BUNCH: A Hierarchical Filtering Algorithm for Identifying Persistent Entities in Interactive Particle Systems

Abstract

Detecting trajectories of hierarchical structures in a dynamical system of multiple interacting particles is an open problem that is typically addressed by imposing strong constraints on the structures to be found. Here, we describe BUNCH, a dynamical filtering algorithm that can efficiently and on-the-fly fit dynamical trajectories of multiple particles to a tree structure of Gaussian clusters that can model a wide range of hierarchically arranged structures, while extracting and calculating hierarchical properties such as complexity, lifespan, and other information- and time-based properties of an entity (an object defined by its structure) and of all of its constituting subentities. Unlike other (hierarchical) clustering algorithms, BUNCH emphasizes independence from adjustable parameters and ascribes equal importance to each hierarchy level and its attending attributes, of the tree of clusters that best fits an evolving particle system. We illustrate the performance of BUNCH via an operational definition of “lifeness” of an entity, as the product of its defining information (algorithmic complexity) integrated over its lifetime, in units of information × time. Thus we provide a proof of concept that measuring and quantifying level-wise properties of hierarchically modeled systems with BUNCH is feasible for small enough particle systems, thereby enabling the classification of entities and subentities via the measurement of hierarchical properties.

1. Introduction

The world can be largely explained as a system of interacting particles or an interactive particle system (IPS), namely a set of massive points governed by the laws of mechanics, where some configurations are more persistent than others. Detecting trajectories of hierarchical structures in a dynamical system of multiple interacting particles is an open problem that is typically addressed by imposing strong constraints on the structures to be found. Here, we present BUNCH, a dynamical filtering algorithm that can efficiently and on-the-fly fit dynamical trajectories of multiple particles to a tree structure that can model a wide range of hierarchically arranged structures, while extracting and calculating the complexity, lifespan, and other information- and time-based properties of an entity (an object defined by its structure) and all of its constituting subentities. BUNCH is not intended to compete with the other hierarchical clustering algorithms, which have varying performances across different tasks and tend to be designed for a narrow range of tasks, but to solve the problem of simultaneously finding a hierarchical structure in a dynamical system and computing its properties in a level-wise manner, with minimal model assumptions.

We illustrate the utility of BUNCH in the problem of measuring “lifeness”, a measure of how lifelike a hierarchical persistent structure constituted by clusters particles is. Our definition of lifeness is based on two assumptions. First, living entities (entities) persist, or exist, for an extended time span (lifespan). Second, they persist while preserving a particular or idiosyncratic structure, that mirrors its environment (good regulator theorem [1] but see [2]). This structure is generally a complex adaptive system: a multiscale hierarchical entity where at each level and between levels an interplay between non-equilibrium dynamics and selective processes continuously reshape all subentities [3,4,5,6]. The currently available hierarchical clustering algorithms require heuristic parameter tuning [7,8] and often cannot build an arbitrary number of hierarchy levels. Here we present a hierarchical clustering algorithm that can identify, tag, and store the location and lineage or relationships between the persistent entities emerging as a hierarchical structure in a system of interacting particles, and to quantify the lifeness of these entities.

2. Modeling Persistent Entities as Hierarchical Mixtures of Gaussian Clusters

Given a dynamical system constituted by a list of moving particles in multi-dimensional space, how can we find the most likely (hierarchy of) clusters that generated them? We need (1) a characterization of how particles are (spatially) distributed over clusters and (2) an algorithm that adheres to this characterization to tractably find and identify likely clusters.

Here we define clusters and entities (classes of equivalence of clusters) using a hierarchical model of Gaussian mixtures and provide a lazy and efficient clustering algorithm that in principle enables fitting dynamically evolving cluster (and entity) trees to the trajectory of an interactive particles dynamical system, and of their subsystems.

We model particle systems as hierarchical mixtures of (elliptical) Gaussian clusters (HMGC) that have no free parameters. A HMGC is structured as a list of Gaussian mixtures, recursively linked such that for each list element or level, the centroid of each (Gaussian) cluster is regarded as a particle (child) amenable to clustering (adoption) by the clusters (parents) of the supraordinate level. In the HMGC or cluster tree, at each level, the weights (the probabilities of children belonging to each possible parent cluster) are determined by the lineage probability, i.e., the product of recursively compounding the nested probabilities of children belonging to their parents, of parents belonging to their grandparents, etc. Thus it explicitly models a genealogy of entities via the probability of nested memberships through a lineage of cluster entities. At each level, clusters are (1) parents that aggregate children elements of the subordinate level, and (2) their centroids are the children of the supraordinate level (Figure 1).

Therefore at the lowest (atomic particle) level the aggregates of particles are modeled as a mixture of scattered bivariate Gaussian functions (clusters or entities), whose iso-density lines are, in general, ellipses. We use Gaussian blobs because they are the most parsimonious (in the entropy maximizing sense) densities that carry information about location, size, anisotropy, and orientation, in virtue of being defined by only the first two moments. This is similar to atomic nuclei that are modeled as balls that can be stretched and squeezed into ellipsoids [10]. Thus, clusters and entities are defined by (1) the location of the centroid, their (2) Gaussian blob or ellipse semi-axes and orientation, and finally by (3) their children. At the second level, the cluster centroids of the first level are in turn modeled as clusters themselves, whose centroids are in turn clustered at the third level, etc. In a mixture, each elliptic blob carries a weight, which allows representation of not only ovals and circles, but also oblong shapes, sticks (near-degenerate ellipses), and annuli (“donuts” made of a wide hill concentric with a narrow pit, akin to a high-pass frequency filter, which requires allowing for negative mixture components). All these in turn can be combined to form arbitrarily complex shapes such as polygons, whorls, tadpoles, or chains. The top (omnicluster or universal cluster) and bottom (atoms) entities are the only eternal structures.

In a two-dimensional IPS, atoms have two properties: atom kind or species and location coordinates, whereas cluster and entity (non-atom) children or members have the properties of kind (cluster or entity identity, defined by the list of its children), two location coordinates (μ), the ellipse’s two semi-axes lengths (Σ), and the ellipse orientation (φ).

A cluster tree is specified by i = 1…L levels, each with clusters j ∈ C_i, each defined by a Gaussian blob with parameters μ_i,j and Σ_i,j. The dynamically evolving tree is a hierarchy of nested clusters. Each cluster of clusters inhabits a particular domain in space and time, with its characteristic scale. The information needed to describe a particular hierarchy of clusters within a cluster tree is the HMGC model complexity, and the surprisal or information associated with describing a particular world (configuration of atoms) with a cluster tree is the likelihood.

We define entities as classes of clusters. Both clusters and entities denote sets defined (up to affine transformations) by their constituting (subcluster or subentity) members. However, entities are invariant under permutations of atoms or entities of the same kind, whereas clusters are not (because two clusters can be of the same kind only by being the same cluster). Hence all clusters are unique and distinguishable, but some entities (at the same level) can be indistinguishable (and hence interchangeable). Note that the indistinguishability of some first-level entities (once their atom-children are given) stems from the inherent indistinguishability of atoms, which allows preserving identity between same-kind atom permutations. This in turn allows for some first-level entities to be indistinguishable (identical copies), which entails the possibility of multisets in the second and all other levels. On the other hand, the distinguishability of clusters stems from the explicit labeling of atoms (e.g., with positive integers) that then bottom-up propagates the distinguishability of clusters at all levels. Thus, while each cluster is a set (of atoms at level 1, otherwise of subordinate sets), entities are multisets (of atoms at level 1, otherwise of subordinate multisets).

We can determine whether a particular child entity/cluster belongs to a particular parent entity/cluster via inference, a procedure to fit the HMGC model’s parameters to the data (atoms) that determines entity memberships. The virtues of HMGC are simplicity, versatility, and adaptability, requiring zero externally adjusted parameters (except perhaps the initial conditions) and perhaps a near-optimal trade-off between simplicity and accuracy. Crucially, not only do the location, size, and orientation of blobs require no parameter adjusting, but neither do the number of blobs at each level and even the number of hierarchy levels (the minimum number of levels is one). This is important because by penalizing “idle” parameters that make little contribution to model accuracy, inference automatically selects the number of levels and blobs at each level, which is a sort of statistical model selection [11,12].

Notice that we have neglected temporal derivatives. Here we use a static HMGC model, i.e., in it no time derivatives are explicitly modeled. Instead, time-dependent changes are implicitly accommodated by iteratively refitting the model to the IPS configuration at each time step. Thus cluster members can belong in a static or dynamic manner by either staying still or moving, e.g., cyclically or chaotically, as long as they remain in the vicinity of the cluster centroid. A more sophisticated model could comprise, besides centroid locations and ellipse orientations, their time derivatives [13], e.g., centroid velocities (and accelerations) and ellipse axes angular velocities.

For describing model complexity priors we just assumed uniform distributions and the Boltzmann entropy (log N). Arbitrarily, we can set N to the typical single-precision floating-point number type, which has a size of 4 bytes or 32 bits and an information content of log 2³²~22.18. Here the HMGC and cluster tree models have no parameters except for the initial conditions, which are simply the five parameters of the starting cluster ellipse blob but after discounting rotation and translation degrees of freedom, this number reduces to two, so we obtain I_p = 2 log 2³² = 64 log 2 for the complexity of priors.

We determine that a particular child entity belongs to a particular parent entity via inference, with a procedure to fit the HMGC model’s parameters to the data (atoms) that determines entity memberships. There are many feasible ways to perform inference; in this article we introduce the BUNCH algorithm for fitting HMGC models.

Lifeness

Given an entity tree D (a class of indistinguishable cluster trees), an entity subtree D_i,j is defined by the subset of D’s nodes that comprises entity C_j at level i and all its descendants (recursively nested children). The largest D_i,j is D itself, the second smallest are any of the first-level entities and the smallest are the atoms (elementary or zeroth level “entities”).

The lifeness L_i,j of an entity subtree D_i,j is defined as L_i,j = I_i,j τ_i,j where I_i,j is the subtree complexity and τ_i,j the cumulative lifespan of the entity subtree D_i,j, which is defined as the sum of all time intervals during which at least one instance (cluster) of the entity subtree D_i,j was alive. Here only the subtrees associated with currently alive clusters D_i,j are considered. The definition of entity suggests that another important clarification is in order: do multiple (cluster) instances of an entity contribute one or multiple lifespan units per simulation frame? Both are sensible ways to define lifeness, bearing different interpretations. For a given entity, the former definition (one-instance) adds a lifeness unit if at least one entity instance is currently alive, whereas the latter (multiple-instances) adds as many lifeness units as entity instances are currently alive. Here we chose the latter, which has a spatial dimension to it that better captures the notion of species.

In practice, we use an approximate and simpler way to compute lifeness Λ_i,j for an entity subtree D_i,j in a two-dimensional world within a tree of i = 1, …, L levels as

$${\Lambda }_{i,j}=n_{i,j}\cdot {\tau }_{i,j}$$

(1)

where τ_i,j is again the cumulative lifespan of the entity subtree D_i,j and n_i,j is a proxy for the cumulative value of the prior complexity I_P of subtrees, recursively defined as

$$n_{i,j}=\left\{\begin{array}{c}160log2+\sum n_{i-1,h}ifi>0\left(nodes\right)\\ 64log2ifi=0\left(leaves\right),\end{array}\right.$$

(2)

where H_i,j is the set of entities that are children of the subtree D_i,j and n_i,j is just the total number of tree nodes comprised within D_i,j (which can be calculated recursively by counting the total number of descendants) multiplied by the complexity of each node. Hence the r.h.s. second term for tree nodes is a sum only over the children of n_i,j. The r.h.s. first term for tree nodes comes from 5 log 2³² parameters, and analogously for tree leaves (i.e., particles) except that they are determined by 2 parameters (spatial coordinates) instead of 5. Note that the reason the approximation Λ_i,j~L_i,j holds reasonably well is related to the reason that small fast fluctuations are not part of persistent entities per se and so their algorithmic complexity or information content can be safely discounted. In other words, although the log-likelihood of a child given its parent is a fluctuating variable, it is approximately on average the same value for all child–parent pairs.

As an example of a potential real world application of lifeness computation, consider the lifeness of an RNA segment entity. We would need an estimate of its cumulative lifespan and its algorithmic complexity. Its complexity can be derived from our knowledge of molecular biology that it is a chain defined by some specific sequence of four nucleotide bases. In turn each of the nucleotide bases is itself a persistent subentity constituted by multiple atoms in a specific spatial configuration. Although physical atoms are not atomic in the sense of elemental particles, they behave as such in biotic systems. Hence the three levels of the dendron entity would be constituted by atoms, nucleotide bases, and RNA, respectively, and we can calculate the dendron complexity of our RNA segment using the formulas Equations (1) and (2). Finally we obtain our RNA segment’s lifeness by simply multiplying its estimated lifespan of, e.g., some 4 billion years, and its dendron complexity. Note that here we are assuming that this specific segment did not become extinct and then reappear, i.e., its lifespan is uninterrupted, and we are using the one-instance definition of lifeness.

3. The BUNCH Algorithm

The Bisect Unite Nodes Clustered Hierarchically (BUNCH) algorithm is a dynamical filter that estimates on-the-fly the parameters of a hierarchy of nested Gaussian blobs or HMGC that fits a trajectory of a particle system, by maximizing its log-evidence. Because this inference problem quickly becomes intractable as the number of particles (and hence model complexity) increases, BUNCH accomplishes approximate inference via heuristics such as point estimation, stochastic sampling, and lazy estimation [14].

Briefly, starting from the first (atomic) level, BUNCH performs a bottom-up sweep, where cluster features and the identity of their children are estimated in a hybrid Bayesian and maximum likelihood fashion. Then the number of clusters and levels is adjusted via a lazy scheme that performs checks to decide whether to split or merge pairs of randomly picked clusters. The output of BUNCH is a dynamically evolving cluster tree or tree whose leaves are the atoms and nodes are the hierarchically nested clusters or entities (with higher degree or thicker branches typically representing more complex and persisting entities) that define the current best model or explanation of the IPS configuration.

Each level is modeled as a Gaussian mixture [15] and estimated via an elliptical K-means algorithm [16], which is the Expectation–Maximization (EM) algorithm [17] for Gaussian mixtures with general covariance matrices and an E-step where atoms are categorically (hard) assigned to clusters [15]. We set the maximum number of EM iterations to 100 and the surprisal convergence criterion to a difference between consecutive iterations of less than 0.1. The covariance matrices were computed via singular value decomposition (SVD; Appendix A). In our case, each EM iteration consists of two steps: the E-step for children element reallocation among the parent clusters, which reuses both children and parents from the previous iteration, and the M-step, which updates the clusters’ sizes and positions [15]. Due to the tree topology of the cluster hierarchy, at every E-step iteration a cluster may adopt new children only among the children of its sibling clusters (i.e., grandchildren of its parent cluster). Similarly to the EM algorithm, BUNCH is a combination of Bayesian and maximum likelihood approaches in an iterative scheme that yields a HMGC density together with maximum a posteriori (MAP) estimates of their parameters (e.g., centroids) and latent variables (e.g., cluster membership), such that the MAP estimates at one level become the data for the supraordinate level.

BUNCH enables tractable estimation of a HMGC, a tree of nested Gaussian mixture densities. This is achieved via dynamical updates, which combine (1) cycling through the cluster tree parameters at each hierarchy level during a bottom-up sweep, similarly to dynamical filtering approaches resting on variational inference, (2) random sampling of log-evidence in the current neighborhood via the stochastic heuristics used during splitting and merging clusters, and (3) local exploration of the parameter space with step size determined by a learning rate.

BUNCH is a dynamical filter that blends features of both agglomerative and divisive clustering approaches:

• Initial condition: The cluster tree is initialized with a single cluster that fits all atoms of the world.
• Bottom-up sweep: All clusters are nested and, at any level, solely determined by the configuration of all potential children (in the subordinate level), so each iteration of the algorithm must proceed bottom-up.
• Random selection of cluster candidates for merging and splitting: At each level and iteration step, one cluster pair is randomly selected for potential merging and then a likelihood ratio test between the log-likelihood of the merged parent cluster given the combined children and the separate two parent clusters given their respective children (similarly to Bayesian agglomerative clustering [18]) is virtually calculated to decide whether to merge (if positive) or not (if negative). Then one cluster is randomly selected for potential splitting (into randomly selected two halves) and a decision to split or not based on an analogous likelihood ratio test is made.

At every time step, clusters may (1) be born, (2) be forwarded to the next time step (stay alive), or (3) die. Clusters are born when (1) one cluster comes out from a merge, (2) two clusters come out from a split, and (3) the world is initialized with a single cluster and starts up. Any change to the cluster tree is guided by the direction in which the log-evidence of the atoms conditioned on the cluster tree is on average increased. A cluster is carried over to the next time step as long as it better predicts or models the configuration of its children relative to other clusters. Otherwise, it dies as a result of being split, merged, or “killed”. A childless cluster (that has lost all its children) is killed because its existence does not explain anything.

3.1. Bisect-Unite, Birth-Death, and Hierarchy Updating Routine Details

Lazy cluster bisection: There is only one way to merge two clusters, but many to split one. In the current version of BUNCH, the selection of the candidate two halves (bipartitions) that determine the bisection is random. This is a lazy approach: computationally cheap but short-sighted. An approach that better optimizes log-evidence would be splitting the ellipse along its minor (or smallest) axis, informed by SVD (cf. Appendix A).

Few-children cluster killing rule: In d dimensions, cluster parents with d children or less are degenerate, i.e., have a measure of zero. So for two dimensions, SVD (cf. Appendix A) on any cluster with two children or less will yield at least one zero singular value. Two-children clusters, which have one zero singular value, are simply modified so that the collapsed (minor) axis is arbitrarily set to a small number (somewhat arbitrarily, the atom radius of three pixels, which itself was chosen just for visualization purposes). Single-child clusters are assigned an isotropic (circular) blob, with a radius that collapses at a fixed rate per iteration: 1 − α = 0.05 (where α is an adjustment or learning rate) which entails an exponential rate of collapse of 0.95. With an adjustment rate of α = 1, single-child clusters would collapse immediately in one time step. By setting α = 0.05, we allow single-child clusters to carry over and possibly to adopt more children in the next time step, thereby avoiding death. This is because the jittering of children (atoms or subclusters) positions prevents blobs from totally collapsing into singularities—thermal motion adds an irreducible variance or noise to the position of children because temporal derivatives such as velocity are not modeled here. Finally, childless clusters and clusters with zero radius (axes) are immediately killed.

Bottom-up cluster tree updating: There must always be a single cluster at the top level: the top cluster. If there is only one level, this is the omnicluster. If the top cluster is split, then its two halves automatically become the two children of a newly added top cluster, which also results in adding a new level to the hierarchy. Conversely, if the next-to-top level has only one cluster (due, e.g., to a recent merge) then it becomes the new top cluster because its former parent is automatically killed, which also results in removing a level from the hierarchy.

In typical hierarchical clustering algorithms, besides the distance metric, a linkage criterion—which specifies the dissimilarity of sets as a function of the pair-wise distances of observations in the sets—is employed to decide which clusters are merged or split [19]. In BUNCH, the linkage criterion is effectively the local shift in the cluster tree’s log-evidence. However, the selection of candidates is uniformly random and the log-evidence is only used to decide whether to perform merges and splits or not.

Optimization heuristics: Unlike the steepest ascent schemes on continuous manifolds, BUNCH does not make use of gradients and attempts to maximize log-evidence via discontinuous leaps while roving the parameter space, which is a hybrid of discrete (e.g., number of levels, clusters at each level, and ways to allocate children to parents) and continuous (cluster positions and covariance matrices) coordinates. Because the model evidence function is not differentiable (e.g., with respect to cluster births and deaths), BUNCH simply evaluates model evidence at stochastically sampled neighborhood locations to decide whether to take a step, similar to pattern search or random search approaches [20]. Similarly to the EM algorithm and variational Bayesian methods, this is accomplished iteratively: at each time step we bottom-up sweep the layers and at each layer we reallocate children and update sequentially each cluster. Discrete coordinates naturally enforce the leap sizes (e.g., a child being transferred to another parent, or two cluster parents being merged) while precluding the calculation of directional derivatives. The ascent step size along continuous coordinates (e.g., cluster centroid speed and bearing and shrinking/growth rate) is determined by a learning rate parameter α = 0.05 that pertains to and bears on the performance of the algorithm, similar to typical gradient descent schemes.

Algorithm complexity: The computational complexity of an algorithm, i.e., the amount of space or storage, and time or number of operations or flops, used during execution, as a function of the input size. For a d-dimensional simulation of n particles ran during t time steps, the time computational complexity of the IPS is O(n²·d·t) flops, whereas the computational complexity of BUNCH is O(n· log n·d²·t) flops. The bottleneck of the IPS algorithm is the n²-costing calculation of pair-wise interactions between the n atoms, whereas the bottleneck for BUNCH is the SVD calculation in elliptical K-means, whose typical cost is O(n·d²), assuming that d > n [21]. The log factor for BUNCH reflects that the number of clusters in a tree hierarchy is a logarithmic function of the total number of atoms.

3.2. Pseudocode for the BUNCH Algorithm

• algorithm BUNCH:
  • // initialize cluster tree and entity tree as one Gaussian blob
    clusterTree = omnicluster
    entityTree(clusterTree)
    for frame in [1,duration]: // loop for the world duration
    updateIPS() //step forward the IPS world simulation
    // recompute cluster tree
    // scan upward from the lowest changed level
    for l = 1 to clusterTreetopLevel:
    ellipticalKmeans(l) // clustering via elliptical K-means
    for l = 1 to clusterTreeTopLevel:
    trySplitting1ClusterLazily(l)
    tryMerging2ClustersLazily(l)
    //recompute entities
    for l = LowestChangedLevel to clusterTreeTopLevel:
    for c in clusters at level l:
    // scan entity tree for new live and dead instances
    if c is new cluster (born or transformed):
    entityTree.addNewEntity(c)
    if c is a dead cluster:
    entityTree.writeOffClusterFromEntity(c)
    // scan entity tree for dangling pointers to clusters
    for e in entities at level l:
    if e point to dead cluster:
    entityTree.pruneDeadClusters(e)
     
    function ellipticalKmeans(l)
    i = 0
    while i < 100 or refitting step is not negligibly small:
    for each cluster c at level l:
    // expectation or reassignment step
    c = reassignChildrenFromVoronoiCellToCluster(c)
    // maximization or refitting step, via Spectral Value Decompostion
    c = refitClusterViaSvd(c)
    dsu = updateClusters()
    // dsu: surprisal difference between consecutive iterations
    if dsu < 0.1 then break

3.3. Software

The IPS were inspired by Particle Life [22], a loose replica of Jeffrey Ventrella’s Clusters algorithm [23]. For a webapp implementation of Particle Life, see https://hunar4321.github.io/particle-life/particle_life.html (accessed on 21 April 2025) [22].

We provide JavaScript and C++ implementations of IPS that build on Particle Life code [22] together with the BUNCH algorithm. The JavaScript and C++ source code are available on the web hosting service GitHub repository (https://github.com/mmartinezsaito/racemi, accessed on 16 November 2025) under the MIT license. Both versions include a simple graphical user interface for tweaking the physics and visualizations. The JavaScript version additionally includes online plots for monitoring statistics by means of the open-source library Plotly (v2.20.0 [24]).

The C++ version stands on the open-source image rendering library openFrameworks (v0.12.0 [25]) and enables simulations of a larger number of particles and visualizations of the matrix of interaction force coefficients. To compile the C++ code [22], download the GitHub repository (https://github.com/mmartinezsaito/racemi) and openFrameworks (https://openframeworks.cc/, accessed on 21 April 2025). Then generate a new openFrameworks project, add the addon ofxGui; after the project files are generated replace the /src folder with the one provided on GitHub. At the time of publication, the GUI slider that sets the number of atoms does not allow decreasing it.

3.4. Comparison with Other Hierarchical Clustering Schemes

Now we proceed to a brief survey of the relevant clustering literature. As in agglomerative clustering, the BUNCH algorithm uses a level-wise bottom-up approach, to evaluate the likelihood of the cluster parents of the current level children and to lazily evaluate merges, splits, and deaths. As in divisive clustering [26], BUNCH recursively may split the initial cluster into descendent clusters; in this respect, it is akin to bisecting K-means [27], X-means [28] or G-means [29]. However, BUNCH may also merge pairs of selected clusters at every step. Divisive clustering with exhaustive search is O(2^L), but BUNCH employs a random selection of candidates for splits and merges. Note however that because cluster likelihood is evaluated bottom-up, a given cluster tree can only grow or collapse by at most one level each time step: each top-down recursive split can occur at most once per time step. Just as in cluster reshaping and centroid shifting, in general, splits, merges, and deaths occur whenever model evidence is locally higher at newly sampled points in parameter space.

Hierarchical Gaussian mixtures have also been used in an algorithm for point-cloud registration [7,30], where the goal is finding a typically affine transformation that aligns a set of points (e.g., obtained by Lidar) to another reference set of points. Here transformation is defined as that which maximizes the probability that the transformed point cloud is a sample that was generated by a reference point cloud modeled as a parametric probabilistic model of Gaussian mixtures [30]. An EM algorithm is used to rove the space of transformations, with the latent variables being point-model associations. Like BUNCH initially, the tree of Gaussian mixtures is recursively split top-down, and may describe different cloud regions with different hierarchy levels to adapt to the cloud’s local geometry [7]. However, unlike BUNCH, the tree topology is initialized at the start, typically as a hierarchy of eight-component nodes, with each having its own eight-component child, and then it is pruned via an early-stopping ad hoc heuristic to select the appropriate local scale that fits the pruned tree model to [7]. This contrasts with the lazy splits and merges of BUNCH that dynamically and flexibly refit the HMGC without ad hoc parameters.

Some approaches, such as K-means [31] and its variants (e.g., k-medoids) and mean-shift [32], require a priori specifying the number K of clusters. Other methods such as DBSCAN [33] and its OPTICS [34], allow non-convex shaped clusters by relying on sample density, but nonetheless still require beforehand one or more parameters specifying a density threshold to form clusters. Yet other schemes, such as hierarchical clustering and bisecting K-means [27] altogether may do away with prior settings (as BUNCH does). However most clustering algorithms rely on heuristics or ad hoc distance-based rules. There are nonetheless principled approaches: in Bayesian agglomerative hierarchical clustering a probabilistic model is used to compute and compare the probability of points belonging to existing clusters within the tree, thus enabling a model-based criterion to decide on merging, or not, clusters [18].

But among all hierarchical clustering, perhaps BIRCH (Balanced Iterative Reducing and Clustering using Hierarchies, in particular its clustering feature tree phase [8]) is conceptually closest to BUNCH. The nodes or branches of the tree created by BUNCH are analogous to BIRCH’s Clustering Feature Nodes. Like BIRCH [8], BUNCH clusters only keep statistics of subclusters, and it is bottom-up and hierarchically built. However BIRCH uses two parameters, viz. branching and threshold factor, to, respectively, limit the number of children of a cluster parent and the distance or eligibility of a child to become adopted by the candidate clusters parents, whereas BUNCH is parameter-free.

Note that BUNCH is not intended to compete with most other hierarchical clustering algorithms, which are typically designed to solve specific clustering problems in their area of application, which typically are static configurations at the first or atomic level, as expounded in Section 3.4. Instead, BUNCH emphasizes independence from adjustable parameters and allots the same importance to the attributes of each level of the hierarchy of clusters that best fits an evolving particle system.

The BUNCH filtering algorithm yields, for each time step, a tree graph where each node is a cluster, with its distance from the nearest leaf indicating its level in the tree hierarchy. For the example of computing the lifeness of a given node, its number of children (in general, descendants) determines its complexity and identity, whereas its lifespan is determined by keeping track of the births and deaths of its children (so for a parent to be considered alive all its children must be alive). Can the most similar algorithms to BUNCH’s tree of Gaussian mixtures for point-cloud registration [30] or PCR-TGM, and BIRCH achieve something comparable? PCR-TGM maximizes the probability that a transformed distribution of particles is generated by the leaves of a hierarchical mixture of Gaussians. In PCR-TGM, the non-terminal nodes are just a means toward achieving a good fit. This is reflected in its early-stopping heuristic (with adjustable parameter λ_C), which induces tree branches of disparate length. Although this would not preclude computing the complexity of all tree nodes, it would make necessary redefining the set of tree graphs considered entities, and the allowed transitions between consecutive simulation steps. But most importantly, this heuristic is optimized for fitting only once, which bars it from working as a filter. Also, its adjustable parameter has to be tuned to the current dataset. Although BIRCH was designed to incrementally and dynamically cluster incoming new data points, its main aim is to hierarchically cluster one single dataset. Its emphasis is on making clustering decisions locally, i.e., with knowledge of only data points and other clusters in the neighborhood of the currently considered cluster. The main and first phase of BIRCH has two parameters: the branching factor and the threshold, which constrain the number of children each parent is allowed to have, and the height of the tree. Although this phase is similar to BUNCH’s bottom-up tree building routine, its adjustable parameters, many optional subroutines (removing outliers, reducing the initial tree size, regrouping subclusters, etc.) and two or three more clustering phases, make it much more complicated and parameter-dependent than BUNCH. As such, BIRCH is also suboptimal for accommodating small changes to the tree graph and clustering features, as an online filter. In summary, both PCR-TGM and BIRCH would require to be substantially modified to be capable of rapidly producing a tree graph that reflects the small temporal variations characteristic of the trajectory of a multiple particle in a dynamical system.

4. Example Numerical Simulation

Here we illustrate the computations of the BUNCH algorithm for two dimensions. We fixed the friction coefficient to 0.7, the total number of particles or atoms to n_A = 256 from 64 particles of four kinds, and the bounding universe box to 800 pixels (arbitrary unit) of width and 600 pixels of height.

Each “atom” is a particle of mass m = 1 whose dynamics is classically described by a Newtonian equation of motion generalized to allow for friction and external forces, demonstrated by the following second order differential equation:

$$m{\displaystyle \frac{d^2{x}_i}{d{t}^2}}+\zeta {\displaystyle \frac{d{x}_i}{dt}}=\sum f_{ij},$$

(3)

where i = 1…n_A is the atom index, x_i a two-dimensional vector indicating its position, t time, ζ friction coefficient, and f_ij the force vector exerted by atom j on i. Note that an atom does not interact with itself: f_ii = 0. Atoms pair-wise interact through conservative central forces as follows:

$$f_{ij}=-\dot{{\chi }_{ij}}{\displaystyle \frac{\partial V}{\partial x_{ij}}},$$

(4)

where x_ij = x_i − x_j and $\dot{{\mathit{\chi }}_{ij}}$ is the atom-wise interaction matrix of constant real interaction coefficients ($\dot{{\mathit{\chi }}_{ii}}=0$) whose sign determines whether forces are attracting (negative) or repelling (positive). The $\dot{{\mathit{\chi }}_{ij}}$ matrix may, in general, be symmetric, skew-symmetric, or a linear combination thereof. Physical force interactions, such as gravity and electromagnetism, are typically symmetric. Forces with skew-symmetric components allow for behaviors characteristic of non-conservative systems. The forces are derived from a power law function of distance potential so that |f_ij (|x_ij|)| = χ_ij|x_ij|^p, where p is the power law exponent.

We model atoms as solid (yet overlappable) balls of charge to avoid the unphysical jagged dynamics typical of classical singularities associated with vanishing volume or infinite density [35]. For two dimensions the exponent range of interest will be around p ∈ [−1, 0].

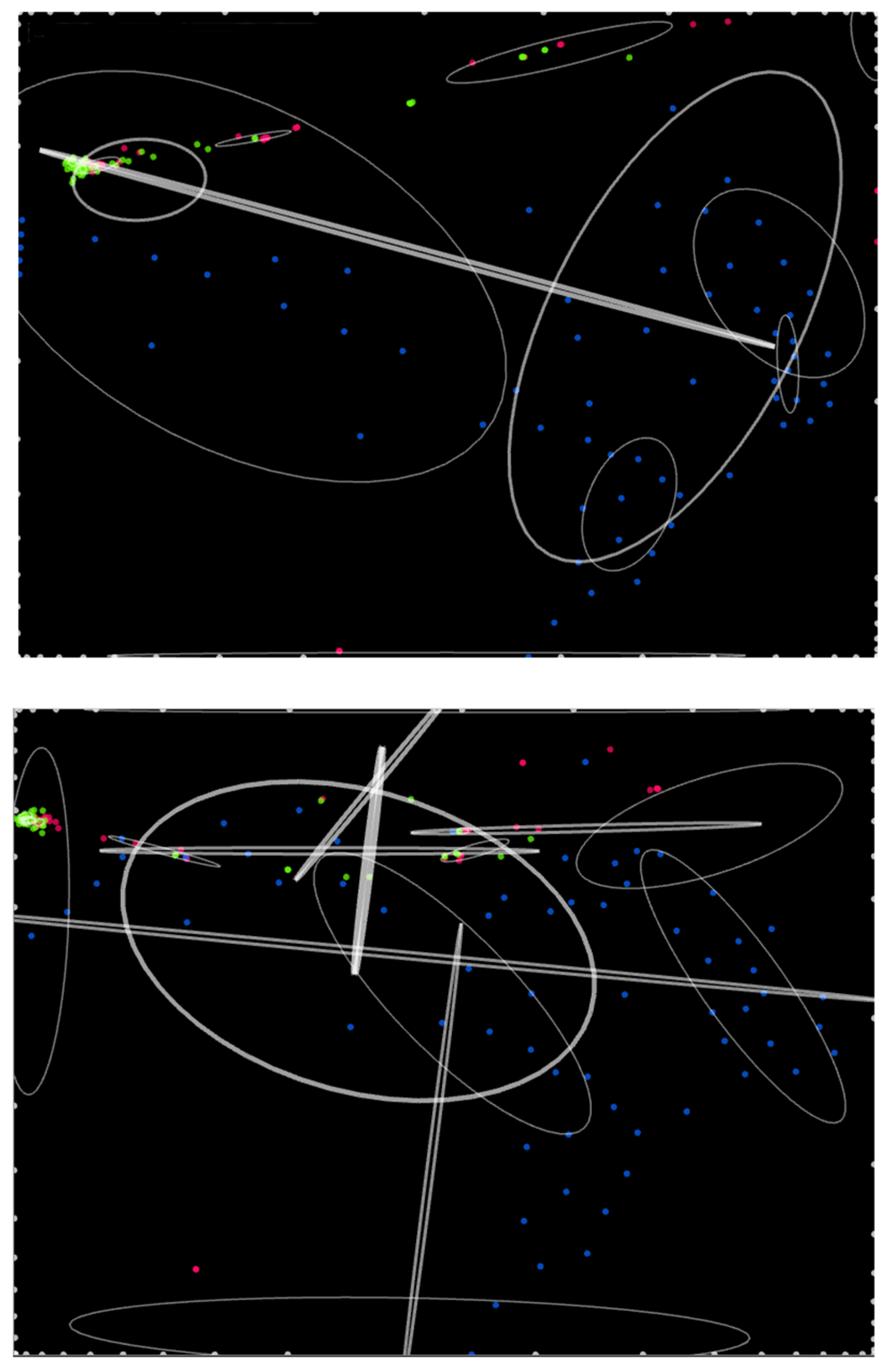
We show a simulation run of an IPS (Figure 2) with interaction force power law exponent p = −1 and matrix χ = $\chi =\left[\begin{array}{c}-0.19-\mathrm{0.550.21}-0.05\\ -0.97-0.94-\mathrm{0.520.34}\\ \mathrm{0.960.200.070.31}\\ \mathrm{0.110.990.790.73}\end{array}\right]$, which is representative of dissipative non-equilibrium steady states with long-range interactions exhibiting chaser–avoider duplets and complex behavior characteristics of skew-symmetric interaction matrices. χ_ij is the coefficient of the force on any atom of kind i exerted by any atom of kind j, with the sole exception that atoms do not exert force on themselves. Here the matrix χ_ij refers to the pair-wise interactions between atom kinds, as opposed to the interactions between individual atoms $\dot{{\mathit{\chi }}_{ij}}$, which is hollow because an individual atom does not interact with itself. A negative (positive) sign indicates attraction (repulsion). Atom kinds are arbitrarily colored: 1 = red, 2 = green, 3 = blue, 4 = white. Here interaction forces are on average slightly more repulsive than attractive and comprise both symmetric and skew-symmetric components, with more of the former [14].

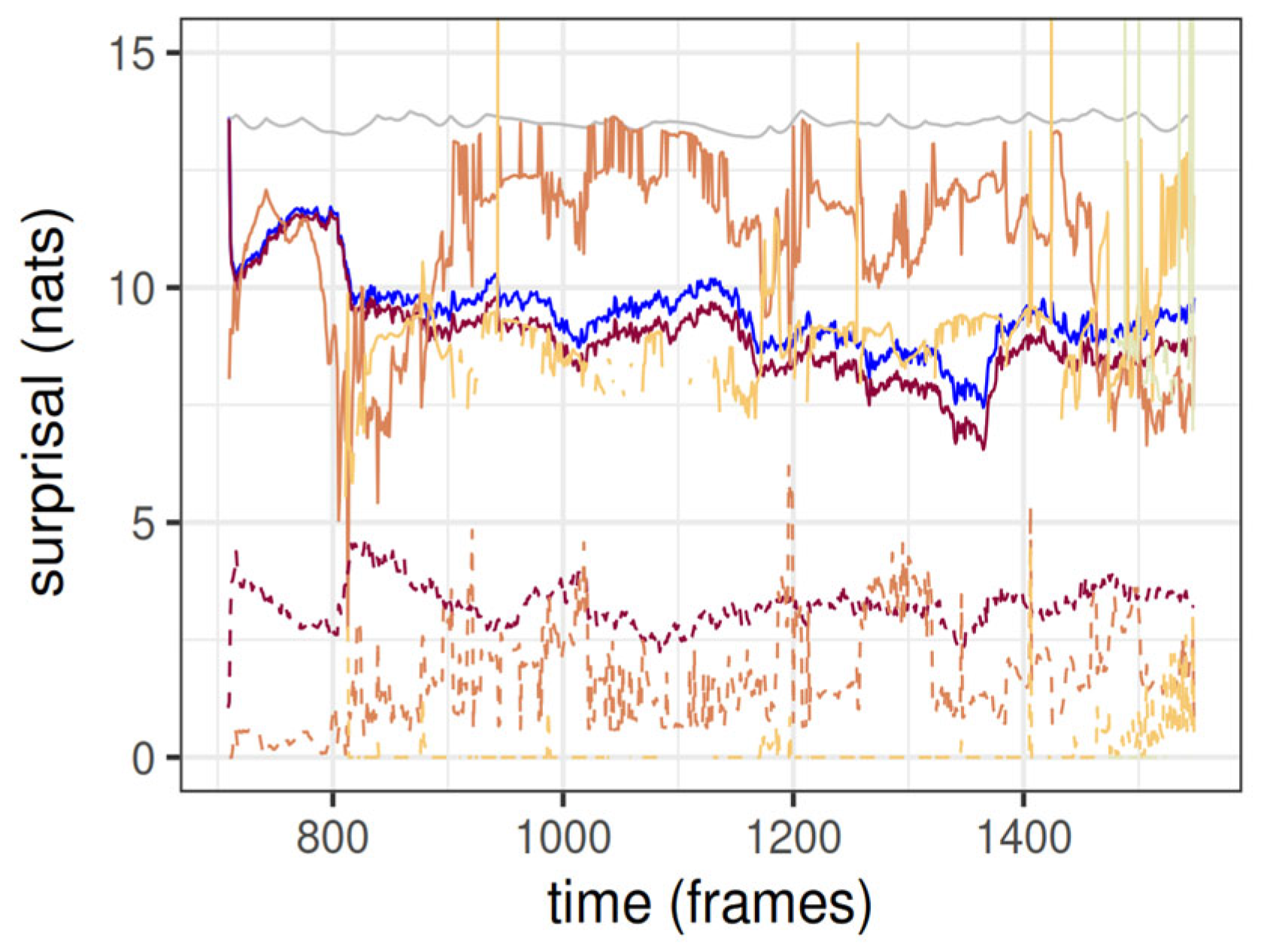
The surprisal (the negative of the log-evidence) of the cluster tree and its constituting clusters dynamically evolving under the BUNCH algorithm is shown in Figure 3. Although not fully shown, in the first few frames of the BUNCH algorithm the total surprisal plummets to a value of around 2400 nats or 9.4 nats per atom, and hence oscillates in its neighborhood. This is a pattern typical of coevolving species in Wright fitness landscapes [26,36]. The rugged plateaus indicate that a steady state has been attained. The hierarchical structure of the tree entails that most of the clusters belong to the first (atomic) level, so the atomic level aggregate surprisal accounts for most of the total surprisal. The cluster tree surprisal is the sum of surprisals for all levels except the atomic, and the total surprisal is the sum of surprisals across all levels. The surprisal associated with the tree components at each level as estimated by the BUNCH algorithm is almost always smaller than that of the reference null model, which is a single Gaussian blob fitting all the particles. The mean surprisal per children (cluster or atom) at each level is typically larger at supra-atomic levels (Figure 3). Because the current version of BUNCH does not model velocities and hence fast atoms cannot be well predicted, one would expect that within-level averaged surprisal is also higher for lower levels. However here this is not the case, likely because continuous smooth models do not explain well sparse data, and cluster blobs have far fewer children at, e.g., the second level than the first.

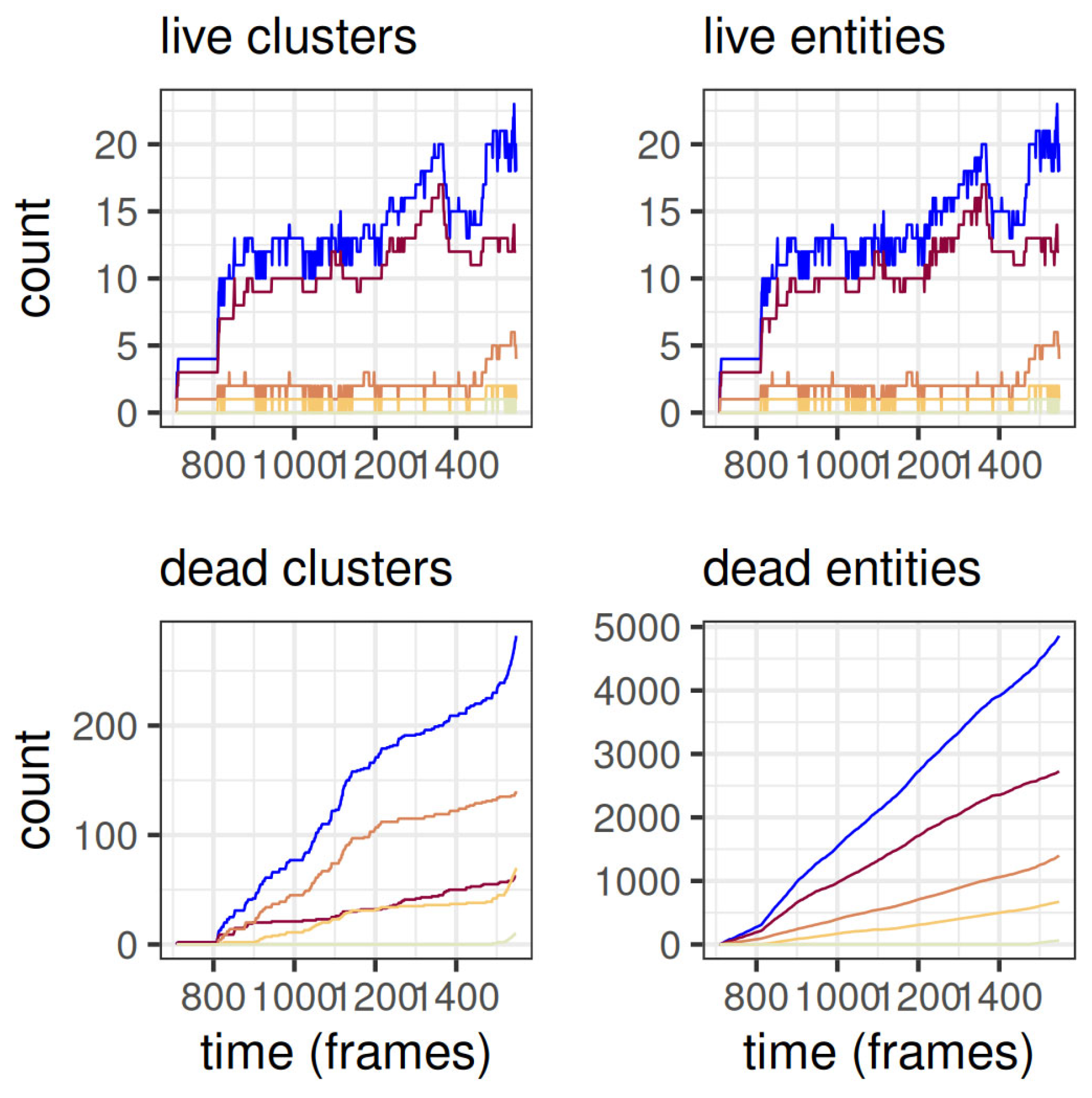
The evolution of the amount of live and dead clusters and entities separately for each level is shown in Figure 4. There are more dead entities than dead clusters because during its lifespan any given cluster typically takes the form of multiple entities as it adopts and loses children.

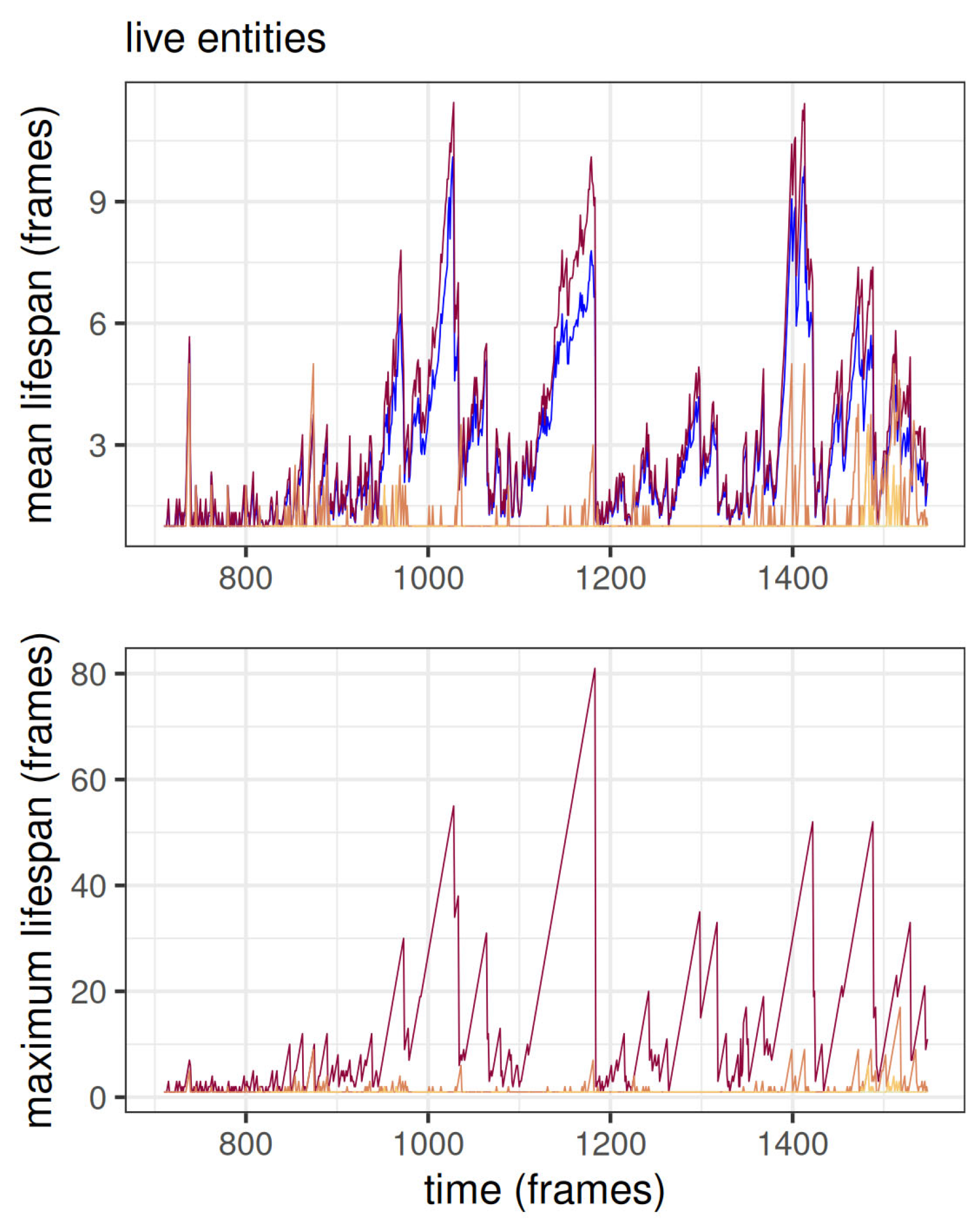
The mean and maximum of current lifespans for each level are shown in Figure 5 for live entities. Most top-level entities have a lifespan of just one frame. This is a common phenomenon also in many other simulations. The top entities are, at least at the beginning of the world, ephemeral because, by the definition of an entity, if any of its children changes the entity “dies”, in the sense that it becomes a different entity.

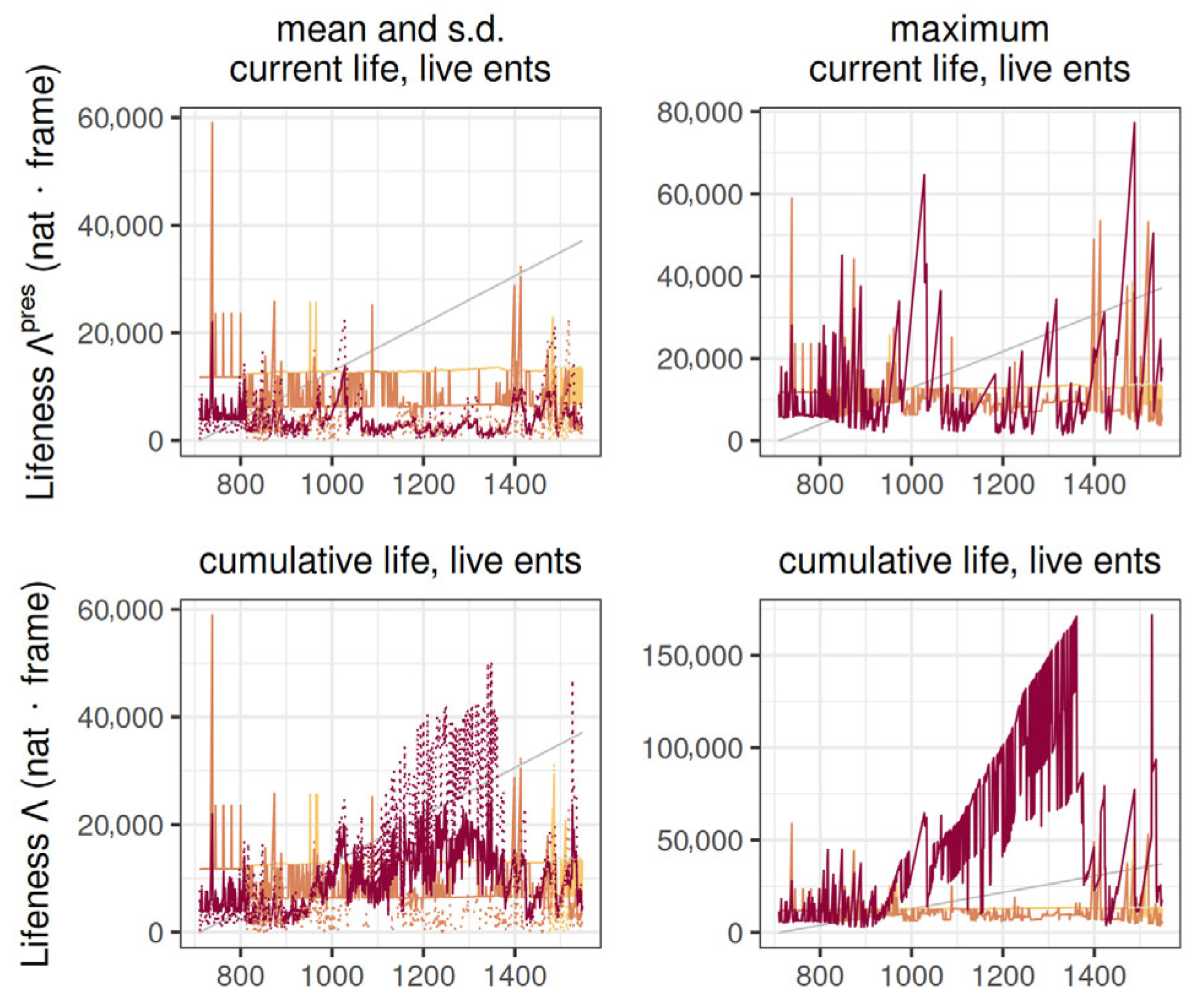
Finally, the evolution of lifeness over simulation frames is shown in Figure 6 for current live entities (top) and cumulative live entities (bottom). The lifeness definition most relevant to biotic complexity is likely the one that rests on cumulative lifespans of live entities (Figure 6, right), because it accounts for an entity’s lived time regardless of the lifespan being continuous or on-off. Here we consider that each entity instance contributes to the lifeness of that entity. Another statistic relevant to biotic complexity is the maximum because the within-level distribution of lifeness is typically a non-uniform or even power law for cluster sizes and lifespans, especially when there is a large number of entities. In Figure 6, there is a large drop for the first level’s maximum cumulative lifeness, indicating that the most complex entity of the level died in that frame, and the second most complex entity was much smaller.

5. Discussion

We simulated multiple IPSs, and measured their level-wise properties by modeling them as hierarchies of clusters via the BUNCH algorithm. In particular, we measured the lifeness of the entities detected in the IPSs and found preliminary evidence suggesting that it is associated with long-range interactions, as roughly measured by the range of the pair-wise interaction forces of the elemental particles of the worlds they inhabit.

5.1. Livable Locations on a Landscape of Lifeness

The vast parameter space and lack of analytical solutions preclude, for now, achieving a comprehensive understanding of which regions of the parameter landscape maximize lifeness, but some parameter statistics illuminate the picture of the non-equilibrium steady states that emerge in the simulations.

First, the interaction force range, parameterized by the power law exponent p, together with the volume and particle number—which we kept fixed here—largely determine the resulting state type, between two relatively uninteresting extremes: strong interconnectivity leads to mean-field-like states where sometimes a generalized central limit theorem-like result yields an asymptotic solution but only probabilistically, and contrarily for no interconnectivity we just obtain independent nodes. By adjusting the interaction strength and frequency, a spectrum of phases from ideal-gas-like states (p < −1) passing through diverging correlation length states (p~0) and onto mean-field-like states emerge which displays a vast diversity also in analogous systems [37]. The exponent p is one measure of distance to criticality because it is associated with correlation strength.

Second, the ratio of repulsion r_χ to attraction largely determines whether the system will gravitate towards a predominantly attractive plasma-star-like clump of convecting particles or contrarily be prone to spread, e.g., as a solid-state-like lattice layout of vibrating particles. Beyond a certain value, the system will sunder out as isolated subsystems.

Third, interaction reciprocity s_χ in many-body systems can be coarsely assessed via the ratio of skew-symmetric to symmetric interactions. A similar index is the averaged difference in the absolute value of symmetric and skew-symmetric matrix elements or d_x. Non-reciprocal or skew-symmetric interactions, which break the action–reaction symmetry, govern the steady-state dynamic properties of entities and can induce self-organized traveling patterns such as itinerant clusters of particles (chaser–avoider duplets). Such effective interactions often are mediated by a non-equilibrium environment and are pervasive in biotic systems. Some degree of interaction non-reciprocity is likely to be essential to life because biotic systems need to replicate the inherent skew-symmetry of their environment. Biotic environments typically evince nonlinear non-conservative feedback functions that, in general, preclude reduction to fluctuations around a single favored state or energy minimum [38]. In short, non-reciprocity is an essential feature of steady states associated with matter and energy flows.

After selecting a fixed representative set of 41 exponent values, with emphasis on p = −1 and its vicinity, we randomly sampled 41 configurations of IPS worlds on the 16-dimensional space of interaction matrices and ran simulations. The loose criterion for stopping the simulation was attaining and staying at non-equilibrium steady state for a long enough timespan to collect useful statistics. The average of the number of frames simulated since the start of BUNCH was 1608. The average of the total number of frames simulated was 8235 because the frames running BUNCH were much slower to compute than those not running it. At steady state, we expect most of the collected statistics to become stationary, such as temperature and surprisal, the number of live clusters, but also the number and complexity of distinct dead and live entities, the maximum attained cluster tree level, and the currently live clusters’ (or entities’) lifespan. The cumulative lifespan should linearly increase with time for subentities that are persisting, but it is likely to increase sublinearly for non-persistent entities (i.e., entities that pop up and fade out intermittently by thermal chance).

What is the effect of the interaction force law range on lifeness? For two dimensions, p = −1 is a special power law because then the flux of a particular atom’s interaction force field through any surface enclosing the atom is constant (Gauss’s Law); in contrast for p < −1 it decreases with distance and for p > −1 it increases with distance. For p > −2, the tail of the interaction law has a characteristic length scale defined by its mean, and for p < −3 it also has a variance. Hence large absolute values of p tend to yield a multiplicity of isolated subsystems. In contrast, smaller absolute values (−1 < p < 0) increase the range and strength of interactions, until at p = 0 the system becomes fully connected regardless of distance. We focused on simple regression analyses for a few selected variables. To test the effect of interaction force power law exponent and other IPS parameters on lifeness, we fitted a generalized linear model with a logarithmic link function for the range p ∈ [−1, 0] (

Table 1. Regression results for a generalized linear model with gamma response distribution, logarithmic link function and linear predictors ${\Lambda }_{\overline{l}}$∼r_χ + s_χ + d_χ + p for levels l = 1,…, 4 and p ∈ [−1, 0]. * indicates p-values less than 0.05.

l	coef.	Estimate	Std. Error	t Value	Pr(>|t|)
	intercept	1.3419	1.4003	0.96	0.3479
	rχ	−1.3688	0.7846	−1.74	0.0944
1	sχ	−3.0670	2.7667	−1.11	0.2791
	dχ	−2.0624	2.6104	−0.79	0.4376
	p	0.0615	0.3491	0.18	0.8617
	intercept	−2.2730	1.9464	−1.17	0.2548
	rχ	0.1303	1.0906	0.12	0.9059
2	sχ	3.6598	3.8455	0.95	0.3511
	dχ	6.0248	3.6283	1.66	0.1104
	p	−0.0821	0.4853	−0.17	0.8672
	intercept	0.9017	3.0525	0.3	0.7703
	rχ	0.8044	1.7103	0.47	0.6425
3	sχ	1.8236	6.0308	0.30	0.7651
	dχ	2.6120	5.6902	0.46	0.6505
	p	2.0219	0.7611	2.66	0.0141 *
	intercept	1.7712	1.1632	1.52	0.1415
	rχ	1.3168	0.6517	2.02	0.0551
4	sχ	−0.5456	2.2981	−0.24	0.8144
	dχ	−1.7924	2.1683	−0.83	0.4169
	p	0.7693	0.2900	2.65	0.0142 *

).

For IPSs with p ∈ [−1, 0], the long-range correlation domain favorable for life(ness), only p for l = 3, 4 (the highest level) was predictive of higher lifeness (Table 1): as p approaches zero in [−1, 0] lifeness becomes higher.

In short, these preliminary analyses suggest that in the range [−1, 0] IPS worlds with interaction force exponent values closer to zero were associated with higher lifeness at higher cluster tree levels, which agrees with the notion that lifeness is related to long-range correlations. Thus we found some evidence that longer interaction range is associated with more lifeness in a subcritical range.

5.2. Caveats and Future Research

Currently the BUNCH algorithm is a proof of concept that complex hierarchical entities embedded in particle systems can be online identified and tracked. As such, it suffers from limitations. First, despite its heuristic routines devised to save computation and time, currently it can only handle IPS in an other order of hundreds or thousands of particles, depending on the computer’s performance. Note however that a substantial part of computational power is devoted to storing the data generated at each simulation frame. Second, BUNCH is currently constrained BUNCH to only fit strictly tree-like graphs—a child can only have at most one parent. Loosening the graph structure constraints would lead to the evolution of a wider range of entities. Third, similarly to other random sampling fitting schemes such as Markov Chain Monte Carlo and particle filtering, and unimodal posterior density schemes such as variational Laplace, BUNCH is a lazy random sampling approximate inference algorithm which yields different results for identical initial conditions. Fourth, the current BUNCH implementation neglects time derivatives such as velocity, which not only would substantially increase goodness of fit, but also they are an essential component of biotic dynamics.

Prospective lines of research should address these shortcomings. In particular, code optimization could be achieved by finding a better way to write the increasing size of the data generated during the simulation. Removing the HMGC constraint of being a tree graph would allow for a wider range of structures to be fit, but at the expense of more computational resources and allowing the likelihood function to become strongly multimodal. Finally, generalizing the cluster tree variables from only position to higher-order temporal derivatives would render BUNCH capable of distinguishing entities not only by their static hierarchical properties, but also by their dynamic hierarchical properties, which would be relevant, e.g., for computing lifeness and, in general, any attribute that encapsulates dynamic behavior.

5.3. Conclusions

The problem of finding and tracking hierarchical structures of arbitrary height embedded in trajectories of dynamical systems can be addressed with BUNCH, a dynamical filtering algorithm that can efficiently and on-the-fly fit trajectories of multiple particles to a tree graph that can model a wide range of hierarchically arranged structures. To illustrate its applicability, we propose an operational definition of lifeness of an entity as a scalar, namely the product of its defining information (algorithmic complexity) integrated over its lifetime. We demonstrated the feasibility of BUNCH by simulating multiple interactive particle systems, fitting them to a hierarchy of Gaussian mixtures, measuring and quantifying lifeness, and providing some evidence suggesting that the lifeness of entities is associated with the correlation length of the system. However, this result should be regarded as preliminary because time and computational power considerations constrained the total number of simulated atoms, number of IPS configurations and length of the simulations, which lead to not enough data to make strong statistical claims and too shallow cluster trees (too few levels) to give rise to persistent entities exhibiting adaptive inference. In conclusion, we have presented a proof of concept that the BUNCH algorithm enables on-the-fly assessing of hierarchically embedded properties and classifying subentity types for interactive particle systems.