Metaheuristic Hyperparameter Optimization Using Optimal Latin Hypercube Sampling and Response Surface Methodology

Abstract

Hyperparameters allow metaheuristics to be tuned to a wide range of problems. However, even though formalized tuning of metaheuristic parameters can affect the quality of the solution, it is rarely performed. The empirical selection method and the trial-and-error method are the primary conventional parameter selection techniques for optimization heuristics. Both require a priori knowledge of the problem and involve multiple experiments requiring significant time and effort, yet neither guarantees the attainment of optimum parameter values. Of the studies that perform formal parameter tuning, experimental design is the most commonly used method. Although experimental design is feasible for systematic experimentation, it is also time-consuming and requires extensive effort for large optimization problems. The computational effort in this study refers to the number of experimental runs required for hyperparameter tuning, not the computational time for each run. This study proposes a simpler, faster method based on an optimized Latin hypercube sampling (OLHS) technique augmented with response surface methodology for estimating the best hyperparameter settings for a hybrid simulated annealing algorithm. The method is applied to solve the aircraft landing problem with time windows (ALPTW), a combinatorial optimization problem that seeks to determine the optimal landing sequence within a predetermined time window while maintaining minimum separation criteria. The results showed that the proposed method improves sampling efficiency, providing better coverage and higher accuracy with 70% fewer sample points and only 30% of the total runs compared to full factorial design.

1. Introduction

Metaheuristics are multipurpose techniques used in a wide variety of problems. One reason these techniques are so versatile is that they include hyperparameters that can be adjusted to fit a problem instance. Metaheuristic practitioners often employ previously used hyperparameter settings established through conventions, ad hoc choices, and empirical comparisons [1]. Most such studies, however, do not report on the process used to set the hyperparameter values. Another common practice is to use hyperparameter values presented in other studies without first ensuring that the values are also appropriate in the context of the current analysis [2].

The “no free lunch” theorem for optimization acknowledges that there is no universally superior approach to all problems [3]. Consequently, there is not a single best metaheuristic hyperparameter configuration for all optimization problems. Instead, optimal settings for hyperparameters can differ substantially from problem to problem. Meta-optimization is the search for such optimal hyperparameter values. Identifying an appropriate set of these values is a complex optimization problem and is an example of a computationally difficult task [4,5,6].

This study aims to propose a hyperparameter tuning strategy for metaheuristic algorithms, in particular Simulated Annealing (SA). SA parameter adjustment and its relation to the specific problem characteristics make the method a good solution for situations where computational cost and maintaining effectiveness are the primary concerns. It is important to note that, although our method was specifically designed for SA, its characteristics allow its use in other metaheuristics. Future studies might investigate this possibility.

Although SA is one of the earliest metaheuristics, it remains relevant in the field of combinatorial optimization due to its structural simplicity, flexibility, and ability to escape local optima. Recent studies have shown that SA continues to be used effectively in real-world problems. For example, Bastianetto et al. [7] used SA to optimize energy consumption schedules in residential environments, achieving cost-effective configurations. Zeng et al. [8] applied SA to improve the mechanical performance of composite structures by optimizing their internal configuration. Xu et al. [9] developed a hybrid SA-ANFIS model to enhance the prediction accuracy of corrosion rates in natural gas pipelines. More recently, Wang et al. [10] applied SA to allocate urban water resources in a multi-objective optimization setting, balancing supply efficiency and sustainability.

In SA studies that employed meta-optimization, the full factorial design (FFD) was the most commonly used method [11]. When the number of hyperparameters is large, FFDs can become impractical due to the exponential growth of the size of such analyses [2,5,11]. This study proposes a method for hyperparameter tuning that is both easy to apply to combinatorial optimization problems and provides more efficient, higher-quality solutions than FFDs. Our proposed method uses candidate parameters’ values generated by a combination of Latin hypercube sampling optimized to minimize the wrap-around L2-discrepancy using an enhanced stochastic evolutionary (ESE) algorithm, as proposed by Jin et al. [12], and a response surface methodology (RSM) based on a second-degree polynomial regression.

F-Race, REVAC, SPO, and BONESA are examples of techniques that are used for hyperparameter tuning. These methods were created to be mainly used in evolutionary algorithms and machine learning models. Our method proposes, through the use of design of experiments techniques, not to depend on iterative adaptive tuning, reduce computational cost, and maintain efficiency in the search for the best hyperparameters.

Compared with adaptive racing and automated configuration methods such as SMAC, irace, and ParamILS, the proposed method follows a fixed-design philosophy. Adaptive methods iteratively update the set of tested configurations based on performance feedback and predefined run budgets. It often requires several sequential evaluations that extend the total execution time. In contrast, our method uses a single optimized space-filling design and an RSM to approximate performance across the entire parameter space. This fixed-design surrogate approach provides higher reproducibility and interpretability, with a shorter and more predictable execution time. It can be used as a practical alternative when fast tuning is required or adaptive configuration is not feasible.

We implemented our method on a hybrid SA application for solving the aircraft landing problem with time windows (ALPTW), a combinatorial optimization problem that seeks to determine the optimal aircraft landing sequence on a specific airport runway within a predetermined time window while maintaining the minimum separation criteria between successive aircraft. To validate the effectiveness and efficiency of our proposed method, we used 20 instances based on real data from São Paulo-Guarulhos International Airport in Brazil. We compared the results of the proposed parameter-tuning method with those provided by FFD.

Our work complements the SA parameter tuning method proposed by Bellio et al. [13], Jamili et al. [14], and Jamili et al. [15]. Bellio et al. [13] first introduced the use of space-filling techniques with low discrepancy for SA parameter tuning in opposition to classical designs, which involved full factorial or Taguchi designs. Bellio et al.’s method proved to be efficient and robust enough to tune an SA algorithm. The problem with Bellio et al.’s approach, however, is the method’s laborious implementation. Our work proposes the use of an optimized Latin hypercube sampling (LHS) with minimal wrap-around discrepancy instead of the classical Hammersley point set. This implementation enables a small design size with a quick and easy application.

As in Jamili et al. [14] and Jamili et al. [15], we use the relative deviation index (RDI) as a performance metric. Departing from those studies, however, we use the parameters’ candidate values generated by an OLHS instead of the entire collection of parameter values as the search space. Neither of the aforementioned studies used replication; instead, each examined 15 datasets (instances). We ran five replications per candidate parameter solution per dataset. Due to the stochastic nature of metaheuristics, replications are an important factor to verify an answer’s quality.

Both studies referenced above used the analysis of variance (ANOVA) technique to choose the best parameter values. However, our method uses an RSM based on a second-degree polynomial regression. With these improvements, we were able to generate equal or better results on the 20 instances of the ALPTW we tested using just 30% of the total runs of the FFD and only 13% of the total runs required by the methods presented by Jamili et al. [14] and Jamili et al. [15].

Recently, some studies have shown interesting implementations in the search for the best hyperparameters. However, these techniques require complex implementation and, in some cases, high computational resources. Yoshitake et al. [16] used a reinforcement learning-based framework with dynamic adjustments for SA hyperparameter tuning. Huri and Mankovits [17] developed a surrogate model-based support vector regression for the SA parameter tuning method. Their method was tested for the shape optimization of automotive rubber bumpers and demonstrated its capability to reduce computational time while providing good results. Onizawa et al. [18] developed a method that, based on local energy distribution, analyzes the characteristics of the search space and optimizes the SA hyperparameters.

Our proposed method combines the strengths of OLHS in exploring the search space and RSM in fine-tuning, with the objective of achieving high computational efficiency and optimized hyperparameters. In addition, the method is a viable alternative to FFD, requiring a smaller number (70%) of points in the search space while achieving performance levels equal to or greater than the classical method. The proposed method offers a simpler, faster, and more efficient approach than other methods, making it a valuable tool for those working with metaheuristics.

In this study, we make the following key contributions:

• Presents an efficient hyperparameter tuning approach using OLHS with RSM, optimized for SA implementation.
• Provides an efficient alternative to FFD, reducing the number of runs while preserving its accuracy and performance.
• Provides a better option for ad hoc trial-and-error methods.

This article is structured as follows: Section 2 describes our novel parameter tuning method, Section 3 presents the results, Section 4 analyzes the results, and Section 5 reports the study’s conclusions.

2. Materials and Methods

Our meta-optimization framework comprises two levels: a meta level (preparation phase) and a base level (optimization phase). At the meta level, a framework is designed to produce the best parameter set and fix parameter ranges. At the base level, the parameter values are optimized for the metaheuristic of interest.

Let h_i be the vector of the base-level parameters to be optimized. Then the meta-level objective function f_meta(hi) is defined by Equation (1) [19].

$$f_{meta}\left(h_i\right)=\underset{\mathit{i}\in \mathit{S}}{\mathit{Minimize}} f_{base}\left(h_i\right)$$

(1)

where

f_meta = meta-level objective function;

S = set of all hyperparameter values;

h_i = set i of hyperparameter values;

f_base = objective function result produced by the base level heuristic.

Intuitively, the h_i associated with $f_{\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{a}}\left(h_{\mathrm{i}}\right)$ can be viewed as the best-found vector of parameters for the base level metaheuristic. In our context, $f_{\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{a}}\left(h_{\mathrm{i}}\right)$ corresponds to the value of the objective function obtained by executing the metaheuristic with hyperparameter configuration hᵢ. Thus, minimizing f_meta means identifying the hyperparameters that result in the metaheuristic to produce the best solution x to the original optimization problem.

The aim of our method is to build a surrogate model for metaheuristic parameter tuning that is efficient enough to replace the use of traditional DOE techniques.

To ensure the necessary clarity for correct execution, the methodology is presented in a sequential format, with each step representing a distinct phase of the process. Figure 1 presents our procedure for finding and selecting metaheuristic parameter values.

We demonstrate that the combination of an optimized LHS and a second-order polynomial RSM improves the efficiency with which the design space is sampled by using fewer sample points, providing better coverage of the design space, and increasing the accuracy of the resulting surrogate model by using a nonlinear function.

All steps of the optimized LHS with the RSM meta-level tuning technique are presented in complete detail within the following subsections.

2.1. Step 1: Select the Parameters and Parameter Range to Be Optimized

The method begins with the selection of the metaheuristic parameters of interest. The academic literature, the researcher’s experience, and preliminary experiments all help to determine the set of parameters to be optimized along with feasible parameter ranges.

2.2. Step 2: Choose the Number and Characteristics of the Training Dataset

The number and characteristics of the datasets used for training are key in determining how the algorithm will behave based on the values of the selected parameters. There is no strict minimum or maximum number of training datasets. That said, our literature review showed a minimum of four training datasets [20,21] and a maximum of 24 [11]. The training datasets must encompass a variety of situations that will be optimized using the algorithm being tuned.

For each training dataset, the algorithm is executed several times (replication) for every parameter candidate solution (Step 3) to account for the stochastic nature of metaheuristic procedures. These replications ensure that the performance metric used in the RSM fitting stage (Step 6) reflects consistent and comparable results across different training datasets. The number of replications is not fixed and should be defined by the researcher according to the desired balance between the total number of runs and the reduction in execution time, which is one of the main goals of the proposed method.

2.3. Step 3: Generate Parameter Candidate Solutions Using an Optimal Latin Hypercube Sampling

Our method uses the optimal Latin hypercube sampling (OLHS) as the technique to sample the candidate parameter values. OLHS was adopted due to its minimal required problem knowledge; the sole precondition for OLHS is knowledge of an appropriate scope of values.

McKay et al. [22] introduced the Latin hypercube sampling (LHS) method. LHS is recognized as an expansion of stratified sampling that assures that each of the input variables involves all segments of its represented range. LHS are computationally cheap to generate, can handle many input variables [23], and cover the entire spectrum of each input variable [24]. In addition, its sample mean has a smaller variance than the sample mean of a simple random sample [25]. In the context of statistical sampling, a square grid containing sample positions is a Latin square if and only if there is only one sample in each row and each column. A Latin hypercube is the generalization of this theory to a random number of dimensions, whereby each sample is the only one in each axis-aligned hyperplane containing it [26]. LHS produces a solid stratification over the space of each uncertain variable with a relatively small sample size while retaining the beneficial probabilistic aspects of a simple random sampling [27].

The drawback is that LHS does not reach the smallest possible variance for the sample mean. For this reason, many authors have tried to improve LHS by incorporating an optimality criterion for LHS development. Such an optimal LHS (OLHS) optimizes some criterion function over the design space [28]. Several optimality criteria have been used, including entropy [29,30], integrated mean squared error (IMSE) [31], and maximin or minimax distance [32], among others.

Discrepancy is one such criterion that can be used to optimize an LHS. Discrepancy is defined within the context of the following experiment: Consider an experiment consisting of s factors for which the experimental region χ is a measurable subset of ℝ^s. The goal is to choose a set of n points P_n = [x₁, …, x_n] ⊆ χ such that these points are ‘uniformly distributed’ throughout the domain χ. In the literature, several discrepancies have been proposed as measures of such uniformity, such as star L_p-discrepancies, star L_∞-discrepancies, generalized L₂-discrepancies, wrap-around L₂-discrepancies (WD), centered L₂-discrepancies (CD), symmetrical L₂-discrepancies (SD), discrete discrepancies (DD), Lee discrepancies (LD), and mixture discrepancies (MD) [33].

The OLHS used in our method aims to minimize the wrap-around L2-discrepancy. The wrap-around L2-discrepancy was introduced by Hickernell [34], and its analytical formula is as follows:

$${\left(WD\left(P_n\right)\right)}^2= -{\left({\displaystyle \frac{4}{3}}\right)}^s+ {\displaystyle \frac{1}{n^2}}\sum _{k=1}^n\sum _{j=1}^n\prod _{i=1}^s\left[{\displaystyle \frac{3}{2}}-\left|x_{ki}-x_{ji}\right|\left(1- \left|x_{ki}- x_{ji}\right|\right)\right]$$

(2)

where

n = number of points of experimental design;

s = number of factors; and

x_k = (x_k1, …, x_ks)

It is a nondeterministic polynomial time hard (NP-hard) problem to find an LHS design achieving the minimum discrepancy [33]. In the present work, we used the OLHS search technique proposed by Jin et al. [12]. They developed an efficient global optimal search algorithm called the enhanced stochastic evolutionary (ESE) algorithm.

The ESE algorithm is an enhancement of the stochastic evolutionary (SE) algorithm introduced by Saab and Rao [23] for general combinatorial optimization applications. The ESE algorithm employs a refined warming/cooling schedule to adjust the initial threshold so that the algorithm can be self-adapted to fit different experimental design problems [12].

In space-filling designs such as OLHS, there is no strict rule for how many design points are required. The choice depends on the problem dimension, the smoothness of the response, and the desired balance between design coverage and the total number of experiments [28,35].

2.4. Step 4: Re-Scale Parameter Candidate Solutions

To make use of the results from the OLHS, adaptations are necessary. Samples obtained by the OLHS are restricted to the hypercube [0, 1]^d. To adapt to the factor values, we use the following transformation, initially proposed by Miyazaki et al. [25]:

$$h_i= \left\{\begin{array}{c}\left(u_i-l_i\right) . x_i \left(linear case\right)\\ floor \left[\left(u_i-l_i\right) . x_i\right] \left(discrete case\right)\end{array}\right\}$$

(3)

$$floor \left(x\right)=max\left\{z \in \mathsf{{\rm Z}} | z \le x\right\}$$

(4)

where

h_i = hyperparameter i;

x_i = candidate setting generated by OLHS;

u_i = upper bound of hyperparameter i; and

l_i = lower bound of hyperparameter i.

These adaptations are necessary to run the base-level algorithm.

2.5. Step 5: Run the Base-Level Algorithm and Calculate the Relative Deviation Index

In this step, the base-level metaheuristic algorithm is run using the parameters’ candidate setting generated by the OLHS. Because different training datasets represent distinct problem characteristics, the values of the corresponding objective functions are not directly comparable. To normalize these results and provide a unified performance measure, the relative deviation index (RDI), as employed by Jamili et al. [14] and Jamili et al. [15], is used to produce a common performance measure. This measure is obtained through the following equation:

$${RDI}_K^l= {\displaystyle \frac{F_K^l- {Min}_k}{{Max}_k-{Min}_k}} \times 100$$

(5)

where

$F_K^l$is the value of the kth instance of the optimization problem of interest using the lth combination of parameters;

Min_k is the best value obtained for each instance; and

Max_k is the worst value obtained for each instance.

The RDI expresses the relative deviation of each result with respect to the best and worst observed performances within the same dataset, producing a normalized scale (0–100). Lower RDI values indicate better algorithm performance. These normalized results are later used as the response variable in the RSM fitting stage (Step 6).

2.6. Step 6: Optimize the Parameter Values Using Response Surface Methodology

The last stage combines the respective RDI and candidate values of the metaheuristic parameters, optimizing these values using response surface methodology.

RSM is a sequential search heuristic. Although there is no assurance that RSM will produce the global optimal solution, it typically produces very good solutions, especially in cases where it may be impractical to search for the very best solution. RSM seeks to minimize the expected value of a single point, with continuous inputs and without constraints [33]. Combining with the derivatives of the fitted second-order polynomial to predict the optimum input combination, we also employ the mathematical technique of canonical analysis to the polynomial to investigate the shape of the optimal subregion.

For each dataset, the objective function results obtained from all runs are normalized using the RDI (described in Steps 2–5). The RDI values are then used as the response variable (Y) in the RSM, while the decision variables defined by the experimental design serve as the predictors (X). This procedure enables the estimation of the polynomial coefficients and the identification of the stationary point that represents the optimized configuration. Equation (6) shows the general form of the second-order RSM.

$${RDI}_i={\beta }_0+\sum _{i=1}^k{\beta }_i{X}_i+\sum _{i=1}^k{\beta }_{ii}{X}_i^2+\sum _{i=1}^{k-1}\sum _{j=i+1}^k{\beta }_{ij}{X}_i{X}_j$$

(6)

where

${RDI}_i$: Relative Deviation Index of the i-th experimental run;

$X_i$: parameters of the experiment;

${\beta }_0$: intercept;

${\beta }_i$: coefficients of the linear terms;

${\beta }_{ii}$: coefficients of the quadratic terms (curvature)

${\beta }_{ij}$: coefficients of the interaction terms between factors i and j;

$k$: number of parameters investigated.

A second-order polynomial model was selected for the RSM because the relationship between metaheuristic hyperparameters and algorithm performance is inherently nonlinear. A quadratic surface allows the identification of the curvature and interaction effects that define the region with the best performance. This choice follows common practice in RSM for optimization problems, where second-order models provide the simplest analytical form [36].

The foundation of the proposed method lies in experimental efficiency, where the goal is to reduce the number of runs. In a full second-order model, the number of coefficients (intercept, linear terms, two-way interactions, and pure quadratics) is directly linked to the number of parameters k, following Equation (7):

$$N_{coefficients}= 1+k+ {\displaystyle \frac{k(k-1)}{2}}+k$$

(7)

It is important to verify for multicollinearity and model stability before fitting the regression. Common diagnostic tests include the variance inflation factor (VIF), the condition number of the design matrix, and the correlation matrix among predictors. High VIF values (greater than 10) or large condition numbers (above 1000) indicate strong collinearity and unstable estimation [36,37,38]. When such dependencies are detected, the non-estimable interaction or quadratic terms should be removed. This procedure ensures numerical stability and prevents overparameterization of the response surface.

The classical RSM assumes that the method is only implemented after the critical inputs and their experimental areas have been determined (i.e., screening phase) [35]. Our adaptation of the RSM method does not perform a screening phase since it is mandatory that all parameters have a determined value to run the SA to solve the base-level problem. A similar philosophy exists in the Taguchi Method. The classical RSM uses a central composite design to generate the input/output data [35]. Our revised RSM method places more sample points in the design’s interior space using an OLHS with fewer runs.

In this framework, the OLHS does not replace the traditional DOE design with a smaller version but rather serves as an alternative space-filling strategy to generate the experimental data. The RSM is then fitted to the responses obtained from these OLHS points. It acts as a surrogate model that approximates the relationship between the hyperparameters and the algorithm performance.

2.7. Case Study

We investigated the effectiveness of our parameter-tuning method by applying it to a hybrid simulated annealing (SA) to solve the aircraft landing problem with time windows (ALPTW).

Our SA implementation is controlled by five parameters: λ, T0, α, M, and N. Where λ is a penalty parameter ensuring the final solution adheres to operational time window constraints. T0 is the SA initial temperature parameter, α is the SA cooling parameter, N controls the number of steps between cooling steps, and M is a temperature change rate. The range of the parameters is as follows: λ: (280, 1400); T0: (100, 2000); α: (0.9, 0.99); M: (100, 500); and N: (5, 150). The parameters λ, T0, and α all have continuous values, and the parameters M and N take integer values.

We compared a traditional two-level FFD against our method. A center point was used in the FFD to verify the presence of curvature in the design. The optimum design of the FFD was based on a regression model using both main effects and interactions of the parameters.

For the dataset, we developed a schedule generator that used Monte Carlo simulation to generate instances based on real data from São Paulo-Guarulhos International Airport, the busiest Brazilian airport for commercial traffic. Schedule generator inputs were drawn from a year-long analysis. We examined both the 7 a.m. and 7 p.m. schedules, the top two busiest schedule times of the year. The 7 a.m. schedule contained 30 aircraft, with an aircraft mix of 25% heavy and 75% medium, and the 7 p.m. schedule had 32 scheduled arrivals, with an aircraft mix of 15% heavy and 85% medium. For the present study, we used 10 datasets for training and 10 datasets for validation.

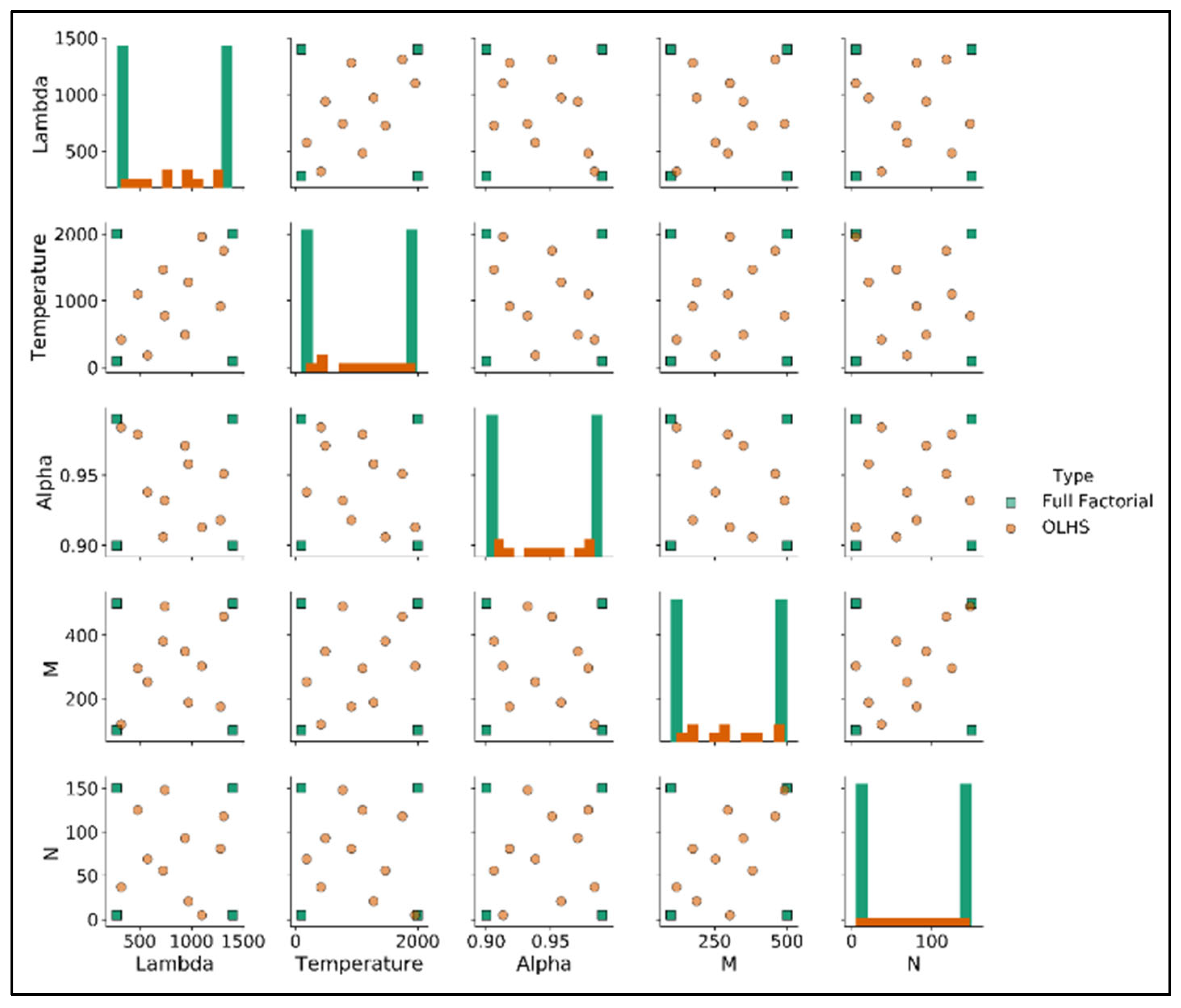
For the parameters’ candidate values, we generated 10 solutions using the OLHS, as previously described. For each method, we used five replication runs. The number of OLHS points was defined in this case study, considering the number of hyperparameters and the need to reduce the total runs. Ten candidate settings were considered enough to explore the five-dimensional parameter space with good coverage.

Figure 2 shows the experimental domain of both methods.

In the FFD, because we investigated five parameters at two levels, a total of 32 (2⁵) runs were necessary. Since SA displayed randomness, we added five points of replication for each run and added five center points. A total of 165 (32 × 5 + 5) runs were thus necessary for each dataset. In the OLHS method, we used 10 candidate solutions and added five replications per candidate solution. A total of 50 runs were thus necessary for each dataset; hence, our novel method required only 30% of the total runs when compared with the FFD.

After selecting the best parameter configurations, we generated 10 new datasets using the schedule generator and ran them 100 times for each dataset using the best parameter values from each method. To compare the quality of the solution from the FFD and the proposed method, we used the paired t-test with a threshold of p < 0.05.

The computational effort in this study refers to the number of experimental runs required for hyperparameter tuning, not the computational time for each run. While both methods (OLHS with RSM and FFD) are computationally efficient in terms of execution time per run, the key advantage of our proposed method lies in the significant reduction in the number of experimental runs required. This reduction minimizes the setup time and experimental workload, making the OLHS with the RSM method a more efficient choice for hyperparameter tuning, without compromising solution quality.

All simulations and analyses were conducted on a Dell G7 7588 laptop equipped with an Intel Core i7-8750H processor, 16 GB of RAM, and an Intel UHD Graphics 630 GPU. The implementation was developed in Python 3.7 and in Minitab 19.1.1 (64-bit). The optimization process was executed within a Windows 11 Home 64-bit environment.

3. Results

A different optimal set of parameters was found for each dataset using the two-level factorial design.

Table 1. Two-Level FFD results.

Dataset	$\mathit{\lambda }$	T0	α	M	N
GRU1	280	100	0.99	500	5
GRU2	280	100	0.99	500	5
GRU3	280	100	0.99	500	5
GRU4	280	2000	0.99	500	5
GRU5	1400	2000	0.99	500	5
GRU6	1400	2000	0.99	500	5
GRU7	280	2000	0.99	500	5
GRU8	1400	100	0.99	500	5
GRU9	1400	100	0.99	500	5
GRU10	1400	100	0.99	500	5

shows the two-level factorial design results for the training set.

All factorial experiments were performed with the addition of a center point to verify the linearity of the model. All center points presented p-values greater than 0.05. This showed that the first-order equation was an appropriate model and that there was no statistical indication of quadratic effects.

The center-point tests in the FFD (p > 0.05) indicated that a first-order model was adequate for the two-level domain, confirming the absence of curvature between the extreme parameter values. However, this result applies only to that discrete factorial region ($\pm$levels). The OLHS explores the continuous interior of the parameter search space, where nonlinear effects become more evident. Therefore, a second-order RSM was used to model the curvature and identify the stationary point within this broader region.

The α, M, and N hyperparameter values were identical for all training datasets, while different values were found for the λ and T0 parameters. As proposed by Coy et al. [39], the final parameter settings using the FFD were determined by using the average across all training datasets. The averaged FFD configuration used for comparison was λ = 840, T₀ = 860, α = 0.99, M = 500, and N = 5.

For our novel method, we ran the OLHS with the RSM meta-level tuning technique through step 5 (executing the hybrid SA algorithm) for each of the 10 candidate configuration sets of hyperparameter values for each training dataset, five times (five replicates). The RDI was calculated for each run. Each OLHS point represents a complete set of SA hyperparameters. The results obtained from these points were used to fit the second-order surface in the RSM stage, which acts as a surrogate model of the algorithm performance.

Table 2. Average RDI for each candidate set at each training set.

Dataset	1	2	3	4	5	6	7	8	9	10
GRU1	20	0	0	0	20	20	0	0	0	0
GRU2	46.67	40	53.33	40	33.33	40	33.33	46.67	80	53.33
GRU3	30	10	20	10	20	40	20	30	20	10
GRU4	10	0	30	0	10	0	10	10	20	0
GRU5	0	0	0	0	0	0	30	10	0	0
GRU6	0	0	0	0	0	20	0	0	0	0
GRU7	0	0	0	0	0	0	0	20	0	0
GRU8	40	33.33	46.67	53.33	13.33	26.67	13.33	26.67	40	60
GRU9	50	60	40	40	20	40	50	40	30	30
GRU10	40	33.33	46.67	53.33	13.33	26.67	13.33	26.67	40	60

shows the average of the five replicates of RDI for each parameter candidate set for all of the training datasets.

These results show that each candidate set of parameters performed differently when applied against the various training sets. A zero value means the candidate set of hyperparameters was able to maintain the lowest RDI value found for the associated training set across the five runs. Higher values show worse performance of the hybrid SA for the given candidate hyperparameter set. Fixing the algorithm and only altering the values of the hyperparameters produced, on average, an 82% drop in solution quality across different instances. This highlights that the problem instance details (i.e., the sequence of aircraft and the total number of aircraft sequenced) dramatically affected the performance of the metaheuristic, reinforcing the need to tune parameters not just to the problem but also to the instance.

These results also illustrate the stochastic behavior of the SA algorithm and the influence of different datasets on the obtained performance. Even though all instances represent the same optimization problem, the same parameter configuration did not yield equivalent results across the datasets. This variability reflects the random nature of the algorithm and the heterogeneity among instances. This confirms the need for systematic hyperparameter tuning rather than ad hoc parameter selection.

Step 6 of the OLHS with RSM meta-level tuning technique involved creating the second-order polynomial RSM, which presented the optimized parameter settings. The performance results obtained from all runs are directly used as observations in the regression model, while the corresponding decision variables defined by the experimental design serve as predictors in the RSM.

When multicollinearity and estimability checks were performed in the full quadratic model, with 21 parameters (Equation (7)), some terms could not be estimated and were removed. The final fitted model is expressed as follows (Equation (8)):

$$RDI= {\beta }_0+{\beta }_{1}Lambda+{\beta }_{2}Temperature+{\beta }_3 Alpha+{\beta }_4 M+{\beta }_5 N+{\beta }_{11}{Lambda}^2+{\beta }_{22}{Temperature}^2+{\beta }_{33}{Alpha}^2$$

(8)

Equation (8) should not be interpreted as a general form. Each tuning experiment must be analyzed separately and will produce its own RSM equation based on the available data and parameter ranges.

The resulting model captured the main curvature of the response surface and provided a well-conditioned regression (VIF < 10 for all retained terms), allowing the identification of the stationary point corresponding to the optimized hyperparameter values.

Table 3. Optimized parameter settings for the proposed method.

Hyperparameter	Setting
Lambda	1268.52
Temperature	1964.47
Alpha	0.984
M	240
N	148

presents the optimized parameter settings obtained for the proposed method.

The optimized parameter configuration provides useful insights into the search behavior of the SA algorithm. The high value of the initial temperature, combined with a cooling factor (Alpha) of 0.984, suggests a slow cooling schedule. This setup allows the algorithm to accept uphill moves more frequently at the beginning of the search and to explore a wider region of the solution space.

The number of neighborhood evaluations (N) before each temperature reduction is relatively large. This indicates that more moves are tested per level, which increases the chance of escaping local minima. The moderate value obtained for the penalty weight (Lambda) helps the SA to avoid premature convergence caused by overly restrictive penalties. This parameter controls the balance between solution feasibility and search diversification. A moderate value penalizes constraint violations enough to maintain feasible schedules while still allowing the algorithm to explore neighboring infeasible solutions that can lead to better solutions in the search strategy.

Finally, the moderate number of temperature cycles (M) indicates an equilibrium between search depth and exploration time, allowing sufficient exploration without excessive computational cost. Larger M values extend the search and delay convergence, while smaller values reduce runtime but may increase the risk of premature convergence.

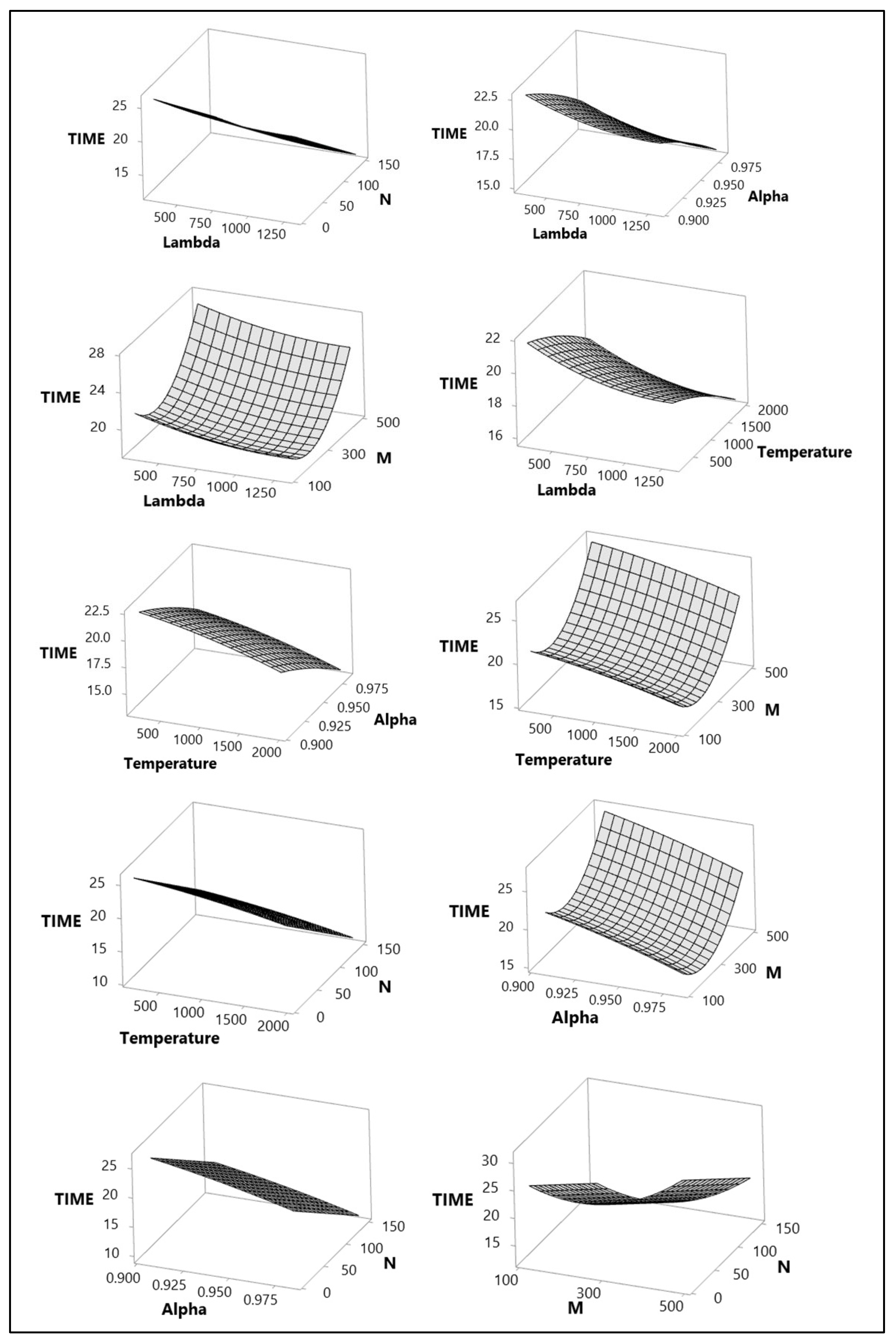
The following surface plots show the interaction and curvature between the parameters, as shown in Figure 3.

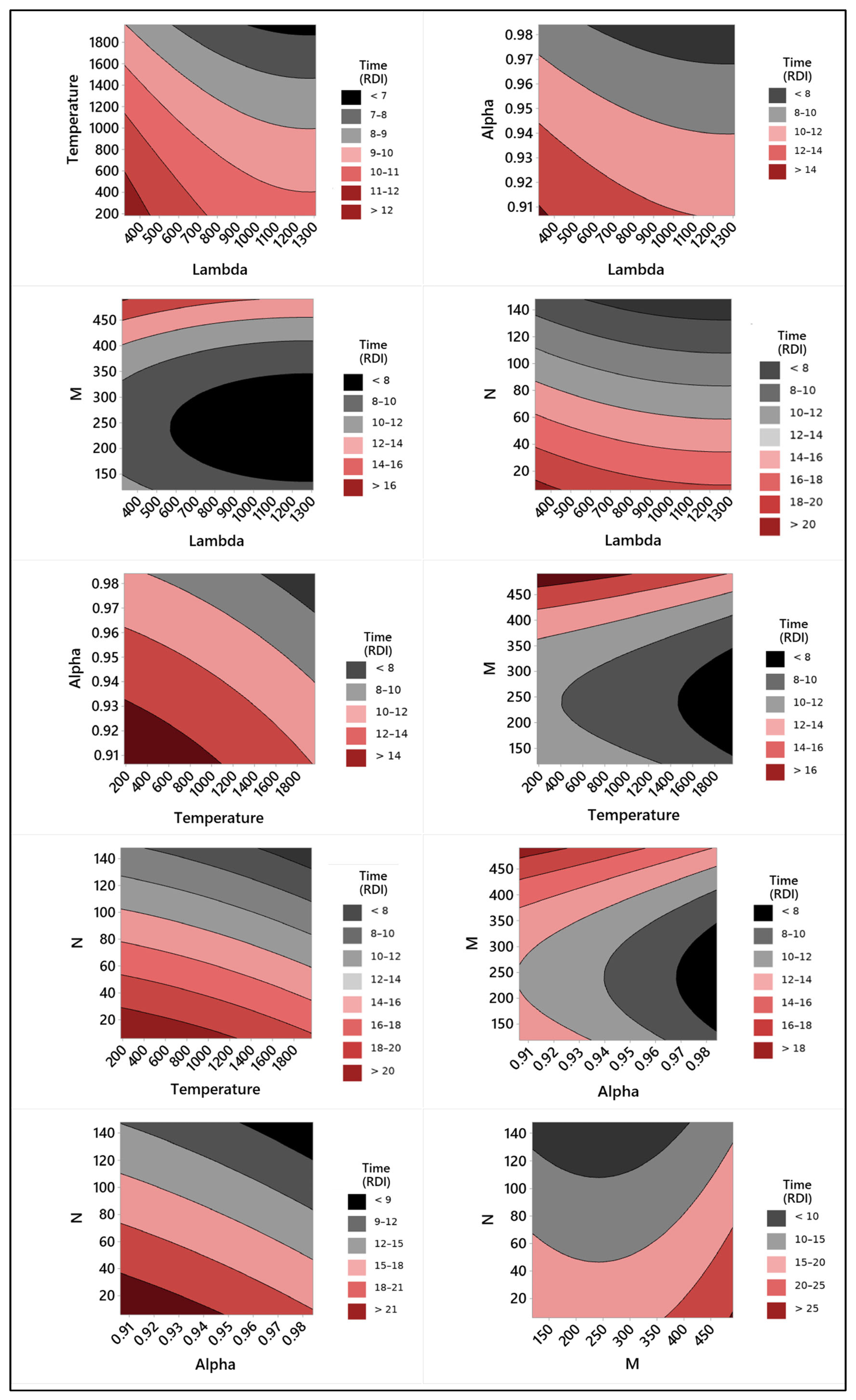
Varying hyperparameters impacted the performance of the metaheuristic. Poor performance was linked with the inability of the metaheuristic to escape from local minima. The optimized hyperparameter settings were the minimum point in the fitted second-order polynomial, in which the partial derivatives were equal to zero. Figure 4 presents the contour plots of the hyperparameters. The optimized parameter settings were used to establish them as the base values.

The contour plots in Figure 4 show that there is a relationship between the values of the hyperparameters. For lambda, small values influenced the hybrid SA algorithm’s ability to yield feasible solutions, especially in the aircraft landing problem with time windows in which a single change in the aircraft sequence could produce infeasible solutions. For our datasets, Lambda must have a value greater than 600. The temperature parameter was linked to the probability of accepting a worse solution to escape local minima. For the studied problem, the temperature must be higher than 1400. The alpha parameter controlled the temperature cooling factor. In the present case, alpha must be greater than 0.97, indicating that the temperature must be slowly reduced. The results also showed that the algorithm performed better when it maintained a certain temperature for longer (parameter N). The temperature change range (parameter M) was between the extreme values surveyed.

Using the optimized hyperparameter values found via both the FFD and our novel method, we generated 10 more test datasets and ran each dataset 100 times for each method. To compare the quality of the solutions obtained by the two methods, we used the paired t-test. This statistical test was applied to verify whether the differences between the results were statistically significant. The p-values corresponding to each dataset are presented in

Table 4. Average makespan value for each method across 10 test instances.

Dataset	Full Factorial (Mean RDI)	Proposed Method (Mean RDI)	Relative Improvement (%)	p-Value	Cohen’s d	Adjusted p-Value
GRU1	2291.8	2291	0.035	0.614	0.074	1.0
GRU2	2287.8	2287.2	0.0265	0.567	0.083	1.0
GRU3	2336.4	2333.2	0.1378	0.042	0.281	0.291
GRU4	2333.6	2333.2	0.017	0.817	0.034	1.0
GRU5	2475.6	2470.8	0.194	0.025	0.312	0.229
GRU6	2475.7	2470.9	0.194	0.025	0.312	0.23
GRU7	2463.6	2460.8	0.114	0.255	0.166	1.0
GRU8	2460.6	2458.2	0.0981	0.363	0.128	1.0
GRU9	2437.8	2435.2	0.107	0.022	0.328	0.229
GRU10	2426.2	2424.4	0.074	0.416	0.115	1.0

, where values lower than 0.05 represent statistical significance among the averages.

A performance comparison was conducted to evaluate the efficacy of the proposed OLHS compared to the RSM method, our method, against FFD, a classical approach. The results showed that our proposed method achieved, on average, results equal to or slightly better than those obtained with the two-level factorial design (lower RDI values are preferred). Although several datasets initially showed p-values below 0.05 in the paired t-tests, none of the differences remained significant after applying the Holm–Bonferroni correction for multiple comparisons. The effect sizes were small (Cohen’s d < 0.35), and the relative improvement ranged between 0.02% and 0.19%. These results indicate that both methods provide statistically equivalent performance.

Crucially, however, our proposed method required only 30% of the total runs utilized by the FFD. These characteristics demonstrated the viability of the proposed method for hyperparameterization of a local search algorithm for solving a combinatorial optimization problem.

4. Discussion

The proposed method combines an OLHS with RSM. When compared to the conventional FFD, it produced better results in terms of computational effort, the number of experimental runs required for hyperparameter tuning, and solution quality. While both methods (ours and FFD) are computationally efficient in terms of execution time per run, the key advantage of our proposed method lies in the significant reduction in the number of experimental runs required. This reduction minimizes the setup time and experimental workload, making the proposed method a more efficient choice for hyperparameter tuning without compromising solution quality.

Due to the combinatorial nature of the problem under study, there is no guarantee that any method, ours or classical, will reach the true global optimum. The objective of the proposed technique is not to discover the “ideal” configuration in an absolute sense, nor to define universal parameter ranges. Rather, it is to efficiently identify high-quality configurations that perform equal to or better than those produced by traditional approaches such as full factorial design, while using substantially fewer simulation runs.

The present study focuses specifically on applying OLHS with RSM to SA. SA was chosen due to its simplicity, flexibility, and robustness in escaping local minima, which makes it suitable for benchmarking tuning strategies in combinatorial optimization problems. OLHS offers good space-filling properties with minimal prior knowledge and fewer samples, making it well-suited for expensive simulation-based evaluations. RSM is an efficient surrogate modeling approach that enables parameter tuning without requiring iterative or adaptive processes, which is particularly valuable when computational resources are constrained.

The authors believe that the demonstration presented in this article provides a clear foundation for further research in this area. This approach was chosen to clearly illustrate the methodology in the context of a well-known problem. The present study may benefit the area of metaheuristic hyperparameter optimization as a whole, as it can be applied to other metaheuristic methods.

5. Conclusions

Metaheuristics are a very important technique that can be applied to a wide range of optimization problems. Their versatility is linked to the presence of parameters that are adjusted according to the problems to be solved. Despite being an important task in the search for the best results in the solutions to these types of problems, the optimization of the parameter values is still underutilized, due in large part to its high demands on time and resources.

Hyperparameterization requires previous knowledge of the metaheuristic and how it was previously implemented for the type of problem being studied. One of the most important steps in hyperparameterization techniques is the identification of the range of values for each parameter.

The hyperparameterization activity is very dynamic and is connected to the training dataset. Parameters for problems with a wide range of configurations, such as the ALPTW, in which airport demand is influenced by seasonality, thus increasing the number of aircraft to be sequenced for landing, must periodically undergo a new hyperparameterization process for adjustments. Another alternative would be to have the training datasets encompass as many as possible of the future situations to be solved by the metaheuristic. The authors believe that an easy-to-implement procedure, such as the proposed method, will facilitate the fine-tuning of metaheuristics.

The objective of the present article was to develop a simple, more efficient method based on an optimized Latin hypercube sampling (OLHS) technique for estimating the best parameter setting for performing a hybrid simulated annealing algorithm. The results showed that the use of an optimized space-filling-based method produces very good results compared with those of traditional techniques such as the two-level FFD. However, our study was restricted to solving a combinatorial optimization problem with the use of a local search metaheuristic. Future research could investigate the application of this method to fine-tuning parameters in other types of problems and in other metaheuristics.