Privacy-Preserving Classification of Medical Tabular Data with Homomorphic Encryption

Abstract

Machine learning (ML) offers significant potential for disease prediction, clinical decision support, and medical data classification, but its reliance on sensitive patient data raises privacy and security concerns, particularly under strict healthcare regulations. Traditional encryption methods require data to be decrypted prior to computation, such as in ML workflows, thereby introducing risks of exposure and undermining data confidentiality. Homomorphic Encryption (HE) addresses this challenge by enabling computations directly on encrypted data, ensuring end-to-end privacy. This paper explores the integration of the Cheon-Kim-Kim-Song (CKKS) HE scheme into the inference phase of medical tabular data classification. We evaluate the performance of Logistic Regression (LR), Support Vector Machine (SVM), and a lightweight multilayer perceptron (MLP) under HE-based inference, and compare their classification accuracy, computational overhead, and latency against plaintext counterparts. Additionally, we propose two hybrid models (LR-MLP and SVM-MLP) to accelerate training convergence and enhance inference performance. Experimental results demonstrate that while HE-based inference introduces moderate computational cost and data transmission overheads, it maintains accuracy comparable to plaintext inference. These outcomes affirm the practical feasibility of HE for privacy-preserving machine learning in healthcare, while also highlighting key implementation trade-offs. Furthermore, the findings support the advancement of secure AI systems and promote the adoption of cryptographic techniques in digital health and other privacy-critical fields.

1. Introduction

Artificial intelligence (AI) is reshaping healthcare through a wide range of applications, including early disease detection, data-driven diagnosis, and personalized treatment recommendations [1]. These examples illustrate the broader potential of AI in enhancing clinical decision-making and patient outcomes, especially as machine learning performance continues to improve and services become increasingly accessible. However, processing sensitive medical data via cloud platforms raises serious privacy concerns. There is a pressing need for machine learning solutions that balance predictive power with strong data protection, particularly under stringent ethical and regulatory frameworks.

Privacy-preserving machine learning (PPML) techniques have emerged to address this challenge. Methods such as secure multi-party computation (SMPC), differential privacy (DP), homomorphic encryption (HE), and federated learning (FL) enable secure data analysis without exposing sensitive patient information [2,3]. Each method offers distinct privacy guarantees and operational trade-offs. SMPC and FL rely on collaborative computation across multiple parties without directly sharing their private data. However, even though the raw data stays local, some intermediate information, like gradients, masked inputs, or model updates, can still be exposed during the process. This information can potentially be exploited by attackers to infer or reconstruct the original data. These methods also require synchronization and trust in the correctness of the underlying protocols. DP, on the other hand, provides formal privacy guarantees by injecting noise into data or computation, making individual data points indistinguishable even to adversaries with auxiliary information. However, this protection comes at the expense of model accuracy, especially in small or sensitive datasets. In contrast, HE [4] offers a uniquely promising approach by enabling direct computations on encrypted data. In an HE-based workflow, the data owner encrypts the input, and all computations are performed entirely within the encrypted domain. The output remains encrypted and can only be decrypted by the data owner, ensuring end-to-end confidentiality. At no point is raw data exposed to the computing party, making HE particularly suitable for scenarios involving untrusted servers or cloud environments. Its non-interactive nature, strong cryptographic protection, and ability to preserve data confidentiality without sacrificing accuracy or requiring multi-party coordination distinguish HE within the PPML space. HE can also be effectively combined with other techniques, such as FL or SMPC, to further enhance privacy and security, especially in complex or distributed settings. Recent advances in approximate HE schemes have significantly improved computational efficiency, enabling practical applications across various domains such as feature extraction, text processing, image recognition, and audio analysis [5]. Its compatibility with cloud-based infrastructures and growing computational efficiency make HE a compelling choice for secure medical data processing [6].

While HE offers strong privacy guarantees, its application in machine learning model training remains computationally intensive due to the overhead of encrypted arithmetic and the depth of iterative optimization algorithms. Key challenges include limited support for non-linear functions, difficulty in gradient-based optimization, and restricted model complexity [7]. Recent research has investigated advanced techniques such as pruning, quantization, batching, and ciphertext packing [8] to reduce training costs and latency, yet practical deployment remains limited. Consequently, many PPML systems prioritize HE for model inference, where computation depth is lower and privacy benefits are retained.

In this work, we focus on HE-based model inference for medical tabular data classification. While both medical tabular and image data often suffer from limited labeled samples, image analysis has greatly benefited from transfer learning. Pretrained models such as ResNet and Inception, originally trained on large-scale natural image datasets like ImageNet [9], can be fine-tuned and achieve strong performance on medical imaging tasks [10]. Furthermore, curated medical image datasets such as MedMINST [11] have accelerated progress in this domain. In contrast, medical tabular data poses unique challenges: It is typically derived from heterogeneous sources, leading to frequent issues with missing values, inconsistencies, and variable data quality. Despite these difficulties, tabular data remains essential for clinical decision-making, particularly in scenarios where diagnosis relies more on patient history, laboratory results, and textual records than on imaging. Moreover, tabular data often offers greater interpretability, which is essential for explainable AI in healthcare [12]. Recent studies also suggest that combining tabular and imaging data can lead to improved predictive performance, highlighting the complementary nature of these modalities [13]. These factors motivate our emphasis on secure tabular data classification using HE, enabling privacy-preserving yet effective disease prediction.

HE-based machine learning inference was first introduced by CryptoNets [14], demonstrating the feasibility of applying neural networks to encrypted image data. Subsequent research has focused on improving the accuracy and efficiency of HE-based learning with deeper neural network architectures [15,16,17]. While neural networks excel in domains like image and speech recognition, their advantage diminishes for tabular data [18]. Structured datasets often favor tree-based models such as gradient boosting (e.g., XGBoost [19], LightGBM [20]), which naturally handle heterogeneous features, missing values, and non-linear interactions with minimal preprocessing. In contrast, neural networks often demand extensive normalization, substantial training datasets, and offer limited interpretability, making them less competitive for many tabular tasks. However, extending HE-based inference on decision trees introduces significant challenges because splits rely on comparisons and data-dependent branching, which are not natively supported by HE schemes that operate over additions and multiplications. Emulating comparisons requires either polynomial approximations of step functions or evaluate-all-branches-with-masking strategies [21,22], both of which increase multiplicative depth, ciphertext count, and noise, often necessitating costly bootstrapping. Ensembles such as random forests and gradient-boosted trees further amplify complexity and require oblivious evaluation to avoid access-pattern leakage. These constraints motivate training-inference co-design [23,24], where model topology and HE parameters are jointly optimized to achieve practical latency without compromising privacy.

Fortunately, recent studies have shown that simple models such as logistic regression (LR) and support vector machines (SVM) can deliver strong inference performance on medical tabular data classification, even under HE [25,26]. These models are well suited for HE because they rely on linear or low-degree polynomial operations, which align with the arithmetic constraints of HE schemes. This combination of computational efficiency and HE compatibility makes LR and SVM attractive for privacy-preserving healthcare applications. In [25], the authors proposed a HE-based LR framework leveraging the Cheon-Kim-Kim-Song (CKKS) scheme [27], a widely adopted HE scheme for efficient computation on real-valued data. They evaluated its performance against a baseline LR model without HE and compared it to HE-enabled SVM inference across three heart disease datasets. Their results indicate that the proposed framework achieves a practical balance between privacy, computational efficiency, and predictive accuracy. Similarly, SVM inference was investigated in [26] for privacy-preserving medical data classification using the CKKS scheme. The study compared SVM models with different kernels on two medical tabular datasets and two image datasets, demonstrating that their approach maintains accuracy comparable to unencrypted SVM prediction while preserving input confidentiality. However, both studies focused on individual models and did not explore architecture variations on hybrid approaches.

Our work addresses this gap by systematically evaluating multiple model types, including LR, SVM, and a lightweight multilayer perception (MLP), for HE-based inference on medical tabular data. In addition to assessing traditional models, we investigate the feasibility of shallow neural architectures that introduce minimal complexity while capturing non-linear feature interactions beyond the capabilities of linear models. By maintaining a low-depth architecture, these models remain compatible with HE constraints, avoiding excessive multiplicative depth and preserving practical inference latency.

A key novelty of our approach lies in the design of two hybrid models (LR-MLP and SVM-MLP), where the MLP is initialized with weights and biases derived from pretrained LR or SVM models. This initialization accelerates convergence during training and can improve inference accuracy while adding little complexity compared to standalone models. Unlike prior work that primarily focused on individual models under HE, our approach advances the state of the art by exploring hybrid architectures that combine the interpretability and efficiency of linear models with the feature learning capabilities of neural networks in an HE setting.

To validate our HE-based privacy-preserving classification framework, we conducted comprehensive experiments on two publicly available medical tabular datasets with varying sizes and class imbalance levels, namely the Wisconsin breast cancer (WBC) dataset [28] and the Cleveland heart disease (CHD) dataset [29]. We applied careful preprocessing and training strategies, including feature selection, normalization, stratified sampling, and k-fold cross-validation, to ensure reliable performance. The implemented ML models were assessed based on inference performed on test data under both plaintext and CKKS-based HE scenarios. Our findings demonstrate that while CKKS encryption introduces moderate computational overhead and increased data transmission costs, it preserves classification accuracy comparable to plaintext models. These findings confirm the practical feasibility of HE for privacy-preserving machine learning in healthcare.

Key contributions of our study are:

• A unified framework for HE-based inference on medical tabular data, integrating traditional and neural models (LR, SVM, and MLP) in a privacy-preserving setting.
• Novel hybrid MLP architectures (LR-MLP and SVM-MLP) that combine linear and non-linear components to enhance training efficiency and model expressiveness under HE constraints.
• Comprehensive performance evaluation of HE-based classification, conducted on two distinct medical datasets, focusing on classification accuracy and generalization capability despite encryption-induced noise and computational constraints. The evaluation also includes an analysis of the computational overhead and communication cost introduced by encryption. Practical implications and strategies to mitigate these challenges are discussed to enhance performance and scalability.

The remainder of this paper is organized as follows: Section 2 provides background on the CKKS scheme, conventional ML models for classification, and strategies for integrating these models with encrypted computation. Section 3 introduces the proposed framework for integrating encryption into the inference pipeline. Section 4 details the implementation process, covering dataset selection, preprocessing steps, model architecture, and the configuration of CKKS parameters and key generation. Section 5 presents the experimental results, including classification performance metrics, computational overhead, and communication cost analysis. It also examines the impact of different CKKS parameter configurations on the performance of HE-based inference. Finally, Section 6 summarizes the key findings, discusses the limitations of the study, and outlines directions for future research.

2. Background

This section presents the essential preliminaries, including an overview of the CKKS homomorphic encryption scheme and various classification models employed—logistic regression (LR), support vector machine (SVM), and multilayer perceptron (MLP). Together, these components establish the foundational elements necessary for our framework of secure and effective encrypted inference.

2.1. CKKS Scheme

The Cheon-Kim-Kim-Song (CKKS) scheme [27] is a leveled homomorphic encryption method designed for approximate arithmetic on encrypted real or complex numbers with controlled error. It leverages the computational hardness of the ring learning with errors (RLWE) problem [30] to maintain cryptographic security.

CKKS achieves efficiency by packing multiple values into a single ciphertext using a SIMD (Single Instruction, Multiple Data) approach. The workflow consists of four main steps:

• Encode: An input vector $\mathbf{a}\in {\mathbb{R}}^{N/2}$ is encoded into a plaintext polynomial $p=\mathrm{E}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}\left(\mathbf{a}\right)$ in the ring $\mathcal{R}=\mathbb{Z}\left[X\right]/(X^N + 1)$, via canonical embedding with a scaling factor.
• Encryption: The plaintext is encrypted into a ciphertext $c={\mathrm{E}\mathrm{n}\mathrm{c}\mathrm{r}\mathrm{y}\mathrm{p}\mathrm{t}}_{pk}\left(p\right)$ using a public key $pk$.
• Decryption: The ciphertext is decrypted back into a plaintext $p={\mathrm{D}\mathrm{e}\mathrm{c}\mathrm{r}\mathrm{y}\mathrm{p}\mathrm{t}}_{sk}\left(c\right)$ using a secret key $sk$.
• Decode: The plaintext is decoded to recover the approximate vector $\mathbf{a} =\mathrm{D}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}\left(p\right)$.

CKKS supports homomorphic addition, homomorphic multiplication, and slot rotations in the encrypted domain:

• Addition: $\mathrm{A}\mathrm{d}\mathrm{d}(c_1,c_2)={\mathrm{E}\mathrm{n}\mathrm{c}\mathrm{r}\mathrm{y}\mathrm{p}\mathrm{t}}_{pk}\left(\mathrm{E}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}\right({\mathbf{a}}_1⨁{\mathbf{a}}_2\left)\right)$
• Multiplication: ${\mathrm{M}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}}_{evk}\left(c_1,c_2\right)={\mathrm{E}\mathrm{n}\mathrm{c}\mathrm{r}\mathrm{y}\mathrm{p}\mathrm{t}}_{pk}\left(\mathrm{E}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}\right({\mathbf{a}}_1⨂{\mathbf{a}}_2\left)\right)$, where $evk$ is a multiplication evaluation key for noise management. After each multiplication, two additional operations are needed: relinearization and rescaling. Relinearization reduces the ciphertext size back to its original form to prevent growth in computational complexity, while rescaling adjusts the modulus and scale to control precision and noise growth. The supported multiplicative depth is therefore limited by the chosen modulus chain unless bootstrapping is employed.
• Rotation: ${\mathrm{R}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}}_{rk}(c,i,d)$ performs a cyclic shift in slots by $i$ along direction $d$ using rotation keys $rk$. These keys enable homomorphic automorphisms on ciphertexts, which are essential for implementing vectorized operations while preserving the original packed structure.

Key design considerations for CKKS include selecting an appropriate polynomial degree and modulus chain to accommodate the required multiplicative depth, and setting an initial scale that balances precision and dynamic range. This study uses TenSEAL (version 0.3.16) [31], a Python library built on top of Microsoft SEAL [32], which implements CKKS but does not natively support bootstrapping. Therefore, circuits must be carefully parameterized to operate within a finite depth.

2.2. Logistic Regression

Logistic regression (LR) is a supervised learning method widely used for classification tasks [33]. For each class label $y_i$, for $i=1,\dots ,n$, LR models the conditional probability that an input ${\mathit{x}}_{\mathit{i}}\in {\mathbb{R}}^d$ belongs to the class as [33]:

$$\mathrm{Pr}\left[y_i|\mathit{x}\right]=\sigma (y_i·({\mathit{w}}^{\mathrm{T}}{\mathit{x}}_{\mathit{i}}+b\left)\right),$$

(1)

where $\mathit{w}\in {\mathbb{R}}^d$ represents the model weights, $b\in \mathbb{R}$ is the bias term, and $\sigma \left(x\right)= {\displaystyle \frac{1}{1 + \mathrm{e}\mathrm{x}\mathrm{p}(-x)}}$ denotes the sigmoid function. The parameters $\mathit{w}$ and $b$ are estimated during training using maximum likelihood estimation, typically implemented via gradient descent.

Once trained, the model predicts the class label by comparing the output probability against a threshold value—commonly 0.5 in binary classification. If the predicted probability exceeds the threshold, the instance is classified as positive; otherwise, it is classified as negative.

LR is computationally efficient, interpretable, and performs well on linearly separable data, making it a common baseline for classification models.

However, since the CKKS scheme supports only polynomial arithmetic, LR inference must be adapted by replacing the sigmoid function with a suitable polynomial approximation to enable encrypted computation, or alternatively, leave it to the client side for post-decryption processing.

2.3. Support Vector Machine

Support vector machines (SVM) are supervised learning models widely used for both classification and regression tasks [34]. The core idea behind SVM is to identify an optimal hyperplane that maximizes the margin between different classes in a high-dimensional feature space.

For binary classification, the decision function for an input $\mathit{x}\in {\mathbb{R}}^d$ is evaluated as [34]:

$$c\left(\mathit{x}\right) =\mathrm{sign}\left({\sum }_{i=1}^l{w}_i{y}_i\mathbb{K}\left(〈{\mathit{x}}_i,\mathit{x}〉\right) + b\right),$$

(2)

where $\mathbb{K}$ is the kernel function, ${\mathit{x}}_i$ is the i-th support vector and $y_i$ is its corresponding class label, $w_i$ are the learned weight coefficients, and $b$ is the bias term. In addition to linear kernels, SVM leverages polynomial and radial basis function (RBF) kernels to capture non-linear relationships by implicitly mapping input data into higher-dimensional spaces where linear separation becomes feasible. Training involves solving a convex optimization problem in either primal or dual form, yielding a subset of training samples (the supporting vectors), associated weights, and the bias. SVM is known for strong generalization performance, especially in cases with limited data and high-dimensional features.

To ensure compatibility with the CKKS scheme, SVM must be adapted in two key ways: A linear kernel or an approximate kernel with low-degree polynomials should be used to conform to polynomial arithmetic constraints. In addition, the sign function used in decision evaluation must be approximated by a polynomial, or alternatively, leave to the client side for post-decryption processing.

2.4. Multilayer Perceptron

Artificial neural networks (ANNs) are computational models inspired by the structure and function of biological neurons, designed to learn complex patterns from data [35]. An ANN typically consists of multiple layers of interconnected nodes (neurons), where each neuron applies a weighted sum of inputs followed by a non-linear activation function. Through iterative training using algorithms such as backpropagation, ANN adjusts the weights to minimize prediction error.

In this study, we focus on a specific subclass of ANN known as multilayer perceptron (MLP). An MLP consists of an input layer, one or more hidden layers, and an output layer. Each neuron in a given layer is fully connected to all neurons in the subsequent layer, forming a dense feedforward architecture. This structure enables the MLP to learn hierarchical representations of the input features, making it particularly effective for classification tasks, especially when relationships between features and target classes are complex and non-linear.

Two fundamental operations in an MLP are:

• Weighted-sum: Each neuron computes a linear combination of inputs from the previous layer [35]:

$$z={\mathit{w}}^{\mathrm{T}}\mathit{x}+b,$$

(3)

where $\mathit{w}$ denotes the weight vector, $\mathit{x}$ is the input vector, and $b$ is the bias term.

• Non-linear activation function: The computed weight-sum $z$ is then passed through a non-linear activation function to introduce nonlinearity. Commonly used activation functions include ReLU, sigmoid, and tanh.

To ensure CKKS compliance, the non-linear activation functions in an MLP must be substituted with polynomial functions, and network depth must be carefully constrained to avoid exceeding the modulus chain, which limits the number of homomorphic operations that can be performed securely.

3. Methodology

This research aims to demonstrate that homomorphic encryption (HE) is an effective solution for privacy-preserving machine learning (PPML) in healthcare, particularly during the inference phase on medical tabular data classification. The goal is to enable accurate disease diagnosis using classification techniques while minimizing any degradation in model performance.

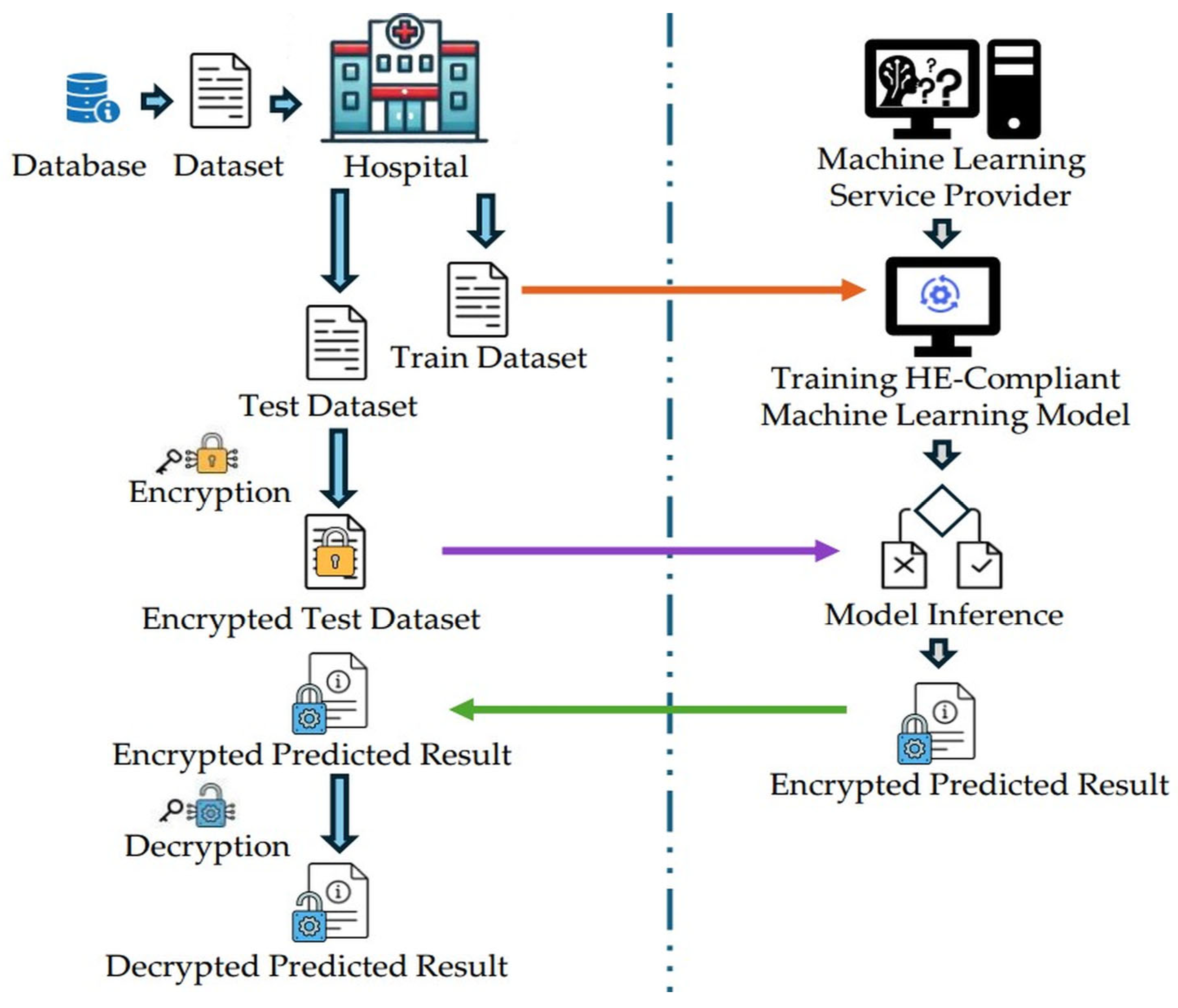
The proposed workflow, illustrated in Figure 1, consists of four main stages: data acquisition, encryption, model training and inference, and result decryption.

The hospital initially retrieves a medical dataset from a database containing non-sensitive, publicly shareable information. This dataset is transmitted in plaintext to the ML service provider for model training. Concurrently, privacy-sensitive data from current patients is collected for evaluation purposes. To ensure compliance with privacy regulations, this evaluation dataset remains encrypted throughout the process and is never exposed in plaintext to external entities.

The privacy-sensitive evaluation dataset is encrypted using the CKKS scheme and transmitted to the ML service provider for inference, while the plaintext training dataset was provided for model training. Prior to training, the ML model is adapted for HE compatibility, ensuring that the learned parameters can be directly applied to encrypted data during inference without requiring structural modifications.

The ML service provider trains a classification model using the plaintext training dataset to achieve optimal predictive performance. After training, the model was applied to the encrypted evaluation dataset without any decryption, thereby ensuring patient privacy throughout the inference process. Finally, the encrypted prediction results are returned to the hospital, where decryption is performed locally to obtain the final disease diagnosis outcomes.

Throughout this paper, $\mathit{x}$ and $\widehat{y}$ denote the plaintext test dataset and the final decrypted prediction results, respectively, while $z_{\mathrm{e}\mathrm{n}\mathrm{c}}$ represents the encrypted predictions. The encryption and decryption operations that are performed using the CKKS scheme are denoted as $\mathrm{E}\mathrm{n}\mathrm{c}\mathrm{r}\mathrm{y}\mathrm{p}\mathrm{t}(·)$ and $\mathrm{D}\mathrm{e}\mathrm{c}\mathrm{r}\mathrm{y}\mathrm{p}\mathrm{t}(·)$, respectively. For each model, $\mathit{w}$ refers to the weight vector and $b$ is the bias term learned during training.

4. Implementation

This section describes the implementation of the proposed evaluation framework. It begins by outlining the two medical tabular datasets and the preprocessing steps applied. The training and inference procedures for the ML models are then presented, along with the modifications introduced to ensure compatibility with homomorphic encryption. To enhance classification performance, two hybrid models (LR-MLP and SVM-MLP) are proposed, and their implementation details are discussed. Finally, the configuration of CKKS parameters and the key generation process required to enable encryption, decryption, and homomorphic operations are provided.

4.1. Dataset Description

This study uses two publicly available medical tabular datasets of different sizes: the Wisconsin breast cancer (WBC) dataset [28] and the Cleveland heart disease (CHD) dataset [29]. Both are widely recognized benchmarks in machine learning for disease diagnosis based on patient records.

The WBC dataset contains 569 instances with no missing values, each described by 30 continuous-valued features, an ID column, and a categorical target variable. All 30 features were derived from 10 real-valued measurements of cell nuclei. The target variable named diagnosis has two classes: benign (non-cancerous) and malignant (cancerous). The dataset includes 357 benign and 212 malignant cases, indicating a moderate class imbalance.

The CHD dataset consists of 303 instances. Among these, six entries include randomly distributed missing values. To maintain data integrity and simplify preprocessing, these incomplete entries were removed, resulting in a cleaned dataset of 297 instances. Each instance is described by 13 features and a categorial target variable named condition, which has two classes: no disease and with disease. This dataset contains 160 benign cases with no heart disease and 137 cases with heart disease. Compared with the WBC dataset, the CHD dataset exhibits a more balanced class distribution.

4.2. Dataset Preprocessing and Splitting

Several preprocessing steps were applied to the WBC and CHD datasets prior to model training and inference to ensure data quality and improve predictive performance. The ID column was removed as it does not provide predictive information. In contrast, all features were retained for the CHD dataset.

Each dataset was split into training and testing subsets using an 80/20 split. This resulted a 455 training cases and 114 testing cases for the WBC dataset, and 237 training cases and 60 testing cases for the CHD dataset.

Given the class imbalance in the WBC dataset, stratified sampling was employed to ensure that both the training and testing subsets preserved the original class distribution. This approach maintained proportional representation of each class across both subsets. The same stratification procedure was applied to the CHD dataset for consistency.

Before feeding the data into the models, all features in both the training and testing datasets were standardized to ensure uniform scaling. Standardization was performed by computing the mean and standard deviation calculated from the training data, which were then applied to transform both the training and testing subsets.

4.3. Model Setup, Training, and Inference

A unified framework was developed for implementing all ML models. Three traditional models (LR, SVM, and MLP) together with two proposed hybrid models (LR-MLP and SVM-MLP) were implemented with HE adaptations. Each model was trained and evaluated separately on both datasets for binary classification tasks.

4.3.1. HE-Compliant Model Accommodation

To enable the processing of the encrypted test dataset, model adaptations were necessary. Since the CKKS scheme supports only addition and multiplication, each model was modified to ensure compatibility with these operations. Consequently, all models were restricted to prioritize linear computations and to utilize extracted weights and biases in plaintext, thereby facilitating encrypted inference without violating HE constraints. The modifications adopted in our implementation are presented below:

1.

LR: The input features from the plaintext training dataset were initially passed through a linear function followed by a sigmoid function, as shown in Equation (1). After training, the learned weights and biases were extracted for encrypted inference. Next, each sample of the test dataset was encrypted using the CKKS scheme. Each encrypted test sample was multiplied (dot product) with the plaintext weight vector and added to the plaintext bias:

$${\mathrm{z}}_{\mathrm{enc}}={\mathit{w}}^T\mathrm{E}\mathrm{n}\mathrm{c}\mathrm{r}\mathrm{y}\mathrm{p}\mathrm{t}\left(\mathit{x}\right) +b.$$

(4)

The sigmoid function was not applied in the encrypted domain. Instead, it can be performed on the client side after decryption, followed by thresholding at 0.5, as shown below:

$$\widehat{y} = \left\{ \begin{array}{c}1; \mathrm{i}\mathrm{f} \sigma \left(\mathrm{Decrypt}\left(z_{\mathrm{e}\mathrm{n}\mathrm{c}}\right)\right) \ge 0.5\\ 0; \mathrm{i}\mathrm{f} \sigma \left(\mathrm{Decrypt}\left(z_{\mathrm{e}\mathrm{n}\mathrm{c}}\right)\right) < 0.5\end{array} \right.,$$

(5)

where $\sigma (·)$ denotes the sigmoid function. Alternatively, since the sigmoid function is monotonic, this is equivalent to applying a threshold of 0 directly to the decrypted value without computing the sigmoid.

2.

SVM: A linear kernel was employed in the SVM model to separate the two classes with a linear decision boundary. The plaintext input features were used to compute the linear function. Encrypted inference followed the same process as LR, except that thresholding was applied at zero after decryption, since the decision boundary is defined by the hyperplane. No probability transformation was needed. The decision rule is:

$$\widehat{y}=\left\{ \begin{array}{c} 1; \mathrm{i}\mathrm{f} \mathrm{D}\mathrm{e}\mathrm{c}\mathrm{r}\mathrm{y}\mathrm{p}\mathrm{t}\left({\mathrm{z}}_{\mathrm{enc}}\right) \ge 0 \\ 0; \mathrm{i}\mathrm{f} \mathrm{D}\mathrm{e}\mathrm{c}\mathrm{r}\mathrm{y}\mathrm{p}\mathrm{t}\left({\mathrm{z}}_{\mathrm{enc}}\right) < 0\end{array}\right..$$

(6)

3.

MLP: A shallow MLP was designed to minimize computation during encrypted inference. Input features first pass through a linear layer, followed by a square activation (as also performed in similar research [13,27]) to form a hidden layer of $m$ neurons. This is then mapped to a single output neuron for binary classification, and predictions are converted to probabilities using a sigmoid function.

For encrypted inference, the prediction is computed as:

$$\begin{gathered} {\mathit{z}}_1 = {\mathit{W}}_1\mathrm{E}\mathrm{n}\mathrm{c}\mathrm{r}\mathrm{y}\mathrm{p}\mathrm{t}\left(\mathit{x}\right)+ {\mathit{b}}_1, \\ {z}_{\mathrm{enc}} = {{\mathit{w}}_{\mathbf{2}}}^T\left({\mathit{z}}_1·{\mathit{z}}_1\right) + b_2, \end{gathered}$$

(7)

where ${\mathit{W}}_1 \in {\mathbb{R}}^{m\times d},{\mathit{b}}_1 \in {\mathbb{R}}^m, {\mathit{w}}_{\mathbf{2}} \in {\mathbb{R}}^m, b_2\in \mathbb{R}$ are the trained weights and biases of the input layer and the hidden layer. In our experiments, the parameter $m$ was set to 16 for the MLP models trained on the WBC dataset, and to 12 for those trained on the CHD dataset. Note that rather than applying the sigmoid function to produce an encrypted probability, the server returns the weighted sum directly. After decryption, the client applies the sigmoid function and a threshold of 0.5 to determine the predicted class, as in Equation (6), or alternatively, applies a threshold of 0 directly to the decrypted value without computing the sigmoid.

4.3.2. Hybrid ML Models

LR and linear-kernel SVM are computationally efficient and effective for linearly separable data. These models are simple, interpretable, and converge quickly due to their convex optimization landscapes. However, they are limited in their ability to model complex, non-linear relationships. In contrast, MLPs are capable of capturing non-linear patterns through their layered architecture and activation functions. While powerful, MLPs are more computationally demanding and often require careful initialization and tuning to avoid issues such as slow convergence or getting trapped in poor local minima. To leverage the strengths of both linear and non-linear modeling, we propose two hybrid architectures, LR-MLP and SVM-MLP, where the MLP’s input layer is initialized with weights and biases derived from a pretrained LR or SVM model. This initialization serves as a form of knowledge transfer, embedding the linear decision boundaries learned by LR or SVM into the MLP’s structure.

In LR-MLP, an LR model is first trained, and its learned parameters initialize the MLP’s first layer, replacing random initialization with a decision boundary that already generalizes well. Similarly, SVM-MLP uses weights and bias from a linear SVM to initialize the MLP, embedding a margin-based decision boundary into the network. Subsequent MLP design and training follow standard practices. To ensure a fair comparison, the MLP architectures used in the hybrid models were kept identical to those employed in the traditional MLP baseline.

This hybrid approach offers several advantages:

• Starting from a meaningful initialization reduces the burden on the optimizer to discover useful patterns from scratch. The model begins training closer to a good solution, which can significantly reduce training time.
• The pretrained weights encode a prior understanding of the data’s linear structure, which can guide the MLP toward more generalizable solutions, especially in cases where the data has both linear and non-linear components.
• Random initialization can lead MLPs to converge to suboptimal local minima. By initializing with pretrained weights, the model is likely to start in a more favorable region of the parameter space, leading to better performance and potentially converging toward a global optimum.
• This integration introduces minimal overhead, as it leverages existing models and only modifies the initialization step. The rest of the training pipeline and the inference process remain unchanged.

4.3.3. k-Fold Cross-Validation and Model Training

The training dataset remained in plaintext without any encryption, and model training was conducted on unencrypted data. To ensure a robust evaluation of model performance, k-fold cross-validation was employed. In this method, the training dataset is partitioned into $k$ equal-sized subsets, or folds. The model is trained on $k - 1$ folds and validated on the remaining fold, repeating the process $k$ times so that each fold serves as the validation set once. The resulting performance metrics from each iteration are then averaged to yield a reliable estimate of the model’s generalization ability. Specifically, 10-fold cross-validation was applied to both the WBC dataset and the CHD dataset. This approach is particularly beneficial for small medical datasets, as it maximizes the use of limited data for both training and validation, reduces variance in performance estimates, and offers a more reliable measure of generalization than a single train–test split.

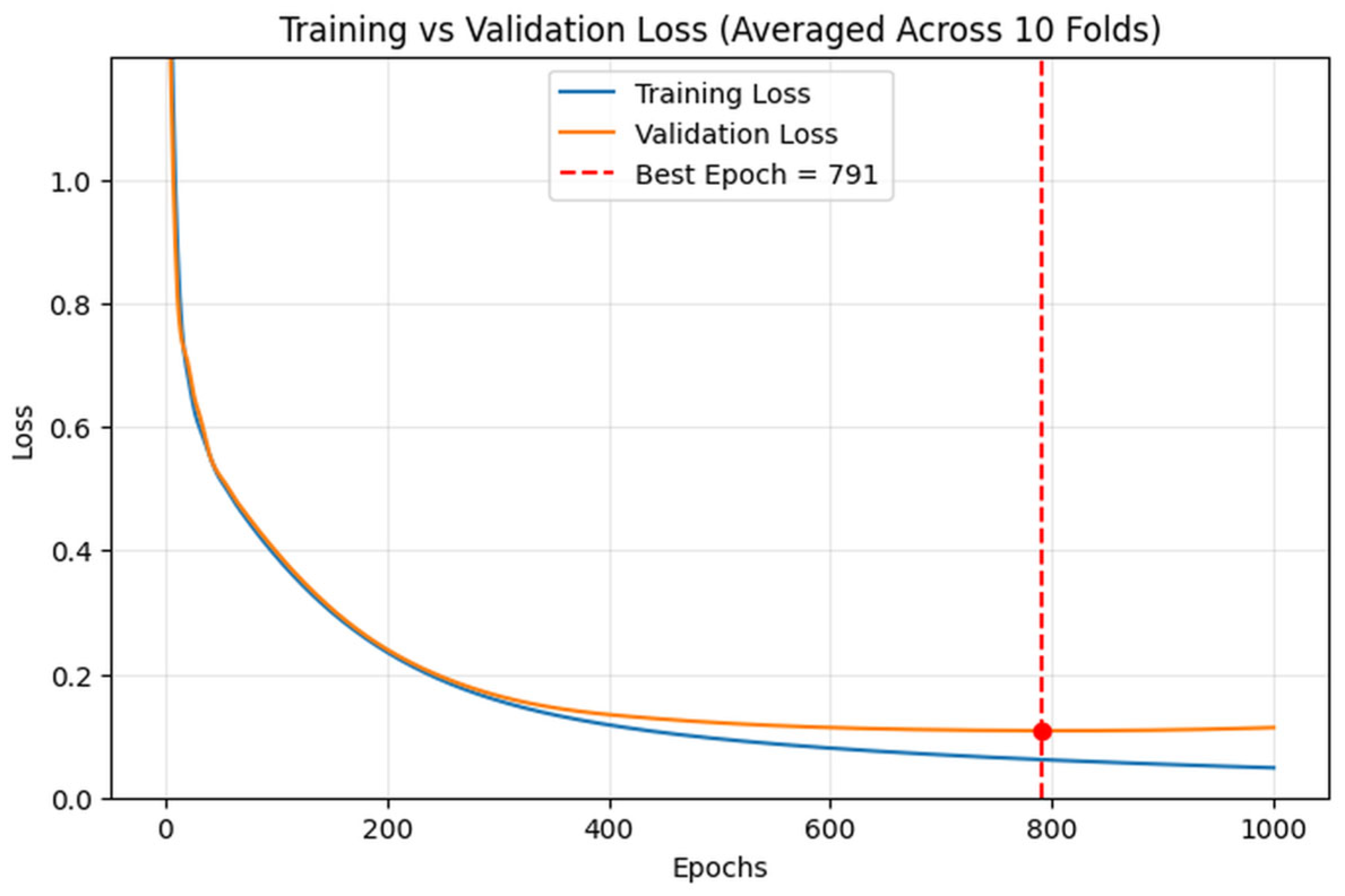
For each model, the number of training epochs was determined based on the average losses observed across the $k$ folds during training and validation. Following cross-validation, the model is retrained on the entire training set using the selected epoch value before being deployed on the held-out test data. For example, in the case of the LR-MLP model, we initialized the input layer of the MLP with pre-trained weights and biases from the LR model. To determine the best number of training epochs, we tracked the average loss across 10 folds during cross-validation. As illustrated in Figure 2, with a learning rate of 0.01, the validation loss stabilized and began to slowly increase around epoch 791, indicating the point where further training might lead to overfitting. Based on this observation, we retrained the MLP model on the full training dataset and stopped training after 791 epochs, thus ensuring strong generalization without overfitting. This data-driven approach helps align training duration with empirical performance trends, effectively mitigating both underfitting and overfitting.

4.3.4. Model Inference and Performance Evaluation

Following model training, evaluation was conducted on an unseen test set. To assess performance, inference metrics obtained from encrypted test samples were compared against those derived from the same dataset in plaintext, using the corresponding trained ML models.

4.4. Encryption Configuration

This section details the key parameters and configuration procedures for implementing CKKS homomorphic encryption in TenSEAL [31], as they play a critical role in ensuring both security and computational efficiency.

4.4.1. CKKS Parameters

The core parameters for configuring CKKS homomorphic encryption include the polynomial modulus degree, the coefficient modulus chain, and the scaling factor [36]. The polynomial modulus degree, which must be a power of two, is the degree of the cyclotomic polynomial. It directly impacts security level, ciphertext size, and computational throughput. The coefficient modulus chain consists of a sequence of prime moduli whose sizes define both the ciphertext size and the supported multiplicative depth; a larger total modulus improves depth but weakens security. Finally, the scaling factor controls how real numbers are encoded as integers prior to encryption and should be chosen based on the desired precision and the available coefficient modulus chain.

The selection of suitable CKKS parameters is a non-trivial task. We adopted an intuitive approach similar to that described in [37]. Specifically, we fixed the polynomial modulus degree at 8192, ensuring approximately 128 bits of security for homomorphic operations. This value also sets an upper limit on the total bit-length of the coefficient modulus chain. The required multiplicative depth determines the minimum number of primes in the chain. while the scale factor controls the precision of the fractional part of the encoded value. In TenSEAL, all middle values in the modulus chain should be equal to support ciphertext rescaling, and their bit-length typically matches the exponent of the scale factor. The first prime in the chain is often slightly larger to accommodate initial noise, while the difference between the first (and the last) prime and the middle ones influences the range of the integer part in the encoding. These parameters were carefully tuned to balance accuracy and efficiency, and remained consistent across models within each dataset. Furthermore, the coefficient modulus chain and the scaling factor were tailored to dataset characteristics such as size, feature count, and required multiplicative depth.

The CKKS parameter configurations used in our experiments are summarized in

Table 1. CKKS parameters configuration.

Polynomial Modulus Degree	Coefficient Modulus Chain	Scaling Factor
8192	31, 26, 26, 26, 26, 26, 26, 31	226

. In our experiment, the same parameters are used across different models and for both datasets (WBC and CHD), including a modulus chain of eight primes: two 31-bit primes at the ends and six 26-bit primes in the middle, and a global scaling factor of 2²⁶.

As discussed in Section 4.3.1, both LR and SVM models require a multiplicative depth of 1, while the MLP models require a depth of 3. To support all models, at least three middle primes (26-bit) are needed in the coefficient modulus chain. In our implementation, we opted for six middle primes to provide redundancy, as the client often lacks precise knowledge of the ML model and its multiplicative depth at the server side. To gain deeper insight into the implications of parameter selection, a detailed analysis of how different CKKS parameter configurations affect HE-based inference is provided in Section 5.5 of this paper.

4.4.2. CKKS Key Generation

Implementing the CKKS scheme requires several types of keys. First, encryption is performed using a public key, while decryption requires a corresponding secret key. To support efficient homomorphic operations, additional evaluation keys are generated. Specifically, relinearization keys are used to reduce ciphertext size after multiplications, preventing growth in ciphertext dimension and improving computational efficiency. Rescaling is applied after each multiplication to manage scale and control noise accumulation, ensuring numerical stability throughout the computation. Furthermore, Galois keys, explicitly generated via the generate_galois_keys() function in TenSEAL, enable advanced operations such as slot rotations and conjugations, which are essential for vectorized computations and batching in CKKS.

5. Results

This section evaluates the implemented ML models based on inference performed on the testing dataset, both with and without CKKS-based homomorphic encryption. The assessment includes a comparison of classification performance metrics and analysis of computational overhead introduced by encryption. Specifically, we measure the execution time difference between encrypted and plaintext inference, as well as the variation in data size between transmitted and received encrypted payloads. All experiments were conducted on Google Colab Pro using an NVIDIA A100 GPU.

5.1. Performance Evaluating Metrics

Classification performance was evaluated using standard metrics: accuracy, precision, recall, F1-score, and specificity [38]. Additionally, curve-based metrics were considered, including the Receiver Operating Characteristic (ROC) curve with corresponding Area Under the Curve (AUC), and the Precision-Recall (PR) curve with corresponding Average Precision (AP) [39]. These metrics were derived from the fundamental counts of True positive (TP), False positive (FP), False negative (FN), and True negative (TN). In this context, TP represents correctly identified disease cases, while TN denotes correctly classified healthy cases. Misclassifications are captured by FN, indicating disease cases incorrectly labeled as healthy, and FP, denoting healthy cases incorrectly labeled as diseased.

5.1.1. Accuracy

Accuracy measures the proportion of correctly classified instances among all samples and is defined as:

$$\mathrm{Accuracy} = {\displaystyle \frac{\mathrm{TP} + \mathrm{TN}}{\mathrm{TP} +\mathrm{TN} + \mathrm{FP} + \mathrm{FN}}}.$$

(8)

A higher accuracy generally indicates better overall model performance. However, in cases of class imbalance or small datasets, accuracy can be misleading; therefore, additional metrics should also be considered.

5.1.2. Precision

Precision represents the proportion of correctly predicted positive instances predicted as positive. It is mathematically defined as:

$$\mathrm{Precision} = {\displaystyle \frac{\mathrm{TP} }{\mathrm{TP} + \mathrm{FP} }}.$$

(9)

5.1.3. Recall

Recall, also referred to as sensitivity or the true positive rate, measures the proportion of actual positive instances that are correctly classified as positive. It is mathematically defined as:

$$\mathrm{Recall} = {\displaystyle \frac{\mathrm{TP} }{\mathrm{TP} + \mathrm{FN}}}.$$

(10)

Recall is highly critical in medical studies, as minimizing missed positive cases, reflected by a high recall, is often a key priority.

5.1.4. F1-Score

The F1-score is the harmonic mean of precision and recall, providing a single metric that balances both measures. It is particularly useful for evaluating models on imbalanced datasets, as it accounts for both false positives and false negatives. It is mathematically defined as:

$$\text{F1-Score} = 2 \times {\displaystyle \frac{\mathrm{Precision} \times \mathrm{Recall}}{\mathrm{Precision} + \mathrm{Recall}}}.$$

(11)

5.1.5. Specificity

Specificity, also known as the true negative rate, measures the proportion of actual negative instances that are correctly identified as negative by a model. It is mathematically defined as:

$$\mathrm{Specificity} = {\displaystyle \frac{\mathrm{TN}}{\mathrm{TN} + \mathrm{FP}}}.$$

(12)

5.1.6. ROC Curve and AUC

The ROC curve evaluates the discriminative ability of a classification model by plotting the true positive rate (sensitivity) against the false positive rate ($1-\mathrm{specificity}$) across varying decision thresholds. A curve along the diagonal line ($y=x$) indicates no discriminative power, whereas curves closer to the upper-left corner reflect better performance. AUC provides a single quantitative measure, where 0.5 corresponds to random guessing and 1.0 indicates perfect discrimination. ROC curves and AUC scores are generally effective for balanced datasets, as they consider both true positive and false positive rates across thresholds. However, in imbalanced datasets, ROC/AUC can be misleading because the false positive rate may appear due to the abundance of negative samples.

5.1.7. PR Curve and AP

The PR curve illustrates the trade-off between precision and recall across different decision thresholds. AP, defined as the area under the PR curve, summarizes this performance in a single value, with a higher AP indicating better detection of positive instances while minimizing false positives. PR curves and AP scores offer a more insightful evaluation in the context of imbalanced datasets, especially when positive instances are rare and of high importance. Unlike metrics that can be skewed by the abundance of negative samples, PR/AP focus on the model’s ability to accurately detect the minority class, emphasizing precision and recall without being diluted by the majority class.

5.2. Classification Performance Comparison

The impact of CKKS-based homomorphic encryption on model performance is presented in

Table 2. Performance comparison of models with and without CKKS for the WBC dataset.

Model	Test Dataset	Accuracy	Precision	Recall	F1-Score	Specificity
LR	Plaintext	0.9211	0.9231	0.8571	0.8889	0.9583
	Ciphertext	0.9211	0.9231	0.8571	0.8889	0.9583
SVM	Plaintext	0.9649	0.9750	0.9286	0.9512	0.9861
	Ciphertext	0.9649	0.9750	0.9286	0.9512	0.9861
MLP	Plaintext	0.9737	0.9535	0.9762	0.9647	0.9722
	Ciphertext	0.9737	0.9535	0.9762	0.9647	0.9722
LR-MLP	Plaintext	0.9825	0.9545	1.0000	0.9767	0.9722
	Ciphertext	0.9825	0.9545	1.0000	0.9767	0.9722
SVM-MLP	Plaintext	0.9825	0.9545	1.0000	0.9767	0.9722
	Ciphertext	0.9825	0.9545	1.0000	0.9767	0.9722

and

Table 3. Performance comparison of models with and without CKKS for the CHD dataset.

Model	Test Dataset	Accuracy	Precision	Recall	F1-Score	Specificity
LR	Plaintext	0.7883	0.8261	0.6786	0.7451	0.7768
	Ciphertext	0.7883	0.8261	0.6786	0.7451	0.7768
SVM	Plaintext	0.7667	0.7500	0.7500	0.7500	0.7812
	Ciphertext	0.7667	0.7500	0.7500	0.7500	0.7812
MLP	Plaintext	0.8167	0.8696	0.7143	0.7843	0.8103
	Ciphertext	0.8167	0.8696	0.7143	0.7843	0.8103
LR-MLP	Plaintext	0.8667	0.9545	0.7500	0.8400	0.9688
	Ciphertext	0.8667	0.9545	0.7500	0.8400	0.9688
SVM-MLP	Plaintext	0.8667	0.9545	0.7500	0.8400	0.9688
	Ciphertext	0.8667	0.9545	0.7500	0.8400	0.9688

for the WBC and CHD datasets, respectively. All models achieved strong results on plaintext data, with overall performance on the WBC dataset generally exceeding that on the CHD dataset. This aligns well with previously reported baseline results associated with the two datasets [28,29]. Notably, across both datasets, the proposed hybrid models (i.e., LR-MLP and SVM-MLP) consistently outperformed the traditional MLP model across both datasets. Remarkably, inference conducted on encrypted data using CKKS did not lead to any observable performance degradation for either the WBC or CHD datasets. This favorable outcome may be attributed to the careful configuration of the CKKS encryption parameters, which ensure that the noise introduced during encryption and computation remains sufficiently low. As a result, the models are able to maintain their predictive accuracy even when operating on encrypted inputs. However, it is important to note that this result may not generalize to other datasets or model architectures, particularly those that depend on more complex feature interactions or are more sensitive to the distortion introduced by approximate encryption.

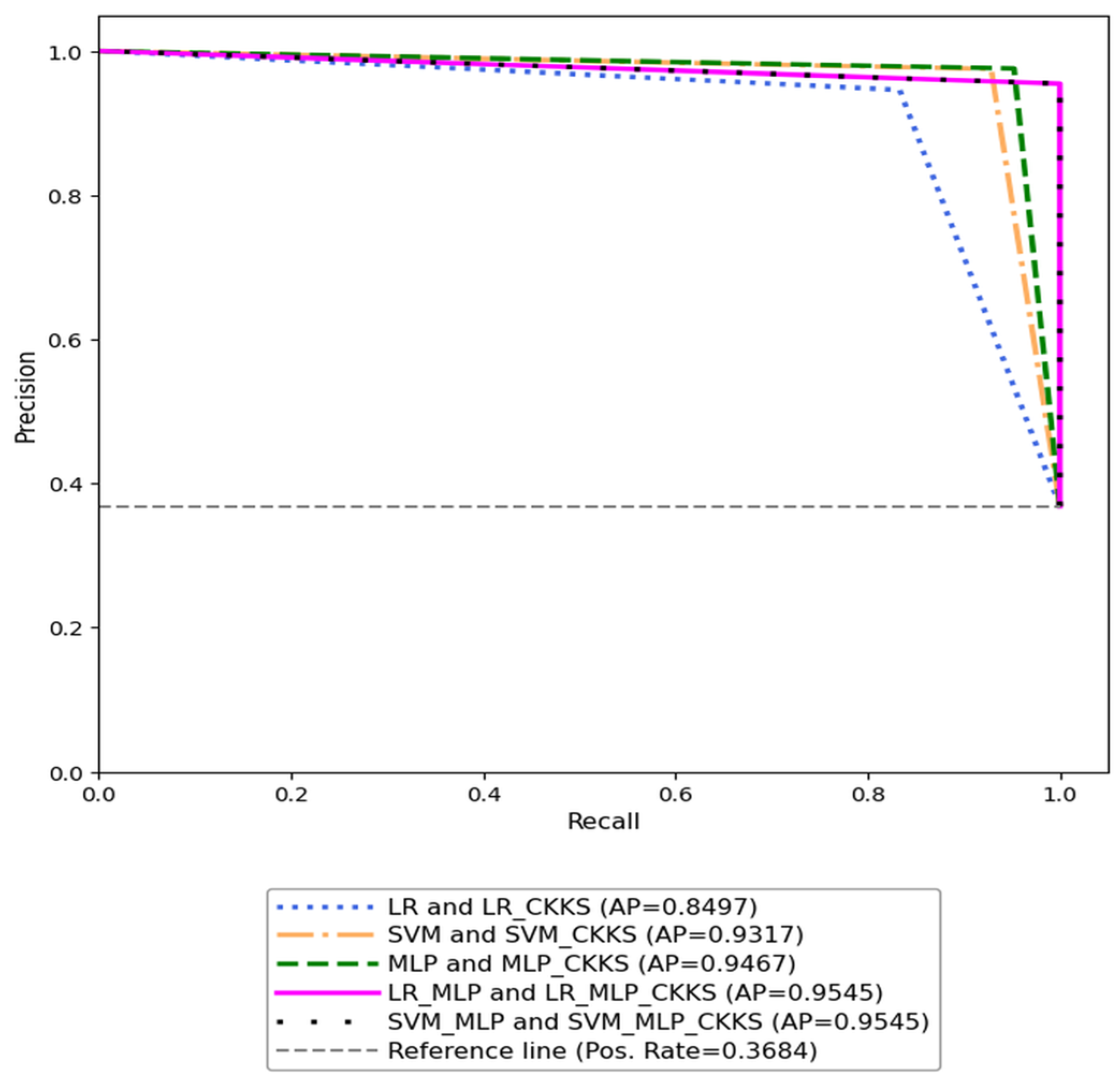
Given the moderate class imbalance in the WBC dataset, we also evaluated model performance using the PR curve, as shown in Figure 3. All curves are concentrated in the upper-right region, indicating strong model performance for both plaintext and encrypted test data, with consistently high recall. Consistent with the results presented in Table 2, the AP for encrypted inference matches that of plaintext inference for each ML model, demonstrating that CKKS-based encryption introduces negligible impact on model performance. Furthermore, the proposed hybrid models outperform traditional models, as evidenced by higher AP values.

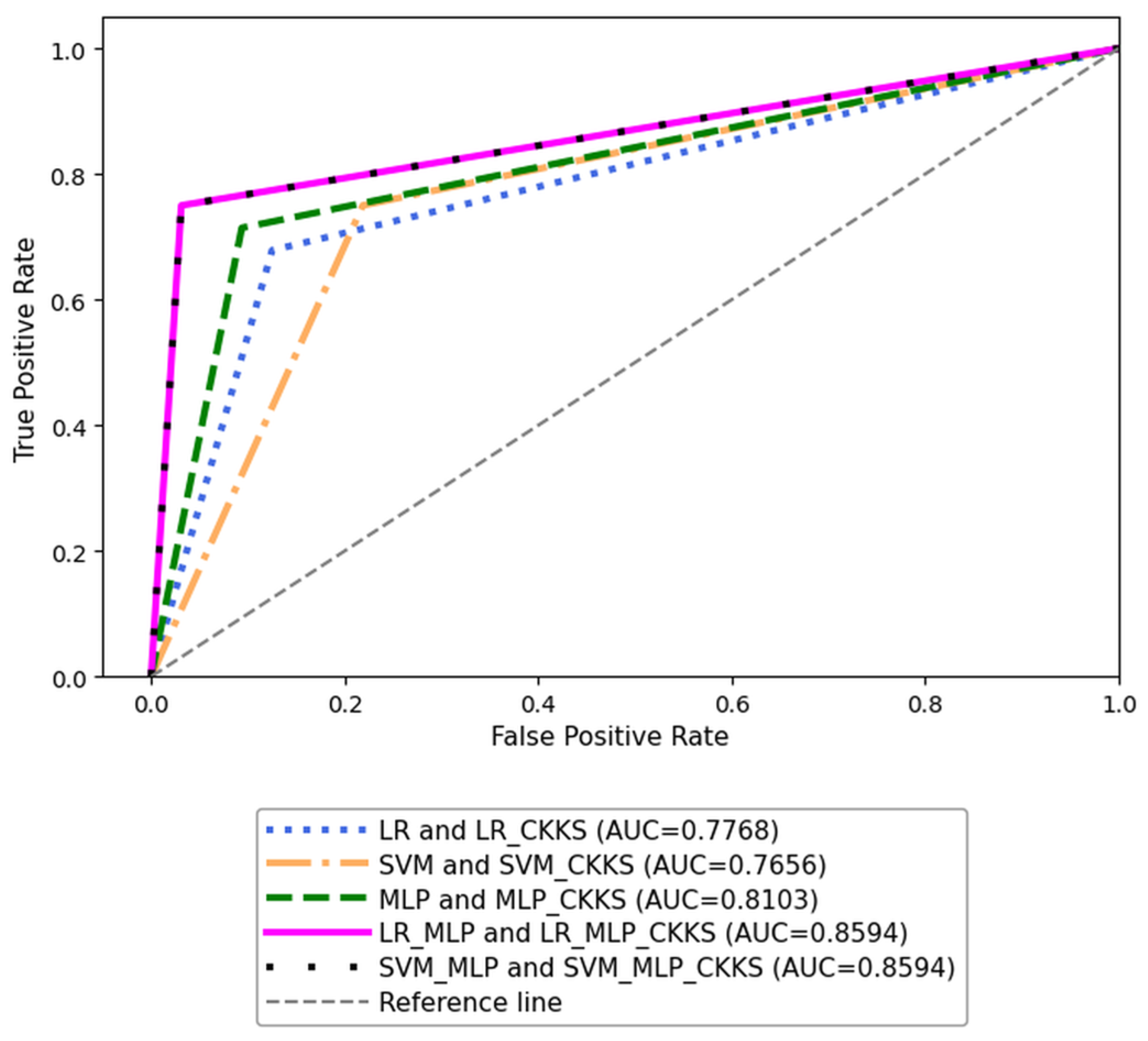
Since the CHD dataset is relatively balanced, model performance was evaluated using the ROC curve, as illustrated in Figure 4. Consistent with the results in Table 3, all models demonstrated strong performance on plaintext test data. Notably, encrypted inference showed no reduction in AUC, indicating that the CKKS encryption had minimal impact on predictive accuracy. Additionally, hybrid models consistently outperformed traditional models in both plaintext and encrypted scenarios, as evidenced by higher AUC values.

5.3. Inference Time Comparison

Inference execution time was compared between plaintext and encrypted scenarios, with results reported in

Table 4. Inference time comparison for the WBC dataset.

Model	Inference Time for Plaintext Test Dataset (s)	Inference Time for Encrypted Test Dataset (s)
LR	0.0002	15.60
SVM	0.0002	15.66
MLP	0.0005	280.22
LR-MLP	0.0012	279.81
SVM-MLP	0.0007	285.51

and

Table 5. Inference time comparison for the CHD dataset.

Model	Inference Time for Plaintext Test Dataset (s)	Inference Time for Encrypted Test Dataset (s)
LR	0.0003	4.71
SVM	0.0002	4.71
MLP	0.0005	65.62
LR-MLP	0.0006	66.28
SVM-MLP	0.0011	66.56

for the WBC and CHD datasets, respectively. As shown in the tables, the introduction of CKKS-based homomorphic encryption significantly increased computational time compared to plaintext inference, reflecting the substantial overhead associated with encrypted operations. This discrepancy underscores the tradeoff between privacy and computation efficiency.

This comparison is particularly relevant in medical applications. While HE enables secure inference without exposing sensitive data, it imposes a notable cost due to the complexity of encrypted arithmetic and data encoding. The results emphasize the need to balance security requirements with practical constraints on latency and resource usage, especially in time-sensitive clinical settings like diagnostics or emergency care.

From a deployment perspective, the findings suggest that HE-based solutions may be best suited for scenarios where data confidentiality is critical and latency tolerance is higher, such as batch processing or offline analysis. For real-time applications, hybrid approaches that combine HE with other PPML techniques, such as FL or SMPC, may offer a more practical balance between privacy and computational efficiency.

5.4. Data Size Overhead in Encrypted Transmission

CKKS-based encryption significantly increases the size of transmitted data.

Table 6. Data size comparison for the WBC dataset.

Model	Plaintext Sample Size (Bytes)	Encrypted Sample Size (Bytes)	Encrypted Prediction Size (Bytes)
LR		476,922	409,928
SVM		477,108	409,943
MLP	120	477,038	276,270
LR-MLP		477,128	276,311
SVM-MLP		477,037	276,446

and

Table 7. Data size comparison for the CHD dataset.

Model	Plaintext Sample Size (Bytes)	Encrypted Sample Size (Bytes)	Encrypted Prediction Size (Bytes)
LR		477,107	410,045
SVM		477,109	409,993
MLP	52	477,044	276,232
LR-MLP		477,296	276,390
SVM-MLP		477,004	276,237

report the plaintext sample size, the encrypted sample size sent from the client to the server, and the encrypted prediction size returned from the server back to the client for the WBC and CHD datasets, respectively.

Compared with plaintext inference, encrypted inference introduces a substantial increase in data size during both transmission phases: when the hospital sends the test dataset to the ML service provider and when it receives the encrypted predictions in return. The increased data size introduced by CKKS encryption has practical implications for deployment, including higher bandwidth usage, longer transmission times, and greater storage demands on both client and server sides. These overheads can be especially challenging in resource-constrained environments, such as rural healthcare facilities, mobile health applications, or edge devices with limited connectivity and computational capacity. In such settings, the communication and storage burden may hinder system responsiveness, scalability, and user experience.

To address these challenges, several strategies can be employed. Pre-encryption data compression can reduce the volume of information processed. Batching operations that pack multiple values into a single ciphertext can significantly lower the number of encrypted transmissions. Careful tuning of encryption parameter can help balance security, precision, and performance. In addition, selectively encrypting only sensitive fields while leaving non-sensitive components in plaintext can reduce the overall encryption footprint. When designing secure and scalable medical AI systems, it is crucial to carefully evaluate the trade-offs between privacy guarantees, system performance, and deployment constraints to ensure practical feasibility across diverse real-world settings.

5.5. Impact of CKKS Parameter Configurations

To better understand the impact of parameter selection, we explored how different CKKS configurations influence HE-based inference performance. Following the hybrid approach of intuitive and iterative testing described in Section 4.4.1, we evaluated several viable CKKS parameter sets. Due to space constraints, this paper includes results from six alternative configurations applied to the WBC dataset, primarily for illustrative purposes. These configurations are summarized in

Table 8. Various alternative CKKS parameter configurations tested.

Parameter Set	Polynomial Modulus Degree	Coefficient Modulus Chain	Scaling Factor
Base set	8192	31, 26, 26, 26, 26, 26, 26, 31	226
Alternative set 1	8192	31, 26, 26, 26, 26, 26, 31	226
Alternative set 2	8192	31, 26, 26, 26, 26, 31	226
Alternative set 3	8192	31, 26, 26, 26, 31	226
Alternative set 4	8192	31, 26, 26, 26, 26, 26, 26, 31	227
Alternative set 5	8192	31, 26, 26, 26, 26, 26, 26, 31	224
Alternative set 6	8192	31, 22, 22, 22, 22, 22, 22, 22, 31	222

, where the base set is identical to that in Table 1 and used as a reference.

In our implementation, all tested parameter sets are with the same polynomial modulus degree of 8192. At least three middle primes are required to support the multiplicative depths of all the ML models on the server side. Alternative sets 1 through 3 share the same scaling factor and coefficient modulus values, differing only in the number of middle primes in the modulus chain. Across these sets, inference performance, as measured by accuracy, precision, recall, F1-score, and specificity, remains consistent with the base configuration as shown in Table 2, achieving results comparable to plaintext inference. However, the computational overhead and data size introduced by CKKS encryption vary across these sets. As illustrated in

Table 9. Inference time and data size comparison with different CKKS parameters (WBC dataset).

Model	Parameter Set	Inference Time for Encrypted Test Dataset (s)	Encrypted Sample Size (Bytes)	Encrypted Prediction Size (Bytes)
LR	Base set	15.60	476,922	409,928
	Alternative set 1	11.84	409,624	343,372
	Alternative set 2	8.59	343,532	276,292
	Alternative set 3	5.88	276,395	209,971
SVM	Base set	15.66	477,108	409,943
	Alternative set 1	11.95	409,785	343,513
	Alternative set 2	8.63	343,532	276,153
	Alternative set 3	5.85	276,361	210,057
MLP	Base set	280.22	477,038	276,270
	Alternative set 1	213.50	410,056	209,925
	Alternative set 2	154.74	343,528	142,800
	Alternative set 3	104.53	276,661	70,386
LR-MLP	Base set	279.81	477,128	276,311
	Alternative set 1	212.53	409,835	209,930
	Alternative set 2	154.48	343,658	142,862
	Alternative set 3	104.87	276,425	70,475
SVM-MLP	Base set	285.51	477,037	276,446
	Alternative set 1	217.33	409,847	209,953
	Alternative set 2	157.10	343,532	142,927
	Alternative set 3	106.80	276,531	70,569

, reducing the length of the modulus chain generally leads to shorter inference times and smaller encrypted sample and prediction sizes, indicating lower computational time and memory demands. Nevertheless, this reduction may come at the cost of decreased noise tolerance and precision, limiting the ability to support deeper models and potentially affecting robustness in more complex scenarios.

Alternative sets 4 and 5 in Table 8 retain the same modulus chain as the base configuration but vary the scaling factor. In contrast, alternative set 6 introduces additional redundancy by extending the modulus chain to support deeper multiplicative depths, while using smaller primes and a reduced scale factor. As shown in

Table 10. Performance comparison with different CKKS parameters (WBC dataset).

Model	Parameter Set	Accuracy	Precision	Recall	F1-Score	Specificity
LR	Base set	0.9211	0.9231	0.8571	0.8889	0.9583
	Alternative set 4	0.9123	0.9000	0.8571	0.8780	0.9444
	Alternative set 5	0.8860	0.9677	0.7143	0.8219	0.9861
	Alternative set 6	0.8246	0.9583	0.5476	0.6970	0.9861
SVM	Base set	0.9649	0.9750	0.9286	0.9512	0.9861
	Alternative set 4	0.9649	0.9750	0.9286	0.9512	0.9861
	Alternative set 5	0.8860	1.0000	0.6905	0.8169	1.0000
	Alternative set 6	0.8596	1.0000	0.6190	0.7647	1.0000
MLP	Base set	0.9737	0.9535	0.9762	0.9647	0.9722
	Alternative set 4	0.9561	0.9512	0.9286	0.9398	0.9722
	Alternative set 5	0.6842	1.0000	0.1429	0.2500	1.0000
	Alternative set 6	0.3509	0.2949	0.5476	0.3833	0.2361
LR-MLP	Base set	0.9825	0.9545	1.0000	0.9767	0.9722
	Alternative set 4	0.8947	0.8125	0.9286	0.8667	0.8750
	Alternative set 5	0.7895	1.0000	0.4286	0.6000	1.0000
	Alternative set 6	0.1842	0.1507	0.2619	0.1913	0.1389
SVM-MLP	Base set	0.9825	0.9545	1.0000	0.9767	0.9722
	Alternative set 4	0.9298	0.8542	0.9762	0.9111	0.9028
	Alternative set 5	0.6404	1.0000	0.0238	0.0465	1.0000
	Alternative set 6	0.1667	0.1159	0.1905	0.1441	0.1528

, these alternative configurations lead to reduced inference performance compared with the base set. The performance degradation is especially noticeable for alternative sets 5 and 6, and is more severe in MLP-based models, which require deeper multiplicative depth than LR and SVM. This highlights that accuracy comparable to plaintext inference is not always guaranteed when using CKKS encryption; careful tuning of CKKS parameters is essential to preserve model performance.

6. Conclusions and Future Work

This research study focused on secure classification of medical tabular data using the CKKS HE schemes to enable privacy-preserving yet effective disease prediction. We evaluated three traditional models (LR, SVM, and MLP) alongside two hybrid models (LR-MLP and SVM-MLP), which combine the interpretability of linear models with the feature learning capabilities of MLP in an encrypted setting.

The findings of our research study are summarized below:

• The hybrid models (LR-MLP and SVM-MLP) consistently outperformed the traditional models (LR, SVM, and MLP) in both plaintext and encrypted inference scenarios.
• By carefully configuring the parameters of the CKKS encryption scheme, it is possible to ensure that the noise introduced during encryption remains sufficiently low, allowing decrypted predictions to achieve accuracy comparable to that obtained from plaintext inputs. However, suboptimal parameter choices can significantly compromise classification performance.
• Introducing CKKS encryption significantly increased computational time, particularly for MLP-based models. Encrypted inference also led to a substantial increase in sample size due to ciphertext expansion. These performance impacts are closely tied to the configuration of CKKS parameters.

In conclusion, hybrid models demonstrated superior classification performance under both plaintext and encrypted conditions. While CKKS-based privacy preservation incurs additional computational and memory costs, the trade-off is justified by the enhanced data confidentiality and maintained predictive accuracy.

This study has several limitations.

• First, the evaluation was conducted on relatively small medical tabular datasets with fractional feature values, which may not fully capture the complexity and variability of real-world healthcare data. Consequently, the generalizability of the findings to larger, high-dimensional datasets remains uncertain.
• Second, model performance may be influenced by dataset characteristics. For example, it has been pointed out that neural networks often perform better on datasets with more regular and continuous features, whereas gradient-boosted decision trees typically excel on irregular or heterogeneous datasets and tend to scale better with larger data volumes [18]. Future work should address these limitations by including larger and more diverse datasets, exploring additional model architectures, and employing advanced validation techniques to strengthen the reliability and applicability of the proposed framework.
• Third, model validation relied on k-fold random cross-validation. While this method is effective for small datasets, it may not account for all sources of variability. Incorporating independent validation sets or employing more robust strategies such as nested cross-validation [40] could enhance the reliability of performance assessments.
• Additionally, the selection of CKKS encryption parameters in our work was guided by a combination of intuitive reasoning and iterative trial-and-error experimentation. This hybrid process is critical, as CKKS configuration directly influences the security level, noise tolerance, and computational efficiency of HE-enabled ML systems. While manual tuning can yield acceptable results, it remains time-consuming and lacks systematic guidance. To better understand the implications of parameter choice, we also investigated the influence of CKKS parameter configurations on inference performance. Our findings highlight the importance of careful parameter selection, as suboptimal configurations can significantly degrade classification accuracy. To streamline broader adoption and improve reproducibility, it is essential to develop more specific guidelines and automated methods for configuring CKKS parameters based on the characteristics of the ML models and input datasets.

Recent advances in HE have expanded beyond inference to enable privacy-preserving model training across diverse ML paradigms. For example, researchers have introduced an accelerated gradient method to reduce the number of iterations and overall computational cost [41] and developed parallelized packing strategies to mitigate the overhead of expensive HE operations [42,43]. Innovative techniques have also been introduced to support fully homomorphic training and inference on decision tree models [23,24]. Beyond individual models, integrated frameworks that support both encrypted training and inference are emerging, aiming to deliver end-to-end privacy guarantees in collaborative and cloud-based environments. To make HE-based training practical for large-scale, real-world applications, future work should focus on improving scalability, supporting heterogeneous model architectures, and optimizing parameter selection.

Another promising research direction is the development of advanced privacy-preserving strategies to reduce the computational and communication overhead of HE schemes at the client site. Hybrid HE schemes (e.g., in [44]) combine symmetric cryptography with HE to significantly lower encryption costs and data transfer overhead while maintaining strong security guarantees. These approaches are particularly relevant for resource-constrained and real-time environments. Similarly, privacy-preserving transfer learning (e.g., [45]) enables encrypted fine-tuning of pre-trained models, reducing training time and improving adaptability. Integrating these techniques into unified frameworks that support both encrypted training and inference could provide comprehensive privacy protection while enhancing efficiency and scalability.