Abstract
This paper presents a robust and reliable voltage regulation method in DC–DC converters, for which a multiloop control strategy is developed and analyzed for a boost converter. The proposed control scheme consists of an inner current loop and an outer voltage loop, both systematically designed using the control Lyapunov function (CLF) methodology. The main contributions of this work are (1) the formulation of a control structure capable of maintaining performance under variations in load, reference voltage, and input voltage; (2) the theoretical demonstration of global asymptotic stability of the closed-loop system in the Lyapunov sense; and (3) the experimental validation of the proposed controller on a physical DC–DC boost converter, confirming its effectiveness. The results support the advancement of high-efficiency nonlinear control methods for power electronics applications. Furthermore, the experimental findings reinforce the practical relevance and real-world applicability of the proposed approach.
1. Introduction
The design of robust controllers for DC–DC boost converters remains a fundamental challenge in power electronics, particularly in applications requiring precise voltage regulation under dynamic and uncertain conditions, such as photovoltaic systems, energy storage, and electric mobility. The inherent nonlinear dynamics of the boost converter, combined with external disturbances such as load or input voltage variations, complicate the tuning of nonlinear controllers. This highlights the need for advanced control strategies that guarantee global stability, fast transient response, and robustness against disturbances.
The main objective of this research is to design, analyze, and experimentally validate a nonlinear multiloop control strategy based on CLFs for a DC–DC Boost converter. The proposed controller aims to ensure global asymptotic stability, robust performance under parameter variations, and accurate voltage regulation in the presence of load and input disturbances.
The novelty of this work lies in the formal hierarchical construction of two structurally coupled Lyapunov functions, each governing one of the control loops—current and voltage—within a unified stability framework. Unlike traditional cascaded or PI/PID-based designs, this approach establishes a mathematically consistent interaction between loops, where the stabilized current dynamics act as a virtual control input for the voltage regulation stage. Additionally, the inclusion of integral error variables in both extended state representations enables zero steady-state error and enhances disturbance rejection capabilities, while maintaining smooth and continuous control action through hyperbolic functions. Finally, the experimental validation on a physical Boost converter prototype confirms the feasibility and robustness of the proposed method, demonstrating stable and efficient operation under real-world dynamic conditions. This combination of formal stability guarantees and experimental verification differentiates the present study from previous works that remain limited to simulation-level implementations or single-loop Lyapunov control designs.
Among the available nonlinear control methodologies, several strategies—such as sliding-mode control, backstepping, and passivity-based control (PBC)—have been widely applied to DC–DC converters. Each presents particular advantages but also inherent limitations. Sliding-mode control provides strong robustness but suffers from chattering and discontinuous actuation. Backstepping offers recursive stability design but often involves complex algebraic expressions and is sensitive to parameter uncertainties. Passivity-based control ensures energy consistency but typically requires explicit knowledge of the system’s storage function, which may not be straightforward to derive for all converter topologies. In contrast, the CLF framework combines the rigor of Lyapunov stability theory with a constructive synthesis procedure, enabling the direct design of control laws that ensure global asymptotic stability. CLFs allow the systematic inclusion of integral error variables, active compensation of disturbances, and smooth control action without discontinuities, thus offering a balanced trade-off between robustness, simplicity, and theoretical formalism. These properties make the CLF-based approach particularly suitable for high-performance power conversion systems, where both stability guarantees and practical implementability are critical requirements.
In recent years, various nonlinear control methodologies have been proposed for DC–DC converter topologies such as Boost, Buck, and Buck-Boost, aiming to improve robustness and dynamic performance. For instance, Lyapunov-based adaptive sliding mode control has been employed to achieve disturbance rejection and chattering mitigation in Boost converters [1]. Composite nonlinear feedback control schemes have also been explored to enhance transient response and minimize overshoot without increasing system complexity [2]. Similarly, improved passivity-based controllers and disturbance observers have been designed to handle constant power loads and input voltage variations in DC–DC converters [3].
Other researchers have focused on energy-based nonlinear frameworks, such as the port-Hamiltonian and passivity-based formulations [4], and on control laws with inherent current limiting that maintain safe operating conditions under high dynamic stress [5]. Recent developments also include nonlinear cascaded control structures that integrate current and voltage loops under a unified design framework [6], and Lyapunov-function-based designs that ensure smooth control actions without discontinuities [7].
Despite these advances, most existing approaches rely on local linearization, switching logic, or discontinuous control laws, and therefore do not guarantee global asymptotic stability. In contrast, the methodology proposed in this work introduces a formally structured Lyapunov-based multiloop controller that ensures global stability, smooth dynamics, and robust performance under real operating conditions while maintaining experimental feasibility.
In [8], a CLF-based multiloop control strategy is proposed for a boost converter under simulation conditions, in which both the inner current loop and the outer voltage loop are designed. The proposed approach demonstrates stability, with future work focused on analyzing the conditions required to guarantee global asymptotic stability and validation of the method through experimental tests. In a follow-up study [9], the same authors delve deeper into the design of the inner current loop using CLF theory, developing an extended system representation and demonstrating its effectiveness under perturbations, thereby reinforcing the applicability of the proposed approach. Separately, ref. [10] addresses the stabilization of boost converters under constant power load (CPL) conditions, a highly unstable operating scenario. The proposed nonlinear controller is based on a gain-scheduling strategy that dynamically adjusts the duty cycle according to the output voltage, ensuring stability in both continuous and discontinuous conduction modes. Complementarily, ref. [11] proposes an improved Lyapunov-based switching scheme for converters with LC input filters, aiming to mitigate instabilities caused by reactive coupling. From a more classical design perspective, the authors in [12] propose a Lyapunov-based controller for boost converters with resistive loads, demonstrating stability under nominal conditions. In a broader context, the article [13] develops a family of Lyapunov-based control schemes for buck converters in maximum power point tracking (MPPT) applications, with convergence to the desired operating point guaranteed. Likewise, ref. [14] integrates Lyapunov control with backstepping and sliding mode techniques into a robust hybrid scheme, applied to boost converters under constant power load conditions.
Despite recent advances, several common limitations can be identified in the literature: (i) many studies focus solely on a single control loop, lacking a structured integration between the voltage and current loops; (ii) extended system representations that incorporate integral error variables are generally not included; (iii) external disturbances are often assumed to be negligible or constant, without explicit active compensation mechanisms; and (iv) in several cases, experimental validation is limited or performed under non-demanding scenarios.
In response to this situation, the present paper proposes a fully structured nonlinear multiloop control architecture based on Control Lyapunov Functions (CLFs), which addresses the previously identified limitations. The proposed methodology is based on:
- An extended system representation that includes integral errors in both the current and voltage control loops, achieved by hierarchically designing both CLFs under a common stability framework, where the inner current loop dynamics explicitly define the virtual control input of the outer voltage loop, ensuring coherent and stable interaction between both subsystems;
- A hierarchical control design, in which each loop (current and voltage) is governed by its own CLF and associated control law;
- A nonlinear control law with explicit compensation for external disturbances;
- A rigorous experimental validation conducted under realistic conditions, including variations in load, input voltage, and reference voltage.
Overall, the proposed approach constitutes an integral, robust, and formally stable solution, oriented toward real-world applications where control reliability is a critical requirement.
2. Nonlinear Averaged Model of the DC-DC Boost Converter
The design of the proposed multiloop controller, based on CLFs, begins with the formulation of the dynamic model of the boost converter using a nonlinear averaged approach. This modeling strategy allows for the description of the system’s continuous-time behavior through differential equations, which is essential for subsequent stability analysis and systematic controller synthesis [15,16].
The boost converter (Figure 1) is a widely used topology in DC–DC conversion applications, designed to raise the output voltage above the input voltage . The energy conversion process is carried out by temporarily storing energy in an inductor L, and then transferring it through a diode D, a controlled switch S (typically a MOSFET), and an output capacitor C, which is connected in parallel to the load .
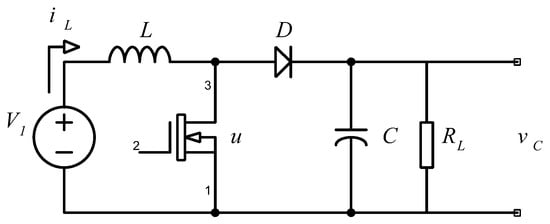
Figure 1.
DC–DC Boost Converter.
The system dynamics are directly governed by the switching cycle of the transistor, which is modeled using the average duty cycle , under the assumption of continuous conduction mode (CCM). This averaged model is well suited for the design of continuous control laws, providing an effective representation of system trajectories and their response to disturbances [17,18].
The derivation of the averaged model is based on the analysis of the converter’s behavior in its two fundamental modes of operation (Figure 2): when the switch is closed (active mode) and when it is open (passive mode). Assuming a sufficiently high switching frequency such that the state variables change slowly relative to the switching period, the time-averaging technique is applied over one switching cycle , yielding a continuous-time model [19]. The state variables chosen for the modeling are the average inductor current and the average capacitor voltage . Under these assumptions, the nonlinear averaged model of the boost converter is expressed as:
where d is the averaged duty cycle, L is the inductance, C is the output capacitance, R is the equivalent load resistance, and is the input voltage source. These equations describe a nonlinear dynamic system, whose structure motivates the use of nonlinear control strategies such as those based on Lyapunov functions [20,21].
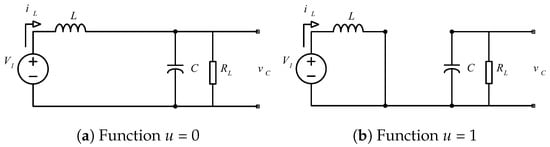
Figure 2.
Operating modes of the proposed converter.
3. Control Design Based on Control Lyapunov Functions
Historically, the theory developed by Lyapunov was originally applied exclusively to the stability analysis of dynamical systems without external inputs, i.e., autonomous systems. However, when considering systems with control variables, a generalization arises, known as Control Lyapunov Functions (CLFs), which not only preserve the analytical value of traditional Lyapunov functions, but also enable a constructive framework for controller design.
A CLF is characterized by admitting a negative time derivative through the appropriate application of a control input, thereby ensuring asymptotic stability. Under certain conditions, the existence of a CLF implies the possibility of designing a stabilizing controller, making it a necessary and sufficient condition for the stabilization of nominal models [22,23,24].
This section describes the control strategy developed to regulate the dynamic behavior of a DC–DC boost converter. The proposed method is based on the nonlinear averaged model of the system and adopts a hierarchical control architecture composed of two coupled loops: an inner loop that regulates the inductor current and an outer loop that controls the output voltage. Both loops are designed within the CLF framework, allowing formal stability conditions to be established. Figure 3 illustrates the general structure of the proposed CLF-based control scheme, where the block represents the normalization (linear model) for the discretization stage required to implement the continuous control law in a pulse-width modulation (PWM)-based converter. The control signal generated by the Lyapunov-based design (CLF), originally defined in a continuous domain, must be converted into a dimensionless reference that can be compared with a periodic sawtooth carrier of amplitude used in the PWM generator. By dividing the control signal by , a normalized duty cycle in the range is obtained, enabling its direct implementation through discrete switching of the power switch. This procedure ensures a structured correspondence between the theoretical control law and its physical execution in the converter.
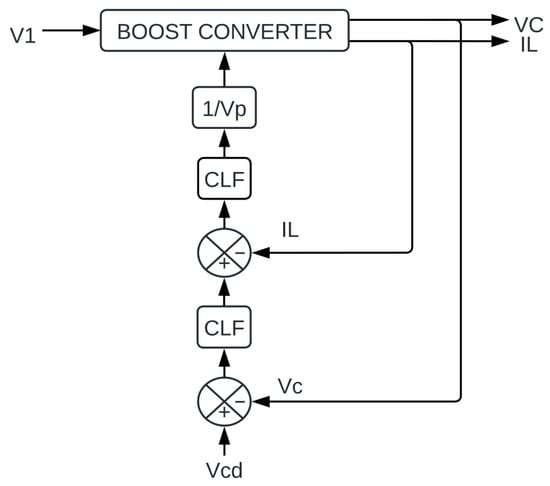
Figure 3.
Proposed CLF-based control scheme.
The development of the proposed controller conceptually builds upon the general framework presented in [25], where a universal method is introduced for constructing CLFs for nonlinear systems in affine form through a structured transformation of the system into a set of auxiliary coordinates. In that work, the authors establish conditions under which it is possible to design a quadratic CLF in the transformed variables using auxiliary functions, thus enabling the derivation of stabilizing control laws.
In this study, the theoretical framework is extended to a real and highly nonlinear physical system: the DC–DC boost converter, whose dynamics do not conform to the triangular structure assumed in [25]. The main contribution lies in the hierarchical design of a multilayer controller, where two independent Lyapunov functions are constructed: one for the inner current loop and another for the outer voltage loop. Each function is tailored to the specific dynamics of its corresponding subsystem, incorporating an extended representation with integral errors, and implementing explicit disturbance compensation. This results in a structured, practical, and robust solution for the design of CLF-based controllers in power electronic systems.
The control strategy developed in this section constitutes the foundation of the experimental case study presented in Part 5, where the proposed CLF-based controller is implemented on a physical Boost converter prototype to verify its stability, robustness, and practical feasibility under real operating conditions.
3.1. CLF-Based Inner Current Loop Control
In the design of the inner current loop (Figure 4) of the boost converter using the CLF technique, the process begins with a structured formulation of the system that enables the definition of a control law ensuring the stability of the current error. This section develops the formulation step by step, starting from the definition of the current error, followed by the extension of the system, and concluding with its rewriting into an affine-in-input form suitable for the application of the CLF framework.
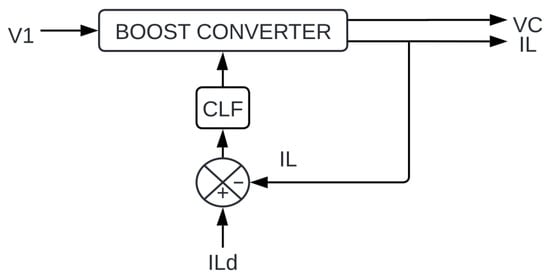
Figure 4.
Current control loop design using control Lyapunov functions.
The objective of the inner loop is to ensure that the inductor current tracks a desired trajectory , which is dynamically provided by the outer voltage loop. To this end, the current error is defined as:
This error is the stabilization target for the inner loop, such that when , the actual current accurately follows the reference generated by the outer controller. For regulation tasks, the desired current is considered constant, yielding the time derivative of the current error as:
Using the averaged model from Equation (1), the error dynamics are given by:
To improve disturbance rejection capabilities against constant perturbations and ensure zero steady-state error, an additional variable is introduced to represent the integral of the current error:
Redefining the states of the extended system as:
the system dynamics can be expressed as:
Equation (8) can be rewritten in affine state-space form as:
In this formulation, the presence of exogenous disturbances is evident, represented by the term:
This term does not depend on the state , nor is it multiplied by the control input d. Therefore, it cannot be absorbed into either or , which prevents the direct application of structured methods such as Control Lyapunov Function (CLF)-based design. To eliminate the disturbance and transform the system into a structured form, an auxiliary input is introduced, defined as:
Solving Equation (11) for d and substituting the result into the representation provided in (9), we obtain
which leads to the following reformulated dynamic system:
This restructuring is fundamental for the application of the CLF framework, as it allows for the construction of quadratic Lyapunov functions over the extended state space x and the design of nonlinear control laws that guarantee global asymptotic or uniformly global stability in the presence of structured disturbances and integral-augmented states.
With the extended current loop system formulated in coordinates , a coordinate transformation is introduced with the objective of structuring a Lyapunov function suitable for the design of a stabilizing control law. The transformed state vector is defined through the following nonlinear relation:
where is a scalar design function, possibly dependent on the current tracking error. This transformation can be expressed in matrix form as:
The inverse transformation is given by:
By substituting (16) this relation into the extended state-space dynamics (13)
and noting that , , we obtain:
Finally, the following quadratic Lyapunov function is proposed over the transformed state space:
which is positive definite and suitable for the stability analysis of the transformed system. Substituting the definitions of and in terms of the physical variables, we obtain
This function is positive definite, continuous, and differentiable, and it is therefore valid as a CLF. Its structured time derivative will be used in the next step to design a nonlinear control law that stabilizes the system.
To ensure global asymptotic stability of the system, it must hold that
where . Therefore, it is necessary to compute . To do so, we start from the relation (15)
The total derivative is:
After algebraic manipulations, we obtain the equivalent form:
where
Recalling that the extended system dynamics in the coordinates is given by:
and substituting this into the expression for , we obtain:
Evaluating the matrix product:
Now, the state vector is expressed in terms of using the inverse transformation:
Substituting (29) into Equation (28), the system dynamics in transformed coordinates are obtained:
The matrix A characterizes the autonomous dynamics of the transformed system, i.e., the evolution of the system in the absence of control input (). The time derivative of the CLF (19), along with Equation (29), after further algebraic manipulations, results in
and when developed in terms of the analyzed system, becomes
where, recalling, .
The development carried out in this step has allowed the transformation of the inner current-loop dynamics of the boost converter into a system expressed in coordinates , which possesses structural properties desirable for nonlinear design based on Lyapunov functions. The next step will focus on computing , analyzing its structure, and designing a control law that ensures the asymptotic convergence of the system to the origin. can be reconfigured (through the appropriate selection of certain terms) so that it is guaranteed to be negative definite, thereby achieving the global asymptotic stability of the closed-loop system. The analysis of the aforementioned aspects is carried out from this point onward. Note that the first term of (the autonomous term),
depends exclusively on the system states and the design parameters and . The structural effect of setting the function as a globally negative constant is examined, namely:
This choice offers the advantage of significantly simplifying the dynamic structure of the system in the transformed coordinates. However, it is essential to rigorously evaluate whether, under this choice, the autonomous term in the Lyapunov function derivative guarantees passive stability of the system; that is, whether it contributes negatively to energy dissipation. Under the assumption that is a negative constant (), we obtain:
thus, the matrix M takes the explicit form:
Since M is symmetric, its definiteness can be characterized by the signs of its eigenvalues. Two fundamental spectral properties are considered:
- Trace:which implies that the sum of the eigenvalues is zero. Therefore, if one eigenvalue is positive, the other must be negative.
- Determinant:This expression is strictly negative for all , as it consists of negative-definite terms and a negative constant.
From these results, it follows that the matrix M always has two real eigenvalues of opposite sign. Thus, M is indefinite for all real values of k and, consequently, it cannot be negative definite or negative semidefinite.
Therefore, the matrix M cannot be negative definite, as it has at least one positive eigenvalue. The immediate consequence of this result is that the system in transformed coordinates does not exhibit total autonomous dissipation. That is, the derivative of the Lyapunov function may become positive in certain directions of the state space, in the absence of control input. This implies that:
- Stability and convergence cannot be guaranteed without active control input.
- The autonomous term alone cannot ensure equilibrium stability.
- Global asymptotic stability can only be achieved through appropriate design of the control input .
Now, based on Equation (32), considering the control term
and selecting
the derivative of the Lyapunov function becomes
This design provides effective dissipation when is large (since ), but near the origin, the dissipation degrades to a quadratic term:
which may be insufficient to counterbalance the possible growth of the autonomous term , which can be positive. To address this issue, a double-dissipation control law is proposed:
where:
- : saturated damping coefficient,
- : gain of the hyperbolic core,
- : additional linear gain.
With this modification, the derivative of the Lyapunov function becomes:
The dissipation term now contains two components:
- : Effective dissipation when is large (saturation regime).
- : Strictly positive dissipation over the entire domain, including near the equilibrium.
This structure guarantees that, for any , the total term
can be selected sufficiently large to dominate the autonomous term , which is continuous and bounded.
Recalling that:
where is the current tracking error and its integral, the explicit control law becomes:
This form is directly implementable, continuous, and guarantees for all , thus fulfilling the conditions of LaSalle’s Invariance Principle.
In the initial analysis of the extended state-space model, it was observed that the current error dynamics exhibited a term that could not be embedded into a standard affine control form. To apply the CLF-based design, the system must be expressed in affine form. To achieve this, the control input u is redefined as:
Having previously designed a Lyapunov-based control law with enhanced dissipation, the complete control input to be applied to the physical system becomes:
This additional term ensures that the Lyapunov-based analysis remains consistent with the actual system dynamics. Omitting it would imply applying a control law derived from a model that does not accurately represent the physical plant, thereby undermining the global asymptotic stability guarantees previously established.
3.2. CLF-Based Control of the Outer Voltage Loop
The design of the outer control loop (Figure 5) aims to regulate the output voltage of the boost converter to a desired reference level . Unlike the inner loop, which rapidly affects the inductor dynamics, the outer loop operates over a slower timescale, associated with the output capacitor and the load.
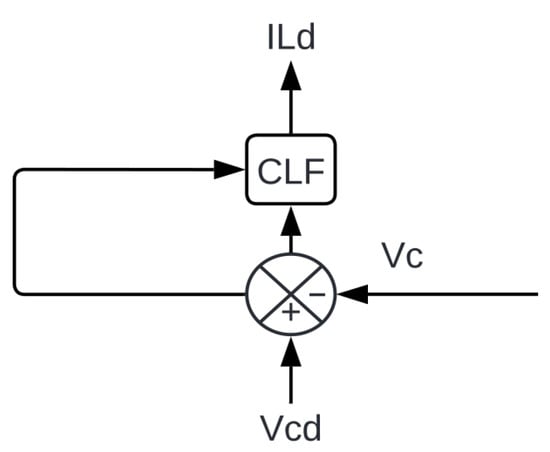
Figure 5.
Voltage control loop based on CLF.
First, the voltage error is defined as:
where denotes the desired reference voltage across the output capacitor, and is the actual system voltage. Under the common control assumption that the reference is either constant or slowly varying, we assume . Accordingly, the error dynamics become:
and therefore, the voltage error dynamics can be expressed as:
where denotes the averaged control signal representing the switch conduction duty cycle. It is important to recall that the signal d is no longer a free input but has been determined by the controller designed in the previous section to stabilize the inner current loop. The control law implemented in the current loop is:
Assuming that the inner loop is well-tuned and sufficiently fast, one can consider and , which simplifies to:
Substituting into the voltage error dynamics:
yields the final expression:
The resulting equation clearly highlights the contribution of each physical component to the evolution of the voltage error :
- The term accounts for the resistive dissipation through the load.
- The term reflects the capacitor discharge due to conduction.
- The term represents energy transfer from the input source to the capacitor, modulated by the action of the inner current loop.
- The outer voltage loop generates the reference current .
- The inner current loop ensures that .
Given the above, if the inner loop is sufficiently fast, it can be assumed that
and substituting this into the voltage error dynamics yields:
Defining the system states as and , the state-space representation becomes:
This form is affine in but contains an autonomous perturbation . To compensate for this term, the following control law is proposed:
which, when substituted into the state-space model, yields:
This representation is ideal for designing an external control law based on Lyapunov functions, as it is affine in control and free from structural perturbations. To proceed, a transformation vector is defined to construct a Lyapunov function suitable for stabilizing control design. The transformed state vector is defined as:
where is a design scalar function that may depend on the voltage error. This transformation can be written in matrix form as:
The inverse transformation is given by:
Substituting into the extended state-space representation yields:
The following quadratic Lyapunov function is proposed:
By substituting the definitions of and in terms of physical variables:
we obtain:
This function is positive definite, continuous, and differentiable, and it is thus valid as a Control Lyapunov Function (CLF). Its structured derivative will be used in the next step to design the nonlinear control law that stabilizes the system.
To ensure the global asymptotic stability of the system, it is required that:
where ; hence, it is necessary to obtain . To do so, we start from the relation:
The total derivative is:
After algebraic manipulations, we arrive at:
where
Recall that the extended system dynamics are:
substituting into , we obtain:
Evaluating:
Now, expressing in terms of :
We finally obtain:
The derivative of the Control Lyapunov Function, after algebraic manipulations, is given by:
Expanding the expression explicitly in terms of the components yields:
where, recall, .
Note that the first term in (the autonomous term):
depends exclusively on the system states and on the design terms and . We analyze the structural effect of fixing the function as a globally negative constant, i.e.,
Under this hypothesis, where , it follows that:
Therefore, the matrix M takes the explicit form:
For the autonomous term to be strictly negative definite, the matrix M must satisfy two simultaneous conditions:
- Negative trace:
- Positive determinant:
It is evident that for any , the determinant of M is strictly negative:
Therefore, matrix M cannot be negative definite, as it has at least one positive eigenvalue. As a result, the derivative of the Lyapunov function may be positive in certain directions of the state space in the absence of control action.
To ensure system stability, the following expression must be negative definite:
Since the multiplier of is defined as:
it follows that:
For a boost converter operating under nominal conditions, , therefore:
However, during transients such as startup (when ), it may happen that . Hence, it is critical that the design of the control law adapts to the sign of a.
A purely nonlinear control law based on tanh is proposed as:
with and as gain constants. This law possesses the following properties:
- It is continuous and smoothly differentiable.
- It is naturally saturated, enhancing robustness to disturbances.
- It guarantees that for all , since and the product −sign is negative.
Therefore, this choice of ensures dissipation in the Lyapunov derivative, even if the system transitions across operating regions, and it is suitable for implementation in nonlinear power controllers. Finally, the complete control law for the virtual input is consolidated as the sum of two terms:
This structure includes:
- A structural compensation term that cancels the perturbation from the original dynamics, allowing the system to take an affine form with respect to .
- A nonlinear stabilizing term based on tanh, ensuring dissipation in the Lyapunov derivative while adapting to the sign of a across any operating region.
This complete formulation allows the direct application of the CLF methodology, guaranteeing robust system stability even in the presence of state or parameter variations.
4. Global Asymptotic Stability Analysis of the Proposed Control Strategy
This section rigorously establishes the global asymptotic stability of the closed-loop system under the multi-loop architecture based on Control Lyapunov Functions (CLF) [22,23]. The adopted approach considers the current and voltage loops hierarchically, both stabilized through nonlinear control laws derived from Lyapunov functions specifically designed for each subsystem.
4.1. Stability of the Internal Current Loop
The following Lyapunov candidate function is defined:
where and , with representing the current error.
This function satisfies the following properties:
- Positive definiteness: it is the sum of two quadratic terms and vanishes only at .
- Radially unbounded: it increases indefinitely as .
The system dynamics in z-coordinates are given by:
The time derivative of is:
Using the following control law:
and defining , we obtain:
Given that and for all , it follows that for all . According to the classical Lyapunov theorem [17], the origin of the current subsystem is globally asymptotically stable.
4.2. Stability of the Outer Voltage Loop
The following function is considered:
where and .
This function satisfies the following properties:
- Positive definiteness: it vanishes only at the origin.
- Radially unbounded: it tends to infinity as .
The system dynamics are:
The time derivative of is:
With the control law:
and defining , we obtain:
Since and , it follows that for all . Therefore, the origin of the voltage subsystem is also globally asymptotically stable.
4.3. Conclusion of the Multiloop System
Both Lyapunov functions are valid: positive definite, radially unbounded, and with strictly negative derivatives under the proposed control laws. Moreover, the hierarchical design ensures that the current loop—being faster—stabilizes the internal subsystem before the voltage control acts significantly. It is concluded that the entire closed-loop system is globally asymptotically stable.
5. Experimental Results
In order to verify the correct operation of the proposed controller, real-time experimental tests were carried out. The characteristics of the tests, as well as those of the system, are described in this section. Figure 6 shows the experimental control system architecture.
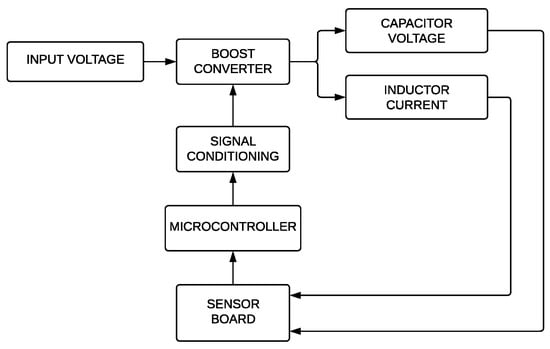
Figure 6.
Architecture of the experimental control system.
Figure 7 shows the system under test, which is composed by the boost converter prototype, load, PWM module, sensor modules and an auxiliary source. The experimental Boost converter prototype was implemented using an IRF540N N-channel MOSFET as the main switching device and an MUR1560 ultrafast recovery diode. The PWM signal generated by the controller was isolated and conditioned through an optocoupled TLP250 driver and a custom PWM signal conditioning board. The control algorithm implementing the proposed CLF strategy was developed in MATLAB/Simulink 2023b using Embedded Coder and executed on a Texas Instruments F28379D digital signal controller (Texas Instruments, Dallas, TX, USA) at a switching frequency of 50 kHz. Voltage sensing was achieved using a precision resistor divider network, while the inductor current was measured by a Honeywell CSNE151 Hall-effect sensor (Honeywell, Charlotte, NC, USA). The converter was powered by a regulated DC source, and a 50 resistive load was connected at the output. Its passive elements include a 160.9 H inductor and a 44 F output capacitor.
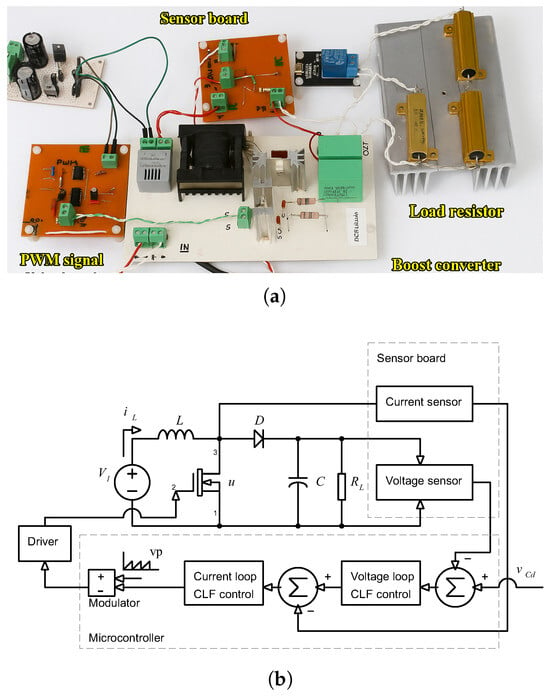
Figure 7.
Experimental prototype of boost converter. (a) Experimental setup. (b) Circuit diagram.
To validate the effectiveness of the proposed nonlinear controller, designed based on a CLF, experimental tests were conducted on a DC–DC boost converter under adverse and representative operating conditions typically encountered in real-world applications. These tests included variations in the supply voltage, step changes in the output reference, and abrupt modifications of the resistive load.
5.1. Voltage Regulation Test
The control objective was to regulate the output voltage at 24 V. Figure 8b shows the voltages measured in the semiconductor devices (diode and MOSFET) of the converter. The yellow trace corresponds to the anode–cathode voltage in the diode, whereas the blue trace corresponds to the drain-source voltage of the active switch. These voltages show the complementary operation of the semiconductor devices, where the operation frequency is imposed by the PWM signal applied to the active switch (MOSFET). The complementary operation of the semiconductor devices confirms the proper operation of the boost converter. The duty ratio can theoretically vary between 0 and 1 to regulate the output voltage. In this topology, no dead-time or simultaneous conduction occurs because the diode conducts only when the MOSFET is turned off and is naturally reverse-biased when the switch is on.
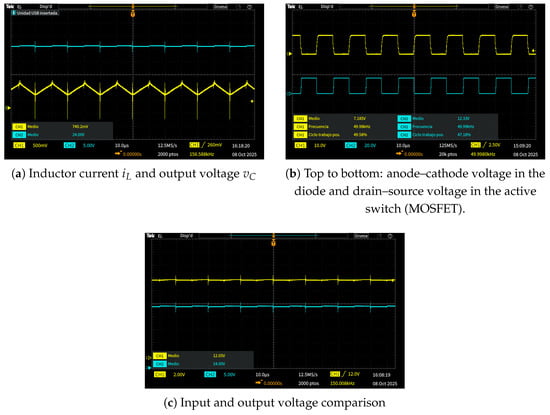
Figure 8.
Steady-state voltage regulation under nominal conditions. (a) Inductor current and capacitor voltage. (b) Complementary PWM waveforms at 50 kHz. (c) Input and output voltage comparison.
Figure 8a presents the inductor current and the capacitor voltage under closed-loop operation. The inductor current exhibits the expected triangular waveform characteristic of continuous conduction mode (CCM), while the capacitor voltage remains practically constant at 24 V with minimal ripple, confirming that the proposed Lyapunov-based controller achieves a stable steady-state equilibrium and ensures smooth voltage regulation. It is important to note that the inductor current waveform shown in Figure 8a was obtained as a voltage-proportional signal, due to the characteristics of the Honeywell CSNE151 Hall-effect current sensor and the oscilloscope input configuration. The sensor was powered with V and used a 220 load resistor, yielding a nominal output current of 25 mA at 5 A input. Under these conditions, the measured voltage is linearly related to the inductor current according to the calibration factor , where is the voltage measured at the sensor output. Therefore, the waveform captured by the oscilloscope represents the proportional voltage corresponding to the instantaneous inductor current. Using this factor, the average measured voltage of approximately 0.74 V corresponds to an inductor current of about 0.67 A, consistent with the theoretical value for continuous conduction mode operation under 12 V input and 24 V regulated output.
Additionally, Figure 8c illustrates the measured input and output voltages, highlighting the correct step-up operation (from 12 V to 24 V). The absence of low-frequency oscillations or instability confirms that the proposed nonlinear Lyapunov-based control maintains accurate steady-state voltage regulation, ensuring global stability and smooth response under constant load. Compared to conventional linear PI regulators, the proposed method provides precise regulation without overshoot or steady-state error while preserving high efficiency and continuous conduction. Quantitatively, the voltage regulation test yielded a settling time of approximately 180 ms and a maximum deviation below 2% of the nominal output voltage. These results confirm the controller’s ability to maintain fast and well-damped voltage regulation under nominal operating conditions.
5.2. Test 1: Input Voltage Variation
To evaluate the robustness of the proposed Lyapunov-based controller under input-voltage disturbances, an experimental test was conducted by applying stepped variations to the DC supply voltage of the Boost converter. This test verifies the ability of the proposed control law to preserve voltage regulation when the input source fluctuates, a condition often encountered in renewable and battery-powered systems.
Figure 9 shows the experimental waveforms recorded during the test. The yellow trace (CH1) corresponds to the voltage signal proportional to the inductor current , while the blue trace (CH2) represents the output voltage . The input voltage was sequentially varied from 12 V down to 11 V, then back to 12 V, increased to 13 V, and finally returned to 12 V, while maintaining a constant resistive load of 50 . The red circles in the figure mark the instants when each voltage step occurred. As observed, the proposed controller successfully maintained the output voltage regulated around 24 V despite the input-voltage perturbations. When the input voltage decreased to 11 V, the inductor current increased to compensate for the reduced input energy, and when the voltage rose to 13 V, the current decreased accordingly. This complementary behavior demonstrates that the control strategy dynamically adjusted the PWM duty cycle to stabilize the energy transfer through the inductor, preserving constant output voltage and continuous conduction.
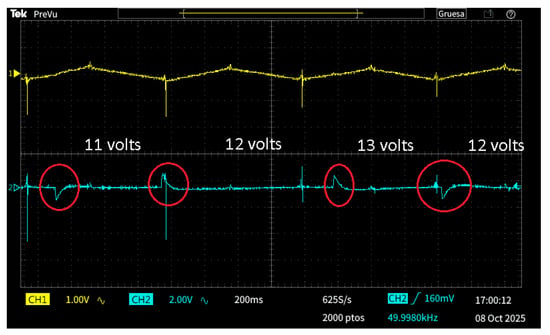
Figure 9.
Experimental time response of the output voltage under input voltage variation.
Throughout all transitions, remained tightly regulated, exhibiting a transient deviation below 2% and a settling time of approximately 180 ms. The waveforms show no overshoot or oscillatory behavior, confirming that the nonlinear controller ensures a stable and well-damped response. These results validate the predicted asymptotic stability of the closed-loop system and its ability to reject input disturbances effectively.
Unlike conventional PI controllers, whose fixed gains typically degrade performance when the operating point changes, the proposed CLF approach preserves global stability and accurate regulation without any parameter retuning. The experimental results confirm that the control law provides strong immunity to source-voltage fluctuations while maintaining smooth voltage regulation and stable current dynamics, thereby demonstrating its practical feasibility and robustness for real-world power conversion systems.
5.3. Test 2: Reference Voltage Changes
To assess the dynamic tracking performance of the proposed Lyapunov-based control strategy, an experimental test was conducted in which the reference voltage was intentionally varied. This test evaluates the controller’s ability to maintain accurate regulation and fast transient response when the reference value changes abruptly.
Figure 10 shows the experimental results obtained when the reference voltage was decreased from 24 V to 22 V and then restored to 24 V. The yellow trace (CH1) represents the voltage signal proportional to the inductor current , while the blue trace (CH2) corresponds to the output voltage . The converter operated with a constant resistive load of 50 and an input voltage of 12 V during the test.
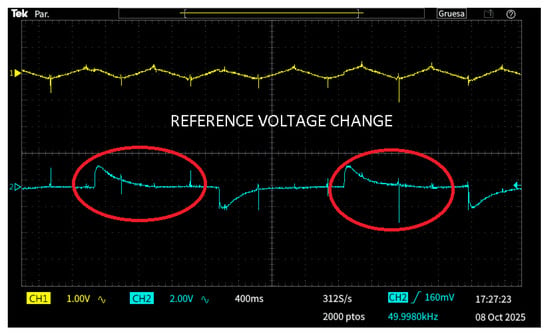
Figure 10.
Experimental time response of the output voltage under reference voltage change.
When the reference voltage dropped from 24 V to 22 V, the controller promptly reduced the inductor current to avoid excessive energy delivery to the output capacitor. Subsequently, when the reference returned to 24 V, the inductor current increased smoothly, reestablishing the steady-state energy balance without overshoot or oscillatory behavior. The output voltage accurately followed the reference transitions, exhibiting a transient deviation below 2% and a settling time of approximately 200 ms.
These results confirm that the proposed control structure achieves precise reference tracking with excellent damping characteristics and no steady-state error. The coordination between the inner current loop and the outer voltage loop allows a fast adjustment of the inductor energy, ensuring smooth voltage recovery after each change in the reference. This behavior experimentally validates the asymptotic convergence predicted by the Lyapunov stability analysis. During the reference change experiment (24 V → 22 V → 24 V), the measured settling time was approximately 200 ms, with a maximum deviation of about 2%. The system achieved smooth tracking of the reference without overshoot or oscillation, validating the robustness of the CLF design.
5.4. Test 3: Change in Resistive Load
This test allows the assessment of the controller’s ability to maintain voltage regulation and dynamic stability when the output current demand changes abruptly.
Figure 11 presents the experimental waveforms obtained during the test. The yellow trace (CH1) corresponds to the voltage signal proportional to the inductor current , while the blue trace (CH2) represents the output voltage . The converter initially operated with a load of 50 ; the resistance was then reduced to 25 to increase the output current demand and subsequently restored to 50 . The red circles indicate the instants when the load transitions occurred. When the load decreased from 50 to 25 , the inductor current increased sharply to supply the higher output current required by the load, while the controller adjusted the PWM duty cycle to stabilize the capacitor voltage. Conversely, when the load was returned to 50 , the current decreased accordingly, and the controller compensated for the excess stored energy, preventing any overshoot in the output voltage. In both cases, the voltage remained regulated around 24 V, exhibiting only minor transients with a deviation below 2.5% and a settling time of approximately 220 ms.
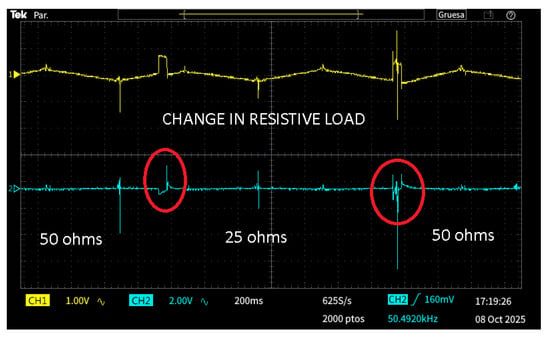
Figure 11.
Experimental time response of the output voltage under change in resistive load.
These results confirm the strong disturbance rejection capability of the proposed multiloop control structure. The inner current loop reacted instantaneously to balance the inductor energy flow, while the outer voltage loop ensured steady-state regulation without oscillations or steady-state error. The well-damped transient behavior experimentally verifies the asymptotic stability predicted by the Lyapunov design.
Although the tests shown in Figure 11 were conducted with a purely resistive load, the proposed CLF-based multiloop controller is load-independent under continuous conduction mode (CCM). The fast current loop isolates the converter dynamics from the load characteristics, allowing the outer voltage loop to operate over an equivalent first-order system even for RL loads. The experimental setup is already equipped for RL load operation, and these tests are considered for future work as an extended validation campaign.
The experimental results presented show oscillations and voltage ripple, which are mainly attributed to analog sensing noise, semiconductor nonidealities, and the limited resolution of the ADC in the digital controller. These effects are inherent to the physical prototype and do not originate from the control algorithm. The observed settling time and transient deviations (around 25% overshoot and undershoot) remain within the expected range for a Boost converter operating under nonlinear Lyapunov-based control without additional predictive or feedforward compensation. Despite these physical limitations, the converter maintains global stability, adequate voltage regulation, and robustness under load and input perturbations. Future improvements will focus on optimizing the sensing and filtering stages to further reduce measured noise while preserving the same control structure. In the load variation scenario, the converter exhibited a settling time of roughly 220 ms and a maximum voltage deviation below 2.5%. These measurements demonstrate the controller’s strong disturbance rejection capability and confirm the global stability predicted by the Lyapunov analysis.
5.5. Discussion and Analysis
The results obtained allow for strong conclusions to be drawn regarding the validity of the proposed strategy:
- The multi-loop architecture ensures effective dynamic decoupling, allowing each loop to fulfill its specific function optimally.
- The CLF-based design provides theoretical guarantees of global stability, overcoming the local limitations inherent to conventional PI/PID regulators.
- The inclusion of integral errors in the extended system representation enables accurate reference tracking and robust disturbance rejection.
- The practical implementation demonstrated that the derived control laws are not only theoretically sound but also computationally feasible and stable in real hardware, even under demanding operating conditions.
Overall, the results support the use of the CLF strategy as an advanced, reliable, and highly efficient solution for power converter control, particularly in applications where global stability and high precision are critical requirements.
It should be emphasized that the purpose of the proposed CLF-based controller is not solely to surpass classical PID or PI schemes in transient performance but also to establish a formally grounded nonlinear control strategy with guaranteed global asymptotic stability and robustness to parameter variations. It is worth noting that classical linear control theory provides several formal and well-established tools for controller tuning, such as gain and phase margins, unit gain crossover frequency, and the well-known k-factor method. These methods allow precise shaping of the transient response and ensure satisfactory robustness under moderate parameter variations. However, such techniques are generally derived from small-signal linearization of the converter dynamics and therefore guarantee stability only locally, around the nominal operating point. When large perturbations, input fluctuations, or strong nonlinearities occur—as in nonminimum-phase Boost converters—their performance and stability margins may degrade due to the inherent local nature of the design. In contrast, the proposed Lyapunov-based multiloop control formulation provides a nonlinear and globally stable control law derived directly from the full system dynamics. By avoiding frequency-domain approximations, the proposed approach ensures global asymptotic convergence, continuous control action, and robustness against load and input variations. Thus, while classical tuning techniques remain valuable within linear control practice, the contribution of this work lies in providing a formally verifiable framework that extends stability guarantees to the global nonlinear regime.
In contrast, the CLF framework adopted in this work provides a systematic and mathematically verifiable design procedure, ensuring global stability of the full nonlinear dynamics. Moreover, the explicit inclusion of integral error variables within the extended system representation enhances the steady-state accuracy and disturbance rejection capability beyond what can be achieved by standard PID controllers. Experimental results confirm that the transient behavior obtained with the proposed control law is comparable in speed to optimized PID tuning, while exhibiting superior robustness and guaranteed theoretical stability. These characteristics make the proposed strategy not merely an alternative to conventional controllers, but a formally validated solution for demanding nonlinear power conversion applications.
The total power loss in the converter semiconductors primarily includes conduction losses in the MOSFET and diode and switching losses during the transitions at 50 kHz. While these losses are mainly determined by the physical characteristics of the power devices, the proposed CLF-based control strategy indirectly contributes to their reduction. By minimizing current oscillations and ensuring smooth duty cycle modulation, the controller decreases both conduction and switching losses. Additionally, by maintaining stable operation near the optimal conversion point, the control law promotes a more energy-efficient switching regime. Although quantitative thermal measurements were not performed, the experimental results—showing reduced current ripple and stable duty cycle behavior—provide clear evidence of lower semiconductor dissipation and improved overall efficiency under dynamic operating conditions.
In practical scenarios, many power converters supply loads with inductive components. The proposed CLF-based control architecture remains valid under RL loading conditions because the fast inner current loop ensures that accurately tracks even when the load introduces an additional time constant . As long as the bandwidth relationship is satisfied, the converter exhibits the same global stability and voltage regulation properties demonstrated experimentally with resistive loading. The experimental platform used in this work is already configured to support RL load testing, which will be reported as an extended experimental validation in future work.
Although the main contribution of this work lies in the formal CLF design and stability guarantees, the proposed control law also contributes indirectly to improving the converter’s efficiency. By reducing current oscillations, ensuring smooth duty cycle transitions, and maintaining steady operation under disturbances, the controller minimizes switching and conduction losses. The smooth control action prevents saturation effects and excessive stress on the power switch, leading to a more efficient and thermally stable operation. These effects were observed experimentally through the reduction of ripple amplitudes and fast convergence to the desired operating point.
Although the proposed Lyapunov-based control strategy may appear mathematically complex, its implementation is computationally simple. The control law only involves basic arithmetic operations and a smooth hyperbolic function, which can be executed in real time using standard digital controllers. The apparent complexity resides in the analytical derivation, not in the practical realization. Unlike conventional linear controllers, which depend on local linearization and empirical tuning, the CLF-based approach provides formal global stability guarantees, continuous control action, and robustness against parameter variations. Therefore, this methodology should not be interpreted as a replacement for linear schemes in simple applications but as a systematic and generalizable framework for nonlinear systems where guaranteed stability and robustness are essential.
At first glance, the CLF strategy may appear mathematically elaborate; however, its practical implementation is computationally straightforward. The control law relies only on basic operations and a smooth hyperbolic function, which can be efficiently executed in real time using standard digital controllers. The perceived complexity lies in the analytical derivation, not in the implementation itself. In contrast to conventional linear controllers, which depend on local linearization and empirical gain tuning, the proposed CLF-based design provides formal guarantees of global stability, continuous control action, and robustness against load and input variations. This methodological rigor ensures consistent performance even under nonlinear or highly dynamic operating conditions. Rather than being intended as a direct substitute for traditional linear schemes in simple applications, the proposed approach establishes a systematic and generalizable framework for nonlinear systems where guaranteed stability and robustness are of primary importance.
6. Conclusions
This work presents a nonlinear multi-loop control strategy for DC–DC boost converters, rigorously designed using the Control Lyapunov Function (CLF) framework. The proposed methodology enables the formulation of control laws that ensure global asymptotic stability without relying on local linear approximations or reduced-order models. The implementation comprises an inner current loop based on an extended state representation with integral terms and an outer voltage loop responsible for reference tracking. This hierarchical structure not only provides modular control but also enables decoupling of the system’s fast and slow dynamics, thereby improving the controller’s precision, stability, and adaptability.
From a theoretical perspective, the design is grounded on conditions that ensure a strictly negative derivative of the Lyapunov function, with an explicit construction of nonlinear coordinates that allows handling perturbation terms not grouped in the affine model. This detail is highly relevant to the control community, as it addresses one of the main limitations of classical linear feedback or standard backstepping-based designs. Furthermore, the proposed controller avoids abrupt saturations through the inclusion of smooth functions of the form tanh, enabling continuous and efficient control action without discontinuities, even in the presence of severe disturbances.
Experimental validation demonstrated that the controller is capable of rejecting external disturbances such as supply voltage drops with fast reconvergence of the output voltage; tracking step references without significant overshoot; and maintaining stability under abrupt changes in the resistive load without compromising regulation quality. In all evaluated scenarios, the system exhibited highly robust behavior, with no sustained oscillations, bifurcations, or loss of regulation, thus empirically supporting the theoretical guarantees of global stability established during the design phase.
Furthermore, although the proposed control strategy has been developed and experimentally validated for a boost converter, the underlying CLF design methodology is general and can be extended to other DC–DC converter topologies such as buck, buck-boost, or Ćuk by adapting the corresponding state-space representations and control variables. Consequently, this work not only provides a rigorous and practical solution to the specific regulation problem of boost converters but also establishes a replicable and scalable methodological foundation for future research in nonlinear control applied to power electronics.
The experimental results obtained confirm that the objectives of this research were fully achieved, validating the effectiveness of the proposed Lyapunov-based multiloop control strategy. The system consistently preserves global stability, continuous voltage regulation, and robustness against load and input variations, demonstrating stable and predictable dynamic behavior under real operating conditions.
Unlike conventional linear controllers, the proposed CLF-based approach combines theoretical rigor, modular structure, and straightforward implementation, without relying on empirical tuning or local linearization. This synergy between analytical design and experimental validation establishes a substantial and verifiable contribution to the field of nonlinear control for DC–DC power converters, reinforcing the integration of Lyapunov stability theory with practical energy conversion applications.
Author Contributions
Conceptualization, M.I.N.-B., J.L.M.-M. and R.L.-P.; methodology, M.I.N.-B., J.L.M.-M. and R.L.-P.; software, M.I.N.-B. and C.A.H.-J.; validation, M.I.N.-B., C.A.H.-J. and R.L.-P.; formal analysis, M.I.N.-B., J.L.M.-M. and R.L.-P.; investigation, M.I.N.-B.; resources, R.L.-P. and J.A.M.-S.; writing—original draft preparation, M.I.N.-B.; supervision, J.L.M.-M., R.L.-P. and J.A.M.-S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Acknowledgments
This research was carried out at the División de Estudios de Posgrado e Investigación, Tecnolǵico Nacional de México/Instituto Tecnológico de La Laguna. It was also supported by SECIHTI through the Ph.D. scholarship granted to the student with CVU 957182.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sahraoui, H.; Meghriche, K.; Ayad, M.Y.; Meziane, A. Lyapunov-Based Adaptive Sliding Mode Control of a DC–DC Boost Converter. Machines 2025, 13, 734. [Google Scholar] [CrossRef]
- Vazani, A.; Salmasi, F.R.; Shamsi, P. Composite Nonlinear Feedback Control of a DC–DC Boost Converter. Int. J. Electr. Power Energy Syst. 2024, 162, 108204. [Google Scholar] [CrossRef]
- Wang, M.; Li, X.; Wu, J.; Wang, L.; Yang, Y. A Nonlinear Control Strategy for DC–DC Converters with Constant Power Loads Based on Improved Passivity and Disturbance Observation. Energies 2021, 14, 3031. [Google Scholar] [CrossRef]
- Ortega, R.; van der Schaft, A.J.; Mareels, I.; Maschke, B. Putting Energy Back in Control. IEEE Control Syst. Mag. 2002, 21, 18–33. [Google Scholar] [CrossRef]
- Konstantopoulos, G.C.; Papadopoulos, G.D.; Alexandridis, A.T.; Alexandridis, A. Nonlinear Control of DC/DC Power Converters with Inherent Current Limiting. In Proceedings of the 2016 24th Mediterranean Conference on Control and Automation (MED), Athens, Greece, 21–24 June 2016; pp. 949–954. [Google Scholar] [CrossRef]
- Mansouri, A.; Gavagsaz-Ghoachani, R.; Phattanasak, M.; Pierfederici, S. Nonlinear Cascaded Control for a DC-DC Boost Converter. Available online: https://pdfs.semanticscholar.org/804d/62de4bd0186bc0f376071a394f06bf9d980b.pdf (accessed on 5 September 2025).
- Komurcugil, H.; Guler, N.; Bayhan, S. Lyapunov-Function-Based Control Strategy for Four-Switch Buck–Boost DC–DC Converters. In Proceedings of the 2022 IEEE 31st International Symposium on Industrial Electronics (ISIE), Anchorage, AK, USA, 1–3 June 2022; pp. 546–551. [Google Scholar] [CrossRef]
- Nava-Bustamante, M.I.; Loera-Palomo, R.; Meza-Medina, J.L. Control strategy based on Control Lyapunov Functions applied to a DC-DC Boost Converter. In Proceedings of the 2023 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 18–20 October 2023. [Google Scholar]
- Nava-Bustamante, M.I.; Loera-Palomo, R.; Meza-Medina, J.L. Lyapunov-Based Current Control Applied to a DC-DC Boost Converter. In Proceedings of the 2024 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 11–13 November 2024. [Google Scholar]
- Parada-Salado, J.G.; Herrera-Ramírez, C.A.; Soriano-Sánchez, A.G.; Rodríguez-Licea, M.A. Nonlinear Stabilization Controller for the Boost Converter with a Constant Power Load in Both Continuous and Discontinuous Conduction Modes. Micromachines 2021, 12, 522. [Google Scholar] [CrossRef] [PubMed]
- Gavagsaz-Ghoachani, R.; Phattanasak, M.; Martin, J.-P.; Pierfederici, S. Lyapunov function-based improved switching command for a boost converter with an inductor–capacitor input filter. IET Power Electron. 2020, 13, 3940–3953. [Google Scholar] [CrossRef]
- Sabzi, S.; Asadi, M.; Moghbelli, H. Design and Analysis of Lyapunov Function-Based Controller for DC-DC Boost Converter. Indian J. Sci. Technol. 2016, 9, 1–6. [Google Scholar] [CrossRef]
- Álvarez, J.; Ruiz, J.; Bernal, M. A family of Lyapunov-based control schemes for maximum power point tracking in buck converters. Kybernetika 2023, 59, 294–313. [Google Scholar] [CrossRef]
- Alam, M.Z.; Ghosh, S.K.; Alkhateeb, A.F.; Roy, T.K.; Islam, M.S.; Saha, S.; Hussain, M.A. Robust hybrid nonlinear control approach for stability enhancement of a constant power load DC-DC boost converter. Alex. Eng. J. 2023, 74, 535–545. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimović, D. Fundamentals of Power Electronics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Ortega, R.; Schaft, A.V.; Maschke, B.; Escobar, G. Interconnection and damping assignment passivity-based control of port-controlled Hamiltonian systems. Automatica 2002, 38, 585–596. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Hoboken, NJ, USA, 2002. [Google Scholar]
- den Bossche, A.V.; Keybus, J.V.d.; Melkebeek, J. Averaged modeling of PWM converters operating in discontinuous conduction mode. In Proceedings of the 2000 IEEE 31st Annual Power Electronics Specialists Conference, Galway, Ireland, 18–23 June 2000; pp. 1092–1097. [Google Scholar]
- Krein, P.T. Elements of Power Electronics; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Isidori, A. Nonlinear Control Systems, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Ortega, R.; García-Canseco, L. Interconnection and damping assignment passivity-based control: A survey. Eur. J. Control 2004, 10, 432–450. [Google Scholar] [CrossRef]
- Artstein, Z. Stabilization with relaxed controls. Nonlinear Anal. Theory Methods Appl. 1983, 7, 1163–1173. [Google Scholar] [CrossRef]
- Sontag, E.D. A Lyapunov-like characterization of asymptotic controllability. SIAM J. Control Optim. 1983, 21, 462–471. [Google Scholar] [CrossRef]
- Bacciotti, A.; Rosier, L. Lyapunov Functions and Stability in Control Theory, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Cai, X.; Wang, X.; Zhang, H. Universal construction of control Lyapunov functions for a class of nonlinear systems. J. Syst. Eng. Electron. 2007, 18, 598–602. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).