Hybrid Artificial Bee Colony Algorithm for Test Case Generation and Optimization

Abstract

The generation of high-quality test cases remains challenging due to combinatorial explosion and difficulty balancing exploration-exploitation in complex parameter spaces. This paper presents a novel Hybrid Artificial Bee Colony (ABC) algorithm that uniquely combines ABC optimization with Simulated Annealing temperature control and adaptive scout mechanisms for automated test case generation. The approach employs a four-tier categorical fitness function discriminating between boundary-valid, valid, boundary-invalid, and invalid values, with first-occurrence bonuses ensuring systematic exploration. Through comprehensive empirical validation involving 970 test suite generations across 97 parameter configurations, the hybrid algorithm demonstrates 68.3% improvement in fitness scores over pairwise testing (975.9 ± 10.6 vs. 580.0 ± 0.0, p < 0.001, d = 42.61). Statistical analysis identified three critical parameters with large effect sizes: MutationRate (d = 106.61), FinalPopulationSelectionRatio (d = 42.61), and TotalGenerations (d = 19.81). The value discrimination system proved essential, uniform weight configurations degraded performance by 7.25% (p < 0.001), while all discriminating configurations achieved statistically equivalent results, validating the architectural design over specific weight calibration.

1. Introduction

Despite the wide application of classical test design techniques and metaheuristic optimization algorithms, the literature reveals a lack of a unified and configurable solution that combines these approaches into a single framework for automated test case generation. Tools based on pairwise combination do not account for semantic validity or boundary values, while existing value generators and property-based libraries do not provide built-in mechanisms for optimizing the test suite. This challenge is magnified by combinatorial explosion, a system with 10 parameters having 5 values each requires 5¹⁰ (approximately 10 million) exhaustive test cases, making comprehensive testing impractical for real-world applications.

The Artificial Bee Colony (ABC) algorithm has proven its effectiveness in discrete optimization problems, but its application in software testing remains underexplored, particularly regarding its integration with test strategies such as Boundary Value Analysis and Equivalence Partitioning. At the same time, while hybrid approaches based on Genetic Algorithms (GA) and Simulated Annealing (SA) show potential for achieving better balance between exploration and exploitation, they are rarely adapted to the specific requirements of test design. These observations highlight a clearly defined gap, there is no solution that simultaneously employs an intelligent optimization mechanism, considers value characteristics (validity, boundary relevance, uniqueness), and is capable of generating a compact yet effective set of test cases. This gap raises fundamental research questions about how evolutionary algorithms can efficiently navigate high-dimensional discrete test spaces while maintaining diversity and avoiding local optima.

To address these challenges, this work investigates three specific research questions: Can a hybrid metaheuristic approach combining ABC with Simulated Annealing achieve superior test case generation compared to traditional techniques? How can fitness function design with categorical value discrimination guide effective exploration-exploitation balance? What is the relative importance of algorithm parameters for robust performance across diverse scenarios?

The present work aims to address this gap through a hybrid ABC algorithm that integrates Simulated Annealing temperature control with concepts from classical test design. Our approach uniquely combines ABC’s global search with SA’s temperature-controlled exploitation and adaptive scout mechanisms, employing a four-tier categorical fitness function that discriminates between boundary-valid, valid, boundary-invalid, and invalid values. The use of global and local search in a hybrid mode has already proven effective in boundary value analysis, where automated frameworks combine generative sampling with local derivation of boundary values [1]. A similar architecture underlies our sampling approach, which could also support future clustering of boundary candidates. The main contributions of this work, validated through 970 experimental test suite generations, are: (1) a hybrid ABC-SA algorithm that integrates classical test design strategies with intelligent optimization, achieving 68.3% improvement over pairwise testing (975.9 ± 10.6 vs. 580.0 ± 0.0, p < 0.001, d = 42.61); (2) a four-tier categorical fitness function that discriminates between boundary-valid, valid, boundary-invalid, and invalid values, demonstrating robustness to ±50% weight variations; (3) an adaptive mutation mechanism controlled by SA temperature that enables temporary acceptance of weaker solutions for global optimization; (4) a stagnation-triggered scout phase ensuring targeted diversification when the population converges prematurely; (5) comprehensive sensitivity analysis identifying three critical parameters, MutationRate (d = 106.61), FinalPopulationSelectionRatio (d = 42.61), and TotalGenerations (d = 19.81), from eight algorithm parameters.

The rest of the paper is organized as follows: Section 2 reviews related works in the field of test case generation including classical test design techniques as well as metaheuristic algorithms for test optimization. Section 3 outlines the proposed hybrid artificial bee colony algorithm for test case generation and optimization. Section 4 details the program implementation and algorithm logic. Section 5 discusses the evaluation of the experimental results, challenges encountered, and proposed solutions. Finally, Section 6 summarizes the paper’s contributions and outlines directions for future research. Having established the critical gaps and our contributions, we now examine existing solutions to position our work within the broader research landscape.

2. Related Work

Existing tools for test coverage in .NET, such as unit testing frameworks (e.g., NUnit [2], MSTest [3], xUnit [4]) and data generators (e.g., Bogus [5], AutoFixture [6]), support parts of the process but do not provide automated generation of test inputs with guaranteed coverage or semantic validity. Pairwise tools such as PICT [7] efficiently generate test suites, but they fail to account for boundary values or negative scenarios. Evolutionary generators such as EvoSuite [8] and FsCheck [9] apply property-based or genetic approaches, but they often require manual specification and cannot ensure coverage of critical combinations. The literature lacks a comprehensive approach that combines automated generation, semantic validation, and optimization through an intelligent algorithm. This gap highlights the need for a solution that integrates classical and hybrid strategies for effective testing in complex input spaces.

2.1. Classical Test Design Techniques

For complex systems with many parameters, exhaustive testing is infeasible due to the exponential growth of possible combinations. To reduce the test suite size without compromising coverage, four classical approaches are typically applied: equivalence partitioning, boundary value analysis, pairwise testing, and the identification of bug masking.

2.1.1. Equivalence Partitioning

This technique groups input values into classes expected to exhibit identical behavior (valid, boundary, invalid), with each class represented by a single value. This significantly reduces the number of tests. Its main drawback lies in the difficulty of defining truly equivalent values when parameter dependencies exist [10].

2.1.2. Boundary Value Analysis

Test cases are designed around values at or near the edges of allowed ranges (min, min+, nominal, max−, max). This technique is effective for independent parameters but limited in scenarios involving interdependent inputs, such as date validation or geometric constraints [11].

2.1.3. Pairwise Testing

This combinatorial technique ensures coverage of all pairs of values across parameters and drastically reduces the number of test cases. For example, with three parameters each having two values, the total is reduced from 8 to 4 tests [10]. Limitations include the lack of coverage for higher-order interactions, sensitivity to the selection of values, and the risk of a false sense of completeness.

2.1.4. Bug Masking

Masking occurs when one defect conceals another, particularly when multiple invalid values appear in a single test. This phenomenon is common in automated optimized tests. Mitigation strategies include separating boundary values, employing adaptive algorithms, and using fitness functions that penalize redundancy and defect accumulation [12].

2.2. Metaheuristic Algorithms for Test Optimization

The generation of effective test cases in software testing has long been a challenge, particularly in systems with high combinatorial complexity. Classical techniques such as equivalence partitioning, boundary value analysis, and pairwise testing achieve substantial reduction in the test set, but they are limited in their ability to uncover defects arising from parameter interdependencies or boundary scenarios. Consequently, a number of metaheuristic approaches have been proposed in the literature as intelligent alternatives for optimization. Metaheuristic algorithms represent a class of stochastic optimization techniques inspired by biological, physical, or evolutionary processes. Unlike classical methods, which often require gradient information or structural knowledge of the objective function, metaheuristics operate through population-based exploration or iterative transformations of current solutions, relying solely on performance evaluation. Their main characteristics include balancing global exploration and local exploitation, incorporating randomness to increase diversity, and functioning as “black-box” optimizers.

Three primary categories of metaheuristic algorithms are identified in the literature: population-based algorithms such as Genetic Algorithms and Artificial Bee Colony; local search algorithms such as Simulated Annealing and Tabu Search (TS); and hybrid methods that combine the strengths of both approaches. Population-based algorithms are effective for global search but are often computationally intensive. Local search algorithms are suitable for fine-tuning but are prone to premature convergence. Hybrid strategies aim to achieve synergy by integrating global and local mechanisms. Genetic Algorithms have been successfully applied to automated test generation and optimization, particularly through the definition of fitness functions that account for path coverage, branch coverage, or defect detection probability. As demonstrated by Mala and Mohan [13], such algorithms can be adapted to different testing goals, though they suffer from premature convergence when mutation diversity is insufficient or selection pressure is overly aggressive. Simulated Annealing is inspired by the physical process of cooling metals and employs a probabilistic mechanism to accept worse solutions, controlled by a temperature parameter. This allows the algorithm to avoid local optima, particularly in the early stages. Kirkpatrick et al. [14] showed that SA is effective for discrete tasks and can be adapted through dynamic adjustment of the cooling rate. The combination of GA and SA has been frequently explored for test optimization, especially in problem spaces with numerous local optima and complex structures. Such hybrid approaches achieve a better balance between exploration and exploitation, which is crucial for tasks requiring both diversity and focused search.

Individual metaheuristics have demonstrated significant success in test case generation. Genetic Algorithms achieve complete coverage in complex logical structures with execution times of 50.878 s, outperforming adaptive GA variants by 0.18 s while significantly reducing iterations [15]. Ant Colony Optimization with fuzzy logic (ACOF) dynamically adjusts exploration-exploitation balance based on tuple coverage percentages, improving convergence in combinatorial test suite generation [16]. Latin Hypercube Sampling enhanced Jaya Algorithm (LHS-JA) improves search diversity in t-way testing, preventing premature convergence through systematic sampling of the parameter space [17]. Evolutionary approaches show consistent improvements in test optimization, multi-objective evolutionary clustering achieves 4.61–9.44% fault detection improvement with 4.10–10.64% better reduction ratios compared to traditional methods [18]. Modern frameworks like EvoGPT combine LLM-based generation with genetic optimization, achieving 10% improvements in both code coverage and mutation scores over conventional search-based testing [19]. Simulated Annealing approaches excel in resource-constrained environments, with large search spaces and multiple iterations achieving optimal results for regression test prioritization in industrial settings [20]. A Hybrid Genetic Algorithm integrating Cuckoo Search Optimization (CSO) achieves 0.271% APFD improvement and 6.35% coverage effectiveness gains over standard approaches [21].

2.3. Artificial Bee Colony Algorithm

The Artificial Bee Colony algorithm, proposed by Karaboga in 2005, is a stochastic optimization method inspired by the foraging behavior of real bee colonies. Similarly to other nature-inspired algorithms, ABC is particularly effective for optimization in discrete and weakly structured solution spaces [13]. The ABC model simulates the interaction of three main types of bees—employed, onlooker, and scout. Each type performs a specific function within an iterative process that combines local search with mechanisms for global adaptation. Employed bees explore existing solutions and generate modified variants through small transformations. Onlooker bees select among the solutions discovered by the employed bees using a probability model based on their fitness. Scout bees are responsible for discovering new regions in the search space when current solutions cease to improve. This tripartite structure ensures an effective balance between exploitation and exploration, which is essential for avoiding local optima while maintaining convergence efficiency. The algorithm’s simplicity and parameter parsimony have made it attractive for various optimization problems, including test case generation.

2.4. Hybrid Metaheuristic Approaches in Test Generation

Recent advances have demonstrated that hybrid metaheuristic variants significantly outperform individual algorithms. Certain modifications of the ABC algorithm demonstrate significant improvements, including the introduction of collaborative group strategies [22]. While ABC-SA hybridization has been explored in various domains, Alabbas and Abdulkareem [23] applied this approach to cryptanalysis, achieving improved scalability (100% vs. 88%) in their specific problem domain. Although their application differs from software testing, their work demonstrates that SA integration can enhance ABC performance in combinatorial problems, employing SA in two phases: initial population repair and modified employed bee phase with probabilistic acceptance mechanisms [23]. GA-ABC hybrids have shown particular promise, with Cross-over-based ABC (CbABC) yielding genetic algorithm crossover operations to strengthen exploitation phases [24]. Recent implementations in wireless sensor networks demonstrate superior performance, outperforming LEACH and PSO baselines in energy-efficiency and network-lifetime metrics [25]. ABC-Bat Algorithm hybrids leverage ABC’s global search capabilities with Bat Algorithm’s local exploitation through periodic solution exchanges, achieving improved convergence and resource utilization in computing environments [26]. In test case generation specifically, a systematic review by Yahaya et al. [27] covering 41 studies from 2014–2024 found that hybrid metaheuristics in pairwise test generation typically achieve 50–85% test suite size reductions. The review establishes hybridization as a major trend, with approaches such as Pairwise hybrid ABC (PhABC), GA-PSO, HOA, and PCFHH consistently outperforming single algorithms [27]. The Improved Cuckoo Search-PSO hybrid (PSOICSA) demonstrates superior performance in t-way test suite generation compared to individual algorithms [28]. Notably, the review identified only two studies mentioning ABC-SA combinations without detailed performance reporting, highlighting a gap our work contributes to filling. These successful hybridizations motivate our approach, which combines ABC with Simulated Annealing temperature-based mutation control and an adaptive scout bee mechanism inspired by Guided Local Search principles for escaping local optima. Among the test generation studies we reviewed, including those covered in Yahaya et al.’s systematic review of 41 papers [27], detailed implementations of ABC-SA hybrids with comprehensive performance evaluation remain limited. Our approach achieves a 68.3% improvement in fitness scores over the pairwise baseline (975.9 ± 10.6 vs. 580.0 ± 0.0, p < 0.001), situating our ABC-SA implementation within the expected performance profile of hybrid metaheuristics while addressing the specific challenges of balancing exploration-exploitation in combinatorial test space. Having established the critical gaps and our contributions, we now examine existing solutions to position our work within the broader research landscape.

3. Proposed Method

This section presents the Hybrid ABC algorithm in detail. We first describe the fundamental phases and bee types (Section 3.1), followed by the fitness evaluation mechanism (Section 3.2), the integrated metaheuristics (Section 3.3), and conclude with usage guidelines (Section 3.4).

3.1. Phases and Types of Bees

The ABC algorithm involves three primary types of bees, each performing a specific role in the optimization process. These phases are repeated cyclically until a predefined number of iterations is reached or satisfactory convergence is achieved. Employed bees apply local mutations to current test cases in order to improve them. Onlooker bees select among existing solutions based on their fitness; in the hybrid version, a Restricted Candidate List (RCL) mechanism is employed, which brings their behavior closer to Guided Local Search (GLS) [29]. Scout bees are activated when a given solution stagnates and generate new alternatives. Unlike the original algorithm, the hybrid approach employs a diversity-oriented strategy based on historical value analysis [30,31]. The combination of these roles ensures an effective balance between local refinement and global exploration of the search space.

3.2. Evaluation of Solutions and Selection

Solutions are evaluated through a multi-component fitness function that incorporates coverage, value diversity, penalties for defective inputs, and bonuses for discovering new scenarios. This evaluation guides the selection, replacement, and mutation of test cases within the algorithm. Each value in a given test case is categorized and assigned points according to the system presented in

Table 1. Scoring system based on value category.

Category	Examples	Contribution
Boundary Valid	14, 99	+20 points
Valid	25, “test@example.com”	+2 points
Boundary Invalid	−1, 1000	−1 point
Invalid	null, “!”	−2 points

. This scoring scheme corresponds to the Boundary Value Analysis and Equivalence Partitioning techniques discussed in earlier sections, encouraging the inclusion of boundary and valid values while limiting excessive use of invalid inputs [11]. Similar ideas for structured evaluation, balancing effectiveness and complexity, have also been observed in genetic algorithm approaches, where the fitness function combines the mutation score with the number of steps required to detect a defect [32]. Each test value in our scoring system is classified into one of four mutually exclusive categories based on its relationship to the parameter’s valid range and boundary conditions. These categories form the foundation of our fitness function’s discrimination mechanism.

To encourage diversity, values that have not yet appeared in the global population receive an additional bonus of 25 points, while those occurring for the first time within the current generation are assigned an extra multiplier. This approach is consistent with the concept of diversity-preserving selection, as discussed in the literature on both ABC and genetic algorithms. If a test case contains more than one invalid value, a global penalty is applied:

P(t) = 50 × (n − 1)

(1)

where n is the number of invalid parameters.

This constraint limits excessive negative testing unless the option AllowMultipleInvalidValues is enabled. The final score for each test case t is calculated as:

F(t) = Σ S(vi) + Σ B(vi) − P(t)

(2)

where

• S(vi) represents the base score of value vi;
• B(vi) is the uniqueness bonus;
• P(t) is the global penalty for defects.

This model closely aligns with multi-criteria evaluation schemes commonly used in constraint-based generation [30,31]. The weight values in Table 1 were empirically validated through 7200 controlled experiments testing eight different weight configurations. Our investigation revealed that the specific weights (+20, +2, −1, −2) are less critical than the categorical discrimination they create. The uniform weight configuration (10/10/10/10) performed significantly worse (7.28% below baseline, p < 0.001, d = 1.484), while five of six configurations maintaining categorical discrimination achieved statistically equivalent performance (differences < 0.06%, p > 0.77). The only exception was the Boundary Focused configuration with its extreme 30:1 ratio, which showed a small but significant difference (0.63%, p = 0.0003). The 10:1 ratio between boundary and normal values (+20 vs. +2) aligns with empirical evidence that approximately 80% of software faults cluster at boundaries [11]. Our sensitivity analysis tested ratios from 3:1 to 30:1, finding no statistical improvement over the baseline ratio. The first-time bonus (+25) ensures systematic exploration without overwhelming quality indicators. Remarkably, varying these weights by ±50% yielded less than 1% performance difference, demonstrating that the four-tier categorical architecture (BoundaryValid, Valid, BoundaryInvalid, Invalid) drives effectiveness rather than precise weight calibration. This robustness provides practitioners flexibility for domain-specific tuning while maintaining the essential discrimination structure. Once all test cases are evaluated using the defined fitness function, selection for the next generation is performed based on two strategies. The first is elite selection, in which a fraction of the best solutions, determined by the parameter EliteSelectionRatio, are preserved automatically. This increases the stability of the algorithm and prevents the loss of high-quality test cases already discovered [13]. The second is onlooker-based selection, where the remaining test cases are chosen with weighted probabilities proportional to their fitness values. In the hybrid implementation, this process is further constrained by the parameter OnlookerSelectionRatio, which regulates the balance between exploitation and exploration. For example, a test case containing a boundary valid value for age (+20 points), a valid name (“Ivan”, +2 points), an invalid email (“abc”, −2 points), and a unique phone number (+25 points) yields a final score of F(t) = 45 points. This scoring and selection system ensures that the chosen population is both high in quality and diverse.

3.3. Integrated Metaheuristics

The first major enhancement is the introduction of an extended elite selection strategy. In the standard implementation of ABC, high-quality solutions can be lost during mutation or replacement. The hybrid version preserves these high-performing test cases across generations, ensuring stability and accumulation of quality throughout the optimization process. With respect to selection in the onlooker phase, classical ABC relies solely on probability-based choice proportional to fitness. The hybrid version introduces dynamic weighting with added randomness, which maintains diversity and prevents premature convergence to local optima, even when dominant solutions exist in the population.

Another improvement concerns mutation. While the standard ABC algorithm does not include a dedicated mutation phase, the hybrid variant employs adaptive mutation controlled by a temperature mechanism inspired by Simulated Annealing. This enables the temporary acceptance of weaker solutions in the interest of global optimization and helps avoid local minima. The scout phase is also refined. Unlike the original ABC, where scout bees are triggered randomly, the hybrid approach applies a controlled exploration mechanism that activates only upon detected stagnation. This ensures timely and targeted diversification of the population with new test cases. Finally, the hybrid approach incorporates a final selection step that reduces the output population based on a configurable selection threshold (FinalPopulationSelectionRatio). Unlike the classical version, which returns the full population, this mechanism guarantees compactness and high quality of the resulting test suite [22]. Comparable strategies for balancing exploitation and exploration through adaptive mechanisms have also been adopted in advanced ABC variants, where the population is partitioned into groups, each following a different search method—global, local, or intensification [22]. Additionally, XOR-based mutation operators have been used to more precisely perturb solutions in binary search spaces [33].

3.3.1. Influence of Parameters on the Final Outcome

The tuning of parameters in metaheuristic algorithms plays a critical role in their convergence, stability, and overall efficiency. In the hybrid version of the ABC algorithm applied to test case generation and optimization, several control parameters regulate the behavior of individual phases, the intensity of mutation, the depth of exploration, and the balance between exploration and exploitation (

Table 2. Key parameters and their influence.

Parameter	Valid Range	Default	Optimal	Description
FinalPopulationSelectionRatio	0.1–0.9	0.5	0.6–0.8	Proportion of population retained in final test suite
EliteSelectionRatio	0.0–0.8	0.5	0.3–0.6	Share of best test cases preserved between generations
TotalGenerations	10–150+	50	100–150	Number of ABC algorithm iterations
MutationRate	0.0–1.0	0.3	0.5–0.8	Probability of changing a value in a test case
CoolingRate	0.5–0.99	0.95	0.9–0.95	Rate of decreasing mutation activity (SA component)
OnlookerSelectionRatio	0.0–0.95	0.1	0.3–0.4	Proportion of solutions selected during onlooker phase
ScoutSelectionRatio	0.0–0.95	0.3	0.1–0.3	Proportion of stagnant solutions replaced by scouts
StagnationThresholdPercentage	0.3–0.9	0.75	0.3–0.75	Fraction of generations after which scout phase activates
EnableOnlookerSelection	true/false	false	true	Enables or disables the onlooker phase
EnableScoutPhase	true/false	false	true	Enables or disables the scout phase
EnforceMutationUniqueness	true/false	true	false	Allows only improving mutations (SA behavior)
AllowMultipleInvalidValues	true/false	true	false	Determines if multiple invalid values allowed per test

). Throughout this paper, algorithm parameters are denoted using PascalCase notation (e.g., MutationRate) when referring to specific implementation variables, while lowercase is used for general conceptual discussion.

Parameter importance was established through systematic sensitivity analysis comprising 970 test suite generations across 97 configurations, with 10 independent runs per configuration using different random seeds. Statistical significance was assessed using Welch’s t-tests with Cohen’s d effect sizes, revealing three distinct categories: Critical Impact Parameters (d > 15, p < 0.001) including MutationRate (d = 106.61), FinalPopulationSelectionRatio (d = 42.61), and TotalGenerations (d = 19.81) which require careful tuning; Moderate Impact Parameters like OnlookerSelectionRatio (d = 12.63, p < 0.05) providing measurable benefits; and Minimal Impact Parameters including EliteSelectionRatio, ScoutSelectionRatio, and StagnationThresholdPercentage (all d < 1.5, p > 0.05) where default values suffice. Particular attention should be given to the CoolingRate parameter, which implements Simulated Annealing behavior enabling controlled diversification at execution start and intensification toward completion [14]. The optimal configuration achieved 975.9 ± 10.6 points versus pairwise baseline of 580.0, representing 68.3% improvement (t(9) = 118.1, p < 0.001). These enhancements integrate techniques from multiple metaheuristic algorithms, combining advantages of global and local search while avoiding key limitations of the original ABC model.

3.3.2. Adaptive Scout Phase

In the classical ABC algorithm, the scout phase replaces stagnant solutions with entirely new ones generated at random. In the proposed approach, this phase is adapted and is activated only when the population does not improve beyond a predefined threshold (StagnationThresholdPercentage). Instead of performing a completely random replacement, the new solution is selected through an analysis of historical values in the population, thereby guiding the search toward unexplored or rarely occurring values [13,31]. The historical value analysis employs a three-tier tracking mechanism that evaluates diversity within each generation. A per-generation dictionary tracks unique values for each parameter position within the current population, awarding +25 points for first occurrences to incentivize diversity. Population-level tracking identifies covered values, enabling the algorithm to count novel contributions, while a diversity multiplier (1 + 0.25n, where n represents new values) amplifies scores for test cases introducing multiple unexplored values. A test case with three new values, for instance, receives +25 for each first-time value (75 points) plus an additional diversity bonus of 43.75 points (25 × 1.75 multiplier), totaling 118.75 bonus points. This per-generation resetting allows previously explored but discarded values to be reconsidered in new combinations as the population evolves, while elite selection preserves successful patterns across generations. When stagnation is detected, scout bees replace the bottom-performing solutions with mutated variants, maintaining systematic exploration while avoiding redundant testing of previously failed configurations. Having established the evaluation mechanism, we now describe how the hybrid algorithm integrates multiple metaheuristic strategies.

3.3.3. Directed Onlooker Selection via Restricted Candidate List

Instead of selecting solutions based on proportional probability relative to their fitness, the onlooker phase employs an approach inspired by the Restricted Candidate List. Only a subset of the best solutions is considered, which reduces the risk of oversaturation with homogeneous test cases and enables more controlled selection. This technique is characteristic of constructive metaheuristics and is frequently used to achieve a balance between exploitation and exploration [29].

3.3.4. Scout Bee Mechanism for Escaping Local Optima

In the classical ABC algorithm, the scout phase replaces stagnant solutions with entirely new ones generated at random. In our implementation, this phase is adapted and activated only when the population does not improve beyond a predefined threshold (StagnationThresholdPercentage). Instead of performing completely random replacement, the scout phase applies targeted mutations to the bottom-performing solutions, maintaining algorithmic continuity while still enabling escape from local optima [13,31]. The scout mechanism operates as follows: once the stagnation threshold is reached (typically after 30% of total generations), the algorithm identifies the poorest-performing test cases based on fitness scores. For each identified solution, scouts apply controlled mutations using the same mutation operator employed in the main evolution phase, ensuring consistency in the search strategy. The mutated variants are then added to the non-elite population pool, expanding the search neighborhood around poor solutions rather than abandoning them entirely. This mutation-based scout approach differs from classical ABC by maintaining partial information from existing solutions while injecting controlled diversity. The historical value tracking mechanism continues to operate, with the per-generation dictionary tracking unique values for each parameter position within the current population, awarding +25 points for first occurrences to incentivize diversity. Population-level tracking identifies covered values, enabling the algorithm to count novel contributions, while a diversity multiplier (1 + 0.25n, where n represents new values) amplifies scores for test cases introducing multiple unexplored values. A test case with three new values, for instance, receives +25 for each first-time value (75 points) plus an additional diversity bonus of 43.75 points (25 × 1.75 multiplier), totaling 118.75 bonus points. This scoring system ensures that even scout-generated mutations exploring new value combinations receive appropriate recognition. When stagnation is detected, scout bees apply mutations to the bottom-performing solutions, with these variants competing for inclusion in the next generation alongside elite and onlooker-selected solutions. This adapted scout mechanism balances exploration through targeted mutations with exploitation of existing knowledge, avoiding the complete information loss that random replacement would cause. Having established the evaluation mechanism, we now describe how the hybrid algorithm integrates multiple metaheuristic strategies.

3.3.5. Simulated Annealing and Hill Climbing (HC)

Simulated Annealing employs a decreasing temperature parameter that, in the early stages, allows the acceptance of weaker solutions to avoid premature convergence to local optima. As the temperature decreases over time, the process becomes more stable. This technique is particularly effective for multimodal functions and has been widely applied to test case optimization [14]. Hill Climbing is activated when the EnforceMutationUniqueness setting is enabled, such that only improving solutions are accepted. This behavior is characteristic of HC, a local search method where each step must lead to an improvement. Despite its simplicity, the algorithm is effective for fine-tuning and is commonly applied in the later phases of the search process [29].

3.3.6. Avoiding Duplicate Solutions (Tabu Search)

The algorithm incorporates a mechanism for detecting and avoiding previously used solutions by storing their hash representation. This behavior resembles Tabu Search, a technique in which a “tabu list” of prior solutions or moves is maintained in order to prevent cycling. Tabu Search is particularly effective in tasks where local convergence is rapid but undesirable [34].

3.3.7. Fast Local Search (FLS)

Although no dedicated local search phase is defined, the mutation logic acts as a Fast Local Search mechanism, since each mutation modifies only a single value. This results in a neighboring solution whose fitness is immediately evaluated. FLS accelerates exploration within a limited radius and is effective in large discrete spaces [29].

3.3.8. Combined Strategy with Genetic Algorithm Components

The hybrid implementation also incorporates elements from Genetic Algorithms, including the preservation of elite individuals, controlled mutation to maintain diversity, and selection of “parent” solutions based on fitness. Although crossover is not applied, the principles of natural selection and selective reproduction are present in the form of elite preservation and customized mutation [13,30]. By integrating additional strategies such as SA, GA, GLS, TS, HC, and FLS into the ABC algorithm, a hybrid optimization mechanism is created that can adapt its behavior to the specifics of the given problem. These techniques operate synergistically: SA and TS support global search and help avoid traps, while HC and FLS provide local refinement. GLS and RCL guide the selection process without restricting diversity. The combined use of these strategies makes the algorithm stable, flexible, and effective, particularly in tasks characterized by numerous input parameters and high combinatorial complexity.

3.4. Summary: When and Why to Use ABC

The Artificial Bee Colony algorithm provides an adaptive and extensible approach for addressing complex combinatorial problems in test design. By combining global and local search, adaptive selection mechanisms, and additional strategies such as elitism, mutation, temperature control, and negative selection, ABC has established itself as an effective tool for automated test case generation and optimization. The ABC algorithm is particularly suitable in the following scenarios. Multi-parameter input spaces where the number of possible test combinations grows exponentially. Situations requiring a balance between coverage and minimization of the test suite without compromising effectiveness. Cases where traditional techniques such as pairwise or boundary value analysis fail to adequately cover all boundary and negative scenarios. Situations that demand adaptive and automated value selection based on specific criteria such as uniqueness, category, or frequency. As highlighted in the studies of Mala and Mohan [13], as well as Srikanth et al. [31], the ABC approach not only produces more compact and informative test suites but also reduces the risk of missed defects, particularly in the presence of complex parameter interactions. Furthermore, the ability to integrate ABC with other metaheuristics such as Simulated Annealing, Guided Local Search, and Tabu Search makes the approach versatile and scalable, with strong potential for adaptation to diverse project requirements. To validate our theoretical contributions and demonstrate practical applicability, we conducted extensive experiments across diverse testing scenarios with rigorous statistical analysis.

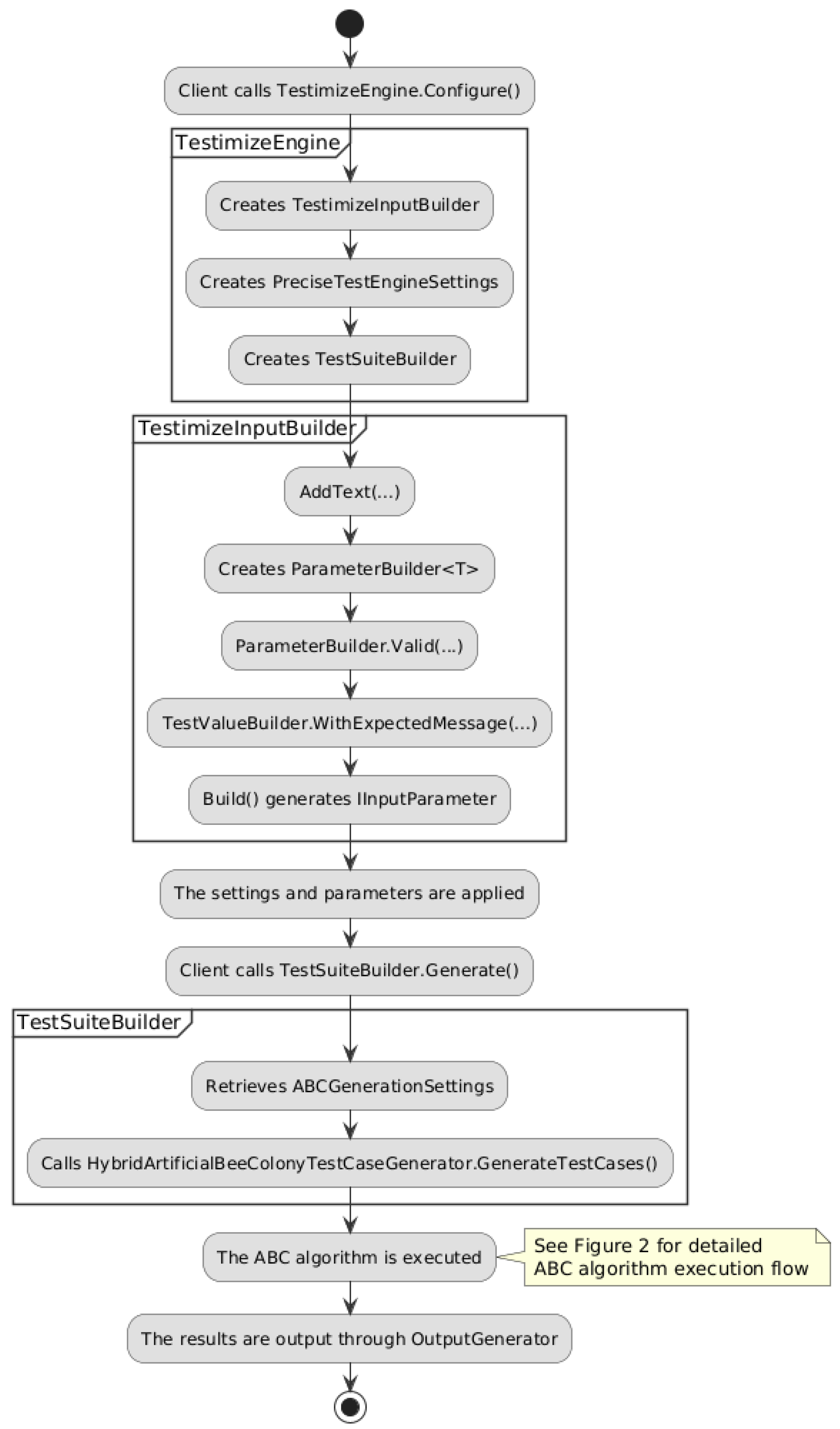
4. Program Implementation and Algorithm Logic

This section details the practical realization of our algorithm. We begin with the implementation architecture (Section 4.1), followed by the algorithm phases (Section 4.2), configuration parameters (Section 4.3), fitness evaluation (Section 4.4), and stagnation handling mechanisms (Section 4.5).

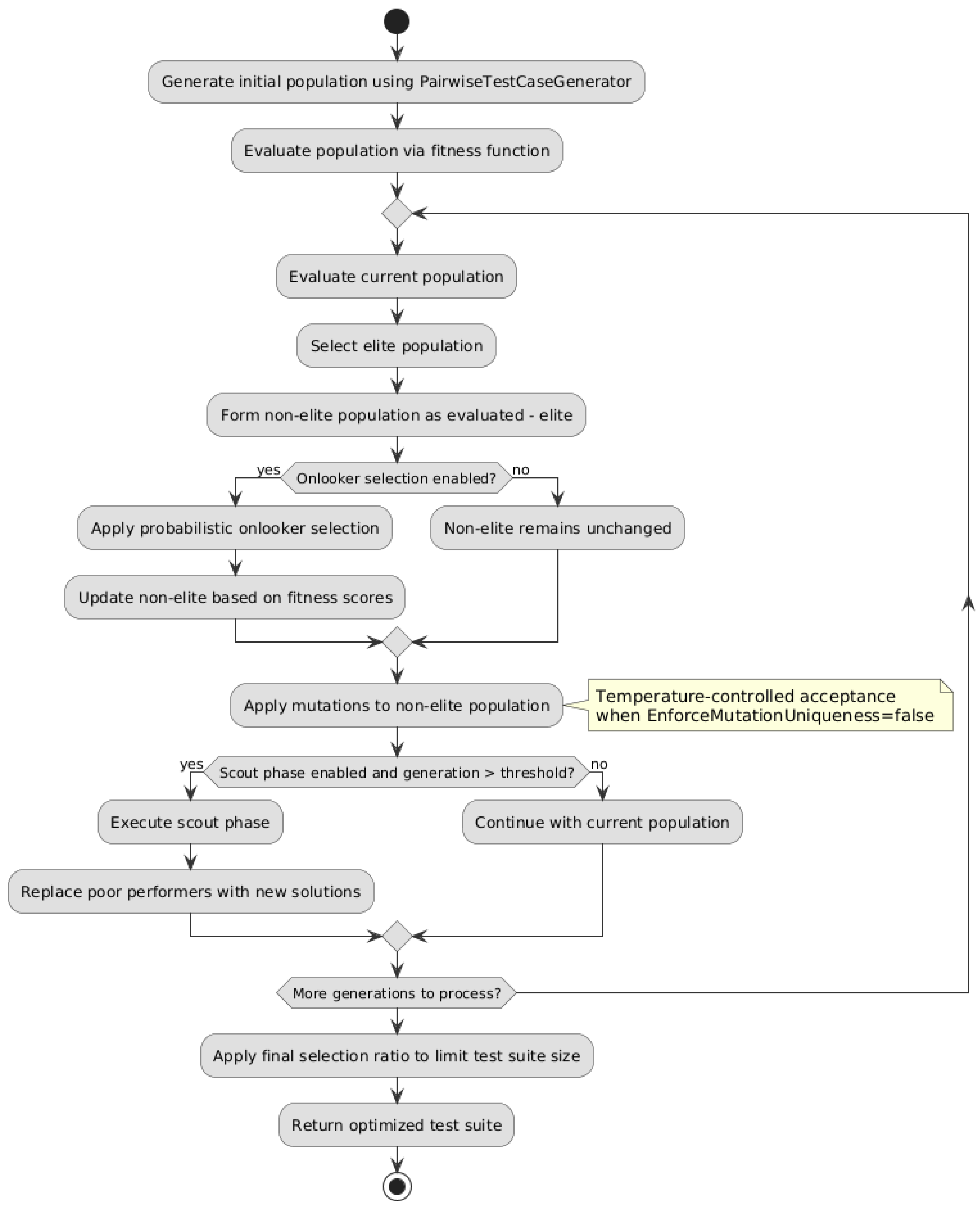
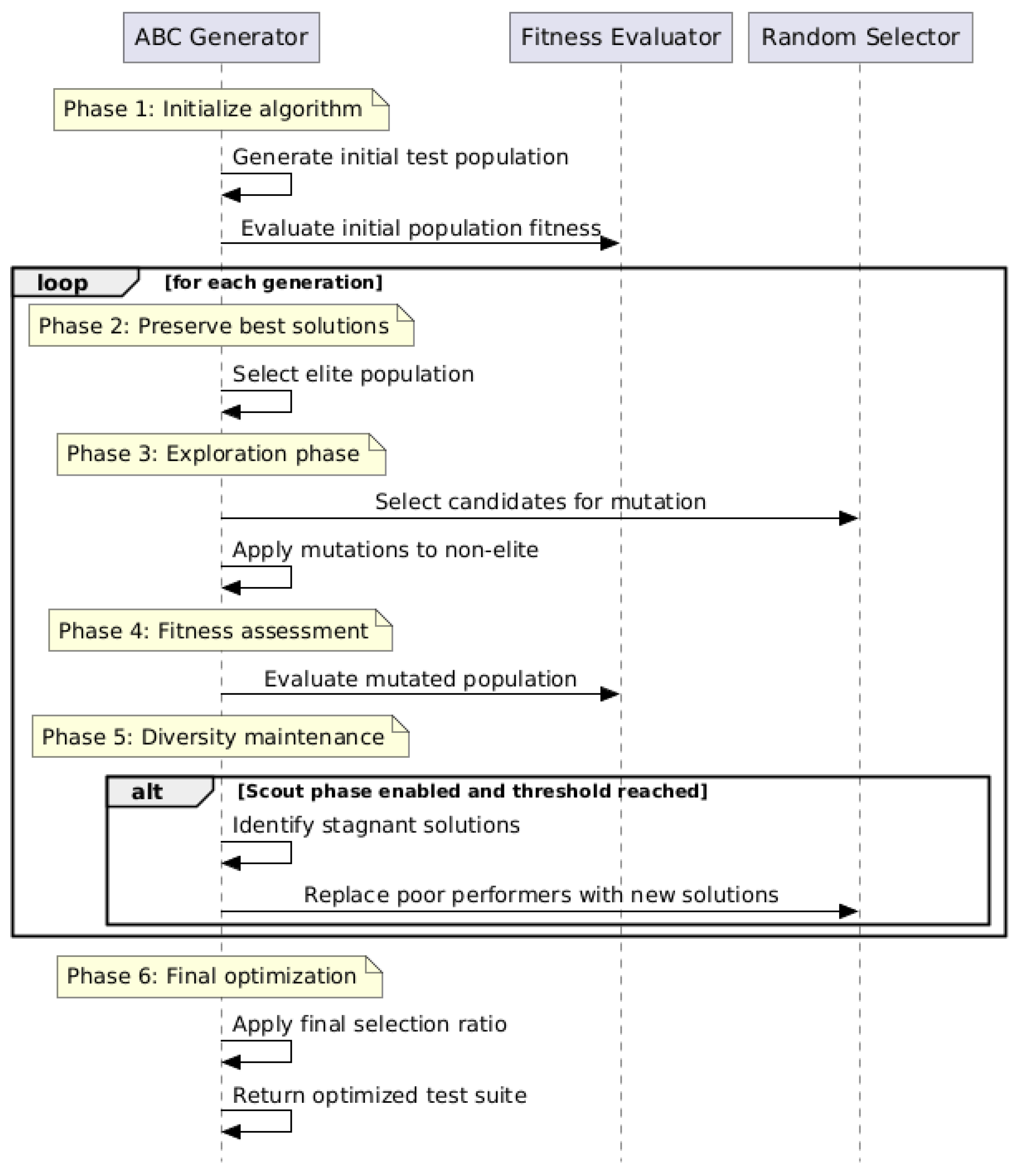
4.1. Implementation of the Hybrid Algorithm

The hybrid ABC algorithm has been implemented in a modular tool for automated test case generation called Testimize [35]. The architecture of the solution supports loosely coupled components through the use of interfaces for input parameters, generation, evaluation, and output. The generator, HybridArtificialBeeColonyTestCaseGenerator, employs IInputParameter, ITestCaseEvaluator, and ITestCaseOutputGenerator, which enables its application across different domains and testing environments. Configuration is performed through a declarative programming interface (Fluent API), allowing the user to define input parameters, the selected generator (e.g., ABC), and the algorithm settings. Once initiated, the tool invokes the configured generator, evaluator, and output generator. The entire process is illustrated in Figure 1. The generator is controlled by a configuration object that includes parameters such as the number of iterations, the percentage of elite selection, MutationRate, and the activation of scouting and onlooker phases. This design allows the algorithm to be adapted to diverse scenarios and objectives within the testing process.

4.2. Main Phases of the Hybrid ABC Algorithm

The diagram illustrates the flow of the hybrid ABC algorithm, highlighting the key steps and decisions made during the optimization of test cases (Figure 2).

This diagram on Figure 2 visualizes the internal logic of the RunABCAlgorithm() method in the HybridArtificialBeeColonyTestCaseGenerator class. It presents the principal phases of the algorithm: initialization and evaluation of the initial population; mutation; bee selection (elite, onlooker, scout); evaluation of the new population; stagnation checking; and final selection. Through loops, decision nodes, and clearly separated actions, the diagram depicts the complete control flow of the metaheuristic optimization. The detailed presentation of the algorithm in pseudocode is given as Algorithm 1.

Algorithm 1.  Hybrid ABC Test Case Generation

Input: Parameters P, TestValues V, Settings S Output: Optimized test suite T      population ← GeneratePairwiseSeeds(P, V)      for generation = 0 to S.TotalGenerations − 1 do        // Evaluate population (history cleared once at start)        EvaluatePopulation(population)        // Elite Selection        eliteSize ← max(1, |population| × S.EliteRatio)        elites ← SelectTop(population, eliteSize)        nonElites ← population \ elites        // Onlooker Phase − Modify non-elite pool        if S.EnableOnlookerSelection then         nonElites ← ProbabilisticSelection(nonElites, population, S.OnlookerRatio)        end if        // Mutation Phase with SA        temperature ← max(0.1, 1.0 × S.CoolingRate^generation)        for each tc in nonElites do         mutant ← ApplyMutation(tc, S.MutationRate) // Mutation rate check inside         if mutant ≠ tc AND mutant ∉ population then           if S.EnforceMutationUniqueness then             if Fitness(mutant) > Fitness(tc) then               Replace(population, tc, mutant)             end if           else             Δf ← Fitness(mutant) − Fitness(tc)             if Δf > 0 OR Random() < exp(Δf/temperature) then               Replace(population, tc, mutant)             end if           end if         end if        end for        // Scout Phase        threshold ← S.TotalGenerations × S.StagnationThreshold        if S.EnableScoutPhase AND generation ≥ threshold then         scoutCount ← max(1, |population| × S.ScoutRatio)         poorPerformers ← SelectBottom(population, scoutCount)         for each tc in poorPerformers do           mutant ← ApplyMutation(tc, S.MutationRate)           Add(nonElites, mutant)         end for        end if      end for      // Final Selection      finalSize ← max(1, |population| × S.FinalPopulationRatio)      T ← SelectTop(population, finalSize)      return T

Algorithm 1 presents the main flow of the Hybrid ABC algorithm. The algorithm begins by initializing the population using pairwise test cases (line 1) to ensure baseline coverage. The use of pairwise testing for initial population generation leverages an established combinatorial testing technique [7] that guarantees coverage of all two-way parameter interactions with a minimal test suite. While debates exist about pairwise testing’s limitations [10], recent systematic reviews confirm its effectiveness as a foundation for further optimization [27]. This approach provides the ABC algorithm with a structured, high-coverage starting point (typically 30–50 test cases) that can be enhanced through evolutionary refinement, achieving better results than either technique alone while maintaining computational feasibility essential for CI/CD integration. The main loop (lines 2–40) executes for the specified number of generations, where each iteration consists of three phases: the mutation phase (lines 15–29) where non-elite solutions undergo mutation with either strict improvement enforcement or Simulated Annealing probabilistic acceptance based on temperature; the onlooker bee phase (lines 10–12) that modifies the non-elite pool through probabilistic selection weighted by fitness scores with added randomness to maintain diversity; and the scout bee phase (lines 31–39) that activates after a stagnation threshold to add mutated variants to the non-elite pool. The temperature calculation (line 14) implements the Simulated Annealing component, progressively reducing exploration intensity through exponential decay. The population evaluation (line 4) maintains a global history that persists across all generations to track and reward discovering values not yet seen throughout the entire optimization process. The final population selection (lines 42–43) uses FinalPopulationSelectionRatio to balance test suite size against quality.

4.3. Configuration Parameters and Adaptive Behavior

The behavior of the hybrid ABC algorithm is governed by the configuration class ABCGenerationSettings, which provides detailed control over phases, mutation dynamics, and selection mechanisms. Proper parameter configuration directly affects the balance between exploitation (using the best solutions) and exploration (searching for new values), as well as the efficiency and stability of the algorithm. The parameter TotalGenerations defines the number of iterations (generations) in which the algorithm searches for improvements. Values above 50 typically lead to more stable optimization in complex input spaces. The MutationRate determines the probability of mutating values in test cases. Typical values between 0.4 and 0.6 foster diversity, while excessively high rates may compromise stability. The EliteSelectionRatio controls the percentage of top-performing solutions preserved unchanged for the next generation. Higher values (e.g., 0.6) accelerate convergence but limit the exploration of new solutions. The FinalPopulationSelectionRatio specifies what portion of the final population is returned as output. Lower ratios result in smaller but higher-quality test sets. The parameters EnableOnlookerSelection and OnlookerSelectionRatio activate the selection of non-elite solutions based on their fitness, which enhances adaptive selection and leads to more informative value combinations. Similarly, EnableScoutPhase and ScoutSelectionRatio manage the scout phase, where part of the population is replaced with random values. This phase is triggered in cases of stagnation and is particularly effective for avoiding local optima. The activation threshold for the scout phase is defined by the parameter StagnationThresholdPercentage, which specifies the fraction of generations without improvement before replacement occurs. A typical value is 0.75 (75%). When EnforceMutationUniqueness is enabled, the algorithm only accepts improving mutations, making its behavior equivalent to Hill Climbing. When disabled, probabilistic mechanisms inspired by Simulated Annealing allow the acceptance of weaker solutions in the early search phases. In addition, the parameter CoolingRate regulates mutation aggressiveness across generations through gradual “cooling.” Finally, AllowMultipleInvalidInputs indicates whether more than one invalid value is permitted in a single test case. When set to false, the algorithm applies stricter control over negative testing. Through careful tuning of these parameters, the hybrid ABC algorithm can be adapted to various objectives, such as minimizing the number of tests, maximizing coverage, or focusing on boundary and invalid scenarios. In practice, parameter values are best calibrated empirically, depending on the specific characteristics of the input data and the requirements for test case quality. With parameters configured, the algorithm evaluates solutions through the multi-component fitness function described next.

4.4. Evaluation of Solutions: Fitness Function

The evaluation function plays a central role in the evolution of the population of test cases. It determines the utility of each test based on several criteria: the category of values (valid, boundary, invalid), the global and local uniqueness of the inputs, and possible penalties for the excessive use of defective values. The inclusion of bonuses for newly introduced values encourages diversity, increases coverage, and improves the likelihood of detecting defects. An illustrative algorithm for computing the fitness score is presented in Algorithm 2.

Algorithm 2. Evaluate Test Case Fitness

Input: TestCase tc, Population P, GlobalHistory H Output: Fitness score 1: score ← 0 2: firstTimeCount ← 0 3: invalidCount ← Count(tc.Values where Category ∈ {Invalid, BoundaryInvalid}) 4: // Initialize count for population-unique values 5: if NOT AllowMultipleInvalid AND invalidCount > 1 then 6:  return -50 × invalidCount 7: end if 8: coveredValues ← GetCoveredValues(P) 9: for i = 0 to |tc.Values| − 1 do 10:  value ← tc.Values[i] 11:  // Base score by category 12:  switch value.Category do 13:    BoundaryValid: score ← score + 20 14:    Valid:     score ← score + 2 15:    BoundaryInvalid: score ← score − 1 16:    Invalid:     score ← score − 2 17:  end switch 18:  // Initialize global history for this parameter position if needed 19:  if i ∉ H.SeenValues then 20:    H.SeenValues[i] ← ∅ 21:  end if 22:  // Global first-time bonus (across all generations) 23:  if value ∉ H.SeenValues[i] then 24:    H.SeenValues[i].Add(value) 25:    score ← score + 25 26:  end if 27:  // Check if value is new to current population 28:  if i ∉ coveredValues OR value ∉ coveredValues[i] then 29:    firstTimeCount ← firstTimeCount + 1 30:    coveredValues[i].Add(value) 31:  end if 32: end for 33: // Diversity amplification 34: if firstTimeCount > 0 then 35:  multiplier ← 1 + firstTimeCount × 0.25 36:  score ← score + (25 × multiplier) 37: end if 38: return score

Algorithm 2 defines the fitness evaluation function central to the optimization process. The algorithm first counts invalid values (line 3) and checks for multiple invalid values (lines 5–7), applying severe penalties (−50 per invalid) when AllowMultipleInvalidValues is disabled to guide generation toward realistic test scenarios. The core scoring mechanism (lines 12–17) implements a four-tier categorical discrimination system: BoundaryValid (+20), Valid (+2) for normal equivalent values, BoundaryInvalid (−1) for edge cases needing coverage, and Invalid (−2) for error handling paths. The evaluation employs two distinct diversity mechanisms. First, the global first-time bonus (lines 23–26) rewards discovering values not yet seen throughout the entire optimization process with +25 points per value, maintaining a persistent history (GlobalHistory H) that tracks all values encountered across all generations. Second, population-level uniqueness tracking (lines 28–31) identifies values that are new to the current population being evaluated, incrementing a counter for each unique contribution. The diversity amplification mechanism (lines 34–36) then applies a compound bonus of 25 × (1 + 0.25 × firstTimeCount) based on the number of population-unique values, significantly boosting scores for test cases that introduce multiple new values to the current population. These two mechanisms work synergistically, a value that is globally novel receives both the +25 global bonus and contributes to the population-level diversity multiplier, while a value that was seen in previous generations but is new to the current population only contributes to the multiplier. This dual-layer approach ensures both long-term exploration across the entire search space and short-term diversity within each generation. To prevent duplicate test cases in the population, each solution is validated through a hash function based on its parameter values, enabling efficient duplicate detection using HashSet in a manner analogous to tabu search [34].

4.5. Stagnation Handling and Cooling Mechanisms

The mutation phase is applied to the non-elite portion of the population with the aim of generating new, diverse, and potentially superior test cases. In the hybrid implementation, two main strategies are employed: hill climbing, in which only improving solutions are accepted, and simulated annealing, which allows for the controlled acceptance of temporary deteriorations. Temperature control is governed by the parameter CoolingRate, which affects the probability of accepting weaker solutions as iterations progress. When EnforceMutationUniqueness is enabled, the algorithm accepts only improving mutations; when disabled, it employs a temperature-based probability model for acceptance. The pseudocode of the core mutation logic is shown in Algorithm 3.

Algorithm 3. Mutate Population

Input: nonElitePopulation, parameters, iteration Output: updatedPopulation  1: temperature ← max(0.1, 1.0 × CoolingRate^generation)  2: for each original in nonElitePopulation do  3:   mutated ← ApplyMutation(original, parameters) // MutationRate check inside  4:   if mutated ≠ original and mutated ∉ evaluatedPopulation then  5:     originalScore ← Evaluate(original)  6:     mutatedScore ← Evaluate(mutated)  7:     if EnforceMutationUniqueness then  8:       accept ← mutatedScore > originalScore  9:     else  10:      Δ ← mutatedScore − originalScore  11:      acceptance ← exp(Δ / temperature)  12:      accept ← Δ > 0 or random() < acceptance  13:    end if  14:    if accept then  15:      Replace original with mutated in evaluatedPopulation  16:    end if  17:  end if  18: end for

Algorithm 3 implements the mutation phase (employed bee phase) of the hybrid ABC algorithm. The algorithm processes each test case in the non-elite population, with ApplyMutation internally applying mutations based on MutationRate probability by randomly selecting a parameter position and replacing its value with another valid value from that parameter’s test value set. The decision to accept mutations follows one of two modes controlled by EnforceMutationUniqueness: when enabled, only fitness improvements are accepted; when disabled, the algorithm employs Simulated Annealing acceptance where improvements always succeed and degradations are accepted based on temperature-controlled probability. The temperature calculation uses Algorithm 1’s cooling schedule, progressively decreasing exploration probability through exponential decay. In the Simulated Annealing mode, high temperatures early in the search allow frequent inferior moves for exploration while low temperatures in later iterations restrict acceptance to exploitation. Successfully accepted mutations immediately replace their originals in the population, maintaining constant population size while preventing duplicates through validation checks. A visual representation of this process is provided in Figure 3, which illustrates the iterative algorithm flow and the synergy between mutation and other phases using a UML sequence diagram. With the implementation complete, we now present comprehensive experimental results demonstrating the algorithm’s effectiveness across various scenarios.

5. Analysis of Experimental Results

Our experimental evaluation addresses the three research questions through systematic analysis. We first describe the configuration and evaluation criteria (Section 5.1), present the experimental scenarios (Section 5.2), analyze comparative results (Section 5.3), discuss key findings (Section 5.4), and examine advantages and limitations (Section 5.5).

5.1. Configuration and Evaluation Criteria

The experiments employed a hybrid version of the Artificial Bee Colony algorithm, which combines its classical phases (employed, onlooker, and scout) with additional mechanisms such as elite selection, adaptive mutation with temperature control, and dynamic weighting during selection. The objective was to minimize the number of generated test cases without compromising coverage. The specific configuration included a total number of generations of 100, a MutationRate of 0.5, a preserved population ratio of 0.6, and an elite selection ratio of 0.6. Both the onlooker and scout phases were activated, thereby ensuring a balance between diversity and stability throughout the evolutionary process. The input parameters used in the experiments covered typical scenarios such as a name field (length between 5 and 20 characters), email address (between 6 and 20 characters, including both valid and invalid formats), age (in the range of 14–99), and phone number (between 5 and 10 digits, including boundary and invalid values). The values were classified according to the techniques of Equivalence Partitioning and Boundary Value Analysis. The fitness function combines several components to determine the utility of a given test case. The main criteria include: (i) classification of values according to their validity (valid, boundary valid, invalid, boundary invalid), (ii) global and local uniqueness with respect to previously generated tests, (iii) diversity among individual test cases, (iv) penalties for an excessive number of invalid values, and (v) bonuses for discovering new values. The result of the function is a numerical score that is used to rank and select tests according to their quality. For comparison of results, the following quantitative metrics are applied: the average score achieved by the ABC algorithm (ABC Avg Score), the corresponding score obtained with the Pairwise approach (Pairwise Avg Score), and the percentage improvement of ABC over Pairwise (Improvement Over Pairwise).

5.2. Experimental Scenario and Results

To evaluate the effectiveness of the proposed hybrid ABC algorithm, a series of experiments were conducted under different configurations. The impact of key parameters was investigated, including the number of generations, MutationRate, the ratios of elite selection and preserved population, as well as the effect of enabling or disabling specific algorithm phases (onlooker and scout). For each configuration, a set of test cases was automatically generated using the ABC algorithm and compared with an equivalent set obtained through the baseline pairwise approach. The test parameters covered combinations of valid, boundary, and invalid values, with the effectiveness of the generated tests measured using the defined fitness function. The methodology consisted of four main steps: generation of an initial set of parameters, execution of pairwise generation as a baseline, application of optimization via the hybrid ABC algorithm, and calculation of average results, followed by comparative analysis.

5.3. Comparative Analysis of Results

The highest score for scenarios with mixed input values was observed under a configuration with 100 generations, a MutationRate of 0.5, and both onlooker and scout phases enabled. Under these conditions, the Hybrid ABC algorithm achieved a mean fitness value of 975.9 ± 10.6 points across 10 independent runs, compared to 580.0 ± 0.0 points for the pairwise baseline, corresponding to an improvement of 68.3% (t(9) = 118.1, p < 0.001). The 95% confidence interval [968, 984] demonstrates consistent performance with low variance (CV = 1.09%). Lower scores were obtained with fewer generations (e.g., 50 generations yielding 896.3 ± 11.0), reduced MutationRate values (0.35–0.4), or when the additional phases were disabled. The phase ablation study (configurations 2–5 in

Table 3. Statistical Analysis of ABC Algorithm Performance with Mixed Input Scenarios (n = 10 seeds).

ID	Gen	MR	FPR	ESR	Onlk	Scout	ABC	Pairwise	95% CI	Δ%	t	p
*1	150 *	0.80	0.60	0.60	Y	Y	976.0 ± 10.5	580 ± 0	[968–984]	68.3	118.8	<0.001
*2	100 *	0.50	0.60	0.30	Y	Y	975.9 ± 10.6	580 ± 0	[968–983]	68.3	118.1	<0.001
3	100	0.50	0.60	0.30	Y	N	973.5 ± 7.9	580 ± 0	[968–979]	67.8	157.4	<0.001
4	100	0.50	0.60	0.30	N	Y	971.6 ± 2.3	580 ± 0	[970–973]	67.5	545.4	<0.001
5	100	0.50	0.60	0.30	N	N	970.9 ± 0.3	580 ± 0	[971–971]	67.4	390.9	<0.001
*6	100 *	0.50	0.60	0.60	Y	Y	976.0 ± 10.5	580 ± 0	[968–984]	68.3	118.8	<0.001
7	50	0.45	0.50	0.50	Y	Y	896.3 ± 11.0	775 ± 0	[888–904]	15.7	34.9	<0.001
8	50	0.35	0.55	0.45	Y	Y	922.2 ± 7.3	780 ± 0	[917–927]	18.2	61.7	<0.001
9	50	0.40	0.50	0.50	Y	Y	895.5 ± 12.1	775 ± 0	[887–904]	15.5	31.6	<0.001
10	60	0.50	0.50	0.70	Y	Y	887.1 ± 11.4	775 ± 0	[879–895]	14.5	31.0	<0.001
11	70	0.60	0.50	0.60	Y	Y	895.5 ± 12.1	775 ± 0	[887–904]	15.5	31.6	<0.001
12	100	0.70	0.50	0.60	N	N	898.0 ± 10.5	775 ± 0	[890–906]	15.9	36.9	<0.001
13	100	0.80	0.40	0.60	N	N	743.5 ± 12.1	678 ± 0	[735–752]	9.7	17.2	<0.001
14	100	0.40	0.50	0.50	N	N	898.0 ± 10.5	775 ± 0	[890–906]	15.9	36.9	<0.001
15	100	0.40	0.40	0.50	N	N	746.0 ± 12.9	678 ± 0	[737–755]	10.0	16.7	<0.001

Gen = Generations, MR = MutationRate, FPR = Final Population Ratio, ESR = EliteSelectionRatio, Onlk = Onlooker Phase, Scout = Scout Phase. * Best performing configurations (68.3% improvement). Pairwise baseline is deterministic, producing consistent output across all runs. All scores represent mean ± standard deviation from 10 independent runs. Statistical significance assessed using Welch’s t-test (df = 9).

) reveals that while both phases contribute to performance, their impact is marginal, removing both phases reduces improvement by only 0.9% (from 68.3% to 67.4%) but dramatically reduces variance (SD from 10.6 to 0.3), suggesting the phases primarily contribute exploration capability rather than core optimization power. The weakest performance, 743.5 ± 12.1 points, was recorded at a high MutationRate of 0.8 combined with a low final population ratio of 0.4, which led to the loss of stable and effective test cases. All configurations demonstrated statistically significant improvements over the baseline (p < 0.001), confirming the robustness of the hybrid ABC approach across diverse parameter settings.

For input data containing only valid values, the optimal configuration again includes 100 generations and a MutationRate of 0.5, achieving a mean score of 1052.5 ± 17.7 points across 10 independent runs compared to 885.0 ± 0.0 with the pairwise approach. This corresponds to an improvement of 18.9% (t(9) = 30.0, p < 0.001), with a 95% confidence interval of [1040, 1065]. Interestingly, the configuration with only the onlooker phase enabled slightly outperformed the full algorithm (18.9% vs. 18.6%), though this difference is not statistically significant. The onlooker and scout phase analysis (configurations 2–5) reveals minimal impact on performance for valid-only inputs, both phases achieve 18.6%, onlooker-only achieves 18.9%, scout-only achieves 17.8%, and neither phase achieves 17.5%, suggesting that for valid-only scenarios, the phases provide marginal benefit. A decline in performance is observed when the MutationRate is excessively high (0.8 yielding only 763.0 ± 10.5 points) or when the final population ratio is reduced to 0.4. All configurations demonstrated statistically significant improvements over their respective baselines (p < 0.001). The detailed measured results and their analysis are presented in

Table 4. Statistical Analysis of ABC Algorithm Performance with Valid-Only Inputs (n = 10 seeds).

ID	Gen	MR	FPR	ESR	Onlk	Scout	ABC	Pairwise	95% CI	Δ%	t	p
1	150	0.80	0.60	0.60	Y	Y	1040.0 ± 16.7	885 ± 0	[1028–1052]	17.5	29.4	<0.001
2	100	0.50	0.60	0.30	Y	Y	1050.0 ± 21.1	885 ± 0	[1035–1065]	18.6	24.8	<0.001
*3	100	0.50	0.60	0.30	Y	N	1052.5 ± 17.7	885 ± 0	[1040–1065]	18.9	30.0	<0.001
4	100	0.50	0.60	0.30	N	Y	1042.5 ± 18.5	885 ± 0	[1029–1056]	17.8	27.0	<0.001
5	100	0.50	0.60	0.30	N	N	1040.0 ± 20.4	885 ± 0	[1025–1055]	17.5	24.0	<0.001
6	100	0.50	0.60	0.60	Y	Y	1050.0 ± 12.9	885 ± 0	[1041–1059]	18.6	40.4	<0.001
7	50	0.45	0.50	0.50	Y	Y	914.5 ± 24.9	807 ± 0	[897–932]	13.3	13.7	<0.001
8	50	0.35	0.55	0.45	Y	Y	952.6 ± 15.1	833 ± 0	[942–963]	14.4	25.1	<0.001
9	50	0.40	0.50	0.50	Y	Y	912.0 ± 11.8	807 ± 0	[904–920]	13.0	28.2	<0.001
10	60	0.50	0.50	0.70	Y	Y	922.0 ± 12.9	807 ± 0	[913–931]	14.3	28.2	<0.001
11	70	0.60	0.50	0.60	Y	Y	912.0 ± 11.8	807 ± 0	[904–920]	13.0	28.2	<0.001
12	100	0.70	0.50	0.60	N	N	927.0 ± 12.9	807 ± 0	[918–936]	14.9	29.4	<0.001
13	100	0.80	0.40	0.60	N	N	763.0 ± 10.5	696 ± 0	[755–771]	9.6	20.1	<0.001
14	100	0.40	0.50	0.50	N	N	914.5 ± 18.5	807 ± 0	[901–928]	13.3	18.4	<0.001
15	100	0.40	0.40	0.50	N	N	773.0 ± 12.9	696 ± 0	[764–782]	11.1	18.9	<0.001

Gen = Generations, MR = MutationRate, FPR = FinalPopulationRatio, and ESR = EliteSelectionRatio. * Best performing configurations (18.9% improvement). Pairwise baseline is deterministic, producing consistent output across all runs. All scores represent mean ± standard deviation from 10 independent runs. Statistical significance assessed using Welch’s t-test (df = 9).

.

5.3.1. Behavior with Activation/Deactivation of Onlooker and Scout Phases

A clear impact of the additional Onlooker and Scout phases on the quality of the generated test cases has been observed. Activating these phases improves results by reducing the loss of valuable test cases. Conversely, when these phases are deactivated, the algorithm demonstrates weaker performance and lower improvement compared to pairwise testing. In the conducted experiments, configurations without Onlooker and Scout reported significantly lower average scores and smaller improvement percentages (in some cases only ~12% improvement of ABC over pairwise, in contrast to ~67% when the phases were enabled). This demonstrates that the phases contribute to maintaining population diversity and preventing the premature loss of potentially valuable test cases.

5.3.2. Influence of Parameters Such as MutationRate, EliteRatio, CoolingRate, and Others

The experimental results indicate that the parameters of the ABC algorithm have a substantial effect on its efficiency. A higher number of iterations (e.g., 100 generations) combined with a moderate MutationRate (≈0.5) yields the best results, with the algorithm achieving both high scores and significant improvements over pairwise testing under these conditions. Reducing the number of generations (e.g., to 50) or employing a low MutationRate (e.g., 0.3–0.4) leads to weaker results and incomplete utilization of the defect-detection potential. Conversely, an excessively high MutationRate (>0.7) has a negative effect, resulting in a decline in solution quality due to the loss of high-quality test cases and instability across generations. Other parameters also play a role. The EliteSelectionRatio (the percentage of the best test cases carried over to the next generation) and the FinalPopulationSelectionRatio (the portion of the population preserved after each generation) need to be balanced. Very low values (e.g., preserving less than 50% of the population) may lead to the loss of valuable information and diversity, while overly high values diminish the effect of selection. An additional parameter, the CoolingRate, has been introduced as a factor for adaptively decreasing the MutationRate during execution (similar to the concept of simulated annealing). Although its effect is not central to this study, in principle, decreasing the MutationRate over successive generations helps stabilize the search around an optimal solution. Overall, proper parameter tuning (e.g., TotalGenerations = 100, MutationRate = 0.5, Onlooker/Scout phases enabled, and balanced selection ratios) provides the best trade-off between diversity and stability of the generated test cases. These comparative analyses reveal important patterns that warrant deeper examination.

5.4. Results and Observations

One of the primary aspects in evaluating the effectiveness of the proposed hybrid algorithm is its comparison with the traditional pairwise approach in terms of the number of generated test cases. In the considered experimental scenario involving four input parameters with valid and invalid values, the pairwise method produced 37 test cases, whereas the hybrid ABC algorithm achieved comparable functional coverage with only 11 test cases. This more than threefold reduction clearly demonstrates the advantage, particularly in large-scale systems where test execution and analysis time is critical. Beyond the quantitative reduction, significant differences in coverage quality are observed. While the pairwise approach, by design, ensures the combination of all parameter pairs, it does not guarantee comprehensive inclusion of boundary and invalid values. In certain configurations, frequent repetition of common values and omission of extreme inputs are observed, which are critical for defect detection. The hybrid ABC algorithm, through its fitness function and adaptive mechanisms, incorporates a wide spectrum of valid, boundary, and invalid values, with a targeted emphasis on critical cases. The resulting tests show a more balanced distribution and considerably higher efficiency in anomaly detection, despite their smaller number. As the number of parameters and values increases, the advantages of the ABC approach become even more pronounced. While pairwise testing leads to a combinatorial increase in the number of test cases particularly in scenarios with multifactor interactions the ABC algorithm applies evolutionary search to select only the most informative test cases. This enables better scalability and adaptability in highly complex systems where traditional techniques become less practical. The concept of test prioritization through evolutionary algorithms has been successfully applied in comparisons of Genetic Algorithms and the Bat Algorithm for regression testing [36]. Their analysis, based on the APFD metric, demonstrated the importance of prioritization over brute-force strategies. A similar analysis can be employed when comparing ABC with other baseline techniques.

5.5. Advantages and Limitations of Each Approach

The proposed hybrid ABC algorithm offers several significant advantages. First, it enables adaptive optimization of tests through the use of a fitness function and evolutionary mechanisms that direct the search toward more informative combinations. This leads to higher coverage of rare and boundary cases with a minimal number of tests. Second, the algorithm significantly reduces the total number of tests without compromising quality, focusing on critical values and interactions. Third, it ensures a high degree of diversity by including unique values and unconventional combinations, thereby increasing the likelihood of defect detection. Fourth, the method is flexible and extensible, it allows parameter tuning according to the specific context and can be easily integrated with automated testing tools. Among the limitations of the ABC approach are the need for parameter tuning, where improper configuration may lead to suboptimal results; the stochastic nature of the algorithm, which causes variability between executions unless initial conditions are fixed; and the lack of a guarantee for complete pairwise coverage, which may result in the omission of certain specific interactions between values. In contrast, the pairwise method has its own distinctive advantages. It is systematic, easy to apply, and fully deterministic always generating the same set of test cases for given input values. It guarantees coverage of all parameter pairs, which is sufficient in many typical scenarios. Furthermore, for a moderate number of parameters, the method provides a good compromise between exhaustiveness and applicability. Its main limitations include the inability to combine multiple boundary values simultaneously, which may lead to omission of critical scenarios; the lack of a mechanism for prioritizing values according to risk or importance; and the tendency to generate a large number of test cases when input spaces become more complex. The strong experimental results confirm our approach’s effectiveness. We now reflect on the implications, limitations, and future research directions.

6. Conclusions

This study investigated three fundamental research questions about hybrid metaheuristic approaches in test case generation. Our hybrid ABC-SA algorithm achieved 68.3% improvement over pairwise testing (975.9 ± 10.6 vs. 580.0 ± 0.0, p < 0.001, d = 42.61), demonstrating that the synergy between ABC’s global exploration and SA’s temperature-controlled exploitation creates a robust optimization framework. The four-tier categorical discrimination system proved essential, with uniform weight configurations degrading performance by 7.25% (p < 0.001), validating that the architecture of value categorization matters more than precise weight calibration. Statistical analysis across 970 test suite generations identified three critical parameters: MutationRate (d = 106.61), FinalPopulationSelectionRatio (d = 42.61), and TotalGenerations (d = 19.81) while five parameters showed negligible impact, enabling simplified configuration. The primary contribution lies in demonstrating that hybrid metaheuristic approaches, when properly adapted with categorical fitness functions and rigorous statistical validation, can achieve substantial improvements over traditional methods. Implementation challenges included managing parameter interdependencies through comprehensive sensitivity analysis and addressing stochastic variability through multiple seed validation. Current limitations include sensitivity to initial configuration of critical parameters, the stochastic nature requiring multiple runs for stable results, and potential scalability challenges for very large parameter spaces not yet tested.

Future research directions include developing adaptive fitness functions that dynamically adjust weights based on test suite characteristics, implementing parallel execution strategies to improve scalability, and extending the approach to multi-objective optimization where coverage, diversity, and test count are simultaneously optimized. Integration with AI-assisted testing tools could enable context-aware test generation, though this requires further investigation. This work demonstrates that hybrid metaheuristic approaches, when properly adapted with categorical fitness functions and rigorous statistical validation, can achieve substantial improvements over traditional methods, positioning this research as a foundation for more intelligent and adaptive automated testing solutions.