Optimized Hybrid Deep Learning Framework for Short-Term Power Load Interval Forecasting via Improved Crowned Crested Porcupine Optimization and Feature Mode Decomposition
Abstract
1. Introduction
1.1. Review
1.2. Research Gap and Contributions
- (1)
- Proposed a three-strategy improved CPO Algorithm, which is used to optimize the hyperparameters of other algorithms in the forecasting model, enhancing its performance in complex optimization problems.
- (2)
- Adopted the ICPO-FMD algorithm for load value decomposition.
- (3)
- Designed an ICPO-QR-CNN-BiGRU-Attention interval forecasting model combined with ICPO-GMM and ICPO-FMD algorithms.
- (4)
- Comparative experiments, supported by sensitivity and interpretability analyses, demonstrate the proposed algorithm’s superiority over traditional methods.
2. Short-Term Electricity Load Interval Forecasting via Improved Crowned Crested Porcupine Optimization and Feature Mode Decomposition
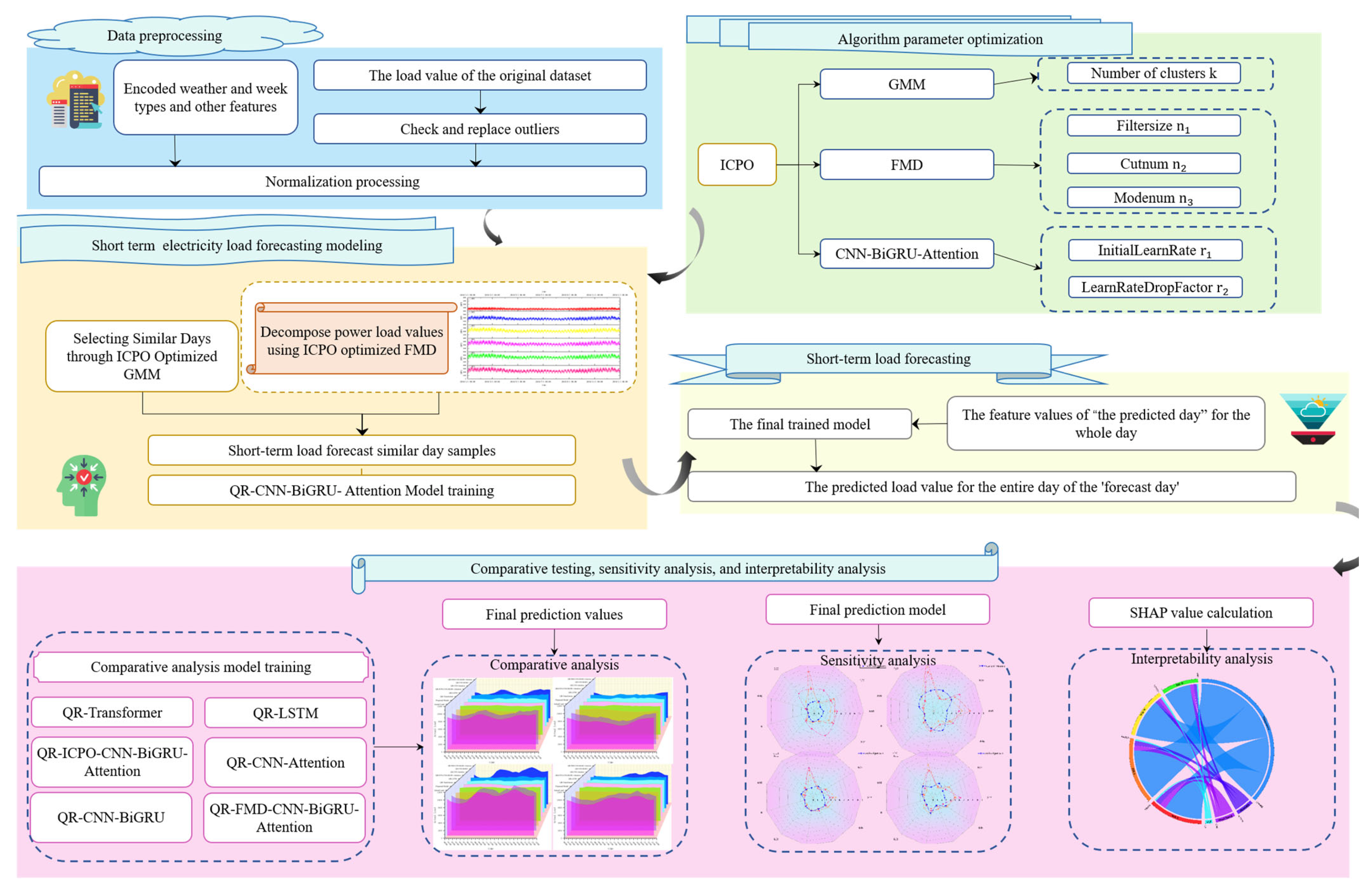
2.1. Data Preprocessing
2.1.1. Outlier Handling
2.1.2. Normalization
2.2. Related Work
2.2.1. GMM
2.2.2. FMD
- (1)
- Finite Impulse Response Filter Initialization
- (2)
- Correlated Kurtosis(CK)
2.2.3. CNN

2.2.4. BiGRU
- (1)
- Reset Gate
- (2)
- Update Gate
- (3)
- Candidate Hidden State
2.2.5. Attention Mechanism
2.2.6. Three-Strategy Improved CPO Algorithm and Its Optimization
| Algorithm 1: CPO Optimization Algorithm for Three Strategy Optimization |
| Input: Initialize Use chaotic mapping to initialize the solutions’ positions, . Output: . |
|
2.3. Short-Term Load Interval Forecasting Model
2.3.1. Input Data Structure
2.3.2. Forecasting Model Framework
3. Simulation Analysis
3.1. Data Source
3.2. Forecast Evaluation Metrics
- (1)
- RMSE
- (2)
- MAE
- (3)
- MAPE
- (4)
- PICP
- (5)
- MPIW
3.3. Model Selection and Hyperparameters
- (1)
- Transformer Quantile Regression Model
- (2)
- LSTM Quantile Regression Model
- (3)
- ICPO-CNN-BiGRU-Attention
- (4)
- CNN-Attention Quantile Regression Model
- (5)
- CNN-BiGRU Quantile Regression Model
- (6)
- FMD-CNN-BiGRU-Attention Quantile Regression Model
- (7)
- Proposed model
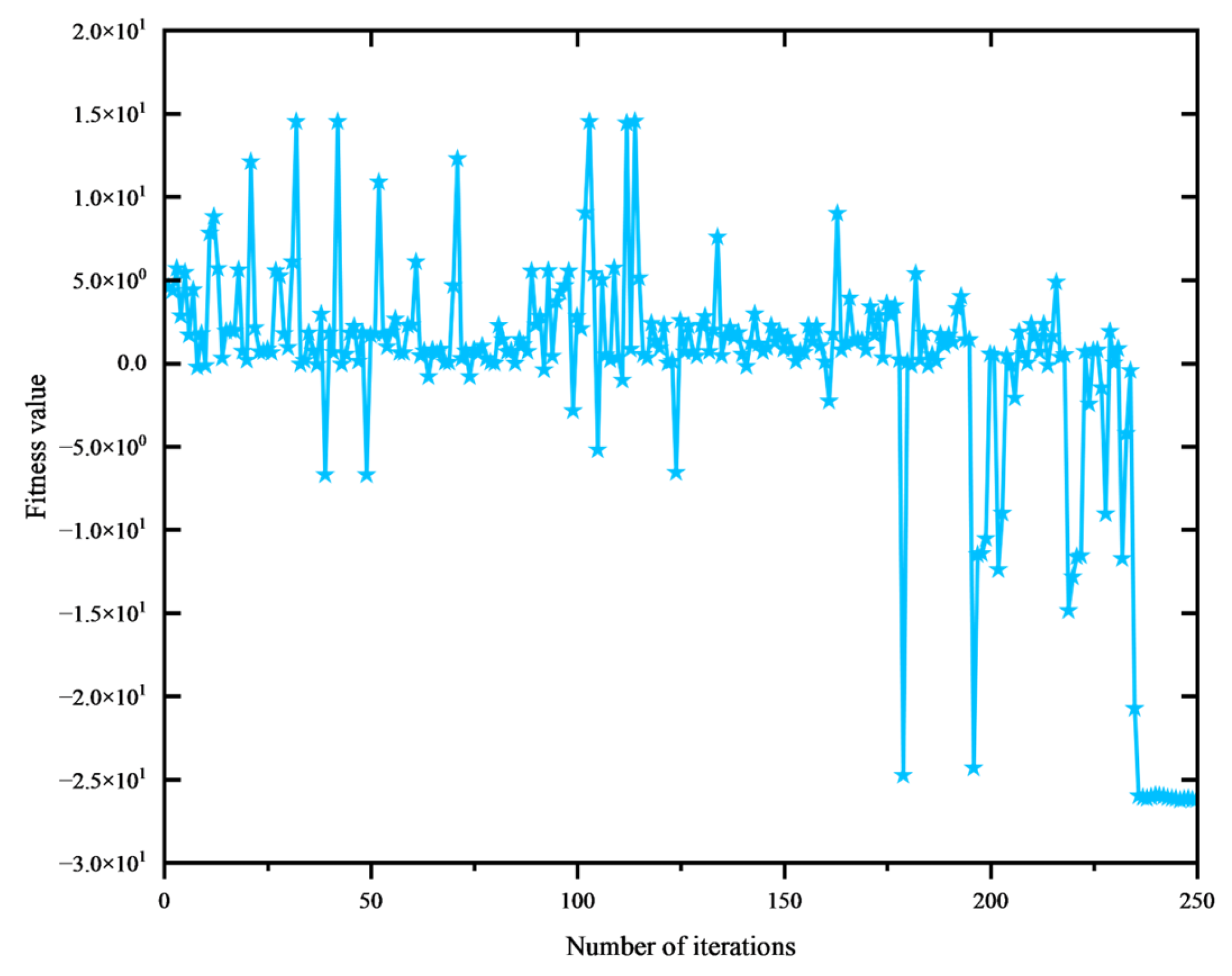
- ①
- ICPO Optimizing GMM Hyperparameters
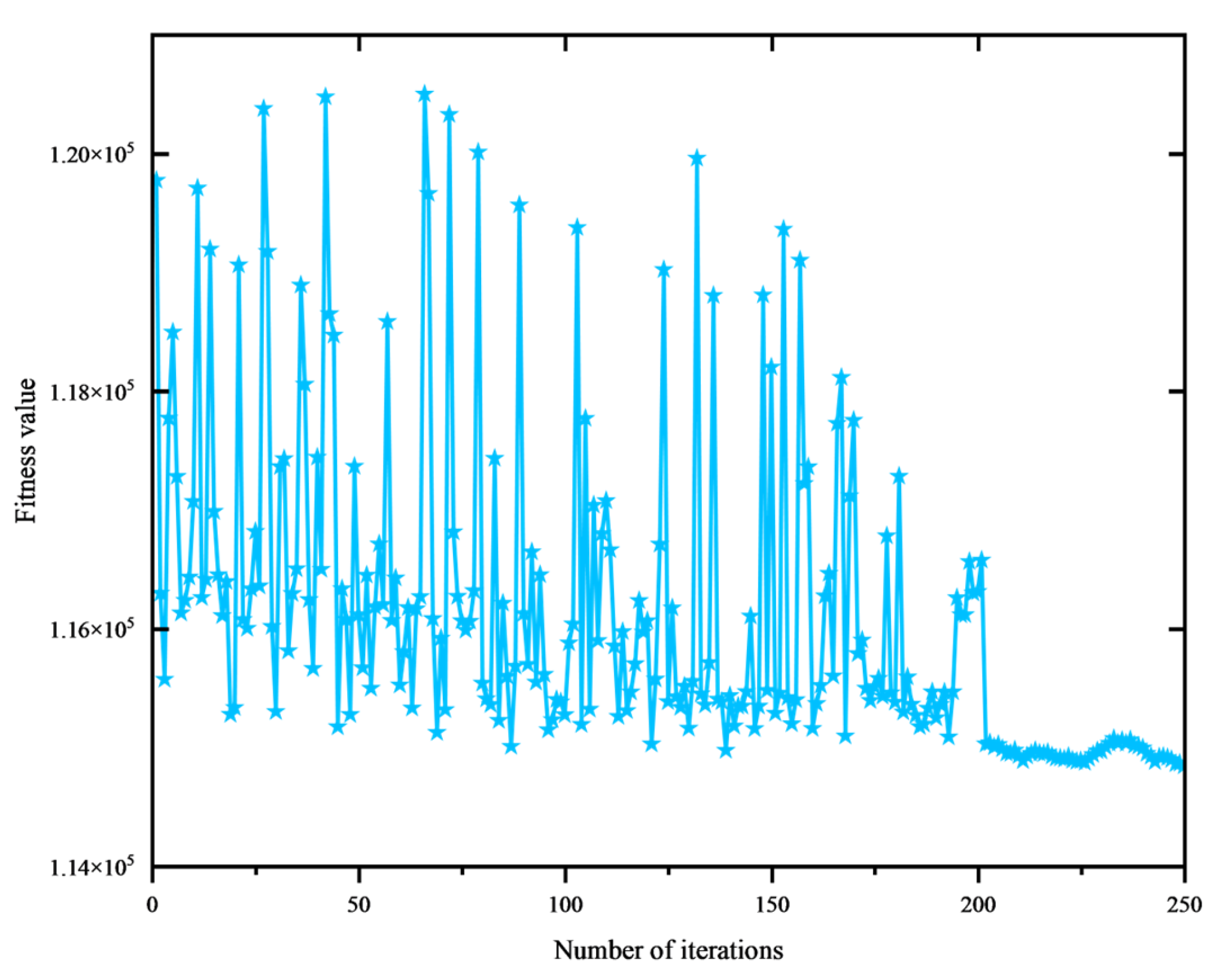
- ②
- ICPO Optimizing FMD Hyperparameters
- ③
- ICPO Optimizing CNN-BiGRU-Attention Hyperparameters

3.4. Forecasting Results Analysis
- (1)
- Summer Weekdays and Weekends (Figure 14a,b)
- (2)
- Winter Weekdays and Weekends (Figure 14c,d)

3.5. Sensitivity Analysis
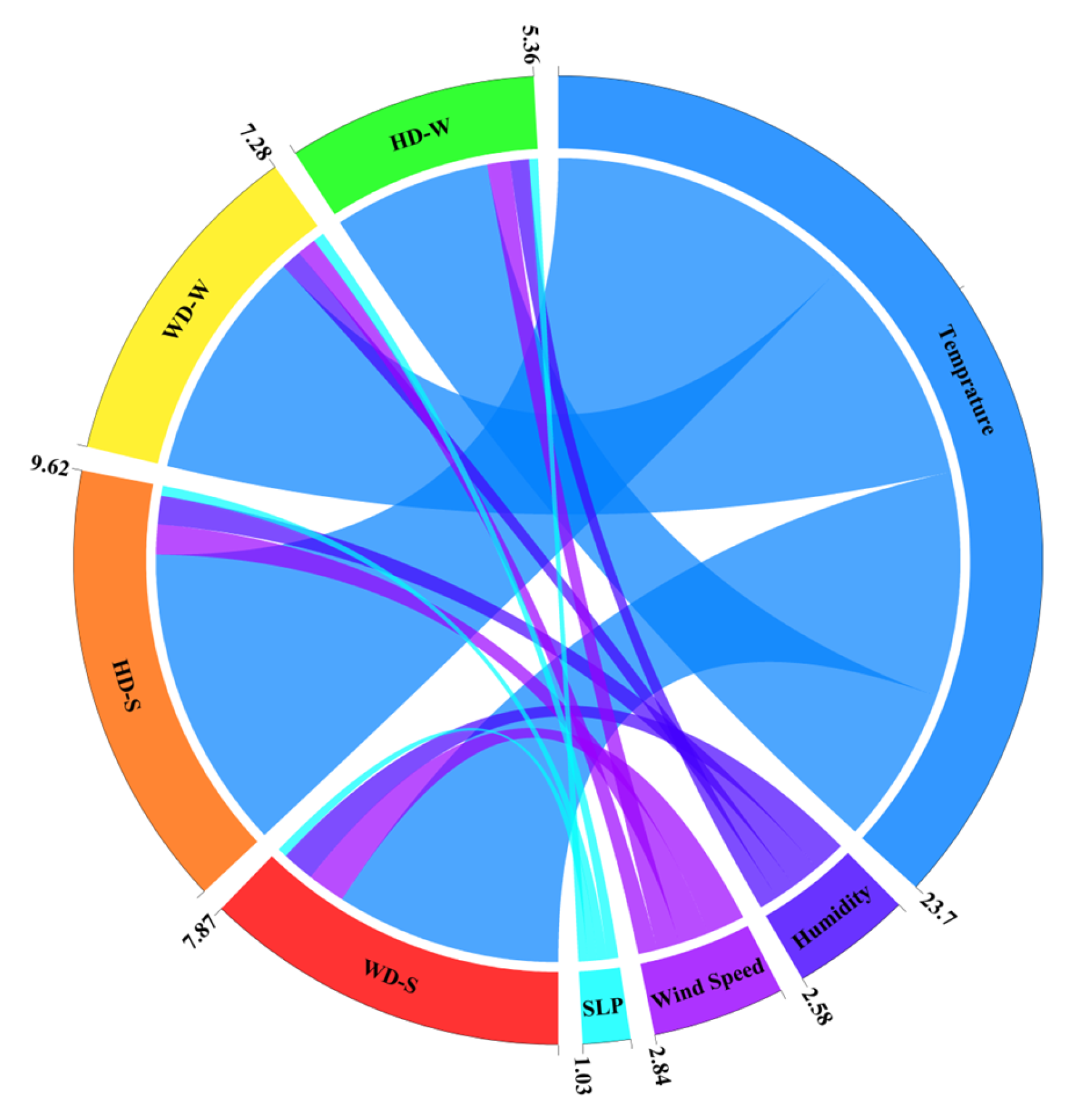
3.6. Interpretability Analysis
4. Conclusions
- (1)
- Effectiveness of the Improved Optimization Algorithm
- (2)
- Model Integration and Performance Improvement
- (3)
- Model Adaptability and Robustness
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FMD | Feature Mode Decomposition |
| CNN | Convolutional Neural Network |
| BiGRU | Bidirectional Gated Recurrent Unit |
| CPO | Crested Porcupine Optimizer |
| ICPO | Improved Crested Porcupine Optimizer |
| GMM | Gaussian Mixture Model Clustering |
| ICPO-GMM | GMM optimized using ICPO |
| ICPO-FMD | FMD optimized using ICPO |
| IMFs | Intrinsic Mode Functions |
| CNN-BiGRU-Attention | Convolutional Neural Network—Bidirectional Gated Recurrent Unit—Attention Mechanism |
| RMSE | Root Mean Squared Error |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| PICP | Forecasting Interval Coverage Probability |
| MPIW | Mean Forecasting Interval Width |
| ARIMA | AutoRegressive Integrated Moving Average |
| SARIMA | Seasonal AutoRegressive Integrated Moving Average |
| SVM | Support Vector Machine |
| PSO | Particle Swarm Optimization |
| GA | Genetic Algorithm |
| K-means | K-means Clustering |
| FCM | Fuzzy C-means Clustering |
| DBSCAN | Density-Based Spatial Clustering of Applications with Noise |
| ISODATA | Iterative Self-Organizing Data Analysis Technique |
| DBFCM | Density-Based Fuzzy C-means Clustering |
| NAR | Nonlinear Autoregressive Model |
| GRA | Grey Relational Analysis |
| LSC | Least Squares Classification |
| AHC | Agglomerative Hierarchical Clustering |
| RBF-ARX | Radial Basis Function AutoRegressive with Exogenous Inputs |
| LSTM | Long Short-Term Memory |
| GRU | Gated Recurrent Unit |
| QR-CNN-BiGRU-Attention | Quantile Regression Convolutional Neural Network-Bidirectional Gated Recurrent Unit-Attention |
| ICPO-QR-CNN-BiGRU-Attention | Improved Catch Fish Optimization-Quantile Regression Convolutional Neural Network-Bidirectional Gated Recurrent Unit-Attention |
| CK | Clustering Kernel |
| CPR | Cumulative Forecasting Residual |
| QR-transformer | Quantile Regression Transformer |
| QR-LSTM | Quantile Regression Long Short-Term Memory |
| QR-CNN-Attention | Quantile Regression Convolutional Neural Network-Attention |
| QR-CNN-BiGRU | Quantile Regression Convolutional Neural Network-Bidirectional Gated Recurrent Unit |
| QR-FMD-CNN-BiGRU-Attention | Quantile Regression Feature Mode Decomposition Convolutional Neural Network-Bidirectional Gated Recurrent Unit-Attention |
| SHAP | Shapley Additive exPlanations |
| 2D | Two-dimensional diagram |
| 3D | Three-dimensional diagram |
References
- Tang, J.; Saga, R.; Cai, H.; Ma, Z.; Yu, S. Advanced integration of forecasting models for sustainable load forecasting in large-scale power systems. Sustainability 2024, 16, 1710. [Google Scholar] [CrossRef]
- Mordjaoui, M.; Haddad, S.; Medoued, A.; Laouafi, A. Electric load forecasting by using dynamic neural network. Int. J. Hydrogen Energy 2017, 42, 17655–17663. [Google Scholar] [CrossRef]
- Han, L.; Peng, Y.; Li, Y.; Yong, B.; Zhou, Q.; Shu, L. Enhanced deep networks for short-term and medium-term load forecasting. IEEE Access 2019, 7, 4045–4055. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, H.; Liu, Y.; Fan, G. Minute-level ultra-short-term power load forecasting based on time series data features. Appl. Energy 2024, 372, 123801. [Google Scholar] [CrossRef]
- Rafi, S.H.; Masood, N.A.; Deeba, S.R.; Hossain, E. A Short-Term load forecasting method using integrated CNN and LSTM network. IEEE Access 2021, 9, 32436–32448. [Google Scholar] [CrossRef]
- Saxena, A.; Shankar, R.; El-Saadany, E.F.; Kumar, M.; Al Zaabi, O.; Al Hosani, K.; Muduli, U.R. Intelligent load forecasting and renewable energy integration for enhanced grid reliability. IEEE Trans. Ind. Appl. 2024, 60, 8403–8417. [Google Scholar] [CrossRef]
- Yin, L.; Xie, J. Multi-temporal-spatial-scale temporal convolution network for short-term load forecasting of power systems. Appl. Energy 2021, 283, 116328. [Google Scholar] [CrossRef]
- Eren, Y.; Küçükdemiral, İ. A comprehensive review on deep learning approaches for short-term load forecasting. Renew. Sustain. Energy Rev. 2024, 189 Pt B, 114031. [Google Scholar] [CrossRef]
- Parmezan, A.R.S.; Souza, V.M.A.; Batista, G.E.A.P.A. Evaluation of statistical and machine learning models for time series forecasting: Identifying the state-of-the-art and the best conditions for using each model. Inf. Sci. 2019, 484, 302–337. [Google Scholar] [CrossRef]
- Memarzadeh, G.; Keynia, F. Short-term electricity load and price forecasting by a new optimal LSTM-NN based forecasting algorithm. Electr. Power Syst. Research 2021, 192, 106995. [Google Scholar] [CrossRef]
- Dhaval, B.; Deshpande, A. Short-term load forecasting using multiple linear regression. Int. J. Electr. Comput. Eng. 2020, 10, 3911. [Google Scholar] [CrossRef]
- Xie, Z.; Wang, R.; Wu, Z.; Liu, T. Short-Term power load forecasting model based on fuzzy neural network using improved decision tree. In Proceedings of the 2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019; pp. 482–486. [Google Scholar]
- Samantaray, S.; Sahoo, A.; Satapathy, D.P.; Oudah, A.Y.; Yaseen, Z.M. Suspended sediment load forecasting using sparrow search algorithm-based support vector machine model. Sci. Rep. 2024, 14, 12889. [Google Scholar] [CrossRef] [PubMed]
- Si, C.; Wang, H.; Chen, L.; Zhao, J.; Min, Y.; Xu, F. Robust co-modeling for privacy-preserving short-term load forecasting with incongruent load data distributions. IEEE Trans. Smart Grid 2024, 15, 2985–2999. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, Y.; Xiao, T.; Wang, H.; Hou, P. A novel short-term load forecasting framework based on time-series clustering and early classification algorithm. Energy Build. 2021, 251, 111375. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Z.; Gao, Y.; Wu, J.; Zhao, S.; Ding, Z. An effective dimensionality reduction approach for short-term load forecasting. Electr. Power Syst. Res. 2022, 210, 108150. [Google Scholar] [CrossRef]
- Li, W.; Zuo, Y.; Su, T.; Zhao, W.; Ma, X.; Cui, G.; Wu, J.; Song, Y. Firefly Algorithm-based semi-supervised learning with transformer method for shore power load forecasting. IEEE Access 2023, 11, 77359–77370. [Google Scholar] [CrossRef]
- Pang, X.; Sun, W.; Li, H.; Liu, W.; Luan, C. Short-term power load forecasting method based on Bagging-stochastic configuration networks. PLoS ONE 2024, 19, e0300229. [Google Scholar] [CrossRef]
- Luo, S.; Wang, B.; Gao, Q.; Wang, Y.; Pang, X. Stacking integration algorithm based on CNN-BiLSTM-Attention with XGBoost for short-term electricity load forecasting. Energy Rep. 2024, 12, 2676–2689. [Google Scholar] [CrossRef]
- Mamun, A.A.; Sohel, M.; Mohammad, N.; Sunny, S.H.; Dipta, D.R.; Hossain, E. A comprehensive review of the load forecasting techniques using single and hybrid predictive models. IEEE Access 2020, 8, 134911–134939. [Google Scholar] [CrossRef]
- Bu, X.; Wu, Q.; Zhou, B.; Li, C. Hybrid short-term load forecasting using CGAN with CNN and semi-supervised regression. Appl. Energy 2023, 338, 120920. [Google Scholar] [CrossRef]
- Sekhar, C.; Dahiya, R. Robust framework based on hybrid deep learning approach for short term load forecasting of building electricity demand. Energy 2023, 268, 126660. [Google Scholar] [CrossRef]
- Shakeel, A.; Chong, D.; Wang, J. District heating load forecasting with a hybrid model based on LightGBM and FB-prophet. J. Clean. Prod. 2023, 409, 137130. [Google Scholar] [CrossRef]
- Han, F.; Pu, T.; Li, M.; Taylor, G. Short-term forecasting of individual residential load based on deep learning and K-means clustering. CSEE J. Power Energy Syst. 2020, 7, 261–269. [Google Scholar]
- Hu, L.; Wang, J.; Guo, Z.; Zheng, T. Load forecasting based on LVMD-DBFCM load curve clustering and the CNN-IVIA-BLSTM Model. Appl. Sci. 2023, 13, 7332. [Google Scholar] [CrossRef]
- Han, Z.; Cheng, M.; Chen, F.; Wang, Y.; Deng, Z. A spatial load forecasting method based on DBSCAN clustering and NAR neural network. J. Phys. Conf. Ser. 2020, 1449, 012032. [Google Scholar] [CrossRef]
- Bedi, J.; Toshniwal, D. Energy load time-series forecast using decomposition and autoencoder integrated memory network. Appl. Soft Comput. 2020, 93, 106390. [Google Scholar] [CrossRef]
- Chen, H.; Huang, H.; Zheng, Y.; Yang, B. A load forecasting approach for integrated energy systems based on aggregation hybrid modal decomposition and combined model. Appl. Energy 2024, 375, 124166. [Google Scholar] [CrossRef]
- Yang, D.; Guo, J.; Li, Y.; Sun, S.; Wang, S. Short-term load forecasting with an improved dynamic decomposition-reconstruction-ensemble approach. Energy 2023, 263, 125609. [Google Scholar] [CrossRef]
- Liu, Y.; Pu, H.; Sun, D.W. Efficient extraction of deep image features using convolutional neural network (CNN) for applications in detecting and analysing complex food matrices. Trends Food Sci. Technol. 2021, 113, 193–204. [Google Scholar] [CrossRef]
- Lin, J.; Ma, J.; Zhu, J.; Cui, Y. Short-term load forecasting based on LSTM networks considering attention mechanism. Int. J. Electr. Power Energy Syst. 2022, 137, 107818. [Google Scholar] [CrossRef]
- Ma, X.; Dong, Y. An estimating combination method for interval forecasting of electrical load time series. Expert Syst. Appl. 2020, 158, 113498. [Google Scholar] [CrossRef]
- Dong, F.; Wang, J.; Xie, K.; Tian, L.; Ma, Z. An interval forecasting method for quantifying the uncertainties of cooling load based on time classification. J. Build. Eng. 2022, 56, 104739. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, M.; Wang, S.; Dai, S.; Luo, L.; Zhu, E.; Xu, H.; Zhu, X.; Yao, C.; Zhou, H. Gaussian mixture model clustering with incomplete data. ACM Trans. Multimed. Comput. Commun. Appl. 2021, 17, 6. [Google Scholar] [CrossRef]
- Miao, Y.; Zhang, B.; Li, C.; Lin, J.; Zhang, D. Feature mode decomposition: New decomposition theory for rotating machinery fault diagnosis. IEEE Trans. Ind. Electron. 2023, 70, 1949–1960. [Google Scholar] [CrossRef]
- Kattenborn, T.; Leitloff, J.; Schiefer, F.; Hinz, S. Review on Convolutional Neural Networks (CNN) in vegetation remote sensing. ISPRS J. Photogramm. Remote Sens. 2021, 173, 24–49. [Google Scholar] [CrossRef]
- Zou, Z.; Wang, J.; Ning, E.; Zhang, C.; Wang, Z.; Jiang, E. Short-Term power load forecasting: An integrated approach utilizing variational mode eecomposition and TCN–BiGRU. Energies 2023, 16, 6625. [Google Scholar] [CrossRef]
- Niu, Z.; Zhong, G.; Yu, H. A review on the attention mechanism of deep learning. Neurocomputing 2021, 452, 48–62. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M. Crested Porcupine Optimizer: A new nature-inspired metaheuristic. Knowl. Based Syst. 2024, 284, 111257. [Google Scholar] [CrossRef]
- Li, C.; Feng, B.; Li, S.; Kurths, J.; Chen, G. Dynamic Analysis of Digital Chaotic Maps via State-Mapping Networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 2322–2335. [Google Scholar] [CrossRef]
- Singh, N.; Kaur, J. Hybridizing sine-cosine algorithm with harmony search strategy for optimization design problems. Soft Comput. 2021, 25, 11053–11075. [Google Scholar] [CrossRef]
- Zhou, Z.; Jia, Y.; Lu, W.; Lei, J.; Liu, Z. Enhancing the crack initiation resistance of hydrogels through crosswise cutting. J. Mech. Phys. Solids 2024, 183, 105516. [Google Scholar] [CrossRef]
- ELIA. Measured and Forecasted Total Load on the Belgian Grid (Historical Data). Available online: https://opendata.elia.be/explore/dataset/ods001/analyze/?dataChart=eyJxdWVyaWVzIjpbeyJjaGFydHMiOlt7InR5cGUiOiJsaW5lIiwiZnVuYyI6IkFWRyIsInlBeGlzIjoidG90YWxsb2FkIiwic2NpZW50aWZpY0Rpc3BsYXkiOnRydWUsImNvbG9yIjoiI2U3NTQyMCJ9XSwieEF4aXMiOiJkYXRldGltZSIsIm1heHBvaW50cyI6bnVsbCwidGltZXNjYWxlIjoibW9udGgiLCJzb3J0IjoiIiwiY29uZmlnIjp7ImRhdGFzZXQiOiJvZHMwMDEiLCJvcHRpb25zIjp7fX19XSwiZGlzcGxheUxlZ2VuZCI6dHJ1ZSwiYWxpZ25Nb250aCI6dHJ1ZX0%3D (accessed on 15 March 2024).
- Timeanddate. Weather in Belgium. Available online: https://www.timeanddate.com/weather/belgium (accessed on 15 March 2024).
- Ran, P.; Dong, K.; Liu, X.; Wang, J. Short-term load forecasting based on CEEMDAN and Transformer. Electr. Power Syst. Res. 2023, 214, 108885. [Google Scholar] [CrossRef]
- Jin, Y.; Guo, H.; Wang, J.; Song, A. A Hybrid System Based on LSTM for Short-Term power load forecasting. Energies 2020, 13, 6241. [Google Scholar] [CrossRef]
- Lin, Z. A hybrid CNN-LSTM-Attention model for electric energy consumption forecasting. In Proceedings of the 2023 5th Asia Pacific Information Technology Conference, Ho Chi Minh, Vietnam, 9–11 February 2023; pp. 167–173. [Google Scholar]
- Li, C.; Li, G.; Wang, K.; Han, B. A multi-energy load forecasting method based on parallel architecture CNN-GRU and transfer learning for data deficient integrated energy systems. Energy 2022, 259, 124967. [Google Scholar] [CrossRef]
- Niu, D.; Yu, M.; Sun, L.; Gao, T.; Wang, K. Short-term multi-energy load forecasting for integrated energy systems based on CNN-BiGRU optimized by attention mechanism. Appl. Energy 2022, 313, 118801. [Google Scholar] [CrossRef]











| Reference | Decomposition Algorithm | Optimization Algorithm | Method Type | Specific Algorithm |
|---|---|---|---|---|
| Bhatti Dhaval et al. [11] | None | None | Statistical | Multiple Linear Regression (MLR) |
| Xie Z et al. [12] | None | None | Hybrid | Fuzzy Neural Network + MID3 |
| Sandeep Samantaray et al. [13] | None | Sparrow Search Algorithm | Hybrid | SVM + SSA |
| Si C et al. [14] | k-Means Clustering | None | Hybrid | PPK-Fed with CNN |
| Chen Z et al. [15] | Time-Series Clustering | None | Hybrid | Early Classification with LightGBM |
| Yang Y et al. [16] | VMD | None | Hybrid | VMD + VAE |
| Li W et al. [17] | None | Firefly Algorithm | Hybrid | Semi-supervised learning with Transformer |
| Pang X et al. [18] | None | None | Hybrid | Bagging-SCNs |
| Luo S et al. [19] | None | None | Stacking Integration | CNN-BiLSTM-Attention + XGBoost |
| Mamun AA et al. [20] | None | None | Review | Analysis of Single and Hybrid Models |
| Bu X et al. [21] | VMD | None | Hybrid | CGAN + CNN + Semi-Supervised Regression |
| Sekhar C et al. [22] | None | Grey Wolf Optimization | Hybrid | GWO-CNN-BiLSTM |
| Shakeel A et al. [23] | None | Grid Search | Hybrid | LightGBM + FB-Prophet |
| Han F et al. [24] | k-Means Clustering | None | Hybrid | Deep Learning + k-Means Clustering |
| Hu L et al. [25] | LVMD | IVIA | Hybrid | LVMD-DBFCM + CNN-IVIA-BLSTM |
| Han Z et al. [26] | None | None | Hybrid | DBSCAN + NAR Neural Network |
| Bedi J et al. [27] | VMD | None | Hybrid | VMD + Autoencoder + LSTM |
| Chen H et al. [28] | ICEEMDAN + SVMD | None | Hybrid | ICEEMDAN + SVMD + TCN-BiGRU + MHA |
| Yang D et al. [29] | Dynamic Decomposition-Reconstruction | Automatic Hyperparameter Optimization | Hybrid | Decomposition-Reconstruction-Ensemble with Neural Network |
| This study | ICPO-FMD | ICPI | Hybrid | ICPO-GMM + ICPO-FMD + QR-ICPO-CNN-BiGRU-Attention |
| Scene | Evaluation Index | Proposed Model | QR-LSTM | QR-ICPO-CNN-BiGRU-Attenion | QR-CNN-Attention | QR-CNN-BiGRU | QR-FMD-CNN-BiGRU-Attetnion | QR-Transformer |
|---|---|---|---|---|---|---|---|---|
| July 12th | RMSE | 132.30 | 769.24 | 605.21 | 693.27 | 672.14 | 557.45 | 434.44 |
| MAE | 120.53 | 655.12 | 505.01 | 577.06 | 549.01 | 477.80 | 421.25 | |
| MAPE | 1.40 | 7.44 | 5.74 | 6.52 | 6.20 | 5.48 | 4.94 | |
| PICP | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| MPIW | 0.35 | 0.45 | 0.39 | 0.39 | 0.38 | 0.36 | 0.36 | |
| July 14th | RMSE | 196.99 | 953.58 | 1072.33 | 1025.45 | 1119.60 | 1095.02 | 348.67 |
| MAE | 157.61 | 837.21 | 887.43 | 868.58 | 935.38 | 913.25 | 337.86 | |
| MAPE | 2.18 | 11.96 | 12.89 | 12.55 | 13.56 | 13.23 | 4.57 | |
| PICP | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| MPIW | 0.42 | 0.50 | 0.49 | 0.51 | 0.46 | 0.43 | 0.43 | |
| December 11th | RMSE | 245.83 | 1680.13 | 1471.37 | 1615.36 | 1517.79 | 1494.24 | 548.29 |
| MAE | 214.24 | 1500.60 | 290.00 | 158.68 | 140.25 | 141.68 | 1009.04 | |
| MAPE | 2.01 | 13.70 | 12.38 | 13.43 | 12.44 | 12.09 | 5.03 | |
| PICP | 0.89 | 0.83 | 0.88 | 0.82 | 0.83 | 0.79 | 0.82 | |
| MPIW | 0.36 | 0.41 | 0.42 | 0.44 | 0.40 | 0.43 | 0.43 | |
| December 16th | RMSE | 220.99 | 791.43 | 799.62 | 864.16 | 774.04 | 778.22 | 367.34 |
| MAE | 194.75 | 673.53 | 648.10 | 715.43 | 614.17 | 635.02 | 344.63 | |
| MAPE | 2.03 | 7.40 | 7.20 | 7.96 | 6.87 | 7.04 | 3.71 | |
| PICP | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| MPIW | 0.43 | 0.45 | 0.45 | 0.48 | 0.45 | 0.43 | 0.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, S.; Meng, X.; Pang, X.; Li, H.; Zheng, Z. Optimized Hybrid Deep Learning Framework for Short-Term Power Load Interval Forecasting via Improved Crowned Crested Porcupine Optimization and Feature Mode Decomposition. Algorithms 2025, 18, 659. https://doi.org/10.3390/a18100659
Luo S, Meng X, Pang X, Li H, Zheng Z. Optimized Hybrid Deep Learning Framework for Short-Term Power Load Interval Forecasting via Improved Crowned Crested Porcupine Optimization and Feature Mode Decomposition. Algorithms. 2025; 18(10):659. https://doi.org/10.3390/a18100659
Chicago/Turabian StyleLuo, Shucheng, Xiangbin Meng, Xinfu Pang, Haibo Li, and Zedong Zheng. 2025. "Optimized Hybrid Deep Learning Framework for Short-Term Power Load Interval Forecasting via Improved Crowned Crested Porcupine Optimization and Feature Mode Decomposition" Algorithms 18, no. 10: 659. https://doi.org/10.3390/a18100659
APA StyleLuo, S., Meng, X., Pang, X., Li, H., & Zheng, Z. (2025). Optimized Hybrid Deep Learning Framework for Short-Term Power Load Interval Forecasting via Improved Crowned Crested Porcupine Optimization and Feature Mode Decomposition. Algorithms, 18(10), 659. https://doi.org/10.3390/a18100659





