Quantifying Statistical Heterogeneity and Reproducibility in Cooperative Multi-Agent Reinforcement Learning: A Meta-Analysis of the SMAC Benchmark

Abstract

This study presents the first quantitative meta-analysis in cooperative multi-agent reinforcement learning (MARL). Undertaken on the StarCraft Multi-Agent Challenge (SMAC) benchmark, we quantify reproducibility and statistical heterogeneity across studies using the five algorithms introduced in the original SMAC paper (IQL, VDN, QMIX, COMA, QTRAN) on five widely used maps at a fixed 2M-step budget. The analysis pools win rates via multilevel mixed-effects meta-regression with cluster-robust variance and reports Algorithm × Map cell-specific heterogeneity and 95% prediction intervals. Results show that heterogeneity is pervasive: 17/25 cells exhibit high heterogeneity (I² ≥ 80%), indicating between-study variance dominates sampling error. Moderator analyses find publication year significantly explains part of residual variance, consistent with secular drift in tooling and defaults. Prediction intervals are broad across most cells, implying a new study can legitimately exhibit substantially lower or higher performance than pooled means. The study underscores the need for standardized reporting (SC2 versioning, evaluation episode counts, hyperparameters), preregistered map panels, open code/configurations, and machine-readable curves to enable robust, heterogeneity-aware synthesis and more reproducible SMAC benchmarking.

1. Introduction

Multi-agent reinforcement learning (MARL) has experienced significant growth in recent years, driven largely by its abilities to model, learn, and coordinate in the presence of a complex and interactive environment where several agents must operate together or in competition. As researchers increasingly tackle real-world applications such as autonomous vehicles, smart grids, distributed robotics, and large-scale simulations, the field of MARL has proven to be especially functional and has gained rapid prominence as a result [1,2]. Such an explosion of interest is visible in a precipitous increase in published research, adoption in cooperative and competitive domains, and current advances within scalable algorithms that are handling ever-increasing populations of agents [3]. As challenges within the field with non-stationarity and credit assignment continue to be addressed, MARL is extending its reach into broader, more dynamic, and higher-impact settings, showing all the signs of a vibrant and accelerating field of research.

A prominent benchmark in this domain is the StarCraft Multi-Agent Challenge introduced by Samvelyan et al. (2019) [4]. The SMAC suite provides dozens of StarCraft II scenarios that test micromanagement, where each agent controls a single game unit with access only to local observations, while a built-in AI controls the enemy units. By focusing on “decentralized execution” problems and offering a diverse set of battle scenarios, SMAC poses high-dimensional, partially observable challenges requiring sophisticated coordination strategies. Crucially, SMAC was open sourced with a deterministic game engine and standardized APIs, making it in principle a reproducible testbed that multiple researchers can use under identical conditions. This combination of accessibility and breadth of scenarios led to SMAC’s rapid adoption: since its 2019 release, SMAC has become the de facto cooperative MARL benchmark, featured in over 30–40% of published papers in the area [5].

Despite SMAC’s initial design as a challenging “standardized testbed” [4], recent developments hint that it is at a saturation point. Many of the originally difficult SMAC scenarios have been essentially “solved” by state-of-the-art (SOTA) algorithms. The development of several novel algorithms have mastered scenarios grouped in the originally “hard” category with nearly perfect scores [6,7]. This rapid progress raises a natural question: how much of the apparent improvement on SMAC benchmarks reflects true algorithmic advances versus overfitting or exploitable quirks of the environment? The risk is that SMAC win-rate increments could become misleading if hidden experimental variability or environment idiosyncrasies account for the differences.

Recent meta-research audits in Reinforcement Learning (RL) revealed disturbingly low rates of independent replication: for example, a 2019 study by Raff attempted to reimplement 255 ML papers and succeeded in only about 63% of cases [8]. In other words, over one-third of claimed results could not be reproduced without authors’ code or clarifications, highlighting how “progress” in the literature can be overstated. MARL is not exempt from these issues. Gorsane et al. (2022) [5] conducted the first large-scale survey of evaluation practices in cooperative MARL, examining 75 papers from 2016 to 2022. The study revealed that MARL saw “wildly different reported performances” for the same algorithm on identical SMAC maps, attributing these variances largely to unreported implementation details.

Prior audits have identified inconsistent reporting practices and performance variability for the same algorithms on identical SMAC scenarios, but these were qualitative observations. As of to date, no study has systematically quantified the reproducibility, statistical heterogeneity, or true effect sizes of published results. To address this gap, our study undertakes a comprehensive meta-analysis of published SMAC results from 2019 to 2024. We aggregate an extensive database of effect sizes (win rates) for a fixed set of algorithm-map combinations in the SMAC benchmark. Prior meta-research has cataloged reporting deficiencies and variance between identical algorithm-map combinations but not measured heterogeneity itself. Standard tools from biomedical meta-analysis, the between-study variance τ², Higgins’ I², and 95% prediction intervals, remain virtually unused in MARL [9].

High irreducible variance compromises the interpretability of incremental win-rate gains, encouraging “benchmark gaming” rather than genuine innovation. Similar crises in single-agent RL spurred the creation of Procgen and RL-Unplugged [10,11], initiatives driven by the realization that without common standards and an accounting of variability, reported SOTA results can be misleading. In cooperative MARL, no analogous community-wide enforcement or benchmark distribution exists yet; SMAC has served as a de facto standard, but until now there has been little formal scrutiny of how results on SMAC should be interpreted given underlying variance. Meta-analysis, a statistical approach designed to synthesize findings across independent studies, operates by weighting and pooling effect estimates while evaluating between-study heterogeneity. Widely used in epidemiology and clinical research, it provides a principled framework to assess consistency, quantify irreducible variance, and generate prediction intervals that reflect real-world variability. These features, especially the explicit evaluation of heterogeneity (τ², I²) and the ability to integrate dispersed evidence, make meta-analysis both implementable and meaningful in this setting. By introducing such evidence-based measures into the evaluation of MARL algorithms, this work aims to bridge a methodology gap between machine learning and fields like epidemiology and clinical research, where meta-analysis is routinely used to aggregate evidence.

This paper’s objectives are to make the following contributions to MARL evaluation and reproducibility research:

• A robust database of SMAC performance results (win rates) from 2018 to 2024, covering 25 unique algorithm-map pairs across dozens of publications;
• Systematically quantify reproducibility, statistical heterogeneity, and effect sizes in published results;
• Identify evaluation practices and incorporate moderator analysis to contextualize variability and guide transparency and reproducibility improvements across studies.

The remainder of this paper is structured as follows. Section 2 introduces the methodology used for our study selection and data extraction. Section 3 details the statistical methodology used in the meta-analysis. Section 4 presents heterogeneity results, prediction intervals, and moderator analyses. Section 5 offers a discussion of key findings, limitations, and recommendations for improving SMAC benchmarking. Finally, Section 6 is the conclusion.

2. Study Selection and Data Extraction

We conducted and reported on our meta-analysis as per the guidelines of the PRISMA (Preferred Reporting Items for Systematic Reviews and Meta-Analyses) statement [12]. This section elaborates on the methodology and describes the setup for our meta-analysis.

2.1. Algorithm Selection

The selection of IQL [13], VDN [14], QMIX [15], COMA [16], and QTRAN [17] as baseline algorithms are justified by their collective status as canonical reference points within the MARL and SMAC literature. These five algorithms were not only the exclusive baselines adopted in the original SMAC benchmark, but also collectively span the principal learning paradigms of MARL, thereby ensuring conceptual breadth rather than redundancy. Additionally, they together span the entire empirically observed difficulty spectrum on SMAC maps, from near-zero win rates on “super-hard” scenarios (IQL) to near-perfect scores on “easy” tasks (QMIX, QTRAN), a spread that is essential for reliable estimation of between-study variance and prediction intervals in meta-analytic models. Moreover, survey/introductory treatments of cooperative MARL and SMAC regularly list IQL, VDN, QMIX, COMA, and QTRAN as the standard baselines and compare new methods against them [18,19]. Collectively, the 5 selected algorithms deliver historical continuity, methodological diversity, and community validation, criteria indispensable for a rigorous assessment of statistical heterogeneity in reported SMAC performance.

In contrast, more recent architectures such as QPLEX, RODE, or MAPPO are only sporadically co-reported with the selected baseline algorithms. Consequently, their current evidence base lacks sufficient density across the five focal maps to support valid cell-level pooling or heterogeneity estimation. Restricting analysis to the foundational baselines therefore ensures consistency, preserves interpretability of cross-study variance, and establishes a reproducible anchor to which newer methods can later be added once reporting practices and coverage become sufficiently standardized.

Beyond their conceptual coverage, the selected baselines also cover a range of algorithmic complexity. IQL represents the simplest paradigm, training fully independent agents without explicit coordination, and thus has minimal computational overhead. VDN and QMIX introduce increasing representational complexity through value decomposition and non-linear mixing networks, requiring centralized training but decentralized execution. COMA and QTRAN further increase complexity by incorporating policy-gradient and constrained value-factorization formulations, respectively, both demanding higher gradient-estimation cost and more extensive credit-assignment computation. This gradation, from tabular-style independent learners to joint value or policy-based models, ensures that the meta-analysis captures variance across not only learning paradigms but also algorithmic and computational scales.

2.2. Map Selection

To determine the benchmark scenarios analyzed in the meta-analysis, we first constructed a frequency matrix that cross-tabulated every SMAC map against the selected studies. The resulting tally revealed that the maps 1c3s5z, MMM2, 2c_vs_64zg, 5m_vs_6m, and 3s_vs_5z were, by a clear margin, the five most frequently employed across the selected studies. Selecting these scenarios therefore maximizes overlap among studies, thereby increasing the number of paired effect sizes per algorithm-map cell and enhancing the precision of estimates accounting for random-effects from studies. Importantly, the chosen subset spans the entire SMAC difficulty continuum, as categorized in the original SMAC paper, from relatively “easy” micromanagement tasks such as 1c3s5z to “super-hard” large-scale engagements like MMM2, ensuring that heterogeneity assessments are not confined to a single performance regime. Restricting the analysis to five maps also keeps data extraction manageable: each additional scenario multiplies the required digitization effort and inflates the variance-covariance matrix yet yields diminishing returns once the difficulty spectrum is already covered. Hence, the final set of five maps represents an empirically grounded compromise that preserves benchmark representativeness while maintaining a manageable workload for effect-size retrieval.

2.3. Eligibility Criteria

To ensure the meta-analysis yields robust and comparable effect estimates, we screened candidate publications against a set of inclusion and exclusion criteria tailored to the SMAC domain. Our inclusion criteria (IC) are as follows:

• IC1. The study reports empirical results on the SMAC benchmark and specifies the map sets evaluated.
• IC2. A full win-rate-versus-environment-step curve is provided that extends to ≥2 million environment steps (training timesteps).
• IC3. The map curves include results for ≥4 of the five selected algorithms: IQL, VDN, QMIX, COMA, and QTRAN.
• IC4. The paper presents independent experimental runs (seeds) and reports dispersion statistics (e.g., mean ± SD, 95% CI) for each algorithm.
• IC5. The experiments are conducted with unmodified SMAC environment code for the 5 selected algorithms.

Similarly, our exclusion criteria (EC) are as follows:

• EC1. The study does not evaluate any SMAC scenario.
• EC2. Win-rate curves terminate before 2 million steps.
• EC3. Fewer than four of the target algorithms are evaluated by the curves
• EC4. Win-rates are reported only as scalar end-point metrics.
• EC5. The paper aggregates results from multiple algorithms without per-algorithm statistics, preventing extraction of algorithm-specific effect sizes.

2.4. Search Strategy

Our search aimed to curate a focused yet comprehensive body of primary studies that empirically evaluate SMAC. Because the broader SMAC literature numbers in the thousands, we limited scope to studies that benchmark at least four of the pre-specified five algorithms: IQL, VDN, QMIX, QTRAN, and COMA. Including only studies that benchmarked at least four of the five algorithms restrict inclusion to studies that benchmark a near-identical algorithm set. The review thus obtains balanced within-study panels that yield multiple paired effect sizes, enabling direct head-to-head contrasts (e.g., QMIX versus QTRAN) and precise estimation of within-study variance without imputed covariances. This design treats each study as its own control, lowering standard-error inflation that would otherwise arise if algorithms were reported across disjoint paper subsets.

The retrieval phase was executed manually in Google Scholar’s interface using five Boolean queries, one for every unique four-algorithm combination, set up as follows: “ALG1 AND ALG2 AND ALG3 AND ALG4 AND (SMAC OR “StarCraft Multi-Agent Challenge”)”. No date filter was required because SMAC debuted in 2019, naturally bounding the timeframe. Duplicate titles appearing across multiple queries were removed automatically in Zotero, which served as the reference manager for deduplication and metadata storage.

To curb retrieval bias we relied on three safeguards. First, algorithmic breadth ensured that all five algorithms were represented across the query set. Second, the exhaustive four-way conjunction prevented any single algorithm from dominating the pool. Third, a secondary search was conducted through Scopus to recover any missing articles that were not found during the primary search via Google Scholar.

2.5. Selection Process

The non-duplicate articles retrieved from the search strategy were subjected directly to full-text assessment because most prespecified criteria: presence of win-rate-versus-environment-step curves, inclusion of at least four of the five target algorithms (IQL, VDN, QMIX, QTRAN, COMA), coverage of at least 2 million training steps, inclusion of dispersion statistics with stated seed counts, and use of the unmodified SMAC codebase, cannot be verified from titles or abstracts alone. For each paper, the reviewer sequentially confirmed these requirements by inspecting the figures, methods, and appendix materials; studies failing any single criterion were excluded at this stage.

2.6. Data Extraction

For each eligible study and for every one of the five focal SMAC maps, raw win-rate curves and their associated uncertainty bands were digitized with WebPlotDigitizer (v5.2) [20]. The point-selection tool was used to capture the median or mean with the study-specific dispersion measure: standard deviation, 95% confidence interval, interquartile range, 75% confidence interval, or 50% confidence interval, depending on how the authors had reported variability. All measurements were taken explicitly at 2 million environment time steps. Because these statistics were rendered graphically as ribbons enveloping the central curve, the same digitization pass yielded both point estimates and spread. Resulting coordinate pairs were synthesized into a spreadsheet, recording for each algorithm-map-study triple, the central tendency at 2 million environment steps, the matched dispersion values at 2 million environment steps, and the number of random seeds. No automation beyond WebPlotDigitizer was employed, and no attempts were made to contact original investigators for missing data; all entries derive exclusively from published materials.

3. Meta-Analysis

3.1. Overview

Our meta-analysis seeks to derive pooled performance estimates which generalize beyond the studies originally publishing those results and to evaluate the degree of between-study heterogeneity that characterizes SMAC studies. Each effect size corresponds to a single win rate measured at 2,000,000 (2M) environment steps for a given Algorithm × Map combination within a specific paper, so that every Algorithm × Map combination contributes one observation, with observations clustered by study. The primary estimand is therefore the mean win rate an algorithm achieves on a given map after 2M steps when averaged over the full population of SMAC research settings; a random-effect for study is used to account for irreducible variability stemming from design choices, hardware, or implementation details that differ across studies.

Effect sizes are primarily analyzed using a restricted-maximum-likelihood (REML) multilevel meta-regression with fixed effects for each Algorithm × Map combination (i.e., an interaction-only parameterization), together with random-effects at the study-level. Cluster-robust variance estimation (RVE) supplies standard errors that remain valid in the presence of within-study correlations engendered by multiple algorithms sharing the same experimental context.

A moderator analysis will examine whether reporting completeness, SC2 engine version, and publication year explain variation in win rates beyond the Algorithm × Map structure. These moderators are incorporated through multilevel meta-regression to test their contribution to reducing between-study heterogeneity and to assess their overall statistical significance.

3.2. Standard Training Budget

The decision to anchor all effect sizes at 2M environment steps is motivated by methodological, statistical, and community-norm considerations. First, the original SMAC benchmark defined 2M environment steps as its standard training budget, so retaining this horizon ensures the meta-analysis remains directly comparable to the benchmark’s own reports and the large body of follow-up studies that adopted the same convention. Second, learning curves in SMAC display inconsistent temporal dynamics: some algorithms plateau early whereas others improve gradually, so extracting win rates at inconsistent checkpoints, or at each study’s “best” timestep, could introduce selection bias and spuriously inflate between-study heterogeneity. By enforcing a uniform, pre-specified budget, the analysis ensures that observed performance disparities reflect algorithmic and environmental properties rather than arbitrary evaluation schedules.

3.3. Primary Meta-Regression Model

We employ a two-level mixed-effects meta-analytic model [21], nesting individual win-rate observations inside the studies that report them. Each observation $\mathrm{i}$ corresponds to a single Algorithm × Map combination evaluated in a given study. We estimate cell-specific pooled means (one per Algorithm × Map) while accounting for between-study heterogeneity and within-study sampling variance. Let ${\mathrm{y}}_{\mathrm{i}}$ denote the reported win rate at 2M steps for observation $\mathrm{i}$, with known within-study variance ${\mathrm{v}}_{\mathrm{i}}$ obtained from Appendix A and let $\mathrm{s}\left(\mathrm{i}\right)$ index the study contributing observation $\mathrm{i}$. We define ${\mathrm{X}}_{\mathrm{i}}$ as the row vector of indicator variables representing the Algorithm × Map cell for observation $\mathrm{i}$. The intercept is suppressed so that each coefficient in the parameter vector $\mathsf{\beta }$ corresponds directly to a specific Algorithm × Map cell mean. This parameterization is appropriate for SMAC because algorithms exhibit markedly map-dependent behavior; imposing a shared intercept or additive main-effects structure would pool across scientifically distinct cells and potentially mask meaningful cell-level differences. Formally, the model is

$${\mathrm{y}}_{\mathrm{i}}={\mathrm{X}}_{\mathrm{i}}^{\mathrm{T}}\mathsf{\beta }+{\mathrm{u}}_{\mathrm{s}\left(\mathrm{i}\right)}+{\mathsf{\epsilon }}_{\mathrm{i}},{\mathrm{u}}_{\mathrm{s}}\sim \mathcal{N}\left(0,{\mathsf{\tau }}^2\right),{\mathsf{\epsilon }}_{\mathrm{i}}\sim \mathcal{N}\left(0,{\mathrm{v}}_{\mathrm{i}}\right),$$

(1)

where $\mathsf{\beta }$ is the vector of fixed effects (Algorithm × Map cell means), ${\mathrm{u}}_{\mathrm{s}\left(\mathrm{i}\right)}$ is a random intercept for study $\mathrm{s}\left(\mathrm{i}\right)$ capturing between-study differences such as variations in implementation or hardware, ${\mathsf{\tau }}^2$ is the between-study variance component, and ${\mathsf{\epsilon }}_{\mathrm{i}}$ represents within-study sampling error with known variance ${\mathrm{v}}_{\mathrm{i}}$. The notation $\mathcal{N}(\mathsf{\mu },{\mathsf{\sigma }}^2)$ denotes a normal distribution with mean $\mathsf{\mu }$ and variance ${\mathsf{\sigma }}^2$. The study-level random intercept is crucial in SMAC because papers will report multiple algorithms under identical experimental conditions (framework, environment version, and tuning defaults), inducing correlation among observations from the same paper; ignoring this dependence would underestimate uncertainty. We estimate variance components by REML because, with a moderate number of studies typical of SMAC evidence syntheses, REML yields less biased and more stable τ² than method-of-moments alternatives, improving downstream heterogeneity and prediction-interval calculations.

For fixed-effect inference we employ cluster-robust variance estimators with CR2 small-sample corrections (Satterthwaite degrees of freedom) [22], clustering on study identifiers. This guards against anticonservative standard errors when the number of studies (clusters) is limited and when multiple correlated effects arise within papers due to the shared experimental conditions that were previously described.

To characterize heterogeneity at the cell level we quantify heterogeneity for each Algorithm × Map cell $\mathrm{c}$, a univariate random-effects model to its subset:

$${\mathrm{y}}_{\mathrm{i}}={\mathsf{\mu }}_{\mathrm{c}}+{\mathrm{u}}_{\mathrm{s}\left(\mathrm{i}\right)}{+\mathsf{\epsilon }}_{\mathrm{i}},{\mathrm{u}}_{\mathrm{s}}\sim \mathcal{N}\left(0,{\mathsf{\tau }}_{\mathrm{c}}^2\right),{\mathsf{\epsilon }}_{\mathrm{i}}\sim \mathcal{N}\left(0,{\mathrm{v}}_{\mathrm{i}}\right),$$

(2)

yielding $\widehat{{\mathsf{\tau }}_{\mathrm{c}}^2}$ and ${\mathrm{I}}_{\mathrm{c}}^2$. Here, ${\mathsf{\mu }}_{\mathrm{c}}$ denotes the pooled mean win rate for Algorithm × Map cell $\mathrm{c}$, ${\mathsf{\tau }}_{\mathrm{c}}^2$ is the between-study variance specific to that cell, and ${\mathrm{I}}_{\mathrm{c}}^2$ quantifies the proportion of total variability attributable to between-study differences within the cell.

Following standard variance-decomposition logic, we compute I² as the proportion of total variability attributable to between-study differences rather than sampling error, which is more interpretable and widely used in meta-analytic reporting [23]:

$${\mathrm{I}}^2=100\mathrm{\%}\times {\displaystyle \frac{{\mathsf{\tau }}^2}{{\mathsf{\tau }}^2+\overline{\mathrm{v}}}},$$

(3)

where $\overline{\mathrm{v}}$ is the mean within-study variance over the relevant subset.

All models were implemented in R (version 4.5.1) [24] using the metafor package [25] for multilevel random and mixed-effects estimation and the clubSandwich [26] package for cluster-robust variance estimation with small-sample (CR2) corrections.

3.4. Moderator Analysis

To probe potential sources of between-study heterogeneity beyond the Algorithm × Map structure, we examine three study-level moderators: reporting completeness, StarCraft II (SC2) engine version, and publication year.

The Reporting Completeness Index (RCI) operationalizes transparency and reproducibility practices on a 0–4 scale, summing four binary rubric items scored at the paper level: (1) whether key hyperparameters (e.g., learning rate, optimizer, discount factor, batch size) are explicitly listed; (2) whether the number of evaluation episodes averaged at each checkpoint is stated; (3) whether the SC2 version is reported; and (4) whether a code repository is provided. Each item contributes one point if present, yielding an integer score between 0 and 4. Because incomplete reporting leaves key implementation details (e.g., hyperparameter specifications, evaluation episode counts, SC2 version) unspecified, independent labs may fill in these gaps differently, yielding divergent outcomes. In this sense, higher reporting completeness could reduce unexplained between-study variance by making evaluation protocols more transparent and replicable. We treat RCI as a linear moderator; interpreted continuously, a one-point increase in RCI corresponds to the average change in win rate associated with disclosing one additional transparency practice.

The SC2 runtime is coded as a categorical moderator with two observed levels (2.4.10 and 2.4.6.2.69233) and an explicit “Missing” level when the version is not reported. These releases are not interchangeable [27]: minor-version changes in unit scripts, pathing, physics, and bug fixes can affect micro-level dynamics and, consequently, SMAC task performance. Modeling SC2 version allows for a better view of whether algorithmic effects are being conflated with environment-version differences, while the “Missing” level preserves sample size and allows us to test whether non-disclosure itself is associated with atypical outcomes.

Publication year is included to capture systematic trends in tooling, compute, default implementations, and community norms. We center publication year at its sample mean to improve interpretability and reduce collinearity with Algorithm × Map indicators. Because the model already conditions on Algorithm × Map, the year coefficient reflects whether there is an average drift in reported win rates per year holding Algorithm × Map identity fixed.

Moderator analyses are conducted via multilevel meta-regression that augments the baseline model with additive moderator terms while retaining cell fixed effects and a study-level random intercept. Similarly to Equation (1), let ${\mathrm{y}}_{\mathrm{i}}$ denote the reported win rate for observation $\mathrm{i}$ with within-study variance ${\mathrm{v}}_{\mathrm{i}}$, and let $\mathrm{s}\left(\mathrm{i}\right)$ index the study contributing that observation. The model introduces a new vector of study-level moderators, ${\mathrm{M}}_{\mathrm{i}}$, which includes the Reporting Completeness Index (RCI), SC2 version indicators, and centered publication year, together with a corresponding coefficient vector $\mathsf{\gamma }$ that quantifies their effects on the reported win rate conditional on Algorithm × Map. Formally, we fit

$${\mathrm{y}}_{\mathrm{i}}={\mathrm{X}}_{\mathrm{i}}\mathsf{\beta }+{\mathrm{M}}_{\mathrm{i}}\mathsf{\gamma }+{\mathrm{u}}_{\mathrm{s}\left(\mathrm{i}\right)}+{\mathsf{\epsilon }}_{\mathrm{i}},{\mathrm{u}}_{\mathrm{s}\left(\mathrm{i}\right)}~\mathcal{N}\left(0,{\mathsf{\tau }}^2\right),{\mathsf{\epsilon }}_{\mathrm{i}}~\mathcal{N}\left(0,{\mathrm{v}}_{\mathrm{i}}\right).$$

(4)

Here, ${\mathrm{X}}_{\mathrm{i}}$ is the vector of Algorithm × Map indicators as before, $\mathsf{\beta }$ represents the corresponding fixed effects, and ${\mathrm{u}}_{\mathrm{s}\left(\mathrm{i}\right)}$ and ${\mathsf{\epsilon }}_{\mathrm{i}}$ retain their previous interpretations as defined with Equation (1). Variance components are estimated by REML, and the between-study variance ${\mathsf{\tau }}^2$ and heterogeneity measure ${\mathrm{I}}^2$ are reported analogously to the baseline model.

Statistical significance of moderator sets (RCI, SC2 version, year, and all jointly) is assessed via nested likelihood-ratio tests (LRTs) fit under maximum likelihood (ML), since REML likelihoods are not comparable across models with different fixed effects structures. Let ${\mathrm{M}}_0$ denote the null model containing only the Algorithm × Map fixed effects and the study-level random intercept, and let ${\mathrm{M}}_1$ represent the augmented model that additionally includes one or more moderators. The LRT statistic is

$$\mathsf{\Lambda }=2\{{\mathrm{l}}_{\mathrm{M}\mathrm{L}}\left({\mathrm{M}}_1\right)-{\mathrm{l}}_{\mathrm{M}\mathrm{L}}\left({\mathrm{M}}_0\right)\}\sim {\mathsf{\chi }}_{\mathrm{d}\mathrm{f}}^2$$

(5)

where ${\mathcal{l}}_{\mathrm{M}\mathrm{L}}\left(\mathrm{M}\right)$ is the maximized log-likelihood of model $\mathrm{M}$ under ML estimation, $\mathsf{\Lambda }$ is the likelihood-ratio test statistic, and $\mathrm{d}\mathrm{f}$ equals the number of additional fixed-effect parameters introduced by the moderator(s). Under the null hypothesis that the moderator coefficients $\left(\mathsf{\gamma }\right)$ are zero, $\mathsf{\Lambda }$ approximately follows a chi-square distribution with $\mathrm{d}\mathrm{f}$ degrees of freedom. This procedure tests whether including a given moderator (or set of moderators) significantly improves model fit beyond the Algorithm × Map structure alone.

3.5. Prediction Intervals

A 95% prediction interval is employed to communicate the expected effects and dispersion for a future study conducted under comparable conditions, which is critical in the presence of between-study heterogeneity where confidence intervals for the mean alone can be misleading about generalizability across laboratories and implementations [28]. A prediction interval quantifies the range in which the true study-level effect is expected to fall in new settings [29], thereby directly addressing external validity, an essential concern for SMAC evaluation where irreducible design variability across papers is non-negligible as described in Gorsane et al. (2022) [5].

We identify that publication year significantly moderates reported performance (Section 4.4), so we condition the heterogeneity component of the prediction interval on this factor. Specifically, we re-estimate cell-level between-study variance ($\widehat{{\mathsf{\tau }}_{\mathrm{c}}^2}$) from univariate REML fits that include centered publication year as a moderator.

In this analysis, the target quantity is the study-level true mean win rate at 2M environment steps for a given Algorithm × Map cell, and the interval is constructed for the true mean of a future study from the same population of research designs. The interval center is the cell-specific expected mean, and the predictive variance sums the sampling uncertainty of that mean and the between-study variance for the cell, with small-sample critical values obtained via Satterthwaite-adjusted t-quantiles to improve coverage under limited numbers of studies. Concretely, for cell $\mathrm{c}$ the interval is

$$\widehat{{\mathsf{\mu }}_{\mathrm{c}}}\pm {\mathrm{t}}_{{\mathsf{\nu }}_{\mathrm{c}},0.975}\sqrt{\widehat{{\mathrm{Var}}_{\mathrm{CR}2}}\left(\widehat{{\mathsf{\mu }}_{\mathrm{c}}}\right)+\widehat{{\mathsf{\tau }}_{\mathrm{c}}^2}}$$

(6)

which treats the future-study target as a true mean (hence no addition of within-study sampling error), where $\widehat{{\mathrm{Var}}_{\mathrm{CR}2}}\left(\widehat{{\mathsf{\mu }}_{\mathrm{c}}}\right)$ is the cluster-robust CR2 variance of the cell mean, $\widehat{{\mathsf{\tau }}_{\mathrm{c}}^2}$ is the REML estimate of the cell-specific between-study variance, and ${\mathrm{t}}_{{\mathsf{\nu }}_{\mathrm{c}},0.975}$ uses Satterthwaite degrees of freedom ${\mathsf{\nu }}_{\mathrm{c}}$ derived from the robust variance estimator.

4. Results

4.1. Overview of Included Evidence

The final evidence base comprised 25 independent Algorithm × Map cells drawn from N = 324 screened studies, of which a subset of 22 studies meeting all eligibility criteria contributed to the meta-analysis. Specifically, references [4,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50] correspond to the 22 studies that satisfied all inclusion criteria, and Figure 1 provides the PRISMA flow diagram detailing the screening and selection process [12]. Each cell corresponds to a pooled estimate of win rate at the 2M environment-step horizon for one of the five canonical SMAC baselines (IQL, VDN, QMIX, QTRAN, COMA) evaluated on one of the five most frequently employed scenarios (1c3s5z, 2c_vs_64zg, 3s_vs_5z, 5m_vs_6m, MMM2).

4.2. Original SMAC Means Vs. Pooled Means

To interpret the pooled means in context, we contrast them with the results first reported in the original SMAC paper [4]. That study introduced the benchmark, defined the training protocol, and provided the initial performance profiles for IQL, VDN, QMIX, COMA and QTRAN, which have since served as the field’s reference points for algorithmic comparison. Nearly all subsequent SMAC publications situate their contributions relative to a combination of these baseline algorithms. By systematically comparing our multi-study pooled estimates to those original single-study figures, we evaluate not only how central tendencies have shifted across independent replications but also whether the benchmark’s foundational claims remain valid under broader evidence.

This subsection quantifies how the multi-study mean performance of the original baselines (IQL, VDN, QMIX, COMA; with QTRAN where applicable) compares to the single-study results that introduced SMAC, as summarized in

Table 1. Comparison of pooled multi-study means with original SMAC results [4]. ∆ denotes pooled minus original. Cells not reported in the original paper are marked with “—“ and ∆ shown as “n/a”.

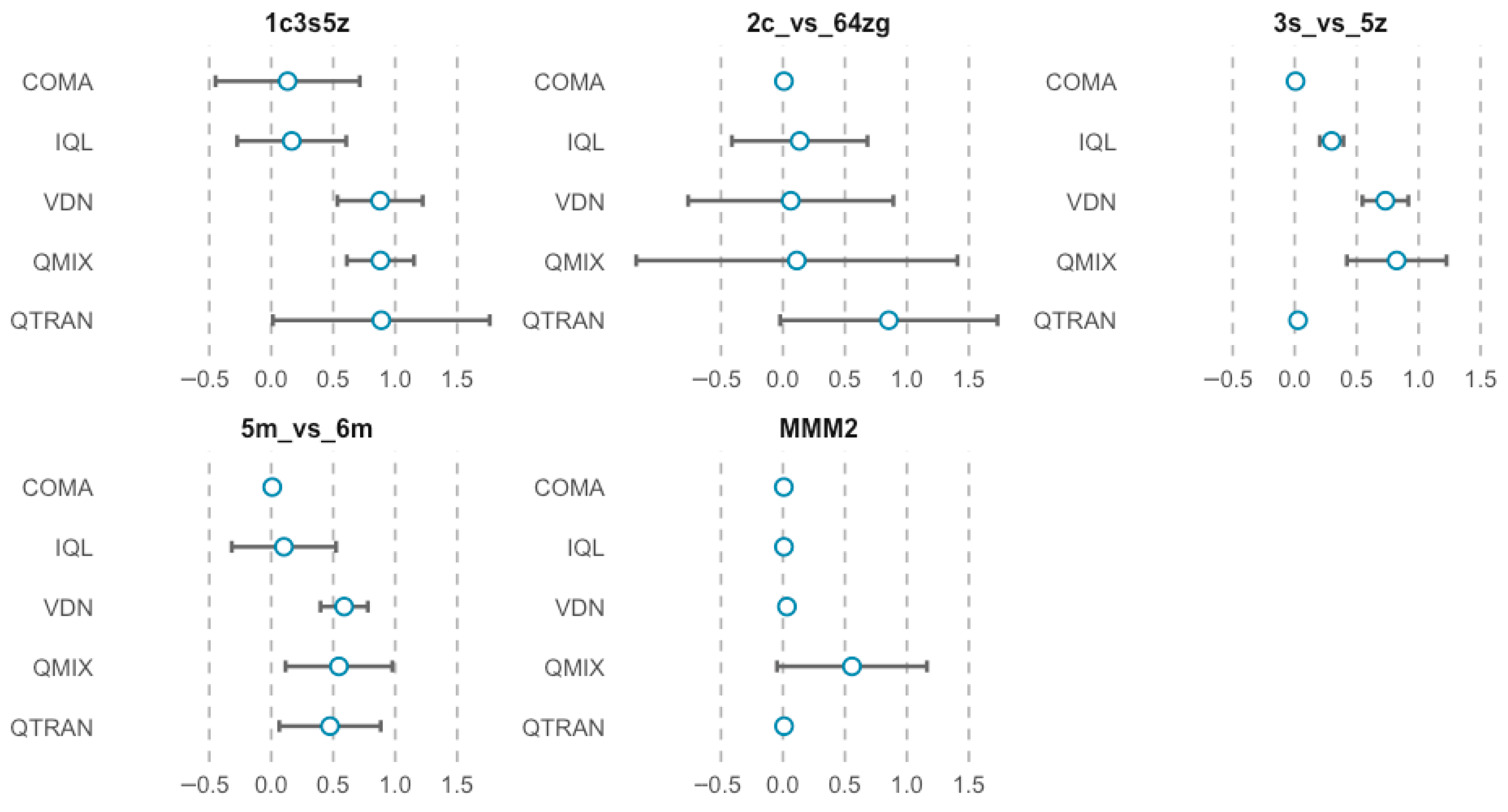
Map	Algorithm	Original	Pooled	Δ
1c3s5z	IQL	0.124	0.165	+0.041
	VDN	0.646	0.878	+0.232
	QMIX	0.719	0.881	+0.162
	COMA	0.174	0.132	−0.042
	QTRAN	—	0.888	n/a
2c_vs_64zg	IQL	0.026	0.135	+0.109
	VDN	0.159	0.063	−0.096
	QMIX	0.455	0.112	−0.343
	COMA	0.000	0.008	+0.008
	QTRAN	—	0.854	n/a
3s_vs_5z	IQL	0.321	0.298	−0.023
	VDN	0.664	0.732	+0.068
	QMIX	0.634	0.823	+0.189
	COMA	0.000	0.007	+0.007
	QTRAN	—	0.027	n/a
5m_vs_6m	IQL	0.357	0.102	−0.255
	VDN	0.507	0.588	+0.081
	QMIX	0.494	0.546	+0.052
	COMA	0.000	0.008	+0.008
	QTRAN	—	0.474	n/a
MMM2	IQL	0.003	0.008	+0.005
	VDN	0.009	0.032	+0.023
	QMIX	0.434	0.557	+0.123
	COMA	0.000	0.007	+0.007
	QTRAN	—	0.009	n/a

. Standard errors of the pooled means can be found in Appendix B,

Table A1. Pooled means and corresponding robust variance–estimated standard errors for each Algorithm × Map cell.

Map	Algorithm	Pooled Mean	RVE SE
1c3s5z	IQL	0.165	0.054
	VDN	0.878	0.050
	QMIX	0.881	0.044
	COMA	0.132	0.105
	QTRAN	0.888	0.011
2c_vs_64zg	IQL	0.135	0.102
	VDN	0.063	0.144
	QMIX	0.112	0.260
	COMA	0.008	0.008
	QTRAN	0.854	0.040
3s_vs_5z	IQL	0.298	0.028
	VDN	0.732	0.030
	QMIX	0.823	0.086
	COMA	0.007	0.008
	QTRAN	0.027	0.013
5m_vs_6m	IQL	0.102	0.088
	VDN	0.588	0.037
	QMIX	0.546	0.051
	COMA	0.008	0.008
	QTRAN	0.474	0.030
MMM2	IQL	0.008	0.008
	VDN	0.032	0.011
	QMIX	0.557	0.018
	COMA	0.007	0.008
	QTRAN	0.009	0.008

.

On 1c3s5z, our pooled means indicate marked uplift for value-decomposition methods relative to the original SMAC paper: VDN (0.878 vs. 0.646; +0.232) and QMIX (0.881 vs. 0.719; +0.162) now average near-ceiling, while IQL rises slightly (0.165 vs. 0.124; +0.041) and COMA is marginally lower (0.132 vs. 0.174; −0.042). On 3s_vs_5z, pooled means are higher for QMIX (0.823 vs. 0.634; +0.189) and VDN (0.732 vs. 0.664; +0.068), while IQL is slightly lower (0.298 vs. 0.321; −0.023) and COMA remains effectively at zero.

On 5m_vs_6m, the synthesis yields modestly higher pooled estimates for VDN (0.588 vs. 0.507; +0.081) and QMIX (0.546 vs. 0.494; +0.052), a large decrease for IQL (0.102 vs. 0.357; −0.255), and negligible change for COMA (0.008 vs. 0.000). For the super-hard MMM2, pooled means are somewhat higher for QMIX (0.557 vs. 0.434; +0.123), while VDN (0.032 vs. 0.009; +0.023) and IQL (0.008 vs. 0.003; +0.005) remain close to zero, and COMA remains negligible (0.007 vs. 0.000).

The most pronounced divergence from the original report appears on 2c_vs_64zg. Whereas the SMAC paper reported moderate means for QMIX (0.455) and VDN (0.159) with IQL near zero (0.026), our pooled estimates reverse this profile: QMIX averages 0.112 (−0.343), VDN 0.063 (−0.096), while IQL rises to 0.135 (+0.109). Moreover, though QTRAN was evaluated only on a few easy scenarios in the original study, our expanded corpus indicates QTRAN pools very high on 2c_vs_64zg (0.854), revealing a strong map-specific advantage not captured in the original baseline comparison.

These overall performance patterns align with well-established characteristics of the baseline algorithms. IQL, which trains agents independently without shared credit assignment, tends to perform adequately on maps with limited coordination requirements but struggles when inter-agent dependencies are strong. VDN and QMIX introduce centralized value decomposition, linear in VDN and monotonic non-linear in QMIX, allowing more effective coordination and higher average win rates on structured cooperative tasks such as 1c3s5z and 3s_vs_5z, though both remain constrained by their inability to model non-monotonic interactions. QTRAN relaxes QMIX’s monotonicity assumption, enabling richer joint value representations and sometimes superior results on complex maps, but its optimization instability often leads to inconsistent performance across studies. COMA, a counterfactual policy-gradient approach, directly addresses credit assignment but exhibits high gradient variance and poor sample efficiency, explaining its comparatively low and variable outcomes. Overall, our pooled means broadly reinforce these known tendencies—strong value-decomposition methods dominate simpler or moderately hard maps, policy-gradient methods remain less stable, and algorithmic design continues to shape relative success across SMAC’s diverse coordination regimes.

Together, the pooled cell means support two central claims of the original SMAC paper while qualifying a third. First, they affirm that value-decomposition methods dominate COMA and often achieve high average win rates on easier or moderately hard scenarios. Second, they confirm the persistence of genuinely hard content in the context of these baseline algorithms (e.g., MMM2), where average win rates remain near zero at 2M steps despite being evaluated across multiple independent studies. Third, they complicate the notion of QMIX (or any algorithm, for that matter) as the superior baseline algorithm by showing map-contingent reversals, most notably on 2c_vs_64zg, once multi-study evidence is aggregated. We emphasize that these contrasts are about only central tendencies; questions of stability and generalizability are developed next via heterogeneity metrics and prediction intervals.

4.3. Heterogeneity

Heterogeneity is central to interpreting SMAC results because our target of inference is not a single laboratory’s outcome but the distribution of study-level outcomes that arises under the field’s diverse implementations.

As summarized in

Table 2. Cell-level heterogeneity estimates (I² percentage) across Algorithm × Map.

Map	Algorithm
	IQL	VDN	QMIX	QTRAN	COMA
1c3s5z	78.4	95.4	96.2	85.5	89.6
2c_vs_64zg	97.1	96.9	97.6	90.0	65.2
3s_vs_5z	0.0	91.5	81.2	23.3	0.0
5m_vs_6m	83.5	87.0	86.4	77.4	80
MMM2	92.6	24.6	87.6	94.3	72.2

, across the 25 Algorithm × Map cells, 17 have I² ≥ 80% (i.e., in most cases between-study variance dominates sampling error). Cell-level heterogeneity is high even when pooled means are high: for example, on 1c3s5z the factorization baselines (QMIX/VDN/QTRAN) achieve near-ceiling means yet still post I² in the >80% range, showing that “easy” scenarios can yield unstable literature estimates. More broadly, heterogeneity is elevated across nearly the entire benchmark, underscoring that instability is a structural property across several SMAC evaluations rather than an exception tied to specific maps or algorithms. As a result, cell means alone provide limited guidance about expected performance, and heterogeneity-aware metrics are indispensable for interpreting reported results.

Uniquely, cells with consistently near-zero performance tend to display the dramatically lowest I² values compared to all other cells, for example, COMA:3s_vs_5z (0%) and IQL:3s_vs_5z (0%), QTRAN:3s_vs_5z (23.3%), and VDN:MMM2 (24.6%). These cases indicate reproducible failure: when algorithms systematically fail on a map, they tend to do so consistently across labs. Regardless, there are notable exceptions to this rule on several Algorithm × Map combinations, notably COMA:MMM2 (72.2%), IQL:MMM2 (92.6%), QTRAN:MMM2 (94.3%), and COMA:5m_vs_6m (80%), however these cases point more to a methodological flaw as opposed to true low reproducibility as explained further in Section 5.3.

4.4. Moderator Analysis

We assessed whether study-level moderators explain residual dispersion beyond Algorithm × Map fixed effects by comparing a cells-only model with augmented specifications. Summary statistics are displayed in

Table 3. Model heterogeneity estimates under alternative moderator specifications relative to the null model. ${∆\mathrm{I}}^2$ denotes percent reduction relative to the null model. Bold indicates the best performing value for each metric.

Model	τ2	I2 (%)	vs. Null
			ΔI2	LRT	p-Value
Null (cells only)	0.00689	39.3	—	—	—
+RCI	0.00713	40.1	−0.83	0.32	0.572
+SC2 Version	0.00723	40.4	−1.16	1.12	0.570
+Publication Year	0.00572	34.9	4.34	5.06	0.024
+All	0.00636	37.4	1.88	6.33	0.176

. In the baseline, the between-study variance was τ² = 0.00689 with I² = 39.3%. Adding publication year significantly improved fit (LRT = 5.06, p = 0.0244), reduced τ² to 0.00572, and lowered I² to 34.9%. This indicates a secular, time-dependent component to reported win rates that persists even after conditioning on the Algorithm × Map identity of each observation, possibly consistent with gradual drift in tooling, defaults, implementations, or community practices that shape outcomes over calendar time.

By contrast, augmenting with the Reporting Completeness Index (RCI) or SC2 runtime version did not improve model fit (LRTs: p = 0.572 and p = 0.570, respectively), and each increased τ² slightly relative to the null (RCI: τ² = 0.00713; SC2 version: τ² = 0.00723). The all-moderators model (year + RCI + version) yielded τ² = 0.00636 and I² = 37.4% but did not significantly outperform the null (LRT = 6.33, p = 0.176). Taken together, these results suggest that calendar time captures a nontrivial share of between-study variation, whereas our coarse measures of reporting quality and versioning offer limited explanatory leverage in this sample once cells are controlled.

Of note, even with publication year included, substantial heterogeneity remains (I² ≈ 35%), underscoring that time trends explain only a portion of the cross-study variability in SMAC outcomes.

4.5. Prediction Intervals

Prediction intervals provide a distributional perspective on how widely outcomes vary across laboratories using the same baseline algorithms. Our data suggests that intervals are broad across nearly all Algorithm × Map cells, reflecting substantial instability in the literature. Figure 2 displays the calculated prediction intervals.

As displayed in Figure 2, on maps often categorized as “easy,” such as 1c3s5z, pooled means for QMIX, VDN, and QTRAN approach ceiling means, yet their intervals extend downward to include values near and well below 50%. This shows that even for scenarios widely regarded as straightforward, a new study could obtain dramatically lower results than the literature average. In other words, high means do not imply reproducibility of high performance.

On the more challenging maps, including 2c_vs_64zg and MMM2, the intervals widen further, in several cases extending outside the [0, 1] bounds of a win-rate scale. They indicate that cross-lab outcomes on these maps can range from near-total failure to near-perfect success depending on implementation choices. This volatility is especially important to be aware of given that these tasks are used to stress-test new algorithms; the breadth of the PIs highlights the difficulty of attributing gains to methodological advances rather than to experimental variability.

Prediction intervals complement the limitations of using means alone to summarize expected performance. For baseline algorithms, intervals reveal that outcomes remain highly lab-dependent even after years of reuse, and that generalization across studies is much weaker than single-study reports would suggest. Also note that the same cells with characteristically low PI intervals are the same that are attributed with unusually low heterogeneity. These cases will be described further in Section 5.3.

5. Discussions

5.1. Finding Highlights in Context

Taken together, the evidence shows that SMAC outcomes are dominated by irreducible, cell-level variability: across the 25 Algorithm × Map cells, a clear majority exhibit very high heterogeneity (17/25 with I² ≥ 80%), meaning that differences between laboratories and implementations typically outweigh sampling error. Consequently, high average win rates do not reliably generalize to a new lab. This is made explicit by the cell-specific 95% prediction intervals, which frequently remain broad even where pooled means approach ceiling; on canonical “easy” cells, intervals commonly include near and sub-50% study-level means, and on harder cells the intervals widen further, underscoring that a new laboratory may legitimately observe outcomes that differ qualitatively from the literature average. These results quantify, in a variance-aware way, the field’s perception of “solved” scenarios rests largely on mean-centric summaries that obscure substantial cross-study dispersion.

The moderator analyses reinforce this picture. After conditioning on Algorithm × Map, neither our Reporting Completeness Index nor SC2 version accounts for a meaningful portion of the between-study variance in this sample, both fail to improve fit relative to the cells-only model, indicating that no tangible reporting/versioning covariate, as currently measured, explains the heterogeneity. By contrast, publication year is statistically significant and reduces residual τ², providing evidence of secular drift: outcomes shift over calendar time, plausibly reflecting evolving defaults, toolchains, and community practices. Importantly, however, substantial heterogeneity persists after adding year (residual I² ≈ 35%), so temporal drift explains only part of the instability.

5.2. Why RCI and SC2 Version Did Not Explain Variance

Several features of the evidence base may have caused the null findings for the Reporting Completeness Index (RCI) and SC2 moderator analyses. First, measurement coarseness and restricted range likely attenuated associations. The RCI is a 0–4 additive rubric of binary items and may be too blunt to capture the implementation choices that plausibly drive between-study dispersion. In addition, our eligibility criteria (≥4 baselines, dispersion reported at a fixed 2M-step horizon) likely select for relatively careful studies, compressing the empirical range of RCI and weakening any detectable relationship with outcomes.

Additionally, dominant cell identity and collinearity with time likely overwhelm modest reporting/version signals. Algorithm × Map fixed effects absorb large systematic differences in difficulty and algorithm-task interactions; if reporting practices and SC2 versions are unevenly distributed across cells or trend with publication year, their incremental explanatory power after conditioning on cells (and, in augmented specifications, on year) will be small. In our data, publication year captures a non-trivial share of residual variance (significant LRT); once this is accounted for, little independent signal remains for RCI or SC2 version. Power is further constrained because both moderators are study-level variables, the number of contributing studies is moderate, and CR2 small-sample corrections reduce effective degrees of freedom.

The implication is not that reporting quality or runtime versions are unimportant, but that our current proxies are underspecified. Future syntheses would benefit from richer reporting taxonomies that we will further describe in Section 5.4.

5.3. Methodological Limitations

Several methodological considerations shape the interpretation of this meta-analysis, particularly those related to data extraction and variance handling. First, all effect sizes were digitized from plotted ribbons at the 2M-step horizon, an approach that introduces a degree of extraction noise. While WebPlotDigitizer allows fine-grained capture of central tendencies and uncertainty bands, resolution constraints and graphical rounding can yield minor distortions in reported values. This digitization process may therefore introduce a small but systematic bias, since uneven sampling density along the plotted curve can give disproportionate weight to smoother or more visually distinct regions. This noise is likely small in magnitude relative to the between-study variance but nonetheless contributes to within-study dispersion and should be acknowledged as a limitation of the digitization procedure.

Second, variability was not always directly reported in the primary sources. In several instances, standard deviations required conversion from alternative uncertainty formats or approximation from available statistics. Although such transformations were implemented using established formulas, they introduce an additional layer of imprecision beyond direct reporting. This limitation is not unique to SMAC but reflects broader challenges in meta-analytic synthesis where reporting practices vary. These conversion formulas are summarized in Appendix A.

Third, the handling of zero-variance cases merits emphasis. In SMAC, many Algorithm-Map combinations, especially those associated with near-universal failure, yield across-seed standard deviations of zero. Left untreated, such cells would imply infinite inverse-variance weights and destabilize estimation. To address this, we applied a conservative two-stage rule in which zeros were replaced by a sentinel floor and then substituted with the within-cell median variance. This preserves the empirical scale of dispersion characteristic of each cell while ensuring strictly positive variances for model fitting. However, the phenomenon that arises at the boundary of proportion data has important implications for heterogeneity metrics. Cell-level I² is conceptually defined as ${\displaystyle \frac{{\tau }^2}{{\tau }^2+\overline{v}}}$, where τ² denotes the between-study variance and $\overline{v}$ the mean within-study variance. In low-mean cells where nearly all studies report failure (means ≈ 0, SD ≈ 0), $\overline{v}$ approaches zero. Under these conditions, even minuscule τ² values (on the order of ${10}^{-5}$ to ${10}^{-4}$) inflate I² toward very high percentages. This explains why cells such as IQL:MMM2 or QTRAN:MMM2 exhibit I² > 90% despite negligible absolute dispersion—rare deviations from universal failure generate non-zero τ² that proportionally dominates $\overline{v}$. By contrast, in cases like COMA:3s_vs_5z, every study reports exactly zero with SD = 0, producing both τ² = 0 and I² = 0.

5.4. Recommendations for Benchmarking Practices

The results of this meta-analysis highlight several actionable steps that can be taken to improve the rigor and reproducibility of SMAC benchmarking. A first priority is version control and disclosure. Authors should explicitly state the StarCraft II runtime version used, along with all wrapper and configuration dependencies, so that differences in environment dynamics can be disentangled from algorithmic effects. Equally critical is full disclosure of evaluation protocols: the number of episodes averaged at each checkpoint, the random seed schedule, and any deviation from default evaluation practices. These details are routinely omitted yet strongly influence the stability of reported win rates.

Second, we recommend map-set preregistration and retention of the 2M-step evaluation anchor. Predefining a balanced set of scenarios across the difficulty spectrum guards against map selection bias, whereby authors emphasize only those tasks that advantage their method. The original SMAC benchmark fixed evaluation at 2M environment steps; retaining this anchor remains essential for comparability across studies, while preregistration of map panels ensures that both easy and hard cases are represented in a fair and transparent way.

Third, authors should provide measures of dispersion (e.g., standard deviation, confidence intervals), the number of evaluation episodes, exact SC2 version and configuration files, and access to full learning curves in machine-readable form (CSV) so that a future systematic meta-analysis like this could be conducted more easily and thoroughly.

Finally, we strongly encourage open code and configuration dumps. Public repositories should include not only the algorithm implementation but also training scripts, evaluation pipelines, and complete hyperparameter and scheduler settings. Configuration transparency ensures that future studies can reproduce reported results under identical conditions, and open repositories allow for independent verification of claims and extension to new settings.

With all of these elements, researchers would not only be able to compute prediction intervals and heterogeneity metrics with far greater precision, but also to explore richer moderator structures such as seed protocols, optimizer schedules, or replay specifications. More thorough reporting practices would allow subsequent syntheses to disentangle methodological from algorithmic variance, quantify reproducibility under more granular conditions, and establish robust cross-lab baselines. In effect, the availability of transparent reporting would enable meta-analyses that are not only more comprehensive but also more diagnostic, turning benchmarks like SMAC into cumulative scientific resources rather than collections of isolated performance claims.

6. Conclusions

In sum, this study provides a variance-aware reassessment of SMAC at a time when the benchmark is widely used yet often read through mean-centric summaries. By pooling multi-study evidence for the canonical baselines, we show that cell-level heterogeneity is the norm and that 95% prediction intervals are generally broad, implying that high reported win rates often do not generalize to a new laboratory. More broadly, the findings highlight that progress in cooperative MARL cannot be judged by isolated mean scores but requires systematic attention to heterogeneity, uncertainty, and reproducibility across laboratories. Conventional proxies for methodological quality or runtime (RCI, SC2 version) do not significantly account for this instability, whereas a year effect signals secular drift in defaults and toolchains. These results underscore the need for richer reporting standards, stronger version control, and open dissemination of code and configurations.

In future works, addressing these gaps will allow future syntheses to partition variance more precisely, distinguish methodological from algorithmic effects, and establish reproducible baselines. Additionally, building off this research, future works may extend the evidence base to include more recent architectures such as QPLEX, RODE, or MAPPO, enabling direct comparison between classical value-decomposition methods and transformer-based or actor–critic frameworks within a unified meta-analytic model. It would also be relevant to evaluate whether the observed heterogeneity patterns persist across other cooperative benchmarks (e.g., MPE, Hanabi, Melting Pot), helping to determine whether reproducibility challenges stem from SMAC itself or from broader structural issues in MARL experimentation.