Deconstructing a Minimalist Transformer Architecture for Univariate Time Series Forecasting

Abstract

This paper provides a detailed breakdown of a minimalist, fundamental Transformer-based architecture for forecasting univariate time series. It describes each processing step in detail, from input embedding and positional encoding to self-attention mechanisms and output projection. All of these steps are specifically tailored to sequential temporal data. By isolating and analyzing the role of each component, this paper demonstrates how Transformers capture long-term dependencies in time series. A simplified, interpretable Transformer model named ’minimalist Transformer’ is implemented and showcased using a simple example. It is then validated using the M3 forecasting competition benchmark, which is based on real-world data, and a number of data series generated by IoT sensors. The aim of this work is to serve as a practical guide and foundation for future Transformer-based forecasting innovations, providing a solid baseline that is simple to achieve but exhibits a stable forecasting ability not far behind that of state-of-the-art specialized designs.

1. Introduction

Time series forecasting is a key topic in data science and has a wide range of applications in areas such as economics, energy, healthcare, logistics and environmental monitoring. Accurate forecasting enables informed decision-making, efficient resource allocation and risk mitigation. Traditional statistical methods such as ARIMA and exponential smoothing have long been used for this purpose and often produce good results when the necessary assumptions are met. However, these methods often struggle to capture complex patterns and long-term dependencies in the data, an area in which deep learning methods, especially sequence models such as recurrent neural networks (RNNs), have often demonstrated superior performance.

Transformer models, which were initially designed for natural language processing tasks, have recently shown remarkable success in understanding and generating sequential data, demonstrating their effectiveness in modeling long-range dependencies. Transformers are attention-based models that eliminate the need for recurrence and convolution, relying instead on a self-attention mechanism to capture global context across sequences. This architecture has had a revolutionary impact on NLP, and its application to time series forecasting is a rapidly growing area of research.

Unlike natural language, time series are composed of continuous values and frequently exhibit seasonality, trends, and influence from exogenous variables. While recent studies have proposed various adaptations of the Transformer to address the unique properties of time series data, many of these models are treated as opaque black boxes. This means that there is limited clear understanding of how each component relates to temporal information and contributes to forecasting performance. Furthermore, the implementation details are frequently insufficiently specified, which makes reproducibility and interpretability challenging.

The aim of this paper is to ’deconstruct’ the forecasting process of Transformer-based models when applied to univariate time series. The objective is to provide a transparent, modular and pedagogical account of how univariate time series are transformed and processed within these models to generate future trajectories. Each processing step is described in detail, including data normalization, input windowing, positional encoding, encoder and decoder architecture, training strategies, and prediction generation. Both the theoretical basis and the practical design choices are highlighted, showing how each element contributes to predictive accuracy and attempting to bridge the gap between theoretical advancements and practical implementation.

To validate the methodology, a basic Transformer-based model has been implemented and evaluated on a significant benchmark of univariate time series. These were selected from the well-known M forecasting competition benchmarks and included macro- and micro-economic, industrial, financial, and demographic series with varying statistical properties. This work combines theoretical explanation with empirical validation to serve as a comprehensive guide to deconstructing Transformer-based time series forecasting, providing a tutorial for newcomers and a reference for practitioners.

This paper is structured as follows. Section 2 reviews the related works in time series forecasting, with particular emphasis on recent advancements leveraging Transformer architectures. Section 3 presents the workflow of a minimalist Transformer module to produce a multipoint forecast for a univariate time series. Section 4 analyses some results in applying the described architecture on benchmark data series and comparing it with another standard methodology.

2. Related Work

Transformer modules for processing graph-like structures were originally introduced in [1] for a check-reading task; however, it was only in [2] that the current Transformer architecture for sequence modeling was proposed. Already, the very first line of the introduction of this seminal paper frames the transformer architecture among established time series modeling and forecasting algorithms, citing LSTM [3] and GRU [4], i.e., the two main architectures for recurrent neural networks (RNNs) applied to time series modeling.

Indeed, RNNs can be effective in capturing long-term dependencies within data, but they suffer from slow training, vanishing gradients, and high sensitivity to hyperparameter settings. Furthermore, the most well-established statistical methods, such as autoregressive integrated moving average (ARIMA) [5] and exponential smoothing (ETS) [6,7], are highly effective for stationary data but struggle with complex nonlinear patterns.

Transformer architectures are immune to these drawbacks because they do not rely on the assumption of stationarity. They capture global dependencies in input sequences without relying on recurrence, instead leveraging self-attention mechanisms to enable the direct modeling of long-range dependencies. This supports full parallelization during training and allows the model to focus on relevant time steps, regardless of their position in the sequence.

A key challenge in applying Transformers to univariate time series is the absence of the rich semantic tokens found in language. Unlike words in a sentence, time series values are continuous and lack discrete meaning, making it more difficult to learn meaningful attention patterns. Therefore, Transformers need to be adapted for time series forecasting. Some adaptations of Transformers for use with time series data include: Informer [8], which introduces a sparse self-attention mechanism to reduce the quadratic complexity of self-attention, making it more efficient for long sequence time series forecasting; Autoformer [9], which integrates a series decomposition block within the Transformer to separate trend and seasonal components, obtaining decomposition-based attention for better seasonal-trend modeling, improving interpretability and long-horizon forecasting accuracy; FEDformer: [10], which incorporates Fourier transformations into the attention mechanism to better exploit frequency-domain characteristics; PatchTST: [11], which employs a splitting mechanism to time series, converting multiple timesteps (i.e., a patch) into a single token, enabling a vanilla Transformer architecture to capture long-term dependencies with fewer tokens; Chronos [12], a family of pretrained time series forecasting models based on language model architectures. Chronos models have been trained on a large corpus of publicly available time series data, with particular interest in their zero-shot performance; TCANs (Temporal Convolution Attention Networks) [13], which combine temporal convolutional networks and attention mechanisms.

Recently, an explosion of adaptations has appeared, together with dedicated surveys and tutorials [14,15,16]. However, these models are often complex, incorporating multiple components such as static covariates, gating mechanisms, and probabilistic outputs. While these additions have shown empirical gains, they frequently obscure the core dynamics of the attention mechanism and make the models less accessible for analysis or adaptation.

In contrast, there is interest in minimal Transformer implementations, which isolate the effectiveness of self-attention in forecasting tasks. Informer has already demonstrated that a simplified Transformer, devoid of specialized components, can outperform classical models and RNNs on certain benchmarks when properly tuned. Similarly, ref. [17] proposed the ‘Temporal Attention’ module within a lightweight Transformer framework, demonstrating that attention over timesteps alone can achieve comparable performance on univariate series. Other studies, such as iTransformer [18], investigate how the performance of standard Transformers is affected by different initialization, normalization, or positional encoding strategies. This sheds light on the contribution of each component to forecasting accuracy.

This body of work highlights the growing interest in demystifying Transformer-based time series models by removing layers of abstraction. In line with this perspective, a minimalist Transformer specifically designed for univariate forecasting is proposed. A minimal version of the Transformer encoder has been developed by maintaining only the essential self-attention and feedforward components. By simplifying the model, the aim of this study is to understand the fundamental processes that enable Transformers to succeed in this domain and to provide a transparent and reproducible basis for further research.

3. The Transformer Processing Pipeline

This section describes the successive processing phases carried out by a minimalist Transformer module to produce a multipoint forecast of a univariate data series. The relevant Python code can be found in [19]. Successive processing stages are here showcased on a tiny time series obtained by querying Google Trends [20] on the term “restaurant”. The series shows a trend (at the time of writing, it is holiday season in Italy and interest in dining out is increasing) as well as seasonality, due to increased interest on weekends. Only 35 data points are considered, 7 of which are kept for validation and 28 are used for training. The series $s\left(t\right)$ is the following:

$$\begin{array}{cc}\hfill s\left(t\right)= & (44,48,51,48,50,63,66,48,53,56,52,57,70,67,56,60,62,60,58,75,73,59,61,65,\hfill \\ \hfill & 63,63,78,80,63,64,67,65,70,87,84)\hfill \end{array}$$

The data processing cycle consists of three main phases: encoding, decoding, and learning. A view of the whole model can be seen in Figure 1. The following subsections provide details on each phase; the reader is referred to [2] for a more exhaustive exposition.

3.1. Encoding

The objective of the encoding component (i.e., the encoder) in a Transformer architecture is to process an input sequence and convert the raw input into a contextually enriched representation that captures both local and global dependencies. This representation can then be used effectively by the rest of the model.

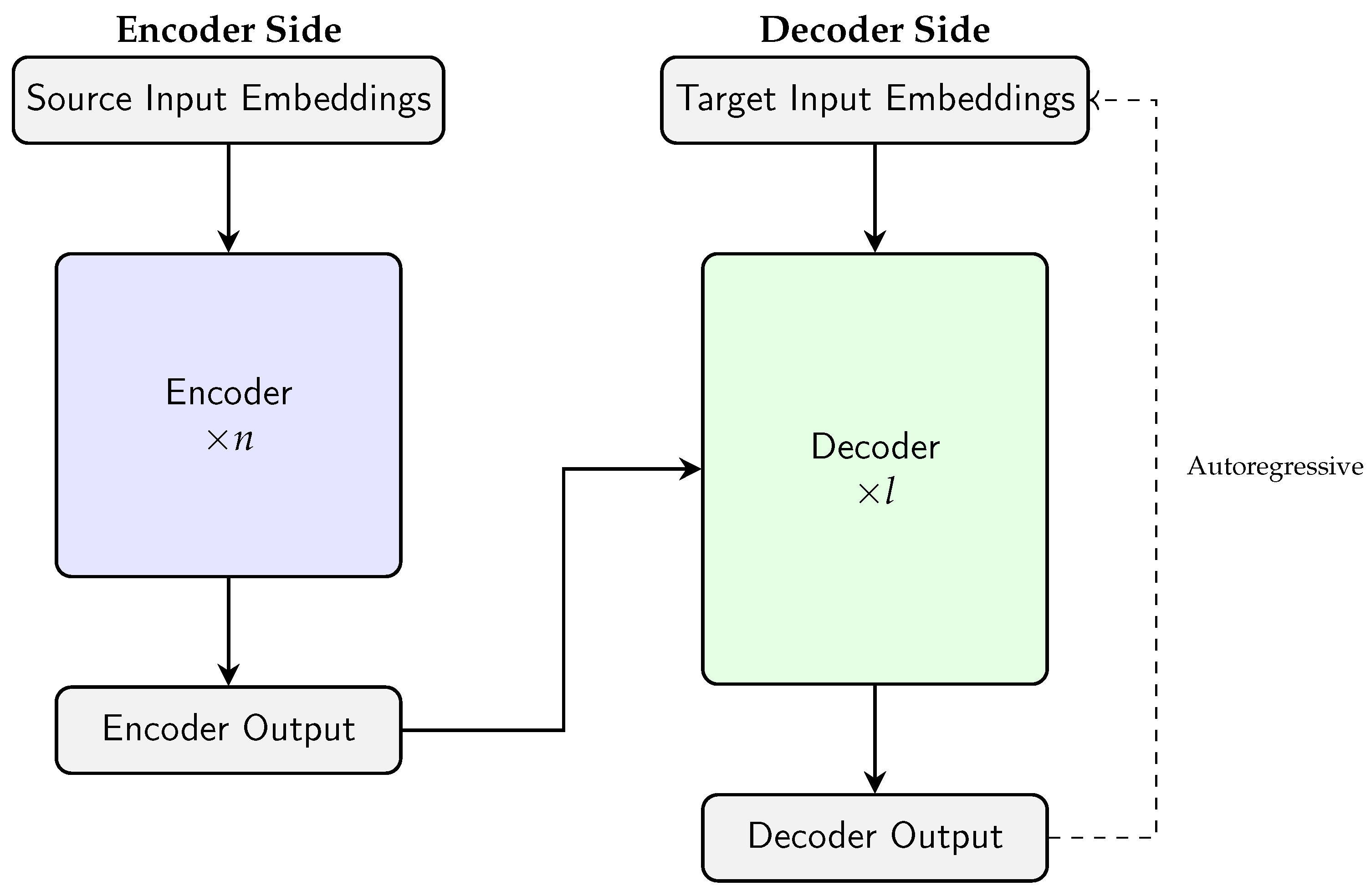
The general structure of the encoding module is represented by the pseudocode in Algorithm 1 and sketched in Figure 2. All intermediate numerical results obtained for the restaurant series case study are reported in the text or in Appendix A when they are too big to be presented inline. This is to enable the interested reader to immediately grasp the dimensionalities and values involved in this tiny example, and possibly to follow the corresponding evolution of a run of the code provided in [19].

In the case of the running example, the following input parameter values are used: n = 7, m = 4, k = 2, $d_k$ = $d_v$ = 2, p = 16.

The individual steps are detailed below.

Algorithm 1: The encoding module

• (Input arguments)

The input consists of the data series to be forecast—in this case, it is an array $s\in {\mathbb{R}}^n$ and of six control hyperparameters.

For the restaurant time series, a straightforward preprocessing step has been applied: min-max normalization of the raw data. Subsequently, each sequence was constructed using a sliding window of length $n=7$ over the series.

• Lines 2–4: (Input Projection)

Single scalar values for each single timestep may not be expressive enough to capture contextual information. Each data point is projected into a higher-dimensional space where nonlinear dependencies between features can be easier to identify.

In the minimalist Transformer model proposed in this study, the projections, also known as embeddings, were obtained by multiplying each datapoint by a shared real-valued vector $W_i\in {\mathbb{R}}^m$ initialized as a random Gaussian vector, and by adding a bias array $b_i\in {\mathbb{R}}^m$. These values can later be learned. In this way, a matrix $X\in {\mathbb{R}}^{n\times m}$ is computed, which contains, for each original timestep, its m-dimensional representation.

In the restaurant series, the projections were based on vectors of 4 values, obtaining a set of matrices, each of which with $n=7$ rows and $m=4$ columns, leaving 4 parameters to be learned for the projection vector and the other 4 for the bias array. Each matrix X represents a window over the input time series; the first of these matrices is presented in the Appendix A as Equation (A1). The learned arrays $W_i,b_i$ are also shown in the Appendix A, as Equation (A2).

• Line 5: (Positional Encoding)

The basic attention mechanism, which will be implemented in lines 12–14, is insensitive to the permutation of the input values [2] and is in itself unusable for modeling data series. Therefore, the model does not inherently deal with the sequential position of the elements: the attention only depends on the set of elements, not on their order. To inject ordering information, each input embedding $X^j$ is added to a positional vector. This is obtained by means of a matrix $P\in {\mathbb{R}}^{n\times m}$, which yields the transformed input:

$$X^{\prime }=X+P$$

(1)

where n denotes the sequence length and m denotes the embedded dimension.

The matrix P can be either static, remaining fixed during the training phase, or learnable, changing at each step to better adapt to the task at hand. It can also be either absolute, depending solely on the element’s position, or relative, in which case the element itself influences the values of the matrix’s rows.

In the proposed minimalist architecture, matrix $P\in {\mathbb{R}}^{7\times 4}$ is an absolute, learnable positional encoding, in the restaurant use case consisting of 7 rows and 4 columns. This equates to a further 28 parameters that need to be learned. The matrix P used in the running example is presented in the Appendix A as Equation (A3).

• Lines 6–21: (Encoding Blocks)

The main loop of the algorithm repeats a block of code called an Encoding Block n times. In it, matrix X is first passed to a module implementing Multihead Attention (Lines 7–15). The outputs of the heads are then concatenated and projected to keep the size consistent (Lines 16–17). Next, a residual connection with a normalization is applied (Line 18). The output is then passed through a small feedforward network, after which another residual connection and normalization are applied (Lines 19–20). It is important to note that each iteration uses its own set of parameters for the projections, attention weights, and feedforward layers; parameters are not shared between iterations. All these steps are detailed in the following.

• Lines 7–15: (Multihead Attention)

This loop iterates a basic attention mechanism that dynamically weighs the contribution of each past point in the series when computing the representation of those under scrutiny. It computes a set of attention scores relating the “query” vector of the current point and “key” vectors of all sequence values. In the sample application, a query comes from the embedding of the last known observation, while the keys correspond to those of all past observations. The resulting attention weights determine which points matter most and the forecast is then given by a weighted sum of the corresponding “value” vectors.

Queries (the elements currently focused on), keys (descriptors of the corresponding values), and values (the actual information) are all represented as matrices. Typically, queries and keys share the same inner dimension $d_k$, while values may have a different dimension $d_v$. At each iteration, the corresponding set of query, key, and value is referred to as a head. The matrices and the bias identified for the two heads used in the running example are reported in the Appendix A in Equations (A4) and (A5).

• Line 8: generates the $h-th$ query matrix and projects the input embeddings into vectors that represent what has been looked for in the past. This is achieved by using a dynamic parameter matrix $W_q^h\in {\mathbb{R}}^{m\times d_k}$ and a bias array $b_q^h\in {\mathbb{R}}^{d_k}$, which are learnt.
• Line 9: generates the $h-th$ key matrix and projects the input embeddings into vectors that represent the information content of each corresponding embedding. This is achieved by using a dynamic parameter matrix $W_k^h\in {\mathbb{R}}^{m\times d_k}$ and a bias array $b_k^h\in {\mathbb{R}}^{d_k}$, which are learnt.
• Line 10: generates the $h-th$ value matrix and projects the input embeddings into vectors that represent the relevant information of each available embedding. This is achieved by using a dynamic parameter matrix $W_v^h\in {\mathbb{R}}^{m\times d_v}$ and a bias array $b_v^h\in {\mathbb{R}}^{d_k}$, which are learnt.
• Line 11: initializes the scaling factor.
• Line 12: implements the first part of the attention function, in this case using the Scaled Dot-Product Attention [2]. The similarity between sequence elements is computed from Q and K through a dot product. The key matrix is transposed so that the operation compares each feature of every query with the corresponding feature of every key. This initial A matrix will contain similarity values $a_{ij}\in \mathbb{R}$ between every query vector and every key vector.
• Line 13: transforms the similarity values into ‘probability’ scores. The $\mathit{softmax}\left(\right)$ operator is applied to all elements $a_{ij}$ over every row: $a_{ij}=e^{a_{ij}}/{\sum }_k{e}^{a_{kj}},\forall i,j=1,\dots ,n$. In this way, for every query vector, normalized weights of similarity towards key vectors are obtained.
• Line 14: completes the computation of the attention function by implementing a weighted sum of the value vectors, $A^h=A^h·V^h$, thereby aggregating information from the relevant timesteps.
• Line 16: lines 7–15 are repeated k times, each time obtaining an attention matrix $A^h$, $h=1,\dots ,k$. This line concatenates all these matrices into a single bigger one, $A=[A^1{A}^2\dots A^h]$. The matrix A obtained for the running example is reported in the Appendix A as Equation (A6).
• Line 17: since concatenation may modify the dimensionality, a final output projection $W^O\in {\mathbb{R}}^{h{d}_v\times m}$ is applied to ensure that the original size is kept $X^{\prime }=A·W^O$.
• In the running example, we set $h=d_k=d_v={\displaystyle \frac{m}{2}}=2$. This produced 6 matrices, all of size $4\times 2$, totaling 48 more parameters to learn. The output matrix $W^O$ is, instead, of size $4\times 4$. Matrix $W^O$ for the running example is reported in Equation (A7) of the Appendix A.
• Lines 18, 20: (Add and Norm)

This block tries to stabilize training by normalizing activations while keeping a residual path. It is implemented by a layer function $LayerNorm:{\mathbb{R}}^{n\times m}\to {\mathbb{R}}^{n\times m}$, which operates independently for each row i (i.e., for each embedding), computing the mean ${\mu }_i\in \mathbb{R}$ and the variance ${\sigma }_i\in \mathbb{R}$, and updating the features of row i as $x_{ij}={\gamma }_j·{\displaystyle \frac{x_{ij}-{\mu }_i}{{\sigma }_i}}+{\beta }_j$, where $\gamma ,\beta \in {\mathbb{R}}^m$ are learnable parameters.

In the running example, having set $m=4$, and having two different LayerNorm blocks, 16 parameters were set to be learned. For the first layer:

$$\gamma =\left[\begin{array}{cccc}0.8659& 1.1768& 0.4843& 1.2575\end{array}\right]\beta =\left[\begin{array}{cccc}-0.3721& 0.1294& -0.0496& 0.3132\end{array}\right]$$

While for the second layer:

$$\gamma =\left[\begin{array}{cccc}0.8747& 0.7511& 0.6320& 0.7074\end{array}\right]\beta =\left[\begin{array}{cccc}-0.1117& -0.1993& 0.0806& 0.1641\end{array}\right]$$

• Line 19: (Feedforward Network)

The final processing step of the minimalist Transformer architecture implements a two-layer network with a ReLU activation function between them:

$$s^{\prime }\leftarrow \max (0,s^{\prime }·W_1+b_1)·W_2+b_2$$

(2)

where:

$$W_1\in {\mathbb{R}}^{m\times p},b_1\in {\mathbb{R}}^p$$

$$W_2\in {\mathbb{R}}^{p\times m},b_2\in {\mathbb{R}}^m$$

The ReLU function is applied element-wise. The intermediate dimension p is typically chosen to be larger than m to improve model capacity and generalization.

In the model, we set $p=4\times m=16$, meaning a total number of $16\times 4\times 2+(16+4)=148$ parameters, as resulting also in Figure 2. The values learned by the sample architecture is reported in the Appendix A in Equations (A8) and (A9).

• Line 22: (Output)

The full output, stored in matrix $X^{\prime }$, contains the encoded representation of the input timesteps. In order to distinguish it thereafter, it will be denoted as Z.

3.2. Decoding

The objective of the decoding component (i.e., the decoder) in a Transformer architecture is to generate an output sequence step by step. This is achieved by using the encoded representation of the input and the output data generated by the encoding component.

The general structure of the decoding module is represented by the pseudocode in Algorithm 2 and in Figure 3. The individual steps are detailed below.

• Lines 1–2: (Input)

The decoder takes the encoder output $Z\in {\mathbb{R}}^{n\times m}$ as its main input (Line 1) and iteratively updates a sequence represented by matrix $\mathbf{Y}\in {\mathbb{R}}^{no+1\times m}$, where each row $Y_{i+1}$ represents the i-th output embedding, except for the first row, which has a special row. Initially, the matrix is zero-initialized (Line 2). The first row is set as the <CLS> token (Line 3), a learnable embedding used in order to kick-start the learning process. The sequence is then updated autoregressively, i.e., one timestep at a time, with each new element depending on the previously generated ones.

The learned <CLS> token for the restaurant series is the following vector:

$$<\mathtt{CLS}>=\left[\begin{array}{cccc}0.3162& -0.1322& 0.3443& 0.2043\end{array}\right]$$

• Lines 5–24: (Decoding Blocks)

Just as in the encoding phase, the main loop of the algorithm updates for l iterations (Lines 5–24) the matrix $\mathbf{Y}$. The block of code implementing each iteration is called a Decoding Block. In the block, Matrix Y is first processed by the Multihead Masked Self-Attention, which enables the decoder to process to previous positions in the output sequence while preventing it from attending to future positions, thereby enforcing autoregressive generation. Next, $\mathbf{Y}$ interacts with the encoder output $\mathbf{Z}$ through a Multihead Cross-Attention module, which enables the model to selectively focus on relevant parts of the input sequence (as encoded by the encoder) when generating each output token. This is the key mechanism that connects the encoder and decoder. Finally, the output is passed through some postprocessing steps to produce the final result of the single iteration.

The general procedure outlined above is explained in more detail below.

• Lines 6–20: (Masked Self-Attention)

The Masked Self-Attention mechanism works in the same way as a Multihead Attention function, but it ensures that the generation of each successive sequence value can only consider the present or the past, never the future. This is achieved using a look-ahead mask that prevents feedback in time. The following operations are performed inside each loop (i.e., each head).

• Line 7: generates the query, key, and value matrices, projecting the already-generated embeddings into semantic vectors. This projection is achieved by using dynamic parameter matrices and a dynamic bias array, both of which must be learnt.
• Line 8: computes the first part of the Scaled-Dot Product Attention function.
• Line 9: masks out any similarity values computed between a query vector from a timestep and a key vector coming from a future timestep. During the subsequent softmax step, the value $-\infty$ becomes 0, thus avoiding dependency on the future.
• Line 10: computes the last part of the attention function.
• After the loop of Lines 7–10 is completed, the $h^1$ different output matrices must be aggregated together.
• Line 12: the $h^1$ matrices are concatenated by row, obtaining the complete A matrix.
• Line 13: the matrix A is multiplied by $W_{o1}\in {\mathbb{R}}^{h^1{d}_v\times m}$. The latter matrix is a learnable parameter.

The operations above are referred to as ‘Self-Attention’ because the projections of $Q,K$ and V all come from the same input vector, $\mathbf{Y}$. In the example architecture, we set the number of heads for the self-attention layers to $h^1=2$.

• Lines 14, 21, 23: (Add and Norm)

Each operation in the decoding stage is followed by a residual connection and a normalization step. The $\mathrm{LayerNorm}\left(\right)$ function works row-wise on the embeddings, standardizing them with learnable scaling and shifting parameters ($\gamma ,\beta$).

• Lines 15–20: (Cross-Attention)

The second Attention step in the decoding phase links the partially generated output with the encoder’s representation of the input. Specifically, the decoder’s current output is projected into queries, while the encoder’s output provides the keys and values. Similar to Multihead Attention, this process involves a loop (Lines 15–18) and an aggregation step at the end (Lines 19–20).

• Line 16: generates the query, key, and value matrices, projecting the decoder’s current output into queries and the encoder’s output into keys and values. Each projection uses a learnable parameter matrix to transform the embeddings into semantic vectors.
• Line 17: computes the attention function, using the already computed matrices.

The above operations are repeated $h^2$ times, getting $h^2$ attention outputs.

• Line 19: All the head’s outputs are concatenated by the rows in a single matrix $\mathbf{A}$.
• Line 20: The attention matrix $\mathbf{A}$ is multiplied by $W_{o2}\in {\mathbb{R}}^{h^2{d}_v\times m}$, which is a learnable parameter.

The name Cross-Attention is due to the fact that the output of the encoding phase Z and the decoding current output $\mathbf{Y}$ are combined, crossing the two matrices together. In the example, we set the number of heads of the Cross-Attention layer to $h^2=2$.

• Line 22: (Feedforward Network)

The decoder applies a position-wise two-layer feedforward network with ReLU activation, as was done in the encoder (Line 22):

$$\mathbf{Y}\leftarrow \max (0,\mathbf{Y}·W_1+b_1)·W_2+b_2$$

• Line 25: (Projecting the Output)

At the end of the decoding loop, matrix $\mathbf{Y}\in {\mathbb{R}}^{o\times m}$ is obtained. Before mapping the j-th embedding back into its scalar prediction, $Y_j$ is passed through a final feedforward network and regularized (Line 25):

$$Y_j\leftarrow feedforward\left(Y_j\right)\ast scale\left(\mathbf{Z}\right)+bias\left(\mathbf{Z}\right)$$

For enhanced regularization purposes, a scale value and a bias value are determined through two learnable matrices $W_{\mathrm{scale}},W_{\mathrm{bias}}\in {\mathbb{R}}^{m\times m}$, based upon the mean across the timesteps of the encoded input series $\mathbf{Z}$:

$$scale\left(\mathbf{Z}\right)=\sigma \left(W_{\mathrm{scale}}·\sum _i{\displaystyle \frac{{\mathbf{Z}}_i}{d}}\right),bias\left(\mathbf{Z}\right)=W_{\mathrm{bias}}·\sum _i{\displaystyle \frac{{\mathbf{Z}}_i}{d}}$$

where $\sigma$ represents the sigmoid function.

If we are at the i-th iteration of the outer output cycle (Lines 4–27), the output matrix $\mathbf{Y}$ contains in position i the predicted embedding $Y_i$ for timestep i.

Algorithm 2: The decoding module

3.3. Learning

The encoding and decoding processes described in Section 3.1 and Section 3.2 are actually included in an overarching loop that implements learning by adjusting all parameters (e.g., weights of projection matrices, attention heads, feed-forward layers, etc.) to minimize a loss function over the training data. This is typically achieved through stochastic gradient descent (SGD)-based optimization, usually backpropagation.

The process is the standard neural learning process, flowing through three main phases:

• a forward pass where input sequences (time series points) are embedded into vectors, flowing through layers of multi-head self-attention and feed-forward networks obtain a forecasted value.
• loss computation, where the loss function measures how far the predictions are from the ground truth. In the case of forecasting data series, the most commonly used loss functions are Mean Squared Error (MSE) or Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), and Huber loss, which combines the robustness of MAE with the smoothness of MSE.
• a backward pass, where gradients of the loss with respect to the parameters are computed via backpropagation and parameters are updated using an optimization algorithm (usually a variant of gradient descent).

The backward pass implements the actual learning process by reversing the computation flow that was used to make the forecast, as presented in Figure 2. A Transformer’s computation graph has many layers, including an embedding layer, multiple self-attention blocks (each with projections $W_Q,W_K,W_V,W_O$), feed-forward networks, layer norms, residual connections, etc. During backpropagation, the chain rule of calculus is applied to each layer, as with standard MLPs, and the gradient flows backwards through each operation. This means that the $W_Q,W_K,W_V,W_O$, feed-forward weights, embedding matrices, and LayerNorm parameters all receive gradient-based updates depending on the value of the loss function.

Learning is a computationally intensive phase based on standard gradient descent optimizers, and it greatly benefits from GPU-optimized codes. In the minimalist architecture, the backward computations have been delegated to the relevant PyTorch classes [21].

The embedding matrices $W_i$ and $W_o$ are initialized such that $W_i·W_o=1$ to represent exactly the same projection. Specifically, $W_i$ is initialized by drawing each of its elements from a uniform distribution, and $W_o$ is set to be ${\displaystyle \frac{W_i}{\left|\right|W_i{\left|\right|}^2}}$ since the bias arrays $b_i,b_o$ are zero-initialized. Then, during training, they are set to change without any constraint.

The training technique is as follows. The input sequence $\mathbf{X}$ of fixed length n is given to the model. The predicted element at the i-th timestep ${\widehat{y}}_i$ is looked at, and the loss function between the ground truth element $y_i$ is computed. The employed loss is the MSE. The backpropagation step, which updates the internal parameters of the mode, follows. Then, with probability p, the $\mathbf{Y}$ matrix is filled not with the predicted element ${\widehat{y}}_i$ but with the actual one, $y_i$. The probability of that happening is gradually decreased during the training phase in order to let the model be more reliant on its own predictions, as it will be during inference.

In the case of the running example, the total number of parameters to learn in the Transformer model was 737.

3.4. Forecasting

Section 3.1, Section 3.2 and Section 3.3 describe the complete process to obtain one forecasted value. If more than one value is to be forecast, each additional forecast is appended to the end of the series, after which the process is repeated using the same fixed parameter matrices.

Figure 4 shows the results for the tiny example data series. The blue line depicts the training set, the green line the validation set, and the dashed line the model’s results. Training was implemented using windows consisting of seven inputs and one output; therefore, the first seven values are not modeled. The forecast was made using seven validation values in the recursive forecasting fashion outlined above.

Despite the limited data and restrictive configuration, the Transformer is highly effective in modeling the input series, though its forecasting abilities are, as would be expected, less accurate. More significant tests are reported in Section 4.

4. Computational Results

This section presents results obtained using the minimalist Transformer architecture in forecasting well-known univariate benchmark data series.

First, we showcase the successive processing stages on the archetypal Airline Passenger data series [5]. Then, we present illustrative quantitative results on standard forecasting benchmark instances. Unless otherwise specified, the hyperparameters were optimized using the Optuna package [22], and all experiments were performed on a machine equipped with 32 GB of RAM and a GPU featuring 16 GB of dedicated memory. All models were trained using PyTorch 2.8.0 on CUDA-enabled devices (with CUDA version 12.8) to leverage GPU acceleration.

4.1. The Airline Passengers Test Case

The Airline Passengers time series is one of the most famous and widely used in data analysis and forecasting. It consists of 144 observations of the monthly total number of international airline passengers in thousands between 1949 and 1960. As it is a real-world case that is very easy to model and predict (it is known to be an ARMA(1,1)), it is commonly used as a first validation for new forecasting approaches.

When the model is applied to this series, setting aside the last 12 values for validation and accounting for the obvious 12-month seasonality, the successive encoding steps through the positional embedding–multi-head attention–layer norm pipeline produce the results shown in Figure 5.

The series was preprocessed only via standard min–max normalization, then it was projected into embeddings of size $m=12$. Employing only $n=12$ timesteps at a time, 118 matrices $X\in {\mathbb{R}}^{12\times 12}$ are obtained. Matrix P used for positional embedding has the same dimensionality.

Next comes multi-head attention. We used 2 heads, and for each head, we set $d_k=d_v={\displaystyle \frac{12}{2}}=6$. Therefore, all matrices $W_Q^h$, $W_K^h$, and $W_V^h$ had dimensions $12\times 6$. These provide the bases for computing the attention function, where each h-$th$ head gives rise to the matrix $A^h={\displaystyle \frac{Q_h{K}_h^{\prime }}{d_h}}\in {\mathbb{R}}^{n\times n}$, in this study $A^h\in {\mathbb{R}}^{12\times 12}$. The successive softmax function does not change its dimensionality. After multiplying by $V_h$, we obtain the output of each head, of dimension $12\times 6$. All outputs are then concatenated by row, giving rise to a matrix $A\in {\mathbb{R}}^{12\times 12}$. The input dimension is then kept, when the output attention matrix is multiplied by matrix $W_O\in {\mathbb{R}}^{h{d}_v\times m}$—in the example, of dimension $12\times 12$. In summary, the values used for the parameters were n = 12, m = 12, k = 2, $d_k$ = $d_v$ = 6, p = 48.

The number of epochs set for learning was 400, and the total number of parameters to learn in the transformer model resulted to be 5413.

4.2. Benchmark Results

This study aims to provide a basic, simple architecture that can be used to fully understand the internal functioning of the Transformer and possibly form the basis for improvements, rather than a best-of-class architecture. However, it is important to validate its effectiveness in order to determine how representative it is of the possibilities offered by the Transformer approach to data series forecasting. To this end, we ran both the described system and a standard random forest forecaster, the RandomForestRegressor from scikit-learn [23], on a standard forecasting benchmark.

The benchmark consisted of the monthly series from the M3 forecasting competition [24]. The M3 dataset comprises a variety of time series from different domains and frequencies, including yearly, quarterly, monthly, and other intervals. It contains the kind of seasonal and noisy data commonly encountered in business forecasting. The monthly data subset includes 1428 real-world time series collected at monthly intervals covering a wide range of domains, classified as:

• Macroeconomics (e.g., unemployment rates, inflation, industrial production),
• Microeconomics (e.g., sales, orders, inventory levels for individual companies),
• Industry (e.g., combined production, sales, or demand in a broader industrial sector, not just a single firm)
• Finance (e.g., stock prices, exchange rates, interest rates),
• Demographics (e.g., population statistics, birth/death rates),
• Others, i.e., diverse, real-world time series that do not belong to traditional economic or financial domains (e.g., energy consumption, transportation data)

The length of the monthly series varies, typically ranging from 48 to 126 observations (i.e., 4 to over 10 years of data), and for each series, participants were asked to forecast the next 18 months. This same forecast horizon has been used in all relevant tests, along with the following argument values: n = 24, m = 36, k = 4, $d_k$ = $d_v$ = 12, p = 144. The number of epochs set for network learning was 400, and the total number of parameters to learn in the Transformer model was 46,189.

We ran each model on all the benchmark series, computing the RMSE on both the training and test sets. To determine whether the difference in forecast effectiveness was significant, a Mann–Whitney U-test was conducted on the RMSE results for each aggregate separately.

Table 1. Minimalist Transformer and random forest, aggregate results.

Type	Num	Len	Train	Test	Perc	Pval
MICRO	474	92.65	6	134	28.27	0.000
INDUSTRY	334	140.02	3	123	36.83	0.042
MACRO	312	130.88	3	101	32.37	0.021
FINANCE	145	124.40	1	68	46.90	0.247
DEMOGRAPHIC	111	123.33	3	33	29.73	0.021
OTHER	52	82.98	0	29	55.77	0.661

shows the results of the comparison aggregated over the type feature. The columns show:

• type: type of the aggregate,
• num: number of series in the aggregate,
• len: average length of the series of the aggregate,
• train: number of series where the Transformer had a lower RMSE on the training set,
• test: number of series where the Transformer had a lower RMSE on the number of series where the Transformer had a lower RMSE on the training set,
• perc: percentage of aggregate series where the Transformer had a lower RMSE on the training set
• pval: p-value of the Mann–Whitney U test.

The results in Table 1 show that, despite being outperformed as a modeler of the known part of the series, the Transformer solution can already be competitive in forecasting, despite the limiting operational restrictions. The quality of the forecast depends on the structure of the data, resulting from dependency on the application domain. In the MICRO and DEMOGRAPHIC domains, Transformers performed better than random forest in less than one-third of cases, whereas in FINANCE, it was almost one-half, and in the OTHER domain, it was even more than half the time. There is no statistical difference in performance between the two approaches for these last two domains, while random forest has a significantly lower average RMSE for the other four. The results of the tests are highly dependent on sample size. It is not surprising that the greatest indifference is observed for the least numerous sample. However, no aggregate has a sample size that renders the test irrelevant.

As the M3 benchmark has been studied in depth, we can tentatively interpret these observations. Financial data is characterized by high volatility and weak or non-existent trends or seasonality. They therefore have a higher noise component, which appears to be better handled by Transformers. In contrast, industry and macro data have stronger deterministic components, such as trends and seasonality (due to business cycles, yearly production seasonality, etc.), which are better captured by a decision tree-based model. Seasonality is in fact much more pronounced in industry and demographics series, while finance has very weak seasonality and is often dominated by idiosyncratic shocks. A similar situation applies to trends in the series, where demographic and macroeconomic series exhibit clear long-term growth or decline. Finally, and most significantly, financial and ‘other’ series are subject to frequent regime shifts, whereas industry and macroeconomic series undergo structural breaks less frequently and exhibit more persistent regimes.

Table 2. Minimalist Transformer and random forest, aggregate results, scaled data.

id	Type	Trtrain	Trtest	Rftrain	Rftest	ΔTrain	ΔTest	Trtime	Rftime
N1652	MICRO	0.061	0.262	0.062	0.335	−0.001	−0.072	0.07	0.15
N1546	MICRO	0.168	0.526	0.068	0.306	0.1	0.219	0.04	0.14
N1894	INDUSTRY	0.133	0.290	0.058	0.433	0.074	−0.142	0.11	0.22
N2047	INDUSTRY	0.144	0.667	0.056	0.428	0.088	0.238	0.12	0.21
N2255	MACRO	0.068	0.088	0.021	0.494	0.046	−0.406	0.13	0.20
N2492	MACRO	0.130	0.626	0.054	0.249	0.076	0.377	0.18	0.21
N2594	FINANCE	0.074	0.597	0.015	0.737	0.059	−0.140	0.13	0.19
N2658	FINANCE	0.126	0.656	0.046	0.435	0.080	0.220	0.03	0.13
N2737	DEMOGRAPHIC	0.074	0.129	0.046	0.209	0.028	−0.079	0.32	0.21
N2758	DEMOGRAPHIC	0.214	1.007	0.034	0.310	0.180	0.696	0.05	0.13
N2817	OTHER	0.079	0.125	0.036	0.441	0.043	−0.315	0.06	0.13
N2823	OTHER	0.116	0.166	0.066	0.081	0.050	0.085	0.11	0.13

shows details of the instances in each category for which Transformers achieved the best and worst test results compared to random forest. The columns of the table contain data that refer to scaled series and are:

• id: the id of the data series in the M3 collection;
• type: the category of the data series;
• trtrain: the absolute RMSE of the Transformer model on the training part;
• trtest: the absolute RMSE of the Transformer model on the test part, i.e., on the last 18 data points;
• rftrain: the absolute RMSE of the random forest model on the training part;
• rftest: the absolute RMSE of the random forest model on the test part, i.e., on the last 18 data points;
• Δtrain: the RMSE difference between Transformers and random forest on the training part;
• Δtest: the RMSE difference between Transformers and random forest on the test part;
• trtime: the average time in seconds needed to train the Transformer on the respective series for a single epoch;
• rftime: the time in seconds needed to fit the random forest model on the training set.

The results in the table confirm that the RMSE values are comparable in all cases and that there are never differences in the order of magnitude, with values remaining relatively low, even when considering that they were computed on max–min scaled series. In all categories, the Transformers achieved a lower RMSE in at least one series. Figure 6 and Figure 7 show plots of the actual series and the forecasts of the Transformers and the random forest in cases where the Transformers performed better and worse than the random forest, respectively.

To evaluate the scalability of the attention mechanism in capturing patterns, we conducted experiments on four longer time series. The series were produced in the context of the SMARTLAGOON project [25], an EU H2020 project with the objective of real-time monitoring, analysis, and prediction of the socio-environmental evolution of the vulnerable area Mar Menor area, the largest saltwater coastal lagoon in Europe. As part of the project, smart buoys were deployed in the lagoon, and their sensors generated IoT series on different physical variables at different sampling frequencies from August 2022 to April 2023.

Table 3. Minimalist Transformer results over longer time series.

Name	Trtrain	Trtest	Rftrain	Rftest	ΔTrain	ΔTest	Trtime	Rftime
SDI_Temp_1m	0.047	0.143	0.012	0.170	0.035	−0.027	5.06	2.52
Vapor_Pressure	0.114	0.167	0.038	0.170	0.076	−0.003	4.93	10.99
WS_ms	0.175	0.190	0.061	0.191	0.114	−0.001	4.96	19.28
WTemp_C1	0.047	0.157	0.011	0.195	0.036	−0.038	4.93	12.73

below reports the results of forecasting the series in relation to water temperature at a depth of 1 m ($SDI\_Temp\_1m$), steam pressure ($Vapor\_Pressure$), wind speed ($WS\_ms$), and water temperature at a depth of 1 m ($WTemp\_C1$). Each run had 24 timesteps as input and had to predict 18 points in time. Each dataset, instead, had 870 samples in the training set and 187 in the test set. Two plot examples of long series can be seen in Figure 8. The results presented in Table 3 show much lower variance than those in Table 2, as they refer to a single application domain. Interestingly, in this particular domain, the minimalist Transformer performs particularly well in comparison to the random forest regressor. Despite achieving a higher RMSE error in the training phase, it was able to deliver better forecasting performance across all series.

To provide a more comprehensive view of the forecasting models, further comparisons have been made against different forecasting models, including recent Transformer-based approaches, in addition to the random forest baseline. These include the Chronos model [12], TCAN (Temporal Convolution Attention Network) [13], the ARIMA (AutoRegressive Integrated Moving Average) (ARIMA), and an ETS model (Exponential Smoothing), specifically a Holt and Winters forecaster. The autoregressive models relied on their statsmodels implementation [26] using the stepwise approach of pmdarima for hyperparameter tuning [27]. The RMSE test results are shown for the series listed in

Table 4. Minimalist Transformer compared to other baseline models.

id	Trtest	Chronos	Tcan	Arima	Ets
N1652	0.262	0.523	0.074	0.119	0.120
N1546	0.526	0.410	0.170	0.238	0.234
N1894	0.290	0.380	0.250	0.408	0.364
N2047	0.667	0.463	0.254	0.133	0.150
N2255	0.088	0.409	0.106	0.201	0.033
N2492	0.626	0.317	0.220	0.284	0.223
N2594	0.597	0.364	0.115	0.013	0.047
N2658	0.656	0.362	0.191	0.248	0.369
N2737	0.129	0.211	0.117	0.238	0.306
N2758	1.007	0.410	0.358	0.212	0.193
N2817	0.125	0.538	0.158	0.143	0.126
N2823	0.166	0.449	0.304	0.302	0.325
avg.	0.428	0.403	0.193	0.211	0.207

.

As shown in Table 4, there is no clear dominance among the different methods. Even though the specialized convolutional Transformer architecture achieves the lowest average error, the two autoregressive approaches follow closely behind. Fine-tuned models are clearly more effective than the zero-shot approach used with Chronos; even the minimalist architecture achieves comparable performance to their specialized one.

4.3. Ablation Studies

In

Table 5. Ablation studies.

id	Single Head	No FF	No Add&Norm 1	No Add&Norm 2	1-Sized Embeddings	No PE	No Output	Baseline
N1652	0.175/0.327	0.188/0.329	0.183/0.332	0.180/0.327	0.410/0.568	0.183/0.301	0.183/0.323	0.179/0.337
N1546	0.194/0.353	0.185/0.290	0.211/0.480	0.190/0.330	0.605/0.319	0.190/0.301	0.195/0.407	0.197/0.354
N1894	0.142/0.496	0.188/0.385	0.132/0.325	0.156/0.524	0.243/0.370	0.108/0.512	0.149/0.260	0.152/0.211
N2047	0.161/0.252	0.157/0.448	0.168/0.255	0.134/0.432	0.181/0.253	0.099/0.488	0.141/0.324	0.173/0.344
N2255	0.117/0.619	0.126/0.587	0.124/0.603	0.121/0.608	0.775/0.208	0.068/0.596	0.097/0.566	0.119/0.577
N2492	0.157/0.438	0.113/0.272	0.154/0.571	0.143/0.598	0.267/0.340	0.097/0.559	0.133/0.380	0.114/0.167
N2594	0.133/0.728	0.125/0.800	0.115/0.640	0.154/0.656	0.542/0.121	0.082/0.615	0.118/0.523	0.137/0.653
N2658	0.143/0.547	0.210/0.268	0.182/0.313	0.184/0.418	0.215/0.246	0.166/0.428	0.190/0.234	0.186/0.380
N2737	0.164/0.226	0.137/0.245	0.131/0.316	0.116/0.255	0.168/0.198	0.099/0.199	0.160/0.215	0.154/0.193
N2758	0.238/0.392	0.273/0.335	0.276/0.401	0.253/0.479	0.371/0.221	0.091/0.711	0.272/0.366	0.229/0.357
N2817	0.267/0.422	0.254/0.414	0.262/0.428	0.240/0.294	0.588/0.200	0.167/0.466	0.226/0.386	0.268/0.341
N2823	0.300/0.200	0.307/0.221	0.308/0.347	0.293/0.178	3.025/2.723	0.233/0.177	0.286/0.218	0.308/0.220
avg.	0.183/0.417	0.189/0.383	0.187/0.418	0.180/0.425	0.616/0.481	0.132/0.446	0.179/0.350	0.185/0.345

it is possible to see the effects of removing or editing computational blocks of the encoder, as shown in Figure 2, on the performance of the entire model. Each cell reports the training and the testing loss of the configuration in the respective row and column, and the corresponding loss, while the columns show:

• id: the id of the data series in the M3 collection;
• 1-sized embeddings: results using embeddings of a single value (i.e., no embedding), lines 2–4 of Algorithm 1;
• No PE: results without positional encoding, line 5 of Algorithm 1;
• Single Head: results with single head instead than mutihead attention, lines 7–15 of Algorithm 1;
• No Add&Norm 1: results removing the first Add and Norm block, line 18 of Algorithm 1;
• No FF: results removing the feedforward network, line 19 of Algorithm 1;
• No Add&Norm 2: results removing the second Add and Norm block, line 20 of Algorithm 1;
• Baseline: results of the complete model.

As the model is quite small, comprising just a single encoder block and a single decoder block, the overall effect is visible but not particularly impactful. As expected, the baseline model achieves the best loss value over the validation data, while the model without the feedforward network is still almost equivalent to it, and removing any other component has a comparable highly disruptive effect. Furthermore, the full model has the fourth highest training loss value. This, alongside the validation result, indicates the model’s ability to generalize over the training data.

4.4. Interpretability

Figure 9 provides an additional view of the effects of learning. It illustrates the contribution of each timestep provided by the decoder to each generated output value. These contributions are made by both the encoded input time series and by the autoregressively generated output timestep, and are demonstrated using the Google Trends restaurant series. The larger the circle around a certain timestep, the greater the attention weight given by the trained model for inference.

More specifically, the attention contribution of the input series-in blue-is extracted from the weights of the Cross-Attention layer, while the attention contribution of the generated series—in green—is extracted from the Self-Attention layer.

The results align with what one might expect the model to learn about a seasonal trajectory. For example, it can be seen that, when generating the first timestep (labeled “Step 1” in Figure 9), the model relies on the timestep seven days prior, when a slight seasonal increase occurs. A similar argument could be made by observing that, from the generation of the fifth timestep onwards, the model relies heavily on the peak value of the input series, probably in order to extract information about the correct value of the new seasonal peak.

Another interesting observation that emerges from the above example is that the model focuses on specific timesteps while ignoring others entirely. Since the difference between these timesteps is small, the model attempts to gather as much information as possible from a few significant timesteps rather than relying on too many similar ones.

4.5. Scalability

The model has also been evaluated in terms of the scalability of its components, i.e., how the number of parameters relates to training and inference time and performance. These tests were performed on the M3 dataseries with ID $N2047$, against which the minimalist model produced unfavorable testing results. The outcomes of these tests are reported in

Table 6. Scalability results.

Encoder	Decoder	Trtrain	Trtest	Nparams	Trtime	Inftime
1	1	0.181	0.397	2697	0.32	0.028
2	2	0.200	0.365	4745	0.37	0.049
3	3	0.191	0.251	6793	0.53	0.051
4	4	0.188	0.162	8841	0.69	0.078

and

Table 7. Scalability results.

Encoder	Decoder	Embed	Trtrain	Trtest	Nparams	Trtime	Inftime
1	1	4	0.175	0.592	805	0.21	0.023
1	1	40	0.135	0.417	57001	0.21	0.033
2	2	4	0.164	0.508	1381	0.34	0.037
2	2	40	0.176	0.422	103081	0.37	0.043
4	4	4	0.132	0.433	2533	0.68	0.083
4	4	40	0.180	0.294	195241	0.70	0.093

. In Table 6, the embedding size was 8 and the number of training epochs was 20. The columns show:

• Encoder: number of encoder layers;
• Decoder: number of decoder layers;
• trtrain: absolute RMSE of the Transformer model on the training part;
• trtest: absolute RMSE of the Transformer model on the test part, i.e., on the last 18 data points;
• nparams: number of model parameters to train;
• trtime: training time, in seconds per epoch;
• inftime: inference time, in seconds.

A brief examination of the above results shows that as the number of encoder and decoder blocks increases, so does the number of parameters (nparams), which directly influences the training time (trtime) and inference time (inftime). While the training loss remains largely stable, the model’s ability to generalize is reflected in the decreasing test loss values. As will also be apparent from the following Table 7, there is no direct correlation between training and testing loss.

Table 7, which includes a new embed column to report the size of the embeddings, shows the results of a model in which both the model size and the size of the internal embeddings change. In this case, the number of epochs is set to 100: this leads to better convergence on the training set, but worse results (with respect to Table 6). It should also be noted that the series in question is relatively short; therefore, increasing the network size—and thus the number of parameters—beyond a certain threshold does not affect performance.

5. Conclusions

This work presents a minimalist Transformer architecture that is specifically designed for univariate time series forecasting. Rather than trying to propose yet another cutting-edge variant, the contribution of this study lies in systematically reducing the architecture to its essential components and documenting all relevant steps of the encoder, decoder and learning procedures in pseudocode. This study aimed to provide a transparent and replicable baseline for researchers, and practitioners interested in understanding the core mechanisms of transformers when applied to forecasting tasks.

The model is evaluated using a set of standard forecasting benchmarks and its performance is compared with that of a random forest forecaster. Although the minimalist Transformer does not outperform the most sophisticated state-of-the-art models, it consistently achieves comparable accuracy, particularly for time series with long-term dependencies, where attention mechanisms can exploit global context more effectively than purely tree-based methods.

Beyond raw predictive performance, the computational findings highlight two key outcomes: clarity and accessibility. By explicitly exposing each functional step, the proposed framework lowers the barrier for newcomers to the Transformer literature and the field of time series forecasting.

The robustness of the Transformer paradigm is also evident, as even a stripped-down version of the model demonstrates stable forecasting ability. This suggests that many performance gains in advanced variants stem from relatively minor architectural refinements.

Although the proposed architecture is designed for univariate forecasting, it can be readily extended to include external predictors and the multivariate case. This can be achieved by adapting the input encoding to represent both the target variable and the external predictors, or multiple variables. This enables the model to explicitly learn and exploit correlations between them.

In a research landscape often dominated by increasingly complex architectures, this study highlights the importance of transparent baselines. Future work may explore the impact of specific enhancements, such as seasonal embeddings, multi-head configurations or hybridization with statistical components, on forecasting performance when added to this minimalist core.