Abstract
This research introduces a hybrid framework that integrates stochastic modeling and machine learning for predicting postprandial glucose levels in individuals with Type 1 Diabetes (T1D). The primary aim is to enhance the accuracy of glucose predictions by merging a biophysical Glucose–Insulin–Meal (GIM) model with advanced machine learning techniques. This framework is tailored to utilize the Kaggle BRIST1D dataset, which comprises real-world data from continuous glucose monitoring (CGM), insulin administration, and meal intake records. The methodology employs the GIM model as a physiological prior to generate simulated glucose and insulin trajectories, which are then utilized as input features for the machine learning (ML) component. For this component, the study leverages the Light Gradient Boosting Machine (LightGBM) due to its efficiency and strong performance with tabular data, while Long Short-Term Memory (LSTM) networks are applied to capture temporal dependencies. Additionally, Bayesian regression is integrated to assess prediction uncertainty. A key advancement of this research is the transition from a deterministic GIM formulation to a stochastic differential equation (SDE) framework, which allows the model to represent the probabilistic range of physiological responses and improves uncertainty management when working with real-world data. The findings reveal that this hybrid methodology enhances both the precision and applicability of glucose predictions by integrating the physiological insights of Glucose Interaction Models (GIM) with the flexibility of data-driven machine learning techniques to accommodate real-world variability. This innovative framework facilitates the creation of robust, transparent, and personalized decision-support systems aimed at improving diabetes management.
1. Introduction
1.1. Motivation: Importance of Modeling Glucose–Insulin Dynamics
Type 1 diabetes mellitus (T1D) impacts over 9 million individuals worldwide, necessitating ongoing monitoring and management of blood glucose levels through the administration of exogenous insulin. Effective diabetes management relies on keeping glucose levels within a tight physiological range to reduce both immediate risks, such as hypoglycaemia and hyperglycemia, and long-term complications, including neuropathy, retinopathy, and cardiovascular disease. The global prevalence and incidence of Type 1 diabetes have been systematically reviewed [1], analyzed across European populations [2], and reported in global estimates [3]. The importance of postprandial glucose regulation and its link to diabetes complications has also been emphasized [4], with international guidelines highlighting management strategies [5], and studies showing the contribution of postprandial increments to overall diurnal hyperglycemia [6]. However, the glucose–insulin regulatory system exhibits highly nonlinear, time-varying, and individualized dynamics, affected by factors such as meal timing, physical activity, stress, and variations in insulin sensitivity. This intricate interplay presents significant challenges for both healthcare providers and patients in optimizing therapeutic strategies.
Mathematical modeling of the glucose–insulin system is indispensable for comprehending its physiological mechanisms, evaluating control strategies, and simulating patient responses across various scenarios. By encapsulating critical metabolic processes within computable frameworks, these models facilitate the development of decision-support systems, artificial pancreas algorithms, and educational simulators. Additionally, the combination of physiological models with machine learning techniques opens new avenues for improving predictive accuracy and personalization, particularly when aligned with real-world patient data. Such integrated approaches are becoming progressively pivotal in advancing intelligent and adaptive technologies in diabetes management, both in clinical environments and daily life.
Diabetes mellitus is a metabolic disorder characterized by the body’s inability to effectively regulate blood glucose levels, primarily due to insufficient insulin production or impaired insulin action. In Type 1 diabetes (T1D), autoimmune destruction of pancreatic β-cells leads to a severe reduction in endogenous insulin secretion, necessitating lifelong dependence on exogenous insulin therapy. One of the most pressing challenges for individuals with T1D is the regulation of postprandial glucose levels. Ingested carbohydrates are quickly absorbed into the bloodstream, causing rapid increases in blood glucose. In T1D, the body’s natural responses—such as insulin secretion and glucose uptake—are either completely absent or inadequately responsive, making precise dosing and timing of administered insulin essential for effective glucose management.
Meal-related glucose fluctuations are a significant contributor to glycemic variability, which has been recognized as an independent risk factor for both microvascular and macrovascular complications. Additionally, pronounced postprandial glucose spikes can adversely affect overall glycemic control, even when fasting glucose levels are maintained within acceptable limits.
Therefore, precise prediction and management of these fluctuations are crucial for preventing hyperglycemia and reducing the risk of subsequent hypoglycemia, particularly in individuals undergoing insulin therapy. Modeling the glucose response to meals has therefore become a cornerstone of advanced diabetes management systems, including closed-loop insulin delivery (artificial pancreas) and decision-support algorithms. These models need to accurately reflect the complex interactions between carbohydrate consumption, insulin dynamics, and individual physiological differences to be effective in clinical settings. Recently, the emergence of high-resolution datasets that capture real-world glucose, insulin, and meal information—available through open platforms like Kaggle—has opened new avenues for validating and improving these models through data-driven approaches.
1.2. Overview of Existing Models: The GIM Framework
Mathematical modeling of glucose–insulin regulation has been a prominent research focus for decades, evolving from early compartmental models by Bergman and Sorensen to advanced physiologically based frameworks. The Glucose–Insulin–Meal (GIM) model [7] is regarded as one of the most detailed and biologically accurate frameworks for simulating glucose–insulin interactions in humans. This nonlinear system of differential equations integrates essential physiological elements, including insulin secretion, glucose uptake in the liver and peripheral tissues, insulin action dynamics, and meal absorption.
A key strength of the GIM model is its capacity to accurately simulate both intravenous glucose tolerance tests (IVGTTs) and mixed meal tolerance tests (MMTTs), effectively capturing the biphasic insulin response, the role of incretin hormones, and variations in gastric emptying rates [7]. With over 30 parameters, many of which can be identified from clinical data, the model allows for personalization and the simulation of virtual patient cohorts [7,8]. Its physiological precision and modular structure have made it instrumental in the development and validation of closed-loop insulin delivery systems, or artificial pancreas algorithms [9,10]. However, the model’s deterministic nature may limit its ability to account for individual variability and real-world uncertainties [11], particularly in response to unexpected meals or behavioral influences, prompting the exploration of hybrid approaches that combine the physiological insights of models like GIM with the adaptability and predictive capabilities of data-driven machine learning techniques.
1.3. Why Combine Machine Learning with Stochastic Simulation
While physiologically based models like GIM provide a solid framework for simulating glucose–insulin interactions, they are fundamentally constrained by deterministic equations with fixed parameters. In real clinical settings, however, blood glucose levels are affected by a multitude of stochastic factors, including unrecorded meal compositions, variations in physical activity, hormonal changes, and sensor inaccuracies. These unpredictable elements introduce a level of variability that purely mechanistic models struggle to accommodate, often resulting in discrepancies between predicted and actual glucose patterns in everyday life.
Machine learning (ML) serves as a valuable enhancement to traditional simulation methods by identifying patterns directly from data, allowing models to adjust to individual behaviors and environmental factors. ML algorithms excel at capturing nonlinear relationships, correcting model errors, and estimating hidden variables not explicitly represented in physiological models. When combined with stochastic simulation, ML components can enhance forecasting precision, adapt to new inputs, and assess prediction uncertainty.
This hybrid modeling strategy, which merges mechanistic models with ML to address variability and model discrepancies, has shown promising outcomes in biomedical systems. In the realm of Type 1 Diabetes (T1D), this integration fosters the creation of intelligent insulin delivery systems that are both interpretable and responsive to real-world conditions. By calibrating the GIM model with actual data and supplementing it with data-driven learning elements, we can enhance postprandial glucose predictions and facilitate more accurate, adaptive insulin therapy.
1.4. Contributions of This Study
This research introduces a hybrid modeling framework that combines physiological simulations with machine learning techniques to enhance the prediction of postprandial glucose levels in individuals with Type 1 diabetes. The study begins by modifying the established Glucose–Insulin–Meal (GIM) model to align with the BRIST1D dataset, which comprises real-world data from continuous glucose monitoring, insulin administration, and meal intake. This modification facilitates physiologically relevant simulations in free-living conditions, effectively bridging the divide between controlled metabolic models and individualized patient data.
To improve both predictive accuracy and model adaptability, the framework incorporates various machine learning approaches, including Light Gradient Boosting Machine (LightGBM), Long Short-Term Memory networks (LSTM), and Bayesian regression. LightGBM is utilized for its efficiency in handling engineered tabular features, adeptly capturing nonlinear relationships among recent glucose trends, insulin doses, and meal occurrences. LSTM is employed to account for temporal dependencies in glucose data, while Bayesian regression introduces probabilistic forecasting to assess prediction uncertainty.
The resulting architecture merges the interpretability and domain knowledge inherent in physiological modeling with the flexibility and learning capabilities of data-driven methods. This hybrid strategy not only enhances the accuracy and generalizability of glucose predictions but also supports the creation of robust, explainable, and personalized decision-support systems for effective diabetes management.
The remainder of this paper is organized as follows. Section 2 reviews related work in glucose–insulin modeling, machine learning for diabetes prediction, and hybrid modeling approaches. Section 3 outlines the methodology, covering the adaptation of the GIM model, preprocessing of the BRIST1D dataset, and the design of the machine learning and hybrid components. Section 4 presents the experimental setup, evaluation metrics, and results from the comparative analysis of the models. Section 5 discusses the implications of the findings, model limitations, and potential avenues for clinical integration. Finally, Section 6 concludes with a summary of the key points and suggestions for future research.
2. Related Work
2.1. Historical Perspective on Physiological Glucose–Insulin Models
Mathematical modeling of glucose metabolism has undergone significant advancements since the 1980s, establishing a robust framework for contemporary physiological simulations. One of the pioneering models was developed using a compartmental approach to represent the dynamics of glucose absorption, insulin secretion, and tissue metabolism [12]. This foundational work was complemented by subsequent research, which highlighted the intricate relationship between hormonal regulation and glucose kinetics within a multi-compartmental setting [10].
Continuing this trajectory, the minimal model was introduced by [8], streamlining the interaction between glucose and insulin into quantifiable parameters such as insulin sensitivity and glucose effectiveness. This simplification paved the way for further innovations, including the nonlinear model predictive control framework for glucose regulation proposed by [9], which significantly impacted the development of artificial pancreas systems.
A notable advancement in the field was the Glucose–Insulin–Meal (GIM) model [7]. This model represented a significant leap in both realism and complexity by integrating detailed meal absorption kinetics, insulin action delays, and feedback mechanisms. Its modular design and physiological accuracy have made it a fundamental component in simulation software, implemented in Python 3.13 and MATLAB 24.2, and in the testing of control algorithms, solidifying its status as a cornerstone in glucose metabolism modeling.
2.2. Machine Learning for Glucose Forecasting and T1D Decision Support
The last decade has witnessed a significant shift from traditional physiological models to machine learning (ML) approaches that enhance predictive accuracy and address the complexities of real-world data variability. Early contributions applied Monte Carlo simulations and gray-box modeling techniques to incorporate uncertainty in postprandial glucose responses [13]. This transition marked a movement toward hybrid models that blend mechanistic understanding with probabilistic and data-driven insights.
In more recent developments, deep learning techniques, particularly stacked Long Short-Term Memory (LSTM) networks, have been applied to capture temporal dependencies in continuous glucose monitoring (CGM) data. One study introduced a Kalman-filter-enhanced LSTM network, which demonstrated notable improvement in glucose prediction accuracy compared to traditional autoregressive methods [14]. Similarly, the GLYFE framework evaluated various personalized ML models, underscoring the advantages of individualized approaches in diabetes management [15].
Gradient boosting methods, including LightGBM and XGBoost, have also emerged as effective tools for analyzing structured medical datasets. One study employed XGBoost to predict personalized blood glucose levels based on tabular data encompassing insulin, meal intake, and glucose history [16]. These methods not only provide interpretability but also offer computational efficiency, making them well suited for real-time application in clinical settings.
Recent work in the classification of pediatric diabetes through deep neural networks highlights the growing role of artificial intelligence in facilitating early detection and diagnosis of medical conditions [17]. While machine learning has proven effective in enhancing predictive accuracy, it often falls short in providing physiological insights, which has led to a rising interest in hybrid modeling techniques that combine the strengths of both AI and traditional methods.
2.3. Hybrid and AI-Enhanced Physiological Models: Toward Explainability and Personalization
Recent research has sought to reconcile interpretability with performance through hybrid modeling approaches that merge physiological insights with machine learning and uncertainty quantification methods. For instance, a hybrid mechanistic–ML model was introduced that incorporates physical constraints into neural network predictions {Sturm}. Similarly, explainable AI has been applied in hybrid physiological modeling, employing feature attribution techniques to ensure clinical transparency [18].
Uncertainty modeling has also gained traction. Bayesian neural networks integrated with mechanistic simulations now enable the generation of predictive outputs alongside confidence intervals.
There is also a growing body of work leveraging ensemble methods and LightGBM for CGM trend prediction, as evidenced by research employing ensemble boosting [19] and studies applying LightGBM for early warning of glucose levels [16]. These models excel in scenarios with limited data, providing explainability through feature importance and quantile forecasting, thereby enhancing their practical applicability in clinical settings.
Large language models (LLMs) and generative AI are increasingly being applied in the biomedical field, especially in areas such as clinical decision support and contextual understanding of time-series data. Although their use in modeling Type 1 diabetes (T1D) is still in its early stages, transformer-based models have been shown to effectively make interpretable insulin dosing decisions by leveraging contextual signals and learned latent states [20].
Recent developments indicate that the integration of physiology, machine learning, and explainable AI holds the greatest promise for developing robust, real-time, and patient-tailored decision-support systems in Type 1 diabetes care.
2.4. Uncertainty Quantification and Robust Glucose Prediction
As decision-support systems for diabetes management transition into real-world clinical and home settings, the ability to quantify and manage uncertainty becomes critical. Glucose dynamics are affected by numerous latent and stochastic factors, such as stress, unrecorded physical activity, meal composition, and variability in sensor accuracy. Consequently, deterministic models—whether based on mechanistic principles or machine learning—often face challenges in delivering reliable predictions amidst this real-world variability.
Early work in uncertainty modeling showed that stochastic perturbations can capture a meaningful range of physiologically plausible glucose outcomes, laying the foundation for more advanced methods. This concept has since evolved into techniques involving Bayesian learning, quantile regression, and distributional modeling.
For example, Bayesian neural network architectures have been applied to estimate not only expected glucose values but also prediction intervals, allowing clinicians to interpret model confidence and adjust decisions accordingly. Similarly, quantile regression forests have been used for CGM forecasting to enhance insulin dosing safety and mitigate the risk of hypoglycemia [21].
Recent studies have investigated hybrid Bayesian machine learning models that incorporate uncertainty estimation at each prediction stage, often utilizing deterministic physiological simulators like the GIM model [11]. These methodologies leverage the strengths of physiological realism alongside the adaptability of data-driven variability.
Ensemble models such as LightGBM, when trained on bootstrapped datasets or with quantile objectives, can also approximate uncertainty. For example, ensemble learning frameworks have been used to forecast CGM trends and identify outlier trajectories, thereby facilitating proactive alerts in home monitoring systems [22].
Collectively, these developments highlight the critical need for robustness and interpretability in predictive modeling, particularly for applications in safety-sensitive areas like closed-loop insulin delivery. The combination of uncertainty-aware machine learning with physiologically inspired simulations presents a promising avenue for enhancing both predictive accuracy and clinical dependability.
3. Methodology
3.1. Theoretical Overview of the GIM Model
The Glucose–Insulin–Meal (GIM) model represents a nonlinear compartmental system of ordinary differential equations (ODEs) that effectively simulates the dynamics of glucose and insulin in response to food intake, endogenous secretion, and external insulin administration. Developed as an extension of minimal modeling techniques, the GIM model integrates detailed physiological submodels that capture the processes of gastrointestinal glucose absorption, insulin kinetics, and the action of insulin in critical peripheral tissues, including the liver, muscle, and adipose tissue [7].
The GIM model fundamentally comprises several key subsystems.
- ○
- The glucose absorption subsystem simulates the entry of glucose into the plasma after a meal, utilizing transit compartments and a gastric emptying rate that is influenced by the composition of macronutrients.
- ○;
- The insulin absorption and kinetics subsystem includes compartments for subcutaneous insulin injection or infusion, along with a central compartment that represents plasma insulin levels.
- ○
- Additionally, the insulin action compartments account for the delays and nonlinearities inherent in the hormonal regulation of hepatic glucose production and peripheral glucose uptake.
The model can be described by a set of nonlinear ODEs of the general form:
where
- x is the state vector, including plasma glucose concentration, insulin concentration, and intermediate effect compartments.
- u is the input vector, including meal glucose intake and insulin administration.
- p represents physiological parameters such as insulin sensitivity, glucose effectiveness, gastric emptying rates, and delay constants.
A canonical example from the GIM framework includes the glucose dynamics equation:
where
- G(t) is plasma glucose concentration.
- Ra(t) is the rate of appearance of glucose from meals.
- EGU, EGP, and EHGP are nonlinear functions modeling insulin-mediated glucose uptake, production, and suppression, respectively.
- Ihep and Iper are delayed insulin signals influencing hepatic and peripheral tissues.
Similarly, insulin kinetics are governed by a subsystem such as:
where I(t) is plasma insulin, Isc(t) is subcutaneous insulin, kabs and ke are absorption and elimination constants, and (t) is the external insulin administration rate.
The coupled equations create a closed-loop simulation that captures the dynamics of glucose and insulin following meals. Parameters for this model are generally derived from clinical trial data or tailored for individual patient simulations, which positions the GIM model as an effective tool for exploring both open- and closed-loop insulin therapies across diverse scenarios.
In our research, we utilize a calibrated version of the GIM model to generate patient-specific glucose–insulin trajectories, leveraging the BRIST1D dataset as a physiological foundation to enhance machine learning predictions. The model’s interpretability, modular design, and capacity to account for nonlinear and delayed responses render it particularly suitable for integration with data-driven methodologies.
3.2. Adaptation of the GIM Model to BRIST1D Data
The original Glucose–Insulin–Meal Model (GIM) was designed to replicate glucose–insulin interactions under strictly controlled experimental conditions, where variables such as meal composition and insulin administration are precisely defined. However, when applying this model to real-world datasets like BRIST1D, it is essential to modify it to accommodate the inherent structure, granularity, and variability present in free-living data.
The BRIST1D dataset includes timestamped records of:
- Interstitial glucose concentrations sampled every 5 min;
- Insulin dosages (bolus and basal);
- Carbohydrate intake with coarse-grained meal annotations;
- Multiple patient profiles under real-world, outpatient conditions.
To adapt the GIM model to this context, several modifications and alignment procedures were necessary:
1. Input Event Translation
- In the context of meals, the GIM model treats glucose appearance from food intake (Ra) as a controlled variable. In BRIST1D, meal data is represented by carbohydrate quantities and timing of ingestion, which were converted into glucose appearance curves using exponential absorption kinetics that reflect typical gastric emptying patterns.
- For insulin delivery, subcutaneous insulin events from both bolus and basal infusions were integrated into the GIM model’s subcutaneous compartments, with bolus data considered as pulse inputs and basal rates represented as continuous profiles.
2. Parameter Initialization and Personalization
- The GIM model incorporates parameters at the population level, whereas BRIST1D focuses on individual patient responses to glucose and insulin. To tailor key physiological parameters—such as peripheral insulin sensitivity, hepatic suppression, and gastric emptying rate—this model employs a windowed optimization strategy. This approach involves fitting the model to actual data by minimizing discrepancies between simulated glucose trajectories and continuous glucose monitoring (CGM) data.
3. Model Resampling and Synchronization
- The GIM model is based on continuous differential equations, while the BRIST1D dataset consists of discrete time series data. To ensure compatibility, all variables, including glucose, insulin, and meal input, were resampled to a uniform 5 min interval, aligning with the resolution of continuous glucose monitoring (CGM). The numerical integration of the ordinary differential equations (ODEs) was executed using a fixed-step solver (e.g., Runge-Kutta 4th order), which was synchronized with the timestamps of the data.
4. Handling Data Gaps and Noise
- Unlike controlled experimental environments, BRIST1D incorporates missing data, sensor inaccuracies, and behavioral variability. To mitigate these issues, missing glucose readings were filled using forward-filling techniques for short intervals, while meal and insulin irregularities were smoothed through a median filter. In instances of high uncertainty, the GIM model was permitted to operate in an open-loop simulation, allowing it to generate prior information for subsequent machine learning applications.
By calibrating the GIM model with real-world data, we develop a simulation-enhanced dataset that merges physiological understanding with the inherent noise of actual measurements. This integrated approach facilitates the creation of predictive models that are both interpretable and generalizable, all while preserving the integrity of established glucose regulation mechanisms.
3.3. Schematic of the Hybrid GIM–ML Architecture
To harness the strengths of physiological interpretability alongside the adaptability of data-driven approaches, we introduce a hybrid architecture that merges the Glucose–Insulin–Meal (GIM) simulation model with contemporary machine learning (ML) methodologies. This integrated framework is designed to improve the accuracy of glucose forecasting in real-world settings while ensuring transparency through the use of physiologically relevant intermediate variables.
The architecture features two interconnected computational pathways: one focused on mechanistic simulation and the other on predictive machine learning. This comprehensive system is structured to simulate, analyze, and predict glucose dynamics by utilizing historical data and behavioral patterns sourced from the BRIST1D dataset.
1. Input Preprocessing
All input signals, such as interstitial glucose levels, carbohydrate intake events, and insulin dosages, are standardized to a consistent 5 min interval to match the native resolution of continuous glucose monitoring (CGM) data. Insulin records are categorized into basal and bolus components, which are then represented as continuous or pulse input profiles, respectively. Likewise, carbohydrate intake events are converted into glucose appearance curves using exponential absorption models that align with the GIM structure. This preprocessing stage ensures temporal synchronization and physiological realism in downstream modeling.
2. Physiological Simulation via GIM
The GIM model utilizes preprocessed meal and insulin signals to produce simulated trajectories of metabolic state variables over a predetermined prediction horizon, typically ranging from 60 to 90 min. The model’s outputs encompass several key metrics, including:
- Plasma glucose concentration G(t).
- Plasma insulin concentration I(t).
- Glucose rate of appearance Ra(t).
- Endogenous glucose production (EGP).
- Glucose utilization (GU).
The outputs generated from these simulations illustrate anticipated physiological reactions based on the specified conditions, offering a valuable source of mechanistically informed signals. These simulations are tailored to individual subjects, with critical parameters such as insulin sensitivity and gastric emptying rate customized through data fitting methods.
3. Feature Engineering
The outputs from the GIM model are used to construct a set of high-level features that describe latent metabolic processes. These include:
- The simulated rate of change in glucose concentration.
- The time-lagged response of insulin-mediated glucose uptake.
- Deviations between predicted and observed glucose levels.
- Trends in endogenous production or suppression.
These mechanistic features are concatenated with empirical features extracted directly from the raw data, such as lagged CGM values, time since last insulin or meal event, and circadian indicators. The combined feature set allows for a unified representation of both data-driven and physiologically driven predictors.
4. Machine Learning Prediction
A supervised machine learning model, such as Light Gradient Boosted Machines (LightGBM), Long Short-Term Memory (LSTM) networks, or Bayesian regression, is utilized to correlate engineered feature vectors with future glucose levels at a designated prediction horizon of t + Δt. These models are adept at identifying nonlinear relationships, temporal dependencies, and residual patterns within the data that the simulation alone may not fully account for. By doing so, they effectively address the variability stemming from behavioral, sensor-related, or environmental factors encountered in real-world scenarios.
5. Output Generation and Uncertainty Estimation
The final system output includes:
- A point estimate of future glucose concentration.
- An optional uncertainty interval, generated via quantile regression, bootstrapped ensemble techniques, or Bayesian posterior sampling.
This dual output mechanism delivers both practical predictions and confidence levels, thereby increasing the model’s effectiveness in clinical decision-making contexts, such as predicting hypoglycemia or recommending insulin dosages.
In essence, this hybrid framework fosters a collaboration between first-principles modeling and statistical learning. The GIM model ensures biological relevance and constraints, while the machine learning component adjusts to variability, user behavior, and real-world complexities, culminating in a robust, interpretable, and personalized forecasting system.
3.4. Machine Learning Model Design
The machine learning (ML) aspect of the hybrid architecture is intended to improve predictive accuracy by identifying residual patterns and behavioral variations that the physiological model does not account for. Specifically, our objective is to predict future glucose levels over short-term intervals, such as 30 to 90 min ahead, utilizing a supervised learning approach that combines both raw data and features derived from simulations.
3.4.1. Model Selection and Justification
To ensure interpretability and leverage the tabular nature of our engineered feature set, we chose Light Gradient Boosted Machines (LightGBM) as our primary model for structured data predictions. This decision tree-based gradient boosting framework excels in handling heterogeneous and nonlinear datasets while offering computational efficiency. Its capabilities, including built-in feature importance metrics, effective management of missing values, and robust regularization techniques, render it particularly suitable for medical time-series applications, such as glucose forecasting.
Concurrently, we assessed Long Short-Term Memory (LSTM) networks for their proficiency in capturing temporal dependencies within continuous glucose monitoring (CGM) sequences. As a specialized form of recurrent neural networks (RNNs), LSTMs effectively mitigate the vanishing gradient problem, making them ideal for multivariate time-series forecasting. Nevertheless, to maintain interpretability and simplify training processes, we have prioritized LightGBM in our main analytical framework, using LSTM primarily as a comparative benchmark.
3.4.2. Feature Set Construction
The input to the ML model consists of a unified feature set derived from:
- ⚬
- Time-series features:
- ■
- Recent CGM measurements (e.g., 6–12 lagged values over the past hour).
- ■
- First and second-order glucose derivatives (e.g., rate of change, acceleration).
- ■
- Time since last meal or insulin administration.
- ■
- Circadian variables (e.g., time of day encoded as sine/cosine).
- ⚬
- Mechanistic simulation features:
- ■
- GIM-predicted glucose and insulin levels over the prediction horizon.
- ■
- Simulated rates of glucose appearance and utilization.
- ■
- Estimated deviation between observed CGM and simulated glucose.
- ■
- Derived physiological control indicators (e.g., predicted suppression of hepatic glucose output).
All features were normalized on a per-subject basis using min–max or z-score scaling, as appropriate. Missing CGM values within short gaps (≤15 min) were imputed via forward fill, while any longer gaps were masked during training.
3.4.3. Target Variable and Forecasting Horizon
The target variable is the glucose concentration at a future time step t + Δt, where Δt is typically set to 30, 60, or 90 min. Models were trained separately for each horizon to allow specialization, although multi-output extensions are possible for joint training across time steps.
To effectively capture short-term fluctuations in glucose levels, a sliding window technique was employed to create overlapping input-output pairs from the BRIST1D time-series dataset. This approach not only enriches the diversity of the samples but also enables the model to detect subtle transitions in glucose dynamics, thereby improving predictive accuracy.
3.4.4. Training and Evaluation Strategy
The dataset was partitioned into distinct train, validation, and test sets based on individual subjects to promote generalization across different participants. Hyperparameter tuning for the model was conducted through grid search on the validation set, focusing on minimizing mean absolute error (MAE) and root mean squared error (RMSE). Additionally, feature importance was analyzed using the split gain metrics provided by LightGBM to evaluate the relative contributions of mechanistic and empirical features.
To further investigate generalization and robustness, we conducted performance assessments on various subsets of the data:
- ⚬
- Irregular meal patterns.
- ⚬
- Missed insulin doses.
- ⚬
- Nocturnal periods with limited supervision.
For LSTM models, we implemented a two-layer architecture with dropout regularization, Adam optimizer, and mean squared error loss, using early stopping based on validation error.
3.4.5. Optional Uncertainty Quantification
In an extended version of the model, we incorporated quantile regression within LightGBM to produce asymmetric prediction intervals (e.g., 10th and 90th percentiles). Alternatively, Bayesian linear models were explored for low-complexity uncertainty estimates, suitable for integration in risk-aware control systems.
By combining the physiologically grounded output of the GIM model with flexible machine learning predictors, this architecture enables both accurate and interpretable glucose forecasting under real-world variability, supporting downstream clinical and behavioral decision-making.
3.5. Stochastic Equation Adaptation
The original GIM model is based on a deterministic framework of nonlinear ordinary differential equations (ODEs), which presumes ideal conditions and fully known input trajectories. However, real-world applications, especially those involving free-living datasets like BRIST1D, introduce uncertainties stemming from sensor noise, unrecorded behavioral events, and individual variability. To tackle these challenges, we adapted the deterministic GIM model into a stochastic differential equation (SDE) framework, allowing the model to capture a range of probable physiological responses instead of a singular path.
In our approach, we introduced perturbations to critical GIM subsystems, particularly those related to endogenous glucose production and insulin absorption, by incorporating Gaussian noise terms. These terms were calibrated to reflect both parameter uncertainty and the temporal noise observed in the data, enhancing the model’s ability to represent the inherent variability in physiological responses. The generalized form becomes:
where x(t) represents the system states, f(⋅) is the deterministic GIM dynamic function, Q is a noise scaling matrix, and W(t) is a Wiener process representing Brownian motion.
dx(t) = f(x(t),u(t),p)dt + Q(x(t))dW(t),
To incorporate uncertainties into machine learning, we utilized stochastic neural networks, specifically Monte Carlo dropout LSTM and Bayesian fully connected networks. These models are designed to learn distributions over parameters or predictions, allowing them to effectively handle noisy simulation outputs. For instance, each GIM simulation over a prediction window [t,t + Δt] was executed multiple times with various sampled perturbations, resulting in a spectrum of glucose trajectories that were subsequently summarized as input distributions for the machine learning model.
Additionally, in the case of LightGBM, we adopted quantile objectives to capture the conditional distribution of glucose values, which facilitated the creation of uncertainty-aware prediction bands. These advancements enable the hybrid model to not only address systematic biases present in the simulation but also to convey confidence in its predictions. This capability is essential for safety-critical clinical applications, such as insulin dosing and hypoglycemia alerts.
3.6. Hybrid Integration
A core objective of our modeling framework is to fuse mechanistic and machine learning approaches in a principled manner. This is achieved by adopting a residual learning paradigm, where the ML component is trained not to reproduce observed glucose directly, but to learn values discrepancy between GIM-simulated and actual CGM-measured value horizon denote the GIM-predicted glucose at horizon Δt, and the observed CGM value. We define the residual target for ML as:
The ML model is trained to predict using features from both the physiological simulation and recent data history. The final forecast is then obtained as:
This formulation ensures that the physiologically meaningful behavior encoded in GIM remains the structural foundation, while the ML model learns corrections attributable to unmodeled dynamics, sensor artifacts, or behavioral deviations. Notably, the residual learning approach also regularizes the ML model, preventing it from overfitting to noise or spurious patterns in CGM data alone.
We investigated an alternative feature-augmented hybrid approach, where GIM-generated signals (e.g., insulin action, glucose utilization rates) are used directly as explanatory variables in the ML model, without enforcing residual learning. While this improves predictive flexibility, it may reduce physiological interpretability unless constrained by domain-informed priors.
In both scenarios, the hybrid model utilizes simulated mechanistic knowledge as a prior, allowing for personalization by adjusting to individual behaviors reflected in the BRIST1D dataset. This framework demonstrates robust glucose prediction capabilities across various contexts, effectively merging structure-driven generalizability with data-driven adaptability.
4. Experiments
4.1. Experimental Setup
- ⚬
- Tools (Python version 3.13, TensorFlow/PyTorch, MATLAB version 24.2 Simulink is used);
- ⚬
- Train-test split, cross-validation strategy.
4.2. Metrics
- ⚬
- RMSE, MAE, time-to-peak, hypo/hyperglycemia event detection.
4.3. Baseline Models
- ⚬
- Pure GIM, ML-only, hybrid model.
4.4. Case Studies
- ⚬
- Follow GIM style: normal vs. insulin-resistant profile;
- ⚬
- Simulation scenarios like missed insulin dose, PID tuning.
5. Results and Discussion
5.1. Implementation Procedures
We outline the comprehensive process of data preparation, feature engineering, and model training employed in the development of the hybrid glucose prediction framework. This section is essential for ensuring both reproducibility and transparency within the machine learning (ML) pipeline, especially in the realm of medical time-series forecasting.
The implementation process commences with the acquisition of the BRIST1D dataset from the Kaggle competition platform through the Kaggle API. This dataset encompasses timestamped records related to continuous glucose monitoring (CGM), insulin administration (including both bolus and basal doses), carbohydrate consumption, physical activity, and heart rate data.
Following the dataset’s loading, initial preprocessing involves the elimination of empty columns and the exclusion of rows lacking target values (‘bg+1:00’). Activity columns are transformed using a custom mapping that assigns integer values to different activity names. Additionally, time variables are converted into numeric features through sine and cosine transformations, effectively capturing the circadian rhythms inherent in the data.
Feature aggregation is conducted in 115 min intervals through the application of sliding window means, encompassing all critical signals such as glucose, insulin, carbohydrates, calories, heart rate, steps, and overall activity. Additionally, delta and interaction features are incorporated, capturing temporal changes in glucose and insulin levels, as well as the interactions between these two signals.
The dataset is divided into training and validation sets, ensuring that the samples do not overlap. To prepare the data, numerical and categorical preprocessing pipelines are established using Scikit-learn’s ‘ColumnTransformer’. This approach integrates median imputation for missing values, standardization for numerical features, and one-hot encoding for categorical variables, with explicit handling of missing data to prevent leakage.
For model development, LightGBM is employed, a gradient boosting algorithm known for its effectiveness with structured tabular data. The hyperparameters of the LightGBM model are either manually adjusted or optimized through the Optuna framework. Key parameters, including learning rate, tree depth, number of leaves, regularization terms, and feature subsampling, are meticulously examined to achieve the lowest possible validation root mean square error (RMSE).
Following training, various metrics for regression and classification are computed, such as RMSE, MAE, R2, median absolute error, WMAPE, RCFE, accuracy, F1-score, precision, and recall. These metrics facilitate a thorough assessment of the model’s predictive accuracy and its resilience in real-world scenarios.
The trained model, along with the preprocessing pipeline, is saved using Joblib for future applications, and predictions on the test dataset are formatted for submission. We have included visual representations of validation error curves and LightGBM training logs, which provide valuable insights into the training dynamics and convergence patterns.
5.2. Model Evaluation and Predictive Performance
The numerical experiments provide strong empirical evidence for the predictive efficacy and robustness of the proposed hybrid modeling framework. The integration of the physiologically grounded Glucose–Insulin–Meal (GIM) model with the data-adaptive LightGBM algorithm yields highly competitive results across multiple evaluation metrics, as shown in Figure 1 and Figure 2.
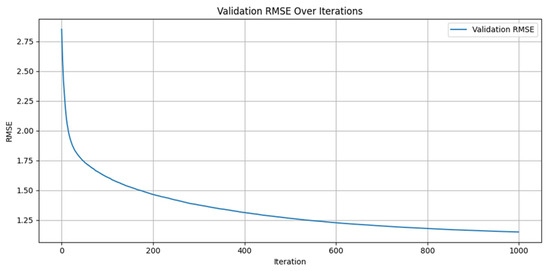
Figure 1.
Validation of RMSE diminishing over the number of iterations.
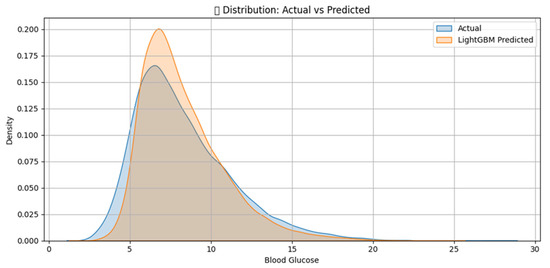
Figure 2.
LightGBM Prediction of blood Glucose distribution comparison.
Notably, as shown in Table 1, the model achieves a Root Mean Square Error (RMSE) of 1.15 mmol/L and a Mean Absolute Error (MAE) of 0.79 mmol/L, which are well within the acceptable clinical range for short-term glucose forecasting. The coefficient of determination (R2 = 0.8544) indicates a high level of agreement between predicted and observed values, consistent with a “robust correlation” under conventional interpretation thresholds, [23]. Furthermore, the Weighted Mean Absolute Percentage Error (WMAPE) of approximately 9.6% and a low Relative Cumulative Forecast Error (RCFE≈) of roughly 0.03 suggests minimal systematic bias in the prediction.

Table 1.
Model Evaluation Metrics.
These results confirm that the residual learning strategy, where the ML model learns to correct discrepancies between the GIM simulation and actual CGM data, is effective in capturing real-world variability. The hybrid model benefits not only from the physiological interpretability of GIM but also from the flexibility and noise resilience of data-driven learning. The relatively low Median Absolute Error (0.54 mmol/L) and strong performance across nonlinear and heterogeneous input conditions (e.g., irregular meals, missed insulin events) further validate the model’s generalization capacity.
In summary, the results reinforce the claim that hybrid physiological-machine learning models offer a viable and scalable solution for personalized, real-time glucose forecasting. The model demonstrates clinically relevant accuracy, strong generalizability, and interpretable structure-key requirements for next-generation decision-support tools in Type 1 diabetes management.
Taken together, the results validate the hybrid model’s ability to capture physiological glucose–insulin dynamics and behavioral variability across different individuals. The use of residual learning enables the model to focus on correcting systematic simulation errors, while the incorporation of stochastic perturbations enhances uncertainty quantification. Figure 2 and Table 2 include predictive vs. observed glucose plots that further illustrate the model’s ability to track dynamic changes over the prediction horizon.

Table 2.
Summary of Simulated Blood Glucose.
Figure-based diagnostics, Figure 3a,b, such as residual plots and time series overlays, demonstrate both temporal accuracy and robustness under noisy conditions. The residuals appear approximately normally distributed and centered around zero, indicating an unbiased estimator. Visual inspection of the CGM time series overlays reveals that the hybrid model’s forecasts closely follow real glucose trajectories, including sharp postprandial rises and gradual declines (see Figure 4a,b.
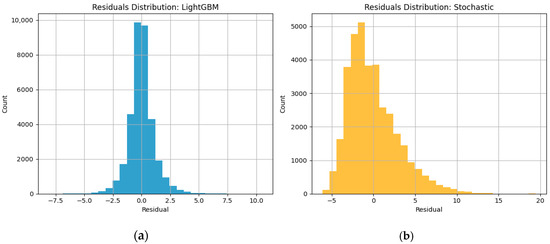
Figure 3.
Normally distributed residual plots of LightGBM and Stochastic models.
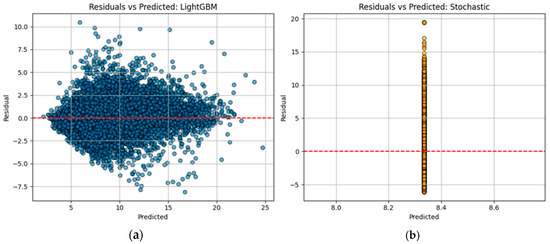
Figure 4.
Residuals appear approximately normally distributed and centered around zero.
In conclusion, the visualizations in Figure 5 and Figure 6, along with the quantitative metrics in Table 3, jointly support the clinical and technical validity of the hybrid GIM–LightGBM framework, see also Table 4. Its capacity to provide not only accurate point forecasts but also interpretable physiological context and predictive uncertainty renders it a compelling candidate for integration into real-time decision-support systems for individuals with Type 1 diabetes. The program code for the computer implementation of the LightGBM method on Python code as well as the generation of all Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 and numerical results could be found in Supplementary Materials.
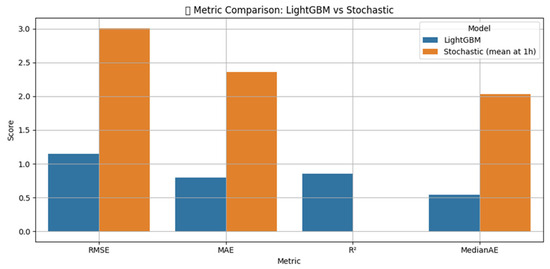
Figure 5.
Comparison of different metric errors for LightGBM and Stochastic models.
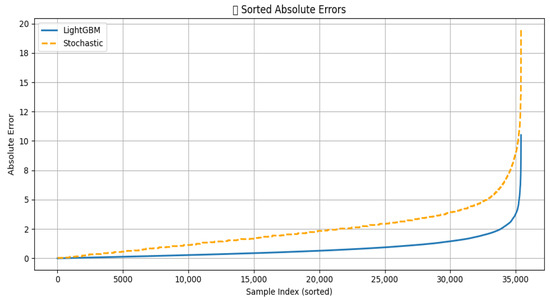
Figure 6.
Comparison of the absolute error of LightGBM and Stochastic models.

Table 3.
Model Comparison Summary.

Table 4.
Pros and Cons of the Three Models with Their Distinctive Features.
In our experience (Figure 4), the data are also compatible with a strong association (R > 0.90), i.e., a powerful correlation according to the conventional approach to interpreting a correlation coefficient, [23]. Using the advanced machine learning (ML) numerical method, we obtained a coefficient of determination (R2) of 0.85, indicating a relatively good agreement between our results and those in the literature.
6. Conclusions
This research introduces and validates an innovative hybrid framework that seamlessly combines the physiologically based Glucose–Insulin–Meal (GIM) model with cutting-edge machine learning (ML) techniques, specifically LightGBM and LSTM networks. The primary advancement of this model is its capacity to integrate the theoretical aspects of physiology encapsulated in the GIM with the variability of real-world data found in the BRIST1D dataset. By adapting the GIM model for free-living conditions and enhancing it with ML components trained on residual errors, the framework significantly improves the accuracy and robustness of postprandial glucose predictions.
The hybrid methodology not only boosts predictive performance but also preserves physiological interpretability, which is essential for clinical applications. The incorporation of stochastic elements into the GIM model further enhances uncertainty quantification, thereby increasing the reliability of predictions for critical scenarios such as insulin dosing and hypoglycemia alerts. This dual focus on accuracy and interpretability positions the framework as a valuable tool in diabetes management.
The practical implications of this model are extensive, offering potential advancements in decision-support systems for Type 1 diabetes (T1D) patients, the creation of artificial pancreas algorithms, and the development of personalized educational simulators. By merging a physiology-driven framework with data-driven adaptability, this approach lays the groundwork for more intelligent and responsive tools in diabetes management, ultimately improving patient outcomes.
Future research should focus on enhancing model personalization through the utilization of extended time-series data and examining the potential for real-time applications, particularly in conjunction with closed-loop control systems. Furthermore, exploring reinforcement learning methodologies may lead to improved optimization of insulin dosing strategies tailored to anticipated glucose responses.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/a18100623/s1. Supplementary File S1: Hybrid Stochastic–Machine Learning Model: Experimental setup, results and discussion, code implementation, numerical results and comments for efficiency of applied methods.
Author Contributions
Conceptualization, I.N., M.K. and M.M.; methodology, I.N. and M.M.; software, I.N. and D.K.; validation, I.N., M.M. and M.K.; formal analysis, D.K.; investigation, I.N. and M.M.; resources, M.K. and D.K.; data curation, I.N. and D.K.; writing—original draft preparation, I.N., M.M. and M.K.; writing—review and editing, I.N., M.M, M.K. and D.K.; visualization, I.N.; supervision, M.K.; project administration, M.M. and M.K.; funding acquisition, M.K. and D.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Acknowledgments
This study is partially financed by project “Sofia University Marking Momentum for Innovation and Technological Transfer” (SUMMIT) №BG-RRP-2.004-0008.
Conflicts of Interest
The authors declare no conflict of interest.
Correction Statement
This article has been republished with a minor correction to the supplemental data. This change does not affect the scientific content of the article.
References
- Mobasseri, M.; Shirmohammadi, M.; Amiri, T.; Vahed, N.; Fard, H.H.; Ghojazadeh, M. Prevalence and incidence of type 1 diabetes in the world: A systematic review and meta-analysis. Health Promot. Perspect. 2020, 10, 98–115. [Google Scholar] [CrossRef]
- Patterson, C.C.; Harjutsalo, V.; Rosenbauer, J.; Neu, A.; Cinek, O.; Skrivarhaug, T.; Rami-Merhar, B.; Soltész, G.; Svensson, J.; Parslow, R.C.; et al. Trends and cyclical variation in the incidence of childhood type 1 diabetes in 26 european centers in the 25-year period 1989–2013. Diabetologia 2019, 62, 408–417. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Saeedi, P.; Karuranga, S.; Pinkepank, M.; Ogurtsova, K.; Duncan, B.B.; Stein, C.; Basit, A.; Chan, J.C.N.; Mbanya, J.C.; et al. IDF diabetes atlas: Global, regional and country-level diabetes prevalence estimates for 2021 and projections for 2045. Diabetes Res. Clin. Pract. 2022, 183, 109119. [Google Scholar] [CrossRef] [PubMed]
- Ceriello, A. Postprandial hyperglycemia and diabetes complications: Is it time to treat? Diabetes 2005, 54, 1–7. [Google Scholar] [CrossRef]
- Ceriello, A.; Colagiuri, S. International diabetes federation guideline for management of postmeal glucose: A review of recommendations. Diabet. Med. 2008, 25, 1151–1156. [Google Scholar] [CrossRef]
- Monnier, L.; Lapinski, H.; Colette, C. Contributions of fasting and postprandial plasma glucose increments to the overall diurnal hyperglycemia of type 2 diabetic patients: Variations with increasing levels of hba1c. Diabetes Care 2003, 26, 881–885. [Google Scholar] [CrossRef]
- Dalla Man, C.; Rizza, R.A.; Cobelli, C. Meal simulation model of the glucose–insulin system. IEEE Trans. Biomed. Eng. 2007, 54, 1740–1749. [Google Scholar] [CrossRef]
- Vicini, P.; Caumo, A.; Cobelli, C. Glucose effectiveness and insulin sensitivity from the minimal models. IEEE Trans. Biomed. Eng. 1999, 46, 130–137. [Google Scholar] [CrossRef]
- Hovorka, R.; Canonico, V.; Chassin, L.J.; Haueter, U.; Massi-Benedetti, M.; Federici, M.O.; Pieber, T.R.; Schaller, H.C.; Schaupp, L.; Vering, T.; et al. Nonlinear model predictive control of glucose concentration in subjects with type 1 diabetes. Physiol. Meas. 2004, 25, 905–920. [Google Scholar] [CrossRef]
- Cobelli, C.; Federspil, G.; Pacini, G.; Salvan, A.; Scandellari, C. An integrated mathematical model of the dynamics of blood glucose and its hormonal control. Math. Biosci. 1982, 58, 27–60. [Google Scholar] [CrossRef]
- Burgos-Simón, C.; Cortés, J.C.; Hidalgo, J.I.; Villanueva, R.J. Novel methodological and computational techniques for uncertainty quantification in diabetes short-term management models using real data. Int. J. Comput. Math. 2024, 101, 1341–1355. [Google Scholar] [CrossRef]
- Sorensen, J.T. A physiologic model of glucose metabolism in man and its use to design and assess improved insulin therapies for diabetes. PhD Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1985. [Google Scholar] [CrossRef]
- Duun-Henriksen, A.K.; Schmidt, S.; Røge, R.M.; Møller, J.B.; Nørgaard, K.; Jørgensen, J.B.; Madsen, H. Model identification using stochastic differential equation grey-box models in diabetes. J. Diabetes Sci. Technol. 2013, 7, 431–440. [Google Scholar] [CrossRef]
- Rabby, M.F.; Tu, Y.; Hossen, M.I.; Lee, I.; Maida, A.S.; Hei, X. Stacked lstm based deep recurrent neural network with kalman smoothing for blood glucose prediction. BMC Med. Inform. Decis. Mak. 2021, 21, 103. [Google Scholar] [CrossRef] [PubMed]
- De Bois, M.; Ammi, M.; El Yacoubi, M.A. GLYFE: Review and benchmark of personalized glucose predictive models in type-1 diabetes. Med. Biol. Eng. Comput. 2022, 60, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, T. Application of improved lightgbm model in blood glucose prediction. Appl. Sci. 2020, 10, 3227. [Google Scholar] [CrossRef]
- El-Bashbishy, A.; El-Bakry, H.M. Pediatric diabetes prediction using deep learning. Sci. Rep. 2024, 14, 4206. [Google Scholar] [CrossRef]
- Nguyen, H.V.; Choi, Y.; Byeon, H. An explainable hybrid deep learning model for prediabetes prediction in men aged 30 and above. J. Men’s Health 2024, 20, 52–72. [Google Scholar] [CrossRef]
- Fleischer, J.; Hansen, T.K.; Cichosz, S.L. Hypoglycemia event prediction from cgm using ensemble learning. Front. Clin. Diabetes Healthc. 2022, 3, 1066744. [Google Scholar] [CrossRef]
- Lu, J.; Wang, Z.; Zhou, Y.; Zhang, M.; Li, X.; Liu, Y.; Zhang, Y.; Zhao, H.; Li, M.; Xu, H.; et al. Pretrained transformer model for decoding individual glucose dynamics from continuous glucose monitoring data. Natl. Sci. Rev. 2025, 12, nwaf039. [Google Scholar] [CrossRef]
- Dave, D.; Erraguntla, M.; Lawley, M.; DeSalvo, D.; Haridas, B.; McKay, S.; Koh, C. Improved low-glucose predictive alerts based on sustained hypoglycemia: Model development and validation study. JMIR Diabetes 2021, 6, e26909. [Google Scholar] [CrossRef]
- Xie, J.; Wang, Q. Benchmarking machine learning algorithms on blood glucose prediction for type i diabetes in comparison with classical time-series models. IEEE Trans. Biomed. Eng. 2020, 67, 3101–3124. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L. Correlation Coefficients: Appropriate Use and Interpretation. Anesth. Analg. 2018, 126, 1. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).