A Hybrid Steffensen–Genetic Algorithm for Finding Multi-Roots of Nonlinear Equations and Applications to Biomedical Engineering

Abstract

A new hybrid of a Steffensen-type method and genetic algorithm is developed for the efficient simultaneous computation of roots of nonlinear equations, particularly in all cases involving non-differentiable functions and multiple roots. Traditional numerical methods often fail to handle these complexities effectively, highlighting the need for a more robust solution. The proposed algorithm combines the global search strength of the genetic algorithm (GA) with the local refinement capabilities of a derivative-free optimal fourth-order Steffensen method. This integration enhances both exploration and exploitation capabilities, leading to improved convergence and computational accuracy. By uniting the GA’s global optimization with the local refinement of iterative solvers, the algorithm forms a higher-order framework capable of locating all roots concurrently. This study validates the performance of this hybrid strategy through diverse applications in biomedical engineering problems.

1. Introduction

Numerical analysis is fundamental to numerous disciplines, such as engineering, applied mathematics, business, the physical sciences, and medicine. It involves a variety of iterative methods that are crucial for tackling complex mathematical challenges, particularly when exact analytical solutions are either impractical or unavailable. For example, in engineering, numerical analysis is used in structural design, power flow analysis, fluid dynamics, and control systems; in applied mathematics, it is fundamental to optimization and computational modeling; in business, it supports financial forecasting, risk assessment, and operations research; in the physical sciences, it is applied to simulate phenomena such as heat transfer, quantum mechanics, and astrophysical models; and in medicine, it underpins medical imaging, tumor detection, and the modeling of biological systems. While certain problems can be addressed using a finite number of analytical steps, many are too complicated for direct methods. In such situations, numerical analysis provides valuable iterative approaches that yield approximate solutions through progressive refinements.

A wide range of real-world phenomena can be described using nonlinear equations, typically represented as $f\left(x\right)=0.$ The iterative methods for obtaining the solution can be categorized into two main types: those designed to find a single root and those intended for finding all roots simultaneously. Among the most widely used techniques for finding simple roots is Newton’s method, known for its quadratic convergence and effectiveness when dealing with functions that have continuous derivatives. This method improves an initial estimate, $x_0$, through repeated iterations, using the following formula:

$$x_{n+1}=x_n-{\displaystyle \frac{f\left(x_n\right)}{f^{\prime }\left(x_n\right)}}.$$

(1)

However, Newton’s method relies on the function being differentiable, which can restrict its applicability. To overcome this limitation, Steffensen’s method [1] provides an alternative by approximating the derivative using forward differences while retaining the same order of convergence:

$$x_{n+1}=x_n-{\displaystyle \frac{f^2\left(x_n\right)}{f(x_n+f\left(x_n\right))-f\left(x_n\right)}}.$$

(2)

The first optimal fourth-order convergent Steffensen-type method was given by Ren et al. [2] in 2009.

$$\begin{array}{cc}\hfill y_n& =x_n-{\displaystyle \frac{f\left(x_n\right)}{f\left[x_n,z_n\right]}},\hfill \\ \hfill x_{n+1}& =y_n-{\displaystyle \frac{f\left(y_n\right)}{f\left[x_n,y_n\right]+f\left[y_n,z_n\right]-f\left[x_n,z_n\right]+a\left(y_n-x_n\right)\left(y_n-z_n\right)}},\hfill \end{array}$$

(3)

where $z_n=x_n+f\left(x_n\right)$ and $a\in R$ is an arbitrary constant. For more optimal fourth-order Steffensen-type simple root-finding methods, one may refer to [3,4,5,6,7].

Simultaneous-root-finding iterative methods are generally more accurate, stable, and reliable than methods focused on finding a single root. These techniques begin with a set of initial approximations and generate sequences of iterations that, under suitable conditions, converge simultaneously to all the roots of a given equation. One of the earliest derivative-free simultaneous methods was introduced by Karl Weierstrass [8] and is widely known in the literature as the Weierstrass method for solving polynomial equations. This approach was later independently rediscovered by Kerner [9], Durand [10], Dochev [11], and Prešić [12] for estimating all roots of nonlinear equations. In 1962, Dochev [11] demonstrated that the Weierstrass method converges locally with a convergence order of two. Subsequently, Dochev and Byrnev [13], along with Börsch-Supan [14], developed derivative-free simultaneous methods with a convergence order of three. In contrast, Ehrlich [15] proposed a simultaneous method for polynomial equations that incorporates derivatives. Similarly, Aberth [16] introduced a simultaneous-root-finding method with third-order convergence that utilizes derivatives. This method was later enhanced by Anourein [17] in 1977 to achieve fourth-order convergence and further improved by Petković [18] in 2010, who developed a sixth-order variant. A tenth-order method was given by Mir et al. [19] in 2020 whereas Cordero et al. [20] gave a method of the general order 2p in 2022. Recently, Shams et al. [21,22,23] have introduced parallel and neural network-based algorithms for simultaneous root finding.

Iterative methods have also been proposed for multiple-root-finding for nonlinear equations. Some multiple-root-finding derivative-free optimal fourth-order methods [24,25,26,27,28] were obtained in the recent past but are mostly for the case when the multiplicity is known. Some derivative-free methods [29,30] based on transformation methods for handling unknown multiplicity were also proposed but these methods are also initial-guess-dependent.

A genetic algorithm (GA) [31] is a metaheuristic search technique inspired by Darwin’s theory of natural selection. It mimics biological evolutionary processes such as mutation, crossover, and selection to evolve solutions over time. GAs are renowned for their strong global search abilities, although they may encounter difficulties with convergence speed, particularly in the later stages of the search. They are commonly employed to identify optimal or near-optimal solutions for complex problems that would otherwise demand extensive computational effort.

Despite their robustness, evolutionary algorithms face several implementation challenges, including premature convergence, sensitive parameter tuning, and the need to balance exploration with exploitation [32]. While capable of delivering reliable solutions, they are often computationally intensive, which can limit their applicability in real-time scenarios. Therefore, selecting an appropriate method requires careful consideration of the trade-offs among accuracy, efficiency, and robustness.

Identifying multiple simultaneous roots of nonlinear equations remains a significant challenge in mathematical and engineering contexts, with broad applications in fields like physics, economics, and design. Traditional simple root-finding methods with quadratic convergence, such as the Newton–Raphson and Steffensen methods [33], often struggle with convergence when dealing with complex root structures, multiple roots, or non-differentiable/discontinuous functions whereas the multiple-root-finding methods require the information of multiplicity. Also, the simultaneous-root-finding methods are mostly developed for polynomial functions only. Altogether, all of these classical methods are highly dependent on the choice of initial guess. These limitations have spurred interest in more robust computational approaches, leading to the development of hybrid algorithms that blend the strengths of genetic algorithms with other optimization techniques.

The literature reports several innovative hybrid strategies for root-finding [34]. One prominent approach integrates genetic algorithms with local search methods, such as gradient descent or Newton’s method [35], which significantly enhances convergence speed. In some studies, the root-finding problem is framed as a multi-objective optimization task [32], where the goal is to minimize the residuals of the nonlinear equations, thereby identifying multiple roots simultaneously. Hybrid genetic algorithms are particularly well-suited for this approach, as they are capable of navigating complex and irregular optimization landscapes.

The effectiveness of a hybrid genetic algorithm [36] lies in combining the rapid convergence of local optimizers such as non-optimal higher order variants of Steffensen’s method with the broad search capacity of genetic algorithms. This fusion is especially beneficial for tackling non-differentiable, discontinuous, or combinatorial problems.

In this study, we propose a novel hybrid Steffensen–genetic algorithm (SGA), which integrates the global search capability of the GA with the local search refinement of the optimal fourth-order Steffensen method developed by Ren et al. [2] to find all roots. In Section 2, the new hybrid algorithm is described. In Section 3, we apply the new hybrid method to some applications from biomedical engineering problems such as osteoporosis in Chinese women, a blood rheology model, a drug concentration profile, and ligand binding. Moreover, to express the capability of the new method to handle non-differentiability, we also consider a standard test problem with these characteristics. Section 4 gives the conclusion.

2. A New Hybrid Steffensen–Genetic Algorithm (SGA)

For better understanding, a flow chart is given in Figure 1 below.

Let us now describe the algorithm step-wise in Algorithm 1.

Algorithm 1 Hybrid Steffensen–genetic algorithm for simultaneous root-finding

1:  Input: Function $f\left(x\right)$, population size N, maximum generations/iterations G, crossover probability $cp$, mutation probability $mp$, Bounds $[a,b]$, tolerance, distinct tolerance 2:  Initialize: Population $P\leftarrow \{x_1,x_2,\dots ,x_N\}$ randomly in $[a,b]$ 3:  for generation = 1 to G do 4:     Calculate fitness and cost for each individual: $Cost=\left|f\left(x\right)\right|,Fitnessf\left(x\right)=e^{{\displaystyle \frac{1}{\left|f\right(x\left)\right|}}}$ 5:     Select individuals using tournament selection 6:     Perform linear crossover and random mutation 7:     Update individuals using fitness function 8:     repeat 9:        Screen top individuals and refine roots using Steffensen-type method RM 10:     until convergence or instability 11:     return x 12:     Replace population with refined roots 13:  end for 14:  return best solution, best cost, and all qualified roots

The new algorithm presented is a hybrid evolutionary method designed to solve nonlinear equations and optimization problems. It begins by initializing a random population within specified bounds and iteratively evolves this population over a fixed number of generations. In each iteration, the objective function is the nonlinear function $f\left(x\right)$ whose simultaneous roots are to be calculated; the cost of the objective function is $\left|f\left(x\right)\right|$ while the fitness of individuals is evaluated using an exponential fitness function, $e^{{\displaystyle \frac{1}{\left|f\right(x\left)\right|}}}$, to avoid division by zero. Selection is performed using tournament selection. Genetic operators such as linear crossover and random mutation are applied to generate new individuals. To enhance convergence and accuracy, the algorithm incorporates a refinement step, the first optimal fourth-order Steffensen method developed by Ren et al. [2] (RM), for the top-performing individuals with the parameter a chosen as zero for computaional efficiency. The population is then updated with these refined solutions. The algorithm outputs the best solution, its corresponding cost, and all distinct qualified roots that meet the given tolerance criteria. The algorithm employs a standard GA enhanced with adaptive crossover and mutation operators to maintain population diversity and ensure efficient convergence. During the local refinement phase, the top-performing individuals from the GA are further optimized using the fourth-order Steffensen-type method, improving the accuracy of root approximations. This combined strategy yields a robust solver capable of efficiently locating and refining multiple distinct roots of nonlinear equations. Let us discuss the conditional stability of the new hybrid algorithm, i.e., under what conditions on the function f(x), its domain, and the algorithm’s parameters does the sequence of approximations converge (stably) to a root. The local refinement step in the algorithm is governed by the optimal fourth-order Steffensen-type method (3). It is locally fourth-order-convergent if the initial guess is close enough; the underlying function f is smooth and differentiable near the required root. In contrast, the genetic algorithm provides global exploration. Its stability is not analysed with derivatives but with population dynamics such as selection that ensure robust convergence, cross-probability to balance exploration and exploitation, mutation probability which ensures diversity and avoids stagnation, and a large enough population size which ensures stability. Stability here means that the GA maintains population diversity long enough to supply candidates close to actual roots, where Steffensen’s method can take over. Therefore, altogether, the new hybrid method is conditionally stable if the GA generates at least some candidates close enough to true roots (exploration condition). The Steffensen iteration at those candidates ensures local stability, and the algorithmic parameters prevent population collapse before convergence. In short, local conditional stability comes from the Steffensen-type method whereas the global conditional stability comes from GA parameters ensuring diversity and exploration until the Steffensen-type method can screen and converge to the required roots. It is worth mentioning that the hybrid approach eliminates the dependency of the Steffensen-type method on the choice of the initial guess, smoothness and non-differentiability near the root, and the demerit of premature or slow convergence of the genetic algorithm, whereas on the other hand, it is dependent on the choice of underlying parameters. This aspect is handled by utilizing a high crossover rate and low mutation rate to balance exploration, exploitation, and diversity. In any case, such a type of hybrid approach lacks rigorous global convergence proofs which is common in metaheuristic-based hybrids.

3. Numerical Experiments

In this section, we examine several test problems listed in

Table 1. Test functions.

Nonlinear Functions	Domain	Solutions
$f_1\left(x\right)=0.0039x^3-0.78x^2+39.9x-612.5$	$\left(0,150\right)$	$35,35,125$
$f_2\left(x\right)=0.0039x^3-0.78x^2+39.9x-467$	$\left(0,150\right)$	$16.7023433744267$
		$56.5740667166546$
		$126.723589908919$
$f_3\left(x\right)={\displaystyle \frac{1}{441}}{x}^8-{\displaystyle \frac{8}{63}}{x}^5-0.05714285714x^4+{\displaystyle \frac{16}{9}}{x}^2$	$\left(0,5\right)$	$0.104698651533921$
$-3.624489796x+0.3600$		$3.82238923462577$
$f_4\left(x\right)={(x^2-e^{60x}-3x+2)}^5$	$\left(0,1\right)$	$0.01188653001928682$
$f_5\left(x\right)=\left(2x\right|cosx|+x^2{-1)}^2-2$	$\left(-3,3\right)$	$-2.704784856524704$
		$-1.821166332738140$
		$-1.562296722714125$
		$-0.840953096992933$
		$-0.244153167113250$
		$1.350786955284248$
$f_6\left(x\right)=x^2-10x+25$	$\left(0,10\right)$	$5,5$
$f_7\left(x\right)=x^2-0.0003x+0.00000001$	$\left(0,0.0003\right)$	$2.62\times {10}^{-4}$, $3.82\times {10}^{-5}$

and describe them below to compare the performance of Steffensen’s method (SM) (2), the genetic algorithm (GA), and the proposed hybrid Steffensen–genetic algorithm (SGA). The experiments were performed using Python 3.0. We present a variety of examples to demonstrate the effectiveness of the SGA. Some problems are drawn from biomedical engineering applications, while two are standard benchmark problems used to evaluate the method’s ability to handle multiple roots and non-differentiable functions. The comparison is given in terms of numbers of iterations or generations, the best solution provided with the best cost or absolute residual error, and computational time in milliseconds. The convergence plots of the SGA for all the functions are also given. In the convergence plots, the best cost or absolute residual error of the function is shown as it converges to all its roots.

To systematically evaluate the performance of the hybrid SGA, we define key parameters influencing the evolutionary process in

Table 2. Parameter selections.

Parameter	Value
Selection	Tournament Selection
Crossover	Linear Crossover (0.7)
Mutation	Random (0.1)
Domain	Problem-Based
Parent-to-Offspring Ratio	1:1
Initial Population Size	200
Maximum Generations	10
Distinct Tolerance	0.1
Tolerance	${10}^{-5}$

. These parameters include the selection operator, the function domain, crossover and mutation probabilities and techniques, the parent-to-offspring ratio, the maximum number of generations, and the total population size. Additionally, stopping criteria and tolerance levels are specified. The tolerance ${10}^{-5}$ is for the RM to screen out the roots and the distinct tolerance is used to obtain different qualified roots. The careful selection of these parameters ensures robust convergence and the stability of the algorithm. We take a high crossover rate of 0.7 to encourage exploration, whereas a low mutation rate of 0.1 is considered which helps to maintain diversity by not becoming stuck in the local extremum. Additionally, low mutation rates also ensure avoiding disrupting good solutions.

Example 1. 

Osteoporosis in Chinese Women: Wu et al. (2003) [37] investigated changes in age-related speed of sound (SOS) at the tibia as well as the prevalence of osteoporosis in native Chinese women. They discovered the following link between SOS and age in years, x:

$$SOS\left(x\right)=3383+39.9x-0.78x^2+0.0039x^3,$$

(4)

where SOS is expressed in units of m/s. For one research subject, SOS was measured to be 3995.5 m/s. The age of the research subject can be determined using the following equation:

$$f_1\left(x\right)=0.0039x^3-0.78x^2+39.9x-612.5.$$

$f_1\left(x\right)$ has a simple root, $\alpha =125$, and a multiple root at $\alpha =35$ with the multiplicity $m=2.$

Let us take another research subject where SOS was measured to be 3850 m/s. Then, we obtain the following equation:

$$f_2\left(x\right)=0.0039x^3-0.78x^2+39.9x-467.$$

(5)

The required roots are $\alpha =16.7023433744267,56.5740667166546,126.723589908919.$ Let us take the bounds for both cases as $\left(0,150\right).$ The initial guess for Steffensen’s method is taken as $75.$ In

Table 3. Performance of root-finding methods for $f_1\left(x\right)$.

Methods	No. of Iterations	Best Solution	Best Cost	Time/(ms)
SM	6	$34.98824391$	4.97604 $\times {10}^{-5}$	78
GA	10	$34.99999725$	2.95585 $\times {10}^{-12}$	73
Hybrid SGA	10	$125.00000004$	6.82121 $\times {10}^{-13}$	122

and

Table 4. Performance of root-finding methods for $f_2\left(x\right)$.

Methods	No. of Iterations	Best Solution	Best Cost	Time/(ms)
SM	5	$16.70234332$	8.60640 $\times {10}^{-7}$	39
GA	10	$56.57407937$	1.38029 $\times {10}^{-4}$	90
Hybrid SGA	10	$56.57406671$	1.00044 $\times {10}^{-11}$	92

, we now compare our results for $f_1\left(x\right)-f_2\left(x\right)$.

All qualified roots using the SGA are 35.000001317434396 and 125.0000000276387, whereas the qualified root from the GA is 34.99999725.

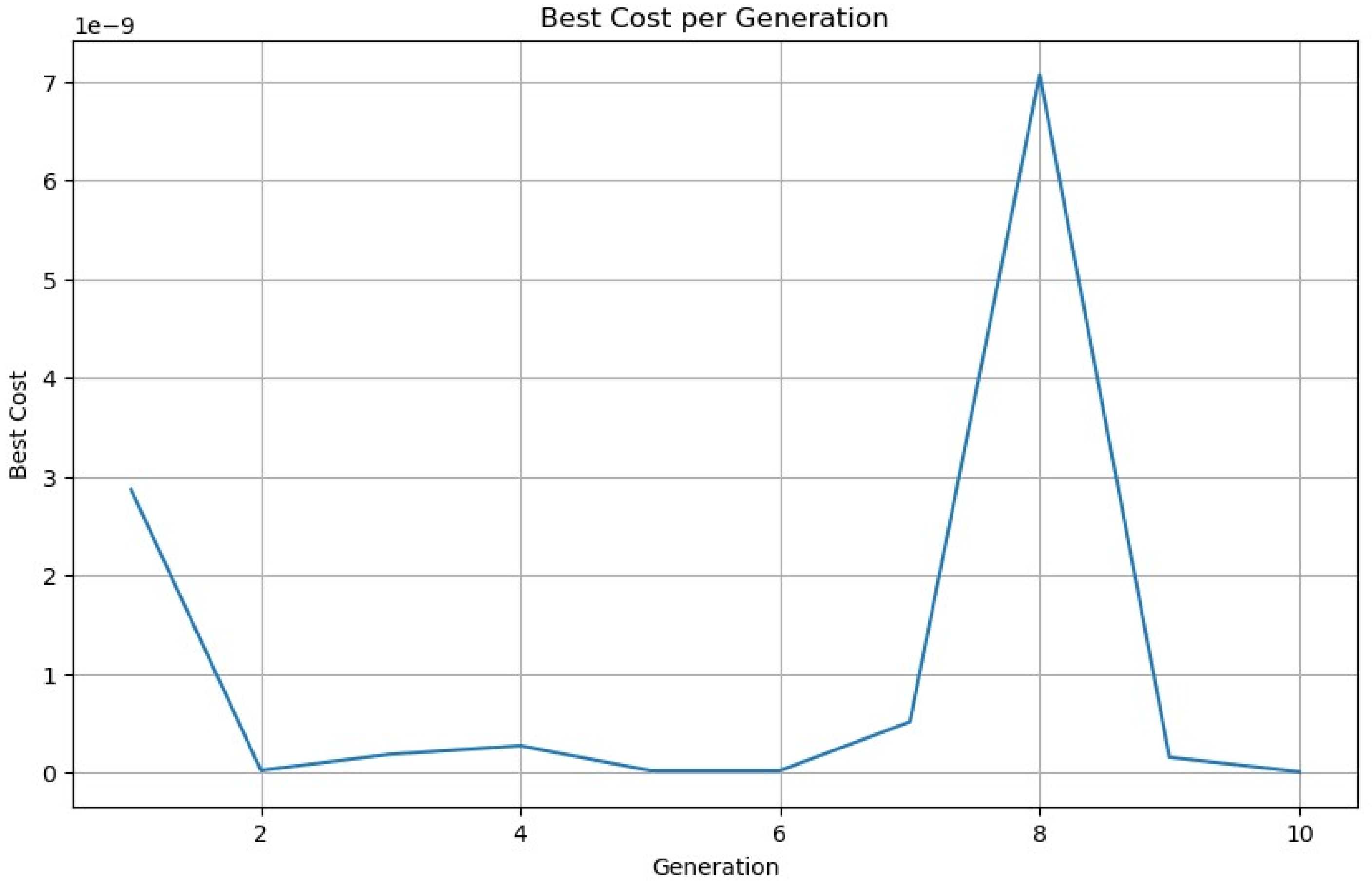
As we can see from Figure 2, the SGA converges to one root until generation 6, and for the next four generations, it switches to the second root of $f_1\left(x\right)$. The roots obtained at the end have residual errors less than ${10}^{-5}.$ We obtain that the residual error for the root 125.0000000276387 is 8.95492 $\times {10}^{-7}$. In this way, in the 10 generations, the SGA finds all the roots of a function. A similar trend can be seen in Figure 3.

All qualified roots using the SGA are 16.70234326657741, 126.7235899088235, and 56.57406671665363, whereas for the GA, only one root is screened, 56.57407937.

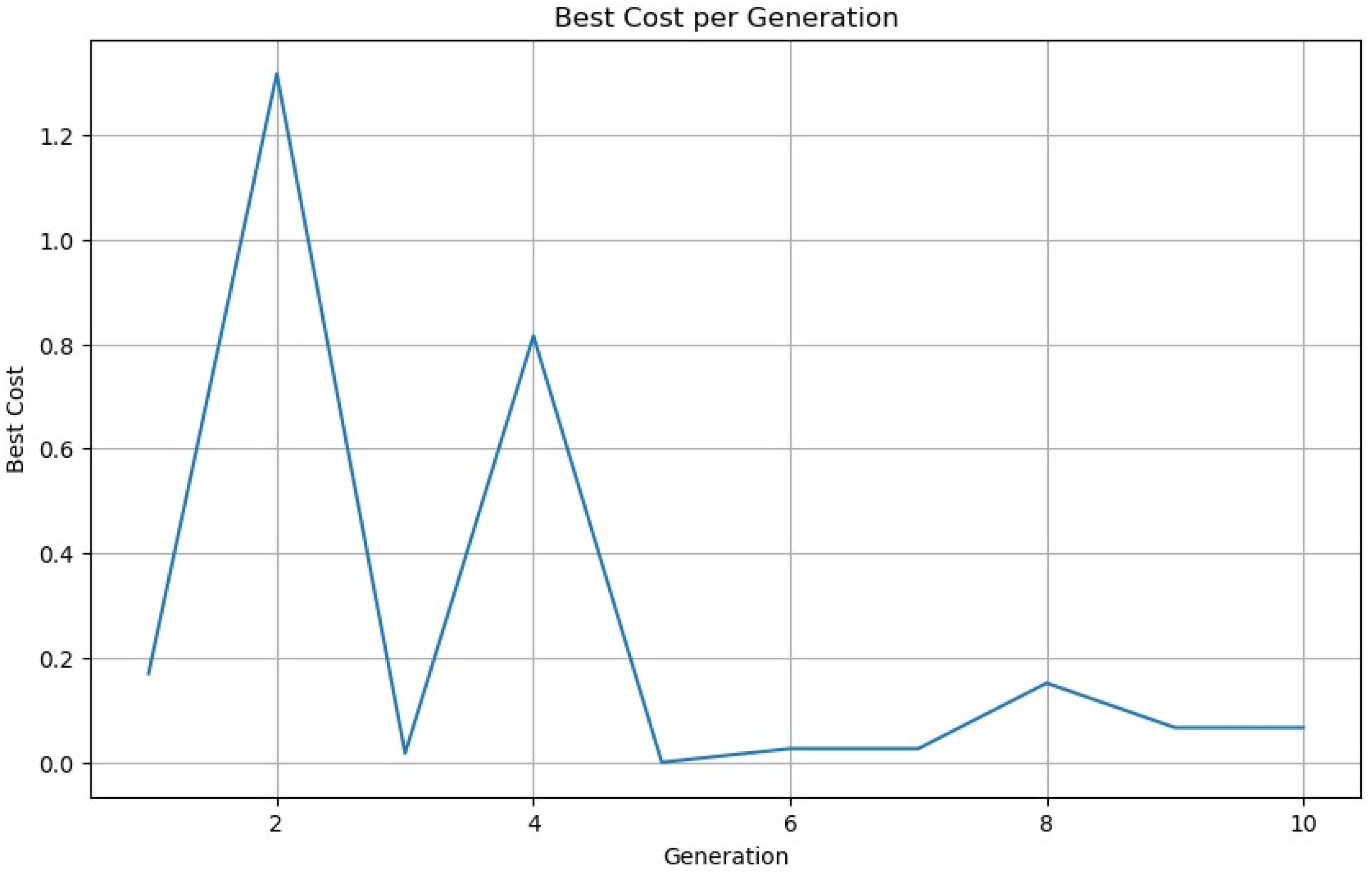
Example 2. 

Blood Rheology Model: Blood rheology is a branch of medicine that studies the structural and flow characteristics of blood. In this context, blood is often modeled as a non-Newtonian Caisson fluid, exhibiting plug flow behavior and moving through a tube with minimal deformation in the core region and a significant velocity gradient near the tube walls. To analyze this plug flow of a Caisson fluid, we consider the following nonlinear equation:

$$H=1-{\displaystyle \frac{16}{7}}\sqrt{x}+{\displaystyle \frac{4}{3}}x-{\displaystyle \frac{1}{21}}{x}^4,$$

where H is the rate of flow. For $H=0.40$, we get

$$f_3\left(x\right)={\displaystyle \frac{1}{441}}{x}^8-{\displaystyle \frac{8}{63}}{x}^5-0.05714285714x^4+{\displaystyle \frac{16}{9}}{x}^2-3.624489796x+0.3600.$$

(6)

The required roots are $0.104698651533921$, $3.82238923462577$, $-2.2786946878959-i1.9874764502574$, $-2.2786946878959+i1.9874764502574$, $-1.23876910501397-i3.40852356845107$, $-1.23876910501397+i3.40852356845107$, $1.55391984983002-i0.940414989869743$, and $1.55391984983002+i0.940414989869743.$ We take the bounds as $\left(0,5\right).$ The initial guess for Steffensen’s method is taken as $3.$ In

Table 5. Performance of root-finding methods for $f_3\left(x\right)$.

Methods	No. of Iterations	Best Solution	Best Cost	Time/(ms)
SM	3	$0.10469864$	2.23659 $\times {10}^{-8}$	8
GA	10	$0.15755396$	7.11793 $\times {10}^{-4}$	66
Hybrid SGA	10	$0.10469865$	2.28041 $\times {10}^{-16}$	94

, we compare our results for $f_3\left(x\right)$ and the convergence plot is shown in Figure 4.

All qualified real roots using the SGA are 0.10469865153392068 and 3.8223892882212724, whereas there are many qualified roots from the GA, out of which we list only a few: 2.544809535345575, 0.9129866801828956, 2.2939664289668364, 0.7079208610382137, and 0.15755396604688204.

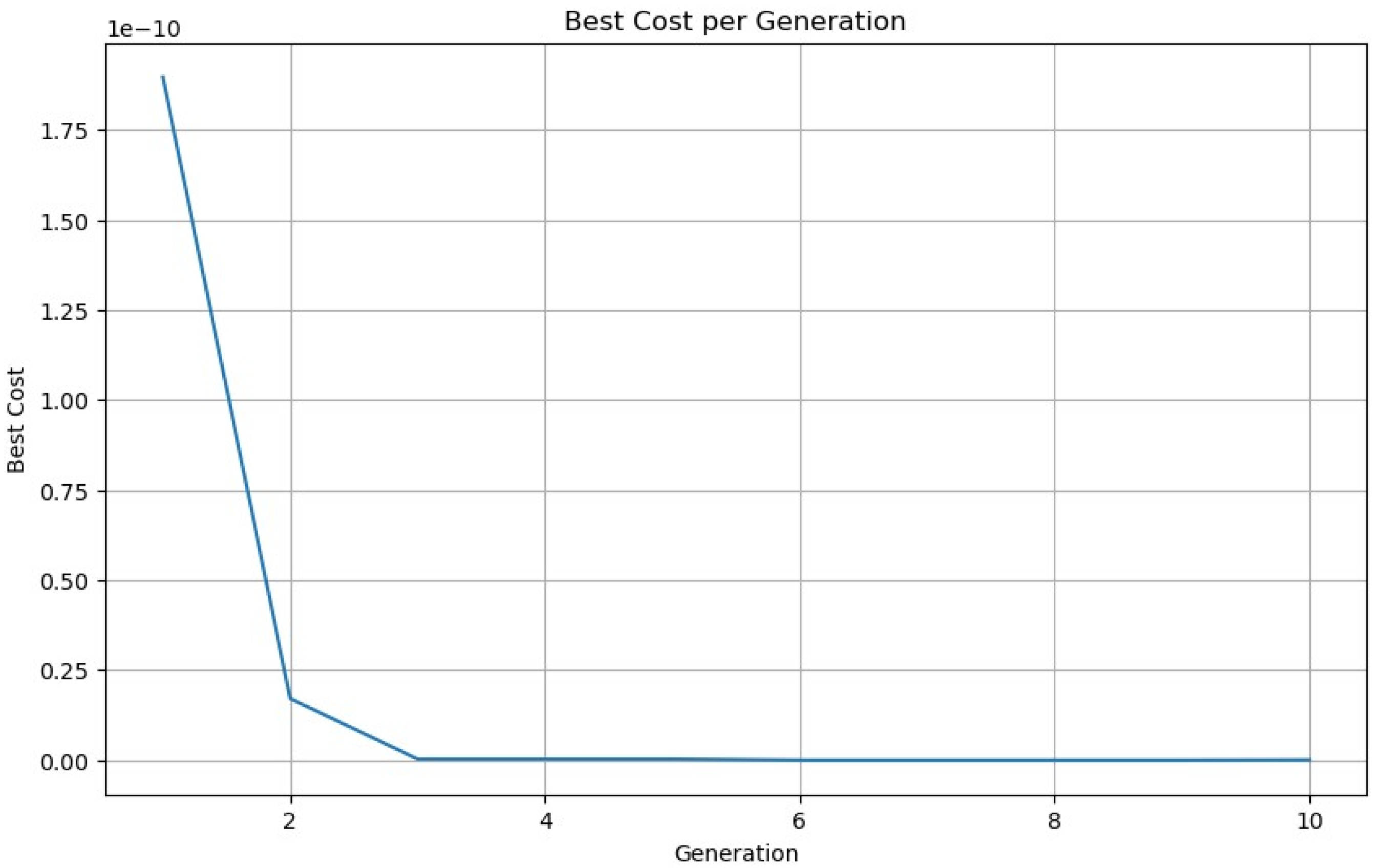
Example 3. 

We now give a problem of finding multiple roots of a function in $(0,1)$. Consider

$$f_4\left(x\right)={(x^2-e^{60x}-3x+2)}^5.$$

(7)

$f_4\left(x\right)$ has a multiple zero at $\alpha =0.01188653001928682$ with the multiplicity $m=5$. The initial guess for Steffensen’s method is taken as 0.

In

Table 6. Performance of root-finding methods for $f_4\left(x\right)$.

Methods	No. of Iterations	Best Solution	Best Cost	Time/(ms)
SM	1	$-1.0$	$7776.0$	$1.5$
GA	10	$0.01150897$	2.11681 $\times {10}^{-8}$	480
Hybrid SGA	10	$0.01180960$	1.40332 $\times {10}^{-13}$	752

, we compare our results for $f_4\left(x\right)$ and the convergence plot is shown in Figure 5.

The qualified real root using the SGA is 0.011809602025173279, whereas there are many qualified roots from the GA, out of which we list only a couple: 0.011508971188723183 and 0.022973611744519395.

Example 4. 

We consider a non-differentiable function in the domain $(-3,3)$. Consider

$$f_5\left(x\right)=\left(2x\right|cosx|+x^2{-1)}^2-2$$

(8)

The initial guess for Steffensen’s method is taken as 0. The required roots are $-2.704784856524704$, $-1.821166332738140$, $-1.562296722714125$, $-0.840953096992933,$$-0.244153167113250$, and $1.350786955284248$.

In

Table 7. Performance of root-finding methods for $f_5\left(x\right)$.

Methods	No. of Iterations	Best Solution	Best Cost	Time/(ms)
SM	5	$-0.24415316$	1.49213 $\times {10}^{-13}$	10
GA	10	$-1.88825542$	2.24249 $\times {10}^{-4}$	77
Hybrid SGA	10	$-0.24415316$	4.44089 $\times {10}^{-16}$	188

, we compare our results for $f_5\left(x\right)$ and the convergence plot is shown in Figure 6.

All qualified roots using the SGA are −1.8211662981990546, −2.7047848787147117, −0.24415316638857587, −1.5622966641710239, 1.3507869552962921, and −0.8409530966864265, whereas the GA produces a long list of qualified roots, out of which some are listed as −0.1193353144222078, −1.662712573906333, −1.4137017600934054, −2.6788354270453563, −0.2395835561741988, −1.872134685585508, 1.2882981230503905, and −2.5694103698386206.

Example 5. 

Drug Concentration Profile: Let us take a look at the drug concentration in a patient’s bloodstream x hours following injection:

$$C\left(x\right)={\displaystyle \frac{50x}{25+x^2}}.$$

We determine the period of time during which the drug’s concentration drops to 5%, and the equation becomes

$$f_6\left(x\right)=x^2-10x+25.$$

$f_6\left(x\right)$ has a multiple zero at $\alpha =5$ with the multiplicity $m=2$. We take the bounds as $\left(0,10\right).$ The initial guess for Steffensen’s method is taken as 8. In

Table 8. Performance of root-finding methods for $f_6\left(x\right)$.

Methods	No. of Iterations	Best Solution	Best Cost	Time/(ms)
SM	10	$5.03505455$	$0.00122882$	11
GA	10	$5.00252358$	1.18810 $\times {10}^{-9}$	33
Hybrid SGA	10	$5.00000010$	7.10542 $\times {10}^{-15}$	117

, we compare our results for $f_6\left(x\right)$ and the convergence plot is shown in Figure 7.

The qualified root using the SGA is 5.000000104713321. All qualified roots using the GA are 5.002523589641892, 4.56067847431556, 4.091058561028491, 5.43454858473575, 5.30337503407576, and 4.870839379610281.

Example 6. 

Ligand Binding: The ligand binding problem explores how a receptor (R) interacts with a ligand (L) to form a complex (x = RL) at equilibrium. This interaction is quantified using the dissociation constant (Kd), which reflects the affinity between the receptor and ligand; a lower Kd indicates stronger binding. The central question involves determining the equilibrium concentrations of the free receptor, free ligand, and the receptor–ligand complex, given total concentrations and Kd. This foundational biochemical concept is crucial for understanding molecular interactions in biological systems, such as enzyme–substrate binding and hormone–receptor signaling. Let us consider that the receptor and ligand are added to a total concentration of $1.0\times {10}^{-4}$ M and the Kd for the RL complex is $1.0\times {10}^{-4}$ M. We obtain the following nonlinear equation.

$$f_7\left(x\right)=x^2-0.0003x+0.00000001.$$

The required roots are $x=RL=2.62\times {10}^{-4}$ M and $x=RL=3.82\times {10}^{-5}.$ We consider the bounds of the problem as $\left(0,0.0003\right).$ The initial guess for Steffensen’s method is taken as $0.1$. In

Table 9. Performance of root-finding methods for $f_7\left(x\right)$.

Methods	No. of Iterations	Best Solution	Best Cost	Time/(ms)
SM	10	2.93775500 $\times {10}^{-4}$	8.17135 $\times {10}^{-9}$	$1.5$
GA	10	3.0 $\times {10}^{-4}$	8.91434 $\times {10}^{-12}$	64
Hybrid SGA	10	2.61802497 $\times {10}^{-4}$	2.01569 $\times {10}^{-13}$	92

, we compare our results for $f_5\left(x\right)$ and the convergence plot is shown in Figure 8.

All qualified roots using the SGA are 0.00026180249742358783 and 3.8105698683110196 $\times {10}^{-5}$. All qualified roots using the GA are 0.0002529336946341387 and 0.0003.

4. Conclusions

A comparative analysis of Steffensen’s method, the genetic algorithm (GA), and the proposed hybrid Steffensen–genetic algorithm (SGA) demonstrates that the hybrid approach is more reliable and robust in locating all the roots of nonlinear problems. Unlike Steffensen’s method, which converges to only one root at a time, and the GA, which either fails to filter out irrelevant solutions or produces an excessively large set of candidate roots, the SGA effectively balances exploration and exploitation.

The convergence plots indicate that the hybrid method is capable of approaching multiple roots simultaneously during intermediate generations with relatively low error, before refining and screening them to obtain accurate solutions at termination. This screening mechanism prevents the accumulation of irrelevant candidates, a drawback often observed in GAs. Furthermore, the results confirm that the SGA maintains computational efficiency by justifying its runtime with improved accuracy and controlled convergence behavior.

Importantly, the hybrid algorithm performs well for both multiple and simple roots, without requiring prior knowledge of multiplicity. This makes it a flexible tool for diverse nonlinear problems. Moreover, the SGA can serve as an effective initial guess generator for higher-order deterministic root solvers, thus bridging global metaheuristic exploration with the fast local convergence of iterative methods. In future work, we aim to develop a deep learning-based hybrid algorithm that can also incorporate hyperparameter tuning of underlying parameters.