Abstract
Spiking Neural Networks (SNNs), with their event-driven and energy-efficient characteristics, have shown great promise in processing data from neuromorphic sensors. However, the sparse and non-stationary nature of event-based data poses significant challenges to optimization, particularly when using conventional algorithms such as AdamW, which assume smooth gradient dynamics. To address this limitation, we propose MemristiveAdamW, a novel algorithm that integrates memristor-inspired dynamic adjustment mechanisms into the AdamW framework. This optimization algorithm introduces three biologically motivated modules: (1) a direction-aware modulation mechanism that adapts the update direction based on gradient change trends; (2) a memristive perturbation model that encodes history-sensitive adjustment inspired by the physical characteristics of memristors; and (3) a memory decay strategy that ensures stable convergence by attenuating perturbations over time. Extensive experiments are conducted on two representative event-based datasets, Prophesee NCARS and GEN1, across three SNN architectures: Spiking VGG-11, Spiking MobileNet-64, and Spiking DenseNet-121. Results demonstrate that MemristiveAdamW consistently improves convergence speed, classification accuracy, and training stability compared to standard AdamW, with the most significant gains observed in shallow or lightweight SNNs. These findings suggest that memristor-inspired optimization offers a biologically plausible and computationally effective paradigm for training SNNs on event-driven data.
1. Introduction
With the rapid development of low-power and high-efficiency intelligent perception systems, Spiking Neural Networks have emerged as a major research direction in neuromorphic computing due to their brain-inspired characteristics such as event-driven processing and sparse activation [1]. Unlike traditional Artificial Neural Networks (ANNs), SNNs encode temporal information using discrete spikes, offering superior energy efficiency and faster response, making them particularly suitable for real-time applications such as autonomous driving, robotic perception, and edge computing [2]. The advancement of neuromorphic sensors, such as event cameras, has further expanded the potential of SNNs. These sensors provide high temporal resolution, low latency, and a wide dynamic range, making them well-suited for object detection in complex and dynamic environments [3]. However, the highly sparse and non-stationary nature of event data poses significant challenges to model training. Under standard backpropagation frameworks, SNNs often suffer from large gradient fluctuations and slow convergence [4,5]. As a result, designing optimization algorithms that are better adapted to the non-stationary gradient characteristics of SNNs has become a critical research focus.
Mainstream optimization algorithms such as Adam [6] and its improved variant AdamW [7] are widely used in deep neural networks, leveraging first- and second-moment estimations to adaptively control the learning rate. AdamW decouples the weight decay term from the gradient update, thereby improving generalization performance and becoming the default optimization algorithm in many mainstream architectures such as Transformers. However, these algorithms generally assume smooth gradient dynamics and stable statistical distributions. When applied to event-driven SNN training, where gradient signals fluctuate abruptly and non-stationarily, such fixed adjustment strategies often fail to respond in real time, leading to unstable training dynamics or convergence stagnation [8,9].
To address these issues, several optimization algorithms have proposed targeted improvements. RAdam [8] mitigates early-stage instability through a dynamic warm-up mechanism, while AdaBound [9] constrains the learning rate within adaptive upper and lower bounds, effectively combining the advantages of SGD and Adam. Lookahead [10] enhances training stability by introducing a two-level update scheme. Optimization algorithms such as Yogi [11], QHAdam [12], and AdaMod [13] incorporate perturbation terms and history-sensitive adjustment strategies to alleviate training oscillations. For task-specific performance enhancements, Bu et al. proposed an automatic gradient clipping method [14] that alleviates gradient explosion and reduces the need for manual hyperparameter tuning. Meanwhile, CG-Adam and AdamW_AGC, proposed by Sun et al. [15,16], have demonstrated strong performance in medical image analysis. Furthermore, optimization algorithms like Adan [17], ELRA [18], and AMSGrad [19] focus on improving momentum estimation and convergence guarantees, while AdaBelief [20] adjusts the step size based on the confidence in observed gradients. Lion [21], a recent optimization algorithm, has also achieved notable progress in large model compression. Although these methods have enhanced robustness and generalization, most of them remain rooted in statistical optimization frameworks and lack the integration of neuromorphic mechanisms.
In recent years, some studies have begun drawing inspiration from neuromorphic hardware, incorporating biologically inspired plasticity mechanisms—such as spike-timing-dependent plasticity (STDP)—and memristor dynamics into the training and optimization of neural networks [22]. As a synapse-like device with nonlinear modulation capability and history dependence, the memristor exhibits conductance changes not only based on the current input but also influenced by the direction, magnitude, and duration of past signals, endowing it with inherent direction-aware and memory-retentive properties [23,24]. In simulating synaptic dynamics, memristor-based systems offer advantages such as low power consumption and high integration density at the hardware level, while also inspiring dynamic adjustment strategies for optimization algorithms [25,26]. For instance, the PRIME framework [27] constructs input-driven SNN architectures using stochastic memristor topologies and incorporates runtime learning to enhance energy efficiency and robustness. Other research combines CMOS with memristor-based hybrid accelerator architectures, showcasing the potential for hardware-algorithm co-optimization and highlighting the value of memristor nonlinearity in designing adaptive training strategies [28]. Despite these advances, most existing approaches still focus on hardware-level neuromorphic design or synaptic weight modulation. Few studies have systematically integrated memristor behavioral models into mainstream optimization frameworks—particularly not into core parameter update mechanisms such as those in AdamW.
To address the limitations of traditional optimization algorithms in training spiking neural networks with event-driven data, this paper proposes a novel algorithm—MemristiveAdamW—which integrates memristor-inspired mechanisms into the AdamW framework. Existing adaptive algorithms, such as AdaMod [13], AdaBelief [20], and Adan [17], mainly refine update magnitudes through moment- or variance-based corrections to capture historical sensitivity. Specifically, AdaMod introduces a long-term memory of learning rates by bounding the step size with an exponential moving average to prevent overly aggressive updates; AdaBelief modifies the variance estimate by measuring the deviation of the gradient from its exponential moving average, thereby improving adaptability to local geometry; and Adan incorporates a gradient-difference term (Δg) into its momentum prediction, using it as an additional signal to refine update direction and accelerate convergence in large-scale models.
By contrast, MemristiveAdamW departs from this moment-centric paradigm. Instead of simply adding Δg into the momentum update as in Adan, it introduces a direction-aware modulation factor that explicitly evaluates the consistency of consecutive gradients and selectively suppresses or amplifies parameter updates based on their alignment. This mechanism is further coupled with a memristor-inspired perturbation model that embeds a nonlinear, state-dependent memory effect analogous to physical memristors, and a progressive decay strategy to gradually weaken the memristor effect during training. As a result, MemristiveAdamW not only enhances historical sensitivity but also models the dynamics of gradient transitions through a state-dependent modulation process, which is fundamentally different from prior adaptive algorithms.
The main contributions of this work are as follows:
We propose MemristiveAdamW, an optimization algorithm that integrates memristor-inspired behavioral modeling with gradient-based optimization. This method enables the effective training of SNNs on event-driven data through biologically motivated mechanisms.
We introduce direction-aware modulation, a memory decay mechanism, and gradient fluctuation modeling, which together allow the optimization algorithm to dynamically adapt to the non-stationary training dynamics commonly observed in SNNs.
We design a learning rate scaling strategy based on training steps and gradient state, which enhances exploration in the early stages of training and improves convergence stability in the later stages.
2. Method
This section provides a detailed description of the AdamW algorithm and our proposed improvements leading to the MemristiveAdamW optimization algorithm. In addition, Algorithm 1 presents the pseudocode implementation of the MemristiveAdamW algorithm.
| Algorithm 1: MemristiveAdamW |
| Input: Model parameters , gradients , learning rate , Adam coefficients , , Epsilon , weight decay , memristor hyperparameters , , . 1: Initialize , , , 2: For each iteration 3: 4: 5: 6: 7: 8: 9: Clamp to 10: 11: Clamp to 12: Clamp to 13: 14: 15: end for Output: Optimized parameters . |
The following Table 1 summarizes the key symbols used in the methodology of the proposed MemristiveAdamW optimization algorithm.

Table 1.
Symbol Definition Table.
2.1. AdamW
AdamW can be regarded as a refined regularization variant of the Adam algorithm, preserving its adaptive learning capabilities while significantly improving model generalization.
The Adam optimization algorithm [6] is an adaptive learning rate algorithm designed for optimizing stochastic objective functions. It integrates the advantages of Adagrad [29] and RMSProp [30], enabling per-parameter learning rate adjustment while leveraging both the first-order (mean) and second-order (variance) moment estimates of the gradients to dynamically control update magnitudes. Specifically, Adam simultaneously considers the moving average of the gradients (first moment) and the squared gradients (second moment), applying exponential moving averages to estimate both, thereby achieving dual regulation of direction and scale during parameter updates.
Compared with standard stochastic gradient descent (SGD) [31], Adam’s first-moment estimation is equivalent to a momentum mechanism, which accelerates convergence by accumulating past gradients and smooths the update trajectory. By assigning higher weights to more recent gradients, the momentum term allows updates to better align with the current optimization direction.
In addition, Adam introduces a second-moment–based adaptive learning rate mechanism to address the issue of varying gradient magnitudes across different parameter dimensions. When the gradient of a particular parameter remains small, suggesting a relatively flat loss landscape in that direction, the algorithm increases the corresponding learning rate to amplify updates. Conversely, when gradients become large, the accumulated squared gradients increase accordingly, and the second-moment estimate in the denominator reduces the effective learning rate, preventing excessively aggressive updates that may lead to oscillations or divergence. Such mechanisms have proven effective in enhancing training stability and efficiency in complex optimization tasks [32].
First, Adam estimates the first-order and second-order moments of the gradients:
In Equations (1) and (2), t is a positive integer representing the current time step. and denote the first-order and second-order moment estimates, respectively. and are the decay rates for the first and second moments. represents the gradient of the loss function with respect to the parameters at the t-th iteration.
Next, to mitigate the bias introduced in the early stages, Adam applies bias correction to both the first- and second-moment estimates:
Finally, the bias-corrected first- and second-moment estimates obtained from Equations (3) and (4) are used in the parameter update step of the Adam algorithm:
In the Adam parameter update Equation (5), denotes the model parameters at the t-th iteration, is the learning rate, and is a small non-zero constant used for numerical stability.
However, standard Adam suffers from a coupling issue in its handling of weight decay, where the decay term is incorrectly applied to the gradient update, potentially degrading the model’s generalization performance. To address this limitation, Loshchilov and Hutter proposed the AdamW algorithm [7], which decouples weight decay from the gradient-based update process, thereby improving the regularization effect. In this way, AdamW retains the adaptive learning rate and fast convergence properties of Adam, while applying weight decay in a more principled manner, ultimately enhancing the model’s generalization ability.
The AdamW algorithm retains the same formulations as Adam in Equations (1)–(4), while modifying the parameter update step from Equation (5) to the following new form shown in Equation (6):
The decoupled weight decay in the AdamW algorithm enhances regularization and, combined with momentum-based estimation, enables adaptive step sizes that accelerate convergence. AdamW has demonstrated strong stability and robustness across various deep learning tasks. However, it implicitly assumes relatively smooth gradient dynamics. In event-driven or SNNs, gradient signals are often sparse, noisy, and subject to abrupt changes. Under such conditions, fixed learning rate scheduling strategies struggle to adapt to the highly dynamic gradient trends, potentially leading to unstable training or slow convergence, and ultimately affecting both training efficiency and final model accuracy.
To address these challenges, we propose MemristiveAdamW, an algorithm that incorporates memristor-inspired mechanisms by introducing history-dependent and direction-aware adaptive modulation strategies, thereby improving training stability and performance in highly dynamic learning environments.
2.2. MemristiveAdamW
2.2.1. Design Motivation and Mechanism
The MemristiveAdamW optimization algorithm proposed in this study is a novel variant built upon the classical AdamW framework, enhanced by incorporating a memristor-inspired dynamic adjustment mechanism. Its design is motivated by the physical characteristics of memristors in neuromorphic hardware: memristors exhibit the ability to nonlinearly modulate their conductance based on the accumulation of historical current or voltage inputs. This behavior resembles biological synapses, demonstrating properties such as short-term memory and adaptive response. Inspired by these features, we augment the momentum estimation and bias correction process of AdamW with a dynamic modulation strategy that is direction-aware, history-sensitive, and perturbation-driven. The goal is to enhance the algorithm’s responsiveness to gradient variations, improving exploration in the early stages of training and stability during later convergence.
Direction-Aware Modulation Mechanism: This mechanism models the directional and magnitude differences between consecutive gradients to determine whether the training process is undergoing gradient ascent, oscillation, or convergence. Based on this analysis, it dynamically adjusts the scaling of parameter updates—increasing the learning rate when gradients exhibit consistent directions, and suppressing aggressive updates in the presence of oscillations. This strategy mimics biological synapses’ behavior, specifically long-term potentiation (LTP) in response to consistent stimulation and long-term depression (LTD) in reaction to noisy or interfering signals. It enhances the algorithm’s ability to respond adaptively to non-stationary loss landscapes.
Memristor Effect Modeling: Memristors are non-volatile electronic devices whose resistance (or conductance) evolves according to the history of applied electrical stimuli rather than the instantaneous input alone. In other words, its internal state is history-dependent: the conductance change is determined jointly by the polarity, magnitude, and duration of past current or voltage excitations [33,34]. This property distinguishes memristors from conventional passive components such as resistors and capacitors, since memristors effectively encode a memory of prior inputs in their physical state. Inspired by this principle, we incorporate a memristor-inspired perturbation factor into our algorithm. Concretely, MemristiveAdamW models history sensitivity by combining two signals: (i) the current first-order momentum (representing long-term accumulated gradient information), and (ii) the gradient difference between consecutive steps (capturing short-term, direction-sensitive variations). Their nonlinear interaction mimics the way memristor conductance responds differently depending on whether successive stimuli reinforce or counteract each other. This perturbation factor then modulates the effective step size during parameter updates, providing an adaptive mechanism that couples cumulative memory with sensitivity to gradient changes. Unlike existing adaptive optimization algorithm such as AdamW [7], which focus on statistical adaptation of gradient magnitudes, our approach explicitly encodes history-dependent dynamics inspired by memristive systems.
Dynamic Learning Rate Scaling: Building upon the mechanisms described above, MemristiveAdamW introduces a unified dynamic scaling factor that integrates both the training step and the current gradient state.
MemristiveAdamW retains the adaptive momentum estimation and weight decay strategy of the original AdamW algorithm, while further incorporating biologically inspired modulation components. These enhancements enable the algorithm to adaptively recognize dynamic patterns during training and adjust its update behavior accordingly. As a result, the overall optimization process becomes more aligned with the dynamic adjustment needs of neural networks operating on non-stationary loss surfaces. This makes MemristiveAdamW particularly suitable for non-traditional architectures such as SNNs, which are characterized by sparse and highly volatile gradients.
2.2.2. Gradient Variation Modeling and Direction-Aware Adjustment
The change between the current gradient and the previous gradient is computed to capture the trend of gradient evolution.
This difference reflects the trend in both the direction and magnitude of gradient changes. Based on the sign of the gradient variation, we construct a direction-aware modulation factor using the Sigmoid and Tanh functions, respectively:
Here, denotes the Sigmoid function, and denotes the hyperbolic tangent function. When the gradient variation exhibits a positive jump, the Tanh function is triggered to enhance the suppression mechanism, stabilizing the training process. Conversely, when a negative jump in the gradient occurs, the Sigmoid function is activated to enhance acceleration, thereby promoting faster convergence. These responses are combined to form the direction-aware adjustment factor . To ensure numerical stability, . is constrained within a bounded range, specifically , to prevent the learning rate from being excessively amplified or diminished, which could otherwise lead to divergence or stagnation during training.
Figure 1 illustrates the direction-aware modulation curve of the proposed MemristiveAdamW. The x-axis denotes the mean gradient difference (Δg), reflecting the consistency between current and historical gradients, while the y-axis represents the adjustment factor applied to the learning rate. When Δg < 0 (left side), the gradients are directionally consistent and the factor exceeds 1 (red region), thereby enlarging the step size and encouraging faster convergence. Conversely, when Δg > 0 (right side), the gradients are inconsistent and the factor drops below 1 (blue region), suppressing updates to mitigate oscillations. The baseline factor of 1.0 (gray dashed line) corresponds to the standard AdamW update without modulation, while the adjustment factor is constrained within [0.8, 2.0] to ensure numerical stability.
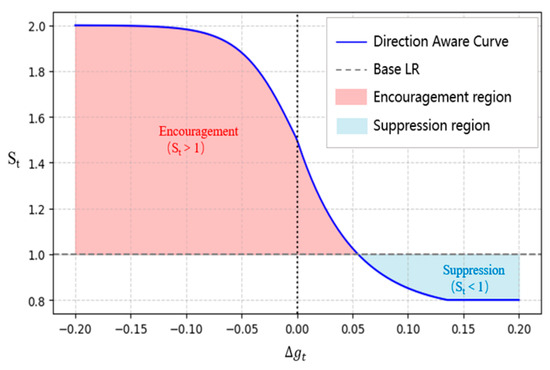
Figure 1.
Direction aware Curve.
2.2.3. Memristor Effect Modeling and Memory Decay Mechanism
In physical memristors, especially volatile types, the conductance tends to gradually decay once the external stimulus is removed, which can often be approximated by exponential or power-law attenuation [35,36]. This biologically inspired behavior motivates the design of a memory decay mechanism, which dynamically attenuates the strength of perturbations to improve optimization stability in the later stages of training. Let denote the initial memristor factor; at training step , the adaptively adjusted coefficient is computed as:
As shown in Figure 2, This curve mimics the natural forgetting process of memristors, this adaptive decay mechanism, based on training progress and iteration count, resembles the natural decline of synaptic plasticity in biological neurons. As training progresses, the influence of the memristive perturbation factor is progressively reduced, forming a biologically inspired memory decay process. This facilitates a smooth transition of the optimization behavior—from exploration in the early stages to convergence in the later stages.
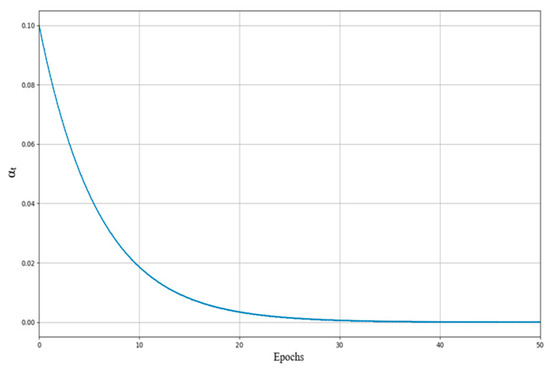
Figure 2.
Memory Decay Curve.
In this study, we introduce a perturbation modeling mechanism inspired by memristor behavior to dynamically adjust the learning rate, thereby enhancing the algorithm’s sensitivity and adaptability to gradient variations. This mechanism takes into account two key signals: the magnitude of the historical gradient momentum and the intensity of the current gradient fluctuation. The specific definition of the memristive perturbation term is given as follows:
Figure 3 depicts the memristive perturbation surface defined in Equation (10), where the effect factor EtE_tEt is determined jointly by two components: the historical momentum term , which represents the long-term accumulation of past updates, and the instantaneous fluctuation term , which captures the short-term intensity of the current gradient variation. Their interaction produces a nonlinear surface that modulates the perturbation strength according to both accumulated state and instantaneous input.
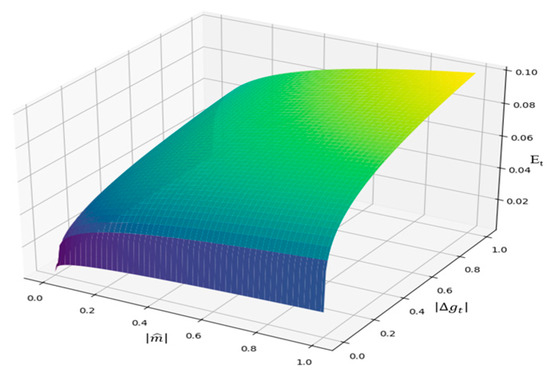
Figure 3.
Memristor Effect Surface.
This construction is directly motivated by the physical behavior of volatile memristors, in which conductance changes depend not only on the present stimulus but also on the device’s internal state shaped by prior excitations. In particular, the coupling of long-term memory and short-term input intensity has been widely reported in oxide-based memristors and artificial synapses, where the cumulative history governs baseline conductance while transient input strength determines the degree of additional modulation [37,38]. By abstracting this dual dependency into the optimization process, the memristor effect surface provides a biologically and physically inspired mechanism that balances exploration and convergence during training.
To prevent the perturbation term from excessively amplifying or diminishing the learning rate, the value of the memristive perturbation factor is constrained within the range . This restriction helps ensure numerical stability during training by avoiding overly strong perturbations that may cause model divergence, as well as overly weak perturbations that could lead to training stagnation.
2.2.4. Dynamic Learning Rate Update Mechanism
Based on the direction-aware factor and the perturbation factor , we define the dynamic learning rate adjustment formula as follows:
Here, denotes the initial learning rate, and the direction-aware factor is introduced to further fine-tune the learning rate based on the direction of gradient variation. represents the average response strength of the perturbation term across the current batch. This dynamic adjustment mechanism integrates the nonlinear response characteristics of memristors with gradient direction sensitivity, enabling real-time adaptation of the learning rate to the training state. In the early training phase, this mechanism significantly improves convergence speed, while in the later stages, it automatically reduces the step size to enhance convergence stability. The approach is particularly well-suited for neuromorphic networks characterized by highly volatile and sparse gradients.
Dynamic learning rate adjustment may pose numerical risks: if the modulation is too strong, the learning rate could be excessively amplified, leading to instability or divergence; if too weak, it may cause the update magnitude to stagnate. To address this, we impose upper and lower bounds, constraining the final learning rate within a safe and reasonable range of .
2.2.5. Parameter Update and Decoupled Weight Decay
In the parameter update stage, MemristiveAdamW adopts the same decoupled regularization strategy as AdamW, applying weight decay directly to the parameters:
Here, denotes the weight decay coefficient, and is the dynamically adjusted learning rate. By adopting the AdamW-style decoupled weight decay strategy, regularization is directly applied to the parameters, which helps control model complexity and improve generalization performance.
Compared to traditional optimization methods, this update scheme adaptively adjusts the step size based on both the historical parameter behavior and the current training dynamics. The direction-aware adjustment term prevents excessive updates during periods of gradient oscillation, while the memristive perturbation term promotes exploration in the early training phase and enhances stability in the later stages.
2.2.6. Summary
In summary, MemristiveAdamW builds upon the convergence and regularization advantages of AdamW by introducing memristor-inspired multi-dimensional modulation mechanisms. These enhancements not only improve the optimization algorithm’s robustness under highly volatile gradient conditions but also strengthen its adaptability to complex loss landscapes. The complete optimization process—covering gradient modeling, direction-aware adjustment, perturbation computation, dynamic step size modulation, and parameter update—is outlined in Algorithm 1.
3. Experiments
The MemristiveAdamW algorithm is an extension and improvement of the AdamW algorithm, incorporating an adaptive perturbation factor, a direction-aware modulation mechanism, and a dynamic learning rate adjustment strategy. These enhancements make the algorithm more flexible and comprehensive, improving its generalization capability and accelerating model convergence.
To evaluate the advantages of MemristiveAdamW over AdamW, we conduct comparative experiments on two datasets—Prophesee NCARS and Prophesee GEN1—using three network architectures: Spiking VGG-11, Spiking MobileNet-64, and Spiking DenseNet-121.
3.1. Dataset Description
3.1.1. Prophesee NCARS
NCARS is a binary classification dataset released by Prophesee, designed for evaluating event-based vision algorithms in autonomous driving scenarios. It is collected using a Dynamic Vision Sensor (DVS) mounted behind the windshield of a moving vehicle. Each sample in the dataset is a short-duration stream of events captured within a temporal window of approximately 100 milliseconds. The dataset contains a total of 24,029 samples, evenly split into 12,019 positive samples (containing cars) and 12,010 negative samples (no car present). Each event is represented as a 4-tuple: (x, y, polarity, timestamp), where (x, y) are pixel coordinates, polarity indicates the direction of brightness change (ON or OFF event), and timestamp records the time of the event with microsecond-level resolution.
For our experiments, we use the official split of the dataset, with 80% of the samples for training and 20% for testing, i.e., 19,223 training samples and 4806 test samples. This dataset provides a clean and balanced benchmark for evaluating binary classification performance in event-based scenarios.
3.1.2. Prophesee GEN1
GEN1 is the first large-scale event-driven object detection dataset released by Prophesee, collected in real-world traffic scenarios. It is designed to evaluate the performance of event-based object detection algorithms. The dataset is captured using high-resolution dynamic vision sensors, offering microsecond-level temporal precision. Each frame is annotated with bounding boxes, class labels, and scene metadata. GEN1 includes various traffic targets (e.g., cars, pedestrians, two-wheelers) under diverse lighting and weather conditions (e.g., daytime, nighttime, rain, backlight), reflecting high scene complexity and realism.
Due to the large size of the original GEN1 dataset (over 200 GB), using the entire dataset for training and evaluation would impose a significant computational burden. To ensure reasonable training time and experimental reproducibility under limited computational resources, we adopt a stratified random sampling strategy, using one-third of the original dataset to construct the training and test sets. This strategy preserves the relative class distribution and scene diversity of the full dataset, thereby maintaining representativeness while improving efficiency.
3.1.3. Dataset Selection Rationale
We selected NCARS and GEN1 as representative datasets for event-based vision because both offer microsecond-level temporal resolution, high spatial sparsity, and broad scene diversity, making them well-suited for evaluating the temporal dynamics and computational efficiency of SNNs.
To examine the generalization capability of our algorithm, we deploy three representative SNN backbones with varying architectural depth and computational complexity: Spiking VGG-11, Spiking MobileNet-64, and Spiking DenseNet-121. These models are trained on both datasets to comprehensively evaluate the effectiveness of the proposed MemristiveAdamW algorithm.
3.1.4. Experimental Platform and Configuration
In this study, all models were trained and evaluated using the widely adopted deep learning framework PyTorch 2.4.1, with all experimental code written in Python 3.12. The development process was conducted within PyCharm 2024.2.4 to enhance programming efficiency. All experiments were performed on an NVIDIA RTX 4060 Ti GPU (NVIDIA Corporation, Santa Clara, CA, USA) with 16 GB of memory. The training time and convergence speed for each model are reported in Section 3.4.
During model training, all experiments were conducted under identical hyperparameter settings (learning rate, weight decay, number of epochs, etc.) to ensure a fair comparison between the proposed MemristiveAdamW and the baseline AdamW algorithm. After each training epoch, the system automatically saved the current model weights and evaluated performance on the validation set. If the current evaluation result outperformed the previous best, the model state was updated accordingly, ensuring that the final evaluation was based on the best-performing model.
Two types of metrics were used for performance evaluation: For classification tasks, accuracy and training loss were the primary evaluation criteria. Accuracy reflects the model’s ability to correctly classify samples in the test set, while training loss indicates the convergence and stability of the optimization process. For detection tasks, we adopted mAP@0.5 (mean Average Precision at an IoU threshold of 0.5) as the key metric, which jointly evaluates both precision and recall performance.
3.1.5. Experimental Settings
Application Domain: This study uses two publicly available event-based datasets: Prophesee NCARS and Prophesee GEN1, both of which can be accessed from the official Prophesee website.
Optimization Algorithms: The objective of the experiments is to compare the performance of the standard AdamW algorithm with the proposed MemristiveAdamW algorithm. Therefore, we evaluate and contrast these two algorithms throughout all experiments.
Neural Network Models: To validate the effectiveness of the proposed MemristiveAdamW algorithm, experiments were conducted on three representative SNN architectures: Spiking VGG-11, Spiking MobileNet-64, and Spiking DenseNet-121. These models differ in architectural depth and computational complexity, allowing a comprehensive comparison of the convergence behavior and final accuracy between MemristiveAdamW and the baseline AdamW.
Learning Rate: For the NCARS dataset, the initial learning rate was set to 0.0005 across all three network architectures. For the GEN1 dataset, the initial learning rate was set to 0.001 for all networks.
Epochs: The number of training epochs was uniformly set to 50 across all experiments to ensure consistency in training duration across different algorithms and models.
Weight Decay: The weight decay coefficient was set to 0.0001 for all experiments.
Experimental Results: For each model-dataset combination, training was conducted independently five times with different random seeds. Comparative analysis of the averaged results highlights the differences in convergence performance and final accuracy between the proposed MemristiveAdamW and the standard AdamW algorithm.
3.2. Experimental Results and Analysis on NCARS
To comprehensively evaluate the performance of the proposed MemristiveAdamW algorithm, we conducted comparative experiments on the NCARS dataset using several representative SNN architectures, including Spiking VGG-11, Spiking MobileNet-64, and Spiking DenseNet-121.
Figure 4 and Figure 5 illustrate the loss curves and classification accuracy curves during training for both optimization algorithms across different network architectures. Table 2 lists the highest classification accuracy achieved by the three networks on the NCARS dataset using MemristiveAdamW and the baseline AdamW.
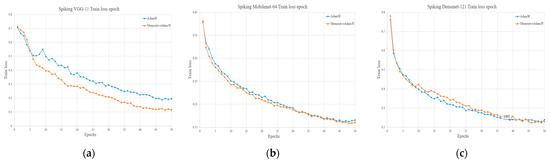
Figure 4.
Loss curves on the NCARS dataset using Spiking VGG-11 (a), Spiking MobileNet-64 (b), and Spiking DenseNet-121 (c).
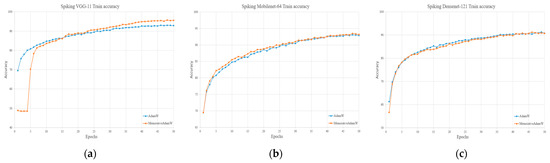
Figure 5.
Training accuracy on the NCARS dataset using Spiking VGG-11 (a), Spiking MobileNet-64 (b), and Spiking DenseNet-121 (c).

Table 2.
Highest classification accuracy of the three networks on the NCARS dataset.
The experimental results show that MemristiveAdamW outperforms the baseline AdamW algorithm in most network configurations. In the case of the Spiking VGG-11 model, MemristiveAdamW demonstrates significant improvements over AdamW: the training loss is reduced from 0.187 to 0.115, and the classification accuracy increases from 92.68% to 95.72%. Both the convergence speed and final performance exhibit clear advantages. This performance gain is mainly attributed to the direction-aware gradient modulation mechanism introduced in MemristiveAdamW, which dynamically adjusts the learning rate direction by analyzing the trend of consecutive gradients. Combined with memristor-inspired perturbation modeling, the algorithm enhances exploration during early training, leading to faster convergence and more stable updates. In the Spiking MobileNet-64 model, MemristiveAdamW also achieves modest improvements, reducing training loss from 0.181 to 0.170, and improving accuracy from 93.05% to 93.49%. This suggests that the algorithm remains robust even in lightweight models, potentially due to the fewer residual connections in Spiking MobileNet-64, which help maintain controlled gradient flow—enabling both the direction-aware and perturbation mechanisms to function effectively. However, in the Spiking DenseNet-121 model, the performance of the two algorithms is nearly identical. The training loss remains at 0.224 for both, and the accuracy slightly decreases from 91.27% (AdamW) to 91.23% (MemristiveAdamW). This suggests that the benefits of MemristiveAdamW may diminish in more complex network architectures such as DenseNet-121. DenseNet aggregates features through extensive shortcut connections, which inherently stabilize gradient propagation and mitigate vanishing gradients. While this property is generally beneficial, it also leads to a high degree of gradient redundancy. When MemristiveAdamW is applied in this context, the added modulation may no longer provide complementary regularization. Instead, it can amplify minor gradient inconsistencies across the densely connected layers, resulting in oscillatory or less stable convergence.
Figure 6 presents the test accuracy curves across 50 training epochs. The results indicate that MemristiveAdamW produces more stable accuracy trends compared to AdamW across all network structures.
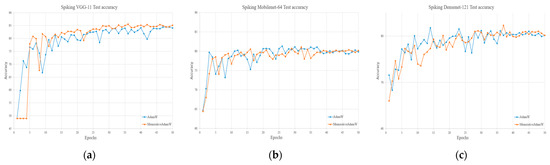
Figure 6.
Test accuracy on the NCARS dataset using Spiking VGG-11 (a), Spiking MobileNet-64 (b), and Spiking DenseNet-121 (c).
In summary, our algorithm achieves the highest accuracy values on both Spiking VGG-11 and Spiking MobileNet-64 architectures. Compared to AdamW, the proposed MemristiveAdamW algorithm demonstrates notable improvements in both convergence and final accuracy.
3.3. Experimental Results and Analysis on GEN1
On the GEN1 dataset, we conducted a comparative evaluation of the proposed MemristiveAdamW algorithm against the conventional AdamW algorithm across multiple spiking neural network architectures, including Spiking VGG-11, Spiking MobileNet-64, and Spiking DenseNet-121. The experiments employed training loss and mAP@0.5 (mean Average Precision at an IoU threshold of 0.5) as the primary performance evaluation metrics.
Table 3 lists the experimental results on the GEN1 dataset. In the experiments conducted on the GEN1 dataset, MemristiveAdamW also demonstrated strong adaptability and robustness. Figure 7 and Figure 8 present the loss curves and mAP@0.5 curves during training across different network architectures for both optimization algorithms. In the Spiking VGG-11 model, the AdamW algorithm achieved a minimum training loss of 1.11 and a best mAP@0.5 of 0.564. In contrast, MemristiveAdamW significantly reduced the training loss to 0.625, while also achieving a higher detection accuracy, with mAP@0.5 improved to 0.640. These results indicate that MemristiveAdamW substantially enhanced convergence and object detection performance for this architecture. The performance gain can be attributed to the algorithm’s effective response to gradient fluctuations through its memristor-inspired perturbation mechanism. This dynamic adjustment mechanism is particularly effective under the highly sparse and volatile gradients commonly encountered in event-driven data, accelerating convergence in such conditions. For the Spiking MobileNet-64 model, the minimum training losses achieved by AdamW and MemristiveAdamW were 1.55 and 1.54, respectively—showing only a slight difference. However, MemristiveAdamW still provided better detection performance, improving mAP@0.5 from 0.280 to 0.297, suggesting that the proposed method offers performance advantages even in lightweight architectures. In the Spiking DenseNet-121 model, both algorithms achieved the same minimum training loss of 0.838, but MemristiveAdamW significantly outperformed AdamW in detection accuracy, with mAP@0.5 reaching 0.536, compared to 0.412 with AdamW. This result demonstrates that MemristiveAdamW can effectively enhance generalization and detection performance in deep network structures. In more complex and realistic event-based detection tasks, the synergy between the perturbation mechanism and the direction-aware adjustment contributes to overcoming the limitations of standard AdamW, particularly in handling intricate target recognition scenarios.

Table 3.
Best mAP@0.5 achieved by the three networks on the GEN1 dataset.
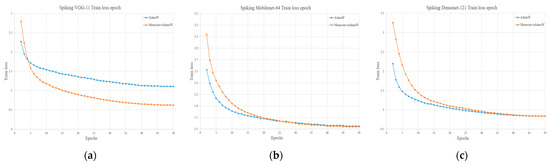
Figure 7.
Loss curves on the GEN1 dataset using Spiking VGG-11 (a), Spiking MobileNet-64 (b), and Spiking DenseNet-121 (c).
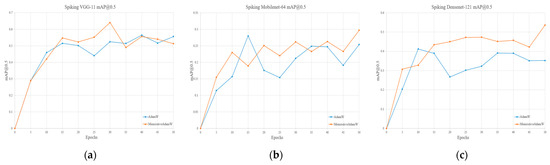
Figure 8.
mAP@0.5 on the GEN1 dataset using Spiking VGG-11 (a), Spiking MobileNet-64 (b), and Spiking DenseNet-121 (c).
In summary, MemristiveAdamW achieves better training convergence and higher detection accuracy on the GEN1 dataset, validating its practicality and robustness for event-driven object detection tasks.
3.4. Analysis of Training Efficiency and Convergence Speed
In this section, we analyze the MemristiveAdamW algorithm from the perspective of computational efficiency. Training time is defined as the amount of time required to reach a specified threshold in either accuracy or loss. Different datasets and network architectures use different thresholds. Specifically, for the NCARS dataset, Spiking VGG-11 uses an accuracy threshold of 92.5%, Spiking MobileNet-64 uses 92%, Spiking DenseNet-121 uses 91%. For the Prophesee GEN1 dataset, since mAP@0.5 is evaluated every 5 epochs and tends to fluctuate significantly, we instead adopt training loss thresholds, the training loss threshold used by Spiking VGG-11 is 1.11, that used by Spiking MobileNet-64 is 1.55, and that used by Spiking DenseNet-121 is 0.838.
The selected thresholds are not unique; they are chosen to ensure that both algorithms—AdamW and MemristiveAdamW—can reasonably reach them. The results for training time comparisons are summarized in the accompanying Table 4.

Table 4.
Training time across different experimental configurations.
All training times in the table are recorded in seconds. On the NCARS dataset, using accuracy thresholds as the evaluation criterion:
For Spiking VGG-11, the MemristiveAdamW algorithm reached the threshold in 4355 s, whereas AdamW required 5979 s, representing a 27.2% reduction in training time.
For Spiking MobileNet-64, MemristiveAdamW reached the threshold in 3519 s, compared to 4025 s for AdamW, achieving a 12.6% speed-up.
For Spiking DenseNet-121, MemristiveAdamW completed training in 7999 s, slightly faster than AdamW’s 8283 s, yielding a 3.4% improvement.
These results demonstrate that the dynamic adjustment mechanisms in MemristiveAdamW can significantly accelerate convergence, particularly in shallower networks or models with relatively stable gradient behavior, where the advantages of adaptive modulation are more pronounced.
On the Prophesee GEN1 dataset, using training loss thresholds as the evaluation criterion:
For Spiking VGG-11, the AdamW algorithm required 38,914 s to reach the threshold, whereas MemristiveAdamW achieved it in only 10,368 s, resulting in a 73.4% speed-up. This demonstrates the strong training efficiency and acceleration capability of MemristiveAdamW, primarily due to the memristor-inspired perturbation mechanism, which effectively activates adaptive regulation in response to sharp gradient changes—dramatically improving early-stage convergence.
For Spiking MobileNet-64, MemristiveAdamW required 12,264 s, slightly outperforming AdamW’s 12,554 s, with a 2.3% improvement, indicating modest gains in lightweight architectures.
For Spiking DenseNet-121, however, MemristiveAdamW took 30,510 s to reach the loss threshold, slightly longer than AdamW, which took 28,094 s. This suggests that in more complex networks, where dense connectivity already stabilizes gradient propagation, the additional perturbation mechanism may introduce redundant fluctuations, leading to reduced efficiency and slower convergence.
In summary, MemristiveAdamW demonstrates faster convergence and improved training efficiency across most models and datasets, with particularly significant advantages observed in Spiking VGG-11. These improvements are primarily attributed to the algorithm’s rapid responsiveness to training dynamics and its multi-stage adaptive learning rate strategy. However, in more complex architectures with higher parameter complexity, performance fluctuations suggest that further research is needed to develop structure-sensitive perturbation modulation mechanisms, in order to enhance the algorithm’s generalization ability and stability in more complex settings.
4. Conclusions
This paper proposed MemristiveAdamW, a novel optimization algorithm that extends AdamW with memristor-inspired mechanisms, including direction-aware gradient modulation, perturbation modeling, and progressive learning rate refinement. These enhancements enable dynamic adaptation to sparse and non-stationary gradients, improving convergence stability and training robustness in spiking neural networks.
Experiments on NCARS and GEN1 datasets with Spiking VGG-11, MobileNet-64, and DenseNet-121 show that MemristiveAdamW generally outperforms AdamW, particularly on lightweight architectures, where it achieves higher accuracy, faster convergence, and lower training loss. For more complex models such as DenseNet-121, the performance was comparable to AdamW, likely due to the stabilizing effect of dense shortcut connections on gradient flow. This suggests that the perturbation mechanism may require architecture-aware adaptation to fully realize its benefits in highly connected networks.
Overall, MemristiveAdamW provides an effective optimization paradigm for event-driven learning and offers a promising direction for scaling to more complex neuromorphic models and large-scale event-based tasks.
Author Contributions
Conceptualization, J.Z. and F.J.; methodology, J.Z.; software, F.J.; validation, F.J., Z.M. and Z.G.; formal analysis, Z.M.; investigation, Z.G.; resources, F.J.; data curation, F.J.; writing—original draft preparation, F.J.; writing—review and editing, J.Z.; visualization, F.J.; supervision, J.Z.; project administration, J.Z.; funding acquisition, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Natural science Foundation of Zhejiang province of China, grant number LY23F040003.
Data Availability Statement
The data used in this study are openly available in the Prophesee repository. Prophesee GEN1: https://www.prophesee.ai/2020/01/24/prophesee-gen1-automotive-detection-dataset/ accessed on 27 September 2025; Prophesee NCARS: https://www.prophesee.ai/2018/03/13/dataset-n-cars accessed on 27 September 2025.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gallego, G.; Delbrück, T.; Orchard, G.; Bartolozzi, C.; Taba, B.; Censi, A.; Leutenegger, S.; Davison, A.J.; Conradt, J.; Scaramuzza, D.; et al. Event-based vision: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 154–180. [Google Scholar] [CrossRef] [PubMed]
- Lichtsteiner, P.; Posch, C.; Delbruck, T. A 128 × 128 120 dB 15 μs latency asynchronous temporal contrast vision sensor. IEEE J. Solid-State Circuits 2008, 43, 566–576. [Google Scholar] [CrossRef]
- Krishnan, K.S.; Krishnan, K.S. Benchmarking Conventional Vision Models on Neuromorphic Fall Detection and Action Recognition Dataset. arXiv 2022, arXiv:2201.12285. [Google Scholar] [CrossRef]
- Neftci, E.O.; Mostafa, H.; Zenke, F. Surrogate gradient learning in spiking neural networks: Bringing the power of gradient-based optimization to spiking neural networks. IEEE Signal Process. Mag. 2019, 36, 51–63. [Google Scholar] [CrossRef]
- Zenke, F.; Ganguli, S. Superspike: Supervised learning in multilayer spiking neural networks. Neural Comput. 2018, 30, 1514–1541. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Liu, L.; Jiang, H.; He, P.; Chen, W.; Liu, X.; Gao, J.; Han, J. On the variance of the adaptive learning rate and beyond. arXiv 2019, arXiv:1908.03265. [Google Scholar]
- Luo, L.; Xiong, Y.; Liu, Y.; Sun, X. Adaptive gradient methods with dynamic bound of learning rate. arXiv 2019, arXiv:1902.09843. [Google Scholar] [CrossRef]
- Zhang, M.; Lucas, J.; Ba, J.; Hinton, G.E. Lookahead optimizer: K steps forward, 1 step back. Adv. Neural Inf. Process. Syst. 2019, 32, 1–12. [Google Scholar]
- Zaheer, M.; Reddi, S.; Sachan, D.; Kale, S.; Kumar, S. Adaptive methods for nonconvex optimization. Adv. Neural Inf. Process. Syst. 2018, 31, 1–11. [Google Scholar]
- Ma, J.; Yarats, D. Quasi-hyperbolic momentum and Adam for deep learning. arXiv 2018, arXiv:1810.06801. [Google Scholar]
- Ding, J.; Ren, X.; Luo, R.; Sun, X. An adaptive and momental bound method for stochastic learning. arXiv 2019, arXiv:1910.12249. [Google Scholar] [CrossRef]
- Bu, Z.; Wang, Y.X.; Zha, S.; Karypis, G. Automatic clipping: Differentially private deep learning made easier and stronger. Adv. Neural Inf. Process. Syst. 2023, 36, 41727–41764. [Google Scholar]
- Sun, H.; Yu, H.; Shao, Y.; Wang, J.; Xing, L.; Zhang, L.; Zhao, Q. An improved Adam’s algorithm for stomach image classification. Algorithms 2024, 17, 272. [Google Scholar] [CrossRef]
- Sun, H.; Cui, J.; Shao, Y.; Yang, J.; Xing, L.; Zhao, Q.; Zhang, L. A Gastrointestinal Image Classification Method Based on Improved Adam Algorithm. Mathematics 2024, 12, 2452. [Google Scholar] [CrossRef]
- Xie, X.; Zhou, P.; Li, H.; Lin, Z.; Yan, S. Adan: Adaptive nesterov momentum algorithm for faster optimizing deep models. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 9508–9520. [Google Scholar] [CrossRef]
- Kleinsorge, A.; Kupper, S.; Fauck, A.; Rothe, F. ELRA: Exponential learning rate adaption gradient descent optimization method. arXiv 2023, arXiv:2309.06274. [Google Scholar] [CrossRef]
- Reddi, S.J.; Kale, S.; Kumar, S. On the convergence of adam and beyond. arXiv 2019, arXiv:1904.09237. [Google Scholar] [CrossRef]
- Zhuang, J.; Tang, T.; Ding, Y.; Tatikonda, S.C.; Dvornek, N.; Papademetris, X.; Duncan, J. Adabelief optimizer: Adapting stepsizes by the belief in observed gradients. Adv. Neural Inf. Process. Syst. 2020, 33, 18795–18806. [Google Scholar]
- Chen, X.; Liang, C.; Huang, D.; Real, E.; Wang, K.; Pham, H.; Dong, X.; Luong, T.; Hsieh, C.-J.; Le, Q.V.; et al. Symbolic discovery of optimization algorithms. Adv. Neural Inf. Process. Syst. 2023, 36, 49205–49233. [Google Scholar]
- Prezioso, M.; Merrikh-Bayat, F.; Hoskins, B.D.; Adam, G.C.; Likharev, K.K.; Strukov, D.B. Training and operation of an integrated neuromorphic network based on metal-oxide memristors. Nature 2015, 521, 61–64. [Google Scholar] [CrossRef] [PubMed]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Diehl, P.U.; Cook, M. Unsupervised learning of digit recognition using spike-timing-dependent plasticity. Front. Comput. Neurosci. 2015, 9, 99. [Google Scholar] [CrossRef] [PubMed]
- Zidan, M.A.; Strachan, J.P.; Lu, W.D. The future of electronics based on memristive systems. Nat. Electron. 2018, 1, 22–29. [Google Scholar] [CrossRef]
- Xia, Q.; Yang, J.J. Memristive crossbar arrays for brain-inspired computing. Nat. Mater. 2019, 18, 309–323. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, X.; Wang, S.; Lin, N.; Li, Y.; Yu, Y.; Zhang, Y.; Yang, J.; Wu, X.; Shang, D.; et al. Topology optimization of random memristors for input-aware dynamic SNN. Sci. Adv. 2025, 11, eads5340. [Google Scholar] [CrossRef]
- Nowshin, F.; An, H.; Yi, Y. Towards energy-efficient spiking neural networks: A robust hybrid CMOS-memristive accelerator. ACM J. Emerg. Technol. Comput. Syst. 2024, 20, 1–20. [Google Scholar] [CrossRef]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Tieleman, T.; Hinton, G. Rmsprop: Divide the Gradient by a Running Average of its Recent Magnitude. Coursera: Neural Networks for Machine Learning. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; PMLR: San Diego, CA, USA, 2017. [Google Scholar]
- Bottou, L. Large-Scale Machine Learning with Stochastic Gradient Descent. In Proceedings of the COMPSTAT’2010, Paris, France, 22–27 August 2010; pp. 177–186. [Google Scholar]
- Zhang, Y.; Chen, C.; Li, Z.; Ding, T.; Wu, C.; Kingma, D.P.; Ye, Y.; Luo, Z.-Q.; Sun, R. Adam-mini: Use fewer learning rates to gain more. arXiv 2024, arXiv:2406.16793. [Google Scholar] [CrossRef]
- Chua, L. Memristor-the missing circuit element. IEEE Trans. Circuit Theory 2003, 18, 507–519. [Google Scholar] [CrossRef]
- Yang, J.J.; Strukov, D.B.; Stewart, D.R. Memristive devices for computing. Nat. Nanotechnol. 2013, 8, 13–24. [Google Scholar] [CrossRef]
- Dutta, M.; Brivio, S.; Spiga, S. Unraveling the roles of switching and relaxation times in volatile electrochemical memristors to mimic neuromorphic dynamical features. Adv. Electron. Mater. 2024, 10, 2400221. [Google Scholar] [CrossRef]
- Ali, S.; Ullah, M.A.; Raza, A.; Iqbal, M.W.; Khan, M.F.; Rasheed, M.; Ismail, M.; Kim, S. Recent advances in cerium oxide-based memristors for neuromorphic computing. Nanomaterials 2023, 13, 2443. [Google Scholar] [CrossRef] [PubMed]
- Jeong, D.S.; Kim, K.M.; Kim, S.; Choi, B.J.; Hwang, C.S. Memristors for energy—Efficient new computing paradigms. Adv. Electron. Mater. 2016, 2, 1600090. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, S.; Zhao, X.; Wu, F.; Wu, Q.; Wang, W.; Cao, R.; Fang, Y.; Lv, H.; Liu, M.; et al. Emulating short-term and long-term plasticity of bio-synapse based on Cu/a-Si/Pt memristor. IEEE Electron Device Lett. 2017, 38, 1208–1211. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).