Abstract
Due to the similar characteristics of chaotic systems and cryptography, public key encryption algorithms based on chaotic systems are worth in-depth research and have high value for the future. Chebyshev polynomials have good properties and are often used in the design of public key algorithms. This paper improves the Bose Multi-Chaotic Public Key Cryptographic Algorithm (BMPKC) by applying Chebyshev polynomials. The proposed algorithm (CMPKC-) introduces the selective coefficient based on the properties of Chebyshev polynomials, allowing the special functions that need to be negotiated in the original system to be freely and randomly chosen as Chebyshev polynomials, and can also be expanded to m levels. The improved cryptographic algorithm also utilizes chaotic hash functions and logistic mapping to generate pseudo-random sequences and overcomes shortcomings of the Bose algorithm by iteratively iterating the selected Chebyshev polynomials based on the number of 0s or 1s in the pseudo-random sequence, thus providing better security. Analysis and software testing results indicate that this algorithm has strong robustness against brute force attacks, achieving a higher attack time for breaking the private key compared to the CEPKC, BMPKC, and CMPKC algorithms. Compared to the CMPKC algorithm, our proposal algorithm achieves better performance in the encryption and decryption phases. Furthermore, we combine this Multi-Chaotic System Key Exchange Protocol with the Advanced Encryption Standard (AES) algorithm, while providing a demonstration, offering more possibilities for practical applications of this system.
1. Introduction
With the advent of cloud computing, the Internet of Things, the mobile internet, and the big data era, security threats brought by the deployment of new technologies are constantly expanding, and designing new high-performance encryption schemes has become an important problem to be urgently solved. Compared with traditional encryption systems, chaotic public key cryptography has higher security, better resistance to attacks, a longer validity period, and more application areas [1,2]. As a new direction in the field of public key cryptography research, it is still in the initial stage and has very important exploratory value.
Cryptography is a very active research field, with traditional ciphers mainly including DES, AES, RSA, and other algorithms [3]. In recent years, new ideas have stimulated many new forms of cipher systems, primarily including quantum cryptography [4], visual cryptography [5], biometric cryptography [6], DNA cryptography [7], homomorphic cryptography [8], attribute-based encryption [9], and Post-Quantum Cryptography [10,11].
Chaos theory is considered the third revolution in physics in the 20th century, following relativity and quantum mechanics. It is the seemingly random behavior generated by deterministic systems. It has extreme sensitivity to initial conditions and parameters, and long-term unpredictability, which conforms to some characteristics of cryptography, opening a new field of research in chaotic cryptography. In 1949, Shannon [12] pointed out the confusion and diffusion principles in cipher design, which correspond precisely to the pseudo-randomness and sensitivity to initial conditions of chaotic systems: the ergodicity and topological mixing of chaotic systems correspond to the confusion properties of ciphers; on the other hand, the extreme sensitivity of chaotic systems to initial conditions and control parameters corresponds to the diffusion properties of ciphers. Diffusion can create an avalanche effect, producing completely different outputs from tiny changes to the initial input. This suggests that chaos can be applied to the field of cryptography. Alvarez et al. [13] summarized some relationships between chaotic systems and cryptography. Chaotic cryptography theory emerged in the mathematics and physics fields in the early 1960s, and it is known as one of the three major scientific revolutions of the 20th century along with quantum theory and relativity. In 1989, Matthews proposed the chaotic cipher algorithm, which provided a chaotic sequence cipher scheme based on modified logistic mappings [14]. In particular, Pecora and Carroll published an article on chaotic synchronized secure communication in 1990 [15], sparking a research wave in chaotic cryptography. At the same time, analysis of chaotic cipher systems has also been carried out, proving the insecurity of some chaotic cipher systems and proposing improvement measures. In recent years, significant progress has been obtained in the research of chaotic cryptography [16,17,18,19,20,21], but there are still some challenging problems to be solved, such as the problem of finite precision digitization of chaotic systems, the security and efficiency of chaotic cipher design, etc. Therefore, compared with traditional cryptography, the development of chaotic cryptography is still not mature and perfect, lacking sufficient persuasiveness. On the other hand, compared with symmetric cryptography, the study of chaotic public key cryptography is relatively weak. Designing public key cryptographic systems based on chaotic systems is a new scientific exploration attempt, which has important research value and significance.
1.1. Trend
Currently, traditional public key encryption algorithms may have some potential issues, such as the threat of quantum computing, increasing key length requirements, and having specific algorithmic characteristics that are vulnerable to targeted attacks. Although the capability of chaotic cryptography to resist quantum computing is still under research, it offers a new approach that is different from traditional public key encryption. Chaotic encryption algorithms can provide more efficient computational performance than traditional public key algorithms, especially in resource-constrained environments such as IoT devices. Certain characteristics of chaotic systems allow for the design of lightweight encryption schemes, thereby saving computational and energy resources. Therefore, it is necessary to find new practical public key cryptographic algorithms as a supplement or replacement to current public key cryptographic algorithms. Table 1 lists the development of chaotic public key cryptography in chronological order, with people attempting to design public key cryptographic algorithms using cellular automata, chaotic iterative structures, distributed dynamical systems, multi-chaos systems, Chebyshev polynomials, torus automorphisms, etc. However, there are security flaws or low efficiency problems in all of them, which is why chaotic public key cryptography cannot match traditional public key cryptography. As a new direction in the field of public key cryptography research, chaotic public key cryptography is still in its early stages and has very important exploratory value.

Table 1.
Major research history of chaotic public key cryptography.
According to Table 1, the development of chaotic public key cryptography, especially the Chebyshev-based public key cryptography discussed in this paper, can be roughly divided into three time periods, as shown in Figure 1.

Figure 1.
Diagram of the development history of chaotic public key cryptography.
- In the embryonic stage, researchers started to explore the design of public key cryptography algorithms using different chaotic systems, such as cellular automata, distributed dynamical system models, Chebyshev chaotic mappings, chaotic synchronization systems, etc.
- In the development stage, more attention was paid to the security of chaotic public key cryptography algorithms, especially the analysis and improvement of Chebyshev-based public key cryptography algorithms, to achieve higher security and efficiency.
- In the expansion stage, chaotic public key cryptography algorithms were extended to other aspects of cryptography, such as identity-based public key encryption schemes, key exchange protocols, digital signature schemes, provable security, etc.
In the early schemes of chaotic public key cryptography, Puhua proposed a chaotic public key algorithm based on cellular automata, which was not practical due to its limitations [22]. Tenny et al. proposed a distributed dynamical model chaotic synchronization public key encryption scheme [40], but it did not adhere to the principle of “all secrets are embedded in the keys” and had potential vulnerabilities against digital attacks. Subsequently, Bose proposed a public key cryptography algorithm based on multiple chaotic systems [27], but it also suffered from security and efficiency issues. Public key cryptography based on multiple chaotic systems and Chebyshev polynomials remains of high value in chaotic public key cryptography research and is the focus of this project. Currently, Kumar et al. has further extended Chebyshev-based public key cryptography and proposed new encryption schemes [41], Islam has proposed new identity-based encryption and signature schemes [33], and Hong Lai et al. has proposed a three-party key exchange protocol based on Chebyshev polynomials and proved its security in the standard model, driving the advancement of chaotic public key cryptography theoretical research [34]. Chatterjee et al. proposed a new multi-server authentication scheme based on Chebyshev chaotic mappings, which is low in computation and communication costs and has been widely cited by scholars [42]. Attaullah et al. proposed a new cryptographic technique based on improved Chebyshev mapping and verified the effectiveness of the expected algorithm [43]. Louzzani et al. proposed a new chaotic Chebyshev polynomial-generating function and applied it to image encryption with good resistance against various attacks [44]. In recent years, chaotic public key cryptography has achieved some new research results [45,46,47,48].
1.2. Contribution
Our approach includes evaluating and discussing several modified Chebyshev public key cryptographic algorithms and understanding their performance and security compared to our proposed algorithm. Specifically, in our proposed improved chaotic multiple public key cryptographic algorithm based on Chebyshev polynomials (CMPKC-), we aim to design a multiple chaotic public key algorithm using Chebyshev polynomials. The algorithm introduces the concept of selective coefficient based on the properties of Chebyshev polynomials, allowing the original system’s special functions and that need to be negotiated to be freely chosen as Chebyshev polynomials and , where the selection of and is randomly determined by and can also be extended to m levels. The improved cryptographic algorithm also utilizes chaotic hash functions and logistic mapping to generate pseudo-random sequences and overcomes the four shortcomings of the Bose algorithm by iteratively iterating and based on the number of 0s or 1s in the pseudo-random sequence, thus providing better security. Analysis and experimental results show that the algorithm has strong robustness against common attacks, achieving a higher attack time to break private keys compared to other variants, proving the algorithm’s security against such attacks. Compared to other similar variants of Chebyshev polynomial public key algorithms, our proposal achieves better performance in the encryption and decryption stages. Furthermore, we combine this multiple chaotic system key exchange protocol with the Advanced Encryption Standard (AES) algorithm and provide a demonstrative example.
1.3. Organization
The remainder of this paper is organized as follows: Section 2 focuses on demonstrating Chebyshev chaotic mapping, the CEPKC algorithm, and the corresponding research work performed to upgrade and improve public key encryption schemes using the Chebyshev system. Then, we improved a public key encryption algorithm and provide related examples and flowcharts in Section 3. Section 4 emphasizes the software implementation and example verification of the proposed method, while Section 5 presents the performance, analysis, and discussion of the method in terms of security. Finally, Section 6 summarizes this paper and proposes future directions for work.
2. Preliminary
2.1. Chebyshev Chaotic Mapping
Definition 1.
Let be a positive integer, , and the order Chebyshev polynomial is defined as:
can also be defined using the following recursive relation:
where in . from Equation (2), it can be observed that the first terms of the Chebyshev polynomial are:
Chebyshev polynomials possess two important properties: the semi-group property and the chaotic property [49].
2.1.1. Semi-Group Property
, where and are positive integers and . To utilize the properties of Chebyshev polynomials in the subsequent context, it is necessary to generalize their properties.
Theorem 1.
Chebyshev polynomials satisfy the semi-group property everywhere in the interval , i.e.,
2.1.2. Chaotic Property
The Chebyshev map is a one-dimensional chaotic map with favorable nonlinear dynamic properties. Chaos occurs when the control parameter is greater than 1. When greater than 2, the map remains in a chaotic state. Figure 2 shows the bifurcation diagram of the Chebyshev map. Figure 3 shows the bifurcation diagram of the improved Chebyshev chaotic map .
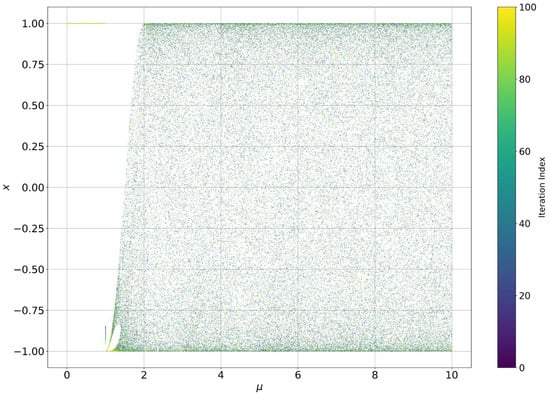
Figure 2.
Bifurcation diagram for the Chebyshev map.
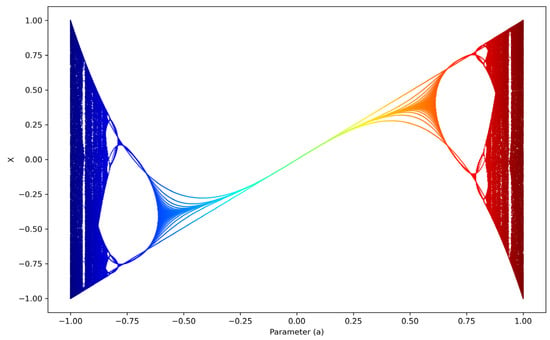
Figure 3.
Bifurcation diagram of the improved Chebyshev chaotic map.
2.1.3. Lyapunov Exponent
The Lyapunov exponent is an important indicator of the dynamic behavior of nonlinear systems. In this section, the Lyapunov exponent (LE) is further used to analyze the predictability of the Chebyshev chaotic system. When , the Chebyshev polynomial has an invariant density distribution of and a positive Lyapunov exponent of , indicating its chaotic property. Figure 4 shows the Lyapunov Exponent of the Chebyshev Map.
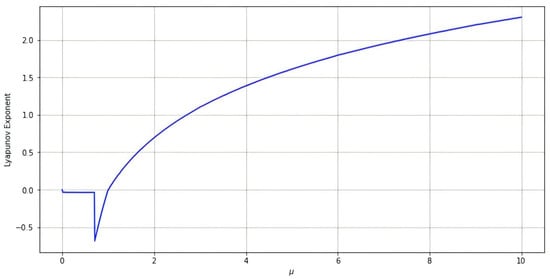
Figure 4.
Lyapunov Exponent of the Chebyshev Map.
2.1.4. Information Entropy
Information entropy is usually used to measure the uncertainty of a variable. The greater the uncertainty of variables, the higher the information entropy, which is defined as , where , is the probability of and for grayscale images. The maximum value of information entropy is 8 for grayscale images.
Figure 5 shows the information entropy diagrams of the Chebyshev chaotic maps. It can be seen that the entropy values of the output sequence generated by the Chebyshev map stabilize within a good range when , indicating that the Chebyshev map exhibits a high degree of unpredictability.
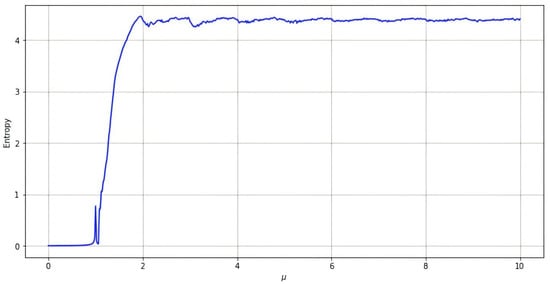
Figure 5.
Information entropy of the Chebyshev map.
2.2. Chebyshev-ElGamal Public Key Cryptographic Algorithm (CEPKC)
In [50], Kocarev et al. utilized the semi-group properties and chaotic characteristics of Chebyshev chaotic mapping to propose a Chebyshev polynomial-based ElGamal-like public key cryptography algorithm, with the ElGamal public key cryptography algorithm as a blueprint. This algorithm does not require the generation of large prime numbers as private keys, and has high computational efficiency. In the algorithm, r and s are large random integers, and . Due to the chaotic characteristics, and can be seen as independent random numbers. However, the inverse operation of the trigonometric function definition in the Chebyshev chaotic mapping leads to the ciphertext information being , from which an adversary can compute:
as and the adversary can recover the plaintext . Similarly, the adversary can compute using Equation (4) to steal Bob’s equivalent private key. To enhance security, Kocarev et al. extended the definition of Chebyshev polynomials from the real field to the finite field as shown below:
where and is a large prime number. It can be proven that the semi-group properties of Chebyshev polynomials still hold in the finite field . Since is an algebraic expression, Equation (6) holds.
Therefore, the semi-group expression of Chebyshev polynomials in the finite field can be derived, as shown in Equation (7).
For any Chebyshev polynomial in the finite field , it can also be represented as:
At the current stage, no inverse function expression for finite field Chebyshev polynomials has been found.
2.2.1. CEPKC Algorithm
Assuming Alice is the sender and Bob is the receiver, the communication process of the ElGamal-type public key algorithm based on finite field Chebyshev polynomials (CEPKC) proposed by Kocarev et al. [51] is as follows:
- Key generation. Bob randomly generates a large prime number , chooses positive integers and , such that , , and computes . Bob’s public key is , and the private key is .
- Message encryption. After receiving Bob’s public key , Alice converts the message to be encrypted into an integer . She chooses a random number , such that . Using the public key , she calculates and then sends the ciphertext message to Bob.
- Message decryption. Upon receiving the ciphertext message , Bob can decrypt it using the private key to recover the plaintext message .
2.2.2. Parameter Selection in the Algorithm
The selection of parameters is crucial to ensure the security of the CEPKC public key cryptographic algorithm, and the following principles [25,52] are mainly considered:
- Selection of parameter : If is a prime number, it is desirable to make or have no factors other than 2, in which case is called a strong prime; if is a composite number, , where is a prime number and it is preferable to have as a strong prime, ideally . When properly chosen, the probability of small cycles occurring is minimized.
- Principles for selecting parameter : For the above prime number , is a parameter for the seed of . Randomly choose an integer , where denotes the group on , with . If , where is a prime number, , let and compute . If and , restart. Repeat until the desired parameter is obtained. When and are appropriately chosen, the probability of small cycles is minimized, and the security of the finite field CEPKC encryption scheme can be effectively enhanced.
2.3. Bose Multi-Chaotic Public Key Algorithm (BMPKC)
A public key encryption algorithm based on the multi-chaos system (-CS) [27] is divided into the following basic steps. For ease of reading, let us assume = 2, so -CS is C-CS (a couple of chaotic systems) in this case. Assume there are two different one-dimensional chaotic maps and , such that , where are control parameters, , are initial conditions, and , denote the two chaotic orbits.
Step 1. Alice and Bob determine the linear transformations and , chaotic mappings and , and initial vector through public negotiation , where are control parameters, are initial conditions, and denote the two chaotic orbits.
Step 2. Alice randomly selects key seeds and and a large number , inputs these parameters into a pseudo-random sequence generator, outputs a sequence of length , iterates for times based on the content of to obtain , and passes as the public key to Bob, ,
is the defined pseudo-random sequence , where
Step 3. Similarly, Bob secretly selects key seeds and and a large number , inputs these parameters into a pseudo-random sequence generator, outputs a sequence of length , iterates for times based on the content of to obtain , and passes as the public key to Alice.
Step 4. Alice iterates for times based on to obtain .
Step 5. Bob iterates for times based on to obtain .
Since and are both linear transformations, and , we have
where are the numbers of 0s and 1s in and . Obviously, , . Similarly, , so , which is used as the actual key.
The process of the algorithm is shown in Figure 6.
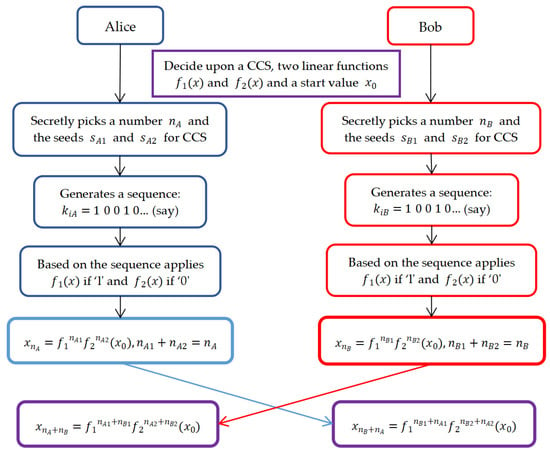
Figure 6.
The proposed key exchange protocol using CCS [27].
Similarly, by extending the function in the algorithm to times , the linear function count becomes and the corresponding selection functions are
The choice of is given by the defined pseudo-random sequence , where follows the conditions described in Equation (13).
2.4. Multi-Chaotic Public Key Cryptographic Algorithm Based on Chebyshev Polynomials
In [27], Bose proposes a specific design case, where the key point of the algorithm lies in both and being linear transformations and satisfying . In fact, and do not need to be strictly linear transformations, so the commutative property becomes particularly important. The semi-group property of Chebyshev polynomials happens to satisfy this property.
To avoid attacks based on the 2-norm as presented by Wang et al. [53], Su et al. propose a multi-chaos public key algorithm based on Chebyshev polynomials (CMPKC). The key exchange step of this algorithm is like Bose’s multi-chaos public key algorithm, as shown in Figure 7 for = 2.
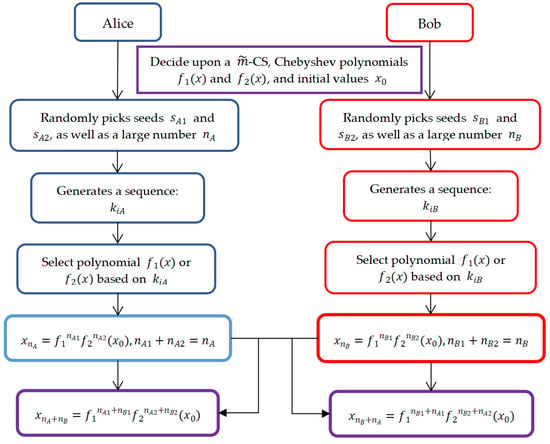
Figure 7.
Key exchange process of a multi-chaotic system.
It is easy to see that the basic ideas of these two algorithms are consistent, with the difference being that the former involves Alice and Bob publicly negotiating linear functions that satisfy the commutative property, while the latter involves Alice and Bob publicly negotiating choice functions as Chebyshev polynomials with mutually prime degrees. Since Chebyshev polynomials have the semi-group property, they still satisfy the requirements of a public key encryption scheme. At this point, .
2.5. Security Analysis of the Algorithm Above
The Bose algorithm (RMPKC) combines the Diffie–Hellman protocol framework. The authors of Reference [53] point out that attacking this algorithm is equivalent to solving the Diffie–Hellman problem, and the difficulty is , where and represent the key space size and the complexity of the linear transformation, respectively. However, the algorithm still has the following shortcomings [28]:
Let be a complex field, and be the -dimensional vector space of . At this point, the linear transformation can be represented as , . Since , this means that ; therefore,
- If and are linear transformations on the vector space , it is difficult to choose suitable linear transformations and , since does not hold in this space.
- Let be any norm of , if and , when and are two large integers, the statistical characteristics of the -tuple vector are poor. In fact, in the instances given by Bose, despite being secret, there are still potential security issues, such as when and , ; when and , . This requires that cannot be a large integer, otherwise the statistical characteristics of the public key will be compromised.
- Although it is difficult for an attacker to infer the specific operational steps from the seed to the public key , they can still calculate by conducting single-bit tests on Alice’s pseudo-random sequence generator. Letting , denote the number of 0s and 1s in an arbitrary bit sequence of length , the statistic is
This approximately follows a distribution with 1 degree of freedom, so and . Let , then . Furthermore, based on Equation (15), we have
where , such that .
We can see that the algorithm provides three design parameters: the size of the key, the computational complexity of linear functions, and the number of linear functions. By analyzing the properties of the -CS pseudo-random sequence generator, we deduce that the computational degree of the algorithm is , which is lower than . In fact, the attacker can be computed as
where , .
Based on , the computational complexity of breaking the private key can be calculated as
- 4.
- Since it requires step-by-step adaptation to the selection rules, Alice cannot use a fast algorithm to encrypt messages. Nonetheless, the attacker can estimate and calculate the weight of the matrix through a sum of squares algorithm. In the worst case scenario, the time consumed for encryption and decryption are equal, so this mode cannot withstand brute force attacks.
Regarding the four shortcomings mentioned above, the CMPKC public key algorithm replaces the linear transformations in the original algorithm with Chebyshev polynomials, inheriting the security performance of multiple chaotic systems in the original algorithm. Transforming to the real finite field can greatly increase the security of the algorithm. In this case, and are no longer linear transformations, making it very difficult to choose orthogonal linear transformations. Nevertheless, attackers can still decipher this encryption system through points 3 and 4 mentioned above, indicating that the encryption mode mentioned does not have sufficient security yet.
3. An Improved Multi-Chaotic Public Key Cryptographic Algorithm Based on Chebyshev Polynomials (CMPKC-ki)
3.1. Selection of Coefficient ki
Before introducing the improved algorithm, we need to clarify the use of the coefficient . The detailed selection scheme of is described as follows:
- Alice chooses two large prime numbers and , and sets . She generates a large integer randomly.
- Calculate , where are the public key and is the private key.
- Bob randomly selects , calculates , and selects based on Equation (20).
- Calculate and send it to Alice.
- Alice calculates based on the private key and selects based on Equation (20).
The selection rule of is as follows:
In Equation (20), is a large number and is the number of . It is easy to see from the semi-group property of Chebyshev that .
, where represents the Chebyshev polynomial and , and are two large prime numbers.
3.2. Chaotic Hash Function for Generating a Sequence
In the algorithm’s design, we will use a chaotic hash function to generate a sequence. The specific Algorithm 1 is as follows.
| Algorithm 1 Chaotic hash function generates a sequence |
| Input: seed_value, sequence_length, Chaotic parameters Output: binary sequence 1: ChaoticHash(seed, length): 2: x: = seed 3: bit_sequence:= “” 4: for I from 1 to length do 5: x: = logistic_map(x) 6: if x > 0.5 then 7: bit_sequence:= bit_sequence + ‘1’ 8: else 9: bit_sequence: = bit_sequence + ‘0’ 10: end if 11: end for 12: return bit_sequence: 13: Function logistic_map(x): 14: : = // Chaotic parameters 15: return r * x * (1 − x) |
3.3. Improved Algorithm (CMPKC-ki)
The improved public key encryption system adopts the coefficient selection based on the equality , where the size of is determined, and is the Chebyshev polynomial. The specific value selection rule of and the size of are shared secrets among participants. A pseudo-random sequence is generated using chaotic hash functions and logistic mapping. The initial value is iterated and times based on the sequence content to obtain and , and then iterated and times again to obtain and .
The key exchange process of this improved multi-chaos public key system is illustrated in Figure 8.
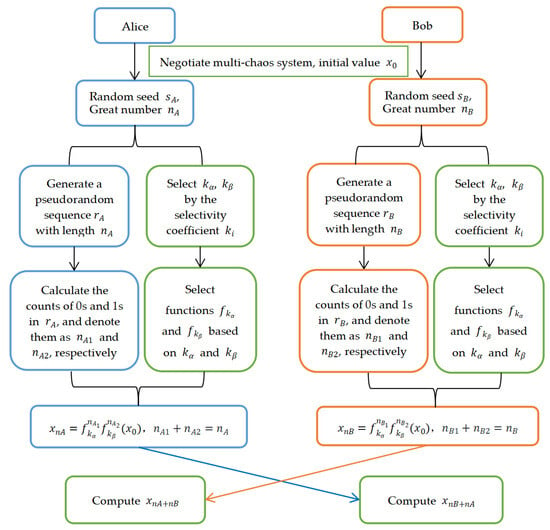
Figure 8.
Key exchange process of the improved multi-chaos system.
The algorithm is described as follows (assuming Alice wants to communicate with Bob):
Let be a large positive number, and the chaotic system is of m levels.
Step 1. Alice and Bob choose coefficients through public negotiation and calculation and determine the initial value and selection functions , where are Chebyshev polynomials.
Step 2. Alice randomly selects a key seed and a large number , inputs these parameters into a pseudo-random sequence generator, and outputs a sequence of length . Select by the selectivity coefficient , select functions and based on and . Iterating over times according to the content of in to obtain , and pass as the public key to Bob.
Step 3. Similarly, Bob randomly selects a key seed and a large number , inputs these parameters into a pseudo-random sequence generator, and outputs a sequence of length . Select by the selectivity coefficient , select functions and based on and . Iterating over times according to the content of {0, 1} in to obtain , and pass as the public key to Alice.
Step 4. Alice iterates over times according to to obtain .
Step 5. Bob iterates over times according to to obtain .
Since are Chebyshev polynomials, it is known from preliminary knowledge that Chebyshev polynomials satisfy the semi-group property on . Therefore, we have , that is
where are the numbers of 0s and 1s in and , respectively. Similarly, it can be proven that
therefore, we have .
Combined with the process in Figure 8, this improved algorithm can be used for both encryption and decryption, and can be combined with the AES algorithm for further applications.
3.3.1. Improved Algorithm for Encryption and Decryption
Assuming plaintext , the steps are as follows:
- Bob selects private key , calculates , and passes it to Alice.Similarly, Alice selects private key , calculates , and passes it to Bob.
- Encrypt , then Alice passes and ciphertext c to Bob.
Bob calculates based on his private key , and uses it to recover plaintext .
3.3.2. Combination with the AES Algorithm to Obtain the Improved Algorithm
Based on steps 1 to 5 of the improved public key encryption algorithm in Section 3.3, and can be used as the keys for encryption and decryption in the AES algorithm, thus achieving the combination of chaotic public key encryption and AES private key encryption. The specific process is shown in Figure 9.
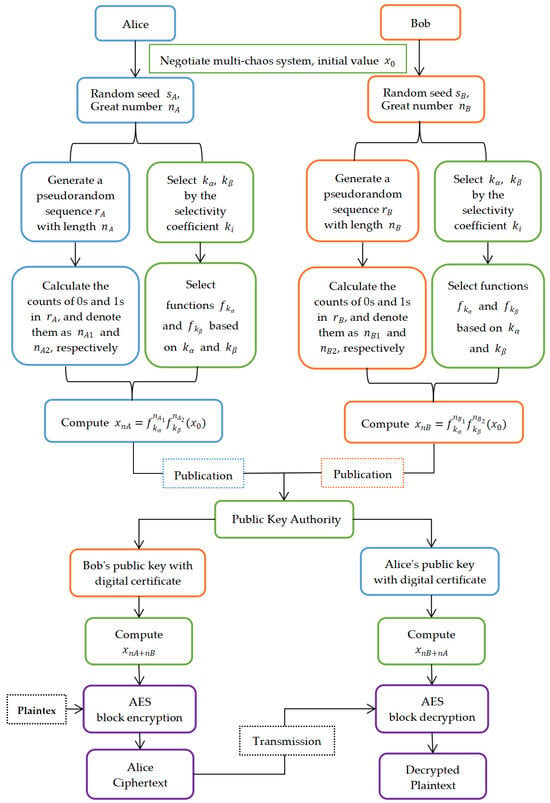
Figure 9.
Combined application of the improved multiple chaotic system key exchange process and AES algorithm.
It is worth noting that after calculating and , they cannot be directly applied to the AES algorithm in most cases. This is because, in practical applications, AES keys need to be represented as hexadecimal strings, Base64 encoded strings, or raw byte sequences. Thus, we need to continue to convert the values of and into the corresponding format.
Step 6: Alice and Bob each transcode the exchanged keys and into 32-byte random binary keys using Algorithm 2.
| Algorithm 2 Convert a decimal number to a 32-byte random binary key |
| Input: decimal_number, random_key Output: 32-byte random binary key, Hexadecimal representation 1: Function decimal_to_random_key(decimal_number): 2: decimal_bytes: = Convert decimal_number to byte array(decimal_number) 3: hash_object: = Create SHA-256 hash object (decimal_bytes) 4: hash_result: = Get digest from hash_object 5: random_key: = First 32 bytes of hash_result 6: return random_key |
Step 7: Alice inputs the plaintext into the AES algorithm for encryption.
Step 8: Bob, upon receiving the ciphertext, uses the key to recover the plaintext using Algorithm 3.
| Algorithm 3 Encrypt and decrypt using the AES algorithm. |
| Input: plaintext, key Output: ciphertext, decrypted_data 1: Function encrypt (plaintext, key): 2: cipher: = Create AES cipher object with key in CBC mode 3: iv: = Generate random initialization vector (IV) 4: padded_plaintext: = Pad plaintext to AES block size 5: ciphertext: = Encrypt padded_plaintext with cipher using the IV 6: Return iv, ciphertext 7: Function decrypt(ciphertext, key, iv): 8: cipher: = Create AES cipher object with key in CBC mode and IV 9: decrypted_bytes: = Decrypt ciphertext with cipher 10: decrypted_data: = Unpad decrypted_bytes to AES block size 11: Return decrypted_data |
4. Software Implementation
4.1. Feasibility Analysis
4.1.1. Fast Algorithm for Chebyshev Polynomials
In Section 3, we presented the improved multiple chaotic public key algorithm, which no longer uses the orthogonal linear exchange designed by Bose in [27]. Instead, it is replaced by Chebyshev polynomials and a set of enhancements (e.g., the introduction of the selective coefficient , freely selectable Chebyshev polynomials , and the chaotic hash function). Since Chebyshev polynomials also possess the semi-group property, they still meet the requirements of the public key encryption scheme.
As the semi-group property of Chebyshev polynomials holds in the interval , decryption computation is feasible. Evaluating the Chebyshev polynomials to reduce the calculation time of is an important challenge. This paper adopts a fast algorithm consistent with the work proposed in [54] to calculate Chebyshev polynomials.
4.1.2. Selection of Parameters
To enhance the readability of this article and facilitate understanding, let the chaotic series in Equation (21) and the modulus . Pseudo-random sequences are generated by the chaotic hash function, detailed in Algorithm 1, where seed_value = 0.123456789, sequence_length = 100, and Chaotic parameters 3.8.
4.1.3. Applications of the Selection of Coefficient ki
The calculation process for selecting coefficient follows the scheme described in Section 3.1. An example is provided below for illustration.
Selection process for :
- Alice chooses two large prime numbers and and sets . She generates a large integer at random.
- Alice computes .The public key is , and the private key is .
- Bob randomly selects an integer and computes . According to Equation (20), he selects the value of . For clarity, let us assume , and select as an arithmetic sequence. Let us calculate coefficient shown in Equation (24) by applying Equation (20), and since , we choose .
- Calculate and send it to Alice.
- Alice computes based on the private key . Similarly, according to Equation (20) and the assumptions made in Section 3.1, can still be selected as .
Through the above process, Alice and Bob can select the same value of while preserving their private key, which will support the subsequent improvement of the Chebyshev polynomial multi-chaos public key algorithm.
Assume that, in the case of , , the value of the coefficient is randomly selected through arbitrary transformations of and . Here, the generation method of two large prime numbers in the Rivest–Shamir–Adleman algorithm can be used to select and . This not only ensures strong randomness but also avoids unpredictable troubles caused by arbitrary value selection. Table 2 presents five sets of experimental results under arbitrary transformations of and .

Table 2.
Values of coefficient under arbitrary transformations of and .
From the values in Table 2, it is easy to see that when , the choice of already exhibits preliminary randomness. In practical applications, as long as , theoretically, the value of can be arbitrarily large and the values of and can also be arbitrarily large. This means that the choice of coefficient has strong randomness in practical applications.
4.2. An Example
PYTHON is a popular and powerful programming language that can be used for mathematical calculation and analysis. In our software implementation, we used algorithm libraries under the Windows environment. Below, we provide a specific example to verify the effectiveness of the proposed algorithm.
Step 1. Alice and Bob publicly negotiate and determine the initial values and . They select two functions in Equation (25), where the selection rule for is as described in Section 4.1.3.
where are Chebyshev polynomials and are calculated using the fast algorithm described in Section 4.1.1.
Step 2. Alice randomly selects a key seed and a large number . She inputs these parameters into a pseudo-random sequence generator (as described in Section 4.1.2) and obtains a sequence of length . The output of this example is as follows:
According to Table 2, we select and the functions and based on and . Then, calculate the number of 0s and 1s in the sequence , denoted as and , respectively.
Next, we compute and and iterate these calculations, respectively, and times to obtain . Finally, is transmitted as the public key to Bob.
Step 3. Similarly, Bob randomly selects a key seed and a large number , and inputs these parameters into a pseudo-random sequence generator (as in Section 4.1.2). This generates a sequence of length consisting of , denoted as , and the results are as follows:
According to Section 4.1.3, Bob calculates based on Alice’s public key. Similarly, Bob selects the functions and based on and .
Bob counts the number of 0s and 1s in , which are and , respectively. By applying the functions and , Bob iterates these calculations and times. This results in , with then transmitted as the public key to Alice.
Step 4. Alice iterates over times based on to obtain . According to Equation (14), we have:
Step 5. Similarly, Bob iterates over times based on to obtain . At this point:
4.2.1. Applying the Improved Algorithm Directly to Encryption and Decryption
Assuming the plaintext , the steps are as follows:
- Bob selects the key seed to calculate and , thus obtaining , and passes to Alice;Similarly, Alice selects the key seed to calculate and , thus obtaining , and passes to Bob;
- Encryption: . Then, Alice passes and the ciphertext to Bob;
- Decrypt: Bob calculates and based on his private key , and computes . Using this value, he recovers the plaintext as .
4.2.2. Combining the Improved Algorithm with the AES Algorithm
In the improved public key encryption algorithm, we have calculated and provided an example of its direct use for encryption. Now, we will combine the improved algorithm with AES and continue with step 5 of the improved algorithm.
Step 6. Alice and Bob each transcode the exchanged keys and into 32-byte random binary keys using Algorithm 2. The transcoding results are shown in Table 3.

Table 3.
Converting decimal numbers to 32-byte random binary keys.
The transcoded result of is as follows:
“,\xa6ZE\xa9]\x83\xa5\xfd\x9c\xe2nZ\xe9\r\xe26\xb9\xe6{t\xf8g\xd1q\xd6h\xda\x0f\xd1\xfcj”
Step 7. Assuming the plaintext is “hello world”,
Alice inputs the plaintext into the AES algorithm for encryption, resulting in the following ciphertext:
“B\x88\x0e\xd0|\xc6\xd9\xbb\x19R\xf6m\x04xD\xda”
Step 8. Bob, upon receiving the ciphertext, uses the key to recover the plaintext “hello world”.
The combined result of transcoding the keys and and applying the AES encryption algorithm is shown in Table 4.

Table 4.
Combined test results of transcoded key with AES encryption algorithm.
5. Implementation Results and Analysis
This paper uses a Xiaomi laptop produced by Tianmi Technology Co., Ltd. in Beijing, China, for verification and analysis. The processor is an 11th generation Intel® Core™ i5-11320H @ 3.20 GHz, with 16.0 GB RAM (15.8 GB available) (Intel Corporation, Santa Clara, CA, USA), and the operating system is Windows 10, 64-bit. The implementation and analysis are carried out on this hardware and software system. The next two sections focus on the performance and security evaluation of CMPKC-Ki compared to RMPKC and its variants.
5.1. Performance Analysis
5.1.1. Key Generation
To maintain consistency in the comparison, we unified the value of the multi-chaos level of the algorithm as 2, and used the same principles for selecting parameters and as the CEPKC algorithm in Section 2.2. We generated and analyzed initial random primes for each of the three cases. Each test was performed for different bit sizes of the initial primes within the range of 128, 256, 512, 1024, and 2048. Table 5 shows the comparison analysis of CMPKC- with CEPKC and CMPKC. Figure 10 shows the comparison of key generation times under different key sizes. It is easy to see that the key generation time of the standard CEPKC algorithm is the lowest, while the CMPKC- algorithm falls in the middle, and the key generation time of CMPKC is the highest. Through analysis, our proposed CMPKC- algorithm adds a selective coefficient , which increases an initial parameter compared to CEPKC and CMPKC, thus resulting in a longer key generation time. However, due to adjustments made in the multiple chaotic selection and pseudo-random sequence generation stages, the time cost of key generation is lower compared to the CMPKC algorithm. Although there is an increase in key generation time cost relative to the CEPKC scheme, the added security is significant, so we consider the limited increase in time to be tolerable.

Table 5.
Analysis and comparison of the CMPKC- model with the CEPKC and CMPKC models.
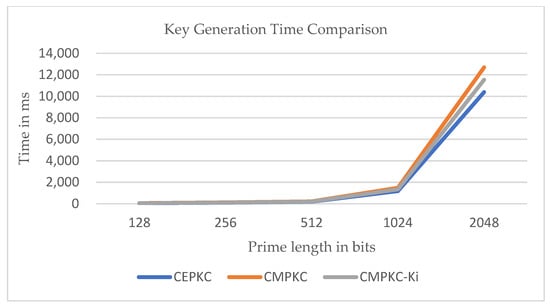
Figure 10.
Key Generation Time Comparison.
5.1.2. Encryption and Decryption
From the encryption and decryption time trends shown in Figure 11 and Figure 12, the standard CEPKC has the lowest execution time for encryption and decryption, especially after 1024 bits, making it the best in terms of encryption and decryption time. Since the CMPKC- scheme involves additional computational steps for coefficient selection during the encryption and decryption phases, increasing the overall complexity of the algorithm, attackers are unable to guess the private key or plaintext by multiplying the public key and prime numbers. Furthermore, until the typical size of 1024 bits, our proposed CMPKC- scheme performs comparably to CEPKC in terms of encryption and decryption times. For higher bit sizes, CMPKC- demonstrates better efficiency in both encryption and decryption processes compared to CMPKC, slightly lagging behind the standard CEPKC scheme. However, it is worth noting that our proposed encryption scheme is generally applied in lightweight encryption environments, with the recommended modulus size being 1024 bits. Therefore, our CMPKC- scheme stands out as efficient and high-performing among all the discussed algorithms. In an overall performance evaluation, among the three algorithms discussed, the CMPKC- algorithm proves to be the most efficient and effective, positioning it as the best algorithm after the standard CEPKC, while CMPKC emerges as the least efficient variant. The reasonable increase in key generation time in CMPKC-, compared to standard CEPKC, is justified as the introduction of adds complexity, making the CMPKC- system more time-consuming to break and enhancing overall security.
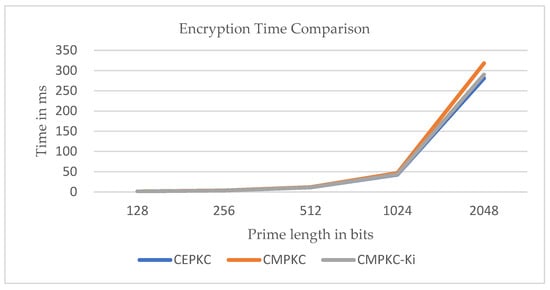
Figure 11.
Encryption Time Comparison.
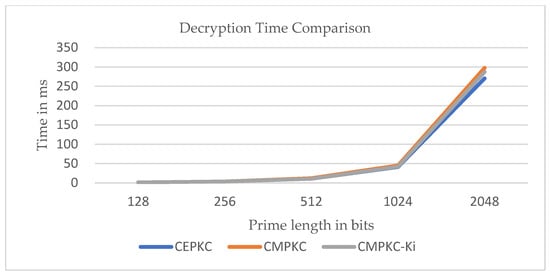
Figure 12.
Decryption Time Comparison.
5.2. Security Analysis
Since we use Chebyshev polynomials based on finite fields, with the domain and range extended to , it effectively avoids the breaking method mentioned in Section 2.2 that utilizes inverse trigonometric functions. In this paper, the selection coefficient is chosen based on the value of , which can only be obtained through calculations by the communicating parties. It is impossible for any third party to know , thus ensuring the security of the selection of .
In the calculation process, the computational complexity of is equivalent to that of the ElGamal public key cryptosystem and does not add an additional computational load. However, it is computationally infeasible to determine from . However, the resonant characteristics of Chebyshev polynomial points in finite fields still exist. That is, given the public key , by calculating and , enough points can be obtained on the Chebyshev polynomial curve, allowing for curve fitting to derive the key . The autocorrelation function of exhibits binary characteristics, and the normalized autocorrelation function for is given by:
In the formula, when is sufficiently large, it can be shown that:
where is a constant, such that . In other words, when is sufficiently large, exhibits binary characteristics. In practical public key encryption systems, the field values are extremely large. Therefore, it can be assumed that the points on the curve are difficult to predict and count during the effective lifespan of the key. Even if an attacker gains access to many points on the curve, they cannot fit the curve and deduce the private key within the limited lifespan of the key.
Furthermore, considering the range of values for , as long as the maximum value of , , and given that can be theoretically arbitrarily large, the values of and can also be arbitrarily large. This means that in practical applications, the selection of the coefficient is highly random, further ensuring the security of the algorithm.
In Section 2.5, we have observed four shortcomings of previous algorithms. By replacing the corresponding linear transformations with finite field Chebyshev polynomials, we can overcome shortcomings 1 and 2. For shortcoming 3, we use chaotic hash functions and logistic mappings to generate pseudorandom sequences. By analyzing the properties of multi-chaos systems, we hypothesized that attackers can calculate , where and . However, in our proposed new algorithm, have been replaced with , where , with sufficiently large ranges and good randomness. This makes it impossible for attackers to effectively attack the algorithm based on the assumptions.
Regarding shortcoming 4, the performance test of the algorithm shows that the improved algorithm has stronger resistance to brute force attacks compared to previous algorithms. Table 6 represents the comparison of brute force attack times from 4-bit prime numbers to 7-bit prime numbers. When attacking prime numbers of 7 bits or more, the execution result requires a long time, and the time trend of brute force attacks is already clear within 7 bits, so we will analyze it within 7 bits. Figure 13 also shows the advantage of the results through a line chart. To compare the results more easily, a logarithmic scale with a base of 10 is used for the vertical axis when plotting.

Table 6.
Brute force attack time comparison in milliseconds.
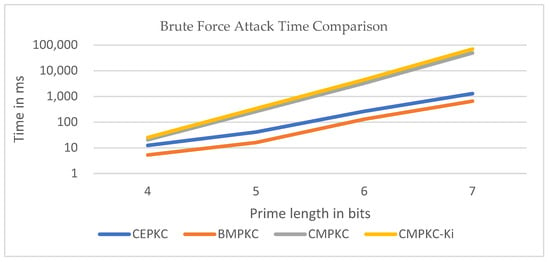
Figure 13.
Brute Force Attack Time Comparison.
From the corresponding Table 6 and Figure 13, for all prime number lengths, CEPKC takes the least amount of time to brute force decrypt its private key components, and BMPKC also shows results close to CEPKC. This means that standard CEPKC and BMPKC have similar complexity and security, and therefore, they have the lowest security among all discussed algorithms. Compared with the other three algorithms, our proposed CMPKC- algorithm shows a significantly longer decryption time on all prime number bits. Therefore, relative to other algorithms, the proposed CMPKC- algorithm has the longest brute force attack time and, therefore, the highest security. CMPKC has the second-longest attack time, only slightly shorter than CMPKC-.
6. Conclusions and Future Work
Due to the similar characteristics between chaotic systems and cryptography, chaos-based public key encryption is currently a hot topic. This paper improves the performance and security of the Bose Multi-Chaotic Public Key Cryptographic Algorithm (BMPKC) from the aspects of efficiency and reliability. The proposed algorithm is named CMPKC-, which overcomes the shortcomings of previous algorithms by using selective coefficient , chaotic hash functions, and logistic mapping to generate pseudo-random sequences. CMPKC- provides better security because it leads to more complex algorithms and the process of public key generation is sent in parallel, making it difficult for attackers to obtain much information about the key or decrypt the message. Compared to the standard CEPKC and BMPKC, CMPKC- takes longer to break private keys. Meanwhile, we also explore the combination of the improved chaotic public key encryption system with the AES encryption method, which provides more possibilities for practical applications of the system.
In summary, this solution has the characteristics of strong practicality and high security, making contributions to the field of information encryption. We believe that its advantage lies in the fact that even if attackers guess the chaotic sequence within the same period, they still need to obtain the specific from the selective coefficient and break the chaotic hash function, which is almost impossible within the limited time. Therefore, the security of the algorithm is greatly improved. Although the overall design of this solution is satisfactory, it requires more time for key generation due to parallel computation and the occurrence of selective coefficients through several generation stages. In the case of large prime numbers, the efficiency of the algorithm will decrease, so the selective coefficient cannot be too large or it will have a negative impact on the required time for the algorithm, as seen in Figure 10, which can be considered as a drawback and an issue that needs continuous improvement. In conclusion, after performance and security analysis, the proposed CMPKC- algorithm demonstrates superior results with improved security.
As future research work, we plan to compare the proposed public key encryption system with other common advanced public key encryption schemes in different application scenarios for performance analysis and conduct a more detailed assessment of security aspects. The algorithm will also be extended to parallel machines so that multiple related operations can be parallelly computed on multi-core processors. Compared to similar public key encryption systems, this will result in lower computational costs and wider acceptability in IoT devices. Additionally, we can explore the potential of combining other chaotic mappings, fractals, and traditional encryption methods (such as AES, DES, and Blowfish) to achieve higher efficiency and security in the field of encryption. Interested researchers can implement this algorithm on hardware platforms such as field-programmable gate arrays (FPGAs) and application-specific integrated circuits (ASICs) to optimize its performance for practical applications. In conclusion, this research brings possibilities for continual exploration and advancement in the digital security field.
Author Contributions
Conceptualization, C.Z., Y. L, A.T. and L.W.; methodology, C.Z. and L.W.; software, C.Z., J.B., T.G. and S.P.; validation, Y.L., A.T. and L.W.; formal analysis, C.Z., J.B. and L.W.; investigation, J.B., Y.L. and A.T.; resources, Y.L., A.T., J.B. and S.P.; writing – original draft, C.Z. and J.B.; writing – review & editing, C.Z., J.B., Y.L., A.T., L.W., T.G. and S.P.; supervision, Y.L., A.T. and L.W.; project administration, Y.L., A.T., L.W., T.G. and S.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 62372494, the Guangdong Province College Youth Innovative Talent Project, grant number 2023KQNCX132, the Guangdong Province College Youth Innovative Talent Project, grant number 2024KQNCX013, the Guangdong Key Disciplines Project, grant number 2021ZDJS138, the Guangdong Key Disciplines Project, grant number 2022ZDJS139, and FCT—Foundation for Science and Technology within the R&D Units Project Scope, grant number UIDB/00319/2020.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kocarev, L. Chaos-based cryptography: A brief overview. IEEE Circuits Syst. Mag. 2001, 1, 6–21. [Google Scholar] [CrossRef]
- Pisarchik, A.N.; Zanin, M. Chaotic map cryptography and security. In Encryption: Methods, Software and Security; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2010; pp. 1–28. [Google Scholar]
- Mahajan, P.; Sachdeva, A. A study of encryption algorithms AES, DES and RSA for security. Glob. J. Comput. Sci. Technol. 2013, 13, 15–22. [Google Scholar]
- Sonko, S.; Ibekwe, K.I.; Ilojianya, V.I.; Etukudoh, E.A.; Fabuyide, A. Quantum cryptography and US digital security: A comprehensive review: Investigating the potential of quantum technologies in creating unbreakable encryption and their future in national security. Comput. Sci. IT Res. J. 2024, 5, 390–414. [Google Scholar] [CrossRef]
- Ibrahim, D.R.; Teh, J.S.; Abdullah, R. An overview of visual cryptography techniques. Multimed. Tools Appl. 2021, 80, 31927–31952. [Google Scholar] [CrossRef]
- Sharma, S.; Saini, A.; Chaudhury, S. A survey on biometric cryptosystems and their applications. Comput. Secur. 2023, 134, 103458. [Google Scholar] [CrossRef]
- Singh, A.; Kumar, A.; Namasudra, S. DNACDS: Cloud IoE big data security and accessing scheme based on DNA cryptography. Front. Comput. Sci. 2024, 18, 181801. [Google Scholar] [CrossRef]
- Chillotti, I.; Gama, N.; Georgieva, M.; Izabachène, M. TFHE: Fast fully homomorphic encryption over the torus. J. Cryptol. 2020, 33, 34–91. [Google Scholar] [CrossRef]
- Shruti; Rani, S.; Srivastava, G. Secure hierarchical fog computing-based architecture for industry 5.0 using an attribute-based encryption scheme. Expert Syst. Appl. 2024, 235, 121180. [Google Scholar] [CrossRef]
- Bernstein, D.J.; Lange, T. Post-quantum cryptography. Nature 2017, 549, 188–194. [Google Scholar] [CrossRef]
- Joseph, D.; Misoczki, R.; Manzano, M.; Tricot, J.; Pinuaga, F.D.; Lacombe, O.; Leichenauer, S.; Hidary, J.; Venables, P.; Hansen, R. Transitioning organizations to post-quantum cryptography. Nature 2022, 605, 237–243. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Matthews, R. On the derivation of a “chaotic” encryption algorithm. Cryptologia 1989, 13, 29–42. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Liu, L. Chaos-Based Image Encryption: Review, Application, and Challenges. Mathematics 2023, 11, 2585. [Google Scholar] [CrossRef]
- Salman, D.S.; Naif, J.R. Comparative study of chaotic system for encryption. Iraqi J. Comput. Inform. 2023, 49, 83–92. [Google Scholar] [CrossRef]
- Alexan, W.; Alexan, N.; Gabr, M. Multiple-Layer Image Encryption Utilizing Fractional-Order Chen Hyperchaotic Map and Cryptographically Secure PRNGs. Fractal Fract. 2023, 7, 287. [Google Scholar] [CrossRef]
- Corona-Bermúdez, E.; Chimal-Eguía, J.C.; Corona-Bermúdez, U.; Rivero-Ángeles, M.E. Chaos Meets Cryptography: Developing an S-Box Design with the Rössler Attractor. Mathematics 2023, 11, 4575. [Google Scholar] [CrossRef]
- Kotadai, Z.; Yves, E.J.; Fischer, C.; Rodríguez-Muñoz, J.D.; Moreno-Lopez, M.F.; Tlelo-Cuautle, E.; De Dieu, N.J. Fractional order 1D memristive time-delay chaotic system with application to image encryption and FPGA implementation. Math. Comput. Simul. 2024, 227, 58–84. [Google Scholar]
- Sambas, A.; Miroslav, M.; Vaidyanathan, S.; Ovilla-Martínez, B.; Tlelo-Cuautle, E.; El-Latif, A.A.A.; Abd-El-Atty, B.; Benkouide, K.; Bonny, T. A New Hyperjerk system with a half line equilibrium: Multistability, Period doubling reversals, antimonotonocity, electronic circuit, FPGA design and an application to image encryption. IEEE Access 2024, 12, 9177–9194. [Google Scholar] [CrossRef]
- Puhua, G. Cellular automaton public-key cryptosystem. Complex Syst. 1987, 1, 51–57. [Google Scholar]
- Kocarev, L.; Tasev, Z. Public-key encryption based on Chebyshev maps. In Proceedings of the 2003 International Symposium on Circuits and Systems, 2003, ISCAS’03, Bangkok, Thailand, 25–28 May 2003; p. III. [Google Scholar]
- Kocarev, L.; Makraduli, J.; Amato, P. Public-key encryption based on Chebyshev polynomials. Circuits Syst. Signal Process. 2005, 24, 497–517. [Google Scholar] [CrossRef]
- Bergamo, P.; D’Arco, P.; De Santis, A.; Kocarev, L. Security of public-key cryptosystems based on Chebyshev polynomials. IEEE Trans. Circuits Syst. I Regul. Pap. 2005, 52, 1382–1393. [Google Scholar] [CrossRef]
- Kocarev, L.; Sterjev, M.; Fekete, A.; Vattay, G. Public-key encryption with chaos. Chaos Interdiscip. J. Nonlinear Sci. 2004, 14, 1078–1082. [Google Scholar] [CrossRef]
- Bose, R. Novel public key encryption technique based on multiple chaotic systems. Phys. Rev. Lett. 2005, 95, 098702. [Google Scholar] [CrossRef]
- Zhang, L. Cryptanalysis of the public key encryption based on multiple chaotic systems. Chaos Solitons Fractals 2008, 37, 669–674. [Google Scholar] [CrossRef]
- Ariffin, M.R.K.; Abu, N.A. -cryptosystem: A chaos based public key cryptosystem. Int. J. Cryptol. Res. 2009, 1, 149–163. [Google Scholar]
- Blackburn, S.R. The discrete logarithm problem modulo one: Cryptanalysing the Ariffin–Abu cryptosystem. J. Math. Cryptol. 2010, 4, 193–198. [Google Scholar] [CrossRef][Green Version]
- Algehawi, M.B.; Samsudin, A.A. new Identity Based Encryption (IBE) scheme using extended Chebyshev polynomial over finite fields Zp. Phys. Lett. A 2010, 374, 4670–4674. [Google Scholar] [CrossRef]
- Haifeng, Q. Pitfalls in identity based encryption using extended Chebyshev polynomial. China Commun. 2012, 9, 58. [Google Scholar]
- Islam, S.K.H. Identity-based encryption and digital signature schemes using extended chaotic maps. Cryptol. ePrint Arch. 2014, 2014, 275–280. [Google Scholar]
- Lai, H.; Orgun, M.A.; Xiao, J.; Pieprzyk, J.; Xue, L.; Yang, Y. Provably secure three-party key agreement protocol using Chebyshev chaotic maps in the standard model. Nonlinear Dyn. 2014, 77, 1427–1439. [Google Scholar] [CrossRef]
- Lee, T.F.; Lin, C.Y.; Lin, C.L.; Hwang, T. Provably secure extended chaotic map-based three-party key agreement protocols using password authentication. Nonlinear Dyn. 2015, 82, 29–38. [Google Scholar] [CrossRef]
- Abd-El-Atty, B.; Amin, M.; Abd-El-Latif, A.; Ugail, H.; Mehmood, I. An efficient cryptosystem based on the logistic-chebyshev map. In Proceedings of the 2019 13th International Conference on Software, Knowledge, Information Management and Applications, 2019, SKIMA, Island of Ulkulhas, Maldives, 26–28 August 2019; pp. 1–6. [Google Scholar]
- Tan, Z. Privacy-preserving two-factor key agreement protocol based on chebyshev polynomials. Secur. Commun. Netw. 2021, 2021, 6697898. [Google Scholar] [CrossRef]
- Meshram, C.; Ibrahim, R.W.; Meshram, S.G.; Imoize, A.L.; Jamal, S.S.; Barve, S.K. An efficient remote user authentication with key agreement procedure based on convolution-Chebyshev chaotic maps using biometric. J. Supercomput. 2022, 78, 12792–12814. [Google Scholar] [CrossRef]
- Meshram, A.; Alouane-Turki, M.H.; Wazalwar, N.M.; Chandrashekhar, M. An Efficient Three-Party Authenticated Key Exchange Procedure Using Chebyshev Chaotic Maps with Client Anonymity. Comput. Mater. Contin. 2023, 75, 5337. [Google Scholar] [CrossRef]
- Tenny, R.; Tsimring, L.S.; Larson, L.; Abarbanel, H.D.I. Using distributed nonlinear dynamics for public key encryption. Phys. Rev. Lett. 2003, 90, 047903. [Google Scholar] [CrossRef]
- Kumar, A.; Ansari, M.M. Multi message signcryption based on chaos with public verifiability. Int. J. Sci. Technol. Res. 2013, 2, 194–198. [Google Scholar]
- Chatterjee, S.; Roy, S.; Das, A.K.; Chattopadhyay, S.; Kumar, N.; Vasilakos, A.V. Secure biometric-based authentication scheme using Chebyshev chaotic map for multi-server environment. IEEE Trans. Dependable Secur. Comput. 2016, 15, 824–839. [Google Scholar] [CrossRef]
- Attaullah; Javeed, A.; Shah, T. Cryptosystem techniques based on the improved Chebyshev map: An application in image encryption. Multimed. Tools Appl. 2019, 78, 31467–31484. [Google Scholar] [CrossRef]
- Louzzani, N.; Boukabou, A.; Bahi, H.; Boussayoud, A. A novel chaos based generating function of the Chebyshev polynomials and its applications in image encryption. Chaos Solitons Fractals 2021, 151, 111315. [Google Scholar] [CrossRef]
- Khan, M.; Alanazi, A.S.; Khan, L.S.; Hussain, I. An efficient image encryption scheme based on fractal Tromino and Chebyshev polynomial. Complex Intell. Syst. 2021, 7, 2751–2764. [Google Scholar] [CrossRef]
- Ren, H.; Niu, S.; Chen, J.; Li, M.; Yue, Z. A Visually Secure Image Encryption Based on the Fractional Lorenz System and Compressive Sensing. Fractal Fract. 2022, 6, 302. [Google Scholar] [CrossRef]
- Guillén-Fernández, O.; Tlelo-Cuautle, E.; de la Fraga, L.G.; Sandoval-Ibarra, Y.; Nuñez-Perez, J.-C. An Image Encryption Scheme Synchronizing Optimized Chaotic Systems Implemented on Raspberry Pis. Mathematics 2022, 10, 1907. [Google Scholar] [CrossRef]
- Mohamed, N.A.E.-S.; El-Sayed, H.; Youssif, A. Mixed Multi-Chaos Quantum Image Encryption Scheme Based on Quantum Cellular Automata (QCA). Fractal Fract. 2023, 7, 734. [Google Scholar] [CrossRef]
- Zhao, G.; Ma, Y. Introduction to chaotic cryptographic algorithms. In Chaotic Applied Cryptography, 1st ed.; Cheng, J., Ed.; Science Press: Beijing, China, 2021; pp. 176–194. [Google Scholar]
- Kocarev, L.; Shiguo, L. Chaos-Based Cryptography: Theory, Algorithms and Applications, 1st ed.; Springer: Berlin, Germany, 2011; pp. 33–40. [Google Scholar]
- Kocarev, L.; Jakimoski, G.; Stojanovski, T.; Parlitz, U. From chaotic maps to encryption schemes. In Proceedings of the 1998 IEEE International Symposium on Circuits and Systems, ISCAS, Monterey, CA, USA, 31 May–3 June 1998; pp. 514–517. [Google Scholar]
- Cheong, K.Y.; Koshiba, T. More on security of public-key cryptosystems based on Chebyshev polynomials. IEEE Trans. Circuits Syst. II Express Briefs 2007, 54, 795–799. [Google Scholar] [CrossRef]
- Wang, K.; Pei, W.; Zou, L.; He, Z. Cryptanalysis of multiple chaotic systems based public key encryption technique. Acta Phys. Sin. 2006, 55, 6234–6247. [Google Scholar] [CrossRef]
- Zhang, C.; Liang, Y.; Tavares, A.; Wang, L.; Gomes, T.; Pinto, S. An Improved Public Key Cryptographic Algorithm Based on Chebyshev Polynomials and RSA. Symmetry 2024, 16, 263. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).