1. Introduction
The neural network using artificial intelligence, which originated in the 1940s as part of a widespread computerization effort, is a sophisticated bionic computational structure that is able to resolve complicated logical and nonlinear issues. It has a structure made up of a variety of small, simple neurons that are interrelated with one another in specific ways [
1].
ANNs have widely been used throughout forecasting models in the building sector during the past several decades. Scientists utilized this approach across every facet of the building industry to maximize the benefits associated with its superiority over traditional modelling techniques. Some of the instances of ANNs utilized in the building sector are financial performance prediction, risk analysis, resources improvement, and procurement predicted results including performance evaluation [
2].
ANN is a flexible computational tool that simulates the human mind’s capacity to use reasoning and methods of pattern identification efficiently. Although knowledge of ANNs has already been present for a while, their utilization in civil engineering only really began in the late 1980s, predominantly within the construction industry [
3].
Two aspects of neural networks bear similarities to the human’s brain: Learning is the method by which a neural system gets information: Knowledge of a neural network is held in what are called synaptic weights, which are inter-neuron interaction strengths [
4]. Neural network representation that includes linear as well as non-linear relations, along with the capacity to infer such relationships based on modelled data oneself, are the actual characteristics and advantages of neural networks as a tool. For the goal of modelling data with non-linear features, conventional linear mathematical models are merely insufficient [
4].
In addition to providing an overview of the uses of artificial intelligence (AI) and neural networks (ANNs) in many fields, Elmusalami [
5,
6] and Naqvi et.al [
7] also attempted to investigate novel applications of these technologies.
Regarding building projects, cost will frequently be the initial factor that must be taken into account. The accomplishment of any construction project depends critically on a reliable estimation of the materials and expenditures involved [
8]. The intricate design of the construction business and the uniqueness of each project endeavor suggest that a variety of factors could influence the project’s total cost [
8].
In order to obtain the most accurate results in this field, the aim of this paper was to compare two ANN-based tools for cost prediction focused on building renovation projects in Greece. This is since, as far as the authors are cognizant, no such models exist, which led to an extensive literature review.
To create a comparable type of cost estimating model, information from prior remodeling projects needs to be collected. As ANN models are able to identify patterns and relationships, they can generate projections that are more precise when they use historical project data. Whenever there are few project details accessible, they may require adjustments even in the early phases of a project.
Comparing by using ANN models to estimate renovation costs necessitates making adequate use of data for model training and validation. Builders and engineers may benefit from the most optimal ANN model by using its realistic forecasts after it has been implemented and identified. As of this writing, no such model which resulted from the comparison of RBF and MLP approaches in order to implement it in a building’s renovation cost estimation based on a particular set of work packages exists.
A substantial dataset of actual project cost data was obtained from a Greek contractor involved in building renovations in order to fill the gap in the field of research. In order to create ANNs for cost prediction, the information gathered was organized, evaluated, and suitably encoded. The network was developed, trained, and tested using IBM SPSS Statistics software 28.0.0.0. Finally, the dependent variable is the final cost. The initial cost, estimated completion time, actual completion time, delay time, initial demolition-drainage costs, final demolition-drainage costs, cost of expenses, initial plumbing costs, final plumbing costs, initial heating costs, final heating costs, initial electrical costs, final electrical costs, initial masonry costs, final masonry costs, initial construction costs of plasterboard construction, final cost of plasterboard construction, initial cost of bathrooms, final cost of bathrooms, initial cost of flooring, final cost of flooring, initial cost of frames, final cost of frames, initial cost of doors, final cost of doors, initial cost of paint, final cost of paint, initial cost of kitchen construction, and final cost of kitchen construction are the independent factors. First, the radial basis function (RBF) is the process that is used. With up to 6% sum of squares error and nearly 0% relative error in the training sample—which makes up approximately 70% of the entire sample—the model’s efficiency throughout training and testing was assessed and analyzed. Secondly the multi-layer perceptron (MLP) is the approach that is applied. The model’s efficiency throughout training and testing was evaluated and analyzed, with the sum of squares error to be ranged between 1% and 5% and 0–7% relative error in the training sample, which accounts for roughly 70% of the total sample. As an instance, it has been shown that ANNs are a very useful technique for estimating total costs, especially for building renovation projects. Specifically, there is the highly precise RBF approach, in which the error value in the model with 43 units in the hidden layer remains steady.
In this regard, and centered on what is presented above, in the construction sector, building renovation is a primary importance, yet accurate cost estimation is a major challenge. To decrease economic disparities, the usage of artificial neural network (ANN) models is highlighted for forecasting the costs of renovations. ANN models were developed and tested, according to the substantial real project cost data that Greek contractors provided. Radial basis function (RBF) and multi-layer perceptron (MLP) are two ANN techniques that were evaluated in the present research. The RBF model was far more accurate in cost estimation than the MLP model.
The sections of this article are organized as follows: A comprehensive assessment of the literature is given in
Section 2 regarding RBF and MLP ANNs as a tool for building projects in particular and the construction industry in general. The problem formulation is presented in
Section 3. The methodology as the data collection and analysis processes for developing the RBF and MLP ANN models to predict and compare the ultimate costs of building renovations are outlined in
Section 4.
Section 5 present the results as well as clarifying them. Conclusions, limitations, and recommendations for additional study are included in
Section 6.
2. Literature Review
In the twentieth century, there has been a dramatic increase in academics’ interest in utilizing ANNs for estimation. ANNs have a lot of potential, but there are a lot of unknowns as well, according to Zhang et al. [
9] who held this belief even in 1998. It is still unknown to researchers what significant components mean in terms of ANN prediction efficacy. However, as the subsequent paragraphs will explain, ANNs have been utilized extensively in construction research [
10].
Adeli [
11] attempted to demonstrate multiple uses for ANNs. The ANNs focused on managing, engineering for construction, and building engineering categories. The simple backpropagation technique represents the foundation for an increasing amount of ANN usages in building engineering. The current research has primarily concentrated on methods to integrate ANN into various other approaches of programming, including fuzzy logic, evolutionary algorithms, and wavelet. The combinations that result improved the effectiveness of models based on ANN.
In contrast to traditional causality and effect theories, Buscema [
12] claims that ANNs represent multifarious, complicated, and dynamic phenomena that are unanticipated and uncontrollable. It is likely that in their basis, they are nonlinear. Whenever linear-based methodologies apply to planned interventions involving nonlinear dynamics, they claim, it is conceivable to employ ineffective approaches to intervention and make incorrect conclusions regarding what has transpired [
12].
ANNs are considered indispensable in the building industry. Time series, classification, and forecasting are the three types of challenges that ANNs have already been used to solve. The ANN needs to be trained in order this process to occur. Considering that the qualities of ANNs are not dependent on a formal development procedure, there is a well-established technique. An ANN’s typical form is a multi-layer perceptron. Several instances have demonstrated their flexibility [
13]. A type of supervising ANN called radial basis function structures is significant because it utilizes guided machine learning (ML) to operate as a nonlinear categorization method. A more thorough evaluation is performed by nonlinear approaches to classification as by basic techniques by using complicated equations.
The primary reasons for inaccurate cost estimation remain to be the following: inadequate time to create cost estimates, inadequate paperwork for tenders, and a large range of pricing from contractors. These factors have been related to the estimating function’s inadequate practical knowledge about the process of building [
14].
Cost estimate is usually a multidisciplinary process that involves feedback from the design team and is based on previous information. The category of project will influence the cost estimation, which is linked to evolving elements of construction and expertise [
14].
Advances in models for predictions have been made possible by the combination of fundamental computational methods including fuzzy logic (FL), ANNs, and evolutionary algorithms (EAs). Different hybrid systems have been developed as a result of such comprehensive simulations, which allow the shortcomings of one approach to be offset by a variety of techniques. It is dependent on the software sector and the unique characteristics of the data available to decide which structure is best and provides accurate information for cost estimation [
2].
In fact, a very prevalent category of construction projects, for which there are numerous cost prediction models, remains building. This was discovered in that 40 of the 92 papers that were examined made reference to buildings in the relevant review of literature that Hashemi et al. [
15] collected. Furthermore, Antoniou et al. [
16] discovered in their research that 31 further articles out of 51 that were published in 2021 and 2022 included models for estimating construction costs for building projects. Eleven studies out of the thirty-one included ANNs in the models they developed. Once an illustrative non-exhaustive content evaluation was conducted on the research projects that were determined to be able to generate cost of construction predictions over buildings utilizing ANNs, the subsequent research findings were identified as distinguished.
It is well acknowledged that construction companies utilize cost estimation mostly to determine the price to assess for estimates of quantities that are created using a standard technique of measurement.
According to Chua et al. [
17], it is critical for developers, suppliers, and stakeholders to recognize and comprehend particular traits that may be crucial to a building construction’s ultimate completion. In an attempt to identify the critical managerial characteristics associated with successful financial efficiency, they then used an ANN approach. They recommended several of factors, such as the quantity of organizational levels between the project leader and the builders, the quantity of thorough planning finished before building, the extent of managerial discussions during constructing, the rate of funds revisions, the implementation of a constructability plan, group employee turnover, the amount of income allocated for project leadership, and the supervisor’s expertise in the field.
Forty-eight building initiatives from builders and twenty-seven from shareholder organizations were included in Chua et al.’s study [
17]. Upon completion of training, the finished model was applied as a predictor for estimating the manner in which a building cost will function. Even if the functional connection amongst the inputs and their results are not clearly defined, a financial performance model continues to be constructed through to this methodology [
17].
Using data from 300 structures, Emsley et al. [
18] employed ANNs to forecast the overall cost of construction. The data from building costs, construction documents, and the outcomes of a widely circulated interview questionnaire comprised the information that was gathered. The ultimate sum totals in the data allowed for the creation of a model that could evaluate the customer’s overall expenses, which included both internal and external expenses in addition to building expenditures. The ANN approach’s ability to simulate nonlinearity in the data was found to be its main advantage, as they used linear regression (LR) techniques to construct additional models to evaluate the models built using ANN. With an uncertain degree of accounting for customer modifications, the best model generated a mean absolute percentage error (MAPE) of 16.6%. The standard estimating method, which finds that the MAPE results fluctuate between 20.8% to 27.9%, differs sharply via findings.
Günaydin and Doħan [
19] investigated the effectiveness of ANN techniques in resolving cost estimating problems in the early phases of building planning processes. Utilizing cost and architectural information coming from 30 projects, an ANN-based simulation that included eight design factors was created and validated to determine the square meter cost of a building’s concrete reinforcement support systems for four- to eight-story apartment buildings in Turkey. The model achieved a 93% accuracy rate.
In addition, Kim et al. [
20] evaluated into the effectiveness of three cost estimation methods in an effort to show how important realistic cost forecasting could be for building tasks. They employed ANNs, multiple regression analysis (MRA), and case-based reasoning (CBR) utilizing past cost information for 530 structures. Construction companies in Seoul, Korea, built the household structures between 1997 and 2000. Although the most effective ANN forecasting model produced more precise forecasting outcomes compared to either the MRA as well as the CBR forecasting versions, the CBR estimating structure accomplished more in terms of lengthy utilization, time in addition to accuracy decisions, and available data derived from outcomes.
To improve the precision of cost estimation, Cheng et al. [
21] proposed the AI process known as the evolutionary fuzzy neural inference model (EFNIM). In order to help the EFNIM locate workable solutions in difficult circumstances, the advantageous properties of ANNs, evolutionary algorithms, and fuzzy logic were successfully added to the model. Whenever these approaches were combined, they enhanced the advantages of each approach and somewhat offset any shortcomings that resulted from using them alone. Fuzzy logic (FL) handled risks as well as roughly inferences, genetic algorithms (GA) have been utilized for optimization, and ANNs were implemented for fuzzy input–output visualization. Because of the above, Cheng et al. [
21] provided two approaches that might be used to determine conceptual building expenses prior to projects even starting.
An early-stage building initiative’s cost was estimated using an ANN-based model by Arafa and Algedra [
22]. Seventy-one building projects across the Gaza Strip were taken from a database. These included household buildings, schools, preschools, and government or NGO buildings. Key characteristics from architectural plans were identified. These were used to calculate building costs. The parameters included the number of stories, area, basement space, groundwork type, column quantity, elevators, and typical flooring size. An ANN model was developed with these inputs. It approximated building costs with a single output neuron, one hidden layer, and seven input neurons. The model showed that ANNs could estimate early construction costs using basic data. The most important factors were the number of stories, ground level dimensions, groundwork type, and elevator count.
Wang et al. [
23] presented an intriguing perspective. They innovated by developing models that used support vector machine (SVM) models and ANNs to anticipate construction costs as well as performance utilizing early planning information as parameter inputs. By gathering preliminary scheduling and building feedback from 92 building endeavors via a pertinent business questionnaire research, they found that the initial preparation stage could potentially effectively be employed to forecast successful completion of projects via ANNs. The 92 building initiatives consisted of 80 novel building endeavors and 12 renovations, of which 32 were private and 60 public. It was demonstrated that models constructed with bootstrap-aggregated ANNs proved more reliable and precise than models made from single ANNs.
A wide range of both qualitative and quantitative measures were implemented to identify ANN algorithms by Shehatto and by El-Sawalhi and Shehatto [
24,
25] in order to obtain cost information for each phase of the building process and precise building construction expenditure estimates. The database consisted of 169 accomplished building initiatives in the region of Gaza. Past projects of building examples from districts, federal offices, engineering education institutions, outside contractors, and specialists served as the source material for the structures. As independent input variables, eleven significant parameters were taken into consideration, and the overall project cost was considered the dependent output parameter. The software called NeuroSolutions was utilized to train the created models. As the mean inaccuracy for the improved model remained overall acceptable, or less than 6%, their ANN models additionally showed that an ANN could accurately calculate building project expenses despite demanding major definite drawings. The sensitivity analysis’s findings showed that the number of stories and the typical ground area provided the most effects on building costs. Eleven elements should be considered distinct inputs that impact the overall project price, the researchers concluded.
It was firmly held by Elfaki et al. [
26] that a number of unique elements influence cost estimation in construction projects. The factors unique to estimation methods and the variables unique to concepts and projects could be separated into two distinct groups. They centered on the necessity of developing a cost forecast methodology that could take into consideration all predicting elements from every standpoint and included a standard validation technique that might have been utilized to assess the level of precision of cost prediction proposition.
In order to predict the total architectural cost of building projects in the Philippines, Roxas and Ongpeng [
27] also used an ANN model. Thirty building projects’ worth of data were collected and divided into three categories: sixty percent for training, twenty percent for performance verification, and twenty percent for an entirely independent test of network generalization. They included six independent variables in their ANN model, which was carried out in MATLAB for simulation: the overall ground region, the number of floors and basements, the total cement, the size of the structure, and the whole weight of the reinforcing steel. Applying the feedforward backpropagation method, the optimal model for the total building cost was developed. The amount of surface area, quantity of the flooring and foundations, amount of concrete, size of structure, thickness of reinforcing steel, post-tensioned sector, number of piles, etc., are some of the factors that the scientists proposed affect structural or civil engineering costs. However, additional building costs involve architectural fees, which vary according to the type and quality of supplies chosen for the exterior walls, ceilings, windows and doorways, flooring, the painting process, and other architectural elements. In conclusion, the building’s entire construction cost is completed by the setting up of elevators, electricals, climate control, heating infrastructure, and wastewater and water supply networks.
In a determination to use ANNs for building project cost planning, Ambrule and Bhirud [
28] looked into and addressed problems in cost estimation at the very beginning of building planning during the preliminary design stage. For upgraded buildings made of concrete, a graphical user interface (GUI) cost prediction model was also developed and validated during the early design phase. As early as the engineering process, Ambrule and Bhirud [
28] demonstrated that the ANN GUI model might be useful for managers in advising on the project’s completion.
Utilizing the first estimations of the costs of 25 construction factors, Abd and Naseef [
29] created an ANN-based mathematical model to calculate the total price of building development. They collected data from 501 building endeavors in Iraq that were completed among 2005 and 2015. The data contained the entire amount invested in different kinds of construction, such as excavation of foundations, filling landfills, filling them with subbase, creating moisture-proof layers, elements of construction, regular concrete for boundaries, building foundations, etc. With respect to the estimation of construction project costs in Iraq, the ANN algorithm demonstrated exceptional performance, as evidenced by the correlation values between the variable results of almost 100%, the error rate of roughly 5.81%, and a level of accuracy that was 94.19%.
An ANN approach to forecast building construction costs was also developed by Indian researchers. In particular, using survey questionnaires and the guidance of building developers and experts, Chandanshive and Kambekar [
30] gathered the amount and cost information from 78 buildings, comprising cottages and smaller and mid-sized homes developed near and inside Mumbai, India, between 2017 and 2019. The following 11 independent variables were linked to the quantities of particular construction functions: the number of levels, the standard surface area, the elevator wall size, the wall’s exterior size, the external plaster amount, the amount of floor area, the quantity of columns, the foundation’s category, and the number of homes. The entire project’s total expenditure was the sole outcome parameter. They utilized a backpropagation approach to build a multilayer feedforward artificial neural network for their model. To increase the ANN’s generalization performance and avoid overfitting, early ending and Bayesian regularization procedures were applied. It was shown that early stopping during the building cost forecast was not as effective as the Bayesian regularization process. The results showed that the trained ANN model could accurately predict the overall cost of building construction [
30].
With the help of historical information from 136 structures built between 2011 and 2015, a study was conducted in Yemen, another growing economy, to present a cost forecasting tool using ANN models via Hakami and Hassan [
31]. To provide an initial estimate of the entire building expense, they incorporated 17 independent factors into their model. The project’s classification, number of stories, length of floors, kind of foundation, number of lifts, outside finishing structure, decorating style, air conditioning category, HVAC, bottom floor, flooring height, foundation type, location region, tile kind, electrical and mechanical installations, and project’s address were the 17 independent factors. Using the NeuroSolutions 6 tool, they designed, trained, tested, and conducted sensitivity assessments on the building. The results of the evaluation, sensitivity analysis, and education were quite satisfactory, having less than 1% inaccuracy and good effectiveness and validity.
The cost predicted model that was determined to be specific to public buildings was offered by Sitthikankun et al. [
32]. They indicated that there are two commonly used methods for determining the expenditures for publicly owned buildings: a thorough prediction that has the benefits of a more accurate cost approximation, yet negative consequences concerning the demand for a definitive successful completion and a related demand for an extended period to complete, and consequently being absent of set financing deadlines. The study employed data from 50 governmental buildings that were finished in Thailand in 2020. There were eleven independent variables that were considered: total space usable, mean perimeter size, mean story height, entire height of the construction, the number of floors, total area under roofing, total area in bathrooms, ground surface slab, entire area of apertures, the kind of roof, and kind of slab construction. Utilizing a model with two hidden layers of ten and eight nodes, the artificial neural network (ANN) approach was employed to forecast the outcomes. With a correlation coefficient (R
2) of 0.914 and a root mean square error (RMSE) of 0.331, the model’s accuracy was demonstrated. For estimating building costs, lowering tolerances, and minimizing effort, this approach provides a safe option for public tendering.
Building Cost Estimation—The Present State of Research: The Special Issue of Building Renovation Cost Estimation
The issue of cost estimation in the construction sector has been extensively studied over the past few decades by many researchers from a variety of professions [
16,
18,
20,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42,
43] who designed and developed a variety of models.
One considerable gap involves the fact that neither of the previously mentioned studies address cost estimation in building renovation projects during the predesign process [
10,
44]. Furthermore, as long that it is aware, the accuracy of the final cost after completing a building renovation project has also not been confirmed. This testing is essential to verify the model’s accuracy and prevent future forecasting errors. The comparative evaluation of two ANN methods, radial basis function and multi-layer perceptron, for prediction is remarkable. Specifically, the evaluation of outcomes, using initial and final costs as independent variables, is interesting as it resulted in the following paragraphs. Moreover, upon completion of a project, a verification may be conducted to ensure that the model remains capable of accurately estimating the project’s final cost.
Aiming to offer cost estimation methods for new building development, the studies mentioned previously all made this endeavor. A research project examining the cost performance of renovation projects, also referred to as building reconstruction, was located. Attalla et al. [
45] attempted to examine this difficult setting and suggested an ANN-based model to compute a cost performance score using information known at the start of the building process. They conducted a survey among industry experts. The goal was to understand overspending and subpar work in 50 reconstruction programs. They recorded every real expense variation from the estimated numbers. They also noted the project control techniques used. Two measures of financial deviation were employed: client fee delays and building constructor repair expenses. Out of 36 independent variables, 18 were selected. These were believed to impact cost-effectiveness. The variables were related to project management methods and tools. These included timeline, quality, cost, safety, and interaction methods and tools. They also included scope definition, bidding, and project completion methods. To construct their models, they used statistical analysis (Systat) and an ANN (Neuro Shell2). The ANN’s model proved more sensitive to a greater variety of factors, even if the two techniques’ performance was equivalent. Utilizing the schedule and cost predictions given at the beginning of construction, this study served as the inspiration for research work to design an ANN model for actual cost prediction and mostly ex-post verification of building renovation projects in the field to predict and mostly verify final cost variances.
In the field of building renovation project cost estimation, an effort was made by the authors [
44] that utilizes IBM SPSS Statistics tools to create, train, and test an ANN model. It relies on extensive review of the literature and actual renovation data from construction businesses. The model employs starting cost, projected duration, and initial demolition cost as a radial basis function technique to provide the foundation for inputs. The model demonstrates excellent accuracy with near 0% relative error and up to 2% sum of squares error, proving the practicality of the ANN in estimating the overall cost of renovations. It was the initial ANN model for building renovation project final cost prediction that has been published, as far as the authors are aware.
Table 1 provides an overview of the methods, sources of data, and other components that the aforementioned researchers and more employed.
As the
Table 1 illustrates, in the context of the building construction sector, there has been limited research focusing on the comparative evaluation of radial basis function (RBF) and multi-layer perceptron (MLP) methods. Notably, researchers such as Bayram et al. [
55] have made contributions in this area. However, it is important to highlight that, to the best of our knowledge, there has been a significant gap in research specifically targeting the buildings renovation sector.
MLP neural network models are among the most frequently employed approaches in these analyses. These models are often utilized alongside other methods, such evolutionary fuzzy neural inference system mechanisms (EFNSM) [
21], support vector machines (SVMs) [
23], generalized regression neural networks (GRNNs) [
18], adaptive neuro fuzzy inference system (ANFIS) and simple linear regression analysis (SLRA) [
56]. These approaches are all differentiable and have been applied to various aspects of buildings construction; at present, there is still a lack of comparative analysis about the relative efficacy of these approaches, especially in the building renovation sector.
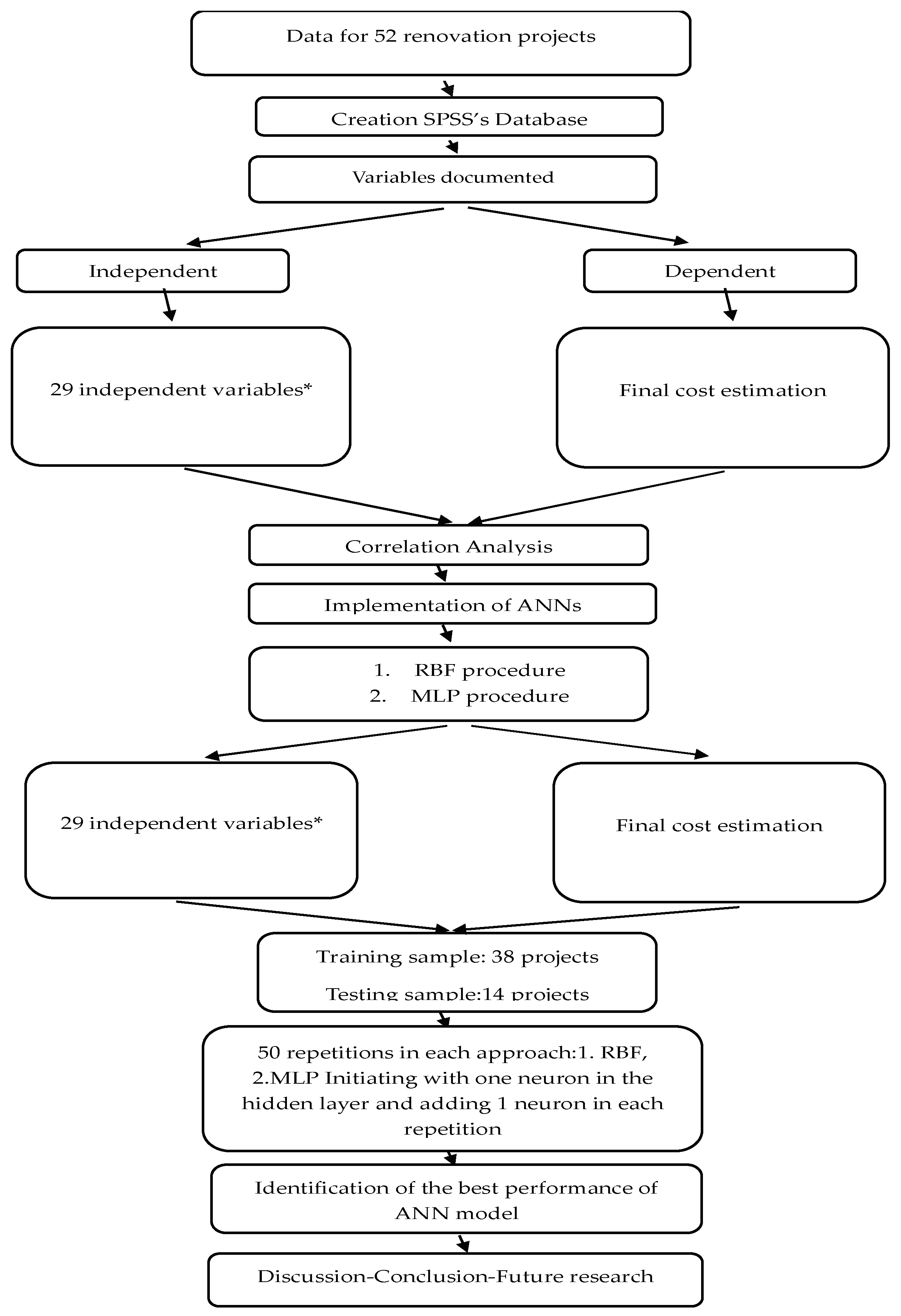
4. Methodology
4.1. Artificial Neural Network Construction for Buildings’ Renovation Cost Estimation
The modelling procedure using neural networks consists of five primary components. These are (1) collecting, analyzing, and representing data; (2) determining the architecture; (3) determining the learning method; (4) training the model; and (5) testing the model that was trained to assess generalization [
50].
The current paper produces a number of ANN models. An independent building firm that specialized in building renovations provided an account of fifty-two renovation projects. That particular company has decades of knowledge regarding renovations. Given that the firm used a consistent approach across all its projects, the data were easily processed. Every one of them was a private undertaking. A thorough survey and measurement of every building construction produced an analytical cost. Both the owner and the builder approved the initial price. The additional expenses as described within the Greek legislation regarding private projects have also been considered to determine the overall cost of each project.
Twenty-nine parameters, namely, initial cost, estimated completion time (in days), actual completion time (in days), delay time (in days), initial demolition-drainage costs, final demolition-drainage costs, cost of expenses (fuel and parking), initial plumbing costs, final plumbing costs, initial heating costs, final heating costs, initial electrical costs, final electrical costs, initial masonry costs, final masonry costs, initial construction costs of plasterboard construction, final cost of plasterboard construction, initial cost of bathrooms, final cost of bathrooms, initial cost of flooring, final cost of flooring, initial cost of frames, final cost of frames, initial cost of doors, final cost of doors, initial cost of paint, final cost of paint, initial cost of kitchen construction, and final cost of kitchen construction, were all entered into a database. A database with the aforementioned technical specifications was created using IBM SPSS Statistics software [
58]. The buildings are primarily urban residential apartment complexes located primarily in the region of Thessaloniki, Greece. The requirement for energy improvement was the primary driver behind the renovations, but there was also modernity; redevelopment; and, very infrequently, alteration in utilization factors. Particularly in terms of those located in the historic city center, the buildings are frequently older by a few decades. The projects had begun in 2018 and were terminated in 2023.
4.2. Factor Determination and Evaluation Influencing the Estimation of Building Rehabilitation Costs
Using an ANN model, nonpredictive or inefficient variables could be eliminated through cutting down from the model, unlike regression methods, which require verification of the covariance between the variables. On the other hand, lower correlation values provide the foundation for the variable choices. Since solely those that are crucial variables are taken into account, this validates the incorporation in the model and greatly expedites the training procedure.
The analysis of correlation was accomplished first.
Table 2 displays the outcomes.
Table 2 indicates that the dependent variable final cost and the independent variables related to project such as initial cost, estimated completion time, actual completion time, delay time, initial demolition-drainage costs, final demolition-drainage costs, cost of expenses, initial plumbing costs, final plumbing costs, initial heating costs, final heating costs, initial electrical costs, final electrical costs, initial masonry costs, final masonry costs, initial construction costs of plasterboard construction, final cost of plasterboard construction, initial cost of bathrooms, final cost of bathrooms, initial cost of flooring, final cost of flooring, initial cost of frames, final cost of frames, initial cost of doors, final cost of doors, initial cost of paint, final cost of paint, initial cost of kitchen construction, and final cost of kitchen construction have a significant link.
The intricate connections between numerous variables must be acknowledged when managing a project. The total performance of the project is impacted by all of the elements mentioned, including the starting cost, ultimate cost, expected completion time, actual completion time, delay time, and several other charges. Throughout the course of the project, they have an impact on one another and are related. A project’s ability to remain within budget and fulfil deadlines does not constitute its only mark of success. It additionally entails producing excellent outcomes that are consistent with the project’s goals.
On the contrary hand, efficiency describes achieving these objectives by utilizing the best advantage of available resources. For example, the cost of demolition per contract and the total cost of renovations has a modest association. In light of the reason that there exists a direct proportionality among the tender offer and project agreement period, this association is significant. An increase in project time results in a raise in construction costs. The renovation project’s final cost would therefore be impacted. During a building renovation project, there are numerous categories that could impact the final cost, and the cost of demolition is just one of them. The other parameters such as the aforementioned have a significant effect as well. The expected or budgeted cost of a project at its inception is referred to as the initial cost. The project’s start-up costs encompass expenses for supplies, labor, machinery, and additional resources. When a project is finished, its final cost is the entire amount that was actually spent. Along with all other unforeseen charges that might have come up during the completion of the project, it comprises all direct and indirect costs.
Cost overruns or savings can be discerned from the discrepancy between the initial and final expenses. The estimated time needed to complete the project in its entirety is referred to as the estimated completion time. It takes into account the resource’s availability, dependencies between tasks, and project partition structure. Precise estimation facilitates scheduling, resource allocation, and project deadline compliance. The real period of time required for completing the project has been established as the actual completion time. It takes into consideration any modifications, issues, or delays that happened throughout implementation. Project performance can be assessed by comparing the expected and actual completion times. The term delay time denotes the additional period of time that is needed over the projected completion date as a result of unanticipated events such as bad weather, a lack of resources, or other problems. Schedule delays have an effect on projects and might result in cost overruns. The initial expenditures of demolition and disposal involve cleansing the region of any existing structures or prepare for construction. Any additional costs incurred throughout the demolition and disposal stages are included in the final demolition-drainage costs. For precise forecasting and project planning, these expenses are crucial. The cost of expenses includes all project-related expenditures, including overhead, administrative fees, licenses, and permits. Monitoring these expenditures provides effective budgetary management and transparency in finances.
The project’s initial and final water supply, heating, and electrical costs cover the systems’ installation, upkeep, and repairs. While final costs represent actual expenditures, initial costs are estimated at the beginning of the project. Masonry expenses are associated with building walls, foundations, and other structures out of stone, brick, or concrete blocks.
Whereas final expenses take into consideration any variations during building, initial masonry costs are only estimates. Gypsum-based boards are used in plasterboard construction for the walls, ceilings, and partitions. Though labor and material estimates are included in the initial construction costs, the actual costs of installing plasterboard are taken into account in the final costs. In addition, variables such as initial and final cost of bathrooms, initial and final cost of flooring, initial and final cost of frames, initial and final cost of doors, initial and final cost of paint, and initial and final cost of kitchen construction work together to influence on schedule, cost containment, and the project’s accomplishment. Project management is enhanced, resource allocation is optimized, and cost drivers are found by analyzing their association. Throughout the duration of a project, accurate monitoring, estimation, and adaptability are essential.
Below, an attempt has been made to verify the correlation between these 29 dependent parameters and the final cost of a building project.
There is a definition for both the independent and dependent variables. The IBM SPSS software was utilized to construct, train, and test the models. It was determined to use the RBF and the MLP in order to compare the results from those two applications. The total final cost of renovation for each project, as per the company’s reports, is the dependent variable. Initial cost, estimated completion time (in days), actual completion time (in days), delay time (in days), initial demolition-drainage costs, final demolition-drainage costs, cost of expenses (fuel and parking), initial plumbing costs, final plumbing costs, initial heating costs, final heating costs, initial electrical costs, final electrical costs, initial masonry costs, final masonry costs, initial construction costs of plasterboard construction, final cost of plasterboard construction, initial cost of bathrooms, final cost of bathrooms, initial cost of flooring, final cost of flooring, initial cost of frames, final cost of frames, initial cost of doors, final cost of doors, initial cost of paint, final cost of paint, initial cost of kitchen construction, and final cost of kitchen construction are the independent factors. For the training sample, 38 projects in total were selected and 14 of those had been chosen for testing. As per the results of the literature review indicated above, the percentage of 70% of the project sample allocated for training and 30% for testing was deemed appropriate. In the hidden layer, the number of neurons (units) is the main area of change.
Deciding the number of hidden layers along with nodes on the hidden layers constitutes one of several critical decisions in neural network architecture. In this regard, Li [
41] reports two useful principles: (1) adding nodes to every hidden layer has little influence on the forecasting success of neural network models; (2) raising the number of hidden layers advances a neural network’s estimation success to a certain degree; however, it would lengthen the neural network’s training procedure.
The ideal number of hidden nodes could not be precisely determined, but trial and error have revealed that it ought to range among the mean and the total of the outputs and inputs nodes [
59].
The hidden layers of an ANN model can display a nonlinear connection among inputs and outputs, making it more advantageous and straightforward compared to multilinear and nonlinear regression models, respectively [
59].
4.3. Implementation of the Radial Basis Function Method (RBF)
Beginning with the RBF and with one neuron in the hidden layer, the analysis proceeds on by adding one neuron for each additional time and analysis. The hidden layer activation function refers to the normalized radial basis function, used to connect the values of the units in a single layer to the values in the one that follows. The identity function roles as the output layer’s activation function, and thus the output units are simply the weighted sums of the hidden units. Within the current design of the model, the normalized radial basis function serves as the activation function for the hidden layer. This function utilizes the SoftMax activation function to normalize all concealed unit activations in order to ensure their sum equals 1. The overlapping factor is the multiplier of the breadth of the radial basis functions. The overlapping factors were computed automatically. The amount of input data, denoted by d, is 1 + 0.1d.
The hyperbolic tangent sigmoid transfer function, which specifies the behavior of the network model and produces output values within −1 and 1, was chosen as the function for the current model. Equation (1) defines the hyperbolic tangent sigmoid transfer function, which is the function that has been adopted [
58]:
The search finally arrived at a hidden layer ANN with 50 neurons. The research essentially yielded fifty models. According to the study, the ANN with 43 neurons in the hidden layer produced the most accurate outcomes based on relative error and sum of squares error.
The data collected by the trained model showed that the method using ANN was effective in predicting the buildings’ cost estimate with the least amount of construction data available and without requiring a more detailed architecture. We carefully selected attributes to maximize the model’s ability to learn from the sparse input. To accomplish such a feat, the most pertinent independent variables had to be chosen. Additionally, in an attempt to eliminate errors or variations, we verified using high-quality data that were as accurate as possible. Ensuring the accuracy and consistency of our data source was the initial goal. When a building renovation construction company with decades of expertise provides high-quality data, it may significantly improve the performance of models, especially when the dataset is small to prevent overfitting. Furthermore, we employed regularization approaches such as early stopping, notably in the MLP approach. The proposed methodological approach’s flowchart is shown in
Figure 1:
4.4. Implementation of the Multi-Layer Perceptron Method (MLP)
In a subsequent phase, the multilayer perceptron method (MLP) was implemented. By using the same input data and, as an output parameter, the final cost of each renovated building as mentioned in the preview paragraphs, the analysis commenced with one neuron in the hidden layer and added one neuron for every incremental time and analyses.
The hyperbolic tangent sigmoid transfer function, which specifies the behavior of the network model and produces output values within −1 and 1, was chosen as the function for the current model.
The one hidden layer activation function refers to the hyperbolic tangent function, used to connect the values of the units in a single layer to the values in the one that follows. Within the current design of the model, the hyperbolic tangent function serves as the activation function for the hidden layer. This function might be expressed as follows [
58]:
The range of values (–1, 1) is obtained by transforming real-valued arguments. It demonstrates the way each of the units in the hidden levels are activated when automatic architectural selection is applied.
The hyperbolic tangent function acts as the output layer’s activation function, and thus the output units are simply the weighted sums of the hidden units. The function can also be expressed in the same form as described above in (2).
It is necessary to identify more than one scale-dependent variable in order to access the rescaling of scale dependent variables controls. We adjusted a normalized method of division by the range
[
58] by subtracting the minimum. Normalized adjusted values range from −1 to 1. When the output layer employs the hyperbolic tangent activation function, then this rescaling approach must be utilized for scale-dependent variables. To guarantee that all rescaled dependent variable values fall within the activated function’s range, the adjustment option applies a small number, as an alteration to the rescaling calculation. Specifically, the uncorrected formula’s values −1 and 1, which at first appear when x reaches its minimum and maximum value, establish the boundaries of the hyperbolic tangent function’s spectrum yet exist outside of it
[
58] is the updated formula. It should be given an integer that is bigger than or equal to 0.
Decisively, an artificial neural network (ANN) with 50 neurons in its hidden layer was the final result of the search. A total of fifty models came from the study’s completion. Relative error and sum of squares error revealed the fact that by applying the MLP method there is a periodicity as seen in the errors (sum of square and relative error) according to the analysis.
5. Problem Solution—Results
The data collection encompassed 52 unique initiatives in all. The network had already formed a testing procedure, and this significant data collection gave it structure. The primary objective of this testing process was to facilitate the comparison of the actual project expenses with the ANN model’s cost projections.
Each project in this collection of data was a single occurrence with an individual set of variables and outcomes. The testing method has a reliable and robust baseline because to the meticulous collection and assembly of these projects’ actual expenditures.
In order to estimate the accuracy of the ANN model, the sum of squares error and relative error were utilized in the present research. The relative error is a measure of the accuracy of a measurement compared to the size of the measurement itself. The relative error is calculated using the following expression:
where Absolute Error is the difference between the measured or predicted value and the actual value (actual and estimated cost) and Actual Value is the true value (actual final cost) [
58].
A metric for measuring the difference between values predicted by a model and actual data points is the sum of squares error, or SSE. The computation involves the summation of the squares representing the discrepancies between the anticipated and observed values. It is calculated utilizing the following expression:
where
represents the actual observed values (actual final cost),
represents the predicted values (estimated final cost) from the model, and n is the number of observations [
58].
Figure 2 and
Figure 3 illustrate how the training sample’s sum of squares error and relative error are maintained at a low level after RBF implementation.
The testing sample’s sum of squares error and relative error were kept low with a concern of overfitting after 43 neurons in the hidden layer following RBF implementation, as seen in
Figure 4 and
Figure 5.
Figure 6 and
Figure 7 below show how the relative error of the training sample and the sum of squares error have a periodic variation with MLP adoption.
Figure 8 and
Figure 9 below illustrate how the implementation of MLP also causes a periodic fluctuation in both the sum of squares error and the relative error of the testing sample.
Various causes may contribute to the periodic variation seen in
Figure 6 and
Figure 7 (training sample) and also
Figure 8 and
Figure 9 (testing sample), depending on the characteristics of the figures and the context of the data. The model architecture selection may introduce periodicity since the results prior in the figures are dependent on model predictions, such as neural networks. Because of their layered nature, neural networks—including multi-layer perceptrons (MLPs)—can display complicated behavior. Among the many types of ANNs, MLPs are particularly intricate and versatile. Their nonlinearity, layered architecture, feature extraction, and backpropagation algorithm—which computes gradients with respect to the loss function and modifies weights to minimize prediction errors—all contribute to their effectiveness and increases in weight. Due to their complicated decision boundaries, MLPs are able to learn extremely nonlinear and irregular limits on decisions [
60]. Complicated decision districts that encircle various data points can be produced by them for classification issues. While MLPs are capable of modelling complicated performance, a large number of hidden neurons and layers in the model might cause overfitting. Improved generalization and the avoidance of overfitting are two benefits of regularization approaches like dropouts and weight decaying.
The performance of the models was evaluated via following
Figure 10,
Figure 11,
Figure 12 and
Figure 13, which illustrate the comparison between the anticipated final costs estimated by the RBF approach, the MLP method, and the actual costs observed in both the training and testing samples. The projects selected for this analysis exhibited a significant variation in their real costs, presenting a challenging scenario for ANNs to develop accurate forecasting models. The effectiveness of the RBFNN model was assessed and examined both during training and testing. In the training sample, the sum of squares error ranged up to 0.006 and nearly 0 relative error, while in the testing sample, which made up around 30% of the total sample, the sum of squares error ranged between 0.02–0.81 and 0.62–22.07 relative error. The evaluation and analysis of the MLP model’s performance during training and testing revealed that the training sample’s sum of squares error ranged between 0.001 and 0.005 and had a 0–0.007 relative error, accounting for approximately 70% of the total sample, while the testing sample’s sum of squares error ranged between 0.001 and 0.1 and had a 0.21–3.15 relative error, accounting for approximately 30% of the total sample. Despite these challenges, the results depicted in
Figure 10,
Figure 11,
Figure 12 and
Figure 13 demonstrate that the RBF method was able to make predictions and perform ex-post verifications that closely simulated the actual costs. This contrasts with the MLP approach, which produced less accurate outcomes. The superior performance of the RBF method in this context highlights its robustness and reliability in cost estimation, even when faced with substantial variability in project costs.
6. Discussion, Conclusions, and Future Research
The primary allure of utilizing neural networks is their potential to autonomously generate information via training data, devoid of preconceived notions. Finding every relevant component that serves as the logical foundation for choices in cost estimating, nevertheless, is challenging and demanding on time. One sector that is particularly vulnerable to changes in the global economy is the building sector, where cyclical economic conditions are common. While the developers are currently in an era of low interest rates and minimal price inflation, data on costs might have been collected during instances of significant interest rates with elevated inflation in previous years, which would be necessary to construct a useful training database. Undoubtedly, that could influence the high accuracy on the cost modelling that rely on neural networks. Converging with Li’s [
41] perspective future research efforts should attempt to create a method for normalizing and softening data used as training to ensure variables like alterations in the economy might be taken into consideration.
Because project costs and unpredicfi engineering parameters have nonlinear correlations and interactions, it is advised that practitioners adopt ANNs. The training process allows for deficiencies in the ANN due to its high precision and capacity to learn complex functions. They speed up and increase the evaluation’s reliability.
The proposed models are in summary accurate, easy to use, and time-saving. An appropriate method for addressing problems arising from multiple uncertainties, such as early cost estimation, may be the ANN models used above. Therefore, the findings support the need for more study on project management that incorporates a hybrid RBF-MLP model, or fuzzy logic and other cutting-edge methodologies.
In the present research, the ANNs utilizing RBFs and MLPs incorporate known input variables that have a noteworthy influence on building renovation costs. This study also demonstrated how these factors are utilized to calculate the building costs of civic projects in Greece. Consequently, professionals ought to think about using these factors when evaluating the total cost of building renovation. The results in
Section 5 illustrate an adequate coinciding with the actual cost in the training and testing sample and the predicted final cost determined using the RBF and MLP methods. The real expenses of the chosen projects varied significantly. For this reason, the ANNs found it very challenging to build predicting models that could also have a usage for an ex-post verification of building renovation total final cost. In contrast to the MLP approach, which yields less accurate results, the RBF method makes predictions that simulate the real cost. As Bayram et al. also concluded, the estimated costs derived from RBF showed a 0.28% variance in excess of the real costs, but the estimated costs derived from MLP showed a 1.11% variance in excess of the actual values [
55].
This emphasizes the necessity to constantly enhance artificial neural network techniques in order to increase their precision and usefulness in the field of building rehabilitation cost prediction and verification. There is an enormous amount of a forum for improvement, as seen by the present limits found in the predictive models. To better handle the unpredictability and complexity of real-world data, these procedures could be improved by adding advanced algorithms, integrating new data sources, and using advanced methods. Rendering this modification could strengthen and bolster the prediction models, allowing them to be more accurate in estimating costs. Ensuring that the projected costs accurately resemble the actual end costs would result from this, as well as improving the models’ ex-post verification efficacy and renovation expense predictions. Ultimately, these developments would help in renovating buildings more accurately and efficiently in terms of financial planning.
Through comprehensive project cost estimation, the building sector may experience significant transformation through the conversion of realistic field data into real-time data. All measurable functions can be approximated by ANNs that may even imitate complex non-linear interactions. A user could arrive at more informed planning decisions with the aid of the predictive estimate of the total cost of a building project. The cost of labor, steel, cement, and other significant resources could all fluctuate, and different stakeholders might be interested in investigating the impact of these changes on project costs in the future.
In order to provide their cost-estimating operations as a benchmark, building organizations should create cost forecasting evaluation standards, as Akintoye et al. also insists [
14].
Additional enhancements might provide additional functions including enhanced managing databases, a user experience, and clarification capabilities. Continuous maintenance is necessary for networks. It is necessary to document information about recently completed buildings. To improve its capacity for generalization, the network might need to be updated utilizing additional data. Currently, the accessibility of training and test samples as well as the output places restrictions on the architecture of the guided back-propagation structure. As Bhoka et al. [
59] mentioned, further construction samples could be utilized to train and test models with various output categories.