Abstract
Amazons is a computerized board game with complex positions that are highly challenging for humans. In this paper, we propose an efficient optimization of the Monte Carlo tree search (MCTS) algorithm for Amazons, fusing the ‘Move Groups’ strategy and the ‘Parallel Evaluation’ optimization strategy (MG-PEO). Specifically, we explain the high efficiency of the Move Groups strategy by defining a new criterion: the winning convergence distance. We also highlight the strategy’s potential issue of falling into a local optimum and propose that the Parallel Evaluation mechanism can compensate for this shortcoming. Moreover, We conducted rigorous performance analysis and experiments. Performance analysis results indicate that the MCTS algorithm with the Move Groups strategy can improve the playing ability of the Amazons game by 20–30 times compared to the traditional MCTS algorithm. The Parallel Evaluation optimization further enhances the playing ability of the Amazons game by 2–3 times. Experimental results show that the MCTS algorithm with the MG-PEO strategy achieves a 23% higher game-winning rate on average compared to the traditional MCTS algorithm. Additionally, the MG-PEO Amazons program proposed in this paper won first prize in the Amazons Competition at the 2023 China Collegiate Computer Games Championship & National Computer Games Tournament.
1. Introduction
Amazons is a two-player board game that was introduced by Walter Zamkauskas of Argentina in 1988 [1,2]. It is the designated game for the Olympia computer game programming competition. Due to its complex gameplay, Amazons is very challenging for humans [3], making it a popular subject for computer game competitions and research. The game rules are as follows: The game is played on a 10 × 10 square board. Each player controls four identical pieces called “Amazons”. These pieces and arrows follow the same rules as a queen in chess: They can move any number of squares in any direction—horizontal, vertical, or diagonal—but cannot jump over other pieces or arrows. The objective is to restrict the opponent’s movement by shooting arrows until none of the opponent’s four pieces can move. If, on a player’s turn, all four of their pieces are immobilized, that player loses, and the other player wins. Notably, there are no ties in Amazons.
The main challenge of the Amazons game lies in its complexity: Each move offers a vast number of possible choices, typically more than 500 [4,5], and the game can extend for over 80 moves [6,7]. This high level of complexity makes Amazons an excellent experimental sample for testing search strategy algorithms [8,9]. Since its invention, it has garnered significant attention from computer scientists [10] and computer science students [11].
The Monte Carlo method [12] is a computational technique that produces numerical results through repeated random sampling. When integrated with tree search algorithms and suitable evaluation functions, the Monte Carlo tree search (MCTS) algorithm has yielded impressive results in board games with a high-branching factor (such as Go) [13,14,15], and in real-time strategy games (such as StarCraft [16]). For instance, in 2016, DeepMind’s AlphaGo program [17] defeated the Korean world champion of Go, Lee Sedol, with a score of 4:1. In 2018, OpenAI’s OpenAI Five program [18] defeated the world champion team in Dota 2 with an overwhelming advantage; both accomplishments are based on the Monte Carlo tree search algorithm.
The ‘Move Groups-Parallel Evaluation’ optimization strategy (MG-PEO) accommodates the rules of the Amazons board game by subdividing a complete move into two parts: Amazon Movement and Arrow Shot. Both Amazon Movement and Arrow Shot are treated as tree nodes, rather than considering a complete move as a single tree node. This approach is known as the Move Groups strategy in the literature [19]. While this strategy has been applied to the Amazons game [20], it still lacks an objective analysis of its effectiveness. Moreover, there is a widespread belief that this method only possesses advantages without any drawbacks. In this paper, we explain the high efficiency of the Move Groups strategy in Amazons by defining a new criterion: the winning convergence distance. We also identify certain shortcomings of this strategy. To address these, we propose using a Parallel Evaluation mechanism to compensate for the limitations of the Move Groups strategy. Our experimental results demonstrate that MG-PEO is an effective fusion optimization strategy.
The main contributions of this paper are as follows:
- •
- We propose an effective optimization of the Monte Carlo tree search algorithm for the Amazons game: the MG-PEO algorithm optimization, which combines the Move Groups strategy with the Parallel Evaluation strategy.
- •
- We provide a performance analysis of the Move Groups strategy in Amazons. By defining a new criterion, the winning convergence distance, we explained the high efficiency of the strategy. Moreover, we also highlight that this strategy has certain shortcomings. The Move Groups strategy involves refining the rules of the Amazons game and using simulations to assign corresponding value scores to additional layer nodes. By utilizing these value scores (e.g., the Upper Confidence Bound Apply to Tree (UCT) strategy [15]), we can achieve effective pruning to save time. However, the addition of extra layer nodes means that more nodes need to be traversed and evaluated in the worst-case scenario, where pruning has not occurred, potentially leading to increased time-consuming overhead. This overhead is incurred as the algorithm strives to find the local optimal solution.
- •
- We propose using a Parallel Evaluation mechanism to address the potential shortcomings of the Move Groups strategy. By parallelizing the evaluation function for the Amazons game, we aim to accelerate the expansion process of the Monte Carlo tree search and minimize the likelihood of the Move Groups strategy falling into a local optimum.
Additionally, we conducted rigorous performance analysis and game experiments. The performance analysis indicates that—compared to the traditional MCTS algorithm—the MCTS algorithm with the Move Groups strategy can enhance the playing ability of Amazons by 20–30 times, while the Parallel Evaluation optimization component can improve the playing ability of Amazons by 2–3 times. Experimental results demonstrate that—compared to the traditional MCTS algorithm—the MCTS algorithm with the MG-PEO strategy achieves an average 23% increase in the game-winning rate and exhibits stronger playing ability.
The remainder of this paper is structured as follows: In Section 2, we present preliminary information about the Amazons game and discuss its relevance to the MCTS algorithm. In Section 3, we provide a detailed description of the MCTS algorithm with the MG-PEO strategy. In Section 4, we offer performance analyses of the Move Groups strategy and Parallel Evaluation strategy, respectively. Section 5 outlines a series of experiments conducted to verify the efficiency of the MCTS algorithm with the MG-PEO strategy. Finally, conclusions and avenues for future research are summarized in Section 6.
2. Related Work
In this section, we provide an overview of the relevant research that forms the basis of our work. Specifically, we will discuss three key modules in the literature that are relevant to Amazons: historical research on Amazons algorithms, the application of the MCTS algorithm to Amazons, and knowledge about game situation evaluation.
2.1. Amazons Playing Algorithm
The Amazons game has undergone extensive study; its algorithm development can be roughly categorized into three stages. Initially, traditional methods rooted in mathematical theory, such as the minimax search algorithm [21], dominated the field. The second phase saw the emergence of Monte Carlo algorithms, including various variants of the Monte Carlo tree search [19,20,22,23,24]. In the third stage, deep learning techniques leveraging Amazons game databases came to the forefront [25,26]. Notably, the most representative Amazons program, Invader [27,28,29], relies on MCTS for prospective exploration, supplemented by neural network training on chess databases, resulting in formidable playing ability in the Amazons game. It can be said that further optimization of Monte Carlo algorithms remains crucial for advancing research on Amazons.
2.2. Monte Carlo Tree Search Algorithm
The development of the Monte Carlo tree search algorithm in Amazons can be roughly divided into two lines of research: algorithm optimization in terms of tree search and algorithm optimization in terms of evaluation functions. In terms of tree search algorithm optimization, researchers have worked on improving search algorithms to improve the performance of Amazons. For example, Guo et al. divided the game into early, middle, and late stages, employing different strategies in each stage [30]. Li et al. applied the UCT algorithm to Amazons [31]; Quan et al. demonstrated the superiority of the UCT algorithm in Amazons [32]. On the other hand, optimizing the evaluation function is also one of the focuses of the research. By optimizing the evaluation function, the current game can be evaluated more accurately and the search algorithm can be guided to make more informed decisions. Lieberum et al. dedicate their research to this aspect [33,34], focusing mainly on improving hyperparameter tuning and designing new evaluation functions. Overall, the Monte Carlo tree search algorithm cannot be improved without any one aspect, and in this paper, our proposed fusion of the Move Groups strategy and the Parallel Evaluation strategy represents a comprehensive consideration of the two historical research focuses. This fusion of the Monte Carlo tree search algorithm is cutting-edge and effective.
2.3. Evaluation Function
At present, almost all search algorithms are faced with a problem: situation evaluation. Good situation evaluation is very important in the Amazons game and can even determine the quality of the game program [33].
Similar to many board games, Amazons can be roughly divided into three stages: opening, middle, and ending, with distinct strategies for each stage. The main indicators of the Amazons evaluation function include territory, position, and mobility, and the importance of these three characteristics varies across different stages. Based on these ideas, Guo et al. [30] proposed a phased evaluation function, as shown in Equation (1):
where and are territory metric values, which, respectively, represent the evaluation of each side’s control over space, based on the QueenMove Method and KingMove Method. and are position metric values, reflecting the strategic position of each side’s pieces, also based on the QueenMove and KingMove Methods relative to the space. is the flexibility evaluation value of both Amazon pieces. , , , , and are the corresponding weight values. How these values are calculated is described below.
According to the literature [2], calculating territory and position values involves two types of methods: QueenMove and KingMove. QueenMove means that a move can be made as long as there are no obstacles to be crossed in any of the eight directions (the obstacles include pieces and arrows), while KingMove means that the distance of a single move is one, i.e., only one move can be made to a neighboring square. The QueenMove value represents the minimum number of moves a player’s four pieces need to reach a given space (i.e., no pieces or arrows); the KingMove value represents the minimum number of moves a player’s four pieces need to make to reach a given space. As shown in Figure 1 on the left side, value 2 in the upper-left corner of the upper-left (A, 1) square indicates that the white piece needs at least two moves to reach this space via the QueenMove method, and value 4 in the lower-right corner indicates that the black piece needs four moves. Similarly, values 2 and 7 in the same square in Figure 1 on the right side indicate the situation when the KingMove method is used.

Figure 1.
Calculation results of the QueenMove and KingMove methods. The left is the result of the KingMove calculation, and the right is the result of the QueenMove calculation.
Accordingly, we can use the following calculation formula for all the indicators:
represents the difference in the control of the territory using the QueenMove method. represents the difference in the control of the territory using the KingMove method. As shown in Equations (2) and (3):
where B represents black pieces, W represents white pieces, with the subscript 1 indicating the QueenMove method and 2 indicating the KingMove method. A represents empty squares. k represents the preponderance of the leading square, and the value range is greater than −1 and less than 1. When the player with the first move is white, k is greater than 0, otherwise, it is less than 0.
represents the positions of the two pieces on control space A using the QueenMove method. represents the positions of the two pieces on control space A using the KingMove method. As shown in Equations (4) and (5):
means the flexibility of the pieces. As shown in Equations (6) and (7):
where F denotes flexibility, denotes the set of spaces that can be reached by a piece using the QueenMove method, and is the minimum number of moves by a to s using the KingMove method.
We retained the hyper-parameterization settings according to the literature [2]; detailed information about each assessment indicator is shown in Table 1.

Table 1.
Weight coefficient table.
Table 1 shows that gradually increases in importance as the game progresses, starting smaller in the opening, becoming larger in the middle, and reaching its peak in the endgame. This is because as the game progresses, board control becomes more crucial to victory or defeat. is extremely crucial in the opening phase to ensure the safety of neighboring regions and territorial boundaries, but its role decreases as the game progresses, and it can be almost ignored in the endgame. It reflects the urgency of the initial layout defense and territorial competition. and denote piece positions, which mainly play roles in the opening phase when a balanced distribution of pieces is crucial to the subsequent strategic deployment; in the endgame, the pattern of the game has already been determined, and the distribution of pieces is no longer a key point; denotes flexibility, which is the most significant in the early stage of the game, as blocking the pieces can be seriously disadvantageous; as the game progresses and the initial layout is established, the distribution of pieces becomes increasingly critical. As the game progresses and the layout is completed, the impact of piece mobility on the game’s situation is weakened, so its weight is reduced to negligible in the middle and late game. This reflects the need for strategic flexibility in the early stages of freedom of movement.
3. Research Methodology
In this section, we first describe the overall framework of the MCTS algorithm enhanced with the MG-PEO strategy. We then elaborate on the optimization details, focusing on two aspects: Move Groups and Parallel Evaluation.
3.1. Overall Framework of Algorithm
We propose an MG-PEO algorithm optimization strategy based on the Monte Carlo tree search [22]. As shown in Figure 2, the optimized Monte Carlo tree search algorithm involves iteratively constructing a search tree, creating a new tree each round until the time constraint is reached or the game ends. At this point, the search stops and returns the best-performing root operation (a combination of actions from certain nodes in the second and third layers).
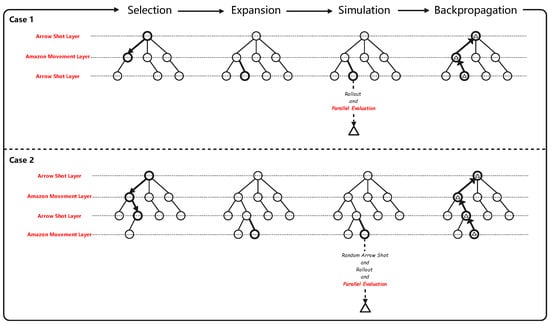
Figure 2.
MCTS plus MG-PEO general framework.
Specifically, the following four steps are performed for each search iteration:
- (1)
- Selection: Starting from the root node, a certain strategy is applied to recursively go down through the tree for expandable node selection. A node is expandable if it represents a non-terminal state and has unvisited children.
- (2)
- Expansion: Expand the tree by adding one (or more) child node(s), depending on the available operations.
- (3)
- Simulation: Run a simulation from a new node to produce results according to the default strategy.
- (4)
- Backpropagation: Back up the simulation results through the selected nodes to update their statistics.
As seen in Figure 2, due to the use of the Move Groups strategy, the algorithm operates under two scenarios during the simulation phase: if the current node is an Arrow Shot layer node, it executes Rollout and Parallel Evaluation; if the current node is an Amazon Movement layer node, it performs Random Arrow Shot, Rollout, and Parallel Evaluation.
The pseudo-code for the overall framework is described in Algorithm 1.
| Algorithm 1: General Algorithm Framework |
| Input: (The current game State) |
| Output: Optimal decision |
| 1: function MCTSSEARCH () |
| 2: create root node with state |
| 3: while within the computational budget do |
| 4: ← Selection () |
| 5: ← Expansion (, ) |
| 6: ←Simulation (, ) |
| 7: Backup (,) |
| 8: return BESTCHILD() |
3.2. Move Groups Strategy in Algorithm
The core idea of the Move Groups strategy is as follows: according to the rules, a node in the original search tree (Amazon Movement and Arrow Shot combined) is decomposed into two nodes (representing Amazon Movement and Arrow Shot, respectively). By utilizing the simulation phase of MCTS to assign value scores to an additional layer (the newly added layer), we can achieve the goals of pruning and saving time, based on the value scores of the extra layer (e.g., using the UCT strategy).
Specifically, when an extra layer node has not yet expanded its child nodes, its value score is initially infinite. Therefore, each extra layer node will first expand its child nodes once and employ a Shallow Rollout strategy to obtain an initial value score. Subsequently, we can select the extra layer node with the highest value score for further expansion and Rollout, until a particular extra layer node’s child nodes are fully generated and the node is selected again. At this point, we can then derive the optimal decision from the child nodes, which is the core of early pruning. It should be noted that due to the dynamic MCTS backpropagation mechanism, the value scores of the extra layer nodes will dynamically change as their child nodes expand. Therefore, early pruning may also occur at the second, third, or other extra layer nodes. For details on the computation and updating of the value scores, please refer to Section 3.3. Since the complete step is a combination of two steps, namely, Amazon Movement and Arrow Shot, and the extra layer represents only one step, the total number of nodes in the extra layer must be less than the total number of nodes, thus enhancing the performance of early pruning in the Monte Carlo tree search algorithm.
However, the Move Groups strategy also increases the number of total tree nodes (for a complete one-step operation) due to the introduction of the extra layer, and if all nodes are expanded without pruning in advance, the extra overhead (expansion and evaluation) incurred by the nodes in the extra layer will negatively affect the algorithm, which will also lead to the fact that—in the worst-case scenario—the addition of the Move Groups strategy to the MCTS will perform slightly worse than the MCTS algorithm without the Move Groups policy. A complete theoretical analysis of the Move Groups policy is detailed in Section 4.1.
3.3. Parallel Evaluation Strategy in Algorithm
The core idea of the Parallel Evaluation strategy is that the time-consuming evaluation part of the MCTS simulation is processed in parallel optimization. It has been shown in the literature [35] that accelerating this labor-intensive evaluation function allows the Monte Carlo Tree Search algorithm to be iterated more frequently. This metric is very beneficial in compensating for the fact that the Move Groups strategy might fall into a local optimum (worst case); specifically, speeding up the evaluation function enables the Monte Carlo Tree Search to scale as quickly as possible, minimizing the impact of the worst-case scenario associated with the Move Groups strategy. The pseudo-code for the Parallel Evaluation part is as shown in Algorithm 2.
| Algorithm 2: SituationEvaluation |
| Input: (The current Game State) |
| Output: Situation Evaluation Value |
| 1: function SituationEvaluation() |
| 2: , , , , ← ParallelEvaluationMetrics () |
| 3: |
| 4: return Value |
Nodes undergo evaluation, and the resulting value scores guide node selection. Traditional Monte Carlo tree search algorithms typically choose the child node with the highest node score (winning rate) based on the current game state [36]. However, this selection method is not ideal, as it tends to prioritize immediate gains and can lead to local optima. To address this issue, this paper incorporates the “Shallow Rollout strategy” [37] and the “tree-based upper confidence interval” algorithm [19] to refine node selection. Specifically, the utilization value derived solely from decision-level nodes may be inaccurate. To enhance precision, a Shallow Rollout strategy is employed, simulating scenarios closer to the endgame. Additionally, the algorithm considers the magnitude of a node’s exploratory value, which is elevated for nodes exhibiting high uncertainty and numerous future possibilities. In summary, the approach assesses both partial equilibrium utilization value and exploration value to facilitate more informed decision-making.
- 1.
- “Shallow Rollout Strategy”: This means that the utility value is not calculated, not only based on the next move but also on the position of the game after randomly simulating the move several times. In this algorithm, we set the number of Rollouts to be two, and the depths to be 4 and 5. Specifically, after expanding the complete decision node (Amazon Movement plus Arrow Shot), we perform two Rollouts for the current situation. In each Rollout, we simulate two steps: the opponent’s next decision (Amazon Movement plus Arrow Shot) and our subsequent decision (Amazon Movement plus Arrow Shot), to obtain a more forward-looking utility value. See pseudo-code Algorithm 3 for details. For the analysis of the relevant parameters, see Appendix A.
- 2.
- “Tree-based Upper Confidence Interval”: As shown in Equation (8), the calculation formula of UCT consists of two components. The first term, , represents the utility value of the information in the constructed search tree, and the second term represents the exploration value of the unvisited nodes. The constant C is used to adjust the proportion of the algorithm’s trade-off between the two values. Note that the value of the root formula is infinite because of the presence of unreachable child nodes, which ensures that unreachable child nodes under the current node will be visited at least once.
Here, we can provide the complete pseudo-code as shown in Algorithm 3.
| Algorithm 3: MCTS with the MG-PEO strategy |
| 1: function Selection(v) |
| 2: while v is nonTerminal do |
| 3: if v is not fully expanded then |
| 4: return v |
| 5: else |
| 6: v ← BESTCHILD(v) |
| 7: return v |
| 8: function Expansion(v,&) |
| 9: if v is an Amazon Movement Node then |
| 10: ← randomly create Arrow Shot Node |
| 11: else if v is an Arrow Shot Node |
| 12: ← randomly create the Amazon Movement Node |
| 13: ← Update the state of the board |
| 14: return |
| 15: function Simulation(v,) |
| 16: S ← |
| 17: //* depth = 4 and 5 (Independent order twice) |
| 18: S ← Rollout(S,) |
| 19: ← SituationEvaluation(S) |
| 20: return |
| 21: function Rollout(S,) |
| 22: repeat |
| 23: if is Terminal (S) then |
| 24: pass |
| 25: if v is the Amazon Movement Node then |
| 26: ← RandomArrow(S) |
| 27: S ← doAction(v,) |
| 28: depth ← depth - 1 |
| 29: else if v is the Arrow Shot Node then |
| 30: ← parent of v |
| 31: S ← doAction(,v) |
| 32: depth ← depth - 1 |
| 33: until depth = 0 or gameover |
| 34: return S |
| 35: function Backup(v,) |
| 36: N(v) ← N(v) + 1 |
| 37: Q(v) ← Q(v) + |
| 38: v ← parent of v |
| 39: function BESTCHILD(v) |
| 40: return |
4. MG-PEO Performance Analysis
In this section, we design two modules to analyze the MG-PEO strategy. First, we analyze the performance of the Move Groups strategy in Amazons. Second, we conduct an in-depth discussion on the performance improvement of the Parallel Evaluation mechanism in Amazons.
4.1. Performance of the Move Groups Strategy in Amazons
The effectiveness of a Monte Carlo tree search algorithm based on the law of large numbers depends largely on the number of situations it can search. The more situations the algorithm can search for, the easier it will be to find “tricks” that are usually hard to find and, thus, beat the opponent. In other words, the more computational the power, the more effective the Monte Carlo algorithm. Therefore, in order to objectively show the influence of the Move Groups strategy on the actual performance of the MCTS algorithm, we provide a new definition (winning convergence distance) to evaluate the performance of the algorithm.
Definition 1.
Winning convergence distance. This calculates the number of tree nodes expanded by the search tree, both in depth and breadth, from the current state (root node) to the winning state (game over). In general, the fewer new nodes the Monte Carlo tree needs to expand to achieve victory as soon as possible, the shorter the winning convergence distance.
To visualize the winning convergence distance, we use the opening first step as an example. Since the number of nodes that can be generated from the first step to the winning state is immeasurable, we use the local optimal solution of the first step instead of the winning state, as shown in Figure 3.

Figure 3.
The local optimal solution assumed in the first step of the opening. From left to right: initial state, after Amazon Movement, and after Arrow Shot.
Based on this, we can plot the Monte Carlo search tree with the Move Groups strategy added and the Monte Carlo search tree without the Move Groups strategy added, and compute the best-case and worst-case expanded node numbers, as shown in Figure 4 and Table 2.
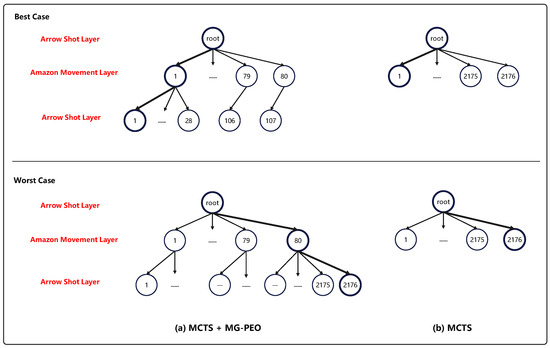
Figure 4.
Plot of the winning convergence distance calculation. The number in the figure refers to the order in which the node is expanded at a certain layer.

Table 2.
Winning convergence distance of two algorithms (unit: nodes).
In Figure 4 and Table 2, for the first step, the Monte Carlo tree search algorithm with the Move Groups strategy added needs to expand 80 Amazon Movement layer nodes first. Since the value score of an Amazon Movement layer node is infinite when it has not yet expanded its child nodes, each Amazon Movement layer node needs to further expand an Arrow Shot layer node to obtain an initial value score. Subsequently, we can select the Amazon Movement layer node with the highest value score for the next child node expansion. In the best case, the first Amazon Movement layer node has the highest value score. During the expansion of its subsequent Arrow Shot layer nodes, the value score of the parent node remains at the maximum observed across all Amazon Movement layer nodes; the other nodes in the Amazon Movement layer do not carry out the expansion of the next layer’s nodes, which is a reflection of early pruning. Finally, the number of nodes expanded is 187. In the worst case, all possible nodes are fully expanded and traversed, resulting in a total of 2256 nodes being expanded.
The Monte Carlo tree search algorithm without the inclusion of the Move Groups strategy needs to select the node with the largest value score as the final decision after generating all possible nodes, regardless of the best or worst-case scenarios; resulting in a total of 2176 nodes being expanded.
In summary, we can conclude the following: in the best case, the winning convergence distance of the MCTS with the Move Groups strategy is significantly shorter than that of the traditional MCTS, while in the worst case, the winning convergence distance of the MCTS with the Move Groups strategy is slightly weaker than that of the traditional MCTS. This indicates that the Move Groups strategy has strong pruning and time-saving abilities, but at the same time, there are some shortcomings.
4.2. Performance of Parallel Evaluation Strategy
In this subsection, we delve into the number of threads required for the Parallel Evaluation mechanism, as well as the speedup ratio that multithreading can bring. Since the time consumption of the evaluation function mainly comes from the time from calculating each evaluation metric, the Parallel Evaluation part is essentially a multi-threaded calculation of evaluation metrics. The pseudo-code for the Parallel Evaluation metric function is shown in Algorithm 4.
| Algorithm 4: Parallel Evaluation Metrics |
| Input: (The current Game State) |
| Output: ,,,, |
| 1: function ParallelEvaluationMetrics() |
| 2: //* The calculation of Territory() and Position() metrics uses the same |
| independent function four times, based on the King Move and QueenMove |
| methods, which are calculated once for black and once for white. |
| 3: //* We optimize its external calls in parallel. |
| 4: Module1 = lambda (range) |
| 5: for the in the range: |
| 6: ← |
| 7: ← |
| 8: CalTP(,) |
| 9: parallel_for(block_range(0,2),Module1) |
| 10: //* The Mobility() metric is calculated one function at a time, and the |
| internal logic is to process each board position ( = 100) independently. |
| 11: //* We optimize its inner loop processing logic in parallel. |
| 12: Module2 = lambda (range) |
| 13: for the in the range: |
| 14: ← |
| 15: ← |
| 16: CalEveryBoardPosition() |
| 17: parallel_for(block_range(0,GridSize),Module2) |
A. Discussion on the number of threads: Since the main metrics of the evaluation function include territory, position, and maneuverability metrics, values of the territory and position metrics can be calculated using a single function; however, as the calculations of these two metrics are related to the colors of the pieces and the calculation method (KingMove method and QueenMove method), four independent calculations are needed for the values of the territory and position metrics. The mobility indicator is calculated by a function that requires one independent calculation. The algorithm is optimized in parallel for the territory and position indicators, which theoretically require a total of four threads. For the maneuverability indicator, ten threads are theoretically needed for internal calculations related to the size of the board.
B. Exploration of the acceleration ratio that multi-threading can bring: In order to accurately explore the acceleration ratio, we counted the time consumed by the computation function of each evaluation metric, and the data are shown in Table 3.

Table 3.
Module execution time and speed-up ratio.
As shown in Table 3, the calculation time for the optimized territory and position metrics achieved a 2.379-fold speedup, while the calculation time for the optimized mobility metric achieved a 1.956-fold speedup. The overall speedup ratio for the evaluation part was 2.111. In section A, we discussed the number of threads and noted that the theoretical speedup of parallelization should correspond to the number of threads. However, the time consumption of each module before and after optimization differed somewhat from the discussion in section A. We consider that the overhead of third-party parallel libraries [38] has consumed some computing resource performance. See Appendix B for details on the CPU usage analysis. Nevertheless, the parallel optimization mechanism reduced the time required to process the same tasks by 2.111 times, resulting in a significant performance improvement in practical applications.
5. Experiment and Results
In this section, in order to verify the effectiveness of the MG-PEO algorithm optimization strategy proposed in this paper, three experiments were designed: the first compares the relevant performance metrics of the MCTS algorithm with the MG-PEO strategy and the traditional MCTS algorithm, and a significance test is carried out on the comparison results. The second experiment focuses on assessing the magnitude of the effect of each optimization module of MG-PEO on MCTS, i.e., the ablation experiment. The third experiment is a generalized experimental analysis of the MG-PEO.
In addition, it is worth mentioning that the MG-PEO Amazons program proposed in this paper won first prize in the Amazons Competition at the 2023 China Collegiate Computer Games Championship & National Computer Games Tournament.
5.1. Experimental Environment Information
In order to ensure the reliability of the experimental results, we conducted all the experiments in a unified environment, and detailed information on the experimental environment settings is shown in Table 4.

Table 4.
Experimental environment information.
5.2. Quantitative and Qualitative Experiments
5.2.1. Winning Percentage Statistics and Analysis
In order to objectively and accurately assess the effectiveness of the MG-PEO algorithm optimization strategy, we selected the MCTS algorithm without Move-Groups optimization and without Parallel Evaluation optimization for comparison, and we played a total of 100 matches under the same conditions, with each match divided into 3 games each (first hand and second hand). Specifically, we chose 33 players who participated in a computer gaming competition and 17 players who open-sourced their rankings (ladder list) on the Botzone platform (https://www.botzone.org.cn/, accessed on 2 March 2024), totaling 50 opponents. Due to the requirement for third-party libraries, we locally exported the exe programs for all players and then conducted the games against each other on the SAU platform (http://computergames.caai.cn/platform/SAU_Game_Platform_2.1.0_r3.rar, accessed on 20 March 2024), and the results of the games are shown in Table 5. Detailed information on all the games can be found in Appendix C.

Table 5.
The winning rate of the two algorithms.
In Table 5, the MCTS algorithm has a winning rate of 74% in Amazons Duel on the SAU matchmaking platform. In the same test environment, the MCTS algorithm with the MG-PEO strategy shows higher stability, and its winning rate in the Amazons Match on the SAU Matchmaking Platform reaches 97%. In summary, the MCTS algorithm with the MG-PEO strategy has more comprehensive and in-depth optimization when considering and utilizing strategies than the MCTS algorithm and, thus, shows a higher winning rate in this test scenario.
It is worth noting that—by observing the matches of the two algorithms—we found that the optimized MCTS algorithm often makes more accurate decisions than the unoptimized MCTS algorithm in some critical rounds. These key rounds often involve crucial positions for “encircle territory” or “block the opponent” strategies. Additionally, during the matches, we noticed that the optimized MCTS algorithm has a clear advantage over some traditional algorithms (such as Minimax and traditional MCTS). However, its performance is slightly lacking when competing against neural network programs trained with a large amount of game data. Nevertheless, this provides a direction for further improving the algorithm’s performance in the next step.
5.2.2. Winning Convergence Distance Visualization and Analysis
In this sub-subsection, we count the number of match point rounds in which the algorithm’s winning percentage assessment reaches 90% or more (the threshold for a solid win) in 100 games played by the two algorithms on the SAU platform, as a way to visualize the definition of the distance of convergence of a win, as well as to compare the strengths and weaknesses of the playing abilities of the two algorithms of the Amazons game. Here, we generally consider the outcome of a game to be clear when the algorithm evaluates a winning rate of 90% or more (barring low-level errors by the dominant side); such moments are considered to be match points and we believe that the earlier this occurs, the stronger the algorithms are. The average resulting data for the number of match point rounds for the two algorithms are shown in Table 6. See Appendix C for complete data:

Table 6.
The average number of match point rounds in 100 matches where the win rate evaluation values of two algorithms exceed 90%.
As can be seen from Table 6, the average number of match point rounds required for the MCTS algorithm to reach the stable winning threshold (evaluation value over 90%) is 42.57 rounds. On the other hand, the MCTS algorithm with the MG-PEO strategy outperforms MCTS in terms of reaching the same stable winning threshold with an average of 39.68 rounds.
This indicates that the MCTS algorithm with the MG-PEO strategy converges faster than MCTS. It requires fewer average rounds than the traditional MCTS algorithm. The MCTS algorithm with the MG-PEO strategy uses the Move Groups strategy and the Parallel Evaluation strategy to optimize the strategy selection process of the MCTS algorithm so that it can find the best search paths in a shorter period of time and reach a stable winning state with a winning rate of more than 90% in advance.
In summary, the MCTS algorithm with the MG-PEO strategy has a shorter winning convergence distance than the traditional MCTS algorithm. It requires fewer rounds to achieve a higher winning rate and, thus, demonstrates superior playing ability.
5.2.3. Significance Test
In this subsection, we perform a significance test on the match point round count data, as counted in Section 5.2.2, to determine whether there is a significant difference between them. We conduct the tests at a significance level of 0.05. The complete match point round count data are detailed in Appendix C. First, we use the Shapiro–Wilk test to assume that both data sets obey a normal distribution. However, neither dataset conforms to a normal distribution. Based on this result, we use the Mann–Whitney U test to assume that there is no significant difference between the two groups of data. We then compare the distribution characteristics of the match point round data of the two algorithms. The detailed results are shown in Table 7.

Table 7.
Significance of the test results.
As a result of the Shapiro–Wilk test, both algorithms tested showed a value of less than 0.05 for the data on the number of match point rounds, leading us to reject the null hypothesis that the data for MCTS+MG-PEO and the data for MCTS both conform to a normal distribution. The results of the Mann–Whitney U test indicate that the value for the data on the number of match point rounds between the two algorithms is significantly smaller than 0.05, so we reject the original hypothesis. That is, there is a significant difference in the average number of winning steps between the two algorithms. Specifically, the average number of winning moves required by MCTS with the MG-PEO strategy is significantly less than that required by traditional MCTS against 100 players, suggesting that MCTS with the MG-PEO strategy outperforms traditional MCTS in terms of playing ability in Amazons.
5.3. Ablation Experiment
In this subsection, to evaluate the effectiveness of the Move Groups strategy and the Parallel Evaluation strategy in Amazons, we design two experiments: one that only employs the Move Groups strategy without using the Parallel Evaluation strategy, and another that only employs the Parallel Evaluation strategy without using the Move Groups strategy. The experimental results are shown in Table 8. On the one hand, the Move Groups strategy focuses on MCTS iterations within a limited time on the sub-nodes of more valuable additional-layer nodes by leveraging their value scores, thus avoiding the expansion of unimportant nodes. While the Move Groups strategy exhibits strong pruning capabilities, the value scores of additional-layer nodes dynamically change with the expansion of their sub-nodes due to the MCTS dynamic backpropagation update mechanism. Consequently, all nodes in the additional layer may be fully expanded and traversed multiple times (pruning has not occurred), potentially resulting in increased time spent compared to MCTS algorithms without the Move Groups strategy. On the other hand, because the proportion of the situation evaluation is limited, using only Parallel Evaluation optimization without adopting the Move Groups strategy offers limited performance improvement. Therefore, the combined optimization of employing both the Move Groups strategy and the Parallel Evaluation is effective and necessary.

Table 8.
Ablation experiment analysis of the Move Groups strategy and Parallel Evaluation strategy.
5.4. Generalization Analysis
In this subsection, we conducted a general analysis of the Move Groups strategy and the Parallel Evaluation strategy, discussing in depth their transferability to other board games.
- 1.
- Move Groups strategy: In some games, the branching factor can be very large, but many moves are similar. The Move Groups strategy creates an additional decision layer where all possible actions are grouped together, allowing us to handle the large branching factor of the game more efficiently. This strategy is beneficial for other games, such as Go [39] and the multi-armed bandit game with Move Groups [40]. We believe that this strategy is still worth exploring and investigating.
- 2.
- Parallel Evaluation strategy: The Parallel Evaluation strategy can provide effective acceleration, whether for simple rule-based games like Gomoku, more complex games like Chess and Go, or even modern innovative board games. Its core advantage lies in its ability to efficiently explore the decision tree, which is a common requirement in various board games.
6. Conclusions and Future Works
In this paper, we propose an efficient optimization of the Monte Carlo Tree Search algorithm for the Amazons game, which refines the Monte Carlo Tree Search capability through the Move Groups strategy. The Parallel Evaluation mechanism addresses the risk of the Move Groups strategy falling into a local optimum (these components are complementary to each other). The experimental results validate that the method proposed in this paper significantly improves the playing ability of the Amazons game.
Future research efforts are also included in our plans. First, to maximize the timesaving potential of the Move Groups strategy pruning, we hope to consider using more intelligent approaches (such as heuristic functions) to guide the pruning behavior of the Move Groups strategy. Secondly, the series of experiments in this paper demonstrate the powerful performance improvement capability of parallel optimization, so we plan to consider more parallel possibilities and more efficient parallel strategies in the future. Finally, we also hope that this algorithm can be further extended to solve more gameplaying problems.
Author Contributions
All authors contributed to the study’s conception and design. Methodology, software, validation, investigation, data analysis, model verification, resources, data curation, visualization, writing—editing, and review: L.Z. and H.Z. Supervision, project administration, funding acquisition: Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Part of the competition code used in this study is the publicly available open source code, which can be found at the following website: https://www.botzone.org.cn/, accessed on 2 March 2024.
Conflicts of Interest
The authors declare that they have no financial interests or personal relationships relevant to the content of this article’s content.
Appendix A
In Appendix A, we discuss and analyze the effect of the depth of Rollout in the simulation phase on the algorithm’s ability to play Amazons, and use the winning convergence distance metric (see Section 4.2 for details) to evaluate the playing ability. Shallow Rollout strategies can consider simulated positions closer to the endgame and more forward-looking games to compute more accurate position evaluation values, which can be used to better guide the node selection for MCTS. Therefore, it is crucial to balance the depth of Rollout; too shallow a depth will make the utilization value (winning rate) in the position evaluation formula less credible, while too deep a depth will lead to a single simulation iteration process that is too long, and the number of nodes expanded out in a finite period of time will become smaller, reducing the accuracy of the Monte Carlo tree search decision. We adjusted the Rollout depth value from 2 to 10 and found that the optimal value of Rollout depth is 4 or 5, as shown in Table A1.

Table A1.
Parametric analysis of the Rollout depth.
Table A1.
Parametric analysis of the Rollout depth.
| Rollout Depth | 1 | 2 | 3 | 4 | 5 | 6 | 7–10 | 4 and 5 |
|---|---|---|---|---|---|---|---|---|
| Match Point Rounds | 40.25 | 40.14 | 40.0 | 39.9 | 39.84 | 40.04 | 40.1 | 39.68 |
Red results indicate the best result in the same column.
In addition, we found in our experiments that Rollout twice (choosing 4 and 5 in-depth) works better than Rollout once (choosing only 4 or 5), i.e., the number of rounds at match points is smaller, the distance of convergence for winning is shorter, and the algorithm is more capable of playing Amazons.
Appendix B
Appendix B shows the detailed CPU usage of the algorithm with and without the Parallel Evaluation strategy. The monitoring environment is the performance profiler in Microsoft Visual Studio 2019, with the algorithm making only one decision, which takes 20 s. As shown in Figure A1, the top part of the image represents the CPU utilization, and the fluctuating part of the CPU utilization values corresponds to the algorithm’s decision-making phase, while the remaining part corresponds to the input and output idle phases.
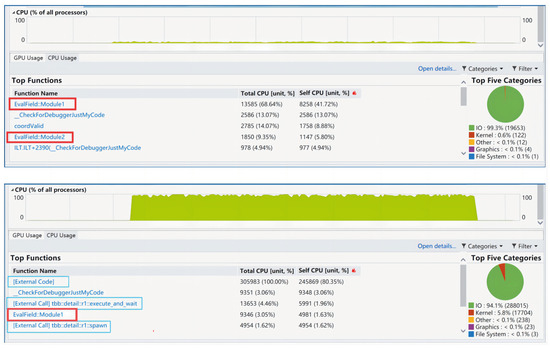
Figure A1.
CPU utilization and top 5 modules occupying CPU resources under [Debug ×64] condition. The upper part shows the monitoring results of the algorithm executed sequentially, while the lower part shows the monitoring results of the algorithm executed in parallel.
From Figure A1, it is evident that the CPU utilization of the algorithm program in parallel execution is significantly higher than in sequential execution. When the algorithm program executes sequentially, both red-framed modules of the evaluation function are among the top 5 modules occupying the most CPU resources. This indicates that parallel optimization of the evaluation part is very necessary. During parallel execution of the algorithm program, the blue-framed third-party parallel library occupies a substantial amount of CPU resources. This indirectly indicates that the performance improvement after parallelization does not achieve the theoretical speedup due to significant resource consumption by external code and external calls.
Appendix C
Appendix C shows the complete game information, as well as the match point round count, as shown in Table A2 and Table A3.

Table A2.
Complete game information (MCTS plus MG-PEO).
Table A2.
Complete game information (MCTS plus MG-PEO).
| ID | First Player | Second Player | Result | Match Point Rounds | Winner |
|---|---|---|---|---|---|
| 1 | Amazons based on Qt’s QMainWindow framework | Divine Move (ours) | 0:3 | 41 | Divine Move (ours) |
| 2 | Divine Move (ours) | Amazons based on Qt’s QMainWindow framework | 3:0 | 39 | Divine Move (ours) |
| 3 | Gomoku | Divine Move (ours) | 0:3 | 39 | Divine Move (ours) |
| 4 | Divine Move (ours) | Gomoku | 3:0 | 36 | Divine Move (ours) |
| 5 | Othello | Divine Move (ours) | 0:3 | 35 | Divine Move (ours) |
| 6 | Divine Move (ours) | Othello | 3:0 | 33 | Divine Move (ours) |
| 7 | God’s Algorithm | Divine Move (ours) | 0:3 | 43 | Divine Move (ours) |
| 8 | Divine Move (ours) | God’s Algorithm | 3:0 | 42 | Divine Move (ours) |
| 9 | Amazons Gaming System | Divine Move (ours) | 0:3 | 39 | Divine Move (ours) |
| 10 | Divine Move (ours) | Amazons Gaming System | 3:0 | 37 | Divine Move (ours) |
| 11 | Advance Little Queens | Divine Move (ours) | 0:3 | 40 | Divine Move (ours) |
| 12 | Divine Move (ours) | Advance Little Queens | 3:0 | 37 | Divine Move (ours) |
| 13 | Checkmate | Divine Move (ours) | 0:3 | 41 | Divine Move (ours) |
| 14 | Divine Move (ours) | Checkmate | 3:0 | 38 | Divine Move (ours) |
| 15 | Cliffhanger Amazons | Divine Move (ours) | 0:3 | 40 | Divine Move (ours) |
| 16 | Divine Move (ours) | Cliffhanger Amazons | 3:0 | 37 | Divine Move (ours) |
| 17 | Qi Kaide’s Victory | Divine Move (ours) | 0:3 | 41 | Divine Move (ours) |
| 18 | Divine Move (ours) | Qi Kaide’s Victory | 3:0 | 36 | Divine Move (ours) |
| 19 | Super Amazon | Divine Move (ours) | 0:3 | 39 | Divine Move (ours) |
| 20 | Divine Move (ours) | Super Amazon | 3:0 | 36 | Divine Move (ours) |
| 21 | God’s Algorithm | Divine Move (ours) | 0:3 | 41 | Divine Move (ours) |
| 22 | Divine Move (ours) | God’s Algorithm | 3:0 | 37 | Divine Move (ours) |
| 23 | Traveler Amazons | Divine Move (ours) | 0:3 | 40 | Divine Move (ours) |
| 24 | Divine Move (ours) | Traveler Amazons | 3:0 | 35 | Divine Move (ours) |
| 25 | Amazon Supreme Chess | Divine Move (ours) | 0:3 | 41 | Divine Move (ours) |
| 26 | Divine Move (ours) | Amazon Supreme Chess | 3:0 | 39 | Divine Move (ours) |
| 27 | Chess Troops Falling from Heaven | Divine Move (ours) | 0:3 | 43 | Divine Move (ours) |
| 28 | Divine Move (ours) | Chess Troops Falling from Heaven | 3:0 | 41 | Divine Move (ours) |
| 29 | Clove Amazons | Divine Move (ours) | 0:3 | 40 | Divine Move (ours) |
| 30 | Divine Move (ours) | Clove Amazons | 3:0 | 37 | Divine Move (ours) |
| 31 | Shao Guang’s Amazons | Divine Move (ours) | 0:3 | 43 | Divine Move (ours) |
| 32 | Divine Move (ours) | Shao Guang’s Amazons | 3:0 | 39 | Divine Move (ours) |
| 33 | AI plays chess | Divine Move (ours) | 0:3 | 43 | Divine Move (ours) |
| 34 | Divine Move (ours) | AI plays chess | 3:0 | 39 | Divine Move (ours) |
| 35 | Canopus One | Divine Move (ours) | 0:3 | 39 | Divine Move (ours) |
| 36 | Divine Move (ours) | Canopus One | 3:0 | 35 | Divine Move (ours) |
| 37 | Win the Opening Team | Divine Move (ours) | 0:3 | 41 | Divine Move (ours) |
| 38 | Divine Move (ours) | Win the Opening Team | 3:0 | 39 | Divine Move (ours) |
| 39 | Wukong Amazons | Divine Move (ours) | 0:3 | 34 | Divine Move (ours) |
| 40 | Divine Move (ours) | Wukong Amazons | 3:0 | 30 | Divine Move (ours) |
| 41 | Traveler Amazons | Divine Move (ours) | 0:3 | 44 | Divine Move (ours) |
| 42 | Divine Move (ours) | Traveler Amazons | 3:0 | 40 | Divine Move (ours) |
| 43 | Yue | Divine Move (ours) | 0:3 | 41 | Divine Move (ours) |
| 44 | Divine Move (ours) | Yue | 3:0 | 40 | Divine Move (ours) |
| 45 | Final Amazon | Divine Move (ours) | 0:3 | 41 | Divine Move (ours) |
| 46 | Divine Move (ours) | Final Amazon | 3:0 | 38 | Divine Move (ours) |
| 47 | Information University - Monte Carlo | Divine Move (ours) | 1:2 | 42 | Divine Move (ours) |
| 48 | Divine Move (ours) | Information University - Monte Carlo | 3:0 | 40 | Divine Move (ours) |
| 49 | Haha Hi | Divine Move (ours) | 1:2 | 42 | Divine Move (ours) |
| 50 | Divine Move (ours) | Haha Hi | 3:0 | 39 | Divine Move (ours) |
| 51 | Dragon Victory | Divine Move (ours) | 0:3 | 41 | Divine Move (ours) |
| 52 | Divine Move (ours) | Dragon Victory | 3:0 | 37 | Divine Move (ours) |
| 53 | Super Amazon | Divine Move (ours) | 0:3 | 43 | Divine Move (ours) |
| 54 | Divine Move (ours) | Super Amazon | 3:0 | 38 | Divine Move (ours) |
| 55 | Base Pairing Team | Divine Move (ours) | 0:3 | 44 | Divine Move (ours) |
| 56 | Divine Move (ours) | Base Pairing Team | 3:0 | 41 | Divine Move (ours) |
| 57 | Pass the Level | Divine Move (ours) | 3:0 | 47 | Pass the Level |
| 58 | Divine Move (ours) | Pass the Level | 0:3 | 47 | Pass the Level |
| 59 | Dalian Jiaotong University Amazons Team 1 | Divine Move (ours) | 0:3 | 41 | Divine Move (ours) |
| 60 | Divine Move (ours) | Dalian Jiaotong University Amazons Team 1 | 3:0 | 39 | Divine Move (ours) |
| 61 | Get Ashore | Divine Move (ours) | 0:3 | 41 | Divine Move (ours) |
| 62 | Divine Move (ours) | Get Ashore | 3:0 | 40 | Divine Move (ours) |
| 63 | Empty | Divine Move (ours) | 0:3 | 44 | Divine Move (ours) |
| 64 | Divine Move (ours) | Empty | 3:0 | 41 | Divine Move (ours) |
| 65 | Bull | Divine Move (ours) | 0:3 | 42 | Divine Move (ours) |
| 66 | Divine Move (ours) | Bull | 3:0 | 40 | Divine Move (ours) |
| 67 | Wukong Amazons | Divine Move (ours) | 1:2 | 34 | Divine Move (ours) |
| 68 | Divine Move (ours) | Wukong Amazons | 3:0 | 31 | Divine Move (ours) |
| 69 | Gangzi Fans Support Team | Divine Move (ours) | 0:3 | 41 | Divine Move (ours) |
| 70 | Divine Move (ours) | Gangzi Fans Support Team | 3:0 | 39 | Divine Move (ours) |
| 71 | Thai Pants Spicy | Divine Move (ours) | 0:3 | 44 | Divine Move (ours) |
| 72 | Divine Move (ours) | Thai Pants Spicy | 3:0 | 41 | Divine Move (ours) |
| 73 | Green Grass Cake | Divine Move (ours) | 0:3 | 34 | Divine Move (ours) |
| 74 | Divine Move (ours) | Green Grass Cake | 3:0 | 30 | Divine Move (ours) |
| 75 | Failed to Grab the Air and Didn’t Grab the Plant Brain Hypoxia Team | Divine Move (ours) | 0:3 | 40 | Divine Move (ours) |
| 76 | Divine Move (ours) | Failed to Grab the Air and Didn’t Grab the Plant Brain Hypoxia Team | 3:0 | 37 | Divine Move (ours) |
| 77 | DG | Divine Move (ours) | 0:3 | 44 | Divine Move (ours) |
| 78 | Divine Move (ours) | DG | 3:0 | 39 | Divine Move (ours) |
| 79 | Why is Tang Yang a God | Divine Move (ours) | 0:3 | 42 | Divine Move (ours) |
| 80 | Divine Move (ours) | Why is Tang Yang a God | 3:0 | 39 | Divine Move (ours) |
| 81 | Dream Team | Divine Move (ours) | 0:3 | 43 | Divine Move (ours) |
| 82 | Divine Move (ours) | Dream Team | 3:0 | 39 | Divine Move (ours) |
| 83 | Horse Face Skirt Daily and Easy to Wear | Divine Move (ours) | 0:3 | 43 | Divine Move (ours) |
| 84 | Divine Move (ours) | Horse Face Skirt Daily and Easy to Wear | 3:0 | 40 | Divine Move (ours) |
| 85 | Genshin Impact Expert | Divine Move (ours) | 0:3 | 41 | Divine Move (ours) |
| 86 | Divine Move (ours) | Genshin Impact Expert | 3:0 | 37 | Divine Move (ours) |
| 87 | Code Apprentice | Divine Move (ours) | 0:3 | 42 | Divine Move (ours) |
| 88 | Divine Move (ours) | Code Apprentice | 3:0 | 41 | Divine Move (ours) |
| 89 | Amazon Drift Notes | Divine Move (ours) | 0:3 | 39 | Divine Move (ours) |
| 90 | Divine Move (ours) | Amazon Drift Notes | 3:0 | 37 | Divine Move (ours) |
| 91 | Love Will Disappear, Right? | Divine Move (ours) | 0:3 | 38 | Divine Move (ours) |
| 92 | Divine Move (ours) | Love Will Disappear, Right? | 3:0 | 33 | Divine Move (ours) |
| 93 | Little Su and the Cat | Divine Move (ours) | 0:3 | 43 | Divine Move (ours) |
| 94 | Divine Move (ours) | Little Su and the Cat | 3:0 | 42 | Divine Move (ours) |
| 95 | Don’t Want Marla | Divine Move (ours) | 0:3 | 44 | Divine Move (ours) |
| 96 | Divine Move (ours) | Don’t Want Marla | 3:0 | 43 | Divine Move (ours) |
| 97 | Parameter Adjustment Team | Divine Move (ours) | 0:3 | 44 | Divine Move (ours) |
| 98 | Divine Move (ours) | Parameter Adjustment Team | 3:0 | 41 | Divine Move (ours) |
| 99 | AlphaAmazon | Divine Move (ours) | 0:3 | 43 | Divine Move (ours) |
| 100 | Divine Move (ours) | AlphaAmazon | 3:0 | 42 | Divine Move (ours) |

Table A3.
Complete game information (MCTS).
Table A3.
Complete game information (MCTS).
| ID | First Player | Second Player | Result | Match Point Rounds | Winner |
|---|---|---|---|---|---|
| 1 | Amazons based on Qt’s QMainWindow framework | MCTS (baseline) | 1:2 | 43 | MCTS (baseline) |
| 2 | MCTS (baseline) | Amazons based on Qt’s QMainWindow framework | 3:0 | 41 | MCTS (baseline) |
| 3 | Gomoku | MCTS (baseline) | 3:0 | 47 | Gomoku |
| 4 | MCTS (baseline) | Gomoku | 3:0 | 45 | MCTS (baseline) |
| 5 | Othello | MCTS (baseline) | 2:1 | 47 | Othello |
| 6 | MCTS (baseline) | Othello | 2:1 | 44 | MCTS (baseline) |
| 7 | God’s Algorithm | MCTS (baseline) | 0:3 | 43 | MCTS (baseline) |
| 8 | MCTS (baseline) | God’s Algorithm | 3:0 | 40 | MCTS (baseline) |
| 9 | Amazons Gaming System | MCTS (baseline) | 0:3 | 42 | MCTS (baseline) |
| 10 | MCTS (baseline) | Amazons Gaming System | 3:0 | 40 | MCTS (baseline) |
| 11 | Advance Little Queens | MCTS (baseline) | 3:0 | 47 | Advance Little Queens |
| 12 | MCTS (baseline) | Advance Little Queens | 3:0 | 43 | MCTS (baseline) |
| 13 | Checkmate | MCTS (baseline) | 2:1 | 47 | Checkmate |
| 14 | MCTS (baseline) | Checkmate | 3:0 | 40 | MCTS (baseline) |
| 15 | Cliffhanger Amazons | MCTS (baseline) | 3:0 | 47 | Checkmate |
| 16 | MCTS (baseline) | Cliffhanger Amazons | 3:0 | 44 | MCTS (baseline) |
| 17 | Qi Kaide’s Victory | MCTS (baseline) | 0:3 | 44 | MCTS (baseline) |
| 18 | MCTS (baseline) | Qi Kaide’s Victory | 3:0 | 41 | MCTS (baseline) |
| 19 | Super Amazon | MCTS (baseline) | 2:1 | 47 | Super Amazon |
| 20 | MCTS (baseline) | Super Amazon | 2:1 | 43 | MCTS (baseline) |
| 21 | God’s Algorithm | MCTS (baseline) | 3:0 | 47 | God’s Algorithm |
| 22 | MCTS (baseline) | God’s Algorithm | 2:1 | 40 | MCTS (baseline) |
| 23 | Traveler Amazons | MCTS (baseline) | 2:1 | 47 | Traveler Amazons |
| 24 | MCTS (baseline) | Traveler Amazons | 3:0 | 42 | MCTS (baseline) |
| 25 | Amazon Supreme Chess | MCTS (baseline) | 0:3 | 40 | MCTS (baseline) |
| 26 | MCTS (baseline) | Amazon Supreme Chess | 3:0 | 41 | MCTS (baseline) |
| 27 | Chess Troops Falling from Heaven | MCTS (baseline) | 0:3 | 43 | MCTS (baseline) |
| 28 | MCTS (baseline) | Chess Troops Falling from Heaven | 3:0 | 39 | MCTS (baseline) |
| 29 | Clove Amazons | MCTS (baseline) | 0:3 | 44 | MCTS (baseline) |
| 30 | MCTS (baseline) | Clove Amazons | 3:0 | 40 | MCTS (baseline) |
| 31 | Shao Guang’s Amazons | MCTS (baseline) | 1:2 | 43 | MCTS (baseline) |
| 32 | MCTS (baseline) | Shao Guang’s Amazons | 3:0 | 40 | MCTS (baseline) |
| 33 | AI plays chess | MCTS (baseline) | 2:1 | 47 | AI plays chess |
| 34 | MCTS (baseline) | AI plays chess | 3:0 | 42 | MCTS (baseline) |
| 35 | Canopus One | MCTS (baseline) | 0:3 | 43 | MCTS (baseline) |
| 36 | MCTS (baseline) | Canopus One | 2:1 | 40 | MCTS (baseline) |
| 37 | Win the Opening Team | MCTS (baseline) | 3:0 | 47 | Win the Opening Team |
| 38 | MCTS (baseline) | Win the Opening Team | 3:0 | 44 | MCTS (baseline) |
| 39 | Wukong Amazons | MCTS (baseline) | 0:3 | 42 | MCTS (baseline) |
| 40 | MCTS (baseline) | Wukong Amazons | 3:0 | 39 | MCTS (baseline) |
| 41 | Traveler Amazons | MCTS (baseline) | 0:3 | 41 | MCTS (baseline) |
| 42 | MCTS (baseline) | Traveler Amazons | 3:0 | 36 | MCTS (baseline) |
| 43 | Yue | MCTS (baseline) | 0:3 | 44 | MCTS (baseline) |
| 44 | MCTS (baseline) | Yue | 3:0 | 41 | MCTS (baseline) |
| 45 | Final Amazon | MCTS (baseline) | 0:3 | 42 | MCTS (baseline) |
| 46 | MCTS (baseline) | Final Amazon | 3:0 | 37 | MCTS (baseline) |
| 47 | Information University - Monte Carlo | MCTS (baseline) | 3:0 | 47 | Information University-Monte Carlo |
| 48 | MCTS (baseline) | Information University-Monte Carlo | 0:3 | 47 | Information University-Monte Carlo |
| 49 | Haha Hi | MCTS (baseline) | 3:0 | 47 | Haha Hi |
| 50 | MCTS (baseline) | Haha Hi | 3:0 | 41 | MCTS (baseline) |
| 51 | Dragon Victory | MCTS (baseline) | 0:3 | 43 | MCTS (baseline) |
| 52 | MCTS (baseline) | Dragon Victory | 3:0 | 38 | MCTS (baseline) |
| 53 | Super Amazon | MCTS (baseline) | 0:3 | 41 | MCTS (baseline) |
| 54 | MCTS (baseline) | Super Amazon | 3:0 | 38 | MCTS (baseline) |
| 55 | Base Pairing Team | MCTS (baseline) | 3:0 | 45 | Base Pairing Team |
| 56 | MCTS (baseline) | Base Pairing Team | 0:3 | 42 | Base Pairing Team |
| 57 | Pass the Level | MCTS (baseline) | 3:0 | 47 | Pass the Level |
| 58 | MCTS (baseline) | Pass the Level | 0:3 | 47 | Pass the Level |
| 59 | Dalian Jiaotong University Amazons Team 1 | MCTS (baseline) | 0:3 | 44 | MCTS (baseline) |
| 60 | MCTS (baseline) | Dalian Jiaotong University Amazons Team 1 | 3:0 | 42 | MCTS (baseline) |
| 61 | Get Ashore | MCTS (baseline) | 3:0 | 47 | Get Ashore |
| 62 | MCTS (baseline) | Get Ashore | 0:3 | 47 | Get Ashore |
| 63 | Empty | MCTS (baseline) | 0:3 | 45 | MCTS (baseline) |
| 64 | MCTS (baseline) | Empty | 3:0 | 41 | MCTS (baseline) |
| 65 | Bull | MCTS (baseline) | 0:3 | 45 | MCTS (baseline) |
| 66 | MCTS (baseline) | Bull | 3:0 | 40 | MCTS (baseline) |
| 67 | Wukong Amazons | MCTS (baseline) | 2:1 | 47 | Wukong Amazons |
| 68 | MCTS (baseline) | Wukong Amazons | 3:0 | 39 | MCTS (baseline) |
| 69 | Gangzi Fans Support Team | MCTS (baseline) | 3:0 | 44 | Gangzi Fans Support Team |
| 70 | MCTS (baseline) | Gangzi Fans Support Team | 1:2 | 41 | Gangzi Fans Support Team |
| 71 | Thai Pants Spicy | MCTS (baseline) | 0:3 | 42 | MCTS (baseline) |
| 72 | MCTS (baseline) | Thai Pants Spicy | 3:0 | 40 | MCTS (baseline) |
| 73 | Green Grass Cake | MCTS (baseline) | 0:3 | 42 | MCTS (baseline) |
| 74 | MCTS (baseline) | Green Grass Cake | 3:0 | 37 | MCTS (baseline) |
| 75 | Failed to Grab the Air and Didn’t Grab the Plant Brain Hypoxia Team | MCTS (baseline) | 0:3 | 41 | MCTS (baseline) |
| 76 | MCTS (baseline) | Failed to Grab the Air and Didn’t Grab the Plant Brain Hypoxia Team | 3:0 | 40 | MCTS (baseline) |
| 77 | DG | MCTS (baseline) | 0:3 | 43 | MCTS (baseline) |
| 78 | MCTS (baseline) | DG | 3:0 | 39 | MCTS (baseline) |
| 79 | Why is Tang Yang a God | MCTS (baseline) | 2:1 | 47 | Why is Tang Yang a God |
| 80 | MCTS (baseline) | Why is Tang Yang a God | 3:0 | 44 | MCTS (baseline) |
| 81 | Dream Team | MCTS (baseline) | 0:3 | 43 | MCTS (baseline) |
| 82 | MCTS (baseline) | Dream Team | 3:0 | 44 | MCTS (baseline) |
| 83 | Horse Face Skirt Daily and Easy to Wear | MCTS (baseline) | 0:3 | 44 | MCTS (baseline) |
| 84 | MCTS (baseline) | Horse Face Skirt Daily and Easy to Wear | 3:0 | 40 | MCTS (baseline) |
| 85 | Genshin Impact Expert | MCTS (baseline) | 0:3 | 44 | MCTS (baseline) |
| 86 | MCTS (baseline) | Genshin Impact Expert | 3:0 | 39 | MCTS (baseline) |
| 87 | Code Apprentice | MCTS (baseline) | 0:3 | 42 | MCTS (baseline) |
| 88 | MCTS (baseline) | Code Apprentice | 3:0 | 40 | MCTS (baseline) |
| 89 | Amazon Drift Notes | MCTS (baseline) | 0:3 | 44 | MCTS (baseline) |
| 90 | MCTS (baseline) | Amazon Drift Notes | 3:0 | 42 | MCTS (baseline) |
| 91 | Love Will Disappear, Right? | MCTS (baseline) | 0:3 | 40 | MCTS (baseline) |
| 92 | MCTS (baseline) | Love Will Disappear, Right? | 3:0 | 38 | MCTS (baseline) |
| 93 | Little Su and the Cat | MCTS (baseline) | 0:3 | 44 | MCTS (baseline) |
| 94 | MCTS (baseline) | Little Su and the Cat | 3:0 | 40 | MCTS (baseline) |
| 95 | Don’t Want Marla | MCTS (baseline) | 0:3 | 41 | MCTS (baseline) |
| 96 | MCTS (baseline) | Don’t Want Marla | 3:0 | 37 | MCTS (baseline) |
| 97 | Parameter Adjustment Team | MCTS (baseline) | 0:3 | 42 | MCTS (baseline) |
| 98 | MCTS (baseline) | Parameter Adjustment Team | 3:0 | 39 | MCTS (baseline) |
| 99 | AlphaAmazon | MCTS (baseline) | 0:3 | 41 | MCTS (baseline) |
| 100 | MCTS (baseline) | AlphaAmazon | 0:3 | 47 | AlphaAmazon |
References
- Li, R.; Gao, M. Amazons search algorithm design based on CNN model. Digit. Technol. Appl. 2022, 40, 164–166. [Google Scholar]
- Guo, Q.; Li, S.; Bao, H. Research on evaluation function computer game of Amazon. Comput. Eng. Appl. 2012, 48, 50–54. [Google Scholar]
- Guo, T.; Qiu, H.; Tong, B.; Wang, Y. Optimization and Comparison of Multiple Game Algorithms in Amazons. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 6299–6304. [Google Scholar]
- Quan, J.; Qiu, H.; Wang, Y.; Li, F.; Qiu, S. Application of UCT technologies for computer games of Amazon. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 6896–6899. [Google Scholar]
- Ju, J.; Qiu, H.; Wang, F.; Wang, X.; Wang, Y. Research on Thread Optimization and Opening Library Based on Parallel PVS Algorithm in Amazons. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 28–30 May 2021; pp. 2207–2212. [Google Scholar]
- Li, Z.; Ning, C.; Cao, J.; Li, Z. Amazons Based on UCT-PVS Hybrid Algorithm. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 28–30 May 2021; pp. 2179–2183. [Google Scholar]
- Ding, M.; Bo, J.; Qi, Y.; Fu, Y.; Li, S. Design of Amazons Game System Based on Reinforcement Learning. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 6337–6342. [Google Scholar]
- Tong, B.; Qiu, H.; Guo, T.; Wang, Y. Research and Application of Parallel Computing of PVS Algorithm Based on Amazon Human-Machine Game. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 6293–6298. [Google Scholar]
- Chen, X.; Yang, L. Research on evaluation function in Amazons. Comput. Knowl. Technol. 2019, 15, 224–226. [Google Scholar]
- Wang, C.; Ding, M. Interface design and implementation of personalized Amazons. Intell. Comput. Appl. 2017, 7, 78–80. [Google Scholar]
- Zhang, L. Research on Amazons Game System Based on Minimax Search Algorithm. Master’s Thesis, Northeast University, Shenyang, China, 2010. [Google Scholar]
- Metropolis, N.; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef] [PubMed]
- Coulom, R. Efficient Selectivity and Backup Operators in Monte-Carlo Tree Search. In Proceedings of the Computers and Games, Turin, Italy, 1–5 April 2007; pp. 72–83. [Google Scholar]
- Gelly, S.; Kocsis, L.; Schoenauer, M.; Sebag, M.; Silver, D.; Szepesvári, C.; Teytaud, O. The grand challenge of computer Go: Monte Carlo tree search and extensions. Commun. ACM 2012, 55, 106–113. [Google Scholar] [CrossRef]
- Gelly, S.; Silver, D. Monte-Carlo tree search and rapid action value estimation in computer Go. Artif. Intell. 2011, 175, 1856–1875. [Google Scholar] [CrossRef]
- Vinyals, O.; Babuschkin, I.; Czarnecki, W.M.; Mathieu, M.; Dudzik, A.; Chung, J.; Choi, D.H.; Powell, R.; Ewalds, T.; Georgiev, P.; et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature 2019, 575, 350–354. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Berner, C.; Brockman, G.; Chan, B.; Cheung, V.; Dębiak, P.; Dennison, C.; Farhi, D.; Fischer, Q.; Hashme, S.; Hesse, C.; et al. Dota 2 with Large Scale Deep Reinforcement Learning. arXiv 2019, arXiv:1912.06680. [Google Scholar]
- Browne, C.B.; Powley, E.; Whitehouse, D.; Lucas, S.M.; Cowling, P.I.; Rohlfshagen, P.; Tavener, S.; Perez, D.; Samothrakis, S.; Colton, S. A Survey of Monte Carlo Tree Search Methods. IEEE Trans. Comput. Intell. AI Games 2012, 4, 1–43. [Google Scholar] [CrossRef]
- Kloetzer, J.; Iida, H.; Bouzy, B. The Monte-Carlo Approach in Amazons. In Proceedings of the Computer Games Workshop, Amsterdam, The Netherlands, 15–17 June 2007; pp. 185–192. [Google Scholar]
- Shannon, C.E. Programming a computer for playing chess. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1950, 41, 256–275. [Google Scholar] [CrossRef]
- Chaslot, G.; Bakkes, S.; Szita, I.; Spronck, P. Monte-Carlo Tree Search: A New Framework for Game AI. In Proceedings of the AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment, California, CA, USA, 22–24 October 2008; pp. 216–217. [Google Scholar]
- Świechowski, M.; Godlewski, K.; Sawicki, B.; Mańdziuk, J. Monte Carlo Tree Search: A review of recent modifications and applications. Artif. Intell. Rev. 2023, 56, 2497–2562. [Google Scholar] [CrossRef]
- Kloetzer, J. Monte-Carlo Opening Books for Amazons. In Computers and Games: 7th International Conference (CG 2010), Kanazawa, Japan, September 24–26 2010, Revised Selected Papers 7; Springer: Berlin/Heidelberg, Germany, 2011; pp. 124–135. [Google Scholar]
- Song, J.; Müller, M. An Enhanced Solver for the Game of Amazons. IEEE Trans. Comput. Intell. AI Games 2014, 7, 16–27. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, X.; Chang, R.; Zhang, Y.; Wang, C.; Bai, L.; Wang, J.; Xu, C. Mastering the Game of Amazons Fast by Decoupling Network Learning. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–8. [Google Scholar]
- de Koning, J. INVADER Prolongs Amazons Title. ICGA J. 2011, 34, 96. [Google Scholar] [CrossRef]
- Kloetzer, J. INVADER Wins Amazons Tournament. ICGA J. 2009, 32, 112–113. [Google Scholar] [CrossRef]
- Lorentz, R. Invader Wins Eighth Amazons Gold Medal. ICGA J. 2017, 39, 228–229. [Google Scholar] [CrossRef]
- Guo, Q.; Li, S.; Bao, H. The Research of Searching Algorithm in Amazons Game. In Proceedings of the 2011 Chinese Control and Decision Conference (CCDC), Mianyang, China, 23–25 May 2011; pp. 1859–1862. [Google Scholar]
- Li, X.; Hou, L.; Wu, L. UCT Algorithm in Amazons Human-Computer Games. In Proceedings of the 26th Chinese Control and Decision Conference (CCDC), Changsha, China, 31 May–2 June 2014; pp. 3358–3361. [Google Scholar]
- Quan, J.; Qiu, H.; Wang, Y.; Li, Y.; Wang, X. Study the Performance of Search Algorithms in Amazons. In Proceedings of the 27th Chinese Control and Decision Conference (CCDC), Qingdao, China, 23–25 May 2015; pp. 5811–5813. [Google Scholar]
- Lieberum, J. An Evaluation Function for the Game of Amazons. Theor. Comput. Sci. 2005, 349, 230–244. [Google Scholar] [CrossRef][Green Version]
- Chai, Z.; Fang, Z.; Zhu, J. Amazons Evaluation Optimization Strategy Based on PSO Algorithm. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 6334–6336. [Google Scholar]
- Sun, Y.; Yuan, D.; Gao, M.; Zhu, P. GPU Acceleration of Monte Carlo Tree Search Algorithm for Amazons and Its Evaluation Function. In Proceedings of the 2022 International Conference on Artificial Intelligence, Information Processing and Cloud Computing (AIIPCC), Kunming, China, 21–23 June 2022; pp. 434–440. [Google Scholar]
- Kocsis, L.; Szepesvari, C.; Willemson, J. Improved Monte-Carlo Search. Univ. Tartu Est. Tech. Rep. 2006, 1, 1–22. [Google Scholar]
- Finnsson, H.; Björnsson, Y. Game-tree properties and MCTS performance. IJCAI 2011, 11, 23–30. [Google Scholar]
- Pheatt, C. Intel® threading building blocks. J. Comput. Sci. Coll. 2008, 23, 164–166. [Google Scholar]
- Childs, B.E.; Brodeur, J.H.; Kocsis, L. Transpositions and move groups in monte carlo tree search. In Proceedings of the 2008 IEEE Symposium on Computational Intelligence and Games, Perth, Australia, 15–18 December 2008; pp. 389–395. [Google Scholar]
- Van Eyck, G.; Müller, M. Revisiting move groups in monte-carlo tree search. In Advances in Computer Games: 13th International Conference, ACG 2011, Tilburg, The Netherlands, November 20–22, 2011, Revised Selected Papers 13; Springer: Berlin/Heidelberg, Germany, 2012; pp. 13–23. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).