Abstract
Procedural Content Generation for video games (PCG) is widely used by today’s video game industry to create huge open worlds or enhance replayability. However, there is little scientific evidence that these systems produce high-quality content. In this document, we evaluate three open-source automated level generators for Super Mario Bros in addition to the original levels used for training. These are based on Genetic Algorithms, Generative Adversarial Networks, and Markov Chains. The evaluation was performed through an Expressive Range Analysis (ERA) on 200 levels with nine metrics. The results show how analyzing the algorithms’ expressive range can help us evaluate the generators as a preliminary measure to study whether they respond to users’ needs. This method allows us to recognize potential problems early in the content generation process, in addition to taking action to guarantee quality content when a generator is used.
1. Introduction
Research on Procedural Content Generation for video games consists of studying procedural generation methods that allow the creation of levels for video games automatically through computational algorithms [1]. Currently, these computational algorithms can potentially save money [2], time, and effort in various areas, such as engineering [1], music [3], and art [4]. The total person-hours needed to complete certain activities can be reduced because these AI-driven systems imitate human action to some degree and deliver results as good as those that a game designer could create [5].
Thanks to PCG, companies have adapted their workflows to be more competitive and achieve better results. There are even situations where artists have begun to be replaced by these intelligent systems to create games more quickly and economically while maintaining quality [6]. Nowadays, companies not only settle for the initial release but also add new content to keep their audience captive. We know this strategy as “Downloadable Content” (DLC) [7], where companies offer additional content that is sold separately, allowing them to generate greater profits. PCG can be a powerful tool for creating DLCs and, thus, offering better services to users.
In this article, we carry out a study of the expressiveness of open-source automatic level generators for Super Mario Bros (SMB). These are
- A Multi-Population Genetic Algorithm [8].
- A Deep Convolutional Generative Adversarial Network (DCGAN) and Covariance Matrix Adaptation Strategy (CMA-ES) [9].
- Markov Chains (MCs) (https://github.com/hansschaa/MarkovChains_SMB (accessed on 13 June 2024)).
This article’s main contribution is comparing three generative spaces using Expressive Range Analysis (ERA) [10]. Two of the three evaluated implementations are peer-reviewed [8,9], the third is our implementation of Markov Chains, and finally, these are contrasted with the SMB levels used as training data. The levels were analyzed with nine metrics through heat charts and box/whisker graphs. As seen in Figure 1, we used the tiles from the video game Super Tux [11] throughout this article because of its GPL license.

Figure 1.
Level 1-1 of Super Mario Bros.
To carry out this study, 200 boards were generated with each generator, and then, for each level, the nine metrics were calculated. Finally, these values are graphed to perform a comparative analysis between generators. The results show that GA and MC have a noticeably wider expressive range than GAN. GA benefits from its exploitation and exploration capacity to find diverse levels, and MC, through the training data, creates levels similar to those that a human can design.
This document is structured as follows: Section 2 briefly presents the technique’s state of the art. Then, in Section 3, the implemented algorithms are reported. In Section 4, the experiments carried out and results obtained are presented, and finally, Section 5 and Section 6 show the discussion and conclusions, respectively.
2. Background
Creating PCG systems can be an arduous and challenging task; the literature specifies five characteristics that these should exhibit [1]. These are the following:
- Speed: How fast can the generator deliver the content [12]? This metric measures the time that PCG systems take to generate content. We can categorize these as methods online (the video game has a game loop that allows the generator to create the content at runtime) or offline (the video game does not allow the generator to create the content at runtime), so it must be executed outside of the user experience.
- Reliability: How faithful is the generator to the configuration imposed on it [13]? Sometimes, we need some features to be strictly adhered to. The generator should only produce content that satisfies the previously configured constraints for games to be solvable.
- Controllability: Does the generator allow designers to customize the required content [13]? A highly controllable system will allow greater flexibility and freedom for the designers or engineers using the generator.
- Expressiveness and diversity: Does the expressiveness of the generator allow for the generation of diverse and interesting content [14]? PCG systems are required to give rise to content valued by the audience. For example, one could have an Age of Empires map generator, but if they present the same biomes with different dimensions, it could bore the player.
- Creativity and credibility: In some cases, it is useful to know that the generator produces content similar to that of humans [15].
Creating a quality generator is not easy, and evaluating it is much less so. People are different in different aspects, be they those of psychology, motor skills, ability, or what amuses them. We relate many of these metrics to a subjective factor where the audience is widely diverse, and we, as researchers and developers, must learn to read that to create ad hoc content for each of them. We can broadly divide evaluation methods into the following four groups:
- Static functions: Static functions are widely used in search-based PCG to guide the search toward quality content. Three types of functions can be observed: direct, simulation-based, and interactive functions [1]. Some examples could be the number of pushes needed to solve a Sokoban board [5] or the location of resources on a map for strategy video games [16].
- Expressive Range Analysis: The analysis of the algorithms that generate content is quite useful since it allows us to have an early view of the behavior of a generator [10]. However, these methods should never replace the evaluations the target audience can make. Researchers often use heatmaps to position the generated content based on two variables: linearity and lenience.
- User testing: These methods are often expensive and time-consuming. Although they provide first-hand information, they are methods that require many resources to carry them out. Among these, we can find playtesting, Turing tests, Likert surveys, and post-interviews, among others [2].
- Bots: With advances in machine learning and reinforcement learning, creating bots that allow levels to be evaluated automatically has been made possible. This allows evaluation of the content as if a person were playing the experience [17]. For example, bots have been trained with Reinforcement Learning (RL) to play PCG levels of Super Mario Bros while simulating the actions of a human and, thus, evaluating their playability [18].
2.1. PCG for Super Mario Bros
Super Mario Bros (SMB) is a widely known platformer video game. Its origin dates back to 1985 in Japan, when it was distributed for the Famicon [19]. Its popularity, simplicity, and documentation, among others, make it an attractive study subject. Below are some key events in the study of SMB.
The generation of SMB levels began with the general study of platformer games [20]. The authors created categories of tile patterns: basic patterns (patterns without repetition), complex patterns (repetition of the same component but with certain changed settings, such as a sequence of platforms with holes of increasing length), compound patterns (alternating between two types of basic patterns), and composite patterns (two components are placed close together in such a way that they require a different type of action or a coordinated action, which would not be necessary for each one individually). Then, they establish a link between the game rhythm that they want to deliver and the music inspired by previous research [21]. They report that although relating music to the design of platformer levels seems somewhat discordant, this depends greatly on the rhythm. When the user must jump over obstacles, they must follow a game rhythm. The design applied to video games of this genre creates a rhythmic sequence based on the placement of enemies and obstacles. These were the bases for several later studies that referred to how to evaluate platformer levels. For example, regarding difficulty, the authors of [22] proposed a metric based on the probability of loss that the player has. For this, they created five types of scenarios where each event (jumping, climbing stairs, dodging bullets) had an associated probability of loss. In the same research on measuring difficulty, evolutionary preference was also used in learning via a simple neural network to assess fun, frustration, and challenge levels [23]. In 2009, the Mario AI Competition began, aiming to create bots to play SMB levels. These have allowed the levels to be evaluated according to their playability, expanding the possible analyses of SMB levels.
2.1.1. PCG Algorithms
Various algorithms have been used to generate SMB levels. With the rise of long short-term memory (LSTM) networks, such algorithms have created playable SMB levels similar to those that a human would build by introducing information about the agent’s routes to solve them [24]. Large Language Models (LLMs) have also been used to create levels through different prompts, achieving excellent results [25]; the authors implemented an adjusted GPT2 Large-Scale Language Model, and 88% of the levels were playable. It has also been proven that these architectures can give rise to highly structured content, such as Sokoban levels; the results improve considerably according to the amount of training data provided [26]. The popularity of LLMs is such that a large number of studies showing their potential in video games have been published [27,28,29]. In the same line as the use of ML, through reinforcement learning, agents capable of designing SMB levels have been created, and then a neural-network-assisted evolutionary algorithm repairs them. The authors assert that their proposed framework can generate infinite playable SMB levels with different degrees of fun and playability [30]. Unlike these black-box models, other level generation systems have also been proposed, such as constructive algorithms [31,32,33] and search-based algorithms [34,35,36].
In addition to the aforementioned methods, Markov Chains have been a popular approach for content generation [37]. These are known as a particular example of a Dynamic Bayesian Network (DBN) [38]; they map states through probabilities of transitioning between them. Related to the procedural generation of SMB levels, several works that generally use human-created levels to sample new columns of tiles based on the probability at which they appear can be found [39,40,41]. Given the stochastic nature of the Markov Chain, there may be a problem in that some levels that are created cannot be playable, which is why hybrid strategies that incorporate search algorithms to join segments of levels have been studied [42].
2.1.2. Expressive Range Analysis
Analyzing the expressive range of algorithms as an early quality assessment measure has been one of the most popular strategies within the scientific community for PCG. The steps of performing an ERA are the following [10]:
- Determining the metrics: The set of metrics to be evaluated must be chosen; they ideally emerge from the generator’s point of view since we can control these variables.
- Generating the content: A representative sample of the generator’s ability to calculate the previously defined metrics is created.
- Visualizing the generative space: The scores reflect the expressive range of the generator. This can be displayed through heatmaps or histograms to find patterns or gaps.
- Analyzing the impacts of the parameters: Comparisons can now be made by modifying the generator variables and determining their expressiveness.
To carry out an Expressive Range Analysis, most studies select the variables by intuition or simply try to use free-for-all heat graphics. To achieve a greater knowledge of the PCG system implemented, methods to study the characteristics that have the greatest impact on the video game have been created; thus, they are selected in such a way as to carry out the analysis with a much more representative set of the level qualities desired to be evaluated [43]. Graphically, heatmaps and box/whisker graphs have been used to statistically study generative power when creating SMB levels [44]. In another case, categorizations have been proposed for metrics and neural networks to estimate how good the aesthetics are or how complicated a game level is [45].
3. PCG Algorithms Evaluated
3.1. Multi-Population Genetic Algorithm
This is a multi-population genetic algorithm for the procedural generation of SMB levels. The central idea of this algorithm is to evolve terrain, enemies, coins, and blocks independently. Each of these has its own coding and fitness function. When the evolutionary algorithm finishes the specified generations, the best individuals from each population are chosen to build a level. By combining each population to create the level, the algorithm makes sure to position each element in the correct place. For example, enemies are placed on the highest floor tile in each column, and coins are placed at a height defined by the genotype, as are blocks.
3.1.1. Representation
Each of the individuals is encoded as a vector of integers; thus, the level will be represented by the union of these four vectors. Each one follows the following logic:
- Floor: The vector for the floor is a vector of the length of the level, where each element takes values between 0 and 15. Each position shows the place on the x-axis where the floor tile will go.
- Blocks: The blocks follow a structure similar to that of the vector for the ground. The difference is that each element takes values between 0 and 4 to show the type of block (improvement, coin, solid, destructible). These are placed four spaces above the highest floor tile, so only one block can be placed per column.
- Enemies: The vector of enemies has the same definition as the vector of blocks, except that they are located immediately after the ground. Each of its elements can take values between 0 and 3 because of the three types of enemies.
- Coins: The vector of coins works the same as that of the ground, where each value shows the height at which they are located.
3.1.2. Fitness Function
The fitness function is the same for everything except the floor. It evaluates this under the concept of entropy [46]. This allows the measurement of the unpredictability of an event, and here, it is used to calculate the unpredictability of the ground. The entropy function is applied to parts of the floor. This decision was made to avoid having a straight floor shape (minimum entropy) or a very stepped one (maximum entropy).
The other level elements use the concept of “dispersion” [47]. Its definition contemplates giving a high dispersion to sets of elements with a high average distance. The goal of the algorithm is to minimize dispersion.
3.2. Deep Convolutional Generative Adversarial Network
GANs are novel neural models capable of delivering interesting content by making use of the corpus of levels stored in the Video Game Level Corpus (VGLC) (https://github.com/TheVGLC/TheVGLC (accessed on 13 June 2024)) to create SMB levels. Although the created GAN produces good content, it can be improved through a Covariance Matrix Adaptation Strategy (CMA-ES) so that, through different aptitude functions, it is possible to discover levels in the latent space that maximize the desired properties.
3.2.1. Process
The applied approach is divided into two phases: the first is the training of the GAN with an SMB level. This is encoded as a multidimensional matrix; there is also a generator that operates on a Gaussian noise vector using this same representation and is trained to create SMB levels. Then, the discriminator is used to discern between the existing and generated levels. When this process is completed, we can understand the GAN as a system that maps from genotype to phenotype, takes a latent vector as an input variable, and generates a tile-level description of SMB. The CMA-ES is then used to search through the latent space for levels with different properties [9].
3.2.2. Training
The algorithm that trains the GAN is called Wasserstein GAN (WGAN) and follows the original DCGAN architecture. It also uses batch normalization in the generator and discriminator after each layer. Unlike the original architecture [48], the study’s implementation uses ReLU activation functions in all generator layers, including the output, since this produces better results.
In this phase, each tile is represented by an integer extended to a one-hot encoding vector. So, the inputs for the discriminator are 10 channels of 32 × 32. For example, in the first channel, if there is a floor, they mark it with 1 and the voids with 0. The dimension of the latent vector input to the generator is 32. When running the evolution, the final dimensional output of 10 × 32 × 32 is cut to 10 × 20 × 14, and each vector in each tile is transformed into an integer using the ArgMax function.
3.3. Markov Chains
For this work, an algorithm that implements Markov Chains was programmed to create an SMB level. As in the previous section, we also used the VGLC. The pseudocode in Algorithm 1 shows the procedure for generating an SMB level with a length of 100. We describe it in more detail below.
- ExtractColumns: We extract columns from the VGLC levels and add them to a vector.
- RemoveDuplicates: The repeated columns are removed. This is essential since the transition matrix will then be calculated with the remaining states.
- GetTransitionMtx: The transition matrix is a matrix or data structure that has, for each column, the columns that are successors, along with the frequency with which the element in question precedes them.
- AppendNewColumn: This function finds the next column based on the transition matrix and adds it to the level structure.
- Level construction: Once the columns that will form the level have been specified, the level can be built and exported to the required format.
| Algorithm 1 MC SMB generation pseudocode. |
|
3.4. Metric Computation
Once the generators were running, software was programmed in Java 17.0.11 to extract the metrics of each level and, thus, be able to perform the ERA. This is public and stored on GitHub (https://github.com/hansschaa/SBM-Expressive-Range-Study (accessed on 13 June 2024)). As seen in Table 1, there are 9 metrics related to the difficulty and level structure.

Table 1.
Metrics evaluated for each SMB level.
The metrics were calculated so that a high value indicates a high presence. For example, a linearity of 1 indicates that the level is very linear.
4. Experiments and Results
We generated 200 boards of 100 tiles for each of the generators to have a large amount of information and, thus, capture their true generative nature (Table 2 shows the symbology used). Then, the levels were imported into the software to calculate their metrics. We normalized these values, considering the maximum and minimum of all resulting values as the upper and lower thresholds, respectively. Finally, to create the charts, we divided them into four files (three for each generator and the original levels) and imported them into a Jupyter notebook (https://github.com/hansschaa/SMB-ERA-Graphs (accessed on 13 June 2024)) to create the heatmaps and box/whisker graphs. Finally, the graphs were analyzed, and we describe each one and compare them.

Table 2.
Symbols used for SMB level encoding.
Regarding the format of the levels, the generator based on GA [9] considers a subgroup of the tiles used for the training of the GAN and MC algorithms. We were forced to simplify some game tiles to just one character. For example, ‘Q’ and ‘S’ (blocks that Mario can break and an empty question block) from a study that implemented a GAN [9] were now blocks represented only by the character ‘B’ (block). Likewise, the shapes of the bottom of the pipes are represented only by ‘X’ (floor) and not with [, ], <, >. This logic allows us to unify metrics and make the logical representation of each PCG algorithm comparable.
We also include the original levels used in the MC generator (https://github.com/TheVGLC/TheVGLC/tree/master/Super%20Mario%20Bros/Original (accessed on 13 June 2024)) for an additional point of comparison and analysis. Some final results can be seen in Figure 2. The hyperparameters of the algorithms were extracted from each of the articles [8,9]. Table 3 and Table 4 show the hyperparameters for the GA and the GAN, respectively, and the MC-based algorithm only has one hyperparameter called n-level, which is 2.
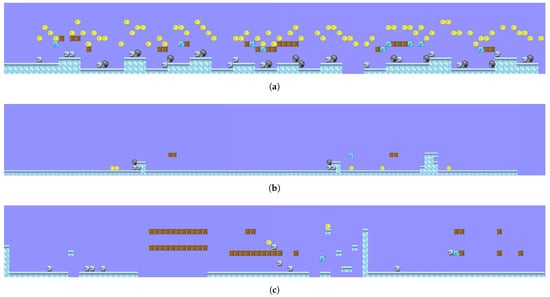
Figure 2.
Examples of the levels generated by each generator. Most levels present similarities, for example, in the absence of structures in the GAN generator or the lack of structural verticality in the GA generator. (a) Level generated by the GA generator. (b) Level generated by the GAN generator. (c) Level generated by the MC generator.

Table 3.
Hyperparameters for the Genetic Algorithm.

Table 4.
Hyperparameters for the Generative Adversarial Network.
Expressive Range
Heatmaps and box/whisker graphs were created to perform a visual reading of the generators. One of the most commonly studied concepts in the generation of video game levels is difficulty. To do this, in Figure 3b, one can see the heatmaps for the three generators and the SMB levels. The GAN produces mostly linear and less diverse levels, while the GA and MC produce semi-linear levels. Regarding lenience, the GAN does not create highly difficult levels in comparison with the GA, which, through the evolutionary method, can build challenging scenarios. The original SMB levels cover a larger area of the generative space with respect to these two metrics; this is very different from the behavior of the other generators, whose respective distributions have a lower variance. Visually, the GAN generator is the most dissimilar. These levels created through Genetic Algorithms and Markov Chains are those that come closest to the characteristics of the original levels. However, a more in-depth analysis must be performed to accurately make this conclusion. Figure 3b,c is also intended to show the degree of difficulty in the generated content. Having enemies too close together can make it difficult to solve the level since the player has a limited jumping height, and rows of enemies can kill them. In this, one can see that the MC generates various configurations on the Y axis, obtaining a wide expressive range regarding the compression of enemies. The GAN obtains poor performance, while the GA concentrates all of the values, giving rise to a low diversity of enemy distribution.
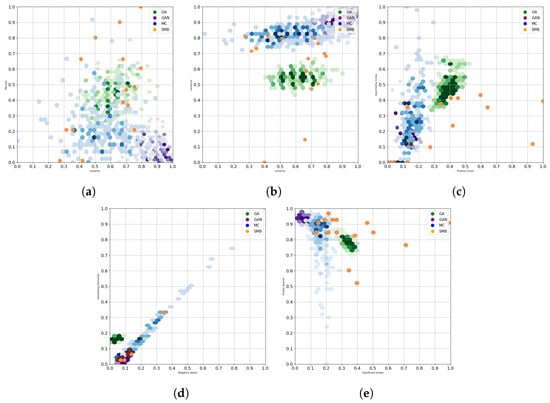
Figure 3.
Expressive range of each generator. Each pair of variables was selected to study relevant characteristics. Density, linearity, and negative space represent the complexity of the level’s navigation; the lenience, average enemy compression, and enemy count variables refer to the degrees of challenge, and finally, interesting elements correspond to the number of interactive elements (power-ups, coins, enemies) in the level. (a) Density vs. linearity. Dense levels with a high linearity can be boring to play. (b) Lenience vs. linearity. Lenience and linearity can help us estimate a level’s hardness. (c) Average EC vs. enemy count. Various enemies can lead to very challenging levels. (d) Interesting elements vs. negative space. Much negative space without interesting elements can result in repetitive structures and is far from being a challenge. (e) Empty spaces vs. significant jumps. A high number of free spaces can result in more complex situations than those that allow greater navigation of the stage without too many jumps.
The heatmaps in Figure 3a,d are related to the levels’ design in appearance and navigation. Figure 3a shows how the GA and MC generators obtain a similar linearity. The GA and MC differ mainly in how the floor tiles are stacked, resulting in denser levels for the GA generator than for the MC. Regarding the GAN, the levels are highly linear with a low density, which results in SMB levels with a low number of columns and complex ground structures. Again, the SMB levels have a wide distribution, as seen on the Y axis, where the density displayed runs along the entire axis. Additionally, the heatmap in Figure 3d shows a limited number of interesting elements with the GA, which produces the greatest number of elements other than soil, but with a low variance in comparison with the MC generator. In this case, there is a similarity in behavior between the original SMB levels and the GAN and MC generators. Still, the MC generator exhibits greater monotony between this pair of variables, covering a larger area of the generative space where its projection is almost linear. Last, Figure 3e shows again how the SMB levels cover a much more uniform space than that of the other generators. This characteristic is desired since a high diversity is needed due to the expressiveness of the algorithms. The three generators distribute their data in a similar way, where the greatest variation with respect to the calculated metrics is given by the MC generator. Curiously, these levels escape the expressive range that the original levels have, since, despite their having been provided as training data, the Markov Chains manage to generate content that has not been seen with respect to the evaluated metrics. This may be caused by the number of columns that the MC considers to create the transition matrix, causing the patterns to be examined locally and not globally, as in the GA and the GAN.
To analyze the generated levels further, we constructed four figures with three box/whisker graphs with normalized data to observe the differences among the generators. The variables studied were the average enemy compression, enemy count, linearity, and lenience. Figure 4d shows how the median of the GA generator is very different from that of the GAN and MC, supporting the idea that this generator creates complex levels concerning difficulty, that is, with high numbers of holes and enemies. This fact is also supported by Figure 4a,b, where it can be seen that the GA obtains levels with many enemies and a high average compression thereof. Figure 4a,c show that the MC generator has a high expressive range when compared to the other generators in terms of linearity and enemy compression, producing diverse levels in terms of structure and difficulty. The data shown by the MC generator are very similar to the original levels, except for Figure 4d, where these seem more challenging.
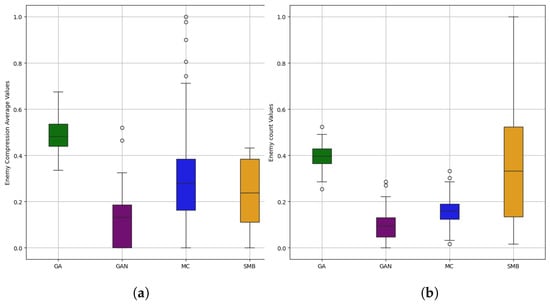
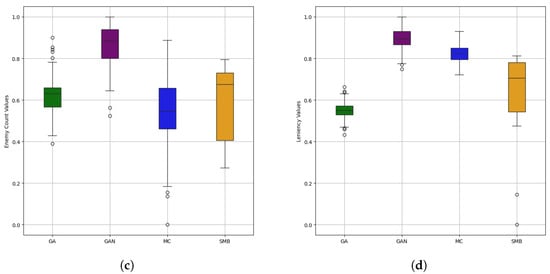
Figure 4.
Boxplots for each generator to compare a single variable of interest. Each of these allows us to observe the dispersion of the data achieved by each generator. The description of each of the variables is found in Table 1. (a) Average enemy compression. (b) Enemy count. (c) Linearity. (d) Lenience.
5. Discussion
The evaluated generators are different in their approaches, each with its own advantages and disadvantages depending on the implementation. For instance, training data can be fed to machine learning algorithms such as a GAN, and the results depend on the quality of this phase. However, they are fast methods capable of execution at runtime. As can be seen in Figure 5, the GAN sometimes produced incoherent content, which would detract from the user experience. This can be fixed through some constructive algorithms or other generative approaches that consider constraints that make the generated content playable [49].

Figure 5.
Incoherent results by the GAN generator.
As observed, the MC generator exhibited a wide expressive range in several metrics. This is the one that distributed the evaluated metrics most uniformly within the plot, the other generators showed a reduced generative space that was concentrated in a small range of values, which did not provide much diversity in the final content. GAs are recognized for being highly configurable, debuggable, and controllable, making them one of the most favored methods for generating content. However, while effective, GAs are slow and tend to fall into local optima easily. To address this, the Quality Diversity algorithms [14] aim to deliver a diverse and high-quality set of individuals as a product.
Conducting an ERA early on can help discern whether to use one method over another depending on the practitioner’s needs. It is not costly and does not require an extensive programming period for calculating metrics and constructing graphs. However, the question of whether there are heuristics that can bring us closer to human thinking remains. These metrics cannot replace user testing but serve as an initial probe in analyzing procedural content generators for video games.
6. Conclusions
This paper evaluates three automatic level generators for Super Mario Bros and their training data. These are based on Genetic Algorithms, Generative Adversarial Networks, and Markov Chains. We tested 200 levels and 9 metrics, performing an evaluation through an Expressive Range Analysis.
Expressive Range Analysis is useful for the early evaluation stages, as heatmaps allow us to clearly visualize how algorithms exhibit uncertain desired characteristics. We observed how genetic algorithms show a wide expressive range despite their early convergence. The presented example uses four different populations, allowing high locality in the search space and generating diverse content. Markov Chains are efficient due to their simplicity and the speed with which they are executed. It is important to have a large corpus of levels to guarantee greater diversity in the results. However, like ML methods, they are complicated to control. GANs produced good content but were sometimes incoherent, not very diverse, and had a limited expressive range.
In future work, it is necessary to include more generators. There is a research gap regarding evaluating machine-learning-based generators for platform levels. It is necessary to include an evaluation of agents to gain more information about the levels, such as their playability and navigation. Although some levels were played, an automatic method is required to obtain metrics regarding the agent and how it overcomes the game level. It is also interesting to investigate the correlations between the metrics studied and humans’ perception, to change them, or to pay attention to those relevant to the study [43]. Also, it would be very useful to carry out a study of the search space that each generator reaches to obtain better-founded conclusions about its generative power.
Author Contributions
Conceptualization, N.A.B. and H.S.; methodology, N.A.B. and H.S.; software, H.S.; validation, N.A.B. and H.S.; formal analysis, N.A.B.; investigation, N.A.B. and H.S.; resources, N.A.B. and H.S.; data curation, H.S.; writing—original draft preparation, H.S.; writing—review and editing, N.A.B. and H.S.; visualization, H.S.; supervision, N.A.B.; project administration, N.A.B. and H.S.; funding acquisition, N.A.B. and H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the National Agency for Research and Development (Agencia Nacional de Investigación y Desarrollo, ANID Chile), ANID-Subdirección del Capital Humano/Doctorado Nacional/2023-21230824, and FONDECYT Iniciación grant 11220438.
Data Availability Statement
The dataset is available from the authors upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PCG | Procedural Content Generation |
| ERA | Expressive Range Analysis |
| DLC | Downloadable Content |
| SMB | Super Mario Bros |
| DCGAN | Deep Convolutional Generative Adversarial Network |
| MC | Markov Chain |
| RL | Reinforcement Learning |
| LSTM | Long Short-Term Memory |
| VGLC | Video Game Level Corpus |
| CMA-ES | Covariance Matrix Adaptation Strategy |
| WGAN | Wasserstein GAN |
| ReLU | Rectified Linear Unit |
| DBN | Dynamic Bayesian Network |
| LLM | Large Language Model |
| EC | Enemy Compression |
References
- Shaker, N.; Togelius, J.; Nelson, M.J. Procedural Content Generation in Games; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Korn, O.; Blatz, M.; Rees, A.; Schaal, J.; Schwind, V.; Görlich, D. Procedural content generation for game props? A study on the effects on user experience. Comput. Entertain. (CIE) 2017, 15, 1–15. [Google Scholar] [CrossRef]
- Scirea, M.; Barros, G.A.; Shaker, N.; Togelius, J. SMUG: Scientific Music Generator. In Proceedings of the ICCC, Park City, UT, USA, 29 June–2 July 2015; pp. 204–211. [Google Scholar]
- Gandikota, R.; Brown, N.B. DC-Art-GAN: Stable Procedural Content Generation using DC-GANs for Digital Art. arXiv 2022, arXiv:2209.02847. [Google Scholar]
- Schaa, H.; Barriga, N.A. Generating Entertaining Human-Like Sokoban Initial States. In Proceedings of the 2021 40th International Conference of the Chilean Computer Science Society (SCCC), La Serena, Chile, 15–19 November 2021; pp. 1–6. [Google Scholar]
- Amato, A. Procedural content generation in the game industry. In Game Dynamics: Best Practices in Procedural and Dynamic Game Content Generation; Springer: Cham, Switzerland, 2017; pp. 15–25. [Google Scholar]
- Tyni, H.; Sotamaa, O. Extended or exhausted: How console DLC keeps the player on the rail. In Proceedings of the 15th International Academic MindTrek Conference: Envisioning Future Media Environments, Tampere, Finland, 28–30 September 2011; pp. 311–313. [Google Scholar]
- Ferreira, L.; Pereira, L.; Toledo, C. A multi-population genetic algorithm for procedural generation of levels for platform games. In Proceedings of the Companion Publication of the 2014 Annual Conference on Genetic and Evolutionary Computation, Vancouver, BC, Canada, 12–16 July 2014; pp. 45–46. [Google Scholar]
- Volz, V.; Schrum, J.; Liu, J.; Lucas, S.M.; Smith, A.; Risi, S. Evolving mario levels in the latent space of a deep convolutional generative adversarial network. In Proceedings of the Genetic and Evolutionary Computation Conference, Kyoto, Japan, 15–19 July 2018; pp. 221–228. [Google Scholar]
- Smith, G.; Whitehead, J. Analyzing the expressive range of a level generator. In Proceedings of the 2010 Workshop on Procedural Content Generation in Games, Monterey, CA, USA, 18 June 2010; pp. 1–7. [Google Scholar]
- The SuperTux Team, SuperTux. Available online: https://www.supertux.org/ (accessed on 10 July 2024).
- Kerssemakers, M.; Tuxen, J.; Togelius, J.; Yannakakis, G.N. A procedural procedural level generator generator. In Proceedings of the 2012 IEEE Conference on Computational Intelligence and Games (CIG), Granada, Spain, 11–14 September 2012; pp. 335–341. [Google Scholar]
- Togelius, J.; Champandard, A.J.; Lanzi, P.L.; Mateas, M.; Paiva, A.; Preuss, M.; Stanley, K.O. Procedural content generation: Goals, challenges and actionable steps. In Artificial and Computational Intelligence in Games. Dagstuhl Follow-Ups; Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik: Wadern, Germany, 2013. [Google Scholar]
- Gravina, D.; Khalifa, A.; Liapis, A.; Togelius, J.; Yannakakis, G.N. Procedural content generation through quality diversity. In Proceedings of the 2019 IEEE Conference on Games (CoG), London, UK, 20–23 August 2019; pp. 1–8. [Google Scholar]
- Craveirinha, R.; Santos, L.; Roque, L. An author-centric approach to procedural content generation. In Proceedings of the Advances in Computer Entertainment: 10th International Conference, ACE 2013, Boekelo, The Netherlands, 12–15 November 2013; Proceedings 10. Springer: Cham, Switzerland, 2013; pp. 14–28. [Google Scholar]
- Togelius, J.; Preuss, M.; Yannakakis, G.N. Towards multiobjective procedural map generation. In Proceedings of the 2010 Workshop on Procedural Content Generation in Games, Monterey, CA, USA, 18 June 2010; pp. 1–8. [Google Scholar]
- Liu, J.; Snodgrass, S.; Khalifa, A.; Risi, S.; Yannakakis, G.N.; Togelius, J. Deep learning for procedural content generation. Neural Comput. Appl. 2021, 33, 19–37. [Google Scholar] [CrossRef]
- Guzdial, M.; Sturtevant, N.; Li, B. Deep static and dynamic level analysis: A study on infinite mario. In Proceedings of the AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment, Burlingame, CA, USA, 8–12 October 2016; Volume 12, pp. 31–38. [Google Scholar]
- Wikipedia. Super Mario Bros. Available online: https://en.wikipedia.org/wiki/Super_Mario (accessed on 27 December 2023).
- Compton, K.; Mateas, M. Procedural level design for platform games. In Proceedings of the AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment, Burlingame, CA, USA, 8–12 October 2016; Volume 2, pp. 109–111. [Google Scholar]
- Iyer, V.; Bilmes, J.; Wright, M.; Wessel, D. A novel representation for rhythmic structure. In Proceedings of the 23rd International Computer Music Conference, Thessaloniki, Greece, 25–30 September 1997; pp. 97–100. [Google Scholar]
- Mourato, F.; Santos, M.P.d. Measuring difficulty in platform videogames. In Proceedings of the 4ª Conferência Nacional Interacção Humano-Computador, Aveiro, Portugal, 13–15 October 2010. [Google Scholar]
- Pedersen, C.; Togelius, J.; Yannakakis, G.N. Modeling player experience in super mario bros. In Proceedings of the 2009 IEEE Symposium on Computational Intelligence and Games, Milan, Italy, 7–10 September 2009; pp. 132–139. [Google Scholar]
- Summerville, A.; Mateas, M. Super mario as a string: Platformer level generation via lstms. arXiv 2016, arXiv:1603.00930. [Google Scholar]
- Sudhakaran, S.; González-Duque, M.; Freiberger, M.; Glanois, C.; Najarro, E.; Risi, S. Mariogpt: Open-ended text2level generation through large language models. In Proceedings of the Advances in Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023; Volume 36. [Google Scholar]
- Todd, G.; Earle, S.; Nasir, M.U.; Green, M.C.; Togelius, J. Level Generation Through Large Language Models. In Proceedings of the 18th International Conference on the Foundations of Digital Games (FDG 2023), Lisbon, Portugal, 12–14 April 2023. [Google Scholar] [CrossRef]
- Gallotta, R.; Todd, G.; Zammit, M.; Earle, S.; Liapis, A.; Togelius, J.; Yannakakis, G.N. Large Language Models and Games: A Survey and Roadmap. arXiv 2024, arXiv:2402.18659. [Google Scholar]
- Nasir, M.U.; James, S.; Togelius, J. Word2World: Generating Stories and Worlds through Large Language Models. arXiv 2024, arXiv:2405.06686. [Google Scholar]
- Nasir, M.U.; Togelius, J. Practical PCG Through Large Language Models. arXiv 2023, arXiv:2305.18243. [Google Scholar]
- Shu, T.; Liu, J.; Yannakakis, G.N. Experience-driven PCG via reinforcement learning: A Super Mario Bros study. In Proceedings of the 2021 IEEE Conference on Games (CoG), Copenhagen, Denmark, 17–20 August 2021; pp. 1–9. [Google Scholar]
- Hauck, E.; Aranha, C. Automatic generation of Super Mario levels via graph grammars. In Proceedings of the 2020 IEEE Conference on Games (CoG), Osaka, Japan, 24–27 August 2020; pp. 297–304. [Google Scholar]
- Shaker, N.; Yannakakis, G.N.; Togelius, J.; Nicolau, M.; O’neill, M. Evolving personalized content for super mario bros using grammatical evolution. In Proceedings of the AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment, Stanford, CA, USA, 8–12 October 2012; Volume 8, pp. 75–80. [Google Scholar]
- Shi, P.; Chen, K. Online level generation in Super Mario Bros via learning constructive primitives. In Proceedings of the 2016 IEEE Conference on Computational Intelligence and Games (CIG), Santorini, Greece, 20–23 September 2016; pp. 1–8. [Google Scholar]
- de Pontes, R.G.; Gomes, H.M. Evolutionary procedural content generation for an endless platform game. In Proceedings of the 2020 19th Brazilian Symposium on Computer Games and Digital Entertainment (SBGames), Recife, Brazil, 7–10 November 2020; pp. 80–89. [Google Scholar]
- Dahlskog, S.; Togelius, J. Procedural content generation using patterns as objectives. In Proceedings of the European Conference on the Applications of Evolutionary Computation, Granada, Spain, 23–25 April 2014; pp. 325–336. [Google Scholar]
- Sarkar, A.; Cooper, S. Procedural content generation using behavior trees (PCGBT). arXiv 2021, arXiv:2107.06638. [Google Scholar]
- Snodgrass, S. Markov Models for Procedural Content Generation; Drexel University: Philadelphia, PA, USA, 2018. [Google Scholar]
- Murphy, K.P. Markov Models. 2007. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=6c4d1f04f5c5004370f03f2e759e6a4b1115cb8c (accessed on 1 June 2024).
- Snodgrass, S.; Ontañón, S. A hierarchical approach to generating maps using markov chains. In Proceedings of the AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment, Raleigh, NC, USA, 3–7 October 2014; Volume 10, pp. 59–65. [Google Scholar]
- Snodgrass, S.; Ontanon, S. A hierarchical mdmc approach to 2D video game map generation. In Proceedings of the AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment, Santa Cruz, CA, USA, 14–18 November 2015; Volume 11, pp. 205–211. [Google Scholar]
- Snodgrass, S.; Ontanón, S. Learning to generate video game maps using markov models. IEEE Trans. Comput. Intell. AI Games 2016, 9, 410–422. [Google Scholar] [CrossRef]
- Biemer, C.F.; Cooper, S. On linking level segments. In Proceedings of the 2022 IEEE Conference on Games (CoG), Beijing, China, 21–24 August 2022; pp. 199–205. [Google Scholar]
- Withington, O.; Tokarchuk, L. The Right Variety: Improving Expressive Range Analysis with Metric Selection Methods. In Proceedings of the 18th International Conference on the Foundations of Digital Games, Lisbon, Portugal, 12–14 April 2023; pp. 1–11. [Google Scholar]
- Horn, B.; Dahlskog, S.; Shaker, N.; Smith, G.; Togelius, J. A comparative evaluation of procedural level generators in the mario AI framework. In Proceedings of the Foundations of Digital Games 2014, Ft. Lauderdale, FL, USA, 3–7 April 2014; pp. 1–8. [Google Scholar]
- Summerville, A.; Mariño, J.R.; Snodgrass, S.; Ontañón, S.; Lelis, L.H. Understanding mario: An evaluation of design metrics for platformers. In Proceedings of the 12th International Conference on the Foundations of Digital Games, Hyannis, MA, USA, 14–17 August 2017; pp. 1–10. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Cook, M.; Colton, S. Multi-faceted evolution of simple arcade games. In Proceedings of the 2011 IEEE Conference on Computational Intelligence and Games (CIG’11), Seoul, Republic of Korea, 31 August–3 September 2011; pp. 289–296. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, ICML, Sidney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Di Liello, L.; Ardino, P.; Gobbi, J.; Morettin, P.; Teso, S.; Passerini, A. Efficient generation of structured objects with constrained adversarial networks. In Proceedings of the Advances in Neural Information Processing Systems, Online, 6–12 December 2020; Volume 33, pp. 14663–14674. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).