Label-Setting Algorithm for Multi-Destination K Simple Shortest Paths Problem and Application
Abstract
1. Introduction
- Propose a label-setting framework for a class of multi-destination KSSP problems and identify optimality conditions to find exact solutions for the identified variants.
- Develop an exact label-setting solution algorithm for solving the one-to-all KSSP problem and analyze its computational complexity.
- Propose a heuristic for practically efficient implementation using bounded labels and appropriate data structures.
- To evaluate the computation performance and solution quality of the proposed approach with state-of-the-art algorithms on various real-world networks.
- To illustrate the application of this algorithm for a practical problem and demonstrate its efficacy for the use case.
2. Review of Related Literature
2.1. KSP Algorithms
2.2. KSSP Algorithms
3. Methodology
3.1. Multi-Destination k Simple Shortest Paths—Problem Definition
3.1.1. Single Destination KSSP
3.1.2. Multi-Destination KSSP
- (i)
- One-to-Many KSSP (KSSP-OM)
- (ii)
- One-to-All Cost Constrained Simple Shortest Paths (CCSSP-OA)
3.2. Label-Setting KSSP Algorithm
| Algorithm 1. Exact_KSSP(, ) | |||||
| Input: The network instance and origin Output: The set of simple shortest path labels | |||||
| 1 | // Create a label corresponding to the first path to the origin | ||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | // Create a temporary set and move into | ||||
| 6 | |||||
| 7 | |||||
| 8 | // Create an empty permanent set | ||||
| 9 | |||||
| 10 | // Initialize the label index and permanent label index for each node | ||||
| 11 | |||||
| 12 | |||||
| 13 | |||||
| 14 | Repeat | ||||
 | |||||
| 29 | Until is or // No more temporary labels to process or at least k permanent labels to every destination are found | ||||
| Algorithm 2. CycleCheck(, , , ) TRUE/FALSE | ||||
| Input: , , , // Label pu of node u is the latest permanent label, v is an adjacent node to u, and s is the source Output: A Boolean value // True if v forms a cycle with pu and false otherwise | ||||
| 1 | ||||
| 2 | ||||
| 3 | While do | |||
| // Backtrack from the end of the path to the origin. Return TRUE if v already exists and FALSE otherwise | ||||
| 4 | If | |||
| 5 | Return | |||
| 6 | Else | |||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 | Return | |||
3.3. Heuristic Approach
| Algorithm 3. KSSP_LL(, ) | |||||
| Input: The network instance and origin Output: The set of simple shortest path labels | |||||
| 1 | // Create a label corresponding to the first path to the origin | ||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | // Create a temporary set and move into | ||||
| 6 | |||||
| 7 | |||||
| 8 | // Create an empty permanent set | ||||
| 9 | |||||
| 10 | // Initialize the label index and permanent label index for each node | ||||
| 11 | |||||
| 12 | |||||
| 13 | |||||
| 14 | Repeat | ||||
 | |||||
| 38 | Until is or // No more temporary labels to process or at least k permanent labels to every destination are found | ||||
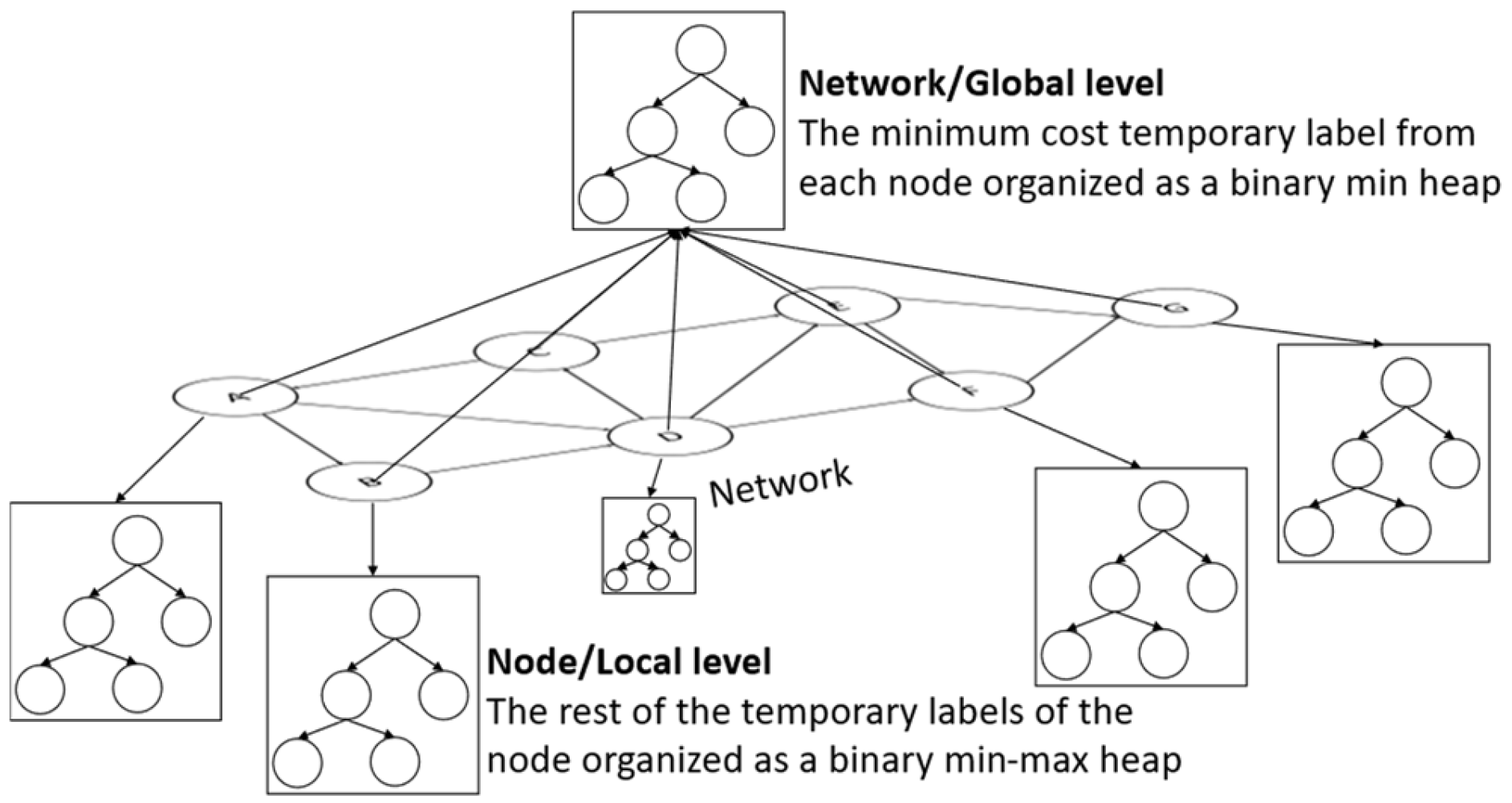
3.4. Data Structures for Scalable Performance
4. Computational Experiments
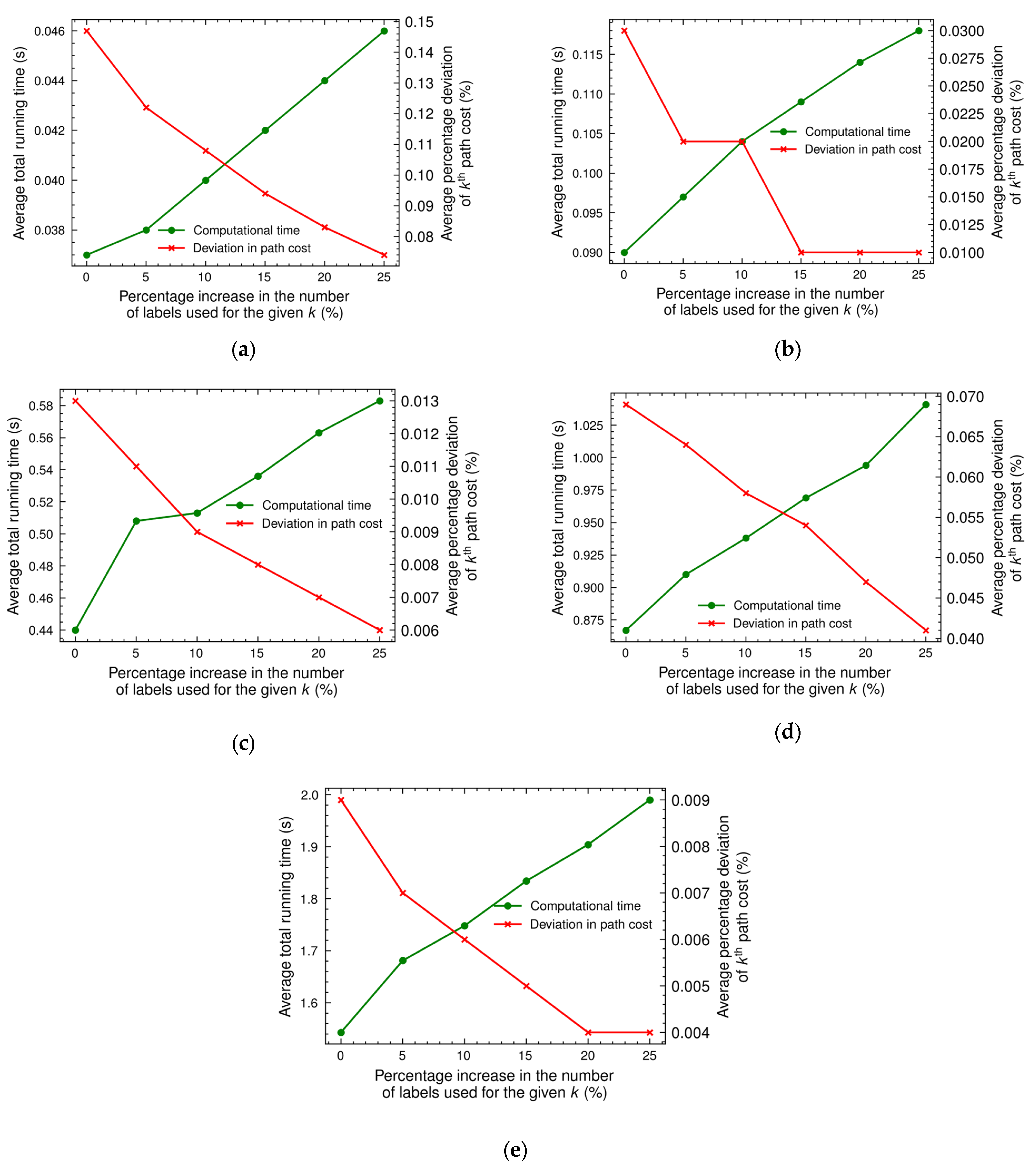
- Average total running time: This metric represents the average time, measured in CPU time, taken to find the required paths. This excludes the time spent reading input data and writing output data.
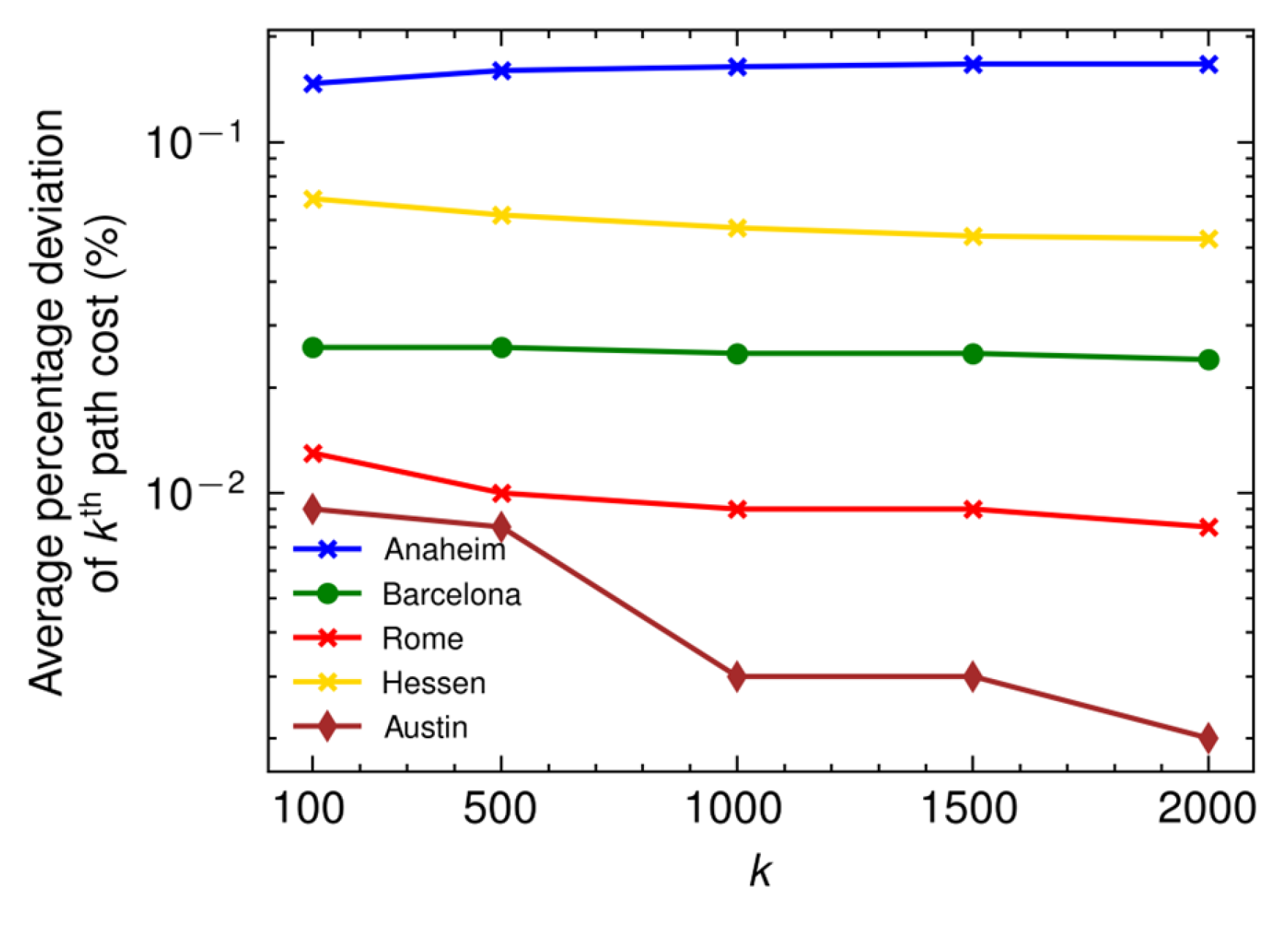
- Average percentage deviation of th path cost: This metric measures the average percentage increase in the th simple shortest path cost obtained by the heuristic algorithm () from the exact th simple shortest path cost (). It is calculated as , expressing the difference as a percentage of the exact cost.
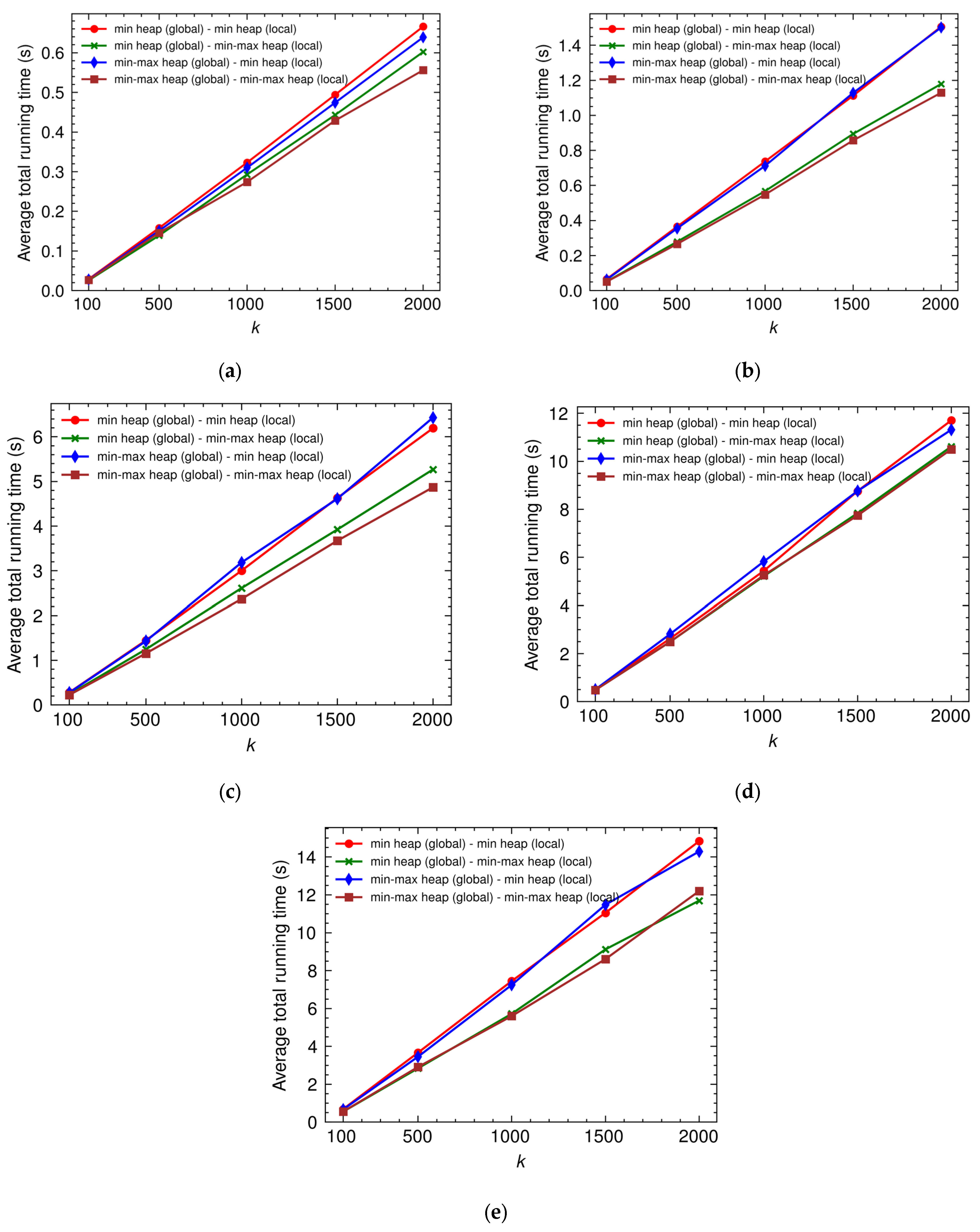
4.1. Evaluation of Data Structures for Temporary Labels
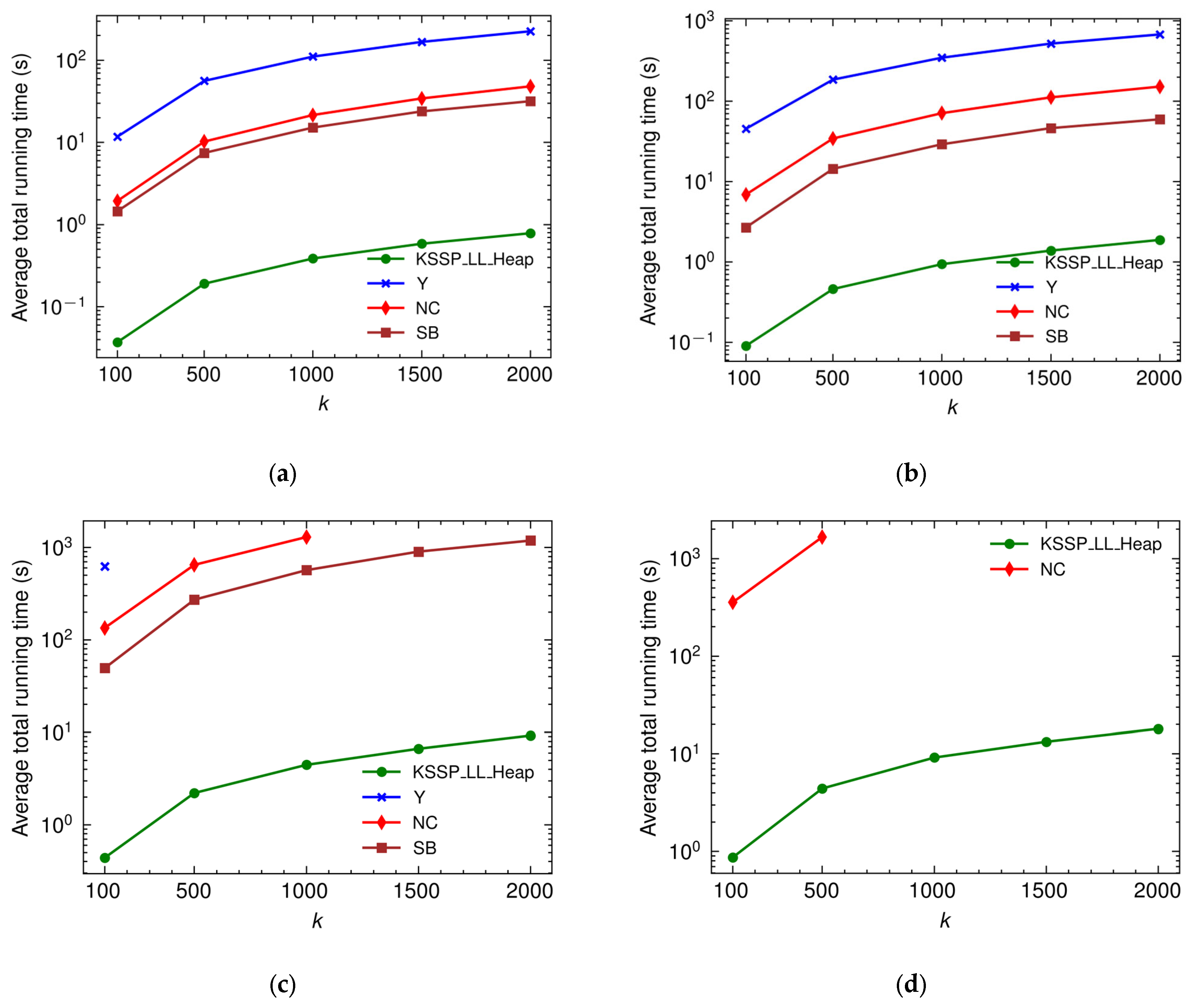
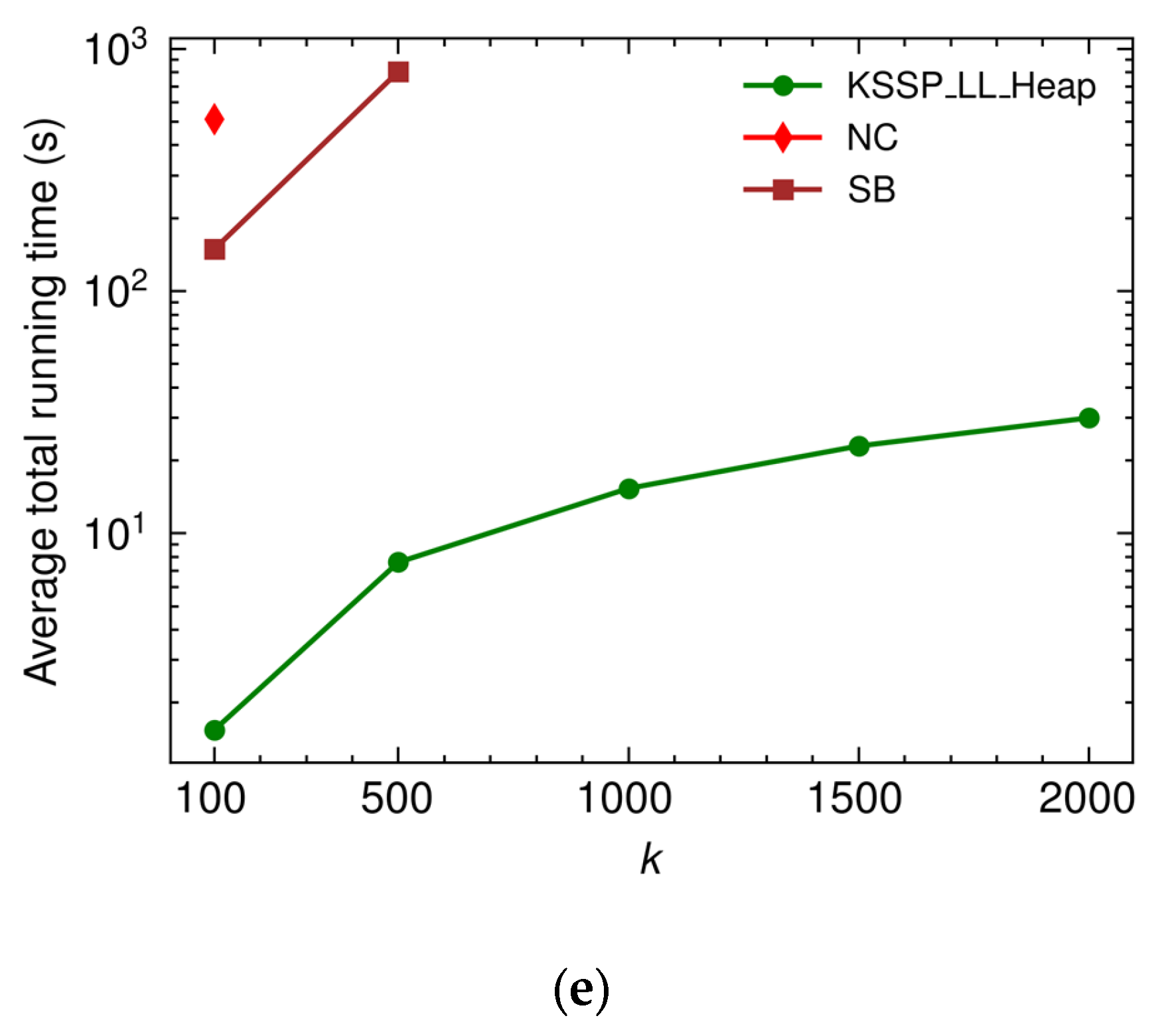
4.2. Evaluation of the Heuristic’s Performance
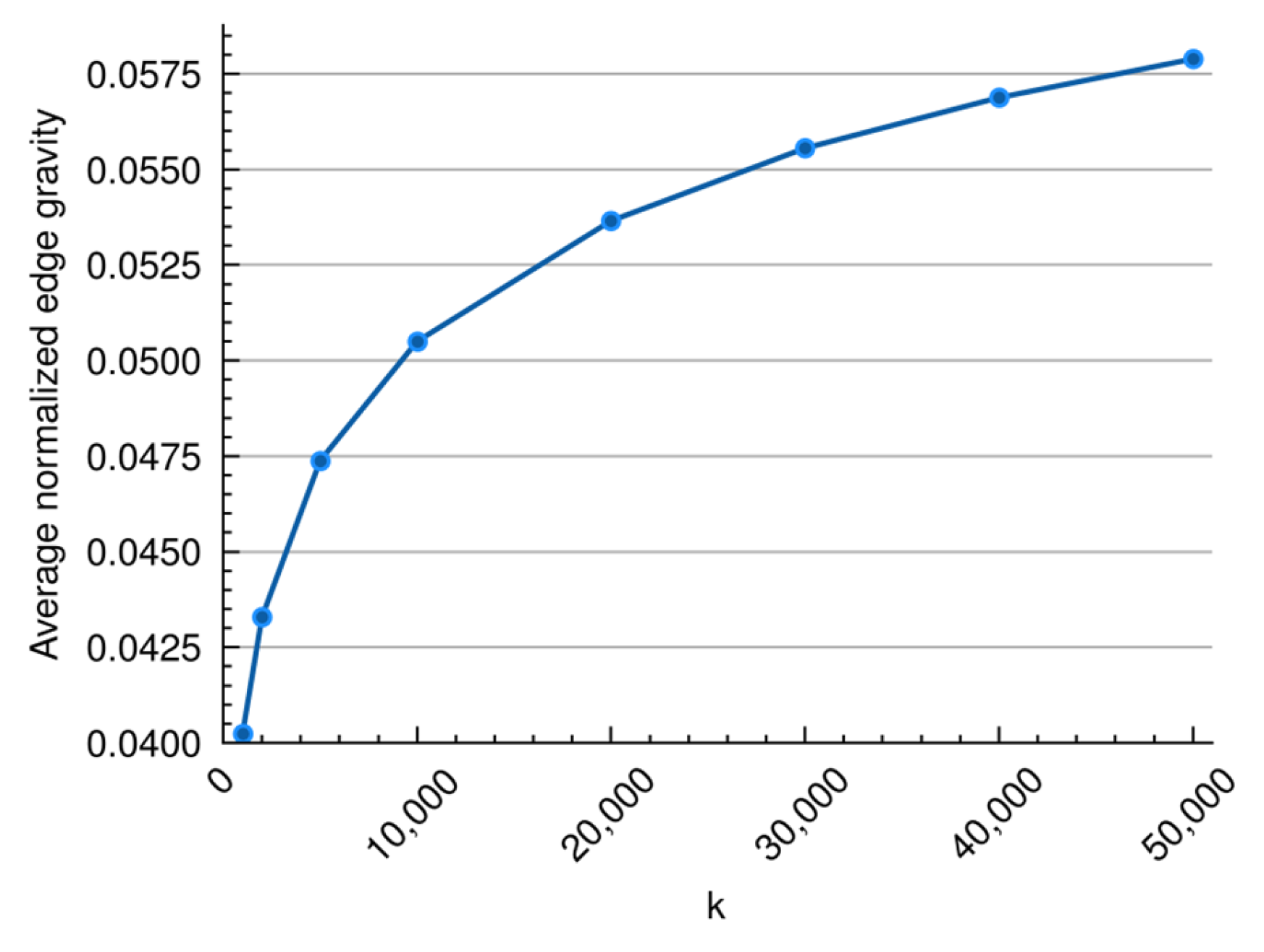
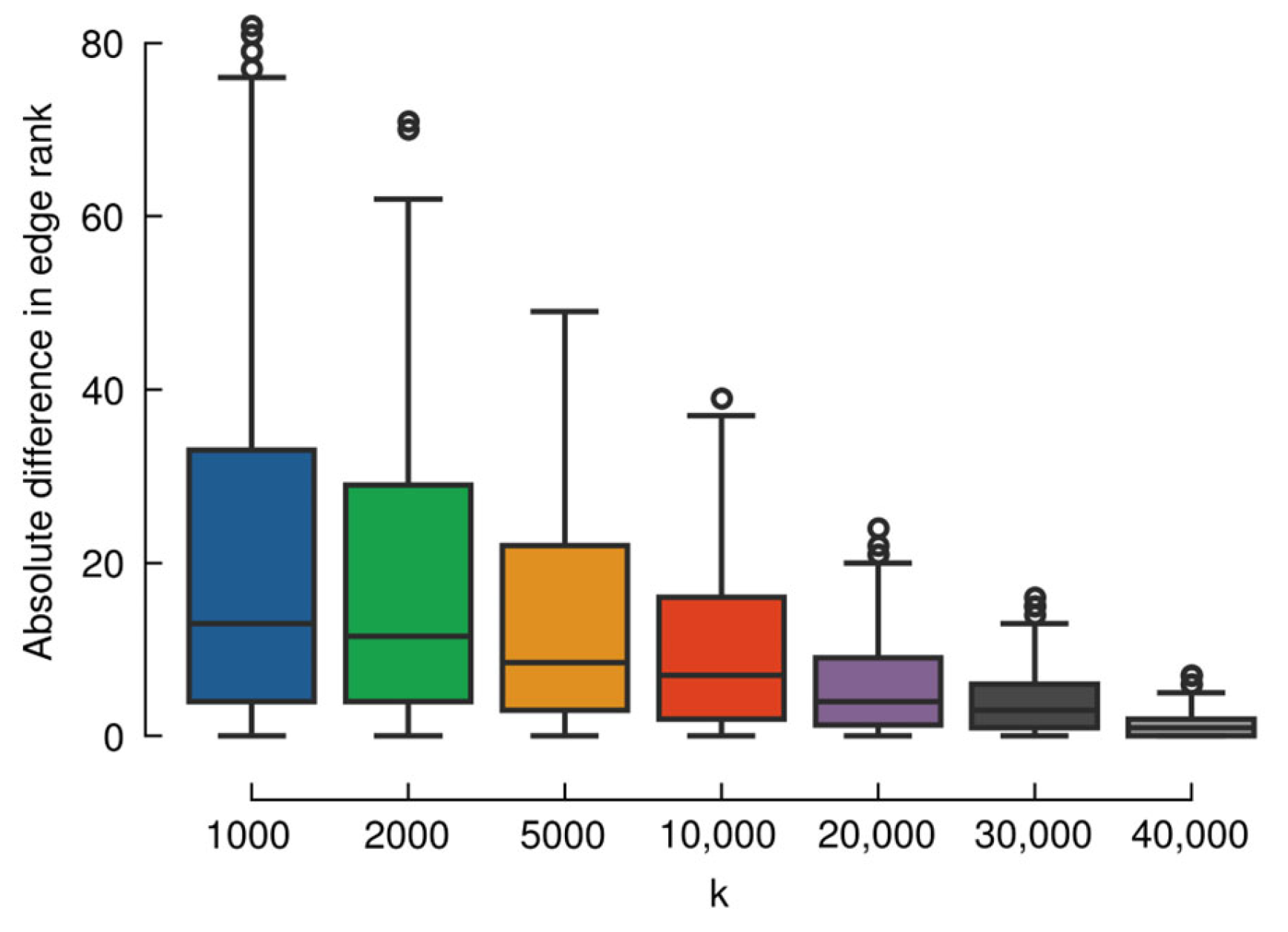
5. Illustrative Practical Application
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- Pseudocode for the implementation of the heuristic using the proposed two-level organization of temporary labels
| Algorithm A1. KSSP_LL_Heap(, ) | ||||||
| Input: The network instance and origin Output: The set of simple shortest path labels | ||||||
| 1 | // Create a label corresponding to the first path to the origin | |||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | // Create a single global temporary set (min heap) and move into | |||||
| 6 | ||||||
| 7 | ||||||
| 8 | // Create a local temporary set (min–max heap) for each node | |||||
| 9 | ||||||
| 10 | // Create an empty permanent set | |||||
| 11 | ||||||
| 12 | // Initialize the label index and permanent label index for each node | |||||
| 13 | ||||||
| 14 | ||||||
| 15 | ||||||
| 16 | Repeat | |||||
| 17 | // Pick the minimum cost label from and move it to , making it permanent | |||||
| // Since labels are permanent for node , is the next smallest temporary label index of | ||||||
| 18 | ||||||
| 19 | ||||||
| 20 | // Increment the permanent label index of node | |||||
| 21 | ||||||
| 22 | // Move the next smallest temporary label of node u from its local level to the global level | |||||
| 23 | ||||||
| 24 | ||||||
| 25 | For each node adjacent to do | |||||
| 26 | If then | |||||
| 27 | If CycleCheck(, , , ) is FALSE then // is not on the path corresponding to | |||||
| 28 | Create a new label | |||||
| 29 | ||||||
| 30 | ||||||
| 31 | ||||||
| 32 | If then // Created label is the new smallest label for | |||||
| // Insert new label into the global level and move the existing label to the local level | ||||||
| 33 | ||||||
| 34 | ||||||
| 35 | ||||||
| 36 | Else | |||||
| 37 | ||||||
| 38 | // Increment the label index of node | |||||
| 39 | ||||||
| 40 | Else if then | |||||
| 41 | If CycleCheck(, , , ) is FALSE then // is not on the path corresponding to | |||||
| 42 | // Create a new label | |||||
| 43 | ||||||
| 44 | ||||||
| 45 | ||||||
| 46 | If then // Created label is the new smallest label for | |||||
| // Insert the new label into the global level and move the existing label to the local level | ||||||
| 47 | ||||||
| 48 | ||||||
| 49 | ||||||
| 50 | Else | |||||
| 51 | ||||||
| 52 | // Max label of is removed to keep | |||||
| 53 | Until is or // No more temporary labels to process or at least k permanent labels to every destination are found | |||||
References
- Mohanta, K. Comprehensive Study on Computational Methods for K-Shortest Paths Problem. Int. J. Comput. Appl. 2012, 40, 22–26. [Google Scholar] [CrossRef]
- Kumawat, S.; Dudeja, C.; Kumar, P. An Extensive Review of Shortest Path Problem Solving Algorithms. In Proceedings of the 2021 5th International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 6–8 May 2021; pp. 176–184. [Google Scholar]
- Magzhan, K.; Jani, H.M. A Review and Evaluations of Shortest Path Algorithms. Int. J. Sci. Technol. Res. 2013, 2, 99–104. [Google Scholar]
- Eppstein, D. Finding the K Shortest Paths. J. SIAM 1998, 28, 652–673. [Google Scholar] [CrossRef]
- Yen, J.Y. Finding the K Shortest Loopless Paths in a Network. Manag. Sci. 1971, 17, 712–716. [Google Scholar] [CrossRef]
- Hu, X.; Chiu, Y.C. A Constrained Time-Dependent K Shortest Paths Algorithm Addressing Overlap and Travel Time Deviation. Int. J. Transp. Sci. Technol. 2015, 4, 371–394. [Google Scholar] [CrossRef]
- Chennai Metro Rail Mulls Introducing More Electric Vehicles to Boost Its Last-Mile Connectivity. Available online: https://www.thehindu.com/news/cities/chennai/chennai-metro-rail-mulls-introducing-more-electric-vehicles-to-boost-its-last-mile-connectivity/article67138761.ece (accessed on 30 July 2023).
- Xie, F.; Xie, Y.; Lam, S.H. K-Shortest Routing for Autonomous Driving. In Proceedings of the 2022 4th International Conference on Machine Learning, Big Data and Business Intelligence, MLBDBI 2022, Shanghai, China, 28–30 October 2022; pp. 212–216. [Google Scholar] [CrossRef]
- Asaduzzaman, M.; Geok, T.K.; Hossain, F.; Sayeed, S.; Abdaziz, A.; Wong, H.-Y.; Tso, C.P.; Ahmed, S.; Bari, M.A. An Efficient Shortest Path Algorithm: Multi-Destinations in an Indoor Environment. Symmetry 2021, 13, 421. [Google Scholar] [CrossRef]
- Gotthilf, Z.; Lewenstein, M. Improved Algorithms for the k Simple Shortest Paths and the Replacement Paths Problems. Inf. Process. Lett. 2009, 109, 352–355. [Google Scholar] [CrossRef]
- Feng, G. Finding k Shortest Simple Paths in Directed Graphs: A Node Classification Algorithm. Networks 2014, 64, 6–17. [Google Scholar] [CrossRef]
- Kurz, D.; Mutzel, P. A Sidetrack-Based Algorithm for Finding the k Shortest Simple Paths in a Directed Graph. Leibniz Int. Proc. Inform. LIPIcs 2016, 64, 49.1–49.13. [Google Scholar] [CrossRef]
- Chen, B.Y.; Chen, X.W.; Chen, H.P.; Lam, W.H.K. Efficient Algorithm for Finding k Shortest Paths Based on Re-Optimization Technique. Transp. Res. E Logist. Transp. Rev. 2020, 133, 101819. [Google Scholar] [CrossRef]
- Helander, M.E.; McAllister, S. The Gravity of an Edge. Appl. Netw. Sci. 2018, 3, 7. [Google Scholar] [CrossRef] [PubMed]
- Bock, F.; Kantner, H.; Haynes, J. An Algorithm (the r-Th Best Path Algorithm) for Finding and Ranking Paths through a Network; Armour Research Foundation: Chicago, IL, USA, 1957. [Google Scholar]
- Hoffman, W.; Pavley, R. A Method for the Solution of the Nth Best Path Problem. J. ACM 1959, 6, 506–514. [Google Scholar] [CrossRef]
- Dreyfus, S.E. An Appraisal of Some Shortest-Path Algorithms. Oper. Res. 1969, 17, 395–412. [Google Scholar] [CrossRef]
- Shier, D.R. Computational Experience with an Algorithm for Finding the k Shortest Paths in a Network. J. Res. Natl. Bur. Stand. Sect. B Math. Sci. 1974, 78 B, 116–139. [Google Scholar] [CrossRef]
- Shier, D.R. Iterative Methods for Determining the k Shortest Paths in a Network. Networks 1976, 6, 205–229. [Google Scholar] [CrossRef]
- Shier, D.R. On Algorithms for Finding the k Shortest Paths in a Network. Networks 1979, 9, 195–214. [Google Scholar] [CrossRef]
- Martins, E.d.Q.V. An Algorithm for Ranking Paths That May Contain Cycles. Eur. J. Oper. Res. 1983, 18, 123–130. [Google Scholar] [CrossRef]
- Gallo, G.; Pallottino, S. Shortest Path Methods: A Unifying Approach. In Netflow at Pisa; Gallo, G., Sandi, C., Eds.; Springer: Berlin/Heidelberg, Germany, 1986; pp. 38–64. ISBN 978-3-642-00923-5. [Google Scholar]
- Guerriero, F.; Musmanno, R.; Lacagnina, V.; Pecorella, A. A Class of Label-Correcting Methods for the K Shortest Paths Problem. Oper. Res. 2001, 49, 423–429. [Google Scholar] [CrossRef]
- De Azevedo, J.; Madeira, J.J.E.R.S.; Martins, E.Q.V.; Pires, F.M.A. A Computational Improvement for a Shortest Paths Ranking Algorithm. Eur. J. Oper. Res. 1994, 73, 188–191. [Google Scholar] [CrossRef]
- Azevedo, J.A.; Madeira, J.J.E.R.S.; Martins, E.d.Q.V.; Pires, F.M.A. A Shortest Paths Ranking Algorithm. In Proceedings of the AIRO’90, Conference on Models and Methods for Decision Support, Sorrento, Italy, 3–5 October 1990; pp. 1001–1011. [Google Scholar]
- Azevedo, J.; Costa, M.E.O.S.; Madeira, J.J.E.R.S.; Martins, E.Q.V. An Algorithm for the Ranking of Shortest Paths. Eur. J. Oper. Res. 1993, 69, 97–106. [Google Scholar] [CrossRef]
- Martins, E.d.Q.V.; Pascoal, M.M.B.; Santos, J.L.E. Dos A New Improvement for a K Shortest Paths Algorithm. Investig. Oper. 2001, 21, 47–60. [Google Scholar]
- Xu, W.; He, S.; Song, R.; Chaudhry, S.S. Finding the K Shortest Paths in a Schedule-Based Transit Network. Comput. Oper. Res. 2012, 39, 1812–1826. [Google Scholar] [CrossRef]
- Jeon, I.; Nam, H.; Jun, C. Improved Public Transit Routing Algorithm for Finding the Shortest K-Path. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2018, 42, 255–264. [Google Scholar] [CrossRef]
- Ivanov, R. An Algorithm for On-the-Fly K Shortest Paths Finding in Multi-Storey Buildings Using a Hierarchical Topology Model. Int. J. Geogr. Inf. Sci. 2018, 32, 2362–2385. [Google Scholar] [CrossRef]
- Pollack, M. The Kth Best Route Through a Network. Oper. Res. 1961, 9, 578–580. [Google Scholar] [CrossRef]
- Clarke, S.; Krikorian, A.; Rausen, J. Computing the N Best Loopless Paths in a Network. J. SIAM 1963, 11, 1096–1102. [Google Scholar] [CrossRef]
- Leo, J. Time-Varying K Shortest Paths Algorithm. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=c39f7ff4e09c5b49573c5db9c3a2b044083d0e51 (accessed on 7 April 2020).
- Martins, E.d.Q.V.; Pascoal, M.M.B.; Santos, J.L.E. Dos Deviation Algorithms for Ranking Shortest Paths. Int. J. Found. Comput. Sci. 1999, 10, 247–261. [Google Scholar] [CrossRef]
- Hershberger, J.; Maxel, M.; Suri, S. Finding the k Shortest Simple Paths: A New Algorithm and Its Implementation. ACM Trans. Algorithms 2007, 3, 45-es. [Google Scholar] [CrossRef]
- Al Zoobi, A.; Coudert, D.; Nisse, N. Finding the k Shortest Simple Paths: Time and Space Trade-Offs. ACM J. Exp. Algorithmics 2023, 28, 1–23. [Google Scholar] [CrossRef]
- Kadivar, M. A New O (M+ Kn Log d) Algorithm to Find the k Shortest Paths in Acyclic Digraphs. Trans. Comb. 2016, 5, 23–31. [Google Scholar]
- de las Casas, P.M.; Sedeño-Noda, A.; Borndörfer, R.; Huneshagen, M. K-Shortest Simple Paths Using Biobjective Path Search. arXiv 2023, arXiv:2309.10377. [Google Scholar]
- Yu, Z.; Yu, X.; Koudas, N.; Chen, Y.; Liu, Y. A Distributed Solution for Efficient K Shortest Paths Computation Over Dynamic Road Networks. IEEE Trans. Knowl. Data Eng. 2024, 36, 2759–2773. [Google Scholar] [CrossRef]
- Feng, W.; Chen, S.; Liu, H.; Ji, Y. PeeK: A Prune-Centric Approach for K Shortest Path Computation. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Denver, CO, USA, 12–17 November 2023; ACM: New York, NY, USA, 2023; pp. 1–14. [Google Scholar]
- Chang, L.; Lin, X.; Qin, L.; Yu, J.X.; Pei, J. Efficiently Computing Top-K Shortest Path Join. In Proceedings of the EDBT 2015—18th International Conference on Extending Database Technology, Brussels, Belgium, 23–27 March 2015; pp. 133–144. [Google Scholar] [CrossRef]
- Gao, J.; Yu, J.; Qiu, H.; Jiang, X.; Wang, T.; Yang, D. Holistic Top-k Simple Shortest Path Join in Graphs. IEEE Trans. Knowl. Data Eng. 2012, 24, 665–677. [Google Scholar] [CrossRef]
- Liang, Q.; Wu, W.; Yang, Y.; Zhang, R.; Peng, Y.; Xu, M. Multi-Player Tracking for Multi-View Sports Videos with Improved K-Shortest Path Algorithm. Appl. Sci. 2020, 10, 864. [Google Scholar] [CrossRef]
- Kontogiannis, S.; Paraskevopoulos, A.; Zaroliagis, C. Time-Dependent Alternative Route Planning: Theory and Practice. Algorithms 2021, 14, 220. [Google Scholar] [CrossRef]
- Jäntschi, L. Graph Theory. 1. Fragmentation of Structural Graphs. Leonardo Electron. J. Pract. Technol. 2002, 1, 19–36. [Google Scholar]
- Bellman, R. On a Routing Problem. Q. Appl. Math. 1958, 16, 87–90. [Google Scholar] [CrossRef]
- Yamane, Y.; Kitajima, H. A New K-Shortest Path Search Approach Based on Graph Reduction. arXiv 2019, arXiv:1908.06460. [Google Scholar]
- Williams, J.W.J. Algorithm 232: Heapsort. Commun. ACM 1964, 7, 347–348. [Google Scholar]
- Transportation Networks for Research Core Team. Transportation Networks for Research. Available online: https://github.com/bstabler/TransportationNetworks (accessed on 28 September 2019).
- Storchi, G.; Dell’Olmo, P.; Gentili, M. 9th DIMACS Implementation Challenge—Shortest Paths. Available online: http://users.diag.uniroma1.it/challenge9/data/rome/rome99.gr (accessed on 9 April 2020).
- Al Zoobi, A.; Coudert, D.; Nisse, N. Space and Time Trade-Off for the k Shortest Simple Paths Problem. Leibniz Int. Proc. Inform. LIPIcs 2020, 160, 13. [Google Scholar] [CrossRef]
- Spearman, C. The Proof and Measurement of Association between Two Things. Am. J. Psychol. 1904, 15, 72. [Google Scholar] [CrossRef]
- Kendall, M.G. The Treatment of Ties in Ranking Problems. Biometrika 1945, 33, 239–251. [Google Scholar] [CrossRef] [PubMed]
| Problem Variant | Termination Condition | Remark |
|---|---|---|
| KSSP-OA | is or | No more temporary labels to process or at least permanent labels to every destination are found |
| KSSP-OM | is or | No more temporary labels to process or at least permanent labels to each destination in are found |
| CCSSP-OA | is or | No more temporary labels to process or the cost of the permanent label in the latest iteration to some node exceeds |
| Network Density | Label-Setting Algorithm | Current State-of-the-Art Algorithm | |
|---|---|---|---|
| Dense, | |||
| Sparse, | |||
| Network | Average Running Time for Algorithm 1 (s) | Average Running Time for the Heuristic (Algorithm 3) (s) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| k = 100 | k = 500 | k = 1000 | k = 1500 | k = 2000 | k = 100 | k = 500 | k = 1000 | k = 1500 | k = 2000 | |
| Anaheim | 4.32 × 102 * | 8.90 × 102 * | 1.13 × 103 * | 1.30 × 103 * | 1.38 × 103 * | 3.75 × 10−1 | 8.88 | 3.38 × 101 | 7.46 × 101 | 1.31 × 102 |
| Barcelona | 9.86 × 102 * | 1.28 × 103 * | 1.44 × 103 * | 1.57 × 103 * | 1.60 × 103 * | 2.27 | 5.56 × 101 | 2.17 × 102 | 5.42 × 102 | 9.91 × 102 * |
| Rome | 1.52 × 103 * | 1.66 × 103 * | 1.70 × 103 * | 1.74 × 103 * | 1.74 × 103 * | 1.19 × 101 | 2.70 × 102 | 1.08 × 103 * | 1.46 × 103 * | 1.63 × 103 * |
| Hessen | 1.57 × 103 * | 1.62 × 103 * | 1.64 × 103 * | 1.66 × 103 * | 1.68 × 103 * | 5.79 | 1.34 × 102 | 5.25 × 102 | 1.19 × 103 * | 1.51 × 103 * |
| Austin | 1.47 × 103 * | 1.58 × 103 * | 1.64 × 103 * | 1.67 × 103 * | 1.70 × 103 * | 3.37 × 101 | 6.59 × 102 * | 1.13 × 103 * | 1.35 × 103 * | 1.47 × 103 * |
| Network | Total Paths Found | Maximum Path Length | CPU Time Reported by Helander and McAllister (s) | CPU Time for Y (s) | CPU Time for KSSP_LL_Heap (s) | |||
|---|---|---|---|---|---|---|---|---|
| Granovetter ’73 example A | 10 | 42 | 416 | 14,796 | 9 | 3.17 × 10−2 | 1.33 × 10−1 | 2.39 × 10−2 |
| Granovetter ’73 example B | 25 | 82 | 17,480 | 2,130,510 | 24 | 124.31 | 94.67 | 6.51 |
| Sioux Falls | 24 | 76 | 4787 | 1,717,464 | 23 | 🗴 | 56.55 | 4.87 |
| Eastern Massachusetts | 74 | 258 | 5000 * | 5,316,354 | 18 | 🗴 | 1417.08 | 10.15 |
| Eastern Massachusetts | 74 | 258 | 10,000 * | 10,633,368 | 20 | 🗴 | 3912.52 | 21.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Udhayasekar, S.V.; Srinivasan, K.K.; Kumar, P.; Chilukuri, B.R. Label-Setting Algorithm for Multi-Destination K Simple Shortest Paths Problem and Application. Algorithms 2024, 17, 325. https://doi.org/10.3390/a17080325
Udhayasekar SV, Srinivasan KK, Kumar P, Chilukuri BR. Label-Setting Algorithm for Multi-Destination K Simple Shortest Paths Problem and Application. Algorithms. 2024; 17(8):325. https://doi.org/10.3390/a17080325
Chicago/Turabian StyleUdhayasekar, Sethu Vinayagam, Karthik K. Srinivasan, Pramesh Kumar, and Bhargava Rama Chilukuri. 2024. "Label-Setting Algorithm for Multi-Destination K Simple Shortest Paths Problem and Application" Algorithms 17, no. 8: 325. https://doi.org/10.3390/a17080325
APA StyleUdhayasekar, S. V., Srinivasan, K. K., Kumar, P., & Chilukuri, B. R. (2024). Label-Setting Algorithm for Multi-Destination K Simple Shortest Paths Problem and Application. Algorithms, 17(8), 325. https://doi.org/10.3390/a17080325






