Enhancing Indoor Positioning Accuracy with WLAN and WSN: A QPSO Hybrid Algorithm with Surface Tessellation
Abstract
1. Introduction
- To extend previously published results on the same dataset by joining our signal optimization results and the concept of tessellation of the search space.
- To develop an optimization algorithm by investigating a suitable tessellation of the research space to reduce the overall error in the Multilayer Perceptron positioning algorithm.
- To introduce a heuristic approach for the determination of regular space meshes in general positioning algorithms. With this fact in mind, a Quantum Particle Swarm Optimization (QPSO) algorithm was integrated into the positioning neural network application.
2. Related Work
3. Research Methodology
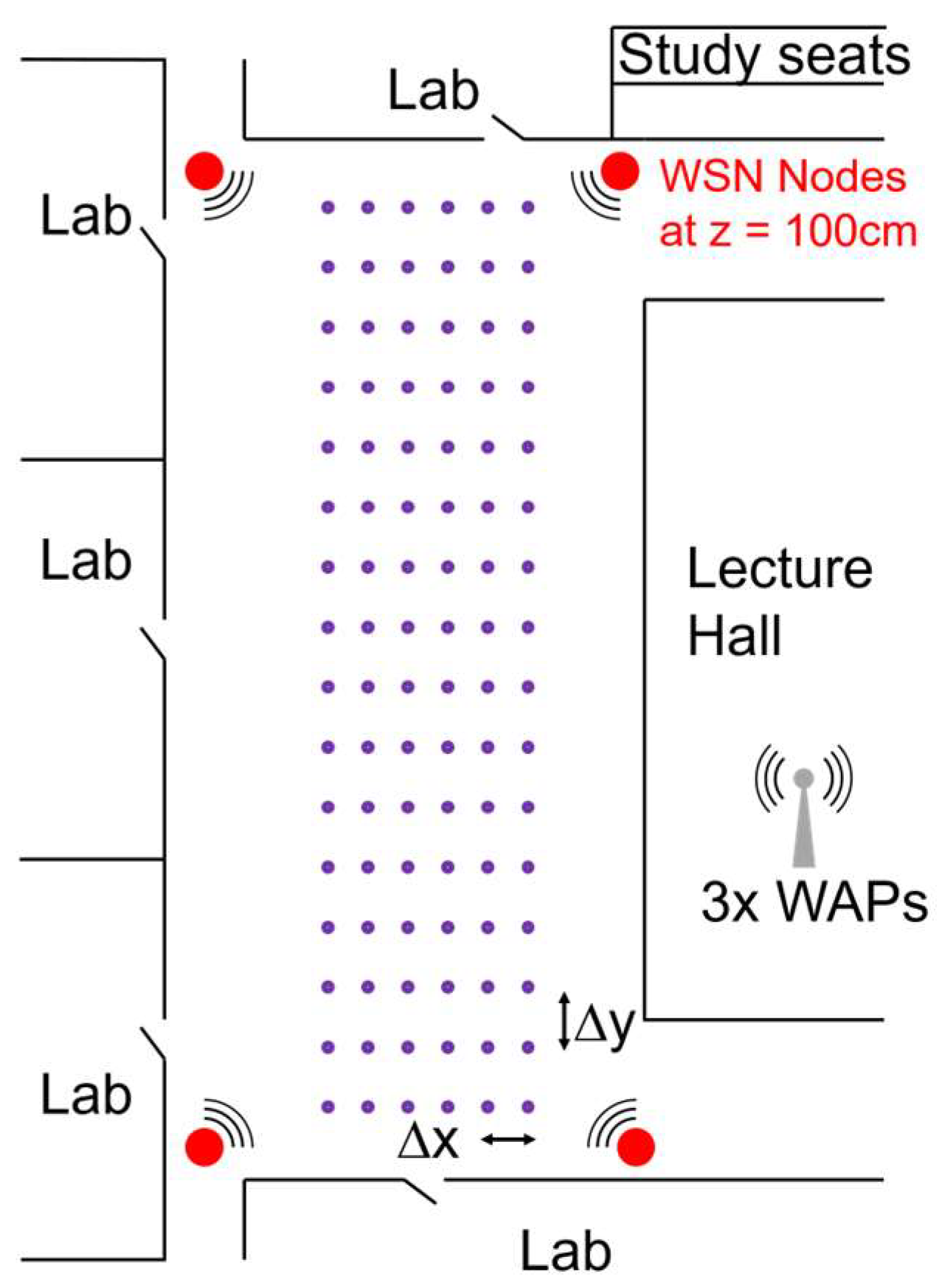
3.1. Signal Acquisition
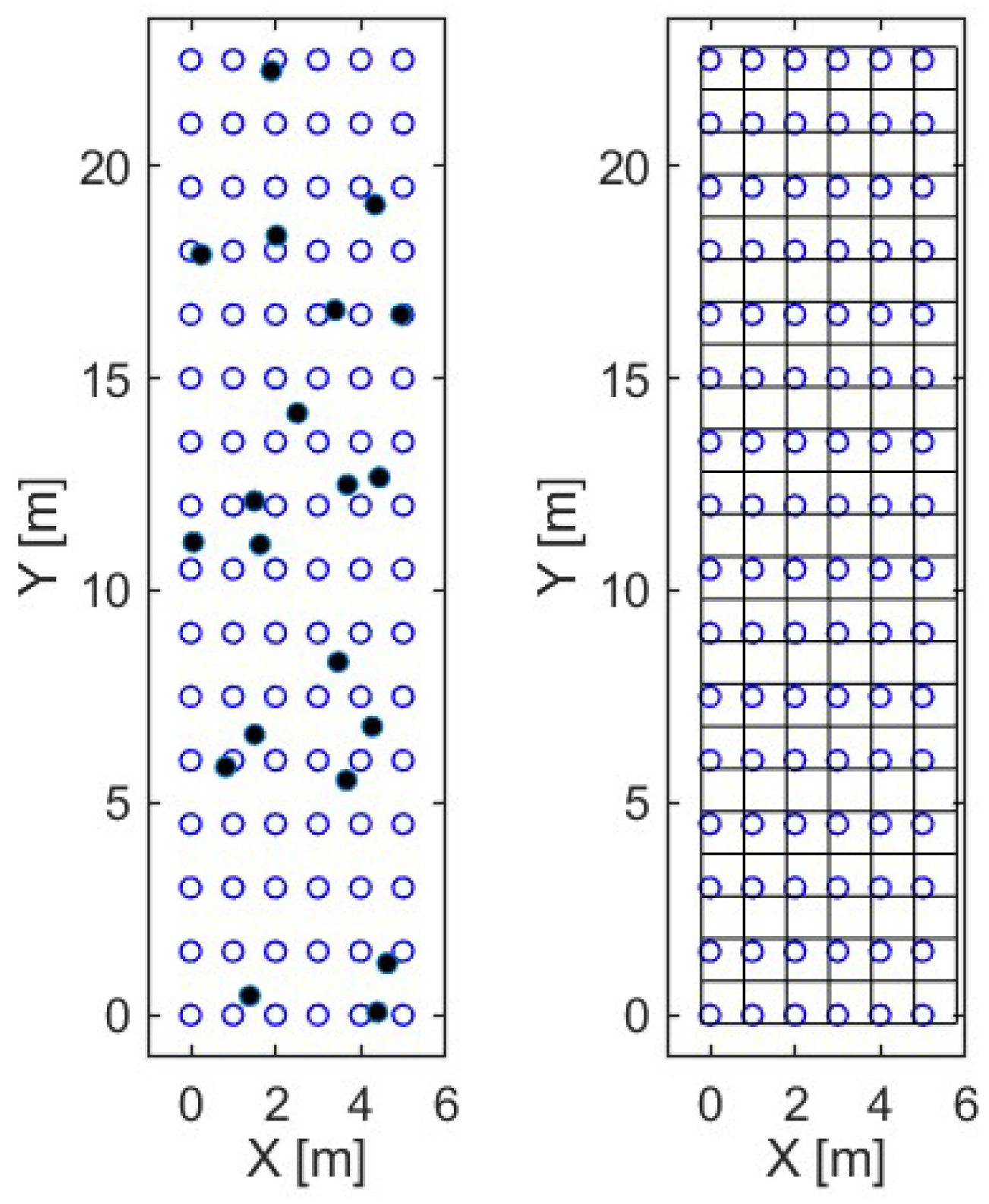
3.2. Data Analysis
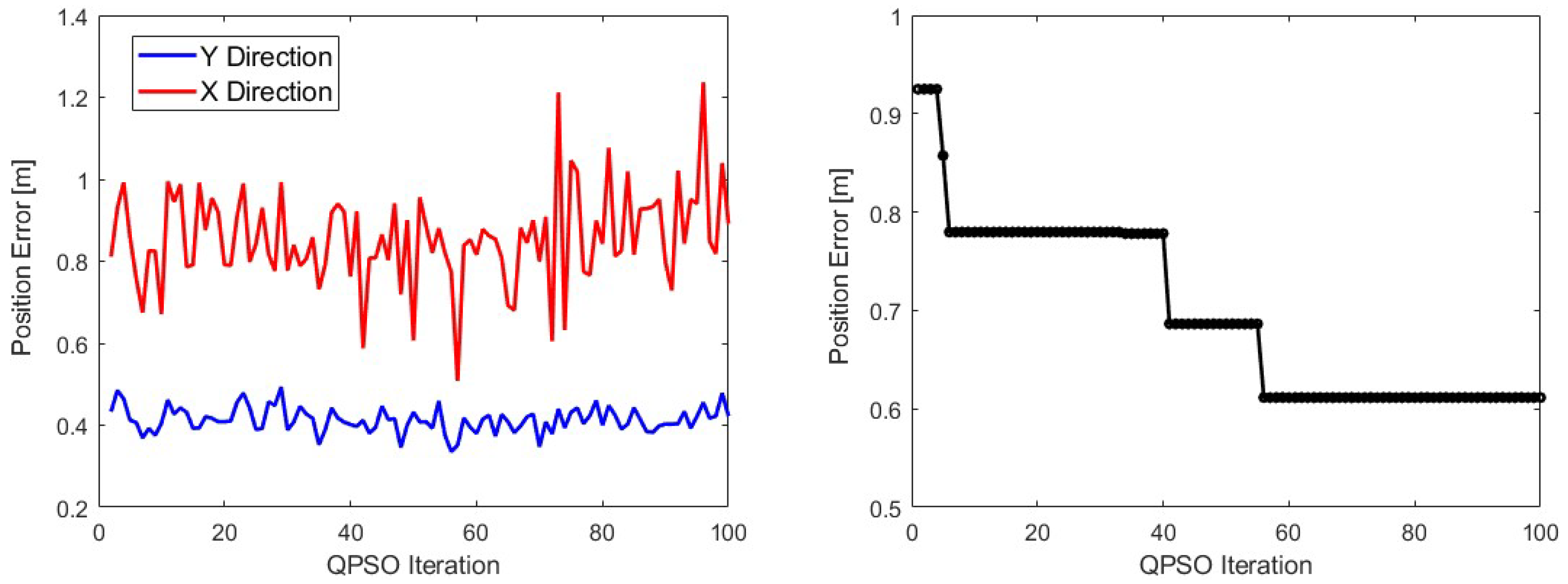
3.3. QPSO Process
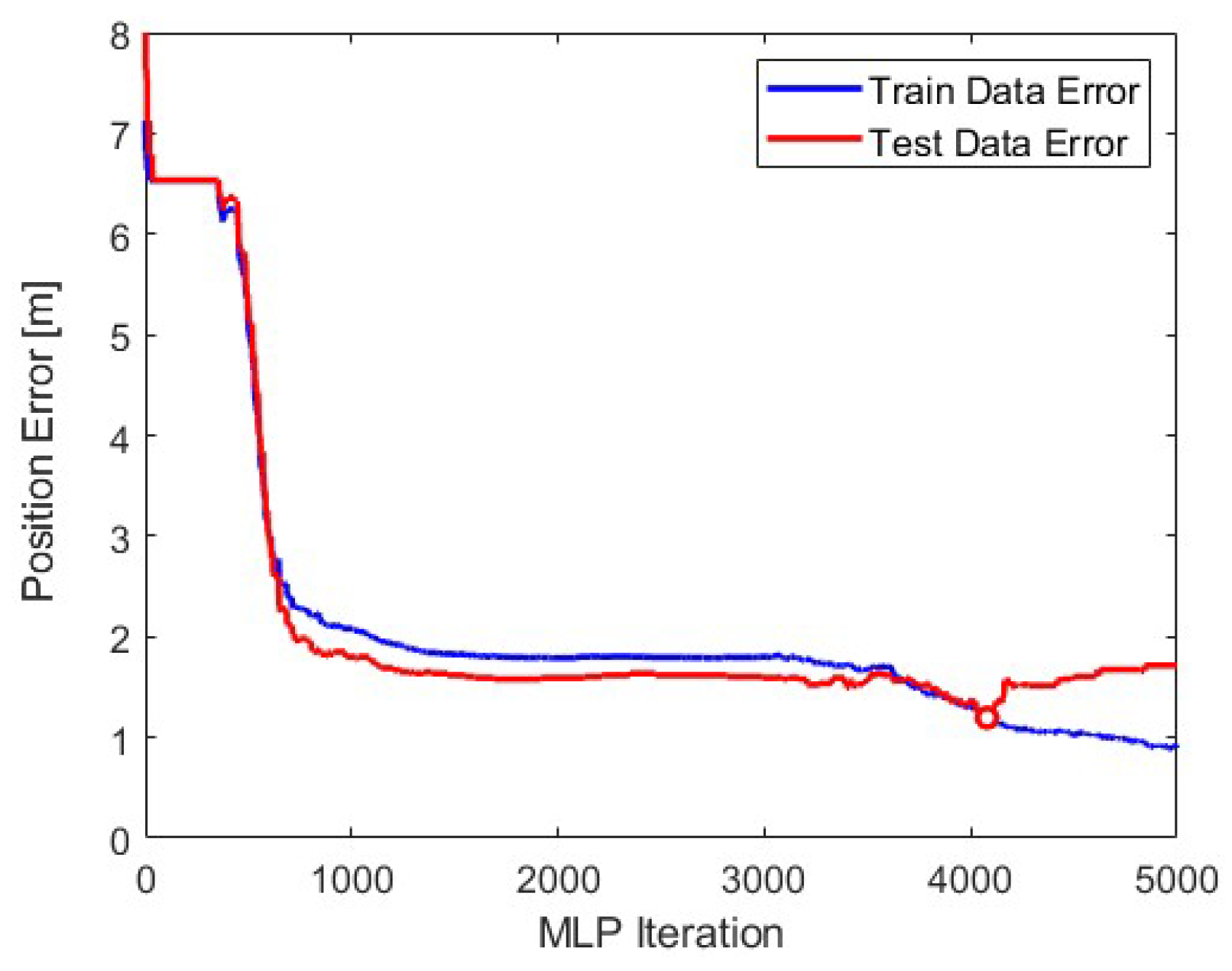
3.3.1. MLP–ADAM-Based Localization
3.3.2. Positioning Algorithm
4. Analysis and Experimental Results
4.1. Experimental Setup
4.2. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, H.; Ning, H.; Lin, Y.; Wang, W.; Dhelim, S.; Farha, F.; Ding, J.; Daneshmand, M. A Survey on the Metaverse: The State-of-the-Art, Technologies, Applications, and Challenges. IEEE Internet Things J. 2023, 10, 14671–14688. [Google Scholar] [CrossRef]
- Qays, M.O.; Ahmad, I.; Abu-Siada, A.; Hossain, M.L.; Yasmin, F. Key communication technologies, applications, protocols and future guides for IoT-assisted smart grid systems: A review. Energy Rep. 2023, 9, 2440–2452. [Google Scholar] [CrossRef]
- Mehannaoui, R.; Mouss, K.N.; Aksa, K. IoT-based food traceability system: Architecture, technologies, applications, and future trends. Food Control 2023, 145, 109409. [Google Scholar] [CrossRef]
- Saleem, F.; Wyne, S. WLAN-based indoor localization using neural networks. J. Electr. Eng. 2016, 67, 299–306. [Google Scholar] [CrossRef]
- Rahman, M.A.A.; Karim, M.K.; Bundak, C.E. Weighted local access point based on fine matching k-nearest neighbor algorithm for indoor positioning system. In Proceedings of the 2019 AEIT International Annual Conference, Florence, Italy, 18–20 September 2019; pp. 1–5. [Google Scholar]
- Gupta, D.; Wadhwa, S.; Rani, S.; Khan, Z.; Boulila, W. EEDC: An Energy Efficient Data Communication Scheme Based on New Routing Approach in Wireless Sensor Networks for Future IoT Applications. Sensors 2023, 23, 8839. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Abdeljawad, T.; Alqudah, M.A. Neural networking study of worms in a wireless sensor model in the sense of fractal fractional. AIMS Math. 2023, 8, 26406–26424. [Google Scholar] [CrossRef]
- Ebied, M.; Elmisery, F.A.; El-Hag, N.A.; Sedik, A.; El-Shafai, W.; El-Banby, G.M.; Soltan, E.; Al-Zubi, N.; Brisha, A.; Zekry, A.; et al. A Proposed Deep-Learning-Based Framework for Medical Image Communication, Storage and Diagnosis. Wirel. Pers. Commun. 2023, 131, 2331–2369. [Google Scholar] [CrossRef]
- Realini, E.; Caldera, S.; Pertusini, L. Precise GNSS positioning using smart devices. Sensors 2017, 17, 2434. [Google Scholar] [CrossRef] [PubMed]
- Yeh, S.; Hsu, W.; Lin, W.; Wu, Y. Study on an indoor positioning system using Earth’s magnetic field. IEEE Trans. Instrum. Meas. 2020, 69, 865–872. [Google Scholar] [CrossRef]
- Tao, Y.; Wu, L.; Sidén, J.; Wang, G. Monte Carlo-based indoor RFID positioning with dual-antenna joint rectification. Electronics 2021, 10, 1548. [Google Scholar] [CrossRef]
- Scherhäufl, M.; Rudic, B.; Stelzer, A.; Pichler-Scheder, M. A blind calibration method for phase-of-arrival-based localization of passive UHF RFID transponders. IEEE Trans. Instrum. Meas. 2019, 68, 261–268. [Google Scholar] [CrossRef]
- Zhou, J.; Ke, Y.; Yu, K.; Tian, D. A solution of high-precision WLAN positioning based on TDOA and PTP. MATEC Web Conf. 2016, 61, 7018. [Google Scholar] [CrossRef]
- Alshami, I.H.; Ahmad, N.A.; Sahibuddin, S.; Firdaus, F. Adaptive indoor positioning model based on WLAN-fingerprinting for dynamic and multi-floor environments. Sensors 2017, 17, 1789. [Google Scholar] [CrossRef] [PubMed]
- Fang, K.T.; Lee, C.T.; Sun, L. An improved hierarchical WLAN positioning method based on apriori knowledge. Electronics 2019, 8, 475. [Google Scholar] [CrossRef]
- Bencak, P.; Hercog, D.; Lerher, T. Indoor positioning system based on Bluetooth low energy technology and a nature-inspired optimization algorithm. Electronics 2022, 11, 308. [Google Scholar] [CrossRef]
- Chen, J.; Wang, S.; Ouyang, M.; Xuan, Y.; Li, K.C. Iterative positioning algorithm for indoor node based on distance correction in WSNs. Sensors 2019, 19, 4871. [Google Scholar] [CrossRef] [PubMed]
- Benatia, M.A.; Sahnoun, M.; Baudry, D. Multi-objective WSN deployment using genetic algorithms under cost, coverage, and connectivity constraints. Wirel. Pers. Commun. 2017, 94, 2739–2768. [Google Scholar] [CrossRef]
- Li, T.; Yan, W.; Ping, L.; Fang, P. A WSN positioning algorithm based on 3D discrete chaotic mapping. EURASIP J. Wirel. Commun. Netw. 2019, 126, 1323. [Google Scholar] [CrossRef]
- Yanbin, H.; Xiaodong, Y.; Abbasi, Q.H. Efficient AoA-based wireless indoor localization for hospital outpatients using mobile devices. Sensors 2018, 18, 3698. [Google Scholar] [CrossRef]
- De Gante, A.; Siller, M. A survey of hybrid schemes for location estimation in wireless sensor networks. Procedia Technol. 2013, 7, 377–383. [Google Scholar] [CrossRef][Green Version]
- Abed, A.; Abdel-Qader, I. RSS-fingerprint dimensionality reduction for multiple service set identifier-based indoor positioning systems. Appl. Sci. 2019, 9, 3137. [Google Scholar] [CrossRef]
- Arai, H. Antennas in Access Points of WLAN/WiFi. In Handbook of Antenna Technologies; Chen, Z., Liu, D., Nakano, H., Qing, X., Zwick, T., Eds.; Springer: Singapore, 2016; pp. 2579–2588. [Google Scholar]
- Ali, R.A.E.Y.; Babiker, A.; Mustafa, A.N. Performance analysis of WiFi network. IOSR J. Electron. Commun. Eng. 2015, 10, 67–76. [Google Scholar]
- Farid, Z. Higher Accuracy Hybrid Wireless Indoor Localization Using Machine Learning. Ph.D. Thesis, Faculty of Engineering, Universiti Kebangsaan Malaysia, Bangi, Malaysia, 2016. [Google Scholar]
- Jiang, L. A WLAN Fingerprinting Based Indoor Localization Technique. Master’s Thesis, Department Computer Science, University of Nebraska, Lincoln, NE, USA, 2012. [Google Scholar]
- Khan, I.U.; Ali, T.; Farid, Z.; Scavino, E.; Rahman, M.A.A. An improved hybrid indoor positioning system based on surface tessellation artificial neural network. Meas. Control 2020, 53, 1968–1977. [Google Scholar] [CrossRef]
- Chen, J.; Song, S.; Yu, H. An indoor multi-source fusion positioning approach based on PDR/MM/WiFi. AEU—Int. J. Electron. Commun. 2021, 135, 153733. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, Z.; Liu, C.; Luo, H. Reliable and cooperative target tracking based on WSN and WiFi in indoor wireless networks. IEEE Access 2018, 6, 24846–24855. [Google Scholar] [CrossRef]
- Guo, T.; Chai, M.; Xiao, J.; Li, C. A hybrid indoor positioning algorithm for cellular and Wi-Fi networks. Arab. J. Sci. Eng. 2022, 47, 2909–2923. [Google Scholar] [CrossRef]
- Gang, H.-S.; Pyun, J.-Y. A smartphone indoor positioning system using hybrid localization technology. Energies 2019, 12, 3702. [Google Scholar] [CrossRef]
- Scavino, E.; Rahman, M.A.A.; Farid, Z. An improved hybrid indoor positioning algorithm via QPSO and MLP signal weighting. Comput. Mater. Contin. 2023, 74, 379–397. [Google Scholar] [CrossRef]
- Farid, Z.; Khan, I.U.; Scavino, E.; Rahman, M.A.A. A WLAN fingerprinting based indoor localization technique via artificial neural network. IJCSNS Int. J. Comput. Sci. Netw. Secur. 2019, 19, 157–165. [Google Scholar]
- Farid, Z.; Nordin, R.; Ismail, M.; Abdullah, N.F. Hybrid indoor-based WLAN-WSN localization scheme for improving accuracy based on artificial neural network. Mob. Inf. Syst. 2016, 2016, 6923931. [Google Scholar] [CrossRef]
- Xiao, P.Y.; Peng, J.; Zhou, G. An improved QPSO algorithm based on social learning and Lévy flights. Syst. Sci. Control. Eng. 2018, 6, 364–373. [Google Scholar]
- Sun, J.; Feng, B.; Xu, W. Particle swarm optimization with particles having quantum behaviour. In Proceedings of the 2004 Congress on Evolutionary Computation, Portland, OR, USA, 19–23 June 2004; pp. 325–331. [Google Scholar]
- Bhatia, A.S.; Saggi, M.K.; Zheng, S. QPSO-CD: Quantum-behaved particle swarm optimization algorithm with Cauchy distribution. Quantum Inf. Process. 2020, 19, 345. [Google Scholar] [CrossRef]
- Russell, S.; Norvig, P. Artificial Intelligence—A Modern Approach, 4th ed.; Pearson Prentice Hall: Hoboken, NJ, USA, 2020. [Google Scholar]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015; pp. 1–13. [Google Scholar]
- Ficco, M.; Palmieri, F.; Castiglione, A. Hybrid indoor and outdoor location services for new generation mobile terminals. Pers. Ubiquitous Comput. 2014, 18, 271–285. [Google Scholar] [CrossRef]
- Xiong, Z.; Song, Z.; Scalera, A.; Ferrera, E.; Sottile, F.; Brizzi, P.; Tomasi, R.; Spirito, M.A. Hybrid WSN and RFID indoor positioning and tracking system. EURASIP J. Embed. Syst. 2013, 1, 6. [Google Scholar] [CrossRef]
| Design Parameters | Architecture Parameters | ||
|---|---|---|---|
| Number of individuals | 20 | 1 | |
| Number of iterations | 100 | 1.5 | |
| Number of cost calculations | 2000 | Initial | 1 |
| Search range (tile size) | (0.3, 1.2) | Final | 0.1 |
| Architecture Parameters | Training Parameters | ||
|---|---|---|---|
| Hidden layers | 3 | Learning rate | |
| Hidden units | 18 per layer | Momenta Adam values | , |
| Activation function | Logistic sigmoid | Runs per individual | 1000 |
| Training points | 96 | Training iterations | 5000 |
| Test points | 20 | Computing time | ~28 h |
| Reference | Chosen Approach and Implementation | Research Area and Anchor Points (AP) | Error |
|---|---|---|---|
| M. Ficco et al. [40] | Source selection, WiFi + Bluetooth | 20 m × 21 m, 26 AP | >4 m |
| L. Jiang [26] | K-NN modeling, WiFi + RSS | 15 m × 40 m, 100 AP | 1.70 m |
| Z. Xiong et al. [41] | Particle filter, WiFi + RFID | 25 m × 12 m, 80 AP | 1.60 m |
| J. Chen et al. [28] | Optimization, IMU + WLAN | 90 m path, 113 AP | 1.48 m |
| Z. Farid et al. (same dataset) [33] | MLP modeling, WiFi + WSN | 6 m × 24 m, 96 AP | 1.22 m |
| I. U. Khan et al. (same dataset) [27] | Tessellation, WiFi + WSN | 6 m × 24 m, 96 AP | 1.01 m |
| E. Scavino et al. (same dataset) [32] | Optimization, WiFi + WSN | 6 m × 24 m, 96 AP | 0.725 m |
| This Research (same dataset) | Variable tessellation, WiFi + WSN | 6 m × 24 m, 96 AP | 0.611 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scavino, E.; Abd Rahman, M.A.; Farid, Z.; Ahmad, S.; Asim, M. Enhancing Indoor Positioning Accuracy with WLAN and WSN: A QPSO Hybrid Algorithm with Surface Tessellation. Algorithms 2024, 17, 326. https://doi.org/10.3390/a17080326
Scavino E, Abd Rahman MA, Farid Z, Ahmad S, Asim M. Enhancing Indoor Positioning Accuracy with WLAN and WSN: A QPSO Hybrid Algorithm with Surface Tessellation. Algorithms. 2024; 17(8):326. https://doi.org/10.3390/a17080326
Chicago/Turabian StyleScavino, Edgar, Mohd Amiruddin Abd Rahman, Zahid Farid, Sadique Ahmad, and Muhammad Asim. 2024. "Enhancing Indoor Positioning Accuracy with WLAN and WSN: A QPSO Hybrid Algorithm with Surface Tessellation" Algorithms 17, no. 8: 326. https://doi.org/10.3390/a17080326
APA StyleScavino, E., Abd Rahman, M. A., Farid, Z., Ahmad, S., & Asim, M. (2024). Enhancing Indoor Positioning Accuracy with WLAN and WSN: A QPSO Hybrid Algorithm with Surface Tessellation. Algorithms, 17(8), 326. https://doi.org/10.3390/a17080326








