Trajectory Classification and Recognition of Planar Mechanisms Based on ResNet18 Network
Abstract
1. Introduction
2. Sample Construction
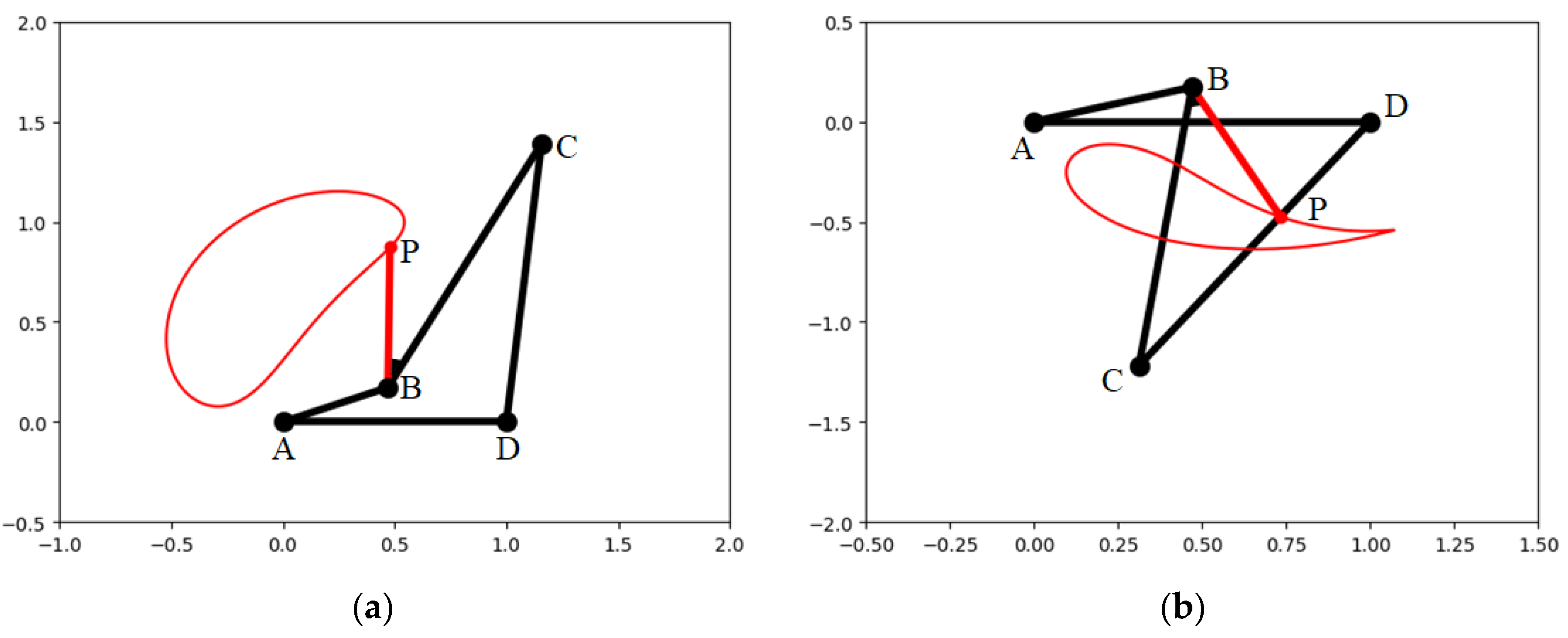
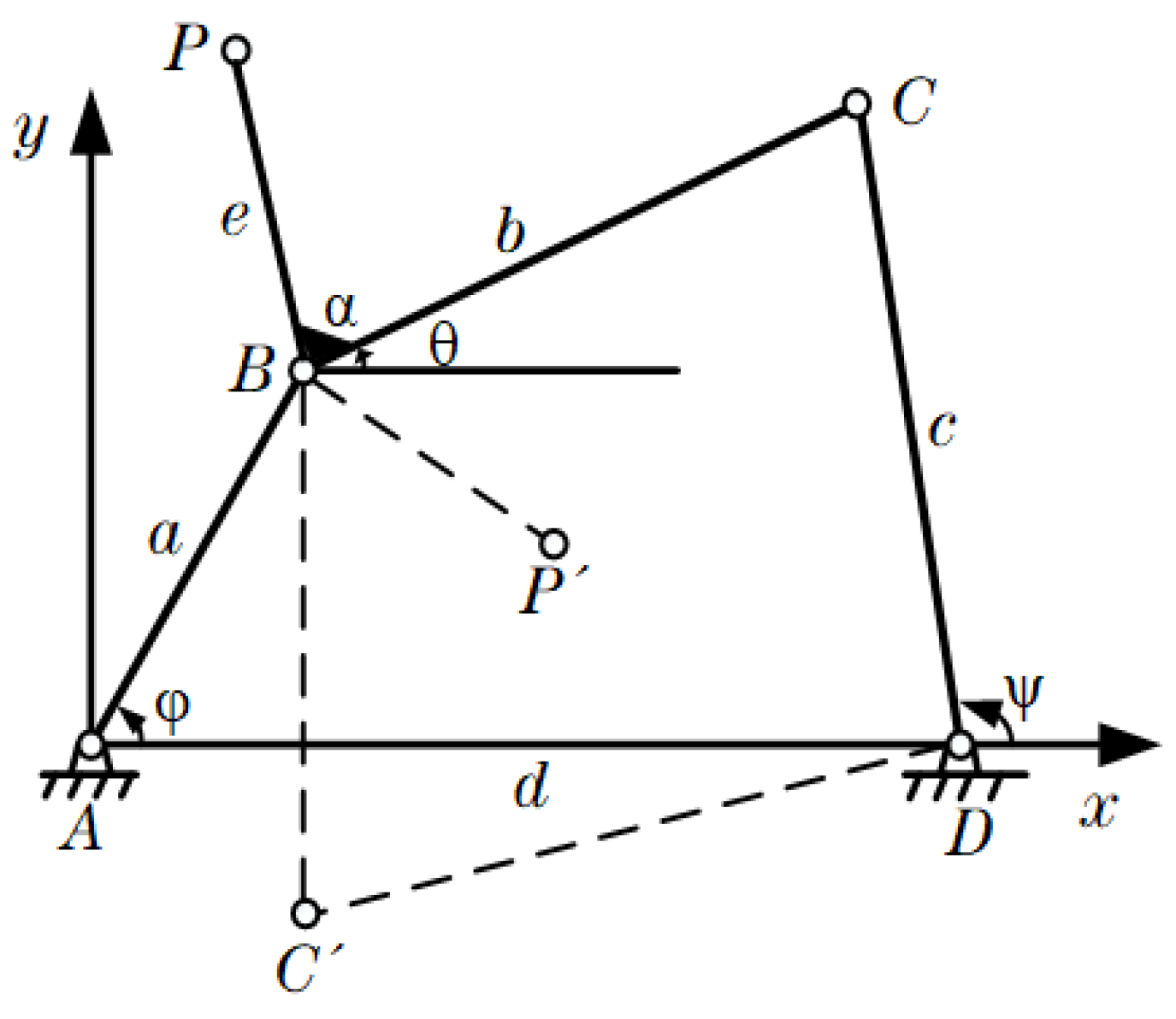
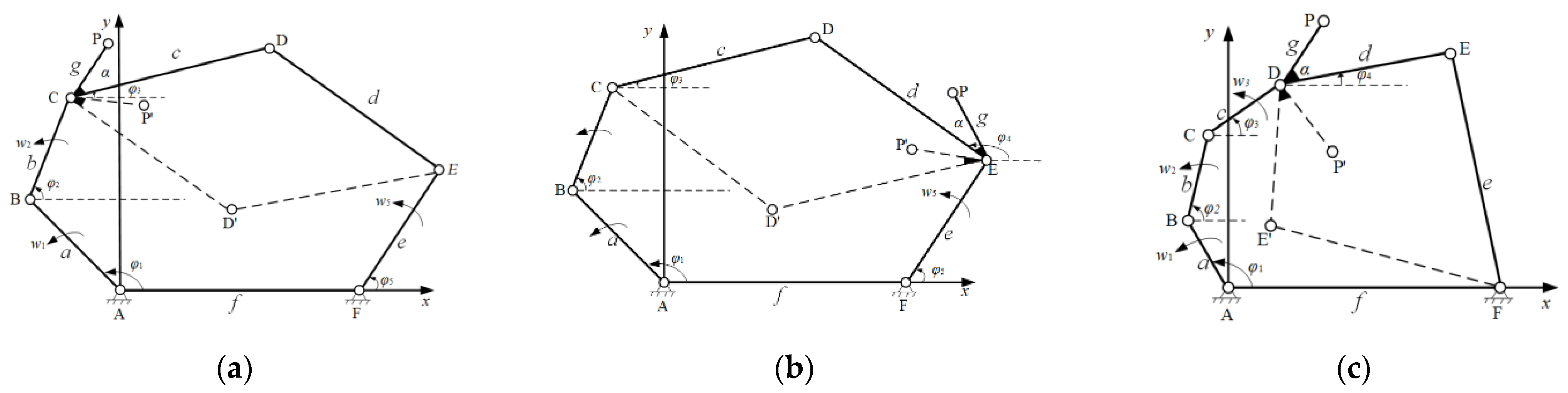
2.1. Hinge Four-Bar Mechanism Sample Construction
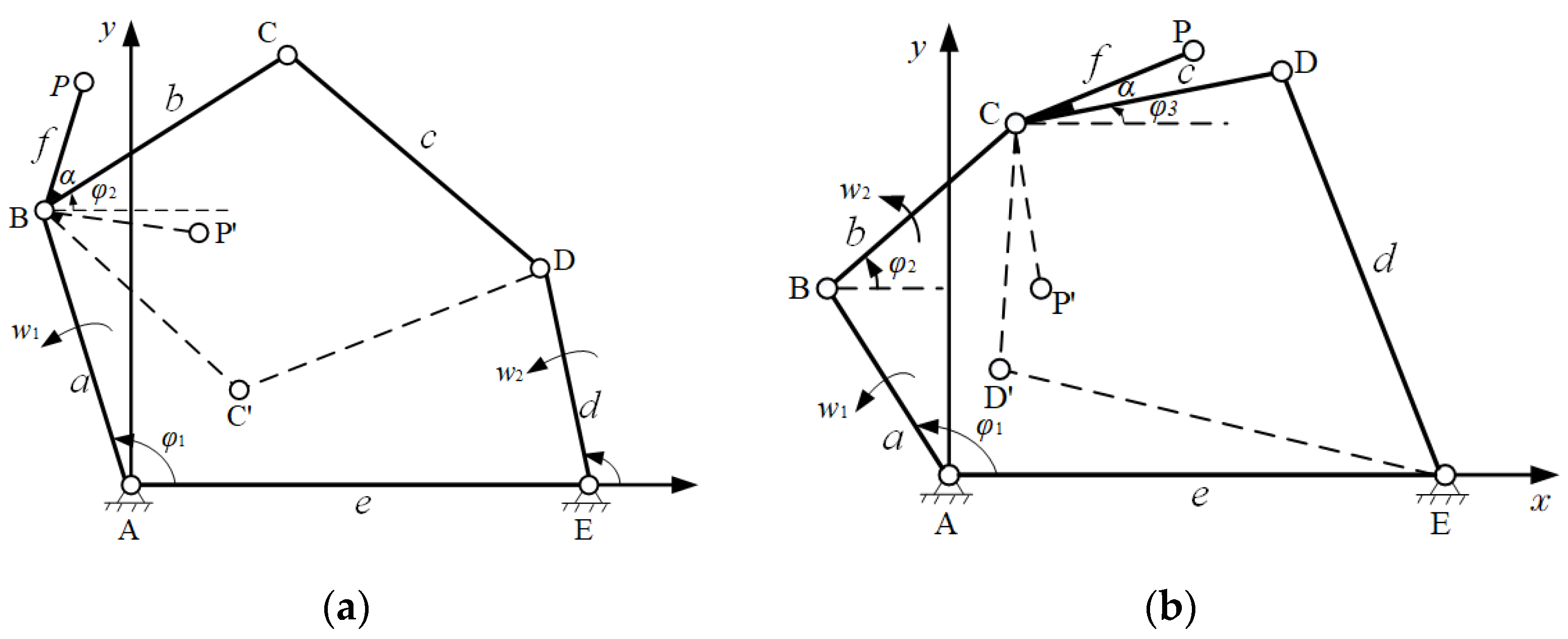
2.2. Construction of Samples for Hyperboloid Crank Hinge Five-Bar Mechanism
2.3. Construction of Samples for Single-Loop Hinge Six-Bar Mechanism
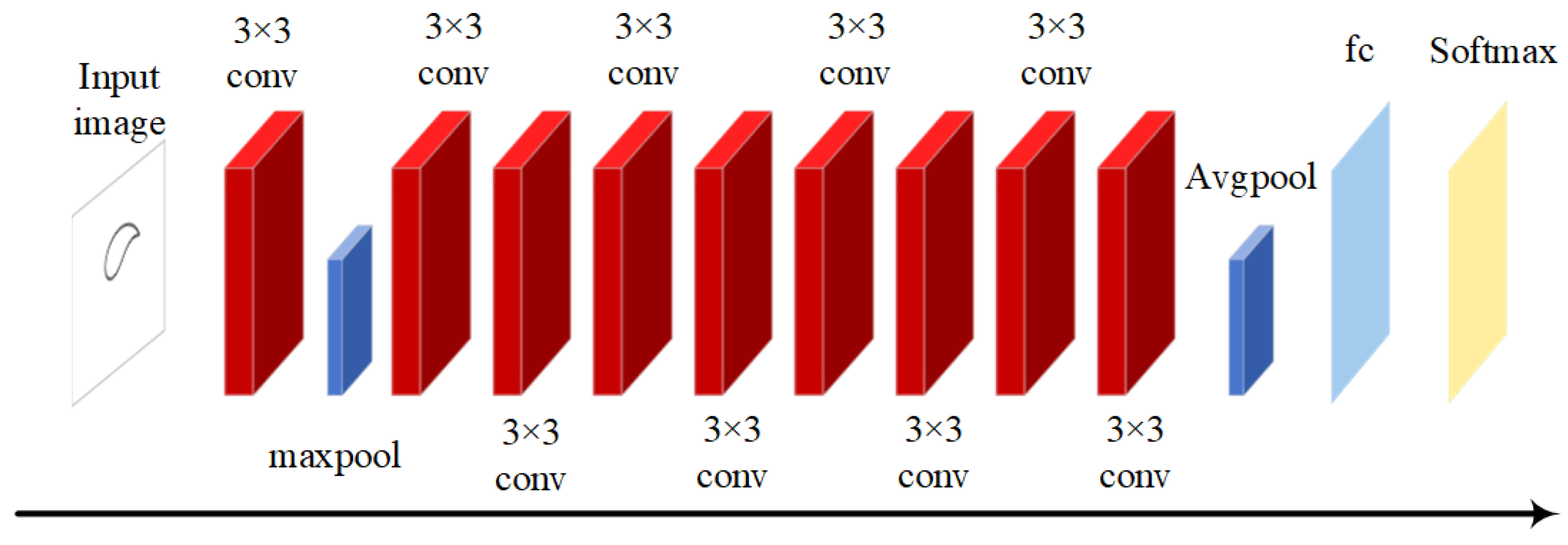
3. Selection of the Network
4. Training Model
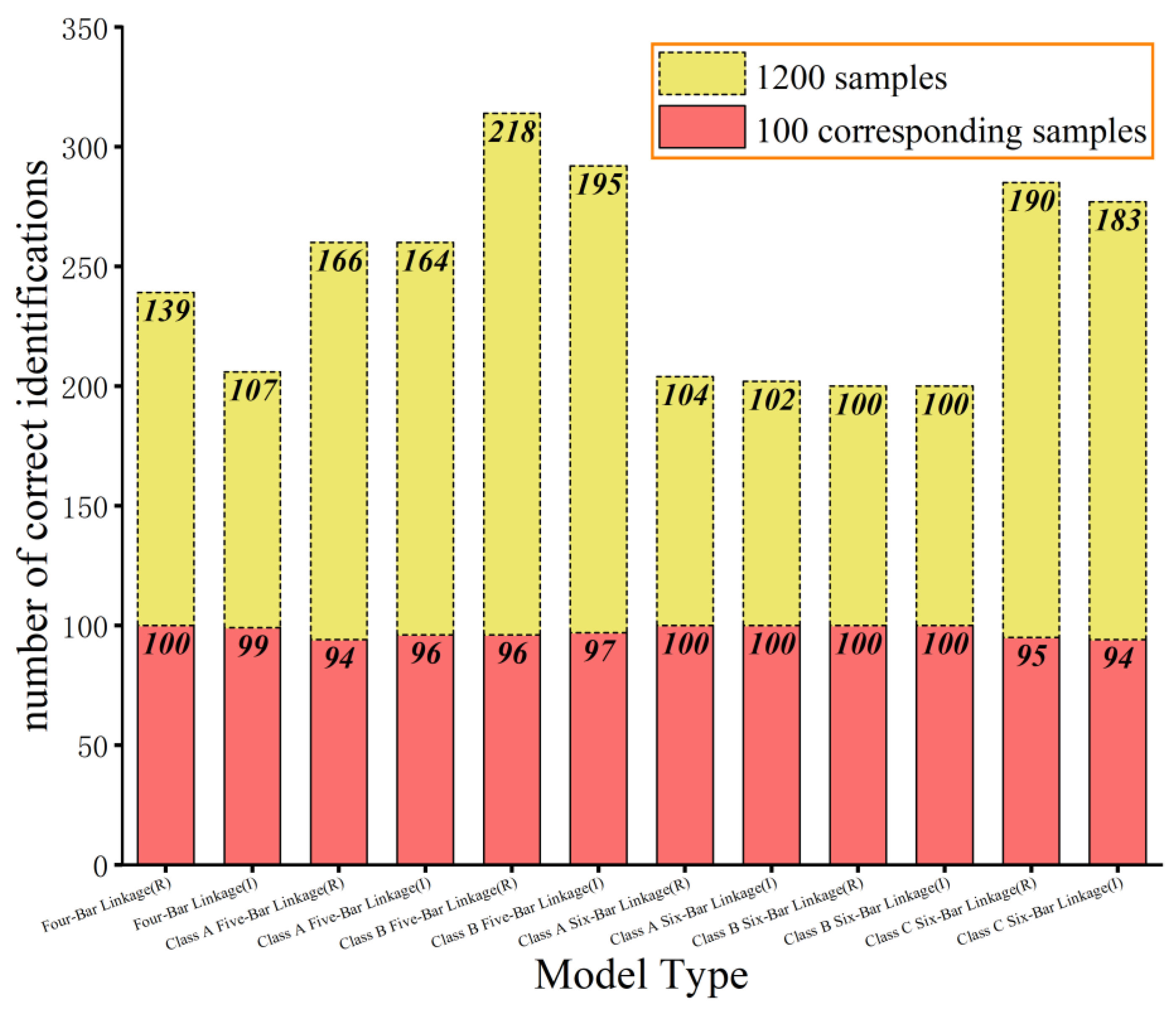
4.1. Classification of Trajectories in Regular and Inverted Configurations
4.2. Recognition of Trajectories in Regular and Inverted Configurations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bulatović, R.R.; Đorðević, S.R. Optimal synthesis of a path generator six-bar linkage. J. Mech. Sci. Technol. 2012, 26, 27–40. [Google Scholar] [CrossRef]
- Tari, H.; Su, H.-J. Complete Solution to the Eight-Point Path Generation of Slider-Crank Four-Bar Linkages. J. Mech. Des. 2010, 132, 081003. [Google Scholar] [CrossRef]
- Sancibrian, R.; Sarabia, E.G.; Sedano, A.; Blanco, J.M. A general method for the optimal synthesis of mechanisms using prescribed instant center positions. Appl. Math. Model. 2016, 40, 6–22. [Google Scholar] [CrossRef]
- Lin, W.; Hsiao, K. A new differential evolution algorithm with a combined mutation strategy for optimum synthesis of path-generating four-bar mechanisms. Proc. Inst. Mech. Eng. 2017, 231, 690–705. [Google Scholar] [CrossRef]
- Bulatović, R.R.; Miodragović, G.; Bošković, M.S. Modified Krill Herd (MKH) algorithm and its application in dimensional synthesis of a four-bar linkage. Mech. Mach. Theory 2016, 95, 1–21. [Google Scholar] [CrossRef]
- Martínez-Alfaro, H. Four-Bar Mechanism Synthesis for n Desired Path Points Using Simulated Annealing; Springer: Berlin/Heidelberg, Germany, 2007; pp. 23–37. [Google Scholar]
- Buśkiewicz, J. A method for optimal path synthesis of four-link planar mechanisms. Inverse Probl. Sci. Eng. 2015, 23, 18–50. [Google Scholar] [CrossRef]
- Qaiyum, A.; Mohammad, A. A novel approach for optimal synthesis of path generator four-bar planar mechanism using improved harmony search algorithm. Aust. J. Mech. Eng. 2022, 22, 95–108. [Google Scholar] [CrossRef]
- Sanchez-Marquez, A.; Vega-Alvarado, E.; Portilla-Flores, E.A.; Mezura-Montes, E. Synthesis of a planar four-bar mechanism for position control using the harmony search algorithm. In Proceedings of the 2014 11th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), Ciudad del Carmen, Mexico, 29 September–3 October 2014; Available online: http://ieeexplore.ieee.org/document/6978286/ (accessed on 3 May 2024).
- Zarkandi, S. A novel optimization-based method to find multiple solutions for path synthesis of planar four-bar and slider-crank mechanisms. J. Mech. Eng. Sci. 2021, 235, 385–405. [Google Scholar] [CrossRef]
- Sharma, S.; Purwar, A.; Ge, Q.J. An Optimal Parametrization Scheme for Path Generation Using Fourier Descriptors for Four-Bar Mechanism Synthesis. J. Comput. Inf. Sci. Eng. 2019, 19, 014501. [Google Scholar] [CrossRef]
- Wu, R.; Li, R.; Liang, H.; Ning, F. Mixed synthesis method of motion and path of planar four-bar linkages. Mech. Sci. 2021, 12, 43–49. [Google Scholar] [CrossRef]
- Daniali, H.M.; Varedi, S.M.; Dardel, M.; Fathi, A. A novel algorithm for kinematic and dynamic optimal synthesis of planar four-bar mechanisms with joint clearance. J. Mech. Sci. Technol. 2015, 29, 59–65. [Google Scholar] [CrossRef]
- Wang, B.; Du, X.; Ding, J.; Dong, Y.; Wang, C.; Liu, X. The Synthesis of Planar Four-Bar Linkage for Mixed Motion and Function Generation. Sensors 2021, 21, 3504. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Liu, W. On the Solution of Eight-Precision-Point Path Synthesis of Planar Four-Bar Mechanisms Based on the Solution Region Methodology. J. Mech. Robot. 2019, 11, 064504. [Google Scholar] [CrossRef]
- Sun, J.; Lu, H.; Chu, J. Variable step-size numerical atlas method for path generation of spherical four-bar crank-slider mechanism. Inverse Probl. Sci. Eng. 2015, 23, 256–276. [Google Scholar] [CrossRef]
- Mundo, D.; Gatti, G.; Dooner, D.B. Optimized five-bar linkages with non-circular gears for exact path generation. Mech. Mach. Theory 2009, 44, 751–760. [Google Scholar] [CrossRef]
- Russell, K.; Sodhi, R.S. Kinematic Synthesis of Planar Five-Bar Mechanisms for Multi-Phase Motion Generation. JSME Int. J. Ser. C 2004, 47, 345–349. [Google Scholar] [CrossRef][Green Version]
- Sun, J.; Xue, N.; Liu, W.; Chu, J. A synthesis method for path generation of a planar five-bar mechanism based on dynamic self-adaptive atlas database. Inverse Probl. Sci. Eng. 2020, 28, 9–32. [Google Scholar] [CrossRef]
- Kapsalyamov, A.; Hussain, S.; Brown, N.A.; Goecke, R.; Hayat, M.; Jamwal, P.K. Synthesis of a six-bar mechanism for generating knee and ankle motion trajectories using deep generative neural network. Eng. Appl. Artif. Intell. 2021, 117, 105500. [Google Scholar] [CrossRef]
- Peón-Escalante, R.; Jiménez, F.C.; Soberanis, M.E.; Peñuñuri, F. Path generation with dwells in the optimum dimensional synthesis of Stephenson III six-bar mechanisms. Mech. Mach. Theory 2020, 144, 103650. [Google Scholar] [CrossRef]
- Sun, J.; Wang, P.; Liu, W.; Chu, J.; Ren, L. Synthesis of multiple tasks of a planar six-bar mechanism by wavelet series. Inverse Probl. Sci. Eng. 2019, 27, 388–406. [Google Scholar] [CrossRef]
- Pickard, J.K.; Carretero, J.A.; Merlet, J.-P. Appropriate analysis of the four-bar linkage. Mech. Mach. Theory 2019, 139, 237–250. [Google Scholar] [CrossRef]
- Liang, C.M.; Li, Y.W.; Liu, Y.H.; Wen, P.F.; Yang, H. Segmentation and weight prediction of grape ear based on SFNet-ResNet18. Syst. Sci. Control Eng. 2022, 10, 722–732. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2015. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015. [Google Scholar] [CrossRef]
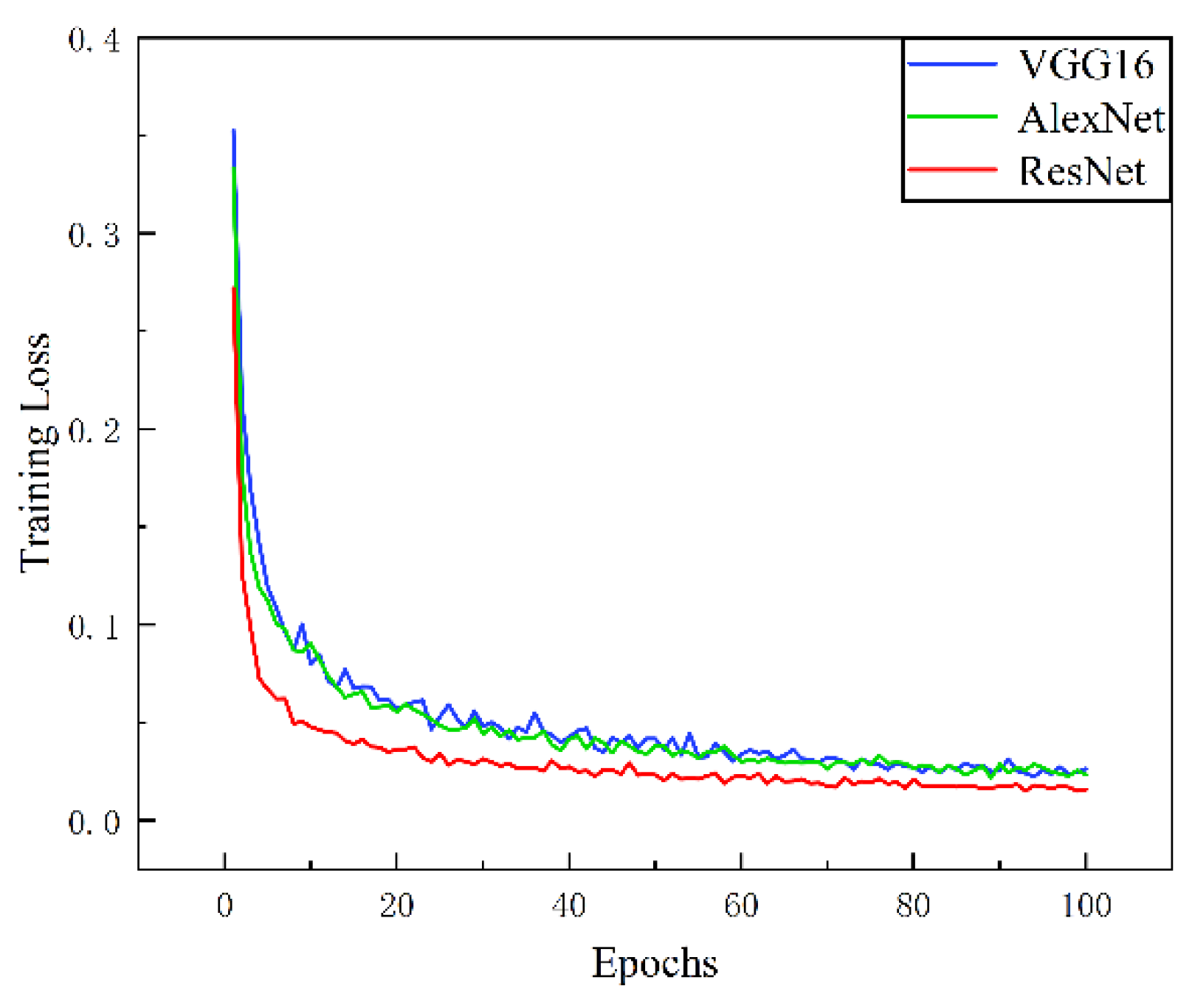
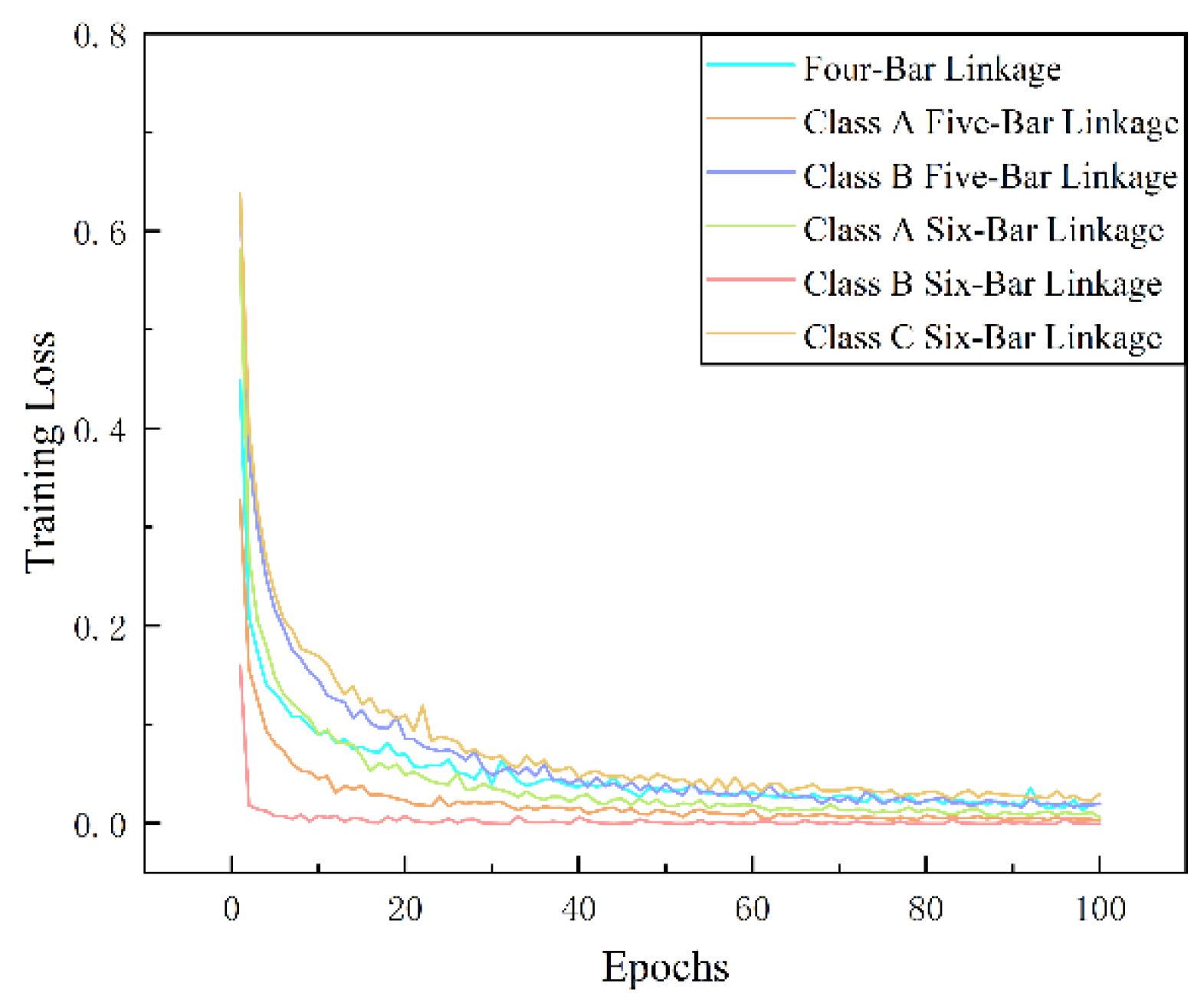

| Sample | Predicted Results | AlexNet | VGG16 | ResNet18 |
|---|---|---|---|---|
| Regular configurations | Regular | 487 | 490 | 497 |
| Inverted | 13 | 10 | 3 | |
| Inverted configurations | Regular | 33 | 17 | 22 |
| Inverted | 467 | 479 | 478 | |
| Training time (s) | 12,012 | 41,642 | 11,423 | |
| Memory (MB) | 222.7 | 524.5 | 43.7 | |
| Accuracy rating | 95.4% | 96.3% | 97.5% | |
| Model Class | Max Loss | Min Loss | Average Loss | |
|---|---|---|---|---|
| Four-Bar Linkage | Regular | 0.27564 | 0.00672 | 0.03224 |
| Inverted | 0.30365 | 0.01774 | 0.04257 | |
| Class A Five-Bar Linkage | Regular | 0.54837 | 0.08741 | 0.19721 |
| Inverted | 0.55185 | 0.09854 | 0.19836 | |
| Class B Five-Bar Linkage | Regular | 0.53649 | 0.14265 | 0.20871 |
| Inverted | 0.54855 | 0.14354 | 0.21043 | |
| Class A Six-Bar Linkage | Regular | 0.32702 | 0.14354 | 0.02249 |
| Inverted | 0.31886 | 0.00370 | 0.02016 | |
| Class A Six-Bar Linkage | Regular | 0.25902 | 0.00387 | 0.01447 |
| Inverted | 0.24952 | 0.00173 | 0.01386 | |
| Class A Six-Bar Linkage | Regular | 0.46131 | 0.13663 | 0.19283 |
| Inverted | 0.47059 | 0.13743 | 0.19212 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wang, Y.; Chen, B.; Jia, X.; Pu, D. Trajectory Classification and Recognition of Planar Mechanisms Based on ResNet18 Network. Algorithms 2024, 17, 324. https://doi.org/10.3390/a17080324
Wang J, Wang Y, Chen B, Jia X, Pu D. Trajectory Classification and Recognition of Planar Mechanisms Based on ResNet18 Network. Algorithms. 2024; 17(8):324. https://doi.org/10.3390/a17080324
Chicago/Turabian StyleWang, Jianping, Youchao Wang, Boyan Chen, Xiaoyue Jia, and Dexi Pu. 2024. "Trajectory Classification and Recognition of Planar Mechanisms Based on ResNet18 Network" Algorithms 17, no. 8: 324. https://doi.org/10.3390/a17080324
APA StyleWang, J., Wang, Y., Chen, B., Jia, X., & Pu, D. (2024). Trajectory Classification and Recognition of Planar Mechanisms Based on ResNet18 Network. Algorithms, 17(8), 324. https://doi.org/10.3390/a17080324






