Supervised Dynamic Correlated Topic Model for Classifying Categorical Time Series

Abstract

In this paper, we describe the supervised dynamic correlated topic model (sDCTM) for classifying categorical time series. This model extends the correlated topic model used for analyzing textual documents to a supervised framework that features dynamic modeling of latent topics. sDCTM treats each time series as a document and each categorical value in the time series as a word in the document. We assume that the observed time series is generated by an underlying latent stochastic process. We develop a state-space framework to model the dynamic evolution of the latent process, i.e., the hidden thematic structure of the time series. Our model provides a Bayesian supervised learning (classification) framework using a variational Kalman filter EM algorithm. The E-step and M-step, respectively, approximate the posterior distribution of the latent variables and estimate the model parameters. The fitted model is then used for the classification of new time series and for information retrieval that is useful for practitioners. We assess our method using simulated data. As an illustration to real data, we apply our method to promoter sequence identification data to classify E. coli DNA sub-sequences by uncovering hidden patterns or motifs that can serve as markers for promoter presence.

1. Introduction

Data on multiple time series or sequences are ubiquitous in various domains, and their classification finds applications in numerous areas, such as human motion classification [1], earthquake prediction [2], and heart attack detection [3]. The classification of multiple real-valued time series have been well studied in the statistical literature (see the detailed review in [4]). However, for analyzing categorical time series, most statistical methods are primarily focused on examining a single time series. A few methods include the Markov chain model [5], the link function approach [6], and the likelihood-based method [7]. In the computer science literature, a number of sequence classification methods have been developed that are black-box in nature and may be difficult to interpret. These include the minimum edit distance classifier with sequence alignment [8,9] and Markov chain-based classifiers [10]. Overall, the classification of multiple categorical time series has not received much attention. Recent work has discussed a novel approach to the classification of categorical time series in the supervised learning framework, using a spectral envelope and optimal scalings [11,12]. We present an alternative approach for classifying multiple categorical time series in the topic modeling framework.

Topic modeling algorithms generally examine a set of documents referred to as a corpus in the natural language processing (NLP) domain. Often, the sets of words observed in documents appear to represent a coherent theme or topic. Topic models analyze the words in the documents in order to uncover themes that run through them. Many topic modeling algorithms have been developed over time, including non-negative matrix factorization [13], latent Dirichlet allocation (LDA) [14], and structural topic models [15]. Topic modeling in the dynamic framework has been extensively studied to model the dynamic evolution of document collections over time [16,17]. However, the dynamic evolution of words over time within each document has not been addressed. The topic modeling literature typically assumes that words are interchangeable. We relax this assumption to model word time series (documents). We build a family of probabilistic dynamic topic models by extending the correlated topic model (CTM) in a supervised framework and modeling the dynamic evolution of the underlying latent stochastic process that reflects the thematic structure of the time series collection, and we classify the documents. Topic models like latent Dirichlet allocation, correlated topic models, and dynamic topic models are unsupervised, as only documents are used to identify topics by maximizing the likelihood (or the posterior probability) of the collection. In such modeling frameworks, we hope that the topics will be useful for categorization and are useful when no response is available and we want to infer useful information from the observed documents. However, when the main goal is prediction, a supervised topic modeling framework is beneficial, as jointly modeling the documents and the responses can identify latent topics that can predict the response variables for future unlabeled documents. The sDCTM framework is attractive because it provides a supervised dynamic topic modeling framework to (i) estimate the evolution of the latent process that captures the dynamic evolution of words in the document; and (ii) classify the time series.

We apply the sDCTM method for promoter sequence identification in E. coli DNA sub-sequences. A promoter is a region of DNA where RNA polymerase begins to transcribe a gene, and it is usually located upstream or at the 5′ end of the transcription initiation site in DNA. DNA promoters are proven to be the primary cause of numerous human diseases, including diabetes [18] and Huntington’s disease [19]. Thus, the identification of DNA sequences containing promoters has gained significant attention from researchers in the field of bioinformatics. Several computational methods and tools have been developed to analyze DNA sequences and predict potential promoter regions. These include the classification of promoter DNA sequences using a robust deep learning model, DeePromoter [20], deep learning, and the combination of continuous FastText N-grams [21] and the position-correlation scoring matrix (PCSM) algorithm [22]. We use the sDCTM model to analyze the E. coli DNA sub-sequences by treating each DNA sub-sequence as a document and the presence/absence of promoter regions as the associated class label.

The format of this paper is as follows: In Section 2, we describe the framework of the supervised dynamic correlated topic model, along with details on inference and parameter estimation. Section 3 discusses the simulation study conducted to assess our method. In Section 4, we present the results of applying the sDCTM method for promoter sequence identification in E. coli DNA subsequences and compare our method with the various classification techniques.

2. Supervised Dynamic Correlated Topic Model

Topic models are traditionally developed by treating words as interchangeable to identify semantic themes within each document. Our method aims to develop a family of probabilistic time series models to analyze the evolution of words over time within document collections. We assume that each document, represented by a categorical time series of words, arises from a generative process that includes latent variables. sDCTM provides a supervised framework for time series classification, allowing it to model class labels associated with each word time series. Alternatively, by removing the response component of the generative process, we can derive an unsupervised dynamic correlated topic model (DCTM).

Suppose we have a corpus $\mathcal{C}$ consisting of M documents. We represent the dth document as ${\mathcal{D}}_d=({\mathit{w}}_{d,1},{\mathit{w}}_{d,2},\dots ,{\mathit{w}}_{d,T})$, where ${\mathit{w}}_{d,t}$ corresponds to a word observed at time point t on the dth document for times $t=1,2,\dots ,T$. Each word is represented by a V-dimensional unit (basis) vector, i.e., ${\mathit{w}}_{d,t}={(w_{d,t}^1,\dots ,w_{d,t}^V)}^{\prime }$ such that,

$$\begin{array}{cc}\hfill w_d^u& =\left\{\begin{array}{cc}1\hfill & \mathrm{if}u=v,\hfill \\ 0\hfill & u\ne v,\hfill \end{array}\right.\hfill \end{array}$$

(1)

when ${\mathit{w}}_{d,t}$ corresponds to the vth word from the vocabulary for $t=1,\dots ,T$ and V denote the number of levels associated with the categorical word time series (document). Additionally, let ${\mathit{y}}_d$ be a multinomial response associated with dth document for $d=1,2,\dots ,M$. Each ${\mathit{y}}_d$ is represented by a $C\times 1$ unit (basis) vector, i.e., ${\mathit{y}}_d={(y_{d,1},\dots ,y_{d,C})}^{\prime }$ such that,

$$\begin{array}{cc}\hfill y_d^g& =\left\{\begin{array}{cc}1\hfill & \mathrm{if}g=c,\hfill \\ 0\hfill & g\ne c,\hfill \end{array}\right.\hfill \end{array}$$

(2)

where ${\mathit{y}}_d$ corresponds to the cth class for $c\in \{1,2,\dots C\}$, where C denotes the number of levels associated with the response variable. Suppose J is the number of assumed latent topics for capturing the hidden thematic structure in the corpus; then, ${\mathit{\delta }}_{d,t}$ is a J dimensional vector corresponding to the latent topic structure for the dth document at time t.

In the promoter identification data, we treat each DNA sub-sequence to be a word time series (document) with $V=4$ levels (indicating nucleotides $a,g,c,$ and t). The response variable ${\mathit{y}}_d$ for $d=1,2,\dots ,M$ indicates the presence/absence of a promoter region with $C=2$ levels. The number of assumed topics J in the sDCTM model capture the hidden patterns within the observed DNA sub-sequences. Under the sDCTM framework, the dth document (DNA sub-sequence) ${\mathcal{D}}_d$ and its associated class label (presence/absence of a promoter) ${\mathit{y}}_d$ for $d=1,2,\dots ,M$ arises from the following generative process. For $d=1,2,\dots ,M$,

• For $t=1,2,\dots ,T$
  • Choose ${\mathit{\delta }}_{d,t}\mid {\mathit{\delta }}_{d,t-1}\sim N(\mathbf{\Phi }{\mathit{\delta }}_{d,t-1},\mathbf{\Sigma })$.
  • Choose a topic ${\mathit{Z}}_{\{d,t\}}\mid {\mathit{\delta }}_{d,t}\sim Mult(1,f\left({\mathit{\delta }}_{d,t}\right))$, where
  • $f\left({\delta }_{d,t,j}\right)={\displaystyle \frac{exp\left({\delta }_{d,t,j}\right)}{{\sum }_{l=1}^{J}exp\left({\delta }_{d,t,l}\right)}}$ for $j=1,2,\dots ,J$.
  • Choose a word ${\mathit{w}}_{d,t}\mid \{{\mathit{Z}}_{\{d,t\}},\mathit{\beta }\}\sim Mult(1,{\mathit{\beta }}_{{\mathit{Z}}_{\{\mathbf{d},\mathbf{t}\}}})$.
• Draw class label ${\mathit{y}}_d\mid {\mathit{Z}}_{d,1:T},\mathit{\eta }\sim softmax({\overline{\mathit{Z}}}_d,\mathit{\eta })$, where

  $${\overline{\mathit{Z}}}_d={\displaystyle \frac{1}{T}}{\sum }_{t=1}^T{\mathit{Z}}_{\{d,t\}},$$

  is the topic frequencies for the dth document. The per-word topic indicator for each word ${\mathit{w}}_{d,t}$ is represented by ${\mathit{Z}}_{d,t}$ for $t=1,\dots ,T$ and $d=1,\dots ,M$. The model parameters include the latent VAR(1) parameter, the $J\times J$ matrices $\mathbf{\Phi }$ and $\mathbf{\Sigma }$, the $J\times V$ matrix of word probabilities $\mathit{\beta }$, and the $J\times C$ matrix of regression coefficients $\mathit{\eta }$. In Section 2.1, we discuss approximate inference techniques based on variational methods and construct the lower bound (Constructing the Lower Bound) to estimate the variational parameters, which can be used to approximate the posterior. In Section 2.2, we discuss the variational EM algorithm to estimate the model parameters. We also discuss simulated annealing (Section 2.2.1), a probabilistic technique employed in optimizing problems to estimate certain model parameters, along with details on selecting initial values (Section 2.2.2) for using this optimization technique.

2.1. Approximate Inference

Given the dth document ${\mathcal{D}}_d$ and the associated response ${\mathit{y}}_d$ for $d=1,2,\dots ,M$, the posterior distribution of the latent variables $({\mathit{\delta }}_{d,1:T},{\mathit{Z}}_{d,1:T})$ is    

$$\begin{array}{ccc}\hfill p({\mathit{\delta }}_{d,1:T},{\mathit{Z}}_{d,1:T}|{\mathcal{D}}_d,{\mathit{y}}_d,\mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta })& =& {\displaystyle \frac{p({\mathit{\delta }}_d,{\mathit{Z}}_d,{\mathcal{D}}_d,{\mathit{y}}_d\mid \mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta })}{p({\mathcal{D}}_d,{\mathit{y}}_d\mid \mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta })}},\hfill \end{array}$$

(3)

for $d=1,2,\dots ,M$. The numerator term in Equation (3), $p({\mathit{\delta }}_d,{\mathit{Z}}_d,{\mathcal{D}}_d,{\mathit{y}}_d\mid \mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta })$, corresponds to the joint distribution of the latent variables $({\mathit{\delta }}_{d,1:T},{\mathit{Z}}_{d,1:T})$ and the observed document–response pair $({\mathcal{D}}_d,{\mathit{y}}_d)$ and is given by

$$\begin{array}{ccc}\hfill p({\mathit{\delta }}_d,{\mathit{Z}}_d,{\mathcal{D}}_d,{\mathit{y}}_d\mid \mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta })& =& \prod _{t=1}^T(p\left({\mathit{w}}_{d,t}\right|{\mathit{Z}}_{d,t},\mathit{\beta })\times p\left({\mathit{Z}}_{d,t}\right|{\mathit{\delta }}_{d,t})\times \hfill \\ & & p({\mathit{\delta }}_{d,t}\mid {\mathit{\delta }}_{d,t-1},\mathbf{\Phi },\mathbf{\Sigma }))\times p({\mathit{y}}_d\mid {\mathit{Z}}_{d,1:T},\mathit{\eta }),\hfill \end{array}$$

for $d=1,2,\dots ,M$. This joint distribution of the latent variables and the document–response pair can be factorized due to the sDCTM framework. The denominator term in Equation (3), i.e., $p({\mathcal{D}}_d,{\mathit{y}}_d\mid \mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta })$, represents the joint distribution of the dth document–response pair $({\mathcal{D}}_d,{\mathit{y}}_d)$ and is given by

$$\begin{array}{ccc}\hfill p({\mathcal{D}}_d,{\mathit{y}}_d\mid \mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta })& =& \int \left(\sum _{{\mathit{Z}}_{d,1:T}}\right(\prod _{t=1}^{T}p\left({\mathit{w}}_{d,t}\right|{\mathit{Z}}_{d,t},\mathit{\beta })\times p\left({\mathit{Z}}_{d,t}\right|{\mathit{\delta }}_{d,t})\hfill \\ & & p({\mathit{\delta }}_{d,t}\mid {\mathit{\delta }}_{d,t-1},\mathbf{\Phi },\mathbf{\Sigma }))\times p({\mathit{y}}_d\mid {\mathit{Z}}_{d,1:T},\mathit{\eta }))d{\mathit{\delta }}_{d,1:T},\hfill \end{array}$$

for $d=1,2,\dots ,M$.

Computing the posterior distribution in Equation (3) is not analytically tractable. Hence, we use variational methods that consider a simple family of distributions over the latent variables, indexed by free variational parameters. The variational parameters are estimated to minimize the Kullback–Leibler (KL) divergence [23] between the variational distribution and the true posterior distribution. The latent variables in the sDCTM framework include the per-word topic structure ${\mathit{\delta }}_{d,t}$ and the per-word topic assignment ${\mathit{Z}}_{d,t}$ for $t=1,2,\dots T$ and $d=1,2,\dots M$. We define the approximate variational posterior for the dth document as

$$q({\mathit{\delta }}_{d,1:T},{\mathit{Z}}_{d,1:T})=q({\mathit{\delta }}_{d,1},{\mathit{\delta }}_{d,2},\dots ,{\mathit{\delta }}_{d,T}\mid {\widehat{\mathit{\delta }}}_{d,1},{\widehat{\mathit{\delta }}}_{d,2},\dots ,{\widehat{\mathit{\delta }}}_{d,T},{\widehat{\sigma }}^2)\times \prod _{t=1}^{T}q({\mathit{Z}}_{d,t}\mid {\mathit{\gamma }}_{d,t}),$$

(4)

for $d=1,2,\dots ,M$, where ${\mathit{Z}}_{d,t}\mid {\mathit{\gamma }}_{d,t}$ is $Mult(1,{\mathit{\gamma }}_{d,t})$, and we obtain $q({\mathit{\delta }}_{d,1:T}\mid {\widehat{\mathit{\delta }}}_{d,1:T})$ using a dynamic model with Gaussian “variational observations” $\{{\widehat{\mathit{\delta }}}_{d,1},$${\widehat{\mathit{\delta }}}_{d,2},\dots ,{\widehat{\mathit{\delta }}}_{d,T}\}$. This dynamic model is defined using a variational Kalman filter, where the variational parameters ${\widehat{\mathit{\delta }}}_{d,1:T}$ are treated as observations. Using the variational distribution, we form a variational state space model as follows. For $t=1,2,\dots T$,

• Observation Equation:

$${\widehat{\mathit{\delta }}}_{d,t}\mid {\mathit{\delta }}_{d,t}\sim N({\mathit{\delta }}_{d,t},{\widehat{\sigma }}^2\mathit{I}).$$

(5)

• State Equation:

$${\mathit{\delta }}_{d,t}\mid {\mathit{\delta }}_{d,t-1}\sim N(\mathbf{\Phi }{\mathit{\delta }}_{d,t-1},\mathbf{\Sigma }).$$

(6)

The Gaussian variational forward filtering distribution $p({\mathit{\delta }}_{d,t}\mid {\widehat{\mathit{\delta }}}_{d,1:t})$ using standard Kalman filter calculations is characterized as follows. For $t=1,2,\dots ,T$,

$$\begin{array}{ccc}\hfill {\mathit{\delta }}_{d,t}\mid {\widehat{\mathit{\delta }}}_{d,1:t}& \sim & N_J({\mathit{m}}_{d,t},{\mathit{V}}_{d,t}),\hfill \\ \hfill {\mathit{m}}_{d,t}& =& (\mathit{I}-{\mathit{K}}_{d,t})\mathbf{\Phi }{\mathit{m}}_{d,t-1}+{\mathit{K}}_{d,t}{\widehat{\mathit{\delta }}}_{d,t},\hfill \\ \hfill {\mathit{V}}_{d,t}& =& (\mathit{I}-{\mathit{K}}_{d,t})[\mathbf{\Phi }{\mathit{V}}_{d,t-1}{\mathbf{\Phi }}^{\prime }+\mathbf{\Sigma }],\hfill \end{array}$$

where

$${\mathit{K}}_{d,t}=[\mathbf{\Phi }{\mathit{V}}_{d,t-1}{\mathbf{\Phi }}^{\prime }+\mathbf{\Sigma }]{(\mathbf{\Phi }{\mathit{V}}_{d,t-1}{\mathbf{\Phi }}^{\prime }+\mathbf{\Sigma }+{\widehat{\sigma }}^2\mathit{I})}^{-1},$$

is the Kalman gain matrix and the initial conditions are specified by ${\mathit{m}}_{d,0}$ and ${\mathit{V}}_{d,0}$.

Similarly, the Gaussian variational backward smoothing distribution $p({\mathit{\delta }}_{d,t-1}\mid {\widehat{\mathit{\delta }}}_{d,1:T})$ using standard Kalman smoothing calculations is characterized as follows. For $t=T,$ $T-1,\dots ,1$,

$$\begin{array}{ccc}\hfill {\mathit{\delta }}_{d,t-1}\mid {\widehat{\mathit{\delta }}}_{d,1:T}& \sim & N_J({\tilde{\mathit{m}}}_{d,t-1},{\tilde{\mathit{V}}}_{d,t-1}),\hfill \\ \hfill {\tilde{\mathit{m}}}_{d,t-1}& =& (\mathit{I}-{\mathit{J}}_{d,t-1}\mathbf{\Phi }){\mathit{m}}_{d,t-1}+{\mathit{J}}_{d,t-1}{\mathit{m}}_{d,t},\hfill \\ \hfill {\tilde{\mathit{V}}}_{d,t-1}& =& {\mathit{V}}_{d,t-1}+{\mathit{J}}_{d,t-1}[{\tilde{\mathit{V}}}_{d,t}-\mathbf{\Phi }{\mathit{V}}_{d,t-1}{\mathbf{\Phi }}^{\prime }-\mathbf{\Sigma }]{\mathit{J}}_{d,t-1}^{\prime },\hfill \end{array}$$

where

$${\mathit{J}}_{d,t-1}={\mathit{V}}_{d,t-1}{\mathbf{\Phi }}^{\prime }{[\mathbf{\Phi }{\mathit{V}}_{d,t-1}{\mathbf{\Phi }}^{\prime }+\mathbf{\Sigma }]}^{-1},$$

and the initial conditions are specified by ${\mathit{m}}_{d,T}={\tilde{\mathit{m}}}_{d,T}$ and ${\mathit{V}}_{d,T}={\tilde{\mathit{V}}}_{d,T}$.

Using the Kalman filter equations, the approximate variational posterior for the dth document is given by

$$q({\mathit{\delta }}_{d,1:T},{\mathit{Z}}_{d,1:T})=q({\mathit{\delta }}_{d,t}\mid {\widehat{\mathit{\delta }}}_{d,1:T},{\widehat{\sigma }}^2)\times \prod _{t=1}^{T}q({\mathit{Z}}_{d,t}\mid {\mathit{\gamma }}_{d,t}),$$

(7)

where ${\mathit{Z}}_{d,t}\mid {\mathit{\gamma }}_{d,t}$ is $Mult(1,{\mathit{\gamma }}_{d,t})$ and ${\mathit{\delta }}_{d,t}\mid {\widehat{\mathit{\delta }}}_{d,1:T},{\widehat{\sigma }}^2\sim N({\tilde{\mathit{m}}}_{d,t},{\tilde{\mathit{V}}}_{d,t})$ for $t=1,2,\dots ,T$ and $d=1,2,\dots ,M.$

Constructing the Lower Bound

Given the variational distribution defined in Equation (4), our goal is to estimate the variational parameters ${\mathit{\gamma }}_{d,t}$, ${\widehat{\mathit{\delta }}}_{d,t}$, and ${\widehat{\sigma }}^2$ for $t=1,2,\dots ,T$ and $d=1,2,\dots ,M$ in order to minimize the KL divergence between the variational distribution $q(.)$ defined in Equation (4) and the true posterior $p(.)$ defined in Equation (3). This optimization problem of minimizing the KL divergence is equivalent to maximizing the evidence lower bound (ELBO) [24] defined below.

$$\begin{array}{ccc}\hfill logp({\mathcal{D}}_d,{\mathit{y}}_d|\mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta })& =& log\int \sum _{{\mathit{Z}}_{d,1:T}}p({\mathit{Z}}_{d,1:T},{\mathit{\delta }}_{d,1:T},{\mathcal{D}}_d,{\mathit{y}}_d\mid \mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta })d{\mathit{\delta }}_{d,1:T},\hfill \\ & =& log\int \sum _{{\mathit{Z}}_{d,1:T}}{\displaystyle \frac{p({\mathit{Z}}_{d,1:T},{\mathit{\delta }}_{d,1:T},{\mathcal{D}}_d,{\mathit{y}}_d\mid \mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta })}{q({\mathit{\delta }}_{d,1:T},{\mathit{Z}}_{d,1:T})}}\times \hfill \\ & & q({\mathit{\delta }}_{d,1:T},{\mathit{Z}}_{d,1:T})d{\mathit{\delta }}_{d,1:T}\hfill \\ & \ge & E_q\left[logp({\mathit{Z}}_{d,1:T},{\mathit{\delta }}_{d,1:T},{\mathcal{D}}_d,{\mathit{y}}_d\mid \mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta })\right]-\hfill \\ & & E_q\left[logq({\mathit{\delta }}_{d,1:T},{\mathit{Z}}_{d,1:T})\right],\hfill \\ & =& L({\widehat{\mathit{\delta }}}_{d,1:T},{\widehat{\sigma }}^2,{\mathit{\gamma }}_d;\mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta },{\mathcal{D}}_d,{\mathit{y}}_d).\hfill \end{array}$$

We estimate the variational parameters ${\mathit{\gamma }}_{d,t}$, ${\widehat{\mathit{\delta }}}_{d,t}$, and ${\widehat{\sigma }}^2$ for $t=1,2,\dots ,T$ and $d=1,2,\dots ,M$ by maximizing the ELBO for approximate inference. In Appendix A, we derive the ELBO and provide the update equations in order to estimate the variational parameters. We estimate the variational parameter ${\mathit{\gamma }}_{d,t}$ using a fixed-point update, ${\widehat{\sigma }}^2$ using a constrained optimization using the DBCPOL routine available in the IMSL library [25] for Fortran 77, and  ${\widehat{\mathit{\delta }}}_{d,1:T}$ using simulated annealing, which we describe in Section 2.2.1.

2.2. Parameter Estimation

In this section, we present a method for parameter estimation. In particular, given the corpus $\mathcal{C}$ with M documents and their associated responses denoted by ${(\mathcal{D},\mathit{y})}_{1:M}$, we wish to estimate the model parameters ${\mathbf{\Phi }}^{J\times J},{\mathbf{\Sigma }}^{J\times J},{\mathit{\beta }}^{J\times V}$, and ${\mathit{\eta }}^{J\times C}$ in order to maximize the log likelihood of the data given by

$$l(\mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta }\mid {(\mathcal{D},\mathit{y})}_{1:M})=\sum _{d=1}^{M}logp({\mathcal{D}}_d,{\mathit{y}}_d|\mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta }).$$

(8)

Because the log likelihood is analytically intractable, we consider a tractable lower bound on the log likelihood by summing the ELBO for $logp({\mathcal{D}}_d,{\mathit{y}}_d|\mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta })$, defined in Section 2.1 over M documents. We estimate the model parameters via an alternating variational EM (VEM) procedure [26] described below:

• E-Step: For each document, we find the optimizing values of the variational parameters described in Section 2.1.
• M-Step: Maximize the resulting lower bound on the log likelihood with respect to the model parameters.

In Appendix A, we derive the lower bound on the log likelihood defined in Equation (8) and provide the updated equations in order to estimate the model parameters. We estimate model parameter $\mathit{\beta }$ using a fixed-point update. The model parameters ${\mathbf{\Phi }}^{J\times J}$ (with the stationarity condition), $\mathbf{\Sigma }$ (with the positive definite condition), and $\mathit{\eta }$ are estimated using a randomized search optimization technique, simulated annealing, which we describe in the next section.

For parameter estimation, we use frequentist methods to estimate the unknown parameters of the sDCTM model. As an alternative, one can set up a Bayesian model for parameters estimation in the sDCTM model by employing the Minnesota prior on $\mathbf{\Phi }$ [27], inverse Wishart or Lewandowski–Kurowicka–Joe (LKJ) prior on $\mathbf{\Sigma }$, Dirichlet prior on $\mathit{\beta }$, and multivariate normal prior on $\mathit{\eta }$.

2.2.1. Simulated Annealing

Simulated annealing (SA) is a probabilistic technique employed for optimizing problems to find a good approximation to the global optimum of a given function [28,29]. It is often used when the search space is discrete and is inspired by the annealing technique in metallurgy, which involves the heating and controlled cooling of a material to increase the size of its crystals and reduce their defects. The algorithm starts with a randomly generated solution and iteratively explores its neighboring states to find better solutions. The acceptance probability mechanism considers solutions that are worse than the current one in order to avoid getting stuck in a local optimum. Algorithm 1 presents a structured pseudocode to execute the simulated annealing technique for optimization problems, and Table 1 describes the initial parameters.

Algorithm 1 Simulated Annealing for Optimization

procedure SIMULATED ANNEALING($\mathit{x},f$)   ${\mathit{x}}_{\mathrm{opt}}=\mathit{x}$ and $f_{\mathrm{opt}}=f$, $count=0$   repeat    for $N_T$ times do      for $N_v$ times do        $x_i^{\prime }=x_i+r\times v_i$, $r_i\sim U(-1,1)$ for $i=1,2,\dots ,n$        $f^{\prime }=\mathrm{CALCULATE}{f}^{\prime }\left({\mathit{x}}^{\prime }\right)$        if $f^{\prime }<f$ then          $\mathit{x}={\mathit{x}}^{\prime }$ and $f=f^{\prime }$          $count=count+1$        end if        if $f^{\prime }<f_{\mathrm{opt}}$ then          $\mathit{x}={\mathit{x}}^{\prime }$ and $f=f^{\prime }$          ${\mathit{x}}_{\mathrm{opt}}={\mathit{x}}^{\prime }$ and $f_{\mathrm{opt}}=f^{\prime }$        end if        if $f^{\prime }\ge f$ then          $p=exp\left(\frac{f-f^{\prime }}{T}\right)$ and $p^{\prime }\sim U(0,1)$          if $p>p^{\prime }$ then            $\mathit{x}={\mathit{x}}^{\prime }$ and $f=f^{\prime }$          end if        end if        Adjust $\mathit{v}$ such that $50\%$ of the moves are accepted        Set $ratio=\frac{count}{N_v}$        if $ratio\ge 0.6$ then          $v_i=v_i\times \left(1+\frac{c\times (ratio-0.6)}{0.4}\right)$ for $i=1,2,\dots ,n$        end if        if $ratio\le 0.4$ then          $v_i=\frac{v_i}{\left(1+\frac{c\times (0.4-ratio)}{0.4}\right)}$ for $i=1,2,\dots ,n$        end if      end for      if $|f-f^{\prime }|<ϵ$ and $|f_{\mathrm{opt}}^{\mathrm{old}}-f_{\mathrm{opt}}|<ϵ$ then        REPORT ${\mathit{x}}_{\mathrm{opt}},f_{\mathrm{opt}}$      else        Set $\mathit{x}={\mathit{x}}_{\mathrm{opt}}$ and $T=r_T\times T$      end if     end for   until convergence or N times end procedure

Table 1. Initial parameters for simulated annealing.

Parameter	Description
$\mathit{x}$	n dimensional initial vector.
$\mathit{v}$	n dimensional initial step length vector.
f	Objective function to minimize.
$ϵ$	Convergence criteria.
T	Temperature
$r_T$	Temperature reduction factor.
N	Maximum number of function evaluations.
$N_T$	Number of function evaluations before T adjustment.
$N_v$	Number of function evaluations before $\mathit{v}$ adjustment.
$count$	Calculate the number of acceptances.
c	Controls how fast $\mathit{v}$ adjusts.

2.2.2. Selecting Initial Values of the Model Parameters

We use the SA technique, one of the top methods for non-derivative-based random search optimization, to estimate the model parameters $\mathit{\eta }$, $\mathbf{\Phi }$, and $\mathbf{\Sigma }$ in the sDCTM framework. To ensure that the optimization works effectively, it is important to select appropriate initial values. We describe the steps to select initial values for $\mathit{\eta }$, $\mathbf{\Phi }$, and $\mathbf{\Sigma }$ below.

• Step 1. We select an initial search space within ${\mathbb{R}}^n$, where n represents the number of variables involved in the estimation (for instance, $n=C\times J$ for $\mathit{\eta }$ and $n=J\times J$ for $\mathbf{\Phi }$ and $\mathbf{\Sigma }$). The initial search space is chosen based on our belief of where the estimates are likely to be found. Then, we divide this search space into $2^n$ smaller subspaces.
• Step 2. For $\mathbf{\Phi }$ and $\mathbf{\Sigma }$, we evaluate the optimization function at the midpoint within each of the subspaces and choose the subspace with the highest (or lowest) value of the function based on the optimization problem as our new search space. In cases where multiple subspaces optimize the function, we consider each of them in the next step for further exploration. In the sDCTM framework, for $\mathit{\eta }$, we consider the training accuracy as our optimization (maximization) function, as $\mathit{\eta }$ plays a crucial role in predicting the response variable. For model parameters $\mathbf{\Phi }$ and $\mathbf{\Sigma }$, we consider the lower bound on the log likelihood as the optimization (maximization) function.
• Step 3. We repeat steps 1 and 2 until no significant improvement in the optimization function value is seen.
• Step 4. If a single subspace is chosen as a search space to select the initial values for optimization, we choose our starting values from this subspace and estimate the parameters using the SA technique. If there are multiple subspaces selected as the initial search space, we choose the initial values from each of these subspaces and run the SA to obtain the parameter estimates. We choose the final parameter estimates from the search space yielding the highest (or lowest) value of the function based on the optimization problem. The sDCTM model is implemented using a standalone code in Fortran 77 [30]. The code for model estimation is posted on https://github.com/NamithaVionaPais/sDTCM (accessed on 10 June 2024).

3. Simulation Study

To evaluate the performance of our model, we conducted a simulation study. We generated a dataset consisting of $M=120$ documents, where each document is represented by a word time series of length $T=100$. The vocabulary size was set to $V=6$, and the documents were divided into $C=2$ classes. Each word time series was governed by an underlying latent topic structure with $J=3$ topics. Our model was evaluated using a six-fold cross-validation with $M_{Tr}=100$ train and $M_{Tst}=20$ test documents. We conducted our analysis in Fortran 77. Given the observed word time series from M documents, we fitted the sDCTM model to estimate the model parameters, $\mathit{\beta }$, $\mathbf{\Sigma }$, $\mathbf{\Phi }$, and $\mathit{\eta }$. As the model parameters are matrices, we assessed the estimation error using the squared Frobenius norm. The squared Frobenius norm lies between two matrices, such as $\mathit{M}$ and $\mathit{N}$, and is defined as

$$d(\mathit{M},\mathit{N})=\mathrm{tr}\left\{{(\mathit{M}-\mathit{N})}^{\prime }(\mathit{M}-\mathit{N})\right\}$$

(9)

The average squared Frobenius norm (over the six-fold cross-validation) for each of the model parameters is shown in Table 2. The low values of the squared Frobenius norm on the model parameters suggest that we are able to estimate the matrices well.

Table 2. Average squared Frobenius norm between the true and estimated model parameters using the sDCTM model on the simulated dataset.

Parameter	Squared Frobenius Norm
$\mathbf{\Phi }$	$0.5270$
$\mathbf{\Sigma }$	$0.3697$
$\mathit{\beta }$	$0.1622$
$\mathit{\eta }$	$0.2385$

We used the estimated model parameter $\mathit{\eta }$ and the variational parameter ${\mathit{\gamma }}_{d,t}$ for $t=1,2,\dots ,T$ and $d=1,2,\dots ,M_{Tr}$ to predict the response associated with the training data containing $M_{Tr}=100$ documents as follows.

$$c_d=\underset{c\in \{1,\dots C\}}{\mathrm{argmax}}{\mathit{\eta }}_c^T{\overline{\mathit{\gamma }}}_d,$$

(10)

for $d=1,2,\dots ,M_{Tr}$ and ${\overline{\mathit{\gamma }}}_d={\displaystyle \frac{T}{{\sum }_{t=1}^T}}{\mathit{\gamma }}_{d,t}$. Table 3 shows the confusion matrix obtained on train data for one of the cross-validations. We were able to achieve a training accuracy of $100\%$, and the average training accuracy across all $k=6$ cross-validation datasets was also $100\%$.

Table 3. Confusion matrix obtained from the sDCTM model on the test data of $M=20$ documents based on a simulation.

	Actual
Predicted	Class 1	Class 2
Class 1	80	0
Class 2	0	20

While classifying the test data, we estimated the variational parameters on the test documents given the estimated model parameters using variational inference. However, because we assume that we do not know the true label in the test documents, we replace the terms in the likelihood function associated with the response variable by the pseudo-label. The pseudo-label assigned to a test document is the class label associated with the nearest train document. We used the hamming distance to calculate the distance between the test and train sequence. Given the word time series, the associated pseudo-label, and the model parameters estimated using the train data, we estimated the variational parameters for each test document. We then obtained the test predictions using Equation (10). Table 4 shows the confusion matrix obtained on the test data for one of the cross-validation test datasets with a test accuracy of $80\%$. The average test accuracy across all $k=6$ cross-validation datasets was $70.83\%$.

Table 4. Confusion matrix obtained from the sDCTM model on the test data in a simulation.

	Actual
Predicted	Class 1	Class 2
Class 1	9	0
Class 2	4	7

The model parameter, denoted as $\mathit{\beta }$, provides an estimate of how words are distributed across a set of J latent topics. Figure 1 illustrates the proportions of words across each of the $J=3$ latent topics. We observed that Word 1 was highly probable within Topic 1, Words 3, 4, and 6 were highly probable within Topic 2, and Word 4 was highly probable within Topic 3.

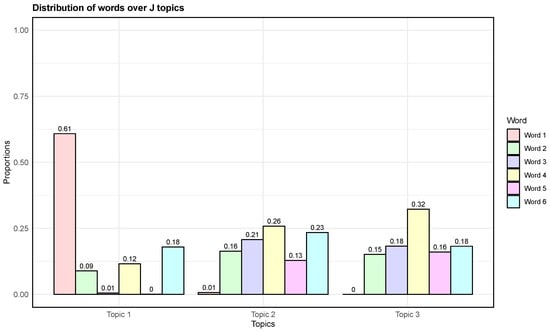
Figure 1. Estimated distribution of words over each of the $J=3$ latent topics on the simulated data.

4. Application for Promoter Sequence Identification in E. coli DNA Sub-Sequences

Proteins are one of the most important classes of biological molecules, being the carriers of the message contained in the DNA. An important process involved in the synthesis of proteins is called transcription. During transcription, a single-stranded RNA molecule, called messenger RNA, is synthesized (using the complementarity of the bases) from one of the strands of DNA corresponding to a gene (a gene is a segment of the DNA that codes for a type of protein). This process begins with the binding of an enzyme called RNA polymerase to a certain location on the DNA molecule. This exact site, which determines which of the two strands of DNA will be a transcript and in which direction, is recognized by the RNA polymerase due to the existence of certain regions of DNA placed near the transcription start site of a gene, called promoters. Because determining the promoter region in the DNA is an important step in the process of detecting genes, the problem of promoter identification is of major importance within the field of bioinformatics.

We considered a dataset of 106 E. coli DNA sub-sequences that is publicly available at https://archive.ics.uci.edu/dataset/67/molecular+biology+promoter+gene+sequences (accessed on 12 March 2023), among which 53 DNA sub-sequences contain promoters and the remaining 53 DNA sub-sequences do not contain promoters. Each sub-sequence consists of 57 nucleotides, represented by the four nucleotide bases: adenine (a), guanine (g), cytosine (c), and thymine (t). Given the two sets of DNA sub-sequences, with and without the presence of promoter regions, we used sDCTM to uncover the hidden patterns or motifs that could serve as markers for promoter presence to classify the sub-sequences. A detailed data description is provided in [31].

We present the results of the sDCTM model applied to analyze the E. Coli DNA sub-sequences. We treated each DNA sub-sequence as a document and the presence/absence of promoter regions as the associated class label. Each word in the document was represented by the nucleotide observed at that position in the sub-sequence. We divided the data into an 80–20 train–test split in order to assess the model performance. We trained the model on data with $M_{tr}=86$ (number of train DNA sub-sequences) and set $T=57$ (length of each DNA sub-sequence), $V=4$ (number of unique nucleotide levels), and $C=2$ (indicating the levels of the response variable). To choose the number of topics J, we ran the model for different values of J and chose J based on the highest test accuracy. We set the number of latent topics as $J=3$. The confusion matrices obtained on the train and test data with $M_{Tst}=20$ (number of test DNA sub-sequences) using the sDCTM model are shown in Table 5 and Table 6. We were able to achieve a training accuracy of $100\%$ and a test accuracy of $90\%$.

Table 5. Confusion matrix obtained from the sDCTM model on the promoter identification train data with $M=86$ DNA sub-sequences.

	Actual
Predicted	Promoter Presence	Promoter Absence
Promoter presence	43	0
Promoter absence	0	43

Table 6. Confusion matrix obtained from the sDCTM model on the promoter identification test data with $M=20$ DNA sub-sequences.

	Actual
Predicted	Promoter Presence	Promoter Absence
Promoter presence	10	0
Promoter absence	2	8

The distribution of nucleotides accross the three topics identified by the sDCTM model is shown in Figure 2. We observed that nucleotide levels a, c, and g were highly probable within Topic 1, nucleotide level t was highly probable within Topic 2, and nucleotide level a was highly probable within Topic 3. In addition, based on the model predictions, we also constructed a sequence logo plot [32] to identify the diversity of sequences between the two predicted groups. The sequence logo plot based on the train model predictions are shown in Figure 3. We can see that that the promoter presence plot demonstrated significantly higher conservation at various positions compared with the promoter absence plot. The higher bits values in the promoter presence plot highlight critical motifs essential for promoter activity. In contrast, the promoter absence plot showed much smaller variability, suggesting fewer conserved elements.

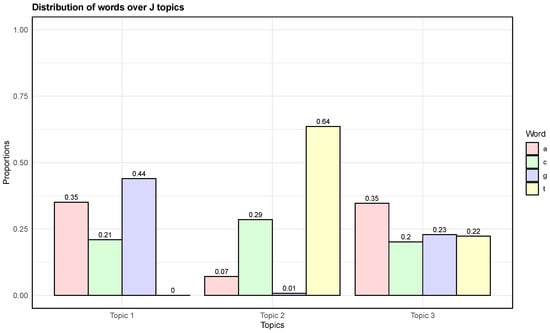
Figure 2. Estimated distribution of $V=4$ nucleotides over each of the $J=3$ latent topics.

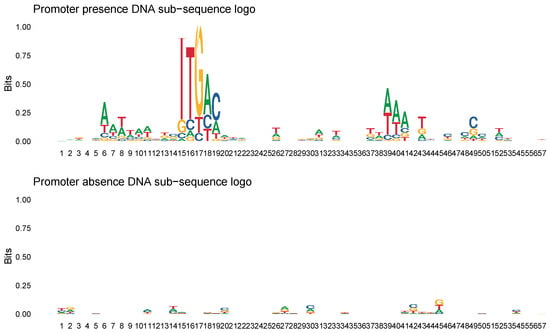
Figure 3. Sequence logo plot based on model predictions on the train data.

Comparison with Other Methods

We compared our sDCTM model with existing classification techniques, such as SVM, k-NN, and classification trees [33]. We used the k-NN classification technique, which is a popular approach used for sequence classification [10] on the observed data. We compared our approach to popular machine learning techniques like SVM and classification trees on the extracted features from the DNA sequence. We used the Haar wavelet transform and the simplest discrete wavelet transform (DWT) to extract features from the observed time series and build a classification model based on these features. We implemented the k-NN classification technique using the R package class [34], which identifies $K=5$ nearest neighbors (in Euclidean distance) to classify the train and test data. We used the R package wavelets [35] to extract the DWT (with Haar filter) coefficients. The classification tree was implemented using the R package party [36], and the SVM was implemented using the R package e1071 [37]. We ran each of these methods using an 80–20 train–test split to assess model performance. The train and test accuracies are shown in Table 7. In comparison with the the other classification techniques, sDCTM performed better on both the train and test data.

Table 7. Comparing accuracy using the sDCTM, k-NN, classification tree, and SVM methods on the train and test data.

Method	Train Accuracy	Test Accuracy
sDCTM	100%	90%
k-NN	84.8%	85%
Classification tree	87.2%	85%
SVM	100%	55%

5. Discussion

In this paper, we introduced the sDCTM model framework, which aims to classify categorical time series by dynamically modeling the underlying latent topics that capture the hidden thematic structure of the time series collection. We demonstrated the applicability of our method to real data by applying it to the promoter identification data to classify E. coli DNA sub-sequences based on promoter presence. Using sDCTM, we estimated the dynamic latent topic structure that serves as markers for promoter presence in a DNA sub-sequence and classify the sub-sequences. Among the $J=3$ latent topics obtained using sDCTM, we observed that nucleotide levels a, c, and g were highly probable within Topic 1, nucleotide level t was highly probable within Topic 2, and nucleotide level a was highly probable within Topic 3. In addition, the logoplot based on the model predictions showed higher conservation at various positions in DNA sub-sequences with predicted promoter presence in comparison with DNA sub-sequences with predicted promoter absence. We compared our method with the k-NN, SVM, and classification tree method on a train–test data setup. Our comparative study results indicated that the sDCTM model performed better than the other classification techniques in both training and test datasets. This indicates that the estimated underlying latent topic structure captured by the sDCTM model is able to identify the promoter presence/absence in a DNA sub-sequence better in comparison with the other classification approaches. An extension of the sDCTM model accommodating word time series of varying lengths can be derived as a part of future work.

Appendix A.1. ELBO

$$\begin{array}{ccc}\hfill L({\widehat{\mathit{\delta }}}_{d,1:T},{\widehat{\sigma }}^2,{\mathit{\gamma }}_d;\mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta })& =& E_q\left[logp({\mathit{Z}}_{d,1:T},{\mathit{\delta }}_{d,1:T},{\mathcal{D}}_d,{\mathit{y}}_d\mid \mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta })\right]-\hfill \\ & & E_q\left[logq({\mathit{\delta }}_{d,1:T},{\mathit{Z}}_{d,1:T})\right]\hfill \\ & =& \sum _{t=1}^T{E}_q\left[logp({\mathit{w}}_{d,t}\mid {\mathit{Z}}_{d,t},\mathit{\beta })\right]+\hfill \\ & & \sum _{t=1}^T{E}_q\left[logp({\mathit{Z}}_{d,t}\mid {\mathit{\delta }}_{d,t})\right]\hfill \\ & & +\sum _{t=1}^T{E}_q\left[logp({\mathit{\delta }}_{d,t}\mid {\mathit{\delta }}_{d,t-1},\mathbf{\Phi },\mathbf{\Sigma })\right]+\hfill \\ & & E_q\left[logp({\mathit{y}}_d={\mathbf{1}}_c\mid {\mathit{Z}}_{d,1:T},\mathit{\eta })\right]\hfill \\ & & -\sum _{t=1}^T{E}_q\left[logq({\mathit{\delta }}_{d,t}\mid {\widehat{\mathit{\delta }}}_{d,1:T},{\widehat{\sigma }}^2)\right]-\sum _{t=1}^T{E}_q\left[logq({\mathit{Z}}_{d,t}\mid {\mathit{\gamma }}_{d,t})\right]\hfill \\ & \ge & \sum _{t=1}^T\sum _{j=1}^J\sum _{i=1}^V{\mathit{\gamma }}_{dtj}{w}_{dt}^{i}log{\mathit{\beta }}_{ji}\hfill \\ & & +\sum _{t=1}^T\sum _{j=1}^J{\mathit{\gamma }}_{dtj}\left[{\tilde{m}}_{dtj}-log\left(\sum _{l=1}^{J}exp[{\tilde{m}}_{dtl}+{\displaystyle \frac{{\tilde{v}}_{dtl}}{2}}]\right)\right]\hfill \\ & & -{\displaystyle \frac{TJ}{2}}log\left(2\pi \right)-{\displaystyle \frac{T}{2}}log\left|\mathbf{\Sigma }\right|-{\displaystyle \frac{1}{2}}\sum _{t=1}^{T}tr\left[{\mathbf{\Sigma }}^{-1}({\tilde{\mathit{V}}}_{dt}+\mathbf{\Phi }{\tilde{\mathit{V}}}_{dt}{\mathbf{\Phi }}^{\prime })\right]\hfill \\ & & -{\displaystyle \frac{1}{2}}\sum _{t=1}^T{({\tilde{\mathit{m}}}_{dt}-\mathbf{\Phi }{\tilde{\mathit{m}}}_{dt-1})}^{\prime }{\mathbf{\Sigma }}^{-1}({\tilde{\mathit{m}}}_{dt}-\mathbf{\Phi }{\tilde{\mathit{m}}}_{dt-1})\hfill \\ & & +{\displaystyle \frac{1}{T}}{\mathit{\eta }}_c^T{\mathit{\gamma }}_{dt}-log\left(\sum _{l=1}^C\prod _{t=1}^T\left(\sum _{j=1}^J{\mathit{\gamma }}_{dtj}exp\left({\displaystyle \frac{1}{T}}{\mathit{\eta }}_{lj}\right)\right)\right)\hfill \\ & & +{\displaystyle \frac{TJ}{2}}log\left(2\pi \right)+{\displaystyle \frac{1}{2}}\sum _{t=1}^{T}log\left|{\tilde{\mathit{V}}}_{d,t}\right|+{\displaystyle \frac{TJ}{2}}-\sum _{t=1}^T\sum _{j=1}^J{\mathit{\gamma }}_{dtj}log\left({\mathit{\gamma }}_{dtj}\right)\hfill \\ & \ge & \sum _{t=1}^T{\mathit{\gamma }}_{dt}^{\prime }log\left(\mathit{\beta }\right){\mathit{w}}_{dt}+\sum _{t=1}^T{\mathit{\gamma }}_{dt}^{\prime }\left[{\tilde{\mathit{m}}}_{dt}-log\left(\mathit{J}exp[{\tilde{\mathit{m}}}_{dtl}+diag{\displaystyle \frac{{\tilde{\mathit{V}}}_{dt}}{2}}]\right)\right]\hfill \\ & & -{\displaystyle \frac{T}{2}}log\left|\mathbf{\Sigma }\right|-{\displaystyle \frac{1}{2}}\sum _{t=1}^{T}tr\left[{\mathbf{\Sigma }}^{-1}({\tilde{\mathit{V}}}_{dt}+\mathbf{\Phi }{\tilde{\mathit{V}}}_{dt}{\mathbf{\Phi }}^{\prime })\right]\hfill \\ & & -{\displaystyle \frac{1}{2}}\sum _{t=1}^T{({\tilde{\mathit{m}}}_{dt}-\mathbf{\Phi }{\tilde{\mathit{m}}}_{dt-1})}^{\prime }{\mathbf{\Sigma }}^{-1}({\tilde{\mathit{m}}}_{dt}-\mathbf{\Phi }{\tilde{\mathit{m}}}_{dt-1})\hfill \\ & & +{\displaystyle \frac{1}{T}}{\mathit{\eta }}_c^T{\mathit{\gamma }}_{dt}-log\left(\sum _{l=1}^C\prod _{t=1}^T{\left(exp\left[{\displaystyle \frac{{\mathit{\eta }}_l}{T}}\right]\right)}^{\prime }{\mathit{\gamma }}_{dt}\right)\hfill \\ & & +{\displaystyle \frac{1}{2}}\sum _{t=1}^{T}log\left|{\tilde{\mathit{V}}}_{d,t}\right|+{\displaystyle \frac{TJ}{2}}-\sum _{t=1}^T{\mathit{\gamma }}_{dt}^{\prime }log\left({\mathit{\gamma }}_{dt}\right)\hfill \end{array}$$

Appendix A.2. Variational Multinomial

$$\begin{array}{ccc}\hfill L\left[{\mathit{\gamma }}_{dtj}\right]& \ge & \sum _{t=1}^T\sum _{j=1}^J\sum _{i=1}^V{\mathit{\gamma }}_{dtj}{w}_{dt}^{i}log{\mathit{\beta }}_{ji}\hfill \\ & & +\sum _{t=1}^T\sum _{j=1}^J{\mathit{\gamma }}_{dtj}\left[{\tilde{m}}_{dtj}-log\left(\sum _{l=1}^{J}exp[{\tilde{m}}_{dtl}+{\displaystyle \frac{{\tilde{v}}_{dtl}}{2}}]\right)\right]\hfill \\ & & +{\displaystyle \frac{1}{T}}{\mathit{\eta }}_c^T{\mathit{\gamma }}_{dt}-log\left(\sum _{l=1}^C\prod _{t=1}^T\left(\sum _{j=1}^J{\mathit{\gamma }}_{dtj}exp\left({\displaystyle \frac{1}{T}}{\mathit{\eta }}_{lj}\right)\right)\right)\hfill \\ & & -{\mathit{\gamma }}_{dtj}log\left({\mathit{\gamma }}_{dtj}\right)\hfill \\ & =& \sum _{t=1}^T\sum _{j=1}^J\sum _{i=1}^V{\mathit{\gamma }}_{dtj}{w}_{dt}^{i}log{\mathit{\beta }}_{ji}\hfill \\ & & +\sum _{t=1}^T\sum _{j=1}^J{\mathit{\gamma }}_{dtj}\left[{\tilde{m}}_{dtj}-log\left(\sum _{l=1}^{J}exp[{\tilde{m}}_{dtl}+{\displaystyle \frac{{\tilde{v}}_{dtl}}{2}}]\right)\right]\hfill \\ & & +{\displaystyle \frac{1}{T}}{\mathit{\eta }}_{cj}{\mathit{\gamma }}_{dtj}-log\left({\mathit{h}}^T{\mathit{\gamma }}_{dt}\right)\hfill \\ & & -{\mathit{\gamma }}_{dtj}log\left({\mathit{\gamma }}_{dtj}\right)\hfill \\ & \ge & \sum _{t=1}^T\sum _{j=1}^J\sum _{i=1}^V{\mathit{\gamma }}_{dtj}{w}_{dt}^{i}log{\mathit{\beta }}_{ji}\hfill \\ & & +\sum _{t=1}^T\sum _{j=1}^J{\mathit{\gamma }}_{dtj}\left[{\tilde{m}}_{dtj}-log\left(\sum _{l=1}^{J}exp[{\tilde{m}}_{dtl}+{\displaystyle \frac{{\tilde{v}}_{dtl}}{2}}]\right)\right]\hfill \\ & & +{\displaystyle \frac{1}{T}}{\mathit{\eta }}_{cj}{\mathit{\gamma }}_{dtj}-{\left({\mathit{h}}^T{\mathit{\gamma }}_t^{old}\right)}^{-1}{\mathit{h}}^T{\mathit{\gamma }}_t\hfill \\ & & -log\left({\mathit{h}}^T{\mathit{\gamma }}_t^{old}\right)+1-{\mathit{\gamma }}_{dtj}log\left({\mathit{\gamma }}_{dtj}\right)\hfill \\ & & +{\mathrm{\Lambda }}_t(\sum _{j=1}^J{\mathit{\gamma }}_{tj}-1).\hfill \end{array}$$

Result used: We know that

$$log\left(x\right)\le {\zeta }^{-1}x+log\left(\zeta \right)-1,\forall x>0,\zeta >0$$

with equality holding iff $x=\zeta$. Then,

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\delta L\left[{\gamma }_{dtj}\right]}{{\gamma }_{dtj}}}& =& log{\beta }_{jv}+{\tilde{m}}_{dtj}-log\left(\sum _{l=1}^{J}exp[{\tilde{m}}_{dtl}+{\displaystyle \frac{{\tilde{v}}_{dtl}}{2}}]\right)+{\displaystyle \frac{1}{T}}{\eta }_{cj}-\hfill \\ & & {\left({\mathit{h}}^T{\mathit{\gamma }}_{dt}^{old}\right)}^{-1}{h}_j-log\left({\gamma }_{dtj}\right)-1+{\mathrm{\Lambda }}_t.\hfill \end{array}$$

Equating to zero, we have a fixed-point estimate:

$$\begin{array}{ccc}\hfill {\gamma }_{dtj}& \propto & {\beta }_{jv}exp[{\tilde{m}}_{dtj}+{\displaystyle \frac{1}{T}}{\eta }_{cj}-{\left({\mathit{h}}^T{\mathit{\gamma }}_{dt}^{old}\right)}^{-1}{h}_j].\hfill \end{array}$$

We can then normalize ${\gamma }_{dtj}$ so that ${\sum }_j{\gamma }_{dtj}=1$.

Appendix A.3. Variational Gaussian

$$\begin{array}{ccc}\hfill L\left[{\widehat{\delta }}_{dtj}\right]& \ge & \sum _{\tau =t-1}^T\sum _{j=1}^J{\mathit{\gamma }}_{d\tau j}\left[{\tilde{m}}_{d\tau j}-log\left(\sum _{l=1}^{J}exp[{\tilde{m}}_{d\tau l}+{\displaystyle \frac{{\tilde{v}}_{d\tau l}}{2}}]\right)\right]\hfill \\ & & -{\displaystyle \frac{1}{2}}\sum _{\tau =t-1}^T{({\tilde{\mathit{m}}}_{d\tau }-\mathbf{\Phi }{\tilde{\mathit{m}}}_{d\tau -1})}^{\prime }{\mathbf{\Sigma }}^{-1}({\tilde{\mathit{m}}}_{d\tau }-\mathbf{\Phi }{\tilde{\mathit{m}}}_{d\tau -1}).\hfill \end{array}$$

We estimate ${\widehat{\delta }}_{dtj}$ using simulated annealing.

$$\begin{array}{ccc}\hfill L\left[{\widehat{\sigma }}^2\right]& \ge & \sum _{t=1}^T\sum _{j=1}^J{\gamma }_{dtj}\left[{\tilde{m}}_{dtj}-log\left(\sum _{l=1}^{J}exp[{\tilde{m}}_{dtl}+{\displaystyle \frac{{\tilde{v}}_{dtl}}{2}}]\right)\right]\hfill \\ & & -{\displaystyle \frac{1}{2}}\sum _{t=1}^{T}tr\left[{\mathbf{\Sigma }}^{-1}({\tilde{\mathit{V}}}_{dt}+\mathbf{\Phi }{\tilde{\mathit{V}}}_{dt}{\mathbf{\Phi }}^{\prime })\right]\hfill \\ & & -{\displaystyle \frac{1}{2}}\sum _{t=1}^T{({\tilde{\mathit{m}}}_{dt}-\mathbf{\Phi }{\tilde{\mathit{m}}}_{dt-1})}^{\prime }{\mathbf{\Sigma }}^{-1}({\tilde{\mathit{m}}}_{dt}-\mathbf{\Phi }{\tilde{\mathit{m}}}_{dt-1})\hfill \\ & & +{\displaystyle \frac{1}{2}}\sum _{t=1}^{T}log\left|{\tilde{\mathit{V}}}_{d,t}\right|.\hfill \end{array}$$

We obtain ${\widehat{\sigma }}^2$ using DBCPOL in Fortran, which minimizes a function using a direct search complex algorithm.

Appendix A.4. Estimation for sDCTM

In this section, we provide update equations to estimate the model parameters based on the lower bound on the log likelihood of the data.

$$\begin{array}{ccc}\hfill l(\mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta })& =& \sum _{d=1}^{M}logp({\mathcal{D}}_d,{\mathit{y}}_d|\mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta }).\hfill \end{array}$$

Then,

$$\begin{array}{ccc}\hfill l(\mathbf{\Phi },\mathbf{\Sigma },\mathit{\beta },\mathit{\eta })& \ge & \sum _{d=1}^M\sum _{t=1}^T\sum _{j=1}^J\sum _{i=1}^V{\gamma }_{dtj}{w}_{dt}^{i}log{\beta }_{ji}\hfill \\ & & +\sum _{d=1}^M\sum _{t=1}^T\sum _{j=1}^J{\gamma }_{dtj}\left[{\tilde{m}}_{dtj}-log\left(\sum _{l=1}^{J}exp[{\tilde{m}}_{dtl}+{\displaystyle \frac{{\tilde{v}}_{dtl}}{2}}]\right)\right]\hfill \\ & & -{\displaystyle \frac{MTJ}{2}}log\left(2\pi \right)-{\displaystyle \frac{MT}{2}}log\left|\mathbf{\Sigma }\right|-{\displaystyle \frac{1}{2}}\sum _{d=1}^M\sum _{t=1}^{T}tr\left[{\mathbf{\Sigma }}^{-1}({\tilde{\mathit{V}}}_{dt}+\mathbf{\Phi }{\tilde{\mathit{V}}}_{dt}{\mathbf{\Phi }}^{\prime })\right]\hfill \\ & & -{\displaystyle \frac{1}{2}}\sum _{d=1}^M\sum _{t=1}^T{({\tilde{\mathit{m}}}_{dt}-\mathbf{\Phi }{\tilde{\mathit{m}}}_{dt-1})}^{\prime }{\mathbf{\Sigma }}^{-1}({\tilde{\mathit{m}}}_{dt}-\mathbf{\Phi }{\tilde{\mathit{m}}}_{dt-1})\hfill \\ & & +\sum _{d=1}^M\left[{\mathit{\eta }}_{c_d}^T{\overline{\mathit{\gamma }}}_d-log\left(\sum _{l=1}^C\prod _{t=1}^T\left(\sum _{j=1}^J{\gamma }_{dtj}exp\left({\displaystyle \frac{1}{T}}{\eta }_{lj}\right)\right)\right)\right]\hfill \\ & & +{\displaystyle \frac{MTJ}{2}}log\left(2\pi \right)+{\displaystyle \frac{1}{2}}\sum _{d=1}^M\sum _{t=1}^{T}log\left|{\tilde{\mathit{V}}}_{d,t}\right|+{\displaystyle \frac{MTJ}{2}}-\sum _{d=1}^M\sum _{t=1}^T\sum _{j=1}^J{\gamma }_{dtj}log\left({\gamma }_{dtj}\right).\hfill \end{array}$$

Appendix A.5. Conditional Gaussian

$$\begin{array}{ccc}\hfill L_{\left[\mathbf{\Phi }\right]}& \ge & \sum _{d=1}^M\sum _{t=1}^T\sum _{j=1}^J{\gamma }_{dtj}\left[{\tilde{m}}_{dtj}-log\left(\sum _{l=1}^{J}exp[{\tilde{m}}_{dtl}+{\displaystyle \frac{{\tilde{v}}_{dtl}}{2}}]\right)\right]\hfill \\ & & -{\displaystyle \frac{1}{2}}\sum _{d=1}^M\sum _{t=1}^{T}tr\left[{\mathbf{\Sigma }}^{-1}({\tilde{\mathit{V}}}_{dt}+\mathbf{\Phi }{\tilde{\mathit{V}}}_{dt}{\mathbf{\Phi }}^{\prime })\right]\hfill \\ & & -{\displaystyle \frac{1}{2}}\sum _{d=1}^M\sum _{t=1}^T{({\tilde{\mathit{m}}}_{dt}-\mathbf{\Phi }{\tilde{\mathit{m}}}_{dt-1})}^{\prime }{\mathbf{\Sigma }}^{-1}({\tilde{\mathit{m}}}_{dt}-\mathbf{\Phi }{\tilde{\mathit{m}}}_{dt-1})\hfill \\ & & +{\displaystyle \frac{1}{2}}\sum _{d=1}^M\sum _{t=1}^{T}log\left|{\tilde{\mathit{V}}}_{d,t}\right|.\hfill \end{array}$$

We estimate $\mathbf{\Phi }$ using simulated annealing.

$$\begin{array}{ccc}\hfill L_{\left[\mathbf{\Sigma }\right]}& \ge & \sum _{d=1}^M\sum _{t=1}^T\sum _{j=1}^J{\gamma }_{dtj}\left[{\tilde{m}}_{dtj}-log\left(\sum _{l=1}^{J}exp[{\tilde{m}}_{dtl}+{\displaystyle \frac{{\tilde{v}}_{dtl}}{2}}]\right)\right]\hfill \\ & & -{\displaystyle \frac{MT}{2}}log\left|\mathbf{\Sigma }\right|-{\displaystyle \frac{1}{2}}\sum _{d=1}^M\sum _{t=1}^{T}tr\left[{\mathbf{\Sigma }}^{-1}({\tilde{\mathit{V}}}_{dt}+\mathbf{\Phi }{\tilde{\mathit{V}}}_{dt}{\mathbf{\Phi }}^{\prime })\right]\hfill \\ & & -{\displaystyle \frac{1}{2}}\sum _{d=1}^M\sum _{t=1}^T{({\tilde{\mathit{m}}}_{dt}-\mathbf{\Phi }{\tilde{\mathit{m}}}_{dt-1})}^{\prime }{\mathbf{\Sigma }}^{-1}({\tilde{\mathit{m}}}_{dt}-\mathbf{\Phi }{\tilde{\mathit{m}}}_{dt-1})\hfill \\ & & +{\displaystyle \frac{1}{2}}\sum _{d=1}^M\sum _{t=1}^{T}log\left|{\tilde{\mathit{V}}}_{d,t}\right|.\hfill \end{array}$$

We estimate $\mathbf{\Sigma }$ using simulated annealing.

Appendix A.6. Conditional Multinomial

$$\begin{array}{ccc}\hfill L_{\left[{\beta }_{ji}\right]}& =& \sum _{d=1}^M\sum _{t=1}^T\sum _{j=1}^J\sum _{i=1}^V{\gamma }_{dtj}{w}_t^{i}log{\beta }_{ji}+\sum _{j=1}^J{\mathrm{\Lambda }}_j(\sum _{i=1}^V{\beta }_{ji}-1)\hfill \\ \hfill {\displaystyle \frac{\partial L}{\partial {\beta }_{ji}}}& =& \sum _{d=1}^M\sum _{t=1}^T{\gamma }_{dtj}{w}_t^i{\displaystyle \frac{1}{{\beta }_{ji}}}+{\mathrm{\Lambda }}_j.\hfill \end{array}$$

This leads to a fixed-point update:

$$\begin{array}{ccc}\hfill {\mathit{\beta }}_{ji}& \propto & \sum _{d=1}^M\sum _{t=1}^T{\mathit{\gamma }}_{dtj}{w}_t^i\hfill \end{array}$$

We can then normalize ${\mathit{\beta }}_j$.

Appendix A.7. Softmax Regression

$$\begin{array}{ccc}\hfill L_{\left[{\eta }_{1:C}\right]}& =& \sum _{d=1}^M\left[{\mathit{\eta }}_{c_d}^T{\overline{\mathit{\gamma }}}_d-log\left(\sum _{l=1}^C\prod _{t=1}^T\left(\sum _{j=1}^J{\gamma }_{dtj}exp\left({\displaystyle \frac{1}{T}}{\mathit{\eta }}_{lj}\right)\right)\right)\right].\hfill \end{array}$$

We estimate the $\mathit{\eta }$ using simulated annealing. We add an $L2$ regularization term to prevent overfitting and prevent the inflation of parameter values.