Abstract
With the global pursuit of renewable energy and carbon neutrality, hydrogen-based microgrids have also become an important area of research, as ensuring proper design and operation is essential to achieve optimal performance from hybrid systems. This paper proposes a distributed control strategy based on multiagent self-triggered model predictive control (ST-MPC), with the aim of achieving demand-side control of hydrogen-based microgrid systems. This architecture considers a hybrid energy storage system with renewable energy as the main power source, supplemented by fuel cells based on electrolytic hydrogen. The primary objective of this architecture is aiming at the supply and demand balance problem under the supply and demand relationship of microgrid, the service life of hydrogen-based microgrid energy storage equipment can be increased on the basis of realizing demand-side control of hydrogen energy microgrid system. To accomplish this, model predictive controllers are implemented within a self-triggered framework that dynamically adjusts the counting period. The simulation results demonstrate that the ST-MPC architecture significantly reduces the frequency of control action changes while maintaining an acceptable level of set-point tracking. These findings highlight the viability of the proposed solution for microgrids equipped with multiple types of electrochemical storage, which contributes to improved sustainability and efficiency in renewable-based microgrid systems.
1. Introduction
With the global pursuit of renewable energy and carbon neutrality, microgrid systems are receiving more and more attention as an efficient and flexible energy distribution solution [1]. The hydrogen-based microgrid system is a potential energy transformation solution because it can realize the storage and distribution of clean energy, thus providing new possibilities for the sustainable development of the energy system [2]. However, the control and management of such systems face many challenges, such as intelligent control on the demand side and distributed control of the system, it is essential to ensure proper design and operation [3].
The development of microgrid control algorithms is a challenge that can integrate multiple methods and requires consideration of many aspects [4]. Existing research has made many attempts at this, such as applying heuristic algorithms to microgrid control in an attempt to obtain a better control method in a shorter time [5]. In order to deal with the uncertain status and parameters of the system, stochastic control algorithms from ref. [6] are introduced into microgrid control. In order to deal with nonlinear problems in microgrid control algorithms, optimal control algorithms such as adaptive optimization algorithms and neural networks are also used [7,8].
In the microgrid control problem, the prediction of power generation, the load of the power grid, and the required energy cost are issues that cannot be ignored. Therefore, it is necessary to develop relevant control algorithms in a targeted manner from the perspective of demand-side control. The system control method that has been widely studied is the island DC microgrid energy management system (EMS) based on hierarchical state machine control algorithm [9]. At the same time, the EMS system can be used to achieve real-time power supply management for power suppliers and demanders in the PV+Wind mode [10]. On this basis, there is also a two-level EMS control method that applies EMS to multiple control levels [11]. As for the demand-side control of hybrid power generation systems, ref. [12] discussed the feasibility of applying dual-mode distributed economic control algorithms. Ref. [13] provides a comprehensive and referenceable process for the design, modeling, and control of DC microgrids.
Based on the above aspects, it is necessary to consider the prediction of power generation and load of microgrids based on the demand side and the required energy costs. If each control node is understood as multiple agents, the multinode power grid control can be transformed into multiagent control with multiple constraints [14], and the model predictive control (MPC) and hierarchical control [15,16], which are widely used in the multiagent field, can be introduced because these can not only combine the above two requirements and consider them together but are also reliable methods to predict and solve the optimal control. And Lyapunov theory can be introduced to prove the feasibility of the control method [17]. There are currently many related research algorithms based on MPC. For example, refs. [18,19], respectively, studied distributed and centralized MPC control methods for renewable energy power generation networks. Refs. [20,21] apply MPC control to hierarchical distributed control. Ref. [22] presented a distributed MPC framework that is suitable for controlling large-scale networked systems such as power systems.
However, while MPC has the above advantages, it also has some disadvantages. For example, because it needs to predict control inputs for many steps in the future, it will inevitably increase the computing cost and communication cost of the system [23,24]. In order to reduce the communication and computing burden of the system, event-triggered and self-triggered controls are widely used [25,26]. Self-triggering control can significantly reduce computing costs because it does not need to detect and control the system status at all times [27,28]. In addition, self-triggering control can determine the precise time of the next triggering moment [29,30], thus making it a popular choice for reducing communication costs and computational costs in system control applications [31].
Based on the above issues and research, this study proposes a distributed control strategy based on multiagent self-triggered model predictive control (ST-MPC), aiming at the supply and demand balance problem under the supply and demand relationship of microgrids, a model predictive control method based on hydrogen-based microgrids is designed. While ensuring that batteries and hydrogen storage tanks are always kept in a safe and sustainable state, the scheduling of each microgrid in the power grid is realized, the demand side control of the hydrogen energy microgrid system is realized, and the purpose of increasing the service life of the storage equipment is achieved. On the other hand, the control algorithm proposed in this paper targets the difference in electricity demand between the energy supply side of photovoltaic (PV)+Wind and the demand side, which can better schedule the microgrid in the power grid to achieve peak shaving and valley filling, thereby making up for these differences, and combining the event triggering algorithm with the MPC algorithm, thereby saving considerable communication resources and control resources in microgrid regulation. The main contributions of this paper can be summarized as follows:
(1) The control method proposed in this article considers the conversion and storage of electricity and hydrogen, which can achieve peak shaving and valley filling in the supply and demand balance of microgrids.
(2) The control method proposed in this article considers state constraints on the battery and hydrogen storage tanks, which can improve the lifespan of storage devices.
(3) The ST-MPC algorithm proposed in this paper effectively reduces the computational burden associated with solving optimization problems.
2. Materials and Methods
2.1. Preliminaries
This section describes a hybrid AC/DC microgrid system that utilizes renewable energy sources such as wind and PV as the primary power source. The AC/DC power generated by the system is rectified to produce a stable DC voltage, which is then transmitted to the DC bus as the power source. The system consists of three main parts: the power generation system, which includes the AC/DC power generation equipment and rectifier; the control and regulation system, which includes energy storage devices such as batteries, electrolyzers, fuel cells, and hydrogen storage tanks, as well as an MPC system; and the load demand side, which consists of the power demand of various loads. Together, these three parts form the hybrid AC/DC microgrid system. The AC/DC hybrid power generation equipment on the power supply side provides stable electrical energy , while the control system is responsible for regulating energy storage or supply in cases of energy surplus or shortage. The loads on the demand side consume electrical energy . The control structure principle is illustrated in Figure 1.
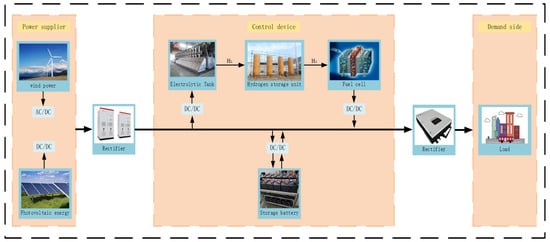
Figure 1.
AC/DC hybrid microgrid electric-to-hydrogen conversion control schematic.
In the aforementioned power distribution system, the energy consumed by the loads is influenced by external factors and electricity usage patterns. For example, the electricity demand of the loads varies across different seasons and time periods. As a result, it becomes challenging to maintain a balance between the power supply and demand, leading to issues of energy surplus or shortage. To address the energy supply–demand imbalance in this power distribution system, this paper presents the following mathematical problem formulation to tackle the aforementioned challenges:
where represents the electrical energy required by the load at time , represents the electrical energy generated by the power generation equipment, represents the energy stored in the battery, represents the energy generated by the fuel cell through hydrogen combustion, and represents the energy consumed by the electrolyzer in electrolyzing water. Therefore, by utilizing the control system composed of energy conversion and storage devices such as batteries, electrolyzers, fuel cells, and hydrogen storage tanks, the control section adjusts these components to achieve a balance between energy supply and demand.
Taking into account the constraints of the lifespan of energy conversion and storage devices, it is necessary to reconstruct a state model that satisfies the supply–demand relationship. In order to prolong the lifespan of the energy conversion and storage devices consisting of batteries, electrolyzers, fuel cells, and hydrogen storage tanks, the following constraints were applied to the battery capacity and hydrogen storage tank capacity:
where represents the capacity of the battery at time , while and represent the lower and upper limits of the battery capacity, respectively. represents the capacity of the hydrogen storage tank at time , while and represent the lower and upper limits of the hydrogen storage tank capacity, respectively.
To constrain the capacity of the battery and hydrogen storage devices within a certain range, this paper establishes the following models for battery and hydrogen storage capacity:
where and , respectively, represent the charge and discharge efficiency of the battery and the energy conversion efficiency of the hydrogen storage device. and represent the total capacity of the battery and the hydrogen storage device, respectively. T represents the time interval. As the electrolyzer and fuel cell cannot operate simultaneously, we use to represent the energy generation or consumption of the electrolyzer, and and to represent the energy generation or consumption of the fuel cell (i.e., when is positive, it represents the energy consumed by the electrolyzer ; when is negative, it represents the energy generated by the fuel cell ). Therefore, by combining Equations (1) and (3), we obtain
where the disturbance term represents the supply–demand mismatch.
2.2. Theory Basics
In this section, an MPC method is studied for addressing the supply–demand balance problem in a microgrid with battery and hydrogen storage tanks, considering the state constraints of these energy conversion and storage devices. This paper proposes the following assumptions:
Assumption 1.
The instantaneous power generation of the power supply side and the electricity consumption of the load on the demand side are observable at each time instant.
Assumption 2.
The power generation of the power supply side and the electricity consumption of the load on the demand side are within a stable and controllable range.
Assumption 3.
The considered topology graph has a directed spanning tree with the leader as the root node of the directed graph.
2.2.1. Model Predictive Control
Consider the following system:
where , , and represent the state input, control input, and the disturbance term, respectively. As it was commented in the preliminaries, there is a disturbance term to deal with. The disturbance would be considered constant over the entire prediction horizon. The augmented model results in
where
The state-space controller is implemented using the incremental formula of the state-space model, which considers the control increment instead of the control signal , where . Using this model, the disturbance term can be coupled to the state input and processed together. Therefore, defining a new state that depends on the previously enhanced state, the incremental model adopts the general form given by
where
Based on the state Equation (8), we formulate the following rolling optimization problem:
Problem 1.
subject to
where represents the prediction horizon, represents the variables to be optimized, and , , and are weight matrices.
Equation (10b) represents the relationship satisfied by the predicted states before and after optimization, while 10c–e represent the corresponding constraints. By solving the cost function , we can obtain the optimal control sequence . The first element is then used as the control input, i.e.,
The algorithm running structure is shown in Algorithm 1
| Algorithm 1. Model Predictive Control |
| 1. Build a control model: , |
| 2. Build a prediction model: , |
| 3. Define the cost function: |
| , |
| 4. Introduce constraints: (10c–f), |
| 5. Solve 3 and get the optimal control sequence: , |
| 6. Repeat steps 3–5. |
2.2.2. Self-Triggered Model Predictive Control
Assumption 4.
Lipschitz continuous functions and are associated with Lipschitz constants and , respectively. Additionally, there exists a function such that the condition holds true.
Lemma 1
([32]). Assuming that Assumption 4 is satisfied, the Lipschitz constant corresponding to the cost Function (10) satisfies the following conditions:
where .
Let denote the self-triggering instant, and represent the sequence of self-triggering instants, i.e., which means updating and optimizing at , and calculating the optimal control. Based on specific self-triggering conditions, the next self-triggering instant, , denoted as , is determined. During the time interval from to , the controller ceases to update but continues to use the effective predicted control input obtained from the previous triggering instant to reduce communication overhead and computational burden.
Definition 1.
If Assumptions 3 and 4 are satisfied, there exist constants and such that
Hence, the subsequent triggering time can be determined based on the following criteria:
where and are defined in Equation (21).
We construct the set of feasible control inputs, denoted as , at time .
where represents the optimal control input obtained by solving the optimization problem at time , and represents the feasible control input at the terminal time . These inputs are then applied to the system (8) to obtain the corresponding feasible state .
Therefore, based on (8), we can construct the following cost function for the ST-MPC:
subject to
where (16c) and (16d) represent the constraints on the control input and state variables, respectively, while (16e) represents the terminal constraint. By minimizing the aforementioned cost function under the given constraints, we can obtain the optimal control sequence . Similarly, at time , only the first element of the control sequence is applied to the control system.
The algorithm running structure is shown in Algorithm 2.
| Algorithm 2. Self-Triggered Model Predictive Control |
| 1. Build a control model: , |
| 2. Build a prediction model: , |
| 3. Define and , |
| 4. Get from , |
| 5. Define the cost function: |
| ; |
| 6. Introduce constraints: (16c,d,e,f), |
| 7. Solve 5 and get the optimal control sequence: , |
| 8. Repeat steps 3–7. |
2.3. ST-MPC for AC/DC Microgrid
2.3.1. MPC for AC/DC Microgrid
Based on the newly constructed supply–demand equilibrium state model (8) that satisfies the lifespan constraints, the following conventional MPC scheme is designed. Firstly, to facilitate the solution of the control problem, Equation (8) is rewritten as the following discrete linear state model:
where is the state vector. , and represent the state matrix, control input matrix, and disturbance matrix, respectively.
As mentioned in (8) and (17), the system contains a state disturbance, which needs to be appropriately addressed. To deal with this problem, the comprehensive process model was expanded to incorporate disturbances. The disturbance is assumed to remain constant throughout the entire prediction horizon, resulting in the augmented model:
Using the prediction model given by Equation (18) and incorporating self-triggered control, we formulate the following optimization problem:
subject to
By solving the optimization problem stated, we obtain the optimal predictive control sequence, denoted as . According to the self-triggered condition given by Equation (14), we select the relevant useful control input as follows:
Subsequently, the obtained useful control input is utilized in the prediction model given by Equation (18) to determine the state.
2.3.2. Self-Triggered Condition
Generally speaking, the trigger condition of the MPC system is that the cost function value of the next trigger moment is smaller than the cost function value of the previous trigger moment, i.e., . By substituting the feasible input (15) at time into the cost function, we can obtain the following feasible value of the cost function:
The inequality indicates that the value of the optimal cost function is not more than the value of the feasible cost function. Based on this fact, it can be expressed in the following form:
where
Hence, the system’s stability can be ensured if the following conditions are satisfied: . These conditions can be expressed as
Since the trigger condition is not satisfied , the system will update the control input. However, in order to simplify the calculation of the next triggered time , we reformulated the condition as follows:
where .
2.4. Analysis of Self-Triggered Model Predictive Control
In general, the stability analysis of MPC is conducted using Lyapunov theory. It aims to ensure that the cost function decreases over time, satisfying .
Based on the theoretical analysis presented in Equations (15)–(18), the sufficient condition for system stability is that Lemma 1 holds. Substituting different initial values and into the MPC system, we can obtain the corresponding cost functions and . Solving these cost functions yields the predictive control inputs and , as well as the corresponding predicted states and , where . Combining these results with the definition of feasible input in Equation , we have , ,
Therefore, we can further obtain the following expressions:
Therefore, it can be further obtained as follows:
Substituting the actual control and optimal control at time into the prediction model equation, we can obtain the actual state and optimal state at time :
Therefore, by utilizing Equation (25) and the Gronwall–Bellman inequality, we can determine the value of .
Lemma 1 holds true, so we can conclude that the system is stable.
3. Results and Discussion
In this section, we provide further explanation and clarification of the ST-MPC control method proposed in this paper for solving the microgrid supply–demand balancing problem with constraints on battery and hydrogen storage capacities using the MATLAB R2024a simulation platform. This simulation example considers three components: the power generation side composed of renewable energy sources such as wind and photovoltaic, the control part consisting of a rolling optimization controller, and the demand side composed of loads. From [9,10,11,12], the simulation will assume that during a short period of control time, the output of the energy supply side remains relatively stable, and the energy input demand on the demand side changes, thereby mobilizing the various microgrids in the power grid to supplement and store energy supply. The relevant parameters used in this simulation example are shown in Table 1.

Table 1.
Parameters of the electrochemical-to-gas conversion devices.
The relevant parameters satisfying the conditions in the article are set as follows: , , , , , , , .
In the current simulation experiment, as shown in Figure 2, the power supply side can continuously provide stable energy within 24 h, while the power consumption by the load side during this period is as follows:
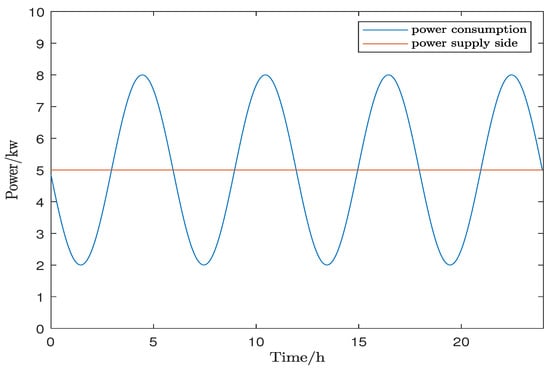
Figure 2.
Power of the supply and demand sides.
Based on the simulation results graph depicting the variation in battery capacity shown in Figure 3, it can be observed that within 24 h, the battery capacity remains within the constraints (i.e., ).
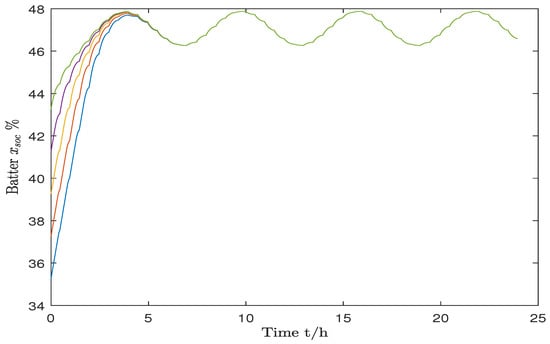
Figure 3.
Battery capacity variation.
The simulation results graph in Figure 4 illustrates the variation in the capacity of the hydrogen storage tank in an AC/DC hybrid microgrid based on ST-MPC. According to the simulation experiment results, it is evident that within 24 h, the hydrogen storage tank capacity remains within the prescribed constraints (i.e., ), and there are no instances of exceeding the constraint boundaries.
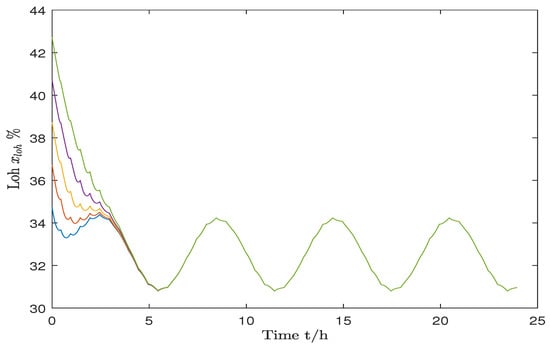
Figure 4.
Hydrogen storage tank capacity variation.
The situation described in Figure 5 is a simulation result graph illustrating the state changes in battery charging and discharging. From this graph, it can be observed that within 24 h, the battery charging and discharging behavior, after a brief adjustment by ST-MPC, effectively tracks the variations in power supply and demand (as shown in Figure 2).
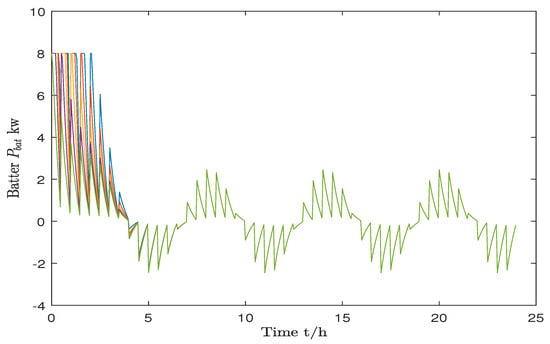
Figure 5.
Battery charging and discharging status.
Figure 6 represents the simulation results of the energy consumption of the electrolyzer or the electricity generation by the fuel cell over a certain time period. From the information presented in the graph, it is evident that the charging and discharging behavior of the electrolyzer, fuel cell, and battery are perfectly synchronized. Thus, the electrolyzer and fuel cell can effectively collaborate with the battery to achieve the conversion and storage of electricity and hydrogen, ultimately accomplishing the peak shaving and valley filling control objective of regulating supply–demand balance.
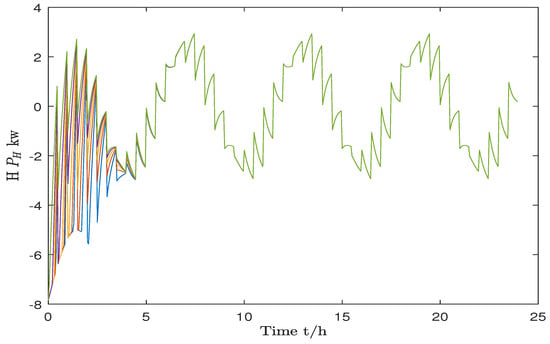
Figure 6.
Energy variation in the electrolyzer and fuel cell.
Figure 7 illustrates the triggering time points under ST-MPC control. It can be clearly seen from the figure that under ST-MPC control, the system does not perform continuous control but only controls when the trigger control is needed, effectively saving control resources.
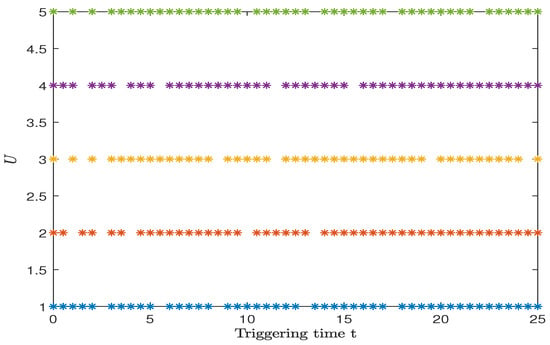
Figure 7.
Trigger time point of ST-MPC.
Figure 8 is a comparison histogram of the number of ST-MPC triggers in this article and the number of MPC triggers in [22]. It can be seen that the number of ST-MPC triggers used in this article is significantly smaller than the number of MPC triggers, which reduces the number of triggers by . At the same time, the control and scheduling of the energy storage module are realized, and it can be concluded that the ST-MPC used in this article can effectively save control resources and communication resources.
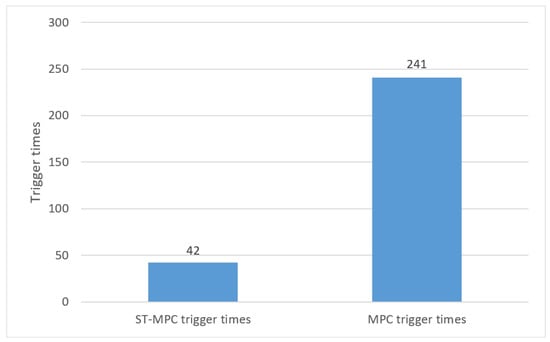
Figure 8.
Comparison histogram of ST-MPC trigger times and MPC trigger times.
4. Conclusions
In this paper, we presented a self-triggered model predictive control architecture for a renewable-based microgrid equipped with a hybrid energy storage system utilizing electricity and hydrogen. The main objective of this architecture is to efficiently manage the energy demand of a load while minimizing reliance on the utility power grid and degradation of storage devices. To achieve this, we implemented model predictive controllers within a self-triggered framework that dynamically adjusts the counting period. Through simulations, we evaluated the performance of the proposed architecture and observed significant reductions in control action changes, minimizing wear and tear on the storage devices. Additionally, the architecture maintained an acceptable level of set-point tracking, ensuring the desired energy demand was met. These findings highlight the promise of the self-triggered model predictive control architecture for microgrids with multiple types of electrochemical storage. By effectively managing energy demand and reducing reliance on external power sources, this architecture offers a viable solution to enhance sustainability and efficiency in microgrid systems.
5. Future Works
Next, we may extend this control algorithm to the energy supply side of PV+Wind, and achieve optimal control of energy generation and distribution on the supply side while improving the service life of microgrid energy storage units in the power grid. At the same time, we will introduce an event trigger mechanism to save communication and control costs, thereby achieving the goal of minimizing total costs. At the same time, we will also consider time-delayed disturbances in future work, thereby continuously improving the practicality of the control algorithm.
Author Contributions
Conceptualization, T.P., J.H., X.J., Z.Y., W.Z. and Z.W.; methodology, T.P.; software, T.P.; validation, T.P.; formal analysis, T.P.; investigation, J.H.; resources, X.J.; data curation, Z.Y.; writing—original draft preparation, T.P.; writing—review and editing, T.P.; visualization, Z.W.; supervision, T.P. and W.Z.; project administration, T.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Science and Technology Project of China Southern Power Grid Corporation under Grant GDKJXM20222125 (CG0300062001548977).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
Authors Jue Hou, Zhenfan Yu, Wei Zhou, Zhijun Wang are employed by the company Power Dispatching Control Center of Guangdong Power Grid Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Núñez-Reyes, A.; Rodríguez, D.M.; Alba, C.B.; Carlini, M.Á.R. Optimal scheduling of grid-connected PV plants with energy storage for integration in the electricity market. Sol. Energy 2017, 144, 502–516. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Canizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in microgrid control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Valverde, L.; Rosa, F.; Bordons, C.; Guerra, J. Energy management strategies in hydrogen smart-grids: A laboratory experience. Int. J. Hydrogen Energy 2016, 41, 13715–13725. [Google Scholar] [CrossRef]
- Gu, W.; Wu, Z.; Yuan, X. Microgrid economic optimal operation of the combined heat and power system with renewable energy. In Proceedings of the IEEE pes General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–6. [Google Scholar]
- Velarde, P.; Valverde, L.; Maestre, J.M.; Ocampo-Martínez, C.; Bordons, C. On the comparison of stochastic model predictive control strategies applied to a hydrogen-based microgrid. J. Power Sources 2017, 343, 161–173. [Google Scholar] [CrossRef]
- Mojica-Nava, E.; Macana, C.A.; Quijano, N. Dynamic population games for optimal dispatch on hierarchical microgrid control. IEEE Trans. Syst. Man Cybern. Syst. 2013, 44, 306–317. [Google Scholar] [CrossRef]
- Chong, L.W.; Wong, Y.W.; Rajkumar, R.K.; Isa, D. An adaptive learning control strategy for standalone PV system with battery-supercapacitor hybrid energy storage system. J. Power Sources 2018, 394, 35–49. [Google Scholar] [CrossRef]
- Pu, Y.; Li, Q.; Chen, W.; Liu, H. Hierarchical energy management control for islanding DC microgrid with electric-hydrogen hybrid storage system. Int. J. Hydrogen Energy 2019, 44, 5153–5161. [Google Scholar] [CrossRef]
- Han, Y.; Chen, W.; Li, Q.; Yang, H.; Zare, F.; Zheng, Y. Two-level energy management strategy for PV-Fuel cell-battery-based DC microgrid. Int. J. Hydrogen Energy 2019, 44, 19395–19404. [Google Scholar] [CrossRef]
- Shi, W.; Li, N.; Chu, C.C.; Gadh, R. Real-time energy management in microgrids. IEEE Trans. Smart Grid 2015, 8, 228–238. [Google Scholar] [CrossRef]
- Yang, H.; Li, Q.; Wang, T.; Qiu, Y.; Chen, W. A dual mode distributed economic control for a fuel cell–photovoltaic-battery hybrid power generation system based on marginal cost. Int. J. Hydrogen Energy 2019, 44, 25229–25239. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, G.; Li, Q.; You, Z.; Chen, W.; Liu, H. Hierarchical energy management for PV/hydrogen/battery island DC microgrid. Int. J. Hydrogen Energy 2019, 44, 5507–5516. [Google Scholar] [CrossRef]
- Negenborn, R.R.; Houwing, M.; De Schutter, B.; Hellendoorn, J. Model predictive control for residential energy resources using a mixed-logical dynamic model. In Proceedings of the 2009 International Conference on Networking, Aachen, Germany, 11–15 May 2009; pp. 702–707. [Google Scholar]
- Ge, M.F.; Gu, Z.W.; Su, P.; Liang, C.D.; Lu, X. State-constrained bipartite tracking of interconnected robotic systems via hierarchical prescribed-performance control. Nonlinear Dyn. 2023, 111, 9275–9288. [Google Scholar] [CrossRef]
- Ge, M.F.; Dong, J.W.; Liu, Z.W.; Yan, H.; Liang, C.D.; Xu, K.T. Hierarchical fuzzy fault-tolerant controller synthesis for finite-time multitarget surrounding of networked perturbed mechanical systems. IEEE Trans. Fuzzy Syst. 2022, 31, 760–773. [Google Scholar] [CrossRef]
- Ge, M.F.; Huang, K.L.; Hu, W.; Yang, C.; Liang, C.D. Hierarchical bipartite formation tracking of networked perturbed robotic systems with nonlinear state-to-output mappings. Int. J. Robust Nonlinear Control 2023, 33, 4541–4561. [Google Scholar] [CrossRef]
- Ge, M.F.; Liu, Z.W.; Wen, G.; Yu, X.; Huang, T. Hierarchical controller-estimator for coordination of networked Euler—Lagrange systems. IEEE Trans. Cybern. 2019, 50, 2450–2461. [Google Scholar] [CrossRef]
- Bordons, C.; Garcia-Torres, F.; Ridao, M.A. Model Predictive Control of Microgrids; Springer: Berlin/Heidelberg, Germany, 2020; p. 358. [Google Scholar]
- Dehghani-Pilehvarani, A.; Markou, A.; Ferrarini, L. A hierarchical distributed predictive control approach for microgrids energy management. Sust. Cities Soc. 2019, 48, 101536. [Google Scholar]
- Jayach, M.; Ravi, G. Decentralized model predictive hierarchical control strategy for islanded AC microgrids. Electr. Power Syst. Res. 2019, 170, 92–100. [Google Scholar]
- Zhang, Y.; Fu, L.; Zhu, W.; Bao, X.; Liu, C. Robust model predictive control for optimal energy management of island microgrids with uncertainties. Energy 2018, 164, 1229–1241. [Google Scholar] [CrossRef]
- Venkat, A.N.; Hiskens, I.A.; Rawlings, J.B.; Wright, S.J. Distributed MPC strategies with application to power system automatic generation control. IEEE Trans. Control Syst. Technol. 2008, 16, 1192–1206. [Google Scholar] [CrossRef]
- Fontenot, H.; Dong, B. Modeling and control of building-integrated microgrids for optimal energy management—A review. Appl. Energy 2019, 254, 113689. [Google Scholar] [CrossRef]
- Xu, J.Z.; Ge, M.F.; Liu, Z.W.; Zhang, W.Y.; Wei, W. Force-reflecting hierarchical approach for human-aided teleoperation of NRS with event-triggered local communication. IEEE Trans. Ind. Electron. 2021, 69, 2843–2854. [Google Scholar] [CrossRef]
- Wang, L.; Ge, M.F.; Zeng, Z.; Hu, J. Finite-time robust consensus of nonlinear disturbed multiagent systems via two-layer event-triggered control. Inf. Sci. 2018, 466, 270–283. [Google Scholar] [CrossRef]
- Wan, X.; Tian, Y.; Wu, J.; Ding, X.; Tu, H. Distributed event-triggered secondary recovery control for islanded microgrids. Electronics 2021, 10, 1749. [Google Scholar] [CrossRef]
- Xu, G.; Ma, L. Resilient self-triggered control for voltage restoration and reactive power sharing in islanded microgrids under denial-of-service attacks. Appl. Sci. 2020, 10, 3780. [Google Scholar] [CrossRef]
- Garcia-Torres, F.; Bordons, C. Optimal economical schedule of hydrogen-based microgrids with hybrid storage using model predictive control. IEEE Trans. Ind. Electron. 2015, 62, 5195–5207. [Google Scholar] [CrossRef]
- Valverde, L.; Rosa, F.; Bordons, C. Design, planning and management of a hydrogen-based microgrid. IEEE Trans. Ind. Inform. 2013, 9, 1398–1404. [Google Scholar] [CrossRef]
- Valverde, L.; Rosa, F.; Del Real, A.J.; Arce, A.; Bordons, C. Modeling, simulation and experimental set-up of a renewable hydrogen-based domestic microgrid. Int. J. Hydrogen Energy 2013, 38, 11672–11684. [Google Scholar] [CrossRef]
- Duan, J.; Zhang, H.; Wang, Y.; Han, J. Output consensus of heterogeneous linear MASs by self-triggered MPC scheme. Neurocomputing 2018, 315, 476–485. [Google Scholar] [CrossRef]
- Castilla, M.; Bordons, C.; Visioli, A. Event-based state-space model predictive control of a renewable hydrogen-based microgrid for office power demand profiles. J. Power Sources 2020, 450, 227670. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).