Automated Personalized Loudness Control for Multi-Track Recordings

Abstract

This paper presents a novel approach to automated music mixing, focusing on the optimization of loudness control in multi-track recordings. By taking into consideration the complexity and artistic nature of traditional mixing processes, we introduce a personalized multi-track leveling method using two types of approaches: a customized genetic algorithm and a neural network-based method. Our method tackles common challenges encountered by audio professionals during prolonged mixing sessions, where consistency can decrease as a result of fatigue. Our algorithm serves as a ‘virtual assistant’ to consistently uphold the initial mixing objectives, hence assuring consistent quality throughout the process. In addition, our system automates the repetitive elements of the mixing process, resulting in a substantial reduction in production time. This enables engineers to dedicate their attention to more innovative and intricate jobs. Our experimental framework involves 20 diverse songs and 10 sound engineers possessing a wide range of expertise, offering a useful perspective on the adaptability and effectiveness of our method in real-world scenarios. The results demonstrate the capacity of the algorithms to mimic decision-making, achieving an optimal balance in the mix that resonates with the emotional and technical aspects of music production.

1. Introduction

Music mixing is an intricate process that transforms multi-track material—recorded, sampled or synthesized—into a cohesive multi-channel format [1]. This process is not merely technical; it significantly influences the emotional connection between the music and its audience. A well-executed mix can profoundly affect the experience of the listener, emphasizing the artistry in sound engineering.

The field of music mixing is experiencing significant changes due to the introduction of automated solutions. The goal of incorporating automation in music mixing is to mimic or assist the complex and artistic process that has traditionally relied on the skill of a professional. This particular expertise is essential for modifying the dynamics, spatial characteristics, timbre and pitch in multi-track recordings. The alteration of these components involves a sequence of procedural stages that employ both linear and nonlinear processes to achieve the desired auditory outcome [2]. The following steps can be outlined:

• Gain Adjustment—this initial stage in mixing involves setting the overall volume levels of different tracks to obtain a well-balanced mix, preventing any single element from dominating the others;
• Equalization (EQ)—this is the deliberate adjustment of specific frequency ranges to improve the clarity and balance of the mix. This technique ensures that each instrument or voice has its own distinct sonic presence;
• Panning—this involves manipulating the stereo position of each track to create a sense of spatial depth in the mix. This technique enhances the listening experience by replicating the placement of sounds in a three-dimensional space, resulting in a more immersive effect;
• Dynamic Range Compression (DRC)—this is a technique that reduces the difference between the softest and loudest sounds in audio signals. It accomplishes this by amplifying soft sounds and attenuating loud sounds, resulting in a more uniform volume level across the mix. This technique is essential for preserving energy and guaranteeing the audible presence of all components;
• Artificial reverberation—this is the process of incorporating reverb effects to imitate different acoustic settings, ranging from compact chambers to large venues. This technique enhances the sonic dimension and ambiance of the audio mix.

Loudness, in the realm of audio engineering, refers to the subjective perception of the power or magnitude of a sound. Unlike objective measures of sound pressure like decibels (dB), loudness is a subjective sense that is affected by frequency and impacted by the unique characteristics of the human auditory system [3]. The intricacy of perceiving loudness has resulted in the creation of multiple standards and models to accurately and meaningfully measure it, such as the International Telecommunication Union’s ITU-R BS.1770 [4] and the European Broadcasting Union’s EBU R128 recommendation [5]. Loudness is not solely determined by amplitude, but rather it is a psycho-acoustic characteristic that reflects how humans perceive the intensity of sound.

The perception of sound is influenced by various elements, including the frequency content, duration and the surrounding context in which it is heard [6]. The challenge of audio mixing is to achieve a harmonic and enjoyable listening experience by balancing the perceptions of diverse audio tracks. Gain adjustment in the mixing process is indeed grounded on loudness measurements, tailored to the auditory perception of the engineer. This phase is crucial in the mixing process, if this step is not executed correctly, it can adversely impact all subsequent stages in the mixing workflow. Loudness management guarantees that the ultimate blend achieves a perceived volume that aligns with industry norms and listener expectations, while preserving the dynamic range and sound quality. The volume of each track in a mix is a crucial factor that can greatly impact the overall sound and clarity of the finished result. Engineers could use diverse strategies to manage track loudness, which might be influenced by their distinct views, target audience and the specific music genre they are working on.

In the domain of automatic music mixing, significant strides have been made towards developing algorithms that can emulate the nuanced decisions of human engineers. The inception of ‘Automatic Mixing’ can be traced back to 1975 with Dugan’s speech application focusing on microphone gain control [7]. Significant contributions to the field include the work of González et al. [8], who introduced an automatic maximum gain normalization technique that forms the basis for many subsequent developments in audio mixing automation. Their methodology, detailed in the Journal of the Audio Engineering Society, provided a cornerstone for gain and fader control algorithms in live and recorded music scenarios. Scott et al. [9] focused on the analysis of acoustic features for automated multi-track mixing, offering insights into how different elements of a mix can be automatically balanced to achieve a desired sonic quality. Their work underscores the importance of understanding the acoustic characteristics of individual tracks for effective automation. Ward et al. [10] contributed to the field with their research on multi-track mixing using models of loudness and partial loudness. Their approach, aiming to improve the clarity and balance of mixes by addressing energetic masking, demonstrates the complexity of achieving a well-balanced mix through automated processes. Fentom et al.’s [11] research on automatic mixing using modified loudness models presents a method for level balancing that considers the psycho-acoustic phenomenon of loudness perception. This work is pivotal in understanding how listeners perceive the loudness of different sources within a mix and how this perception can be modeled and applied in automatic mixing systems. Moffat et al.’s [12] exploration of automatic mixing level balancing, enhanced through source interference identification, adds a layer of sophistication to automated mixing by addressing the issue of source interference. Their work proposes solutions for identifying and mitigating interference between sources, thereby enhancing the clarity and quality of the mix. Wilson et al.’s [13] research addresses the challenge of achieving desired audio outcomes by leveraging the flexibility and efficiency of genetic algorithms, which can evolve solutions based on user preferences and feedback. This method stands out by facilitating a more intuitive interaction between the user and the mixing process, enabling the user to influence the evolution of the mix in real time.

Further emphasizing the role of technological advancements in audio processing, recent studies in uncertainty estimation provide a crucial foundation for enhancing automated mixing systems. Adiloglu et al. [14] discuss the integration of probabilistic source separation with feature extraction to robustly estimate audio features despite errors in separation, particularly useful in under-determined scenarios such as polyphonic music recordings. Extending to multimodal contexts, Fang et al. [15] introduce an uncertainty-driven hybrid fusion model for audio-visual phoneme recognition, which adaptively manages unreliable visual inputs to enhance accuracy. Additionally, Sefidgar et al. [16] tackle the challenge of source feature extraction in multi-source recordings by employing deep learning to handle uncertainty, aiming to improve both the accuracy and robustness of separations. Xu et al. [17] provide a novel approach to the challenge of compressive blind mixing matrix estimation of audio signals, focusing on directly estimating the mixing matrix from compressive measurements without the need for reconstructing the mixtures to enhance the speed and accuracy of audio signal processing. These contributions highlight the increasing reliance on sophisticated algorithms to address complex challenges in audio engineering, aligning well with the ongoing developments in automated mixing technologies.

The significance of our work lies in its personalized approach to automated music mixing, distinguishing it from existing methodologies that generally aim for a one-size-fits-all solution. Unlike the broad strategies employed in previous studies, our research focuses on emulating the unique preferences and styles of individual engineers. This distinction is crucial because artists often seek out specific engineers for their distinctive sound and approach to mixing. The ability of our algorithm to learn and adapt to the preferences of different engineers represents a paradigm shift in automated mixing technology. It not only automates the technical aspects of mixing but also captures the creative signature essence of the engineer, thus offering a more tailored and artistically sensitive solution. Our methodology incorporates the pyloudnorm Python system, which adheres to the ITU-R BS.1770-4 standard and EBU R128 recommendation for measuring loudness [18]. By using the Loudness Units Full Scale (LUFS) meter, we can measure the volume in a manner that is consistent with both human perception and industry norms. Through the process of measuring and standardizing the loudness of each track, we provide a uniform starting point for our algorithm. This guarantees that the final mix attains the intended aural equilibrium and quality.

In this paper, we further investigate the implementation of automation in music mixing by proposing an experimental configuration that evaluates an individualized multi-track leveling method across a total of 20 songs and 10 engineers. This approach, which is based on our prior research [19], aims to improve the automation of the mixing process by focusing on crucial components such as loudness control and reproduction of creative decision-making similar to that of skilled audio engineers. The current experiment aims to evaluate the capacity of the algorithm to adjust to different musical genres and multiple engineering preferences, thus tackling the difficulty of automating music mixing with a sophisticated approach that considers the nuances of creative intention and technological implementation. Through the analysis of the algorithm’s performance on a wide range of songs and mixing styles, our goal is to confirm its effectiveness and adaptability, which is a crucial milestone in addressing the challenges of automating music mixing. In this article we seek to enhance our previous discoveries from [19] and make a substantial contribution to the area by showcasing an advanced technique for obtaining customized loudness control and innovative decision-making in automated music mixing.

This paper is organized as follows. In Section 2, details about the used dataset, signal-processing operations and our applied methods for loudness control are presented. The results of our work are highlighted in Section 3. An analysis of the experiments is carried out as a discussion in Section 4. Finally, Section 5 concludes this work.

2. Materials and Methods

In this section, we provide a comprehensive explanation of the approaches and tools utilized to successfully accomplish our goals in creating a customized automated loudness control system for multi-track recordings. First, we provide a summary of the composition of dataset and the standards used for selecting songs, which guarantee a diverse representation of many musical genres. Subsequently, we explain the standardization procedure used on the audio files to ensure uniformity across all experimental inputs. Next, we analyze the development of the problem by creating a mathematical model that incorporates different variables. This section is essential for establishing a basic understanding of our methodologies and tactics prior to exploring specific algorithms, such as the genetic algorithm and neural network approach, which are explained in later subsections.

2.1. Dataset

For this paper, a dataset of 20 songs was meticulously curated, combining tracks from the Cambridge Music Technology database [20] and recordings from local Romanian bands sourced by the participating engineers. These selections encompass a wide range of genres and styles, providing a robust foundation for examining the nuances of audio mixing. The multi-track collection spans a deliberately broad spectrum of musical genres and styles, including Soul, Indie Pop, Alternative Rock, Country, Hip-Hop, Latin Pop, Funk, Rock ‘n’ Roll, Blues Rock, Indie-Psych Rock, R&B, Soft Rock, Pop Rock, Funk/Soul, Art Rock, Power Pop, Metal and more. This eclectic selection is critical for a comprehensive analysis of the diverse mixing techniques preferred by different sound engineers. The decision to include such a varied range of genres serves multiple purposes. Firstly, it mirrors the wide-ranging musical landscape that sound engineers encounter in professional settings, ensuring our findings have broad applicability. Secondly, it allows us to examine how different musical styles influence the mixing process, particularly in terms of dynamic range, tonal balance and spatialization, which can vary significantly from genre to genre. This diversity not only enriches our dataset but also strengthens our investigation into the adaptability and effectiveness of the personalized multi-track leveling algorithm in mimicking the nuanced approach that engineers bring to projects across the musical spectrum.

The effectiveness of our tailored multi-track leveling process relies heavily on the expertise and subjective assessments of sound engineers. In order to assess the efficacy and versatility of our algorithm, we enlisted the participation of 10 sound engineers with diverse levels of expertise, ranging from beginners to professionals in the music industry. The selection process aimed to include individuals with a range of mixing techniques and preferences, in order to thoroughly evaluate the performance of the algorithm across various artistic approaches. Before starting the experiment, the sound engineers undertook a training session to become acquainted with the details of the algorithm. This encompassed a comprehensive examination of its design concepts and operational mechanics.

2.2. Data Preparation

As a pre-processing step, all audio files in the dataset were uniformly converted to a standard sampling rate in music of 44.1 kHz [21]. This conversion ensures consistency across all tracks, facilitating a more accurate and controlled analysis of the mixing processes employed by the engineers. The standardization of the sampling rate is a crucial step in maintaining the integrity and comparability of the data, as recommended in the Audio Engineering Society’s standard [22]. To avoid unwanted artifacts caused by quantization, we maintained the bit depth at its original value. In order to improve the organization of our dataset, we created a custom Python script to methodically rename audio files, using precise keywords extracted from a comprehensive multi-track database [20]. The process of renaming is not solely administrative; it fulfills a crucial analytical purpose by guaranteeing that tracks of similar categories throughout multiple songs are consistently labeled, hence greatly streamlining data administration and analysis. As an example, the recordings are consistently renamed according to a convention like ‘Index_KickIn’, ‘Index_BassDi’, ‘Index_Piano’, ‘Index_LeadVocals_2’, ‘Index_LeadVocals_3’, enabling quick identification and comparison of related parts throughout the collection. Our track list template consists of 66 general tracks conform to the industry standard and is generated through the analysis of several multi-track recordings. It enables a more focused and nuanced examination of the individual contributions of each group to the overall mix, as well as how engineers approach the process of mixing different instrument kinds in different genres:

• 00–17—Drums and related instruments (e.g., KickIn, SnareUp, HiHat);
• 18–24—Synthesized and electronic percussion (e.g., KickSynth, PercSynthLow);
• 25–30—Bass tracks (e.g., BassDi, BassSynth);
• 31–36—Guitars (e.g., AccGuitarDi, ElGuitarClean);
• 37–45—Keyboards, Piano and synthesized instruments (e.g., ElectricPiano, KeySynthLow);
• 46–58—Orchestral, world instruments and other cinematic instruments (e.g., Woodwinds, Vio1, WorldInstrLow);
• 59–65—Vocals and other (e.g., LeadVox, BackingMed, Other).

This methodical approach addresses the lack of a common naming convention among artists and recording engineers, an issue in the profession that we sought to overcome. By using a systematic naming convention, we enhance the organization and accessibility of the dataset. This ensures that tracks are not only uniformly titled, but also classified and arranged in a manner that reflects industry standards.

As a post-mixing step, for each sound engineer, the loudness parameters for each track of each song were meticulously extracted and documented, in order to properly represent the preferences of each individual. We created a Python script specifically designed to apply ITU loudness standards [4] for quantifying important loudness measures in every engineer’s mix. This script additionally validates the accurate naming of tracks and detects any additional tampering apart from gain adjustment, that might have taken place. The main purpose of this method for loudness extraction was to examine perceptive audio level parameters, offering a quantitative perspective to evaluate the mixing decisions of each engineer. The advantage of this method is represented by its capacity to process a wide range of audio data inputs, guaranteeing consistency in parameter extraction regardless of the file format and duration. Nevertheless, the process was not devoid of obstacles. Novice engineers exhibited inconsistent compliance to protocols, resulting in a deviation from established mixing procedures and causing unanticipated changes in loudness parameters. The extraction algorithm faced considerable obstacles due to inconsistencies in naming standards and unanticipated changes in bit depth, and required human intervention.

One very important step in automatic learning using any type of data is to ensure that all the examples are in the same distribution and within a similar range of values. Because the loudness control is a problem of human perception, we needed to make sure that each song has the same loudness volume. This operation was carried out in order to ensure that the mix created by each engineer is always at the same loudness level, and only the coefficients between tracks are different. Additionally, each original song has its own multi-tracks at different loudness levels, therefore, it is important to normalize all the initial tracks to a fixed loudness. To ensure consistency and optimal listening conditions, we normalized each input track to $-45$ LUFS and set the loudness of every original mix to $-23$ LUFS. The decision to use $-45$ LUFS for individual tracks stems from a widely adopted practice among sound engineers, who prefer to start with lower volumes to have greater control during the mixing process. This initial low volume also surpasses the loudness threshold gate, below which measurements by loudness meters may not be reliable, ensuring accuracy in our loudness assessments. The selection of $-23$ LUFS for the mixed audio volume is rooted in its recognition as a level that aligns closely with human auditory perception, offering a balance that preserves both clarity and dynamic range, without inducing listener fatigue over extended periods. This choice mirrors the standards set forth by international broadcasting guidelines, such as the EBU R128 standard [18], which recommends a target loudness of $-23(\pm 2)$ LUFS to ensure a consistent and comfortable listening experience across various platforms and media types. However, obtaining an accurate loudness reading for audio tracks with only small brief moments of useful signal, such as a single clap or a snare strike, can be quite difficult. It is well known that the length of the useful signal should be at least 3 s for a proper loudness measurement. In the case of such exceptional cases with very brief useful signal and small amplitude levels, the Root Mean Square (RMS) value was used instead of LUFS implementation in order to scale the track. For this paper, we consider the reference mix level at $-23$ LUFS, and the input track level at $-45$ LUFS.

For audio processing, it is usually quite challenging to work with the entire signal, therefore, splitting the audio into multiple overlapped windows is commonly practiced. However, for the problem of a fixed loudness level for the entire track, we discovered that there is no need to look at all the signal windows, but instead, use only one of them, because the scale factor will be the same over the entire track. In other words, instead of processing entire tracks, we focus on key segments, thereby reducing processing time without compromising on the accuracy of loudness estimation. Additionally, based on the human auditory sensitivity differences across frequencies, we also recognized that the maximum loudness perception is between 250 Hz and 4000 Hz [23]. For this reason, as an optimization step, we realized that we could downsample the audio at a lower frequency rate, maintaining quality while reducing computational load. The following multi-step procedure was applied for each track in every song:

• Downsample the entire track to 16 kHz, in alignment with human auditory sensitivity and the equal-loudness contours, which emphasize the 2–5 kHz range where clarity and loudness perception are most significant [3];
• Divide the audio signal into windows of 3 s, with a hop size of 1 s (66% overlap);
• Find the best window within the audio. We consider the best window the one with the highest RMS value, which can approximate the loudness level with some degree (it is a representantion of the power of the signal, without the human perception factor), but is much faster to compute;
• Repeat steps (2) and (3), but with a window size of 1024 samples and hop size of 512 (50% overlap), representing a window of 64 ms in time. This was done in order to further shrink the input data size for a faster training loop.

2.3. Problem Formulation

Music mixing, inherently a blend of art and science, necessitates a nuanced understanding of audio signal interplay. A musical piece, essentially a combination of various frequencies and timbres, can be deconstructed into its constituent tracks. This separation is key to our approach, as it allows for the manipulation of individual elements before reassembling them into a harmonious mixture. At the heart of our method, Equation (1) presents a mathematical model [24] representing a mixed song as a sum of its constituent tracks, each modulated by a specific coefficient:

$$m\left(t\right)=\sum _{i=1}^N{\mathit{\lambda }}_i{x}_i\left(t\right),$$

(1)

where $m\left(t\right)$ denotes the mixed audio at time sample t, $x_i\left(t\right)$ symbolizes an individual track and ${\mathit{\lambda }}_i$ is the corresponding mixing coefficient. N represents the maximum number of possible tracks, and is equal to 66 in our case. This model encapsulates the essence of mixing—blending various elements (tracks) into a cohesive auditory experience.

When analyzing the mixing process from an optimization perspective, we view it as a search for the best combination of ${\mathit{\lambda }}_i$ values that result in a balanced blend. The difficulty lies in automating this process of optimization, which has traditionally been carried out by human professionals. In our situation, the coefficient ${\mathit{\lambda }}_i$ represents the level or loudness of each recording as perceived in the mix.

2.4. Genetic Algorithm for Loudness Optimization

We propose the utilization of genetic algorithms [25,26] to effectively handle this complex and multi-solution problem. Our approach leverages a genetic algorithm to iteratively refine the mixing coefficients, driving towards an optimal mix. The algorithm mimics natural selection, evolving solutions over generations to arrive at a superior mix.

The genetic algorithm begins with a population of randomly generated solutions (mixing coefficient sets). Through processes akin to biological evolution—selection, crossover and mutation—this population evolves over generations. A generic pseudo-code for genetic algorithms is represented in Algorithm 1.

Algorithm 1: Genetic Algorithm

1: Set: Population size, chromosome length 2: Init: Create population using random bounded values 3: while stop criterion not met do 4:     Evaluation: Calculate the fitness of each individual in the population 5:     Parents selection: Choose individuals for reproduction based on their fitness 6:     for i = 0 to length list of parents do 7:         Choose pair of parents 8:         if random probability crossover ≤ crossover probability then 9:            Crossover: Perform crossover between parents to create a new offspring 10:         else 11:            Select a parent as the new offspring 12:         end if 13:     end for 14:     for each offspring do 15:         for each gene in offspring do 16:            if random probability mutation ≤ mutation probability then 17:                Mutation: Apply random mutation to introduce changes in the offspring 18:            end if 19:         end for 20:     end for 21:     Update: Create a new population based on the generated offsprings 22: end while

Our customized genetic algorithm ensures that only the fittest solutions (those producing the most harmonious mixes) survive and propagate their traits. Given the unique demands of music mixing, we customize the standard genetic algorithm to suit our specific needs:

• Population and Solution Representation—the population consists of vectors of mixing coefficients (chromosomes). Each vector represents a potential solution for the problem, where one element (gene) corresponds to a coefficient for a track. For our problem, each solution will always be represented by a vector of 66 elements. Instead of creating a high population, we chose to use a highly competitive small population of only 5 chromosomes, in order to extract the optimal solution from this group of best candidates. Using the model described in Equation (1), we define a chromosome based on the vector representation specified in Equation (2):

  $$c=[{\mathit{\lambda }}_0,{\mathit{\lambda }}_1,\dots ,{\mathit{\lambda }}_{65}].$$

  (2)
• Fitness Function—our fitness function evaluates the quality of a mix based on the Mean Absolute Error (MAE) between the desired and produced audio samples across tracks. The main difference is that instead of computing the loss function for each song and average all the errors, we instead compute the error for each track in all songs (Equations (3) and (4)), in order to better approximate the track coefficients.

  $$e_i^k=\frac{1}{T^k}\sum _{t=0}^{T^k-1}|y_i^k\left(t\right)-{\mathit{\lambda }}_i{x}_i^k\left(t\right)|=\mathrm{MAE}\left(y_i^k,{\widehat{y}}_i^k\right),$$

  (3)

  $$e_i=\sum _{k=1}^M{e}_i^k,$$

  (4)

  where $k\in [1,M]$ represents the index of a song out of M possible examples, and $T^k$ is the length of the signal k. At each track i for a song k, the error $e_i^k$ (MAE function) is calculated between the original track $y_i^k$ and the product of coefficient ${\mathit{\lambda }}_i$ and input track $x_i^k$ at $-45$ LUFS, which represents the predicted track ${\widehat{y}}_i^k$.

The MAE function, defined in both Equations (3) and (5), measures the differences between the ground truth track samples $y_i^k$ and predicted samples ${\widehat{y}}_i^k$. Summing these errors on a track level helps us better minimize a loss function as the average of the track errors over all songs M. In other words, we are trying to reduce the differences between the loudness of the predicted track and the original one, for all available musical pieces.

$$\mathcal{L}=-\frac{1}{N}\sum _{i=0}^{N-1}{e}_i=-\frac{1}{N}\sum _{i=0}^{N-1}\sum _{k=1}^M\mathrm{MAE}\left(y_i^k,{\widehat{y}}_i^k\right).$$

(5)

• Selection Process—we employ a 3-Way Tournament selection, ensuring diversity while favoring higher-fitness solutions. This means that a parent is extracted as the best solution from 3 random candidates. The best solution is always saved to the next generation using the Elitism method, and there are 4 mating parents for the crossover and mutation operations.
• Crossover and Mutation—a tailored crossover strategy ensures optimal trait inheritance, while a controlled mutation process introduces necessary variability, preventing stagnation. Instead of a probability approach, we always apply a custom crossover operation between 2 parents. Each gene is selected from the 2 parents as the best one by comparing the gene error $e_i$ at each track i, using Equations (3) and (4). For the mutation operation, we use an adaptive mutation [27,28] probability of 10% for the parent-crossing solutions and 1% for the elite chromosome.

The customized genetic algorithm can represent a good solution for the loudness control problem because it finds a fixed set of coefficients as the best approximation for multiple songs. However, one of the problem with this approach is that there will always be the same values for the coefficients (unless retraining is demanded). Because of this, if the training songs are very different between each other, the genetic algorithm will try to find the best solution that can obtain the minimal fitness function, but this may not always be the best auditory experience when mixing the tracks with the corresponding coefficients.

2.5. Neural Network for Loudness Optimization

In order to test the eligibility of our proposed method, in addition to the customized genetic algorithm, we also implemented a neural network that can solve the automatic loudness control problem in an adaptive way instead of a fixed solution. We chose a Convolutional Neural Network (CNN) architecture because it has the ability to extract useful information from correlated data, in our case, the successive audio samples. Because stereo channels usually have correlated information with many similarities, we simplified the problem by stacking both channels into a single one using a Fortran-like index order (the left sample is followed by its corresponding right sample). This enables us to use 1D convolution instead of the 2D operation, ensuring a better representation for the extracted time features.

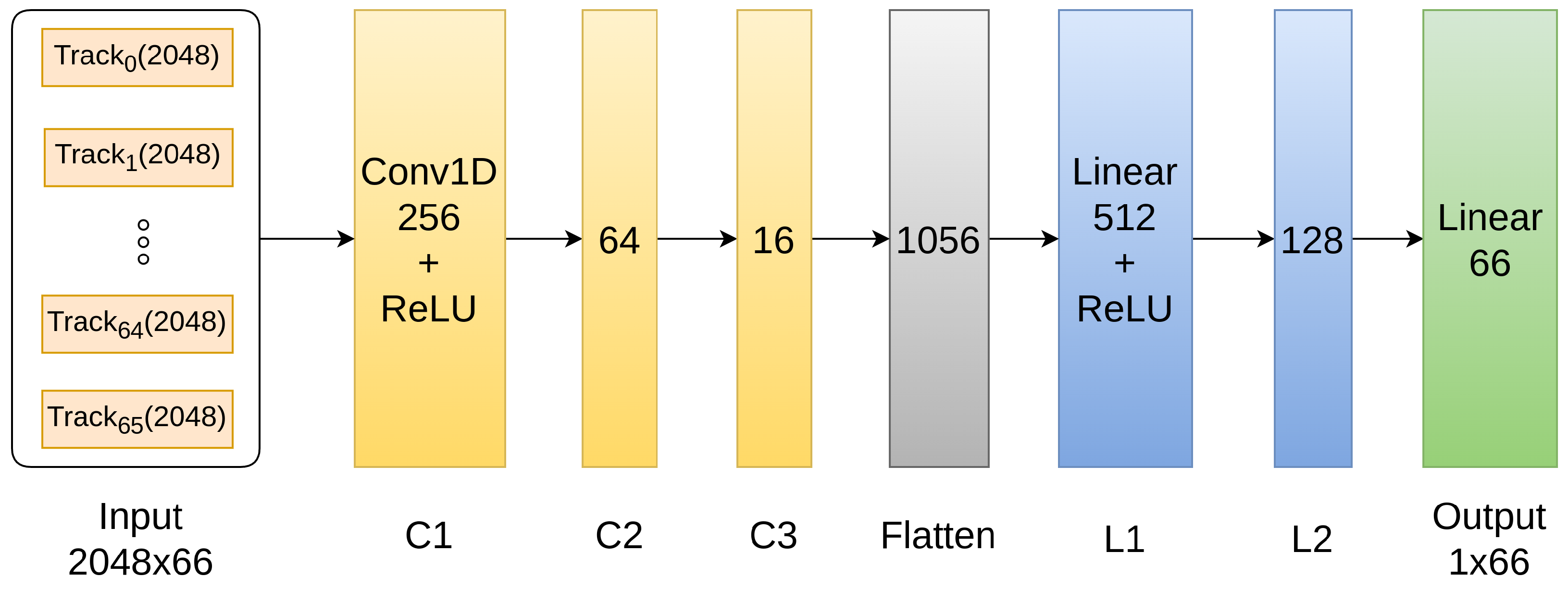
A big advantage when using a neural network is its ability to generalize by learning on a batch of data, instead of one single example. In our case, since the number of audio mixes in the dataset is limited, we chose our batch size as the entire train data size (15 songs), allowing the model to extract information from all musical pieces available for training. The output of our architecture will be represented by a vector of 66 coefficients, ensuring that all the tracks have a corresponding scaling factor (the same as the genetic algorithm output). Usually, augmenting operations for extending the training dataset are applied, e.g., overlapping windows for audio are treated as different examples in the input of the model. However, because we decided to use only the best segment of 1024 stereo samples in the genetic algorithm, we kept the same input for our neural network as well, therefore, only one segment was used from each track. The only difference is that the input for the genetic algorithm is stereo, while the neural network receives the stacked mono signal. The architecture of the model is represented in Figure 1.

Note that we used a simple model in order to learn the track coefficients, because this problem does not require very complex architectures, since this is only a scaling task. However, we mention that any type of architecture can be used here, and more large models might be required for bigger datasets. The loss function used is the same one presented in Equation (5). This means that we did not apply the MAE function between real and predicted coefficients, but rather on the input samples multiplied with the predicted coefficients and compared with the ground truth samples. An explication for this will be the fact that the MAE function between audio signals can give better results than an error between only 66 values. This neural network was implemented only to test its functionality for this problem and can be considered as a baseline for all the next tasks in automatic mixing, e.g., EQ, panning, DRC or even artificial reverberation.

3. Results

Both our methods (genetic algorithm and neural network) were applied for each of the 10 sound engineers, in order to capture the preferences of each individual. For this reason, 10 solutions from the customized genetic algorithm were obtained, as well as 10 trained machine learning models. In order to correctly conduct a comparison of the two methods, we divided the dataset composed of 20 songs in 15 songs used for train and 5 musical pieces for validation purposes, for both algorithms. The 5 mixtures for validation were selected based on their uniqueness and their differences between other songs. Those validation songs were considered outliers, or in other words, musical pieces too difficult to extract the correct coefficients when combined with other songs.

For the training process, it is important to mention that usually songs have multiple versions of the same track (e.g., guitar1, guitar2, violin1, violin2, etc.). When recording or mixing both symphonic and modern music, it is typical to combine similar instrument tracks to make the best use of technical resources and improve artistic expression. For instance, when there are several violinists in an orchestra section or multiple guitar parts in a song, they are frequently combined into a single track during the mixing process. This method saves the channels of the mixing console, decreases the amount of processing required and reduces the size of files, making it easier to handle and save them. From an artistic standpoint, when tracks that perform the same part, such as double tracking guitar riffs or a violin section, are combined, it results in a cohesive and more dense sound. To address this issue, we consider a single track $x^k$ (e.g., guitar) which represents the mean of all the possible versions $x_j^k$ of the corresponding track, as presented in Equation (6):

$$x_i^k=\frac{1}{V}\sum _{j=0}^{V-1}{x}_{i,j}^k,$$

(6)

where j represents the index of the current variant from all possible V versions for track k of song i.

By doing this, we are always able to keep the same number of 66 tracks, no matter the song. However, one constraint is that for both methods, the algorithm will optimize one single coefficient value for the corresponding track, instead of a multitude of them. While all sound engineers had the possibility to change all available tracks (including their variants), the automatic approaches can only approximate the track composed from grouping all available variants. This means that all track versions will have the same mean coefficient at prediction, therefore, it will always be at least a small difference between the predicted mix and its reference. Nevertheless, having the same coefficient value for a group of the same tracks can give a smooth audio sensation and might actually be better perceived by the listener.

For the subjective listening test, each engineer participating in the project received four distinct forms of a mix: the RAW, unedited tracks summed after recording; the artist’s MIX, which is the engineer’s personal mix used as a reference for the algorithms; and the versions generated by the GA and NN algorithms. The engineers were given the songs in a random order and labeled in a manner that prevented them from knowing what version they were reviewing. In order to preserve consistency and assure reliable assessment, each engineer examined the songs in their private studio using their familiar setup that they are used to for mixing. This method helped in reducing any variations in the listening environment that could potentially impact their evaluations of the audio quality. For the subjective listening test described, the engineers used the same digital audio workstation (DAW) software that they are most accustomed to for mixing to conduct the evaluations. This choice is significant as it ensures that the engineers are working within a familiar audio processing environment, reducing the learning curve and potential biases that might arise from unfamiliarity with new software tools. This ensured an impartial evaluation. The engineers were instructed to listen to each version 3 times in order to acquaint themselves with the subtleties of each mix. After participating in these listening sessions, participants were given the task of evaluating each version using the ITU standard grading scale, which ranges from 1 to 5. A rating of 1 indicates the lowest quality, while a rating of 5 indicates the highest quality. The average of these three scores was then calculated to generate a final score for each mix version for every engineer. The results for the training dataset are presented in

Table 1. Mean listening scores over the training dataset of 15 songs. The last column represents the average over all 10 subjects for each of the 4 versions.

Version	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	All
original (RAW)	3.5	3.9	3.5	3.1	3.5	2.9	3.7	1.2	3.5	1.5	3.0
artist’s mix (MIX)	4.3	4.1	4.0	3.7	3.3	3.3	4.3	2.2	4.0	4.0	3.7
genetic algorithm (GA)	4.6	3.9	4.2	3.6	3.1	3.4	3.9	2.9	4.2	4.5	3.9
neural network (CNN)	4.5	4.2	4.5	3.7	3.1	3.7	4.1	3.3	4.5	3.7	3.9

and

Table 2. Mean listening scores over the validation dataset of 5 songs. The last column represents the average over all 10 subjects for each of the 4 versions.

Version	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	All
original (RAW)	3.4	3.7	3.6	3.2	2.2	1.6	3.5	1.4	3.6	1.6	2.8
artist’s mix (MIX)	4.7	4.0	4.3	3.8	2.9	3.2	4.6	2.8	4.3	4.0	3.9
genetic algorithm (GA)	4.3	3.2	3.8	2.8	3.2	2.6	3.8	2.2	3.8	2.2	3.2
neural network (CNN)	4.3	3.5	4.0	3.8	2.0	3.0	3.7	2.2	4.0	2.2	3.3

for validation.

Upon reviewing the listening test results for the 15 songs used to train the algorithms, we observe that the genetic algorithm achieved a score that was equal to or greater than the human-engineered mix in half of the cases, specifically for 5 out of the 10 engineers. The CNN also performed notably, matching or surpassing the MIX in 4 out of the 10 instances. In the scenarios where the GA and CNN did not outscore the MIX, their performance remained close to the reference, indicating a marginal difference. This tight competition between the algorithms and the human MIX scores underscores the sophistication and potential of these automated mixing tools to closely approximate, if not enhance, the nuanced craft of human audio engineering.

In the validation phase of our study, we assessed the performance of the algorithms on a set of 5 complex songs, selected for their challenging nature in terms of mixing. The results for these songs are revealing in terms of the capability of both GA and CNN to handle complicated audio tasks. The RAW tracks, which had no processing, received scores that highlight the inherent difficulties present in the unaltered recordings, with mean scores ranging from 1.4 to 3.7 across the engineers. In contrast, the human-engineered MIX versions, which represent the benchmark of professional quality, scored significantly higher, with means spanning from 2.8 to 4.7, reflecting the engineers’ ability to enhance and refine the tracks. Notably, the GA and CNN both showed strong performances in this challenging scenario. The scores from GA were consistently competitive, ranging from 2.2 to 4.3, closely trailing the MIX scores and, in some cases, matching them. The CNN mirrored this robust performance with scores from 2.0 to 4.3, demonstrating that the advanced modeling and learning capabilities of CNNs are effective even with the most complex mixes.

These results suggest that both automated methods are adept at navigating the intricacies of sophisticated song structures and mixing requirements. Their performance in this validation set reinforces the potential of these algorithms to act as valuable tools in the mixing process, providing high-quality results even when confronted with demanding audio material. In the realm of audio engineering, professionals are often distinguished by varying levels of proficiency, each characterized by distinct skill sets, experiences and contributions to the music-production process. Our participant engineers might be categorized based on their competence level as follows:

• S1 and S6: Professional Engineers (Pro);
• S8, S9 and S10: Semi-Professional Engineers (Semi-Pro);
• S5 and S7: Aspiring Engineers (Aspiring);
• S2, S3 and S4: Amateur Engineers (Amateur).

In reinterpreting the data based on the level of proficiency, we observe distinct trends in how the different engineer categories perceive the quality of mixes produced by the algorithms compared to the raw and human-engineered mix. The Pro engineers rated their mix highest, which is expected as it aligns with their high standards and experience in creating polished mixes. However, it is noteworthy that both the GA and CNN also received high ratings from these engineers, often very close to their MIX scores. This suggests that the algorithms are producing results that approach professional quality, even in the eyes of seasoned engineers. Semi-Pro engineers provided a diverse range of scores. Interestingly, the algorithms, especially CNN, received scores that were competitive with the MIX, occasionally surpassing them. This indicates that the Semi-Pro engineers found the automatic mixed tracks to be of a high standard, suggesting that these tools could be particularly beneficial for those in this category looking to enhance their output. Aspiring engineers demonstrated a wide range of responses, possibly reflecting their developing ears and mixing preferences. The algorithms’ scores were generally favorable, sometimes matching the MIX, which could indicate that these tools might serve as educational aids, helping aspiring engineers understand and achieve better mixing standards. For the Amateur engineers, the MIX and the algorithmic outputs were also rated better than the RAW version, with the algorithms often scoring on par with the human mixes. This reflects the potential for the GA and CNN to serve as effective tools for amateurs, helping them achieve a more professional sound that might otherwise be beyond their current skill level.

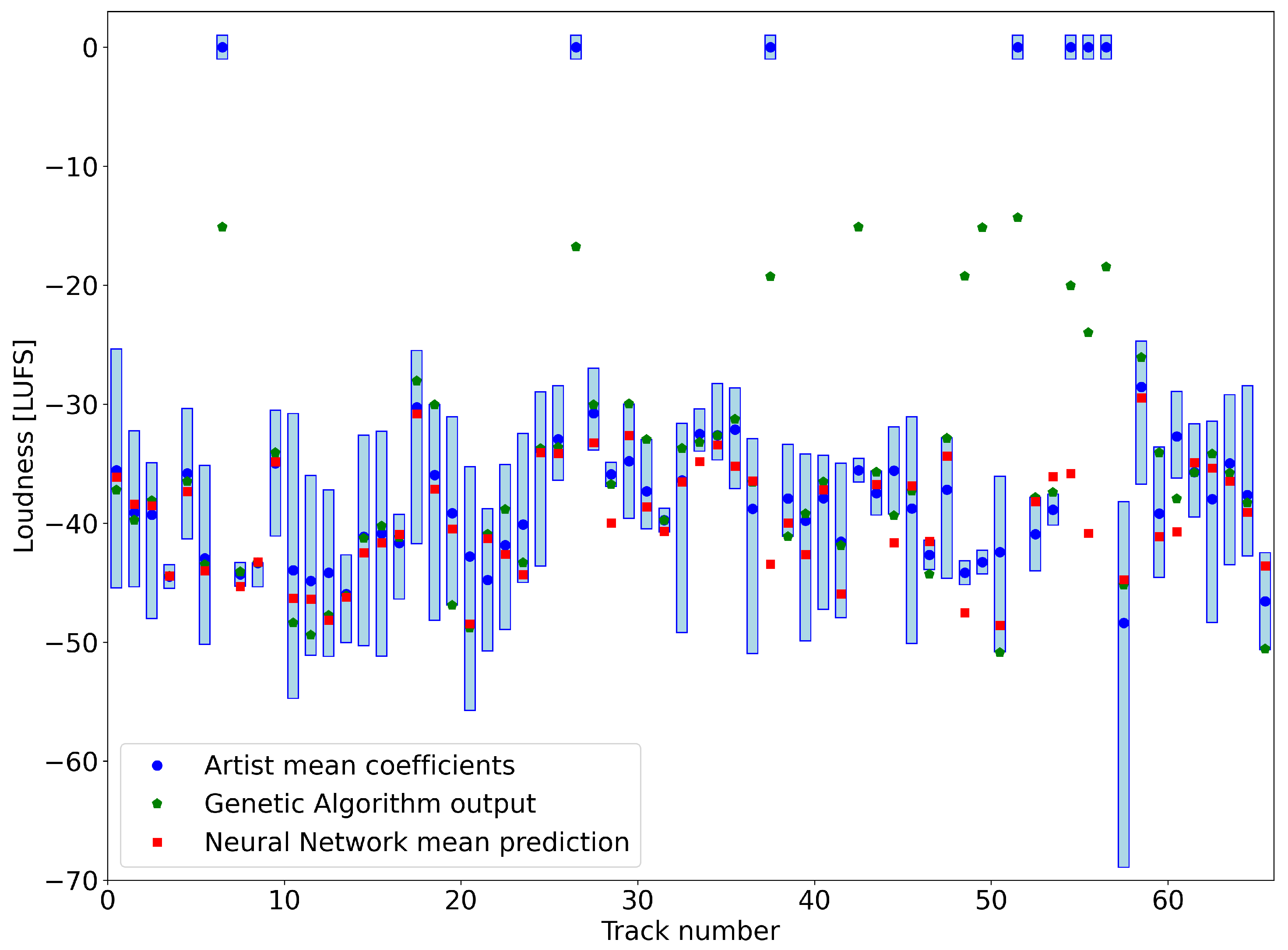
In Figure 2, we chose to illustrate a comparison between the mean preferences of one Pro artist over the 20 songs, and the two automatic proposed methods (GA and NN). The loudness variance of the original artist mixes for all 20 songs is delimited in the rectangle blue boxes, showing significant variations between songs.

The blue dots represent the mean computed over the 20 songs for the artist’s coefficient for each track. The green pentagons are illustrated by the output of the genetic algorithm, and the red squares are the mean predicted coefficients from the neural network. As you can notice, both automatic methods are close to the user’s mean preferences. The genetic algorithm will always output the same constant coefficients, which makes it a consistent method. On the other hand, the neural network always tries to adjust to the received input, therefore, the prediction will be different based on audio, which makes it an interesting adaptive algorithm. The advantage of GA is that the prediction is very fast because it only loads the best solution, but it has the disadvantage that it is not adaptable. On the other hand, the neural network is very flexible, but requires more time to predict because it needs to receive the audio input, which has to go through all the pre-processing operations previously mentioned. Our findings showed that Pros spent about 5 min on simpler songs and up to 30 min on more complex tracks to achieve their mix. In contrast, amateur engineers sometimes required up to an hour to reach satisfactory results, illustrating the steep learning curve and time investment needed without the aid of automation. Once trained, our methods significantly reduced this time expenditure, showing the potential of these algorithms not only to assist engineers by automating the initial, labor-intensive steps of mixing but also to expedite the overall mixing process.

The training and inference processes were conducted on a laptop with Nvidia GeForce RTX 2060 as GPU, which proves that both our methods can be used on common computers, representing a big advantage for artists because they can use this program on their personal laptops. The custom genetic algorithm was trained for 30,000 iterations, while the neural network was trained for 200 epochs. For training the NN, we used the Adam [29] optimizer with a learning rate of $1\times {10}^{-4}$ and a batch size of 20. We minimized a MAE loss function between the ground truth audio samples and the input samples multiplied by the predicted coefficients, as depicted in Equation (5).

4. Discussion

Our comprehensive analysis yielded compelling results: both GA and CNN displayed a remarkable ability to not only improve upon the raw, unprocessed tracks, but also to meet—and occasionally exceed—the quality of mixes engineered by humans. This was evidenced across a training set of 15 songs and a validation set of 5 complex songs, where the automated algorithms consistently achieved scores close to or surpassing those of the human-engineered mix. The findings from our study are not an indicator that the role of the audio engineer is being replaced by algorithms, but rather that these technologies are emerging as sophisticated assistants in the mixing process. The GA and CNN demonstrate an ability to lay the groundwork according to an engineer’s preferences, effectively setting the stage for them to concentrate on the more creative and subjective aspects of mixing. This symbiosis could see engineers leveraging AI (Artificial Inteligence) to handle initial and time-consuming tasks, such as balancing levels and applying basic EQ settings, thereby freeing up more time for them to delve into the artistic nuances that truly define a mix. Despite the promising outcomes, our results are not without limitations. The current algorithms, while proficient in technical execution, may not yet fully replicate the creative and intuitive aspects of human mixing—the ‘art’ that goes beyond the ‘science’. Moreover, the listening tests were confined to specific genres and mixing styles, which may not represent the full spectrum of music production. Future research should explore the incorporation of creative and stylistic decision-making into the algorithms to capture the artistry of human engineers more faithfully. Additionally, expanding the dataset to include a wider variety of musical genres and engineering styles could provide a more comprehensive understanding of the capabilities of the algorithms. Investigating user-friendly interfaces for these technologies could also facilitate their adoption by professionals in the field, enhancing the collaborative potential between humans and AI in audio engineering. As we look to the future, our research will not rest at the threshold of leveling algorithms. We plan to expand this personalized approach to encompass other critical aspects of mixing, including equalization, compression and saturation. By extending the scope of our algorithm to these domains, we aim to offer an even more comprehensive and intuitive mixing tool, one that further blurs the lines between professional studio quality and accessible home recording setups.

5. Conclusions

In this paper, we present a novel approach that centers around a highly personalized multi-track leveling algorithm for automatic mixing. This implementation is designed to reflect the individual preferences of any user by learning their specific style and applying these preferences to the mixing process. We provide two algorithms for resolving the automatic loudness control: a customized genetic algorithm and a convolutional neural network, where both are adept at adjusting to the unique requirements of the user and executing precision-based loudness control across a multitude of tracks. We created a dataset of 20 songs, ranging from diverse genres and complexity. Both the genetic algorithm and neural network were trained on 15 songs and validated on 5 other songs, where the validation set was chosen as the most different musical pieces compared to the others from the dataset. This creative approach presents a novel multi-track leveling technique specifically designed to greatly simplify the mixing process for music producers and sound engineers. Upon receiving a new set of multi-tracks for a song, our approach not only efficiently organizes and arranges the tracks based on a specific order, but also does preliminary processing on each individual track, a process that is normally carried out manually. This preprocessing aligns each track with the precise mixing preferences of the engineer, guaranteeing that they are optimally prepared for import into the desired DAW. This tailored design enables producers to concentrate more effectively on enhancing and finalizing the remaining activities in the production process. This virtual assistant technology promotes creative freedom and makes high-quality mixing available to a greater variety of music enthusiasts and professionals by responding to the particular styles and requirements of each producer, thereby democratizing access.