Abstract
This paper introduces an algorithm to tackle the boundary condition (BC) problem, which has long persisted in the numerical and computational treatment of smoothed particle hydrodynamics (SPH). Central to the BC problem is a need for an effective method to reconcile a numerical representation of particles with 2D or 3D geometry. We describe and evaluate an algorithmic solution—boundary SPH (BSPH)—drawn from a novel twist on the mesh-based boundary method, allowing SPH particles to interact (directly and implicitly) with either convex or concave 3D meshes. The method draws inspiration from existing works in graphics, particularly discrete signed distance fields, to determine whether particles are intersecting or submerged with mesh triangles. We evaluate the efficacy of BSPH through application to several simulation environments of varying mesh complexity, showing practical real-time implementation in Unity3D and its high-level shader language (HLSL), which we test in the parallelization of particle operations. To examine robustness, we portray slip and no-slip conditions in simulation, and we separately evaluate convex and concave meshes. To demonstrate empirical utility, we show pressure gradients as measured in simulated still water tank implementations of hydrodynamics. Our results identify that BSPH, despite producing irregular pressure values among particles close to the boundary manifolds of the meshes, successfully prevents particles from intersecting or submerging into the boundary manifold. Average FPS calculations for each simulation scenario show that the mesh boundary method can still be used effectively with simple simulation scenarios. We additionally point the reader to future works that could investigate the effect of simulation parameters and scene complexity on simulation performance, resolve abnormal pressure values along the mesh boundary, and test the method’s robustness on a wider variety of simulation environments.
1. Introduction
The smoothed particle hydrodynamics (SPH) approach is a widely used, mesh-free, Lagrangian representation of gaseous or fluid media that enjoys applications in a variety of simulation tasks, which range from theoretical astrophysics to material science and computational fluid dynamics (CFD) [1,2,3,4]. In particular, SPH is broadly appreciated for its ability to provide numerical and computational support where model interactions between fluid particles and simulated solids, walls, and structures are called for. Nonetheless, SPH is troubled by an open, non-trivial challenge in the form of the “Boundary Condition” (BC) or “Fluid-Surface Interactions” (FSI) problem [5]. FSI arises from a conundrum in the numeric representation of fluid particles, wherein they have no direct means of interacting with 2D or 3D representations of boundary manifolds. FSI creates significantly thorny issues for applications of SPH. At a minimum, two main criteria are expected for boundaries. First, the boundary must prevent fluid particles from intersecting completely with the boundary and therefore escaping the fluid domain. Second, the boundary must minimize truncation of the density kernel of fluid particles close to or intersecting with the boundary manifold [3,6]. If these criteria are not met, the resulting hydrodynamics markedly deviate from real-world properties, often in ways that are visually and empirically unrealistic in simulation.
One of the earliest known BC methods is Peskin’s “Immersed Boundary Method” (IBM), which approximates boundary forces via a Dirac delta function [7,8]. The IBM has seen success in various application fields [9] but exhibits unexpected spring-like behavior in elastic boundaries [10]. Since the IBM, three broad perspectives dominate popular BC methodologies: (1) Monaghan’s “Boundary Particles” method [11]; (2) fictitious “dummy” particles, commonly referred to as “Ghost Particles” or “Mirror Particles” [12,13]; and (3) semi-analytical wall boundaries via boundary integrals [14,15]. Hybrid variations of these methods are also common, such as Yildiz et al.’s combination of boundary and ghost particles [16] or Dalrymple and Knio’s “staggered” boundary particle rows approach [17,18], which share resemblance with Marrone et al.’s “fixed” ghost particles variation for SPH [19,20].
Yet, for all their successes in advancing computational representations of hydrodynamics, many of these methods are limited in one key respect: their ability to treat the complexity of the boundary manifold. Consider, for example, the case of ghost particles. They are incompatible with boundary manifolds that feature sharp edges, turns, or points. Moreover, methodologies that involve 3D boundary particles suffer in computational performance due to the difficulty of interpolating across 3D surfaces. There have been noble attempts to circumnavigate this issue. For example, Müller attempted to resolve the 3D interpolation issue by using a Gaussian kernel to dictate the placement of boundary particles, but alas, this method involves the subdivision of mesh triangles and can lead to complications with bigger meshes [21]. Alongside challenges with absolute boundary properties, it is often observed that boundary particles also suffer from aberrant effects in the fluid particles as they grow close to the boundary. Invariably, this near-boundary problem manifests in a range of compromising knock-on effects that are often unsatisfactory for application domains. These issues may present as (1) the bouncing of fluid particles due to the “bumpy” surface formed by boundary particles; (2) unexpected pressure forces acting on fluids at the beginning of simulations; (3) tensile instability, wherein fluid particles close to the boundary sometimes clump together; and (4) the density kernel of fluid particles close to the boundary being “truncated” beyond the initial layer of boundary particles. As a result, corrections are needed, such as Monaghan and Katjar’s strategy of having boundary forces dependent solely on fluid particles’ perpendicular distance to the boundary [22]. Alongside the obvious deviation from empirical properties of known hydrodynamic processes, We note that these four problems are largely unacceptable for simulations that are designed to produce visual hydrodynamics, as in computer graphics and special effects. Additionally, we point the reader to Vacondio et al.’s [23] summary of key issues that still persist among existing boundary conditions, including whether a boundary condition can remain consistent without compromising stability, how an initial distribution of particles can avoid “shocks” due to initial interactions with boundaries, and the need for a methodology for solid wall BCs representing actual 2D and 3D geometries. The last point is of particular importance for certain fields where 3D meshes are the primary means of representing geographic data or dynamic entities.
With the aforementioned open challenges for SPH modeling as motivation, in this paper, we introduce, demonstrate, and then evaluate a BC methodology that is compatible with triangle-based 3D polygon meshes that affords for rapid prototyping of particle interactions between concave and convex boundary manifolds. This method—which we refer to as boundary SPH, or BSPH—involves the direct calculation of the closest point of a particle on a 3D boundary manifold, thereby also affording a signed distance calculation to determine whether a particle is intersecting or encased by the boundary manifold. As the online performance of the method in graphics applications is a topic of concern, we also evaluate BPSH in Unity3D, where BPSH may be utilized to drive parallelized particle operations via HLSL compute shaders. Our focus on 3D meshes as the primary representation of the boundary manifold is driven by three core motivations. First, in our implementation of BSPH, the boundary manifold is already discretized through its triangle faces, removing the need for the approximation of the boundary, as seen with the IBM or boundary integrals. Second, BSPH does not rely on boundary particles, which can be computationally expensive to manage in 3D simulations due to the need to interpolate across the 3D manifold. Third, BSPH shows broad compatibility with manifolds that feature complex geometry such as sharp edges, points, or concave segments, with which ghost particles sometimes have compatibility issues. We propose the BSPH methodology with the idea that simple scenarios involving 3D meshed objects can be rapidly developed and implemented with game engines such as Unity3D, thus widening the range of possible applications for SPH-driven simulation in demanding application environments that call for realistic-behaving, realistic-looking, real-time performance in front of everyday users.
2. Materials and Methods
This paper describes BSPH as an FSI methodology that enables interactions between SPH fluid particles and mesh-based 3D geometries. Specifically, BSPH decomposes the FSI problem into two smaller problems: (1) detecting a particle’s closest projection onto the 3D mesh surface; and (2) deriving the reflected velocity based on the boundary normal at this closest projection. Key to this method is the concept of “Voronoi Regions” [24,25], or the segmentation of a 2D or 3D space such that all points encased within a segment are closest to one of a set of feature points. In this case, this FSI method can be generalized to the following steps:
- For each fluid particle and mesh triangle , project p onto the 2D plane defined by t () and determine the closest point on the triangle to this projection (). Voronoi region tessellation is needed here to divide the 2D plane of each triangle into regions that identify if is closest to either a vertex or edge or if is located inside the triangle.
- For each fluid particle , determine the closest point on the mesh such that the distance between p and is minimized.
- For each fluid particle, determine the boundary normal based on the closest ’s position on the mesh as well as the signed distance from p to the closest based on .
This methodology shares conceptual similarities with the Gilbert–Johnson–Keerthi (GJK) distance algorithm: both methodologies rely on Voronoi region tessellation [26]. However, the GJK algorithm is only applicable to convex geometries. We instead follow concepts exhibited by a field of collision detection algorithms known as “Discrete Signed Distance Fields” [27]. Such methods attempt to detect minimum signed distances between query points and a 2D or 3D manifold by first “extruding” the faces, wedges, and vertices of the manifold outward and inward, then querying which extrusion each query point is located inside [28]. Mauche’s “Characteristic/Scan-Conversion” (CSC) method [29] is a notable application of the concept that uses “scan-conversion” for the point-extrusion check.
We combine the strategies for the signed distance calculation from Payne and Toga [30] and Baerentzen and Aanaes [31]. Payne and Toga’s strategy compares query points with each triangle on a mesh to determine the closest point and offers suggestions for optimization, such as calculating the sign of the distance separately from the distance measurement and precomputing triangle vertices and normal components prior to runtime. Both suggestions are realized through Baerentzen and Aanaes’ strategy of calculating the “pseudonormal” vectors of edges and vertices of a mesh and deriving the signed distance based on boundary normals and closest point alone. This is in agreement with Thürrner and Wüthrich’s original method [32]. Particle–boundary interactions are adapted from Furhmann et al.’s method [33], which also mentions the use of Voronoi Regions for fast detection of closest mesh points but leaves this step ambiguous in its implementation. More importantly, Furhmann et al.’s application re-positions particles based on the boundary normal of the closest point on the mesh for each particle, which we also adopt in our implementation.
2.1. Triangle Mesh Basics
In 3D computer graphics and modeling, a polygonal mesh is a collection of vertices, edges, and faces that define a volume in three-dimensional space. The “faces” of the mesh are the rendered surface of the mesh, whose appearance may then be controlled by factors such as color, material, and UV coordinates. Mesh types are usually defined by:
- Choice of face type: Meshes can be defined based on their face type. Typical face types include triangles, quads, or n-gons.
- Choice of representation: This refers to the explicit format and type of data that are stored about the mesh. Types include but are not limited to vertex–vertex (“VV”), face–vertex meshes, and winged-edge meshes [34].
In our implementation, we strictly refer to the face–vertex mesh representation. Face–Vertex triangle meshes store vertices as an array of float3 positions relative to the mesh center. The faces (triangles) of the mesh are stored separately as an integer array three times longer than the vertex list. A triangle is represented as a set of three integers, each corresponding to an entry in the vertex array. Edges are not contained in this representation and therefore have to be interpreted from the triangle array.
2.2. Pre-Processing 3D Meshes
Prior to the start of a BSPH simulation, we must pre-process each 3D mesh to better fit our scheme. In particular, we must calculate and cache the following properties of each mesh:
- Vertices: In mesh data, vertices are stored as float3 vectors that may overlap based on how the mesh data was created. We must filter vertices into a condensed list where each vertex is unique and no overlaps exist among vertices. For example, Unity3D’s “Cube” primitive is originally represented by 24 vertices, which can be condensed into 8 vertices. We also must calculate the pseudonormal vector of each vertex that represents the boundary normal vector at the vertex. This pseudonormal vector is the average of the pseudonormal vectors of all triangles connected to a vertex, weighted by the angle of influence that the vertex has on the face area (see Figure 1).
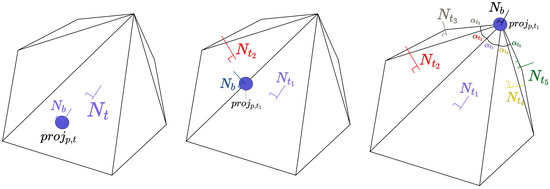 Figure 1. Calculation of pseudonormal vectors of faces, edges, and vertices. The face pseudonormal is the cross-product of two edges, while the edge pseudonormal is the unweighted sum of the two triangles connected to the edge. The vertex pseudonormal is the weighted sum of all triangle face pseudonormals, whose triangles are connected to the vertex, weighted by the vertex’s angle in each triangle.
Figure 1. Calculation of pseudonormal vectors of faces, edges, and vertices. The face pseudonormal is the cross-product of two edges, while the edge pseudonormal is the unweighted sum of the two triangles connected to the edge. The vertex pseudonormal is the weighted sum of all triangle face pseudonormals, whose triangles are connected to the vertex, weighted by the vertex’s angle in each triangle. - Edges: Edges are not stored in face–vertex triangle meshes and must be computed manually. Edges are composed of two vertices, with a midpoint calculated based on the average of its two vertices’ positions. We must also calculate the pseudonormal vector of each edge that represents the boundary normal vector. We take advantage of the idea that an edge can only connect two triangles at maximum and calculate the pseudonormal vector as the average of the two faces’ pseudonormal vectors. If a mesh is incomplete and is compsed of only one triangle, we simply set the pseudonormal vector as the same as the connected triangle’s pseudonormal vector.
- Triangles: Triangles are stored as a tuple of index values that point to vertices in the mesh’s vertices array. In our scheme, mesh triangles also feature a centroid position based on the average positions of its vertices, a pseudonormal vector orthogonal to the plane defined by the triangle, a signed distance float value from the triangle’s 2D plane to the origin, and 2D pseudonormal vectors of each edge along the 2D plane defined by the triangle. All of these properties need to be manually calculated.
When handling multiple meshes, we conduct this pre-processing operation on each mesh individually, then concatenate the vertices, edges, and triangle arrays into global lists of vertices, edges, and triangles. These global lists are segmented such that the vertices, edges, and triangles of each mesh remain grouped together. References to these segments are indexed by an additional fourth global list representing the mesh objects themselves, with each item in this list storing the starting indices of that mesh’s vertices, edges, and triangles in the global lists. Once aggregated, these global lists can be inserted into HLSL compute buffers that may then be stored in a GPU for use during the simulation step. For reference, Table 1 and Figure 1 and Figure 2 highlight the general formulae to calculate these pseudonormal vectors, their 3D representations, and an overview of the pre-processing step, respectively. See Appendix A for the pseudocode on this pre-processing operation.

Table 1.
List of triangle properties that are involved in particle–mesh interactions.
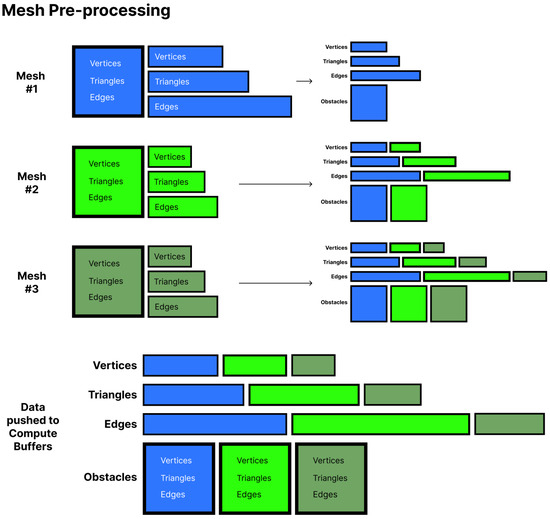
Figure 2.
Visual representation of the pre-processing steps described for three mesh obstacles. The first mesh is represented with blue, the second with light green, and the third with dark green. Each mesh’s vertex, edge, and triangle data are stored into global lists that are then buffered into the GPU.
2.3. Single Particle–Triangle Scenario
Let us define a single pair of a particle and triangle , where P is the set of all particles in the fluid simulation and T is the set of all mesh triangles. p is a float3 position with some radius that represents either the particle’s smoothing kernel or visual radius, while t is a triplet of three vertices . The 2D plane of t is notated as .
2.3.1. Calculating Plane Projection
The first step is to project p onto to determine (see Figure 3). The projection equation is defined as follows:
where:
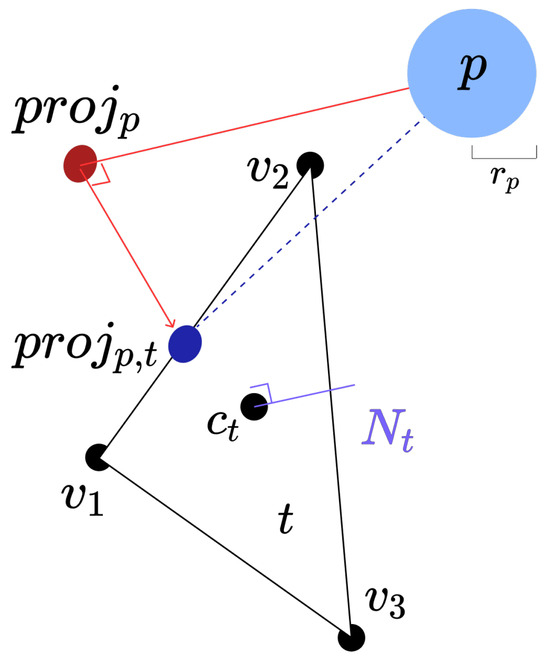
Figure 3.
Depiction of a single triangle t with three vertices, a centroid calculated from the average position of the three vertices, and a face normal vector. With particle p with radius , the steps are to first find and then calculate , which lies on either a vertex, edge, or within t.
- p: The particle’s current position in 3D space; it also represents the vector from world origin to the particle’s current position.
- : The triangle’s face pseudonormal vector.
- : The triangle’s centroid.
- : The signed distance between p and . A negative (−) distance means that the particle is “above” the mesh triangle, while a positive (+) distance means the particle is “below” the mesh triangle. Note that a positive sign does not necessarily mean that the particle is submerged or intersecting with the mesh obstacle as the particle may simply be in a concave segment of the mesh.
2.3.2. Calculating the Closest Point and Corresponding Boundary Normal
After determining , we can calculate the closest point on t, or , and the corresponding boundary normal . This requires the tessellation of into seven Voronoi regions, discretized by t’s edges and their planar 2D normals (see Figure 4). An edge’s planar 2D normal vector is calculated with the following equation:
Normally, we check the six outer regions before defaulting to being in the triangle. We introduce an optimization step where we first check which vertex is closest to , then check the connected regions to that vertex. This reduces the number of calculations required from a 7-region check to a 4-region check.
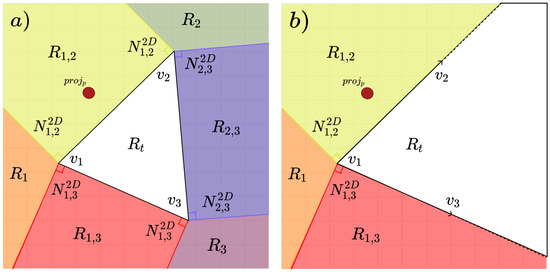
Figure 4.
The Voronoi Region tessellation of based on the planar 2D normal vectors of each edge. Regions are colored to distinguish them from one another in the visualization. The red dot represents , a particle’s projection onto the 2D plane. (a) The original 7 regions that need to be checked. (b) An optimization that considers a 4-region rather than 7-region check.
To calculate and the resulting boundary normal , let us assume that the closest vertex is designated as , with its assigned Voronoi region as . The two other vertices of t are designated and , the two edges connected to are designated as and , their planar 2D normal vectors as and , and their resulting Voronoi regions as and . The region contained by t is designated as . Refer to Table 2 for how to check which region lies in and the resulting and . Figure 5 shows a visual representation of the steps listed.

Table 2.
Region checks to identify which Voronoi region lies within.
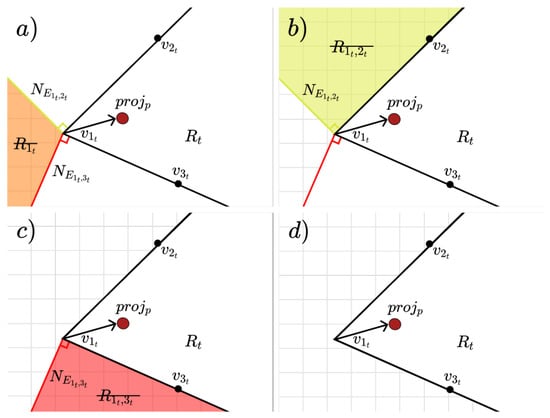
Figure 5.
Example process of checking which Voronoi region lies in. Regions are colored to distinguish them from one another in the visualization, and the red dot represents . The process starts with Panel (a) and shows that region is rejected. Panels (b) and (c) show the same with regions and , respectively. The algorithm ends in Panel (d) where is determined to be in region . Therefore, and .
2.3.3. Calculating the Signed Distance
The signed distance from particle to triangle can be combined into a single expression as provided by Baerentzen and Aanaes [31]:
This assumes that we are looking at a singular point without a radius to consider and that the signed distance is negative if the point is contained inside the mesh boundary. However, in the SPH scheme, we are dealing with particles with radius . To prevent the kernel truncation issue, we need to detect the moment the smoothing kernel intersects with the boundary manifold. Therefore, we provide an alternative form of the signed distance function in consideration with :
where , which represents the innermost point on the smoothing kernel of particle p. We follow the convention that the negative sign indicates that the particle’s smoothing kernel is submerged into the boundary manifold, while a positive sign indicates that the particle and its smoothing kernel are outside the boundary manifold.
2.4. SPH Fluid Interaction
For proper integration with any SPH scheme, this particle–triangle check must be extended to all particles and all mesh triangles . The boundary condition must be accounted for the scenario where, for each single particle p, its is within some radius of the particle. Depending on the implementation, it is highly recommended to make equivalent to the smoothing kernel of the particle in order to prevent kernel truncation. p is therefore intersecting with the boundary if the distance between p and is less than or equal to .
The general operational flow from mesh pre-processing to simulation runtime is visualized in Figure 6. As a general rule of thumb, the mesh pre-processing step occurs prior to the first frame of the simulation. The global mesh vertices, edges, triangles, and obstacles arrays are buffered into the GPU and referenced during every simulation frame. During the simulation, SPH particles are compared with every obstacle to identify whether they are intersecting with any meshes in the scene.
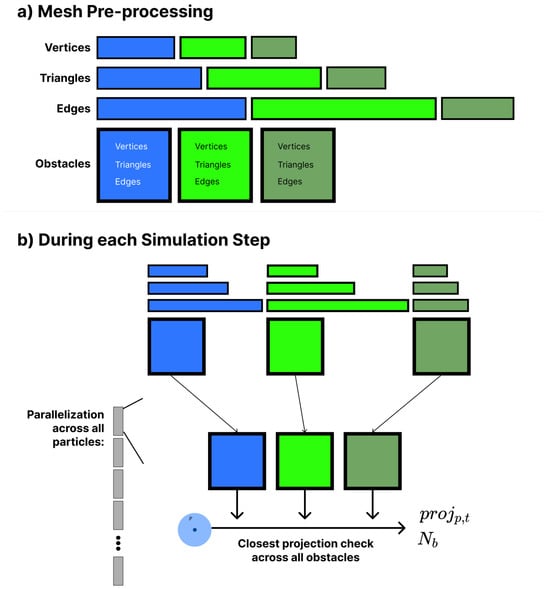
Figure 6.
Overview of the general operational pipeline from the pre-processing to simulation step. In this visualization, three mesh obstacles are represented by blue, light green, and dark green. (a) Pre-processing occurs prior to the first simulation step. (b) During each simulation step, parallelization allows for each particle to be compared with each mesh obstacle and their vertices, edges, and triangles in thread groups on the GPU. The final determination of the closest mesh and its corresponding closest projection and boundary normal vector is calculated for each particle.
When a particle is detected to be intersecting with (or submerged in) the boundary manifold, the particle must be reflected away from the boundary to prevent truncation. The simplest approach is to (1) reposition the particle so that its smoothing kernel is just beyond the boundary manifold; and (2) adjust its velocity to reflect off of the boundary manifold (see Figure 7). We take inspiration from Fraga Filho’s implementation of reflective boundary conditions to implement particle–boundary interactions with respect to the boundary manifold’s friction and restitution coefficients [35]. Given the velocity for particle p, the reflected vector is the component of two orthogonal sub-vectors:
where is the restitution coefficient that influences the strength of the reflection along the boundary normal and is the friction coefficient that influences the strength of the reflection along the tangent line of the boundary method at .
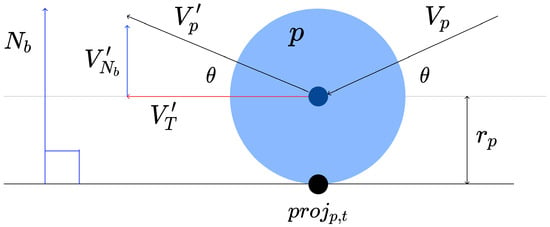
Figure 7.
Calculation of the reflected velocity vector based on the particle’s initial velocity , the projected point of p on the boundary manifold , and the boundary normal vector . Particle p is represented by the light blue circle whose center is the darker, inner circle. is derived from combining , the tangential component of the reflected velocity that is affected by the boundary’s friction coefficient, and , the normal component of the reflected velocity that is affected by the boundary’s restitution coefficient.
3. Results
In order to assess its robustness in application, we evaluated the BSPH method in different 3D environments that vary in simulation size and complexity of meshes. The goal of this evaluation was to identify how successfully BSPH could prevent particles from intersecting with a given mesh boundary manifold and how the average frames per second (FPS) of the simulation would be affected. To yield empirical output, the resulting pressure gradients of the fluid manifold were measured to test for pressure irregularities around the mesh boundary. Each simulation was run with Müller’s weakly compressible SPH variant [36], which uses Desbrun and Gascuel’s “Spiky” kernel for pressure force operations [37], Müller’s custom kernel for viscosity force operations, and a Poly6 kernel for all other operations, such as density calculations. Müller also stabilizes pressure operations by modifying the ideal gas state equation to the following:
where p represents pressure, k represents the bulk modulus, represents density, and represents the expected or ideal density of the fluid medium at rest.
The experimental setup was implemented in Unity3D (ver.2021.3.11f1), where meshed objects were placed in the 3D world space and BSPH calculations were conducted using an HLSL compute shader. To enable particle–mesh interactions, the mesh data of all 3D meshed entities in the simulation space were pre-loaded into HLSL compute buffers and transformed from local to world space whenever a mesh entity was updated in the 3D scene; all particle–mesh calculations were also subsequently conducted in the GPU. Note that double-precision values cannot be used as input or output data for HLSL data streams when passing data between the CPU and GPU; thus, single-precision float values had to be used instead in this version of the implementation. The setup was run on a PC with an AMD Ryzen 5 5600G processor with 16 Gb of RAM alongside an NVIDIA GeForce RTX 3070 GPU with 8 Gb of VRAM.
3.1. Simple Setups
This series of evaluations focuses on particle–mesh interactions on flat and inclined planes. In the ideal case, the mesh boundary method would prevent particles from intersecting with the plane, allow for the smooth movement of particles as they flow down an inclined plane with a 10-degree slope, and prevent particles from flowing down the incline in a no-slip condition. Unlike existing boundary particle methods where the boundary particle manifold would create irregularities in the surface and cause particles to bound erratically, our BSPH method should ideally prevent such erratic particle movements. Simulation parameters for all simple setups are provided in Table 3.

Table 3.
Simple setups—simulation parameters.
Figure 8 depicts the results of the flat-plane simulation, which shows 64 particles in an 8 × 8 grid arrangement falling onto a completely horizontal plane. In this simulation, the particles were spaced 0.125 m apart and also had a kernel radius of 0.125 m. The plane was a 2 m × 2 m quad divided into two separate mesh triangles, such that the edge connecting the two mesh triangles followed the diagonal of the quad. This also means that some particles will fall directly onto this edge. Despite this fact, the particles’ pathlines and positions indicate that the particles do not erratically move after landing and remain in their original grid formation, even after coming to rest. No particles appear to penetrate the mesh boundary, which in this case is the horizontal plane positioned above the ground level of the simulation. This verifies the mesh boundary’s ability to repel particles and prevent erratic interactions between particles and the mesh.
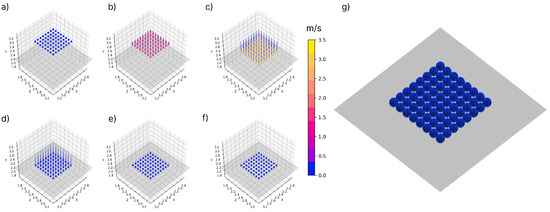
Figure 8.
The flat-plane simulation run with an 8 × 8 grid of particles placed 0.125 m apart and forced to fall onto a horizontal plane. Panels (a–f) depict the pathlines of the 64 particles as they fall, while panel (g) shows the final result in Unity3D that corresponds with panel (f).
A similar setup was conducted with the plane at an angle of 10 degrees. This time, the plane was a 5 m × 5 m quad, and a 5 × 5 grid of particles were placed 0.2 m away from each other. The plane had a friction coefficient of zero. The particles were placed further uphill from the quad center and are expected to “roll” down the incline. Figure 9 depicts the results of the inclined plane simulation, which shows the pathlines of 5 particles among the 25 particles. The pathlines do not depict any erratic or abnormal behavior in the particles’ movements and depict a consistent trajectory, fulfilling our expectations of the interaction between rolling spheres and a smooth surface.
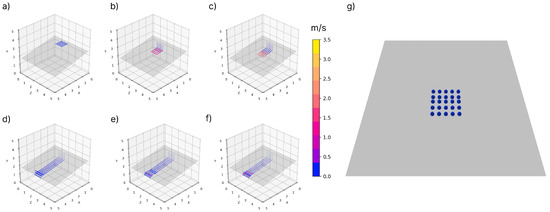
Figure 9.
The inclined plane simulation run with a 5 × 5 grid of particles placed slightly further than the smoothing kernel radius and forced to fall onto the plane inclined at 10 degrees and with a friction coefficient of 0. Panels (a–f) depict the pathlines of five of particles as they fall and “roll” down the incline path, while panel (g) shows the screenshot of the particles during movement in Unity3D.
A third setup was conducted with the same parameters as the inclined plane, but with a friction coefficient of 1.0. In this scenario, one should expect particles to “stick” to the plane and not move when they land on the plane. Figure 10 depicts the results of this scenario and shows that as the particles land, they do not move from their original formation and stick in formation. This validates the idea that the velocity reflection equation managed to suitably cancel out the tangential velocity component of the reflected velocity vector for each particle, thus leaving them stuck in place.
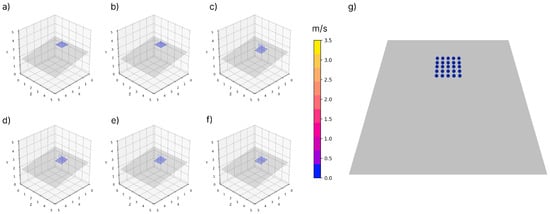
Figure 10.
The inclined plane simulation run with a 5 × 5 grid of particles placed slightly further than the smoothing kernel radius and forced to fall onto the plane inclined at 10 degrees with a friction coefficient of 1. Panels (a–f) depict the pathlines of five of particles as they fall and “stick” onto the inclined plane. Panel (g) shows the screenshot of the particles at the end of the simulation run, where they still remain uphill and in formation.
3.2. Water Tank Setups
Our BSPH method, despite its efficacy in the plane-based trials, still does not account for pressure irregularities in particles close to the boundary manifold. To verify this, two water tank simulations were conducted: one with an empty tank, and another with a 90-degree wedge placed on the floor in the middle of the tank. A third water tank setup was also created to simulate a dam break scenario with the wedge acting as a slope, for which we measured whether the mesh boundary method could handle fluid movement from dam breaks. The tank itself was represented by an inverted mesh cube stretched to fit a 10 m × 7.5 m × 2.5 m area. This means that the limits of the experiment space were contained by mesh triangles, and therefore, all particle interactions with the water tank were effectively particle–mesh boundary interactions. The tank and wedge mesh boundaries both had a friction coefficient of 0 and restitution coefficient of 0.25. Simulation parameters for all water tank simulations are provided in Table 4.

Table 4.
Water tank setups—simulation parameters.
In the first two water tank tests, particles had a kernel support radius of 0.2 m and were initialized with 0.2 m of space between particles. The resulting pressure gradients were measured at the end of the simulation, when the particles no longer exhibited any movement and the fluid was still. The pressure gradients visualized here are calculated based on the original pressure equation:
and are expressed in Pascal units, though the SPH implementation in Unity3D still uses Müller’s modified variant.
The empty tank scenario (Figure 11) was initialized with 15,750 particles, while the tank with the wedge scenario (Figure 12) was initialized with 13,500 particles. Visual analysis of both results show that irregular pressure values are most prominent along the edges of the simulation area, where particles would interact with the inverted cube and wedge meshes. Irregular pressure values can also be seen along the bottom of the simulation space as well. This falls within expectation, as the mesh boundary method does not account for the loss in pressure due to empty kernel space for particles touching the boundary. Nonetheless, the simulation is stable enough to be at a standstill, and particles show no sign of escaping the boundary manifold. The wedged tank simulation shows that the particles do not penetrate the boundary formed by the wedge and instead follow its contour as expected.
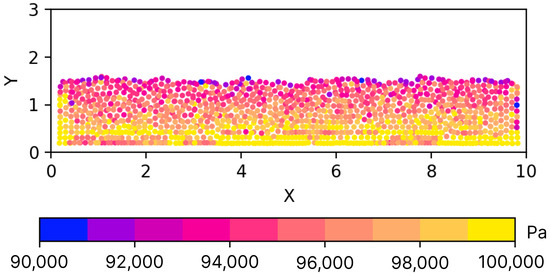
Figure 11.
A slice of the empty tank simulation depicting particles along the middle of the Z-axis and the resulting pressure gradient at the end of the simulation run. Visual observation shows that while the pressure gradient decreases with elevation, the sides of the simulation feature irregular pressure values among particles closest to the mesh edge. Irregular pressure values can also be seen along the bottom of the tank, where particles are touching the bottom of the cube mesh.
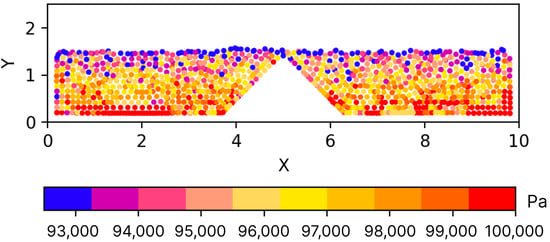
Figure 12.
A slice of the wedged tank simulation depicting particles along the middle of the Z-axis and the resulting pressure gradient at the end of the simulation run. Visual observation shows similar results to the empty tank scenario, where the particles are directly touching or are in close proximity to the mesh boundaries experience irregular pressure values. The particles successfully conform to the manifold shape of the tank, following the general contour of the boundary in 3D space.
The final tank-based setup that we explored was a traditional dam break scenario with the same incline wedge placed in the middle of the scene. Rather than identifying pressure gradients along the boundary, the focus of this evaluation was to observe whether particles penetrated the boundary due to excessive pressure and viscosity forces generated from the fluid motion. In this setup, 20,445 particles were placed on one side of the tank and were placed at intervals of 0.15 m. This means that the particles, upon initialization of the simulation, were expected to expand outward and thus generate the necessary fluid motion to simulate a dam break scenario. Figure 13 shows the status of the simulation in Unity3D at 1-second intervals. As illustrated in screen captures, we can show that the inverted cube and wedge meshes that represented the water tank dimensions successfully contained all particles.

Figure 13.
Screen captures of the dam break simulation from Unity3D, with each frame (a–d) depicting the status of the simulation at 1-second intervals. Coloration is indicative of particle speed from 0 m/s (blue) to 5 m/s (green). The wedged slope shows particles following the sloped contour to produce the wave-like flow that collides with the other side of the tank. The tank’s mesh boundary successfully prevents all particles from escaping the tank.
3.3. Concave Mesh and Fluid Flow Setups
A key value of our BSPH method is sourced in its ability to handle concave boundary manifolds. To demonstrate this capability for BSPH, we established three fluid tests with three different types of mesh objects: a convex sphere, a concave elongated torus, and a concave bowl. Particles were parameterized with a support kernel radius of 0.2 m and initialized in a 125 × 25 × 5 grid arrangement at the start of the simulation, totaling to 31,250 particles. Particles would flow rightward at an acceleration of 9.8 m/s, similar to that of gravity. The sphere, torus, or concave bowl was placed along the particle path to interact with the particles. The simulation parameters for all three fluid flow tests are provided in Table 5.

Table 5.
Fluid flow setups—simulation parameters.
A first setup was designed to depict the resulting flow field around a concave sphere of 7.5 m radius. It was expected that particles would flow around the curvature of the sphere and not intersect or be submerged within the sphere’s mesh manifold. Figure 14 shows the resulting flow fields at approximately 3 s after the start of the simulation, when particles are interacting with the sphere. As expected, the particles appear to flow around the sphere and form two distinct flow fields as they proceed past the sphere. No penetration of the mesh boundary was visually observed.
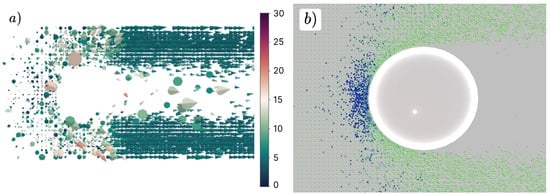
Figure 14.
Screen captures of the flow field simulation with a concave sphere with a radius of 7.5 m. This visual was generated approximately 3 s after the start of the simulation. Panel (a) visualizes the flow field as a cone field, while Panel (b) is a screen capture of the Unity3D simulation. The Unity3D simulation uses a transparent sphere to highlight possible submerged particles. Both visualizations’ coloration represent particle speeds within a range of 0–30 m/s.
A second setup uses an elongated torus with a tunnel formed by the elongated inner cavity of the torus. We established the torus with a depth of 1.32 m while being set to 0.35 m × 0.35 m in width and height. In addition, the torus was rotated off-axis by 45 degrees around the y-axis, creating a diagonal path that particles would be expected to flow through, while particles outside the torus flow around the outer curvature of the mesh. Figure 15 shows how particles flow through the cavity formed by the inner ring of the torus, and visual observation shows that particles collide strongly with the lip of the torus near the tunnel entrance and proceed to flow through the mesh, as expected. Due to the arrangement of the torus, particles outside of the tunnel follow the diagonal orientation of the torus and reach a choking point near the end of the torus’ tunnel. Visual analysis indicates that no particles appear to intersect or be submerged within the mesh boundary manifold of the torus.
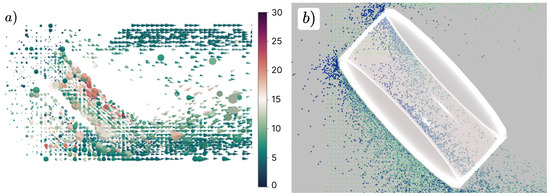
Figure 15.
Screen captures of the flow field simulation with an elongated torus forming a tunnel that particles are expected to flow through. This visual was generated approximately 3 s after the start of the simulation. Panel (a) visualizes the flow field as a cone field, while Panel (b) is a screen capture of the Unity3D simulation. The Unity3D simulation uses a transparent torus to highlight possible submerged particles. Both visualizations’ coloration represent particle speed within a range of 0–30 m/s.
A third setup uses a bowl mesh meant to appear as a cooking pot. The opening of the bowl was approximately 5 m in radius, and the bowl reached a depth of 3 m. Particles were expected to initially hit the interior of the bowl, scatter, and remain in the bowl as particles outside the bowl radius flowed past it. The results are shown visually in Figure 16; particles hit the bowl and consequently bounce around in it. Within expectation, the bowl mesh manages to prevent particles from moving through the bowl and creates a scattering effect among particles within the bowl’s curvature.
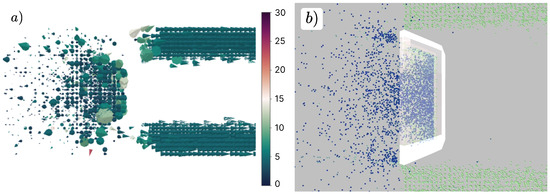
Figure 16.
Screen captures of the flow field simulation with a cooking pot mesh creating a cavity where particles were expected to fall into and remain. This visual was generated approximately 3 s after the start of the simulation. Panel (a) visualizes the flow field as a cone field, while Panel (b) is a screen capture of the Unity3D simulation. The Unity3D simulation uses a transparent mesh to highlight possible submerged particles. Both visualizations’ coloration represent particle speeds within a range of 0–30 m/s.
3.4. Mesh Boundary Performance
To quantify the performance of BSPH, we measured the average frames per second (FPS) of each simulation scenario during runtime, when particle–mesh interactions were most prominent. We parameterized the simulation complexity based on the number of vertices, triangles, and edges present in each scene, as well as the number of particles used in the simulation. The full results are reported in Table 6.

Table 6.
Mesh boundary performance by scene.
Initial analysis indicates that the number of particles in the simulation affects the average FPS of every simulation. Among scenario groupings (i.e. plane, tank, and flow field), average FPS does not appear to change significantly. For example, we showed that the FPS only dips by about 5 FPS between “Flow Field (bowl)” and “Flow Field (Sphere)”, despite the jump in the number of triangles, edges, and vertices. The jump in FPS between the “Dam Break” and “Tank (with Wedge)” scenarios appears to be largely driven by the number of particles, though it is also possible that this jump could be affected by particle–particle interaction calculations driven by the initial arrangement of particles in either scenario. For example, in the “Dam Break” scenario, particles are condensed into one side of the tank, while in the “Tank (with Wedge)” scenario, particles are more broadly dispersed across the length of the tank. Further analysis is required to explain the effect of initial simulation parameters on overall average performance of the simulation. Holistically, the average FPS values for each scenario show that the affected mesh boundary method can still be effectively run in tandem with parallelization schemes for SPH, insofar as when simpler simulations, such as those covered in this report, are concerned.
4. Conclusions
This paper describes a new approach of implementing the SPH boundary method. Our scheme, BSPH, takes advantage of 3D mesh architecture to create boundary manifolds that may be concave and feature complex geometry such as bowls or tunnels. The method is inspired by existing work in graphics and uses concepts from discrete signed distance fields, Payne and Toga’s closest point querying algorithm, and Baerentzen and Aanaes’s methods for calculating normal vectors for faces, edges, and vertices. To evaluate and establish robustness for BSPH in application, we tested a variety of simulations in a Unity3D implementation that utilizes compute shaders to optimize kernel neighborhood calculations and parallelize particle operations. Our performance and empirical results show promise in BSPH’s agility and ability to prevent submersion of particles into the boundary manifold, and we were successful in demonstrating that BSPH operates with similar effectiveness with both concave and convex mesh types. The average FPS performance indicates that BSPH can be run effectively over commonplace scenarios that are routine in computer graphics applications, for example in gaming and in special effects. We plan to further test the limitations of the mesh boundary method to identify how initial simulation parameters as well as the number of mesh vertices, edges, and triangles affect the runtime performance of the simulation. Our future efforts will also study whether edge cases can be identified through testing a more varied sample of mesh objects and whether the particle–mesh projection step can be further parallelized for additional flexibility in optimization. Furthermore, we will investigate the behavior of BSPH when integrated with double-precision values during mesh data pre-processing and during simulation. Finally, we aim to address the issue of irregular pressure values for particles close to the boundary in future iterations of the mesh boundary method.
Author Contributions
R.K.: Conceptualization, idea brainstorming, and formation; methodology, conceptualization, and mathematical formulation of the mesh boundary algorithm; software, implementation of the Unity3D build for prototyping, and result aggregation; writing—original draft preparation, submission drafting, and write-up; and literature review of existing boundary condition methods. P.M.T.: Supervision, project oversight, and guidance; project administration, providing the necessary computational hardware required to run SPH; and funding acquisition, aiding R.K. in achieving GAANN fellowship funding. All authors have read and agreed to the published version of the manuscript.
Funding
Ryan Kim was supported by a U.S. Department of Education Graduate Assistance in Areas of National Need (GAANN) fellowship under award P200A210096.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Mesh Pre-Processing Algorithm
| Algorithm A1: Mesh Pre-Processing during Initialization |
 |
| Algorithm A2: PreprocessMesh() |
 |
| Algorithm A3: PreprocessVertices() |
 |
| Algorithm A4: PreprocessTriangles() |
| Data: : Current triangle index, : original mesh triangles, : mesh’s condensed list of vertices, : mapper from original vertex indices to condensed vertices, ref : reference to mesh’s triangle data Result: Extending with angle, center, and normal data // Retrieving positions of triangle’s vertices ; ← First vertex’s position; ← Second vertex’s position; ← Third vertex’s position; // Updating vertex angles for this triangle ; // Updating triangle’s centroid and orthogonal normal vector ; ← Right-hand Rule; |
| Algorithm A5: PreprocessEdges() |
 |
References
- Reynolds, C. Big fast crowds on PS3. In Proceedings of the 2006 ACM SIGGRAPH Symposium on Videogames, New York, NY, USA, 30–31 June 2006; pp. 113–121. [Google Scholar] [CrossRef]
- Monaghan, J. Smoothed Particle Hydrodynamics and Its Diverse Applications. Annu. Rev. Fluid Mech. 2012, 44, 323–346. [Google Scholar] [CrossRef]
- Shadloo, M.; Oger, G.; Le Touzé, D. Smoothed particle hydrodynamics method for fluid flows, towards industrial applications: Motivations, current state, and challenges. Comput. Fluids 2016, 136, 11–34. [Google Scholar] [CrossRef]
- Ye, T.; Pan, D.; Huang, C.; Liu, M. Smoothed particle hydrodynamics (SPH) for complex fluid flows: Recent developments in methodology and applications. Phys. Fluids 2019, 31, 011301. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, Y.J.; Wu, D.; Adams, N.A.; Hu, X. Smoothed particle hydrodynamics: Methodology development and recent achievement. J. Hydrodyn. 2022, 34, 767–805. [Google Scholar] [CrossRef]
- Boregowda, P.; Liu, G.R. On the accuracy of SPH formulations with boundary integral terms. Math. Comput. Simul. 2023, 210, 320–345. [Google Scholar] [CrossRef]
- Peskin, C.S. Numerical analysis of blood flow in the heart. J. Comput. Phys. 1977, 25, 220–252. [Google Scholar] [CrossRef]
- Peskin, C.S. The immersed boundary method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef]
- Hou, G.; Wang, J.; Layton, A. Numerical Methods for Fluid-Structure Interaction—A Review. Commun. Comput. Phys. 2012, 12, 337–377. [Google Scholar] [CrossRef]
- Stockie, J.M.; Wetton, B.R. Analysis of Stiffness in the Immersed Boundary Method and Implications for Time-Stepping Schemes. J. Comput. Phys. 1999, 154, 41–64. [Google Scholar] [CrossRef]
- Monaghan, J. Simulating Free Surface Flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Morris, J.P.; Fox, P.J.; Zhu, Y. Modeling Low Reynolds Number Incompressible Flows Using SPH. J. Comput. Phys. 1997, 136, 214–226. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Bonet, J.; Kulasegaram, S.; Rodriguez-Paz, M.; Profit, M. Variational formulation for the smooth particle hydrodynamics (SPH) simulation of fluid and solid problems. Comput. Methods Appl. Mech. Eng. 2004, 193, 1245–1256. [Google Scholar] [CrossRef]
- Ferrand, M.; Laurence, D.R.; Rogers, B.D.; Violeau, D.; Kassiotis, C. Unified semi-analytical wall boundary conditions for inviscid, laminar or turbulent flows in the meshless SPH method. Int. J. Numer. Methods Fluids 2013, 71, 446–472. [Google Scholar] [CrossRef]
- Yildiz, M.; Rook, R.A.; Suleman, A. SPH with the multiple boundary tangent method. Int. J. Numer. Methods Eng. 2009, 77, 1416–1438. [Google Scholar] [CrossRef]
- Dalrymple, R.; Rogers, B. Numerical modeling of water waves with the SPH method. Coast. Eng. 2006, 53, 141–147. [Google Scholar] [CrossRef]
- Dalrymple, R.A.; Knio, O. SPH Modelling of Water Waves. In Coastal Dynamics ’01; American Society of Civil Engineers: Reston, VA, USA, 2012; pp. 779–787. [Google Scholar] [CrossRef]
- Marrone, S.; Antuono, M.; Colagrossi, A.; Colicchio, G.; Le Touzé, D.; Graziani, G. δ-SPH model for simulating violent impact flows. Comput. Methods Appl. Mech. Eng. 2011, 200, 1526–1542. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S.; Lugni, C. Propagation of gravity waves through an SPH scheme with numerical diffusive terms. Comput. Phys. Commun. 2011, 182, 866–877. [Google Scholar] [CrossRef]
- Müller, M.; Schirm, S.; Teschner, M.; Heidelberger, B.; Gross, M. Interaction of fluids with deformable solids. Comput. Animat. Virtual Worlds 2004, 15, 159–171. [Google Scholar] [CrossRef]
- Monaghan, J.; Kajtar, J. SPH particle boundary forces for arbitrary boundaries. Comput. Phys. Commun. 2009, 180, 1811–1820. [Google Scholar] [CrossRef]
- Vacondio, R.; Altomare, C.; De Leffe, M.; Hu, X.; Le Touzé, D.; Lind, S.; Marongiu, J.C.; Marrone, S.; Rogers, B.D.; Souto-Iglesias, A. Grand challenges for Smoothed Particle Hydrodynamics numerical schemes. Comput. Part. Mech. 2020, 8, 575–588. [Google Scholar] [CrossRef]
- Torrens, P.M. Exploring behavioral regions in agents’ mental maps. Ann. Reg. Sci. 2016, 57, 309–334. [Google Scholar] [CrossRef]
- Okabe, A.; Boots, B.; Sugihara, K.; Chiu, S.N. Spatial Tessellations: Concepts and Applications of Voronoi Diagrams; John Wiley & Sons: Chichester, West Sussex, England, 2009; ISBN 0-471-98635-6. [Google Scholar]
- Gilbert, E.; Johnson, D.; Keerthi, S. A fast procedure for computing the distance between complex objects in three-dimensional space. IEEE J. Robot. Autom. 1988, 4, 193–203. [Google Scholar] [CrossRef]
- Jones, M.; Baerentzen, J.; Sramek, M. 3D distance fields: A survey of techniques and applications. IEEE Trans. Vis. Comput. Graph. 2006, 12, 581–599. [Google Scholar] [CrossRef]
- Sigg, C.; Peikert, R.; Gross, M. Signed distance transform using graphics hardware. In Proceedings of the IEEE Visualization, Seattle, WA, USA, 19–24 October 2003; pp. 83–90. [Google Scholar] [CrossRef]
- Mauch, S. A Fast Algorithm for Computing the Closest Point and Distance Transform. 2000. Available online: https://www.researchgate.net/publication/2393786_A_Fast_Algorithm_for_Computing_the_Closest_Point_and_Distance_Transform (accessed on 18 July 2023).
- Toga, A.W.; Payne, B.A. Distance Field Manipulation of Surface Models. IEEE Comput. Graph. Appl. 1992, 12, 65–71. [Google Scholar] [CrossRef]
- Baerentzen, J.; Aanaes, H. Signed distance computation using the angle weighted pseudonormal. IEEE Trans. Vis. Comput. Graph. 2005, 11, 243–253. [Google Scholar] [CrossRef] [PubMed]
- Thürrner, G.; Wüthrich, C.A. Computing Vertex Normals from Polygonal Facets. J. Graph. Tools 1998, 3, 43–46. [Google Scholar] [CrossRef]
- Fuhrmann, A.; Sobottka, G.A. Distance Fields for Rapid Collision Detection in Physically Based Modeling. Proc. GraphiCon 2003, 2003, 58–65. [Google Scholar]
- Baumgart, B.G. A polyhedron representation for computer vision. In Proceedings of the May 19–22, 1975, National Computer Conference and Exposition on—AFIPS ’75, Anaheim, CA, USA, 19–22 May 1975. [Google Scholar] [CrossRef]
- Fraga Filho, C.A.D. Reflective boundary conditions coupled with the SPH method for the three-dimensional simulation of fluid–structure interaction with solid boundaries. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 256. [Google Scholar] [CrossRef]
- Müller, M.; Charypar, D.; Gross, M. Particle-based fluid simulation for interactive applications. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, San Diego, CA, USA, 26–27 July 2003; pp. 154–159. [Google Scholar]
- Desbrun, M.; Gascuel, M.P. Smoothed Particles: A new paradigm for animating highly deformable bodies. In Proceedings of the Eurographics Workshop, Poitiers, France, 31 August–1 September 1996; pp. 61–76. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).