Abstract
The problem of finding the best path trajectory in a graph is highly complex due to its combinatorial nature, making it difficult to solve. Standard search algorithms focus on selecting the best path trajectory by introducing constraints to estimate a suitable solution, but this approach may overlook potentially better alternatives. Despite the number of restrictions and variables in path planning, no solution minimizes the computational resources used to reach the goal. To address this issue, a framework is proposed to compute the best trajectory in a graph by introducing the mathematical morphology concept. The framework builds a lattice over the graph space using mathematical morphology operators. The searching algorithm creates a metric space by applying the morphological covering operator to the graph and weighing the cost of traveling across the lattice. Ultimately, the cumulative traveling criterion creates the optimal path trajectory by selecting the minima/maxima cost. A test is introduced to validate the framework’s functionality, and a sample application is presented to validate its usefulness. The application uses the structure of the avenues as a graph. It proposes a computable approach to find the most suitable paths from a given start and destination reference. The results confirm that this is a generalized graph search framework based on morphological operators that can be compared to the Dijkstra approach.
1. Introduction
Path planning in a graph represents one of the most fundamental tasks in a graph space. In the literature, several approaches deal with this task by limiting and conditioning it to particular contexts, rendering it computable in closed scenarios [1,2,3,4,5]. In this context, the main approaches developed to deal with the problem of best-searching path planning are the following.
Global search approaches: This approach considers the full graph as the solution space, where the origin and destination are known, and it uses a global directional cost function such that it minimizes/maximizes in terms of the best direction. The traveling path across the graph is performed by local navigation using the most reliable direction provided by the global cost function. The global approach has the disadvantage that it might grow, becoming difficult to analyze with specific computer resources [6,7,8]; however, it has the advantage that it is always looking for the best path solution, making it less likely to fall into loops or diverge from the destination. These approaches produce a general representation with a low level of detail, prioritizing the global searching reference, making it suitable for scenarios with fixed computational resources [9,10,11].
Local search approaches: These approaches assume that local optimization might drive the global solution. They use a local neighborhood, and it begins by locating the best solution. Each step forward updates the local searching neighborhood by adding new evidence to search for the best path solution. However, these approaches are computationally restricted; they might fall into loops, diverge from the global solution, or locate a sub-optimal solution. The computational complexity depends on the size of the neighborhood and the criterion function cost [12,13,14]. These approaches are helpful when there is no previous knowledge about the scenario, making them feasible in uncertain environments. The low complexity makes it possible to obtain subgraph partitions and instantiate in several initial states [15,16,17].
Hybrid approaches: These combine the above two types of approaches with the local analysis neighborhood, which results in a method that is computationally tractable. Adding some restrictions helps to reflect the global direction to locate the solution. Additionally, prior knowledge can be used several times to define additional criteria as a heuristic for specific scenarios and contexts. Most studies, including [3,18,19], have proposed mixed strategies that combine well-accepted local and global approaches. The cost function can be modified with the introduction of reset criteria whenever partial solution are reached.
Nature-inspired approaches: Finally, this type of approach involves using optimization techniques that are inspired by the principles of nature, including the theory of evolution and the behaviors of living organisms, to efficiently solve problems across various fields of application. This is achieved by imitating the ways in which nature tackles these challenges. Some examples of such techniques are the particle swarm algorithm [20,21], evolutionary algorithms [22], ant colonies [8], and neural networks [23].
On the other hand, mathematical morphology provides a conceptual foundation for the morphological analysis (inner structures) of abstract objects, such as numbers, shapes, or graphs. The morphological analysis consists of defining two basic operators named dilation and erosion. The mixture of basic operators defines other new operators and filters, which are used to detect structures of interest, e.g., in the case of image applications [24] or volumetric reconstructions [25,26,27,28]. Nowadays, morphology represents a generalized framework to manage finite structures disposed into a given space [29,30]. In this context, it has been used in a wide range of image analysis applications [31] where the spaces are expressed as grid structures that might be associated with lattices using morphological operators [32].
A city’s infrastructure requires several electronic, communication, storage, and data analysis resources. Various studies throughout history have adopted technological approaches to sense and monitor urban variables. These urban variables allow, through analysis, the selection of the best decision in an urban context regarding the different events involved. In this context, good communication balances the resources needed and the time response. This situation involves searching for the most reliable path to travel into the city to reach a destination. This task might refer to the transportation of people, traffic, electrical devices, or other goods from a source to a destination via a specific net. A city can be represented as a graph of interconnections. However, the computation of the best-planning path is considered a graph search or traveler’s agent process and represents an NP-algorithm [33,34,35,36]. On the other hand, in recent years, studies have considered the autonomy of electric vehicles, considering variables such as speed, charge, and distance, in the context of energy consumption and the possible carbon emissions associated with these technologies [37,38].
Mathematical morphological operators induce, in a discrete space, an order criterion, which provides the basis for this work, proposing a generalized graph search framework based on morphological operators. The initial reference and the morphological operators induce a lattice such that it is possible locate possible path trajectories in the graph. The approach defines the morphological operators by starting from the minimum connected subgraph denoted for the infimum and by considering the supremum as the total space.
The continuous covering of dilation in the graph space gives the order relation. Next, a bijective mapping is performed on the natural numbers from the covering order induced, which helps to locate the possible path trajectories. The weighted cost applies several morphological operators to generalize the morphological context and provide a general weighted approach to travel within the graph.
This paper proposes a new framework to calculate the shortest path in a complex graph. The main contribution is the creation of a lattice that tracks the frequency of the mathematical operators used. This lattice provides a basis for the analysis of complex graphs and the development of algorithms using a theoretical discrete approach. The proposed morphological framework offers a novel way to navigate graphs and create schemes that can be used to solve problems. The proposal consists of two algorithms: (a) the first assumes that there is at least one solution (the entire space is connected), and (b) in the second, there is no guarantee of a solution (there are regions that are not connected). Finally, an experiment shows the capabilities of the algorithm. This experiment uses the framework to search for the most suitable path trajectories from the geographical image layer of a city in order to study the best trajectory planning. Finally, we discuss the use of the proposed framework as a general search framework based on morphological operators and compare it with another well-accepted approach.
The content is organized into several sections. Section 2 explains the theoretical concepts of mathematical morphology and graph theory. Section 3 presents the experimental analysis and the results obtained from the experiments. Section 4 discusses the findings. Finally, Section 5 provides the conclusions, discusses the proposed framework’s limitations, and outlines any future work that may be required.
2. Morphological Search Framework
In this section, we discuss the framework for a family of morphological search algorithms in graphs. The proposed framework introduces a lattice that begins with a reference point and uses a morphological dilation operator in the graph space. Furthermore, three new operators are defined: the covering dilation, the dilation frequency, and the weighted dilation. These new operators provide the foundation for the development of an algorithm for general searching.
2.1. Preliminary Concepts
Consider a set of nodes and a set of edges . A graph consists of , which is denoted by , and the definition is represented by an enumerated set . An arbitrary graph G represents the coding of a scenario [10,39]. The G graph represents a net topology of connections, where the nodes and edges denote the available places and steps. A particular lattice is denoted by a two-tuple , where is an arbitrary subset and is a partial-order relation in . The partial-order relation considers an arbitrary reference and denotes the allowed movements and directions in the navigation of L. In our case, we consider a lattice that covers all subsets of adjacent nodes that cover the graph space starting from the reference. The order by which adjacent nodes are covered, resulting in subgraphs, depends on L, where the reference defines the order relation. In other words, the supreme element of the lattice is the entire graph L. The intimum represents the element such that there is no other that belongs to ; for simplicity, it is expressed as and , respectively.
As a complement, a path lattice in L is a set of graphs of the step incremental connected graph starting from the reference and ending at references . The path is covered by all steps over to reach the graph. Regarding the order relation , the reference becomes a subset of . The path lattice is expressed as an ordered collection and describes the incremental step cover path resulting from adding the graph neighborhood under a connectivity criterion denoted by the connection order in the graph space. Two subgraphs , become adjacent under the whenever it is found that the relation belongs to the order relation. For simplicity, the path can be expressed as the number of steps from a reference to the ending as . These steps represent all intermediate adjacent steps in p.
The lattice denotes the directionality and availability transitions over the allowed subgraph in G. The graph topology and the order relation depend on the context of each scenario. Using morphological operators in the graph space G, we can define a partial order criterion, establishing the incremental criterion from the boundaries of the current subgraph. As mentioned above, mathematical morphology (MM) introduces two basic operators known as dilation and erosion. Both use a graph structure to navigate the graph neighborhood, called a structural element. The parameter denotes the structural element representing the step-up/-down reached/dismissed nodes from the current subgraph across the basic MM operators.
The operator of dilation () is an increasing function that denotes a step forward following increasing coverage for a given lattice with a unitary step . The dilation on a complete lattice is expressed as follows:
where and all nodes ; denotes the addition of the b isomorphic node referring to a if and only if , from a given neighborhood , where is a graph that denotes the homomorphic structure and G represents the graph space. represents the step forward in the order to cover G, i.e., the dilation operator indicates that the following subset belongs to , which includes the nodes adjacent to the boundary nodes of the A subset. In a complementary definition, the opposite operator is the erosion (), which is defined as follows, taking as a reference the dilation operator:
where , and, for all nodes, . denotes the addition of the b isomorphic node referring to a if and only if or a null element adds ∅, from the given neighborhood , where is a graph that denotes the homomorphic structure that represents a step backward in the relation. Figure 1 illustrates both operators (dilation and erosion) when they are applied in a given graph. The dilation moves a step-forward subgraph across the lattice under the step criterion . In contrast, the erosion operator discards elements with a lower connection criterion defined by the structural element making a step backward.
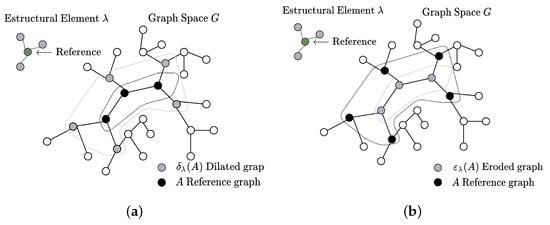
Figure 1.
Morphological basic operators: (a) dilation operator and (b) erosion operator.
These operators represent the step forward/backward to navigate over the lattice . In terms of a graph space, for a given subgraph such that belongs to L and or , where the initial position represents the infinitum inf and the supremum sup is denoted by the entire space G, there are other elements where . Both elements are represented by the dilation and erosion operations, respectively.
2.2. Prior Definitions
Any lattice L resulting from the graph space G represents an order relation with an initial reference subgraph , and the set of subsequent step-forward sorted subgraphs that need to cover the graph space G following a set of finite steps denotes the order . The subgraph covers the entire space in the intermediate steps and is defined by the homomorphic structure defined in . Any intermediate step i provides a subgraph that denotes how the consecutive finite states cover the space G.
Initially, two subgraphs are considered as such that . Here, and are defined as the start and goal nodes in G, respectively. The subgraph can be approximated starting from by applying successive dilation operators, even if does not belong to the order relation. This approximation is obtained via the definition of the covering dilation operator as follows:
such that k represents the number of times that the dilation operator is composed successively, and · denotes the compositional operator. The k-th dilation represents the first step forward until the condition holds. The successive dilation subgraphs to reach the condition represent a step-forward path to .
For all particular nodes involved in reaching , the number of times that each node becomes dilated as a result of is denoted as a set of nodes as . The function becomes such that, for all nodes , the cumulative frequency for a particular node is expressed as a tuple. Each counter is computed for all nodes in a given graph.
where b is a function defined as follows
where is a node. By notation, the expression refers to the particular frequency for the node . Figure 2 depicts the graph’s node dilation frequency during the coverage process. The graph starts from an initial reference (black node) and a destination (double-circle node). The dilated nodes are shown in gray and the available nodes in white. Under successive dilations, the number of times that a node becomes dilated increases. The reference becomes the node with the maximum frequency, and the boundaries represent the lowest frequencies. The morphological coverage by dilation applies successive dilations until the destination is reached; the frequency counter has a zero or greater value.
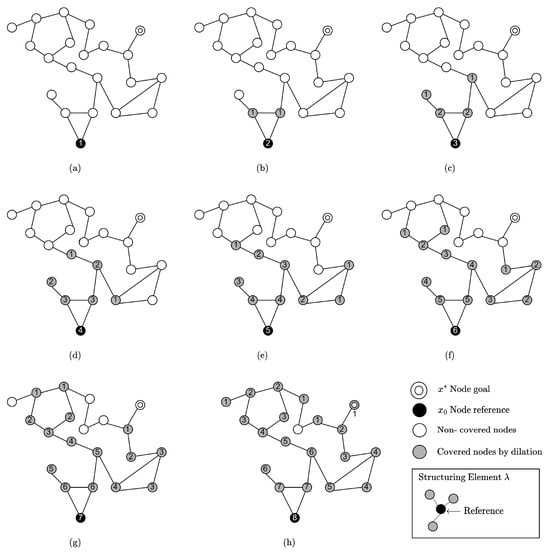
Figure 2.
Covering dilation operator and the frequency with which each node is dilated.
For weighted graphs, the definition extends as a three-tuple , adding the parameter. The formalism remains similar, with the addition of a weighted covering dilation operator, which is denoted by , and the weight is defined as follows:
where is a function defined as follows:
and is a weighted node. represents the weight required to travel across them. This weight can be accumulated, representing the cost of traveling through a given set of nodes, giving the total cost of the solution path.
2.3. Search Criterion
The morphological search criterion uses the dilation and erosion operators to conform to a lattice. The reference (initial state) represents a subgraph that indicates where the trajectory starts in the lattice. All subsequent subgraphs resulting from dilating the reference represent a lattice that denotes all possible paths to search a trajectory. After reaching the destination node, the optimal path trajectory is estimated by following the natural order constituted by the successive dilations and the frequency counters of each dilated node, starting from the destination node to the origin (inverse order).
The proposed framework consists of a given graph , as the origin, for the location of a path trajectory of connected nodes covered by a two-tuple element that denotes, under a specific criterion C, the most reliable path to travel from the node to the destination node, both in G.
The algorithm applies a morphological covering operator starting from the node until successive dilations reach the objective D. The intersection of and D is usually an empty set . In terms of semantics, whenever the intersection of both elements becomes a non-empty set , the starting and destination locations in the graph are the same. The covering dilation generates a graph denoted by , such that , i.e., the destination D has been reached via successive dilations starting from . The algorithm takes as an input a G graph space; represents the coverage by dilation to reach destination starting from , which represents the initial position (or reference); and represents the destination. The last input is a structural graph connection neighborhood. It represents a homomorphic structure for the lattice navigation . The algorithm outputs a path that follows the search criterion and the total cost associated with displacement along this path. The complete algorithm is described in Algorithm 1. This algorithm computes the best trajectory under the assumption that there are one or more solutions. In spaces without a solution, the algorithm becomes computationally infeasible. An example in which the covering dilation operator reaches the minimum path trajectory is presented in Appendix A, as well as other complementary consequences of these definitions.
The function C criterion (line 8 of the algorithm) takes as an input a given node n and a set of adjacent nodes expressed as . The output is the node that denotes the best transition from the current node n to any node belonging to its neighborhood. The function C analyzes the neighborhood, selecting the best node (minima or maxima) to construct the path.
| Algorithm 1 Morphological search with the constraint of and |
|
The algorithm assumes that the destination is a subgraph denoted by . In a blind search, the guarantee of at least one path from to D becomes complicated. In the particular case that , Algorithm 1 becomes infeasible (it falls into an infinite loop), which can be considered a disadvantage. An enhanced algorithm can overcome this based on the modification of the coverage of the dilation operator, as shown in Equation (8):
such that k represents the number of fixed times that the dilation operator is composed successively, and · denotes the compositional operator. The covering operator performs k dilation and the condition might not be satisfied. Consequently, the and functions are similar, with the difference that k denotes the upper bound for the number of times that a given node might be dilated.
The enhanced algorithm becomes useful whenever there is no guarantee of locating a solution because the destination makes it unreachable. Whenever the destination D becomes unreachable by the coverage of the dilation operator expressed by , it indicates that D belongs to a non-connected graph with the reference . There may be no path solution. In contrast, means that there is at least one possible connected path from to the destination. Finally, Algorithm 2 refers to the generalized search process. This algorithm returns an empty set whenever no path solution exists in an unknown scenario. This algorithm is always computationally feasible (i.e., under any input, it generates a response), which makes it suitable for several search applications.
| Algorithm 2 Morphological search with the constraint of |
|
2.4. Implementation Issues
A discussion about the computational complexity of the two above algorithms is presented in the following paragraphs.
The implementation is mainly affected by the expected order of connections in the graph G. A graph is expressed as a finite list of nodes, and its analysis consists of a sequential process operating over one-to-one elements. The computational complexity is addressed in three main stages: (1) the morphological operators (covering dilation and frequency/weighted calculation); (2) the complexity in estimating the best path trajectory; and (3) the evaluation process for the selection of the best forward step from a given node.
For (1), the complexity depends on the number of nodes that denotes the cardinality of the set and the expected order of all nodes involved in expressed by the constant , which represents the structural element size of . Then, the complexity is expressed as . The final complexity multiplies the previous complexity by a factor of k, representing the worst number of dilations needed to cover the search space . In conclusion, the covering dilation complexity is .
The computational complexity of the frequency and weighted operators and operators is the same. In real scenarios, the covering and frequency/weighted operators might compute simultaneously, reducing the necessary computing time. In each iteration, the list of nodes for dilation might be computed separately because the dilation is performed independently; this makes it possible to segment them into m chunks (sublist) for the implementation of a parallel approach, reducing the final complexity by . Whenever the graph order is homogeneous across all elements, the computational complexity for a given dimensionality becomes . The factor m denotes the space dimensionality. These spaces represent structures such as images, volumes, or any grid space.
For (2), the loop to build the best trajectory consists of the backward analysis of the topological structure given by the frequency/weighted calculation. The minimum number of iterations to reach the goal D is given by ; however, it might change according to how we implement the C criterion. Then, for practical purposes, the lower bound of the complexity is multiplied by the complexity of the C criterion.
Finally, (3) refers to the criterion C for the step forward to the destination D. This function requires a complexity of computations to determine the best choice. Then, the total complexity from stages (1) and (2) is .
In summary, the total complexity of Algorithm 1 is
where is a constant that takes values of 2 or 3 if frequency dilation or weighted dilation is needed. In addition, the general search algorithm (see Algorithm 2) adds further complexity due to the loop (lines 3 to 9). Each iteration computes a coverage and its frequency. Hence, for each iteration, the maximum number of computed dilations depends on the k value. In fact, the complexity of computing a frequency and dilation is expressed as for k iterations. Then, the loop requires evaluation times, and denotes the iterations needed to perform the morphological process one time. The complexity is expressed as for the loop, which, after factorizing and rewriting the summation results, becomes .
Finally, substituting the morphological complexity from Algorithm 1 and replacing the complexity for Algorithm 2, we have
with .
3. Experimental Analysis and Results
An experimental model is presented for the performance evaluation and comparison to well-accepted approaches.
3.1. Experimental Process
The experimental process consists of the following stages.
- Testing the location of the best trajectory from a grid topology. This experiment uses the city map encoded as a single binary image that represents a grid space. The starting and final path trajectories are selected according to the most representative topologies. The graph belongs to a part of Querétaro City. This graph is the result of automatic graph generation from a satellite map via avenue segmentation. The scale and resolution refer to the real dimensions of maps expressed in terms of pixels.
- The location of the best trajectory from a graph space. In this stage, the city is encoded as a graph after computing the avenue intersections as nodes. The tested scenario becomes the same as that used in the last point. The weighting considers the distance in a metric space to weigh the graph. The coding process uses the vertex detection since the detection of the maximum values of the distance transformation is given by the segmentation of the road into a connected map. All maxima detected represent the nodes, and the connection arcs result from the connected avenues. Each vertex represents an avenue intersection.
- A comparison with other well-accepted approaches. This process evaluates another search method as a reference. The comparison is considered in terms of their computational complexity.
3.2. Results
The location of the best trajectory from a grid topology. The neighborhood might represent the adjacent local connections of a given node, and it defines the structural element. This representation has the advantage that the grid uniformity might refer directly to the uniform sampling of a physical plane space representation.
Figure 3 illustrates the grid space that conforms to a graph search space. The uniformity of the structure of the connectivity of each node allows a direct association with the image pixels. The representation of four or eight connections might be applied to images, being useful for illustration purposes. The avenue’s directionality is bidirectional. In concrete scenarios, the directionality becomes constrained to the extra layer of information. The first step consists of selecting the initial (the graph) and the destination (the D graph) positions in the graph (see Figure 3a). In this case, the origin and the destination D correspond to the same connected zone, and its intersection is the null set.
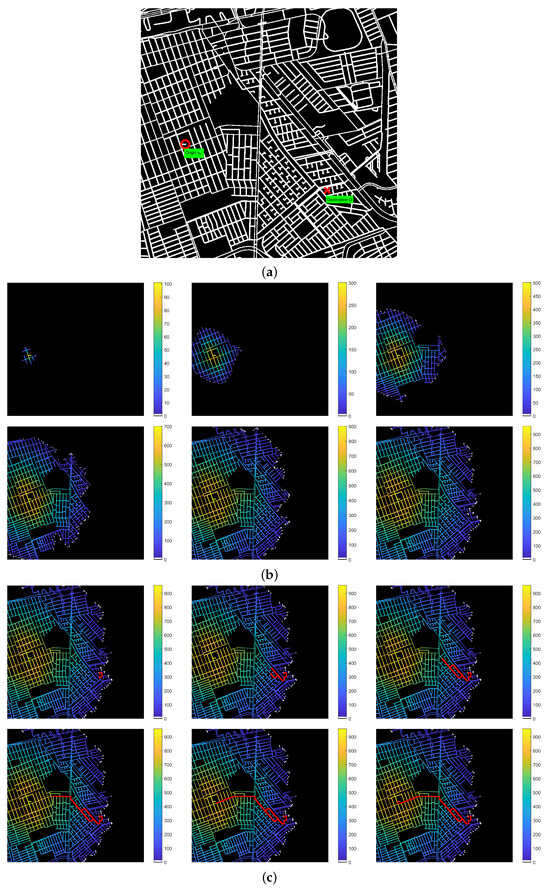
Figure 3.
Example of searching algorithm with (a) avenue scenario with node origin and destination; (b) frequency with which dilation is applied; and (c) dilations required to reach the goal.
The searching algorithm has two principal subprocesses: (1) the morphological covering of the space until, from a given reference, the destination is reached (see Figure 3b). This process generates the dilation operator several times, where, with each iteration, the covering graph increases. The successive dilations represent the searching criterion, such that it is closely similar to a first-width approach. The approach performs a simultaneous path search, expanding in terms of the topology of the structural element. In our example, the border nodes are illustrated in white and represent the dilating nodes. Each node of the border represents a possible path search to locate the destination. With each successive iteration, the node of the border is incremented one step forward according to the space topology. Hence, these increments mean that the border nodes might be divided, merged, or fused. When the border is divided, the approach introduces one possible path. Whenever two paths are joined, the dilation frequency defines which of the two paths is more reliable. Note that when the space limits are reached, a path solution does not exist. This algorithm’s behavior allows the implementation of parallel approaches to benefit the performance. Finally, the first algorithm ends whenever the destination D is reached, meaning that the covering operators introduce a morphological order expressed by a lattice as all covering subgraphs cover the space.
Consequently, the frequency of dilations applied to each node induces an order relation. The infimum corresponds to the destination D node, denoting the origin. The order in the step-forward natural direction of the frequency dilation nodes represents the possible path trajectories, with the cost associated with reaching the reference . The subgraph represents the most dilated nodes, denoting the supremum of the total order. The solution conforms from the subgraph D to the subgraph direction following the frequency of dilations. Sometimes, the solution might not be unique (see Figure 3), and they might all require the same number of steps to reach the destination from the origin; thus, equivalent minimal path trajectories are provided. For multiple solutions, we focus on the red rectangle marked at the center of the last frame in Figure 3c. This figure augments Figure 4, where (a) shows the different solutions located, and, in (b), the frequency is illustrated as level curves. The red arrows represent the different path trajectories. The solid-arrow solution navigates via the lower rectangle and the dotted-arrow solution via the upper rectangle. Both solutions have an equal cost in traveling from the reference to the destination; it is possible that the cost of traveling via the first and second solutions is the same. Similarly, scenarios with multiple solutions can locate all solutions simultaneously. The grid representation becomes practical whenever the dimensions of the maps become smaller because the computational resources have increased. Meanwhile, a graph space representation has a non-uniform connection order.
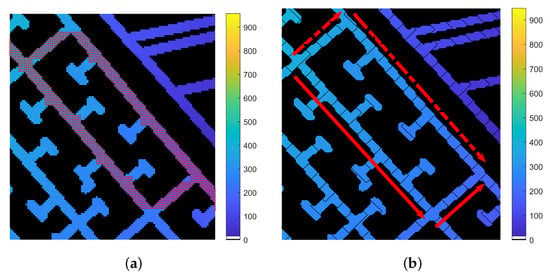
Figure 4.
Multiple solutions for best path trajectory. (a) shows the different solutions located; (b) the frequency is illustrated as level curves.
Testing the location of the best trajectory from a graph space. An encoding process is required to convert a geographical map into a graph. The encoding process takes as input geographical information such that avenues/crossroads are encoded as a graph. The encoding process takes the intersections as nodes and the avenues as arcs. The detection is performed with the distance transformation and maximum zones detected. This representation is a compact representation of the geographical avenue layer with the advantage of requiring minimal computational resources. The avenue intersections denote the local maxima distances in a distance transformation. The positions of all maxima are the result of applying the extended morphological distance. The process of coding the image in a graph is illustrated in Figure 5, where, starting from (a), a geographic binary map layer and (c) the distance transform, considering the avenue as a connected surface, we can compute the minimum distance between each active pixel and the nearest border. The distance transform is illustrated in pseudo-color, where dark zones correspond to small distances, and white zones represent large distances. Consequently, Figure 5d shows the process of maximum detection. The resolution and the thinness of the avenue representation might affect the maxima detection by merging two close maxima. The maximum detection zones are obtained through morphologically extended maxima transformation. This transformation offers a robust process to detect maxima on discrete surfaces. Finally, Figure 5b illustrates the graph representation once the maximum is detected. The connectivity results from the removal of the dilated maximum zones detected. Each arc detected is dilated and the maximum regions that overlap are tested. In a weighted version, the geographical distance might require the conversion of pixel distances into metric units.
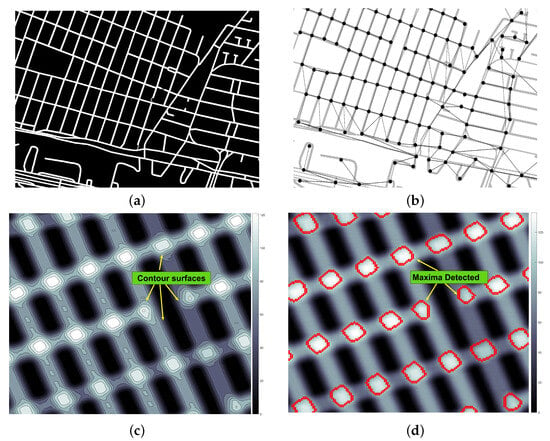
Figure 5.
Map encoding process: (a) geographical binary map layer; (b) built graph connection; (c) computation of distance transformation; and (d) detection of maximum zones.
Similarly, the graph generated from the avenue information is encoded as a graph space. Figure 6 illustrates an example of the searching path in the graph space resulting from encoding a geographical city map. Figure 6 illustrates two positions that represent the start and destination to reach D. In the following graphs, Figure 6b illustrates the covering process, representing the city as a graph, where each node is accompanied by the frequency by which it is dilated. The frequency defines the natural order relation that reconstructs the shortness trajectory in terms of jumps. The solution is marked in red once the destination reaches D. In this particular case, it takes 17 iterations (dilations) to reach the destination. Note that the proposed framework has the advantage of representing a width-first search, resulting in faster convergence.
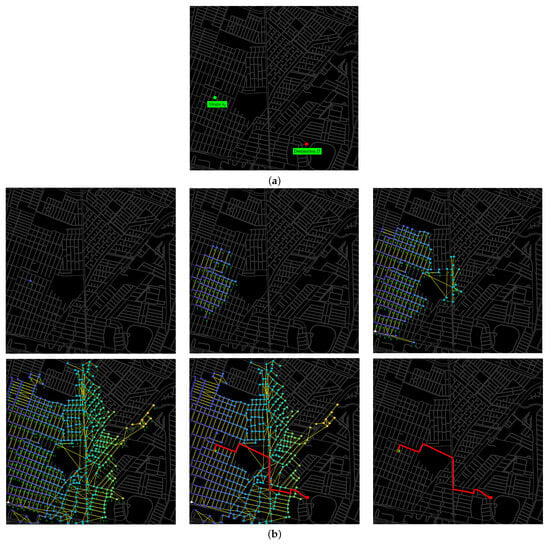
Figure 6.
Example of the searching algorithm in a graph space with (a) an avenue scenario, including the origin and destination nodes, and (b) the frequency with which dilation is applied and the computation of the best path trajectory.
A comparison with other well-accepted approaches. The proposed method matches with well-accepted approaches from the literature. Table 1 shows the main features used to compute the best trajectory. The best path trajectory, as an open task, has three main features to denote: (1) the search space; (2) local constraints for specific environments; and (3) the path searching approach.

Table 1.
Approaches to computing the best path trajectory.
The above features are discussed in the following paragraph and allow the clarification of the contributions of our proposal. Case (1) can be divided into two classes (workspace column in Table 1). (i) Approaches based on structured spaces (grid spaces); (ii) approaches based on non-structured approaches, which establish the upper bound limits to avoid falling into a combinatorial growing space. Therefore, these approaches based on grid spaces become limited in the searching space, with an advantage for (ii) approaches that denote more complicated working spaces.
In (2), the feature reduces the search space to improve the computability and tractability. However, it might bring further complexity associated with the segmentation of the searching space, such that, in some cases, it might considerably increase the total complexity. Particular cases include hybrid approaches [45,46,47] or mixture approaches [6,43,48], which include additional constraints to make the searching space more tractable.
The above approaches only reduce the searching space, without contributing to the computation of the trajectory. In (3), the feature, without loss of generality, uses a Dijkstra-like algorithm [49,50,51,52] at the end to compute the best trajectory. In other words, the foundations and method used to finally locate the best trajectory rely on a variation of the Dijkstra algorithm [53]. An extensive comparison with the Dijkstra algorithm is beneficial because our proposal offers an alternative theoretical framework to deal with this problem. To compare our proposal with the Dijkstra algorithm [54], we perform a complexity analysis of both approaches. The complexity of the algorithm is summarized in Equation (11).
where V is the set of vertices and A is the set of arcs. This complexity refers to the basic algorithm without a priority queue. Several authors denote the computational complexity as [54] when using a priority queue. This complexity is incomplete because it lacks the additional complexity associated with the priority queue building.
The morphological approach has complexity defined by Equation (9), where , , , and k are constant values. The k parameter takes values in the worst case , where is the number of vertices. The and parameters adopt small values. For simplicity, both are rewritten as a constant value . Finally, the parameter represents the neighborhood expressed by the structural element. We assume a constant complexity for path generation for , and in the worst case, has a frequency of . We rewrite the complexity equation as
The final expression becomes simplified to the expression ; the complexity is comparable to that of the Dijkstra algorithm without a priority queue. Finally, the parameter might increase the complexity; however, this parameter represents the number of elements at the border to be analyzed by each iteration (structural element dimension). The considerable increment in the complexity is compensated because, with each iteration, the number of covering steps is reduced in the best case by a factor of . The complexity will likely be increased for higher values, but the number of iterations needed to cover the nodes is reduced in a logarithmic ratio. Figure 7 shows the complexity in terms of the changing value. It is concluded that the total complexity is similar to that of Dijkstra for small values. This analysis confirms that the morphological search framework is equivalent to the Dijkstra algorithm in this particular case.
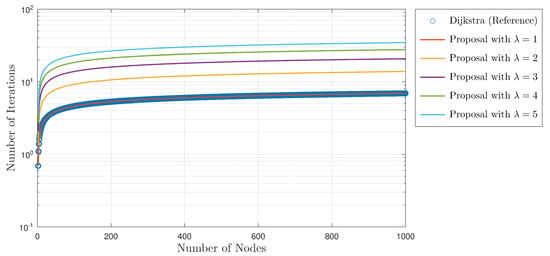
Figure 7.
Complexity for different values, matched with the reference algorithm.
4. Discussion
The results show that the approach is reliable as a general framework to build searching algorithms in a graph. The proposed approach provides a general framework for path searching, offering a compact theoretical reference to define a searching process. This method produces a simplified representation of the searching approach in discrete spaces.
The structural element parameter and the neighborhood connectivity parameter define the criteria for the coverage of the graph space, as mentioned in Section 2 and in Figure 1. This parameter affects the search velocity in the graph: higher values have faster coverage. The symmetrical structural elements become more efficient for grid spaces as compared to irregular shapes, representing the trend in step-forward structures that impose a search tendency that reflects the solution.
The covering dilation operator provides a travel criterion to the graph that avoids loops in the searching space due to the induced lattice. In general terms, a morphological approach is a first-in-width approach to searching; in other words, the first solution is reached in terms of the width of the tree paths generated from the lattice. This drawback is also addressed in the final part of Section 3.2, where the total complexity of the proposed algorithms is analyzed.
The addition of weight values to the graph introduces the possibility to adapt, in terms of cost, the traveling between a pair of nodes, improving the capabilities of the analysis in non-uniform step-forward graph spaces. These areas of opportunity will be considered in future work, as well as improvements applicable to the proposed method.
5. Conclusions
The main objective of this research work was to introduce a search reference framework in a graph based on morphological mathematics. One of the main contributions consists of performing a search for the optimal minimum path based on an approach using a new operator called the dilation coverage operator.
The approach induces a lattice in a graph; it is a result of the definition of the dilation operator and its associated frequency until the destination is reached. After this, the cover subgraphs map into a lattice based on natural numbers, such that it represents the dilation frequencies. Our method defines a criterion to locate the solution path within the context of the minimum path defined by the dilation frequency. This criterion uses the unitary descendant travel of the lattice until it reaches the infimum. Our experimental process and complexity analysis using other approaches demonstrate that the computational complexity is very similar to that of the Dijkstra algorithm without a priority queue in terms of efficiency, and the inclusion of morphological operators makes it feasible to paralyze it.
In a dense graph, the complexity can be tracked easily due to the logarithmic growth. The parameters that affect the complexity also affect the number of neighborhoods considered. When a large neighborhood is selected, the number of iterations required to reach the solution decreases exponentially. If the conditions are similar, then the complexity of the algorithm is the same as that of the Dijkstra algorithm. This makes standard algorithms more feasible. In other cases, it becomes an alternative search graph where the exploration velocity can be controlled by adjusting the neighborhood size.
In the context of the algorithm operation, the proposal locates all possible best path trajectories. Some algorithm variations are implemented by changing the structural element parameter, affecting the search’s convergence velocity and priority directionality. In terms of practical application, the search algorithm is a reliable path trajectory approach for geographical maps. This consideration makes it feasible for use in a computationally limited context, with high efficiency and accuracy for execution.
Despite the above, the proposal presents inherent limitations due to the method used and the complexity of the graph being solved. This has a direct impact on the computational cost when calculating the minimum path. Furthermore, using morphological dilation in a graph-based space may not guarantee the minimum path in all cases.
This approach is based on iteratively covering certain search regions from the origin point , which depends on the complexity, size, and topology of the analyzed scenario. As a result, routes may be obtained that are not minimal in overall terms of cost or distance.
Furthermore, when using mathematical morphology, it is necessary to arbitrarily define the size and shape of the structuring element according to the work context, which may affect the convergence speed of the method, as shown in Figure 7. To address these limitations, it is proposed to dynamically adapt the size and shape of the structural element depending on the graph space presented. This involves analyzing different sizes associated with the desired level of coverage by the dilation operator in each applied iteration. This strategy could improve the robustness of the proposal against large and complex search spaces.
Furthermore, the proposal allows the isolation of processes that could be parallelized in multicore hardware systems. Finally, by including specific variables of the context, such as the vehicle flow, width of the avenue, number of lanes, and direction of circulation, the precision of the proposed method could be improved. This would make it applicable in a wide variety of real-world situations.
Further Works
This framework establishes the basis for a morphological searching approach. Hence, some future research efforts around it include the following. (1) The discussion of parallelization criteria to enhance the algorithm execution in multi-core hardware. This aspect is addressed briefly in Section 2.4, being necessary in strategies for the isolation of the different processes and the execution in parallel of several sub-processes.
(2) The development of graph approach representations from raw data. In the experimental analysis, a single coding scheme was implemented; however, the approach might be extended to the automatic graphs built from information about the traffic flow density, velocity, or other urban variables that are expressed as a fluid.
As a final note, the searching framework offers the possibility to locate or not the path trajectories whenever the destination graph is not reachable. This property represents a new connectivity criterion that establishes the basis of a covering dilation connection for graph-dense clustering analysis or any other grid as a new method for the clustering and labeling of data.
Author Contributions
Conceptualization, J.L.P.-R. and H.J.-H.; Formal analysis, A.M.H.-N. and H.J.-H.; Methodology, J.L.P.-R., S.R.-R. and H.J.-H.; Software, H.J.-H.; Supervision, G.X.-R. and H.J.-H.; Writing—original draft, J.L.P.-R. and A.M.H.-N.; Writing—review and editing, D.C.-E., L.A.D.-J. and G.X.-R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
We wish to give thanks to CIDESI, CONAHCYT, and the Mexican Artificial Intelligence Alliance, with the FORDECYT Project 296737 Consorcio en Inteligencia Artificial, which provided the student scholarships, and CIICCTE (Centro de Investigación e Innovación en Ciencias de la Computación y Tecnología Educativa), which provided technical and infrastructure support. We especially acknowledge the guidance of Hugo Jimenez and the entire work team.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Minimum Path Trajectory Step Demonstration
This appendix demonstrates that Algorithm 1 and its generalized form, Algorithm 2, locate the minimum step-forward path trajectory. Previously, the following definitions were introduced. Consider a function , where N represents a node, and the function returns the number of arcs that start in a given particular node, which is defined as
where is the cardinality of the set. Now, consider the function that is implemented as
where G is a graph, n is a node, and e is an arc. The function becomes the maximum order connection of a given graph. Consider an isomorphic structural element of order, a graph G, a reference, and a destination . Now, let the demonstration be performed in the following two steps.
- Base case: Consider that D becomes reachable in one step forward by the dilation-induced lattice. Algorithm 2 reduces to the one-time application of the dilation operator. Let , and ; this is true. If the intersection is the empty set, D is not reachable in one step. Consequently, this is the minimum path step forward in the lattice. Considering that the solution might not be unique, one or more nodes in one step forward reach the destination.
- Generalized case: Consider the situation in which D becomes reachable in k step forward. Algorithm 2 reduces to the application of the dilation operator k times. Let , and ; this is true. Consider, by contradiction, that there is no optimal path. The algorithm reconstructs the path trajectory by the one-step-forward navigation of the natural order generated by the successive dilation operation. A better step trajectory must travel by another path that advances in the lattice, resulting in more than one step. Consequently, this becomes false because it does not follow the one-step-forward travel condition. Similarly, as in the base case, the path trajectory might not be unique; however, the steps to reach the destination are the minimum in all possible paths.
The consequences of these demonstrations generate the two following cases as corollaries.
- Whenever G becomes a weighted graph. In the case of a weighted graph, consider the same demonstration considering the weighted step forward as the coding of the weighted connection via the introduction of a function , defined as follows:where denotes the minimum weight value of the connection of a node in the graph G. This function translates the weighted values into a positive reference, maintaining the distance relations of the weights. Then, the cost step denotes the weighted magnitude for all steps forward in the lattice increments. All iterations now select the best weight choice under the function criterion C without affecting the number of steps performed.
- Whenever . The structural element represents an isomorphism with a connection order smaller than the maximum connection order of the graph. Then, for a given reference as , a successive is equivalent, i.e., requires, in the worst case, , where is the round operator. The number of extra steps required has, as the lower bound, one (the optimal case), and, as the upper bound, the factor , which denotes the worst case of dilating each note times.
References
- Lyu, D.; Chen, Z.; Cai, Z.; Piao, S. Robot path planning by leveraging the graph-encoded Floyd algorithm. Future Gener. Comput. Syst. 2021, 122, 204–208. [Google Scholar] [CrossRef]
- Galán-García, J.L.; Aguilera-Venegas, G.; Galán-García, M.Á.; Rodríguez-Cielos, P. A new Probabilistic Extension of Dijkstra’s Algorithm to simulate more realistic traffic flow in a smart city. Appl. Math. Comput. 2015, 267, 780–789. [Google Scholar] [CrossRef]
- Li, Y.; Wei, W.; Gao, Y.; Wang, D.; Fan, Z. PQ-RRT*: An improved path planning algorithm for mobile robots. Exper. Syst. Appl. 2020, 152, 113425. [Google Scholar] [CrossRef]
- Ruan, C.; Luo, J.; Wu, Y. Map Navigation System Based on Optimal Dijkstra Algorithm. In Proceedings of the 2014 IEEE 3rd International Conference on Cloud Computing and Intelligence Systems, Shenzhen, China, 27–29 November 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 559–564. [Google Scholar] [CrossRef]
- Szücs, G. Decision Support for Route Search and Optimum Finding in Transport Networks under Uncertainty. J. Appl. Res. Technol. 2015, 13, 125–134. [Google Scholar] [CrossRef][Green Version]
- Fang, Y.; Huang, X.; Qin, L.; Zhang, Y.; Zhang, W.; Cheng, R.; Lin, X. A Survey of Community Search over Big Graphs; Springer: Berlin/Heidelberg, Germany, 2020; Volume 29, pp. 353–392. [Google Scholar] [CrossRef]
- Zhao, Y.; Bi, S.; Zhang, H.; Chen, Z. Dynamic Weight and Mapping Mutation Operation-Based Salp Swarm Algorithm for Global Optimization. Appl. Sci. 2023, 13, 8960. [Google Scholar] [CrossRef]
- Wang, L.; Kan, J.; Guo, J.; Wang, C. 3D Path planning for the ground robot with improved ant colony optimization. Sensors 2019, 19, 815. [Google Scholar] [CrossRef]
- Châari, I.; Koubâa, A.; Bennaceur, H.; Ammar, A.; Trigui, S.; Tounsi, M.; Shakshuki, E.; Youssef, H. On the adequacy of tabu search for global robot path planning problem in grid environments. Procedia Comput. Sci. 2014, 32, 604–613. [Google Scholar] [CrossRef]
- Liu, H.; Jin, C.; Zhou, A. Popular route planning with travel cost estimation from trajectories. Front. Comp. Sci. 2020, 14, 191–207. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, F.; Tong, X.L.; Yun, J.; Liu, Y.; Sun, Y.; Tao, B.; Kong, J.; Xu, M.; Chen, B. Time Optimal Trajectory Planing Based on Improved Sparrow Search Algorithm. Front. Bioeng. Biotechnol. 2022, 10, 852408. [Google Scholar] [CrossRef]
- Liu, X.; Gao, X.; Wang, Z.; Ru, X. Improved local search with momentum for bayesian networks structure learning. Entropy 2021, 23, 750. [Google Scholar] [CrossRef]
- Wu, J.; Yin, M. A restart local search for solving diversified top-k weight clique search problem. Mathematics 2021, 9, 2674. [Google Scholar] [CrossRef]
- Ahmed, A.K.F.; Sun, J.U. Bilayer local search enhanced particle swarm optimization for the capacitated vehicle routing problem. Algorithms 2018, 11, 31. [Google Scholar] [CrossRef]
- Tafreshian, A.; Masoud, N. Trip-based graph partitioning in dynamic ridesharing. Transpo. Res. Part C Emerg. Technol. 2020, 114, 532–553. [Google Scholar] [CrossRef]
- Fan, W.; Jin, R.; Liu, M.; Lu, P.; Luo, X.; Xu, R.; Yin, Q.; Yu, W.; Zhou, J. Application Driven Graph Partitioning. In Proceedings of the SIGMOD/PODS’20: International Conference on Management of Data, Portland, OR, USA, 14–19 June 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 1765–1779. [Google Scholar] [CrossRef]
- Srinivasan, R.; Vivekanandan, M. On Packing Colouring of Transformation of Path, Cycle and Wheel Graphs. Indian J. Sci. Technol. 2021, 14, 1975–1981. [Google Scholar] [CrossRef]
- Karur, K.; Sharma, N.; Dharmatti, C.; Siegel, J.E. A Survey of Path Planning Algorithms for Mobile Robots. Vehicles 2021, 3, 448–468. [Google Scholar] [CrossRef]
- de Oliveira, G.C.R.; de Carvalho, K.B.; Brandão, A.S. A hybrid path-planning strategy for mobile robots with limited sensor capabilities. Sensors 2019, 19, 1049. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Tian, B.; Hou, S.; Li, X.; Li, Y.; Liu, C.; Li, J. Path Planning for Mount Robot Based on Improved Particle Swarm Optimization Algorithm. Electronics 2023, 12, 3289. [Google Scholar] [CrossRef]
- Na, Y.; Li, Y.; Chen, D.; Yao, Y.; Li, T.; Liu, H.; Wang, K. Optimal Energy Consumption Path Planning for Unmanned Aerial Vehicles Based on Improved Particle Swarm Optimization. Sustainability 2023, 15, 2101. [Google Scholar] [CrossRef]
- Liu, Y.; Qi, N.; Yao, W.; Zhao, J.; Xu, S. Cooperative path planning for aerial recovery of a UAV swarm using genetic algorithm and homotopic approach. Appl. Sci. 2020, 10, 4154. [Google Scholar] [CrossRef]
- Li, Q.; Gama, F.; Ribeiro, A.; Prorok, A. Graph Neural Networks for Decentralized Multi-Robot Path Planning; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2020; pp. 11785–11792. [Google Scholar] [CrossRef]
- Hirata, N.S.; Papakostas, G.A. On machine-learning morphological image operators. Mathematics 2021, 9, 1854. [Google Scholar] [CrossRef]
- Delmerico, J.; Isler, S.; Sabzevari, R.; Scaramuzza, D. A comparison of volumetric information gain metrics for active 3D object reconstruction. Auton. Robot. 2018, 42, 197–208. [Google Scholar] [CrossRef]
- Gaikwad, S.K.; Karwankar, A.R. Food image 3D reconstruction using image processing. In Proceedings of the 2019 3rd International Conference on Trends in Electronics and Informatics, Tirunelveli, India, 23–25 April 2019. [Google Scholar] [CrossRef]
- Richard, A.; Morlot, C.; Créon, L.; Beaudoin, N.; Balistky, V.S.; Pentelei, S.; Dyja-Person, V.; Giuliani, G.; Pignatelli, I.; Legros, H.; et al. Advances in 3D imaging and volumetric reconstruction of fluid and melt inclusions by high resolution X-ray computed tomography. Chem. Geol. 2019, 508, 3–14. [Google Scholar] [CrossRef]
- Liu, X.; Yao, H.; Chen, X.; Gao, W. An active volumetric model for 3D reconstruction. In Proceedings of the IEEE International Conference on Image Processing 2005, Genova, Italy, 14 September 2005; Volume 2. [Google Scholar] [CrossRef]
- Hou, Y.; Li, Q.; Zhang, C.; Lu, G.; Ye, Z.; Chen, Y.; Wang, L.; Cao, D. The State-of-the-Art Review on Applications of Intrusive Sensing, Image Processing Techniques, and Machine Learning Methods in Pavement Monitoring and Analysis. Engineering 2021, 7, 845–856. [Google Scholar] [CrossRef]
- Salvi, M.; Acharya, U.R.; Molinari, F.; Meiburger, K.M. The impact of pre- and post-image processing techniques on deep learning frameworks: A comprehensive review for digital pathology image analysis. Comput. Biol. Med. 2021, 128, 104129. [Google Scholar] [CrossRef] [PubMed]
- Ronse, C.; Heijmans, H.J. A lattice-theoretical framework for annular filters in morphological image processing. Appl. Algebr. Eng. Commun. Comput. 1998, 9, 45–89. [Google Scholar] [CrossRef][Green Version]
- Maragos, P. Lattice image processing: A unification of morphological and fuzzy algebraic systems. J. Math. Imag. Vis. 2005, 22, 333–353. [Google Scholar] [CrossRef]
- Dang, T.; Tranzatto, M.; Khattak, S.; Mascarich, F.; Alexis, K.; Hutter, M. Graph-based subterranean exploration path planning using aerial and legged robots. J. Field Robot. 2020, 37, 1363–1388. [Google Scholar] [CrossRef]
- Tawanda, T.; Nyamugure, P.; Kumar, S.; Munapo, E. A Labelling Method for the Travelling Salesman Problem. Appl. Sci. 2023, 13, 6417. [Google Scholar] [CrossRef]
- Shen, Y.; Zhu, Y.; Kang, H.; Sun, X.; Chen, Q.; Wang, D. UAV path planning based on multi-stage constraint optimization. Drones 2021, 5, 144. [Google Scholar] [CrossRef]
- Zieliński, P. The computational complexity of the relative robust shortest path problem with interval data. Eur. J. Oper. Res. 2004, 158, 570–576. [Google Scholar] [CrossRef]
- Li, J.; Wang, F.; He, Y. Electric vehicle routing problem with battery swapping considering energy consumption and carbon emissions. Sustainability 2020, 12, 537. [Google Scholar] [CrossRef]
- Yu, M.; Luo, Q.; Wang, H.; Lai, Y. Electric Logistics Vehicle Path Planning Based on the Fusion of the Improved A-Star Algorithm and Dynamic Window Approach. World Electr. Vehicle J. 2023, 14, 213. [Google Scholar] [CrossRef]
- Adcock, J.C.; Morley-Short, S.; Dahlberg, A.; Silverstone, J.W. Mapping graph state orbits under local complementation. Quantum 2020, 4, 305. [Google Scholar] [CrossRef]
- Lu, X.; Camitz, M. Finding the shortest paths by node combination. App. Math. Comput. 2011, 217, 6401–6408. [Google Scholar] [CrossRef]
- Xu, M.H.; Liu, Y.Q.; Huang, Q.L.; Zhang, Y.X.; Luan, G.F. An improved Dijkstra’s shortest path algorithm for sparse network. Appl. Math. Comput. 2007, 185, 247–254. [Google Scholar] [CrossRef]
- Boria, N.; Blumenthal, D.B.; Bougleux, S.; Brun, L. Improved local search for graph edit distance. Pattern Recognit. Lett. 2020, 129, 19–25. [Google Scholar] [CrossRef]
- Hentous, H.; Merabti, B. A branch and bound heuristic for the flow shop problem. In Proceedings of the Fourth International Conference on Sensor Technologies and Applications, Venice, Italy, 18–25 July 2010; pp. 352–356. [Google Scholar] [CrossRef]
- Fan, D.; Shi, P. Improvement of Dijkstra’s algorithm and its application in route planning. In Proceedings of the 2010 Seventh International Conference on Fuzzy Systems and Knowledge Discovery, Yantai, China, 10–12 August 2010; IEEE: Piscataway, NJ, USA, 2010; Volume 4, pp. 1901–1904. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, F.; Liu, Z.; Li, Y. Efficient Path Planning Method of USV for Intelligent Target Search. J. Geovisualiz. Spat. Anal. 2019, 3, 1–9. [Google Scholar] [CrossRef]
- Singh, K.N.; van Oudheusden, D.L. A branch and bound algorithm for the traveling purchaser problem. Eur. J. Oper. Res. 1997, 97, 571–579. [Google Scholar] [CrossRef]
- Pham, Q.D.; Deville, Y.; Hentenryck, P.V. LS(Graph): A constraint-based local search for constraint optimization on trees and paths. Constraints 2012, 17, 357–408. [Google Scholar] [CrossRef]
- Ravi, R.; Salman, F.S. Approximation algorithms for the traveling purchaser problem and its variants in network design. In Algorithms–ESA’99. ESA 1999; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1643. [Google Scholar] [CrossRef]
- Cheng, P.Y.; Chen, P.J. Navigation of mobile robot by using D++ algorithm. Intell. Serv. Robot. 2012, 5, 229–243. [Google Scholar] [CrossRef]
- Höffmann, M.; Patel, S.; Büskens, C. Optimal Coverage Path Planning for Agricultural Vehicles with Curvature Constraints. Agriculture 2023, 13, 2112. [Google Scholar] [CrossRef]
- Shu-Xi, W. The Improved Dijkstra’s Shortest Path Algorithm and Its Application. Procedia Eng. 2012, 29, 1186–1190. [Google Scholar] [CrossRef]
- Lewis, R. Algorithms for finding shortest paths in networks with vertex transfer penalties. Algorithms 2020, 13, 269. [Google Scholar] [CrossRef]
- Wang, H.; Qi, X.; Lou, S.; Jing, J.; He, H.; Liu, W. An efficient and robust improved a* Algorithm for path planning. Symmetry 2021, 13, 2213. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A Note on Two Problems in Connexion with Graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).