An Innovative Mathematical Model of the Spine: Predicting Cobb and Intervertebral Angles Using the 3D Position of the Spinous Processes Measured by Vertebral Metrics
Abstract
1. Introduction
2. Methods
2.1. Establishing Input Conditions
2.2. Estimating the Spine Biomechanics
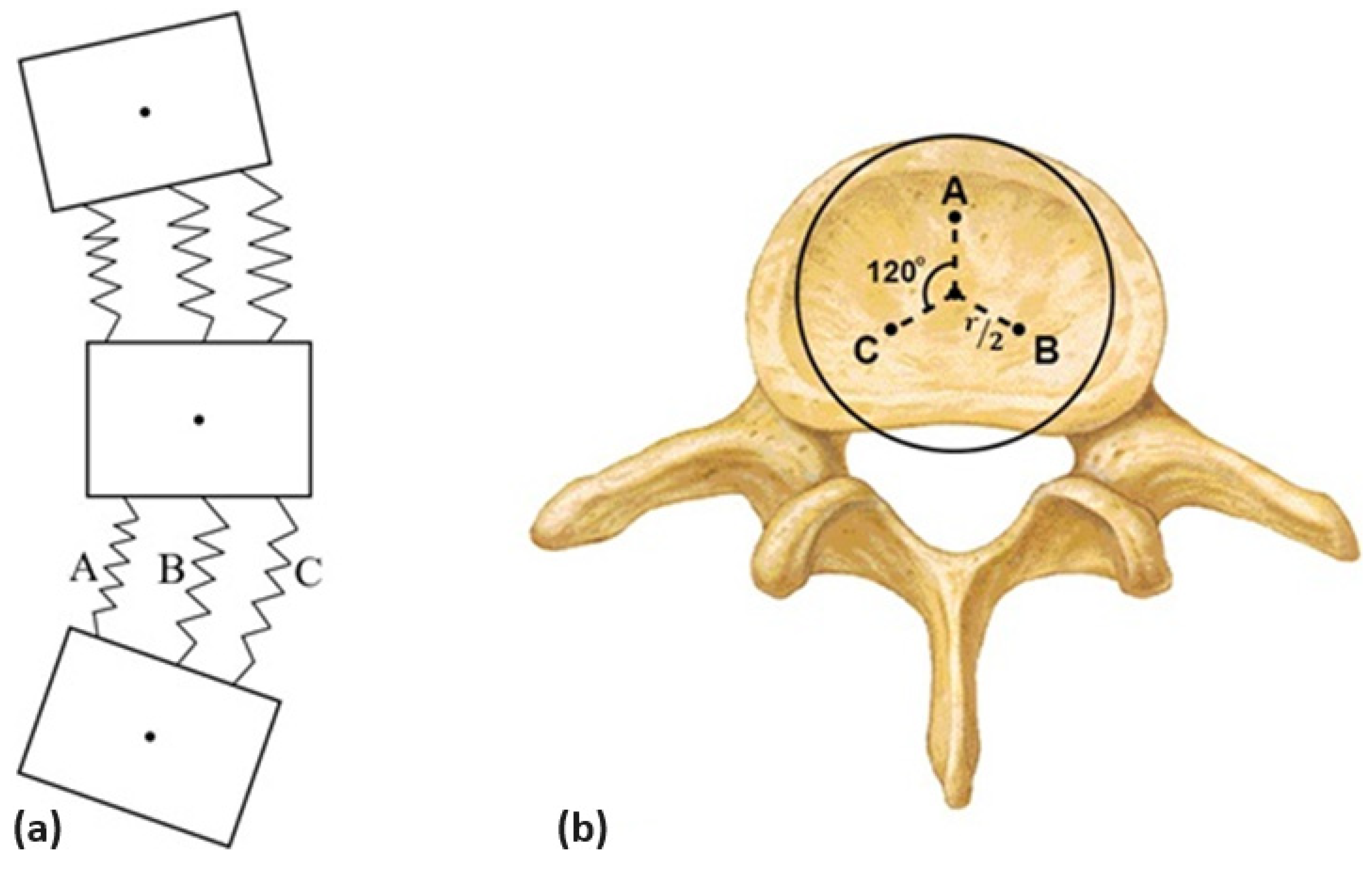
- Definition of an initial spring–mass system;
- Match the initial system and the VM data;
- Modulation in the sagittal plane;
- Modulation in the coronal plane;
- Find the Cobb and the intervertebral angles;
- Three-dimensional representation.
2.2.1. Defining an Initial Spring–Mass System
2.2.2. Matching the Initial System and VM Data
2.2.3. Modelling in the Sagittal Plane
2.2.4. Modeling in the Transversal Plane
2.2.5. Cobb Angles and Intervertebral Angles
- L1 and S1 to the lumbar lordosis;
- D1 and D12 to the dorsal kyphosis;
- C2 and C7 to the cervical lordosis.
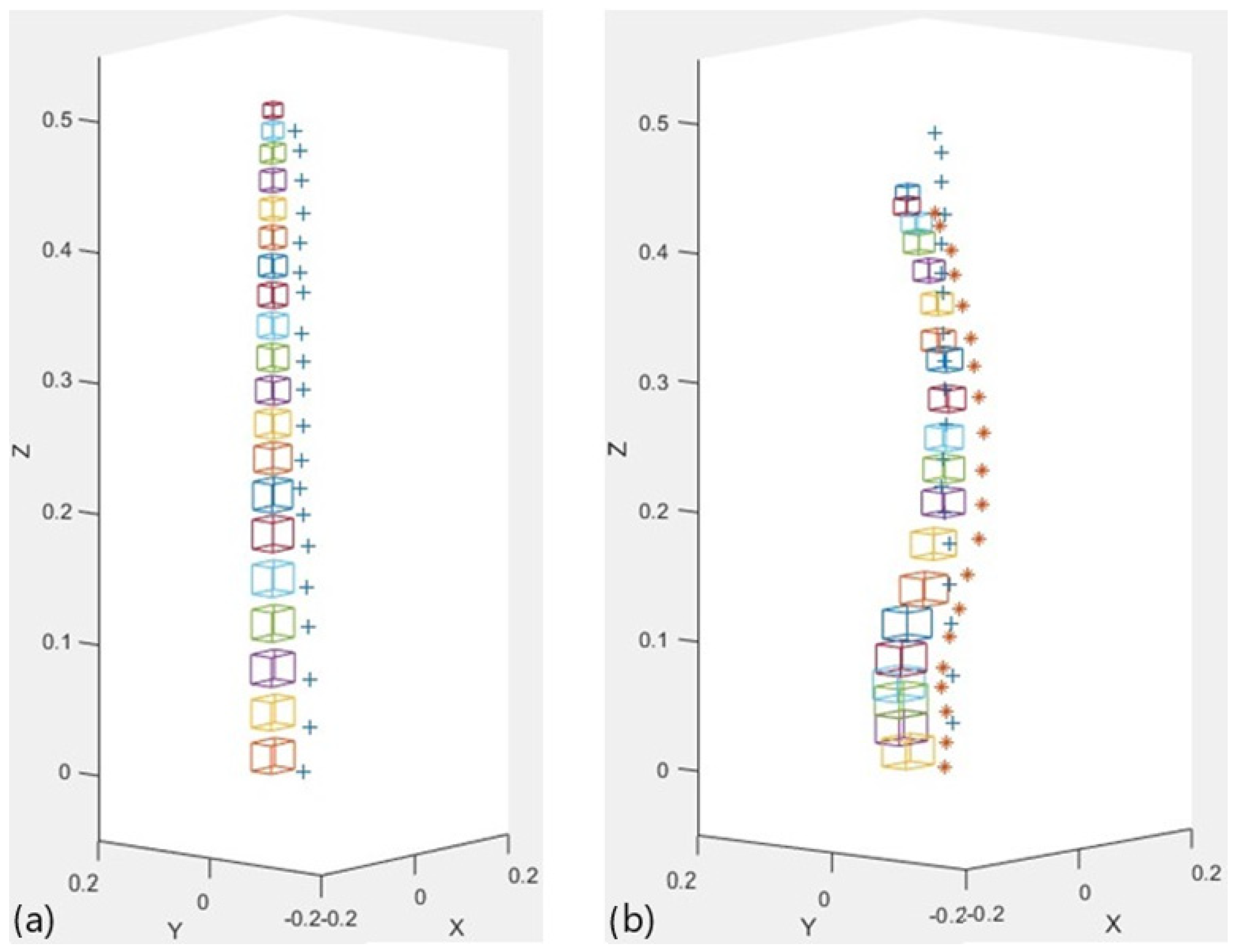
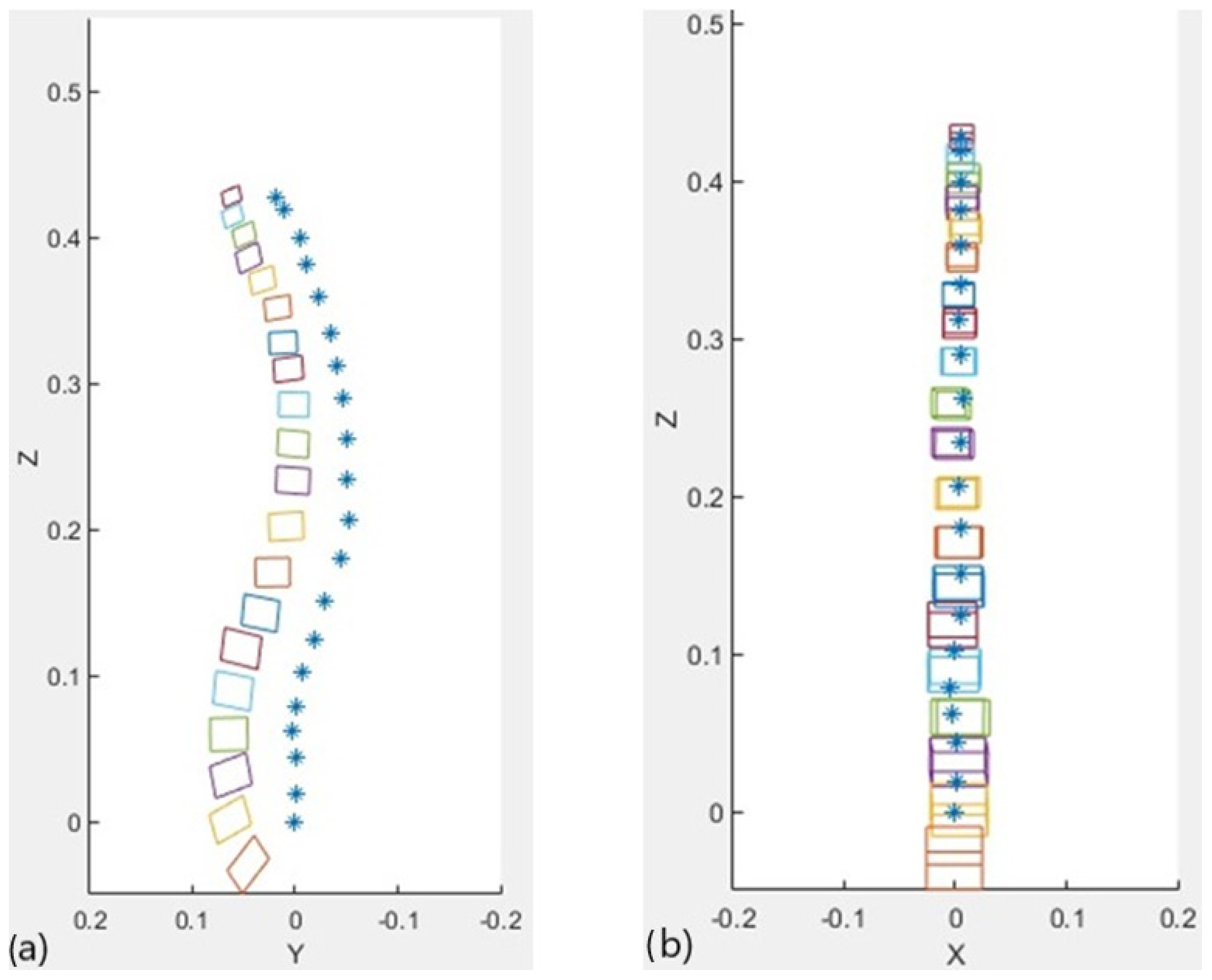
2.2.6. 3D Representation
2.3. Testing and Validation
- Age over 18 years old;
- Body mass index below 35 kg/m2;
- No pregnancy or breastfeeding;
- No infections requiring hospitalisation or antibiotics;
- No uncontrolled medical illness;
- No total ankylosis of the spine;
- X-rays of the spine in the sagittal and coronal planes;
- The same physician identified the cutaneous projection of the apex through palpatory anatomy;
- The same researcher carried out data collection;
- The sampling method was random.
- The upper limits of the surfaces of the vertebral body;
- The lower limits of the surfaces of the vertebral body;
- The upper and lower limits of the apex.
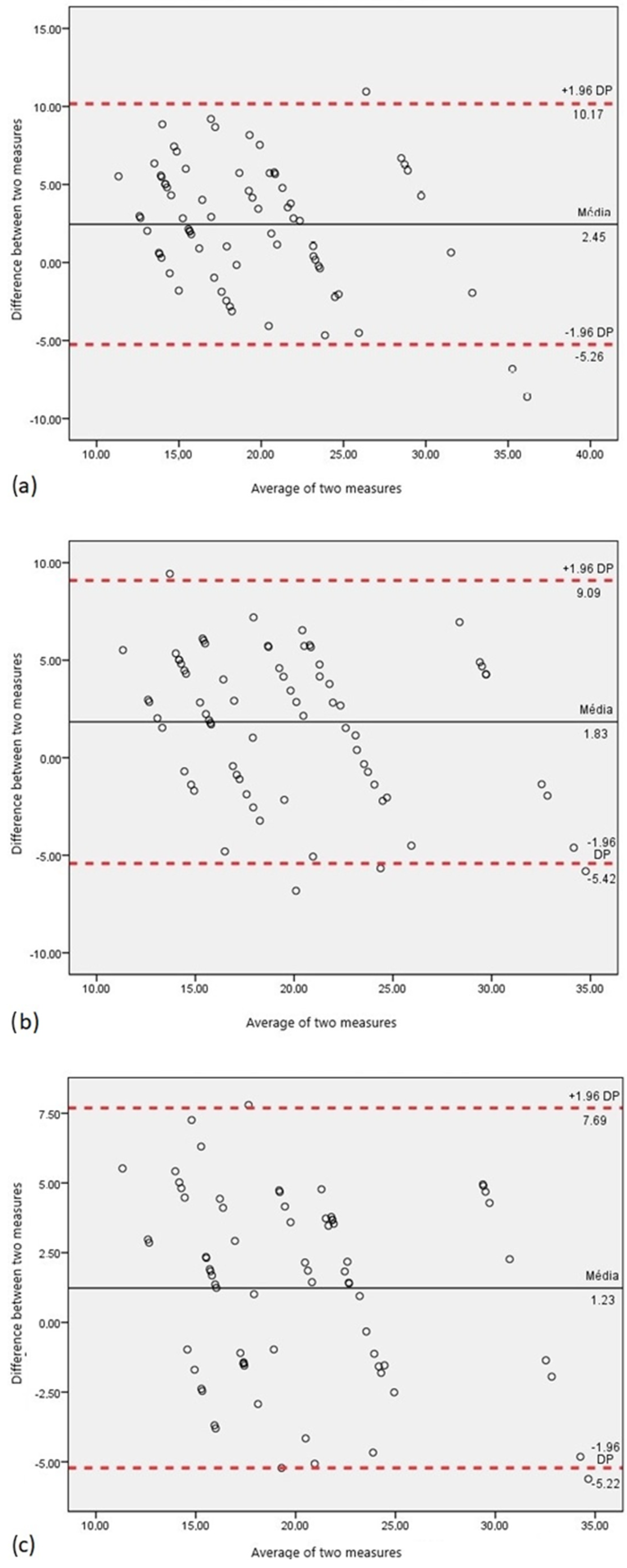
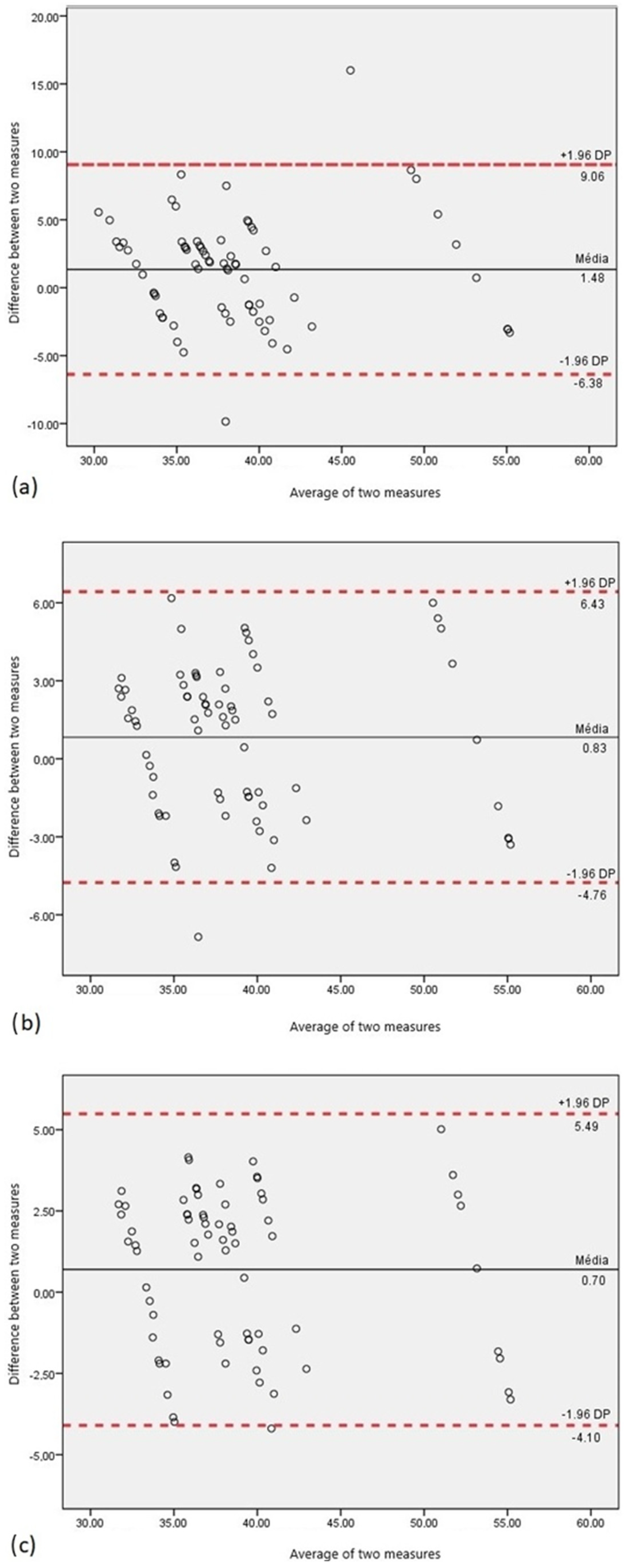
3. Results
- The average of the rotation angles measured on the eight radiographs;
- The angle measured on the radiograph of each patient.
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- American Academy of Orthopaedic Surgeons. Posture and Its Relationship to Orthopaedic Disabilities—A Report of the Posture Committee; American Academy of Orthopaedic Surgeons: Evanston, IL, USA, 1947. [Google Scholar]
- Magee, D.J. Orthopedic Physical Assessment, 4th ed.; Saunders Company: New York, NY, USA, 2002. [Google Scholar]
- Aroeira, R.M.C.; de Las Casas, E.B.; Pertence, A.E.M.; Greco, M.; Tavares, J.M.R. Non-invasive methods of computer vision in the posture evaluation of adolescent idiopathic scoliosis. J. Bodyw. Mov. Ther. 2016, 20, 832–843. [Google Scholar] [CrossRef] [PubMed]
- Singla, D.; Veqar, Z. Effect of playing basketball on the posture of cervical spine in healthy collegiate students. Int. J. Biomed. Adv. Res. 2015, 6, 133–136. [Google Scholar] [CrossRef]
- Ehrlich, G.E. Low back pain. Bull. World Health Organ. 2003, 81, 671–676. [Google Scholar] [PubMed]
- Dionne, C.E.; Dunn, K.M.; Croft, P.R. Does back pain prevalence really decrease with increasing age? A systematic review. J. Am. Geriatr. Soc. 2006, 35, 229–234. [Google Scholar] [CrossRef] [PubMed]
- Hoy, D.; Brooks, P.; Blyth, F.; Buchbinder, R. The Epidemiology of low back pain. Best Pract. Res. Clin. Rheumatol. 2010, 24, 769–781. [Google Scholar] [CrossRef] [PubMed]
- Traeger, A.C.; Buchbinder, R.; Elshaug, A.G.; Croft, P.R.; Maher, C.G. Care for low back pain: Can health systems deliver? Bull. World Health Organ. 2019, 97, 423–433. [Google Scholar] [CrossRef] [PubMed]
- Kheirinejad, S.; Visuri, A.; Suryanarayana, S.A.; Hosio, S. Exploring mHealth applications for self-management of chronic low back pain: A survey of features and benefits. Heliyon 2023, 9, e16586. [Google Scholar] [CrossRef] [PubMed]
- Aspden, R. A new mathematical model of the spine and its relationship to spinal loading in the workplace. Appl. Ergon. 1988, 19, 319–323. [Google Scholar] [CrossRef]
- Ferguson, S.J.; Steffen, T. Biomechanics of the aging spine. Eur. Spine J. 2003, 12 (Suppl. 2), S97–S103. [Google Scholar] [CrossRef]
- Iorio, J.A.; Jakoi, A.M.; Singla, A. Biomechanics of Degenerative Spinal Disorders. Asian Spine J. 2016, 10, 377–384. [Google Scholar] [CrossRef]
- Esperança Pina, J.A. Anatomia Humana da Locomoção, 5th ed.; LIDEL—Edições Técnicas, lda: Lisbon, Portugal, 2014. [Google Scholar]
- Seeley, R.; Stephens, T.; Tate, P. Anatomia e Fisiologia, 6th ed.; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Wolfla, C.; Stemper, B.; Board, D.; Yoganandan, N. Biomechanical properties of human thoracic spine disc segments. J. Craniovertebral Junction Spine 2010, 1, 18–22. [Google Scholar] [CrossRef]
- Najm, W.I.; Seffinger, M.A.; Mishra, S.I.; Dickerson, V.M.; Adams, A.; Reinsch, S.; Murphy, L.S.; Goodman, A.F. Content validity of manual spinal palpatory exams—A systematic review. BMC Complement. Altern. Med. 2003, 3, 1. [Google Scholar] [CrossRef]
- González, A.B.; Darby, S. Risk of cancer from diagnostic X-rays: Estimates for the UK and 14 other countries. Lancet 2004, 363, 345–351. [Google Scholar] [CrossRef]
- Pinel-Giroux, F.-M.; Mac-Thiong, J.-M.; de Guise, J.A.; Berthonnaud, É.; Labelle, H. Computerised assessment of sagittal curvatures of the spine: Comparison between Cobb and tangent circles techniques. J. Spinal Disord. Tech. 2006, 19, 507–512. [Google Scholar] [CrossRef]
- Harlick, J.C.; Milosavljevic, S.; Milburn, P.D. Palpation identification of spinous processes in the lumbar spine. Man. Ther. 2007, 12, 56–62. [Google Scholar] [CrossRef] [PubMed]
- Moura, D.C.; Boisvert, J.; Barbosa, J.G.; Labelle, H.; Tavares, J.M.R. Fast 3D reconstruction of the spine from biplanar radiographs using a deformable articulated model. Med. Eng. Phys. 2011, 33, 924–933. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Brink, Y.; Louw, Q.; Grimmer-Somers, K. The quality of evidence of psychometric properties of three-dimensional spinal posture-measuring instruments. BMC Musculoskelet. Disord. 2011, 12, 93. [Google Scholar] [CrossRef] [PubMed]
- Greendale, G.A.; Nili, N.S.; Huang, M.-H.; Seeger, L.; Karlamangla, A.S. The reliability and validity of three non-radiological measures of thoracic kyphosis and their relations to the standing radiological Cobb angle. Osteoporos. Int. 2011, 22, 1897–1905. [Google Scholar] [CrossRef] [PubMed]
- Coelho, D.M.; Bonagamba, G.H.; Oliveira, A.S. Scoliometer measurements of patients with idiopathic scoliosis. Braz. J. Phys. Ther. 2013, 17, 179–184. [Google Scholar] [CrossRef] [PubMed]
- Giglio, C.A.; Volpon, J.B. Development and evaluation of thoracic kyphosis and lumbar lordosis during growth. J. Child. Orthop. 2007, 1, 187–193. [Google Scholar] [CrossRef] [PubMed]
- Mirbagheri, S.-S.; Rahmani-Rasa, A.; Farmani, F.; Amini, P.; Nikoo, M.-R. Evaluating kyphosis and lordosis in students by using a flexible ruler and their relationship with severity and frequency of thoracic and lumbar pain. Asian Spine J. 2015, 9, 416–422. [Google Scholar] [CrossRef]
- Mannion, A.F.; Knecht, K.; Balaban, G.; Dvorak, J.; Grob, D. A new skin-surface device for measuring the curvature and global and segmental ranges of motion of the spine: Reliability of measurements and comparison with data reviewed from the literature. Eur. Spine J. 2004, 13, 122–136. [Google Scholar] [CrossRef]
- Vutan, A.-M.; Lovasz, E.-C.; Amarandei, M.; Ciupe, V. The methods used for the diagnosis and evaluation of scoliosis. Timis. Phys. Educ. Rehabil. J. 2016, 9, 36–41. [Google Scholar] [CrossRef][Green Version]
- Quaresma, C.; João, F.; Fonseca, M.; Secca, M.F.; Veloso, A.; O’neill, J.G.; Branco, J. Comparative evaluation of the tridimensional spine position measured with a new instrument (Vertebral Metrics) and an optoelectronic system of stereophotogrammetry. Med. Biol. Eng. Comput. 2010, 48, 1161–1164. [Google Scholar] [CrossRef]
- Gabriel, A.; Quaresma, C.; Vieira, P. Vertebral metrics—Automation of a non-invasive instrument to analyse the spine. In BIODEVICES 2015—8th International Conference on Biomedical Electronics and Devices, Proceedings of the 8th International Joint Conference on Biomedical Engineering Systems and Technologies, BIOSTEC 2015, Lisbon, Portugal, 12–15 January 2015; Cliquet, A., Jr., Fred, A., Gamboa, H., Elias, D., Eds.; SciTePress—Science and Technology Publications: Setúbal, Portugal, 2015; pp. 150–155. [Google Scholar]
- Gabriel, A.T.; Quaresma, C.; Secca, M.F.; Vieira, P. Development and clinical application of Vertebral Metrics: Using a stereo vision system to assess the spine. Med. Biol. Eng. Comput. 2018, 56, 1435–1446. [Google Scholar] [CrossRef] [PubMed]
- Gruescu, C.M.; Garaiman, A.; Lovasz, E.C. Modeling of human spinal column and simulation of spinal deformities. Mechanika 2015, 21, 214–219. [Google Scholar] [CrossRef][Green Version]
- Campbell-Kyureghyan, N.; Jorgensen, M.; Burr, D.; Marras, W. The prediction of lumbar spine geometry: Method development and validation. Clin. Biomech. 2005, 20, 455–464. [Google Scholar] [CrossRef]
- Lavecchia, C.E.; Espino, D.M.; Moerman, K.M.; Tse, K.M.; Robinson, D.; Lee, P.V.S.; Shepherd, D.E.T. Lumbar model generator: A tool for the automated generation of a parametric scalable model of the lumbar spine. J. R. Soc. Interface 2018, 15, 20170829. [Google Scholar] [CrossRef] [PubMed]
- Panjabi, M.M. Three-dimensional mathematical model of the human spine structure. J. Biomech. 1973, 6, 671–680. [Google Scholar] [CrossRef]
- Boisvert, J.; Cheriet, F.; Pennec, X.; Labelle, H.; Ayache, N. Principal Deformations Modes of Articulated Models for the Analysis of 3D Spine Deformities. Electron. Lett. Comput. Vis. Image Anal. 2008, 7, 13–31. [Google Scholar] [CrossRef][Green Version]
- Poredoš, P.; Čelan, D.; Možina, J.; Jezeršek, M. Determination of the human spine curve based on laser triangulation. BMC Med. Imaging 2015, 15, 2. [Google Scholar] [CrossRef] [PubMed]
- Panjabi, M.M.; Duranceau, J.; Goel, V.; Oxland, T.; Takata, K. Cervical human vertebrae quantitative three-dimensional anatomy of the middle and lower regions. Spine 1991, 16, 861–869. [Google Scholar] [CrossRef]
- Panjabi, M.M.; Takata, K.; Goel, V.; Federico, D.; Oxland, T.; Duranceau, J.; Krag, M. Thoracic human vertebrae quantitative three-dimensional anatomy. Spine 1991, 16, 888–901. [Google Scholar] [CrossRef] [PubMed]
- Panjabi, M.M. The stabilizing system of the spine. Part I. Function, dysfunction, adaptation, and enhancement. J. Spinal Disord. 1992, 5, 383–389. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Wilamowski, B.M. The Industrial Electronics Handbook—Intelligent Systems, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Moll, J.M.; Wright, V. New York clinical criteria for ankylosing spondylitis. A statistical evaluation. Ann. Rheum. Dis. 1973, 32, 354–363. [Google Scholar] [CrossRef] [PubMed]
- Akgul, O.; Ozgocmen, S. Classification criteria for spondyloarthropathies. World J. Orthop. 2011, 2, 107–115. [Google Scholar] [CrossRef]
- Jang, J.H.; Ward, M.M.; Rucker, A.N.; Reveille, J.D.; Davis, J.C.; Weisman, M.H.; Learch, T.J. Ankylosing spondylitis: Patterns of radiographic involvement—A re-examination of accepted principles in a cohort of 769 patients. Radiology 2011, 258, 192–198. [Google Scholar] [CrossRef] [PubMed]
- Baraliakos, X.; Listing, J.; Brandt, J.; Haibel, H.; Rudwaleit, M.; Sieper, J.; Braun, J. Radiographic progression in patients with ankylosing spondylitis after 4 yrs of treatment with the anti-TNF-α antibody infliximab. Rheumatology 2007, 46, 1450–1453. [Google Scholar] [CrossRef]
- Ramiro, S.; Stolwijk, C.; van Tubergen, A.; van der Heijde, D.; Dougados, M.; Van den Bosch, F.; Landewé, R. Evolution of radiographic damage in ankylosing spondylitis: A 12 year prospective follow-up of the OASIS study. Ann. Rheum. Dis. 2015, 74, 52–59. [Google Scholar] [CrossRef]
- Singer, K.P.; Edmondston, S.J.; Day, R.E.; Breidahl, W.H. Computer-Assisted Curvature Assessment and Cobb Angle Determination of the Thoracic Kyphosis—An In Vivo and In Vitro Comparison. Spine 1994, 19, 1381–1384. [Google Scholar] [CrossRef]
- Hanneman, S.K. Design, Analysis, and Interpretation of Method-Comparison Studies. AACN Adv. Crit. Care 2008, 19, 223–234. [Google Scholar] [CrossRef]
- Doğan, N. Bland-Altman analysis: A paradigm to understand correlation and agreement. Turk. J. Emerg. Med. 2018, 18, 139–141. [Google Scholar] [CrossRef]
- Giavarina, D. Understanding Bland Altman analysis. Biochem. Medica 2015, 25, 141–151. [Google Scholar] [CrossRef]
- Picone, V.; Makris, N.; Boutevin, F.; Roy, S.; Playe, M.; Soussan, M. Clinical validation of time reduction strategy in continuous step-and-shoot mode during SPECT acquisition. EJNMMI Phys. 2021, 8, 10. [Google Scholar] [CrossRef]
- Thirunavukarasu, A.J.; Mullinger, D.; Rufus-Toye, R.M.; Farrell, S.; Allen, L.E. Clinical validation of a novel web-application for remote assessment of distance visual acuity. Eye 2022, 36, 2057–2061. [Google Scholar] [CrossRef]
- Azram, M.; Ahmed, N.; Leese, L.; Brigham, M.; Bowes, R.; Wheatcroft, S.B.; Ngantcha, M.; Stegemann, B.; Crowther, G.; Tayebjee, M.H. Clinical validation and evaluation of a novel six-lead handheld electrocardiogram recorder compared to the 12-lead electrocardiogram in unselected cardiology patients (EVALECG Cardio). Eur. Heart J.-Digit. Health 2021, 2, 643–648. [Google Scholar] [CrossRef] [PubMed]
- Merchant, M.; Parfenov, A.; Bettencourt, A.; Klein, L. Clinical Validation of Non-Invasive Monitor Of Hemodynamic Congestion In Heart Failure Patients. J. Card. Fail. 2023, 29, 557. [Google Scholar] [CrossRef]
- Ghafari, C.; Houissa, K.; Dens, J.; Ungureanu, C.; Kayaert, P.; Constant, C.; Carlier, S. Clinical Validation of a New Enhanced Stent Imaging Method. Algorithms 2023, 16, 276. [Google Scholar] [CrossRef]
- Hadjidimitriou, S.; Pagourelias, E.; Apostolidis, G.; Dimaridis, I.; Charisis, V.; Bakogiannis, C.; Hadjileontiadis, L.; Vassilikos, V. Clinical Validation of an Artificial Intelligence–Based Tool for Automatic Estimation of Left Ventricular Ejection Fraction and Strain in Echocardiography: Protocol for a Two-Phase Prospective Cohort Study. JMIR Res. Protoc. 2023, 12, e44650. [Google Scholar] [CrossRef]
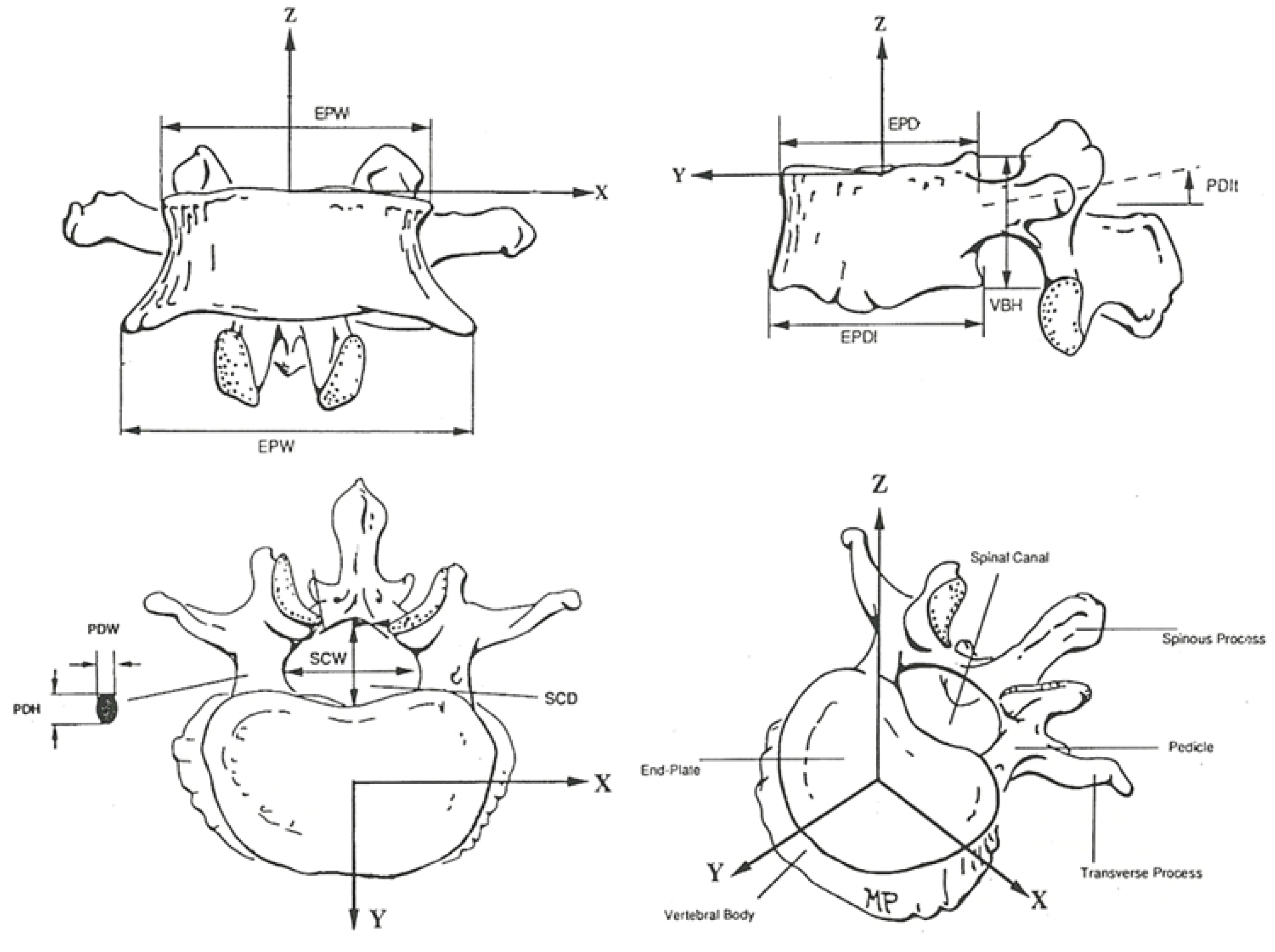

| S1 | L5 | L4 | L3 | L2 | L1 | T12 | T11 | T10 | T9 | T8 | T7 | T6 | T5 | T4 | T3 | T2 | T1 | C7 | C6 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EPW (mm) | 48 | 48 | 48 | 46 | 44 | 42 | 42 | 39 | 35 | 33 | 30 | 29 | 28 | 27 | 26 | 26 | 27 | 28 | 23 | 20 |
| EPD (mm) | 34 | 34 | 35 | 35 | 35 | 35 | 33 | 32 | 32 | 31 | 29 | 28 | 27 | 26 | 24 | 23 | 22 | 20 | 18 | 17 |
| EPA (mm2) | - | 1218 | 1273 | 1290 | 1197 | 1117 | 1024 | 945 | 834 | 754 | 664 | 603 | 552 | 495 | 444 | 412 | 400 | 376 | 280 | 290 |
| VBH (mm) | 23 | 23 | 24 | 24 | 24 | 24 | 23 | 21 | 20 | 19 | 19 | 18 | 17 | 16 | 16 | 16 | 16 | 14 | 13 | 11 |
| SCW (mm) | - | 27 | 25 | 24 | 24 | 24 | 22 | 19 | 18 | 18 | 18 | 17 | 17 | 17 | 17 | 18 | 19 | 22 | 25 | 26 |
| SCD (mm) | - | 20 | 19 | 17 | 18 | 19 | 18 | 16 | 15 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 15 | 16 | 15 | 15 |
| PDW (mm) | - | 16 | 14 | 10 | 8 | 9 | 9 | 10 | 9 | 8 | 7 | 6 | 6 | 6 | 6 | 7 | 8 | 8 | 7 | 6 |
| PDH (mm) | - | 16 | 15 | 14 | 15 | 16 | 17 | 16 | 15 | 14 | 12 | 12 | 12 | 11 | 12 | 12 | 11 | 10 | 7 | 7 |
| PDIt (°) | - | 5 | 4 | 3 | 3 | 3 | 5 | 9 | 7 | 8 | 12 | 11 | 8 | 8 | 8 | 9 | 8 | 8 | 11 | 6 |
| SPW (mm) | 5 | 5 | 6 | 7 | 6 | 7 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 5 | 4 | 5 | 5 | 7 | 6 | 7 |
| SPD (mm) | 27 | 31 | 32 | 33 | 30 | 27 | 27 | 25 | 27 | 30 | 34 | 35 | 35 | 35 | 33 | 32 | 30 | 30 | 30 | 25 |
| SPH (mm) | 10 | 14 | 15 | 14 | 14 | 15 | 15 | 10 | 11 | 9 | 9 | 9 | 8 | 8 | 9 | 9 | 8 | 10 | 8 | 7 |
| SPIt (°) | 10 | 19 | 11 | 13 | 11 | 10 | 2 | 10 | 25 | 29 | 45 | 54 | 57 | 61 | 53 | 38 | 30 | 20 | 20 | 20 |
| S1–L5 | L5–L4 | L4–L3 | L3–L2 | L2–L1 | L1–T12 | T12–T11 | T11–T10 | T10–T9 | T9–T8 | T8–T7 | T7–T6 | T6–T5 | T5–T4 | T4–T3 | T3–T2 | T2–T1 | T1–C7 | C7–C6 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IDH | 9 | 9 | 9 | 9 | 9 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 3 | 3 |
| k (N/mm) | 683 | 714 | 724 | 672 | 627 | 1034 | 954 | 842 | 762 | 671 | 609 | 558 | 500 | 448 | 416 | 404 | 380 | 471 | 488 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gabriel, A.T.; Quaresma, C.; Vieira, P. An Innovative Mathematical Model of the Spine: Predicting Cobb and Intervertebral Angles Using the 3D Position of the Spinous Processes Measured by Vertebral Metrics. Algorithms 2024, 17, 134. https://doi.org/10.3390/a17040134
Gabriel AT, Quaresma C, Vieira P. An Innovative Mathematical Model of the Spine: Predicting Cobb and Intervertebral Angles Using the 3D Position of the Spinous Processes Measured by Vertebral Metrics. Algorithms. 2024; 17(4):134. https://doi.org/10.3390/a17040134
Chicago/Turabian StyleGabriel, Ana Teresa, Cláudia Quaresma, and Pedro Vieira. 2024. "An Innovative Mathematical Model of the Spine: Predicting Cobb and Intervertebral Angles Using the 3D Position of the Spinous Processes Measured by Vertebral Metrics" Algorithms 17, no. 4: 134. https://doi.org/10.3390/a17040134
APA StyleGabriel, A. T., Quaresma, C., & Vieira, P. (2024). An Innovative Mathematical Model of the Spine: Predicting Cobb and Intervertebral Angles Using the 3D Position of the Spinous Processes Measured by Vertebral Metrics. Algorithms, 17(4), 134. https://doi.org/10.3390/a17040134








