Analysis of a Two-Step Gradient Method with Two Momentum Parameters for Strongly Convex Unconstrained Optimization

Abstract

The paper is devoted to the theoretical and numerical analysis of the two-step method, constructed as a modification of Polyak’s heavy ball method with the inclusion of an additional momentum parameter. For the quadratic case, the convergence conditions are obtained with the use of the first Lyapunov method. For the non-quadratic case, sufficiently smooth strongly convex functions are obtained, and these conditions guarantee local convergence.An approach to finding optimal parameter values based on the solution of a constrained optimization problem is proposed. The effect of an additional parameter on the convergence rate is analyzed. With the use of an ordinary differential equation, equivalent to the method, the damping effect of this parameter on the oscillations, which is typical for the non-monotonic convergence of the heavy ball method, is demonstrated. In different numerical examples for non-quadratic convex and non-convex test functions and machine learning problems (regularized smoothed elastic net regression, logistic regression, and recurrent neural network training), the positive influence of an additional parameter value on the convergence process is demonstrated.

1. Introduction

Nowadays, many problems in machine learning [1], optimal control [2], applied linear algebra [3], system identification [4], and other applications lead to the problems of unconstrained convex optimization. The theory of convex optimization is well-developed [5,6,7], but  methods that can be additionally analyzed or improved exist. A typical example of an improvement of the standard gradient descent method is the heavy ball method (HBM), proposed by B.T. Polyak in [7,8], which is based on the inclusion of a momentum term. The local convergence of this method for functions from ${\mathcal{F}}_{l,L}^{2,1}$ (twice continuously differentiable, l-strongly convex functions with Lipschitz gradient) was proved in [7]. Recently, Ghadimi et al. [9] formulated the conditions of global linear convergence. Aujol et al. [10] analyzed the dynamical system associated with the HBM in order to obtain optimal convergence rates for convex functions with some additional properties, such as quasi-strong and strong convexity.

In the last few decades, extended modifications of the HBM have been developed, and interesting results on their behavior have been obtained. Bhaya and Kaszkuremicz [11] demonstrated that the HBM for minimization of quadratic functions can be considered a stationary version of the conjugate gradient method. Recently, Goujand et al. [12] proposed an adaptive modification of the HBM with Polyak stepsizes and demonstrated that this method can be considered a variant of the conjugate gradient method for quadratic problems, having many advantages, such as finite-time convergence and instant optimality. Danilova et al. [13] demonstrated the non-monotonic convergence of the HBM and analyzed the peak effect for ill-conditioned problems. In order to carry out the damping of this effect in [14], an averaged HBM was constructed. A global and local convergence of momentum method for semialgebraic functions with locally Lipschitz gradients was demonstrated in [15]. Wang et al. [16] used the theory of PID controllers for the construction of momentum methods for deep neural network training. A quasi-hyperbolic momentum method with two parameters, momentum and parameter, which performs a sort of interpolation between gradient descent and the HBM, was presented in [17]. A complete analysis of such algorithms for deterministic and stochastic cases was performed in [18], where the influence of parameters on stability and convergence rate was analyzed. Sutskever et al. [19] proposed a stochatic version of Nesterov’s method, where the momentum was included bilinearly with the step. An improved accelerated momentum method for stochastic optimization was presented in [20].

In [21], the authors investigated the ravine method and momentum methods from dynamical system perspectives. A high-resolution differential equation describing these methods was proposed, and the damping effect of the additional term driven by the Hessian was demonstrated. Similar results for Hessian damping were obtained in [22] for the proximal methods.A continuous system with damping for primal-dual convex problems was constructed in [23]. Alecsa et al. [24] investigated a perturbed heavy ball system with a vanishing damping term that contained a Tikhonov regularization term. It was demonstrated that the presence of a regularization term led to a strong convergence of the descent trajectories in the case of smooth functions. An analysis of momentum methods from the positions of Hamiltonian dynamical systems was presented in [25].

Yan et al. [26] proposed a modification of the HBM with an additional parameter and an additional internal stage. In [27], a method with three momentum parameters (the so-called triple momentum method) was presented. This method has been classified as the fastest known globally convergent first-order method. In [28], the integral quadratic constraint method used in robust control theory was applied to the construction of first-order methods. A method with two momentum parameters was introduced. In [29], this scheme was analyzed for a strongly convex function with a Lipschitz gradient, and the range of the possible convergence rate was presented.

Despite the results obtained for different methods with momentum mentioned above, there is a lack of correct understanding of the roles of parameters in computational schemes with momentum. As  mentioned by investigators, understanding the role of momentum remains important for practical problems. For example, in [19], the authors demonstrated that momentum is critical for good performance in deep learning problems. However, in another modification of the HBM, Ma and Yarats [17] demonstrated that momentum in practice can have a minor effect, which is insufficient for acceleration of convergence. Therefore, additional theoretical analysis of methods with momentum is important in our time.

The presented paper is devoted to the analysis of a method with two momentum parameters, as proposed in [28]. For the functions from ${\mathcal{F}}_{l,L}^{1,1}$ (l-strongly convex L-smooth functions), this method was analyzed in [29], where global convergence for the special choice of parameters was proven. In the presented paper, we try to focus our attention on the case of quadratic functions from ${\mathcal{F}}_{l,L}^{1,1}$, in order to obtain the inequalities for parameters that guarantee global convergence, to obtain optimal values of the parameters, and to understand the effect of an additional momentum parameter on the convergence rate. Convergence conditions are obtained, and corresponding theorems are formulated. The constrained optimization problem for obtaining optimal parameters is stated. As  demonstrated in numerical experiments, in the quadratic case, the inclusion of an additional parameter does not improve the convergence rate. The role of this parameter is demonstrated with the use of the ordinary differential equation (ODE), which is equivalent to the method. This parameter provides an additional damping effect on the oscillations, typical for the HBM, according to its non-monotonic convergence, and can be useful in practice. In the numerical experiments for non-quadratic functions, it is demonstrated that this parameter also provides damping of the oscillations and leads to faster convergence to the minimum in comparison with the standard HBM. Additionally, the effect of this parameter is demonstrated for the non-convex function that arises in recurrent neural network training.

The paper has the following structure: Section 2 is devoted to the theoretical analysis method in application to strongly convex quadratic functions. The effect of an additional momentum parameter is analyzed. The results of the numerical experiments for non-quadratic, strongly convex, and non-convex functions are presented in Section 3. Some concluding remarks are made in Section 4.

2. Analysis of Two-Step Method

Let the scalar function $f:{\mathbb{R}}^d\to \mathbb{R}$ from ${\mathcal{F}}_{l,L}^{1,1}$ be considered. We try to find its minimizer $x^{\ast }$. So the unconstrained minimization problem is stated:

$$f\left(x\right)\to \underset{x\in {\mathbb{R}}^d}{min}.$$

(1)

The gradient descent method (GD) for numerical solution of (1) is written as

$$x^{k+1}=x^k-h\nabla f\left(x^k\right),$$

(2)

where $h>0$ is a step. If we additionally propose that $f\left(x\right)\in {\mathcal{F}}_{l,L}^{2,1}$, the optimal step and convergence rate for (2) are presented as in [7]

$$h_{opt}=\frac{2}{l+L},{\rho }_{opt}=\frac{\kappa -1}{\kappa +1},$$

where $\kappa =L/l$ is the condition number and $L,l$ can be associated with the minimum and maximum eigenvalues of a Hessian of $f\left(x\right)$.

Polyak’s heavy ball method is presented as in [7,8]

$$x^{k+1}=x^k-h\nabla f\left(x^k\right)+\beta (x^k-x^{k-1}),$$

(3)

where $\beta \in [0,1)$ is the momentum. The optimal values in the case of strongly convex quadratic function are written as in [7]

$$h_{opt}=\frac{4}{{(\sqrt{L}+\sqrt{l})}^2},{\beta }_{opt}={\left(\frac{\sqrt{\kappa }-1}{\sqrt{\kappa }+1}\right)}^2,{\rho }_{opt}=\frac{\sqrt{\kappa }-1}{\sqrt{\kappa }+1}.$$

Lessard et al. [28] proposed the following method with an additional momentum parameter:

$$x^{k+1}=x^k-h\nabla f\left(y^k\right)+{\beta }_1(x^k-x^{k-1}),y^k=x^k+{\beta }_2(x^k-x^{k-1}).$$

(4)

As can be seen, for the case of ${\beta }_2=0$, method (4) leads to (3). In [29], the global convergence of this method for $f\left(x\right)\in {\mathcal{F}}_{l,L}^{1,1}$ with the convergence rate $\rho \in \left[1-\frac{1}{\sqrt{\kappa }},1-\frac{1}{\kappa }\right]$ is demonstrated for the following specific choice of parameters:

$$h=\frac{\kappa {(1-\rho )}^2(1+\rho )}{L},{\beta }_1=\frac{\kappa {\rho }^3}{\kappa -1},{\beta }_2=\frac{{\rho }^3}{(\kappa -1){(1-\rho )}^3(1+\rho )}.$$

In the theoretical part of the presented paper, we try to analyze the influence of parameter ${\beta }_2$ on the convergence of method (4) for the case of a quadratic function, written as

$$f\left(x\right)=\frac{1}{2}(x,Ax)-(b,x),$$

(5)

where $b\in {\mathbb{R}}^d$, A is a positive definite and symmetric matrix with eigenvalues $0<l={\lambda }_1\le {\lambda }_2\le \dots \le {\lambda }_d=L$. The gradient of this function is computed as $\nabla f\left(x\right)=Ax-b$, and $x^{\ast }$ is treated as the solution of the linear system $Ax=b$. The obtained results can be considered as the results of the local convergence of method (4), applied to $f\left(x\right)\in {\mathcal{F}}_{l,L}^{2,1}$, because in the neighborhood of $x^{\ast }$$f\left(x\right)$ from this class can be presented as (5) with $A={\nabla }^{2}f\left(x^{\ast }\right)$. This approach for obtaining local convergence conditions and optimal parameters values is widely used in literature [7,18].

Method (4), when applied to (5), leads to the following difference system:

$$x^{k+1}=(E-hA)x^k+({\beta }_{1}E-{\beta }_{2}hA)(x^k-x^{k-1})-hb,$$

(6)

where E is the unity matrix.

2.1. Convergence Conditions

The following theorem on the convergence of an iterative method, as presented by (6), can be formulated

Theorem 1. 

For $h>0$, ${\beta }_1\in [0,1)$ and ${\beta }_2\ge 0$, the following inequality takes place:

$$h<\frac{2(1+{\beta }_1)}{(1+2{\beta }_2)L}.$$

(7)

Then, method (6) converges to $x^{\ast }$ for any $x^0$.

Proof of Theorem 1. 

(1)

Let the new variable $z^k={(x^k-x^{\ast },x^{k-1}-x^{\ast })}^T$ be introduced. Then, method (6) can be rewritten as a single-step method:

$$z^{k+1}=T{z}^k,$$

where matrix T is written as

$$T=\left(\begin{array}{cc}(1+{\beta }_1)E-h(1+{\beta }_2)A& h{\beta }_{2}A-{\beta }_{1}E\\ E& 0_{d\times d}\end{array}\right).$$

This method converges if, and only if, $r\left(T\right)$ (spectral radius of matrix T) is strictly less than unity [3].

Matrix A can be represented by the spectral decomposition $A=S\mathsf{\Lambda }{S}^T$, where $\mathsf{\Lambda }$ is the diagonal matrix of eigenvalues of A, S is a matrix of eigenvectors, and $S{S}^T=S^{T}S=E$. The following transformation of T can be introduced: $\overline{T}={\Sigma }^{T}T\Sigma$, where

$$\Sigma =\left(\begin{array}{cc}S& 0_{d\times d}\\ 0_{d\times d}& S\end{array}\right),\overline{T}=\left(\begin{array}{cc}(1+{\beta }_1)E-h(1+{\beta }_2)\mathsf{\Lambda }& h{\beta }_2\mathsf{\Lambda }-{\beta }_{1}E\\ E& 0_{d\times d}\end{array}\right).$$

Matrix $\overline{T}$ has the same eigenvalues, as matrix T.

Let us demonstrate that $\overline{T}$ has the same spectrum as the following matrix:

$$\tilde{T}=\left(\begin{array}{cccc}{T}_1& 0_{2\times 2}& \dots & 0_{2\times 2}\\ 0_{2\times 2}& T_2& \dots & 0_{2\times 2}\\ \dots & \dots & \dots & \dots \\ 0_{2\times 2}& 0_{2\times 2}& \dots & T_d\end{array}\right).$$

where $T_i$ are $2\times 2$ matrices, which are presented as

$$T_i=\left(\begin{array}{cc}1+{\beta }_1-h(1+{\beta }_2){\lambda }_i& h{\beta }_2{\lambda }_i-{\beta }_1\\ 1& 0\end{array}\right).$$

Matrix $\overline{T}-\zeta E$ is presented as

$$\overline{T}-\zeta E=\left(\begin{array}{cc}{T}_{11}& T_{12}\\ T_{21}& T_{22}\end{array}\right),$$

where $T_{11}=(1+{\beta }_1)E-h(1+{\beta }_2)\mathsf{\Lambda }-\zeta E$, $T_{12}=h{\beta }_2\mathsf{\Lambda }-{\beta }_{1}E$, $T_{21}=E$, $T_{22}=-\zeta E$. The determinant of this matrix is computed by the following rule [30]:

$$det(\overline{T}-\zeta E)=det\left(T_{11}\right)det(T_{22}-T_{21}{T}_{11}^{-1}{T}_{12})=$$

$$det\left(T_{11}\right)det\left(\begin{array}{cccc}-\zeta +\frac{{\beta }_1-h{\beta }_2{\lambda }_1}{1+{\beta }_1-h(1+{\beta }_2){\lambda }_1-\zeta }& 0& \dots & 0\\ 0& -\zeta +\frac{{\beta }_1-h{\beta }_2{\lambda }_2}{1+{\beta }_1-h(1+{\beta }_2){\lambda }_2-\zeta }& \dots & 0\\ \dots & \dots & \dots & \dots \\ 0& 0& \dots & -\zeta +\frac{{\beta }_1-h{\beta }_2{\lambda }_d}{1+{\beta }_1-h(1+{\beta }_2){\lambda }_d-\zeta }\end{array}\right)=$$

$$({\beta }_1-h{\beta }_2{\lambda }_1-\zeta {\chi }_1)\dots ({\beta }_1-h{\beta }_2{\lambda }_d-\zeta {\chi }_d),$$

where ${\chi }_i=1+{\beta }_1-h(1+{\beta }_2){\lambda }_i-\zeta$, $i=\overline{1,d}$.

The determinant of the block-diagonal matrix $\tilde{T}-\zeta E$ is written as

$$det(\tilde{T}-\zeta E)=det(T_1-\zeta E_{2\times 2})det(T_2-\zeta E_{2\times 2})\dots det(T_d-\zeta E_{2\times 2}),$$

and, as can be seen, it is equal to $det(\overline{T}-\zeta E)$. So, both matrices have the same eigenvalues ${\zeta }_k$, $k=\overline{1,2d}$ and these eigenvalues are computed as eigenvalues of matrices $T_i$.

(2)

According to the result presented above, the analysis of eigenvalues of T leads to the analysis of roots of an algebraic equation:

$${\zeta }^2-(1+{\beta }_1-h(1+{\beta }_2)\lambda )\zeta +{\beta }_1-h{\beta }_2\lambda =0.$$

(8)

In order to guarantee convergence, parameters should be chosen in a way which guarantees that $|{\zeta }_{1,2}|<1$. For  obtaining these conditions, we perform conformal mapping of the interior of the unit circle $\{\zeta :|\zeta |<1\}$ to the set $Q=\{q:\mathrm{Re}(q)<0\}$ with use of the following function:

$$\zeta =\frac{q+1}{q-1}.$$

(9)

After substitution of (9) into (8), the following equation is obtained:

$$h\lambda q^2+2(1-{\beta }_1+{\beta }_2\lambda h)q+2(1+{\beta }_1-{\beta }_2\lambda h)-h\lambda =0.$$

(10)

The conditions on coefficients of (10) guarantee roots $q_i\in Q$ are provided by the Routh–Hurwitz criterion [30,31]. The Hurwitz matrix for (10) is written as

$$\left(\begin{array}{cc}2(1-{\beta }_1+{\beta }_2\lambda h)& h\lambda \\ 0& 2(1+{\beta }_1-{\beta }_2\lambda h)-h\lambda \end{array}\right).$$

The conditions of the Routh–Hurwitz criterion lead to two inequalities:

$$1-{\beta }_1+{\beta }_2\lambda h>0,$$

(11)

$$2(1+{\beta }_1-{\beta }_2\lambda h)-h\lambda >0.$$

(12)

Inequity (11) is valid $\forall \lambda \in [l,L]$, $\forall h>0$ according to the ranges of values of ${\beta }_i$ stated in the conditions of the theorem. Inequity (12) is rewritten as

$$h<\frac{2(1+{\beta }_1)}{\lambda (1+2{\beta }_2)},$$

and it is valid for values of h chosen from Inequity (7). This, condition (7) guarantees that $q_i\in Q$, and as a consequence that $|{\zeta }_i|<1$ under the stated conditions. This leads to the convergence of (6) for any $x^0\in {\mathbb{R}}^d$.

□

2.2. Analysis of Convergence Rate

Let us analyze the convergence rate of method (6). At first, let us obtain the expression for the spectral radius of matrix T. Let $s=(h,{\beta }_1,{\beta }_2)$ and the spectral radius be presented as the function $r(s,\lambda )$, where $\lambda \in [l,L]$. The expression for r can be obtained with the use of an expression for the roots of (8):

$${\zeta }_{1,2}=\frac{1}{2}\left(A_1\pm \sqrt{D}\right),$$

where $D=A_1^2-4A_2$, $A_1=1+{\beta }_1-h(1+{\beta }_2)\lambda$, $A_2={\beta }_1-h\lambda {\beta }_2$ and is written as

$$r(s,\lambda )=\frac{1}{2}max\left(\right|{\zeta }_1|,|{\zeta }_2\left|\right).$$

(13)

If $r(s,\lambda )$ is considered a function of $\lambda$, the following theorem on its extremal property can be formulated:

Theorem 2. 

The maximum value of $r(s,\lambda )$ as a function of $\lambda \in [l,L]$ takes place for $\lambda =l$ or $\lambda =L$.

Proof of Theorem 2. 

(1)

Let us obtain the expression for $r(s,\lambda )$. For $D>0$ in the case of $A_1>0$, the following inequality takes place: $A_1+\sqrt{D}>0$ and $|A_1-\sqrt{D}|=A_1-\sqrt{D}$ if $A_1>\sqrt{D}$, and in this case $A_1+\sqrt{D}>A_1-\sqrt{D}>0$. If $A_1-\sqrt{D}<0$, we obtain that $|A_1-\sqrt{D}|=\sqrt{D}-A_1$ and $A_1+\sqrt{D}>\sqrt{D}-A_1$. So, if $D>0$ and $A_1>0$, we have that $r(s,\lambda )=\frac{1}{2}(A_1+\sqrt{D})$.

If $D>0$ and $A_1<0$, we have that $|A_1-\sqrt{D}|=\sqrt{D}-A_1$, and for $|A_1+\sqrt{D}|$ we have that if $A_1+\sqrt{D}>0$, then $\sqrt{D}-A_1>A_1+\sqrt{D}$. If $A_1+\sqrt{D}<0$, then $|A_1+\sqrt{D}|=-A_1-\sqrt{D}$ and $\sqrt{D}-A_1>-A_1-\sqrt{D}$. So if $A_1<0$ and $D>0$, we obtain that $r(s,\lambda )=\frac{1}{2}(\sqrt{D}-A_1)$.

For $D<0$, it is easy to see that $r(s,\lambda )=\sqrt{A_2}$. The case of $D=0$ and case $A_1=0$ are trivial to analyze. Thus, it is demonstrated that

$$r(s,\lambda )=\left\{\begin{array}{c}\frac{1}{2}(A_1+\sqrt{D}),A_1\ge 0,D\ge 0,\hfill \\ \frac{1}{2}(\sqrt{D}-A_1),A_1<0,D\ge 0,\hfill \\ \sqrt{A_2},D<0.\hfill \end{array}\right.$$

(2)

Let us analyze the behavior of $r(s,\lambda )$ for $\lambda \in [l,L]$. The expression for D is written as

$$D={(1+{\beta }_2)}^2{\lambda }^2{h}^2-2((1+{\beta }_1)(1+{\beta }_2)-2{\beta }_2)\lambda h+{(1-{\beta }_1)}^2.$$

So, the non-negative values of D are associated with the solutions of the following inequality:

$${(1+{\beta }_2)}^2{t}^2-2((1+{\beta }_1)(1+{\beta }_2)-2{\beta }_2)t+{(1-{\beta }_1)}^2\ge 0.$$

The corresponding discriminant is equal to $16({\beta }_1+{\beta }_2({\beta }_1-1))$. As  can be seen,  solutions to this inequality exist, when

$${\beta }_2\le \frac{{\beta }_1}{1-{\beta }_1}.$$

(14)

The opposite inequality guarantees that it is valid for all $\lambda >0$. For analysis of the general situation of the sign of D this restriction is too strict, so we consider the case of condition (14).

The case of $D<0$ leads to the investigation of function $\psi \left(\lambda \right)=\sqrt{A_2\left(\lambda \right)}=\sqrt{{\beta }_1-\lambda h{\beta }_2}$. Condition $A_2\left(\lambda \right)>0$ leads to the restriction $\lambda <\frac{{\beta }_1}{h{\beta }_2}$, which is valid for $h<\frac{{\beta }_1}{L{\beta }_2}$. It should be noted that this condition correlates with (7) for values of ${\beta }_1\in [0,1)$, ${\beta }_2\ge 0$ under condition ${\beta }_2>\frac{{\beta }_1}{2}$. The derivative of $\psi \left(\lambda \right)$ is written as

$${\psi }^{\prime }\left(\lambda \right)=\frac{-h{\beta }_2}{2\sqrt{A_2\left(\lambda \right)}}$$

and for ${\beta }_2>0$, it is strictly negative, so $\psi$ decreases on the considered interval and its maximum is equal to $\psi \left(l\right)<\psi \left(0\right)=\sqrt{{\beta }_1}<1$.

For $D=0$, we obtain that $r=\frac{1}{2}|A_1\left(\lambda \right)|=\frac{1}{2}|1+{\beta }_1-h(1+{\beta }_2)\lambda |$. The case $A_1>0$ corresponds to the interval $\lambda \in \left(0,\frac{1+{\beta }_1}{h(1+{\beta }_2)}\right]$, where r decreases, and case $A_1<0$ corresponds to $\lambda >\frac{1+{\beta }_1}{h(1+{\beta }_2)}$, where r increases. So, the maximum of r in this situations is realized in point $\lambda =l$ or $\lambda =L$.

For $D>0$, two situations should be considered. For $A_1\ge 0$, the behavior of function ${\phi }_1\left(\lambda \right)=\frac{1}{2}(A_1\left(\lambda \right)+\sqrt{A_1^2\left(\lambda \right)-4A_2\left(\lambda \right)})$ should be analyzed. Its derivative is written as

$${\phi }_1^{\prime }\left(\lambda \right)=\frac{1}{2}\left(A_1^{\prime }\left(\lambda \right)+\frac{A_1^{\prime }\left(\lambda \right)A_1\left(\lambda \right)-2A_2^{\prime }\left(\lambda \right)}{\sqrt{A_1^2\left(\lambda \right)-4A_2\left(\lambda \right)}}\right)$$

and according to $A_1^{\prime }\left(\lambda \right)=-h(1+{\beta }_2)<0$, we can see that if $A_1^{\prime }{A}_1-2A_2^{\prime }\le 0$, ${\phi }_1^{\prime }\left(\lambda \right)$ will be negative, so ${\phi }_1$ decreases. Let us determine where this inequality is valid:

$$A_1^{\prime }{A}_1-2A_2^{\prime }\le 0\iff -(1+{\beta }_1)(1+{\beta }_2)+h\lambda {(1+{\beta }_2)}^2+2{\beta }_2\le 0,$$

so

$$\lambda \le \eta ({\beta }_1,{\beta }_2)=\frac{(1+{\beta }_1)(1+{\beta }_2)-2{\beta }_2}{h{(1+{\beta }_2)}^2}.$$

Function $\eta$ is strictly positive, when

$${\beta }_2<\frac{1+{\beta }_1}{1-{\beta }_1}.$$

(15)

As can be seen, this inequality is valid when condition (14) is realized on values of ${\beta }_2$. So, in the interval $(0,\eta ]$, function ${\phi }_1\left(\lambda \right)$ decreases.

Positive values of ${\phi }_1^{\prime }\left(\lambda \right)$ can be realized when the following inequality is valid:

$$A_1^{\prime }\sqrt{A_1^2-4A_2}+A_1^{\prime }{A}_1-2A_2^{\prime }>0,$$

(16)

which leads to $A_1^{\prime }{A}_1-2A_2^{\prime }>-A_1^{\prime }\sqrt{A_1^2-4A_2}$. According to $A_1^{\prime }=-h(1+{\beta }_2)<0$, this leads to the evident inequality $A_1^{\prime }{A}_1-2A_2^{\prime }>0$, which takes place for $\lambda >\eta ({\beta }_1,{\beta }_2)$ under condition (15).

Let us demonstrate that (16) correlates with (14): Inequity (16) leads to $-A_1^{\prime }{A}_2^{\prime }{A}_1+A_2^{\prime 2}>-A_2{A}_1^{\prime 2}$, which leads to the following inequality:

$$-(1+{\beta }_2+{\beta }_1+{\beta }_1{\beta }_2){\beta }_2+{\beta }_2^2>-{\beta }_1-2{\beta }_1{\beta }_2-{\beta }_1{\beta }_2^2,$$

which is equivalent to

$${\beta }_2+{\beta }_1{\beta }_2<{\beta }_1+2{\beta }_1{\beta }_2,$$

which is equivalent to (14).

It is easy to see that

$$\frac{(1+{\beta }_1)(1+{\beta }_2)-2{\beta }_2}{{(1+{\beta }_2)}^2}<\frac{1+{\beta }_1}{1+{\beta }_2},$$

(17)

so, when $\lambda \in \left(0,\frac{(1+{\beta }_1)}{h(1+{\beta }_2)}\right]$ (corresponds to $A_1\ge 0$), r decreases when $\lambda \in (0,\eta ({\beta }_1,{\beta }_2)]$ and increases when $\lambda >\eta ({\beta }_1,{\beta }_2)$ and its maximum is realized in the boundary point.

The case $A_1<0$ leads to the analysis of function ${\phi }_2\left(\lambda \right)=\frac{1}{2}(\sqrt{A_1^2\left(\lambda \right)-4A_2\left(\lambda \right)}-A_1\left(\lambda \right))$ on the interval, defined by inequality (see case $D=0$)

$$\lambda >\frac{1+{\beta }_1}{h(1+{\beta }_2)}.$$

(18)

The first derivative of ${\phi }_2\left(\lambda \right)$ is written as

$${\phi }_2^{\prime }\left(\lambda \right)=\frac{1}{2}\left(\frac{A_1^{\prime }\left(\lambda \right)A_1\left(\lambda \right)-2A_2^{\prime }\left(\lambda \right)}{\sqrt{A_1^2\left(\lambda \right)-4A_2\left(\lambda \right)}}-A_1^{\prime }\left(\lambda \right)\right).$$

According to $-A_1^{\prime }=h(1+{\beta }_2)>0$, we obtain that if $A_1^{\prime }{A}_1-2A_2^{\prime }>0$ (this takes place when $\lambda >\eta ({\beta }_1,{\beta }_2)$), this derivative is strictly positive. According to (17), it is valid for the interval defined by (18), so ${\phi }_2\left(\lambda \right)$ and, as a consequence, function r increases in the case of $A_1<0$ corresponding to (18) and its maximum takes place in the right boundary point $\lambda =L$, if intervals $[l,L]$ and (18) have an intersection.

Thus, for all values of D, we can see that r reaches its maximum value at the boundaries of interval $[l,L]$.

□

Notation 1. 

Formulated theorems for the case of function (5) provide the conditions that guarantee global convergence [7]:

$$\left|\right|x^k-x^{\ast }\left|\right|\le {(\rho +\epsilon )}^k\left|\right|x^0-x^{\ast }\left|\right|,\forall \epsilon \in (0,1-\rho ),\forall k\le 0,$$

where $\rho =max\left(r\right(s,l),r(s,L\left)\right)$.

If the non-quadratic $f\left(x\right)\in {\mathcal{F}}_{l,L}^{2,1}$ is considered, then these conditions provide a local convergence (see Theorem 1 from subsection 2.1.2 in [7]). Any sufficiently smooth function $f\left(x\right)$ in the neighborhood of $x^{\ast }$ can be presented as

$$f\left(x\right)\approx f\left(x^{\ast }\right)+\frac{1}{2}({\nabla }^{2}f\left(x^{\ast }\right)(x-x^{\ast }),x-x^{\ast }),$$

and according to the following property:

$$f\left(x^k\right)-f\left(x^{\ast }\right)\le \frac{L}{2}\left|\right|x^k-x^{\ast }{\left|\right|}^2,$$

we can see that if ∃ $\delta >0$, $\left|\right|x^0-x^{\ast }\left|\right|\le \delta$, then for method (4) the following inequality is obtained $\forall k\ge 0$:

$$f\left(x^k\right)-f\left(x^{\ast }\right)\le \frac{L}{2}{\delta }^2{(\rho +\epsilon )}^{2k},\forall \epsilon \in (0,1-\rho ).$$

Notation 2. 

Theorem 2 provides an approach to obtain optimal parameters with the solution of the following problem for obtaining an optimal convergence rate:

$${\rho }_{opt}=\underset{s\in \Sigma \subset {\mathbb{R}}^3}{min}max(r(s,l),r(s,L)),$$

(19)

where Σ is defined as:

$$\mathrm{\Sigma }=\left\{({\beta }_1,{\beta }_2,h):{\beta }_1\in [0,1),{\beta }_2\ge 0,h\in \left(0,\frac{2(1+{\beta }_1)}{L(1+2{\beta }_2)}\right]\right\}.$$

(20)

Similar minimax problems arise in the theory of the standard HBM (3) [7] and multiparametric method in [18].

2.3. Optimal Parameters

In this subsection, we discuss the solution of minimization problems (19) and (20) and the following problem, which is stated in order to analyze the effect of parameter ${\beta }_2$:

$$F({\beta }_1,h)=max(r(h,{\beta }_1,{\beta }_2,l),r(h,{\beta }_1,{\beta }_2,L))\to \underset{\Delta }{min},$$

(21)

where

$$\Delta =\left\{({\beta }_1,h):{\beta }_1\in [0,1),h\in \left(0,\frac{2(1+{\beta }_1)}{L(1+2{\beta }_2)}\right]\right\}.$$

So in (21) ${\beta }_2$ is treated as an external parameter, which can be varied. In our computations, problem (21) is solved using the following approach: in the first stage, we obtain three ’good’ initial points in $\Delta$ by random search, and in the second stage, we apply the Nelder–Mead method in order to obtain the optimal point more precisely than in the first stage. For computations at any value of ${\beta }_2$, we use ${10}^5$ random points in $\Delta$ and the accuracy ${10}^{-5}$ for the Nelder–Mead method. The use of a large number of random points provides the possibility of obtaining the initial points in the small neighborhood of the optimal point, and the points obtained with the Nelder–Mead method do not leave $\Delta$. This approach to solving the problem is very simple to realize and eliminates the need to use methods of unconstrained optimization. All computations were realized with the use of codes implemented in Matlab 2021a.

In Figure 1, the plots of optimal values of F are presented for the cases of interval ${\beta }_2\in [0,1]$ (Figure 1a) and ${\beta }_2\in [0,100]$ (Figure 1b) for four values of $\kappa$: 10, ${10}^2$, ${10}^3$, and ${10}^5$. As  can be seen, for both intervals and all considered values of $\kappa$, the minimum values of $F_{opt}$ takes place for ${\beta }_2=0$. The value of $F_{opt}$ becomes smaller at smaller values of $\kappa$. The last feature is also mentioned for the multi-parametric method of [18].

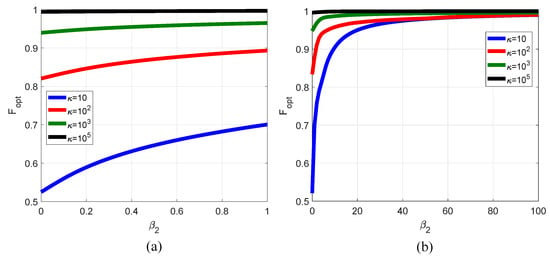
Figure 1. Plots of the dependence of optimal values of F on the value of ${\beta }_2$: (a) ${\beta }_2\in [0,1]$; (b) ${\beta }_2\in [0,100]$.

In addition, we try to compare the optimal convergence rate as a function of $\kappa$ for method (4) with the optimal rates for the GD method (2), the HBM (3), and the following Nesterov methods:

(1)

Nesterov’s accelerated gradient method for $f\in {\mathcal{F}}_{l,L}^{1,1}$ (Nesterov1) [6,28]:

$$x^{k+1}=y^k-h\nabla f\left(y^k\right),y^k=x^k+\beta (x^k-x^{k-1}),$$

$$h_{opt}=\frac{1}{L},{\beta }_{opt}=\frac{\sqrt{\kappa }-1}{\sqrt{\kappa }+1},{\rho }_{opt}=1-\frac{1}{\sqrt{\kappa }}.$$

(2)

Nesterov’s accelerated gradient method for a strongly convex quadratic function (Nesterov2) [28]:

$$x^{k+1}=y^k-h\nabla f\left(y^k\right),y^k=x^k+\beta (x^k-x^{k-1}),$$

$$h_{opt}=\frac{4}{3L+l},{\beta }_{opt}=\frac{\sqrt{3\kappa +1}-2}{\sqrt{3\kappa +1}+2},{\rho }_{opt}=1-\frac{2}{\sqrt{3\kappa +1}}.$$

The numerical solution to problem (19) is realized using the same method as for problem (21), but for the Nelder–Mead method, four ’good’ points are obtained with a random search. The interval on ${\beta }_2\ge 0$ is bounded by 0.5, according to the behavior, illustrated in Figure 1.

Plots of ${\rho }_{opt}$ are presented in Figure 2. As can be seen, the minimum values of ${\rho }_{opt}$ took place for methods (3) and (4), and they were very close. So, from the results of the computations, the following conclusion can be drawn: for the quadratic function $f\left(x\right)$, parameter ${\beta }_2$ does not provide an additional acceleration effect in comparison with the standard HBM (3).

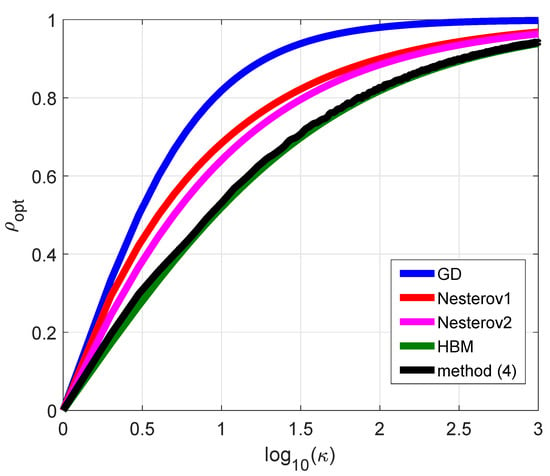
Figure 2. Plots of the dependence of the optimal convergence rate on logarithm of $\kappa$.

2.4. Equivalent ODE

For an additional analysis of the influence of ${\beta }_2$ on the convergence of (4), we consider an approach based on the ODE, which is constructed as a continuous analogue of the iterative method. At present, this approach is widely used for the analysis of optimization methods [7,21,22,23,24,32,33].

Let method (4) for quadratic function $f\left(x\right)=\frac{a}{2}{x}^2$, where $x\in \mathbb{R}$, $a>0$, be considered. This function can be treated as a quadratic approximation of the arbitrarily smooth function, which has its minimum zero value in point $x=0$. Application of (4) leads to the following difference equation:

$$x^{k+1}=x^k-ha(x^k+{\beta }_2(x^k-x^{k-1}))+{\beta }_1(x^k-x^{k-1}).$$

(22)

Let us introduce function $x\left(t\right)$, where t is defined as $t=k\sqrt{h}$, so $x\left(t\right)\approx x^{\frac{t}{\sqrt{h}}}=x^k$ and $x(t+\sqrt{h})\approx x^{k+1}$, $x(t-\sqrt{h})\approx x^{k-1}$. Equation (22) can be rewritten as

$$\frac{x^{k+1}-x^k}{\sqrt{h}}=-\sqrt{h}a{x}^k+({\beta }_1-ha{\beta }_2)\frac{x^k-x^{k-1}}{\sqrt{h}}.$$

(23)

Let the new parameters ${\gamma }_1>0$, ${\gamma }_2\ge 0$ be introduced: ${\beta }_1=1-{\gamma }_1\sqrt{h}$, ${\gamma }_2=\sqrt{h}{\beta }_2$ and the following new variable is considered:

$$m^{k+1}=\frac{x^{k+1}-x^k}{\sqrt{h}}.$$

So, (23) is rewritten as

$$\frac{m^{k+1}-m^k}{\sqrt{h}}=-a{x}^k-({\gamma }_1+a{\gamma }_2)m^k.$$

(24)

For $h\to 0$, we find that (24) is rewritten as $\dot{m}=-ax-({\gamma }_1+a{\gamma }_2)m$ and with the use of $m=\dot{x}$, we obtain the following second-order ODE:

$$\ddot{x}=-ax-({\gamma }_1+a{\gamma }_2)\dot{x}.$$

(25)

The case of HBM corresponds to ${\gamma }_2=0$ [7] and the ODE describes the dynamics of a material point with unit mass under a force with a potential represented by $f\left(x\right)$ and under a resistive force with coefficient ${\gamma }_1$. Thus, if ${\gamma }_2\ne 0$, we have the following mechanical meaning of ${\beta }_2$: this presents an additional damping effect on the solution of the ODE (25) and, as a consequence, on the behavior of method (4). With the use of proper values of ${\beta }_2$, we can realize the damping of oscillations related to the non-monotonic convergence of the method. This is typical for the case of $\kappa \gg 1$ [13]. In Section 3, this will also be illustrated for the minimization of non-quadratic convex and non-convex functions.

3. Numerical Experiments and Discussion

In this section, we tried to apply method (4) to the minimization of non-quadratic functions that arise in test problems for optimization solvers and in machine learning. The main purpose of these numerical experiments was to demonstrate the effect of ${\beta }_2$ on the convergence of method (4) in comparison with the standard HBM (3). The initial point for all test examples (except the RNN) was chosen as a fixed (not random) point, for better illustration of the convergence process. It was chosen far from the minimum points, but not so far that the method had a large number of iterations.

For the numerical examples, only a comparison of method (4) with the HBM (3) was realized, because (4) was treated as an improvement of the HBM, so it was decided to only perform a comparison with this method, in order to demonstrate the practical effect of such an improvement.

3.1. Rosenbrock Function

Let the 2D Rosenbrock function be considered:

$$f(x_1,x_2)={(1-x_1^2)}^2+100{(x_2-x_1^2)}^2.$$

This function has a minimum at the point $x^{\ast }=(1,1)$. For the numerical simulation, we used the following values: $x^0=(1,3)$, $h=2\times {10}^{-4}$, ${\beta }_1=0.97$, ${\beta }_2=1$. The descent trajectories for the methods (3) and (4) are presented in Figure 3a. The plots of the dependence of the logarithm of error, computed as $f\left(x^k\right)-f\left(x^{\ast }\right)$ on the iteration number are presented in Figure 3b. From both figures, it can be seen that the inclusion of ${\beta }_2$ led to the damping of oscillations typical for the HBM, and, as a consequence, to a faster entry of the trajectory in the neighborhood of the minimum point.

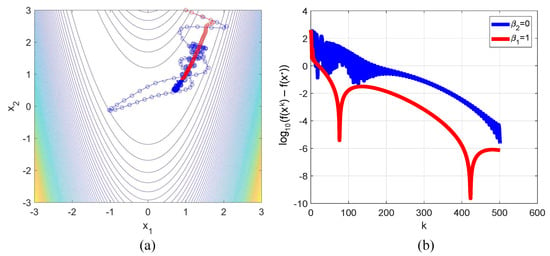
Figure 3. Plots of the descent trajectories (a) and dependence of the error logarithm on iteration number (b) for the minimization of the 2D Rosenbrock function. Blue line corresponds to the HBM, red line—to method (4).

The Rosenbrock function considered in this example can be classified as a ravine function, so the traditional gradient methods (without the application of the ravine method) converge slowly to the minimum point and they need many iterations. As  can be seen from Figure 3b, both methods converged in the neighborhood of the minimum point with good accuracy, but method (4) converged faster according to the damping of the oscillations.

3.2. Himmelblau Function

For the minimization of the non-convex Himmelblau function

$$f(x_1,x_2)={(x_1^2+x_2-11)}^2+{(x_1+x_2^2-7)}^2,$$

which has four local minima, the following parameters were used: $h=0.01$, ${\beta }_1=0.95$, ${\beta }_2=1$. For the initial point $x^0=(0,0)$ both methods converged to the local minimum $x^{\ast }=(3,2)$. The trajectories are presented in Figure 4a, and the plots of the error logarithm are presented in Figure 4b. As  can be seen, the damping effect realized with the proper choice ${\beta }_2$ led to a faster convergence in comparison with the standard HBM.

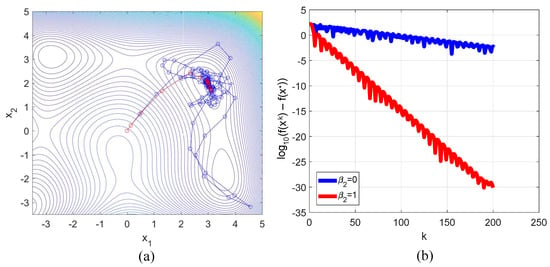
Figure 4. Plots of the descent trajectories (a) and dependence of the error logarithm on iteration number (b) for the minimization of the Himmelblau function. Blue line corresponds to the HBM, red line—to method (4).

3.3. Styblinski–Tang Function

Let the following non-convex function be considered:

$$f\left(x\right)=\frac{1}{2}\sum _{i=1}^d(x_i^4-16x_i^2+5x_i),$$

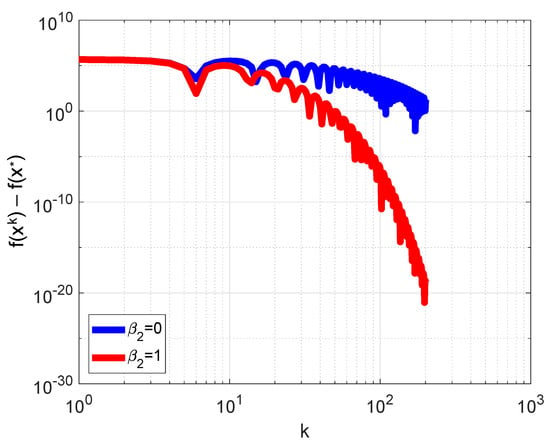
which has a local minimum at $x^{\ast }=(-2.903534,\dots ,-2.903534)$ and $f\left(x^{\ast }\right)=-39.16599·d$. For the case of $d=2$, we used $x^0=(-1,-4)$, $h=0.02$, ${\beta }_1=0.99$, ${\beta }_2=1$. The trajectories for both methods are presented in Figure 5a and plots of the logarithms of error are presented in Figure 5b. As  can be seen, for this situation, parameter ${\beta }_2\ne 0$ had a positive influence on the convergence. For $d=100$, we used the initial vector $x^0=(-1,\dots ,-1)$ and the parameters $h=0.03$, ${\beta }_1=0.95$, ${\beta }_2=1$. Plots of the dependence of error on iteration number in log–log scale are presented in Figure 6. As  can be seen, method (4) for ${\beta }_2=1$ converged to $x^{\ast }$ faster than the  HBM.

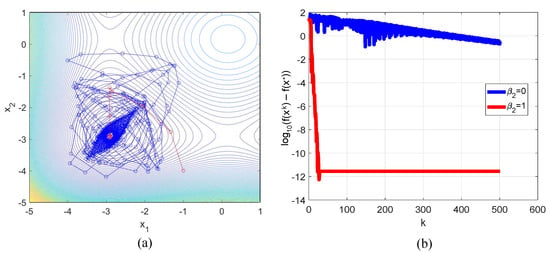
Figure 5. Plots of the descent trajectories (a) and dependence of the error logarithm on iteration number (b) for the minimization of the Styblinski–Tang function. Blue line corresponds to the HBM, red line—to method (4).

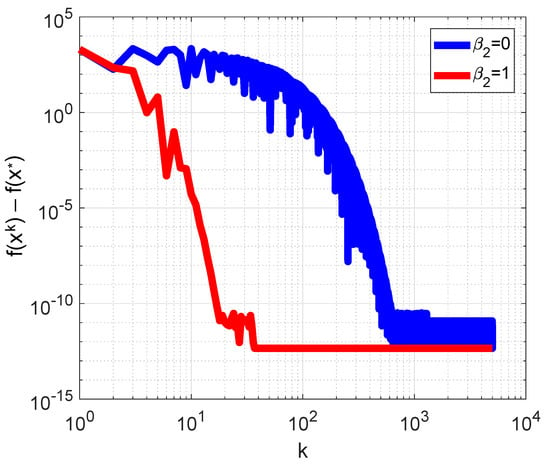
Figure 6. Plots of the dependence of error on iteration number for minimization of Styblinski–Tang function for $d=100$ in log–log axes. Blue line corresponds to the HBM, red line—to method (4).

3.4. Zakharov Function

This convex function is presented as

$$f\left(x\right)=\sum _{i=1}^d{x}_i^2+{\left(\sum _{i=1}^{d}0.5i{x}_i\right)}^2+{\left(\sum _{i=1}^{d}0.5i{x}_i\right)}^4.$$

It has a unique minimum point $x^{\ast }=0$. For $d=2$, we chose $x^0$ as $(4,2)$ and performed computations with the following parameter values: $h={10}^{-4}$, ${\beta }_1=0.985$, ${\beta }_2=15$. The trajectories are presented in Figure 7a and plots of the error logarithm dependence on the iteration number are presented in Figure 7b. As  can be seen, the selected value of ${\beta }_2$ led to a damping of oscillations typical for the HBM and led to a faster entry of the trajectory into the neighborhood of $x^{\ast }$. For $d=10$, computations were performed for $x^0$, selected as the vector of units, $h={10}^{-6}$, ${\beta }_1=0.99$, ${\beta }_2=4$. Plots of the dependence of error on the iteration number in log–log axes are presented in Figure 8. As  can be seen, the value of ${\beta }_2$ led to the damping of oscillations, as in the 2D case.

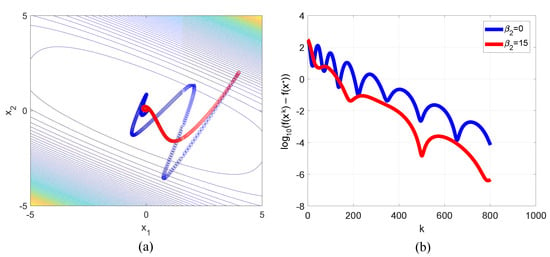
Figure 7. Plots of the descent trajectories (a) and the dependence of the error logarithm on the iteration number (b) for the minimization of the Zakharov function. Blue line corresponds to the HBM, red line—to method (4).

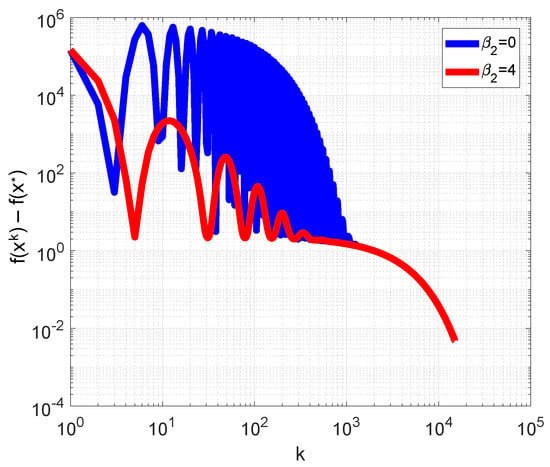
Figure 8. Plots of the dependence of the error on iteration number for the minimization of the Zakharov function for $d=10$ in log–log axes. Blue line corresponds to the HBM, red line—to method (4).

3.5. Non-Convex Function in Multidimensional Space

Let the following function be considered:

$$f\left(x\right)=\sum _{i=1}^{{10}^6}\frac{x_i^2}{1+x_i^2}.$$

(26)

This function has a unique minimum point $x^{\ast }=0$. We performed computations with $x^0$ chosen as a vector of units and for $h=0.1$, ${\beta }_1=0.95$, ${\beta }_2=1$.  Plots of the error’s dependence on the iteration number in log–log axes are presented in Figure 9. As in the previous examples, the inclusion of ${\beta }_2$ led to a faster convergence in comparison with the standard HBM.

Figure 9. Plots of the dependence of error on iteration number for minimization of function (26) in log–log axes. Blue line corresponds to the HBM, red line — to method (4).

3.6. Smoothed Elastic Net Regularization

The following function that arises in machine learning was considered [34]:

$$f\left(x\right)=\frac{1}{2}\left|\right|Ax-{b\left|\right|}_2^2+\alpha {\nu }_{\tau }\left(x\right)+\frac{\gamma }{2}{\left|\right|x\left|\right|}_2^2,$$

where $x\in {\mathbb{R}}^d$, $b\in {\mathbb{R}}^d$ is the vector of values, $dim\left(A\right)=m\times d$ is a matrix of features, $\alpha >0$, $\gamma >0$ are the regularization parameters, function ${\nu }_{\tau }\left(x\right)$, $\tau >0$ is the smooth approximation of ${\ell }_1$-norm (so-called pseudo-Huber function [35]):

$${\nu }_{\tau }\left(x\right)=\sum _{i=1}^d\left(\sqrt{{\tau }^2+x_i^2}-\tau \right).$$

As mentioned in [34,35] $f\left(x\right)\in {\mathcal{F}}_{l,L}$, where $l=\gamma +min\left(\mathrm{eig}\right(A\left)\right)$, $L\approx {(1+\sqrt{m/d})}^2+\gamma +\alpha /\tau$. Datasets, represented by A and b at various values of m and d were simulated using the function randn() in Matlab: matrix A was simulated as a random matrix from the Gaussian distribution normalized by $\sqrt{d}$, and b was simulated as a random vector from the same distribution. Computations were performed with the following parameter values: $\tau ={10}^{-4}$, $\alpha =\gamma ={10}^{-2}$. Steps h and ${\beta }_1$ were computed as optimal values for the quadratic case, and ${\beta }_2$ was chosen to as equal to 0.5. Condition number $\kappa$ for all model datasets was approximately equal to ${10}^4$. The error was computed as $f\left(x^k\right)-f\left(x^{\ast }\right)$, where $x^{\ast }$ was the benchmark solution, obtained by method (4) for $2\times {10}^4$ iterations. For all cases, $x^0$ was chosen as a vector of units. In Figure 10, the plots of the dependence of error on the iteration number are presented in log–log axes. As  can be seen, the presence of ${\beta }_2$ led to an improvement in convergence.

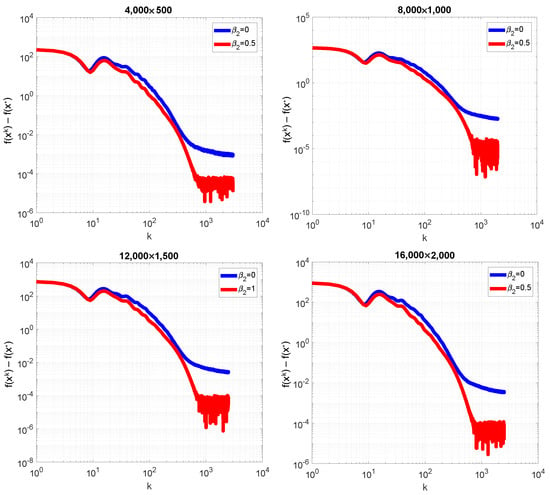
Figure 10. Plots of the dependence of the error on the iteration number for the regression problem with smoothed elastic net regularization in log–log axes for different model datasets. Blue line corresponds to the HBM, red line—to method (4).

3.7. Logistic Regression

For the binary classification, the following convex function related to the model of logistic regression is widely used:

$$f\left(x\right)=\sum _{i=1}^{m}log(1+exp(-y_i{\xi }_i^{T}x)),$$

where ${\xi }_i$ represents the rows of matrix $\mathsf{\Xi }$, $dim\left(\mathsf{\Xi }\right)=m\times d$ and $y_i\in \{-1,1\}$, $i=\overline{1,d}$. Matrix $\mathsf{\Xi }$ and vector y represent the training dataset.

For the computations, we used two datasets: SONAR ($m=208$, $d=60$) and CINA0 ($m=\mathrm{16,033}$, $d=132$). The first was used for a comparison of different methods in [36]. The second is a well-known test dataset, which can be downloaded from https://www.causality.inf.ethz.ch/challenge.php?page=datasets (accessed on 14 March 2024). The error was computed as $f\left(x^k\right)-f\left(x^{\ast }\right)$. For the SONAR dataset, the values $h=0.1$, ${\beta }_1=0.9999$, and ${\beta }_2=10$ were used, and a benchmark solution was obtained with method (4) in the case of $2\times {10}^4$ iterations. For CINA0, the following parameters were used: $h={10}^{-6}$, ${\beta }_1=0.99$, ${\beta }_2=2$ and a benchmark solution was obtained for $5\times {10}^3$ iterations of method (4). For both datasets, $x^0$ was chosen as a vector of zeroes.

In Figure 11, plots of the dependence of error on the iteration number in log–log axes are presented. As can be seen, the adding of ${\beta }_2\ne 0$ led to the damping of oscillations typical for the standard HBM.

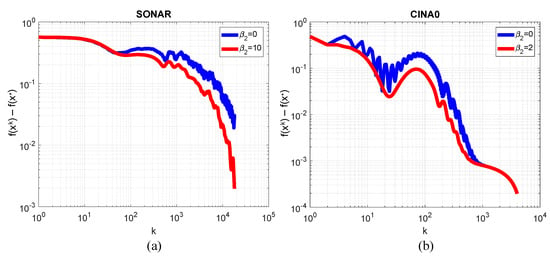
Figure 11. Plots of the dependence of error on the iteration number for the logistic regression problem in log–log axes for datasets SONAR (a) and CINA0 (b). Blue line corresponds to the HBM, red line—to method (4).

3.8. Recurrent Neural Network

Let us consider the model recurrent neural network (RNN) used for the analysis of phrase tone. For details of its architecture and realization, see https://python-scripts.com/recurrent-neural-network (accessed on 16 March 2024). This RNN was realized using the following recurrent relations:

$$h_s=tanh\left(W_{xh}{x}_s+W_{hh}{h}_{s-1}+b_h\right),s=\overline{1,M},y=W_{hy}{h}_M+b_y,$$

where M is the number of words of vocabulary in the phrase; $x_s$ is a vector, which represents the s-th word in the phrase; $h_s$ is a vector used for iterations in the hidden layer; y is the output vector; $W_{xh}$,$W_{hh}$, $W_{hy}$ are the matrices of weights; and $b_h$ and $b_y$ are the vectors of biases. The vector of probabilities of the ’good’ or ’bad’ tone of the phrase was computed as $\mathrm{softmax}\left(y\right)$. The training dataset consisted of 67 phrases from the vocabulary, with 19 unique words. The following dimensions of vectors were used: $dim\left(x\right)=19$, $dim\left(y\right)=2$, the dimension of h was chosen as 64 (the maximum number of words from vocabulary in the phrase; this number can be varied).

As a result of forward propagation, we obtained a 2D vector of probabilities for the phrase tone, computed with the use of the softmax function. The loss function used for the training of this RNN was computed as

$$L(X,\theta )=H_{\mu }(\mu ,p(X;\theta )),$$

where X is a matrix of vectors $x_1,\cdots ,x_M$, which represents the phrase with M words, $\mu \in \{0,1\}$ is a label of phrase; represented by X; $p\left(X\right)=\mathrm{softmax}\left(y\right(X\left)\right)$ is the probability of the phrase tone; $H_{\mu }$ is a proper component of a cross-entropy function

$$H(\nu ,p)=-(\nu log(p)+(1-\nu )log(1-p\left)\right);$$

and $\theta \in {\mathbb{R}}^d$ is a vector of parameters of RNN. The objective function is written as

$$f\left(\theta \right)=\frac{1}{N}\sum _{i=1}^{N}L(X_i,\theta ),$$

where $N=67$ is the size of the training dataset (number of phrases). With all considered dimensions, we minimized the function of $d=5506$ variables.

For minimization, we applied deterministic methods, as was considered in the theoretical part of the presented paper and despite the use of stochastic methods in most works on the training of neural networks. The computations were performed with $h=0.05$, ${\beta }_1=0.9$ and we tried to vary the value of ${\beta }_2$ in order to analyze its effect on the convergence. We realized a numerical experiment for 250 random initializations of weights and biases and performed computations for $3\times {10}^3$ epochs. In Figure 12, the plots of the dependence of the objective function value on the epoch number averaged at all random initializations are presented for the standard GD (2), HBM (3), and method (4) in the case of ${\beta }_2=1$. As can be seen, methods with momentum led to a faster convergence in comparison with the standard GD, as mentioned by many authors (e.g., see [19]), and the presence of ${\beta }_2$ led to a faster convergence to the minimum in practice. In Figure 13, the plots obtained for different values of ${\beta }_2$ are presented. As can be seen, the value of ${\beta }_2$ had an effect on the convergence of method (4).

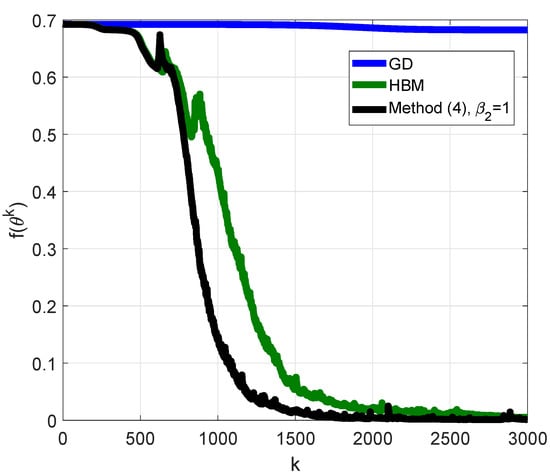
Figure 12. Plots of the dependence of the objective function value on the epoch number for the problem of RNN training.

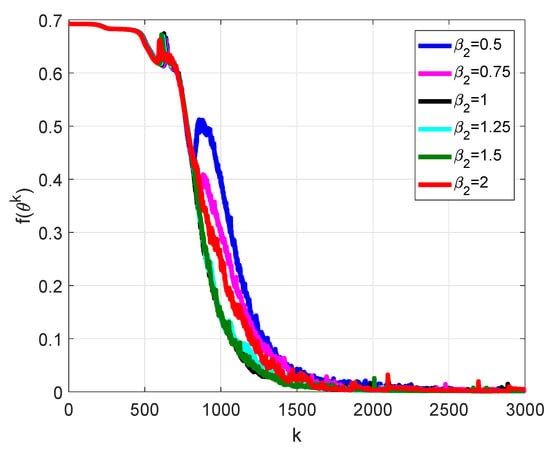
Figure 13. Plots of the dependence of the objective function value on epoch number for the problem of RNN training for method (4) at different values of ${\beta }_2$.

4. Conclusions

In the presented paper, we tried to perform an analysis of the properties of method (4) in theory and practice. Despite the results of the investigations presented in [28,29], this method requires further analysis, so we tried to realize this in the presented paper.

The following new results were obtained:

• It was demonstrated that, in the case of the quadratic function, method (4) can be easily investigated using the first Lyapunov method. As a result of its application, the convergence conditions presented in Theorem 1 were obtained. Such conditions led to the conditions for the HBM (3) in the case of ${\beta }_2=0$ (see [7]). For functions from ${\mathcal{F}}_{l,L}^{2,1}$, such conditions can be treated as the conditions of local convergence.
• In comparison with the HBM, optimal parameters for method (4) can only be obtained numerically by the solution of the 3D constrained problems (19) and (20). As demonstrated, for the quadratic case, the optimal value of ${\beta }_2$ was equal to zero, so method (4) did not provide additional acceleration in comparison to the standard HBM.
• The ’mechanical’ role of ${\beta }_2$ was demonstrated by the consideration of the ODE (25), which is equivalent to (4) in the 1D case. This ODE describes the descent process in the neighborhood of $x^{\ast }$. As can be seen from (25), the presence of ${\beta }_2$ realized an additional damping of oscillations associated with non-monotone convergence of the HBM [13].
• In numerical examples from different applications, it was demonstrated that, with the use of proper values of ${\beta }_2$, a decrease in oscillation amplitudes typical of the HBM can be realized.

The following remarks on future investigations can be made:

• In this paper, a local convergence analysis was presented. For $f\left(x\right)\in {\mathcal{F}}_{l,L}^{1,1}$, global convergence for a specific choice of the parameters was demonstrated in [29]. It is imperative to obtain the general conditions for the parameters that guarantee global convergence.As is known for the HBM (e.g., see [28]), the convergence conditions obtained for strongly convex quadratic functions can lead to a lack of global convergence for $f\left(x\right)\in {\mathcal{F}}_{l,L}^{1,1}$.
• An analysis of method (4) was performed for the case of constant values of ${\beta }_1$ and ${\beta }_2$. But as known [18], it is effective to use methods with adaptive momentum, whose value is dependent on k in order to improve the convergence. Thus, the construction of extensions of method (4) to the case of adaptive parameters is a perspective for future research.
• In this paper, all methods were considered in their deterministic formulations. However, in modern problems, especially those arising in machine learning, stochastic gradient methods are used according to the size of the datasets. Therefore, the extension of method (4) and its modifications for stochastic optimization has potential for future investigation, especially for applications in machine learning.