Modeling of Some Classes of Extended Oscillators: Simulations, Algorithms, Generating Chaos, and Open Problems
Abstract
1. Introduction
2. The Models
2.1. Model A: Mixed Form of Models (3) and (5)
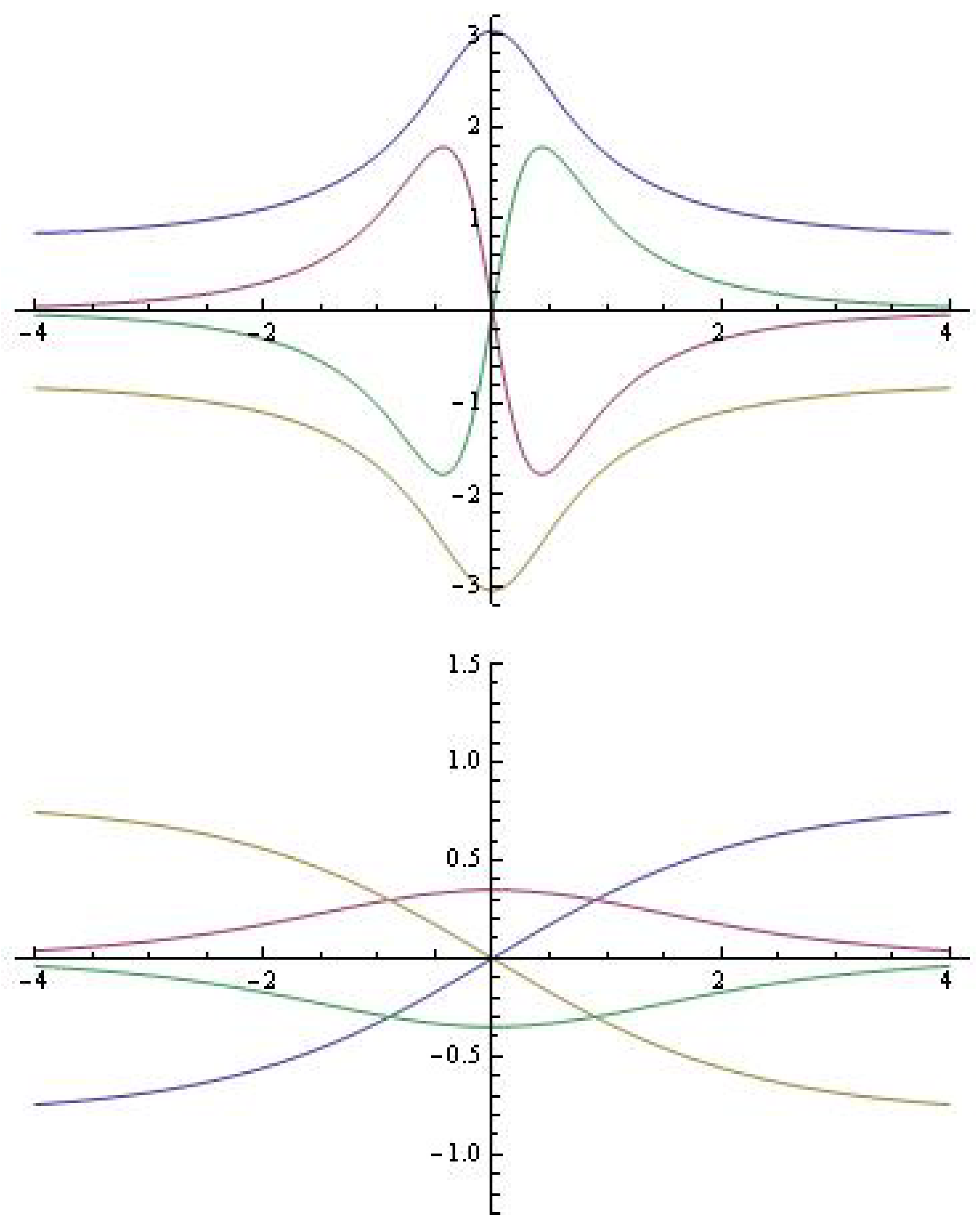
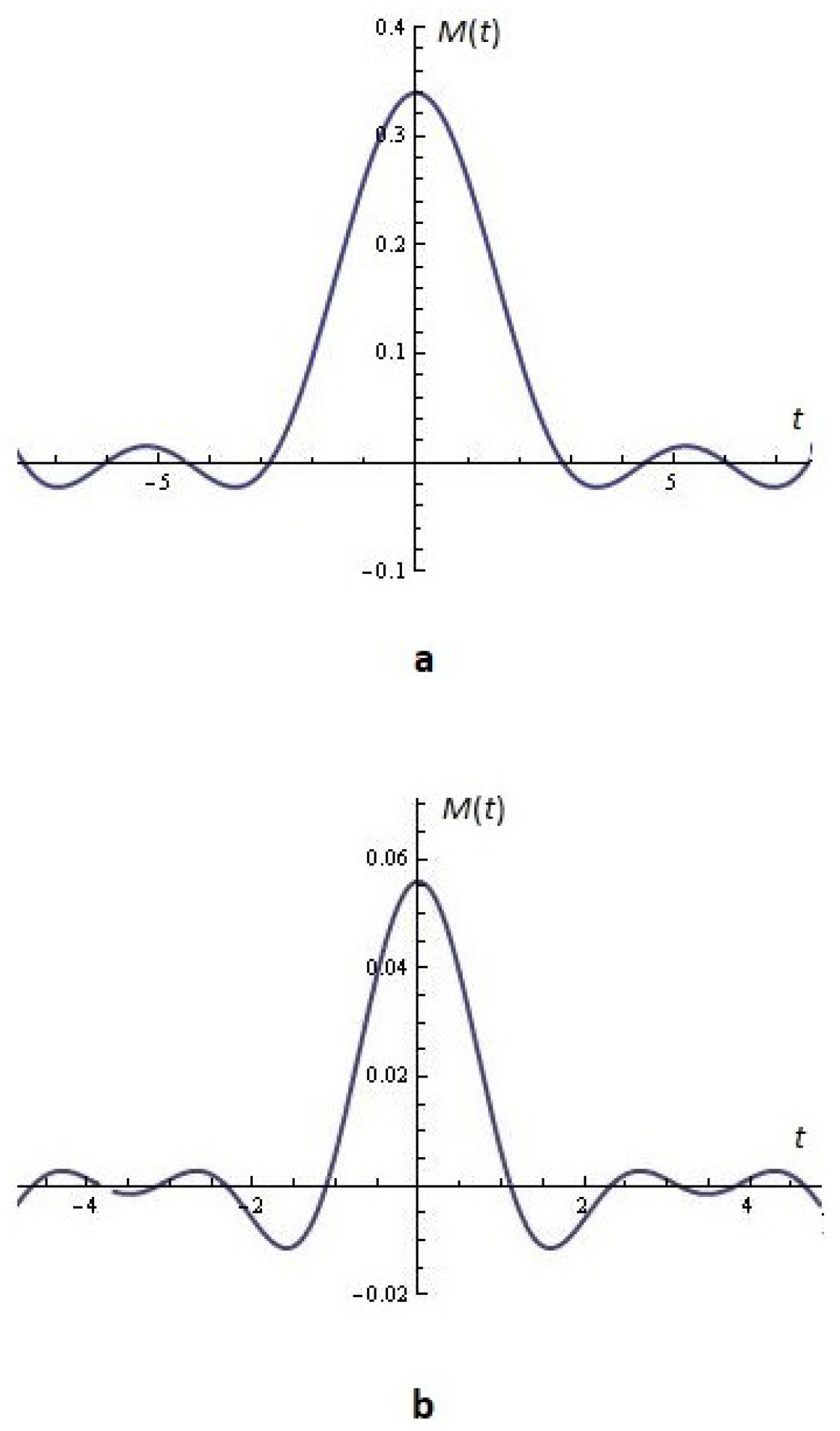
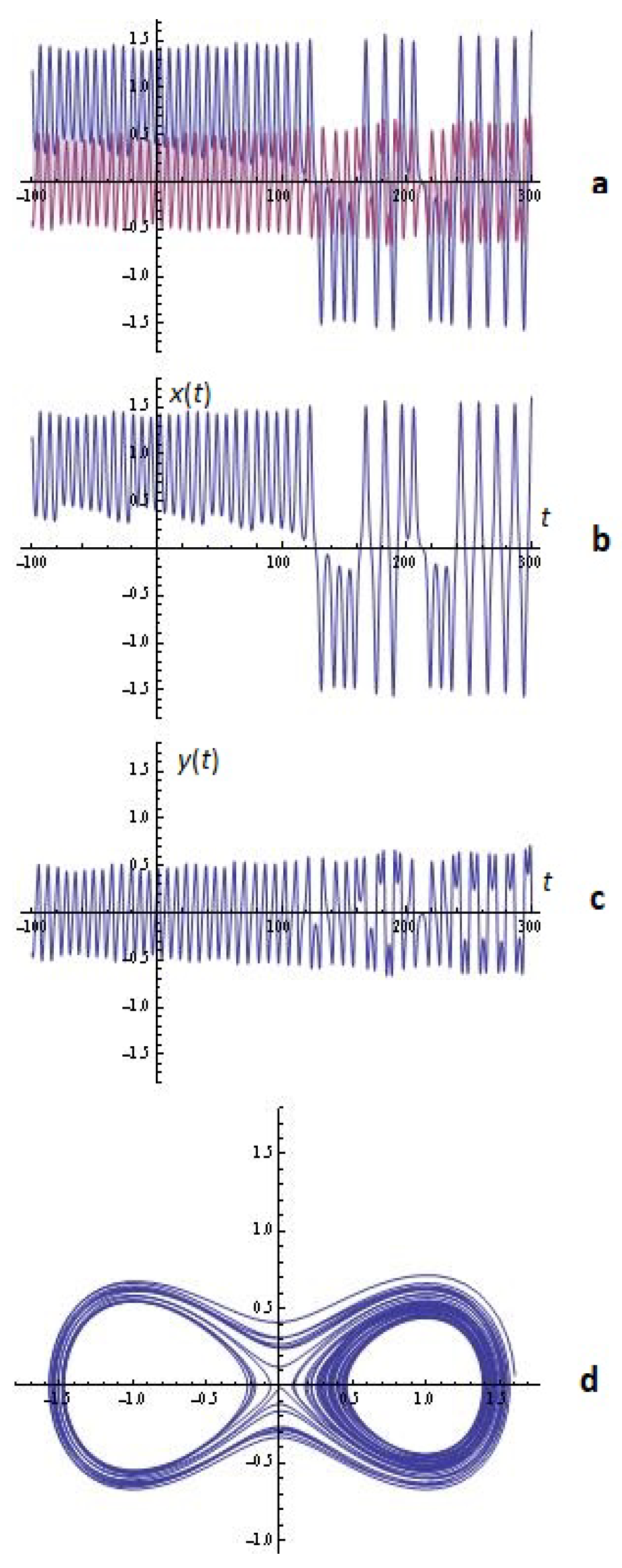
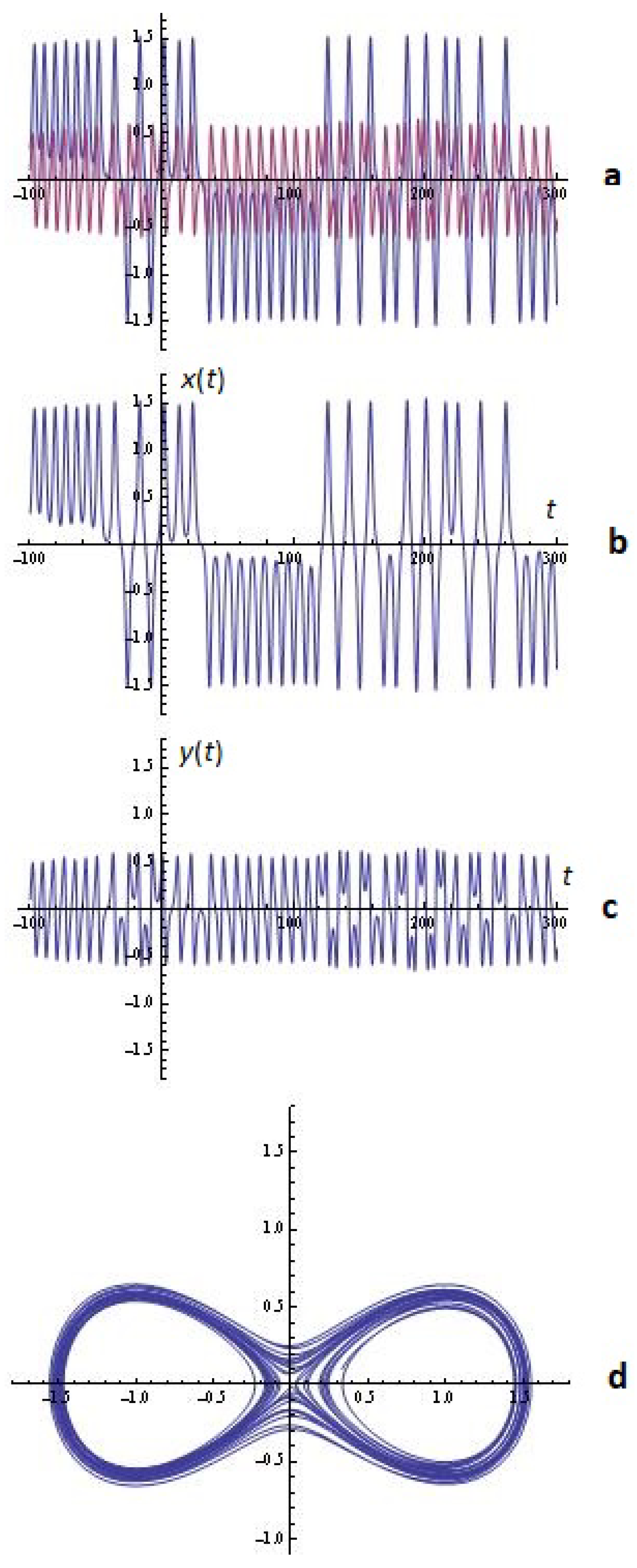
2.1.1. Some Simulations
2.2. A Modified Model
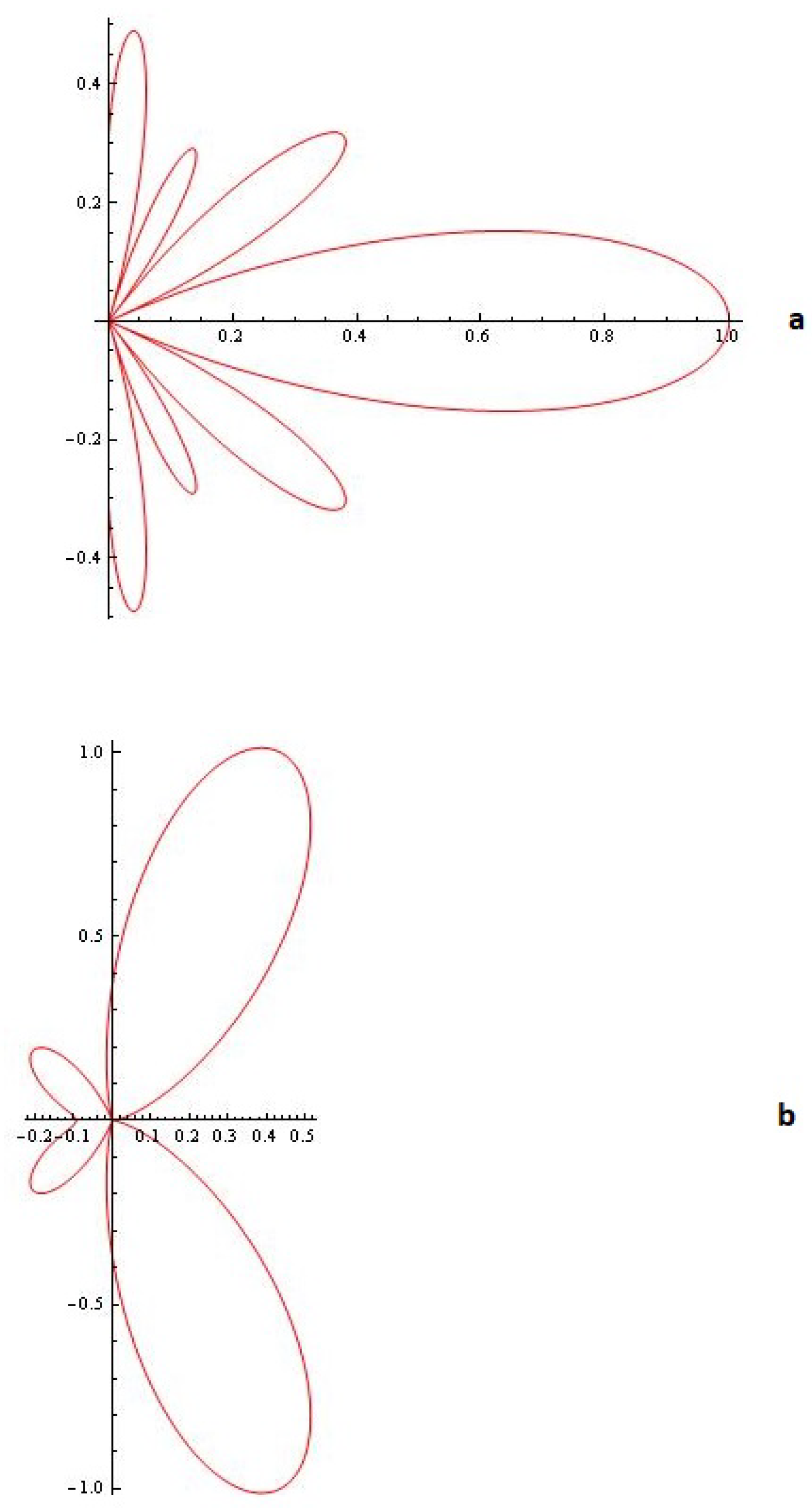
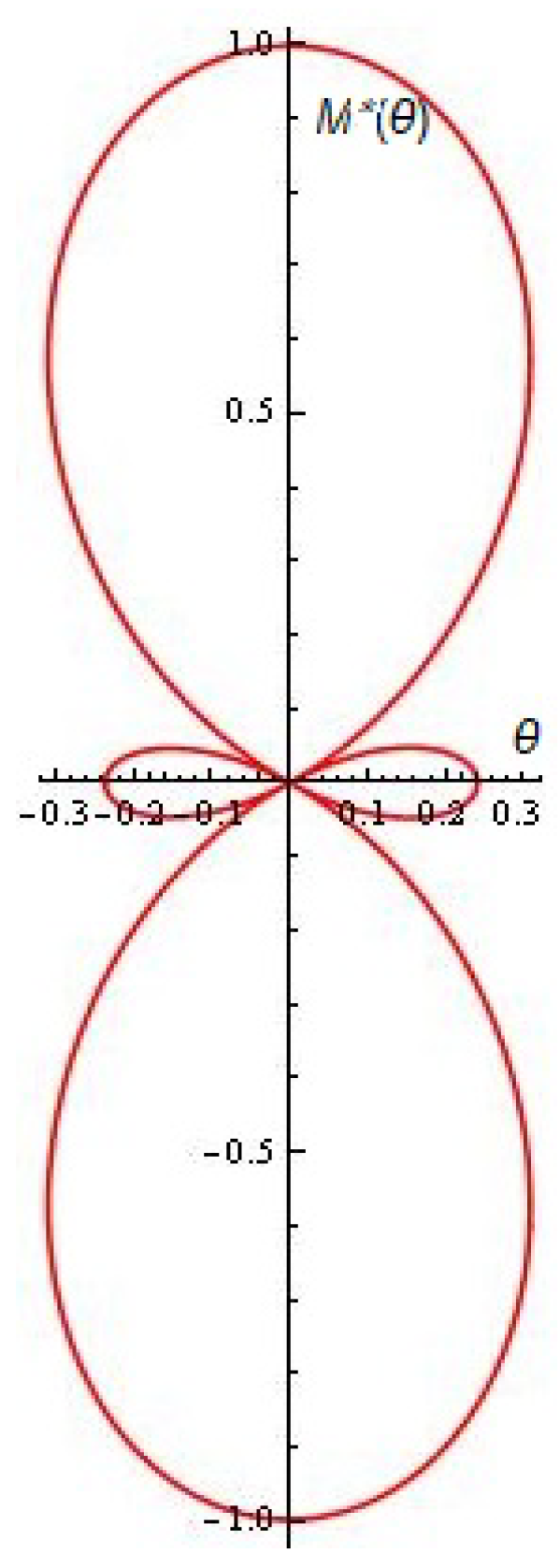
2.3. One Possible Application That Melnikov Functions May Find in the Modeling and Synthesis of Radiating Antenna Patterns
- I.
- (from Proposition 2);
- II.
- (from Proposition 3).
3. One More Note on the Subject: Generating Chaos via
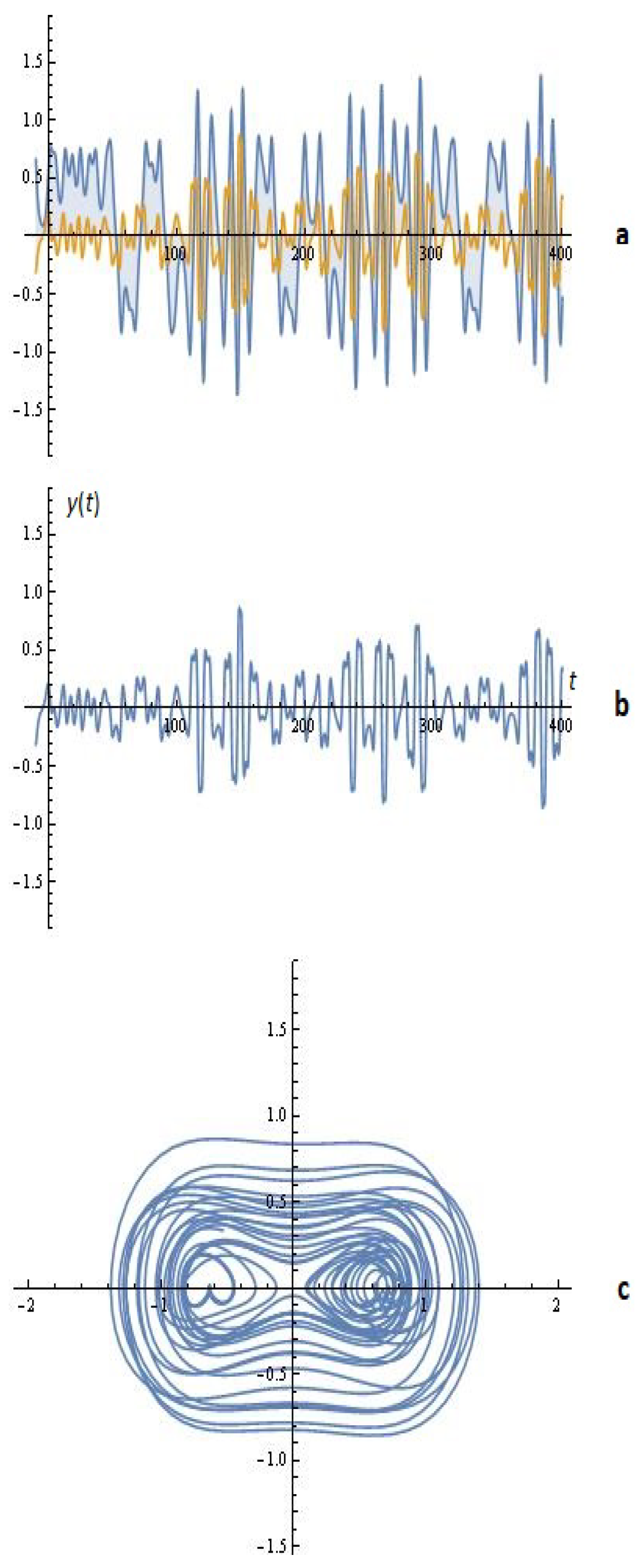
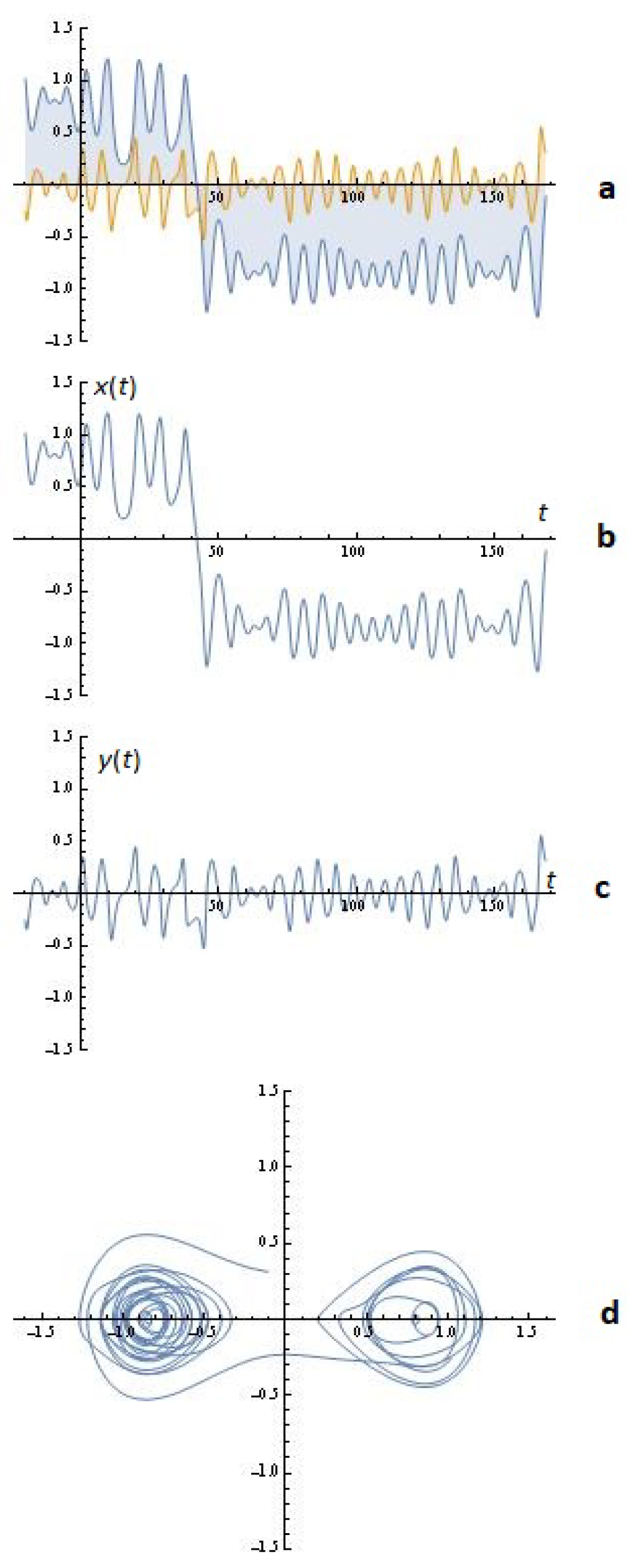
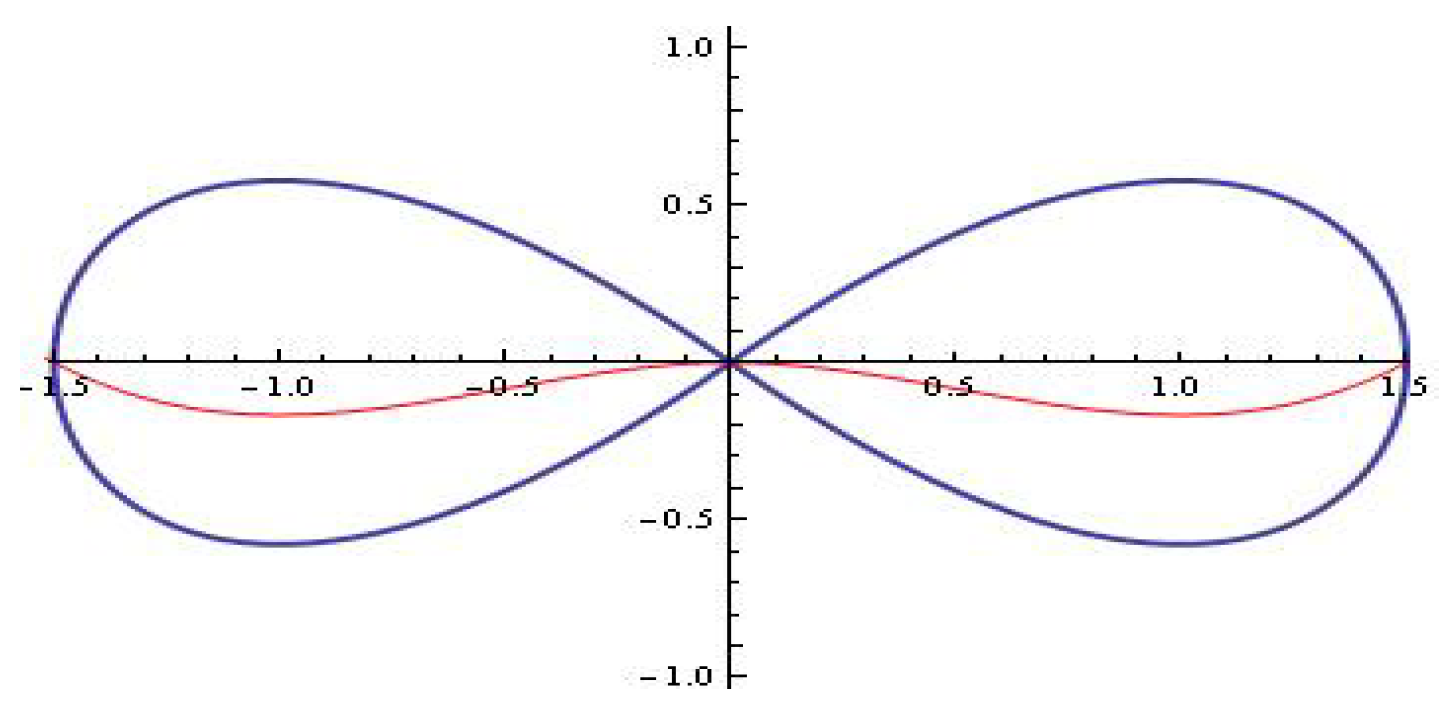
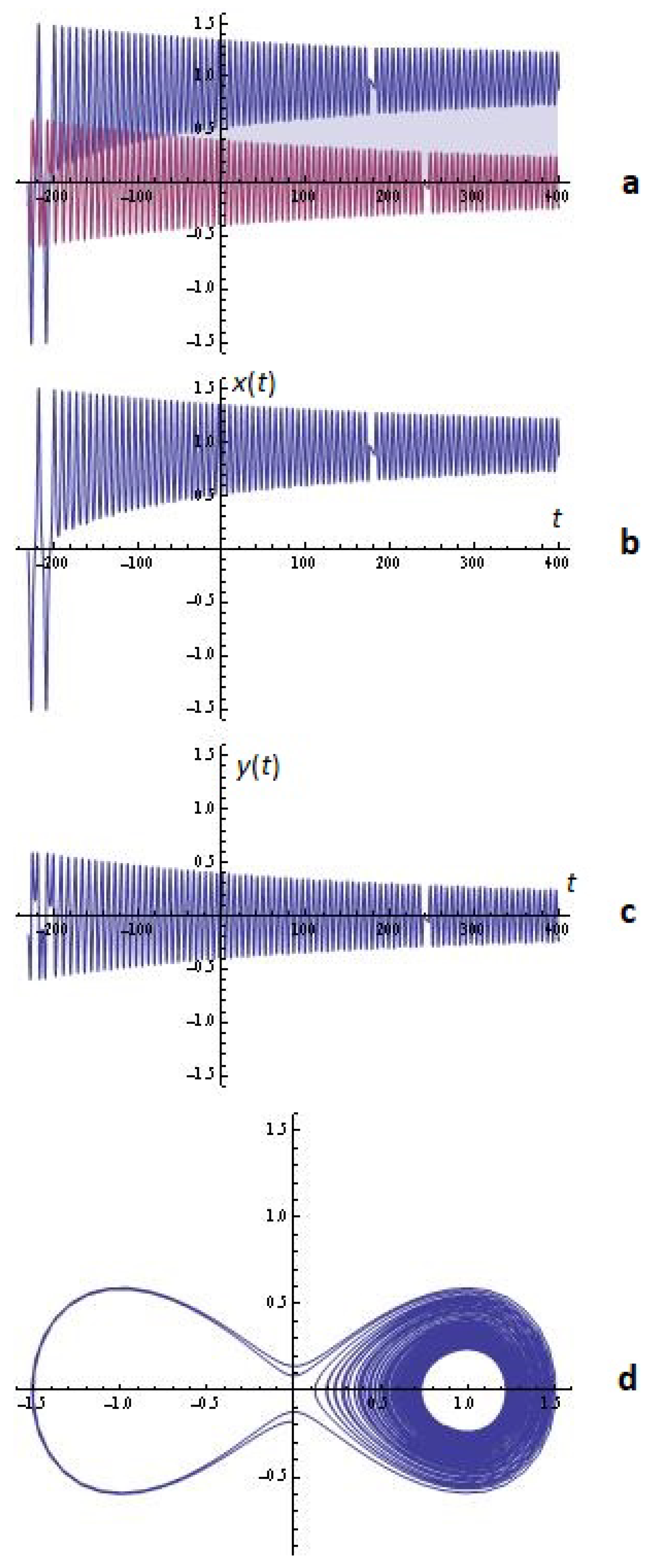
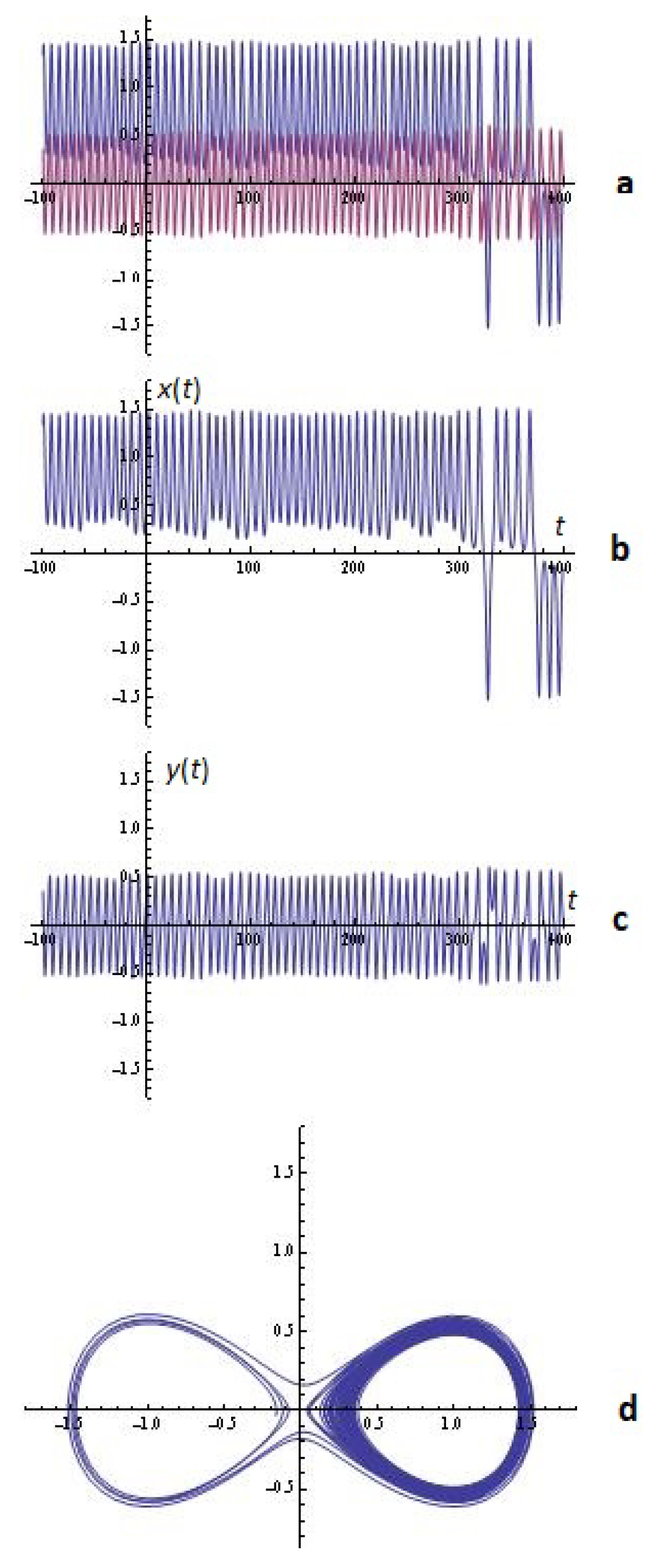
3.1. Some Simulations
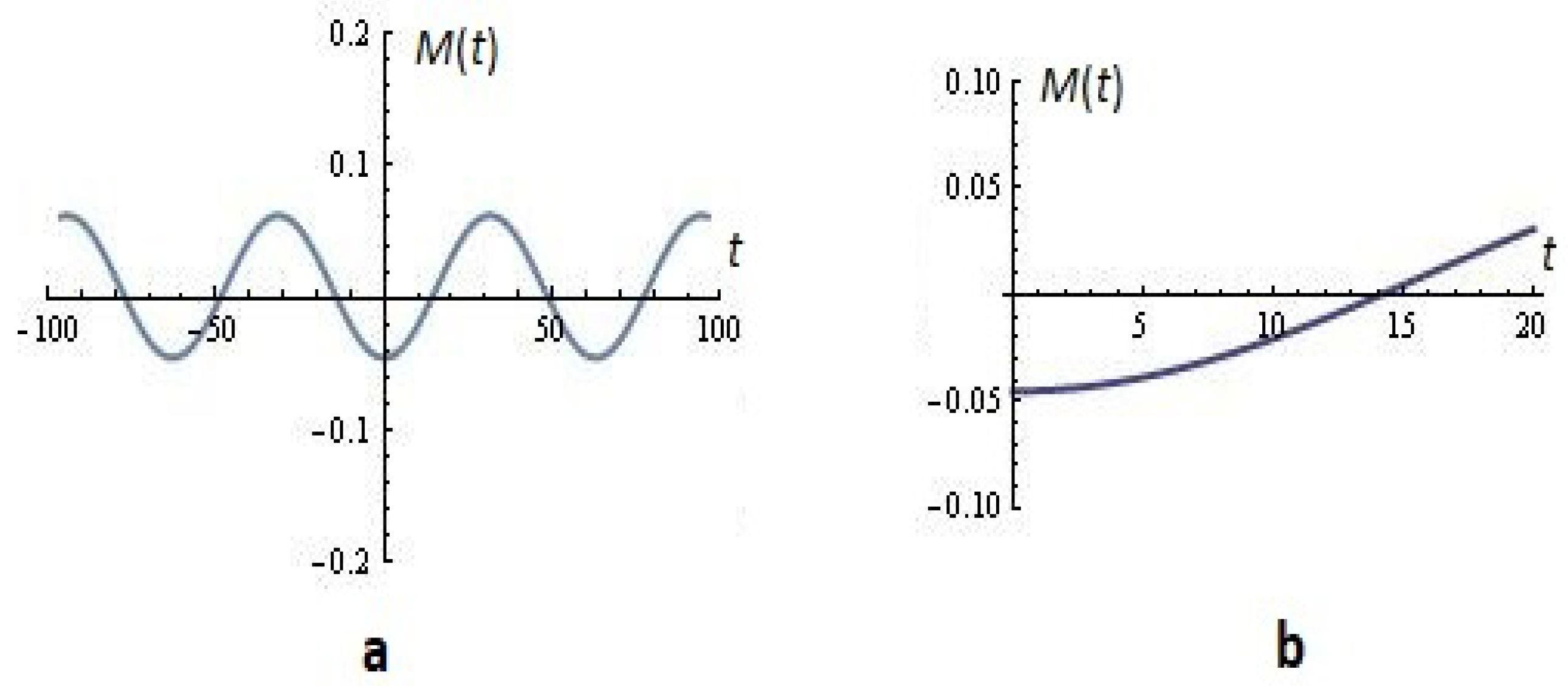
3.1.1. Melnikov’s Approach
4. Some Probability-Based Constructions
5. Concluding Remarks
- -
- is the azimuth angle;
- -
- is the wave length; d is the distance between emitters;
- -
- is the phase difference.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sanjuan, M. The effect of nonlinear damping on the universal oscillator. Int. J. Bifurc. Chaos 1999, 9, 735–744. [Google Scholar] [CrossRef]
- Soliman, M.S.; Thompson, J.M.T. The effect of nonlinear damping on the steady state and basin bifurcation patterns of a nonlinear mechanical oscillator. Int. J. Bifurc. Chaos 1992, 2, 81–91. [Google Scholar] [CrossRef]
- Fangnon, R.; Ainamon, C.; Monwanou, A.V.; Mowadinou, C.H.; Orpu, J.B. Nonlinear dynamics of the quadratic damping Helmholtz oscillator. Complexity 2020, 2020, 8822534. [Google Scholar] [CrossRef]
- Bikdash, M.; Balachandran, B.; Nayfeh, A. Melnikov analysis for a ship with a general roll-damping model. Nonlinear Dyn. 1994, 6, 101–124. [Google Scholar] [CrossRef]
- Ravindra, B.; Mallik, A.K. Stability analysis of a non–linearly clamped Duffing oscillator. J. Sound Vib. 1999, 171, 708–716. [Google Scholar] [CrossRef]
- Ravindra, B.; Mallik, A.K. Role of nonlinear dissipation in soft Duffing oscillators. Phys. Rev. E 1984, 49, 4950–4954. [Google Scholar] [CrossRef]
- Sanjuan, M. Monoclinic bifurcation sets of driven nonlinear oscillators. Int. J. Theor. Phys. 1996, 35, 1745–1752. [Google Scholar] [CrossRef]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer: New York, NY, USA, 1983. [Google Scholar]
- Perko, L. Differential Equations and Dynamical Systems; Springer: New York, NY, USA, 1991. [Google Scholar]
- Holmes, P.; Marsden, J. Horseshoes in perturbation of Hamiltonian systems with two degrees of freedom. Comm. Math. Phys. 1982, 82, 523–544. [Google Scholar] [CrossRef]
- Holmes, P.; Marsden, J. A partial differential equation with infinitely many periodic orbits: Chaotic oscillations. Arch. Ration. Mech. Anal. 1981, 76, 135–165. [Google Scholar] [CrossRef]
- Francescatto, A.; Contento, G. Bifurcations in ship rolling: Experimental results and parameter identification technique. Ocean Eng. 1999, 26, 1095–1123. [Google Scholar] [CrossRef]
- Tang, K.; Man, K.; Zhong, G.; Chen, G. Generating chaos via x|x|. IEEE Trans. Circuit Syst. Fundam. Theory Appl. 2001, 48, 636–640. [Google Scholar] [CrossRef]
- Tricomi, F. Integratione di un’ equazione differenziale presentatasi in elettrotecnica. Ann. Della Sc. Norm. Super. Pisa 1933, 2, 1–20. [Google Scholar]
- Stoker, J. Nonlinear Vibration in Mechanical and Electrical Systems; Interscience: New York, NY, USA, 1950. [Google Scholar]
- Levi, M.; Hoppensteadt, F.; Miranker, W. Dynamics of the Josephson junction. Quart. Appl. Math. 1978, 35, 167–198. [Google Scholar] [CrossRef]
- Siewe, M.; Kakmeni, F.; Tchawoua, C. Resonant oscillation and homoclinic bifurcation in ϕ6—Van der Pol oscillator. Chaos Solut. Fractals 2004, 21, 841–853. [Google Scholar] [CrossRef]
- Yu, J.; Li, J. Investigation on dynamics of the extended Duffing—Van der Pol system. Z. Fur Naturforschung 2009, 64, 341–346. [Google Scholar] [CrossRef]
- Siewe, M.; Tchawoua, C.; Rajasekar, S. Homoclinic bifurcation and chaos in ϕ6 Rayleigh oscillator with three wells driven by an amplitude modulated force. Int. J. Bifurc. Chaos 2011, 21, 1583–1593. [Google Scholar] [CrossRef]
- Kyurkchiev, N.; Zaevski, T. On a hypothetical oscillator: Investigations in the light of Melnikov’s approach, some simulations. Int. J. Differ. Equ. Appl. 2023, 22, 67–79. [Google Scholar]
- Kyurkchiev, N.; Zaevski, T.; Iliev, A.; Kyurkchiev, V.; Rahnev, A. Nonlinear dynamics of a new class of micro-electromechanical oscillators—Open problems. Symmetry 2024, 16, 253. [Google Scholar] [CrossRef]
- Golev, A.; Terzieva, T.; Iliev, A.; Rahnev, A.; Kyurkchiev, N. Simulation on a generalized oscillator model: Applications, Web-based application. Comptes Rendus l’Académie Bulg. Des Sci. 2024, 77, 230–237. [Google Scholar] [CrossRef]
- Melnikov, V.K. On the stability of a center for time—Periodic perturbation. Trans. Mosc. Math. Soc. 1963, 12, 3–52. [Google Scholar]
- Kyurkchiev, V.; Iliev, A.; Rahnev, A.; Kyurkchiev, N. On a class of orthogonal polynomials as corrections in Lienard differential system. Applications. Algorithms 2023, 16, 297. [Google Scholar] [CrossRef]
- Kyurkchiev, N.; Iliev, A. On the hypothetical oscillator model with second kind Chebyshev’s polynomial—Correction: Number and type of limit cycles, simulations and possible applications. Algorithms 2022, 15, 462. [Google Scholar] [CrossRef]
- Abramowicz, A.; Stegun, I. Handbook of Mathematical Functions; Dover: New York, NY, USA, 1970. [Google Scholar]
- Kyurkchiev, N.; Andreev, A. Approximation and Antenna and Filter Synthesis: Some Moduli in Programming Environment Mathematica; LAP Lambert Academic Publishing: Saarbrucken, Germany, 2014; ISBN 978-3-859-53322-8. [Google Scholar]
- Crandall, S. Non–Gaussian closure for random vibration of non-linear oscillators. Int. J. Non-Linear Mech. 1980, 15, 303–313. [Google Scholar] [CrossRef]
- Sobczyk, K.; Trebicki, J. Maximum entropy principle and nonlinear stochastic oscillators. Phys. A Stat. Mech. Its Appl. 1993, 193, 448–468. [Google Scholar] [CrossRef]
- Wang, K.; Masoliver, J. Linear oscillators driven by Gaussian colored noise: Crossovers and probability distributions. Phys. A Stat. Mech. Its Appl. 1996, 231, 615–630. [Google Scholar] [CrossRef]
- Er, G.; Zhu, T.; Iu, V.; Kou, K. Probabilistic Solution of Nonlinear Oscillators Under External and Parametric Poisson Impulses. AIAA J. 2008, 46, 2839–2847. [Google Scholar] [CrossRef]
- Monga, B.; Moehlis, J. Phase distribution control of a population of oscillators. Phys. D Nonlinear Phenom. 2019, 398, 115–129. [Google Scholar] [CrossRef]
- Thangkhenpau, G.; Panday, S.; Bolunduet, L.C.; Jantschi, L. Efficient Families of Multi-Point Iterative Methods and Their Self-Acceleration with Memory for Solving Nonlinear Equations. Symmetry 2023, 15, 1546. [Google Scholar] [CrossRef]
- Akram, S.; Khalid, M.; Junjua, M.-U.-D.; Altaf, S.; Kumar, S. Extension of King’s Iterative Scheme by Means of Memory for Nonlinear Equations. Symmetry 2023, 15, 1116. [Google Scholar] [CrossRef]
- Cordero, A.; Janjua, M.; Torregrosa, J.R.; Yasmin, N.; Zafar, F. Efficient four parametric with and without-memory iterative methods possessing high efficiency indices. Math. Probl. Eng. 2018, 2018, 8093673. [Google Scholar] [CrossRef]
- Proinov, P.; Vasileva, M. On the convergence of high-order Ehrlich-type iterative methods for approximating all zeros of a polynomial simultaneously. J. Inequalities Appl. 2015, 2015, 336. [Google Scholar] [CrossRef]
- Proinov, P.D.; Vasileva, M.T. Local and Semilocal Convergence of Nourein’s Iterative Method for Finding All Zeros of a Polynomial Simultaneously. Symmetry 2020, 12, 1801. [Google Scholar] [CrossRef]
- Proinov, P.D.; Vasileva, M.T. On the convergence of high-order Gargantini-Farmer-Loizou type iterative methods for simultaneous approximation of polynomial zeros. Appl. Math. Comput. 2019, 361, 202–214. [Google Scholar] [CrossRef]
- Proinov, P.; Ivanov, S. On the convergence of Halley’s method for simultaneous computation of polynomial zeros. J. Numer. Math. 2015, 23, 379–394. [Google Scholar] [CrossRef]
- Ivanov, S.I. Families of high-order simultaneous methods with several corrections. Numer. Algor. 2024. [Google Scholar] [CrossRef]
- Kyncheva, V.; Yotov, V.; Ivanov, S. Convergence of Newton, Halley and Chebyshev iterative methods as methods for simultaneous determination of multiple zeros. Appl. Numer. Math. 2017, 112, 146–154. [Google Scholar] [CrossRef]
- Lenci, S.; Lupini, R. Homoclinic and heteroclinic solutions for a class of two-dimensional Hamiltonian systems. Z. Angew. Math. Phys. 1996, 47, 97–111. [Google Scholar] [CrossRef]
- Lenci, S.; Rega, G. Controlling nonlinear dynamics in a two-well impact system. I. Attractors and bifurcation scenario under symmetric excitations. Int. J. Bifur. Chaos Appl. Sci. Eng. 1998, 8, 2387–2407. [Google Scholar] [CrossRef]
- Lenci, S.; Rega, G. Controlling nonlinear dynamics in a two-well impact system. II. Attractors and bifurcation scenario under unsymmetric optimal excitation. Int. J. Bifur. Chaos Appl. Sci. Eng. 1998, 8, 2409–2424. [Google Scholar] [CrossRef]
- Lenci, S.; Rega, G. Higher-order Melnikov analysis of homo/heteroclinic bifurcations in mechanical oscillators. In Proceedings of the 16th AIMETA Congress of Theoretical and Applied Mechanics, Ferrara, Italy, 9–12 September 2003. [Google Scholar]
- Lenci, S.; Rega, G. Optimal control of homoclinic bifurcation: Theoretical treatment and practical reduction of safe basin erosion in the Helmholtz oscillator. J. Vib. Control 2003, 9, 281–315. [Google Scholar] [CrossRef]
- Rega, G.; Lenci, S. Bifurcations and chaos in single-d.o.f. mechanical systems: Exploiting nonlinear dynamics properties for their control. In Recent Research Developments in Structural Dynamics; Luongo, A., Ed.; Research Signpost: Kerala, India, 2003; pp. 331–369. [Google Scholar]
- Soto-Trevino, C.; Kaper, T.J. Higher-order Melnikov theory for adiabatic systems. J. Math. Phys. 1996, 37, 6220–6249. [Google Scholar] [CrossRef]
- Gavrilov, L.; Iliev, I. The limit cycles in a generalized Rayleigh–Lienard oscillator. Discret. Contin. Dyn. Syst. 2023, 43, 2381–2400. [Google Scholar] [CrossRef]
- Thompson, M.T.; Stewart, H.B. Nonlinear Dynamics and Chaos, 2nd ed.; John Wiley & Sons: Chichester, UK, 2002. [Google Scholar]
- Rahneva, O.; Pavlov, N. Distributed Systems and Applications in Learning; Plovdiv University Press: Plovdiv, Bulgaria, 2021. [Google Scholar]
- Pavlov, N. Efficient Matrix Multiplication Using Hardware Intrinsics and Parallelism with C#. Int. J. Differ. Equ. Appl. 2021, 20, 217–223. [Google Scholar]
- Duffy, J. Concurrent Programming on Windows; Addison Wesley: Boston, MA, USA, 2009. [Google Scholar]
- Miller, W. Computational Complexity and Numerical Stability. SIAM J. Comput. 1975, 4, 97–107. [Google Scholar] [CrossRef]
- Mateev, M. Creating Modern Data Lake Automated Workloads for Big Environmental Projects. In Proceedings of the 18th Annual International Conference on Information Technology & Computer Science, Athens, Greece, 9 September 2022. [Google Scholar]
- Stoyanov, S.; Popchev, I. Evolutionary development of an infrastructure supporting the transition from CBT to e-Learning. Cybern. Inf. Technol. 2006, 6, 101–114. [Google Scholar]
- Sandalski, M.; Stoyanova-Doycheva, A.; Popchev, I.; Stoyanov, S. Development of a Refactoring Learning Environment. Cybern. Inf. Technol. 2011, 11, 46–64. [Google Scholar]
- Stoyanov, S.; Popchev, I.; Doychev, E.; Mitev, D.; Valkanov, V.; Stoyanova-Doycheva, A.; Valkanova, V.; Minov, I. DeLC Educational Portal. Cybern. Inf. Technol. 2010, 10, 49–69. [Google Scholar]
- Glushkova, T.; Stoyanov, S.; Popchev, I.; Cheresharov, S. Ambient-oriented Modelling in a Virtual Educational Space. Comptes Rendus l’Académie Bulg. Des Sci. 2018, 71, 398–406. [Google Scholar]
- Stancheva, N.; Stoyanova-Doycheva, A.; Stoyanov, S.; Popchev, I.; Ivanova, V. A Model for Generation of Test Questions. Comptes Rendus l’Académie Bulg. Des Sci. 2017, 70, 619–630. [Google Scholar]
- Apostolov, P. An Addition to Binomial Array Antenna Theory. Prog. Electromagn. Res. Lett. 2023, 113, 113–117. [Google Scholar] [CrossRef]


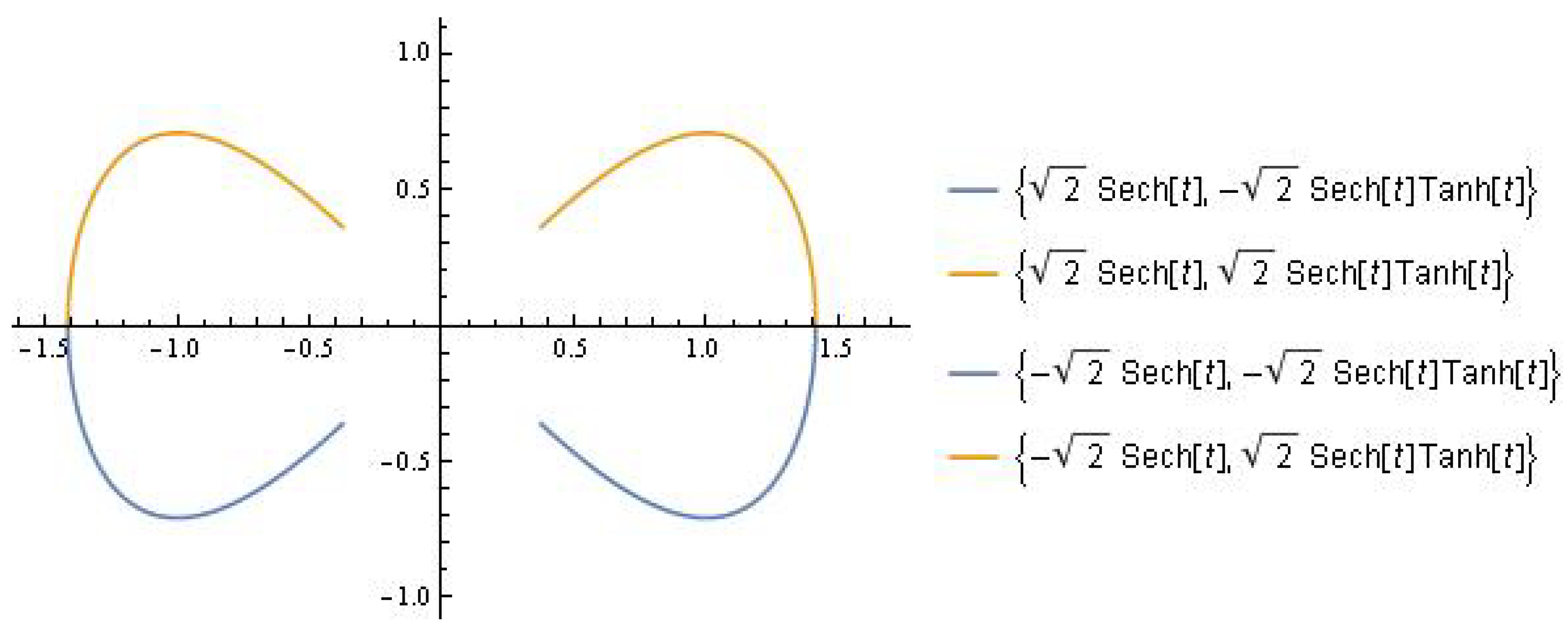



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kyurkchiev, N.; Zaevski, T.; Iliev, A.; Kyurkchiev, V.; Rahnev, A. Modeling of Some Classes of Extended Oscillators: Simulations, Algorithms, Generating Chaos, and Open Problems. Algorithms 2024, 17, 121. https://doi.org/10.3390/a17030121
Kyurkchiev N, Zaevski T, Iliev A, Kyurkchiev V, Rahnev A. Modeling of Some Classes of Extended Oscillators: Simulations, Algorithms, Generating Chaos, and Open Problems. Algorithms. 2024; 17(3):121. https://doi.org/10.3390/a17030121
Chicago/Turabian StyleKyurkchiev, Nikolay, Tsvetelin Zaevski, Anton Iliev, Vesselin Kyurkchiev, and Asen Rahnev. 2024. "Modeling of Some Classes of Extended Oscillators: Simulations, Algorithms, Generating Chaos, and Open Problems" Algorithms 17, no. 3: 121. https://doi.org/10.3390/a17030121
APA StyleKyurkchiev, N., Zaevski, T., Iliev, A., Kyurkchiev, V., & Rahnev, A. (2024). Modeling of Some Classes of Extended Oscillators: Simulations, Algorithms, Generating Chaos, and Open Problems. Algorithms, 17(3), 121. https://doi.org/10.3390/a17030121







