A Novel Higher-Order Numerical Scheme for System of Nonlinear Load Flow Equations
Abstract
1. Introduction
- Gauss–Seidel Method:
- Advantages: Simple implementation, low memory requirement, suitable for small to medium-sized systems.
- Disadvantages: Slow convergence for large and highly nonlinear systems, may not converge for certain network configurations, sensitive to initial guesses.
- Newton–Raphson Method:
- Advantages: Faster convergence compared to Gauss–Seidel, suitable for large and highly nonlinear systems, allows for simultaneous solution of multiple equations.
- Disadvantages: Higher computational complexity, requires initial estimates for all variables, may encounter convergence issues for ill-conditioned systems. Moreover, it starts to lose its ability to converge fast with the increasing system size.
- Fast Decoupled Method:
- Advantages: Improves convergence speed compared to Newton–Raphson, less computational burden, suitable for medium to large systems with moderate nonlinearity.
- Disadvantages: Less accurate than Newton–Raphson, may not converge for highly nonlinear systems, requires assumptions to decouple real and reactive power calculations.
- Modified Newton Method:
- Advantages: Combines advantages of Newton–Raphson and fast decoupled methods, faster convergence than traditional Newton–Raphson.
- Disadvantages: May require more computational resources than fast decoupled method, convergence issues still possible for highly nonlinear systems.
- DC Load Flow Method:
- Advantages: Extremely fast convergence, suitable for initial approximations or preliminary studies, computationally efficient.
- Disadvantages: Limited accuracy due to linearization of power flow equations, not suitable for highly nonlinear systems or systems with voltage deviations.
- Sparse Matrix Techniques:
- Advantages: Memory-efficient for large systems, reduces computational burden by exploiting network sparsity.
- Disadvantages: Requires additional implementation complexity, may not significantly improve computational speed for small to medium-sized systems.
- Constructing a mathematical model that illustrates the relationship between voltages and powers in an interconnected system.
- Specifying the voltage and power conditions for each network bus.
- Calculating the voltage magnitude and phase angle at each bus in a power system under some balanced steady-state conditions
2. Development of Seventh-Order Method and Convergence Analysis
2.1. Special Cases
2.2. Computational Cost
3. Numerical Experiments
Formation of Load Flow Equations
| k | ||||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 1 | ||||
| 2 | ||||
| 3 |
| k | ||||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 1 | ||||
| 2 | ||||
| 3 |
| k | ||||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 1 | ||||
| 2 | ||||
| 3 |
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jarratt, P. Some efficient fourth order multipoint methods for solving equations. BIT Numer. Math. 1969, 9, 119–124. [Google Scholar] [CrossRef]
- Behl, R.; Sarría, Í.; González, R.; Magreñán, Á.A. Highly efficient family of iterative methods for solving nonlinear models. J. Comput. Appl. Math. 2019, 346, 110–132. [Google Scholar] [CrossRef]
- Hueso, J.L.; Martínez, E.; Teruel, C. Convergence, efficiency and dynamics of new fourth and sixth order families of iterative methods for nonlinear systems. J. Comput. Appl. Math. 2015, 275, 412–420. [Google Scholar] [CrossRef]
- Lee, M.Y.; Kim, Y.I. Development of a Family of Jarratt-Like Sixth-Order Iterative Methods for Solving Nonlinear Systems with Their Basins of Attraction. Algorithms 2020, 13, 303. [Google Scholar] [CrossRef]
- Abad, M.; Cordero, A.; Torregrosa, J.R. A family of seventh-order schemes for solving nonlinear systems. Bull. Math. Soc. Sci. Math. 2014, 57, 133–145. [Google Scholar]
- Yaseen, S.; Zafar, F.; Chicharro, F.I. A seventh order family of Jarratt type iterative method for electrical power systems. Fractal Fract. 2023, 7, 317. [Google Scholar] [CrossRef]
- Narang, M.; Bhatia, S.; Kanwar, V. New efficient derivative free family of seventh-order methods for solving systems of nonlinear equations. Numer. Algorithms 2017, 76, 283–307. [Google Scholar] [CrossRef]
- Sharma, J.R.; Arora, H. A novel derivative free algorithm with seventh order convergence for solving systems of nonlinear equations. Numer. Algorithms 2014, 67, 917–933. [Google Scholar] [CrossRef]
- Sharma, J.R.; Arora, H. A simple yet efficient derivative free family of seventh order methods for systems of nonlinear equations. SeMA J. 2016, 73, 59–75. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, T. A family of Steffensen type methods with seventh-order convergence. Numer. Algorithms 2013, 62, 429–444. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, T.; Qian, W.; Teng, M. Seventh-order derivative-free iterative method for solving nonlinear systems. Numer. Algorithms 2015, 70, 545–558. [Google Scholar] [CrossRef]
- Behl, R.; Arora, H. CMMSE: A novel scheme having seventh-order convergence for nonlinear systems. J. Comput. Appl. Math. 2022, 404, 113301. [Google Scholar] [CrossRef]
- Wang, X. Fixed-point iterative method with eighth-order constructed by undetermined parameter technique for solving nonlinear systems. Symmetry 2021, 13, 863. [Google Scholar] [CrossRef]
- Xiao, X.Y. New techniques to develop higher order iterative methods for systems of nonlinear equations. Comp. Appl. Math. 2022, 41, 243. [Google Scholar] [CrossRef]
- Zhanlav, T.; Otgondorj, K. Higher order Jarratt-like iterations for solving systems of nonlinear equations. Appl. Math. Comput. 2021, 395, 125849. [Google Scholar] [CrossRef]
- Zhanlav, T.; Mijiddorj, R.; Otgondorj, K. A family of Newton-type methods with seventh and eighth-order of convergence for solving systems of nonlinear equations. Hacettepe J. Math. Stat. 2023, 52, 1006–1021. [Google Scholar] [CrossRef]
- Sharma, J.R.; Guha, R.K.; Sharma, R. An efficient fourth order weighted-Newton method for systems of nonlinear equations. Numer. Algorithms 2013, 62, 307–323. [Google Scholar] [CrossRef]
- Bergen, A.R. Power Systems Analysis; Pearson Education India: New Delhi, India, 2009. [Google Scholar]
- Glover, J.D.; Overbye, T.J.; Sarma, M.S. Power System Analysis & Design; SI Version; Cengage Learning: Boston, MA, USA, 2015. [Google Scholar]
- Nagsarkar, T.K.; Sukhija, M.S. Power System Analysis, 2nd ed.; Oxford University Press: New Delhi, India, 2014. [Google Scholar]
- Saadat, H. Power System Analysis; The McGraw-Hill Companies, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Ward, J.B.; Hale, H.W. Digital computer solution of power flow problems. AIEE Trans. 1956, 75, 398–404. [Google Scholar]
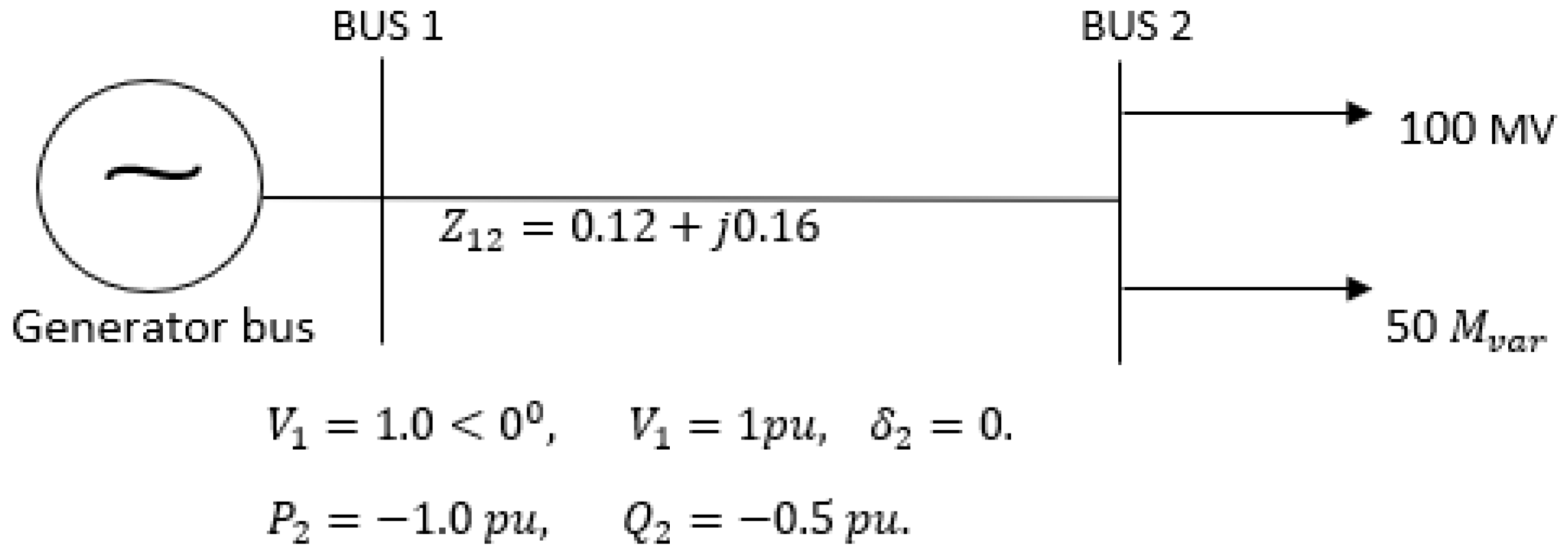


| Types of Bus | Specified Quantities | Unspecified Quantities |
|---|---|---|
| Slack bus | ||
| Generator/ bus | ||
| Load/ bus |
| Multiplication | Division | CC | |
|---|---|---|---|
| LU-decomposition | |||
| Two-triangular system | m | ||
| Matrix–vector multiplication | |||
| Matrix–matrix multiplication | m | m |
| Methods | Convergence Order | Function Evaluations | CC |
|---|---|---|---|
| 7 | |||
| 7 | |||
| 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zafar, F.; Cordero, A.; Maryam, H.; Torregrosa, J.R. A Novel Higher-Order Numerical Scheme for System of Nonlinear Load Flow Equations. Algorithms 2024, 17, 86. https://doi.org/10.3390/a17020086
Zafar F, Cordero A, Maryam H, Torregrosa JR. A Novel Higher-Order Numerical Scheme for System of Nonlinear Load Flow Equations. Algorithms. 2024; 17(2):86. https://doi.org/10.3390/a17020086
Chicago/Turabian StyleZafar, Fiza, Alicia Cordero, Husna Maryam, and Juan R. Torregrosa. 2024. "A Novel Higher-Order Numerical Scheme for System of Nonlinear Load Flow Equations" Algorithms 17, no. 2: 86. https://doi.org/10.3390/a17020086
APA StyleZafar, F., Cordero, A., Maryam, H., & Torregrosa, J. R. (2024). A Novel Higher-Order Numerical Scheme for System of Nonlinear Load Flow Equations. Algorithms, 17(2), 86. https://doi.org/10.3390/a17020086








