A Literature Review on Some Trends in Artificial Neural Networks for Modeling and Simulation with Time Series
Abstract
1. Introduction
- Nonparametric statistical models. Some of these techniques include the following: self-exciting threshold autoregressive (SETAR) models [9], which are a nonlinear extension to the parametric autoregressive linear models; autoregressive conditional heteroskedasticity (ARCH) models [10], which assume that the variance of the current error term or innovation depends on the sizes of previous error terms; and bilinear models [11], which are similar to ARIMA models, but include nonlinear interactions between AR and MA terms.
- ANNs are data-driven methods. They use historical data to build a system that can give the desired result [18].
- ANNs are flexible and self-adaptive. It is not necessary to make many prior assumptions about the data generation process for the problem under study [18].
- ANNs are able to generalize (robustly). They can accurately infer the invisible part of a population even if there is noise in the sample data [19].
- ANNs can approximate any continuous linear or nonlinear function with the desired accuracy [20].
2. Basic Principles and Concepts in Time Series Analysis
2.1. What Is a Time Series?
2.2. Time Series Modeling
- Functional model f: Suppose a function f that represents the dependence of related to ;
- Training phase: For each past value , train f using as inputs the values , and …, , and as target ;
- Predict value : Apply the trained functional model f to predict from , , , …, .
2.3. ARIMA Time Series Modeling
- Linear modeling is always at the forefront of the literature;
- Linear models are easy to learn and implement;
- Interpretation of results coming from linear models relies on well-defined, well-developed, standardized, mechanized procedures with solid theoretical foundations (e.g., there are established procedures that help us build confidence intervals associated with point forecasts, founded on statistical and probabilistic theory centered around the normal distribution).
Since all models are wrong, the scientist cannot obtain a “correct” one by excessive elaboration; on the contrary, following William of Occam, he should seek an economical description of natural phenomena. Just as the ability to devise simple but evocative models is the signature of the great scientist, so over-elaboration and over-parametrization is often the mark of mediocrity.(Box [25], 1976)
3. Popular ANN Architectures Employed for Time Series Forecasting Purposes
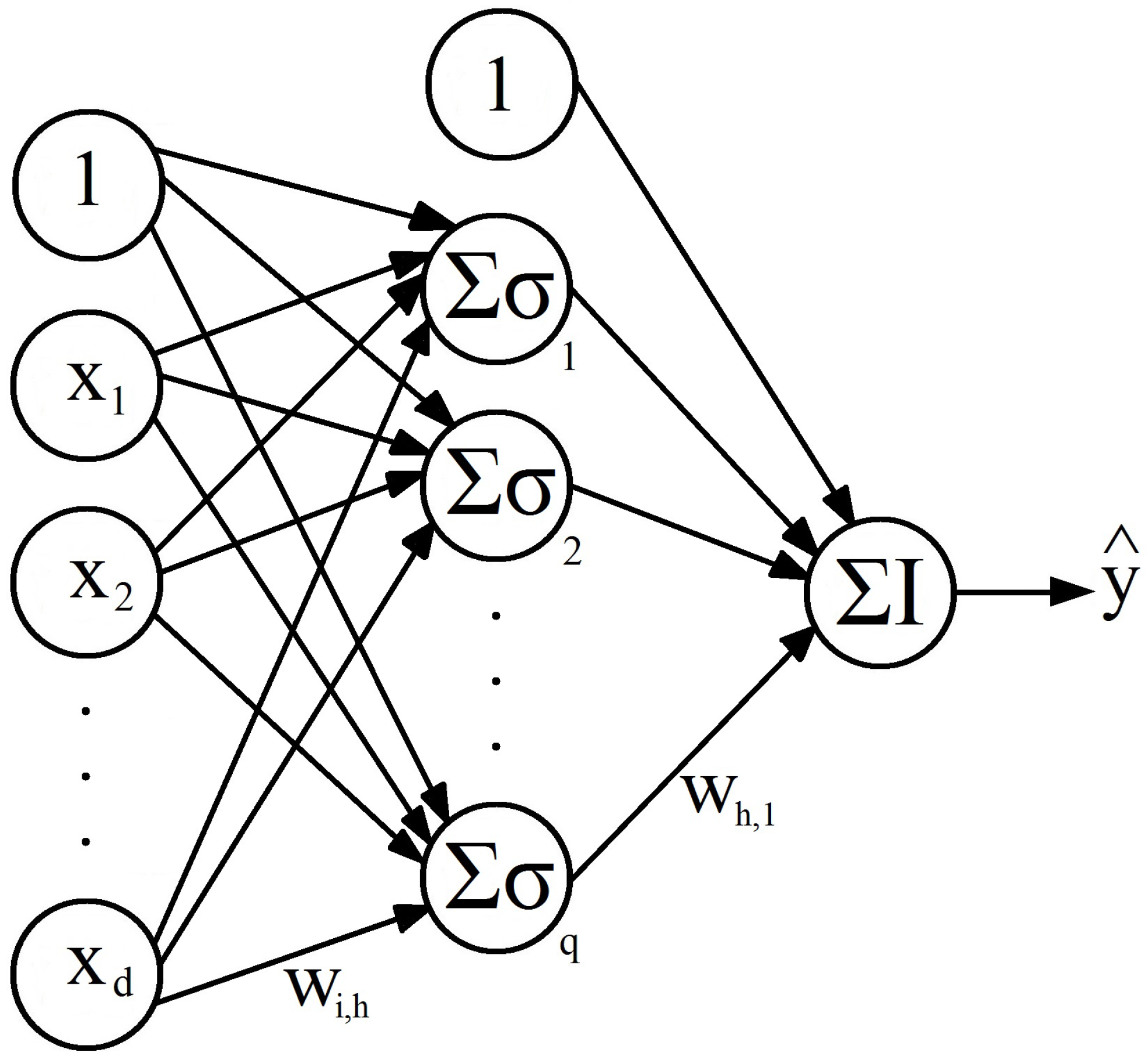
3.1. Feedforward Neural Networks
3.1.1. Basic Model
3.1.2. FFNN Training
- Initialize randomly;
- Repeat (a) and (b) until is below a given threshold T or a pre-established maximum number of iterations M has been reached:
- (a)
- ;
- (b)
- Update all network weights: ;
- Return .
3.1.3. Time Series Training Examples for FFNNs
3.1.4. FFNN Time Series Predictions
3.1.5. Cross-Validation
3.1.6. FFNN Ensembles for Time Series Forecasting
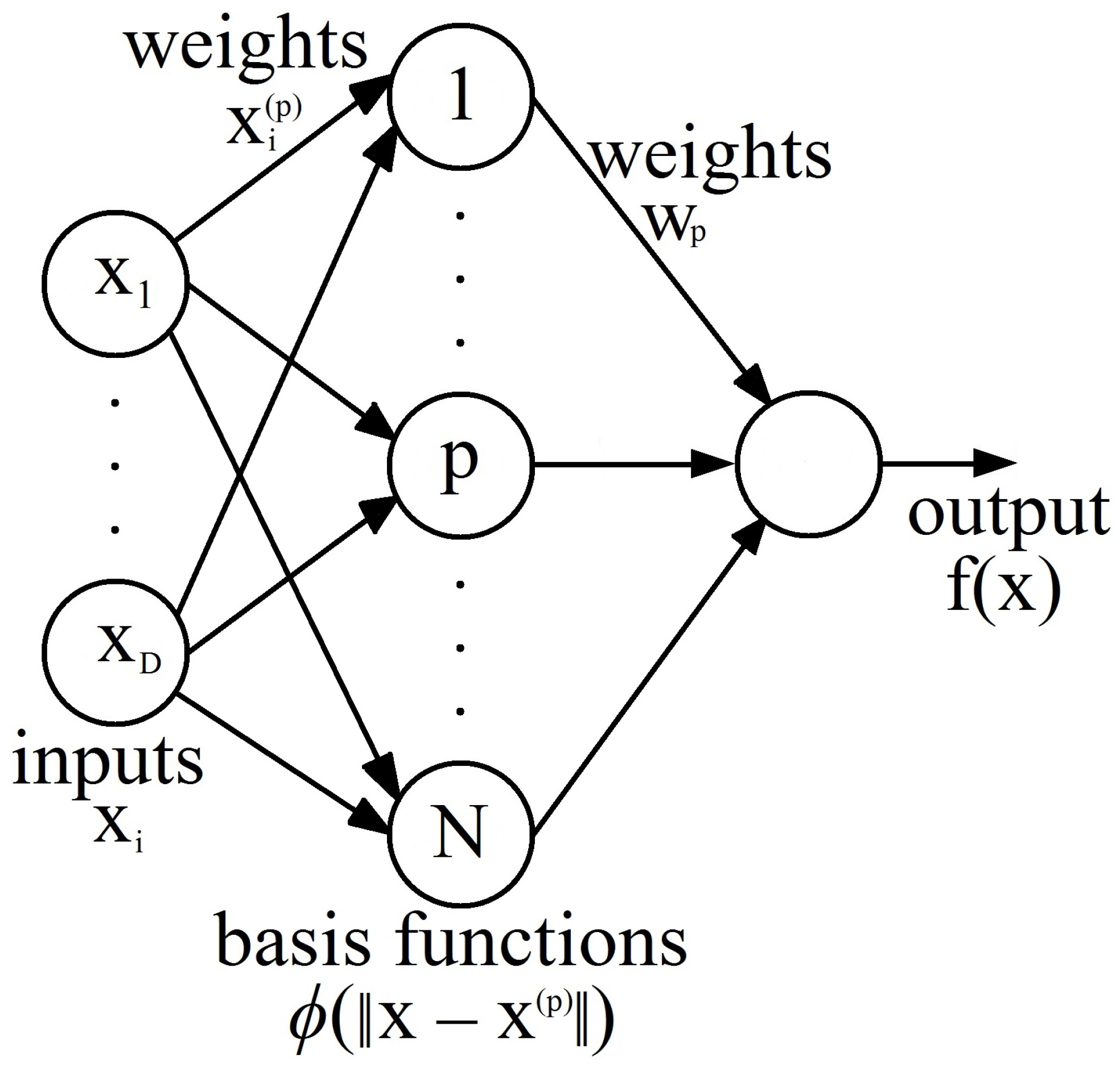
3.2. Radial Basis Function Networks
3.3. How Do We Improve Radial Basis Function Networks?
- The number of basis functions M must be much smaller than the number of data points N, ();
- Determine the centers of the basic functions using a training algorithm; they should not be defined as training data input vectors;
- The basis functions should have a different width parameter , which could be solved by a training algorithm;
- To compensate for the difference between the mean value of all basis functions and the corresponding mean value of the targets, bias parameters can be used in the linear sum of activations in the output layer.
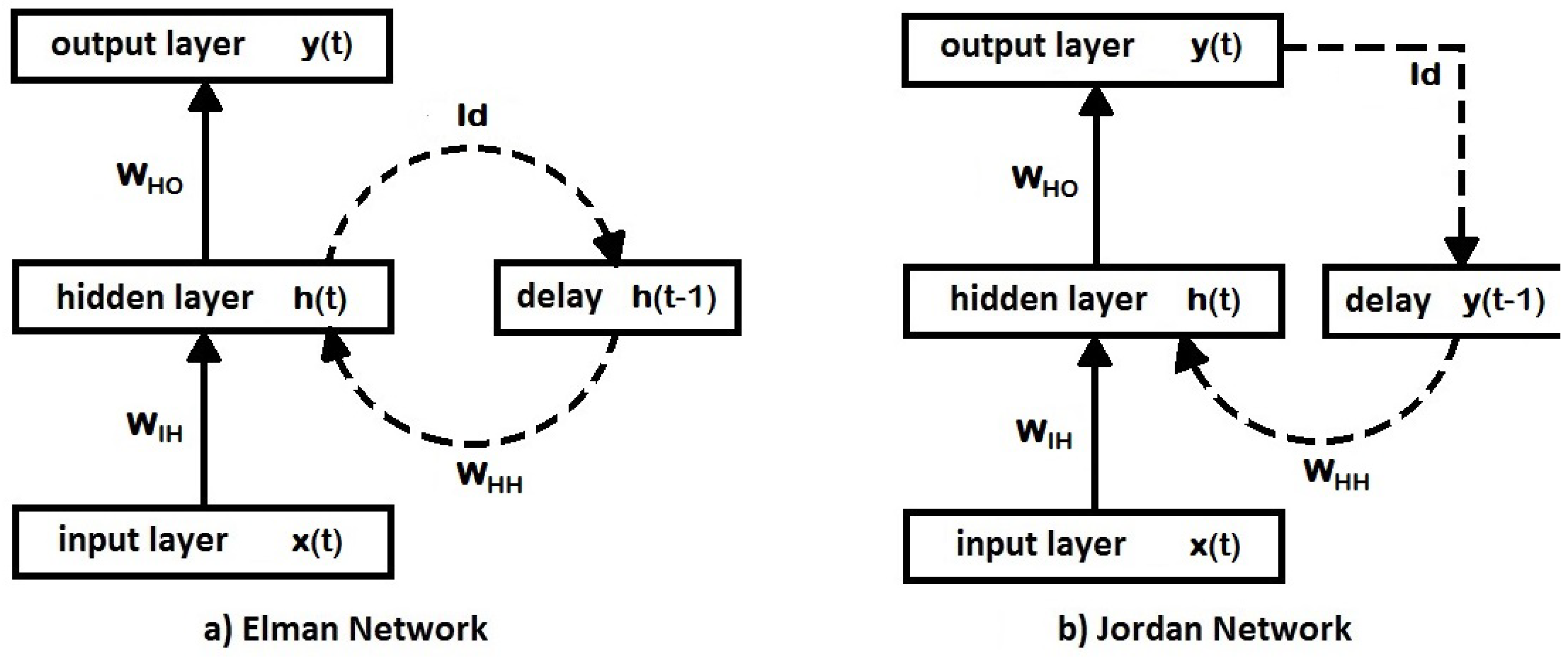
3.4. Recurrent Neural Networks
- RNNs contain a subsystem similar to a static FFNN;
- RNNs can take advantage of the nonlinear mapping abilities of an FFNN, with an added memory capacity for past information.
- Open-loop. Also known as the series-parallel architecture, in this NARX variant, the present and past values of and the true past values of the time series are used to predict the future value of the time series .
- Close-loop. Also known as the parallel architecture, in this NARX variant, the present and past values of and the past predicted values of the time series are used to predict the future value of the time series .
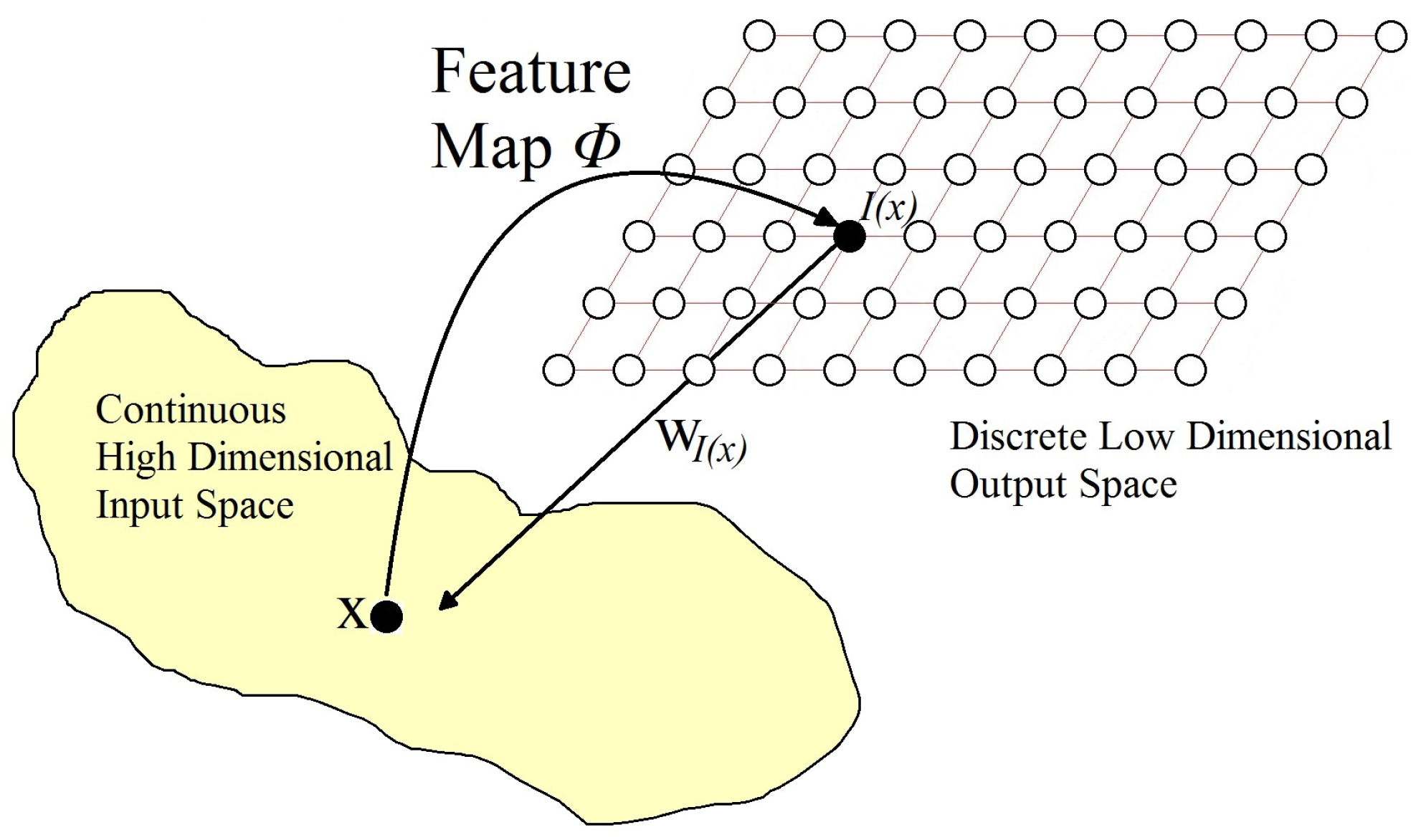
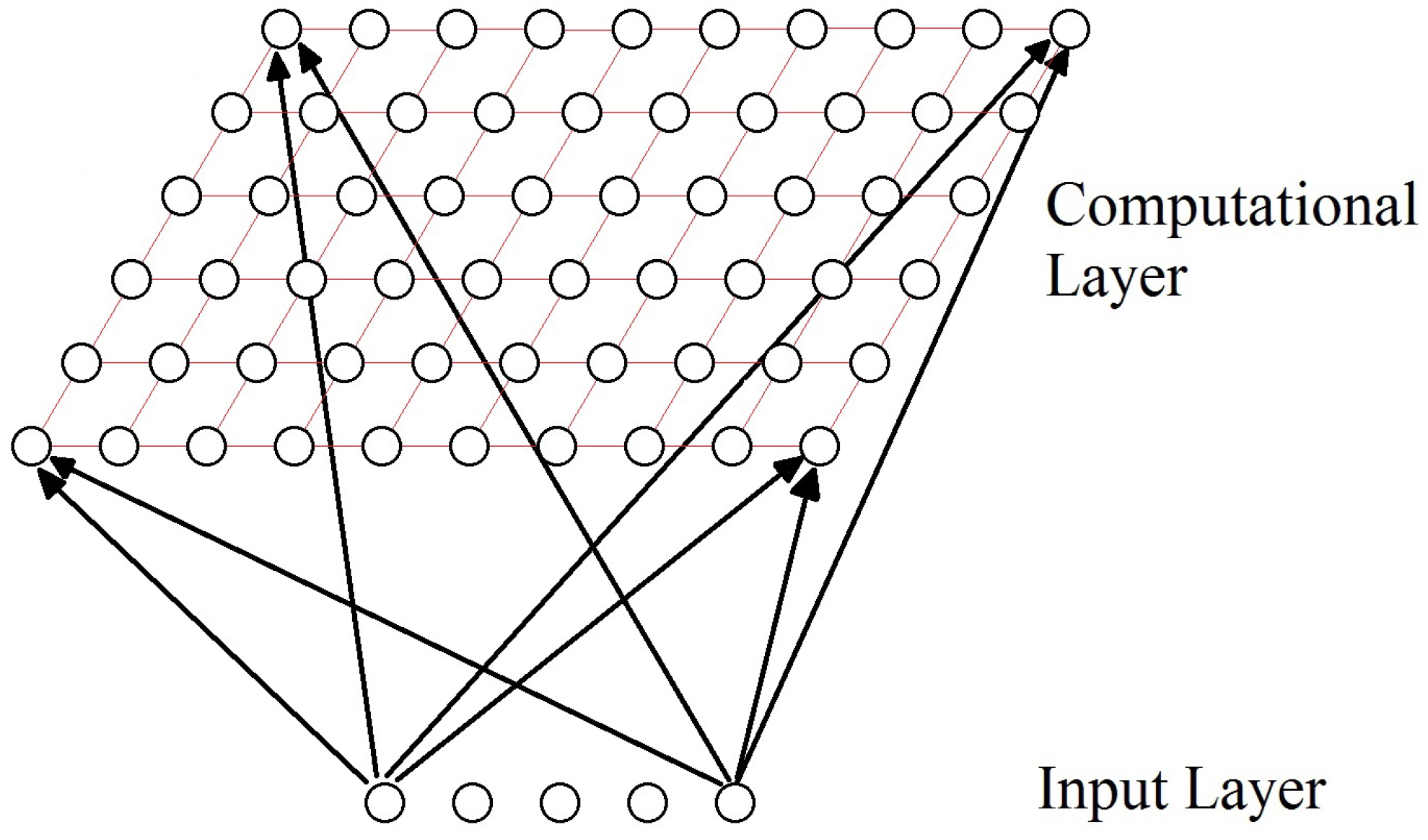
3.5. Self-Organizing Maps
3.5.1. Essential Characteristics and Training of an SOM
- Initialization. At first, the connection weights are set to small random values.
- Competition. For a D dimensionality input space, represents the input patterns and represents the connection weights between the input units and the neuron j in the computational layer; , where N is the total number of neurons. The difference between for each neuron can be calculated as the Euclidean distance squared, which will represent the discriminant function .The neuron with the lowest discriminant function is declared the winner-takes-all neuron. Competition between neurons allows mapping the continuous input space to the discrete output space.
- Cooperation. In neurobiological studies, it was observed that, within a set of excited neurons, there can be lateral interaction. When a neuron is activated, the neurons in its surroundings tend to become more excited than those further away. A similar topological neighborhood that decays with distance exists for neurons in an SOM. Let be the lateral distance between any pair of neurons i and j, then defines our topological neighborhood, where is the index of the winner-takes-all neuron. A special quality of the SOM is that the size of the neighborhood should decrease over time. An exponential reduction is a commonly used time dependence: .
- Adaptation. SOM has an adaptive (learning) process through which the feature map between inputs and outputs is formed through the self-organization of the latter. Due to the topographic neighborhood, when the weights of the winner-takes-all neuron are updated, the weights of its neighbors are also updated, although to a lesser extent. To update the weight, we define , in which we have a time-dependent learning rate t. These updates are applied to all training patterns for various periods. The goal of each learning weight update is to move the weight vectors of the winner-takes-all neuron and its neighbors closer to the input vector .
3.5.2. Application of Self-Organizing Maps to Time Series Forecasting
3.5.3. Comparison between FFNN and SOM Models Applied to Time Series Prediction
3.5.4. SOM Models Combined with Autoregressive Models
3.6. BP Problems in the Context of Time Series Modeling
3.6.1. Vanishing and Exploding Gradient Problems
3.6.2. Alternatives to the BP Problems
- Introduce a time-step sequence of input and output pairs to the network.
- Unroll the network.
- For each time step, calculate and accumulate errors.
- Roll-up the network.
- Update weights.
- Repeat.
4. Brief Literature Survey on ANNs Applied to Time Series Modeling
4.1. Combining Feedforward Neural Networks and Particle Swarm Optimization for Time Series Forecasting
PSO is an optimization algorithm inspired by the motion of a bird flock; any member of the flock is called a “particle”.(Kennedy and Eberhart [101], 1995)
4.1.1. Particle Swarm Optimization for Artificial Neural Networks
| Algorithm 1 Basic particle swarm optimization (PSO) algorithm |
| for each particle in the swarm do |
| initialize particle’s position: uniform random vector in |
| initialize particle’s best-known position: |
| if then |
| update swarm’s best-known position: |
| end if |
| initialize particle’s velocity: uniform random vector in |
| end for |
| repeat |
| for each particle in the swarm do |
| for each dimension do |
| pick random numbers |
| update particle’s velocity: |
| end for |
| update particle’s position: |
| if then |
| update particle’s best-known position: |
| if then |
| update swarm’s best-known position: |
| end if |
| end if |
| end for |
| until a termination criterion is met |
| Now, holds the best found solution |
- Relevant time lags for autoregressive inputs (the total number of relevant time lags defines the FFNN’s input dimension d);
- Number q of hidden units in the FFNN;
- Variant of FFNN architecture employed: 1. An FFNN architecture identical to the one outlined in Section 3.1, with a linear output unit, 2. an FFNN with structural modifications proposed by Leung, Lam, Ling, and Tam [114], or 3. the same FFNN architecture as in 1, but with a sigmoidal output unit;
- Initial FFNN weights and meta-parameter configuration.
- Experiment number 1 tests all six training algorithms on a special ANN architecture called single multiplicative neuron (SMN), which is similar to an FFNN but consists of an input layer and an output layer with a single processing unit (this single neuron has a logistic activation function but multiplies its inputs instead of adding them; additionally, there is a bias for each input node, in contrast to FFNNs, which contain just one bias in the input layer).
- Experiment number 2 also tests all six training algorithms, but this time on a regular FFNN with one to six hidden neurons.
4.1.2. Particle Swarm Optimization Convergence
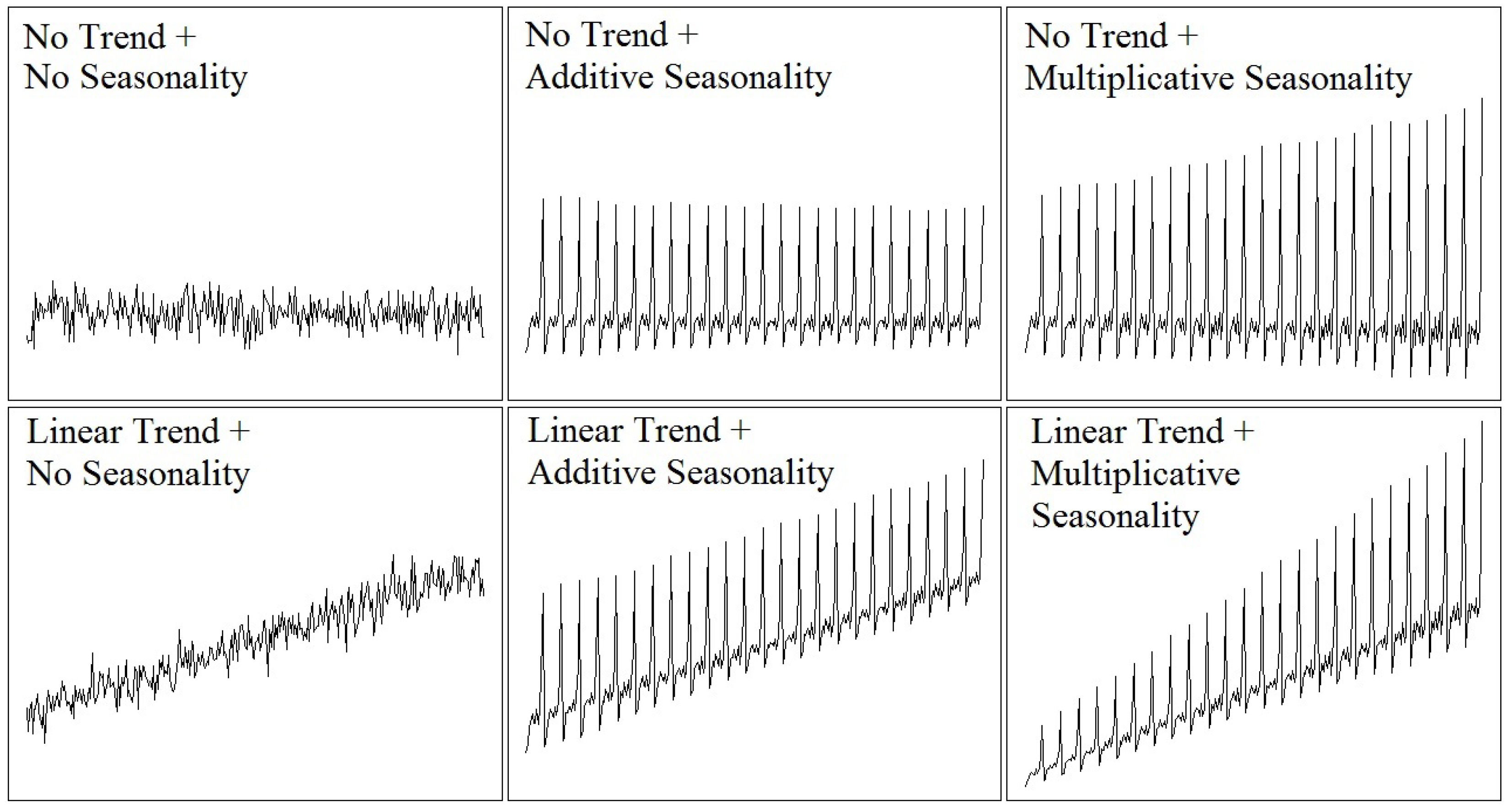
4.2. A Study on the Ability of Support Vector Regression and Feedforward Neural Networks to Forecast Basic Time Series Patterns
- FFNNs;
- SVR models using a radial basis function (RBF) kernel;
- SVR models using a linear function kernel.
- Stationarytime series (constant level);
- Stationary time series with additive seasonality;
- Linear trend;
- Linear trend with additive seasonality;
- Linear trend with multiplicative seasonality.
- The performance of FFNNs and SVRs with linear kernel is similar; they both robustly forecast time series patterns without preprocessing;
- Considering the results obtained in the three error measures of MAE, MSE, and RMSE, the FFNNs outperform the SVR models in the time series forecast of the different patterns tested;
- The results obtained indicate that FFNNs seem to be able to extrapolate seasonal trends and patterns accurately and without preprocessing.
4.3. Forecasting the Economy with Artificial Neural Networks
- Macroeconomics is a non-experimental science. It is a complicated task to observe the behavior of an economy as a whole, and the possibility of carrying out controlled experiments is very remote;
- Lack of a priori models. It is not possible to carry out controlled studies on the effects of the influence that qualitative (non-quantifiable) variables have on economic activity, due to the complexities of the economic system;
- Noise present in data. This is due to two main causes: the way in which information is collected and the number of unobserved (non-measurable) variables in economics. The presence of noise in short time series makes it difficult to control the variance of the model, requiring highly complex models to predict this type of phenomena;
- Nonlinearity. Due to high levels of noise and limited data, neural network models do not capture the nonlinear characteristics of macroeconomic series.
Neural Network Challenges in Economy
- After selecting the number of hidden units, input removal and weight elimination can be carried out in parallel or sequentially;
- In order to avoid an exhaustive search over the exponentially large space of architectures obtained by considering all possible combinations of inputs, we can employ a directed search strategy using the sensitivity-based input pruning (SBP) algorithm;
- We can employ some of the following optimization criteria in order to select competing models: maximum a posteriori probability (MAP), minimum Bayesian information criterion (BIC), minimum description length (MDL), and estimation (from the training data) of generalization ability, also called prediction risk;
- It is easier to over-fit a model to a small training set, so care must be taken to select a model that is not too large;
- The sensitivity analysis provides a global understanding about which inputs are important for predicting quantities of interest, such as the business cycle. Further information can be gained, however, by examining the evolution of sensitivities over time;
- Given the difficulty of macroeconomic forecasting, no single technique for reducing prediction risk is sufficient to obtain optimal performance. Rather, a combination of techniques is required.
4.4. Double SOM for Long-Term Time Series Prediction
- Build regressor at time t;
- Identify centroid corresponding to regressor ;
- Draw randomly a deformation , according to the empirical law of probabilities ;
- and are summed to form vector ;
- The part extracted from the left side of the vector computed in the previous step constitutes the prediction.
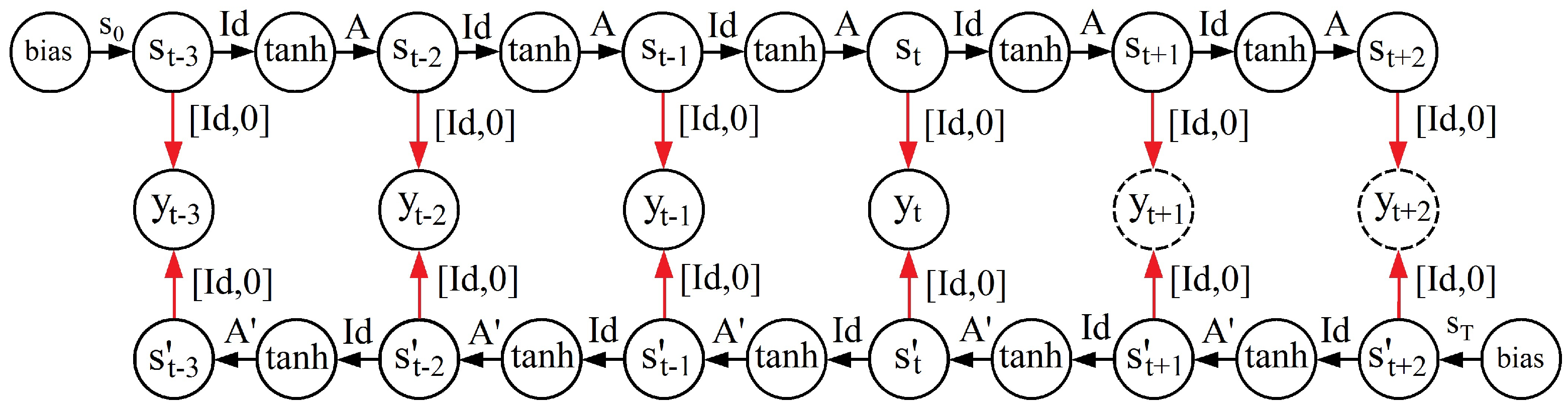
4.5. Time Series Forecasting with Recurrent Neural Networks
- Basic time-delay RNNs in state space formulation, which model open dynamical systems (i.e., partly autonomous and partly externally driven dynamical systems);
- Error-correction neural networks (ECNNs), which refine the basic RNN model by adding an error-correction term in order to handle missing information from unknown external drivers of open dynamical systems;
- Historically consistent neural networks (HCNNs), which refine ECNNs by internally modeling external drivers, thus transforming ECNNs (and basic RNNs) into closed dynamical systems;
- Causal-retro-causal neural networks (CRCNNs), which refine HCNNs by incorporating into their usual information flow from past into future (causal flow) the effects of rational decision-making and planning via an information flow from future into past (retro–causal flow).
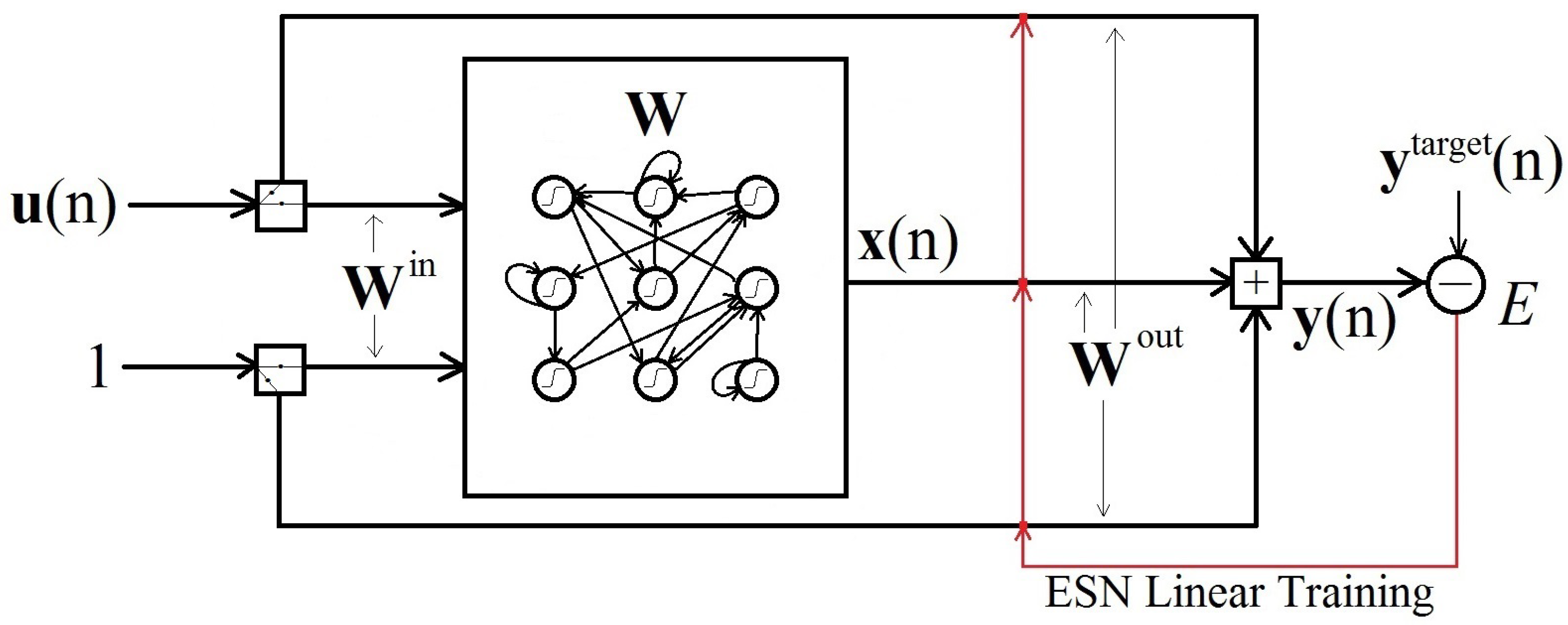
4.6. Applying Echo State Networks to Time Series Forecasting
- Generate a random reservoir RNN ;
- Run the reservoir using the training input and collect the corresponding reservoir activation states ;
- Compute the linear readout weights from the reservoir, minimizing the MSE between and ;
- Use the trained network on new input data to compute by using the trained output weights .
5. Discussion
- First razor: Starting from the fact that simplicity is desirable in itself, the simpler model should be preferred between two models with the same generalization error.
- Second razor: Starting from the fact that you are likely to have a smaller generalization error in the simpler model, it should be preferred between two models with the same error in the training set.
6. Conclusions
| Study | Main Model Employed | Time Series Forecasting Application |
|---|---|---|
| Adhikari et al. [81] | FFNN–PSO, Elman RNN–PSO | Macroeconomic variables |
| Alba-Cuéllar et al. [6] | FFNN–PSO ensemble-bootstrap | Monthly transportation data |
| Barrow and Crone [40] | FFNN ensembles | Transportation data |
| Blonbou [85] | Bayesian NN | Wind-generated power |
| Busseti et al. [169] | Deep RNN | Load forecasting |
| Chandra and Zhang [53] | Elman RNN | Chaotic time series |
| Chatzis and Demiris [170] | Bayesian ESN | Chaotic time series |
| Crone et al. [94] | FFNN, SVR | Monthly retail sales |
| Dablemont et al. [66] | Double SOM–RBFN | German DAX30 index |
| Giovanis [83] | FFNN–GA | Macroeconomic and financial data |
| Guo and Deng [89] | Hybrid FFNN–BP–ARIMA | Traffic flow |
| Jaeger and Haas [164] | ESN | Wireless communication signals |
| Jha et al. [80] | FFNN–PSO | Financial data |
| Kocadağlı and Aşıkgil [87] | Bayesian FFNN–GA | Weekly sales of a finance magazine |
| Lahmiri [41] | RBFN ensemble | NASDAQ returns |
| Leung et al. [114] | FFNN-improved GA | Natural phenomena (sunspots) |
| Maciel and Ballini [19] | FFNN | Stock market index forecasting |
| Mai et al. [48] | RBFN | Electric load |
| de M. Neto et al. [92] | FFNN–PSO | Financial data |
| Niu and Wang [47] | Improved RBFN | Financial data |
| Nourani et al. [68] | SOM–Wavelet Transform–FFNN | Satellite rainfall runoff data |
| Otok et al. [90] | Ensemble ARIMA–FFNN | Monthly rainfall in Indonesia |
| Sermpinis et al. [45] | RBFN–PSO | Global financial data |
| Shi and Han [171] | SVR–ESN hybrid | China Yellow River runoff |
| Simon et al. [64] | Double SOM | Polish electrical load time series |
| Skabar [84] | Bayesian FFNN | Australian Financial Index |
| Song [57] | Jordan RNN | Natural phenomena and sunspots |
| Valero et al. [63] | SOM, FFNN | Load demand in Spain electrical system |
| van Hinsbergen et al. [86] | Bayesian ANN | Urban travel time |
| Yadav and Srinivasan [65] | SOM–AR | Electricity demand in Britain and Wales |
| Yeh [93] | FFNN–ISSO | Natural phenomena and simulated data |
| Yin et al. [46] | RBFN | Tidal level at Canada’s west coast |
| Zhang [88] | Hybrid ARIMA–FFNN | Natural phenomena and financial data |
| Zhao et al. [54] | Elman RNN–Kalman filter | By-product gas flow in the steel industry |
| Zimmermann et al. [96] | ECNN | Demand of products and raw materials |
- ANN modeling is still a fast-evolving field of study;
- Further work still needs to be done in order to employ ANNs as useful tools for understanding and interpreting relationships among time series variables involved in the forecasting task at hand (opening the black box);
- Although ensemble modeling and methods similar to the double SOM technique discussed in Section 4.4 provide solutions for quantifying the uncertainty of time series forecasts generated by ANN models, we think that work still needs to be done in order to construct statistically valid prediction intervals associated with time series point forecasts from ANN models.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABC | Artificial bee colony |
| ANN | Artificial Neural Network |
| ARCH | Autoregressive conditional heteroskedasticity |
| ARIMA | Autoregressive integrated moving average |
| BP | Backpropagation |
| BPTT | Backpropagation through time |
| CV | Cross-validation |
| FFNN | Feedforward neural networks |
| GA | Genetic algorithm |
| MLP | Multilayer perceptron |
| NARX | Nonlinear autoregressive with exogenous inputs |
| PEM | Prediction error measure |
| PCA | Principal component analysis |
| PSO | Particle swarm optimization |
| RBFN | Radial basis function network |
| RNN | Recurrent neural network |
| SOM | Self-organizing map |
| SVM | Support vector machines |
References
- Alba-Cuéllar, D.; Muñoz-Zavala, A.E. A Comparison between SARIMA Models and Feed Forward Neural Network Ensemble Models for Time Series Data. Res. Comput. Sci. 2015, 92, 9–22. [Google Scholar] [CrossRef]
- Panigrahi, R.; Patne, N.R.; Pemmada, S.; Manchalwar, A.D. Prediction of Electric Energy Consumption for Demand Response using Deep Learning. In Proceedings of the 2022 International Conference on Intelligent Controller and Computing for Smart Power (ICICCSP), Hyderabad, India, 21–23 July 2022; IEEE: New York, NY, USA, 2022; pp. 1–6. [Google Scholar]
- Wang, Y.; Chen, J.; Chen, X.; Zeng, X.; Kong, Y.; Sun, S.; Guo, Y.; Liu, Y. Short-Term Load Forecasting for Industrial Customers Based on TCN-LightGBM. IEEE Trans. Power Syst. 2021, 36, 1984–1997. [Google Scholar] [CrossRef]
- Tudose, A.M.; Picioroaga, I.I.; Sidea, D.O.; Bulac, C.; Boicea, V.A. Short-Term Load Forecasting Using Convolutional Neural Networks in COVID-19 Context: The Romanian Case Study. Energies 2021, 14, 4046. [Google Scholar] [CrossRef]
- Panigrahi, R.; Patne, N.; Surya Vardhan, B.; Khedkar, M. Short-term load analysis and forecasting using stochastic approach considering pandemic effects. Electr. Eng. 2023, in press. [Google Scholar] [CrossRef]
- Alba-Cuéllar, D.; Muñoz-Zavala, A.E.; Hernández-Aguirre, A.; Ponce-De-Leon-Senti, E.E.; Díaz-Díaz, E. Time Series Forecasting with PSO-Optimized Neural Networks. In Proceedings of the 2014 13th Mexican International Conference on Artificial Intelligence (MICAI), Tuxtla Gutierrez, Mexico, 16–22 November 2014; IEEE: New York, NY, USA, 2014; pp. 102–111. [Google Scholar]
- Box, G.E.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Holden Day: New York, NY, USA, 1970. [Google Scholar]
- Tong, H. Nonlinear time series analysis since 1990: Some personal reflections. Acta Math. Appl. Sin. 2002, 18, 177–184. [Google Scholar] [CrossRef]
- Tong, H. Non-Linear Time Series: A Dynamical System Approach; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Engle, R.F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econom. J. Econom. Soc. 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- Granger, C.W.J.; Andersen, A.P. An Introduction to Bilinear Time Series Models; Vandenhoeck and Ruprecht: Göttingen, Germany, 1978. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1997, 9, 155–161. [Google Scholar]
- Härdle, W. Nonparametric and Semiparametric Models; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Rosenblatt, F. The Perceptron—A Perceiving and Recognizing Automaton; Technical Report 85-460-1; Cornell Aeronautical Laboratory: Buffalo, NY, USA, 1957. [Google Scholar]
- Lapedes, A.; Farber, R. Nonlinear Signal Processing Using Neural Networks: Prediction and System Modeling; Technical Report LA-UR-87-2662; Los Alamos National Laboratory: Los Alamos, NM, USA, 1987. [Google Scholar]
- As’ad, F.; Farhat, C. A mechanics-informed deep learning framework for data-driven nonlinear viscoelasticity. Comput. Methods Appl. Mech. Eng. 2023, 417, 116463. [Google Scholar] [CrossRef]
- Maciel, L.S.; Ballini, R. Neural networks applied to stock market forecasting: An empirical analysis. Learn. Nonlinear Model. 2010, 8, 3–22. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications (with R Examples), 3rd ed.; Springer Science+Business Media, LLC: Cham, Switzerland, 2011. [Google Scholar]
- Jones, E.R. An Introduction to Neural Networks: A White Paper; Visual Numerics Inc.: Houston, TX, USA, 2004. [Google Scholar]
- Touretzky, D.; Laskowski, K. Neural Networks for Time Series Prediction; Lecture Notes for Class 15-486/782: Artificial Neural Networks; Carnegie Mellon University: Pittsburgh, PA, USA, 2006. [Google Scholar]
- Whittle, P. Hypothesis Testing in Time Series Analysis; Hafner Publishing Company: New York, NY, USA, 1951. [Google Scholar]
- Box, G.E. Science and statistics. J. Am. Stat. Assoc. 1976, 71, 791–799. [Google Scholar] [CrossRef]
- Nisbet, B. Tutorial E—Feature Selection in KNIME. In Handbook of Statistical Analysis and Data Mining Applications, 2nd ed.; Nisbet, R., Miner, G., Yale, K., Eds.; Academic Press: Boston, MA, USA, 2018; pp. 377–391. [Google Scholar]
- Bullinaria, J.A. Neural Computation. 2014. Available online: https://www.cs.bham.ac.uk/~jxb/inc.html (accessed on 1 December 2023).
- Beale, R.; Jackson, T. Neural Computing—An Introduction; Institute of Physics Publishing: Bristol, UK, 1990. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Callan, R. Essence of Neural Networks; Prentice Hall PTR: Hoboken, NJ, USA, 1998. [Google Scholar]
- Fausett, L. Fundamentals of Neural Networks: Architectures, Algorithms, and Applications; Prentice Hall: Hoboken, NJ, USA, 1994. [Google Scholar]
- Gurney, K. An Introduction to Neural Networks; Routledge: London, UK, 1997. [Google Scholar]
- Ham, F.M.; Kostanic, I. Principles of Neurocomputing for Science and Engineering; McGraw-Hill Higher Education: New York, NY, USA, 2000. [Google Scholar]
- Haykin, S.S. Neural Networks and Learning Machines; Pearson Education Upper Saddle River: Hoboken, NJ, USA, 2009; Volume 3. [Google Scholar]
- Hertz, J. Introduction to the Theory of Neural Computation; Basic Books: New York, NY, USA, 1991; Volume 1. [Google Scholar]
- Mazaheri, P.; Rahnamayan, S.; Bidgoli, A.A. Designing Artificial Neural Network Using Particle Swarm Optimization: A Survey; IntechOpen: Rijeka, Croatia, 2022. [Google Scholar]
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Hjorth, J.U. Computer Intensive Statistical Methods: Validation, Model Selection, and Bootstrap; Chapman and Hall: Boca Raton, FL, USA, 1994; pp. 65–73. [Google Scholar]
- Makridakis, S.; Winkler, R.L. Averages of forecasts: Some empirical results. Manag. Sci. 1983, 29, 987–996. [Google Scholar] [CrossRef]
- Barrow, D.K.; Crone, S.F. Crogging (cross-validation aggregation) for forecasting—A novel algorithm of neural network ensembles on time series subsamples. In Proceedings of the 2013 International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013; IEEE: New York, NY, USA, 2013; pp. 1–8. [Google Scholar]
- Lahmiri, S. Intelligent Ensemble Systems for Modeling NASDAQ Microstructure: A Comparative Study. In Artificial Neural Networks in Pattern Recognition; Springer: Cham, Switzerland, 2014; pp. 240–251. [Google Scholar]
- Broomhead, D.S.; Lowe, D. Radial Basis Functions, Multi-Variable Functional Interpolation and Adaptive Networks; Technical Report, DTIC Document; Controller HMSO: London, UK, 1988. [Google Scholar]
- Hartman, E.J.; Keeler, J.D.; Kowalski, J.M. Layered neural networks with Gaussian hidden units as universal approximations. Neural Comput. 1990, 2, 210–215. [Google Scholar] [CrossRef]
- Chang, W.Y. Wind energy conversion system power forecasting using radial basis function neural network. Appl. Mech. Mater. 2013, 284, 1067–1071. [Google Scholar] [CrossRef]
- Sermpinis, G.; Theofilatos, K.; Karathanasopoulos, A.; Georgopoulos, E.F.; Dunis, C. Forecasting foreign exchange rates with adaptive neural networks using radial-basis functions and Particle Swarm Optimization. Eur. J. Oper. Res. 2013, 225, 528–540. [Google Scholar] [CrossRef]
- Yin, J.c.; Zou, Z.j.; Xu, F. Sequential learning radial basis function network for real-time tidal level predictions. Ocean Eng. 2013, 57, 49–55. [Google Scholar] [CrossRef]
- Niu, H.; Wang, J. Financial time series prediction by a random data-time effective RBF neural network. Soft Comput. 2014, 18, 497–508. [Google Scholar] [CrossRef]
- Mai, W.; Chung, C.; Wu, T.; Huang, H. Electric load forecasting for large office building based on radial basis function neural network. In Proceedings of the 2014 IEEE PES General Meeting—Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; IEEE: New York, NY, USA, 2014; pp. 1–5. [Google Scholar]
- Zhu, J.Z.; Cao, J.X.; Zhu, Y. Traffic volume forecasting based on radial basis function neural network with the consideration of traffic flows at the adjacent intersections. Transp. Res. Part C Emerg. Technol. 2014, 47 Pt A, 139–154. [Google Scholar] [CrossRef]
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Sprott, J.C. Chaos and Time-Series Analysis; Oxford University Press: Oxford, UK, 2003; Volume 69. [Google Scholar]
- Ardalani-Farsa, M.; Zolfaghari, S. Chaotic time series prediction with residual analysis method using hybrid Elman–NARX neural networks. Neurocomputing 2010, 73, 2540–2553. [Google Scholar] [CrossRef]
- Chandra, R.; Zhang, M. Cooperative coevolution of Elman recurrent neural networks for chaotic time series prediction. Neurocomputing 2012, 86, 116–123. [Google Scholar] [CrossRef]
- Zhao, J.; Zhu, X.; Wang, W.; Liu, Y. Extended Kalman filter-based Elman networks for industrial time series prediction with GPU acceleration. Neurocomputing 2013, 118, 215–224. [Google Scholar] [CrossRef]
- Jordan, M.I. Attractor Dynamics and parallelism in a connectionist sequential machine. In Proceedings of the Eight Annual Conference of the Cognitive Science Society, Amherst, MA, USA, 15–17 August 1986; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1986. [Google Scholar]
- Tabuse, M.; Kinouchi, M.; Hagiwara, M. Recurrent neural network using mixture of experts for time series processing. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics—Computational Cybernetics and Simulation, Orlando, FL, USA,, 12–15 October 1997; IEEE: New York, NY, USA, 1997; Volume 1, pp. 536–541. [Google Scholar]
- Song, Q. Robust initialization of a Jordan network with recurrent constrained learning. Neural Netw. IEEE Trans. 2011, 22, 2460–2473. [Google Scholar] [CrossRef]
- Song, Q. Robust Jordan network for nonlinear time series prediction. In Proceedings of the 2011 International Joint Conference on Neural Networks (IJCNN), San Jose, CA, USA, 31 July–5 August 2011; IEEE: New York, NY, USA, 2011; pp. 2542–2549. [Google Scholar]
- Boussaada, Z.; Curea, O.; Remaci, A.; Camblong, H.; Mrabet Bellaaj, N. A Nonlinear Autoregressive Exogenous (NARX) Neural Network Model for the Prediction of the Daily Direct Solar Radiation. Energies 2018, 11, 620. [Google Scholar] [CrossRef]
- Kohonen, T. Self-Organizing Maps; Springer Series in Information Sciences; Springer: Berlin/Heidelberg, Germany, 1995; Volume 30. [Google Scholar]
- Barreto, G.A. Time series prediction with the self-organizing map: A review. In Perspectives of Neural-Symbolic Integration; Springer: Berlin/Heidelberg, Germany, 2007; pp. 135–158. [Google Scholar]
- Burguillo, J.C. Using self-organizing maps with complex network topologies and coalitions for time series prediction. Soft Comput. 2014, 18, 695–705. [Google Scholar] [CrossRef]
- Valero, S.; Aparicio, J.; Senabre, C.; Ortiz, M.; Sancho, J.; Gabaldon, A. Comparative analysis of Self Organizing Maps vs. multilayer perceptron neural networks for short-term load forecasting. In Proceedings of the Modern Electric Power Systems (MEPS), 2010 Proceedings of the International Symposium, Wroclaw, Poland, 20–22 September 2010; IEEE: New York, NY, USA, 2010; pp. 1–5. [Google Scholar]
- Simon, G.; Lendasse, A.; Cottrell, M.; Fort, J.C.; Verleysen, M. Double SOM for long-term time series prediction. In Proceedings of the Conference WSOM 2003, Kitakyushu, Japan, 11–14 September 2003; pp. 35–40. [Google Scholar]
- Yadav, V.; Srinivasan, D. Autocorrelation based weighing strategy for short-term load forecasting with the self-organizing map. In Proceedings of the 2010 the 2nd International Conference on Computer and Automation Engineering (ICCAE), Singapore, 26–28 February 2010; IEEE: New York, NY, USA, 2010; Volume 1, pp. 186–192. [Google Scholar]
- Dablemont, S.; Simon, G.; Lendasse, A.; Ruttiens, A.; Blayo, F.; Verleysen, M. Time series forecasting with SOM and local non-linear models—Application to the DAX30 index prediction. In Proceedings of the Workshop on Self-Organizing Maps, Kitakyushu, Japan, 11–14 September 2003. [Google Scholar]
- Cherif, A.; Cardot, H.; Boné, R. Recurrent Neural Networks as Local Models for Time Series Prediction. In Neural Information Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 786–793. [Google Scholar]
- Nourani, V.; Baghanam, A.H.; Adamowski, J.; Gebremichael, M. Using self-organizing maps and wavelet transforms for space–time pre-processing of satellite precipitation and runoff data in neural network based rainfall–runoff modeling. J. Hydrol. 2013, 476, 228–243. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training Recurrent Neural Networks. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; IEEE: New York, NY, USA, 2013. [Google Scholar]
- Hu, D.; Wu, R.; Chen, D.; Dou, H. An improved training algorithm of neural networks for time series forecasting. In MICAI 2007: Advances in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2007; pp. 550–558. [Google Scholar]
- Nunnari, G. An improved back propagation algorithm to predict episodes of poor air quality. Soft Comput. 2006, 10, 132–139. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, ICML-2015, JMLR, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Yang, G.; Pennington, J.; Rao, V.; Sohl-Dickstein, J.; Schoenholz, S.S. A Mean Field Theory of Batch Normalization; Cornell Uiversity: Ithaca, NY, USA, 2019. [Google Scholar]
- Werbos, P. Backpropagation through time: What it does and how to do it. Proc. IEEE 1990, 78, 1550–1560. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Calin, O. Deep Learning Architectures: A Mathematical Approach; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Roy, T.; kumar Shome, S. Optimization of RNN-LSTM Model Using NSGA-II Algorithm for IOT-based Fire Detection Framework. IETE J. Res. 2023, in press. [Google Scholar] [CrossRef]
- Jha, G.K.; Thulasiraman, P.; Thulasiram, R.K. PSO based neural network for time series forecasting. In Proceedings of the 2009 International Joint Conference on Neural Networks, IJCNN 2009, Atlanta, GA, USA, 14–19 June 2009; IEEE: New York, NY, USA, 2009; pp. 1422–1427. [Google Scholar]
- Adhikari, R.; Agrawal, R.; Kant, L. PSO based Neural Networks vs. traditional statistical models for seasonal time series forecasting. In Proceedings of the 2013 3rd IEEE International Advance Computing Conference (IACC), Ghaziabad, India, 22–23 February 2013; IEEE: New York, NY, USA, 2013; pp. 719–725. [Google Scholar]
- Awan, S.M.; Aslam, M.; Khan, Z.A.; Saeed, H. An efficient model based on artificial bee colony optimization algorithm with Neural Networks for electric load forecasting. Neural Comput. Appl. 2014, 25, 1967–1978. [Google Scholar] [CrossRef]
- Giovanis, E. Feed-Forward Neural Networks Regressions with Genetic Algorithms: Applications in Econometrics and Finance. SSRN 2010, in press. [Google Scholar] [CrossRef]
- Skabar, A.A. Direction-of-change financial time series forecasting using neural networks: A Bayesian approach. In Advances in Electrical Engineering and Computational Science; Springer: Dordrecht, The Netherlands, 2009; pp. 515–524. [Google Scholar]
- Blonbou, R. Very short-term wind power forecasting with neural networks and adaptive Bayesian learning. Renew. Energy 2011, 36, 1118–1124. [Google Scholar] [CrossRef]
- Van Hinsbergen, C.; Hegyi, A.; van Lint, J.; van Zuylen, H. Bayesian neural networks for the prediction of stochastic travel times in urban networks. IET Intell. Transp. Syst. 2011, 5, 259–265. [Google Scholar] [CrossRef]
- Kocadağlı, O.; Aşıkgil, B. Nonlinear time series forecasting with Bayesian neural networks. Expert Syst. Appl. 2014, 41, 6596–6610. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Guo, X.; Deng, F. Short-term prediction of intelligent traffic flow based on BP neural network and ARIMA model. In Proceedings of the 2010 International Conference on E-Product E-Service and E-Entertainment (ICEEE), Henan, China, 7–9 November 2010; IEEE: New York, NY, USA, 2010; pp. 1–4. [Google Scholar]
- Otok, B.W.; Lusia, D.A.; Faulina, R.; Kuswanto, H. Ensemble method based on ARIMA-FFNN for climate forecasting. In Proceedings of the 2012 International Conference on Statistics in Science, Business, and Engineering (ICSSBE), Langkawi, Malaysia, 10–12 September 2012; IEEE: New York, NY, USA, 2012; pp. 1–4. [Google Scholar]
- Viviani, E.; Di Persio, L.; Ehrhardt, M. Energy Markets Forecasting. From Inferential Statistics to Machine Learning: The German Case. Energies 2021, 14, 364. [Google Scholar] [CrossRef]
- Neto, P.S.d.M.; Petry, G.G.; Aranildo, R.L.J.; Ferreira, T.A.E. Combining artificial neural network and particle swarm system for time series forecasting. In Proceedings of the 2009 International Joint Conference on Neural Networks, IJCNN 2009, Atlanta, GA, USA, 14–19 June 2009; IEEE: New York, NY, USA, 2009; pp. 2230–2237. [Google Scholar]
- Yeh, W.C. New Parameter-Free Simplified Swarm Optimization for Artificial Neural Network Training and its Application in the Prediction of Time Series. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 661–665. [Google Scholar]
- Crone, S.F.; Guajardo, J.; Weber, R. A study on the ability of support vector regression and neural networks to forecast basic time series patterns. In Artificial Intelligence in Theory and Practice; Springer: Boston, MA, USA, 2006; pp. 149–158. [Google Scholar]
- Moody, J. Forecasting the economy with neural nets: A survey of challenges and solutions. In Neural Networks: Tricks of the Trade, 2nd ed.; Montavon, G., Orr, G.B., Müller, K.R., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7700, pp. 343–367. [Google Scholar]
- Zimmermann, H.G.; Tietz, C.; Grothmann, R. Forecasting with recurrent neural networks: 12 tricks. In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 2012; pp. 687–707. [Google Scholar]
- Lukoševičius, M. A practical guide to applying echo state networks. In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 2012; pp. 659–686. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Angeline, P.J. Evolutionary optimization versus particle swarm optimization: Philosophy and performance differences. In Evolutionary Programming VII; Springer: Berlin/Heidelberg, Germany, 1998; pp. 601–610. [Google Scholar]
- Freitas, D.; Lopes, L.G.; Morgado-Dias, F. Particle Swarm Optimisation: A Historical Review Up to the Current Developments. Entropy 2020, 22, 362. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: New York, NY, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Eberhart, R.; Shi, Y. Evolving Artificial Neural Networks. In Proceedings of the International Conference on Neural Networks and Brain, PRC, Anchorage, AK, USA, 4–9 May 1998; Volume 1, pp. PL5–PL13. [Google Scholar]
- Eberhart, R.; Shi, Y. Particle swarm optimization: Developments, applications and resources. In Proceedings of the 2001 Congress on Evolutionary Computation, Seoul, Republic of Korea, 27–30 May 2001; IEEE: New York, NY, USA, 2001; Volume 1, pp. 81–86. [Google Scholar]
- Yu, J.; Wang, S.; Xi, L. Evolving artificial neural networks using an improved PSO and DPSO. Neurocomputing 2008, 71, 1054–1060. [Google Scholar] [CrossRef]
- Munoz-Zavala, A.E. A Comparison Study of PSO Neighborhoods. In EVOLVE—A Bridge between Probability, Set Oriented Numerics, and Evolutionary Computation II; Springer: Berlin/Heidelberg, Germany, 2013; pp. 251–265. [Google Scholar]
- Eberhart, R.; Dobbins, R.; Simpson, P. Computational Intelligence PC Tools; Academic Press Professional: Cambridge, MA, USA, 1996. [Google Scholar]
- Clerc, M.; Kennedy, J. The particle swarm: Explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Slama, S.; Errachdi, A.; Benrejeb, M. Tuning Artificial Neural Network Controller Using Particle Swarm Optimization Technique for Nonlinear System; IntechOpen: Rijeka, Croatia, 2021. [Google Scholar]
- Ahmadzadeh, E.; Lee, J.; Moon, I. Optimized Neural Network Weights and Biases Using Particle Swarm Optimization Algorithm for Prediction Applications. J. Korea Multimed. Soc. 2017, 20, 1406–1420. [Google Scholar]
- Hagan, M.T.; Menhaj, M.B. Training feedforward networks with the Marquardt algorithm. Neural Netw. IEEE Trans. 1994, 5, 989–993. [Google Scholar] [CrossRef] [PubMed]
- Riedmiller, M.; Braun, H. A direct adaptive method for faster backpropagation learning: The RPROP algorithm. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993; IEEE: New York, NY, USA, 1993; pp. 586–591. [Google Scholar]
- Møller, M.F. A scaled conjugate gradient algorithm for fast supervised learning. Neural Netw. 1993, 6, 525–533. [Google Scholar] [CrossRef]
- Battiti, R. One step secant conjugate gradient. Neural Comput. 1992, 4, 141–166. [Google Scholar] [CrossRef]
- Leung, F.H.F.; Lam, H.K.; Ling, S.H.; Tam, P.K.S. Tuning of the structure and parameters of a neural network using an improved genetic algorithm. IEEE Trans. Neural Netw. 2003, 14, 79–88. [Google Scholar] [CrossRef]
- Sitte, R.; Sitte, J. Neural networks approach to the random walk dilemma of financial time series. Appl. Intell. 2002, 16, 163–171. [Google Scholar] [CrossRef]
- de Araujo, R.; Madeiro, F.; de Sousa, R.P.; Pessoa, L.F.; Ferreira, T. An evolutionary morphological approach for financial time series forecasting. In Proceedings of the 2006 IEEE Congress on Evolutionary Computation, CEC 2006, Vancouver, BC, Canada, 16–21 July 2006; IEEE: New York, NY, USA, 2006; pp. 2467–2474. [Google Scholar]
- Yeh, W.C.; Chang, W.W.; Chung, Y.Y. A new hybrid approach for mining breast cancer pattern using discrete particle swarm optimization and statistical method. Expert Syst. Appl. 2009, 36, 8204–8211. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Zhao, L.; Yang, Y. PSO-based single multiplicative neuron model for time series prediction. Expert Syst. Appl. 2009, 36, 2805–2812. [Google Scholar] [CrossRef]
- Mackey, M.C.; Glass, L. Oscillation and chaos in physiological control systems. Science 1977, 197, 287–289. [Google Scholar] [CrossRef] [PubMed]
- Hyndman, R. Time Series Data Library. 2014. Available online: https://robjhyndman.com/tsdl/ (accessed on 1 December 2023).
- Keirn, Z. EEG Pattern Analysis. 1988. Available online: https://github.com/meagmohit/EEG-Datasets (accessed on 1 December 2023).
- Gershenfeld, N.; Weigend, A. The Santa Fe Time Series Competition Data. 1994. Available online: http://techlab.bu.edu/resources/data_view/the_santa_fe_time_series_competition_data/index.html (accessed on 1 December 2023).
- Gudise, V.; Venayagamoorthy, G. Comparison of particle swarm optimization and backpropagation as training algorithms for neural networks. In Proceedings of the 2003 IEEE Swarm Intelligence Symposium. SIS’03 (Cat. No. 03EX706), Indianapolis, IN, USA, 26 April 2003; IEEE: New York, NY, USA, 2003; pp. 110–117. [Google Scholar]
- Liu, C.; Ding, W.; Li, Z.; Yang, C. Prediction of High-Speed Grinding Temperature of Titanium Matrix Composites Using BP Neural Network Based on PSO Algorithm. Int. J. Adv. Manuf. Technol. 2016, 89, 2277–2285. [Google Scholar] [CrossRef]
- Ince, T.; Kiranyaz, S.; Gabbouj, M. A Generic and Robust System for Automated Patient-Specific Classification of ECG Signals. IEEE Trans. Biomed. Eng. 2009, 56, 1415–1426. [Google Scholar] [CrossRef]
- Hamed, H.N.A.; Shamsuddin, S.M.; Salim, N. Particle Swarm Optimization For Neural Network Learning Enhancement. J. Teknol. 2008, 49, 13–26. [Google Scholar]
- Olayode, I.O.; Tartibu, L.K.; Okwu, M.O.; Ukaegbu, U.F. Development of a Hybrid Artificial Neural Network-Particle Swarm Optimization Model for the Modelling of Traffic Flow of Vehicles at Signalized Road Intersections. Appl. Sci. 2021, 11, 8387. [Google Scholar] [CrossRef]
- Van den Bergh, F.; Engelbrecht, A. Cooperative learning in neural networks using particle swarm optimizers. S. Afr. Comput. J. 2000, 2000, 84–90. [Google Scholar]
- van den Bergh, F.; Engelbrecht, A. Training product unit networks using cooperative particle swarm optimisers. In Proceedings of the International Joint Conference on Neural Networks, IJCNN’01, Washington, DC, USA, 15–19 July 2001; IEEE: New York, NY, USA, 2001; Volume 1, pp. 126–131. [Google Scholar]
- Munoz-Zavala, A.; Hernandez-Aguirre, A.; Villa Diharce, E. Constrained optimization via particle evolutionary swarm optimization algorithm (PESO). In Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation, GECCO’05, Washington, DC, USA, 25–99 June 2005; ACM: New York, NY, USA, 2005; pp. 209–216. [Google Scholar]
- Munoz-Zavala, A.; Hernandez-Aguirre, A.; Villa Diharce, E.; Botello Rionda, S. Constrained optimization with an improved particle swarm optimization algorithm. Int. J. Intell. Comput. Cybern. 2008, 1, 425–453. [Google Scholar] [CrossRef]
- Kennedy, J. Methods of agreement: Inference among the EleMentals. In Proceedings of the 1998 IEEE International Symposium on Intelligent Control (ISIC) Held Jointly with IEEE International Symposium on Computational Intelligence in Robotics and Automation (CIRA) Intell, Gaithersburg, MD, USA, 17 September 1998; IEEE: New York, NY, USA, 1998; pp. 883–887. [Google Scholar]
- Ozcan, E.; Mohan, C. Analysis of a Simple Particle Swarm Optimization System. Intell. Eng. Syst. Artif. Neural Netw. 1998, 8, 253–258. [Google Scholar]
- Van den Bergh, F.; Engelbrecht, A.P. A Convergence Proof for the Particle Swarm Optimiser. Fundam. Inform. 2010, 105, 341–374. [Google Scholar] [CrossRef]
- Kan, W.; Jihong, S. The Convergence Basis of Particle Swarm Optimization. In Proceedings of the 2012 International Conference on Industrial Control and Electronics Engineering, Xi’an, China, 23–25 August 2012; IEEE: New York, NY, USA, 2012; pp. 63–66. [Google Scholar]
- Qian, W.; Li, M. Convergence analysis of standard particle swarm optimization algorithm and its improvement. Soft Comput. 2018, 22, 4047–4070. [Google Scholar] [CrossRef]
- Xu, G.; Yu, G. On convergence analysis of particle swarm optimization algorithm. J. Comput. Appl. Math. 2018, 333, 65–73. [Google Scholar] [CrossRef]
- Huang, H.; Qiu, J.; Riedl, K. On the Global Convergence of Particle Swarm Optimization Methods. Appl. Math. Optim. 2023, 88, 30. [Google Scholar] [CrossRef]
- Zhang, G.P.; Qi, M. Neural network forecasting for seasonal and trend time series. Eur. J. Oper. Res. 2005, 160, 501–514. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer-Verlag New York, Inc.: New York, NY, USA, 1995. [Google Scholar]
- US Census Bureau. X-13ARIMA-SEATS Seasonal Adjustment Program. 2016. Available online: https://www.census.gov/srd/www/x13as/ (accessed on 22 October 2016).
- Kiani, K.M. On business cycle fluctuations in USA macroeconomic time series. Econ. Model. 2016, 53, 179–186. [Google Scholar] [CrossRef]
- Moody, J. Prediction risk and neural network architecture selection. In From Statistics to Neural Networks: Theory and Pattern Recognition Applications; Cherkassky, V., Friedman, J.H., Wechsler, H., Eds.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 147–165. [Google Scholar]
- Pi, H.; Peterson, C. Finding the embedding dimension and variable dependencies in time series. Neural Comput. 1994, 6, 509–520. [Google Scholar] [CrossRef]
- Yang, H.; Moody, J. Input Variable Selection Based on Joint Mutual Information; Technical Report; Department of Computer Science, Oregon Graduate Institute: Eugene, OR, USA, 1998. [Google Scholar]
- Mozer, M.C.; Smolensky, P. Skeletonization: A technique for trimming the fat from a network via relevance assessment. In Advances in Neural Information Processing Systems; ACM: New York, NY, USA, 1989; pp. 107–115. [Google Scholar]
- Ash, T. Dynamic node creation in backpropagation networks. Connect. Sci. 1989, 1, 365–375. [Google Scholar] [CrossRef]
- LeCun, Y.; Denker, J.S.; Solla, S.A.; Howard, R.E.; Jackel, L.D. Optimal brain damage. Adv. Neural Inf. Process. Syst. 1989, 2, 598–605. [Google Scholar]
- Hassibi, B.; Stork, D.G. Second order derivatives for network pruning: Optimal brain surgeon. Adv. Neural Inf. Process. Syst. 1993, 5, 164. [Google Scholar]
- Levin, A. Fast pruning using principal components. Adv. Neural Inf. Process. Syst. 1994, 6, 35–42. [Google Scholar]
- Moody, J.E.; Rögnvaldsson, T. Smoothing Regularizers for Projective Basis Function Networks. Adv. Neural Inf. Process. Syst. 1996, 9, 585–591. [Google Scholar]
- Wu, L.; Moody, J. A smoothing regularizer for feedforward and recurrent neural networks. Neural Comput. 1996, 8, 461–489. [Google Scholar] [CrossRef]
- Liao, Y.; Moody, J. A neural network visualization and sensitivity analysis toolkit. In Proceedings of the International Conference on Neural Information Processing (ICONIP’96), Hong Kong, China, 24–27 September 1996; Amari, S.-I., Xu, L., Chan, L., King, I., Leung, K.-S., Eds.; Springer Verlag Singapore Pte. Ltd.: Singapore, 1996; pp. 1069–1074. [Google Scholar]
- Schäfer, A.M.; Zimmermann, H.G. Recurrent neural networks are universal approximators. In Artificial Neural Networks–ICANN 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 632–640. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Internal Representations by Error Propagation; Technical Report, DTIC Document; Institute for Cognitive Science University of California: San Diego, CA, USA, 1985. [Google Scholar]
- Zimmermann, H.G.; Neuneier, R. Neural network architectures for the modeling of dynamical systems. In A Field Guide to Dynamical Recurrent Networks; Wiley-IEEE Press: Hoboken, NJ, USA, 2001; pp. 311–350. [Google Scholar]
- Werbos, P. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1974. [Google Scholar]
- Zimmermann, H.G.; Neuneier, R.; Grothmann, R. Modeling dynamical systems by error correction neural networks. In Modelling and Forecasting Financial Data; Springer: Boston, MA, USA, 2002; pp. 237–263. [Google Scholar]
- Zimmermann, H.G.; Grothmann, R.; Schäfer, A.M.; Tietz, C.; Georg, H. Modeling Large Dynamical Systems with Dynamical Consistent Neural Networks. In New Directions in Statistical Signal Processing; MIT Press: Cambridge, MA, USA, 2007; p. 203. [Google Scholar]
- McNeil, A.J.; Frey, R.; Embrechts, P. Quantitative Risk Management: Concepts, Techniques, and Tools; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Jaeger, H. The “Echo State” Approach to Analysing and Training Recurrent Neural Networks—With an Erratum Note; GMD Technical Report 148; German National Research Center for Information Technology: Bonn, Germany, 2001; p. 13. [Google Scholar]
- Jaeger, H. Echo state network. Scholarpedia 2007, 2, 2330. [Google Scholar] [CrossRef]
- Jaeger, H.; Haas, H. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science 2004, 304, 78–80. [Google Scholar] [CrossRef] [PubMed]
- Jaeger, H.; Lukoševičius, M.; Popovici, D.; Siewert, U. Optimization and applications of echo state networks with leaky-integrator neurons. Neural Netw. 2007, 20, 335–352. [Google Scholar] [CrossRef]
- Hyndman, R.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, VIC, Australia, 2021; Volume 1. [Google Scholar]
- Domingos, P. Occam’s Two Razors: The Sharp and the Blunt. In Proceedings of the Fourth International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 27–31 August 1998; ACM: New York, NY, USA; AAAI Press: Washington, DC, USA, 1998; pp. 37–43. [Google Scholar]
- Lin, H.W.; Tegmark, M. Why does deep and cheap learning work so well? arXiv 2016, arXiv:1608.08225. [Google Scholar] [CrossRef]
- Busseti, E.; Osband, I.; Wong, S. Deep Learning for Time Series Modeling; Technical Report; Stanford University: Stanford, CA, USA, 2012. [Google Scholar]
- Chatzis, S.P.; Demiris, Y. Echo state Gaussian process. Neural Netw. IEEE Trans. 2011, 22, 1435–1445. [Google Scholar] [CrossRef]
- Shi, Z.; Han, M. Support vector echo-state machine for chaotic time-series prediction. Neural Netw. IEEE Trans. 2007, 18, 359–372. [Google Scholar] [CrossRef]
| Example | ⋯ | ||||
|---|---|---|---|---|---|
| 1 | ⋯ | ||||
| 2 | ⋯ | ||||
| 3 | ⋯ | ||||
| ⋮ | ⋮ | ⋮ | ⋯ | ⋮ | ⋮ |
| ⋯ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muñoz-Zavala, A.E.; Macías-Díaz, J.E.; Alba-Cuéllar, D.; Guerrero-Díaz-de-León, J.A. A Literature Review on Some Trends in Artificial Neural Networks for Modeling and Simulation with Time Series. Algorithms 2024, 17, 76. https://doi.org/10.3390/a17020076
Muñoz-Zavala AE, Macías-Díaz JE, Alba-Cuéllar D, Guerrero-Díaz-de-León JA. A Literature Review on Some Trends in Artificial Neural Networks for Modeling and Simulation with Time Series. Algorithms. 2024; 17(2):76. https://doi.org/10.3390/a17020076
Chicago/Turabian StyleMuñoz-Zavala, Angel E., Jorge E. Macías-Díaz, Daniel Alba-Cuéllar, and José A. Guerrero-Díaz-de-León. 2024. "A Literature Review on Some Trends in Artificial Neural Networks for Modeling and Simulation with Time Series" Algorithms 17, no. 2: 76. https://doi.org/10.3390/a17020076
APA StyleMuñoz-Zavala, A. E., Macías-Díaz, J. E., Alba-Cuéllar, D., & Guerrero-Díaz-de-León, J. A. (2024). A Literature Review on Some Trends in Artificial Neural Networks for Modeling and Simulation with Time Series. Algorithms, 17(2), 76. https://doi.org/10.3390/a17020076







