Fractional-Order Fuzzy PID Controller with Evolutionary Computation for an Effective Synchronized Gantry System
Abstract
1. Introduction
2. System Model and Identification
2.1. PMLSM Model
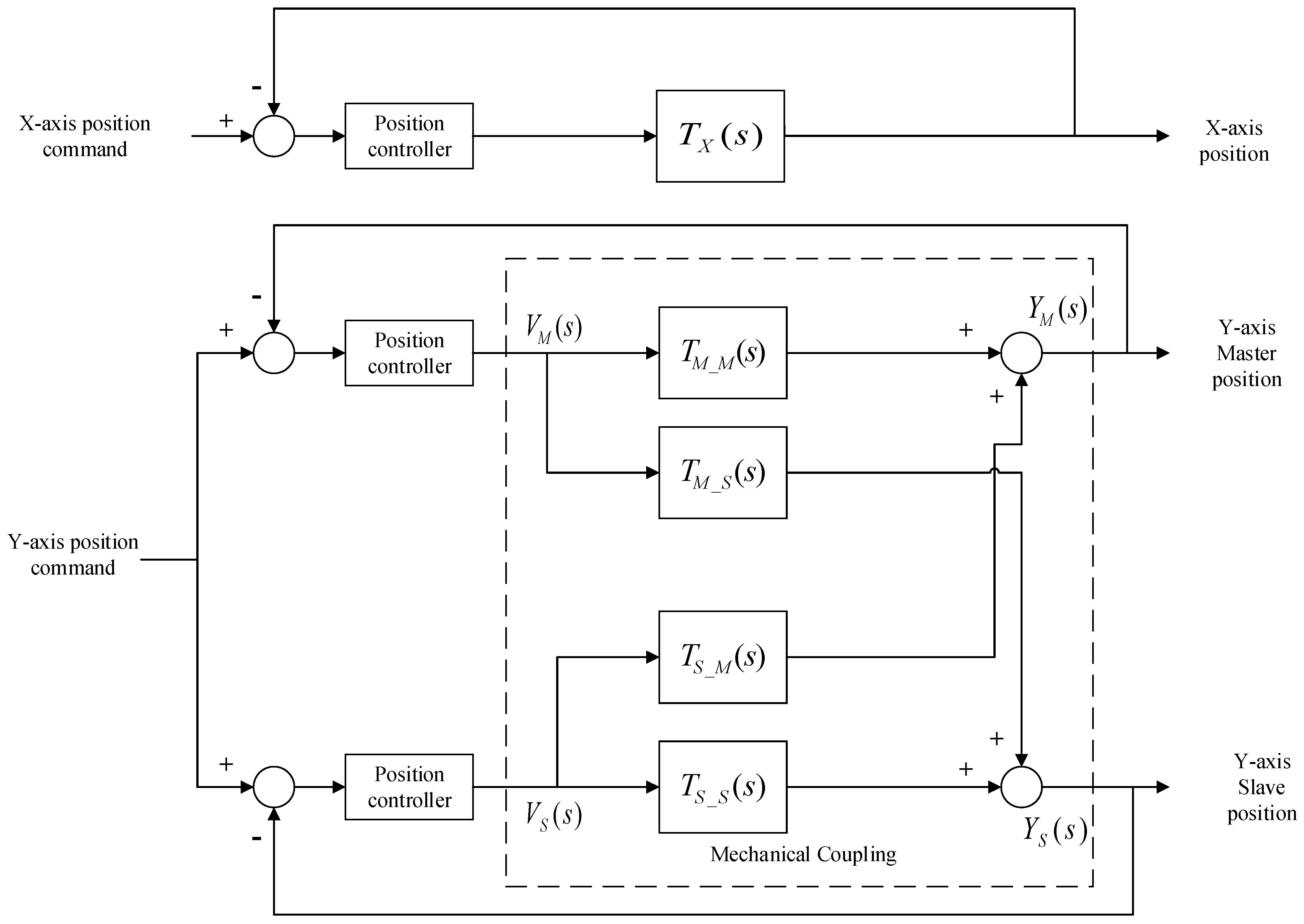
2.2. Mechanical Coupling Model and System Identification
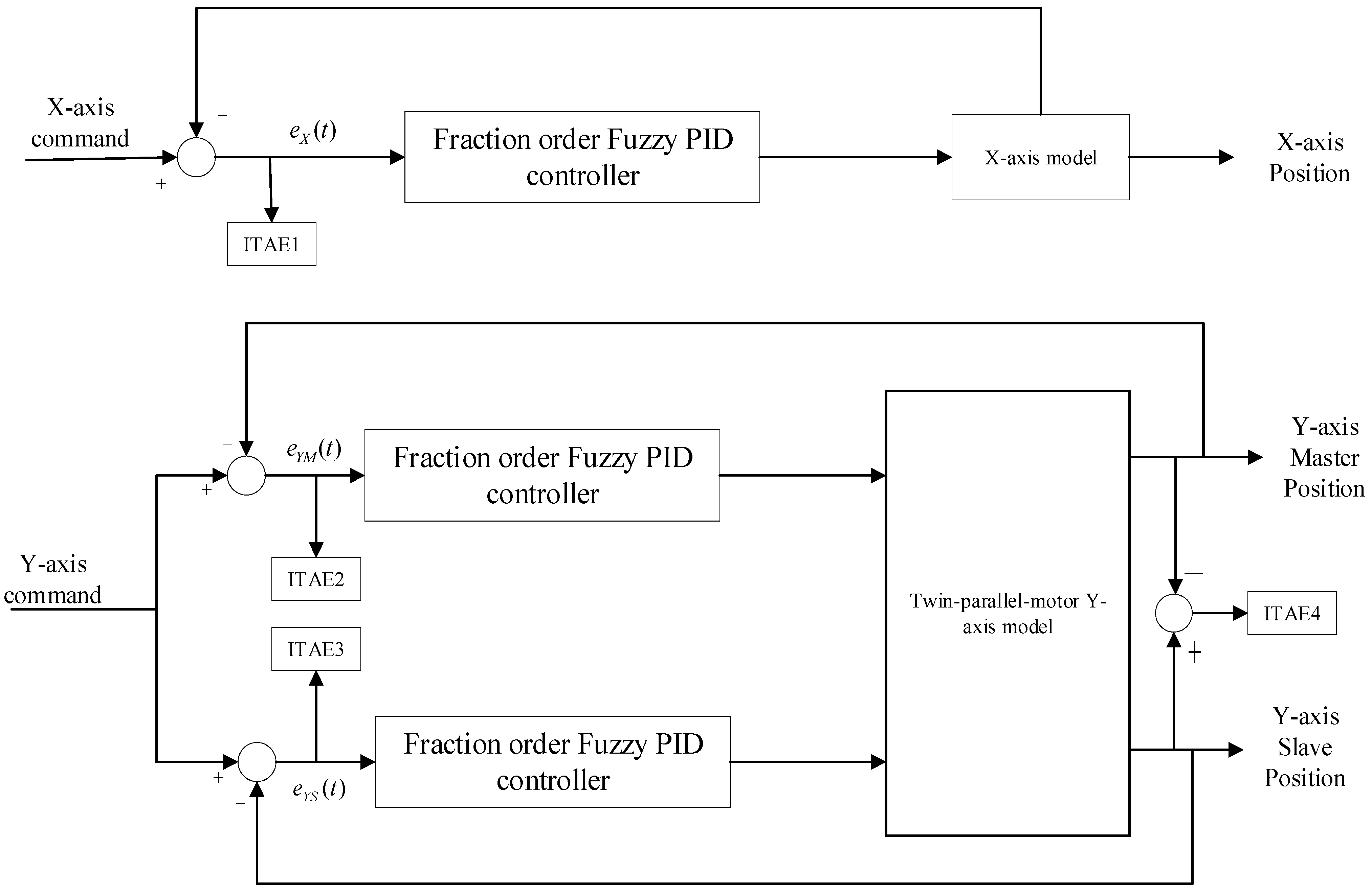
3. Control Design
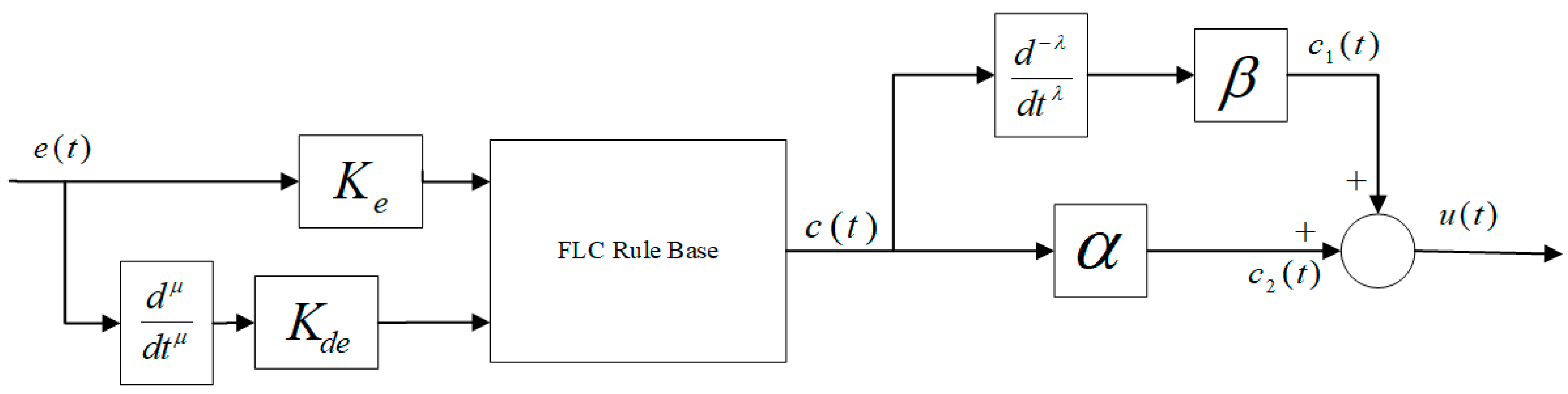
3.1. Fractional Order Fuzzy PID Controller
3.2. The Objective Function
4. Optimization Algorithms
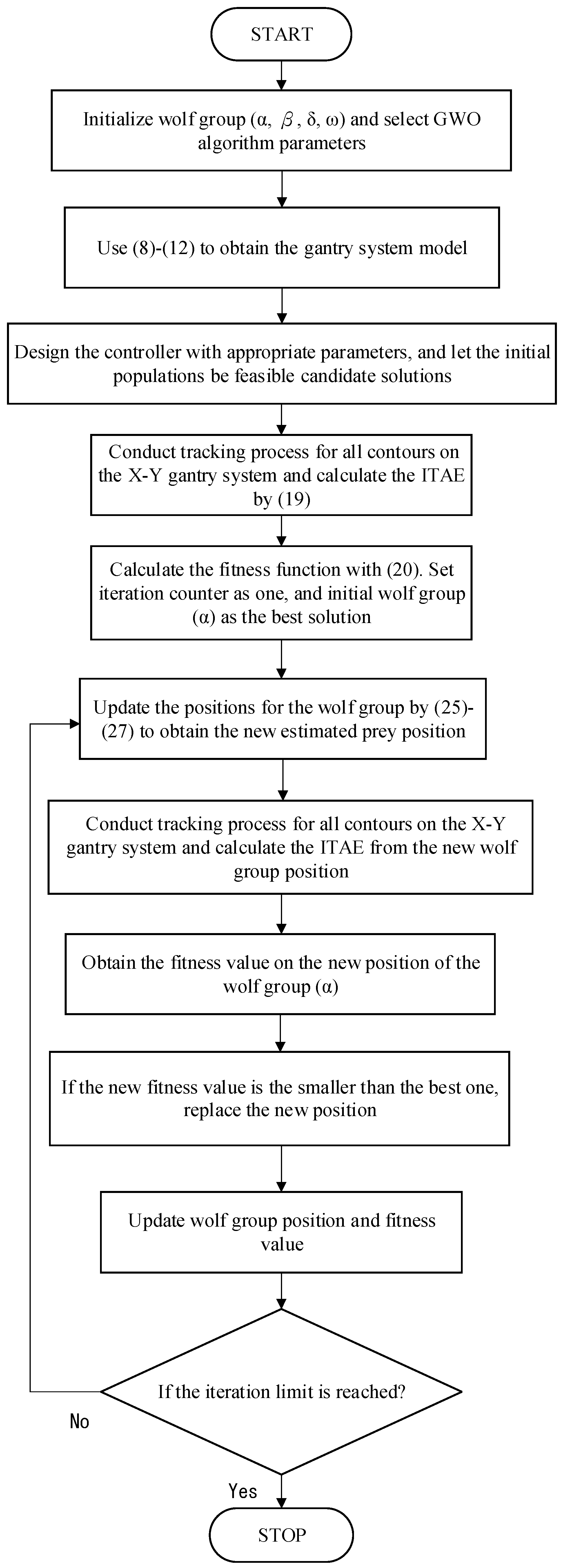
4.1. Grey Wolf Optimizer (GWO) Algorithm
- (1)
- Initialize the wolf group () and select the GWO algorithm parameters.
- (2)
- Design the appropriate parameters (, , , , , , , , , , , , , , , , , ), and let the initial populations be feasible candidate solutions.
- (3)
- Conduct the tracking process for all contours on the X–Y gantry system, calculate the ITAE, and then calculate the fitness function with (20).
- (4)
- Set the iteration counter as one and the initial wolf group () as the best solution.
- (5)
- Update the positions for the wolf group by (25)–(27) to obtain the new estimated prey position.
- (6)
- Again, perform all contour tracking for the X–Y gantry system, compute the ITAE, and calculate the fitness value according to the new wolf group () position.
- (7)
- Check whether the new fitness value is smaller than the best one. If the new fitness value is smaller, then replace the new position with it.
- (8)
- Update the wolf group position and the corresponding fitness values.
- (9)
- If the iteration limit is not reached, increase the iteration counter and return to Step (5).
4.2. Other Optimization Algorithms
5. Experimental Results
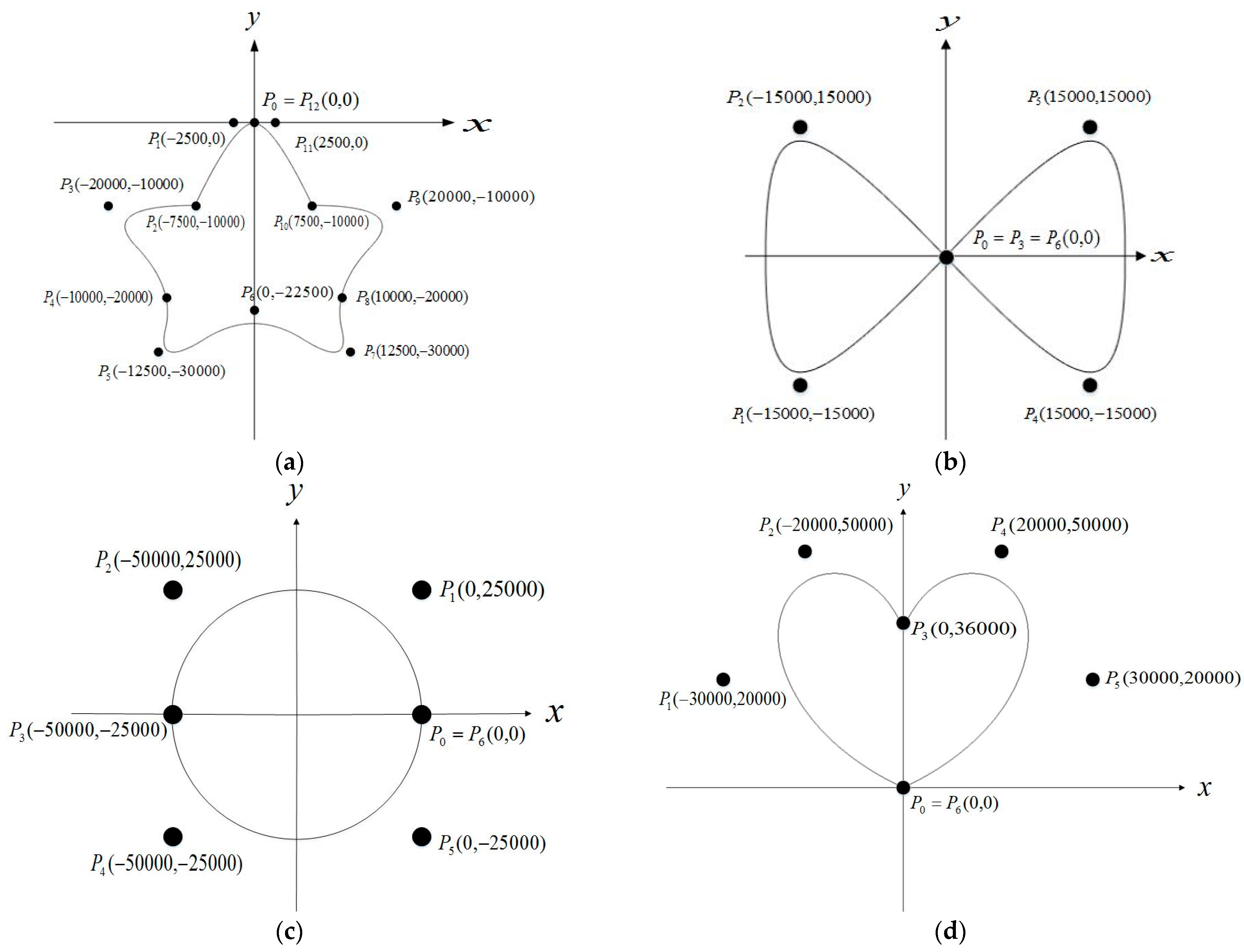
5.1. Contour Planning
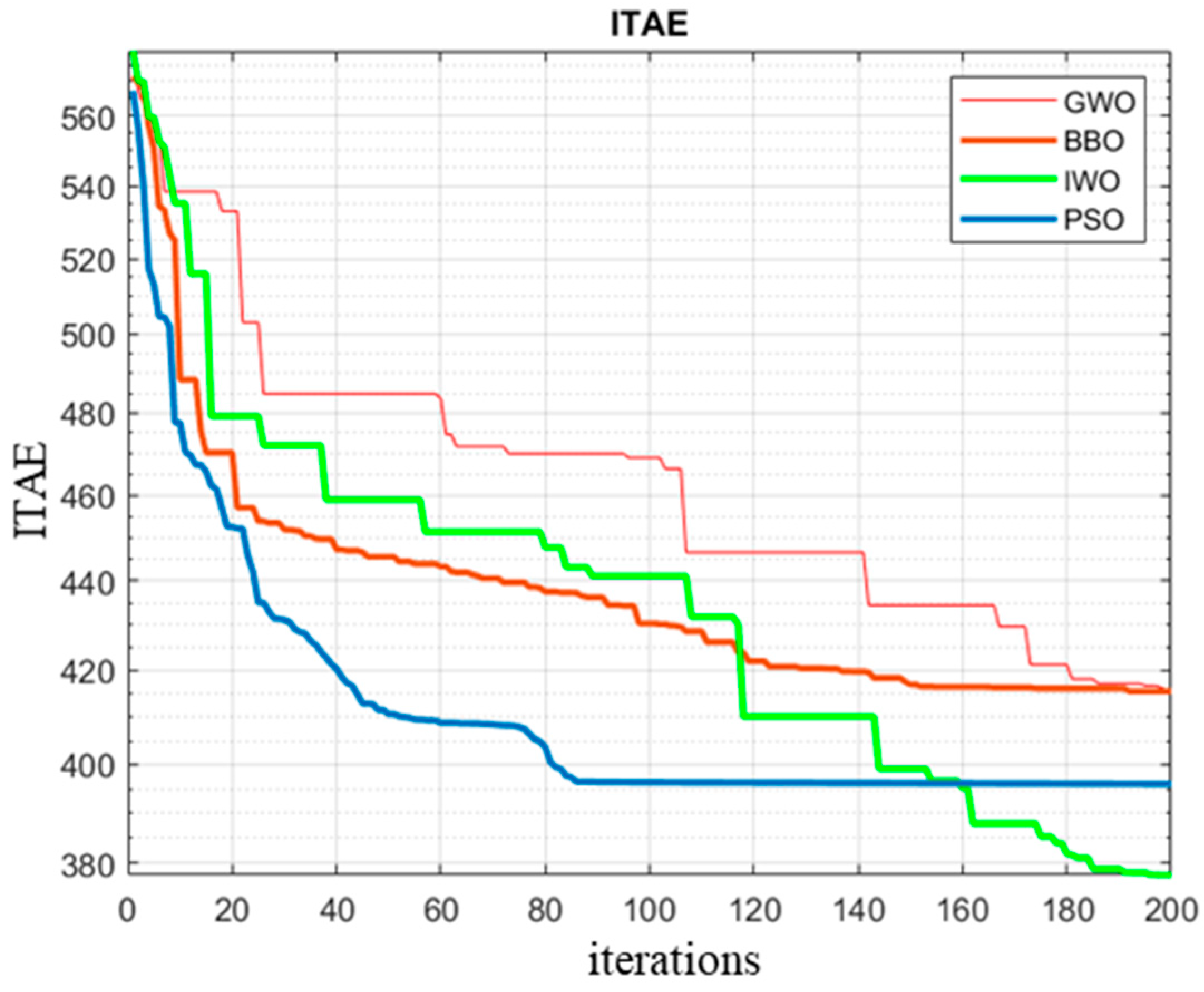
5.2. Optimization and Performance Indices
- (1)
- ATE:
- (2)
- TESD:
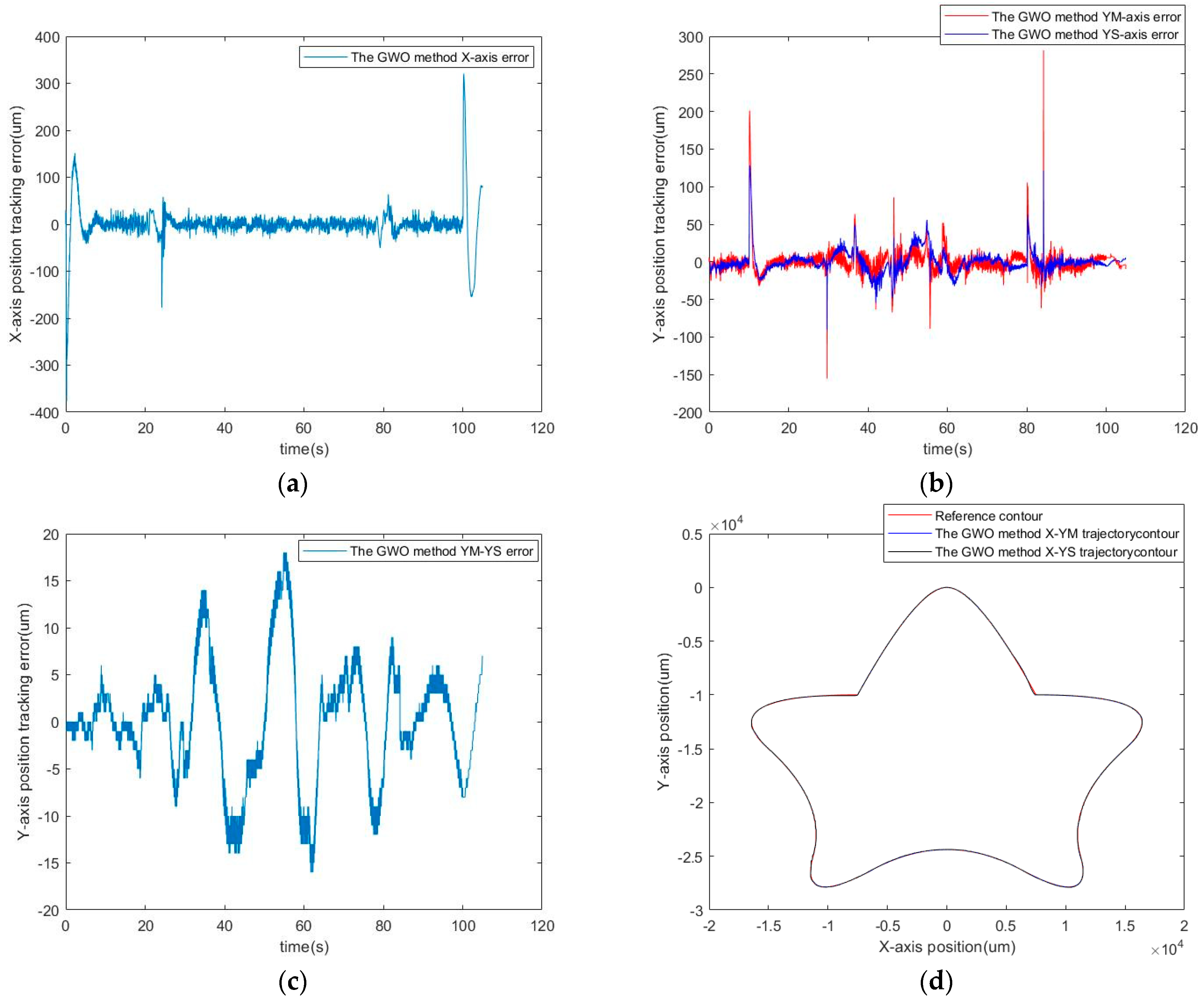
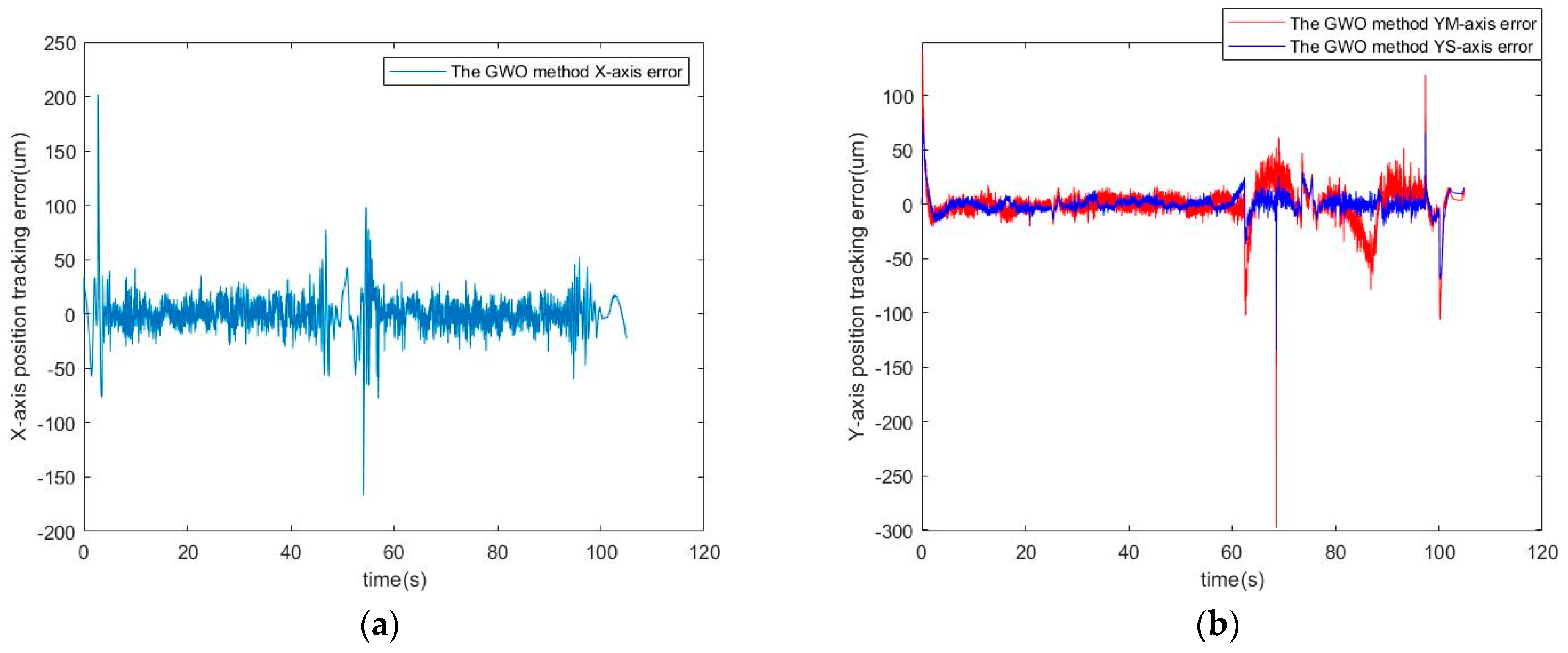
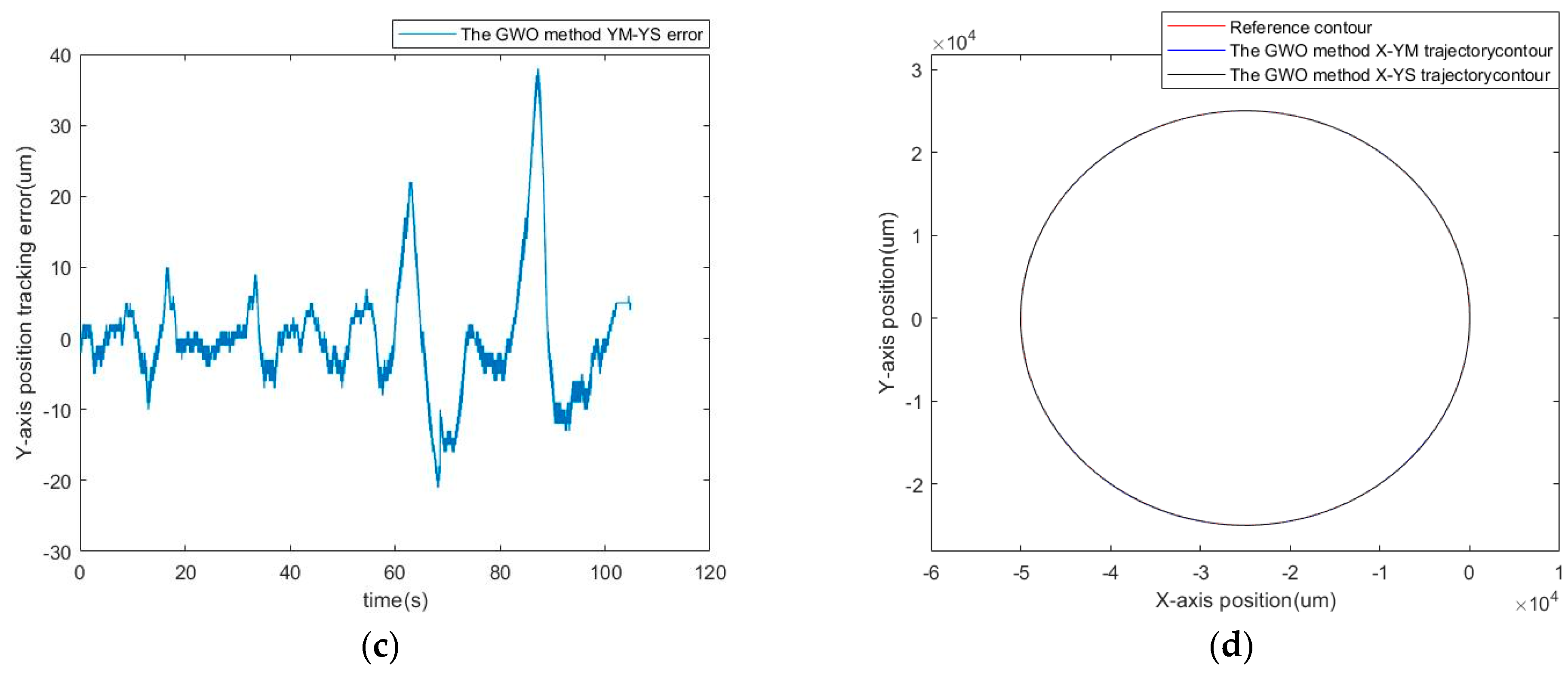
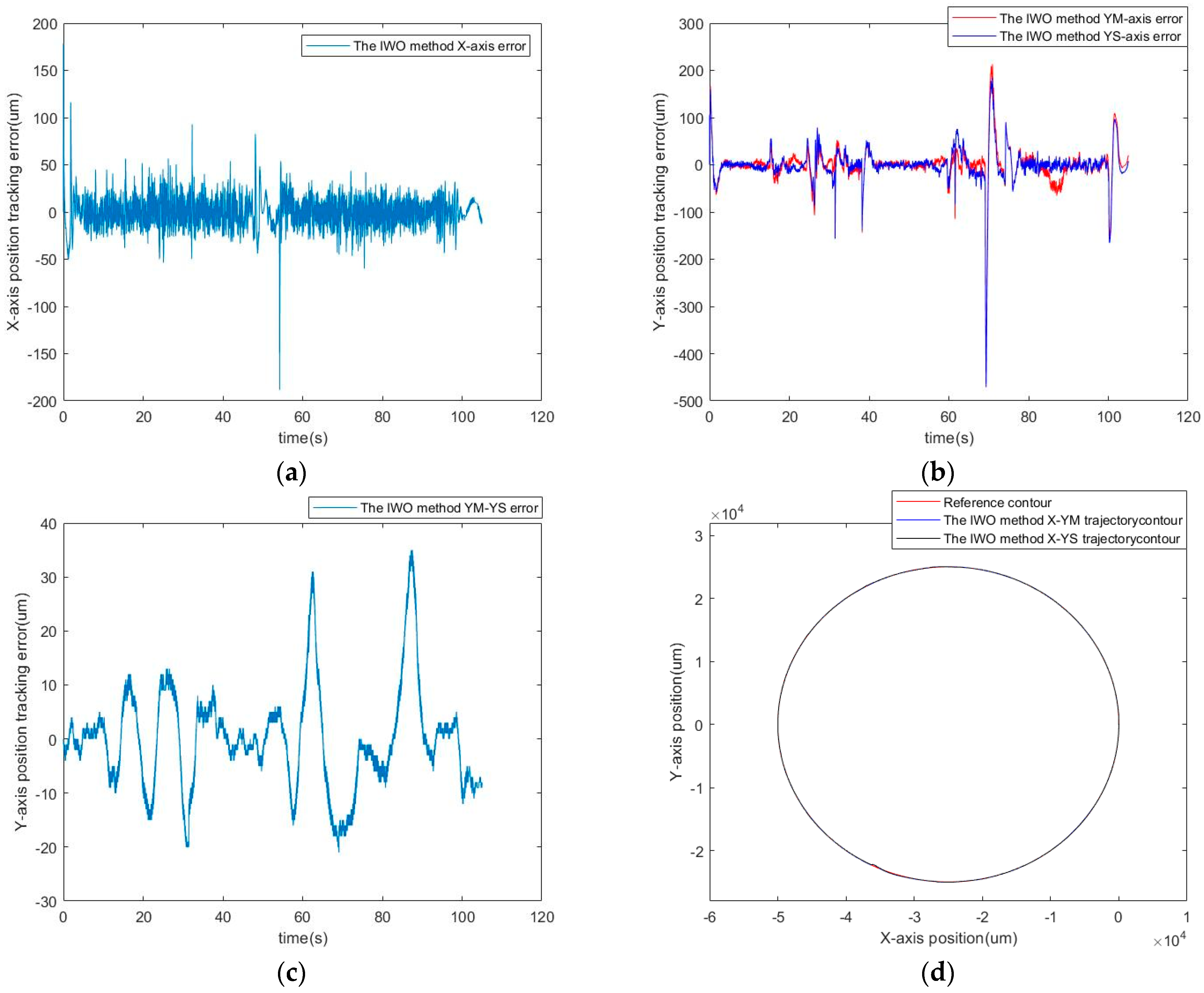
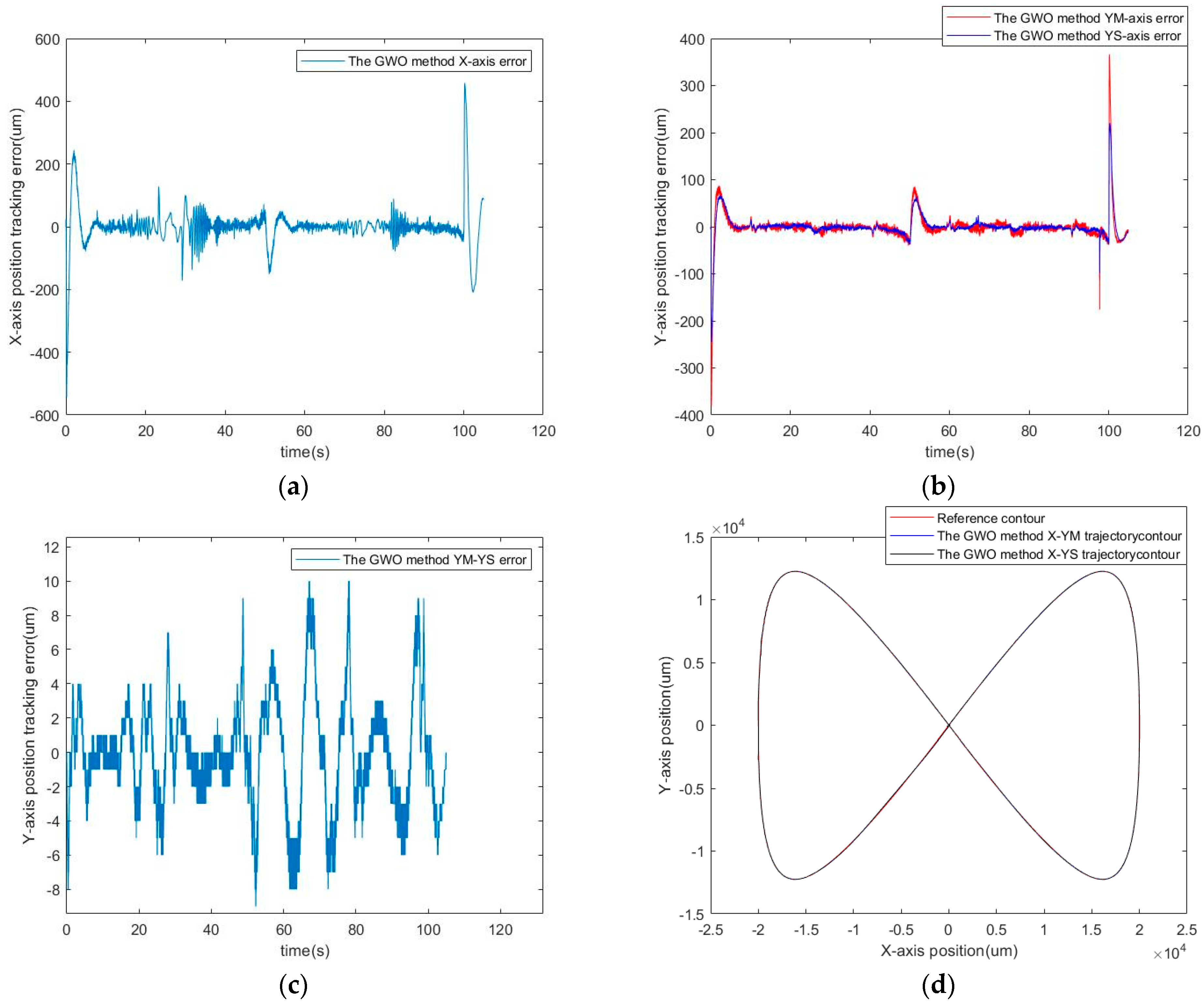
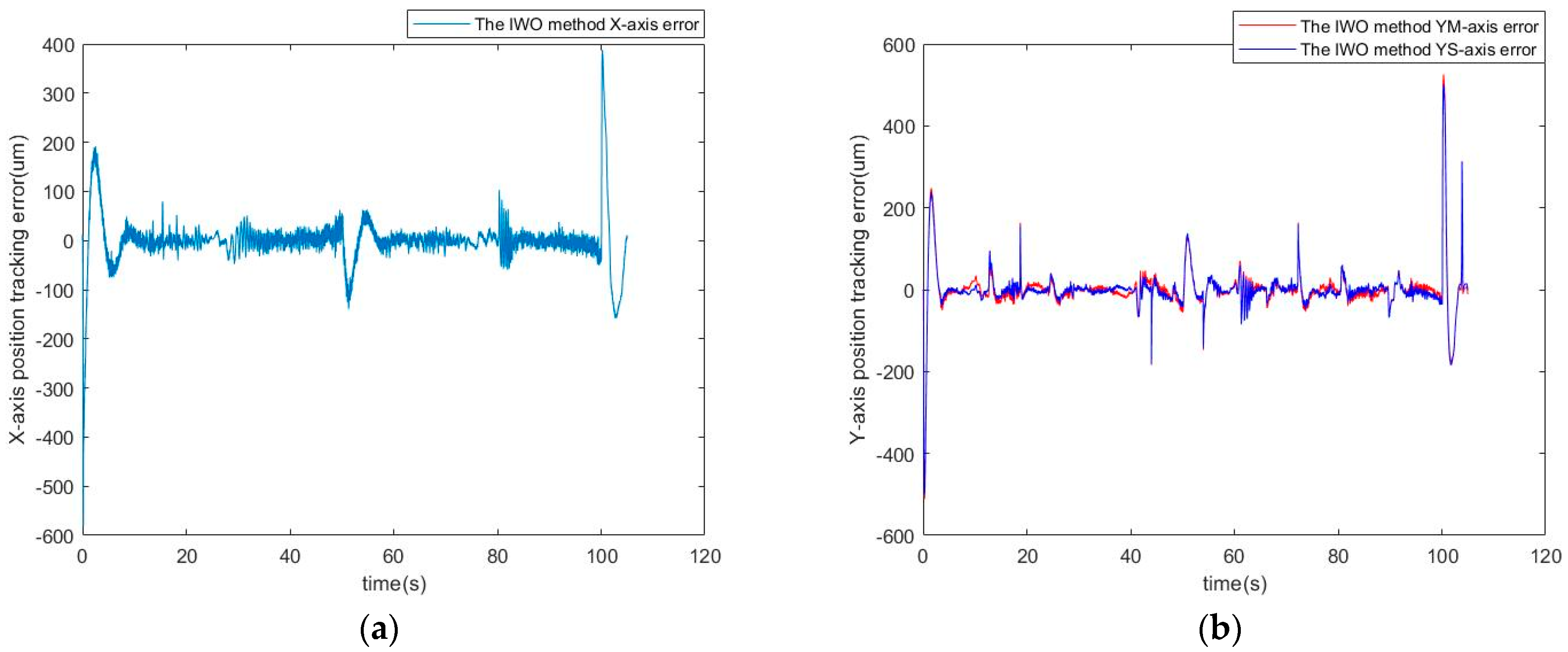
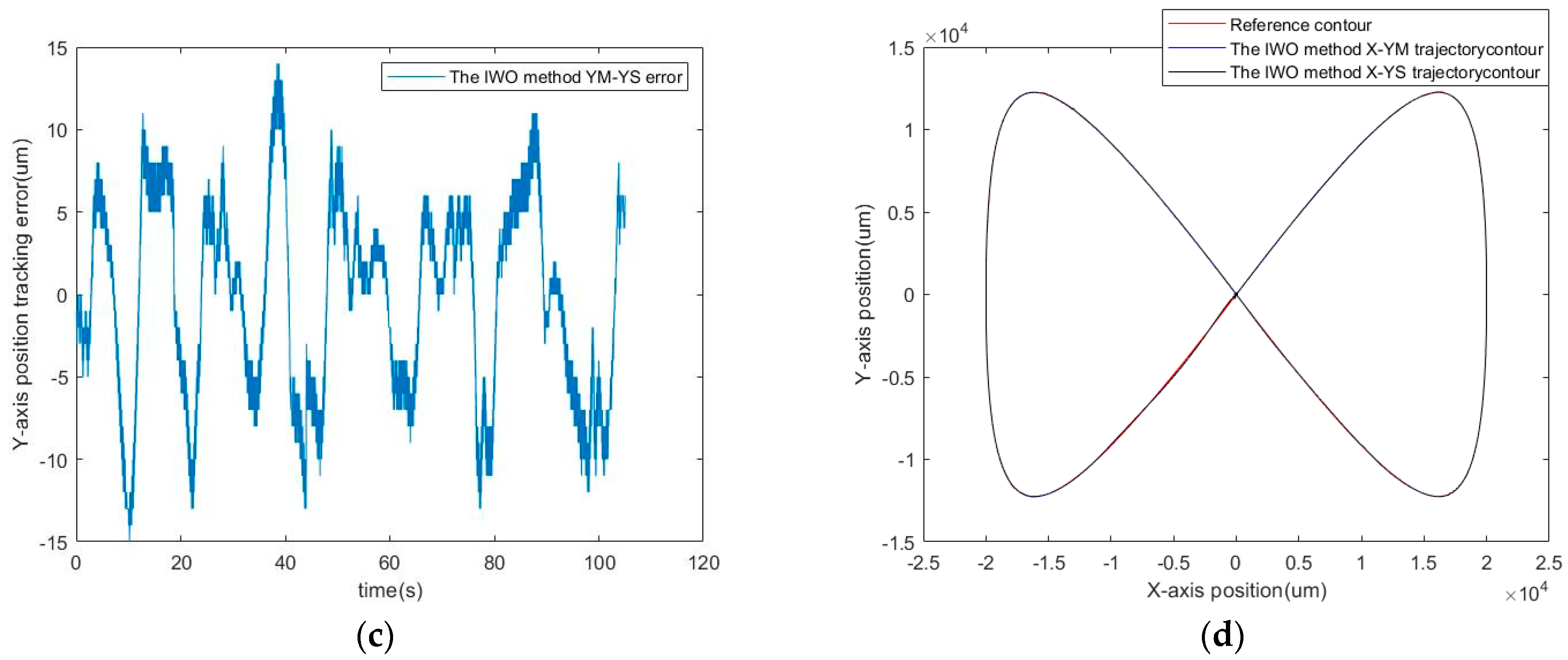
5.3. Simulation Results
5.4. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nunez, C.; Alvarez, R.; Cervantes, I. Multi-motor synchronization techniques. Int. J. Sci. Eng. Technol. Res. 2014, 3, 319–322. [Google Scholar]
- Cheng, M.H.; Chen, C.Y.; Bakhoum, E.G. Synchronization controller synthesis of multi-axis motion control. Int. J. Innov. Comput. I 2011, 7, 4395–4410. [Google Scholar]
- Koren, Y. Cross-coupled biaxial compute control for manufacturing system. J. Dyn. Syst. Meas. Control. 1980, 32, 265–272. [Google Scholar] [CrossRef]
- Lorenz, R.D.; Schmidt, P.B. Synchronized motion control for process automation. In Proceedings of the 1989 IEEE Industry Applications Annual Meeting, San Diego, CA, USA, 1–5 October 1989; pp. 1693–1698. [Google Scholar]
- Kung, Y.S. Design and implementation of a high-performance PMLSM drives using DSP chip. IEEE Trans. Ind. Electron. 2008, 55, 1341–1351. [Google Scholar] [CrossRef]
- Ting, C.S.; Chang, Y.N.; Shi, B.W.; Lieu, J.F. Adaptive backstepping control for permanent magnet linear synchronous motor servo drive. IET Electr. Power Appl. 2015, 9, 265–279. [Google Scholar] [CrossRef]
- Hsieh, M.F.; Yao, W.S.; Chiang, C.R. Modeling and synchronous control of a single-axis stage driven by dual mechanically-coupled parallel ball screw. Int. J. Adv. Manuf. Technol. 2007, 34, 933–943. [Google Scholar] [CrossRef]
- Chu, B.; Kim, S.; Hong, D.; Park, H.K.; Park, J. Optimal cross-coupled synchronizing control of dual-drive gantry system for a SMD assembly machine. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 2004, 47, 939–945. [Google Scholar] [CrossRef][Green Version]
- Lin, F.J.; Chou, P.H.; Chen, C.S.; Lin, Y.S. DSP-based cross-coupled synchronous control for dual linear motors via intelligent complementary sliding mode control. IEEE Trans. Ind. Electron. 2012, 59, 1061–1073. [Google Scholar] [CrossRef]
- Dimeas, I.; Petras, I.; Psychalinos, C. New analog implementation technique for fractional-order controller: A DC motor control. AEU-Int. J. Electron. Commun. 2017, 78, 192–200. [Google Scholar] [CrossRef]
- Said, L.A.; Radwan, A.G.; Madian, A.H.; Soliman, A.M. Fractional order oscillators based on operational transresistance amplifiers. AEU-Int. J. Electron. Commun. 2015, 69, 988–1003. [Google Scholar] [CrossRef]
- Saxena, S. Load frequency control strategy via fractional-order controller and reduced-order modeling. Int. J. Electr. Power Energy 2019, 104, 603–614. [Google Scholar] [CrossRef]
- Li, G.; Li, Y.; Chen, H.; Deng, W. Fractional-order controller for course-keeping of underactuated surface vessels based on frequency domain specification and improved particle swarm optimization Algorithm. Appl. Sci. 2022, 12, 3139. [Google Scholar] [CrossRef]
- Li, H.S.; Luo, Y.; Chen, Y.Q. A Fractional Order Proportional and Derivative (FOPD) Motion Controller: Tuning Rule and Experiments. IEEE Trans. Control Syst. Technol. 2010, 18, 516–520. [Google Scholar] [CrossRef]
- Petráš, I.; Vinagre, B. Practical application of digital fractional-order controller to temperature control to temperature control. Acta Montan. Slovaca 2002, 7, 131–137. [Google Scholar]
- Kumar, A.; Pan, S. Design of fractional order PID controller for load frequency control system with communication delay. ISA Trans. 2022, 129 Pt A, 138–149. [Google Scholar] [CrossRef]
- Swethamarai, P.; Lakshmi, P. Adaptive-Fuzzy Fractional Order PID Controller-Based Active Suspension for Vibration Control. IETE J. Res. 2022, 68, 3487–3502. [Google Scholar] [CrossRef]
- Shalaby, R.; El-Hossainy, M.; Abo-Zalam, B.; Mahmoud, T.A. Optimal fractional-order PID controller based on fractional-order actor-critic algorithm. Neural Comput. Appl. 2023, 35, 2347–2380. [Google Scholar] [CrossRef]
- Das, S.; Pan, I.; Das, S.; Gupta, A. A novel fractional order fuzzy PID controller and its optimal time domain tuning based on integral performance indices. Eng. Appl. Artif. Intell. 2012, 25, 430–442. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Joint Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Mehrabian, A.R.; Lucas, C. A Novel Numerical Optimization Algorithm Inspired from Weed Colonization. Ecol. Inform. 2006, 1, 355–366. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-Based Optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Cao, J.Y.; Cao, B.G. Design of Fractional Order Controllers Based on Particle Swarm Optimization. In Proceedings of the 2006 IEEE Conference on Industrial Electronics and Applications, Singapore, 24–26 May 2006. [Google Scholar]
- Kommula, B.N.; Kota, V.R. Design of MFA-PSO based fractional order PID controller for effective torque controlled BLDC motor. Sustain. Energy Technol. Assess. 2022, 49, 101644. [Google Scholar]
- Obaid, B.A.; Saleh, A.L.; Kadhim, A.K. Resolving of optimal fractional PID controller for DC motor drive based on anti-windup by invasive weed optimization technique. Indones. J. Electr. Eng. Comput. Sci. 2019, 15, 95–103. [Google Scholar] [CrossRef]
- Verma, S.K.; Yadav, S.; Nagar, S.K. Optimization of Fractional Order PID Controller Using Grey Wolf Optimizer. J. Control. Autom. Electr. Syst. 2017, 28, 314–322. [Google Scholar] [CrossRef]
- Yeşil, E.; Güzelkaya, M.; Eksin, İ. Self tuning fuzzy PID type load and frequency controller. Energy Convers. Manag. 2004, 45, 377–390. [Google Scholar] [CrossRef]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F. Frequency-band complex noninteger differentiator: Characterization and synthesis. IEEE Trans. Circuits Syst. L Fundam. Theory Appl. 2000, 47, 25–39. [Google Scholar] [CrossRef]
- Noshadi, A.; Shi, J.; Lee, W.S.; Shi, P.; Kalam, A. Optimal PID-type fuzzy logic controller for a multi-input multi-output active magnetic bearing system. Neural Comput. Appl. 2016, 27, 2031–2046. [Google Scholar] [CrossRef]
- Pieg, L.; Tiller, W. The NURBS Books, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Chen, S.Y.; Lai, Y.H.; Lu, H.T. Contours Planning and Visual Servo Control of XXY Positioning System Using NURBS Interpolation Approach. Invent. J. Res. Technol. Eng. Manag. 2016, 1, 16–23. [Google Scholar]
- Gopi, M.; Manohar, S. A Unified Architecture for the Computation of B-Spline Curves and Surfaces. IEEE Trans. Parallel Distrib. Syst. 1997, 8, 1275–1287. [Google Scholar] [CrossRef]


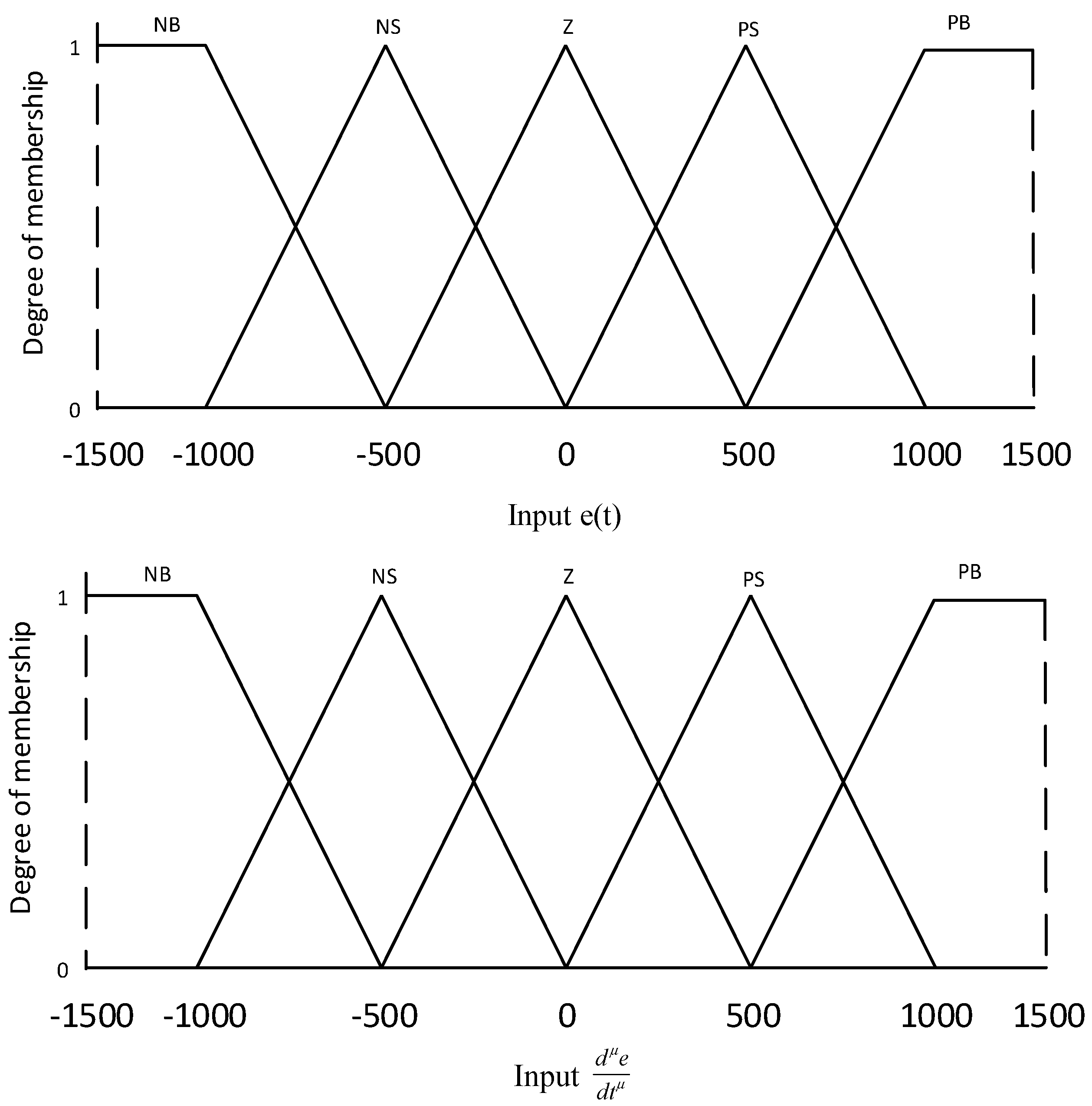
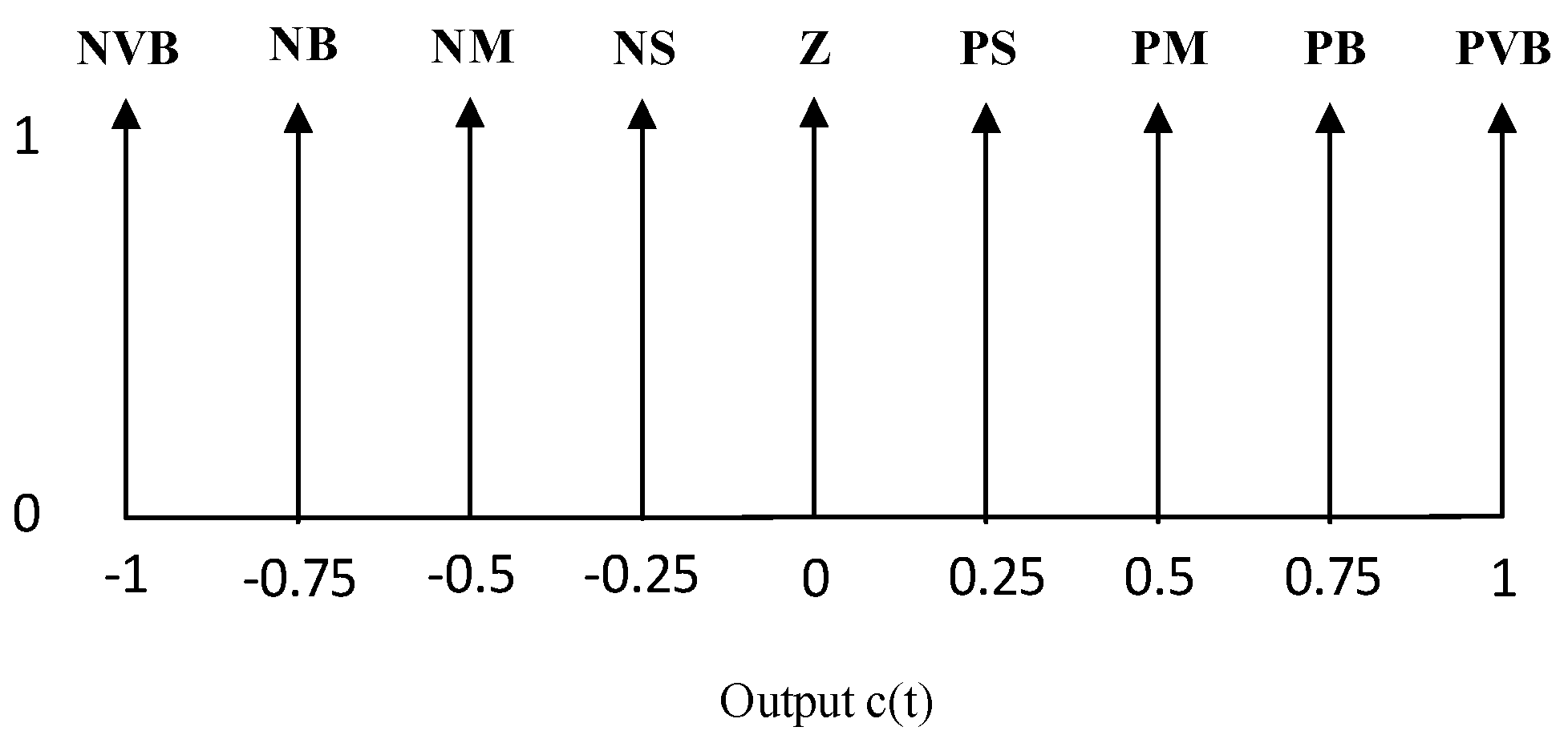



| c(t) | e(t) | |||||
|---|---|---|---|---|---|---|
| NB | NS | Z | PS | PB | ||
| NB | NVB | NB | NM | NS | Z | |
| NS | NB | NM | NS | Z | PS | |
| Z | NM | NS | Z | PS | PM | |
| PS | NS | Z | PS | PM | PB | |
| PB | Z | PS | PM | PB | PVB | |
| Trajectory Type | NURBS Parameters |
|---|---|
| Circle | d = 2, P = [(0,0),(0, 25,000), (−50,000, 25,000),(−50,000, 0), (−50,000, −25,000), (0, −25,000), (0, 0)], k = [0, 0, 0, 0.25, 0.5, 0.5, 0.75, 1, 1, 1], w = [1, 0.5, 0.5, 1, 0.5, 0.5, 1] |
| Heart | d = 2, P = [(0,0), (−30,000, 20,000), (−20,000, 50,000), (0, 36,000), (20,000, 50,000), (30,000, 10,000), (0,0)], k = [0, 0, 0, 0.25, 0.5, 0.5, 0.75, 1, 1, 1], w = [1, 1, 1, 1, 1, 1, 1] |
| Bow | d = 2, P = [(0, 0), (−15,000, −15,000), (−15,000, 1.5), (0, 0), (15,000, −15,000), (15,000, 150,000), (0, 0)], k = [0, 0, 0, 0.25, 0.5, 0.5, 0.75, 1, 1, 1], w = [1, 2.5, 2.5, 1, 2.5, 2.5, 1] |
| Star | d = 2, P = [(0, 30,000), (−2500, −30,000), (−7500, 20,000), (−20,000, 20,000), (−1000, 10,000), (−12,500, 0), (0, 7500),(12,500, 0),(10,000, 10,000), (20,000, 20,000), (7500, 20,000),(2500, 30,000),(0, 30,000)], k = [0, 0, 0, 0.1, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.8, 1, 1, 1], w = [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] |
| Optimization Algorithm | Parameters |
|---|---|
| PSO | population size: leaning parameters: , upper/lower bounds of the random velocity weight: , upper/lower bound of the position: , |
| IWO | population size: maximum group size = 30 nonlinear harmonic parameter initial standard deviation = 0.5 final standard deviation = 0.001 upper/lower bound of weed seeds: / |
| GWO | population size: upper/lower bound of wolf group(alpha): |
| BBO | number of habitats: max/min migration rates: , = 0.1 upper/lower bound of habitat species: |
| value | ||||||
| PSO | 1.8931 | 0.1097 | 0.4520 | 1.5940 | 1.9000 | 0.9726 |
| IWO | 1.8237 | 0.2757 | 1.8330 | 1.6256 | 1.4351 | 1.1889 |
| BBO | 1.8980 | 0.1006 | 1.8914 | 1.6927 | 1.9000 | 0.6967 |
| GWO | 1.3132 | 0.1285 | 1.8970 | 1.6103 | 1.8326 | 1.0344 |
| value | ||||||
| PSO | 0.4488 | 0.1000 | 1.9000 | 1.4877 | 1.9000 | 0.8245 |
| IWO | 1.8866 | 0.1012 | 1.6841 | 1.5311 | 1.8837 | 0.7184 |
| BBO | 1.7297 | 0.4819 | 0.7888 | 1.4647 | 1.6594 | 0.8007 |
| GWO | 1.8825 | 0.1085 | 1.4989 | 1.3023 | 1.8645 | 1.4217 |
| value | ||||||
| PSO | 1.2828 | 0.142 | 1.9000 | 1.4889 | 1.4156 | 0.6118 |
| IWO | 1.8302 | 0.1000 | 1.7325 | 1.5320 | 1.9000 | 0.7267 |
| BBO | 1.8914 | 0.4146 | 1.1917 | 1.4872 | 1.3578 | 0.6606 |
| GWO | 1.8992 | 0.2610 | 1.7539 | 1.3435 | 1.8493 | 1.3241 |
| Method | ) | ) | ITAE |
|---|---|---|---|
| Circle | |||
| PSO | 1.4719 | 3.2174 | 728.4400 |
| IWO | 0.9100 | 1.6635 | 689.4438 |
| BBO | 1.5367 | 3.0456 | 732.9247 |
| GWO | 1.1919 | 1.4536 | 732.1176 |
| Heart | |||
| PSO | 1.3767 | 7.3135 | 687.1533 |
| IWO | 1.2314 | 5.5600 | 662.0899 |
| BBO | 1.4962 | 7.7701 | 706.2485 |
| GWO | 1.2854 | 4.7161 | 716.1556 |
| Star | |||
| PSO | 2.9381 | 9.7067 | 758.2886 |
| IWO | 2.9195 | 6.0844 | 732.7888 |
| BBO | 2.9834 | 9.8334 | 822.2761 |
| GWO | 2.8224 | 6.8502 | 800.8768 |
| Bow | |||
| PSO | 6.2185 | 30.6246 | 726.3240 |
| IWO | 2.0803 | 12.5113 | 686.4565 |
| BBO | 5.9139 | 27.0573 | 778.0170 |
| GWO | 5.0548 | 18.6534 | 795.2960 |
| Average | |||
| PSO | 3.0013 | 12.7156 | 725.0515 |
| IWO | 1.7852 | 6.4548 | 692.6948 |
| BBO | 2.9826 | 11.9266 | 759.8666 |
| GWO | 2.5886 | 7.9183 | 761.1115 |
| Method | ATE () | TESD ( ) | ITAE |
|---|---|---|---|
| Circle | |||
| PSO | 12.33468 | 19.06461 | 1000.13697 |
| IWO | 22.55877 | 39.85242 | 1018.96457 |
| BBO | 13.65512 | 15.22419 | 1009.078 |
| GWO | 7.93084 | 8.69547 | 998.86251 |
| Heart | |||
| PSO | 17.05340 | 23.22570 | 1011.88779 |
| IWO | 23.88164 | 36.07943 | 1015.39364 |
| BBO | 18.09240 | 27.08182 | 1008.25875 |
| GWO | 9.09414 | 16.49567 | 994.75943 |
| Star | |||
| PSO | 19.17965 | 21.18270 | 997.62259 |
| IWO | 23.93769 | 29.72738 | 1007.70703 |
| BBO | 21.82199 | 24.02363 | 1009.45364 |
| GWO | 14.13845 | 15.14002 | 993.72111 |
| Bow contour | |||
| PSO | 16.95719 | 28.80572 | 1018.65117 |
| IWO | 23.79299 | 42.70955 | 1018.99118 |
| BBO | 23.44690 | 39.53237 | 1014.40448 |
| GWO | 14.36346 | 24.53757 | 976.54349 |
| Average | |||
| PSO | 16.38123 | 23.06968 | 1007.07463 |
| IWO | 23.54277 | 37.092195 | 1015.26410 |
| BBO | 19.25410 | 26.46550 | 1010.29870 |
| GWO | 11.38172 | 16.21718 | 990.97163 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, W.-L.; Chen, S.-H.; Kao, C.-Y. Fractional-Order Fuzzy PID Controller with Evolutionary Computation for an Effective Synchronized Gantry System. Algorithms 2024, 17, 58. https://doi.org/10.3390/a17020058
Mao W-L, Chen S-H, Kao C-Y. Fractional-Order Fuzzy PID Controller with Evolutionary Computation for an Effective Synchronized Gantry System. Algorithms. 2024; 17(2):58. https://doi.org/10.3390/a17020058
Chicago/Turabian StyleMao, Wei-Lung, Sung-Hua Chen, and Chun-Yu Kao. 2024. "Fractional-Order Fuzzy PID Controller with Evolutionary Computation for an Effective Synchronized Gantry System" Algorithms 17, no. 2: 58. https://doi.org/10.3390/a17020058
APA StyleMao, W.-L., Chen, S.-H., & Kao, C.-Y. (2024). Fractional-Order Fuzzy PID Controller with Evolutionary Computation for an Effective Synchronized Gantry System. Algorithms, 17(2), 58. https://doi.org/10.3390/a17020058







