A Simulated Annealing Algorithm for the Generalized Quadratic Assignment Problem
Abstract
1. Introduction
- SA, a single solution algorithm, can find “good” solutions quickly compared to population-based algorithms for certain COPs (Delahaye et al. [24]). As indicated in Cordeau et al. [9] and in Silva et al. [14], constructing/finding a population of solutions, especially for tightly constrained GQAP instances, can be computationally costly.
2. Mathematical Models
2.1. Mathematical Programming Models
- One or more facilities may be assigned to each location such that the capacities of the locations are not exceeded.
- The objective is to minimize the sum of the assignment and the transportation costs. The assignment costs consist of the cost of installing each facility (e.g., machine) to each location, and the transportation costs consist of the costs of moving materials processed on the machines between the machines.
- The input data are deterministic and known. That is, the number of units of materials transported between facilities i and j (fij), the distances between locations k and l (dkl), the space requirement of each facility i (ri), the capacity of each location k (Ck), the costs of assigning or installing facility i to location k (aik), and the unit cost per distance unit of transporting materials between each pair of facility i at location k and facility j at location l (cijkl) are deterministic and known.
2.2. Combinatorial Optimization Problem Model
2.3. Illustrative Example
3. Methods
3.1. Construction Algorithm
- The additional notation used in CA are as follows.
- Cap(k) = the remaining capacity of location k.
- SetOfFac = vector of facilities sorted in descending order based on ri.
- SetOfFac(p) = facility in the p-position of the vector SetOfFac.
- s(i) = location assigned to facility i.
- Remove(i) = function used to remove i from the vector SetOfFac.
| Algorithm 1: CA(Ck, ri) | |||
| 1: Initialize Ck and ri | |||
| 2: Construct SetOfFac by sorting facilities in descending order based on ri (break ties by lower i) | |||
| 3: k ← 1 //k is the location index for vector Ck | |||
| 4: while k ≤ N and SetOfFac ≠ {} do //{} is the empty set | |||
| 5: | Cap(k) ← Ck | ||
| 6: | p ← 1 //p is the position index in SetOfFac | ||
| 7: | repeat | ||
| 8: | i ← SetOfFac(p) // i is the facility number in position p in SetOfFac | ||
| 9: | if ri ≤ Cap(k) then | ||
| 10: | s(i) ← k | ||
| 11: | Cap(k) ← Cap(k) – ri | ||
| 12: | Remove(i) // Remove facility i from SetOfFac | ||
| 13: | else | ||
| 14: | p ← p + 1 | ||
| 15: | end if | ||
| 16: | until Cap(k) < ri* do // i* = SetOfFac(Last) (i.e., facility in last position in SetOfFac) | ||
| 17: | k ← k + 1 | ||
| 18: end while | |||
| 19: return S // S = {s(1), s(2), …, s(M)} | |||
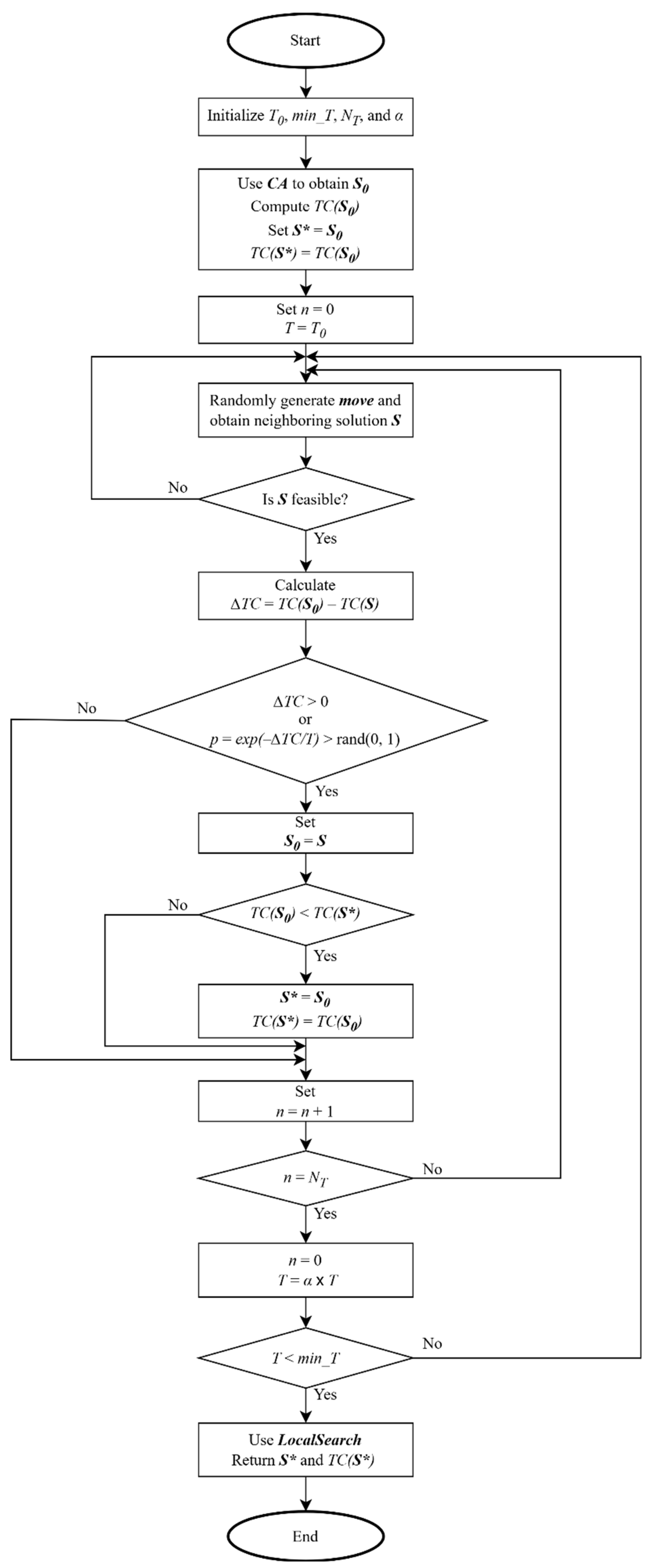
3.2. Simulated Annealing Algorithm
- Shift move consists of changing the assigned location of a facility to a different location. For example, in a solution S0, an assignment which assigns facility i to location k (i.e., s(i) = k) is changed where facility i is reassigned to a different location k’ (i.e., s(i) = k’) which gives the neighboring solution S;
- Swap move consists of exchanging the assigned locations of two facilities assigned to different locations (e.g., in a solution S0, s(i) = k and s(j) = l are changed to s(i) = l and s(j) = k which gives the neighboring solution S).
- Given solution S* and cost of solution TC(S*);
- Find all feasible solutions in the Shift and Swap neighborhoods of S*;
- Pick the best feasible solution S with respect to total cost, TC(S). If TC(S) < TC(S*), set S* = S and TC(S*) = TC(S), and go to Step 2. Else, terminate algorithm and return local optimum S* and its cost TC(S*).
- ∆TC = TC(S0) − TC(S)
- T0 = initial temperature.
- α = cooling ratio where 0 < α < 1. Consider α ≥ 0.90 for slow reduction of temperature.
- T = current temperature where temperature is reduced using the cooling scheduling given in Equation (12).
- min_T = minimum temperature used in stopping criterion. Stop if T > min_T.
- NT = number of iterations at each temperature T.
- p = probability of accepting a worse (non-improving) neighboring solution S. See Equation (11).
- p′= probability of accepting non-improving solution S at initial temperature T.
- rand(0, 1) = a random real number between zero and one.
- LocalSearch(S*, TC(S*)) = function used to perform steepest descent algorithm.
| Algorithm 2: SA(T0, min_T, NT, α) | ||||
| 1: Initialize T0, min_T, NT, and α | ||||
| 2: S0 ← CA(Ck, ri) | ||||
| 3: Compute TC(S0) using Objective function (9) of COP model | ||||
| 4: S* ← S0, TC(S*) ← TC(S0) // update best solution S* and its cost | ||||
| 5: n ← 0, T ← T0 //initialize iteration counter n at each temperature and temperature T | ||||
| 6: while T ≥ min_T do | ||||
| 7: | Randomly generate move and obtain neighboring solution S | |||
| 8: | Check if S is feasible using Constraint (10) of COP model | |||
| 9: | if S is feasible then | |||
| 10: | ∆TC ← TC(S0) – TC(S) | |||
| 11: | if ∆TC > 0 or p = exp(−∆TC/T) > rand(0, 1) then | |||
| 12: | S0 ← S | |||
| 13: | if TC(S0) < TC(S*) | |||
| 14: | S* ← S0, TC(S*) ← TC(S0) // update best solution S* and its cost | |||
| 15: | end if | |||
| 16: | end if | |||
| 17: | n ← n + 1 | |||
| 18: | if n = Nt then | |||
| 19: | n ← 0, T ← α×T // update iteration counter n and temperature T | |||
| 20: | end if | |||
| 21: | end if | |||
| 22: end while | ||||
| 23: S* ← LocalSearch(S*, TC(S*)) | ||||
| 24: return S*and TC(S*) // return best solution S* and its costs | ||||
4. Computational Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Öncan, T. A Survey of the Generalized Assignment Problem and Its Applications. INFOR Inf. Syst. Oper. Res. 2007, 45, 123–141. [Google Scholar] [CrossRef]
- Lee, C.G.; Ma, Z. The generalized quadratic assignment problem. In Research Report, Department of Mechanical and Industrial Engineering; University of Toronto: Toronto, ON, Canada, 2004. [Google Scholar]
- Ünal, Y.Z.; Uysal, Ö. A new mixed integer programming model for curriculum balancing: Application to a Turkish university. Eur. J. Oper. Res. 2014, 238, 339–347. [Google Scholar] [CrossRef]
- Guignard, M. Strong RLT1 bounds from decomposable Lagrangean relaxation for some quadratic 0–1 optimization problems with linear constraints. Ann. Oper. Res. 2020, 286, 173–200. [Google Scholar] [CrossRef]
- Hahn, P.M.; Kim, B.J.; Guignard, M.; Smith, J.M.; Zhu, Y.R. An algorithm for the generalized quadratic assignment problem. Comput. Optim. Appl. 2008, 40, 351–372. [Google Scholar] [CrossRef][Green Version]
- Pessoa, A.A.; Hahn, P.M.; Guignard, M.; Zhu, Y.R. Algorithms for the generalized quadratic assignment problem combining Lagrangean decomposition and the Reformulation-Linearization Technique. Eur. J. Oper. Res. 2010, 206, 54–63. [Google Scholar] [CrossRef]
- Fathollahi-Fard, A.M.; Wong, K.Y.; Aljuaid, M. An efficient adaptive large neighborhood search algorithm based on heuristics and reformulations for the generalized quadratic assignment problem. Eng. Appl. Artif. Intell. 2023, 126, 106802. [Google Scholar] [CrossRef]
- Sahni, S.; Gonzalez, T. P-complete approximation problems. J. ACM 1976, 23, 555–565. [Google Scholar] [CrossRef]
- Cordeau, J.F.; Gaudioso, M.; Laporte, G.; Moccia, L. A memetic heuristic for the generalized quadratic assignment problem. INFORMS J. Comput. 2006, 18, 433–443. [Google Scholar] [CrossRef]
- Zou, D.; Gao, L.; Li, S.; Wu, J.; Wang, X. A novel global harmony search algorithm for task assignment problem. J. Syst. Softw. 2010, 83, 1678–1688. [Google Scholar] [CrossRef]
- Mateus, G.R.; Resende, M.G.; Silva, R.M. GRASP with path-relinking for the generalized quadratic assignment problem. J. Heuristics 2011, 17, 527–565. [Google Scholar] [CrossRef]
- McKendall, A.; Li, C. A tabu search heuristic for a generalized quadratic assignment problem. J. Ind. Prod. Eng. 2017, 34, 221–231. [Google Scholar] [CrossRef]
- Mostafa, R. Metaheuristics for the Generalized Quadratic Assignment Problem. Master’s Thesis, West Virginia University, Morgantown, WV, USA, July 2020. Available online: https://researchrepository.wvu.edu/etd/7717 (accessed on 27 October 2024).
- Silva, A.; Coelho, L.C.; Darvish, M. Quadratic assignment problem variants: A survey and an effective parallel memetic iterated tabu search. Eur. J. Oper. Res. 2021, 292, 1066–1084. [Google Scholar] [CrossRef]
- Greistorfer, P.; Staněk, R.; Maniezzo, V. A Tabu Search Matheuristic for the Generalized Quadratic Assignment Problem. In Metaheuristics International Conference; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Kirpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- McKendall, A.R.; Shang, J.; Kuppusamy, S. Simulated annealing heuristics for the dynamic facility layout problem. Comput. Oper. Res. 2006, 33, 2431–2444. [Google Scholar] [CrossRef]
- Huo, L.; Zhu, J.; Wu, G.; Li, Z. A novel simulated annealing based strategy for balanced UAV task assignment and path planning. Sensors 2020, 20, 4769. [Google Scholar] [CrossRef]
- Dai, Z.; Zhang, Z.; Chen, M. The home health care location-routing problem with a mixed fleet and battery swapping stations using a competitive simulated annealing algorithm. Expert Syst. Appl. 2023, 228, 120374. [Google Scholar] [CrossRef]
- Tole, K.; Moqa, R.; Zheng, J.; He, K. A simulated annealing approach for the circle bin packing problem with rectangular items. Comput. Ind. Eng. 2023, 176, 109004. [Google Scholar] [CrossRef]
- Ghotb, S.; Sowlati, T.; Mortyn, J. Scheduling of log logistics using a metaheuristic approach. Expert Syst. Appl. 2024, 238, 122008. [Google Scholar] [CrossRef]
- van Laarhoven, P.J.M.; Aarts, E.H.L. Simulated Annealing: Theory and Applications, 1st ed.; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1987. [Google Scholar]
- Siarry, P. Simulated Annealing. In Metaheuristics; Siarry, P., Ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 19–50. [Google Scholar]
- Delahaye, D.; Chaimatanan, S.; Mongeau, M. Simulated Annealing: From Basics to Applications. In Handbook of Metaheuristics; Gendreau, M., Potvin, J.Y., Eds.; International Series in Operations Research & Management Science; Springer International Publishing: Cham, Switzerland, 2019; Volume 272, pp. 1–35. [Google Scholar] [CrossRef]
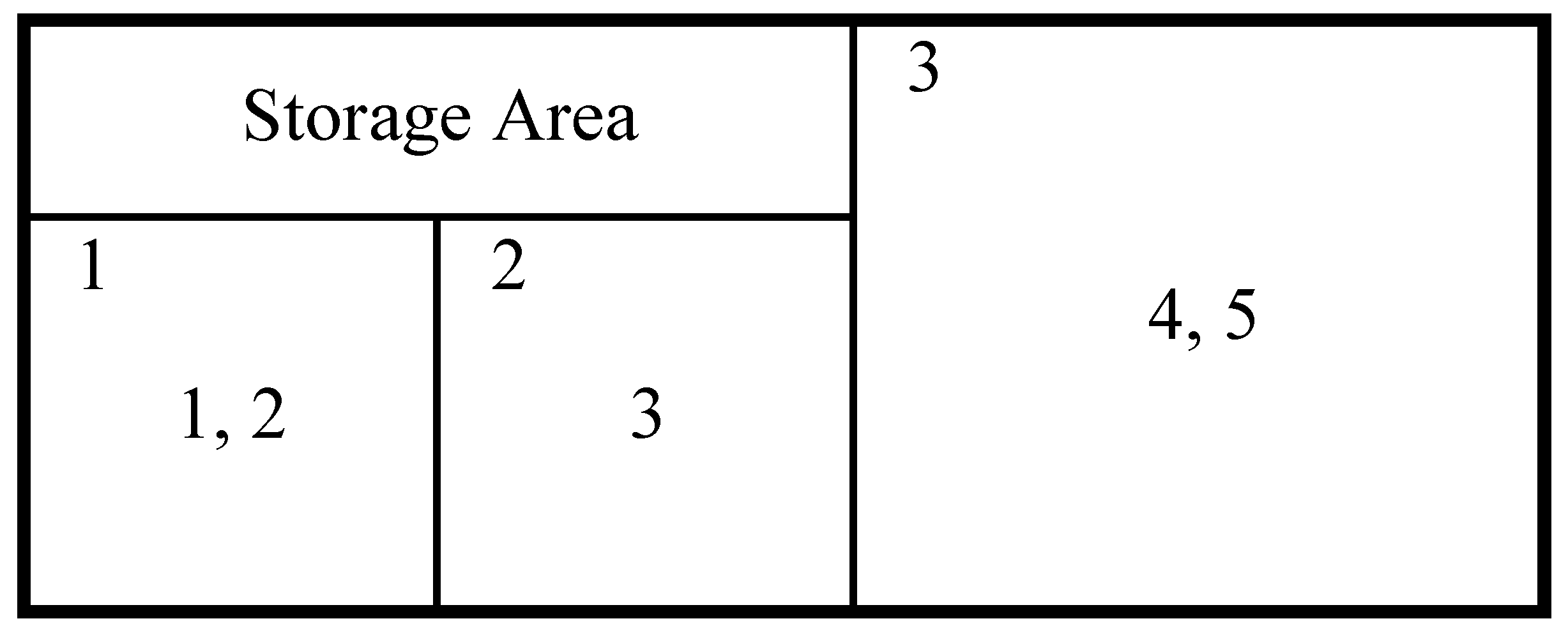

| fij | 1 | 2 | 3 | 4 | 5 | aik | 1 | 2 | 3 | dkl | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 100 | 50 | 20 | 0 | 1 | 1000 | 1800 | 1400 | 1 | 0 | 20 | 50 |
| 2 | 0 | 0 | 100 | 0 | 0 | 2 | 1600 | 1000 | 1200 | 2 | 20 | 0 | 30 |
| 3 | 0 | 0 | 0 | 50 | 0 | 3 | 1200 | 1800 | 2000 | 3 | 50 | 30 | 0 |
| 4 | 0 | 0 | 0 | 0 | 100 | 4 | 2000 | 1200 | 1400 | Ck | 30 | 30 | 50 |
| 5 | 0 | 0 | 0 | 0 | 0 | 5 | 1400 | 2000 | 1000 | ||||
| ri | 20 | 10 | 30 | 10 | 20 |
| Instance | Solution | Time (s) | ||||||
|---|---|---|---|---|---|---|---|---|
| Initial | Max | Avg | Min | BKS | Max | Avg | Min | |
| 20-15-35 | 3,296,339 | 1,554,904 | 1,497,611.9 | 1,471,896 | 1,471,896 | 6.8 | 4.5 | 1 |
| 20-15-55 | 3,811,156 | 1,752,035 | 1,739,005.9 | 1,723,638 | 1,723,638 | 6.4 | 5 | 1.5 |
| 20-15-75 | 3,697,904 | 2,000,519 | 1,965,217.5 | 1,953,188 | 1,953,188 | 11.3 | 8.1 | 2.2 |
| 30-06-95 | 8,502,834 | 5,192,968 | 5,164,120.3 | 5,160,920 | 5,160,920 | 15.1 | 8.9 | 3.2 |
| 30-07-75 | 6,972,953 | 4,442,143 | 4,390,408.3 | 4,383,923 | 4,383,923 | 8.1 | 3.7 | 1.5 |
| 30-08-55 | 7,756,799 | 3,501,695 | 3,501,695 | 3,501,695 | 3,501,695 | 1.6 | 1.5 | 1.3 |
| 30-10-65 | 7,446,408 | 3,708,768 | 3,640,528.8 | 3,620,959 | 3,620,959 | 10.8 | 8.5 | 1.9 |
| 30-20-35 | 6,564,745 | 3,762,510 | 3,564,370.7 | 3,379,359 | 3,379,359 | 14.9 | 11.6 | 2.8 |
| 30-20-55 | 8,921,966 | 3,755,859 | 3,622,121.4 | 3,593,105 | 3,593,105 | 17.8 | 12 | 3.9 |
| 30-20-75 | 8,146,803 | 4,291,942 | 4,110,134.9 | 4,050,938 | 4,050,938 | 28.1 | 23.3 | 5.6 |
| 30-20-95 | 8,627,569 | 6,108,771 | 5,893,437.8 | 5,710,645 | 5,710,645 | 121.5 | 107.7 | 25.9 |
| 35-15-35 | 10,150,194 | 4,515,731 | 4,470,900.9 | 4,456,670 | 4,456,670 | 12.4 | 10.9 | 2.8 |
| 35-15-55 | 10,790,017 | 4,793,770 | 4,679,438.8 | 4,639,128 | 4,639,128 | 14.9 | 11.5 | 3.3 |
| 35-15-75 | 12,170,135 | 6,450,289 | 6,344,300.9 | 6,301,723 | 6,301,723 | 24.3 | 18 | 5.1 |
| 35-15-95 | 12,581,614 | 6,988,554 | 6,833,884.3 | 6,670,264 | 6,670,264 | 67.4 | 58.6 | 16.5 |
| 40-07-75 | 12,467,450 | 7,481,756 | 7,420,285.2 | 7,405,793 | 7,405,793 | 11.4 | 6.4 | 2.4 |
| 40-09-95 | 14,780,911 | 7,856,544 | 7,763,270.2 | 7,667,719 | 7,667,719 | 35.7 | 29.6 | 9.4 |
| 40-10-65 | 15,547,370 | 7,298,103 | 7,270,402.3 | 7,265,559 | 7,265,559 | 14 | 6.7 | 3 |
| 50-10-65 | 25,416,364 | 10,623,768 | 10,530,334 | 10,513,029 | 10,513,029 | 18.9 | 10.6 | 4.8 |
| 50-10-75 | 21,806,545 | 11,458,172 | 11,302,423.7 | 11,217,503 | 11,217,503 | 32.2 | 25.4 | 5.1 |
| 50-10-95 | 23,195,085 | 13,133,213 | 12,947,121.6 | 12,845,598 | 12,845,598 | 51.9 | 37.4 | 12.5 |
| Average | 11,078,626.7 | 5,746,286.4 | 5,650,048.3 | 5,596,821.5 | 5,596,821.5 | 25 | 19.5 | 5.5 |
| Instance | BKS | Time (min) | ||||
|---|---|---|---|---|---|---|
| Memetic [9] | GRASP-PR [11] | TS [12] | PMITS [14] | SA | ||
| 20-15-35 | 1,471,896 | 1.6 | 0.1 | 0 | 0 | 0.1 |
| 20-15-55 | 1,723,638 | 1.7 | 0 | 0 | 0 | 0.1 |
| 20-15-75 | 1,953,188 | 1.7 | 0 | 4.2 | 0 | 0.1 |
| 30-06-95 | 5,160,920 | 1.9 | 0 | 0 | 0 | 0.1 |
| 30-07-75 | 4,383,923 | 2.6 | 0.1 | 0 | 0 | 0.1 |
| 30-08-55 | 3,501,695 | 1.6 | 0 | 0 | 0 | 0 |
| 30-10-65 | 3,620,959 | 3.5 | 2 | 0.1 | 0 | 0.1 |
| 30-20-35 | 3,379,359 | 9.4 | 1.3 | 32.8 | 0 | 0.2 |
| 30-20-55 | 3,593,105 | 7.7 | 0.4 | 24.6 | 0 | 0.2 |
| 30-20-75 | 4,050,938 | 8.7 | 0.7 | 0 | 0 | 0.4 |
| 30-20-95 | 5,710,645 | 44.2 | 926.3 | 0.2 * | 9 | 1.8 |
| 35-15-35 | 4,456,670 | 7.6 | 5.1 | 26.8 | 0 | 0.2 |
| 35-15-55 | 4,639,128 | 6.4 | 0.4 | 0 | 0 | 0.2 |
| 35-15-75 | 6,301,723 | 6.6 | 1.1 | 0 | 0 | 0.3 |
| 35-15-95 | 6,670,264 | 14.4 | 25.9 | 0 | 0 | 1 |
| 40-07-75 | 7,405,793 | 3 | 1 | 0 | 0 | 0.1 |
| 40-09-95 | 7,667,719 | 19 | 7 | 0.1 | 0.1 | 0.5 |
| 40-10-65 | 7,265,559 | 4 | 0.3 | 0 | 0 | 0.1 |
| 50-10-65 | 10,513,029 | 8.4 | 0.4 | 0 | 0 | 0.2 |
| 50-10-75 | 11,217,503 | 10.1 | 23.1 | 0.1 | 0 | 0.4 |
| 50-10-95 | 12,845,598 | 20.9 | 1.5 | 0.4 | 0 | 0.6 |
| Average | 5,596,821.5 | 8.8 | 47.5 | 4.3 | 0.4 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McKendall, A.; Dhungel, Y. A Simulated Annealing Algorithm for the Generalized Quadratic Assignment Problem. Algorithms 2024, 17, 540. https://doi.org/10.3390/a17120540
McKendall A, Dhungel Y. A Simulated Annealing Algorithm for the Generalized Quadratic Assignment Problem. Algorithms. 2024; 17(12):540. https://doi.org/10.3390/a17120540
Chicago/Turabian StyleMcKendall, Alan, and Yugesh Dhungel. 2024. "A Simulated Annealing Algorithm for the Generalized Quadratic Assignment Problem" Algorithms 17, no. 12: 540. https://doi.org/10.3390/a17120540
APA StyleMcKendall, A., & Dhungel, Y. (2024). A Simulated Annealing Algorithm for the Generalized Quadratic Assignment Problem. Algorithms, 17(12), 540. https://doi.org/10.3390/a17120540






