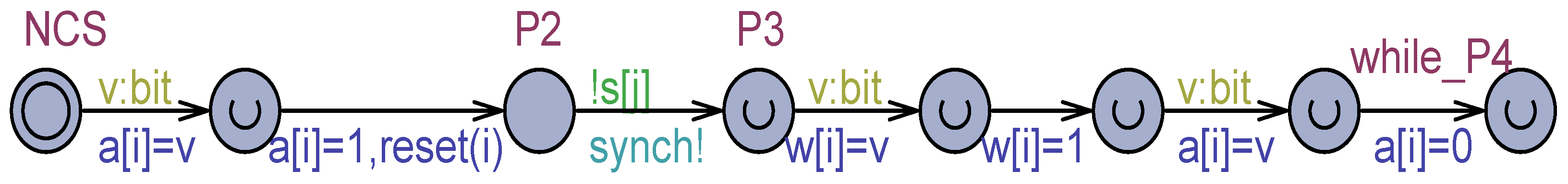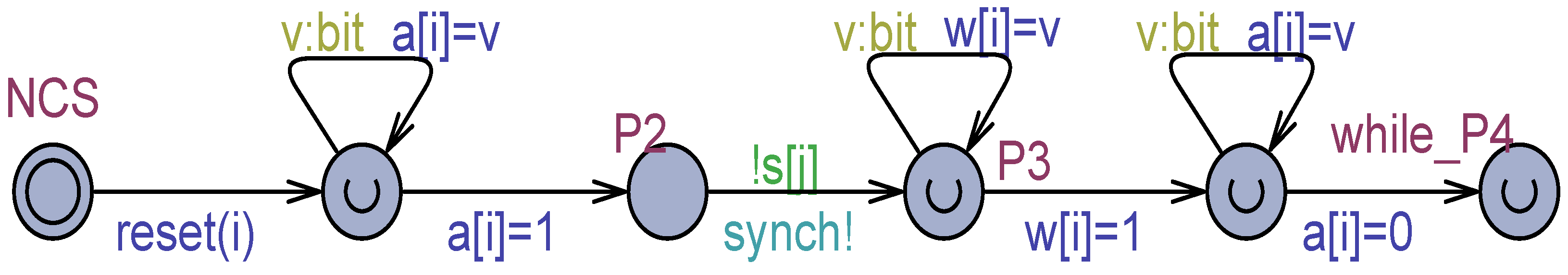Abstract
The work described in this paper develops a formal method for modeling and exhaustive verification of mutual exclusion algorithms. The process is based on timed automata and the Uppaal model checker. The technique was successfully applied to several mutual exclusion algorithms, mainly under the atomic memory model, when the read and write operations on memory cells (registers) are atomic or indivisible. The original contribution of this paper consists of a generalization of the approach to support modeling mutual exclusion algorithms with non-atomic registers, where multiple read operations can occur on a register simultaneously to a write operation on the same register, thus giving rise to the flickering phenomenon or multiple write operations can occur at the same time on the same register, hence determining the scrambling phenomenon. The paper first clarifies some consistency rules of non-atomic registers. Then, the developed Uppaal-based method for specifying and verifying mutual exclusion algorithms is presented. The method is applied to the correctness assessment of a sample mutual exclusion solution. After that, non-atomic register consistency rules are rendered in Uppaal to be embedded in the specification methodology. The paper goes on by presenting different mutual exclusion algorithms that are studied using non-atomic registers. Algorithms are also investigated in the context of a tournament tree organization that can provide standard and efficient mutual exclusion solutions for processes. The paper compares the proposed techniques for handling non-atomic registers and reports about their application to many other mutual exclusion solutions.
1. Introduction
The mutual exclusion problem [1,2,3] arises each time concurrent/parallel processes (or threads) have to access in read/write to a shared resource . For predictability of evolution, only one process at a time must be allowed to use . The code segment executed by a process when using constitutes its (CS). Several algorithms (protocols) have been proposed in the literature for solving the mutual exclusion problem. In this paper, the interest is on algorithms that are based on software mechanisms only, that is, without the support of special hardware instructions like test-and-set. Each particular protocol (see Algorithm 1) consists of a (hopefully minimal) number of (registers), suitably initialized, and a section where the process signals its interest in accessing the resource and starts competing with peers. The process remains (waits) in the prologue until the conditions on the shared variables permit it to enter its critical section. Waiting is normally achieved by loops, with the process actively checking selected variables until an awake situation is sensed which enables it to exit from the busy–waiting. After the critical section, an section is executed, which resets registers, thus allowing other competing processes to possibly resume movement toward their critical section. In the non-critical section (NCS) the process executes actions independent from the resource . For generality, in the NCS the process can also terminate its execution.
| Algorithm 1. Abstract structure of a process using a mutual exclusion protocol. | |
| global shared communication variable : local variables | |
| repeat | |
| NCS Prologue CS Epilogue | //Non Critical Section //Enter section of the protocol //Critical Section //Exit section of the protocol |
| forever | |
The first “pure” software solution to the mutual exclusion problem was due to Dekker [4,5] and was concerned with the handling of processes. Dijkstra proposed a solution [6] for processes, although with a possible unbounded waiting time for a competing process. Knuth [7], de Bruijn [8], and Eisenberg and McGuire [9], respectively, developed improved solutions to the Dijkstra’s algorithm to ensure a bounded waiting time for a competing process, possibly linear in , e.g., [9]. A more simple and elegant solution than Dekker’s algorithm for processes and a general solution for processes were proposed by Peterson in [10]. All such algorithms were mainly studied using atomic registers and through informal mathematical reasoning. Atomic registers have indivisible read/write operations. That is, it is not possible that such operations can overlap on the same register. In addition, informal reasoning has great difficulty in assessing the general properties of a mutual exclusion algorithm. This is due to the intrinsic non-determinism or interleaving that characterizes the execution order of actions of concurrent/parallel processes, which almost always is impossible to predict. This can explain, for example, the different conjectures about the waiting time of a competing process in Peterson’s algorithm for processes [11].
As observed by Lamport in [1], studying the correctness of a mutual exclusion algorithm by assuming atomic read/write operations on registers is a way of achieving mutual exclusion by relying on a lower-level mechanism of mutual exclusion. On the other hand, the widespread diffusion of multi-port memory devices [12] (e.g., cell phones and similar low-cost hardware devices) mandates to adopt mutual exclusion solutions that can tolerate multiple simultaneous read/write operations on the same register. Therefore, the more general context where to check properties of mutual exclusion algorithms is that of working with non-atomic registers and their associated consistency rules.
This paper significantly extends previous authors’ work [11,13,14,15] aimed at the development of a formal method for modeling and verification of mutual exclusion algorithms based on timed automata [16] and model checking [17,18], using the Uppaal toolbox [19,20,21] for the practical experiments. Previous work mainly addressed the correctness assessment of mutual exclusion solutions using atomic registers and a preliminary technique for dealing with non-atomic registers. The original contribution of the current paper is to propose more general techniques to ensure the consistency of non-atomic registers [22]. The new techniques are rendered in the Uppaal modeling method, and their practical usefulness is demonstrated by modeling examples. The new proposed techniques address specifically non-atomic registers where multiple writers and multiple readers (MWMR) can overlap their execution on the same register, or a single writer and multiple readers (SWMR) can access a register simultaneously. The MWMR case can cause the value of the register to be scrambled [22,23], that is, writing in it a non-deterministic value belonging to the register type domain, which can be acquired by readers. The SWMR case is the source of the flickering phenomenon [22,23], where each distinct overlapping reader can obtain a non-deterministic valuation of the register value.
Different mutual exclusion solutions are considered for modeling and correctness assessment. As an example, the paper shows that Szymanski’s algorithm proposed in [24] is correct under atomic registers but becomes incorrect when using non-atomic registers. In addition, the improved solution reported in [25], designed to ensure a linear waiting time for a competing process and which admits a reduced shared data space, effectively guarantees a linear (the number of times competing processes can bypass a given waiting process and precede it in entering their critical section), but, for processes, it does not fulfill mutual exclusion properties even with atomic registers. From the algorithm in [25], a version for (S2) processes is derived in this paper, and its correctness is demonstrated using either atomic or non-atomic registers. Both the Peterson for processes (P2) [10] and the Szymanski algorithm for processes are then exploited, separately, as the arbitration unit in a standard and efficient tournament tree (TT)-based solution [11,14,26,27], thus addressing processes. As an original result of this paper, it is shown that whereas TT-P2 is incorrect when both scrambling and flickering of non-atomic registers are admitted, the TT-S2 solution, which can only be affected by flickering, represents a fully correct mutual exclusion algorithm also with non-atomic registers.
The paper compares the model checking efficiency of three proposed flickering techniques for non-atomic registers with the so-called technique, which is a novel proposal of this paper, that emerges as the best one for application generality, flexibility, and execution performance.
The formal modeling approach developed in this paper is similar to the process algebra method based on the mCRL2 model checker [28], described in [22]. However, this paper argues that the presented approach is more intuitive to use because it rests on processes modeled graphically by timed automata, which are more amenable to understanding and preliminary debugging activities. Visual modeling and exhaustive model checking, that is, systematically investigating all the possible (hopefully finite) execution paths/states in a model, represent the strength of the developed formal method.
The paper is structured as follows. Section 2 describes the consistency rules of non-atomic registers. Section 3 presents the basic formal method, centered on Uppaal, for modeling and verification of mutual exclusion algorithms. A few timed computational tree logic (TCTL) queries are suggested for checking the properties of a mutual exclusion solution. Section 4 proposes some techniques for modeling scrambling and flickering, respectively, in MWMR/SWMR non-atomic registers. The techniques are rendered in Uppaal to be easily integrated within the basic formal method described in Section 3. Section 4 illustrates the application of the MWMR/SWMR consistency techniques to different mutual exclusion algorithms, also in the context of the general and efficient tournament binary tree organization. The section compares the model checking efficiency of the three flickering techniques proposed in Section 4. Section 6 concludes the paper with an indication of ongoing and future work.
2. Register Consistency in Non-Atomic Memory
Shared communication variables (registers) used by a mutual exclusion protocol can (hopefully) be only output variables [29] (also called exterior variables in [26]). Each output variable is owned by a distinct process, which is the only one that can write a value on it. Output variables, though, can be consulted by all the other processes. Instead, a not-output variable can be read/written by any process. It can be anticipated that this is the most complex case that can occur.
Register consistency conditions arise when multiple operations can be executed simultaneously on the same register. The so-called Single Writer Multiple Readers (SWMR) case is the first scenario to be considered [22,30]. A register operated under SWMR is safe if a read that occurs when there is no overlapping write returns the most recently written value, whereas a read that happens concurrently to a write operation may return (flickering) a non-deterministic value belonging to the domain (type) of the register. The register is regular, under SWMR, if it is safe, but, in addition, a read that occurs simultaneously to a write operation returns either the value of the overlapping write or the most recently written value. Finally, a register is atomic under SWMR when the read and write operations never occur simultaneously but are executed according to a definite order.
The most complex scenario is the Multiple Writers Multiple Readers (MWMR) one. As in [22,23], the Raynal condition [3] is assumed. Under MWMR, a register is safe if multiple concurrent writes on the register cause scrambling of its value, that is, a non-deterministic value belonging to the register type is actually written. Any read operation executed in overlapping with one or multiple writes returns a non-deterministic value belonging to the type of the register. The register is regular; if a read occurring in overlapping with write operations, either returns the last value written to the register or the value of any overlapping write. Finally, an MWMR register is atomic if read/write operations never overlap and a read operation always returns the value of the last executed write with respect to the moment the read was issued.
Of course, the use of only output variables requires a mutual exclusion algorithm to be correct under atomic registers and SWMR-safe or SWMR-regular non-atomic registers. When non-output variables are admitted, the atomic algorithm’s correctness has to be checked under the more challenging MWMR-safe or MWMR-regular non-atomic registers.
A specific contribution of this paper is a rendering of the non-atomic SWMR/MWMR registers in an Uppaal model. In particular, the approach starts by transforming a mutual exclusion algorithm into an Uppaal model tailored to only use atomic registers. Model correctness is then thoroughly assessed. After that, the model is modified according to the requirements of the intervening SWMR/MWMR scenarios, and the correctness is re-checked under safe or regular non-atomic registers.
3. Uppaal Modeling with Atomic Registers
The following summarizes the formal approach adopted in this work for modeling and verification by model checking of a mutual exclusion algorithm reduced onto the timed automata language of the Uppaal toolbox [19,20,21]. The goal is to clarify the basic modeling infrastructure based on atomic registers, on top of which the operation of non-atomic registers will subsequently be embedded. The reader is referred to [11,13] for more details about the rationale of the transformation of a mutual exclusion solution into an Uppaal model.
A concurrent system with processes is represented by a network of Process() instances (timed automata), whose unique identifier ranges from 1 to . The processes execute the same algorithm and interact with one another through the shared communication variables used by the mutual exclusion protocol.
Under atomic modeling, any single access (read/write) to a shared communication variable constitutes an atomic action. Therefore, a boolean expression involving multiple shared variables has to be evaluated component-by-component. An exception to the above rule is represented by the management of local variables of a process. Multiple local variables, supposedly held in hardware registers, can be operated simultaneously.
Szymanski’s algorithm for processes, proposed in [24] (page 624, Figure 2), is chosen for demonstration purposes (see Algorithm 2). It is based on output variables only: , . The solution follows the metaphor of a waiting room with two doors: and . Initially, the door_in is open and the door_out is closed. Each process can be in one of 5 states (values of ). State 0 means the process is not interested in the critical section. In state 1, the process wants to enter the waiting room. All the processes that want to enter the waiting room at the same time are allowed to pass through the . In state 2, a process checks if other external processes want to enter. If no other processes are sensed, the process closes the , passes to state 3, and the is opened. From the waiting room, processes exit the according to the order of their IDs. In state 4 the process exits the waiting room and enters the CS. When finishing with the CS, the process switches again to the state 0. At the time the last process exits from its CS, the initial door situation is re-installed.
| Algorithm 2. The Szymanski’s mutual exclusion algorithm [24]. |
| shared communication variables: int [0, 4] flag [1..N];//all 0 initially Process(i:1..N) local variables: j repeat NCS P10: flag[i] = 1; P11: await(); P20: flag[i]=3; P21: if(){ flag[i] = 2; P22: await()} P30: flag[i] = 4; P31: await(); CS E0: await(); E1: flag[i] = 0; forever |
The await() condition at the E0 line takes into account the correction suggested in [31] (page 675).
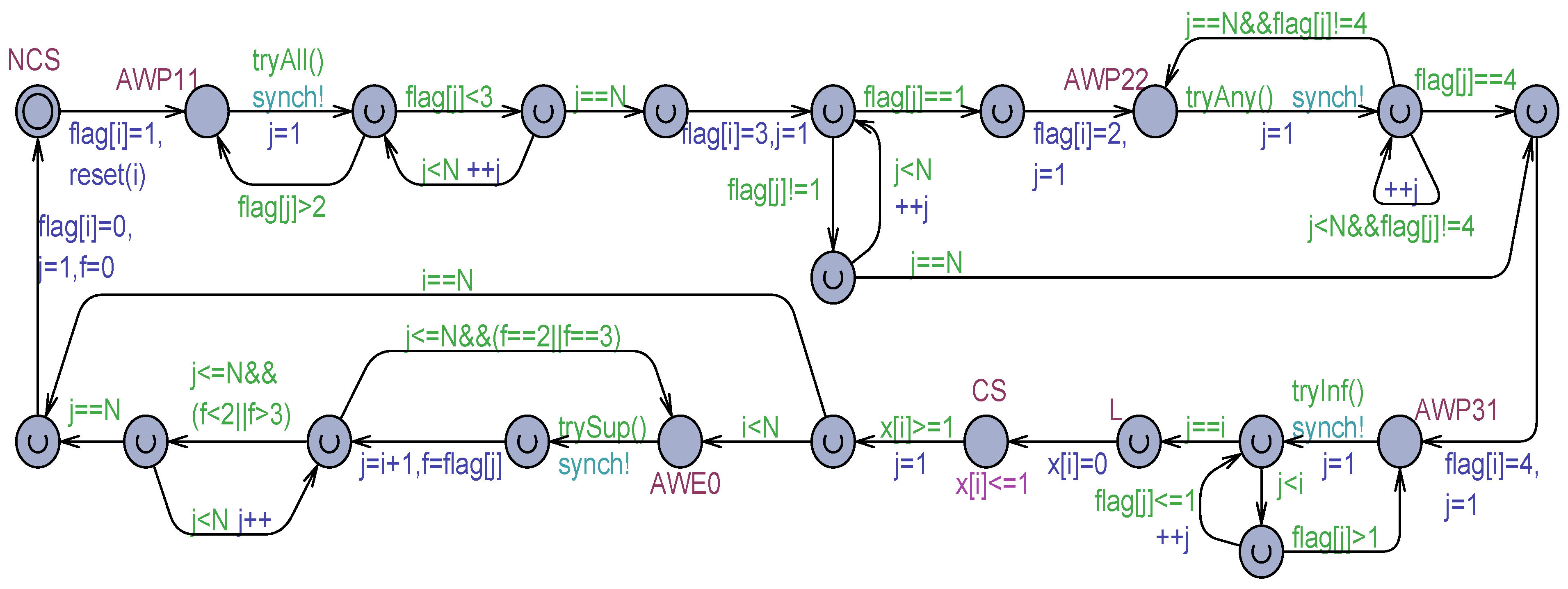
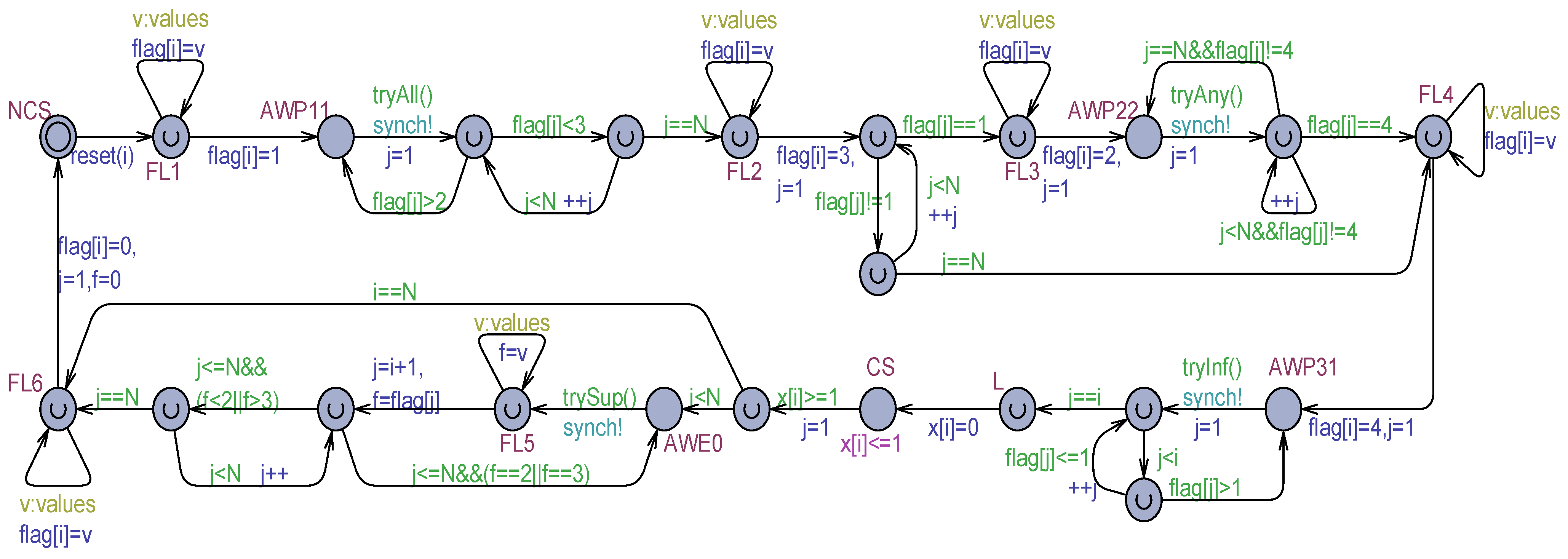
The Algorithm 2 was analyzed informally by the author in [24], and a linear overtaking factor (that is the maximal number of times a process in the waiting room will be by-passed by other competing processes) was predicted: , as a direct consequence of enforcing an exit order from the waiting room directly dependent on the process IDs. Figure 1 shows a transformation of Szymanski’s algorithm of the generic in an Uppaal-timed automaton model made of locations, edges, and clocks. Time can be controlled by clock variables, which measure relative amounts of elapsed time. A clock can be reset. After a reset, the clock grows at the same rate as all the clocks in the model. Edges are annotated by guarded commands. Guards (green-colored in Figure 1) are logical conditions that enable an edge to be possibly taken. A command can contain a synchronization on an urgent broadcast (asynchronous) channel (azure-colored) that constrains the edge to be exited as soon as the guard evaluates to true. A command can also have an update part (blue-colored), which consists of an ordered list of assignments and clock resets. Locations can be normal (see NCS, AWP11, and so forth) or urgent (flagged with an internal U). The automaton ( instance) can remain in a normal location for an arbitrary time. The dwell time in a normal location can be constrained by attaching to it an invariant (see the CS location with the invariant in Figure 1). The process can remain in the location provided the invariant (a logical condition built on data or clocks) continues to be satisfied. An urgent location must be abandoned without time passage. Among the current urgent locations of a set of processes, Uppaal ensures they will be exited in a non-deterministic order. Therefore, for a proper reproduction of the concurrency of the actions of multiple processes, actions can be purposely attached to the edge commands exiting from urgent locations. This way action interleaving and partial order of a concurrent/parallel execution are naturally ensured. It is worth noting that exiting from a normal location with an enabled guard and urgent output synchronization (see, e.g., the AWP11 location in Figure 1) is equivalent to exiting from an urgent location. Thus, non-determinism regulates the execution of all types of urgent actions.
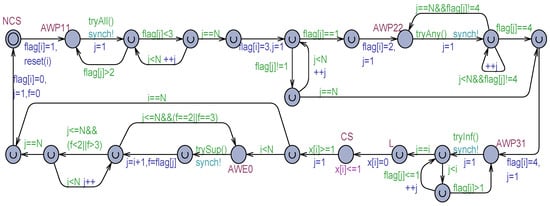
Figure 1.
Uppaal Process model for the Szymanski’s solution of Algorithm 2.
The model in Figure 1 is time-dependent in the following aspects. In the non-critical section (NCS), which is also the initial location, a process can remain an arbitrary time, also infinite. This way, process termination gets naturally modeled. In the critical section (CS) location, the dwell time is constrained to be exactly 1 time unit. This choice was adopted to measure the overtaking factor () of processes easily. Each process is associated with a clock , which is reset just before entering the CS. A target process () can be established and its clock observed for measuring the . All the times the process starts competing, its clock is reset (through the function). Then, gets incremented as competing processes gain the CS before . Finally, the maximum value of is measured just before enters its CS (see the location in Figure 1).
Busy–waiting situations are required in the P11, P22, and P31 points of the Prologue section and the E0 point of the Epilogue of the mutual exclusion protocol (see Algorithm 1). Whereas an internal spin-lock of a process running on a separate core can be practically tolerated, it should conveniently be avoided in an Uppaal model for verification efficiency (by reducing the number of distinct execution paths to be analyzed). The adopted solution consists of introducing a normal location (see AWP11, AWP22, AWP31, and AWE0 in Figure 1) for each busy waiting. Instead of immediate looping, the exit from the location is controlled by a guard function like in AWP11. This function checks “optimistically” (by possibly simultaneously consulting multiple shared variables) if a potential exit from the busy waiting location is possible. If yes, the urgent and asynchronous signal is used to force the exiting without further time passage. However, following the exit from the busy waiting location, the effective evaluation of the await (possibly complex) condition is carried out, component by component. At any moment the condition for abandoning the busy–waiting would be found to be false, the busy–waiting location is immediately re-entered. Algorithm 3 collects all the try functions used in Figure 1.
| Algorithm 3. The try functions of the model in Figure 1. | |||
| bool tryAll(){ int j; for(j = 1; j <= N; ++j) if(flag[j] > 2) return false; return true; }//tryAll | bool tryAny(){ int j; for(j = 1; j <= N; ++j) if(flag[j]==4) return true; return false; }//trayAny | bool tryInf(){ int j; for(j = 1; j < i; ++j) if(flag[j] > 1) return false; return true; }//tryInf | bool trySup(){ int j; for(j = i + 1; j <= N; ++j) if( flag[j]==2|| flag[j]==3) return false; return true; }//trySup |
3.1. System Configuration
Algorithm 4 collects the global declarations of the Uppaal model in Figure 1.
| Algorithm 4. Uppaal global declarations of the model in Figure 1. |
| const int N = 4;//example typedef int[1, N] pid;//process IDs typedef int[0, 4] values;//possible values of flag[.] variables values flag[pid];//all zeros initially by default urgent broadcast chan synch; |
The automaton has only one parameter: , which establishes as the process identifier. instances of the model are automatically created at the system initialization time by using the following statement of system configuration:
3.2. Checking Algorithm’s Correctness
Correctness of the Algorithm 2 and the corresponding Uppaal model in Figure 1 can be assessed through a few timed computational tree logic (TCTL) queries supported by Uppaal [20]. First, the state graph (timed transition system) of the model is built by the verifier, that is the set of all (hopefully finite) execution states and execution paths in the model. Then, specific properties of the mutual exclusion solution are investigated as follows.
3.2.1. Mutual Exclusion Property
The following query asks if it is always true that in all the states of the state graph the number of processes simultaneously found in their critical section, is less than or equal to 1:
A[] (sum(i:pid)Process(i).CS) ≤ 1
3.2.2. Absence of Deadlocks
No state of the state graph is deadlocked provided the following query is satisfied:
A[] !deadlock
3.2.3. Bounded Overtaking (or Absence of Starvation)
The target process experiments a bounded overtaking if the following suprema () query is satisfied with a finite value of :
sup{Process(tp).L}: x[tp]
3.2.4. Liveness-1
Any process eventually enters its critical section provided the following existential query is satisfied, whatever the identity of the target process :
E<> Process(tp).CS
3.2.5. Liveness-2
A process in NCS does not forbid other processes to enter their CS if the following query is satisfied:
E<> exists(i:pid)Process(i).NCS && exists(j:pid)Process(j).CS
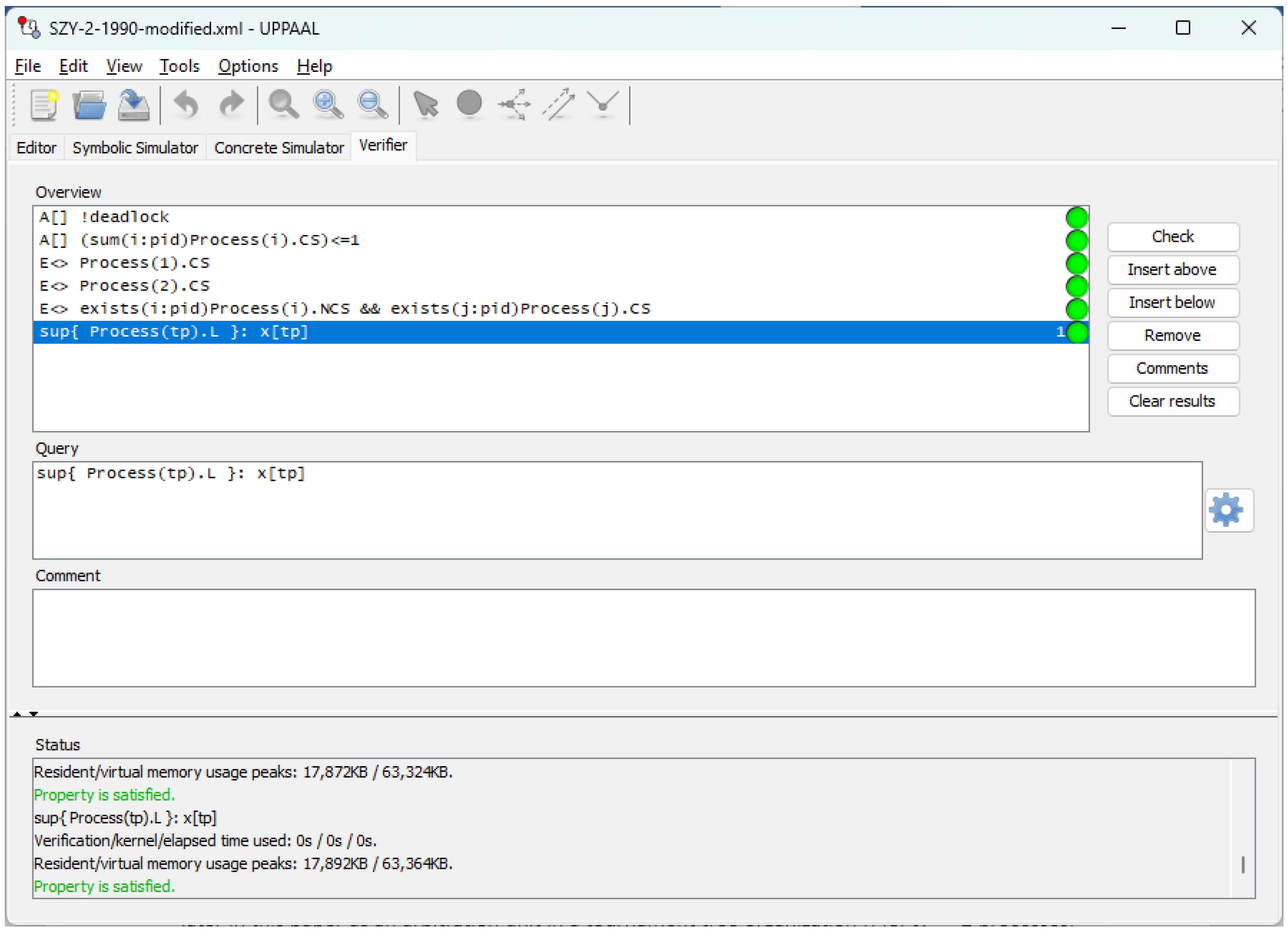
From the model checking of the Uppaal model in Figure 1 it emerged that the solution is correct from all the mutual exclusion properties. Properties were verified both when NCS is normal (an arbitrary time can elapse before the next competition of the process) and in the case the NCS location is urgent (a process immediately re-enters after complete access to its CS). The linear overtaking was confirmed. In the case NCS is urgent, and , the suprema query terminates after 792 s with a memory usage of 12.6 GB, on a Win11 Pro desktop platform, Dell XPS 8940, Intel i7-10700 (8 physical cores), CPU@2.90 GHz, and 32 GB RAM, using version 5 of Uppaal 64 bit.
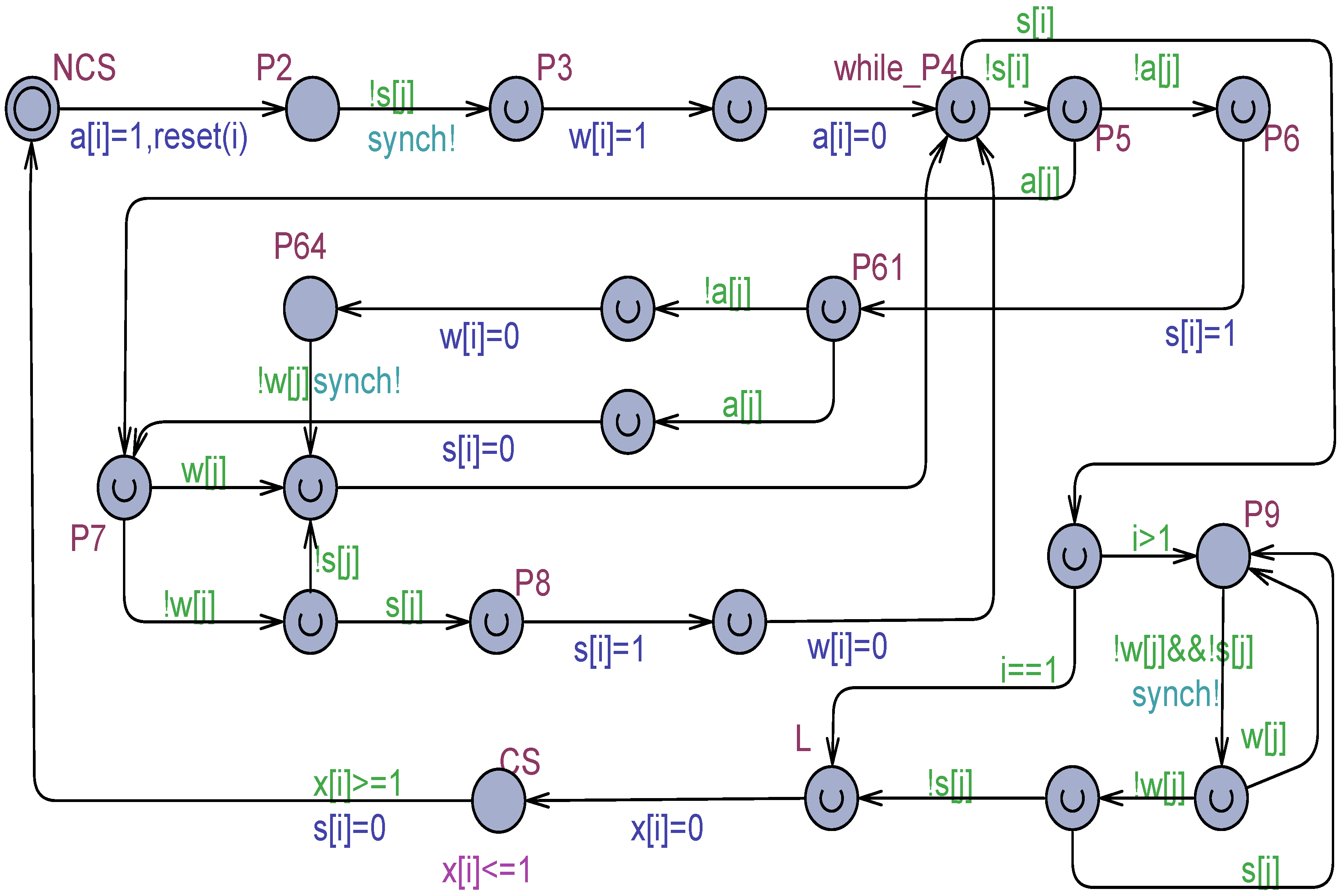
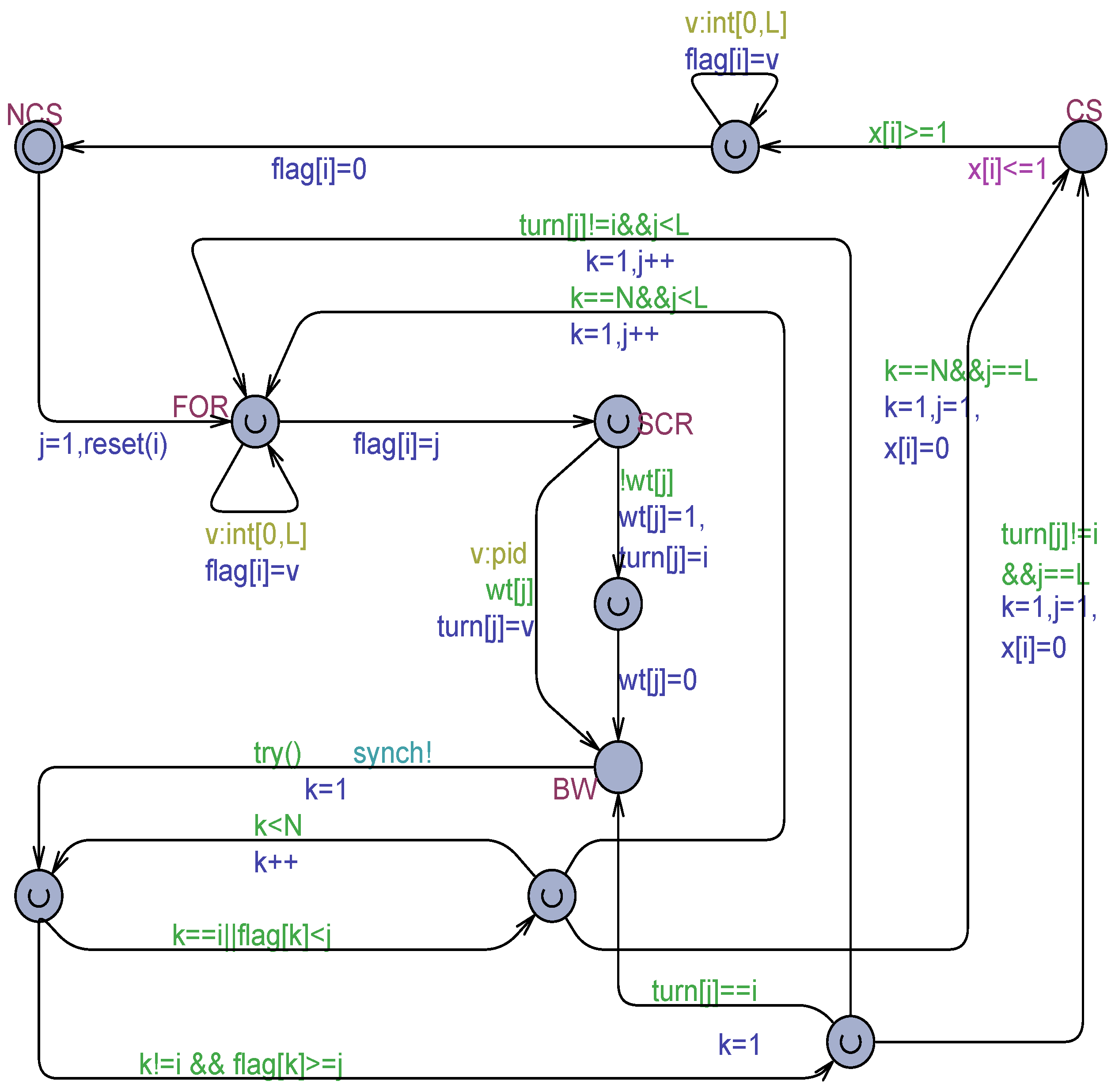
The Algorithm 2 was refined in [25] by using only three output bits per process (: ctive aiting hutting). The waiting room has only the input door. An active process wants to enter the waiting room. While waiting, further processes signaling they would also enter are allowed to gain the waiting room. Otherwise, the door is shut. Processes exit the waiting room according to their IDs. This algorithm too, with the correction noted in [31], was modeled by our proposed Uppaal-based method with atomic memory. Model checking revealed that for the model has no deadlock and admits a linear overtaking, but mutual exclusion can be violated. That is, multiple processes can enter their CS simultaneously.
The Uppaal model shown in Figure 2 was derived from the algorithm in [25] by tailoring it to processes and by modifying the condition for abandoning the busy–waiting in P9. The current process is denoted by and its partner by . The informal algorithm behind Figure 2 can be easily deduced from the model.
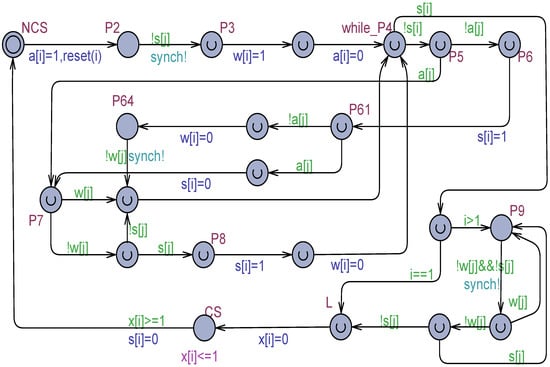
Figure 2.
The Szymanski algorithm in [25] for , adapted for processes.
The model in Figure 2 is a fully correct mutual exclusion solution (see also Figure 3). It will be used later in this paper as the arbitration unit in a tournament tree organization [11,14,26,27] for processes, under both atomic and non-atomic registers.
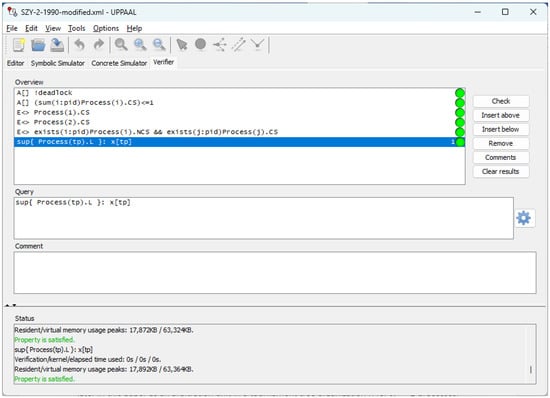
Figure 3.
An Uppaal snapshot witnessing correctness of the model in Figure 2.
4. Modeling Non-Atomic Registers in Uppaal
The following proposes some techniques for rendering SWMR and MWMR register flickering and scrambling in Uppaal.
4.1. Modeling Flickering in SWMR Registers
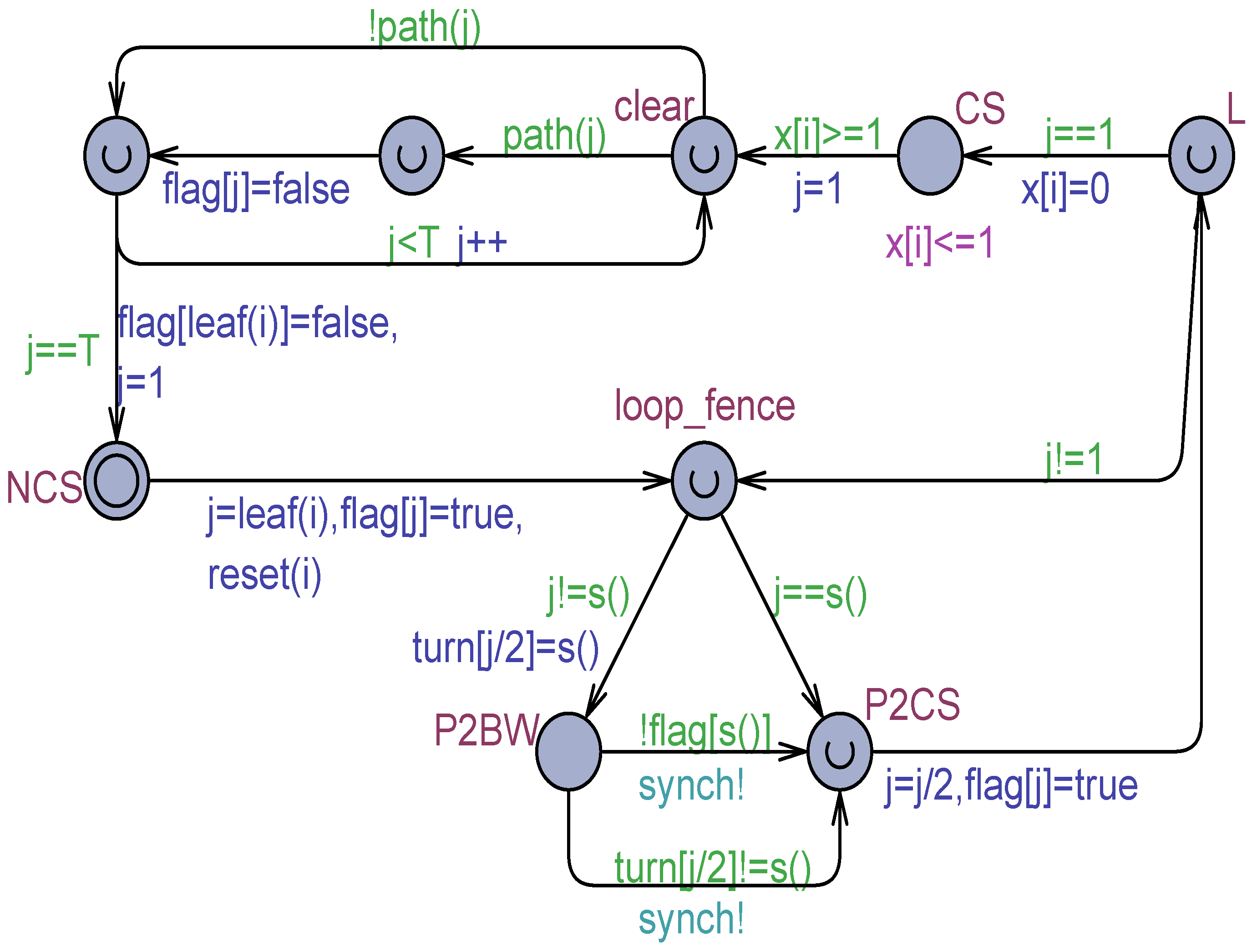
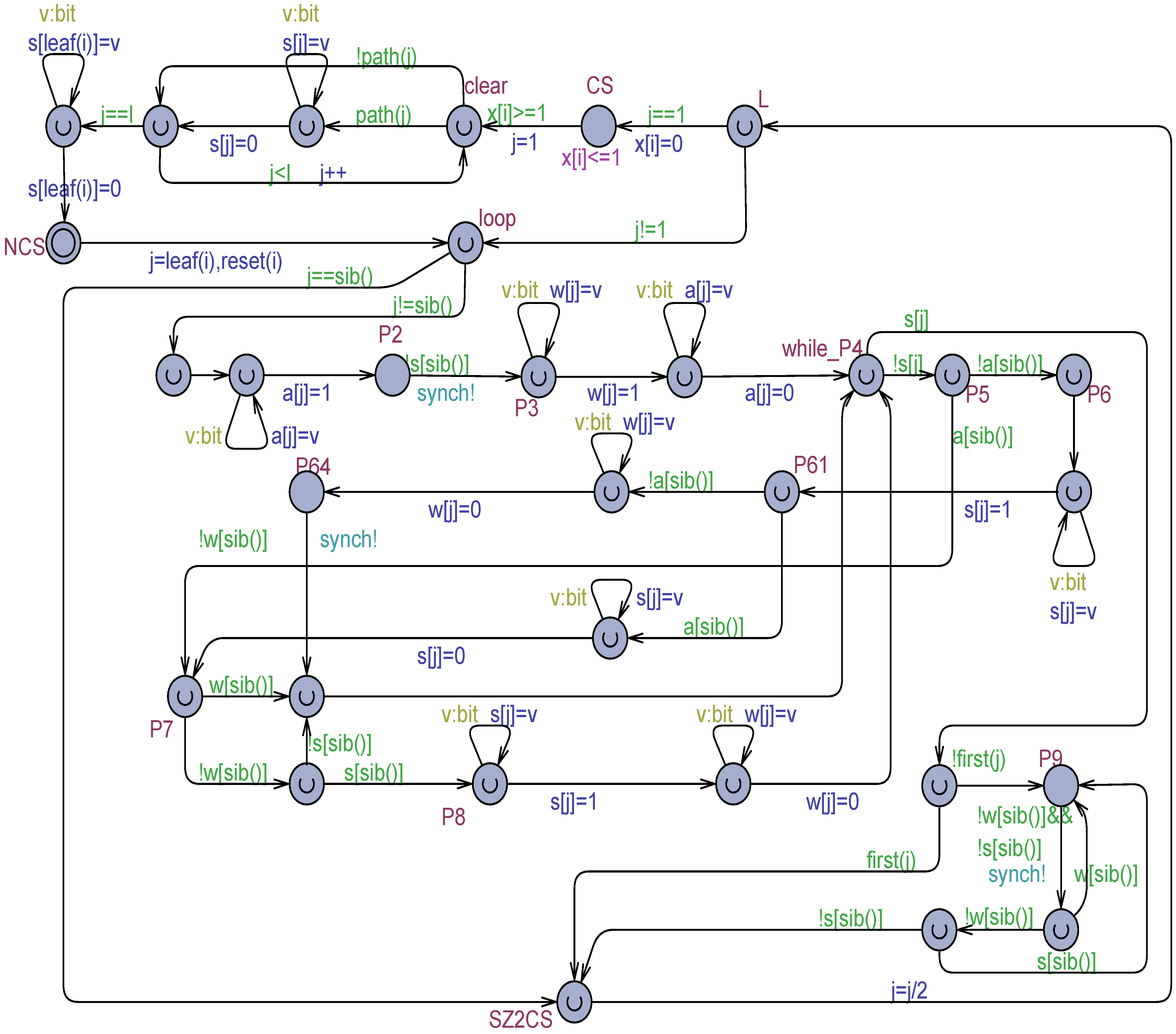
Three techniques were developed. In the first one ( technique), the writer first assigns a non-deterministic value to the register, belonging to the type of the variable, followed by the assignment of the true value. This corresponds to a non-atomic write operation [32,33,34] (e.g., [34] page 3). The technique (see Figure 4) is exemplified in the model of Figure 2, when the process exits the NCS and has to establish the value 1 (true) in the output variables and and again, before while_P4, 0 (false) in . The yellow part of the three commands in Figure 4 expresses the non-deterministic selection of a bit value and its assignment to the temporary variable , whose lifetime is restricted to the command itself.

Figure 4.
An excerpt of using the flickering between NCS and the while_P4 location of Figure 2.
flickering allows an overlapping read, e.g., of to acquire the non-deterministic value instead of the true value. Despite its simplicity, the technique permits multiple readers to actually achieve different values of the register. In fact, due to concurrency and interleaving of process actions (it is recalled that all the execution paths in the state graph are automatically analyzed by the exhaustive model checker), a reader can obtain the previous value, another the non-deterministic (flickering) value, another one the effective written value. The simple flickering technique was adopted, e.g., in [11,14].
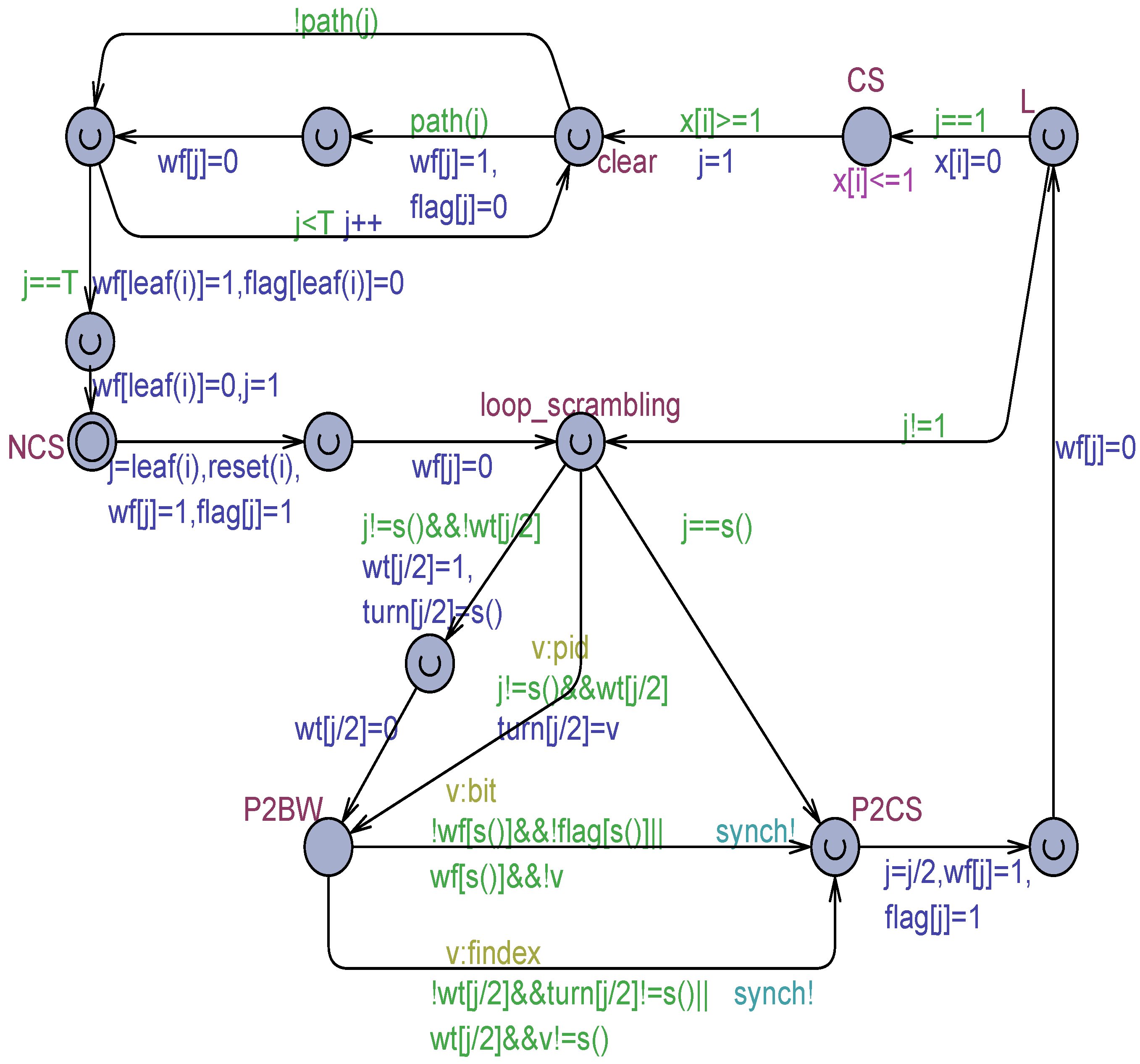
The second technique ( technique) [32] is used, e.g., in [29]. In this case, the writer realizes a loop of non-deterministic assignments to the register (see Figure 5) before writing the true value. The proposal assumes the loop eventually terminates. As a consequence, this technique aims to ensure that multiple readers can achieve, during an overlapping write, a possible different flickering value.

Figure 5.
An excerpt of using flickering between NCS and the while_P4 location of Figure 2.
The use of the technique causes no problem in the Uppaal model of a mutual exclusion algorithm. The model checker, indeed, can consider what happens for any duration of the loop.
The third proposed technique in this paper is the one, which reproduces the intents of the mechanism by first decorating the model with boolean variables (0 false, 1 true) to indicate whether a given register is actually under writing or not. For example, in the model of Figure 2, the boolean arrays , and are introduced (all false initially), which correspond to the output variables , , and , respectively. When the writer, e.g., of wants to assign a value to , it puts true to the corresponding decoration variable and assigns the value to . Then, following this step, is reset to false to reflect the writing to is finished. The technique gives the reader the responsibility of checking the value of If it is true, the reader generates and uses a non-deterministic value for the register (see Figure 6). Otherwise, the actual value of the register is used.
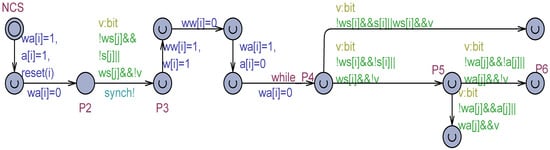
Figure 6.
An excerpt of using flickering by in the model of Figure 2.
This paper advocates the use of the technique for rendering flickering. It has general applicability and can reduce the non-determinism degree in the model: a non-deterministic choice is only used when the corresponding output variable is effectively under writing, as witnessed by the associated decoration variable . It can be expected a reduction both in the memory space required by the state graph and in the verification time (see also later in this paper). To reduce model cluttering, in Figure 6, instead of two distinct edges (see the connection, e.g., between and ), an equivalent disjunction is used in the guard of a single edge. A first piece of the guard is associated with the case , that is, the variable is not under writing and its value can be used directly; a second case occurs when is true and the non-deterministic selection is used instead.
4.2. Modeling MWMR Safe Registers
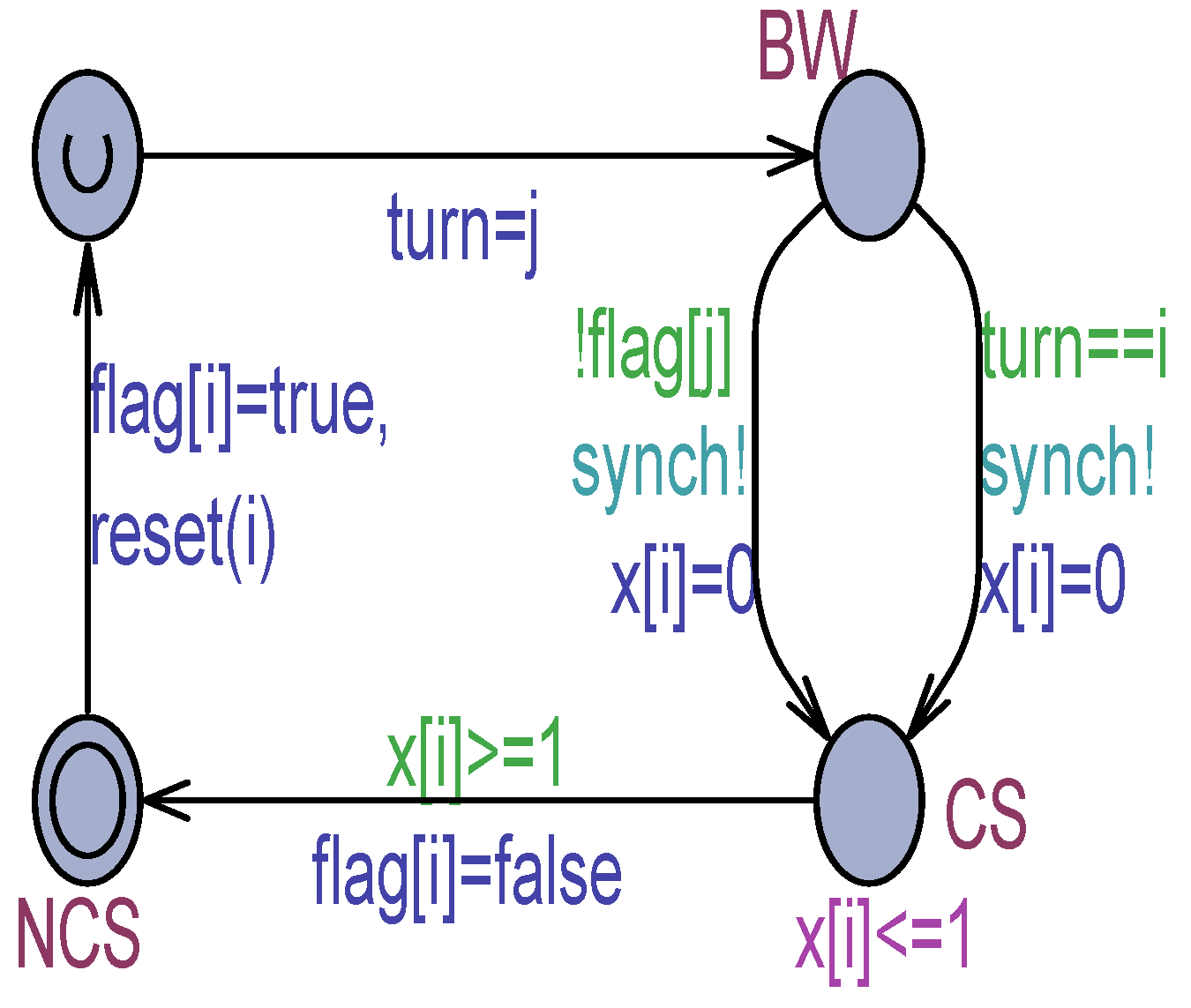
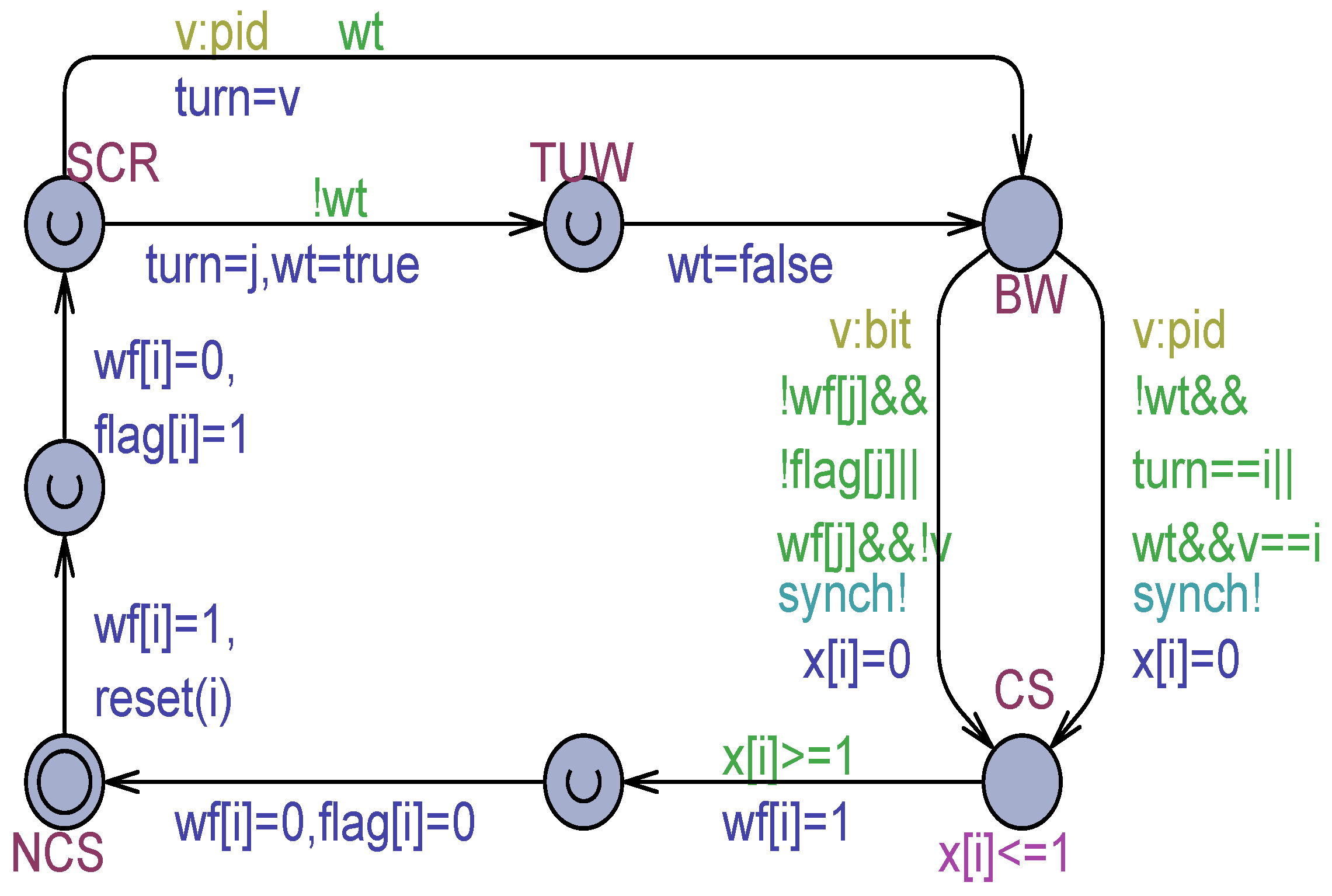
The most challenging case concerns modeling MWMR safe registers. This paper proposes the introduction of decoration variables to reflect both the case of multiple writes on a scrambled register and that of multiple reads of a flickered register. As an example, Figure 7 and Figure 8 show, respectively, the Peterson for 2 processes (Peterson-2) model [10] under atomic memory and its decorated version with scrambling and flickering. Scrambling is modeled according to the Raynal assumption [3] that multiple simultaneous writes assign a non-deterministic value to the register.
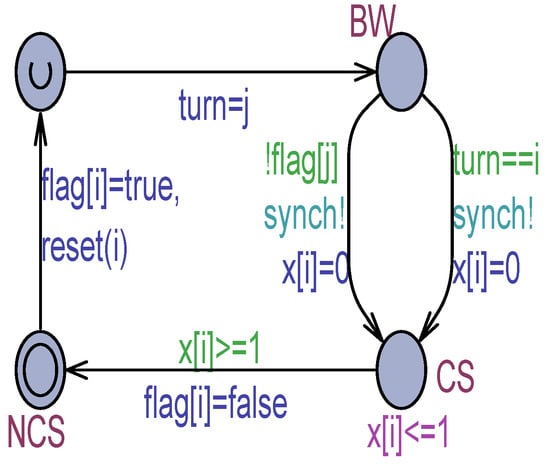
Figure 7.
Peterson-2 process model with atomic registers.
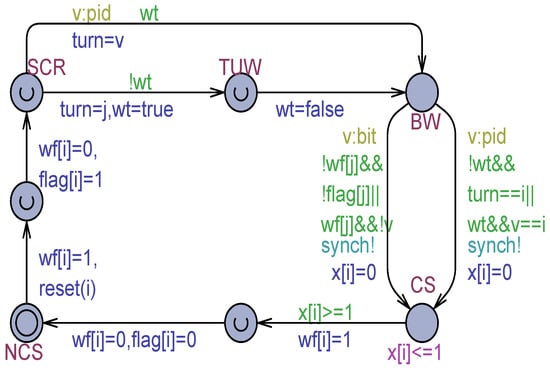
Figure 8.
Peterson-2 process model with MWMR safe registers.
As in other cases, in the models of Figure 7 and Figure 8, denotes this process and indicates the partner process. The Peterson-2’s solution uses two output boolean variables to testify the interest () or not () of each process to enter the critical section. The shared non-output variable is used for yielding to the partner the grant for entering its CS. In a possible case, both processes can write simultaneously to (scrambling). The following decoration variables are used: (scalar) and (array) . As shown in Figure 8, a writer who senses the other writer is not writing to sets to true and assigns the ID of the partner to the variable. Would the second writer arrive simultaneously at the SCR location, it can see is true. In this case, a non-deterministic value is assigned to . The writer who assigned true to is also responsible for lowering it to false in the next step. Of course, being two processes, in the case of scrambling on the register, no simultaneous read can occur. Instead, a write operation on the output variable or the non-output variable can always occur simultaneously with a concurrent read operation issued by the partner process in the busy–waiting (BW) location.
From the model checking of the models in Figure 7 and Figure 8, it emerged that Peterson-2 is correct under atomic memory and it is MWMR-safe under non-atomic memory. This is because being the of type , that is, the domain includes only the two values 1 and 2 of the process IDs, scrambling cannot generate random values, which can cause the algorithm to lose its mutual exclusion, enter a deadlock state, and so forth.
The following TCTL query (satisfied) guarantees effectively that the two processes can simultaneously be in their SCR location, thus generating scrambling in the variable:
E<> Process(1).SCR && Process(2).SCR
4.3. Modeling MWMR Regular Registers
Also in this case, decoration variables could be used to identify the situation where multiple writers are simultaneously writing to the same register. Under regular MWMR registers, though, each writer who finds another write in progress assigns its value to the register. Therefore, a concurrent read can either return the last written value or any of the assigned values to the register. In reality, the modeling of MWMR regular registers naturally falls into what we have called Uppaal modeling with atomic registers. Multiple concurrent write operations will occur one at a time and in any order. Each writer is allowed to assign its value to the register. On the other hand, a concurrent read always returns the last written value to the register, defined after a given order of action execution. Moreover, the Uppaal model checker is capable of investigating all the possible execution orders of the actions of the concurrent/parallel processes.
5. Modeling Examples with Non-Atomic Registers
5.1. Szymanski’s Algorithm
The model of Szymanski’s algorithm [24] in Figure 1, based only on output variables, was adapted to work with SWMR safe registers, using the technique for flickering. The new model is shown in Figure 9. Unfortunately, the model no longer satisfies the mutual exclusion properties. In particular, whatever the value of , the model admits deadlocked states, and the mutual exclusion property is violated.
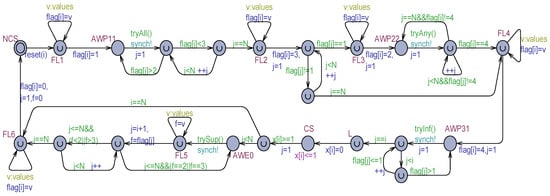
Figure 9.
Szymanski algorithm [24] modeled by using the flickering technique.
The same results were observed by using the and the flickering techniques. Therefore, the Szymanski algorithm [2] was found correct only under atomic memory or non-atomic memory with regular SWMR registers. The source of bad behavior with SWMR safe registers is the rich set of values () of the output variables. Therefore, it is highly probable that flickering can generate unexpected values, which cause the model to fail. For example, processes in AWP22, due to flickering, can be unable to exit from the busy–waiting because no other process is found that has . All of this was confirmed by a diagnostic trace generated by the Uppaal model checker.
The above-reported results comply with the verification experiments carried out with the mCRL2 toolset in [22].
5.2. Peterson Algorithm for Processes
Peterson-N [10] extends the algorithm for processes using the metaphor of climbing a ladder. The ladder is composed of steps or levels. By convention, a process at level 0 is one not interested in the critical section. The process that first arrives at the last level obtains the permission to enter the critical section. Current level occupied by process is reflected by assigning as the value of the output variable: . In addition, process is also assigned the level through the non-output variable . More than one process can occupy simultaneously the level . When this occurs, one of them moves to the next level.
The algorithm was modeled in Uppaal and thoroughly investigated in [11]. It emerged the algorithm is fully correct when it executes with atomic registers or MWMR regular registers. In particular, the overtaking factor was found to be: when the non-critical section NCS can have an arbitrary duration (also infinite), and when NCS is made urgent, meaning that a process exiting from the CS is permitted to immediately re-enter for a new competition. In the more general case of MWMR safe registers, that is, when scrambling in the variables and flickering in the variables are allowed (see the Uppaal model in Figure 10 that is based on the flickering technique), the algorithm continues to be free of deadlocks but loses the fundamental mutual exclusion property, that is, multiple processes can enter simultaneously their critical section. The same results were observed when using the and the technique. These results integrate the results of Peterson-N based on non-atomic memory and flickering reported in [11], where the solution was mainly studied for the assessment of the overtaking factor.
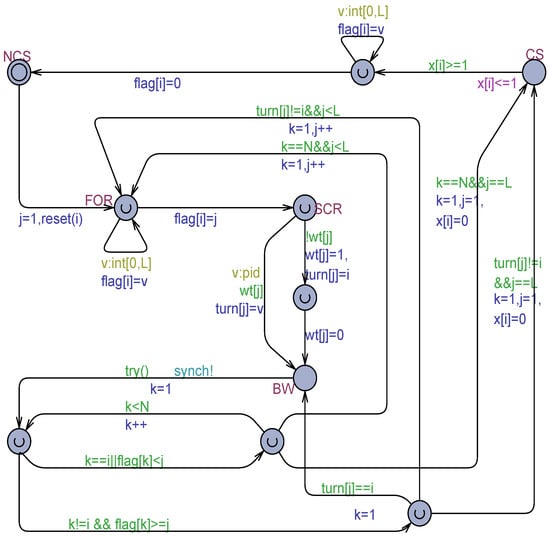
Figure 10.
Uppaal model of Peterson-N algorithm with both scrambling and flickering.
5.3. Tournament Tree-Based Mutual Exclusion Solutions
As shown in [11,14,26,27] a mutual exclusion algorithm for processes can be exploited as the arbitration unit in a binary tournament tree (TT) to achieve a general, standard, and efficient solution for processes. For implementation purposes, the TT can be mapped onto the same linear array often used for supporting the heap sort algorithm. Processes enter the leaf nodes, which are located on the last level of the TT. Intermediate nodes are indexed from 1 (the root node) to . The entering process , , deterministically occupies the leaf node . Position represents the process in its current position in the TT. Process can admit a sibling process at node , provided , that is, processes and share the same ancestor node . Pairs of sibling processes compete using the chosen algorithm for arbitrating processes. The winner moves to the ancestor node, from where it will compete with another sibling and so forth. The process that first arrives at the root node gains permission to enter its critical section. Variables are assumed to represent the nodes the process visited during its movement in the TT. On exiting from the critical section, all the nodes that were previously visited in the upward movement (path) toward the root node are reset exactly in the opposite order, thus possibly awakening processes in arbitration nodes that can resume their advancement in the TT.
Two representative cases are shown in this section. The first one (TT-P2) is related to the use of Peterson-2’s solution in a TT organization. The second one (TT-S2) exploits the algorithm for two processes derived from Szymanski’s solution [25], which was previously described in this paper.
5.3.1. TT-P2’s Solutions
The TT-P2 algorithm under atomic registers or MWMR regular registers is shown in Figure 11. The subrange type of all the TT nodes is denoted by and contains all the integers from 1 to . The subrange type of the intermediate (ancestor) nodes is denoted by and contains the integers from 1 to . The TT is actually represented by the boolean array which stores the process advancements in the TT path toward the root. In addition, the array is introduced. The register regulates the arbitration between the process in position and its sibling, if there are any, whose position is calculated by the function. P2CS is the virtual critical section after an arbitration, modeled as an urgent location. The time unit elapses in the CS location of the overall TT.
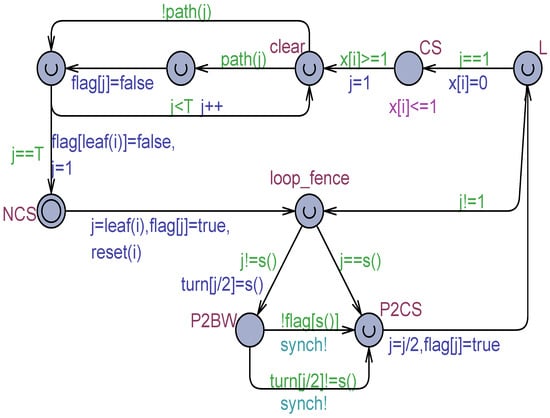
Figure 11.
The basic TT-P2 algorithm based on atomic or MWMR regular registers.
The TT-P2 basic algorithm satisfies all the mutual exclusion properties. Its overtaking factor was found to be: , which becomes when is a power of 2. The model was also studied in [11] under flickering (using the technique) but without scrambling (the MWMR variables were made SWMR registers). Also in this case the TT-P2 model proved to be fully correct.
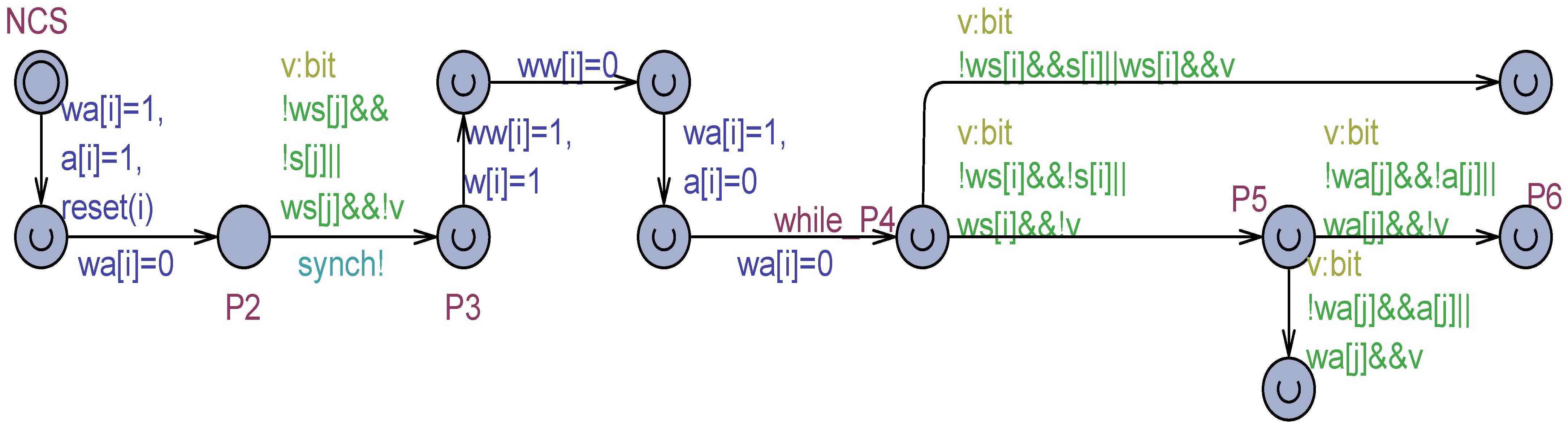
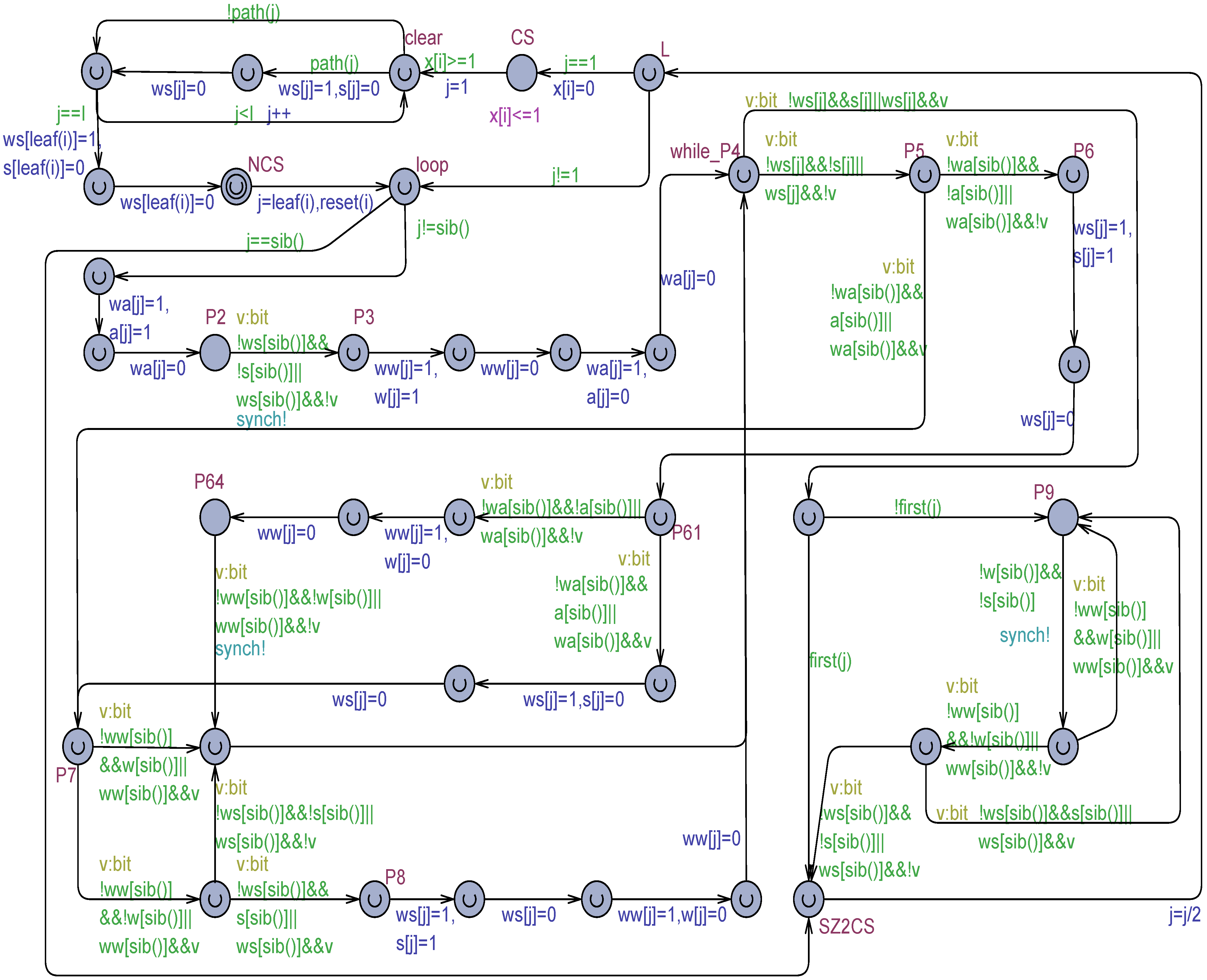
The most general version of the TT-P2 algorithm when both scrambling in the safe registers and flickering (e.g., expressed by the technique) in the output safe registers are allowed, is proposed in Figure 12.
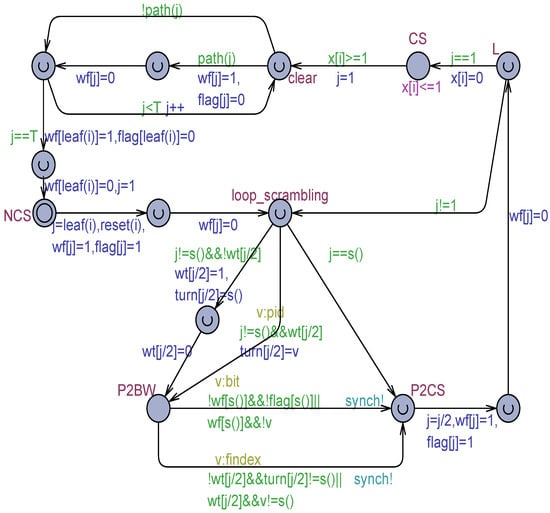
Figure 12.
The TT-P2 algorithm with scrambling and flickering based on the technique.
The TT-P2 model of Figure 12 is without deadlocks, confirms the overtaking factor but violates the mutual exclusion property. Scrambling in the register, in fact, can allow multiple processes to enter simultaneously their critical section CS.
5.3.2. The TT-S2 Algorithm
The TT-S2’s solution, which uses the adapted Szymanski algorithm [25] for processes (see Figure 2) as the arbitration strategy, is presented in Figure 13. The model rests on the 3 bit per process output registers , , SWMR safe registers (all initialized to 0).
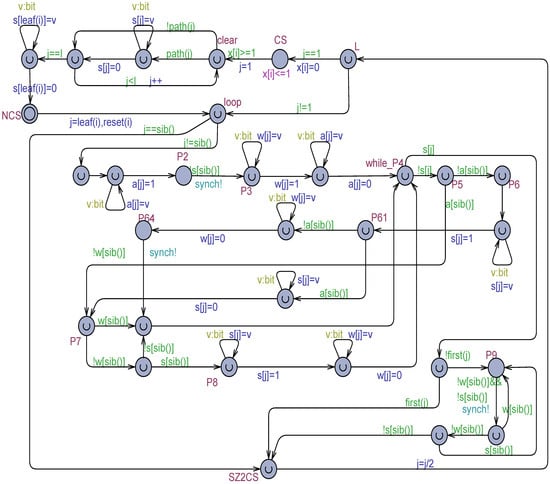
Figure 13.
The TT-S2 formal model based on the SWMR safe registers , , with flickering expressed by the technique.
For simplicity, in Figure 13, flickering is rendered by the technique. The model was also prepared by using the and the flickering techniques as well. Figure 14 shows the TT-S2 model according to the technique.
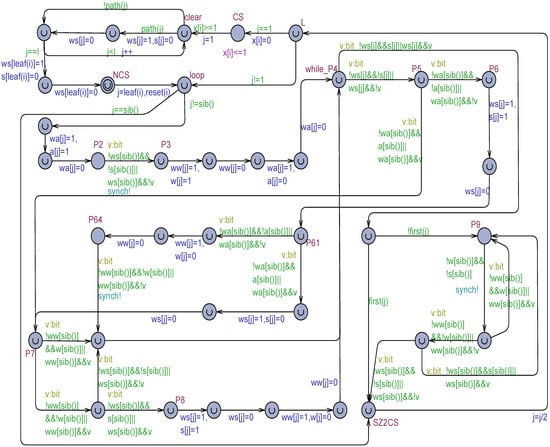
Figure 14.
The TT-S2 formal model based on the SWMR safe registers , , and with flickering expressed by the technique.
The models in Figure 13 and Figure 14 were found fully correct, from all the mutual exclusion properties, with the overtaking factor being . Concerning the TT’s solution based on the Lycklama and Hadzilacos (LH) algorithm [15] for processes, the TT-S2’s algorithm uses fewer shared space variables: 3 bit per process for TT-S2 instead of 4 bit per process required by TT-LH2 [15].
The correct behavior of TT-S2 was also confirmed when flickering is expressed by the technique. The TT-S2 models were verified until . Table 1 collects the execution time () in sec, and the memory usage () in GB required by the model checker in the case with the non-critical section (NCS) supposed to have a 0 duration. After having checked that the model behaves correctly with NCS which has an arbitrary duration (also infinite to model process termination), setting NCS to a 0 duration ensures maximal process competition (a process that exits the CS immediately re-enters to compete). TT-S2 was separately studied in the three cases of formulation of register flickering and for the three basic TCTL queries [20] (see also Section 3.2) devoted to checking the absence of deadlocks (satisfied), the mutual exclusion correctness (satisfied), and the assessment of the overtaking factor ( when ).

Table 1.
Model checking efficiency of the TT-S2 algorithm with the three flickering techniques and processes.
As one can see from Table 1, the and techniques imply similar verification performances. The two flickering techniques are outperformed by the technique, which ensures a reduced verification time and a lower memory usage. It should be noted that the extra variables introduced by the technique do not cause a degradation of the model checking work because they normally stay at their false default value.
As another significant case, the basic Dekker’s algorithm for processes [4,5,14] used as the arbitration unit in a tournament tree (TT-D2) was considered. TT-D2 admits both output variables (, one per node of the TT) and non-output variables (, one per ancestor node). However, as shown in [14], TT-D2 does not suffer from scrambling because only the winner of a local arbitration writes on the of the ancestor node the ID of the sibling process. As a consequence, TT-D2 is only affected by flickering, and it was verified using separately the three techniques proposed in this paper.
Model checking the TT-D2 model for and the NCS with 0 duration, confirmed the corrected behavior of the mutual exclusion solution with all three flickering techniques. Performance results are collected in Table 2. The superior character of the technique emerged. In particular, the scenario with which causes state explosion in the state graph when the or technique is used, produced the results reported in Table 3. With also the TT-D2 model based on generates state explosion.

Table 2.
Model checking efficiency of the TT-D2 algorithm with the three flickering techniques and processes.

Table 3.
Model checking efficiency of the TT-D2 algorithm with the technique and processes.
Similar results were also observed on many other mutual exclusion algorithms [11,13,14,15], which were previously handled by the flickering technique only. The technique emerged to be an improved and general way for handling SWMR non-atomic registers.
6. Conclusions
This paper proposes techniques for specifying register flickering and scrambling in mutual exclusion algorithms executing in non-atomic memory [22]. The techniques are embedded into a formal methodology for modeling and exhaustive verification of mutual exclusion protocols. The methodology is based on timed automata [16] and the Uppaal model checker [19,20,21].
With respect to similar formal methods, e.g., based on process algebra and model checking [22], this paper argues the proposed approach is more intuitive yet powerful to use.
Several examples were thoroughly modeled and verified using the consistency rules of non-atomic registers described in this paper. Observed results comply with results reported in [22]. Some solutions were also extended for them to be used in the context of the tournament tree (TT) organization [11,14,27]. TT provides a standard and efficient way of supporting mutual exclusion for processes by relying on particular solutions for processes used as the arbitration unit. As an original result of this paper, although Szymanski’s algorithm [25] was proved by our work to be incorrect with both atomic and non-atomic registers, its version for processes, modified according to the indications in [31], is not only fully correct with non-atomic registers but exploited as the arbitration unit in TT is capable of furnishing correct mutual exclusion for processes.
The paper also reports some experimental results concerning the verification efficiency of three flickering techniques. The so-called technique, which is a novel contribution of this paper, emerged to be the best one in all the carried-out experiments.
Ongoing and future work will be geared to the following points: first, to continue applying the developed non-atomic register consistency techniques to other mutual exclusion algorithms; second, to make a detailed experimental comparison of the proposed method with the approach described in [22]; third, to consider the modeling of further consistency rules of non-atomic registers as proposed, e.g., in [35].
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The author declare no conflict of interest.
References
- Lamport, L. The mutual exclusion problem: Part I—A theory of interprocess communication. J. ACM 1986, 33, 313–326. [Google Scholar] [CrossRef]
- Lamport, L. The mutual exclusion problem: Part II—Statement and solutions. J. ACM 1986, 33, 327–348. [Google Scholar] [CrossRef]
- Raynal, M. Concurrent Programming: Algorithms, Principles, and Foundations; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Dijkstra, E.W. Co-operating sequential processes. In Programming Languages: NATO Advanced Study Institute: Lectures Given at a Three Weeks Summer School Held in Villard-le-Lans; Genuys, F., Ed.; Academic Press Inc.: Cambridge, MA, USA, 1965; pp. 43–112. [Google Scholar]
- Dekker, T.J. History of Dekker’s algorithm for mutual exclusion. In Tales of Electrologica: Computers, Software and People; Alberts, G., Groote, J.F., Eds.; Springer Nature: Cham, Switzerland, 2022; Chapter 6; pp. 111–120. [Google Scholar]
- Dijkstra, E.W. Solution of a problem in concurrent programming control. Commun. ACM 1956, 8, 569. [Google Scholar] [CrossRef]
- Knuth, D.E. Additional comments on a problem in concurrent programming control. Commun. ACM 1966, 9, 321–322. [Google Scholar] [CrossRef]
- de Bruijn, N.G. Additional comments on a problem in concurrent programming control. Commun. ACM 1967, 10, 137–138. [Google Scholar] [CrossRef]
- Eisenberg, M.A.; McGuire, M.R. Further comments on Dijkstra’s concurrent programming control problem. Commun. ACM 1972, 15, 999. [Google Scholar] [CrossRef]
- Peterson, G.L. Myths about the mutual exclusion problem. Inf. Process. Lett. 1981, 12, 115–116. [Google Scholar] [CrossRef]
- Nigro, L.; Cicirelli, F. Property assessment of Peterson’s mutual exclusion algorithms. Appl. Comput. Intell. 2024, 4, 66–92. [Google Scholar] [CrossRef]
- Frenzel, L.E. Dual-Port SRAM Accelerates Smart-Phone Development. Electronic Design 2004. Available online: https://www.electronicdesign.com/technologies/industrial/boards/article/21774041/dual-port-sram-accelerates-smart-phone-development (accessed on 31 August 2024).
- Nigro, L.; Cicirelli, F. Correctness Verification of Mutual Exclusion Algorithms by Model Checking. Modelling 2024, 5, 694–719. [Google Scholar] [CrossRef]
- Nigro, L.; Cicirelli, F.; Pupo, F. Modeling and Analysis of Dekker-based Mutual Exclusion Algorithms. Computers 2024, 13, 133. [Google Scholar] [CrossRef]
- Nigro, L. Formal modelling and verification of Lycklama and Hadzilacos’s mutual exclusion algorithm. Mathematics 2024, 12, 2443. [Google Scholar] [CrossRef]
- Alur, R.; Dill, D.L. A theory of timed automata. Theor. Comput. Sci. 1994, 126, 183–235. [Google Scholar] [CrossRef]
- Baier, C.; Katoen, J.P. Principles of Model Checking; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Clarke, E.M.; Klieber, W.; Nováček, M.; Zuliani, P. Model checking and the state explosion problem. In LASER Summer School on Software Engineering; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1–30. [Google Scholar]
- Uppaal on-Line. Available online: https://uppaal.org (accessed on 31 October 2024).
- Behrmann, G.; David, A.; Larsen, K.G. A tutorial on UPPAAL. In Formal Methods for the Design of Real-Time Systems; Bernardo, M., Corradini, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; LNCS 3185; pp. 200–236. [Google Scholar]
- Zhou, W.; Zhao, Y.; Zhang, Y.; Wang, Y.; Yin, M. A comprehensive survey of UPPAAL-assisted formal modeling and verification. Softw. Pract. Exp. 2024, 1–26. [Google Scholar] [CrossRef]
- Spronck, M.; Luttik, B. Process-Algebraic Models of Multi-Writer Multi-Reader Non-Atomic Registers. In Proceedings of the 34th International Conference on Concurrency Theory (CONCUR) 2023, Antwerp, Belgium, 18–23 September 2023; pp. 5.1–5.17. [Google Scholar]
- Buhr, P.A.; Dice, D.; Hesselink, W.H. Dekker’s mutual exclusion algorithm made RW-safe. Concurr. Comput. Pract. Exp. 2016, 28, 144–165. [Google Scholar] [CrossRef]
- Szymanski, B.K. A simple solution to Lamport’s concurrent programming problem with linear wait. In Proceedings of the 2nd International Conference on Supercomputing, ICS 1988, Saint Malo, France, 4–8 July 1988; pp. 621–626. [Google Scholar] [CrossRef]
- Szymanski, B.K. Mutual exclusion revisited. In Proceedings of the 5th Conference on Information Technology 1990, Jerusalem, Israel, 22–25 October 1990; pp. 110–117. [Google Scholar] [CrossRef]
- Kessels, D.E. Arbitration without common modifiable variables. Acta Inform. 1982, 17, 135–141. [Google Scholar] [CrossRef]
- Hesselink, W.H. Tournaments for mutual exclusion: Verification and concurrent complexity. Form. Asp. Comput. 2017, 29, 833–852. [Google Scholar] [CrossRef]
- Groote, J.F.; Keiren, J.J.; Luttik, B.; de Vink, E.P.; Willemse, T.A. Modelling and analysing software in mCRL2. In Formal Aspects of Component Software, Proceedings of the 16th International Conference, FACS 2019, Amsterdam, The Netherlands, 23–25 October 2019; Proceedings 16; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 25–48. [Google Scholar]
- Hesselink, W.H. Verifying a simplification of mutual exclusion by Lycklama–Hadzilacos. Acta Inform. 2013, 50, 199–228. [Google Scholar] [CrossRef]
- Lamport, L. On interprocess communication. Part II Algorithms. Distrib. Comput. 1986, 1, 86–101. [Google Scholar] [CrossRef]
- Buhr, P.A.; Dice, D.; Hesselink, W.H. High-performance N-thread software solutions for mutual exclusion. Concurr. Comput. Pract. Exp. 2015, 27, 651–701. [Google Scholar] [CrossRef]
- Lamport, L. The TLA+ Hyperbook. Available online: https://lamport.azurewebsites.net/tla/hyperbook.html (accessed on 31 August 2024).
- Lamport, L. Proving the correctness of multiprocess programs. IEEE Trans. Soft. Eng. 1977, 3, 125–143. [Google Scholar] [CrossRef]
- Anderson, J.H.; Gouda, M.G. Atomic semantics of non-atomic programs. Inf. Process. Lett. 1988, 28, 99–103. [Google Scholar] [CrossRef]
- Shao, C.; Welch, J.L.; Pierce, E.; Lee, H. Multiwriter consistency conditions for shared memory registers. SIAM J. Comput. 2011, 40, 28–62. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).