Abstract
In the present study, a novel parametric family of fuzzy implications is introduced and its properties are examined. The parametric family of implications is produced only via a fuzzy negation. This in turn enables the effortless production of a wide range of implications from which to select the one that best fits a given problem, for example in fuzzy inference systems or fuzzy neural networks. The fuzzy negations that have been selected as a basis for the proposed methodology are strong, i.e., involutions, thus leading, in general, to the generated fuzzy implications possessing many desirable additional properties. We have examined which of these properties hold for the implications produced by our algorithm and under which conditions. Finally, it is demonstrated that the family of implications generated via the proposed methodology generalizes other well-established implications, including the Łukasiewicz implication.
1. Introduction
Fuzzy implications have been developed into an integral and crucial part of fuzzy logic. They generalize the classical logic implication operator and enable “if–then” rules to be applied in a fuzzy inference system [1,2]. Apart from the basic properties that a fuzzy implication has to satisfy by definition, researchers have proposed many additional properties, e.g., [3,4,5], each usually satisfied by a particular subclass of implications. Depending on the specific context of the application, a different set of these properties might be desired. Even within a fuzzy implication subclass, it is often desirable to find the one that fits a given dataset best, i.e., to finetune the fuzzy inference system [6,7].
Thus, it becomes clear that, in such applications, it is imperative for the researcher to have an algorithm capable of producing a wide class of implications from which to select the one that best fits their particular problem. Among the many most commonly used ones, we focus in this paper on the so-called implications [8]. implications are produced using a fuzzy distinction S (fuzzy “or”) in conjunction with a fuzzy negation N based on the well-known logical truth “if P then Q” ≡ “if NOT P then NOT Q”.
In the present study, an algorithmic approach for producing a parametric family of implications is presented. As a basis for the developed algorithm, we have utilized the strong fuzzy negation introduced in [9], which is derived via the parametric form of the conical sections equation. There are other families of parametric negations in the literature, such as the Sugeno or Yager classes [10]. However, as the authors in [9] demonstrated, the examined methodology is more general since it produces some of these classes as a subset of the produced negations.
The introduced parameter enables, as mentioned, many different implications to be chosen from for a particular problem. This is an advantage compared to other methodologies. For example, Yager’s f- and g-generated implications [11] or the implications presented in [12] are not produced by a parametric generator. In addition, the fact that the implications are produced via a strong negation leads to many additional desirable properties being satisfied, as indicated in the present study. Finally, this family of implications generalizes other well-known implications, such as the Łukasiewicz implication, as, for special choices of the parameter, these are produced by our algorithm.
Thus, the contributions of the study presented herein are focused in two main directions. On the one hand, we introduce an algorithm to effortlessly produce an infinite variety of implications, which can be used in an integrated decision-making system in a fuzzy environment. On the other hand, the theoretical mathematical properties of this family of implications are studied, which is a necessary step towards their successful implementation in a practical application.
2. Preliminaries
In this section, we present the necessary mathematical propositions that constitute the basis of the developed algorithm. These fundamental building blocks pertain to fuzzy implications, fuzzy disjunctions, as well as fuzzy negations. Their definitions and some of their well-known properties are examined below. These are included in many well-known textbooks on fuzzy logic, e.g., [10,13,14].
A fuzzy implication expands the notion of the classical implication operator → to the domain of fuzzy logic. In classical logic, the implication operator is expressed via the tautology “IF P THEN Q” ≡ “NOT P OR Q”. Fuzzy implications generalize the truth table of the above relation. Similarly, a fuzzy negation generalizes the truth table of the classical negation ¬ and a fuzzy disjunction generalizes the notion of the classical ∨ (or) operator. We begin by presenting the definition and some additional properties of fuzzy implications.
Definition 1.
A bivariate function is called a fuzzy implication if we have the following conditions:
Equations (J1–J5) correspond to a set of functions denoted by . In addition to the above, there have been many complementary properties in different publications, e.g., [3,4,5]. Each of these properties defines a subset of , i.e., a subclass of the encompassing set of fuzzy implications. Some common ones that we will be using in this paper are provided in the following definition.
Definition 2.
Given a function , it is said to satisfy
- 1.
- the left neutrality property if
- 2.
- the exchange principle if
- 3.
- the identity principle if
- 4.
- the ordering property if
Definition 3.
A univariate function is called a fuzzy negation if
The set of functions that satisfy the above conditions can be denoted as . These conditions are generic and can be true for a wide array of functions. In addition to the above, several properties pertaining to fuzzy negations have been investigated, which define distinct subclasses of . Specifically, as we have mentioned, the fact that the negations that form the basis of the proposed methodology are “strong” leads to many favorable properties for the generated parametric family of implications. To this end, we present below the pertinent definitions.
Definition 4.
A fuzzy negation is called
- 1.
- strict if
- 2.
- strong if
The law of contraposition is another well-known tautology from the realm of classical logic. Formally, for two propositions P and Q, this can be expressed via the formula “IF P THEN Q” ≡ “NOT Q THEN NOT P”. This can be extended in fuzzy logic as follows [10] (p. 20):
Definition 5.
Let . Furthermore, let be a fuzzy negation. Then, J satisfies the following:
- 1.
- law of contraposition if
- 2.
- left law of contraposition if
- 3.
- right law of contraposition if
If J satisfies the (left, right) contrapositive symmetry with respect to N, then we also denote this by CP(N) (respectively, by L-CP(N), R-CP(N)). For a strong fuzzy negation, as shown in [10] (p. 21), the above 3 statements are equivalent.
It is important to highlight that Equations (CP), (L-CP), and (R-CP) are equivalent in the classical logic domain. This is because of the well-known identity . However, as was shown in Equation (N5), this intuitive property only holds for the subclass of strong negations. Thus, the above equivalence does not hold in general.
Definition 6.
A map is called a fuzzy disjunction or triangular conorm (often abbreviated as t-conorm) if ; the following hold:
In addition to the above, we also have many complementary properties of t-conorms. In particular, a property we will use in the sequel is the so-called Archimedean property [10] (p. 45). A t-conorm S is said to satisfy the Archimedean property if such that .
For a continuous function, the above definition is equivalent to . Given the above, we have the following theorem [10] (p. 47):
Theorem 1.
For a map , the propositions presented below are equivalent:
- 1.
- S is a continuous t-conorm that satisfies the Archimedean property.
- 2
- There exists a continuous function g with domain of closed interval and co-domain , such thatFurthermore, the function g is strictly increasing in its domain and must satisfy the boundary condition . Finally, the function g can be determined uniquely, up to a positive multiplicative constant.
In the domain of classical logic, the the law of excluded middle is an additional statement that combines the previously examined notions of negation (“not”) and disjunction (“or”). Formally, for two propositions p and q, the relation is always true. This can be extended in fuzzy logic as follows [10] (p. 52):
Definition 7.
Given a t-conorm S and a function , i.e., a fuzzy negation, the pair obeys the so-called law of excluded middle (LEM) if
As was previously mentioned, in the realm of classical logic, the identity “IF P THEN Q” ≡ “NOT P OR Q” is always true. Thus, it is natural to extend this definition to fuzzy logic as follows [10] (p. 57):
Definition 8.
Given a function , i.e., a fuzzy negation, and a triangular conorm S, a map defined as
will be called an implication. The implications that are generated via the above relationship will be denoted as .
For an implication , the following proposition holds [10] (pp. 57, 61, 64–65):
Proposition 1.
Let N be a fuzzy negation, S a t-conorm, and the associated implication. Then,
3. Main Results
We present an algorithm to produce fuzzy implications of a special form based only on a strong fuzzy negation. The specific strong fuzzy negation employed here is based on the properties of conical sections and was introduced by Souliotis and Papadopoulos in [9]. To this end, first recall that, as demonstrated in Theorem 1, a t-conorm can be generated via a function g as
and note that is a continuous function, which is strictly increasing in its domain. Let , where denotes the strong negations based on conical sections introduced in [9]. As shown by the authors, this can take one of two forms. Specifically, in the first case, we have
which leads to the so-called Sugeno family of negations. In the second case, we have
Note that, using the previous transformation, g is indeed a strictly increasing function, with the additional boundary condition . Finally, recall that was proven to be strong; i.e., . Now, note that we have
This leads to
and finally
Thus, the family of strong negations presented in Equations (2) and (3) is utilized to parametrically produce infinitely many implications. Due to the fact that these negations are strong, the produced family of implications possesses several desirable properties, as shown in the sequel. To this end, for the above implication , the properties presented in the proposition below are true:
Proposition 2.
Proof (Proof of Proposition 2).
The proof of (i) and (ii) is a direct application of the corresponding points in Proposition 1. The proof of (iii) is a direct application of points (iii) and (v) in Proposition 1 and the fact that every strong fuzzy negation is also strict [10] (p. 15). For point (iv), note that, since was proven to be strong in [9], from (vi) and (vii) in Proposition 1, we only need to prove that, if , then the disjunction–negation pair , with S defined as in (5) and defined as in Equations (2) and (3), satisfies Equation (LEM). To this end, first note that, from [9], we have
A straightforward substitution can be performed in (7), which yields the following inequality:
Similarly, an additional substitution can also be performed in (7). In turn, this gives rise to the following series of inequalities:
The inequalities presented in (8) and (9) can be combined, which results in the following relation:
where the last inequality holds due to (7). Therefore, it trivially holds that
From the above, we have
which is exactly (LEM). This completes the proof. □
Thus, the algorithm presented in Equation (6), in conjunction with the conic negations presented in Equations (2) and (3), provide a generic procedure for the parametric production of an infinite number of equations. As was proven in the above proposition, this family of functions not only satisfies the fundamental properties of Equations (J1–J5) and are thus fuzzy implications but they also satisfy several additional desirable properties. Furthermore, the family of implications is generic and can produce other well-known implications as a subclass.
For example, for , we have , which, through straightforward calculations, yields the well-known Łukasiewicz implication . Similarly, for , and using (3), we have . This Yager-type negation leads to the fuzzy implication
The graphs of the above implications and the graphs of the strong negations that produced them are shown in Figure 1 and Figure 2, respectively.
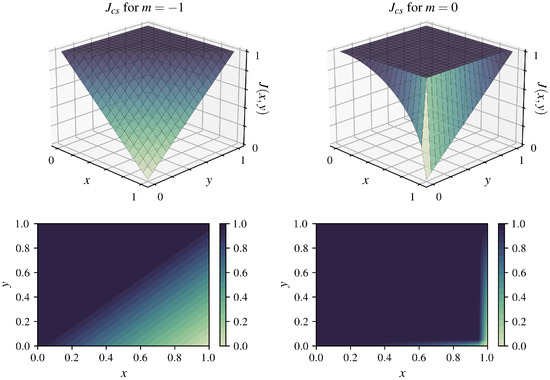
Figure 1.
for (left) using (3), i.e., the Łukasiewicz implication, and for (right).
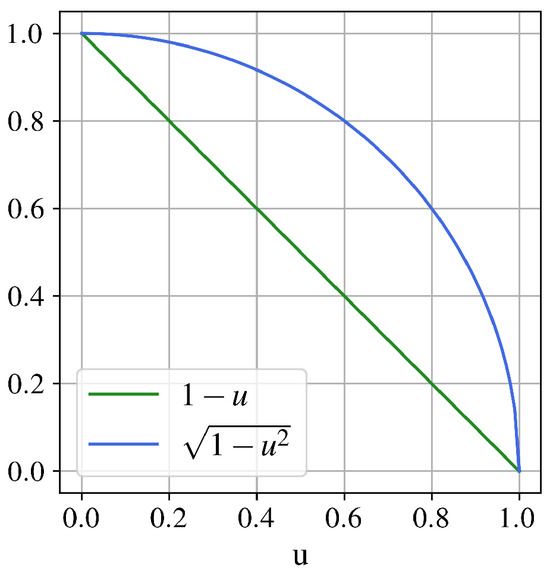
Figure 2.
for and .
4. Conclusions
In the manuscript presented herein, an algorithm for the parametric production of a family of fuzzy implications is introduced. Deviating from the previously established methodologies, the proposed algorithm is based solely on a single fuzzy negation. Specifically, the proposed algorithm is based on the strong fuzzy negations based on the conical sections introduced by Souliotis and Papadopoulos in [9]. This extends the available range of implications for researchers to select the most suitable one for any given application. In addition, it generalizes other well-known implications, which are produced by our algorithm for the special choices of the parameter.
Furthermore, selecting a strong negation as a basis for the proposed formulation has essentially removed all the constraints of Proposition 1. In turn, this has led to the proof of Proposition 2, which includes several other intuitive and desirable properties, in addition to the ones presented in Definition 1 and conditions (J1–J5). Specifically, the generated family of implications was shown to satisfy Equations (ExPr), (NePr), and (CP)-(R-CP)-(L-CP). In addition, we have shown that, for the given family of implications, the ordering property and identity principle are satisfied for a range of the examined parameter m.
A future path of research includes the application of this family of implications in a fuzzy inference system or a fuzzy neural network and comparing the performance obtained by an optimal choice of our parameter m against other well-known implications. It should be noted that the evaluation of the optimal fuzzy implication is carried out individually for each specific application. The proposed methodology offers a tool in order to parametrically, and thus seamlessly, produce infinitely many implications in order to identify the optimal one for each case. Finally, additional theoretical investigations can be conducted and further properties of this family of implications can be established.
Author Contributions
I.K., G.S., B.P. and A.K. co-authored the final manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
The present study did not receive any external funding that might affect the findings presented herein.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare that there are no conflicts of interest that could have influenced the findings presented in the paper.
References
- Azeem, M.F. Fuzzy Inference System: Theory and Applications; BoD–Books on Demand: Norderstedt, Germany, 2012. [Google Scholar]
- Sabri, N.; Aljunid, S.; Salim, M.; Badlishah, R.; Kamaruddin, R.; Malek, M. Fuzzy inference system: Short review and design. Int. Rev. Autom. Control 2013, 6, 441–449. [Google Scholar]
- Trillas, E.; Valverde, L. On implication and indistinguishability in the setting of fuzzy logic. In Readings in Fuzzy Sets for Intelligent Systems; Elsevier: Amsterdam, The Netherlands, 1993; pp. 97–104. [Google Scholar]
- Smets, P.; Magrez, P. Implication in fuzzy logic. Int. J. Approx. Reason. 1987, 1, 327–347. [Google Scholar] [CrossRef]
- Gottwald, S.; Gottwald, P.S. A Treatise on Many-Valued Logics; Research Studies Press: Hertfordshire, UK, 2001; Volume 3. [Google Scholar]
- Herrera, F.; Lozano, M.; Verdegay, J.L. Tuning fuzzy logic controllers by genetic algorithms. Int. J. Approx. Reason. 1995, 12, 299–315. [Google Scholar] [CrossRef]
- Shi, Y.; Mizumoto, M. A new approach of neuro-fuzzy learning algorithm for tuning fuzzy rules. Fuzzy Sets Syst. 2000, 112, 99–116. [Google Scholar] [CrossRef]
- Baczyński, M.; Jayaram, B. On the characterizations of (S, N)-implications. Fuzzy Sets Syst. 2007, 158, 1713–1727. [Google Scholar] [CrossRef]
- Souliotis, G.; Papadopoulos, B. An algorithm for producing fuzzy negations via conical sections. Algorithms 2019, 12, 89. [Google Scholar] [CrossRef]
- Baczynski, M.; Jayaram, B. Fuzzy Implications; Springer: Berlin/Heidelberg, Germany, 2008; Volume 231. [Google Scholar]
- Yager, R.R. On some new classes of implication operators and their role in approximate reasoning. Inf. Sci. 2004, 167, 193–216. [Google Scholar] [CrossRef]
- Dombi, J. On Implication Operators. In Proceedings of the Aggregation Functions in Theory and in Practice, Skövde, Sweden, 12–22 June 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 241–252. [Google Scholar]
- Klir, G.J.; Yuan, B. Fuzzy sets and fuzzy logic: Theory and applications. Possibility Theory Probab. Theory 1996, 32, 207–208. [Google Scholar]
- Nguyen, H.T.; Walker, C.L.; Walker, E.A. A First Course in Fuzzy Logic; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).