Abstract
One of the most significant applications of mathematical numerical methods in biology is the theoretical description of the convectional reaction–diffusion of chemical compounds. Initial biological objects must be appropriately mimicked by digital domains that are suitable for further use in computational modeling. In the present study, an algorithm for the creation of a digital phantom describing a local part of nervous tissue—namely, a synaptic contact—is established. All essential elements of the synapse are determined using a set of consistent Boolean operations within the COMSOL Multiphysics software 6.1. The formalization of the algorithm involves a sequence of procedures and logical operations applied to a combination of 3D Voronoi diagrams, an experimentally defined inner synapse area, and a simple ellipsoid under different sets of biological parameters. The obtained digital phantom is universal and may be applied to different types of neuronal synapses. The clear separation of the designed domains reveals that the boundary’s conditions and internal flux dysconnectivity functions can be set up explicitly. Digital domains corresponding to the parts of a synapse are appropriate for further application of the derived numeric meshes, with various capacities of the included elements. Thus, the obtained digital phantom can be effectively used for further modeling of the convectional reaction–diffusion of chemical compounds in nervous tissue.
1. Introduction
Numerical analysis and scientific computing have been gaining prominence in recent years, especially in the application of different algorithms to find solutions to fundamental problems. One of the most important research interests in this context is convection–diffusion equations (e.g., Burgers’ equation). To numerically solve such problems, different algorithms have been used, including the two-grid method [1,2], three-level conservative difference scheme [3], and non-linear compact difference scheme [4]. Recently, novel methods for solving three-dimensional evolution equations have been proposed [5,6,7]. Other biologically applicable classes of equations describing sub-diffusional processes have been successfully solved using the orthogonal Gauss collocation method [8] and a linearized orthogonal spline collocation method [9]. Additionally, the finite difference scheme is especially useful for evaluation of the three-dimensional time-fractional telegraph equation [10], fourth-order time-fractional diffusion-wave equations [11], and multi-term non-local Nagumo-type equations [12]. Partial integra-differential equations can be solved by applying the time two-grid finite difference algorithm [13] or a space–time Sinc-collocation method [14]. An interesting approach for the approximation of a 2D non-local non-linear wave equation has been developed on the basis of a time two-grid difference method, where coarse grid numerical solutions are used as sources for the construction of a linearized system on the fine grid [15].
Remarkably, biomedical research and the description of various living systems are two areas where mathematical modeling can be successfully applied [16,17]. Numerical algorithms are tools that are capable of describing both macro-objects, such as populations, and micro-objects, such as cells and sub-cellular structures. For instance, recent advancements have been made in various mathematical theories of epidemiology [18,19,20], molecular dynamics of biopolymers [21], cardiac electrophysiology [22,23], convectional reaction–diffusion [24,25], and so on. The creation of a digital object that matches the studied biological system is a key aspect of such a modeling approach. The algorithms used in these cases are developed based on step-by-step analyses of different types of data; for example, through analyzing real measured cell images, the knowledge gained can be combined with the primary knowledge in the fields of molecular biology, physics, and electrical engineering [26]. A biological object usually consists of several separate parts having various properties. This leads to heterogeneity, causing the final digital phantom to be characterized by high geometric complexity. The nervous parenchyma is one of the most complex examples and, for its reconstruction, fluorescence microscopy image stacks are commonly evaluated [27]. For branched cells such as neurons, another approach based on probabilistic filtering by sequential Monte Carlo estimation can be applied, using prediction and update models designed specifically for tracing neuronal branches in microscopic image stacks [28]. A digital phantom of nervous tissue can be created de novo using common experimental data describing the structure and features of the tissue. For this purpose, a novel algorithm based on 3D Voronoi diagrams has been proposed [29]. The main advantage of such an approach is the detailed formation of different cells in the parenchyma (e.g., neurons, astrocytes, oligodendrocytes, and so on), while maintaining scale and compartment localization. It is essential that the proposed algorithm makes it possible to apply the phantom for further numerical modeling using the finite element method (FEM). The local design of an algorithm concerning a synaptic contact between neurons has been previously proposed elsewhere [30,31]. Nevertheless, the potential interconnection of astrocyte leaflets and synaptic contact neurons remains to be addressed. In the present study, a glutamatergic synapse is used as a prototype for the creation of a digital phantom (Figure 1). The mechanism of synaptic transmission consists of several steps. Initially, a presynaptic neuron is filled up with synaptic vesicles containing neuromediators (glutamate, Glu). These vesicles are attached to a presynaptic membrane. The presynaptic release machinery comprises mediating membrane fusion proteins (SNARE and Munc18-like proteins), enabling Ca2+-triggered fusion proteins (synaptotagmines and corresponding complexin cofactors) and AZ scaffold proteins, which tether the synaptic vesicles and recruit Ca2+ channels to neurotransmitter release sites (Rab3-interacting molecules, RIMs; RIM binding proteins; and Munc13-like proteins). The vesicular release machinery is canonical for all types of synapses and neuromuscular junctions, and just one feature distinguishes presynaptic terminals with different specializations—neurotransmitters and matching transporters, which fill vesicles, and synthetizing enzymes (if not glutamate or glycine, as usual cytoplasmic metabolites) [32]. The whole process of vesicular release is generally referred to as SNAR-mediated exocytosis. The released neuromediators diffuse to the postsynaptic membrane, then activate specific membrane receptors (NMDAR and AMPAR, in the considered case). Then, the molecules of Glu move out of the synaptic cleft due to convectional diffusion. This process is accompanied by Glu reuptake through specific transporters (EAAT(i)) on the membranes of astrocytes and neurons [33]. Then, Glu is converted to glutamine (Gln) by glutamine synthetase, as part of the glutamate–glutamine cycle. Gln can be transferred fluently to neurons, where it is converted back to Glu by glutaminase. The physiological functioning of the synapse is strongly regulated by the balance between Glu release, convectional diffusion, and EAAT-mediated reuptake.
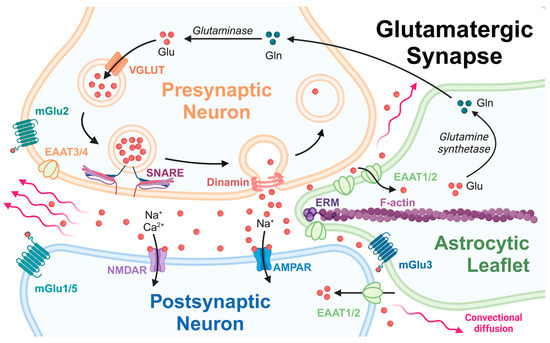
Figure 1.
The scheme of a glutamatergic synapse in the central nervous system (CNS). Created with BioRender.com.
There are significant experimental evidences proving that the activity of glial glutamate transporters (EAATs) ceases under pathological conditions and aging, and the abundance of glutamate may damage the surrounding nervous tissue and hamper normal brain functions [34,35].
The density and mutual distribution of EAATs on an astrocytic leaflet (Figure 1) are the main factors determining the balance of released Glu being included into the glutamate–glutamine cycle [35]. This process makes it possible to avoid excitotoxic damage to brain tissue in the CNS. Knowing the precise position of an astrocyte membrane relating to pre- and postsynaptic membranes makes it possible to correctly digitize a native synapse, which provides a powerful tool for the further modeling of the convectional diffusion of Glu during spillover. The introduced algorithm makes it possible to develop a digital phantom describing the properties of the synaptic cleft correctly. A numerical mesh of different parameters can be further applied to the phantom to solve a boundary convectional reaction–diffusion problem. The purpose of this solution is to provide information on how glutamate transporters are distributed on the surface of astrocyte membranes and how they relate to the neurotransmitter pool in the synaptic cleft.
It is essential to note that, despite the existence of elaborate approaches for solving different boundary PDE problems, examples considering the application of these mathematical methods to real biological objects remain scarce. The explanation of this gap is the difficulties associated with reconstructing real-scale structures of biological prototypes which are suitable for further modeling. The digital model of the object should be three-dimensional with a clear indication of the boundary’s orientation, and the most properties of the initial biological object must be taken into account. In the present study, we developed a method for the creation of an isolated synapse digital phantom, with respect to detailed localization of the contacts between essential cellular structures of the synapse; namely, neurons and astrocytes. For the first time, a precise validated structure of an astrocytic leaflet is described, in terms of an algorithm for the creation of geometric domains. It is essential to note that the main goal of the introduced algorithm is to reveal the informal explicit mutual relation between the digital domains, making it applicable for numerical modeling of biological prototypes. The obtained phantom makes it possible to evaluate the important properties of living nervous tissue, such as the convectional diffusion of mediators in the interstitial fluid. The described algorithm can be considered as a powerful tool for the modeling of different types of synaptic contacts.
A simplified 3D structure of nervous tissue was constructed through the averaging of parameters [36]. However, considering the average fluxes and concentrations in the distributed radial model to correspond to quantities in a lumped model, the authors concluded that varying the locus of the synaptic activity in reference to the capillaries significantly alters the lumped model parameters. Further consideration of the metabolism of neurons was also made for the development of a 3D structure of brain tissue [37]. The diffusion process was numerically executed using spatial discretization based on FEM, and the resulting large system was time integrated using robust stiff solvers. Computational experiments showed the effects of ECS tortuosity, gap junction strength, and spatial anisotropy in the astrocyte network on the energy metabolism of the brain [37]. However, the structure of the domains was essentially simplified, and there was no ability to capture the detailed distributions of metabolites near neurons and astrocytes. For this purpose, a more detailed phantom structure must be established, as is the case for the proposed algorithm.
The scope of the proposed methodology is to create a detailed digital phantom of a local neuron/neuron contact with astrocytic leaflet which is suitable for further numerical modeling. An essential property of such a phantom is its suitability for the direct modeling of convectional diffusion in ISF and reaction–diffusion in neurons and astrocytes.
Thus, in the present study, an algorithm for the creation of a digital synaptic contact is introduced. The main advantages of the proposed method are (i) a clear relationship with the considered biological structures; (ii) validated sizes and distances inside and outside the phantom; (iii) precisely structured localization of presynaptic vesicle–membrane contacts; and (iv) possibility of further application of the meshes in numerical modeling.
2. Materials and Methods
The basic aspects of the introduced algorithm are four simple bodies that should be initially chosen. Three of them are the closest 3D Voronoi diagram elements (Ω1–3), and the fourth is an ellipsoid (Ωellipsoid). Originally, an algorithm for digital synaptic cleft phantom creation, using the example of a glycine synapse, was described in the works of Nartsissov et al. [30,31]. The essential details which must be additionally included in the phantom construction process are the correct localization of an active zone (AZ, 𝜕ΩAZ) of neuromediator release in the presynaptic membrane, properly indicated and localized postsynaptic density (PSD, 𝜕ΩPSD), and the structural placement of an astrocytic leaflet between the neurons. To digitalize these physiological features of a synaptic contact, a number of steps including Boolean operations should be fulfilled. In order to systematize the used geometric objects, we introduce the nomenclature for the list of bodies and surfaces in Table 1. The working elements used in the algorithm are grouped into several units. The main principle of the classification is as follows: the full-body domain is indicated with a Greek letter (for example, Ω), and its surface is indicated with a prefix 𝜕 (for example, 𝜕Ω). Initially, three 3D Voronoi bodies were chosen, as indicated in the Section “Input Voronoi diagram bodies”. The next section (“Auxiliary objects, planes, and surfaces”) describes the auxiliary elements, including the bodies and surfaces. The final obtained digital domains are collected in the Section titled “Digital domains corresponding to nervous tissue’s cells and ISF”. The Section “Digital surfaces coinciding with essential biological areas” points out the essential surfaces which are engaged in further mathematical modeling for indication of the boundary conditions according to biological functions.

Table 1.
Nomenclature of the bodies and surfaces used in the algorithm. The first column indicates the object (full-body, surface, plane), while the second column includes general descriptions of the appropriate objects. The comments describing the Boolean operations, relations between the objects, the positions of the units, and so on are described in the third column.
For the creation of the digital phantom, any kind of CAD Programming Software can be used. In the present study, all Boolean and logical operations were performed using the COMSOL Multiphysics software version 6.1. The proposed algorithm for digital phantom creation consists of several steps, as described below.
2.1. Forming of Pre- and Postsynaptic Endings and an Auxiliary Plane
Pre- and postsynaptic endings (Ωpre and Ωpost) are close neighbors of each other, which capture the AZ (𝜕ΩAZ) and PSD (𝜕ΩPSD) membrane regions at their interface. As indicated above, these objects are created with respect to the two close 3D Voronoi diagram (Ω1 and Ω2) members in the experimentally defined synapse phantom. In addition, they should be scaled to adjust to experimental data. In particular, the digital objects reconstructed on the basis of experimental measurements clearly indicate the existence of plane sheets with a distance of no less than 7 nm combined with tunnels having a width of about 18 nm [27,38]. Initially, the creation of 3D Voronoi diagrams was fulfilled at a large scale; then, for the optimal fit to the indicated conditions, a scale coefficient of 2.1∙10−7 was applied.
An auxiliary plane (𝜕ω) is built between the bodies Ω1 and Ω2 for precise synapse phantom positioning and astrocytic leaflet tip formation. Laying down three points on the boundary edge where Ω1 and Ω2 approach each other, we avoid any rotation steps or construction of pivot points, and align this plane strictly between the pre- and postsynaptic endings.
The space between adjacent Ω1 and Ω2 is not uniform due to the stochastic nature of Voronoi diagram formation. The boundary of the utmost approach area of Ω1 and Ω2 is evaluated using the auxiliary objects intersection procedure. The auxiliary objects Ω′1 and Ω′2 are created with an isotropic scaling procedure, applied to each body separately with the corresponding body midpoints as the center of scaling, and an empirical scale factor (γ = 1.025, Table 1) was chosen, thereby ensuring that the distance from the Ω′i boundaries to Ωi is not less than 14.5 nm. The resulting object Ω1–2 has a peripheral edge trajectory matching the utmost approach of Ω1 and Ω2. Two of three auxiliary plane points are chosen on the Ω1–2 edge on the side of the third Voronoi body position. The last auxiliary point should oppose these, such that the resulting plane cuts the most central part of Ω1–2. The origin of the auxiliary plane coordinates is chosen to collocate with the central point on one of the adjacent boundaries of Ω1 and Ω2 (i.e., 𝜕Ω1–2 and 𝜕Ω2–1).
2.2. Synapse Phantom
A synapse phantom (SP) is a union of three primitive forms, i.e., two ellipsoids and one cylinder between them, as has been previously described [31]. This combination of primitives was chosen due to the observed tendency of the presynaptic and postsynaptic membranes to be closer at the edge of synaptic cleft [39]. We propose a range of synaptic phantoms with different total height and radius. The height of the synaptic phantoms (HSP) varies from 15 to 30 nm, reflecting different stages of the synaptic lifecycle—formation, mature state, or elimination. This difference in synaptic height is sustained with respect to composition and the interaction of synaptic adhesion molecules (SAMs) [32]. For each height value of the phantom, the synaptic radius varies from 50 to 450 nm, as has been postulated earlier [31]. The synapse phantom is constructed in an auxiliary plane 𝜕ω, and should be adjusted along zω within Ω1 and Ω2 such that the surfaces 𝜕ΩPSD and 𝜕ΩAZ are equal to each other.
2.3. Synaptic Cleft
The synaptic cleft is embedded between the first and second (Ω1 and Ω2) 3D bodies from Voronoi diagram synapse phantom track and contained within the AZ (𝜕ΩAZ) and PSD (𝜕ΩPSD) membrane lacunae. The presynaptic 𝜕ΩAZ includes multiple plausible locations for vesicular fusion pore openings (𝜕Ωifusion). The canonical vesicular release protein machinery can vary, with different isoforms expressed throughout CNS, but the underlying principle is always the same [32]. Instead of quantal vesicular release theory, intermediate release modes have been postulated, including a kiss-and-run mode which permits just a small amount of a released neurotransmitter to pass through the transient opening of a tiny fusion pore, and a partial release mode which corresponds to a more pronounced temporal and spatial span. Together with full fusion, the intermediate release modes provide clues for the characterization of synaptic plasticity. At present, partial vesicular neurotransmitter release is suggested as the dominant mode of exocytosis [40]. The vesicular partial fusion pore diameter is restrained by Dinamin 1 and reaches a maximum width of 9 nm with a timescale up to 10 ms [41]. Moreover, the binding of the vesicles appears as regularly spaced cone-shaped structures with a size of approximately 50 nm attached to the presynaptic membrane, which are known as dense projections (DPs) or, collectively, the “presynaptic particle web” or “presynaptic grid” [42]. Interestingly, the same structured localization of receptors is observed in PSD. For example, the PSD region of the glycinergic synapse features precise coordination of glycine receptors by gephyrin [30]. Thus, the collocation of 𝜕Ωifusion on 𝜕ΩAZ complies with the plausible hexagonal grid pattern of tethering synaptic vesicles and Ca2+-channel-recruiting AZ scaffold proteins (DPs) on the presynaptic membrane with unit parameter of 70 nm [42], as well as matching up with rather small vesicles of 40 nm in diameter [41].
For moderate synaptic clefts (about 100 nm in radius), the mean distance between presynaptic and postsynaptic membranes fell to 61 ± 3% at the edge of the cleft, when compared to central part [39]. In our 3D model, this difference was 62%, 47%, 38%, and 32% for synaptic cleft areas designed with 130 nm radius and various heights of the synapse phantom (15 nm, 20 nm, 25 nm, and 30 nm, respectively). Apparently, this prominent difference is a direct result of the synapse phantom geometry for the distance between the adjacent surfaces of Ω1 and Ω2, defined as a sheet with given minimal thickness [38].
According to the 3D EM reconstruction, the opposing 𝜕ΩAZ and 𝜕ΩPSD are very similar in surface estimation, varying from 0.006 to 0.445 µm2, with a mean distribution value of approximately 0.09 µm2 [43]. In our modeling environment corresponding to the synapse phantoms, 𝜕ΩAZ and 𝜕ΩPSD were in a good agreement with the experimental data indicated above. The modeling values are presented in Table 2.

Table 2.
The surface area of AZ and PSD for different chosen geometric parameters of the synapse phantom. The square of AZ is equal to the same as that for PSD.
2.4. Astrocytic Leaflets
The astrocytic leaflet has a spongy structure and protrudes within the presynaptic and postsynaptic endings to the synaptic cleft. They have a very dynamic shape and their protrusion extent varies with synaptic plasticity, circadian rhythms, stress conditions, and neurodegenerative disorders [44,45,46]. According to an EM study, about 20% to 80% of rat hippocampus spines have glia cells opposed to them [47], and only 20% to 65% of synapses could be surrounded by astrocytes at the periphery [48]. The distance between astrocytic and neuronal membranes is no less than 7 nm for ISF diffusion feasibility, as is the case for all cells of the brain parenchyma [38]. Furthermore, the leaflet tip cannot be too thin, as it must have the capacity to contain cell structure elements inside it, and the curvature of the cell membrane is limited. We took the above criteria into consideration for 3D astrocytic leaflet modeling in detail, utilizing a combination of geometric and Boolean operations.
As above, the surrounding synaptic cleft astrocytic geometric object was built by connecting the adjacent faces of 𝜕Ω1–2 and 𝜕Ω2–1 using the loft procedure (Standard Geometry module, COMSOL Multiphysics Software). The number of adjacent faces was allowed to vary, in order to enfold the chosen synaptic periphery distance. In the current work, the surrounding synaptic cleft region leaflets presented 24%, 38%, 48%, and 62% cradle variation. An additional loft operation was used to link this leaflet part to several faces of Ω3. Thus, the intermediate astrocytic leaflet structure, Ω′leaflet, was created. The Boolean subtraction operation was used on the differently scaled Ω1 and Ω2 objects for replication of the space between neuronal and astrocytic 3D objects. Similar to Ω′i, an isotropic scaling procedure was applied to each body separately, with their corresponding scaling center and an empirically chosen scale factor (λ = 1.015), and the resulting bodies are denoted as Ω″1 and Ω″2. The object after subtraction will have the required extracellular distance to Ωpre and Ωpost.
The tip of Ω′leaflet is strikingly edgy and is not suitable for further application in numerical calculations using FEM. Moreover, the leaflet tip is formed with the involvement of cell structure elements, so biologically reasonable restrictions should be applied on the stochastically created object. Responsible for astrocytic leaflet protrusion, F-actin filaments are linked through the ezrin radixin moesin (ERM) family of proteins to astrocytic transmembrane proteins at adhesion sites [49]. Ezrin has been shown to be expressed predominantly in astrocytes and knockout mice displayed glial fibrillary acidic protein (GFAP) upregulation and reactive astrogliosis [50]. Similar changes in astrocyte morphology, GFAP upregulation, and ezrin downregulation have been noticed with aging in human bran [51]. It has also been demonstrated that ezrin depletion has a direct impact on the proximity of astrocytic leaflets to the synapse and boosted extrasynaptic glutamate diffusion [44]. The N-terminal ezrin domain (FERM domain) contains the adhesion protein binding motif and has a cloverleaf shape with overall dimensions for ezrin of ~70 Å by 70 Å, and a thickness of 40 Å [52]. Connected with FERM by a long central helical domain, the helical C-terminal part of ERM protein in phosphorylated active conformation binds to F-actin filaments with diameter of 7 nm [53,54]. Hence, we propose a minimal leaflet tip width of about 15 nm, which conforms to the FERM domain size enclosed within two lipid bilayers of 4–5 nm width.
The Ω1–2 edge projection on the auxiliary plane (𝜕Ωbp ⊂ ω) with solid-type interpolation curve was used for astrocytic leaflet shaping, and a 3D template (Ωbp) for leaflet cutting, created with thickness addition (𝜕h >> HSP) for the boundary projection 𝜕Ωbp, was used to obtain an evenly cut leaflet edge which is no thinner than 15 nm.
Finally, the set of Boolean operations was applied consequently to the chosen bodies and the obtained digital phantom provides four domains on which convectional reaction–diffusion can be evaluated.
3. Results
The results of applying the described Boolean operations and procedures allowed us to obtain a placed set of domains corresponding to the initial biological structures in a one-to-one manner. The functional features of the final structure are the true-distance localization for not only the neuronal membranes, but also for the astrocytic leaflet and presynaptic vesicles (𝜕Ωifusion) on the membrane (Figure 2). The localization of the vesicles indicates the possible locations of neuromediator release, and should be considered as possible areas of incidental connection of some vesicles with further opening and the release of their internal pool. The number of the attached vesicles is also a subject of discussion. The conventional reaction–diffusion of neuromediators out of a synaptic cleft will be modeled in the ISF domain (Figure 3a–c) with consideration of 𝜕Ωifusion (Figure 3b). However, it is also possible to consider the full values of the inter-vesicle pool, including the spheric domains directly (Figure 3c). In such a case, one must consider a physical problem with time-dependent emptying of the vesicles. It is essential to consider that the localization of the attached vesicles can differ, and there is a chance that both neighbor and distant connections appear.
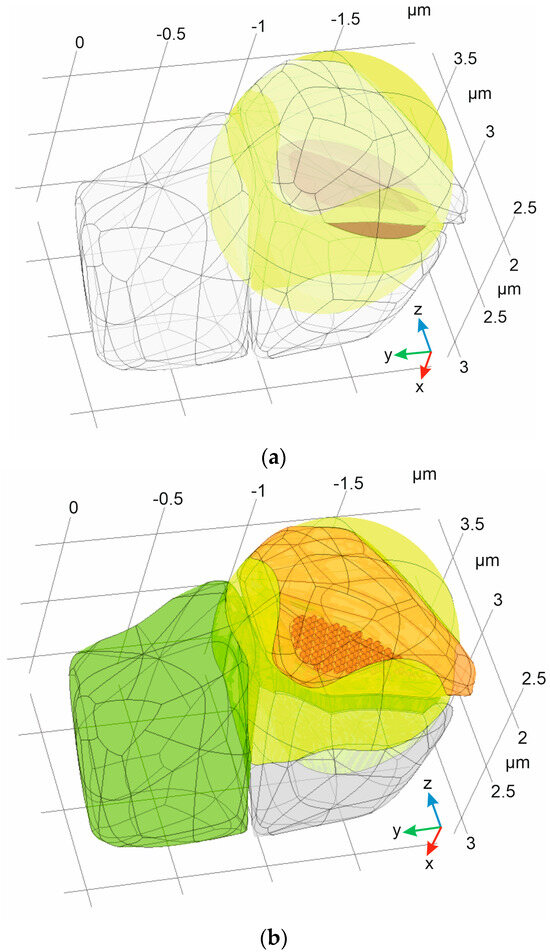
Figure 2.
The digital phantom of a synapse obtained after application of the proposed algorithm to initial set of bodies: (a) The initial set of 3D Voronoi diagram neighbors (Ω1–3, empty bodies), experimentally defined inner synapse area (ΩSP, magenta), and a simple ellipsoid (Ωellipsoid, yellow); (b) the final synapse phantom, including presynaptic neuron (Ωpre, orange), postsynaptic neuron (Ωpost, blue), astrocyte with leaflets (ΩAL, green), and ISF (ΩISF, yellow).
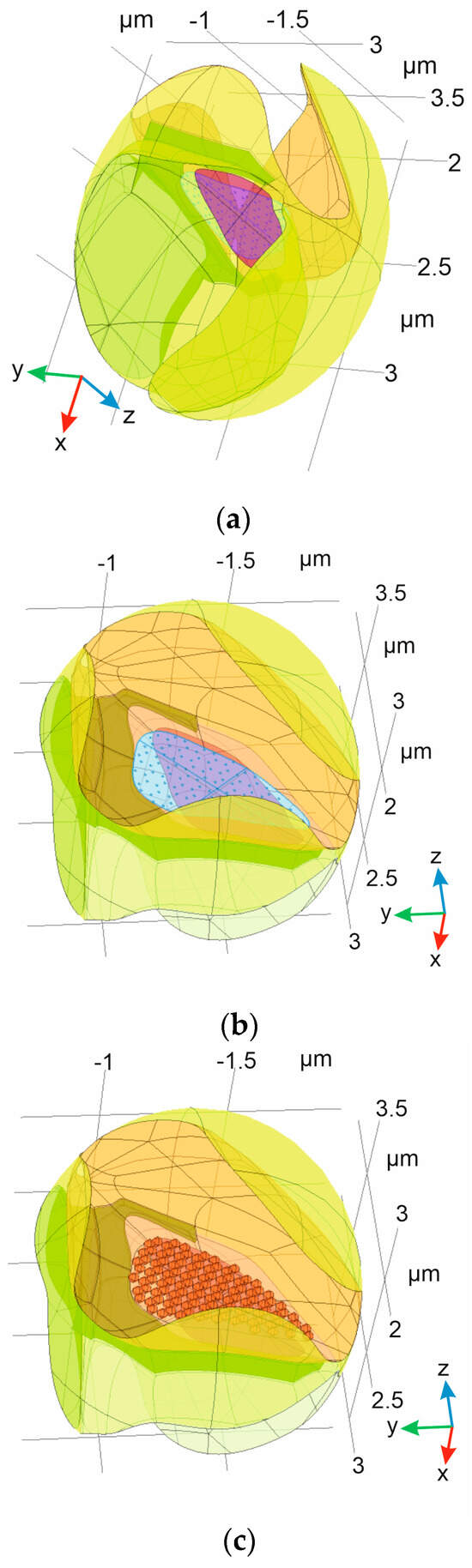
Figure 3.
The digital domain corresponding to the ISF: (a) A separated ISF domain with indication of PSD (magenta); (b) ISF domain with indication of both PSD (magenta, below) and AZ (light blue, under), with areas of localized vesicles attachment on the membrane (𝜕Ωifusion). The astrocyte leaflet is indicated in dark green; and (c) the same indication of ISF, but with presynaptic vesicles positioned on AZ DPs (dark orange spheres) also indicated.
The required astrocytic leaflet object (Ωleaflet) is a result of Boolean subtraction operations: Ωleaflet = Ω′leaflet\(Ω′1 U Ω′2 U Ωbp). In our modeling environment, the distal point of Ωleaflet admittedly does not reach the synaptic cleft area for small synapse phantoms (≤200 nm diameter), such that 𝜕Ωbp Ո 𝜕Ω′bp = ∅ (see Figure 4). Thus, Ωleaflet could be created independently to Ωpre and Ωpost. Furthermore, Boolean subtraction of the adjusted Ω′bp should be performed for bigger synapse phantoms if 𝜕Ωbp Ո 𝜕Ω′bp ≠ ∅. In this case, 𝜕Ω′bp is a solid type of interpolation curve of the Ω′1–2 edge combined with the projections of 𝜕ΩPSD and 𝜕ΩAZ on the auxiliary plane 𝜕ω.
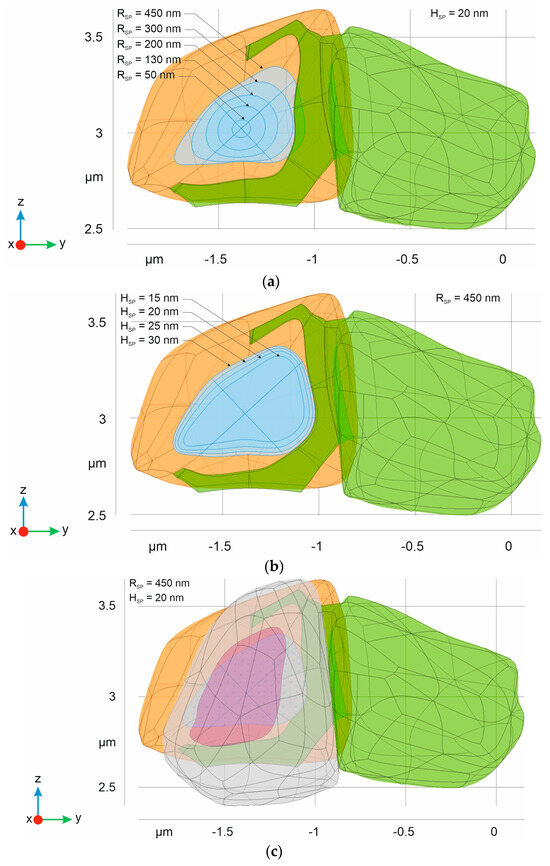
Figure 4.
Different types of synaptic forms composing the final phantom of synaptic contact. The green body indicates an astrocyte with leaflet. The orange domain corresponds to presynaptic neuron and a blue area is equivalent to AZ. The isolines indicate the boundaries retained after different radiuses (a) and heights (b) of synaptic phantoms ΩSP were used; and (c) the full structure of the digital phantom, including a postsynaptic neuron (empty domain) with indication of PSD (magenta).
The most prominent characteristic of astrocytic leaflets is their surface-to-volume ratio (SVR). For rat hippocampal synapses, the astrocyte leaflet SVR has been described through 3D reconstruction of electron microscopic (EM) data [47]. The leaflets created in this work aligned well with these experimental SVR values (see Table 3).

Table 3.
The calculated SVR values for different types of ΩSP. The combination of height (columns) and radius size (rows) describes the total volume of the digital synapse. Then, the volume and surface area of constructed leaflet were measured using the tools in the Geometric module of the COMSOL Multiphysics software. Experimental data indicate that the SVR has a density distribution within the range of 18–60 µm−1 with a maximum at 20–25 µm−1 [47].
The differences in AZ are presented in Figure 4. The results clearly indicate a profound enlargement and change in the shape of the AZ with an increased radius RSP. At the same time, the height of ΩSP is not a crucial parameter affecting the size of AZ under the same radius. Additionally, although the PSD area is similar, it is not equivalent to the AZ.
As follows from Figure 4, there is one remarkable feature of our 3D model—the larger synaptic cleft most likely comes into direct contact with the astrocytic leaflet [47]. This observation correlates with the prominent practical finding that large synapses have increased astroglial synaptic coverage [55]. The leaflet protrusion toward the cleft excludes thick intercellular spaces (tunnels) in close proximity to the astrocyte, leaving only a sheet-like diffusion area, which is also in good agreement with 3D reconstruction data from the rat CA1 hippocampal region [38].
An essential part of the applied algorithm is the adjustment of the astrocytic leaflet and its size to AZ and PSD. The presented method makes it possible to create various types of cradle for the synapse. Conditionally, they can be classified as small, medium, and large. It is intuitively acceptable that a large ΩSP should correspond to a large cradle and vice versa. However, this is not necessarily obvious. For native cases, all types of combinations may be considered. The shape and the size of the leaflet likely depend on the activity of the vesicles and the intensity of convectional diffusion near the cleft. The results of astrocyte leaflet modeling are represented in Figure 5. A notable feature of this part of the algorithm is that the shape and size of the leaflets are determined by the curve traces remaining after Boolean operations with ΩSP and Ωi. This simplification allows additional geometrical modification of the domains to be avoided and, at the same time, a smooth and twisted pattern of the leaflet to form.
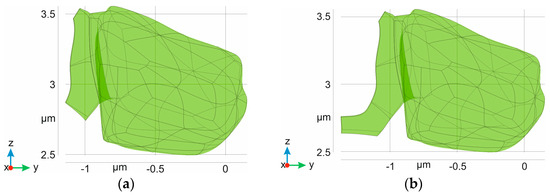
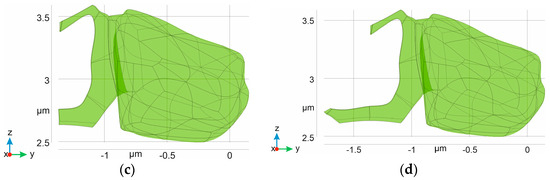
Figure 5.
Digital domains corresponding to an astrocyte body with leaflet. The main body is the same in all cases and the size of the cradle corresponds to 24% (a), 38% (b), 48% (c), and 62% (d) surrounding the AZ (see Section 2. Material and Methods).
The different shapes of the astrocytic leaflets can be applied in the creation of the final synaptic cleft phantom. It is interesting that the same AZ and PSD may be surrounded by various types of cradle (Figure 6). Geometrically, such variation in the mutual position of the astrocyte/neurons is not prohibited. Moreover, this example can be used to evaluate the biological aspect of synaptic plasticity when re-uptake of the neuromediators may be determined not only by the activity level of transporters. The difference in position of astrocytic leaflets reveals a flexibility of spillover flux regulated by the spatial distribution of the transport system. This process can appear as a part of nervous tissue development or pathological changes.
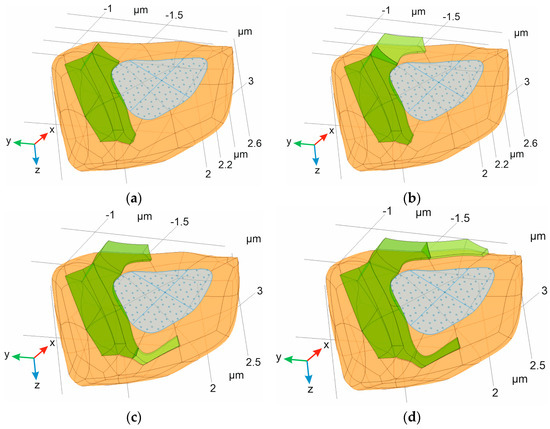
Figure 6.
Several types of astrocytic leaflets surrounding the synaptic cleft. The cases correspond to those indicated in Figure 5. For clarity, the postsynaptic domain (Ωpost) and astrocyte body part of ΩAL are omitted. Only the leaflet parts of ΩAL are shown (in green), and the size of the cradle corresponds to 24% (a), 38% (b), 48% (c), and 62% (d).
The main feature of the created domains is their relative compliance to the initial biological prototypes. Known key parameters, such as cell-to-cell distance, the size of synapse, the size of PSD, and so on, are taken into account in the final phantom. Indeed, a true-to-life geometry of the domains could only be attained through reconstruction on the basis of experimental images. Nevertheless, this approach faces several difficulties. First of all, the format of output files should be acceptable for further numerical modeling. However, transferring between digital image formats is not simple if the shape of the considered object is complex. Moreover, the problem of so-called unsolved surfaces exists. In some cases, the overlapped surfaces formed a slightly shifted cross-section. These areas are usually detected by the solver. However, modeling of the whole phantom then becomes impossible, due to many tiny details in the structures acting as obstacles preventing application of the appropriate meshes. The introduced algorithm allows such a problem to be avoided. It is essential to stress that the constructed domains are suitable for further application. The applied meshes have different capacities of the elements, thus the calculations can be evaluated at various levels of significance and with a range of computational resources. This aspect has particular importance for further numerical modeling.
Several examples of various meshes are shown in Figure 7, which were all generated using the COMSOL Multiphysics software. The results of the algorithm are considered acceptable for applications demanding both coarse and extra fine meshes, with examples of both further represented in Figure 7. Their main characteristics are quite different. In particular, the maximum element size is about 0.14 μm in the coarse mesh, compared 0.03 μm in the extra fine mesh. Furthermore, the minimum element size is 0.04 μm in the coarse mesh, compared to 0.002 μm in the extra fine mesh. The number of elements is also observed to present a significant difference—0.2∙106 (coarse) versus 1.6∙106 (extra fine). However, both types of mesh can be created in the obtained domains. The means that the model can be evaluated with the appropriate calculation resources and at the desired level of quality.
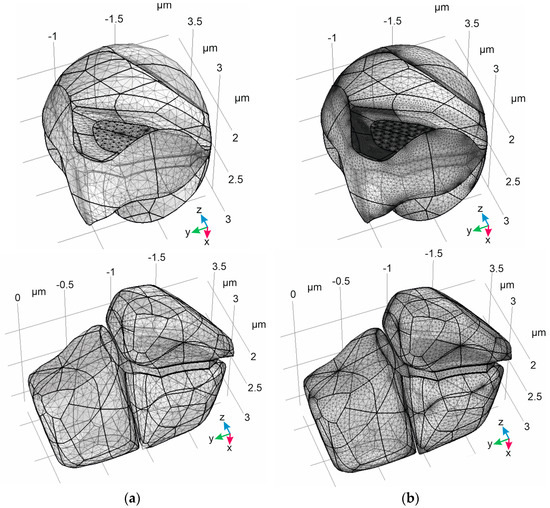
Figure 7.
Application of different meshes to the resulting domains created using the proposed algorithm. The considered meshes are classified, according to the COMSOL Multiphysics software, as “coarse” (a) and “extra fine” (b). The domain of ISF (ΩISF) is represented in the upper panels. The lower panels represent the digital phantom including Ωpre, Ωpost, and ΩAL.
Thus, the represented algorithm facilitates a creation of a digital phantom of a synaptic contact with a high level of biological detail, resolving the complex astrocyte/neuron contact. These detailed boundaries are essential for correct and accurate consideration of convectional reaction–diffusion of neuromediators in the ISF associated with a synaptic cleft area.
4. Discussion
Computational modeling of the diffusion of chemical species in synaptic and perisynaptic spaces, metabolic pathways, reaction compartmentalization in brain parenchyma, receptor activation reactions, or transmitter uptake implies specific geometric decisions. There are many ways to carry out synaptic modeling. The first and simplest is to use a two-dimensional geometry. Although planar models can provide insights on some valuable functional characteristics, more vivid three-dimensional geometry can also be used. Simple spherical 3D synaptic models have been based on quantitative EM observations of the cell membrane patterns in a planar section of the rat hippocampus. The superposition of several synaptic profiles allows for a reasonable approximation using two solid hemispheres, representing the presynaptic and postsynaptic parts of neurons as obstacles to diffusion. They are separated from each other by a cylindrical synaptic cleft area and surrounded with a spherical porous medium representative of brain parenchyma [39,47]. These models have been amended with more elaborate geometric primitives; for example, a bowl-shaped presynaptic ending and spherical dendritic parts of neurons [56], reversed truncated hemispheres [57], or simply cylindrical nerve endings [58,59]. They have also been improved through the addition of glial sheets which envelop the synaptic junction and contain transporters for matching neurotransmitters [56,60,61]. There are also compromising cases which approximate the synaptic space with two infinite planes [62,63], or a combination of a plane and rectangular elements mimicking dendritic spines [64] for transmitter diffusion modeling. The results obtained with such models are of great importance, but more realistic structures can still be generated. Therefore, spherical objects have been used to mimic dendritic spines and axon boutons in association with cylindrical cell parts, including axons, spine necks, dendritic shafts, and astrocyte processes [65,66]. The whole dendritic segments with multiple spines have been constructed using truncated spherical and cylindrical primitives for LTP plasticity modeling [67]. Most native structures are created through 3D reconstruction of ultra-resolution EM data [68]. This type of model is very precise for geometrical definition of brain parenchyma cellular parts—for example, in terms of surface-to-volume ratio (SVR) and spatial distribution or changes in metabolic concentration—yet cannot be used for diffusion modeling. A stochastic model of brain parenchyma with a cylindrical synaptic cleft in the center of a cube filled with randomly scattered, overlapping spheroids representing neuronal and astroglial cell parts with sizes obtained from EM data has been presented recently as more biologically relevant geometric environment for transmitter diffusion simulation [69]; however, it is still not a 3D reconstruction.
In the present study, we produced a stochastic and biologically precise 3D model of a single synaptic cleft including contact with an astrocytic leaflet, which is suitable for use in transmitter reaction–diffusion modeling. It should be noted that, despite the specific type of considered synapse (i.e., glutamatergic synapse), the introduced algorithm will create a digital phantom reflecting any type of synapse in the CNS. The basic steps are the same for each synaptic contact, as the nature of neurotransmission between neurons is similar for various receptors and neuromediator systems. Moreover, the clear separation of the inside and outside areas allows the created phantoms to be used according to the H/H Classification of convectional reaction–diffusion boundary problems introduced earlier [70].
5. Conclusions
In the present study, we proposed an algorithm for the creation of digital synaptic phantoms. The main advantage of the introduced method is its careful consideration of the astrocyte/neurons area, using scaled distances between the membranes. The final form of the phantom includes smoothly shaped AZ and PSD surrounded by the astrocyte leaflet in a fluent manner. The step-by-step procedures of digital phantom creation are represented in Figure 8. It is essential that the set of initial bodies is selected without any special assumption about the geometric shape. This can be performed according to the automatic generation of 3D Voronoi diagrams in any appropriate software package. As only three closest neighbors and an including ellipsoid are required, the presented steps are universal and highly adaptive to various programming demands. Although the process of creating an astrocytic leaflet is precise, the overall formation of the final phantom can be carried out rapidly. As mentioned above, a created digital phantom is suitable for convectional reaction–diffusion modeling; in particular, the phantom designed according to the introduced algorithm will be of Class I, according to the H/H classification [70].
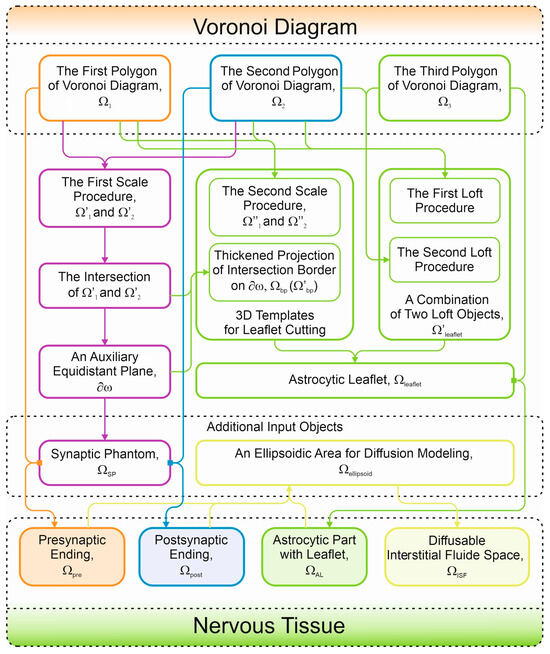
Figure 8.
Summary of the algorithm steps to be fulfilled. The colors of lines and blocks are the same as in the previous Figures, where the domains have been indicated in colors.
A possible application of the introduced algorithm is the creation of a digital phantom of a synaptic contact for modeling the diffusion of mediators in the ISF and their possible consumption and metabolic transformations in both neurons and astrocytes. It should be noted that the presented algorithm can be applied for different types of analyses, such as solutions with distorted meshes [71,72] and PDEs with non-smooth data [73]. Despite the partial example of a glutamate synapse considered in the present study, the method of domain creation is the same for any kind of neurotransmission system in the CNS. It can be applied to both exciting and inhibiting systems with the inclusion of different types of membrane transporters. The activities of the membrane transport system can be considered as the boundary conditions for appropriate surfaces. Moreover, the activities of membrane receptors on the PSD can also be taken into account. The introduced algorithm makes it possible to evaluate mediator gradients in 3D models of convectional reaction–diffusion in nervous tissue.
The clear separation of the designed domains allows the boundary conditions and internal flux dysconnectivity functions to be explicitly set up. The amplitude and form of numerical solutions for boundary partial differential equations problems are greatly influenced by these types of conditions. Notably, the introduced algorithm permits the creation of a digital phantom that is compatible with most living subjects (Class I of the H/H classification). Therefore, the introduced algorithm is a useful tool for preparing a complex three-dimensional digital phantom which is suitable for further use in the mathematical modeling of biological processes.
Author Contributions
Conceptualization, O.A.Z. and Y.R.N.; methodology, Y.R.N.; software, O.A.Z. and Y.R.N.; validation, O.A.Z.; formal analysis, O.A.Z. and Y.R.N.; investigation, O.A.Z. and Y.R.N.; resources, Y.R.N.; data curation, O.A.Z.; writing—original draft preparation, O.A.Z. and Y.R.N.; writing—review and editing, Y.R.N.; visualization, O.A.Z.; supervision, Y.R.N.; project administration, Y.R.N.; funding acquisition, Y.R.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to acknowledge Dmitry Lazarev for his help with the COMSOL Multiphysics software. The authors thank Ilya Kurochkin for a creation of 3D Voronoi diagram samples. Moreover, we would like to thank Elena Mashkovtseva for her critical comments and fruitful discussion.
Conflicts of Interest
Authors Olga A. Zagubnaya and Yaroslav R. Nartsissov were employed by the company BiDiPharma GmbH. All authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Shi, Y.; Yang, X. A time two-grid difference method for nonlinear generalized viscous Burgers’ equation. J. Math. Chem. 2024, 62, 1323–1356. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, X.; Zhang, Z. Construction of a new time-space two-grid method and its solution for the generalized Burgers’ equation. Appl. Math. Lett. 2024, 158, 109244. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, X. Pointwise error estimate of conservative difference scheme for supergeneralized viscous Burgers’ equation. Electron. Res. Arch. 2024, 32, 1471–1497. [Google Scholar] [CrossRef]
- Li, C.; Zhang, H.; Yang, X. A new nonlinear compact difference scheme for a fourth-order nonlinear Burgers type equation with a weakly singular kernel. J. Appl. Math. Comp. 2024, 70, 2045–2077. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, H.; Yang, X.; Wang, F. A second-order finite difference method for the multi-term fourth-order integral–differential equations on graded meshes. Comput. Appl. Math. 2022, 41, 313. [Google Scholar] [CrossRef]
- Yang, X.; Qiu, W.; Chen, H.; Zhang, H. Second-order BDF ADI Galerkin finite element method for the evolutionary equation with a nonlocal term in three-dimensional space. Appl. Numer. Math. 2022, 172, 497–513. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, H.; Yang, X. CN ADI fast algorithm on non-uniform meshes for the three-dimensional nonlocal evolution equation with multi-memory kernels in viscoelastic dynamics. Appl. Math. Comput. 2024, 474, 128680. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Z. Superconvergence Analysis of a Robust Orthogonal Gauss Collocation Method for 2D Fourth-Order Subdiffusion Equations. J. Sci. Comput. 2024, 100, 62. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, X.; Xu, D. Unconditional convergence of linearized orthogonal spline collocation algorithm for semilinear subdiffusion equation with nonsmooth solution. Numer. Methods Partial. Differ. Equ. 2021, 37, 1361–1373. [Google Scholar] [CrossRef]
- Yang, X.; Qiu, W.; Zhang, H.; Tang, L. An efficient alternating direction implicit finite difference scheme for the three-dimensional time-fractional telegraph equation. Comput. Math. Appl. 2021, 102, 233–247. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, H.; Zhou, Z.; Yang, X. A fast compact finite difference scheme for the fourth-order diffusion-wave equation. Int. J. Comput. Math. 2024, 101, 170–193. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Z. On conservative, positivity preserving, nonlinear FV scheme on distorted meshes for the multi-term nonlocal Nagumo-type equations. Appl. Math. Lett. 2024, 150, 108972. [Google Scholar] [CrossRef]
- Wang, F.; Yang, X.; Zhang, H.; Wu, L. A time two-grid algorithm for the two dimensional nonlinear fractional PIDE with a weakly singular kernel. Math. Comput. Simul. 2022, 199, 38–59. [Google Scholar] [CrossRef]
- Yang, X.; Wu, L.; Zhang, H. A space-time spectral order sinc-collocation method for the fourth-order nonlocal heat model arising in viscoelasticity. Appl. Math. Comput. 2023, 457, 128192. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, X.; Wang, F.; Yang, X. The time two-grid algorithm combined with difference scheme for 2D nonlocal nonlinear wave equation. J. Appl. Math. Comp. 2024, 70, 1127–1151. [Google Scholar] [CrossRef]
- Appadu, A.R.; Lebelo, R.S.; Gidey, H.H.; Inan, B. Editorial: Modeling and numerical simulations with differential equations in mathematical biology, medicine, and the environment. Front. Appl. Math. Stat. 2023, 9, 1150552. [Google Scholar] [CrossRef]
- Ehrhardt, M.; Sánchez, L.J.; Villanueva Micó, R.J. Numerical methods and mathematical modelling in biology, medicine and social sciences. Int. J. Comput. Math. 2014, 91, 176–178. [Google Scholar] [CrossRef]
- Huppert, A.; Katriel, G. Mathematical modelling and prediction in infectious disease epidemiology. Clin. Microbiol. Infect. 2013, 19, 999–1005. [Google Scholar] [CrossRef]
- Kucharski, A.J.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Eggo, R.M.; Sun, F.; Jit, M.; Munday, J.D.; et al. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 553–558. [Google Scholar] [CrossRef]
- Saldaña, F.; Velasco-Hernández, J.X. Modeling the COVID-19 pandemic: A primer and overview of mathematical epidemiology. SeMA J. 2022, 79, 225–251. [Google Scholar] [CrossRef]
- Deplazes, E. Molecular simulations of disulfide-rich venom peptides with ion channels and membranes. Molecules 2017, 22, 362. [Google Scholar] [CrossRef] [PubMed]
- Cusimano, N.; Gizzi, A.; Fenton, F.H.; Filippi, S.; Gerardo-Giorda, L. Key aspects for effective mathematical modelling of fractional-diffusion in cardiac electrophysiology: A quantitative study. Commun. Nonlinear Sci. Numer. Simul. 2020, 84, 105152. [Google Scholar] [CrossRef] [PubMed]
- Hurtado, D.E.; Castro, S.; Gizzi, A. Computational modeling of non-linear diffusion in cardiac electrophysiology: A novel porous-medium approach. Comput. Methods Appl. Mech. Eng. 2016, 300, 70–83. [Google Scholar] [CrossRef]
- Nartsissov, Y.R. The Effect of Flux Dysconnectivity Functions on Concentration Gradients Changes in a Multicomponent Model of Convectional Reaction-Diffusion by the Example of a Neurovascular Unit. Defect Diffus. Forum 2021, 413, 19–28. [Google Scholar] [CrossRef]
- Nartsissov, Y.R. Application of a multicomponent model of convectional reaction-diffusion to description of glucose gradients in a neurovascular unit. Front. Physiol. 2022, 13, 843473. [Google Scholar] [CrossRef]
- Ulman, V.; Svoboda, D.; Nykter, M.; Kozubek, M.; Ruusuvuori, P. Virtual cell imaging: A review on simulation methods employed in image cytometry. Cytom. Part A 2016, 89, 1057–1072. [Google Scholar] [CrossRef] [PubMed]
- Mishchenko, Y.; Hu, T.; Spacek, J.; Mendenhall, J.; Harris, K.M.; Chklovskii, D.B. Ultrastructural analysis of hippocampal neuropil from the connectomics perspective. Neuron 2010, 67, 1009–1020. [Google Scholar] [CrossRef]
- Radojević, M.; Meijering, E. Automated Neuron Reconstruction from 3D Fluorescence Microscopy Images Using Sequential Monte Carlo Estimation. Neuroinformatics 2019, 17, 423–442. [Google Scholar] [CrossRef]
- Nartsissov, Y.R. A novel algorithm of the digital nervous tissue phantom creation based on 3D Voronoi diagram application. J. Phys. Conf. Ser. 2021, 2090, 012009. [Google Scholar] [CrossRef]
- Nartsissov, Y.R.; Ivontsin, L.A. Mathematical Modelling of Physiological Effects Caused by a Glycine Receptors Post-Synaptic Density Spatial Polymorphism. Mathematics 2023, 11, 2499. [Google Scholar] [CrossRef]
- Nartsissov, Y.R.; Zagubnaya, O.A. A digital 3D reconstruction of a synaptic cleft which can be used for further modeling of neuromediators convectional diffusion in a nervous tissue. AIP Conf. Proc. 2023, 2872, 120003. [Google Scholar] [CrossRef]
- Südhof, T.C. The cell biology of synapse formation. J. Cell Biol. 2021, 220, e202103052. [Google Scholar] [CrossRef] [PubMed]
- Grewer, C.; Gameiro, A.; Rauen, T. SLC1 glutamate transporters. Pflug. Arch. Eur. J. Physiol. 2014, 466, 3–24. [Google Scholar] [CrossRef]
- Armbruster, M.; Hanson, E.; Dulla, C.G. Glutamate clearance is locally modulated by presynaptic neuronal activity in the cerebral cortex. J. Neurosci. 2016, 36, 10404–10415. [Google Scholar] [CrossRef]
- Belov Kirdajova, D.; Kriska, J.; Tureckova, J.; Anderova, M. Ischemia-Triggered Glutamate Excitotoxicity from the Perspective of Glial Cells. Front. Cell. Neurosci. 2020, 14, 51. [Google Scholar] [CrossRef] [PubMed]
- Calvetti, D.; Cheng, Y.; Somersalo, E. A spatially distributed computational model of brain cellular metabolism. J. Theor. Biol. 2015, 376, 48–65. [Google Scholar] [CrossRef]
- Idumah, G.; Somersalo, E.; Calvetti, D. A Spatially Distributed Model of Brain Metabolism Highlights the Role of Diffusion in Brain Energy Metabolism. J. Theor. Biol. 2022, 572, 111567. [Google Scholar] [CrossRef]
- Kinney, J.P.; Spacek, J.; Bartol, T.M.; Bajaj, C.L.; Harris, K.M.; Sejnowski, T.J. Extracellular sheets and tunnels modulate glutamate diffusion in hippocampal neuropil. J. Comp. Neurol. 2013, 521, 448–464. [Google Scholar] [CrossRef]
- Rusakov, D.A.; Kullmann, D.M. Geometric and viscous components of the tortuosity of the extracellular space in the brain. Proc. Natl. Acad. Sci. USA 1998, 95, 8975–8980. [Google Scholar] [CrossRef]
- Borges, R.; Gu, C.; Machado, J.D.; Ewing, A.G. The dynamic nature of exocytosis from large secretory vesicles. A view from electrochemistry and imaging. Cell Calcium 2023, 110, 102699. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, Q.; Liu, B.; Li, Y.; Wu, X.; Kuo, S.; Zheng, L.; Wang, C.; Zhu, F.; Zhou, Z. Dynamin 1 restrains vesicular release to a subquantal mode in mammalian adrenal chromaffin cells. J. Neurosci. 2019, 39, 199–211. [Google Scholar] [CrossRef] [PubMed]
- Limbach, C.; Laue, M.M.; Wang, X.; Hu, B.; Thiede, N.; Hultqvist, G.; Kilimann, M.W. Molecular in situ topology of Aczonin/Piccolo and associated proteins at the mammalian neurotransmitter release site. Proc. Natl. Acad. Sci. USA 2011, 108, E392–E401. [Google Scholar] [CrossRef]
- Colombo, M.N.; Maiellano, G.; Putignano, S.; Scandella, L.; Francolini, M. Comparative 2D and 3D ultrastructural analyses of dendritic spines from CA1 pyramidal neurons in the mouse hippocampus. Int. J. Mol. Sci. 2021, 22, 1188. [Google Scholar] [CrossRef] [PubMed]
- Aina, B.-S.; Tim, S.H.; Mandy, S.J.K.; Adrian, N.; Huibert, D.M.; Baljit, S.K.; Rogier, M.; August, B.S.; Mark, H.G.V. Proximity of astrocyte leaflets to the synapse determines memory strength. bioRxiv 2022. [CrossRef]
- Toman, M.; Wade, J.J.; Verkhratsky, A.; Dallas, M.; Bithell, A.; Flanagan, B.; Harkin, J.; McDaid, L. The influence of astrocytic leaflet motility on ionic signalling and homeostasis at active synapses. Sci. Rep. 2023, 13, 3050. [Google Scholar] [CrossRef]
- Badia-Soteras, A.; Heistek, T.S.; Kater, M.S.J.; Mak, A.; Negrean, A.; van den Oever, M.C.; Mansvelder, H.D.; Khakh, B.S.; Min, R.; Smit, A.B.; et al. Retraction of Astrocyte Leaflets from the Synapse Enhances Fear Memory. Biol. Psychiatry 2023, 94, 226–238. [Google Scholar] [CrossRef] [PubMed]
- Gavrilov, N.; Golyagina, I.; Brazhe, A.; Scimemi, A.; Turlapov, V.; Semyanov, A. Astrocytic coverage of dendritic spines, dendritic shafts, and axonal boutons in hippocampal neuropil. Front. Cell. Neurosci. 2018, 12, 248. [Google Scholar] [CrossRef]
- Ventura, R.; Harris, K.M. Three-dimensional relationships between hippocampal synapses and astrocytes. J. Neurosci. 1999, 19, 6897–6906. [Google Scholar] [CrossRef]
- Ponuwei, G.A. A glimpse of the ERM proteins. J. Biomed. Sci. 2016, 23, 35. [Google Scholar] [CrossRef]
- Schacke, S.; Kirkpatrick, J.; Stocksdale, A.; Bauer, R.; Hagel, C.; Riecken, L.B.; Morrison, H. Ezrin deficiency triggers glial fibrillary acidic protein upregulation and a distinct reactive astrocyte phenotype. GLIA 2022, 70, 2309–2329. [Google Scholar] [CrossRef]
- Popov, A.; Brazhe, N.; Morozova, K.; Yashin, K.; Bychkov, M.; Nosova, O.; Sutyagina, O.; Brazhe, A.; Parshina, E.; Li, L.; et al. Mitochondrial malfunction and atrophy of astrocytes in the aged human cerebral cortex. Nat. Commun. 2023, 14, 8380. [Google Scholar] [CrossRef] [PubMed]
- Hamada, K.; Shimizu, T.; Matsui, T.; Tsukita, S.; Hakoshima, T. Structural basis of the membrane-targeting and unmasking mechanisms of the radixin FERM domain. EMBO J. 2000, 19, 4449–4462. [Google Scholar] [CrossRef] [PubMed]
- Dominguez, R.; Holmes, K.C. Actin structure and function. Annu. Rev. Biophys. 2011, 40, 169–186. [Google Scholar] [CrossRef]
- Fehon, R.G.; McClatchey, A.I.; Bretscher, A. Organizing the cell cortex: The role of ERM proteins. Nat. Rev. Mol. Cell Biol. 2010, 11, 276–287. [Google Scholar] [CrossRef]
- Fomitcheva, I.V.; Sword, J.; Shi, Y.; Kirov, S.A. Plasticity of perisynaptic astroglia during ischemia-induced spreading depolarization. Cereb. Cortex 2023, 33, 5469–5483. [Google Scholar] [CrossRef]
- Rusakov, D.A. The role of perisynaptic glial sheaths in glutamate spillover and extracellular Ca2+ depletion. Biophys. J. 2001, 81, 1947–1959. [Google Scholar] [CrossRef]
- Zheng, K.; Scimemi, A.; Rusakov, D.A. Receptor actions of synaptically released glutamate: The role of transporters on the scale from nanometers to microns. Biophys. J. 2008, 95, 4584–4596. [Google Scholar] [CrossRef] [PubMed]
- Diamond, J.S. Neuronal glutamate transporters limit activation of NMDA receptors by neurotransmitter spillover on CA1 pyramidal cells. J. Neurosci. 2001, 21, 8328–8338. [Google Scholar] [CrossRef]
- Freche, D.; Pannasch, U.; Rouach, N.; Holcman, D. Synapse geometry and receptor dynamics modulate synaptic strength. PLoS ONE 2011, 6, e25122. [Google Scholar] [CrossRef] [PubMed]
- Herde, M.K.; Bohmbach, K.; Domingos, C.; Vana, N.; Komorowska-Müller, J.A.; Passlick, S.; Schwarz, I.; Jackson, C.J.; Dietrich, D.; Schwarz, M.K.; et al. Local efficacy of glutamate uptake decreases with synapse size. Cell Rep. 2020, 32, 108182. [Google Scholar] [CrossRef]
- Rǎdulescu, A.R.; Todd, G.C.; Williams, C.L.; Bennink, B.A.; Lemus, A.A.; Chesbro, H.E.; Bourgeois, J.R.; Kopec, A.M.; Zuloaga, D.G.; Scimemi, A. Estimating the glutamate transporter surface density in distinct sub-cellular compartments of mouse hippocampal astrocytes. PLoS Comput. Biol. 2022, 18, e1009845. [Google Scholar] [CrossRef] [PubMed]
- Feghhi, T.; Hernandez, R.X.; Stawarski, M.; Thomas, C.I.; Kamasawa, N.; Lau, A.W.C.; Macleod, G.T. Computational modeling predicts ephemeral acidic microdomains in the glutamatergic synaptic cleft. Biophys. J. 2021, 120, 5575–5591. [Google Scholar] [CrossRef]
- Kleinle, J.; Vogt, K.; Lüscher, H.R.; Müller, L.; Senn, W.; Wyler, K.; Streit, J. Transmitter concentration profiles in the synaptic cleft: An analytical model of release and diffusion. Biophys. J. 1996, 71, 2413–2426. [Google Scholar] [CrossRef]
- Nielsen, T.A.; DiGregorio, D.A.; Silver, R.A. Modulation of glutamate mobility reveals the mechanism underlying slow-rising AMPAR EPSCs and the diffusion coefficient in the synaptic cleft. Neuron 2004, 42, 757–771. [Google Scholar] [CrossRef]
- McCauley, J.P.; Petroccione, M.A.; D’Brant, L.Y.; Todd, G.C.; Affinnih, N.; Wisnoski, J.J.; Zahid, S.; Shree, S.; Sousa, A.A.; De Guzman, R.M.; et al. Circadian Modulation of Neurons and Astrocytes Controls Synaptic Plasticity in Hippocampal Area CA1. Cell Rep. 2020, 33, 108255. [Google Scholar] [CrossRef]
- Sweeney, A.M.; Fleming, K.E.; McCauley, J.P.; Rodriguez, M.F.; Martin, E.T.; Sousa, A.A.; Leapman, R.D.; Scimemi, A. PAR1 activation induces rapid changes in glutamate uptake and astrocyte morphology. Sci. Rep. 2017, 7, srep43606. [Google Scholar] [CrossRef]
- Antunes, G.; de Souza, F.M.S. 3d modeling of dendritic spines with synaptic plasticity. J. Vis. Exp. 2020, 2020, e60896. [Google Scholar] [CrossRef]
- Héja, L.; Szabó, Z.; Péter, M.; Kardos, J. Spontaneous Ca2+ Fluctuations Arise in Thin Astrocytic Processes With Real 3D Geometry. Front. Cell. Neurosci. 2021, 15, 617989. [Google Scholar] [CrossRef] [PubMed]
- Savtchenko, L.P.; Rusakov, D.A. Increased Extrasynaptic Glutamate Escape in Stochastically Shaped Probabilistic Synaptic Environment. Biomedicines 2022, 10, 2406. [Google Scholar] [CrossRef]
- Nartsissov, Y.R. A spatial classification applied to convectional reaction-diffusion boundary problems basing on a geometrical polymorphism of biological objects. J. Phys. Conf. Ser. 2024, 2701, 012084. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, H.; Zhang, Q.; Yuan, G.; Sheng, Z. The finite volume scheme preserving maximum principle for two-dimensional time-fractional Fokker–Planck equations on distorted meshes. Appl. Math. Lett. 2019, 97, 99–106. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, H.; Zhang, Q.; Yuan, G. Simple positivity-preserving nonlinear finite volume scheme for subdiffusion equations on general non-conforming distorted meshes. Nonlinear Dyn. 2022, 108, 3859–3886. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, H. The uniform l1 long-time behavior of time discretization for time-fractional partial differential equations with nonsmooth data. Appl. Math. Lett. 2022, 124, 107644. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).