Abstract
Machine learning-based Surrogate Reservoir Models (SRMs) can replace/augment multi-physics numerical simulations by replicating the reservoir simulation results with reduced computational effort while maintaining accuracy compared with numerical simulations. This research will demonstrate SRMs’ potential in long-term simulations and optimization of geological carbon storage in a real-world geological setting and address challenges in big data curation and model training. The present study focuses on CO2 storage in the Smeaheia saline aquifer. Two SRMs were created using Deep Neural Networks (DNNs) to predict CO2 saturation and pressure over all grid blocks for 50 years. 18 million samples and 31 features, including reservoir static and dynamic properties, build the input data. Models comprise 3–5 hidden layers with 128–512 units apiece. SRMs showed a runtime improvement of 300 times and an accuracy of 99% compared to the 3D numerical simulator. The genetic algorithm was then employed to determine the optimal rate and duration of CO2 injection, which maximizes the volume of injected CO2 while ensuring storage operations’ safety through constraints. The optimization continued for the reproduction of 100 generations, each containing 100 individuals, without any hyperparameter tuning. Finally, the optimization results confirm the significant potential of Smeaheia for storing 170 Mt CO2.
1. Introduction
The main target of the Paris Agreement in December 2015 was to concentrate efforts on limiting temperature increases (above pre-industrial levels) below 1.5 °C [1]. Based on research findings [2], if there is not a significant reduction in greenhouse gas emissions before 2030, global warming will exceed 1.5 °C; consequently, the permanent demise of delicate ecosystems is inevitable. Carbon capture and storage (CCS) is an efficient method that targets CO2 emissions at their origin and has the potential to lead to a 15% reduction in overall emissions by 2050 [3]. CCS is a promising strategy for addressing climate change that involves trapping and purifying CO2 emissions from industrial and energy sources, rather than emitting them into the atmosphere. The captured CO2 is then transported and stored permanently in the underground, either onshore or offshore [4,5]. Different techniques for storage and utilization of CO2 underground have been developed, including storing it in saline aquifers, utilizing it to enhance oil and gas recovery, recovering methane from coal beds, using it in geothermal systems, storing it in compressed air energy storage systems, and converting it into carbonate minerals in situ [6].
The geological storage of CO2 presents five possible risks: CO2 and CH4 leakage, seismicity, ground movement, and brine migration [7,8]. Prior to injection, the primary objective is to ensure that CO2 does not flow through pre-existing fractures and faults or newly created fractures in the caprock due to pressures exceeding the fracture pressure. Additionally, it is important to maintain the effectiveness of the caprock seal, as measured by breakthrough capillary pressure values [9,10] and legacy wells [11,12]. Hence, optimizing the storage process can prevent such risks by defining proper objectives and constraints [13,14,15]. Traditionally, the optimization of storage activities has been faced via multi-physical 3D numerical simulation approaches, which allow a holistic vision of the phenomena involving geological, fluid-flow, geochemical and geomechanical aspects. However, the high degree of accuracy in the phenomena simulation could be counteracted by time-consuming computational efforts [16,17]. A promising alternative, Proxy Modeling, reproducing simulation outputs from input features through mathematical or statistical functions, has been used to substitute physics-based reservoir simulations [18,19] and enhance computational time by orders of magnitude [20,21]. There are several types of proxy models including reduced-physics, the reduced-order modeling (ROM) approach, statistics-based techniques, and artificial intelligence (AI)-based methods [22,23].
The Smart Proxy Model (SPM) or Surrogate Reservoir Model (SRM) is a data-driven model that uses machine learning to replace/aid computationally intensive numerical models. It can accurately reproduce the pressure and saturation distribution, for instance, across the grid cells at each time step [24]. Computationally expensive optimization tasks (injection or production) can be performed by SRMs to reduce the computational time. Golzari, et al. [25] developed a field-based SRM and later optimized the reservoir production through the Genetic Algorithm (GA). Ng et al. [26] used adaptive moment estimation (Adam) to build an SPM for a fractured reservoir and optimize production [27]. Based on ten realizations of the Egg Model, Ng et al. [28] showed how multilayer perceptron may be used to create data-driven models. To perform waterflooding optimization, these models were then combined with two nature-inspired algorithms, namely particle swarm optimization and the gray wolf optimizer. In parallel, they compared the optimizers’ performance, which resulted in good prediction accuracy. Ng et al. [29] enhanced proxy modeling applications for waterflooding optimization by utilizing a sophisticated machine learning algorithm, Long Short-Term Memory (LSTM).
Furthermore, SRMs were exploited for injection optimization in CO2 Storage and CO2-EOR by Agada et al. [30], Nait Amar et al. [31], Nait Amar et al. [32], Sun et al. [33]. Various optimization algorithms were used such as GA [30,32,34,35], Ant Colony [31], Hooke–Jeeves Direct Search [36], SIMPLEX (a simple optimization technique by linear programming), and Generalized Reduced Gradient [13]. The main aim of these works was optimizing the CO2 injection rate, Water Alternating Gas (WAG) cycle, slug size, and well location to maximize Field Oil Production Total and CO2 storage capacity based on operational goal and CO2 storage type (in saline aquifer or CO2-EOR).
Various machine learning algorithms, such as Artificial Neural Network (ANN), Support Vector Machine, and Random Forest, can be employed for proxy modeling [37]. Due to the strong performance in highly non-linear problems and precise predictive capabilities of Artificial Neural Networks (ANNs) [38,39,40], much research has utilized this method or its advanced variations, such as Deep Neural Networks (DNNs), Convolutional Neural Networks (CNNs), or Recurrent Neural Networks (RNNs), for surrogate reservoir modeling [41,42].
Gholami [43] integrated a grid-based and a well-based SRM to optimize CO2-EOR by utilizing ANN. They used a cascading (sequential) grid-based approach to simulate the distribution of CO2 mole fraction, pressure, water saturation, and oil saturation in a compositional model. A cascading approach produces distinct SRMs for each time step and parameter. The model output at the preceding time step, t − 1, becomes the model input at time step t. In addition, the robust SRM accurately simulated the production rate and the total amount of oil produced. Amini [44] employed ANN to build grid-based SRMs for coarse and fine grid models using cascading and non-cascading approaches. Unlike cascading, the non-cascading method involves creating a single model for the entire simulation time for each parameter. Only the original state of dynamic features at time step zero is provided to the model. As a result, the cascading grid-based SRM (SRMG) led to the accumulation of errors from each time step with prior time steps, resulting in lower accuracy compared to the non-cascading approach. In addition, the non-cascading SRMG, which was constructed using the fine-grid model, led to greater precision in predicting pressure but a bigger margin of error in predicting saturation when compared to the coarse-grid model.
Matthew, et al. [45] employed DNNs to develop field-based proxy models and address a multi-objective optimization problem through the utilization of NSGA-II (Non-dominated Sorting Genetic Algorithm II) in two reservoir models. The research was conducted to investigate the application of CO2-WAG (Water Alternating Gas) in order to optimize oil recovery and CO2 storage in the reservoir. The study focused on optimizing the injection rates of gas and water, as well as the duration of half-cycles. Naghizadeh et al. [46] proposed an economical optimization framework that combines machine learning models and several optimization techniques to determine the ideal setting for injecting flue gas-WAG into the “Gullfaks” reservoir. Proxy models such as DNN, Cascade Forward Neural Network (CFNN), Radial Basis Function, and Generalized Regression Neural Network were used in this study to develop robust machine learning models. The CFNN and DNN models exhibited the most accurate predictions for recovery factor and CO2 storage.
A limitation of the current SRM studies (presented briefly in this section) lies in their applicability to real-world field development planning, which requires long-term simulation and optimization of numerous temporal and spatial factors. The majority of the aforementioned works have a brief and restricted time span. In addition, the training of intricate SRMs necessitates a substantial number of numerical simulation cases [47]. The Smeaheia storage project, which is part of the Northern Lights’ full-scale CCS project, has been granted a license [48]. The project aims to develop transport and storage solutions for up to 20 million tons of CO2 per year (to be operational by 2028) and covers a large area east of the Troll field off the west coast of Norway. Smeaheia possesses an extensive numerical model, developed by Eqionor and Gassnova [49] that is computationally demanding to conduct long-term simulations. Many simulation runs are necessary to evaluate and optimize the development plan of this project. Additionally, no proxy models have been developed for this aquifer model to reduce the computing costs. This computational challenge will be more significant considering the ambition of 30–50 million tons per annum capacity for CO2 transport and storage by 2035, by storing all the transported CO2 in Smeaheia and other potential storage sites as they are matured, thus making the models bigger and more complex.
The objective of this study is to create the first SRM for the Smeaheia aquifer and enhance the efficiency of long-term CO2 storage simulations. The potential risks associated with this storage project are the migration of CO2 plume towards the leakage points and the fracturing of the caprock [50,51,52]. Hence, the objective of optimization is to maximize the storage of CO2 while simultaneously imposing restrictions on the CO2 saturation and cell pressure below the caprock. This study shall utilize grid-based SRMs to forecast the pressure and CO2 saturation within the cells in a computationally effective way. SRMs will be created for this real-world reservoir model that consists of about 1.5 million grid cells and spans 50 years. Although RNNs can anticipate intermediate time steps and the period after injection, they also result in higher computational expenses for both training and computation. Furthermore, the training of CNNs requires a large number of numerical simulation examples, as demonstrated by Wang et al. [41], who utilized 200 simulation cases. Given the extensive simulation time required for a complex model like Smeaheia, it is not practical to conduct such a large number of simulation cases. Furthermore, it would be impractical to create a proxy model for optimization. Hence, the DNN approach will be employed for the development of SRMs. In this technology, the prediction of features for each grid cell can be performed independently of other cells. This allows for the simulation volume to be targeted specifically to the desired cells and reduces the time required for optimization.
This study (which is mainly based on the results obtained in [53]), will provide a concise introduction to ANN and GA in the second section. Subsequently, the methodology will involve investigating the features of the Smeaheia aquifer and updating its numerical model. This will be carried out by incorporating pore volume multipliers and creating an injection well. The updated model will be utilized for generating training and validation data for two grid-based SRMs that forecast pressure and CO2 saturation. Once the model has been trained and validated without previous knowledge of the data, it will be employed to optimize CO2 storage. Ultimately, the outcome of the proxy-based optimization will be verified against numerical simulation results. After presenting the results, the discussion part offers an analysis of the results and comprehensively elucidates all the limitations and challenges faced in constructing the ultimate model.
2. Theory
2.1. Artificial Neural Network
An ANN is a type of machine learning algorithm that utilizes previous data and examples to learn and predict the future performance of a given phenomenon [54]. It includes three layers: the input layer, hidden layer, and output layer, each with respective units.
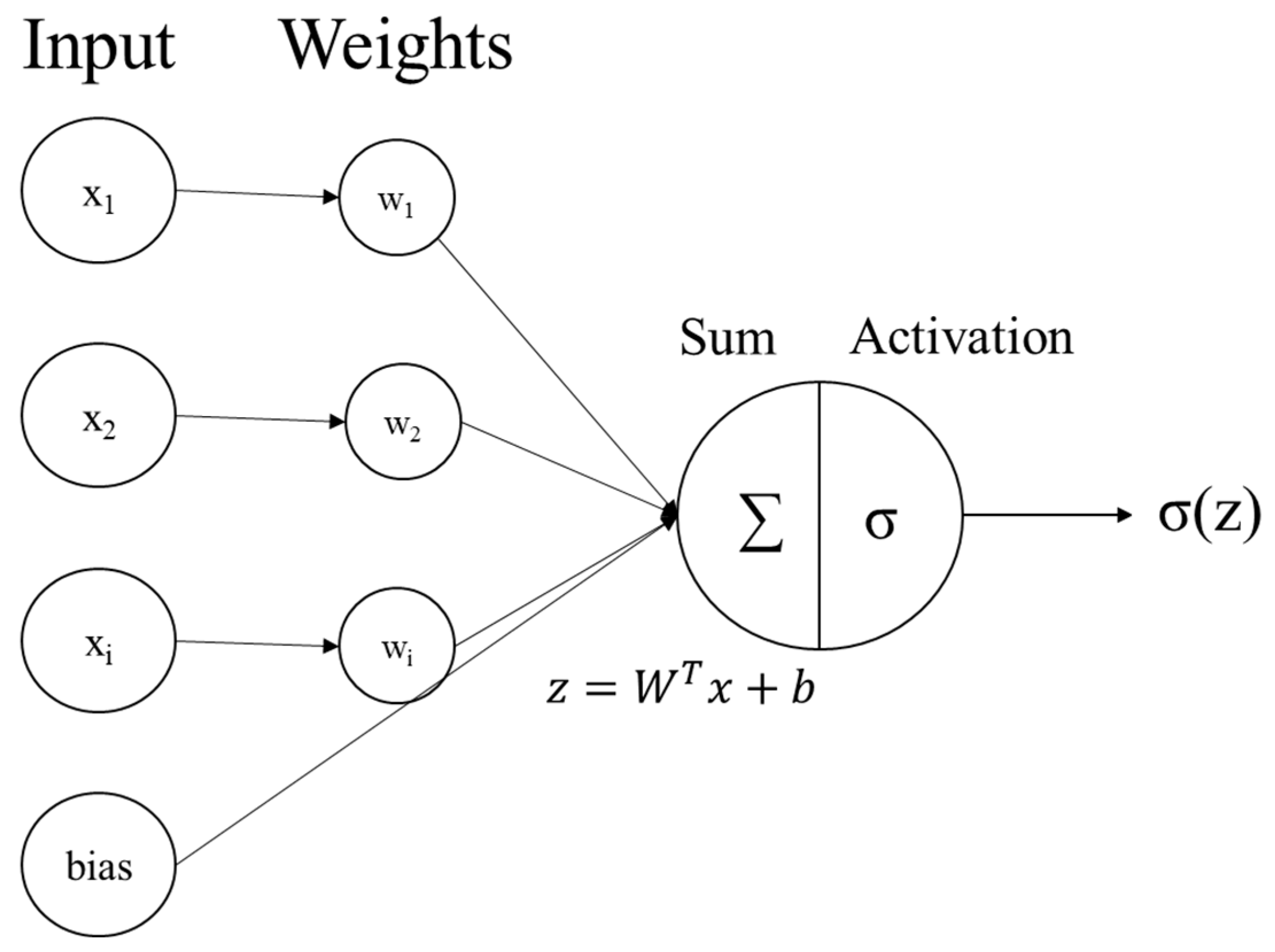
The hidden layer employs an activation function (σ(z)) to activate weighted input data using the kernel (W) and bias (b) matrices (Figure 1). The output layer will apply weights and activation functions to the outcomes of the hidden layer, using units that correspond to the required features for prediction. The model forecast will then be reflected in the output of the last layer.
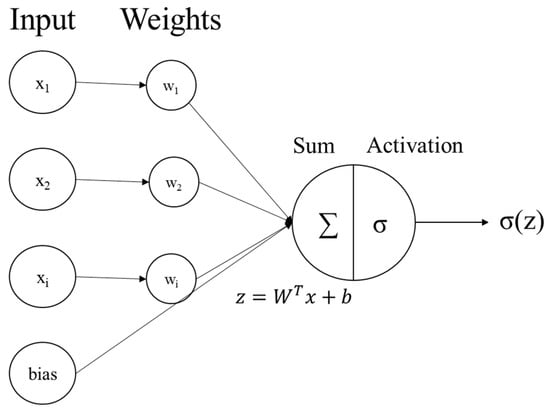
Figure 1.
ANN forward propagation algorithm for computing the next layer units from input data.
The process of Forward Propagation is crucial for generating the expected outcome, while the loss function calculates the discrepancy between the predicted values and the true values. The Back Propagation method improves the matrices and decreases the prediction loss and error in proportion to the learning rate. The method is iterated until reaching the global minimum of the loss; each iteration is referred to as an Epoch [55].
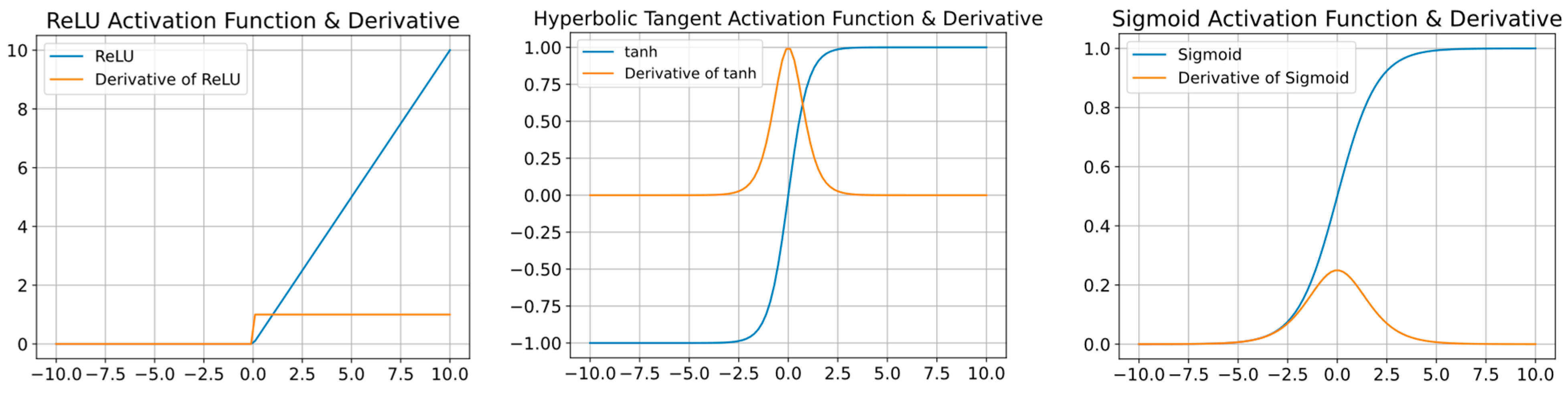
There exist multiple activation functions that can be utilized in the construction of an ANN. The foremost activation functions include the sigmoid, tangent hyperbolic, and rectified linear unit (ReLU). The sigmoid activation function (Equation (1)) maps the input range to the interval [0, 1]. The inherent nature of the phenomenon under consideration is characterized by non-linearity, as visually depicted in Figure 2, where it is evident that the derivative exhibits a continuous and gradual change. The Hyperbolic Tangent function exhibits a structure that closely resembles the Sigmoid function. The function compresses the input value into the interval of [−1, +1] and operates according to Equation (2). Both practitioners and researchers widely employ the ReLU activation function in deep learning. The efficacy of the ReLU stems from its higher performance in training as compared to alternative activation functions, such as the logistic sigmoid and the hyperbolic tangent. The ReLU function can be described as a linear function, namely the identity function, for all positive input values. Conversely, the ReLU function outputs zero for all negative input values, as denoted by Equation (3). Nevertheless, the output numbers span from zero to infinity [56].
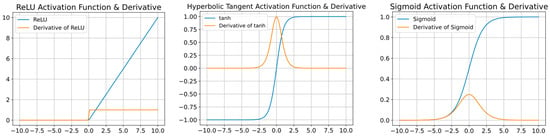
Figure 2.
Common activation functions and their derivatives, from left: ReLU, hyperbolic tangent, and sigmoid.
A Deep Neural Network (DNN) operates in a similar manner by utilizing multiple hidden layers. Hyperparameters, such as the learning rate, number of hidden layers, and optimizer, need to be tuned to suit different scenarios. Underfitting and overfitting are the two primary challenges encountered during model training. Underfitting arises when the ANN is inadequately taught to comprehend the intricacy of the occurrence. Overfitting is the phenomenon where a model achieves high performance during training but fails to generalize effectively. Possible remedies for overfitting encompass augmenting the model’s network, elevating the learning rate, enhancing features, streamlining the model, implementing regularization techniques, and incorporating additional data [57].
2.2. Genetic Algorithm
Holland [58] pioneered the development of the GA, which gained popularity through David Goldberg’s application in solving a challenging gas-pipeline transmission problem [59]. GA is an optimization and search technique that operates on the concepts of genetics and natural selection. It facilitates the reproduction of a population, consisting of a specific number of individuals, to achieve the highest level of fitness or the lowest cost function value. The widespread adoption of GA is due to its numerous benefits, such as its ability to handle both continuous and discrete values, its capacity to simultaneously search multiple samples from a cost surface, its lack of limitations on the number of variables, its ability to avoid becoming stuck in local optima, and its applicability on numerically generated data, experimental data, or analytical functions [60,61].
The genetic algorithm includes a population which comprises Npop individuals or chromosomes, representing all feasible solutions. Each individual or chromosome is composed of Nvar variables or genes. The representation of individual genes can be achieved by many means such as bits, integers, trees, arrays, lists, or other objects. This is accomplished through the process of encoding, which involves the conversion of gene values [62].
The initial population is a randomly generated matrix with dimensions Npop×Nvar. During the initialization process, the objective function will be computed for decoded indiviuals with real numbers. The value obtained for an individual is referred to as its Fitness, which indicates both the quality of the solution and its proximity to the ideal chromosome. The process of decoding gene values is accomplished through Genotype-Phenotype Mapping, which transforms genotypes into phenotypes, the actual solutions [63]. When continuous solutions are used, it is not necessary to decode the genotype to obtain real values. Only normalized data need to be denormalized. Following the evaluation of fitness, two parents will be chosen to create the next generation. The Ranking Selection strategy, considered one of the most effective selection methods, arranges individuals based on their fitness levels. The selection of the best parents is determined by a selection ratio, which randomly chooses two parents from a pool of candidates. The process of reproduction in genetic algorithms involves the use of crossover, which entails swapping single or multiple genes between parents, and mutation, which involves the random evolution of some genes within the solution interval. These mechanisms build a new generation. The primary objective of mutation is to avoid the algorithm from becoming trapped in a local optimum by reducing the propensity of GA to converge rapidly [60]. A straightforward approach to address constraints in genetic algorithms is utilizing the Death Penalty technique. The method involves evaluating the feasibility of constraints after performing crossover and mutation operations. If the constraints are not feasible, the loop will repeat until constraints are satisfied.
3. Methodology
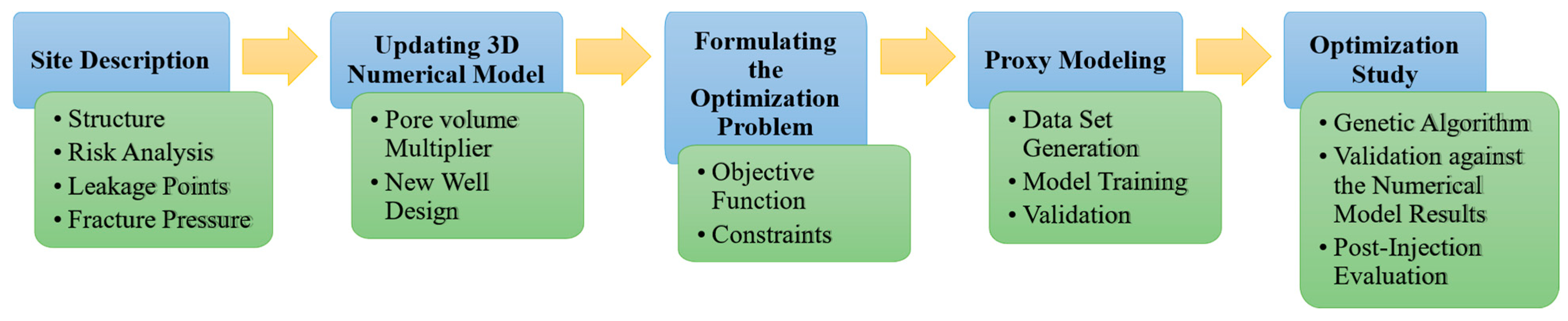
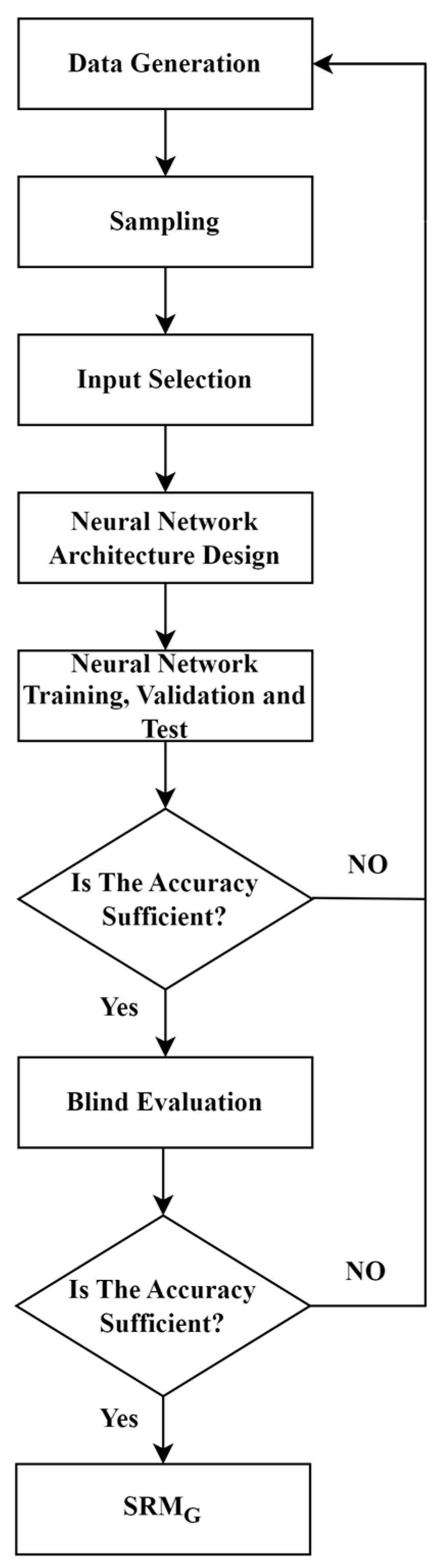
Figure 3 shows the overall worflow. The study commences by examining the Smeaheia aquifer and the available numerical model. Afterwards, the aquifer model will be modified by incorporating pore volume multipliers, determining an appropriate well location using sensitivity analysis, and designing a new injection well. The third phase is formulating the Smeaheia optimization problem by identifying the objective function and constraints. SRMs are designed, trained, and validated based on the input parameters of objectives and constraints. Ultimately, GA is coupled with SRMs to efficiently solve the optimization problem within a remarkably short timeframe.
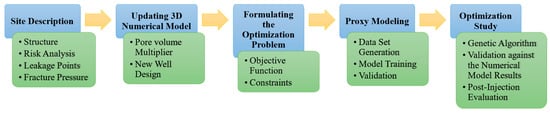
Figure 3.
The workflow implemented in this study.
3.1. Case Study Description and Its Numerical Model
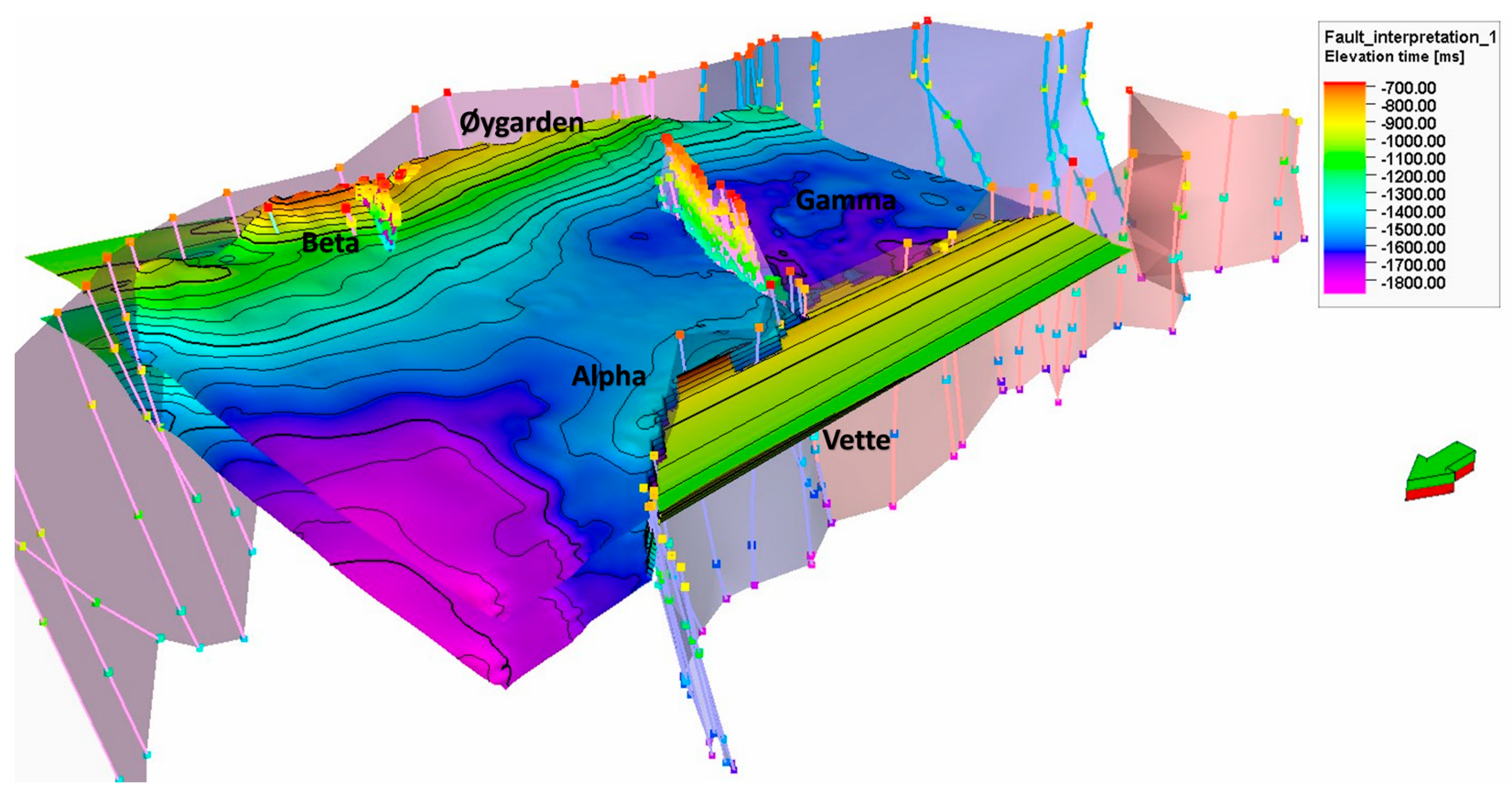
In Smeaheia, the Viking Group is the storage target, which consists of three shallow marine formations: Krossfjord, Fensfjord, and Sognefjord. Moreover, the flooding that occurred across the entire basin resulted in the deposition of mudstones in the Draupne formation, which served as the main caprock. The Troll Field wells prove the efficacy of the main caprock, which extends over the entire fault block. The storage complex is equipped with supplementary seal units made of limestone and shales from the upper groups. Tertiary and Quaternary sediments can also be regarded as having the ability to effectively seal. The gross seal spans approximately 750 m in width and 1200 m in length across the studied region. The primary seal is weakened in both the eastern and western directions, parallel to the thinning of the storage from west to east. The Smeaheia storage site is located within the Troll Kystnaer fault block, specifically in the footwall of the Vette fault (VF) to the north and west, and in the hanging wall of the Øygarden Fault Complex (ØFC) to the east [50].
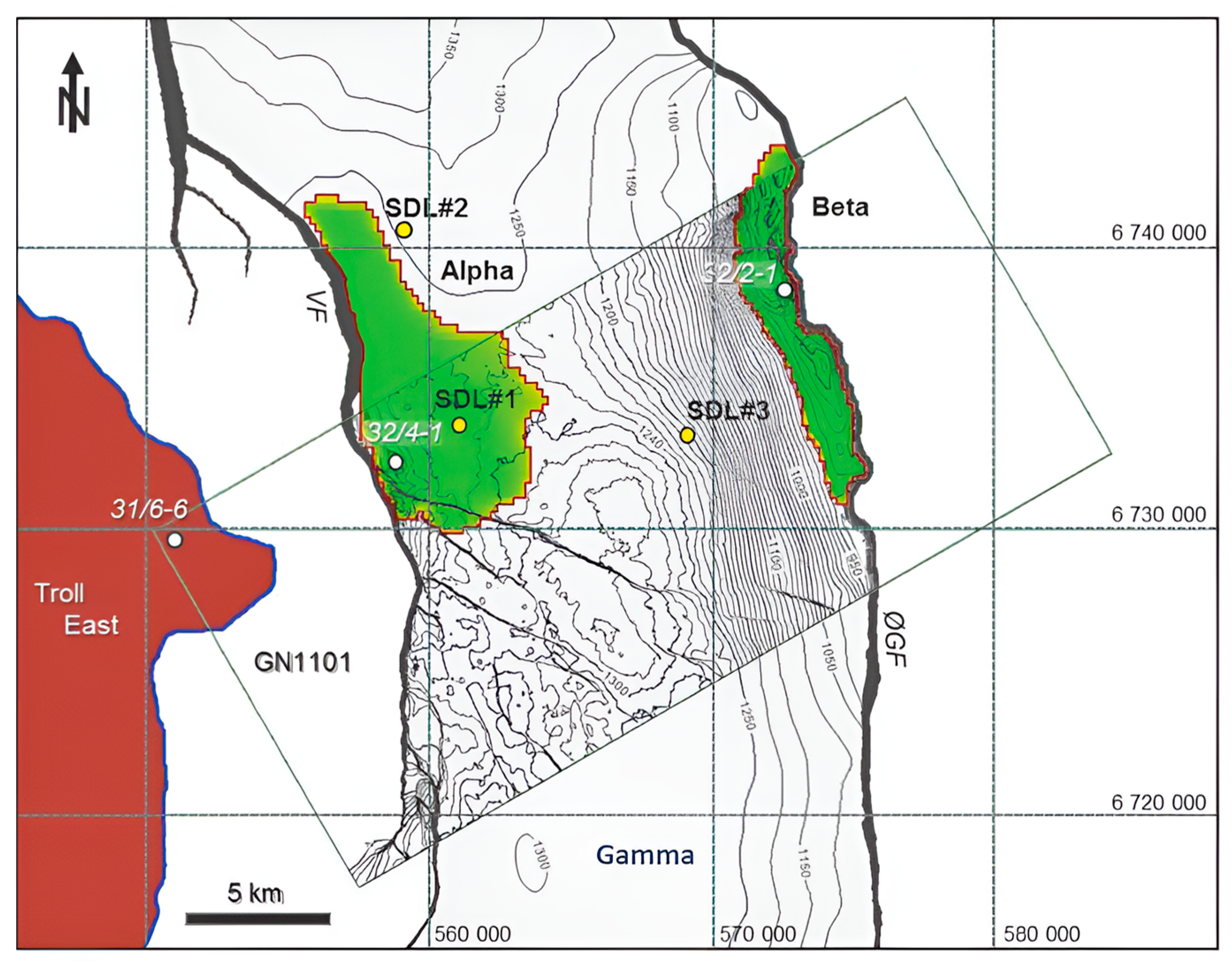
Smeaheia CO2 storage is composed of Alpha, Beta, and Gamma prospects. As shown in Figure 4, the GN1101 seismic survey covers a large portion of Alpha and Beta (green zones), making them more dependable for examination. However, the Gamma zone, despite its enormous storage potential because of its expansion, is not as extensively surveyed.
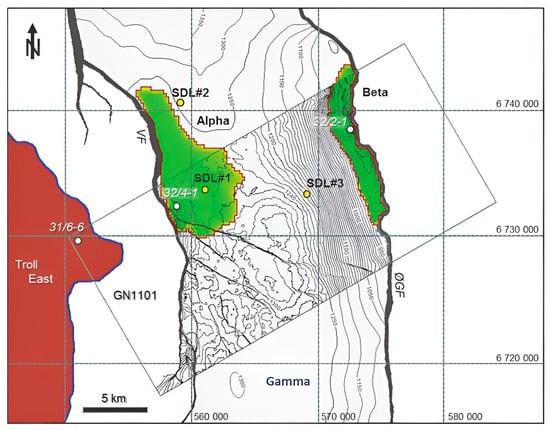
Figure 4.
Smeaheia’s prospects location with respect to GN 101 survey [49,64].
Smeaheia possesses a 3D numerical model with closed boundaries developed by Statoil [49]. This available 3D model consists of 1.5105 × 106 active 3D cells with a 200 × 200 m lateral resolution and 100 layers with a 1.6 m average thickness. The model exhibits significant heterogeneity, with porosity ranging from 0.13 to 0.17 and permeability ranging from 0.18 to 7103 mD. This study has preserved static properties like permeability and porosity in addition to the PVT model. A black oil fluid model is utilized to simulate the injection of CO2 into a saline aquifer, with CO2 density of 1.87 kg/m3 and water density of 1026.03 kg/m3 at surface condition (the model uses “oil” with brine characteristics instead of water). At a depth of 800 m, the reservoir’s initial pressure is 81 bar. Additionally, rock compressibility is 4 × 10−5 bar−1 at a pressure of 10 bar. The Eclipse data file of the model was regenerated in the SLB Petrel 2017.4 software [65] for further analysis, and ECLIPSE100 [66] was used as the numerical solver.
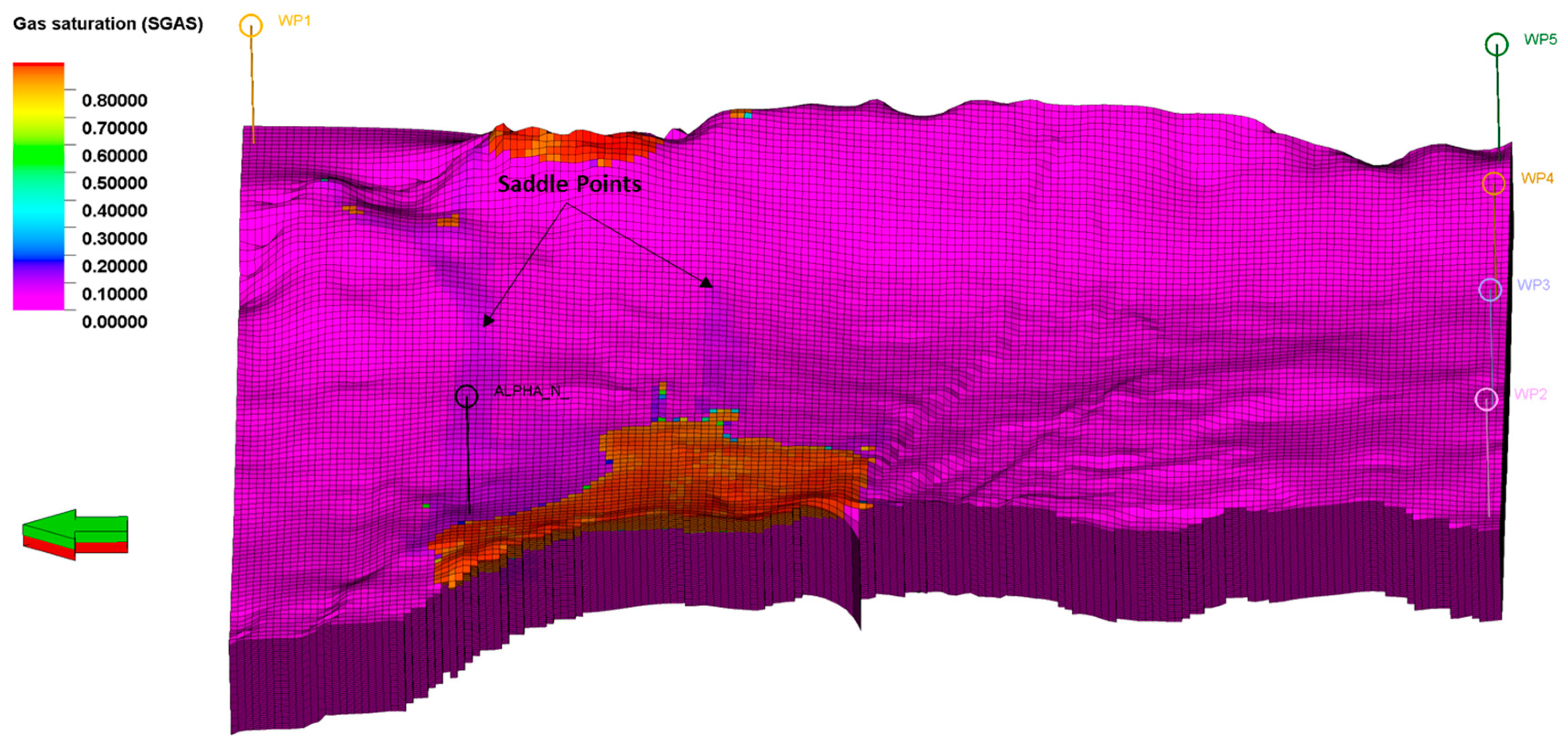
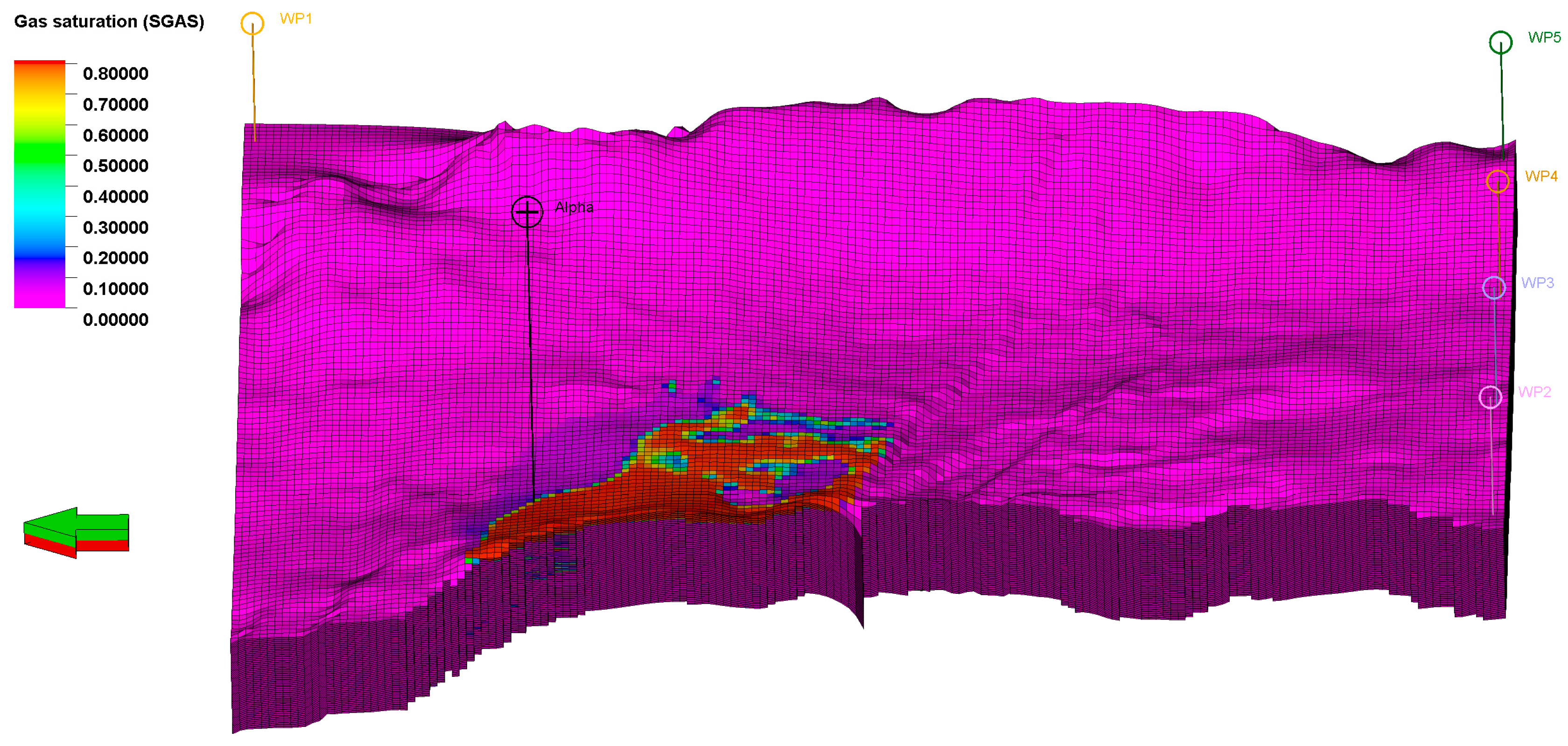
The 3D numerical fluid flow model includes four virtual water production wells in the south and one in the north. These wells are used to induce depletion in the Smeaheia aquifer and Troll East field due to gas production from the Troll field. This depletion is facilitated by the hydraulic communication between the aquifer and the field. The wells commenced production in 1999 and will continue until 2060. At that point, three wells, namely WP1, WP2, and WP5, will be closed. Additionally, in 2122, WP3 and WP4 will also be closed. In addition, pore volume multipliers are present in both the southern and northern regions of the model. These multipliers are used to compensate for the undiscovered reservoir area and to align the pressure decline inside the aquifer. The simulation data file was first executed by the numerical simulator without taking into account pore volume multipliers. From January 2022, CO2 was continuously injected over a period of 25 years at a rate of 5.872 × 106 sm3/day through a well named Alpha-N. The movement of the CO2 after injection was closely observed until the year 2300. Figure 5 depicts the distribution of CO2 saturation in the year 2300, as it migrates to the Beta zone by passing through the saddle points located in the middle of the field.
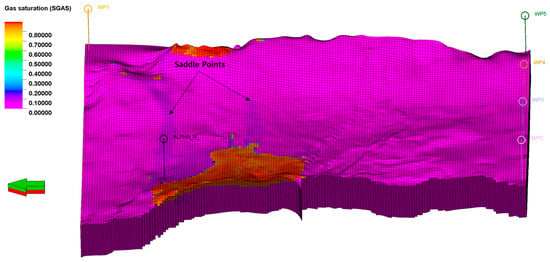
Figure 5.
Gas saturation distribution in year 2300, after 25 years CO2 injection with the rate of 5.872 × 106 sm3/day since 2022.
3.2. Updating the Numerical Model
According to observations, it was projected that the storage complex would undergo an average pressure drop of 14 bar from 1999 to 2022 [67]. Hence, the pore volume multipliers for the southern and northern regions have been set to 50 and 55, respectively, by sensitivity analysis to obtain a more certain model with respect to the original model.
As previously stated, the storage thickness decreases in an easterly direction, along with the caprock. Furthermore, as indicated by Figure 6, there are some minor faults and cracks present in the higher layers of zone Beta, where both the storage formation and caprock have been reduced in thickness. Consequently, it is imperative to avert the dispersion of the CO2 plume into zone Beta to mitigate the risk of probable leakage. Pre-existing faults and fractures, as well as caprock fracturing, contribute to the dangers associated with CO2 storage. Furthermore, during initial simulations, the bottom hole pressure reached a magnitude of 1000 bar, which is unattainable in real-world operations. Therefore, it is necessary to develop a new well design and optimize the injection process.
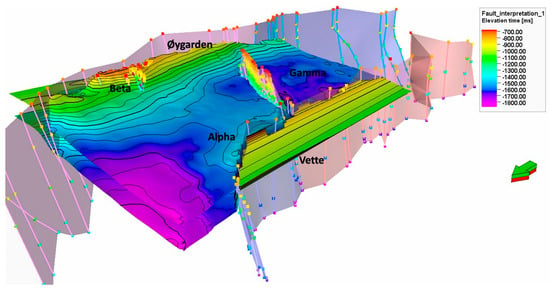
Figure 6.
Storage structure, consisting of top and bottom surfaces, and faults.
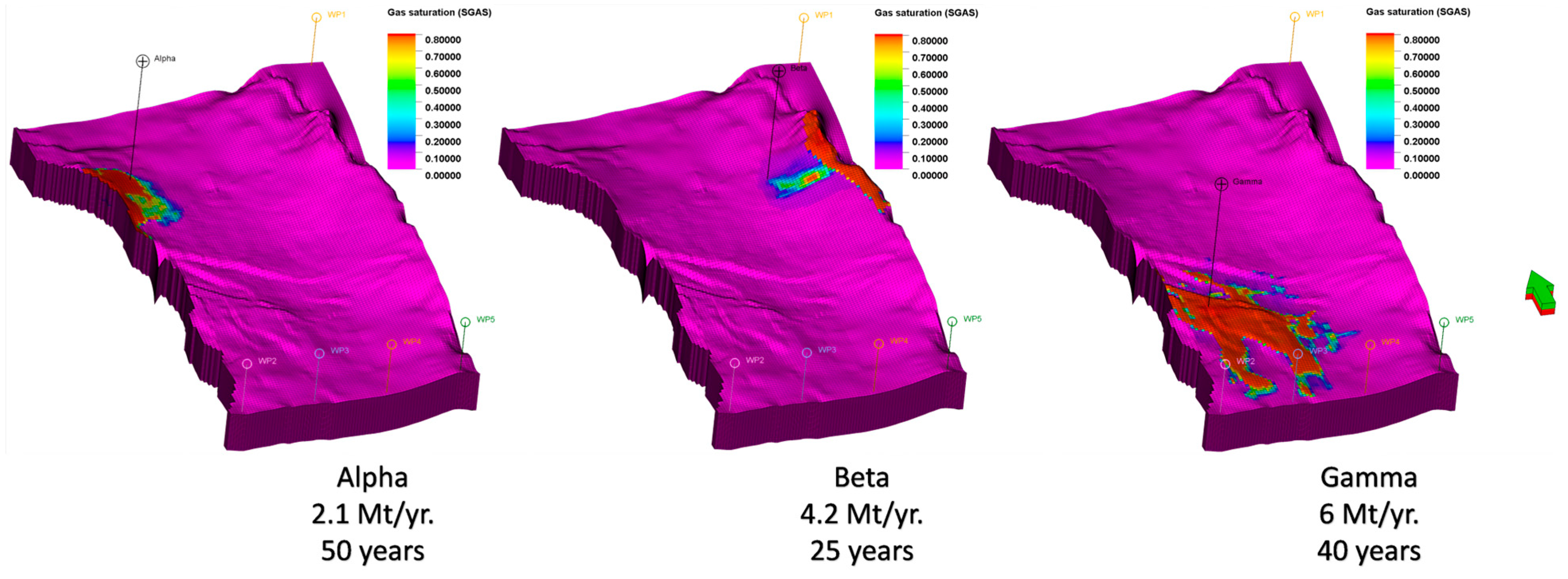
Brobakken [52] analyzed the sensitivity of the field with respect to well placement, although the model used differs from Statoil’s model regarding the presence of the production wells. Statoil’s model was assessed in this study with respect to the injection well location. Figure 7 compares the CO2 plume migration path where the injection well is located in the north of zone Alpha, between zone Alpha and Beta, and in the south of the model.
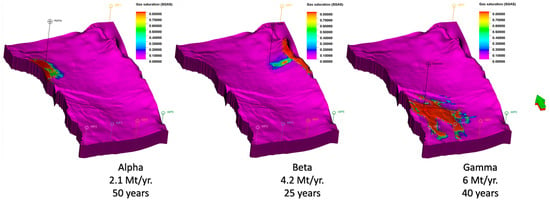
Figure 7.
Well location sensitivity analysis in zones Alpha, Beta, and Gamma.
Evidence suggests that the injection of CO2 in the vicinity of zone Beta will inevitably result in leakage. Zone Gamma is excluded from this analysis due to its unavailability in the seismic survey and the uncertainty surrounding its features, despite its significant storage capacity. In addition, the depletion of virtual wells causes the CO2 plume to vary from its initial route in the absence of virtual wells. Zone Alpha has shown superior performance in controlling the migration path of CO2. However, to optimize its effectiveness, the injection well must be relocated and modified as a down-dip J-shaped directed well in the northern part of the zone. This redesign should include a lengthy tangent section and perforation towards the northwest. The purpose of this was to ensure that the bottom hole pressure did not surpass the fracture pressure. The well Alpha was intentionally redesigned with the top of the perforation positioned at a depth of 1600 m TVD ssl.
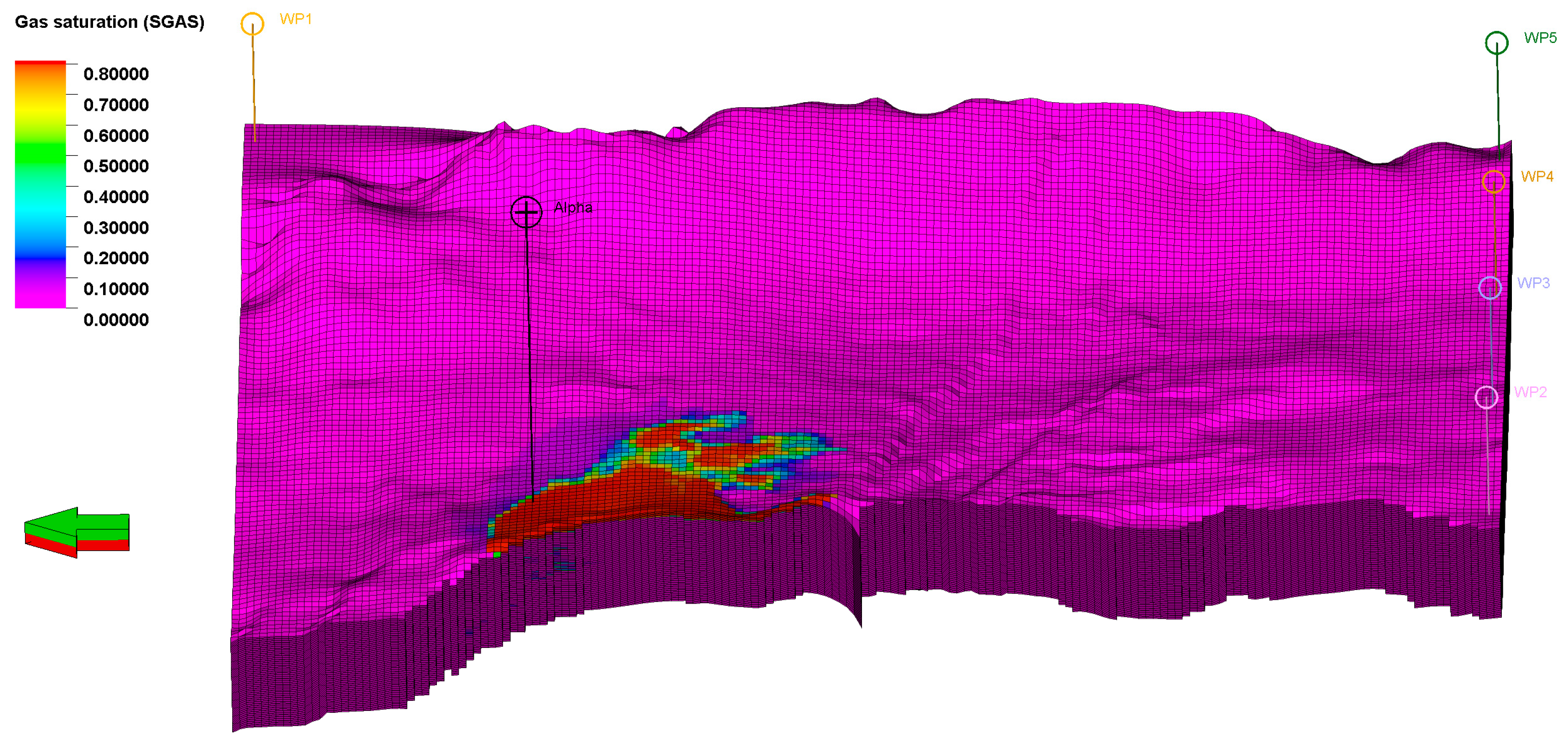
According to the stress model, the minimum horizontal stress (Min SH) can be calculated as the upper limit for bottom hole pressure, while the fracture pressure serves as the limit for field pressure [49]. The Min SH at the depth of 1600 m TVD ssl is 216 bar; by considering a safety factor, 200 bar is fixed as the well bottom hole pressure constraint. A simulation scenario was developed to validate the well design by injecting CO2 at a rate of 5.872 × 106 sm3/day over a period of 35 years (2022–2057). Figure 8 illustrates the CO2 saturation after a 35-year injection in the new model. The highest bottom hole pressure in well Alpha reached 180 bar.
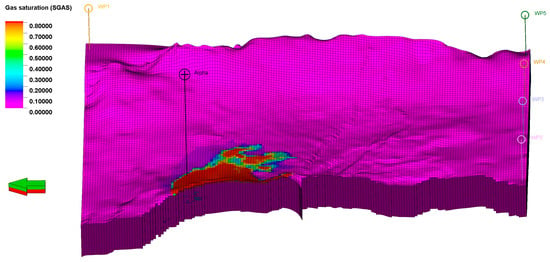
Figure 8.
Saturation distribution in 2072. 35-year CO2 injection in newly designed injection well Alpha.
3.3. CO2 Storage Optimization via Proxy Modeling
According to the CO2 storage goal, the objective of the Smeaheia project can be defined as follows:
- To maximize the amount of CO2 injected while maintaining a safe pressure level at the top of the injection area to avoid fractures in the caprock and to prevent the CO2 plume from moving towards zone Beta.
The risk of fracturing occurring far from the injection well is low as a result of the pressure reduction caused by gas production in the Troll field. The shallowest portion of zone Alpha, which has the only potential for fracturing, is positioned at a depth of 1240 m. This depth is located beneath the caprock, which possesses a fracture pressure of 187 bar. If a safety factor is used, the maximum pressure allowed at the top of zone Alpha will be 150 bar [49].
During CO2 injection in well Alpha, the northernmost spill point is reached first, which is approximately located in a grid with an i-index of 60 (Figure 4). Thus, the i-index of 50 was selected as the saturation constraint to avoid the CO2 plume from extending beyond the 60th i-index.
The injected CO2 volume can be calculated by multiplying the injection rate and the duration of injection, both of which are optimization variables. Furthermore, saturation and pressure distribution can be rapidly predicted utilizing grid-based SRMs. These indicate that the objective function and constraints can be expressed as follows:
where i1, j1, and k1 are cell indexes that address the spill points locations, and k2 defines the top of zone Alpha. The minimum injection rate was considered 2 × 106 Sm3/day, which can be increased up to 7.6 × 106 Sm3/day without exceeding the bottom hole pressure limit. Time is the injection period, which is between 25 and 50 years, with 6-month time steps.
Rate: [1.8 × 106–7.6 × 106] Sm3/day
Time: [0:6:600] month
Subjected to:
This research used a GA as the optimization technique due to its simplicity of implementation, effective constraint handling, and strong convergence capabilities, imported from the Pymoo package [68] in Python 3.10.0, without any hyperparameter tuning during sampling, crossover, and mutation. The requirement for the time step to be an integer necessitates the selection of an integer value for the CO2 injection rate within the specified range, which, in turn, enhances the efficiency of the optimization process. Consequently, an integer simulated binary crossover and polynomial mutation are employed subsequent to an integer random sampling. The crossover and mutation functions utilize a probability of 1.0, which means all variables are involved in crossover and mutation, and an eta value of 3, which controls the distribution of new solutions around parental solutions. The default solution provided by the module for handling constraints is the death penalty. The population size is fixed at 100 individuals, and the optimization process will conclude after replacing 100 generations.
Proxy Modeling
As previously mentioned, there are three distinct categories of SRMs: field-based, well-based, and grid-based. The choice of a single or coupled-type SRM depends on the specific SRM application. Due to the need to control and monitor CO2 saturation and pressure at different sites both horizontally and vertically in order to optimize storage, a grid-based SRM (SRMG) will be constructed for each parameter. Figure 9 demonstrates the proxy modeling workflow.
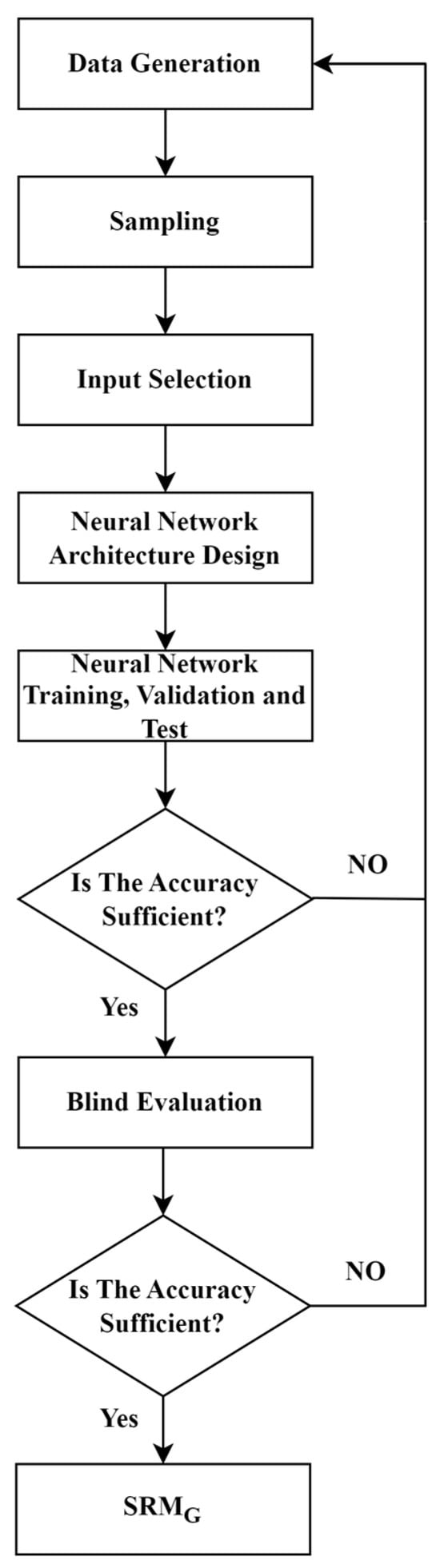
Figure 9.
Proxy modeling workflow.
An ANN requires a wide range of input data in order to effectively learn the behavior of a phenomena and accurately predict outputs under different conditions. If there is a lack of or insufficient actual data, synthetic data are generated using analytical or numerical models. Since the Smeaheia project has not yet started, we will use numerical simulation to generate the necessary data. The optimization variables are injection rate and injection time; so, an adequate number of scenarios were investigated to define the model response as a function of injection rates and times. This dataset represents the training data.
To develop SRMG, Amini [44] used three simulation cases with a fixed injection period and different injection rates and added two more cases to enhance the precision at the periphery of the CO2 accumulation area. According to the workflow (Figure 9), the quantity of numerical simulation cases that impact the ANN’s accuracy and ability to generalize to diverse inputs was tuned while training. Accordingly, in this study, the proxy development began by presenting the outcomes of three simulated scenarios and continued with seven cases until the acceptance of the model’s accuracy.
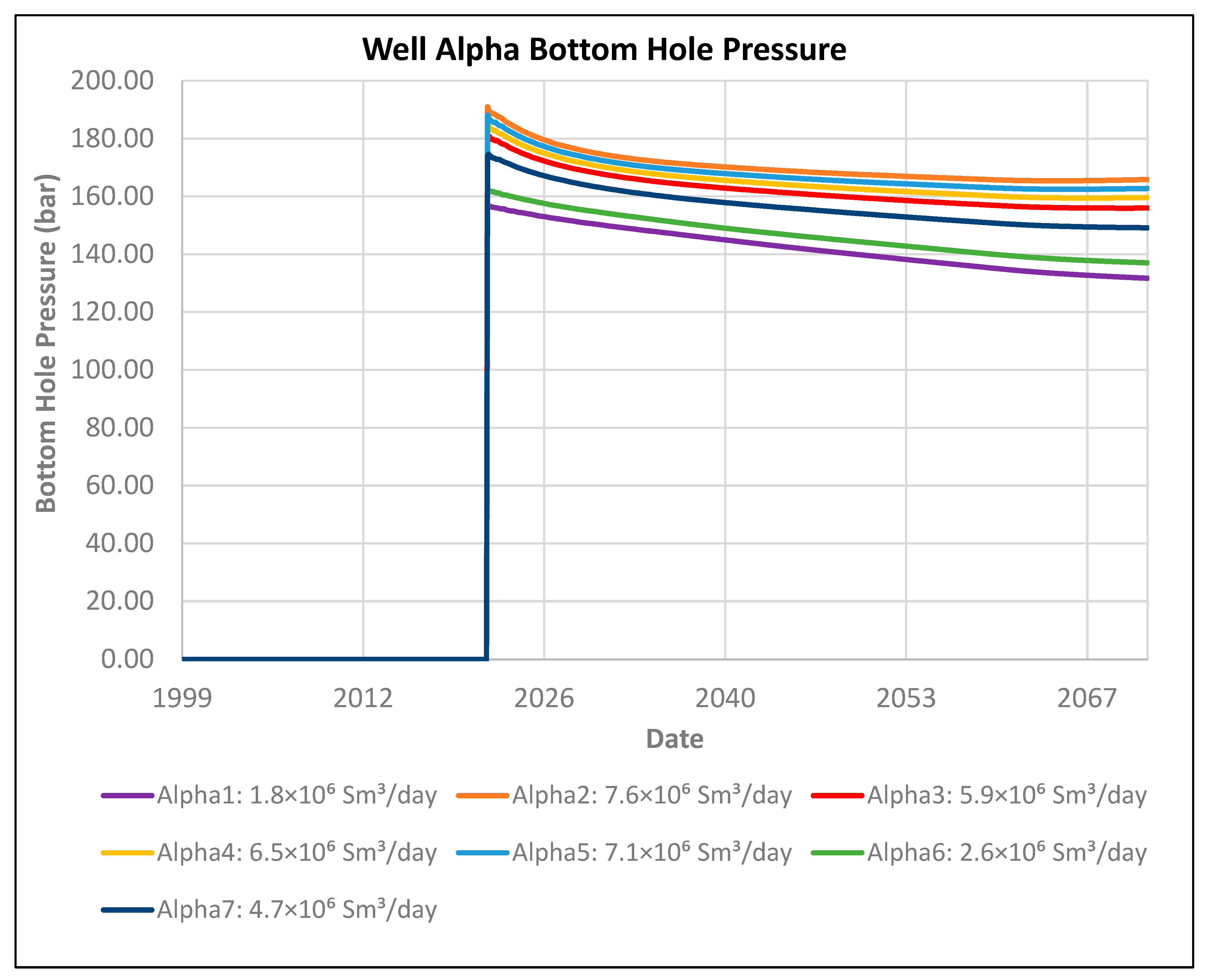
Due to the superior performance of proxy models in interpolation compared to extrapolation, the injection rate range for numerical simulations should be limited to the minimum and maximum admissible rates. The maximum possible rate, without exceeding the bottom-hole pressure constraint, is 5.5 Mt/year. Therefore, seven rates between 1.3 Mt/year and 5.5 Mt/year will be chosen, as shown in Figure 10.
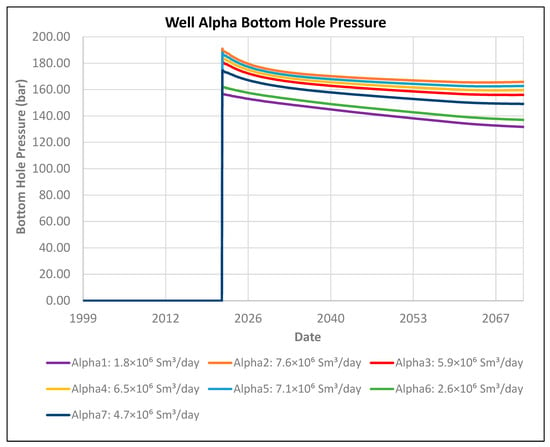
Figure 10.
Bottom hole pressure of numerical simulation cases used for SRM training.
Sensitivity analyses were developed considering time steps in the range from 1 month up to 5 years within the fixed simulation time frame of 50 years of CO2 storage. On the basis of the results, a 6-month time step was selected, balancing accuracy and generated data volume, splitting the simulation time into 100 steps.
Further sensitivity analysis on the cascading and non-cascading SRM method was performed. The cascading approach showed numerous drawbacks in terms of error accumulation, complexity, and time-consuming step-by-step predictions. Therefore, the non-cascading approach was adopted and the input features for training the ANN were selected and listed in Table 1.

Table 1.
Input Features.
The qualities and conditions of neighboring cells surrounding a grid block must be considered as a boundary condition, because they impact the movement of fluids. During the process of injecting and storing CO2, the CO2 moves upwards due to gravitational forces and changes the level of CO2 saturation in the grids, depending on the properties of the layers above and below. A tier model was developed to determine the average pressure, saturation, permeability, and porosity of neighboring grid blocks for each cell in the current layer (the cell layer), as well as the layers directly above and below it. These average properties are referred to as tier-1, tier-2, and tier-3, respectively. Indeed, the average property of cells, which are connected to the main grid block through a surface, line, and point, is computed in three sequential layers. Apart from permeability, which uses a harmonic averaging method shown by this Equation (5), the average of all the other parameters is computed by the arithmetic method.
This study assumes that the boundaries are completely sealed, resulting in a layer above the first layer and a layer below the last layer with negligible permeability and porosity. Consequently, the saturation of CO2 in these layers will be zero. Moreover, in the event of a closed boundary, the reservoir will exhibit a pseudo-steady state condition. The pressure above the topmost layer and below the bottommost layer is assumed to be equal to the pressure of the current layer due to insufficient data.
The reservoir model contains 1.5105 × 106 grid blocks, which makes it unusable for the input dataset. Consequently, the input grids were decreased by implementing sampling techniques and criteria that rely on the model’s output. The input dataset of the saturation model was sampled using the parameter variation that specifically chooses cells that are more influenced by CO2 injection. Performing an injection at the maximum rate has a greater impact on a bigger number of cells and spreads CO2 over a wider area. Thus, only the grids that had a saturation value greater than zero after 50 years of injection at the maximum rate were selected for sampling. Nevertheless, this sampling technique resulted in overfitting for the pressure model input as a consequence of its spread across the whole storage model, rather than being limited to a specific region surrounding the injection well. The pressure model, which was trained using data from cells that showed the highest level of pressure change, failed to generalize in the blind evaluation and was consequently abandoned. Thereby, the grids were randomly sampled in order to train the pressure model; 1.485 × 106 cells were selected randomly and excluded from all cases to ultimately keep 2.55 × 104 random cells.
The final dataset consists of 31 features that exhibit variations across diverse ranges of real numbers, which could potentially result in instability throughout the training process. Based on the physics of the problem, the activation functions ReLU [69] and Sigmoid [70] have been chosen which produce output values ranging from 0 to 1. Thus, the dataset requires normalization between 0 and 1 by the min-max method (Equation (6)). The global nature of each property’s minimum and maximum values allows for their application in denormalizing the ultimate forecast of the pressure model and facilitating comparison with the actual value.
The final stage involves constructing the architecture of the ANN, which ensures an adequate degree of accuracy during the validation, testing, and blind evaluation processes. An attempt was made to train a single ANN for both qualities, which encountered a significant convergence challenge. Furthermore, the sampling technique for saturation and pressure models differs, resulting in distinct training data. Consequently, a distinct ANN was developed for each parameter. To attain this, hyperparameters must be tuned; they include the number of hidden layers, the number of units in each layer, the activation function, and the learning rate, in addition to features and amount of data.
The features and examples of input data were determined based on the reciprocal relationship between accuracy and computer facilities tolerance. The optimal hyperparameters for the artificial neural network (ANN) structure (as shown in Table 2) were determined by multiple trial-and-error iterations during the training, validation, and blind assessment stages, following the SRM development flowchart (refer to Figure 9). Different optimization algorithms can be implemented to minimize the loss function and train an ANN. The SGD, the root mean squared propagation (RMSprop), and Adam are a group of available optimizers. In this study, Adam indicated better performance than the others. In addition, an exponential learning rate decay function was employed to maintain a consistent learning rate and prevent any fluctuations in the trend of learning and validation loss. The models were developed in Python by Keras TensorFlow [71].

Table 2.
Hyperparameters.
4. Results
4.1. Model Training
The process of constructing an Artificial Neural Network (ANN) model consists of distinct stages: training, validation, and testing. Each stage necessitates the use of a distinct dataset. The dataset is divided into training, validation, and testing sets, in this study with ratios of 80%, 10%, and 10% respectively. During the fitting phase, the model undergoes training using the training dataset. After each epoch, the resulting model is evaluated using the validation dataset. After completing the training and validation of the model, it is evaluated using the testing dataset. A suitable model exhibits consistent loss values across all time steps. This fact also must be confirmed by metrics. The primary loss function utilized for this study was the Mean Absolute Error (MAE) (Equation (7)) due to its suitability as a metric for regression tasks. It enables the detection of errors in the initial set of characteristics during the training process. Moreover, the real MAE in bar units for the pressure, which has been normalized for model training, can be computed to offer a more accurate representation of the model’s precision. The Mean Squared Error (MSE) (Equation (8)) is used as a supplementary metric during training to assess the effectiveness of the primary loss function. In addition, the absolute percentage error was used to accurately quantify and visually depict the extent of the problem.
where Y is the output feature, i is the output index in the range from 1 to n, and n is the number of instances. The true output represents the computed variable by the numerical simulation, while the predicted value indicates the proxy model output.
In order to enhance the accuracy assessment of the pressure model, we compute the corresponding MAE using the denormalized data (i.e., pressure in bar):
By replacing the denormalized pressure data (Equation (9)) in the MAE formula (Equation (8)), Equation (10) will be obtained (in bar):
Table 3 and Table 4 represent the performance metrics of CO2 saturation and pressure models. The extremely low MAE and MSE values provide confirmation of the successful training of the models without underfitting. Furthermore, their consistent values for training, validation, and testing effectively eliminate any potential for overfitting. An MAE value below 0.05 demonstrates a high level of competence in pressure model development.

Table 3.
CO2 Saturation SRM Accuracy Evaluation.

Table 4.
Pressure SRM Accuracy Evaluation.
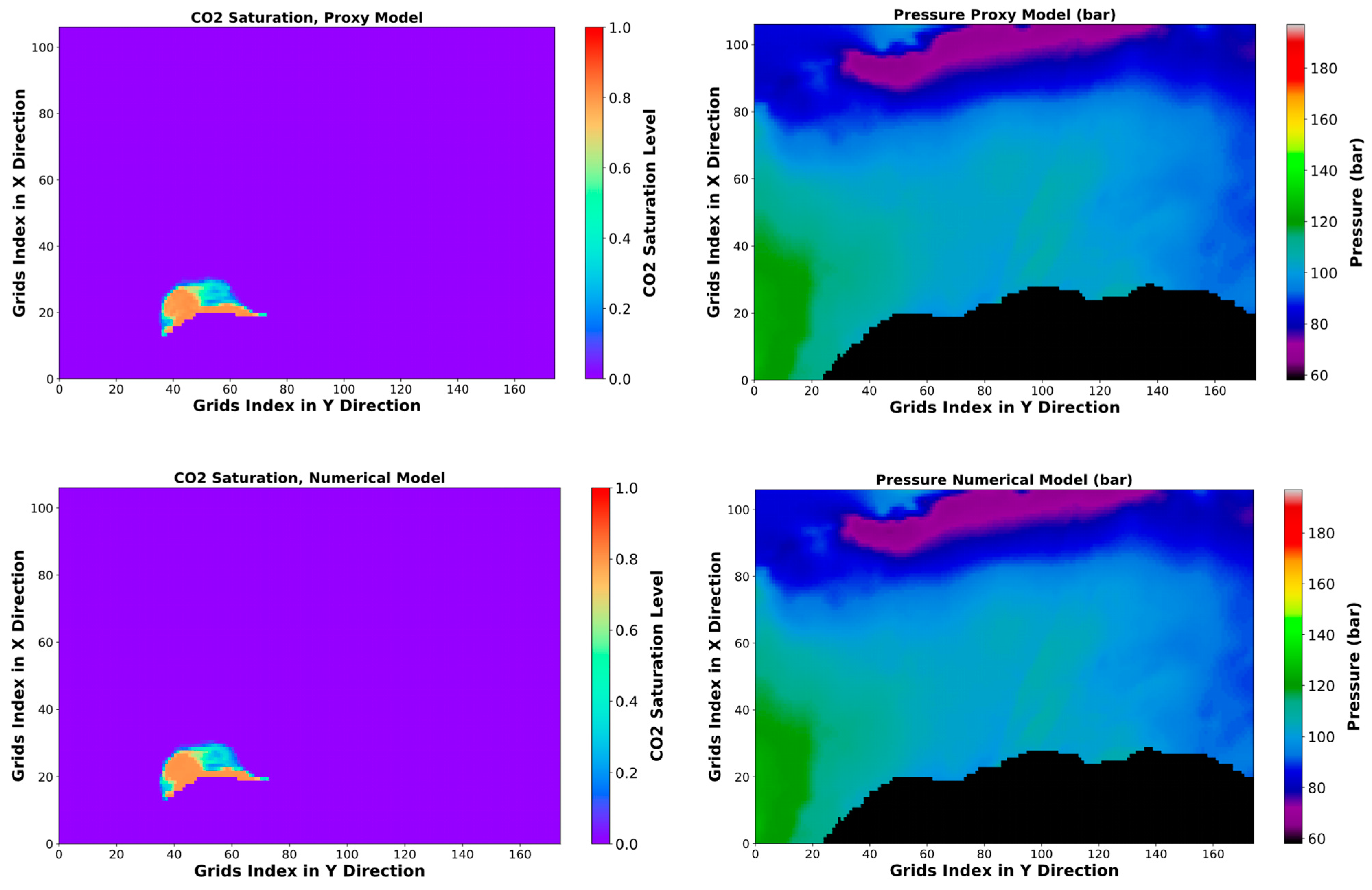
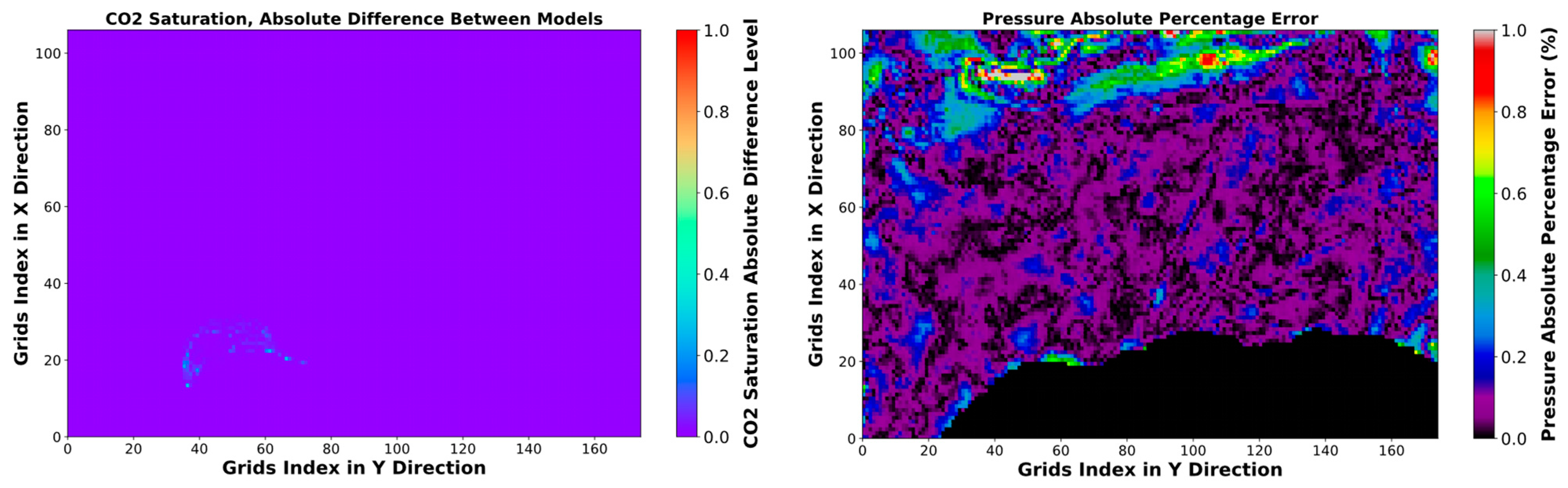
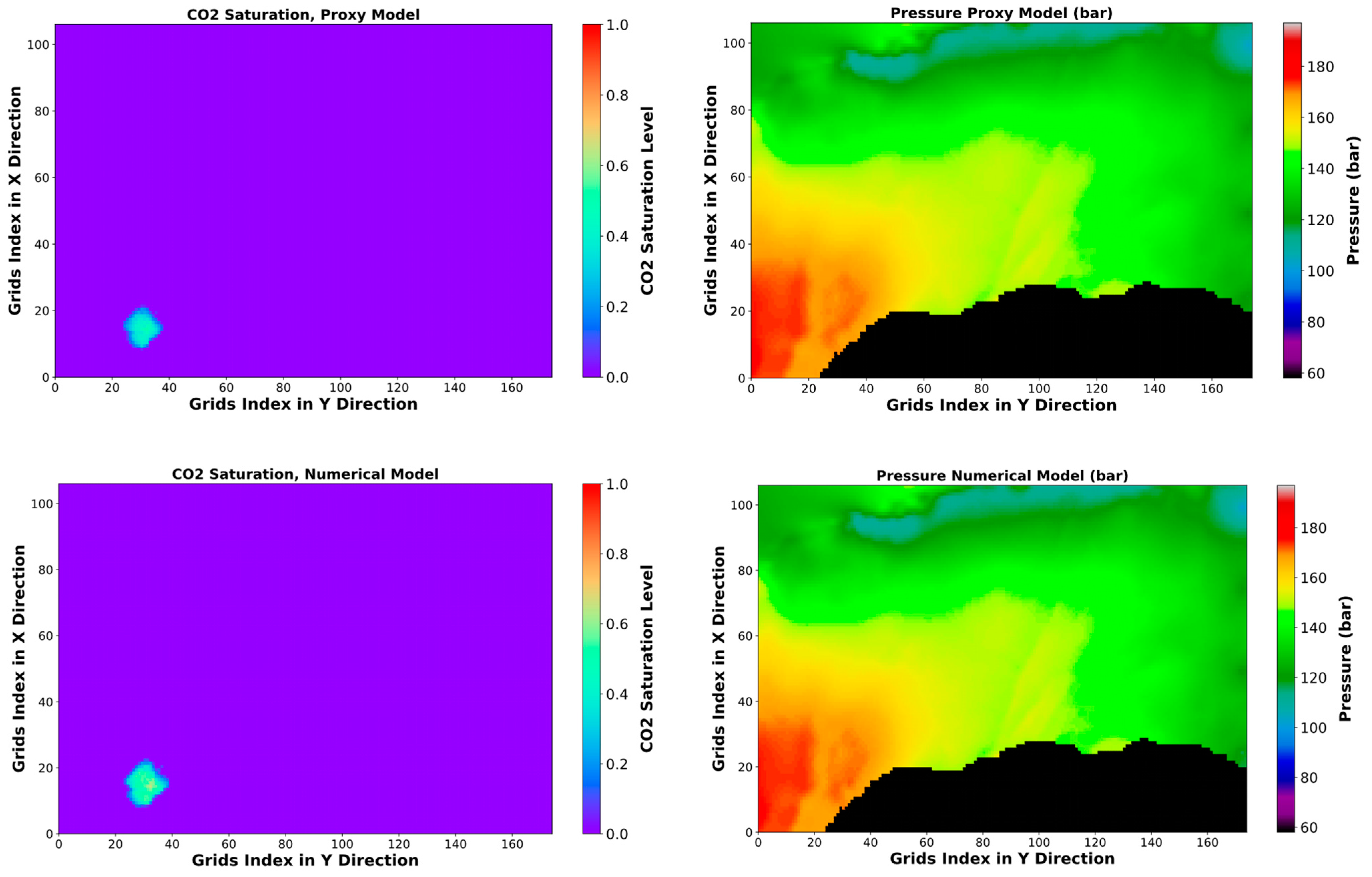
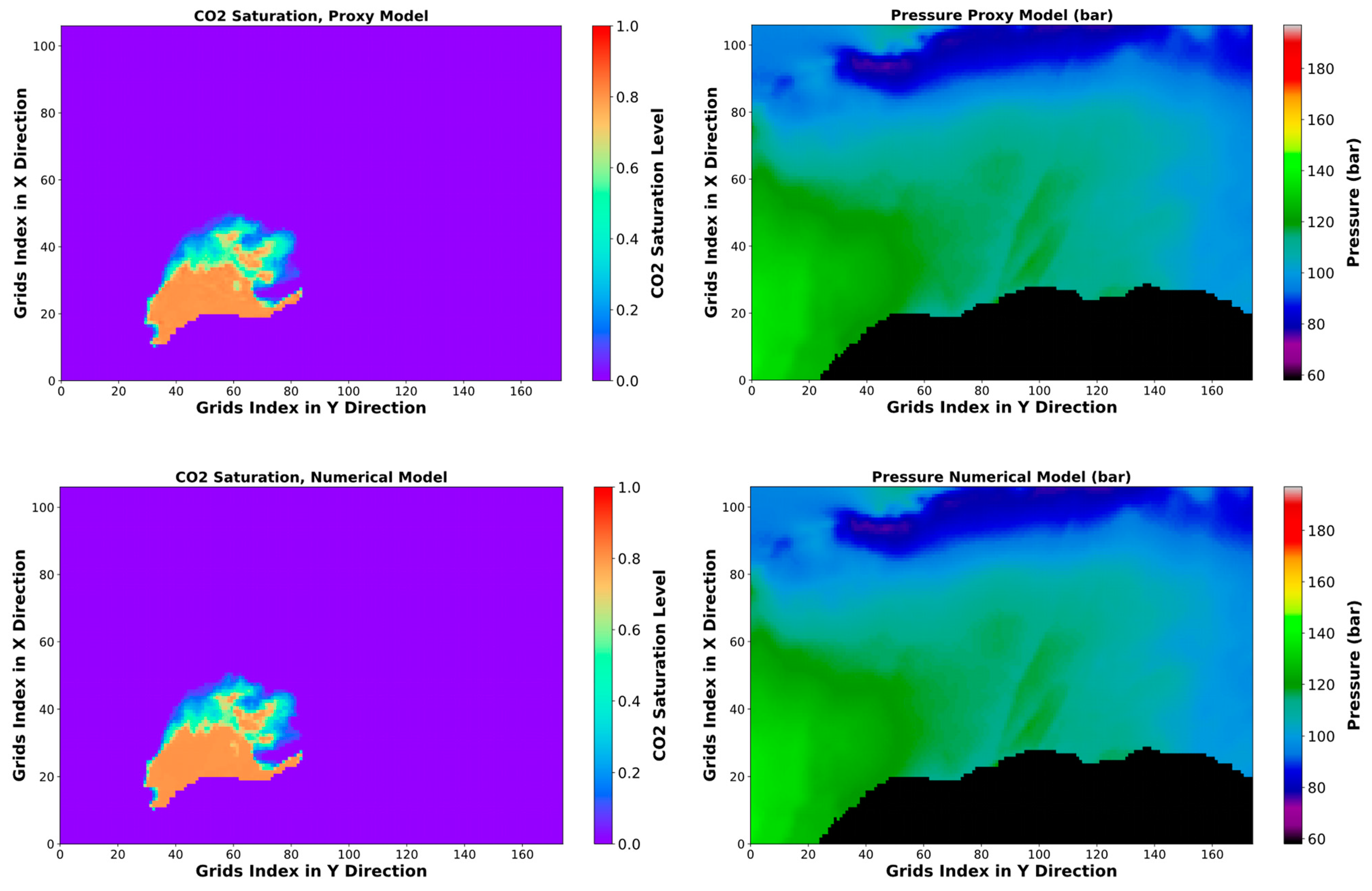
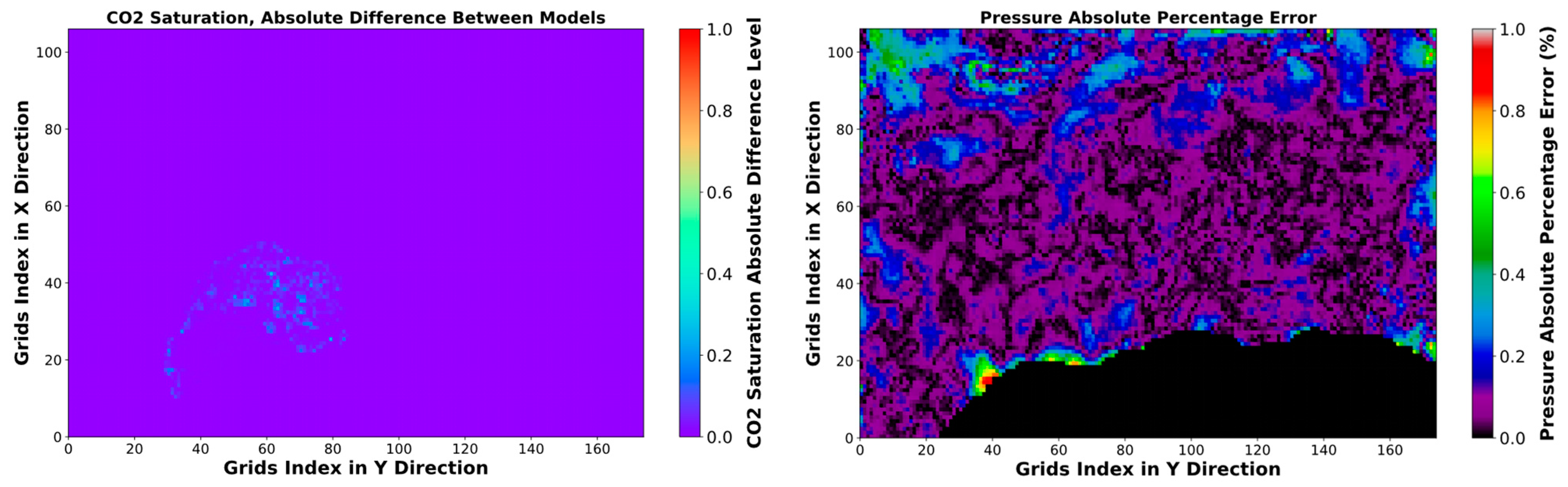
The SRM exhibited a much higher computational speed than the 3D numerical simulator, about 300 times faster when simulating the final outcome at the last time step. Figure 11 and Figure 12 compare the CO2 saturation and pressure distribution maps in two different layers and at two different time steps for training cases, obtained by SRM and the numerical simulation. Moreover, the saturation absolute difference and pressure absolute percentage error between SRM and the numerical simulation are mapped. Based on the saturation absolute difference map, it can be observed that the error for the CO2 plume saturation prediction is either zero or within 0.1 in most locations. Within the CO2 plume, there are, however, specific spots where the absolute difference of CO2 saturation is up to 0.2–0.3. Furthermore, the SRM saturation achieved successful predictions at distant locations (from the CO2 plume) due to its training on cells that contained CO2 saturation values greater than zero. Unlike the MAE of the training, testing, and validation datasets, which only include the area of the CO2 plume, the MAE of the complete field simulation decreases to 1.6 × 10−4. The absolute percentage error of the cells’ pressure is within 1%. The actual MAE of the complete field pressure simulation is 6.9 × 10−2 bar, which closely aligns with the results obtained during training and validation. This verifies the model’s potential to generalize in diverse CO2 injection rate and time.
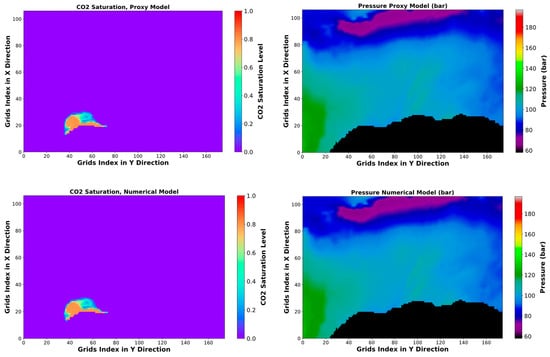
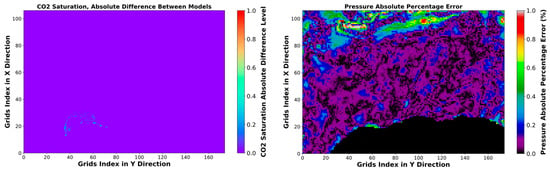
Figure 11.
Pressure and CO2 saturation distribution and error maps after 50 years injection with the rate of 1.79881 × 106 Sm3/day, 1st layer.
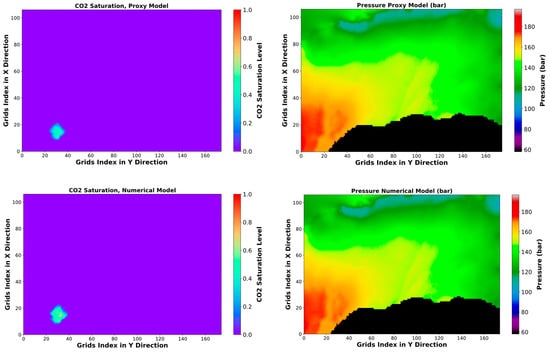
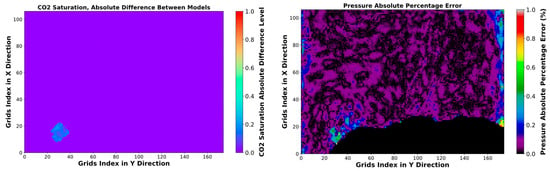
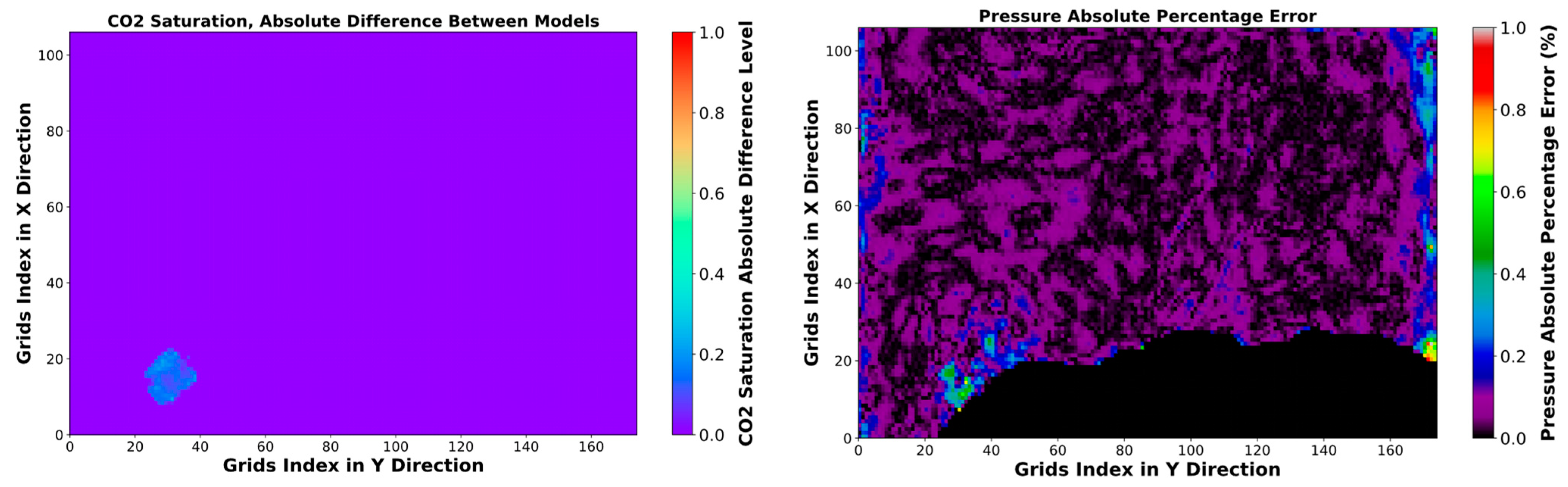
Figure 12.
Pressure and CO2 saturation distribution and error maps after 25 years injection with the rate of 7.61035 × 106 Sm3/day, 70th layer.
4.2. Blind Validation
The accuracy of the SRMs was next confirmed through a blind case that was not included in the training dataset. A numerical simulation case with a distinct rate is generated in order to assess the viability of the proxy model for applications such as optimization and sensitivity study. Table 5 shows the blind evaluation results of SRMs at various time steps for a CO2 injection time frame of 50 years with a rate of 3.45925 × 106 Sm3/day. The MAE of the blind evaluation is of the same order of magnitude as the MAE of the training outcome: it confirms the model’s ability to generalize in various dynamic conditions. Furthermore, upon comparing the MAE observed during the simulation, no discernible evidence of error accumulation can be identified. As previously stated, the training data for the saturation model only includes cells around the injection well that are more significantly impacted by CO2. In contrast, the blind validation data encompasses the whole model. Due to a substantial portion of the model containing zero CO2 saturation and the capability of SRM in predicting these zero saturations, the MAE was reduced compared to the MAE of the training data.

Table 5.
Blind Validation Results.
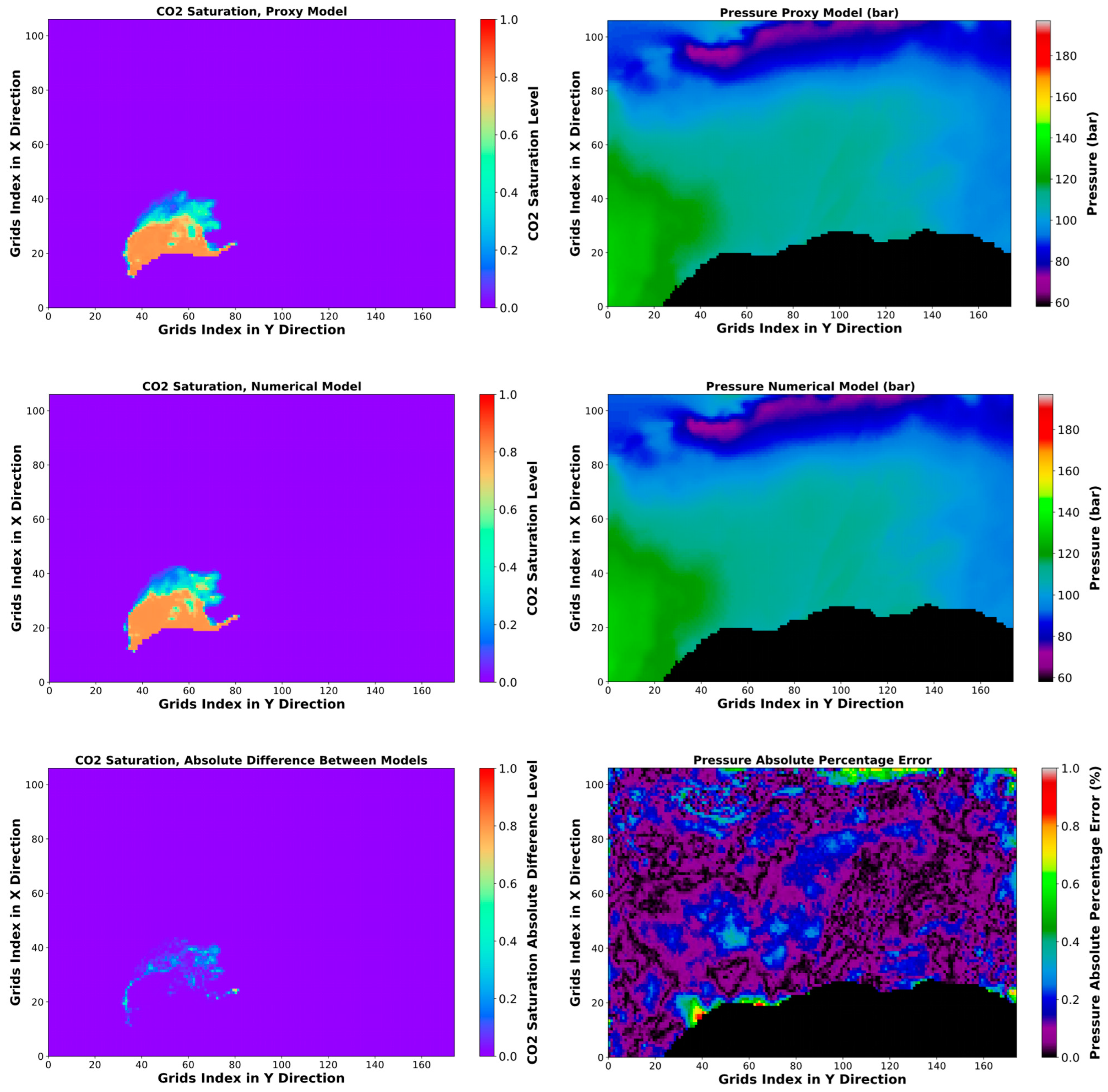
The comparison between CO2 saturation and pressure distribution for the blind case in the first layer obtained from SRM and the numerical simulation is shown in Figure 13. The CO2 saturation and pressure predictions of the proxy models show high consistency with the results of the numerical simulation. The CO2 saturation prediction error is either zero or less than 0.1, in addition to a few points with a difference of about 0.2–0.3, just like the training examples. The absolute percentage error of grid cells pressure is between 0 and 1 percent. Furthermore, the error maps depicted in Figure 13 exhibit significant similarity to the maps shown in Figure 11 and Figure 12.
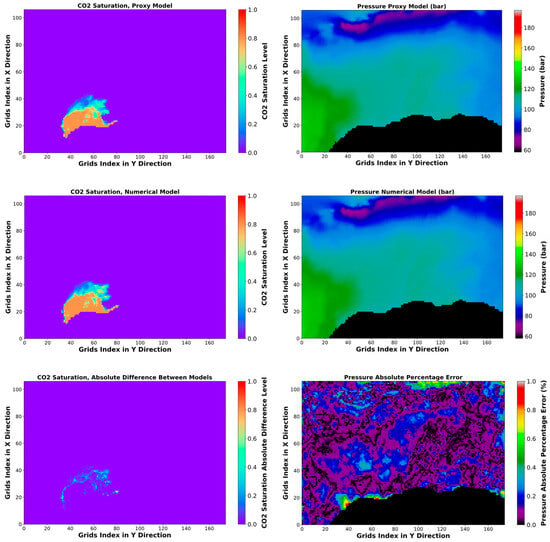
Figure 13.
Pressure and CO2 saturation distribution and error maps after 50 years injection with the rate of 3.45925 × 106 Sm3/day, 1st layer.
4.3. Optimization
The GA identified the optimal population consisting of 100 individuals after undergoing 100 generations replacement. A total of 10,000 iterations were completed within a time frame of 50 min, while a single simulation of CO2 injection in Smeaheia using ECLIPSE100 [66] and SRMs required 6 h and 1 min, respectively. The minimal computational cost is obtained by utilizing SRMs and restricting the simulation region to target grid cells. This is possible because SRMs can simulate the properties of each cell independently from other cells. The first individual in the last population represents the optimal rate and injection period that results in the highest volume of injected CO2, while still adhering to the given limitations. Table 6 displays the initial 20 individuals from the most recent population. Based on the data presented in this Table, injecting CO2 at the optimal rate of 4.683495 × 106 Sm3/day for a duration of 50 years will securely store approximately 170 million Mt of CO2. Consequently, about 3.2 Mt CO2 must be supplied annually.

Table 6.
The final population of the optimization.
The CO2 saturation constraint is approximate, so assessing the CO2 plume migration in the post-injection interval is required. Therefore, a 3D numerical simulation case with the optimal values of CO2 injection rate and time was run not only to validate the SRM during injection but also to monitor CO2 distribution in the post-injection period. In the designed case, the injection started in 2022 until 2072, when no further production activity occurred; the behavior of the system was simulated until 2100 considering no injection/production operations. Figure 14 illustrates the distribution of CO2 saturation in 2100, showing no indication of CO2 movement towards zone Beta. As a result of the closure of wells WP1, WP2, and WP5 in 2060, the depletion impact in the southern part of the storage area is the most significant. The CO2 plume tends to move towards the southern region of the model when the depletion wave of well WP1 diminishes. The injection rate and period that yielded the best results were used to confirm the accuracy of the optimization in Figure 15. The SRM and numerical model estimated the pressure and CO2 saturation after 50 years of injection at a rate of 4.683495 × 106 Sm3/day. CO2 saturation mean, absolute difference, and pressure absolute percentage error were mapped to demonstrate the models’ supreme accuracy in optimization.
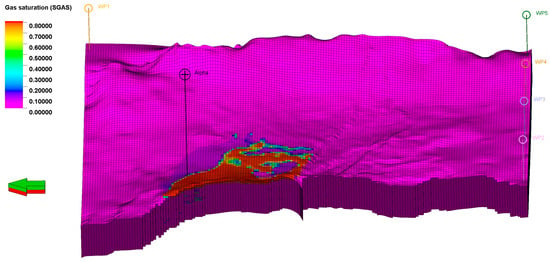
Figure 14.
CO2 Saturation distribution in 2100, 28 years after stopping CO2 injection at rate of 4.683495 × 106 Sm3/day for 50 years.
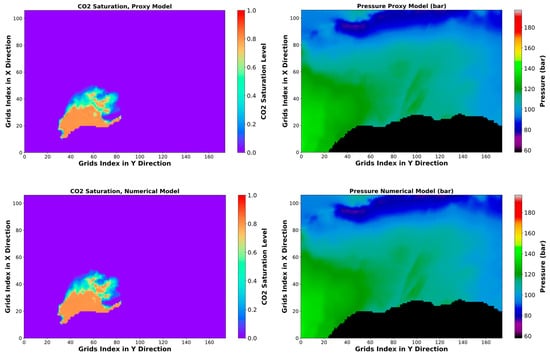
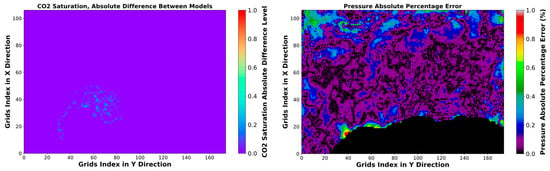
Figure 15.
Pressure and CO2 saturation distribution and error maps after 50 years injection with the rate of 4.683495 × 106 Sm3/day (optimum case), 1st layer.
5. Discussion
In order to achieve Net Zero Emissions (NZE), it is imperative to prioritize the implementation of safe and effective geological CO2 storage. In this context, it is necessary to conduct a sensitivity analysis to examine the challenges associated with candidate sites and impose constraints on them while optimizing the process. This study employed SRMs as a replacement for the standard numerical simulation approach in order to reduce computational time while preserving accuracy. The objective was to facilitate rapid investigation and management of CO2 storage in the Smeaheia saline aquifer.
The development of an ANN-based SRM in this study commenced by employing the cascading method. This method involves dividing the simulation time into numerous time steps and training a separate model for each time step. Subsequently, the strategy was altered to a non-cascading way due to the drawbacks associated with the cascading approach. When using a cascade proxy, multiple models need to be trained and optimized for each parameter. This process can be complex and demanding in terms of computational resources. As previously stated, the approach is particularly hindered by error accumulation, which is especially problematic during long-term simulations. To predict 50 years of CO2 storage, 50 models need to be trained, each with a 1-year time step. MAE was around 1 × 10−2 for training and testing a single CO2 saturation model, whereas it reached 0.9 for sequential blind evaluation of cascading SRM. Additionally, the developed proxy is intended for an optimization study that needs to predict all models’ parameters prior to the desirable time step in the cascading approach. If the proxy models were constructed using the cascade technique, it would require approximately 50 min to sequentially forecast the last time step. Although the cascading method is still faster than numerical simulation (which took 6 h with a dynamic memory allocation of 4000 MB), the non-cascading proxy model simulated each dynamic parameter in only 30 s. It should be mentioned that this study was performed using a computer system with Intel(R) Core (TM) i7-4710HQ CPU 2.50 GHz and 16 GB RAM.
The dataset is influenced by the amount of training scenarios (simulation cases), time step, features, and sampling technique. Multiple time-step durations were examined in order to create the most precise model. No significant improvement was noticed when reducing the time step from 6 months to 3 months. However, by increasing the number of training scenarios, the model was able to accomplish generalization.
The only input features excluded are the cell distance from the boundary and the bottom-hole pressure owing to additional computational efforts compared to the model improvement, and lack of well-based SRM, respectively. It is advisable to integrate this model with a well-established SRM in the future in order to incorporate bottom-hole pressure into the grid-based SRM and assess its effects. Besides that, the well placement, injectivity, wellhead pressure, tubing size, as well as perforation length and position can be assessed and optimized.
The sampling method depends on the dynamic behavior and distribution of the properties. The pressure model’s input was sampled by considering the fluctuation in property values between time steps. This means that only the points near the injection and production wells were chosen, resulting in overfitting and a large inaccuracy for sites located far from the wells. The utilization of random sampling across the reservoir effectively reduced the absolute percentage error of pressure to below 0.5% in the majority of cells by selecting points from various locations.
Amini and Mohaghegh [22] proposed the use of an ANN with a single hidden layer to construct cascading proxies. Nevertheless, when employing the non-cascading approach with a substantial dataset consisting of 1.75 × 107 rows and 31 columns, a basic ANN (resulting in underfitting) was unable to discover the solution. Expanding the model network significantly reduced the model loss. It is important to note that a significant expansion of the ANN can result in overfitting and decreased accuracy in predicting outcomes.
Considering the problem framework, ReLU and Sigmoid are the optimal activation functions. When comparing the two, ReLU performs better in the hidden layer. However, its use in the output layer leads to the algorithm becoming stuck in a plateau and training very slowly. Utilizing the sigmoid function in the output layer resolved the issue. In addition, the model training was extremely responsive to the learning rate, as it was exclusively conducted using the beginning rate of 5 × 10−4. However, to ensure consistent learning, a learning rate decay function was utilized instead of a constant training rate, which led to the successful convergence of the solution.
The absolute difference in the CO2 saturation model is generally less than 0.1 in practically all cells. However, it is mostly accumulated in cells located at the periphery of the CO2 plume. This issue becomes more pronounced when CO2 is delivered at the greatest injection rate in the training scenarios. A maximum rate that is beyond the maximum rate used for model application may be employed to train the model.
This study did not optimize the GA hyperparameters, despite making a few modifications to the population size and number of generations. These modifications were made after confirming the functionality of the code and algorithm using a quick optimization process with a small population and termination generation. A limited population size or a level of termination that is below the optimum may not result in the most ideal solution, but it will still be quite close to it. At first, the optimization was carried out with a saturation limit on the spill point between zones Alpha and Beta. The CO2 plume moved away from the saddle point by monitoring the post-injection period. Therefore, the constraint is established before the spill point in order to create an empty area for the movement of CO2 after injection.
Despite SRMs exhibiting good performance in fast simulation, the optimization process requires thousands of simulations, which still remains a computationally burdensome task. The non-cascading approach employed by our SRMs enables the simulation of individual cell properties independent of other cells and time steps. Consequently, by restricting the simulation area for CO2 saturation to the vicinity of the injection well and confining the pressure prediction region solely to the first layer of the model, the overall optimization time was reduced to 50 min. On the other hand, when taking into account factors such as computational time and the presence of dependent cells, the use of numerical simulation renders the optimization unfeasible.
6. Conclusions
This study examined fast simulation and optimization of CO2 storage in Smeaheia aquifer through the utilization of grid-based proxy models. Furthermore, the work addressed several challenges that arise in the development and application of such SRMs. In brief:
- In this work, a non-cascading grid-based SRM was deemed appropriate for long-term surrogate reservoir modeling and optimization in the context of Smeaheia storage.
- Proxy models built for replicating both CO2 saturation and pressure data showed excellent accuracy compared with the results of the numerical simulator. Data sampling for the former could be conducted by assessing the degree of property fluctuation over time, as opposed to pressure data, which necessitates random samples.
- The pressure SRM exhibited less than 0.5% error, which shows its applicability in future studies, especially when it comes to coupling it with geomechanical models.
- To effectively tackle the issue of accumulated error at the CO2 plume boundary when SRM is applied at high injection rates, it is recommended to use higher maximum injection rates that exceed the maximum rate for model application in the training phase.
- By leveraging the SRMs, an optimization process consisting of 10,000 iterations was successfully completed within a time frame of 50 min, achieved by constraining the simulation volume. This is a huge reduction in computational time compared with optimization using the numerical model.
- Finally, the study demonstrated that CO2 can be injected in Smeaheia at a rate of around 3.4 Mt per year to safely store about 170 Mt CO2 in 50 years.
Regarding the limitations of this study, SRMs are limited in generalizing to different geological contexts (i.e., fit-for-purpose rather than one-size-fits-all). In order to utilize SRMs for simulating a different reservoir, it is necessary to retrain the models, as per the standard approach of proxy modeling. Non-cascading SRMs offer advantages in modeling CO2 storage; nevertheless, they are impaired in post-injection simulation due to the fact that the developed SRMs cannot accurately predict the final time step of the CO2 injection. To make a post-injection prediction, it is necessary to either train an additional SRM or retrain the current SRMs with a more extended network and additional input and output features. Furthermore, a deterministic approach was employed in this study, neglecting geological uncertainty. Also, since there is no historical data available for the project, the numerical model being used is not history matched. These limitations need to be addressed in a computationally efficient manner in future studies.
Author Contributions
Conceptualization, B.A., A.J.G., V.R. and C.S.W.N.; Data curation, B.A.; Formal analysis, A.J.G.; Funding acquisition, B.A.; Investigation, B.A.; Methodology, B.A.; Software, B.A.; Supervision, A.J.G. and V.R.; Validation, C.S.W.N.; Writing—original draft, B.A.; Writing—review and editing, A.J.G., V.R. and C.S.W.N. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Politecnico di Torino [grant number 1490 of 1 October 2021] in a mobility program, and EDISU in International Mobility 2022 program.
Data Availability Statement
The dataset employed in this study is an open-source data from https://co2datashare.org/dataset/smeaheia-dataset (accessed on 23 February 2021), and all rights are possessed by Equinor and Gassnova.
Acknowledgments
The project was conducted at Politecnico di Torino and CEORS Gemini-Center (CO2 Enhanced Oil Recovery and Storage), a strategic collaboration between NTNU and SINTEF (https://www.ntnu.edu/ceors). The authors acknowledge the feedback and suggestions by Bamshad Nazarian (Equinor) and Alv-Arne Grimstad (SINTEF).
Conflicts of Interest
The authors have no competing interests to declare that are relevant to the content of this article.
Nomenclature
| Adam | adaptive moment estimation |
| ANN | artificial neural network |
| b | bias |
| CCS | carbon capture and storage |
| CFNN | cascade forward neural network |
| CNN | convolutional neural network |
| d | distance |
| DNN | deep neural network |
| EOR | enhanced oil recovery |
| GA | genetic algorithm |
| i | cell number in x direction |
| j | cell number in y direction |
| k | cell number in z direction |
| kh | horizental permeability |
| kv | vertical permeability |
| LSTM | long short-term memory |
| MAE | mean absolute error |
| MSE | mean squared error |
| Npop | population size |
| Nvar | number of optimization variables |
| NSGA | non-dominated sorting genetic algorithm |
| P | pressure |
| Q | flow rate |
| ReLU | rectified linear unit |
| RNN | recurrent neural network |
| Sg | gas saturation |
| SIMPLEX | simple optimization technique by linear programming |
| SPM | smart proxy model |
| SRM | surrogate reservoir model |
| SRMG | grid-based surrogate reservoir model |
| T | time step |
| tanh | tangent hyperbolic |
| W | kernel |
| WAG | water alternating gas |
| σ | activation function |
| ϕ | porosity |
References
- UNFCCC. Adoption of the Paris Agreement. In Proceedings of the Paris Climate Change Conference, Paris, France, 12 December 2015. [Google Scholar]
- Masson-Delmotte, V.; Zhai, P.; Portner, H.-O.; Roberts, D.; Skea, J.; Shukla, P.R.; Pirani, A.; Moufouma-Okia, W.; Pean, C.; Pidcock, R.; et al. Global Warming of 1.5 °C; IPCC: Geneva, Switzerland, 2018. [Google Scholar]
- IEA. Net Zero by 2050: A Roadmap for the Global Energy Sector; IEA: Paris, France, 2021. [Google Scholar]
- Bandilla, K.W. Carbon capture and storage. In Future Energy; Elsevier: Amsterdam, The Netherlands, 2020; pp. 669–692. [Google Scholar]
- Metz, B.; Davidson, O.; De Coninck, H.; Loos, M.; Meyer, L. IPCC Special Report on Carbon Dioxide Capture and Storage; IPCC: Geneva, Switzerland, 2005. [Google Scholar]
- Rackley, S. Introduction to geological storage. In Carbon Capture and Storage; Butterworth-Heinemann: Boston, MA, USA, 2017; pp. 285–304. [Google Scholar]
- Li, Q.; Liu, G. Risk assessment of the geological storage of CO2: A review. In Geologic Carbon Sequestration; Springer: Cham, Switzerland, 2016; pp. 249–284. [Google Scholar] [CrossRef]
- Li, Q.; Han, Y.; Liu, X.; Ansari, U.; Cheng, Y.; Yan, C. Hydrate as a by-product in CO2 leakage during the long-term sub-seabed sequestration and its role in preventing further leakage. Environ. Sci. Pollut. Res. 2022, 29, 77737–77754. [Google Scholar] [CrossRef] [PubMed]
- Rocca, V. The sealing efficiency of cap rocks–laboratory tests and an empirical correlation. GEAM (Geoing. Ambient. E Mineraria) 2021, 58, 41–48. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.; Wang, F.; Wu, J.; Usman Tahir, M.; Li, Q.; Yuan, L.; Liu, Z. Effect of thickener and reservoir parameters on the filtration property of CO2 fracturing fluid. Energy Sources Part A Recovery Util. Environ. Eff. 2020, 42, 1705–1715. [Google Scholar] [CrossRef]
- Ajayi, T.; Gomes, J.S.; Bera, A. A review of CO2 storage in geological formations emphasizing modeling, monitoring and capacity estimation approaches. Pet. Sci. 2019, 16, 1028–1063. [Google Scholar] [CrossRef]
- Harding, F.C.; James, A.T.; Robertson, H.E. The engineering challenges of CO2 storage. Proc. Inst. Mech. Eng. Part A J. Power Energy 2018, 232, 17–26. [Google Scholar] [CrossRef]
- Santibanez-Borda, E.; Govindan, R.; Elahi, N.; Korre, A.; Durucan, S. Maximising the dynamic CO2 storage capacity through the optimisation of CO2 injection and brine production rates. Int. J. Greenh. Gas Control 2019, 80, 76–95. [Google Scholar] [CrossRef]
- Nguyen, Q.M.; Onur, M.; Alpak, F.O. Multi-objective optimization of subsurface CO2 capture, utilization, and storage using sequential quadratic programming with stochastic gradients. Comput. Geosci. 2024, 28, 195–210. [Google Scholar] [CrossRef]
- Edouard, M.N.; Okere, C.J.; Ejike, C.; Dong, P.; Suliman, M.A.M. Comparative numerical study on the co-optimization of CO2 storage and utilization in EOR, EGR, and EWR: Implications for CCUS project development. Appl. Energy 2023, 347, 121448. [Google Scholar] [CrossRef]
- Jiang, X. A review of physical modelling and numerical simulation of long-term geological storage of CO2. Appl. Energy 2011, 88, 3557–3566. [Google Scholar] [CrossRef]
- Akai, T.; Kuriyama, T.; Kato, S.; Okabe, H. Numerical modelling of long-term CO2 storage mechanisms in saline aquifers using the Sleipner benchmark dataset. Int. J. Greenh. Gas Control 2021, 110, 103405. [Google Scholar] [CrossRef]
- Zubarev, D.I. Pros and cons of applying proxy-models as a substitute for full reservoir simulations. Presented at the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 4–7 October 2009. [Google Scholar] [CrossRef]
- Jaber, A.K.; Al-Jawad, S.N.; Alhuraishawy, A.K. A review of proxy modeling applications in numerical reservoir simulation. Arab. J. Geosci. 2019, 12, 701. [Google Scholar] [CrossRef]
- Ng, C.S.W.; Nait Amar, M.; Jahanbani Ghahfarokhi, A.; Imsland, L.S. A Survey on the Application of Machine Learning and Metaheuristic Algorithms for Intelligent Proxy Modeling in Reservoir Simulation. Comput. Chem. Eng. 2023, 170, 108107. [Google Scholar] [CrossRef]
- Hosseini Boosari, S.S. Predicting the dynamic parameters of multiphase flow in CFD (Dam-Break simulation) using artificial intelligence-(cascading deployment). Fluids 2019, 4, 44. [Google Scholar] [CrossRef]
- Amini, S.; Mohaghegh, S. Application of Machine Learning and Artificial Intelligence in Proxy Modeling for Fluid Flow in Porous Media. Fluids 2019, 4, 126. [Google Scholar] [CrossRef]
- Mohaghegh, S.D.; Amini, S.; Gholami, V.; Gaskari, R.; Bromhal, G. Grid-Based Surrogate Reservoir Modeling (SRM) for fast track analysis of numerical reservoir simulation models at the grid block level. Presented at the SPE Western Regional Meeting, Bakersfield, CA, USA, 21–23 March 2012. [Google Scholar] [CrossRef]
- Mohaghegh, S. Data-Driven Analytics for the Geological Storage of CO2; CRC Press: Boca Raton, FL, USA, 2018; p. 302. [Google Scholar]
- Golzari, A.; Sefat, M.H.; Jamshidi, S. Development of an adaptive surrogate model for production optimization. J. Pet. Sci. Eng. 2015, 133, 677–688. [Google Scholar] [CrossRef]
- Ng, C.S.W.; Jahanbani Ghahfarokhi, A.; Nait Amar, M.; Torsæter, O. Smart proxy modeling of a fractured reservoir model for production optimization: Implementation of metaheuristic algorithm and probabilistic application. Nat. Resour. Res. 2021, 30, 2431–2462. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ng, C.S.W.; Jahanbani Ghahfarokhi, A.; Nait Amar, M. Adaptive Proxy-based Robust Production Optimization with Multilayer Perceptron. Appl. Comput. Geosci. 2022, 16, 100103. [Google Scholar] [CrossRef]
- Ng, C.S.W.; Jahanbani Ghahfarokhi, A.; Nait Amar, M. Production optimization under waterflooding with long short-term memory and metaheuristic algorithm. Petroleum 2023, 9, 53–60. [Google Scholar] [CrossRef]
- Agada, S.; Geiger, S.; Elsheikh, A.; Oladyshkin, S. Data-driven surrogates for rapid simulation and optimization of WAG injection in fractured carbonate reservoirs. Pet. Geosci. 2017, 23, 270–283. [Google Scholar] [CrossRef]
- Nait Amar, M.; Zeraibi, N.; Redouane, K. Optimization of WAG process using dynamic proxy, genetic algorithm and ant colony optimization. Arab. J. Sci. Eng. 2018, 43, 6399–6412. [Google Scholar] [CrossRef]
- Nait Amar, M.; Zeraibi, N.; Jahanbani Ghahfarokhi, A. Applying hybrid support vector regression and genetic algorithm to water alternating CO2 gas EOR. Greenh. Gases Sci. Technol. 2020, 10, 613–630. [Google Scholar] [CrossRef]
- Sun, Z.; Xu, J.; Espinoza, D.N.; Balhoff, M.T. Optimization of subsurface CO2 injection based on neural network surrogate modeling. Comput. Geosci. 2021, 25, 1887–1898. [Google Scholar] [CrossRef]
- Liu, S.; Agarwal, R.; Sun, B.; Wang, B.; Li, H.; Xu, J.; Fu, G. Numerical simulation and optimization of injection rates and wells placement for carbon dioxide enhanced gas recovery using a genetic algorithm. J. Clean. Prod. 2021, 280, 124512. [Google Scholar] [CrossRef]
- Agarwal, R.K. Modeling, simulation, and optimization of geological sequestration of CO2. J. Fluids Eng. 2019, 141, 100801. [Google Scholar] [CrossRef]
- Cameron, D.A.; Durlofsky, L.J. Optimization of well placement, CO2 injection rates, and brine cycling for geological carbon sequestration. Int. J. Greenh. Gas Control 2012, 10, 100–112. [Google Scholar] [CrossRef]
- Luo, J.; Ma, X.; Ji, Y.; Li, X.; Song, Z.; Lu, W. Review of machine learning-based surrogate models of groundwater contaminant modeling. Environ. Res. 2023, 238, 117268. [Google Scholar] [CrossRef]
- Bertini, J.R.; Ferreira Batista, S.; Funcia, M.A.; Mendes da Silva, L.O.; Santos, A.A.S.; Schiozer, D.J. A comparison of machine learning surrogate models for net present value prediction from well placement binary data. J. Pet. Sci. Eng. 2022, 208, 109208. [Google Scholar] [CrossRef]
- García-Feal, O.; González-Cao, J.; Fernández-Nóvoa, D.; Astray Dopazo, G.; Gómez-Gesteira, M. Comparison of machine learning techniques for reservoir outflow forecasting. Nat. Hazards Earth Syst. Sci. 2022, 22, 3859–3874. [Google Scholar] [CrossRef]
- Shahkarami, A.; Mohaghegh, S. Applications of smart proxies for subsurface modeling. Pet. Explor. Dev. 2020, 47, 400–412. [Google Scholar] [CrossRef]
- Wang, S.; Xiang, J.; Wang, X.; Feng, Q.; Yang, Y.; Cao, X.; Hou, L. A deep learning based surrogate model for reservoir dynamic performance prediction. Geoenergy Sci. Eng. 2024, 233, 212516. [Google Scholar] [CrossRef]
- Omosebi, O.A.; Oldenburg, C.M.; Reagan, M. Development of lean, efficient, and fast physics-framed deep-learning-based proxy models for subsurface carbon storage. Int. J. Greenh. Gas Control 2022, 114, 103562. [Google Scholar] [CrossRef]
- Gholami, V. On the Optimization of CO2-EOR Process Using Surrogate Reservoir Model; West Virginia University: Morgantown, WV, USA, 2014. [Google Scholar]
- Amini, S. Developing a Grid-Based Surrogate Reservoir Model Using Artificial Intelligence; West Virginia University: Morgantown, WV, USA, 2015. [Google Scholar]
- Matthew, D.A.; Jahanbani Ghahfarokhi, A.; Ng, C.S.; Nait Amar, M. Proxy Model Development for the Optimization of Water Alternating CO2 Gas for Enhanced Oil Recovery. Energies 2023, 16, 3337. [Google Scholar] [CrossRef]
- Naghizadeh, A.; Jafari, S.; Norouzi-Apourvari, S.; Schaffie, M.; Hemmati-Sarapardeh, A. Multi-objective optimization of water-alternating flue gas process using machine learning and nature-inspired algorithms in a real geological field. Energy 2024, 293, 130413. [Google Scholar] [CrossRef]
- Mao, J.; Jahanbani Ghahfarokhi, A. A review of intelligent decision-making strategy for geological CO2 storage: Insights from reservoir engineering. Geoenergy Sci. Eng. 2024, 240, 212951. [Google Scholar] [CrossRef]
- Equinor. Smeaheia—Bringing Large Scale CO2 Storage to European Industry. Available online: https://www.equinor.com/energy/smeaheia (accessed on 19 April 2024).
- Equinor; Gassnova. Smeaheia Dataset. Published on CO2 DataShare. 2021. Available online: https://co2datashare.org/dataset/smeaheia-dataset (accessed on 23 February 2021).
- Erichsen, E.; Rørvik, K.L.; Kearney, G.; Haaberg, K. Troll Kystnær Subsurface Evaluation Report; Gassnova SF: Trondheim, Norway, 2013. [Google Scholar]
- Statoil. Report on Subsurface Evaluation of Smeaheia. June 2016. Available online: https://co2datashare.org/dataset/smeaheia-dataset (accessed on 23 February 2021).
- Brobakken, I.I. Modeling of CO2 Storage in the Smeaheia Field; NTNU: Trondheim, Norway, 2018. [Google Scholar]
- Amiri, B. A Fast and Accurate Investigation into CO2 Storage Challenges by Making a Proxy Model on a Developed Static Model with the Application of Artificial Intelligence/Machine Learning; under Creative Commons Attribution Non-Commercial No Derivatives License; Polytechnic of Turin, Webthesis Portal of Polytechnic of Turin: Torino, Italy, 2022. [Google Scholar]
- Géron, A. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media, Inc.: Sevastopol, CA, USA, 2019. [Google Scholar]
- Silva, I.N.; Spatti, D.H.; Flauzino, R.A.; Liboni, L.H.B.; Alves, S.R. Artificial Neural Networks: A Practical Course; Springer: Cham, Switzerland, 2017; pp. XX, 307. [Google Scholar]
- Rasamoelina, A.D.; Adjailia, F.; Sinčák, P. A Review of Activation Function for Artificial Neural Network. In Proceedings of the 2020 IEEE 18th World Symposium on Applied Machine Intelligence and Informatics (SAMI), Herlany, Slovakia, 23–25 January 2020; pp. 281–286. [Google Scholar]
- Aggarwal, C.C. (Ed.) Training Deep Neural Networks. In Neural Networks and Deep Learning: A Textbook; Springer International Publishing: Cham, Switzerland, 2018; pp. 105–167. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Goldberg, D.E. Computer-Aided Gas Pipeline Operation Using Genetic Algorithms and Rule Learning; University of Michigan: Ann Arbor, MI, USA, 1983. [Google Scholar]
- Haupt, R.L.; Haupt, S.E. Practical Genetic Algorithms; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Hendrix, E.M.; Boglárka, G.-T. Introduction to Nonlinear and Global Optimization; Springer: Berlin/Heidelberg, Germany, 2010; Volume 37. [Google Scholar]
- Sivanandam, S.; Deepa, S. Introduction to Genetic Algorithms, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. IX, 92. [Google Scholar]
- Kramer, O. Genetic Algorithm Essentials; Springer: Cham, Switzerland, 2017; pp. IX, 92. [Google Scholar]
- Equinor; Gassnova. Smeaheia Dataset License. Available online: https://co2datashare.org/view/license/26af9426-203f-4993-9d41-2e1bf191ceaf (accessed on 23 February 2021).
- SLB. Software: Petrel 2017.4; 2018. Available online: https://www.software.slb.com/software-news/support-news/petrel/petrel-2017-4_studio-2017-4 (accessed on 5 June 2018).
- SLB. Software: ECLIPSE 2017.1; 2017. Available online: https://www.software.slb.com/software-news/software-top-news/eclipse/eclipse-2017-1 (accessed on 20 July 2017).
- Nazarian, B.; Thorsen, R.; Ringrose, P. Storing CO2 in a Reservoir Under Continuous Pressure Depletion; a Simulation Study. In Proceedings of the 14th Greenhouse Gas Control Technologies Conference, Melbourne, Australia, 21–26 October 2018. [Google Scholar]
- Blank, J.; Deb, K. pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
- Agarap, A.F. Deep Learning using Rectified Linear Units (ReLU). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- Han, J.; Moraga, C. The influence of the sigmoid function parameters on the speed of backpropagation learning. In International Workshop on Artificial Neural Networks; Springer: Berlin/Heidelberg, Germany, 1995; pp. 195–201. [Google Scholar] [CrossRef]
- Chollet, F. Keras. Available online: https://keras.io (accessed on 27 March 2015).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).