Adaptive Compensation for Robotic Joint Failures Using Partially Observable Reinforcement Learning
Abstract
1. Introduction
- Unified approach: By combining fault detection, diagnosis, and control into a single system, we potentially reduce complexity and improve response times.
- Adaptability: The DRL agent can learn to handle a wide range of faults, including those not explicitly modeled during training, enhancing the system’s robustness.
- Efficiency: The direct processing of raw sensory data eliminates the need for complex feature engineering or intermediate representations.
- Scalability: As the complexity of the robotic system increases, the DRL approach can potentially scale more effectively than traditional methods when given sufficient training data and computational resources.
- Continuous learning: The system is designed to update its policies in real time, allowing for ongoing adaptation to new fault scenarios or changing operating conditions.
2. Literature Review
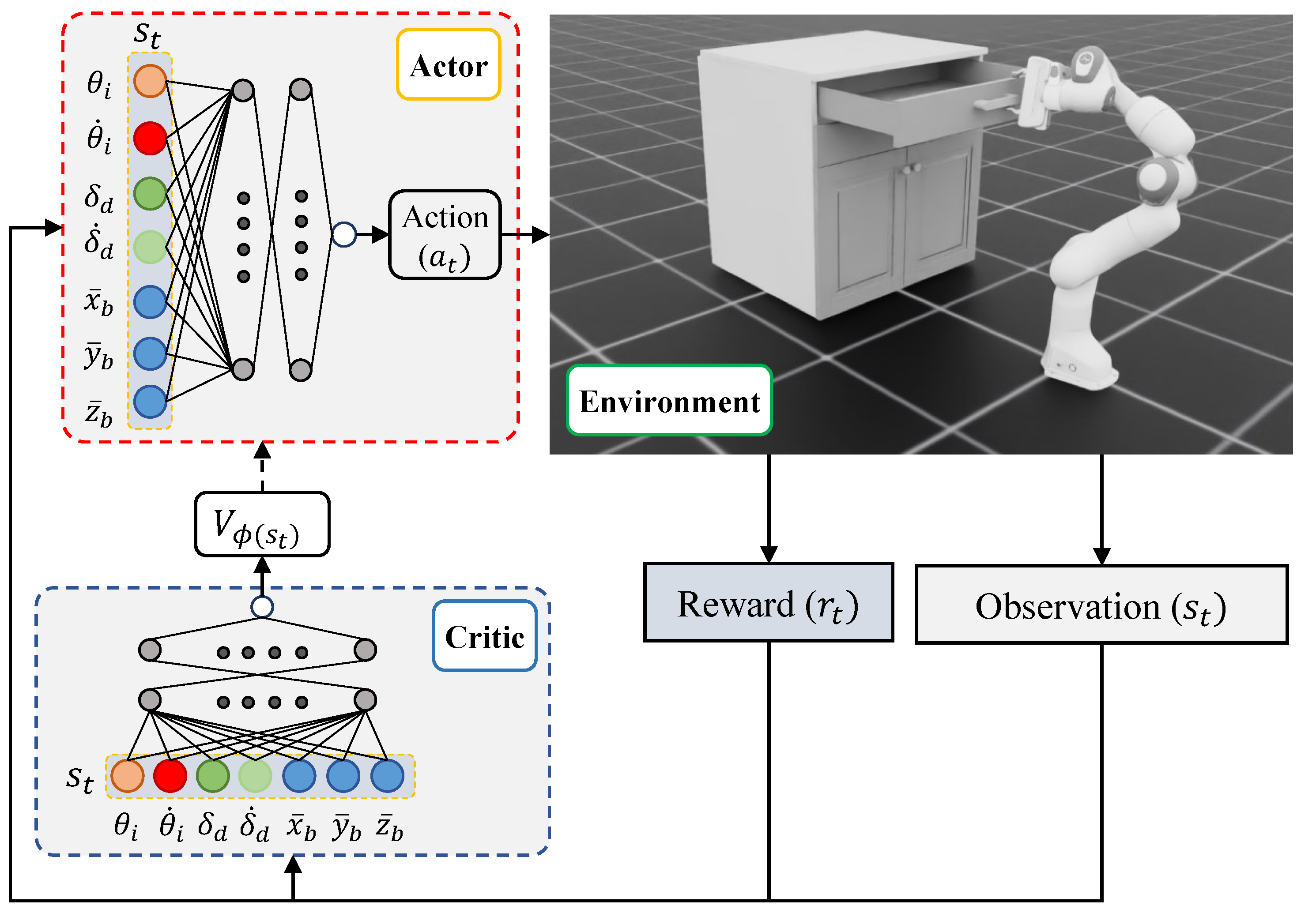
3. Methodology
3.1. Problem Formulation
3.1.1. Observation Space
3.1.2. Action Space
3.1.3. Reward Function
3.2. Reinforcement Learning Framework
3.2.1. PPO Algorithm
3.2.2. Agent Training
3.3. Simulation Setup and Evaluation
- Permanently broken joint: One of the robot’s joints is completely nonfunctional throughout the task execution.
- Intermittently functioning joint: One of the robot’s joints operates intermittently, randomly switching between functional and nonfunctional states.
- The success rate of completing the task (opening the drawer).
- The time taken to complete the task.
4. Inverse Kinematics
4.1. Denavit–Hartenberg Parameters and Inverse Kinematics Solving
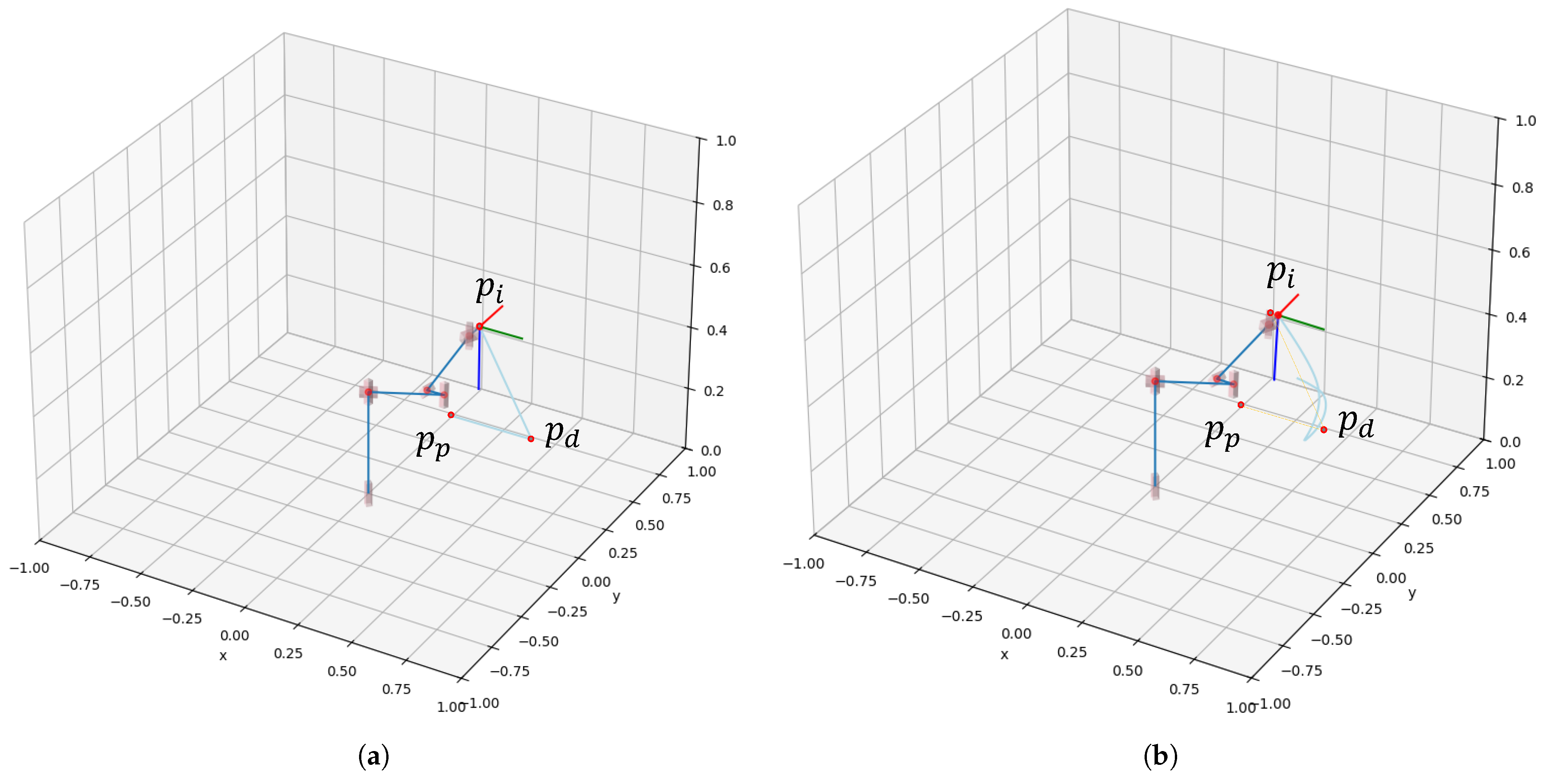
4.2. Inverse Kinematics Simulation and Joint Failure Scenario
5. Results and Discussion
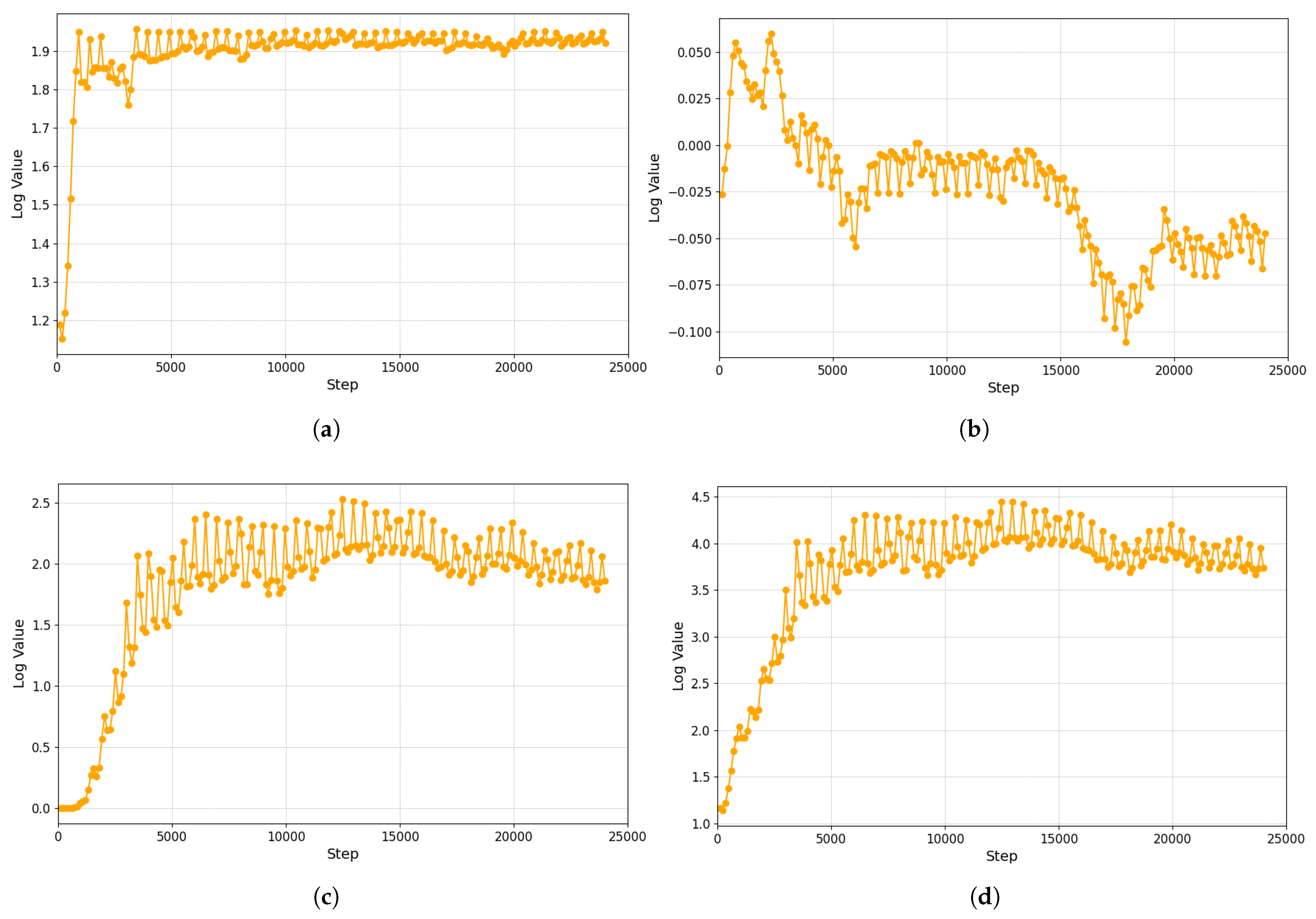
5.1. RL Training Results
5.2. Kinematics Results
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International Federation of Robotics. World Robotics; International Federation of Robotics: Frankfurt, Germany, 2021. [Google Scholar]
- Vasic, M.; Billard, A. Safety issues in human-robot interactions. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 197–204. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, J. Bibliographical review on reconfigurable fault-tolerant control systems. Annu. Rev. Control 2008, 32, 229–252. [Google Scholar] [CrossRef]
- Venkatasubramanian, V.; Rengaswamy, R.; Yin, K.; Kavuri, S.N. A review of process fault detection and diagnosis: Part I: Quantitative model-based methods. Comput. Chem. Eng. 2003, 27, 293–311. [Google Scholar] [CrossRef]
- Blanke, M.; Kinnaert, M.; Lunze, J.; Staroswiecki, M. Diagnosis and Fault-Tolerant Control; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Ding, S.X. Model-Based Fault Diagnosis Techniques: Design Schemes, Algorithms, and Tools; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Amin, A.A.; Sajid Iqbal, M.; Hamza Shahbaz, M. Development of Intelligent Fault-Tolerant Control Systems with Machine Learning, Deep Learning, and Transfer Learning Algorithms: A Review. Expert Syst. Appl. 2024, 238, 121956. [Google Scholar] [CrossRef]
- Piltan, F.; Prosvirin, A.E.; Sohaib, M.; Saldivar, B.; Kim, J.M. An SVM-based neural adaptive variable structure observer for fault diagnosis and fault-tolerant control of a robot manipulator. Appl. Sci. 2020, 10, 1344. [Google Scholar] [CrossRef]
- Fei, F.; Tu, Z.; Xu, D.; Deng, X. Learn-to-recover: Retrofitting uavs with reinforcement learning-assisted flight control under cyber-physical attacks. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: New York, NY, USA, 2020; pp. 7358–7364. [Google Scholar]
- Wang, Y.; Wang, Z. Model free adaptive fault-tolerant tracking control for a class of discrete-time systems. Neurocomputing 2020, 412, 143–151. [Google Scholar] [CrossRef]
- Sardashti, A.; Nazari, J. A learning-based approach to fault detection and fault-tolerant control of permanent magnet DC motors. J. Eng. Appl. Sci. 2023, 70, 109. [Google Scholar] [CrossRef]
- Chen, J.; Patton, R.J. Robust Model-Based Fault Diagnosis for Dynamic Systems; The International Series on Asian Studies in Computer and Information Science; Springer: New York, NY, USA, 1999. [Google Scholar] [CrossRef]
- Yao, X.; Tao, G.; Ma, Y.; Qi, R. An adaptive actuator failure compensation scheme for spacecraft with unknown inertia parameters. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 1810–1815. [Google Scholar] [CrossRef]
- Zhuo-Hua, D.; Zi-Xing, C.; Jin-Xia, Y. Fault diagnosis and fault tolerant control for wheeled mobile robots under unknown environments: A survey. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; IEEE: New York, NY, USA, 2005; pp. 3428–3433. [Google Scholar]
- Ahmed, S.; Azar, A.T.; Tounsi, M. Adaptive Fault Tolerant Non-Singular Sliding Mode Control for Robotic Manipulators Based on Fixed-Time Control Law. Actuators 2022, 11, 353. [Google Scholar] [CrossRef]
- Zhou, K.; Ren, Z. A new controller architecture for high performance, robust, and fault-tolerant control. IEEE Trans. Autom. Control 2001, 46, 1613–1618. [Google Scholar] [CrossRef]
- Sun, S.; Wang, X.; Chu, Q.; Visser, C.D. Incremental Nonlinear Fault-Tolerant Control of a Quadrotor with Complete Loss of Two Opposing Rotors. IEEE Trans. Robot. 2021, 37, 116–130. [Google Scholar] [CrossRef]
- Ali, K.; Mehmood, A.; Iqbal, J. Fault-tolerant scheme for robotic manipulator—Nonlinear robust back-stepping control with friction compensation. PLoS ONE 2021, 16, e0256491. [Google Scholar] [CrossRef]
- Wang, X. Active Fault Tolerant Control for Unmanned Underwater Vehicle with Sensor Faults. IEEE Trans. Instrum. Meas. 2020, 69, 9485–9495. [Google Scholar] [CrossRef]
- Blanke, M.; Christian Frei, W.; Kraus, F.; Ron Patton, J.; Staroswiecki, M. What is Fault-Tolerant Control? IFAC Proc. Vol. 2000, 33, 41–52. [Google Scholar] [CrossRef]
- Abbaspour, A.; Mokhtari, S.; Sargolzaei, A.; Yen, K.K. A Survey on Active Fault-Tolerant Control Systems. Electronics 2020, 9, 1513. [Google Scholar] [CrossRef]
- Esteva, A.; Kuprel, B.; Novoa, R.A.; Ko, J.; Swetter, S.M.; Blau, H.M.; Thrun, S. Dermatologist-level classification of skin cancer with deep neural networks. Nature 2017, 542, 115–118. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.W.; Zhao, T.Z.; Schmidgall, S.; Deguet, A.; Kobilarov, M.; Finn, C.; Krieger, A. Surgical Robot Transformer (SRT): Imitation Learning for Surgical Tasks. arXiv 2024, arXiv:2407.12998. [Google Scholar]
- Pham, T.H.; Li, X.; Nguyen, K.D. seUNet-Trans: A Simple Yet Effective UNet-Transformer Model for Medical Image Segmentation. IEEE Access 2024, 12, 122139–122154. [Google Scholar] [CrossRef]
- Whiting, D.G.; Hansen, J.V.; McDonald, J.B.; Albrecht, C.; Albrecht, W.S. Machine learning methods for detecting patterns of management fraud. Comput. Intell. 2012, 28, 505–527. [Google Scholar] [CrossRef]
- Al Ayub Ahmed, A.; Rajesh, S.; Lohana, S.; Ray, S.; Maroor, J.P.; Naved, M. Using Machine Learning and Data Mining to Evaluate Modern Financial Management Techniques. In Proceedings of the Second International Conference in Mechanical and Energy Technology: ICMET 2021, Greater Noida, India, 28–29 October 2021; Springer: Berlin/Heidelberg, Germany, 2022; pp. 249–257. [Google Scholar]
- Muhammad, K.; Ullah, A.; Lloret, J.; Del Ser, J.; de Albuquerque, V.H.C. Deep learning for safe autonomous driving: Current challenges and future directions. IEEE Trans. Intell. Transp. Syst. 2020, 22, 4316–4336. [Google Scholar] [CrossRef]
- Aloufi, N.; Alnori, A.; Basuhail, A. Enhancing Autonomous Vehicle Perception in Adverse Weather: A Multi Objectives Model for Integrated Weather Classification and Object Detection. Electronics 2024, 13, 3063. [Google Scholar] [CrossRef]
- Aikins, G.; Jagtap, S.; Gao, W. Resilience analysis of deep q-learning algorithms in driving simulations against cyberattacks. In Proceedings of the 2022 1st International Conference on AI in Cybersecurity (ICAIC), Victoria, TX, USA, 24–26 May 2022; IEEE: New York, NY, USA, 2022; pp. 1–6. [Google Scholar]
- Pham, T.H.; Nguyen, K.D. Enhanced Droplet Analysis Using Generative Adversarial Networks. arXiv 2024, arXiv:2402.15909. [Google Scholar]
- Sharma, A.; Jain, A.; Gupta, P.; Chowdary, V. Machine learning applications for precision agriculture: A comprehensive review. IEEE Access 2020, 9, 4843–4873. [Google Scholar] [CrossRef]
- Pham, T.H.; Nguyen, K.D. Soil Sampling Map Optimization with a Dual Deep Learning Framework. Mach. Learn. Knowl. Extr. 2024, 6, 751–769. [Google Scholar] [CrossRef]
- Pham, T.H.; Acharya, P.; Bachina, S.; Osterloh, K.; Nguyen, K.D. Deep-learning framework for optimal selection of soil sampling sites. Comput. Electron. Agric. 2024, 217, 108650. [Google Scholar] [CrossRef]
- Eski, I.; Erkaya, S.; Savas, S.; Yildirim, S. Fault detection on robot manipulators using artificial neural networks. Robot. Comput. Integr. Manuf. 2011, 27, 115–123. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, R.; Yang, Y.; Li, Y.; Xu, M. Intelligent Fault Identification Based on Multisource Domain Generalization Towards Actual Diagnosis Scenario. IEEE Trans. Ind. Electron. 2020, 67, 1293–1304. [Google Scholar] [CrossRef]
- Ahmed, I.; Khorasgani, H.; Biswas, G. Comparison of model predictive and reinforcement learning methods for fault tolerant control. IFAC-PapersOnLine 2018, 51, 233–240. [Google Scholar] [CrossRef]
- Okamoto, W.; Kera, H.; Kawamoto, K. Reinforcement Learning with Adaptive Curriculum Dynamics Randomization for Fault-Tolerant Robot Control. arXiv 2021, arXiv:2111.10005. [Google Scholar]
- Zhu, J.W.; Dong, Z.Y.; Yang, Z.J.; Wang, X. A New Reinforcement Learning Fault-Tolerant Tracking Control Method with Application to Baxter Robot. IEEE/ASME Trans. Mechatron. 2024, 29, 1331–1341. [Google Scholar] [CrossRef]
- Aikins, G.; Jagtap, S.; Nguyen, K.D. A Robust Strategy for UAV Autonomous Landing on a Moving Platform under Partial Observability. Drones 2024, 8, 232. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Albrecht, S.V.; Christianos, F.; Schäfer, L. Multi-Agent Reinforcement Learning: Foundations and Modern Approaches; MIT Press: Cambridge, MA, USA, 2024. [Google Scholar]
- Mittal, M.; Yu, C.; Yu, Q.; Liu, J.; Rudin, N.; Hoeller, D.; Yuan, J.L.; Singh, R.; Guo, Y.; Mazhar, H.; et al. Orbit: A Unified Simulation Framework for Interactive Robot Learning Environments. IEEE Robot. Autom. Lett. 2023, 8, 3740–3747. [Google Scholar] [CrossRef]
- Dubey, S.R.; Singh, S.K.; Chaudhuri, B.B. Activation functions in deep learning: A comprehensive survey and benchmark. Neurocomputing 2022, 503, 92–108. [Google Scholar] [CrossRef]
- Dulęba, I.; Opałka, M. A comparison of Jacobian-based methods of inverse kinematics for serial robot manipulators. Int. J. Appl. Math. Comput. Sci. 2013, 23, 373–382. [Google Scholar] [CrossRef]
- Whitney, D.E. Resolved motion rate control of manipulators and human prostheses. IEEE Trans. Man Mach. Syst. 1969, 10, 47–53. [Google Scholar] [CrossRef]
- Zhao, T.Z.; Kumar, V.; Levine, S.; Finn, C. Learning fine-grained bimanual manipulation with low-cost hardware. arXiv 2023, arXiv:2304.13705. [Google Scholar]

| Joint i | (m) | (m) | (rad) | (rad) |
|---|---|---|---|---|
| 1 | 0.333 | 0 | 0 | 1.157 |
| 2 | 0 | 0 | −1.066 | |
| 3 | 0.316 | 0 | −0.155 | |
| 4 | 0 | 0.0825 | −2.239 | |
| 5 | 0.384 | −0.0825 | −1.841 | |
| 6 | 0 | 0 | 1.003 | |
| 7 | 0 | 0.088 | 0 | 0.469 |
| (rad) | (rad) | (rad) | x | y | z | |
|---|---|---|---|---|---|---|
| 0 | 0 | |||||
| 0 | 0 | 0 | ||||
| 0 | 0 |
| Fault Scenario | Success Rate (%) | Average Completion Time (s) |
|---|---|---|
| No Fault | 98.00 | 3.54 |
| Permanently Broken Joint | 96.00 | 4.62 |
| Intermittently Functioning Joint | 96.00 | 3.77 |
| Joint Works First Half | 96.00 | 4.11 |
| Joint Works Second Half | 82.00 | 8.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, T.-H.; Aikins, G.; Truong, T.; Nguyen, K.-D. Adaptive Compensation for Robotic Joint Failures Using Partially Observable Reinforcement Learning. Algorithms 2024, 17, 436. https://doi.org/10.3390/a17100436
Pham T-H, Aikins G, Truong T, Nguyen K-D. Adaptive Compensation for Robotic Joint Failures Using Partially Observable Reinforcement Learning. Algorithms. 2024; 17(10):436. https://doi.org/10.3390/a17100436
Chicago/Turabian StylePham, Tan-Hanh, Godwyll Aikins, Tri Truong, and Kim-Doang Nguyen. 2024. "Adaptive Compensation for Robotic Joint Failures Using Partially Observable Reinforcement Learning" Algorithms 17, no. 10: 436. https://doi.org/10.3390/a17100436
APA StylePham, T.-H., Aikins, G., Truong, T., & Nguyen, K.-D. (2024). Adaptive Compensation for Robotic Joint Failures Using Partially Observable Reinforcement Learning. Algorithms, 17(10), 436. https://doi.org/10.3390/a17100436






