Distributed Data-Driven Learning-Based Optimal Dynamic Resource Allocation for Multi-RIS-Assisted Multi-User Ad-Hoc Network
Abstract
1. Introduction
2. Related Studies and the Current Contribution
2.1. Related Studies
2.2. Current Contribution
- It formulates a time-varying and uncertain wireless communication environment to address dynamic resource allocation in RIS-assisted mobile ad-hoc networks (MANET).A model has been constructed to depict the dynamic resource allocation system within a multi-mobile RIS-assisted ad-hoc wireless network.
- The optimization problems encompassing RIS selection, spectrum allocation, phase shifting control, and power allocation in both the inner and outer networks have been formulated to maximize the network capacity while ensuring the quality of service (QoS) requirements of mobile devices.As solving mixed-integer and non-convex optimization problems poses challenges, we reframe the issue as a multi-agent reinforcement learning problem. This transformation aims to maximize the long-term rewards while adhering to the available network resource constraints.
- An inner–outer online optimization algorithm has been devised to address the optimal resource allocation policies for RIS-assisted mobile ad-hoc networks (MANET), even in uncertain environments.As the network exhibits high dynamism and complexity, the D-UCB algorithm is employed in the outer network for RIS and spectrum selection. In the inner network, the TD3 algorithm is utilized to acquire decentralized insights into RIS phase shifts and power allocation strategies. This approach facilitates the swift acquisition of optimized intelligent resource management strategies. The TD3 algorithm features an actor–critic structure, comprising three target networks and two hidden layer streams in each neural network to segregate state–value distribution functions and action–value distribution functions. The integration of action advantage functions notably accelerates the convergence speed and enhances the learning efficiency.
3. System and Channel Model
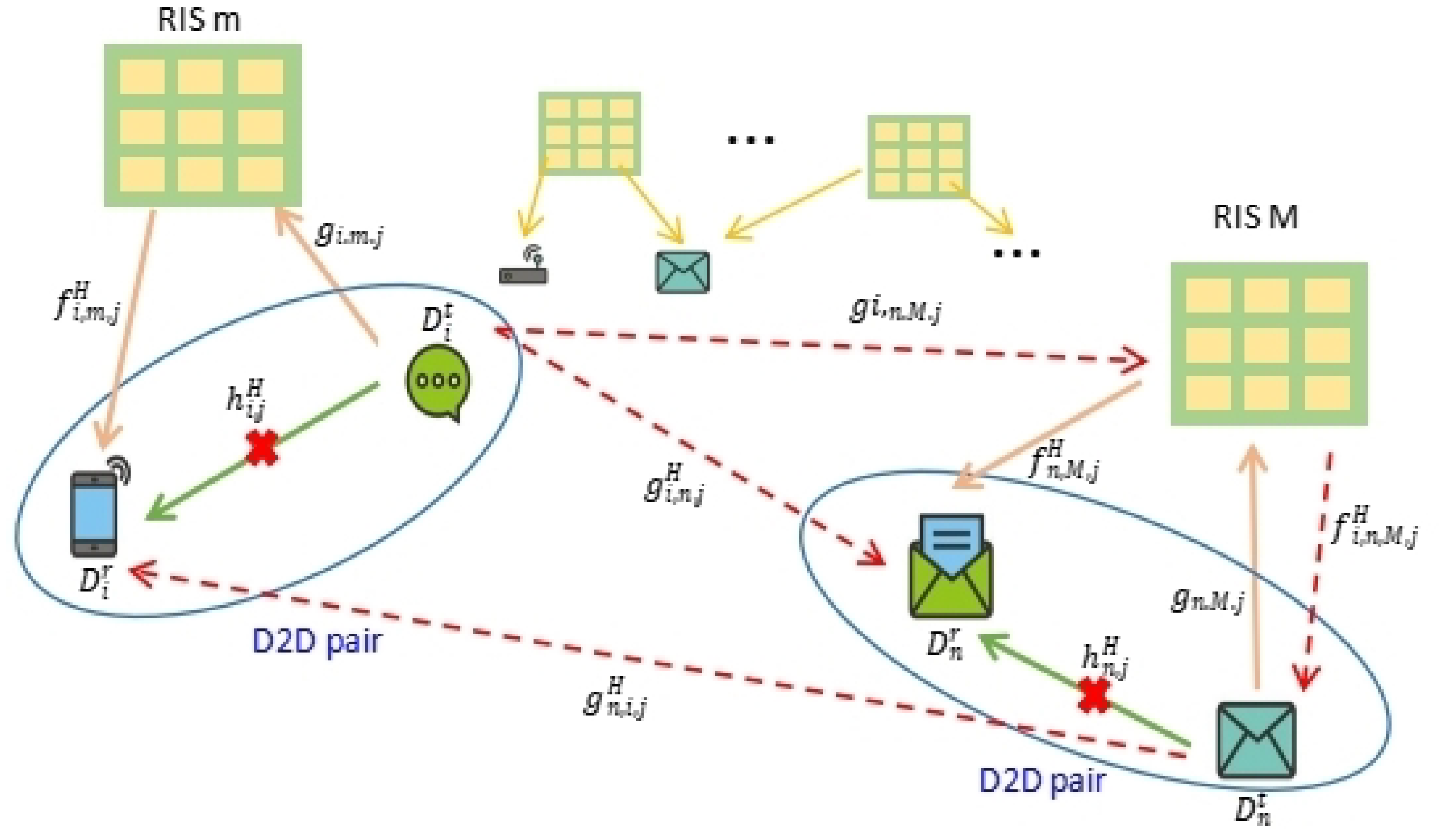
3.1. System Model
3.2. Interference Analysis
4. Problem Formulation
4.1. Outer Loop of Dec-MPMAB Framework
4.1.1. Basic MAB and Dec-MPMAB Framework
4.1.2. Dec-MPMAB Formulation of RIS and RB Selection Problem
4.1.3. Illustration of Reward for i-th D2D Pair
4.2. Inner Loop of Joint Optimal Problem Formulation
4.2.1. Power Consumption
4.2.2. Joint Optimal Problem Formulation for RIS-Assisted MANET
5. Outer and Inner Loop Optimization Algorithm with Online Learning
5.1. Outer Loop Optimization: Novel Dec-MPMAB Algorithm
5.1.1. General Single Player MAB Algorithm
5.1.2. Decentralized-UCB (D-UCB) Algorithm
| Algorithm 1 D-UCB Algorithm |
|
| Algorithm 2 TD3-based RIS phase shifting and power allocation algorithm |
|
5.2. Inner Loop Optimization: A TD3-Based Algorithm for RIS Phase Shifting and Power Allocation
- State space: Let be the state space, which contains the following components: (i) information about the current channel conditions, denoted as and ; (ii) the positions and statuses of device-to-device (D2D) pairs ; (iii) the actions, including the phase-shifting settings of the RIS elements and power allocation of taken at time ; (iv) the energy efficiency at time . Thus, S comprises
- Action space: Denote A as the action space, which consists of the actions that the agent can take. In this case, it includes the phase shifting of each RIS element and the transmission power of the transmitter (Tx) of the device-to-device (D2D) pair. The action is given by
- Reward function: The agent receives an immediate reward , which is the energy efficiency defined in Equation (16). This reward is affected by factors such as the channel conditions, RIS phase shifts, and device-to-device (D2D) power allocations, i.e.,
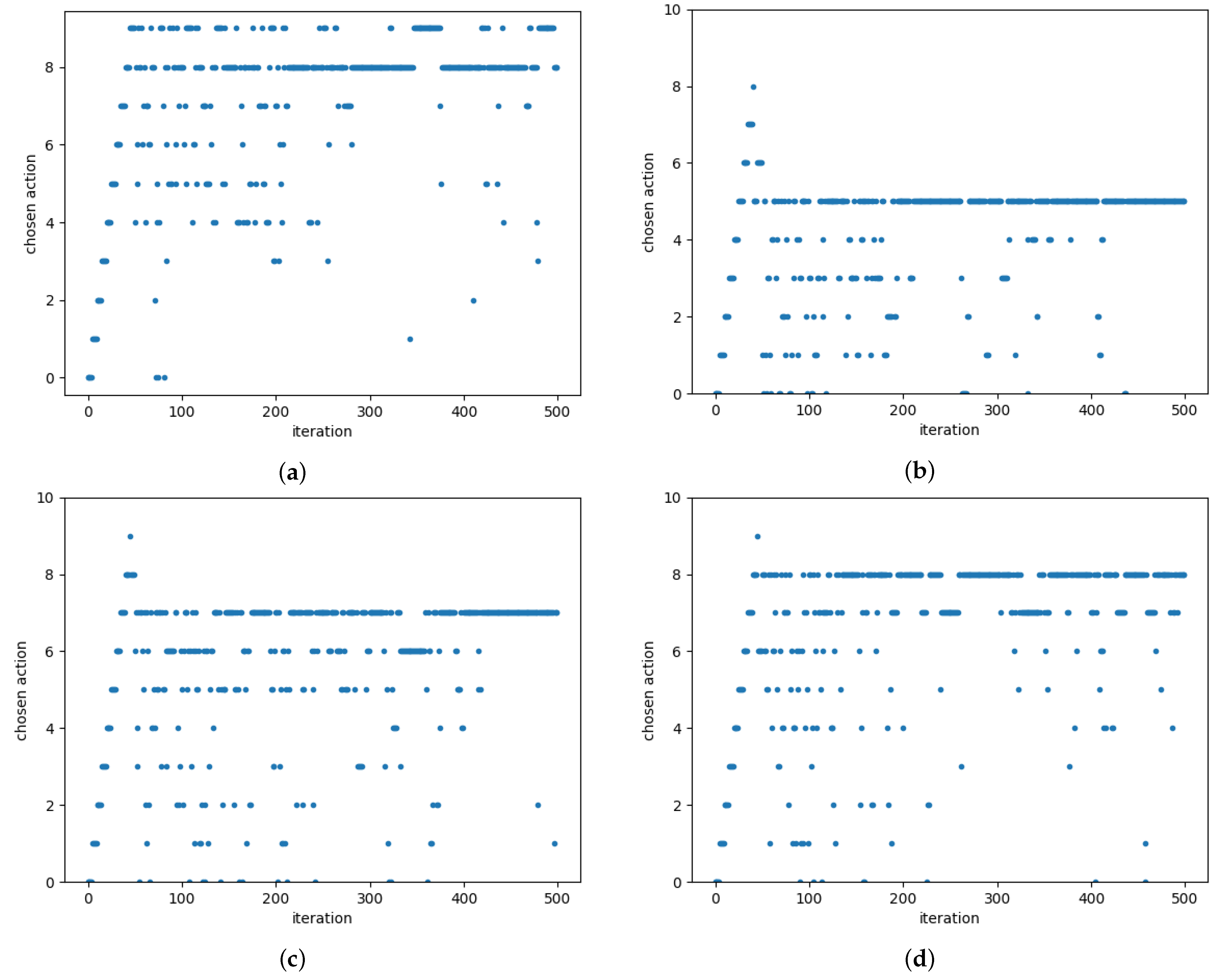
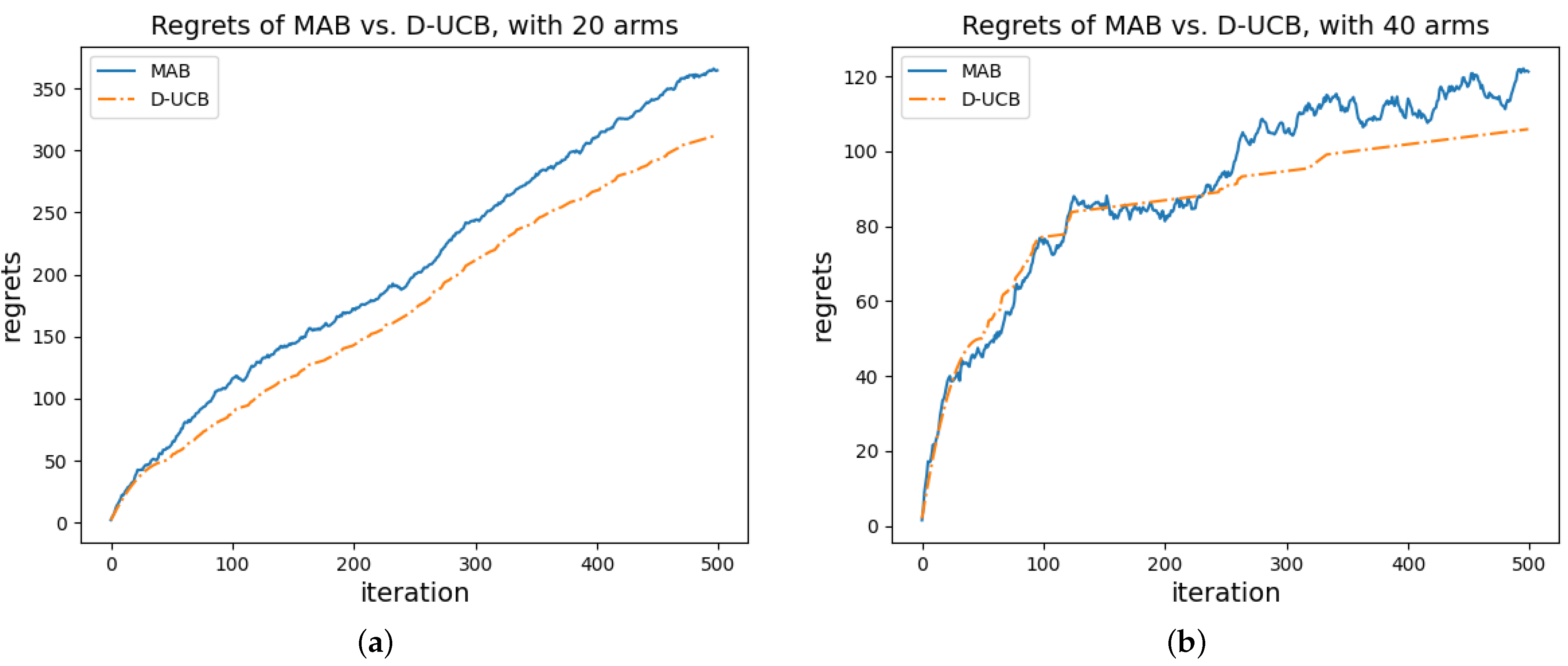
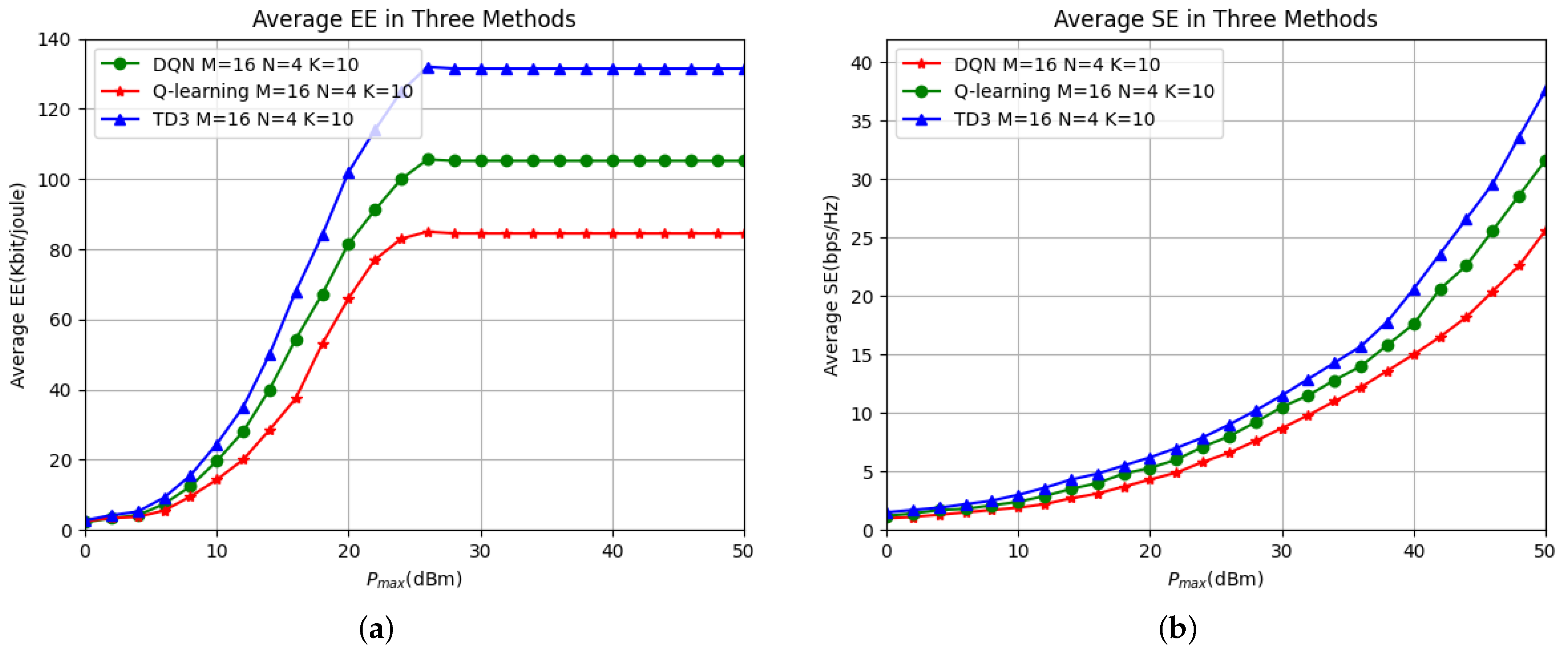
6. Simulation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dogra, A.; Jha, R.K.; Jain, S. A survey on beyond 5G network with the advent of 6G: Architecture and emerging technologies. IEEE Access 2020, 9, 67512–67547. [Google Scholar] [CrossRef]
- Rekkas, V.P.; Sotiroudis, S.; Sarigiannidis, P.; Wan, S.; Karagiannidis, G.K.; Goudos, S.K. Machine learning in beyond 5G/6G networks—State-of-the-art and future trends. Electronics 2021, 10, 2786. [Google Scholar] [CrossRef]
- Madakam, S.; Lake, V.; Lake, V.; Lake, V. Internet of Things (IoT): A literature review. J. Comput. Commun. 2015, 3, 164. [Google Scholar] [CrossRef]
- Laghari, A.A.; Wu, K.; Laghari, R.A.; Ali, M.; Khan, A.A. A review and state of art of Internet of Things (IoT). Arch. Comput. Methods Eng. 2021, 29, 1395–1413. [Google Scholar] [CrossRef]
- Chvojka, P.; Zvanovec, S.; Haigh, P.A.; Ghassemlooy, Z. Channel characteristics of visible light communications within dynamic indoor environment. J. Light. Technol. 2015, 33, 1719–1725. [Google Scholar] [CrossRef]
- Kamel, M.; Hamouda, W.; Youssef, A. Ultra-dense networks: A survey. IEEE Commun. Surv. Tutorials 2016, 18, 2522–2545. [Google Scholar] [CrossRef]
- Hoebeke, J.; Moerman, I.; Dhoedt, B.; Demeester, P. An overview of mobile ad hoc networks: Applications and challenges. J.-Commun. Netw. 2004, 3, 60–66. [Google Scholar]
- Bang, A.O.; Ramteke, P.L. MANET: History, challenges and applications. Int. J. Appl. Innov. Eng. Manag. 2013, 2, 249–251. [Google Scholar]
- Liu, Y.; Liu, X.; Mu, X.; Hou, T.; Xu, J.; Di Renzo, M.; Al-Dhahir, N. Reconfigurable intelligent surfaces: Principles and opportunities. IEEE Commun. Surv. Tutorials 2021, 23, 1546–1577. [Google Scholar] [CrossRef]
- ElMossallamy, M.A.; Zhang, H.; Song, L.; Seddik, K.G.; Han, Z.; Li, G.Y. Reconfigurable intelligent surfaces for wireless communications: Principles, challenges, and opportunities. IEEE Trans. Cogn. Commun. Netw. 2020, 6, 990–1002. [Google Scholar] [CrossRef]
- Huang, C.; Zappone, A.; Alexandropoulos, G.C.; Debbah, M.; Yuen, C. Reconfigurable intelligent surfaces for energy efficiency in wireless communication. IEEE Trans. Wirel. Commun. 2019, 18, 4157–4170. [Google Scholar] [CrossRef]
- Ye, J.; Kammoun, A.; Alouini, M.S. Spatially-distributed RISs vs relay-assisted systems: A fair comparison. IEEE Open J. Commun. Soc. 2021, 2, 799–817. [Google Scholar] [CrossRef]
- Huang, C.; Mo, R.; Yuen, C. Reconfigurable intelligent surface assisted multiuser MISO systems exploiting deep reinforcement learning. IEEE J. Sel. Areas Commun. 2020, 38, 1839–1850. [Google Scholar] [CrossRef]
- Lee, G.; Jung, M.; Kasgari, A.T.Z.; Saad, W.; Bennis, M. Deep reinforcement learning for energy-efficient networking with reconfigurable intelligent surfaces. In Proceedings of the ICC 2020—2020 IEEE International Conference on Communications (ICC), Virtually, 7–11 June 2020; pp. 1–6. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Zhu, Y.; Bo, Z.; Li, M.; Liu, Y.; Liu, Q.; Chang, Z.; Hu, Y. Deep reinforcement learning based joint active and passive beamforming design for RIS-assisted MISO systems. In Proceedings of the 2022 IEEE Wireless Communications and Networking Conference (WCNC), Austin, TX, USA, 10–13 April 2022; pp. 477–482. [Google Scholar]
- Nguyen, K.K.; Khosravirad, S.R.; Da Costa, D.B.; Nguyen, L.D.; Duong, T.Q. Reconfigurable intelligent surface-assisted multi-UAV networks: Efficient resource allocation with deep reinforcement learning. IEEE J. Sel. Top. Signal Process. 2021, 16, 358–368. [Google Scholar] [CrossRef]
- Slivkins, A. Introduction to multi-armed bandits. Found. Trends® Mach. Learn. 2019, 12, 1–286. [Google Scholar] [CrossRef]
- Kuleshov, V.; Precup, D. Algorithms for multi-armed bandit problems. arXiv 2014, arXiv:1402.6028. [Google Scholar]
- Auer, P.; Ortner, R. UCB revisited: Improved regret bounds for the stochastic multi-armed bandit problem. Period. Math. Hung. 2010, 61, 55–65. [Google Scholar] [CrossRef]
- Darak, S.J.; Hanawal, M.K. Multi-player multi-armed bandits for stable allocation in heterogeneous ad-hoc networks. IEEE J. Sel. Areas Commun. 2019, 37, 2350–2363. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep reinforcement learning: A brief survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Smith, J.C.; Taskin, Z.C. A tutorial guide to mixed-integer programming models and solution techniques. Optim. Med. Biol. 2008, 521–548. [Google Scholar]
- Shi, C.; Xiong, W.; Shen, C.; Yang, J. Decentralized multi-player multi-armed bandits with no collision information. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Online, 26–28 August 2020; pp. 1519–1528. [Google Scholar]
- Russo, D.J.; Van Roy, B.; Kazerouni, A.; Osband, I.; Wen, Z. A tutorial on thompson sampling. Found. Trends® Mach. Learn. 2018, 11, 1–96. [Google Scholar] [CrossRef]
- Kalathil, D.; Nayyar, N.; Jain, R. Decentralized learning for multiplayer multiarmed bandits. IEEE Trans. Inf. Theory 2014, 60, 2331–2345. [Google Scholar] [CrossRef]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1587–1596. [Google Scholar]


| Parameter | Value |
|---|---|
| Number of D2D pairs | 10 |
| Number of RIS | (10, 20) |
| Number of RB | (10, 20) |
| Tx transmission power | 20 dBm |
| Rx hardware cost power | 10 dBm |
| RIS hardware cost power | 10 dBm |
| Path loss in reference distance (1 m) | −30 dBm |
| Target SINR threshold | 20 dBm |
| Power of noise | −80 dBm |
| D-UCB time steps | 500 |
| D-UCB exploration parameter C | 2 |
| TD3 time steps | 1000 |
| Reward discount factor | 0.99 |
| Network update learning rate | 0.005 |
| Target network update frequency | 2 |
| Policy noise clip | 0.5 |
| Max replay buffer size | 100,000 |
| Batch size | 256 |
| Variables | n | Mean | SD | Median | Skew | Kurtosis | SE |
|---|---|---|---|---|---|---|---|
| D-UCB | 500 | 300.379 | 12.658 | 300.964 | −0.019 | −1.452 | 1.808 |
| MAB | 500 | 352.055 | 10.459 | 353.225 | −0.199 | −1.106 | 1.494 |
| Variables | n | Mean | SD | Median | Skew | Kurtosis | SE |
|---|---|---|---|---|---|---|---|
| D-UCB | 500 | 97.801 | 5.541 | 97.691 | 0.344 | −0.945 | 0.792 |
| MAB | 500 | 118.593 | 4.189 | 119.456 | −0.532 | −0.703 | 0.598 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Xu, H. Distributed Data-Driven Learning-Based Optimal Dynamic Resource Allocation for Multi-RIS-Assisted Multi-User Ad-Hoc Network. Algorithms 2024, 17, 45. https://doi.org/10.3390/a17010045
Zhang Y, Xu H. Distributed Data-Driven Learning-Based Optimal Dynamic Resource Allocation for Multi-RIS-Assisted Multi-User Ad-Hoc Network. Algorithms. 2024; 17(1):45. https://doi.org/10.3390/a17010045
Chicago/Turabian StyleZhang, Yuzhu, and Hao Xu. 2024. "Distributed Data-Driven Learning-Based Optimal Dynamic Resource Allocation for Multi-RIS-Assisted Multi-User Ad-Hoc Network" Algorithms 17, no. 1: 45. https://doi.org/10.3390/a17010045
APA StyleZhang, Y., & Xu, H. (2024). Distributed Data-Driven Learning-Based Optimal Dynamic Resource Allocation for Multi-RIS-Assisted Multi-User Ad-Hoc Network. Algorithms, 17(1), 45. https://doi.org/10.3390/a17010045






