Abstract
Velocity estimation has a key role in several applications; for instance, velocity estimation in navigation or in mobile mapping systems and GNSSs is currently a common way to achieve reliable and accurate velocity. Two approaches are mainly used to obtain velocity based on GNSS measurements, i.e., Doppler observations and carrier phases differenced in time (that is, TDCP). In a benign environment, Doppler-based velocity can be estimated accurately to within a few cm/s, while TDCP-based velocity can be estimated accurately to within a few mm/s. On the other hand, the TDCP technique is more prone to availability shortage and the presence of blunders. In this work, the two mentioned approaches are tested, using three devices of different grades: a high-grade geodetic receiver, a high-sensitivity receiver, and a GNSS chip mounted on a smartphone. The measurements of geodetic receivers are inherently cleaner, providing an accurate solution, while the remaining two receivers provide worse results. The case of smartphone GNSS chips can be particularly critical owing to the equipped antenna, which makes the measurements noisy and largely affected by blunders. The GNSSs are considered separately in order to assess the performance of the single systems. The analysis carried out in this research confirms the previous considerations about receiver grades and processing techniques. Additionally, the obtained results highlight the necessity of adopting a diagnostic approach to the measurements, such as RAIM-FDE, especially for low-grade receivers.
1. Introduction
Velocity is essential in several applications such as navigation, transportation, or mapping. Global Navigation Satellite System (GNSS)-based velocity estimation is one of the most adopted solutions; according to the technique and measurements used, different performance levels can be obtained. The two most-used measurements for GNSS-based velocity are Doppler shift and carrier phase (CP); the use of Doppler observables allows a cm/s accuracy level [1], while the use of carrier phase (CP) observables differenced in time Time-Differenced Carrier Phase (TDCP) can achieve a mm/s accuracy level [2,3].
Doppler measurements were used as the only source for GNSS positioning in [4], where the geometric weakness of this approach was highlighted. New interest in this approach has emerged regarding the possibility of supporting a GNSS with Low Earth Orbit (LEO) satellites [5]. Doppler measurements have been integrated with advanced algorithms. For example, in [6], they are integrated with inertial measurements in a pedestrian dead reckoning (PDR) system for indoor navigation; in [7] and [8], they are combined with pseudorange measurements; and in [9,10], Doppler is used for smoothing pseudorange. The particular use of Doppler for anti-spoofing applications is explored in [11]. In any case, the most common use of the Doppler shift in the GNSS context is for velocity estimation [1,12].
CP measurements are used for precise positioning; the higher precision and accuracy are obtained at the cost of increasing the navigation engine complexity due to the intrinsically ambiguous nature of CP observables [1,12]. In addition, the loss of lock and cycle slip are additional problems in the usage of this type of measurement.
By exploiting the difference between two consecutive CP measurements, TDCP removes the problem of the unknown ambiguity (in the absence of cycle slips) [3], making this technique very powerful due to its reachable accuracy.
Several research studies have focused on TDCP; it has been used to estimate the velocity of a standalone GPS receiver [2], but it has also been successfully applied to other constellation cases such as BeiDou in the static case, where mm/s accuracy was obtained, and in the kinematic case, where only a cm/s accuracy level was achieved due to the sudden acceleration of the vehicle [13], revealing a possible weakness of this technique. Moreover, the performance of TDCP using Galileo in the static case and on different signal frequencies is analyzed in [14]. One of the main limitations of TDCP is the usage of two consecutive measurements, which are referred to as different epochs. If between the two epochs a new navigation message is received, two different sets of ephemerides are used, resulting in a discontinuity of the TDCP measurement; this problem has been addressed in [15], where a method that considers the same ephemerides set for every couple of epochs is proposed. In 2015, the Leica Geosystems company published a white paper on the Velocity And Displacement Autonomous Solution Engine (VADASE) algorithm [16], which exploits the difference between two consecutive phase measurements, i.e., TDCP, for a precise velocity estimation.
In the sector of inertial and integrated navigation, TDCP also garnered considerable interest due to its capability to improve the accuracy of an integrated solution; in [17], this technique was used to enhance Inertial Navigation System (INS) with an iterative extended Kalman filter (EKF); in [18], a novel TDCP-GNSS/INS integration was designed for a low-cost GNSS receiver and low-accuracy INS, where the role of TDCP was in cycle slip detection and handling.
The TDCP technique has been investigated for several applications: for automotive applications in [19], where TDCP is used for the computation of the heading and pitch angles of an antenna mounted on a vehicle; for critical infrastructural monitoring in [20]; and for seismic motion detection in [21].
Low-cost GNSS devices include mass-market receivers and smartphones. These devices are exploited by billions of users in different operational conditions. Currently, few studies have been performed to analyze the performance of TDCP using such devices, which are usually characterized by noisy and discontinuous measurements. The measurement quality of such devices was analyzed and assessed in several studies; in [22,23,24], exhaustive assessments of several smartphones’ observations are provided in terms of different aspects: carrier-to-noise density power ratio (C/N0), multipath error, positioning performance, and so on. The TDCP potentialities of such devices are also revealed; in [25], a static analysis considering only GPS data was conducted by comparing receivers of different grades, confirming mm/s level accuracies for all the adopted devices, i.e., for the smartphone as well. The GNSS market is evolving very fast, and the capability of low-cost devices is increasing; several manufacturers have enhanced their products, for example, by tracking new constellations and adding different frequencies. These evolutions have led to the wider adoption of low-cost devices (including smartphones) for several applications. The performance and limitations of these devices for velocity estimation are not fully investigated in the specialized literature. In the current research, the objective is to fill this gap, in particular, by extending the available analysis to other constellations and using different devices.
This study assesses the performance of the TDCP technique on three different devices: a Novatel GPS geodetic-grade receiver; a uBlox ZED-F9P high-sensitivity receiver; and a Xiaomi Mi8, equipped with a Broadcom BCM47755 chipset. The motivations of this study are related to the huge number of smartphones exploited by users for navigation purposes. The quality of the measurements collected by such devices is promising, and an analysis of the performance of low-cost devices exploiting advanced techniques and their comparison with higher-grade devices becomes interesting. The assessment was performed using real data collected with an ad hoc setup including the three devices mentioned above. The test duration was about one hour, and the analysis was performed only on L1 frequency. All the adopted devices were able to collect both Doppler shift and CP measurements; hence, velocity was determined with Doppler and TDCP approaches considering all the GNSSs, in single constellation mode. Moreover, further analysis involving the application of a RAIM-FDE algorithm was conducted with the aim of evaluating the contribution of an integrity module able to detect and exclude measurements affected by gross errors.
The paper is organized as follows: in Section 2, the developed methodology is described, providing theoretical aspects related to Doppler-based velocity, TDCP-based velocity, RAIM-FDE, and the selected weighting strategy; Section 3 first provides the experimental setup description and the data analysis, in order to provide an overview of the test conditions, and in the second part, the results and the findings are presented; Section 4 concludes the paper.
2. Velocity Estimation
In this section, the two considered techniques for GNSS-based velocity estimation are described: Doppler-based velocity estimation in Section 2.1 and TDCP-based velocity estimation in Section 2.2. For both algorithms, the measurements are differently weighted according to a suitable criterion, which is explained in Section 2.3. The adopted RAIM-FDE technique, that is, the subset testing, is described in Section 2.4.
The following nomenclature is adopted hereinafter:
Receiver position: .
Satellite position: .
Receiver velocity: .
Satellite velocity: .
Unit vector of the direction from receiver to satellite: .
Geometric distance between receiver and satellite: .
Positions and velocities are expressed in the Earth-centered, Earth-fixed (ECEF) frame.
2.1. Doppler-Based Velocity
The Doppler shift is the apparent frequency change of signals related to the relative motion between the observer and the source. In the GNSS context, satellites are the signal source and receivers are the observers. Doppler shift is exploited to estimate receiver velocity, with the satellite motion being known.
The Doppler shift, , can be expressed as the variation in the receiver–satellite range, , as follows:
where is the signal wavelength.
is not exactly coincident with the receiver–satellite geometric range rate, , owing to errors related to the receiver and satellite clock drift, troposphere, ionosphere, orbits, multipath, and noise. In addition, includes the receiver clock drift, , which is unknown and needs to be estimated together with the receiver velocity. Satellite clock drift is monitored by the GNSS ground segment: it is accurately estimated and broadcasted to users through the navigation message. The remaining error sources are generally negligible.
The measurement equation related to the Doppler shift can be expressed as
where the unmodeled and uncorrected error sources are lumped in .
is the projection of the relative motion between the satellite and the receiver in the receiver–satellite direction, that is,
By replacing the expression of reported in (3) in measurement Equation (2) and rearranging the terms, the following equation is obtained:
Considering the components of , , , , the dot product in (4) can be developed, resulting in the following:
In Equation (5), the left side contains only known entities; the satellite position and velocity are known thanks to the navigation message, and it is assumed that the receiver position has already been estimated. On the right side of (5), the unknowns of the problem, i.e., receiver velocity components and clock drift, are present. In the case of a single GNSS, at least four equations like (5), corresponding to as many simultaneous available measurements, are necessary for computing the unknowns.
A system of measurements like (5) can be written as
As can be seen from (5), the receiver position and the receiver clock bias have already been estimated. So, the receiver clock drift in (6) can be also calculated by differencing two consecutive clock biases and by dividing such difference by the time interval between the considered epochs. However, in this way, a noisier clock drift is obtained in comparison to the use of Doppler measurements.
The Doppler measurements expressed in velocity units, corrected for the satellite motion, are stored in .
is the design matrix whose ith row is and contains information about the satellite geometry observed by the receiver.
is the unknown vector, which can be resumed with and contains the ECEF components of the user velocity and the receiver clock drift .
In case of redundant measurements, a suitable estimation technique should be adopted; in this study, a weighted least squares (WLS) technique is used; the weighting matrix is related to satellite elevation and C/N0 as specified below. The formula for estimating using the WLS technique is reported in (7):
The geometry contribution to the solution quality is quantified by the Dilution Of Precision (DOP) metrics. After the 4 × 4 matrix is defined, the square root of the sum of the diagonal elements of the submatrix of obtained excluding the 4th row and 4th column is the 3D-DOP, which is considered in this study and is shown in Formula (8).
This particular DOP quantifies the effect of geometry on the three components of the estimated velocity.
2.2. TDCP-Based Velocity
CP is, together with pseudorange and Doppler, one of the main GNSS observables, and its equation is
is the CP measurement expressed in length units and is the product between the CP measurement in cycles, , and the signal wavelength, . and are the receiver and the satellite clock biases, respectively; is the integer ambiguity; is the orbital error; and are the ionospheric and tropospheric errors, respectively; is the Broadcast Group.
Delay; is the relativistic error; and are the errors related to multipath phenomenon and to receiver noise, respectively; and includes the unmodeled error sources.
The TDCP observation is obtained by differencing two consecutive CP measurements from the same satellite, thus reducing the common errors. If any cycle slip occurs, is constant in two consecutive CPs, so it can be eliminated. , , , , , and are time-correlated error sources, so they are strongly reduced in the difference, especially if the sampling interval is small, e.g., 1 s or smaller.
Assuming that and are two consecutive epochs, the TDCP measurement equation is
is the difference between CPs at and .
is the range variation proportional to the average Doppler frequency shift due to satellite motion along the receiver–satellite direction.
is a term taking into account the changes in the receiver–satellite geometry.
is the receiver displacement between epochs and .
is the receiver clock bias variation between epochs and .
contains the residual and the unmodeled errors.
Considering the expression of components, Equation (10) becomes
The corrected TDCP measurements are located on the left side of (11), while the unknowns and are on the right side. The average receiver velocity between epochs and , , can be easily computed as
Similar to the case of Doppler-based velocity, at least four equations like (10) are necessary for unknown estimation, in both single and multiple GNSS cases. A system of equations like (11) is shown in (13):
If system (13) is redundant, a suitable estimation technique should be used; the WLS method is adopted for this technique as well, and the formula for estimating is reported in (14):
where the only difference from (7) is the subscript “T”, standing for “TDCP”.
The DOP concept is valid for TDCP too, and the 3D-DOP, defined in (7), is also considered in this case, indicating the design matrix with instead of . The matrices and are formally identical; of course, the 3D-DOP values can be different for Doppler and TDCP cases because of the different available measurements.
2.3. Weighting Strategy
In order to fully exploit the available measurements, it is necessary to weight them differently in the estimation algorithm. In the GNSS context, satellite elevation (El) and are usually adopted as quality indicators for defining the weighting scheme. In the specialized literature, several schemes have been defined, based on El only [26,27], on only [28], or on both [29,30,31]. In this work, the weighting scheme described in [29] is used, and it is scaled to fit Doppler and TDCP measurements. The weights, , are computed as the inverse of the measurement error variance, , , whose expression is
is compared with a threshold . If exceeds , the corresponding is set to ; otherwise, it is increased according to formula (15) as a function of and El. The parameters in (15) have been empirically set as , , and . The value is set to 5 cm/s for Doppler and 5 mm for TDCP. The choice of the value is fundamental for an effective RAIM-FDE application.
2.4. RAIM-FDE
RAIM algorithms are user-level algorithms able to provide integrity information, i.e., the trust that can be placed in the GNSS solution. RAIM algorithms are based on a consistency check on redundant measurements [32]; and if RAIM algorithms are also able to identify and reject anomalous measurements, they are referred to as FDE algorithms.
In this work, the adopted RAIM-FDE algorithm is called “Subset Testing” [28], and it is based on the analysis of residuals, , whose expression is as follows:
where is the measurement vector, is the design matrix, and is the vector of the estimated unknowns.
A decision variable , depending on the residuals and on the weighting matrix , is defined as follows:
is compared with a threshold, whose value depends on the measurement redundancy and on the probability of a false alarm; if exceeds the threshold, the presence of at least one anomalous measurement is reported. In subset testing, such a test is carried out on each possible subset of measurements, until a blunder-free subset is identified; in this way, the possible anomalous measurements are excluded, and they do not contribute to the solution computation. If an inconsistency is revealed but a blunder-free subset is not identified, the solution is indicated as not reliable.
In this study, the RAIM-FDE block is used also for detecting cycle slips; in that context, a cycle slip is considered as a simple blunder affecting the carrier-phase measurements and is rejected by the FDE part of the integrity algorithm. No repair action is performed when a cycle slip is detected.
3. Results
This section is divided into three sub-sections: test description, preliminary data analysis, and velocity domain results. In the first, the performed test is detailed in terms of equipment and scenario. In the second, the collected measurements are preliminarily analyzed by studying the measurement availability, the signal strength, and the satellite geometry. In the last, the estimated velocities are analyzed.
3.1. Test Description
The purpose of this work is to analyze the performance of Doppler-based and TDCP-based algorithms with different grades of GNSS receivers: a geodetic receiver, a consumer-grade receiver, and a smartphone chip. Specifically, the used devices are as follows:
- Novatel geodetic receiver [33], hereinafter briefly referred to as “Novatel”;
- uBlox ZED-F9P GNSS receiver [34], hereinafter briefly referred to as “uBlox”;
- Broadcom BCM47755 chipset [35] (embedded in Xiaomi Mi8 smartphone), hereinafter briefly referred to as “Xiaomi”.
The test was carried out in a rural area in the suburbs of Naples, where the mentioned devices simultaneously acquired about 1 h of GNSS measurements. The test was static, in order to have a null velocity as ground truth. The location of the data collection is shown in Figure 1a. The equipment arrangement is shown in Figure 1b. The adopted antennas were placed nearby on the same plane; a geodetic antenna was connected to the Novatel device, a patch antenna was connected to the uBlox device, and the antenna of the Xiaomi smartphone was embedded in the device.
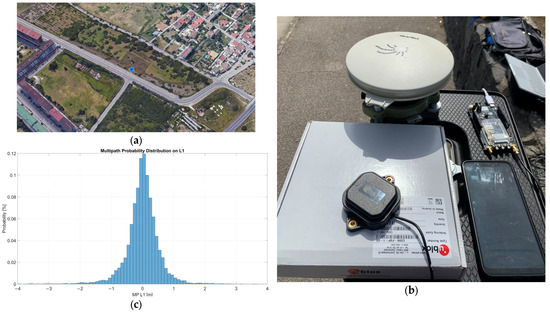
Figure 1.
Panel (a): location of the test; the equipment is placed on point P. Panel (b): equipment deployment. Panel (c): multipath probability distribution for the uBlox receiver.
The data collected by the devices were processed with specifics MATLAB software, i.e. PANGNAV for the Doppler part [36], and by an ad-hoc TDCP algorithm published in [15].
In Figure 1c, the probability distribution of the multipath errors on L1 for uBlox is shown; from that, it can be noted that the multipath errors are small and compliant with an open-sky scenario.
It should be noted that the performance of the uBlox device could be affected by the used setup (shown in Figure 1b); indeed, the adoption of a ground plane, as suggested in [37], could improve the performance of such a device.
3.2. Preliminary Data Analysis: Measurement Availability, Signal Strength, and Geometry
Velocity estimation is strongly affected by the number of available measurements, by the geometry, and by the measurements’ quality. Before the results are presented in the velocity domain, a preliminary analysis of the data is performed. In detail, the following aspects are investigated:
- Availability of raw Doppler shift and CP measurements;
- behavior;
- Availability and geometry of Doppler and TDCP measurements considering mask angle and limit.
As evidenced by Figure 1, the location where the test took place has no significant obstacles, and the multipath level is low, so it is a typical open-sky scenario; consequently, a large number of measurements is expected.
The availability of Doppler and CP observables is shown in Figure 2 for each device, GNSS, and satellite ID. In this analysis, all the tracked measurements are considered, without considering the mask angle and limit. Specifically, panels in the first row refer to GPS satellites, panels in the second row to Glonass, panels in the third row to Galileo, and panels in the fourth row to BeiDou. Moreover, panels in the first column refer to the Novatel device, panels in the second column to uBlox, and panels in the third column to Xiaomi. Only one panel is present in the first column, i.e., panel (a), because the Novatel device is able to acquire only GPS signals. In each panel, a blue dot indicates the availability of both Doppler and CP measurements for a certain epoch, while a red dot indicates the availability of only Doppler measurements and the unavailability of CP measurements in the considered epoch. It never happens that CP is available and Doppler is not.
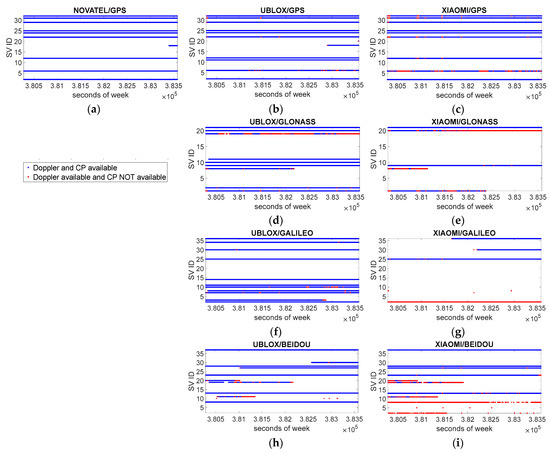
Figure 2.
Availability of Doppler and CP observables (mask angle and limit not applied). Each panel refers to a single device and to a single GNSS. Panels in the first row, (a–c), refer to GPS; panels in the second row, (d,e), to Glonass; panels in the third row, (f,g), to Galileo; and panels in the fourth row, (h,i), to BeiDou. The panel in the first column, (a), refers to the Novatel device; panels in the second column, (b,d,f,h), to uBlox; and panels in the third column, (c,e,g,i), to Xiaomi.
From an analysis of the panels (a), (b), and (c), it is evident that the tracked GPS satellites are roughly the same, except for G11, which is tracked by uBlox but not by Novatel and Xiaomi. There are no red dots for Novatel, while they are present for uBlox and even more for Xiaomi. This highlights that, in the GPS case, the CP observable is continuous for the high-grade device, while discontinuities appear for the high-sensitivity device and, above all, for the smartphone chip. This issue reverberates on the availability of a TDCP solution, which is based on time-differenced CP measurements. The comparison with the geodetic receiver in terms of the other GNSSs is not possible.
An analysis of the panels (d) and (e), regarding Glonass measurements from uBlox and Xiaomi, respectively, indicates that the tracked satellites are significantly different: measurements from R02, R10, R11, and R19 satellites are present for uBlox and not for Xiaomi. Glonass Doppler measurements for Xiaomi are often insufficient for standalone velocity estimation, and CP is often missing even when Doppler is available, causing a long unavailability of TDCP Glonass-only velocity.
A very similar consideration can be made for Galileo measurements, by analyzing panels (f) and (g): for Doppler shift, the uBlox device was able to track up to 11 satellites, while the maximum number of Galileo satellites for the smartphone was 4; for the TDCP case, only a few discontinuities were observed for uBlox, while for the smartphone case, large discontinuities were observed, and even in case of Doppler availability, CP is often missing.
Regarding BeiDou, the available Doppler and CP measurements are similar for uBlox and Xiaomi; only small differences can be noted. Specifically, satellite C30 is tracked by uBlox and not by Xiaomi, and satellites C02 and C05 are tracked by Xiaomi and not by uBlox. C02 and C05 are both geostationary (GEO) satellites, highlighting a uBlox shortage in tracking such satellites, while C30 is a medium Earth orbit (MEO) satellite and is probably not tracked by Xiaomi due to the inherent selection criteria of the device. Xiaomi is not able to store CP for C02, C05, and C08, while CP is discontinuous for C19 and C20. C02, C05, and C08 are all characterized by low values, about 25 dB-Hz, inhibiting the storage of reliable CP measurements; C08 is an inclined geosynchronous orbit (IGSO) satellite. CP discontinuities of C19 and C20 are related to frequent drops in their C/N0 values below 25 dB-Hz. The number of epochs where Doppler is present and CP is missing is significantly smaller in uBlox.
An analysis of the measurements stored by Xiaomi, panels (c), (e), (g), and (i), indicates that a measurement selection criterion appears to be implemented in the device, privileging GPS and BeiDou measurements over Glonass and Galileo ones. This behavior is probably due to the limited number of channels available for tracking.
An additional analysis of measurement availability is carried out by comparing the availability percentages of Doppler and CP measurements of two GPS satellites, G02 and G06, for the three considered devices. In Figure 3a, the measurement availability for G02 is shown, while Figure 3b shows that for G06. These particular satellites have been selected because CP from G02 is continuous for all three devices, while for G06, some discontinuities in CP are evident for uBlox and Xiaomi, as shown in panels (a), (b), and (c) of Figure 2. The graphs in Figure 3 confirm what emerges from Figure 2, relative to satellites G02 and G06. Specifically, the availability of Doppler and CP measurements of G02 is 100% for all the considered devices, with only a few gaps for CP with Xiaomi, which has 99.9% availability. Regarding the G06 satellite, Doppler and CP availabilities are 99.9% for Novatel; they are 99.8% and 97.8%, respectively, for uBlox; and they are 92.2% and 83.1%, respectively, for Xiaomi.
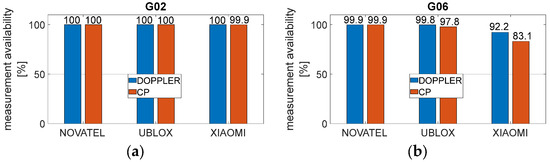
Figure 3.
Availability percentage of Doppler and CP measurements for satellite G02, panel (a), and for satellite G06, panel (b). Mask angle and limit not applied.
The behavior of is shown in Figure 4, which is structured like the previously described Figure 2. In the panels, the values of the tracked satellites are displayed with respect to time; in black, the mean values for each GNSS and device are shown too. Considering the GPS case, panels (a), (b), and (c), the Novatel device shows larger values than uBlox and Xiaomi, with mean values equal to 44.7 dB-Hz, 41.3 dB-Hz, and 37.7 dB-Hz, respectively. This could be related to the different gain antennas characterizing the three devices and to the way is computed by each device. The behavior for Novatel seems more regular with values never below 25 dB-Hz, while the uBlox receiver and the smartphone were able to track very weak signals with values as low as 15 dB-Hz. For uBlox and Xiaomi, the behavior is more fluctuating, with lower values for Xiaomi.
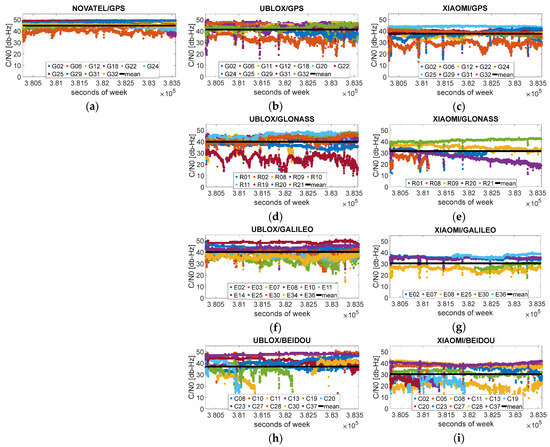
Figure 4.
behavior over time (mask angle and limit not applied). Each panel refers to a single device and to a single GNSS. Panels in the first row, (a–c), refer to GPS; panels in the second row, (d,e), to Glonass; panels in the third row, (f,g), to Galileo; and panels in the fourth row, (h,i), to BeiDou. The panel in the first column, (a), refers to the Novatel device; panels in the second column, (b,d,f,h), to uBlox; and panels in the third column, (c,e,g,i), to Xiaomi.
Considering the Glonass case, in panels (d) and (e), more satellites are tracked by uBlox than by Xiaomi; moreover, values for Xiaomi are lower, e.g., satellite R09 has values between 40 and 50 dB-Hz for uBlox (purple dots in panel (d)) and between 30 and 40 for Xiaomi (yellow dots in panel (e)). The mean values are 39.8 dB-Hz for uBlox and 31.5 dB-Hz for Xiaomi. Such behavior is, as previously mentioned, related to differences in antenna and receiver architecture between the considered devices. Similar behaviors are also evident for Galileo in panels (f) and (g); in this case, the mean value is 40.2 dB-Hz for uBlox and 30.4 dB-Hz for Xiaomi. Even for BeiDou, it is evident that for Xiaomi, panel (h), lower values are present in comparison to uBlox, panel (i); the mean values are 36.6 dB-Hz for uBlox and 30.2 dB-Hz for Xiaomi.
In Table 1, the mean, maximum, and minimum values for each GNSS and for each device are summarized. It is evident that for each GNSS, the higher the device grade, the higher the mean value. GPS measurements have, on average, larger values in comparison to the measurements from the other systems. Glonass and Galileo measurements, fixed the device, have similar mean values, while the lowest values are found for BeiDou. The low mean values of for BeiDou are due to the presence of GEO and IGSO satellites in its constellation.

Table 1.
Mean, maximum, and minimum values in dB-Hz for single GNSS and device (mask angle and limit not applied).
Similar conclusions can be obtained considering the maximum and minimum values: uBlox (and Novatel, even if for the GPS-only case), reported a higher maximum value than Xiaomi; Xiaomi, on the other hand, reported a higher minimum value than uBlox, except for the BeiDou case. Although the devices were able to track very weak signals with close to 10 dB-Hz, the measurements related to signals with such low power are not used in the estimation process because a threshold for the value was set to 25 dB-Hz.
Table 2 reports the mean values for BeiDou measurements, classified by orbit type; it demonstrates that BeiDou measurements from MEO satellites have values similar to those for GPS, while significantly lower values characterize GEO and IGSO cases.

Table 2.
Mean values in dB-Hz for BeiDou system, related to satellite orbit type (mask angle and limit not applied).
An additional analysis of is carried out by comparing its trends for the G02 and G06 GPS satellites, for the three considered devices. In Figure 5, the behavior for G02 is shown in panel (a), and that for G06 is shown in panel (b). As shown in Figure 5a, the values are about 48 dB-Hz with a very stable behavior for Novatel; slightly lower values with more pronounced fluctuations are evident for uBlox and even more for Xiaomi, remaining above 30 dB-Hz in any case. From Figure 5b, it is evident that the values are lower than those for the G02 case: for Novatel, values are higher than those for uBlox and even higher than those for Xiaomi. It can be noticed that for uBlox and Xiaomi, the epochs in which Doppler measurements are available and CP measurements are not, marked by red dots in Figure 2, correspond to values of below 25 dB-Hz.
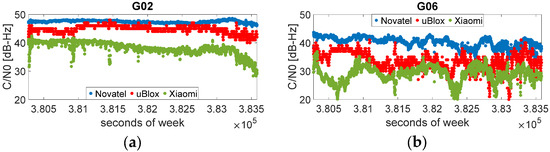
Figure 5.
behavior over time (mask angle and limit not applied) for satellite G02, panel (a), and for satellite G06, panel (b).
Usually, measurements from a satellite elevation below a certain threshold and with a value below a certain limit are not used for solution computation. In this work, a mask angle of 15 degrees and a limit of 25 dB-Hz are adopted. So, the numbers of actually used Doppler and CP measurements are reduced in comparison to the ones shown in Figure 2 and Figure 4.
In Figure 6, the numbers of used Doppler shift and TDCP measurements are shown for each GNSS and for each considered device, following the scheme described in the previous figures. TDCP measurements are obtained by differencing two consecutive CPs, so it is sufficient that at least one of the two CPs is missing for inhibiting TDCP measurement; for this reason, it is expected that the number of TDCP measurements is less than the number of Doppler measurements. In the same figure, the corresponding 3D DOP is shown too. The numbers of used Doppler and TDCP measurements are drawn in cyan and blue, respectively; the corresponding 3D DOP values are drawn in magenta and red, respectively. The number of measurements and the corresponding 3D DOP are strictly related; indeed, DOP increases when the number of measurements decreases and vice versa.
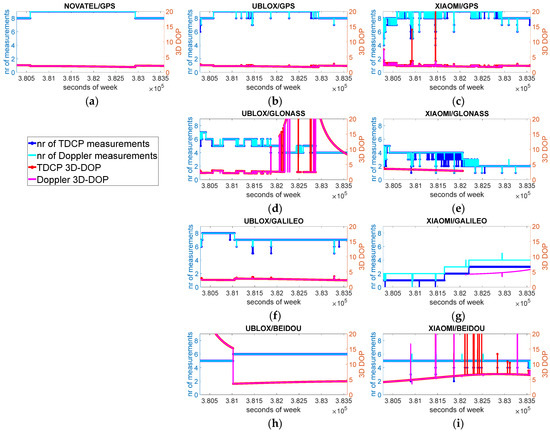
Figure 6.
Numbers of Doppler and TDCP measurements (mask angle and limit applied). Each panel refers to a single device and to a single GNSS. Panels in the first row, (a–c), refer to GPS; panels in the second row, (d,e), to Glonass; panels in the third row, (f,g), to Galileo; and panels in the fourth row, (h,i), to BeiDou. The panel in the first column, (a), refers to the Novatel device; panels in the second column, (b,d,f,h), to uBlox; and panels in the third column, (c,e,g,i), to Xiaomi.
An analysis of the GPS-only case reveals that for the Novatel device (panel (a)), the numbers of Doppler and TDCP measurements are the same (except for the first epoch, when the TDCP measurements cannot be obtained). For uBlox, panel (b), some punctual reductions in measurements, can be noted but the numbers of Doppler and TDCP measurements are always larger than four, allowing the estimation of velocity. For Xiaomi, panel (c), a larger difference between TDCP and Doppler shifts can be appreciated, with the former going down to four. Regarding geometry, for the Novatel device, the 3D DOP behavior, in panel (a), is regular, with values below 2.5 and with two small jumps in correspondence with changes in measurement availability; the red and magenta lines are coincident. For uBlox, only a few additional jumps are visible in panel (b), related to the sudden variations in measurements. The frequent variations in GPS measurements in Xiaomi lead to irregularities in the red and magenta lines; when four TDCP measurements are available, the corresponding DOP value exceeds 15 (panel (c)).
For Glonass, panels (d) and (e), the number of measurements used varies between four and seven for uBlox, and few differences between the Doppler and TDCP cases can be noted. For the Xiaomi case, the number of used Doppler shift measurements is between one and five; the situation is even worse for TDCP measurements, which exhibit significant drops in comparison to the Doppler shift. An analysis of the corresponding geometry reveals that for the uBlox device, the 3D DOP values are about 2.5 for the first part of the session, while they jump to values greater than 15 in the second part, characterized by fewer available measurements (panel (d)). For Xiaomi, the number of Glonass measurements is not sufficient in the second part of the session, making the velocity estimation and DOP computation impossible (panel (e)).
For Galileo, panels (f) and (g), the behavior of the available measurements seems very regular for uBlox, with between six and eight measurements available for Doppler and between five and eight measurements available for TDCP. For Xiaomi, the number of Doppler measurements is often below four, making the estimation of velocity impossible, while TDCP measurements are always insufficient for the velocity estimation. In an analysis of the corresponding geometry, uBlox shows a good DOP behavior, comparable to the GPS-only case (panel (f)). Xiaomi has sufficient Doppler measurements for estimating velocity only in the last part of the session, while the TDCP measurements are insufficient for the entire session, as shown in panel (g).
For BeiDou, the numbers of Doppler and TDCP measurements regularly span between five and six for uBlox (panel (h)), and the number of measurements is most of the time equal to five, with drops to three for Doppler and to two for TDCP, for Xiaomi (panel (i)). For uBlox, the geometry with five measurements is poor, leading to DOP values greater than 15, while with six measurements, DOP values become below 5 (panel (h)). For Xiaomi, when five measurements are available, 3D DOP values are between 2 and 3, and during the sudden measurement drops, DOP values become large, exceeding 15, as shown in panel (i).
The availability of Doppler and TDCP measurements during the session is summarized in Table 3, where the minimum, maximum, and average numbers of measurements are shown for each considered GNSS and device. It is evident that Novatel and uBlox are able to track approximately the same GPS satellites while Xiaomi shows a lower minimum value, just sufficient for velocity estimation. The Xiaomi device demonstrates a deficiency in available Glonass and Galileo measurements in comparison to uBlox, which leads to frequent solution unavailability. Regarding BeiDou, uBlox and Xiaomi devices have comparable measurement availability, which is reduced for Xiaomi mainly because of IGSO C08 satellite unavailability.

Table 3.
Minimum, mean, and maximum numbers of Doppler and TDCP measurements (mask angle and limit applied).
3.3. Velocity Domain Results
In this section, the main outcomes of this study are reported; in particular, the estimated velocities are analyzed for each considered device and for single GNSS cases. In Figure 7 and Figure 8, the behaviors of the horizontal and vertical velocity errors are shown; in all panels, the solution obtained using Doppler shift measurements is represented by the red line, while the blue line represents the solution obtained with the TDCP technique. In this case, the figures are composed as described in the previous section.
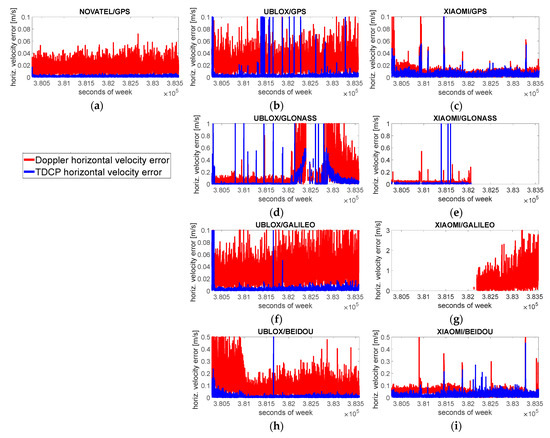
Figure 7.
Horizontal Doppler-based and TDCP-based velocity error. Each panel refers to a single device and to a single GNSS. Panels in the first row, (a–c), refer to GPS; panels in the second row, (d,e), to Glonass; panels in the third row, (f,g), to Galileo; and panels in the fourth row, (h,i), to BeiDou. The panel in the first column, (a), refers to the Novatel device; panels in the second column, (b,d,f,h), to uBlox; and panels in the third column, (c,e,g,i), to Xiaomi.
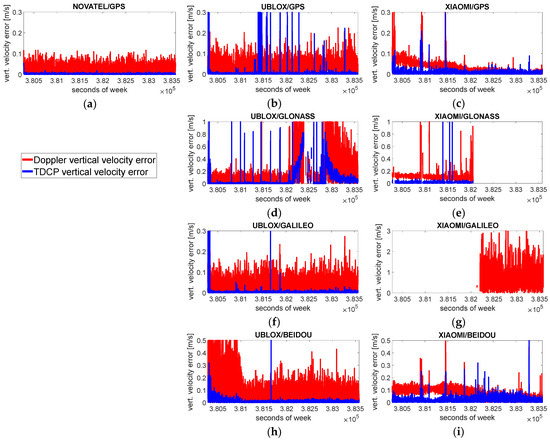
Figure 8.
Vertical Doppler-based and TDCP-based velocity error. Each panel refers to a single device and to a single GNSS. Panels in the first row, (a–c), refer to GPS; panels in the second row, (d,e), to Glonass; panels in the third row, (f,g), to Galileo; and panels in the fourth row, (h,i), to BeiDou. The panel in the first column, (a), refers to the Novatel device; panels in the second column, (b,d,f,h), to uBlox; and panels in the third column, (c,e,g,i), to Xiaomi.
For the performance in the velocity domain using GPS measurements, the panels (a) (b), and (c) of Figure 7 and Figure 8 are considered. From the figures, it is evident that Doppler-based and TDCP-based velocities are accurately estimated when GPS measurements from Novatel are used, while when using GPS measurements provided by uBlox, the TDCP velocity error is mostly about one order of magnitude less than Doppler one, as emphasized by the mean errors. Nevertheless, frequent spikes in the TDCP solution can be noted and are caused by anomalous measurements, supposedly due to cycle slips. For GPS measurements collected by Xiaomi, panel (c), sudden climbs in horizontal and vertical errors are evident in both the Doppler and TDCP cases (more pronounced in the latter), due to poor geometry; indeed, such error increases correspond to the DOP increase shown in Figure 6.
For Glonass measurements with uBlox, the first part of the session is characterized by frequent spikes in the TDCP solution, panel (d), while in the second part, a degradation in both the Doppler and TDCP solutions is present, due to a reduction in the available measurements and to a consequent geometry worsening; maximum errors are higher, being about a few m/s. When using Glonass measurements from the Xiaomi device, panel (e), the number of available Doppler measurements is mainly four in the first part of the session and below four in the second part, making the solution computation impossible. In the first part, sudden jumps in error values indicate the presence of blunders among the measurements. TDCP measurement availability is worse with longer solution unavailability; blunders are also present, leading to a maximum error exceeding 30 m/s.
The solutions obtained using Galileo measurements from the uBlox receiver, panel (f), are very similar to the GPS case with the same device, resulting in fewer and smaller anomalous error peaks. For Galileo with Xiaomi, panel (g), the TDCP solution is impossible to estimate due to an insufficient number of measurements during the session, while the Doppler solution is possible only in the second part of the session, with degraded performance (rms errors of about 1 m/s) due to the probable presence of anomalous measurements.
Considering BeiDou measurements from the uBlox device, panel (h), both Doppler and TDCP are degraded in the initial part of the session because of poor geometry, while in the remaining part, velocity errors are prevalently below 20 cm/s for the Doppler case and 3 cm/s for TDCP case. A large spike is evident in the TDCP solution, related to anomalous measurements. Considering BeiDou measurements from Xiaomi, panel (i), the poor geometry issue in the initial part of the session is not present, but several spikes are present in the TDCP solution. The Doppler velocity estimation seems to be better than the uBlox case, with more bounded errors.
The mean, root mean square (rms), and maximum horizontal and vertical velocity errors are computed and summarized in Table 4 and Table 5, respectively.

Table 4.
Horizontal velocity error (m/s): mean, root mean square, and maximum errors for single devices and single GNSSs.

Table 5.
Vertical velocity error (m/s): mean, root mean square, and maximum errors for single devices and single GNSSs.
Comparing the single GNSS configurations in terms of the considered figures of merit, it is evident that the best performance is obtained by the high-grade device. For uBlox, GPS-only performance and Galileo-only performance are similar, with the Doppler solution prevailing for GPS and the TDCP solution prevailing for Galileo. The GPS-only solution with Xiaomi demonstrates good performance, better than the corresponding uBlox configuration for almost all the figures of merit. The Glonass-only performance is deficient for both the uBlox and Xiaomi devices.
From the tables considering the GPS Novatel case, it can be noted that the rms horizontal and vertical errors are 2 cm/s and 3.6 cm/s, respectively, for Doppler and 2 mm/s and 4 mm/s for TDCP; the maximum errors are 7.2 cm/s and 11.7 cm/s for Doppler and 17 mm/s and 55 mm/s for TDCP. For the uBlox case, the rms errors are at the cm/s level for both the Doppler and TDCP cases. For the TDCP case, larger maximum horizontal and vertical errors of about 1 m/s and 1.8 m/s, respectively, have been observed. Finally, for the smartphone case, Doppler-based performance is good, considering that the horizontal and vertical rms errors are 1.3 cm/s and 4.5 cm/s, comparable with the Novatel case.
In Table 6, the solution availability values for the different configurations are reported. Solution availability is defined as the percentage of available solutions when the number of available measurements is at least four. Herein, a measurement is considered available if it comes from a satellite at an elevation angle above 15 degrees and if it has a C/N0 above 25 dB-Hz. Moreover, in the epochs where the geometry is too poor, specifically with 3D-DOP larger than 15, the solutions are considered not available. TDCP solution availability cannot be 100%, because two consecutive CP measurements should be differenced to obtain a TDCP measurement, and so it is not possible to have TDCP measurements in the first epoch.

Table 6.
Solution availability for single devices and single GNSSs.
From Table 6, it is evident that for the GPS case, the solution availability is very close to 100% for both the Doppler shift and the TDCP case. For the BeiDou case, it can be noted that few solutions are not available for Xiaomi. The situation for Glonass and Galileo is strongly dependent on the type of receiver. Using uBlox in both cases, the solution availability is very high, about 95% for Glonass and about 100% for Galileo; only marginal differences can be appreciated between the Doppler shift and the TDCP case. The situation is completely different when the smartphone solutions are considered: for the Glonass case, the solution availability using Doppler shift measurements is around 50%; this value is reduced in the TDCP case to about 43%. For Galileo, the Doppler shift solution availability is about 42%, and it was not possible to compute the TDCP solution; hence, the solution availability in this case is 0%. Hence, the configurations characterized by the worst solution availability are Glonass-only and Galileo-only with Xiaomi with a percentage of about 50 or lower, and with the TDCP solution never being possible for Galileo-only.
From the errors reported in Table 4 and Table 5 and Figure 7 and Figure 8, the presence of anomalous measurements leading to large velocity errors is evident, above all for the TDCP solution and non-high-grade devices. In this context, the application of RAIM-FDE can be effective in improving the results. In Figure 9 and Figure 10 and Table 7 and Table 8, the same error analysis carried out previously is reported, but with the application of the Subset algorithm. RAIM-FDE evaluates the consistency of the measurements, tries to reject blunders, and indicates reliable solutions. In this error analysis, only reliable solutions are considered.
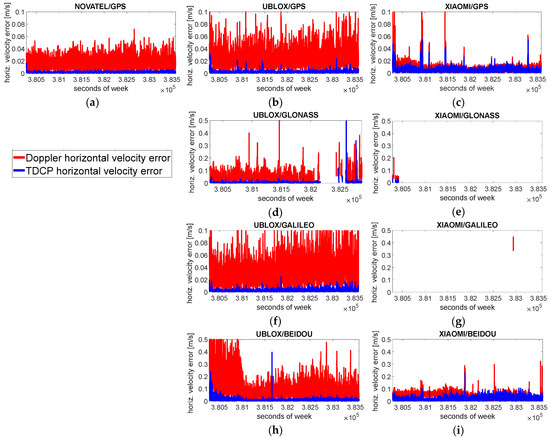
Figure 9.
Horizontal Doppler-based and TDCP-based velocity error with RAIM applied. Each panel refers to a single device and to a single GNSS. Panels in the first row, (a–c), refer to GPS; panels in the second row, (d,e), to Glonass; panels in the third row, (f,g), to Galileo; and panels in the fourth row, (h,i), to BeiDou. The panel in the first column, (a), refers to the Novatel device; panels in the second column, (b,d,f,h), to uBlox; and panels in the third column, (c,e,g,i), to Xiaomi.
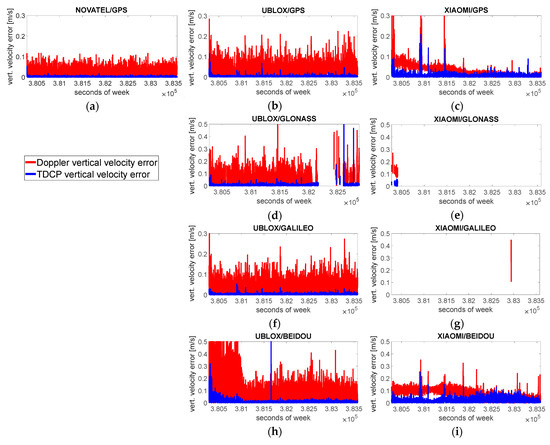
Figure 10.
Vertical Doppler-based and TDCP-based velocity error with RAIM applied. Each panel refers to a single device and to a single GNSS. Panels in the first row, (a–c), refer to GPS satellites; panels in the second row, (d,e), to Glonass; panels in the third row, (f,g), to Galileo; and panels in the fourth row, (h,i), to BeiDou. The panel in the first column, (a), refers to the Novatel device; panels in the second column, (b,d,f,h), to uBlox; and panels in the third column, (c,e,g,i), to Xiaomi.

Table 7.
Horizontal velocity error (m/s): mean, root mean square, and maximum errors for single devices and single GNSSs. RAIM is applied.

Table 8.
Vertical velocity error (m/s): mean, root mean square, and maximum errors for single devices and single GNSSs. RAIM is applied.
RAIM-FDE has no impact on both Doppler shift and TDCP velocities using the Novatel device, as is evident from the identical figures of merit reported in Table 7 and Table 8, because no blunders were detected. The benefits coming from RAIM-FDE can be clearly appreciated when using the measurements of low-cost devices.
For the GPS case with uBlox, the benefits of RAIM-FDE are evident in the TDCP solution where several spikes have been eliminated, improving all the figures of merit; no benefits are evident for Doppler velocity. A similar behavior is demonstrated for the Galileo-only case with uBlox. No significant effect is visible in the GPS case using measurements retrieved from the Xiaomi device, because the error peaks occur when DOP values are high and measurement redundancy is low, making the application of RAIM-FDE ineffective.
For the Glonass-only case with uBlox, several anomalous measurements have been identified and rejected, as demonstrated by the improvements of all the considered figures of merit, but some large errors remain in the solution owing to low redundancy. Both the Doppler and TDCP solutions are discontinuous because RAIM was not able to identify blunders in spite of the presence of measurement inconsistencies. Reliable solutions are almost completely absent for the Glonass and Galileo cases when the Xiaomi device is used; this is mainly due to the limited number of available measurements, as at least five measurements are needed to apply RAIM-FDE.
Finally, considering BeiDou measurements, RAIM has no impact with uBlox but is effective with Xiaomi, as demonstrated by the reduction in the maximum errors.
In Table 9, the reliable availability, defined as the solution percentage indicated by RAIM as reliable, is reported for each considered device, GNSS, and processing technique. Reliable availability is always lower than or equal to solution availability. The most critical configurations, according to reliable availability, are Glonass with both uBlox and Xiaomi, and Galileo with Xiaomi. For Glonass with uBlox, about 35% of the solutions are not reliable; for Glonass with Xiaomi, about 98% of the solutions are not reliable; and for Galileo with Xiaomi, there are no reliable solutions. For Galileo, these low values are due to severe geometric conditions and a limited number of measurements, while for the uBlox Glonass case, several outliers have been identified among the measurements.

Table 9.
Reliable availability for single devices and single GNSSs.
4. Conclusions
In this paper, the performance of TDCP and Doppler shift velocity estimation is analyzed. The performance of the two methods is assessed in terms of horizontal and vertical velocity errors, exploiting mean, rms, and maximum error indicators.
The two techniques were evaluated using real data collected by three different devices: a professional receiver, a low-cost receiver, and a smartphone. A preliminary analysis of the data provided by the three devices was performed and revealed the following:
- The professional receiver provides continuous CP measurements, while discontinuities have been noted for the low-cost receiver and, even more, for the smartphone chip.
- For all the considered devices, Doppler shift measurements are more continuous than CP measurements.
- The signal strength for the professional receiver is in general higher and more stable than that for the low-cost device, and the difference with respect to the smartphone is even more evident.
- For the smartphone, during the test, it was observed that a very limited number of Galileo and Glonass measurements was available, leading to a reduced solution availability and a large error in the velocity solution.
- RAIM-FDE has no impact on both Doppler shift and TDCP velocities when a high-grade device is used, while evident benefits are appreciated considering the measurements of low-cost devices.
- The effects of RAIM-FDE are evident in the uBlox and Xiaomi cases, leading to a reduction in almost all the errors, for both the horizontal and vertical components.
In the velocity domain, TDCP measurements from a professional receiver led to a more accurate solution for both the horizontal and vertical components. The smallest difference between the TDCP and Doppler shift solutions has been observed for the smartphone case. In particular, remarkable performance was obtained using Doppler shift measurements; in this case, the performance of the smartphone is similar to that of the professional receiver. When TDCP measurements from a low-cost device and from a smartphone are used, spikes are evident and lead to a degraded final solution. The spikes were due to erroneous CP observables and cycle slips. In order to mitigate these effects, a RAIM-FDE algorithm was included in the velocity estimation. The algorithm is able to identify and exclude multiple simultaneous outliers, leading to a sensible reduction in the velocity error. For all the configurations using professional and high-sensitivity receivers, the reliable availability is close to 100%, with a reduction in all the statistical parameters in the velocity domain. The performance of the RAIM-FDE block is strongly affected by the measurement redundancy. This effect is particularly evident for the Glonass and Galileo cases using the Xiaomi device, where the reliable availability is more than halved. This work has studied the potentiality of an advanced technique for GNSS velocity, namely TDCP. From the results, it emerges that such a technique could find interesting applications according to the used device: in a geodetic-grade receiver, it could be used for precise applications like mobile mapping; in low-cost devices, it could be used on UAV platforms, increasing the performance of velocity estimation for navigational purposes.
It is also interesting to note that for both Doppler- and TDCP-based velocity, the knowledge of the receiver position could affect the accuracy of the estimated velocity. To prove that, a simulated approach considering an increasing error in the estimated position is needed, and this could be an interesting analysis to address in further studies.
The issue related to the impact of the adopted setup, as discussed in Section 3.1, could be addressed in further empirical analyses in order to assess the possible benefits related to the adoption of a ground plane.
Additional future works will include the performance evaluation of the considered velocity estimation methods using kinematic data.
Author Contributions
Conceptualization, A.A. and G.C.; methodology, A.A. and C.G.; software, A.A. and G.C.; validation, C.G. and S.G.; formal analysis, C.G. and S.G.; investigation, A.A. and C.G.; resources, S.G.; data curation, A.A. and G.C.; writing—original draft preparation, A.A., G.C. and C.G.; writing—review and editing, A.A., G.C., C.G. and S.G.; visualization, A.A. and C.G.; supervision, S.G.; project administration, G.C. and A.A.; funding acquisition, A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The used software tools are available at https://link.springer.com/article/10.1007/s10291-014-0425-1 (accessed on 11 October 2023) and at https://geodesy.noaa.gov/gps-toolbox/ (accessed on 11 October 2023). The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kaplan, E.D.; Hegarty, C.J. Understanding GPS. Principles and Applications, 2nd ed.; Artech House: Norwood, MA, USA, 2006. [Google Scholar]
- Van Graas, F.; Soloviev, A. Precise velocity estimation using a stand-alone GPS receiver. Navigation 2004, 51, 283–292. [Google Scholar] [CrossRef]
- Teunisses, P.J.; Montenbruck, O. Springer Handbook of Global Navigation Satellite Systems; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Hill, J. The principle of a snapshot navigation solution based on Doppler shift. In Proceedings of the 14th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 2001), Salt Lake City, UT, USA, 11–14 September 2001. [Google Scholar]
- Shi, C.; Zhang, Y.; Li, Z. Revisiting Doppler positioning performance with LEO satellites. GPS Solut. 2023, 27, 126. [Google Scholar] [CrossRef]
- He, Z.; Renaudin, V.; Petovello, M.G.; Lachapelle, G. Use of high sensitivity GNSS receiver doppler measurements for indoor pedestrian dead reckoning. Sensors 2013, 13, 4303–4326. [Google Scholar] [CrossRef]
- Li, L.; Zhong, J.; Zhao, M. Doppler-aided GNSS position estimation with weighted least squares. IEEE Trans. Veh. Technol. 2011, 60, 3615–3624. [Google Scholar] [CrossRef]
- Wood, J.; Thompson, S.; Martin, S.; Bevly, D. GPS Positioning in Reduced Coverage Environments Using Batched Doppler and Pseudorange Measurements. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020. [Google Scholar]
- Zhou, Z.; Li, B. Optimal Doppler-aided smoothing strategy for GNSS navigation. GPS Solut. 2017, 21, 197–210. [Google Scholar] [CrossRef]
- Bahrami, M.; Ziebart, M. A Kalman filter-based Doppler-smoothing of code pseudoranges in GNSS-challenged environments. In Proceedings of the 24th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2011), Oregon Convention Center, Portland, OR, USA, 20–23 September 2011. [Google Scholar]
- Qi, W.; Zhang, Y.; Liu, X. A GNSS anti-spoofing technology based on Doppler shift in vehicle networking. In Proceedings of the 2016 International Wireless Communications and Mobile Computing Conference (IWCMC), Paphos, Cyprus, 5–9 September 2016. [Google Scholar]
- Parkinson, B.W.; Spilker, J.J.J. Global Positioning System: Theory and Applications; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 1996. [Google Scholar]
- Ye, S.; Yan, Y.; Chen, D. Performance analysis of velocity estimation with BDS. J. Navig. 2017, 70, 580–594. [Google Scholar] [CrossRef]
- Gioia, C.; Angrisano, A.; Gaglione, S. Galileo-Based Doppler Shifts and Time Difference Carrier Phase: A Static Case Demonstration. Sensors 2023, 23, 6828. [Google Scholar] [CrossRef]
- Freda, P.; Angrisano, A.; Gaglione, S.; Troisi, S. Time-differenced carrier phases technique for precise GNSS velocity estimation. Gps Solut. 2015, 19, 335–341. [Google Scholar] [CrossRef]
- Geosystems, L. Leica VADASE White Paper. August 2015. Available online: https://leica-geosystems.com (accessed on 12 October 2023).
- Soon, B.K.; Scheding, S.; Lee, H.-K.; Lee, H.-K.; Durrant-Whyte, H. An approach to aid INS using time-differenced GPS carrier phase (TDCP) measurements. Gps Solut. 2008, 12, 261–271. [Google Scholar] [CrossRef]
- Chen, K.; Chang, G.; Chen, C.; Zhu, T. An improved TDCP-GNSS/INS integration scheme considering small cycle slip for low-cost land vehicular applications. Meas. Sci. Technol. 2021, 32, 055006. [Google Scholar] [CrossRef]
- Ding, W.; Sun, W.; Gao, Y.; Wu, J. Carrier Phase-Based Precise Heading and Pitch Estimation Using a Low-Cost GNSS Receiver. Remote Sens. 2021, 13, 3642. [Google Scholar] [CrossRef]
- Jiménez-Martínez, M.J.; Quesada-Olmo, N.; Zancajo-Jimeno, J.J.; Mostaza-Pérez, T. Bridge Deformation Analysis Using Time-Differenced Carrier-Phase Technique. Remote Sens. 2023, 15, 1458. [Google Scholar] [CrossRef]
- Dittmann, T.; Liu, Y.; Morton, Y.; Mencin, D. Supervised Machine Learning of High Rate GNSS Velocities for Earthquake Strong Motion Signals. J. Geophys. Res. Solid Earth 2022, 127, e2022JB024854. [Google Scholar] [CrossRef]
- Robustelli, U.; Baiocchi, V.; Pugliano, G. Assessment of dual frequency GNSS observations from a Xiaomi Mi 8 Android smartphone and positioning performance analysis. Electronics 2019, 8, 91. [Google Scholar] [CrossRef]
- Robustelli, U.; Paziewski, J.; Pugliano, G. Observation Quality Assessment and Performance of GNSS Standalone Positioning with Code Pseudoranges of Dual-Frequency Android Smartphones. Sensors 2021, 21, 2125. [Google Scholar] [CrossRef]
- Siddakatte, R.; Broumandan, A.; Lachapelle, G. Performance evaluation of smartphone GNSS measurements with different antenna configurations. In Proceedings of the International Navigation Conference, Brighton, UK, 27–30 November 2017. [Google Scholar]
- Angrisano, A.; Cappello, G.; Del Pizzo, S.; Gaglione, S. Time-differenced carrier phase technique for precise velocity estimation on an android smartphone. Sensors 2022, 22, 8514. [Google Scholar] [CrossRef]
- Hartinger, H.; Brunner, F.K. Variances of GPS phase observations: The SIGMA-ɛ model. GPS Solut. 1999, 2, 35–43. [Google Scholar] [CrossRef]
- Collins, J.; Langley, R. Possible Weighting Schemes for GPS Carrier Phase Observations in the Presence of Multipath; Final contract report for the US Army Corps of Engineers Topographic Engineering Center, No. DAAH04-96-C-0086/TCN 98151; University of New Brunswick: Fredericton, NB, Canada, 1999. [Google Scholar]
- Kuusniemi, H.; Lachapelle, G.; Takala, J.H. Position and velocity reliability testing in degraded GPS signal environments. GPS Solut. 2004, 8, 226–237. [Google Scholar] [CrossRef]
- Realini, E.; Reguzzoni, M. goGPS: Open source software for enhancing the accuracy of low-cost receivers by single-frequency relative kinematic positioning. Meas. Sci. Technol. 2013, 24, 115010. [Google Scholar] [CrossRef]
- Tay, S.; Marais, J. Weighting models for GPS Pseudorange observations for land transportation in urban canyons. In Proceedings of the 6th European Workshop on GNSS Signals and Signal Processing, Munich, Germany, 5–6 December 2013. 4p. [Google Scholar]
- Li, Y.; Cai, C.; Xu, Z. A Combined Elevation Angle and C/N0 Weighting Method for GNSS PPP on Xiaomi MI8 Smartphones. Sensors 2022, 22, 2804. [Google Scholar] [CrossRef]
- Sturza, M.A. Navigation system integrity monitoring using redundant measurements. Navigation 1988, 35, 483–501. [Google Scholar] [CrossRef]
- Novatel. ProPak-G2plus—Quick Start Guide. 2020. Available online: https://hexagondownloads.blob.core.windows.net/public/Novatel/assets/Documents/Manuals/gm-14915048/gm-14915048.pdf (accessed on 11 October 2023).
- uBlox. C099-F9P Application Board (rev. E)—User Guide. 24 November 2022. Available online: https://content.u-blox.com/sites/default/files/documents/C099-F9P-AppBoard_UserGuide_UBX-18063024.pdf (accessed on 11 October 2023).
- Broadcom. BCM47755. Available online: https://www.broadcom.com/products/wireless/gnss-gps-socs/bcm47755 (accessed on 11 October 2023).
- The GPS Toolbox. Available online: https://geodesy.noaa.gov/gps-toolbox/ (accessed on 11 October 2023).
- u-Blox Achieving Centimeter Level Performance with Low Cost Antennas—White Paper. 2016. Available online: https://content.u-blox.com/sites/default/files/documents/AntennasForRTK_WhitePaper_(UBX-16010559).pdf (accessed on 22 November 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).