Abstract
Artificial immune systems (AIS), as nature-inspired algorithms, have been developed to solve various types of problems, ranging from machine learning to optimization. This paper proposes a novel hybrid model of AIS that incorporates cellular automata (CA), known as the cellular automata-based artificial immune system (CaAIS), specifically designed for dynamic optimization problems where the environment changes over time. In the proposed model, antibodies, representing nominal solutions, are distributed across a cellular grid that corresponds to the search space. These antibodies generate hyper-mutation clones at different times by interacting with neighboring cells in parallel, thereby producing different solutions. Through local interactions between neighboring cells, near-best parameters and near-optimal solutions are propagated throughout the search space. Iteratively, in each cell and in parallel, the most effective antibodies are retained as memory. In contrast, weak antibodies are removed and replaced with new antibodies until stopping criteria are met. The CaAIS combines cellular automata computational power with AIS optimization capability. To evaluate the CaAIS performance, several experiments have been conducted on the Moving Peaks Benchmark. These experiments consider different configurations such as neighborhood size and re-randomization of antibodies. The simulation results statistically demonstrate the superiority of the CaAIS over other artificial immune system algorithms in most cases, particularly in dynamic environments.
1. Introduction
Real-world optimization problems often exhibit a dynamic nature, which leads to their modeling as Dynamic Optimization Problems (DOPs). In such problems, a model’s parameters change over time due to the changing environment. Thus, finding an optimal solution is challenging because the objective function and constraints vary with time. As a result, although numerous successful optimization algorithms have been developed for static optimization problems, traditional optimization algorithms could not be effective at reaching an appropriate solution in such scenarios as they do not account for changes in real-time data. Thus, researchers tried to develop suitable algorithms to adapt to changes in dynamic environments.
Moreover, designing suitable optimization algorithms for solving real-world applications is not easy due to these environments’ limitations and constraints. To name a few applications in dynamic environments, one can mention some examples of scheduling problems. These problems are in such a way that stochastic jobs may be inserted/deleted over time. Another example is routing problems, in which routers may fail or change status (from on to off or vice versa) in the whole routing network.
Time-based pricing [1] is a common problem in financial planning. In this problem, customers are divided into multiple groups based on their demand curves, and different prices are charged to each group at different times. This approach allows businesses to optimize their revenue by charging higher prices when demand is strong and lower prices when demand is weak. In channel assignment and multicast routing in multi-channel wireless mesh networks [2], these networks require dynamically efficient multicast routing protocols to ensure data delivery to multiple receivers simultaneously while minimizing network congestion and delay. Dynamic optimization techniques can be applied to address dynamic multicast problems in mobile ad hoc networks (MANETs) [3]. These networks are characterized by their dynamic topology and mobility, which makes multicast routing protocol optimization challenging. In dynamic multicast problems, the network topology is changed frequently due to node mobility or link failures. This requires an adaptive routing protocol to ensure reliable data delivery. Dynamic optimization techniques can improve multicast routing protocols’ efficiency and adaptability in MANETs.
Dynamic optimization techniques can be applied to dynamic vehicle routing problems (VRPs) [4] to improve routing solutions’ efficiency and adaptability. In dynamic VRPs, the number and routes of vehicles change dynamically over time due to various factors such as traffic conditions, weather, and customer demands. By using dynamic optimization techniques, it is possible to achieve more efficient and cost-effective routing solutions, reduce delivery times, and improve overall customer satisfaction. Dynamic job shop scheduling [5] is a scheduling problem in which jobs are processed on different machines in a factory. The goal is to determine the optimal sequence of jobs to be processed on each machine. This is carried out while considering some factors such as machine availability, job release times, and processing times. These problems are particularly challenging because the optimal schedule may change with time due to job requirements or machine availability changes. As a result, these problems require complex algorithms that adapt to changing conditions in real time. For more applications, it can be addressed in aerospace design [6], car distribution systems [7], object detection [8] and pollution control [7], electric vehicle dispatch optimization [9], cold chain logistics scheduling [10], and railway junction rescheduling [11].
The purpose of optimization in dynamic problems has shifted from simply identifying the stationary optimal solution(s) to precisely monitoring the trajectories of the optimal solution(s) over time [12,13,14]. As a result, it is crucial to adequately tackle the extra challenges presented by this scenario to achieve promising results. Reacting to changes is critical to maintaining optimization algorithms’ performance in dynamic environments. The first step toward reacting to changes is to detect changes in the first place and then adopt a suitable strategy to deal with them. Richter [15] discussed two major change detection types: population based and sensor based. In population-based detection, statistical hypothesis testing is performed at each generation to see whether the alteration in the fitness of the individuals was not due to their convergence. In sensor-based detection, some measurements (so-called “fitness landscape sensors”) are placed either randomly or regularly into the landscape. At every generation, the environment changes if any of the sensors detect an altered fitness value. Evolutionary algorithms (EAs) for addressing diverse applications characterized by dynamic behavior have received significant attention in recent years [3]. Conventional population-based algorithms can successfully solve static optimization problems but may fail in dynamic environments since they cannot recognize environmental changes. Different methods have been suggested to detect changes in the dynamic environment. Also, there is no prior knowledge or standard criteria for dealing with changing environments. A simple method can reset the optimization algorithm after detecting any environmental change, which can often be performed correctly [16]. Before reaching optimal regions, another change may occur through the evolution of an optimization algorithm. It is also possible to track the peaks around the optimal instead of locating the optimal using DOP algorithms as an alternative solution. Several techniques and improvements based on the characteristics of each EA are suggested for dynamic optimization [17,18,19], among which, the main approaches dealing with the dynamic environment can be categorized into several groups, including: (1) increasing diversity methods [13], (2) diversity maintenance methods [20], (3) memory-based methods [21], (4) predicting the next optimum solution, (5) self-adaptive mechanisms, (6) multi-population methods [22], and (7) hybridization of the methods [23,24]. This study uses diversity control with parameter adaptation by CAs for the distribution of parameters among the CA cells and their interaction.
A cellular automaton (CA) comprises numerous cells, each possessing a state that evolves through a set of feasible states according to a local rule. CA is especially appropriate for simulating natural systems that can be characterized as a vast collection of essential components interacting locally with one another. The cellular automata-based artificial immune system (CaAIS) proposed in this paper can be viewed as a stochastic cellular automaton [25], where the size of the state set corresponds to the number of points in the search space, and the cells update their states repeatedly until an appropriate predetermined criterion is met.
This paper presents a novel hybrid model of AIS using the cellular automata called cellular automata based on artificial immune system (CaAIS) for dynamic environments. Antibodies are distributed throughout a cellular grid of search space in the proposed model as nominal solutions. They are responsible for different solutions at different times. Based on the local interactions between cells and their local rules, the appropriate parameters and optimal solutions of cells are spread in the cell space. Due to CA properties, the CaAIS inherits the computational power of cellular automata [26] and AIS optimization capability.
In summary, our main contributions are highlighted as follows:
- We proposed a hybrid model of AIS and CA called cellular automata based on the artificial immune system (CaAIS) for dynamic environments.
- We proposed the CA local interactions in the CaAIS to adapt the parameters and increase diversity.
- As the environment changes, we propose a replacement mechanism that incorporates the near-best parameter of the cells and spreads to their neighbors.
The remainder of the paper is structured as follows: Section 2 provides an overview of related work on several studies on dynamic optimization problems. Section 3 introduces cellular automata in brief. The simple artificial immune algorithm is described in Section 4. The proposed algorithm (CaAIS) is described in detail in Section 5. Section 6 reports on the experimental results conducted on MPB and compares the CaAIS results with those of state-of-the-art and selected algorithms. Finally, Section 7 concludes this paper.
2. Related Work
In the literature, there are several studies on dynamic optimization problems. For example, Jin and Branke [27] tackled and deliberated on different forms of uncertainty in evolutionary optimization. Cruz et al. [16] have furthered the progress of the domain by achieving a dual objective, thereby enhancing its significance: (1) Their accomplishment involved the establishment of a vast collection of pertinent references on the subject matter from the previous ten years, which they then classified according to various criteria, including publication type, type of dynamism, dynamic optimization problem-solving approaches, performance metrics, applications, and year of publication. (2) Afterward, they conducted a comprehensive review of the research conducted on dynamic optimization problems using the compiled collection. Nguyen et al. [28] conducted a comprehensive investigation into the field of evolutionary optimization in dynamic environments, presenting an in-depth survey of the field. This research analyzed the latest advancements in the academic literature from four distinct perspectives, namely: (a) benchmark problems, (b) performance metrics, (c) methodologies, and (d) theories. Although their work is very valuable in studying and summarizing different methods for solving MPB, it does not provide categorical information on how different methods work and which mechanisms can improve the performance of different methods. In addition, it does not explain the reasons for specific approaches’ superiority.
Yazdani et al. [29,30], in two parts of survey papers, presented a review of research studies regarding DOPs. Since an efficient dynamic optimization algorithm consists of several parts to cope with dynamic optimization problems, they tried to provide a comprehensive taxonomy to identify the parts of dynamic optimization algorithms. In the second part of this survey, they gave an overview of dynamic optimization problem benchmarks and performance measures. Moser et al. provide another study [31]. In this work, the authors surveyed the existing techniques in the literature for addressing MPB. They categorize the diverse methods into four groups: swarm intelligence algorithms, evolutionary algorithms, hybrid approaches, and other approaches.
In [22], Balckwell et al. introduced the concept of multi-swarms, which involves partitioning the population of particles into multiple subgroups, each with its own information sharing and exploration strategies. The researchers propose using an adaptive partitioning technique that dynamically adjusts the number and size of multi-swarms based on the characteristics of the problem and the environment. Then, they introduced the concept of exclusion, which allows individual particles to temporarily avoid regions of the search space that are not beneficial. By excluding certain areas, particles can avoid premature convergence and explore other areas of the search space. Additionally, the authors addressed the issue of anti-convergence, which occurs when all particles converge to a suboptimal solution. To mitigate this problem, the authors propose a re-initialization mechanism, which randomly disperses particles in the search space to encourage exploration.
In [32], Li et al. focused on improving particle swarm optimization (PSO) algorithms in dynamic environments by incorporating both speciation and adaptation mechanisms. Speciation is a process inspired by biological evolution, where particles are divided into different sub-populations or species based on their similarities. This helps maintain diversity and exploration, even in changing or dynamic environments. Adaptation, on the other hand, enables particles to adjust their behavior and parameters in response to environment changes. It allows particles to quickly react and update their positions and velocities to find better solutions. Nasiri et al. [33] proposed the integration of speciation, a concept from evolutionary biology, into the firefly algorithm. This is a widely used optimization algorithm inspired by fireflies’ behavior. The algorithm partitions the population into different species based on their similar solutions. Fireflies within the same species closely cooperate and share information, while fireflies belonging to different species compete for resources. This division allows for both exploration and exploitation of the search space, improving the algorithm’s ability to adapt to changing environments.
The authors in [34] focused on studying the effectiveness of a multi-population heuristic approach to solving non-stationary optimization tasks. The authors emphasize that real-world optimization problems often have non-stationary characteristics, meaning that the problem landscape changes over time. Thus, they introduced a multi-population heuristic approach, which involves multiple populations working in parallel. Each population adapts and evolves independently, making the approach suitable for solving non-stationary problems where the landscape changes unpredictably.
An appropriate candidate for a nature-inspired algorithm dealing with the changing environment components is an artificial immune system (AIS). An AIS [35] is an adaptive system inspired by vertebrate immune processes developed by researchers to solve complex real-world problems [36]. In this regard, some achievements have been made in AISs dealing with DOPs. Franca et al. have proposed modifications to the artificial immune network (AIN) algorithm for dynamic environments [37]. They utilize particular sub-populations for memory, linear search for parameter control, and novel operators for mutation in AIN. The multi-population strategy of the artificial immune algorithm in a dynamic environment has been suggested by Xhua et al., which obtained relatively successful results [38]. In [39], the authors focused on the improvement of adaptation in optimization problems subject to time-dependent changes. The authors propose a hybrid approach that combines genetic algorithms (GAs) and artificial immune systems (AIS) to enhance optimization. The proposed hybrid approach incorporates a multi-objective optimization framework, which combines exploration and exploitation objectives with AIS components. Specifically, the authors introduce an immune-inspired strategy for maintaining a diverse population of solutions and adaptively reacting to changes in the optimization landscape. The AIS components act as an additional mechanism for preserving diversity, increasing adaptability, and improving the algorithm’s convergence rate.
Kelsey et al. [40] proposed a novel optimization technique called Immune-inspired Somatic Contiguous Hypermutation (ISCH). This technique is inspired by the immune system’s somatic hypermutation process, which generates diverse antibodies to combat various pathogens. ISCH involves the creation of a population of candidate solutions, represented as individuals or antibodies. Each candidate solution corresponds to a specific state within the search space. The somatic contiguous hypermutation operator is then applied to these individuals to generate mutated offspring. Unlike traditional mutation operators, the contiguous hypermutation in ISCH selectively mutates contiguous regions within the candidate solutions. This approach allows for more focused exploration of the search space, potentially yielding better solutions in less time. In [41], De Castro et al. discussed the clonal selection algorithm (CSA) and its various applications in engineering. CSA is a computational optimization technique inspired by the immune system’s clonal selection process. This algorithm mimics the immune system’s ability to generate antibodies to combat infections, and it has been successfully applied to a wide range of engineering problems.
A comprehensive review and performance evaluation of some different mutation behaviors for the clonal selection algorithm, artificial immune network, and B-cell algorithm is reported in dynamic environments [42] by Trojanowski et al. There are some desirable results in a dynamic environment for adaptive operators using learning automata to increase diversity. This is developed for the immune algorithm immune network [13]. The dynamic T-cell algorithm, a novel immune algorithm inspired by the T-cell model, was developed for DOP based on four populations [43]. Another multi-population-based algorithm was introduced as an artificial immune algorithm for the dynamic environment based on the principle of biological immune response [44]. Nabizedeh et al. utilized a clonal selection algorithm as a local search for a search around the optima [45]. An adaptive version of the immune system algorithm utilizing learning automata is presented in [46], in which the hypermutation parameter is adjusted using learning automata as a successful reinforcement learning approach.
However, nature-inspired methods for dynamic optimization problems have certain limitations. One limitation is the exploration–exploitation trade-off. These algorithms may struggle to balance between exploring new regions of the search space to find better solutions and exploiting the current best solutions. In dynamic environments, where the optimal solution may change over time, this trade-off becomes even more challenging. Additionally, these methods may suffer from premature convergence, where they converge to suboptimal solutions too quickly and fail to adapt to changing environments. The lack of effective mechanisms to handle dynamic changes in the search space is another limitation, as these algorithms may struggle to quickly adapt and track the changing optimal solution. Overall, while nature-inspired methods have shown promise in solving optimization problems, their limitations in dynamic environments call for further research and development.
3. Cellular Automata
Cellular automata [47] is a dynamical system with discrete space and time. The CA is a mathematical model with an array of cells with local interactions for investigating sophisticated, complex phenomena. Each cell’s behavior is determined based on its neighbor’s behavior. CA is a decentralized, discrete, self-organized, and parallel system that enables one to create an ordered structure by starting from a random state. It is shown that the property of CA by applying a CA to a set of structures could not affect the set entropy. In this model, space is specified by a regular grid of cells, each representing a memory of states. In each step, the cell considers neighboring cells, and based on the communication rules, the next state is specified. In addition, each cell can work independently of the other cells.
Cellular automata consider different neighborhood configurations. Each set of cells is considered to be neighbors in a specific order. The two most well-known neighborhoods are the Von Neumann and Moore neighborhoods. The Von Neumann neighborhood includes four adjacent cells not diagonal to the central cell, while the Moore neighborhood includes all eight surrounding cells. Each cell in the Von Neumann neighborhood has an equal distance from the central cell. This model takes into account a wider range of neighboring cells, allowing for more complex interactions and patterns within the cellular automaton. These neighborhoods are commonly called the nearest neighbors and are illustrated in Figure 1 [48]. For the CaAIS, the Von Neumann model may be more suitable for scenarios where a more localized and restricted antibody spread is desired. In contrast, the Moore model allows for a more extensive spread of antibodies across cells.
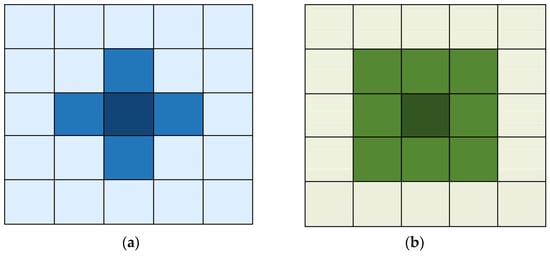
Figure 1.
The typical neighborhood model in a 2-D CA; (a) Von Neumann, (b) Moore.
The CaAIS is not the first evolutionary algorithm to use CA. In [49], CGA is a cellular evolutionary algorithm that utilizes a decentralized population approach. In this method, tentative solutions are introduced in overlapping neighborhoods. The hybrid CA with particle swarm optimization (PSO), called CPSO, is presented in a study to optimize functions [50]. The CPSO algorithm incorporates a CA mechanism into the velocity update process to modify particle trajectories. The CaAIS is similar to CGA and CPSO in that it is parameter dependent and hybridizes with CA. However, the CaAIS differs from CGA and CPSO models in several aspects. 1: The main evolutionary algorithm is based on AIS. 2: Unlike CGA, the CaAIS model does not use crossover and mutation operators. Based on the AIS algorithm, the CaAIS uses only hypermutation operators. 3: Unlike CGA, in the CaAIS, each antibody interacts only with its pre-defined neighboring antibodies. 4: the CaAIS focuses on optimization for dynamic environments.
Several hybridizations of CA and evolutionary algorithms are also reported in the literature, including CLA-EC [51], Cellular PSO [52,53], Cellular DE [19,54], CLA-DE [55], and Cellular fish swarm [56]. This paper proposes a hybrid model using cellular automata and an artificial immune system for optimization in dynamic optimization.
4. Artificial Immune Algorithm
An artificial immune system [35] is a branch of computational intelligence that draws inspiration from the natural immune system. It offers various algorithms for solving complex real-world problems [36]. Several applications of AIS algorithms have been reported by researchers, such as optimization [13], power systems [57], scheduling [58], pattern recognition, bioinformatics [59], data mining [60], psychometric technology [61], sensor networks [62], intrusion detection [63], mobile robot control [64], and clinical diagnostics [65]. Taking inspiration from human immune systems, many AIS algorithms are generated. These algorithms include negative selection algorithms (NCA), clonal selection algorithms (CLONALG), bone marrow, artificial immune networks (AINE), toll-like receptors (TLR), danger theory, and dendritic cell algorithms (DCA) [36,60].
The immune network theory was presented by Jerne [66], while the artificial immune network (AIN) algorithm was developed for multi-model optimization by de Castro and Timmis [67]. This algorithm considers the immune cell as a population and its representation as a real value vector with Euclidian distance. One of the main properties of this algorithm is affinity maturation after random initialization, after which cells suffer mutation based on the affinity of cells to produce colonies according to Equation (1)
where is the mutated cell, is a control parameter for the normalization of fitness value , and specifies a Gaussian distribution by mean and variance 0 and 1, respectively. After the mutation of the clones, cells with maximum fitness values were retained, and cells with fitness values smaller than others were replaced with random cells [37]. Indeed, the AIN algorithm aims to attain a set of representations with the least redundancy. Although the AIN algorithm looks like a clonal selection algorithm, the main difference is attributed to the suppression mechanism for cell interaction. This eliminates certain sets of cells with less fitness than others. Algorithm 1 presents the artificial immune network algorithm pseudo-code [68].
| Algorithm 1. Artificial immune network algorithm |
| 1. Initialize the population as antibodies, and is a control parameter. 2. Repeat for each . 3. Evaluate . 4. Select the best . 5. Clone and mutate . 6. Retain the highest as memories. 7. Remove weak memories. 8. Replace random . 9. Until the termination condition is met |
5. Proposed Model: Cellular Automata-Based on Artificial Immune System (CaAIS)
Parameters in the AIS algorithm play a critical role due to several parameters, such as hypermutation. These parameters affect the AIS algorithm’s performance [35]. On the other hand, there are local interactions between s in the immune system. Thus, in the proposed algorithm, a CA is used for enhancing the parameter adaptations of the algorithm. Each CA cell consists of antibodies denoted by , and their parameters, such as , are control parameters. This concept preserves diversity in the search space through CA local interaction. A general representation of the proposed model for CA deployment in a Von Neumann model is depicted in Figure 2.
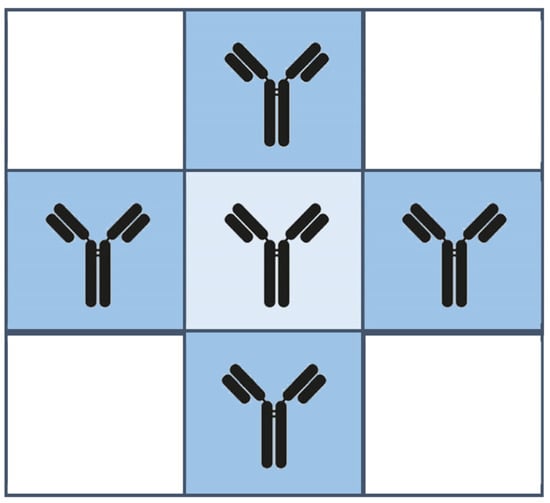
Figure 2.
Deployment of schematic antibodies in a 2D cell space as Von Neumann model.
After initialization, the proposed algorithm iterates in parallel for each cell. Each step is described in the following subsections. The pseudo-code of the proposed algorithm, the CaAIS, is presented in Algorithm 2.
| Algorithm 2. Cellular automata-based artificial immune system (CaAIS) |
| 1. (Initialization): Generate randomly the initial population and initialize the parameters in each cell 2. Repeat for each cell in parallel 3. Evaluate the population 4. (Change Environment) If changing the environment is detected, do the following operations on each 5. (Replacement) Replace a set of s with the best of neighboring cells according to Equation (3), and the remainder set reinitializes the parameters randomly. 6. Generate clones and then perform Hypermutation clones with equal probability to each clone according to the neighboring cells based on Equation (4). 7. Evaluate the fitness of every mutated clone, and select the best s using Equation (3) as a member of the new generation and remove the others. 8. (CA Local interaction) Interact between cells and run local rules transition in each cell for parameter selection value according to Equation (5). 9. Retain the best as memory. 10. Remove a set of weak and replace it with new randomly. 11. Until (Stopping criteria) are met |
The description of each step of the CaAIS is given as follows.
5.1. Initialization
The initial population was randomly generated using random distribution in the corresponding range in each cell as follows
where is a random number distributed in , , are the lower and upper bound of the real variable for cell , respectively. Additionally, in this step, the maximum iteration, mutation probability Pm, and other parameters, such as the control parameter β, are set.
5.2. Change the Environment
In the proposed algorithm, a change in environments is detected by re-evaluating the as the best in the population. So, a change is detected if the fitness value of the has been changed since its last fitness evaluation. By detecting a change in the environment, the fitness value of each also should be re-evaluated. A local search is performed around each individual as well. According to the proposed method, a local search is applied simply by interacting with neighbors. This idea helps to track the previous best search attempts to find the new optimal position quickly.
5.3. Replacement
In a time of changing environment, a set of antibodies in each cell is replaced by the best neighbor. Other antibodies are reinitialized based on the last good neighbor in the memory as for cell , and the remaining are randomly initialized. Indeed, it provides a global search by random search and local search by replacing the cells and spreading in the neighbors. The replacement of antibodies is carried out using Equation (3).
where is the antibody in the central cell, returns the set of neighboring cells for in the central cell. Moreover, the best of each cell as memory is considered as .
5.4. Hypermutation
Since cloning and hypermutation are the main operators of AIS, they are performed on the population according to their fitness values. In this step, the with a higher fitness value suffers more clones because the better s are closer to optimal. Then, hypermutation is applied as in Equation (4).
where is a control parameter for the normalization of fitness value for in cell , specifies a Gaussian distribution by mean and variance 0 and 1, respectively.
5.5. CA Local Interactions
In the proposed algorithm, the is an -dimensional real vector, where is the number of the dimensions of search space. In this discipline, the parameter of is adjusted via local interaction between s in the CA in a parallel manner. The relation between s in a local grid in the Moore model is schematically presented in Figure 3.
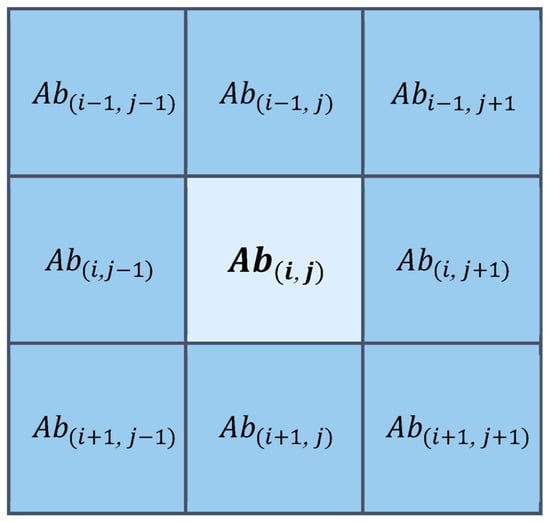
Figure 3.
Representation of deployment of antibodies in Moore model of CA.
In the case of a dynamic environment, the parameters of AIS become different with changing environments adaptively, and the diversity of population increases during the time based on CA. In this method, antibodies are distributed in the grid of cells so that each cell can access its neighboring information by interaction among the cells.
Since the immune algorithm’s performance depends on mutation, values of as the control parameter are chosen adaptively through the algorithm evolution. The first initialization of this parameter is randomly selected since there is no prior knowledge of the environment. When the algorithm proceeds, the value of is updated based on the received feedback from the environment. While all antibodies in each cell are evaluated, information interactions between neighboring cells are performed, and the central cell for each window determines the best value of using Equation (5),
where and are the control parameters of mutated antibodies in the central cell and the control parameters of antibodies in neighboring cells, respectively.
The information interactions and the spread of parameters among cells in the 2D model through the algorithm’s evolution schematically are shown in Figure 4.
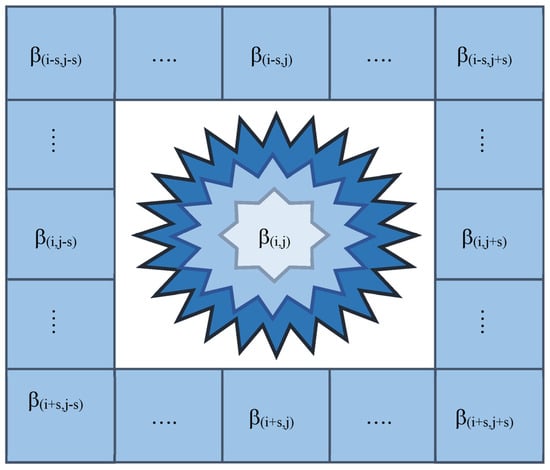
Figure 4.
The representation of the local information interaction and its spread of parameters (i.e., control parameter ) among cells for the 2D model of Moore with s distance from the central cell.
5.6. Stopping Criteria
The process of evaluating the population, detecting the change in environment and re-initialization and replacement, generating clones and hypermutation clones, evaluating the mutated clones, performing CA local interaction, retaining the best s, and removing the set of weak s is repeated until the stopping criteria are met. The proposed algorithm stops when the maximum number of iterations is met.
6. Experimental Study
First, this section introduces (1) the performance measure, (2) MPB as a popular dynamic environment benchmark [67], and (3) an experimental setup that allows the CaAIS to be evaluated. Then, the CaAIS experimental results compared to some well-known algorithms are reported in Section 5.3.
6.1. Performance Measure
Offline error (OE) has been used to evaluate the CaAIS, a popular measure in the literature for dynamic optimization. The average of the best value rather than the last change from optima is indicated in OE, which is defined by Equation (6):
where is the fitness evaluation of a changing environment, is the fitness evaluation for the jth time of environment, specifies the best value of the jth state (between and ), and is the best current fitness value found up to now [16].
6.2. Dynamic Environment
Due to the dynamic nature of many real-world problems and the continuously changing environment, MPB, as a well-known dynamic environment, was developed as a means of algorithm evaluation [69]. MPBs are being presented in the n-dimensional environment with pre-defined peaks in (location), (height), (weight). The peak functions are defined below as Equation (7), and the highest value obtained over all of them specifies the fitness landscape.
where is the coordination related to the location, is the width of the th peak, is the height of th peak, all in time . A uniform distribution is used to generate the height randomly () in the range and width () in the range of each peak.
The width and height are changed, respectively, as Equations (8) and (9)
where is a random number from a Gaussian distribution with a mean of 0 and variance of 1. The position of each peak is updated by vector and it is formulated as follows:
where is defined as Equation (11)
where as the shift vector is a linear combination of a random vector and the previous shift vector and is normalized by the length factor . The severity of change is determined by parameter , while the correlation between each peak’s changes and the previous one is specified by . (i.e., specifies the change of peak is uncorrelated).
An example of the landscape generated by the MPB is illustrated in Figure 5. The peaks are distributed throughout the whole environment, while the peaks’ location, weight, and height change over time.
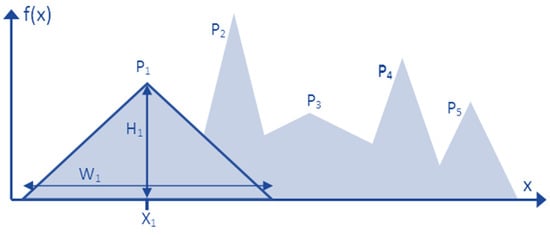
Figure 5.
An example of a landscape generated by the MPB.
The default settings of MPB [70] to facilitate comparison with alternative algorithms are given in Table 1.

Table 1.
The default settings of MPB for experimentation.
6.3. Experiments
In this section, the CaAIS performance is studied in numerous experiments and compared with alternative algorithms reported in the literature. For each experiment, an average offline error over 30 independent runs with a 95% confidence level is presented. Moreover, each experiment contains its assumptions. Two groups of experiments are designed in this section. The first group considered various configurations of the proposed algorithm, and the other experiments employed comparisons with other algorithms with varying MPB scenarios.
6.3.1. Effect of Various Numbers of Initial Antibodies
A first set of experiments is conducted by OE to examine the effect of the initial antibody size (initial population) on the MPB. Although the diversity values of antibody quantities can be considered for initialization, the population of AIS is increasing dynamically, so using multiple values would not be reasonable. Hence, 2–10, 20, and 50 antibodies are selected for initialization in this experiment. The effects of the number of initial antibodies in the proposed algorithm are depicted in Figure 6.
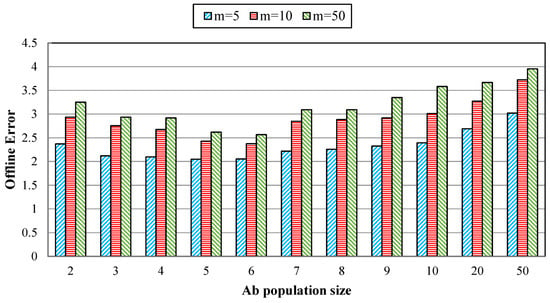
Figure 6.
Offline error for various numbers of initial population size.
As evident from Figure 6, OE has been decreased by raising the initial population to 5–6, and it shows relative improvement. Although it has been further increased, the result has been inversed, and the OE value has increased. By increasing the number of antibodies, it seems that more populations will cooperate to interact with each other and share the optimization solutions. In contrast, for the population increased to more than six, the results are not promising. According to these results of OE for the populations of five to six and with a shorter run time, the initial size of the population is set to five antibodies for the rest of the experiments.
6.3.2. Effect of Varying the Number of Neighborhood Sizes
Other experiments investigated the effects of several neighbor cells in CA. This experiment avoids large neighborhood structures to avoid additional computational challenges and a long run time. Therefore, the numbers of neighbor cells are studied from one to five for the effects of cell neighborhood sizes. The effects of the different cell neighborhood sizes are summarized in Figure 7.
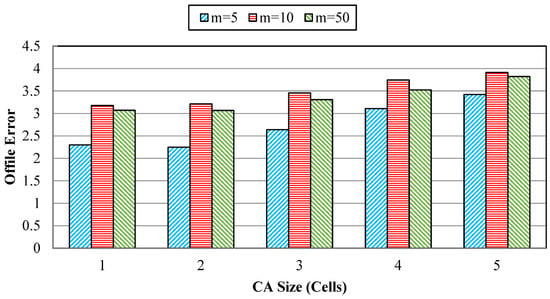
Figure 7.
Effect of varying cell neighborhood sizes.
According to Figure 7, it can be observed that the cell neighborhood size has been increased until size two has relatively improved. However, no more than three to five values will be enhanced, and OE will be increased. Indeed, increasing the cell neighborhood size causes more complexity, and the advantage of local search deteriorates during the changing environment.
6.3.3. Effect of Varying the Re-Randomization of Antibodies
One reaction mechanism for changing the environment is re-randomizing a set of populations. The effects of varying the re-randomization of a set between 10 and 100% of the total population for the proposed algorithm can be seen in Figure 8. As reflected in Figure 8, the rate of re-randomization value replacement of the population has promising results between 30 and 60% of the population. It implies that a lower or higher rate of re-randomization would not be efficient. Smaller rates of replacement value (fewer than 30%) cause negligible effects on enhancing the results. It may due to a lack of diversity in the search space. In comparison, greater replacement values (over 60%) cause significant randomization, and the algorithm can not find a suitable solution, because it may be a candidate solution far from the optimal peaks. Therefore, due to the received proper results for the mid-range of the re-randomization rate, in the rest of the experiments, the rate of re-randomization is set to 50–60 percent of the population.
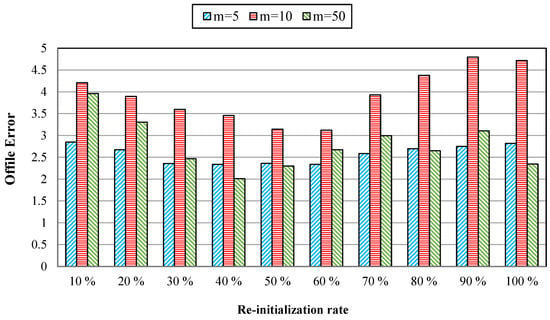
Figure 8.
Comparison of different re-randomization for the CaAIS from 10 to 100%.
6.3.4. Comparison of the CaAIS with Peer Immune Algorithms
In this experiment, the performance of the CaAIS is compared with several algorithms, including the simple artificial immune system (SAIS) [39], artificial iterated immune algorithm (AIIA) [34], B-cell algorithm (BCA) [40], clonal selection algorithm (CLONALG) [41], artificial immune network (opt-aiNet) [67], learning automata-based immune algorithm (LAIA) [46], and the cellular PSO based on clonal selection algorithm (CPSOC) [45]. A statistical test is also applied to validate the significance of the results. The statistical test results of comparing algorithms by one-tailed t-test with 28 degrees of freedom at a 0.05 level of significance are reported in Table 2. Table 2 consists of two main columns for 5 peaks and 50 peaks as different environments. For each environment, the offline error and standard errors are given along with the results of the statistical significance test. The t-test result regarding the CaAIS with each alternative algorithm is shown as “+”, “−”, and “~” when the CaAIS is significantly better than, significantly worse than, and statistically equivalent to the alternative algorithm, respectively. According to Table 2, the results of the proposed method are statistically equivalent to those of BCA. They show better results than other general relativity algorithms. This is due to the cellular structure and immune properties that provide an adaptive balance between local and global search in changing environments.

Table 2.
Comparison of OE ± standard error for the CaAIS versus other AIS algorithms with t-test results.
6.3.5. Effect of Various Severities of Shift
This experiment examines the effect of different values on shift severity. For comparison, it utilizes other methods, such as multi-swarm optimization methods [22], including mPSO, mCPSO, mQPSO [22], PSO with speciation (SPSO) [32], and SFA [33]. Figure 9 shows the average offline error for different algorithms. As seen in Figure 9, an increase in shift length leads to a corresponding increase in offline error across all algorithms. It means that longer shift lengths pose challenges for the environment and thus algorithms with less steep curves are preferred. Amongst these algorithms, the proposed algorithm outperforms other algorithms such as mQSO, mPSO, mCPSO, and SPSO, but not SFA due to its unique algorithm properties. It should be noted that all other methods are based on particle swarm optimization.
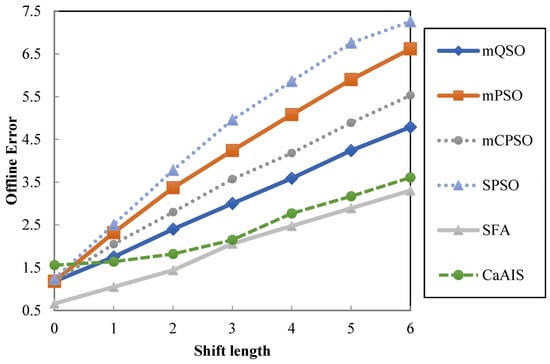
Figure 9.
OE for different values of severity shift.
6.3.6. Effect of Various Numbers of Peaks
In an environment with moving peaks, the number of peaks is essential in determining the results. The numbers of different peaks indicate the algorithm’s scalability in various states. This experiment is designed to examine the performance of the proposed algorithm when several peaks change. According to Table 1, the number of peaks changed within the range from 1 to 200. In this experiment, the proposed algorithm the CaAIS is compared with well-known algorithms such as multi-swarm optimization in two states, mCPSO and mQPSO [22], PSO with speciation (SPSO) [32], cellular differential evolution (CLDE) [54], fast multi-swarm optimization (FMSO) [71], dynamic population differential evolution (DynPopDE) [72], speciation-based firefly algorithm (SFA) [33], particle swarm optimization with composite (PSO-CP) [73], learning automata-based immune algorithm (LAIA) [46], cellular PSO (CLPSO) [53], multi-swarm cellular PSO with local search (CPSOL) [74], and multi-population differential evolution (DE) algorithm with learning automata (Dyn-DE+LA) [75]. The effect of the varying number of peaks is listed in Table 3. It should be noted that the results of the compared algorithms are the same as those of their papers; therefore, in some cases, the results are not presented. According to Table 3, the CaAIS outperforms peer algorithms for 40 and 100 peaks, but for different numbers of peaks, another algorithm may have been the best. Table 3 shows that the CaAIS delivers marginally superior results for different numbers of peaks. The CaAIS produces better results as the number of peaks rises.

Table 3.
Comparing offline error and standard error for varying numbers of peaks.
7. Conclusions
This paper presents a hybrid method using cellular automata and an artificial immune system. Unlike conventional AIS algorithms for dynamic environments, antibodies are distributed through a grid of cells in the proposed algorithm. They try to find environmental peaks by local interaction with antibodies in neighbor cells. The information interaction is implemented in two ways: one, the best value of control parameters and memory in neighbor cells totally after the evaluation of antibodies is replaced in the central cell; and later, during the changing environment, a set of the population is replaced with neighbors’ antibodies. The proposed methods are enforced by both local and global search due to the characteristics of AIS and CA. The results of experiments on the proposed algorithm on MPB compared with well-known algorithms reveal relative improvements in dynamic environments. The simulation results show the superiority of the CaAIS statistically in comparison with peer artificial immune system algorithms in most cases in dynamic environments. To address the potential applications of the CaAIS to real-world dynamic optimization problems, one can optimize the allocation of resources in dynamic environments, such as transportation logistics or energy management systems, or optimize investment portfolios by adapting to changing market conditions and adjusting asset allocations accordingly, to name a few. Finally, for future research directions, techniques should be developed to improve the algorithm’s ability to adapt to rapidly changing environments and handle complex dynamic scenarios. In addition, strategies should be developed to enhance the scalability of the algorithm, particularly for large-scale dynamic optimization problems to be considered.
Author Contributions
Conceptualization, A.R.; methodology, A.R.; software, A.R.; validation, A.R. and S.M.V.; formal analysis, A.R. and S.M.V.; investigation, A.R. and S.M.V.; resources, A.R., S.M.V. and A.M.S.; data curation, A.R., S.M.V. and A.M.S.; writing—original draft preparation, A.R.; writing—review and editing, A.R., S.M.V. and A.M.S.; visualization, A.R., S.M.V. and A.M.S.; supervision, A.R.; project administration, A.R., S.M.V. and A.M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kim, S.-K.; Kim, J.-Y.; Cho, K.-H.; Byeon, G. Optimal Operation Control for Multiple BESSs of a Large-Scale Customer under Time-Based Pricing. IEEE Trans. Power Syst. 2017, 33, 803–816. [Google Scholar] [CrossRef]
- Cheng, H.; Yang, S. Joint QoS Multicast Routing and Channel Assignment in Multiradio Multichannel Wireless Mesh Networks Using Intelligent Computational Methods. Appl. Soft Comput. 2011, 11, 1953–1964. [Google Scholar] [CrossRef][Green Version]
- Cheng, H.; Yang, S. Genetic Algorithms with Immigrants Schemes for Dynamic Multicast Problems in Mobile Ad Hoc Networks. Eng. Appl. Artif. Intel. 2010, 23, 806–819. [Google Scholar] [CrossRef]
- Khouadjia, M.R.; Sarasola, B.; Alba, E.; Jourdan, L.; Talbi, E.G. A Comparative Study between Dynamic Adapted PSO and VNS for the Vehicle Routing Problem with Dynamic Requests. Appl. Soft Comput. 2012, 12, 1426–1439. [Google Scholar] [CrossRef]
- Adibi, M.A.; Zandieh, M.; Amiri, M. Multi-Objective Scheduling of Dynamic Job Shop Using Variable Neighborhood Search. Expert Syst. Appl. 2010, 37, 282–287. [Google Scholar] [CrossRef]
- Mack, Y.; Goel, T.; Shyy, W.; Haftka, R. Surrogate Model-Based Optimization Framework: A Case Study in Aerospace Design. In Evolutionary Computation in Dynamic and Uncertain Environments; Yang, S., Ed.; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2007; Volume 51, pp. 323–342. [Google Scholar]
- Michalewicz, Z.; Schmidt, M.; Michalewicz, M.; Chiriac, C.; Yang, S. Adaptive Business Intelligence: Three Case Studies. In Evolutionary Computation in Dynamic and Uncertain Environments; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2007; Volume 51, pp. 179–196. [Google Scholar]
- Hossain, M.; Dewan, M.; Chae, O. A Flexible Edge Matching Technique for Object Detection in Dynamic Environment. Int. J. Appl. Intell. 2012, 36, 638–648. [Google Scholar] [CrossRef]
- Shi, L.; Zhan, Z.-H.; Liang, D.; Zhang, J. Memory-Based Ant Colony System Approach for Multi-Source Data Associated Dynamic Electric Vehicle Dispatch Optimization. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17491–17505. [Google Scholar] [CrossRef]
- Wu, L.-J.; Shi, L.; Zhan, Z.-H.; Lai, K.-K.; Zhang, J. A Buffer-Based Ant Colony System Approach for Dynamic Cold Chain Logistics Scheduling. IEEE Trans. Emerg. Top. Comput. Intell. 2022, 6, 1438–1452. [Google Scholar] [CrossRef]
- Eaton, J.; Yang, S.; Mavrovouniotis, M. Ant Colony Optimization with Immigrants Schemes for the Dynamic Railway Junction Rescheduling Problem with Multiple Delays. Soft Comput. 2016, 20, 2951–2966. [Google Scholar] [CrossRef]
- Kordestani, J.K.; Rezvanian, A.; Meybodi, M.R. An Efficient Oscillating Inertia Weight of Particle Swarm Optimisation for Tracking Optima in Dynamic Environments. J. Exp. Theor. Artif. Intell. 2015; in press. [Google Scholar] [CrossRef]
- Kordestani, J.K.; Mirsaleh, M.R.; Rezvanian, A.; Meybodi, M.R. Advances in Learning Automata and Intelligent Optimization; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Kordestani, J.K.; Rezvanian, A.; Meybodi, M.R. CDEPSO: A Bi-Population Hybrid Approach for Dynamic Optimization Problems. Appl. Intell. 2014, 40, 682–694. [Google Scholar] [CrossRef]
- Richter, H. Detecting Change in Dynamic Fitness Landscapes. In Proceedings of the IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009; pp. 1613–1620. [Google Scholar]
- Cruz, C.; González, J.R.; Pelta, D.A. Optimization in Dynamic Environments: A Survey on Problems, Methods and Measures. Soft Comput. 2010, 15, 1427–1448. [Google Scholar] [CrossRef]
- Nickabadi, A.; Ebadzadeh, M.; Safabakhsh, R. A Competitive Clustering Particle Swarm Optimizer for Dynamic Optimization Problems. Swarm Intell. 2012, 6, 177–206. [Google Scholar] [CrossRef]
- Ayvaz, D.; Topcuoglu, H.R.; Gurgen, F. Performance Evaluation of Evolutionary Heuristics in Dynamic Environments. Int. J. Appl. Intell. 2012, 37, 130–144. [Google Scholar] [CrossRef]
- Noroozi, V.; Hashemi, A.B.; Meybodi, M.R. Alpinist CellularDE: A Cellular Based Optimization Algorithm for Dynamic Environments. In Proceedings of the Fourteenth International Conference on Genetic and Evolutionary Computation Conference Companion (GECCO 2012), Philadelphia, PA, USA, 7–11 July 2012; ACM: New York, NY, USA, 2012; pp. 1519–1520. [Google Scholar]
- Yang, S. Genetic Algorithms with Memory-and Elitism-Based Immigrants in Dynamic Environments. Evol. Comput. 2008, 16, 385–416. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Cheng, H.; Wang, F. Genetic Algorithms With Immigrants and Memory Schemes for Dynamic Shortest Path Routing Problems in Mobile Ad Hoc Networks. IEEE Trans. Syst. Man. Cybern Part. C Appl. Rev. 2010, 40, 52–63. [Google Scholar] [CrossRef]
- Blackwell, T.; Branke, J. Multiswarms, Exclusion, and Anti-Convergence in Dynamic Environments. IEEE Trans. Evol. Comput. 2006, 10, 459–472. [Google Scholar] [CrossRef]
- González, J.R.; Masegosa, A.D.; García, I.J. A Cooperative Strategy for Solving Dynamic Optimization Problems. Memetic Comput. 2011, 3, 3–14. [Google Scholar] [CrossRef]
- Yu, X.; Tang, K.; Chen, T.; Yao, X. Empirical Analysis of Evolutionary Algorithms with Immigrants Schemes for Dynamic Optimization. Memetic Comput. 2009, 1, 3–24. [Google Scholar] [CrossRef]
- Giacobini, M.; Alba, E.; Tomassini, M. Selection Intensity in Asynchronous Cellular Evolutionary Algorithms. In Proceedings of the Genetic and Evolutionary Computation—GECCO 2003, Chicago, IL, USA, 12–16 July 2003; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2003; Volume 2723, pp. 955–966. [Google Scholar]
- Wolfram, S. Theory and Applications of Cellular Automata; World Scientific Publication: Singapore, 1986. [Google Scholar]
- Jin, Y.; Branke, J. Evolutionary Optimization in Uncertain Environments-a Survey. IEEE Trans. Evol. Comput. 2005, 9, 303–317. [Google Scholar] [CrossRef]
- Nguyena, T.T.; Yangb, S.; Brankec, J. Evolutionary Dynamic Optimization: A Survey of the State of the Art. Swarm Evol. Comput. 2012, 6, 1–24. [Google Scholar] [CrossRef]
- Yazdani, D.; Cheng, R.; Yazdani, D.; Branke, J.; Jin, Y.; Yao, X. A Survey of Evolutionary Continuous Dynamic Optimization over Two Decades—Part A. IEEE Trans. Evol. Comput. 2021, 25, 609–629. [Google Scholar] [CrossRef]
- Yazdani, D.; Cheng, R.; Yazdani, D.; Branke, J.; Jin, Y.; Yao, X. A Survey of Evolutionary Continuous Dynamic Optimization over Two Decades—Part B. IEEE Trans. Evol. Comput. 2021, 25, 630–650. [Google Scholar] [CrossRef]
- Moser, I.; Chiong, R. Dynamic Function Optimization: The Moving Peaks Benchmark. In Metaheuristics for Dynamic Optimization; Springer: Berlin/Heidelberg, Germany, 2013; pp. 35–59. [Google Scholar]
- Li, X.; Branke, J.; Blackwell, T. Particle Swarm with Speciation and Adaptation in a Dynamic Environment. In Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation (GECCO ’06), Seattle, DC, USA, 2–12 July 2006; pp. 51–58. [Google Scholar]
- Nasiri, B.; Meybodi, M.R. Speciation Based Firefly Algorithm for Optimization in Dynamic Environments. Int. J. Artif. Intell. 2012, 8, 118–132. [Google Scholar]
- Trojanowski, K.; Wierzchon, S.T. Studying Properties of Multipopulation Heuristic Approach to Non-Stationary Optimisation Tasks. In Intelligent Information Processing and Web Mining; Springer: Berlin/Heidelberg, Germany, 2003; Volume 22, pp. 23–32. [Google Scholar]
- Timmis, J.; Neal, M. A Resource Limited Artificial Immune System for Data Analysis. Knowl.-Based Syst. 2001, 14, 121–130. [Google Scholar] [CrossRef]
- Zheng, J.; Chen, Y.; Zhang, W. A Survey of Artificial Immune Applications. Artif. Intell. Rev. 2010, 34, 19–34. [Google Scholar] [CrossRef]
- de Franca, F.O.; Von Zuben, F.J.; de Castro, L.N. An Artificial Immune Network for Multimodal Function Optimization on Dynamic Environments. In Proceedings of the 2005 Conference on Genetic and Evolutionary Computation (GECCO ’05), Washington, DC, USA, 25–29 June 2005; ACM: New York, NY, USA, 2005; pp. 289–296. [Google Scholar]
- Xuhua, S.; Feng, Q. An Optimization Algorithm Based on Multi-Population Artificial Immune Network. In Proceedings of the Fifth International Conference on Natural Computation (ICNC ’09), Tianjin, China, 14–16 August 2009; pp. 379–383. [Google Scholar]
- Gasper, A.; Collard, P. From GAs to Artificial Immune Systems: Improving Adaptation in Time Dependent Optimization. In Proceedings of the 1999 Congress on Evolutionary Computation, (CEC 99), Washington, DC, USA, 6–9 July 1999; Volume 3. [Google Scholar]
- Kelsey, J.; Timmis, J. Immune Inspired Somatic Contiguous Hypermutation for Function Optimisation. In Proceedings of the Genetic and Evolutionary Computation—GECCO 2003, Chicago, IL, USA, 12–16 July 2003; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2003; Volume 2723, pp. 207–218. [Google Scholar]
- De Castro, L.N.; Von Zuben, F.J. The Clonal Selection Algorithm with Engineering Applications. In Proceedings of the GECCO00 Workshop on Artificial Immune Systems and Their Applications, Las Vegas, NV, USA, 8 July 2000; Volume 3637, pp. 36–39. [Google Scholar]
- Trojanowski, K.; Wierzchon, S.T. Immune-Based Algorithms for Dynamic Optimization. Inf. Sci. 2009, 179, 1495–1515. [Google Scholar] [CrossRef]
- Aragón, V.S.; Esquivel, S.C.; Coello Coello, C.A. A T-Cell Algorithm for Solving Dynamic Optimization Problems. Inf. Sci. 2011, 181, 3614–3637. [Google Scholar] [CrossRef]
- Shi, X.; Qian, F. Immune Response-Based Algorithm for Optimization of Dynamic Environments. J. Cent. South Univ. 2011, 18, 1563–1571. [Google Scholar] [CrossRef]
- Nabizadeh, S.; Rezvanian, A.; Meybodi, M.R. A Multi-Swarm Cellular PSO Based on Clonal Selection Algorithm in Dynamic Environments. In Proceedings of the 2012 International Conference on Informatics, Electronics & Vision (ICIEV), Dhaka, Bangladesh, 18–19 May 2012; pp. 482–486. [Google Scholar]
- Rezvanian, A.; Meybodi, M.R.; Kim, T. Tracking Extrema in Dynamic Environments Using a Learning Automata-Based Immune Algorithm. In Grid and Distributed Computing, Control and Automation; Communications in Computer and Information Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 121, pp. 216–225. [Google Scholar]
- Ceccherini-Silberstein, T.; Coornaert, M. Cellular Automata and Groups; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Kroc, J.; Hoekstra, A.; Sloot, P.M.A. Simulating Complex Systems by Cellular Automata; Springer: New York, NY, USA, 2010. [Google Scholar]
- Alba, E.; Dorronsoro, B. Cellular Genetic Algorithms; Springer: Berlin/Heidelberg, Germany, 2008; Volume 42. [Google Scholar]
- Shi, Y.; Liu, H.; Gao, L.; Zhang, G. Cellular Particle Swarm Optimization. Inf. Sci. 2011, 181, 4460–4493. [Google Scholar] [CrossRef]
- Rastegar, R.; Meybodi, M.R.; Hariri, A. A New Fine-Grained Evolutionary Algorithm Based on Cellular Learning Automata. Int. J. Hybrid Intell. Syst. 2006, 3, 83–98. [Google Scholar] [CrossRef]
- Hashemi, A.B.; Meybodi, M.R. A Multi-Role Cellular PSO for Dynamic Environments. In Proceedings of the 14th International CSI Computer Conference, Tehran, Iran, 20–21 October 2009; pp. 412–417. [Google Scholar]
- Hashemi, A.; Meybodi, M.R. Cellular PSO: A PSO for Dynamic Environments. In Advances in Computation and Intelligence; Cai, Z., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; pp. 422–433. [Google Scholar]
- Noroozi, V.; Hashemi, A.; Meybodi, M.R. CellularDE: A Cellular Based Differential Evolution for Dynamic Optimization Problems. In Adaptive and Natural Computing Algorithms; Dobnikar, A., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; pp. 340–349. [Google Scholar]
- Vafashoar, R.; Meybodi, M.R.; Momeni Azandaryani, A.H. CLA-DE: A Hybrid Model Based on Cellular Learning Automata for Numerical Optimization. Appl. Intell. 2012, 36, 735–748. [Google Scholar] [CrossRef]
- Yazdani, D.; Golyari, S.; Meybodi, M.R. A New Hybrid Algorithm for Optimization Based on Artificial Fish Swarm Algorithm and Cellular Learning Automata. In Proceedings of the 2010 5th International Symposium on Telecommunications (IST), Tehran, Iran, 4–6 December 2010; pp. 932–937. [Google Scholar]
- Basu, M. Artificial Immune System for Dynamic Economic Dispatch. Int. J. Electr. Power Energy Syst. 2011, 33, 131–136. [Google Scholar] [CrossRef]
- Wu, S.S.; Li, B.Z.; Yang, J.G. A Three-Fold Approach to Solve Dynamic Job Shop Scheduling Problems by Artificial Immune Algorithm. Adv. Mater. Res. 2010, 139, 1666–1669. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Wu, L.; Huo, Y. Artificial Immune System for Protein Folding Model. J. Converg. Inf. Technol. 2011, 6, 55–61. [Google Scholar]
- Dasgupta, D.; Yu, S.; Nino, F. Recent Advances in Artificial Immune Systems: Models and Applications. Appl. Soft Comput. 2011, 11, 1574–1587. [Google Scholar] [CrossRef]
- Chang, T.-Y.; Shiu, Y.-F. Simultaneously Construct IRT-Based Parallel Tests Based on an Adapted CLONALG Algorithm. Int. J. Appl. Intell. 2012, 36, 979–994. [Google Scholar] [CrossRef]
- Wallenta, C.; Kim, J.; Bentley, P.J.; Hailes, S. Detecting Interest Cache Poisoning in Sensor Networks Using an Artificial Immune Algorithm. Int. J. Appl. Intell. 2010, 32, 1–26. [Google Scholar] [CrossRef]
- Zeng, J.; Liu, X.; Li, T.; Li, G.; Li, H.; Zeng, J. A Novel Intrusion Detection Approach Learned from the Change of Antibody Concentration in Biological Immune Response. Int. J. Appl. Intell. 2011, 35, 41–62. [Google Scholar] [CrossRef]
- Fernandez-Leon, J.A.; Acosta, G.G.; Mayosky, M.A. From Network-to-Antibody Robustness in a Bio-Inspired Immune System. Biosystems 2011, 104, 109–117. [Google Scholar] [CrossRef]
- Zhao, W.; Davis, C.E. A Modified Artificial Immune System Based Pattern Recognition Approach–An Application to Clinical Diagnostics. Artif. Intell. Med. 2011, 52, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Jerne, N.K. Towards a Network Theory of the Immune System. Ann. Immunol. 1974, 125C, 373–389. [Google Scholar]
- de Castro, L.N.; Timmis, J. An Artificial Immune Network for Multimodal Function Optimization. In Proceedings of the 2002 Congress on Evolutionary Computation, (CEC ’02), Honolulu, HI, USA, 12–17 May 2002; pp. 699–704. [Google Scholar]
- Timmis, J.; Hone, A.; Stibor, T.; Clark, E. Theoretical Advances in Artificial Immune Systems. Theor. Comput. Sci. 2008, 403, 11–32. [Google Scholar] [CrossRef]
- Branke, J. Memory Enhanced Evolutionary Algorithms for Changing Optimization Problems. In Proceedings of the 1999 Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999; pp. 1875–1882. [Google Scholar]
- The Moving Peaks Benchmark. Available online: http://www.aifb.unikarlsruhe.de/~jbr/MovPeaks/ (accessed on 1 May 2010).
- Li, C.; Yang, S. Fast Multi-Swarm Optimization for Dynamic Optimization Problems. In Proceedings of the Fourth International Conference on Natural Computation, 2008, (ICNC’08), Jinan, China, 18–20 October 2008; Volume 7, pp. 624–628. [Google Scholar]
- du Plessis, M.C.; Engelbrecht, A.P. Differential Evolution for Dynamic Environments with Unknown Numbers of Optima. J. Glob. Optim. 2013, 55, 73–99. [Google Scholar] [CrossRef]
- Liu, L.; Wang, D.; Tang, J. Composite Particle Optimization with Hyper-Reflection Scheme in Dynamic Environments. Appl. Soft Comput. 2011, 11, 4626–4639. [Google Scholar] [CrossRef]
- Nabizadeh, S.; Rezvanian, A.; Meybodi, M.R. Tracking Extrema in Dynamic Environment Using Multi-Swarm Cellular PSO with Local Search. Int. J. Electron. Inf. 2012, 1, 29–37. [Google Scholar]
- Kordestani, J.K.; Ranginkaman, A.E.; Meybodi, M.R.; Novoa-Hernández, P. A Novel Framework for Improving Multi-Population Algorithms for Dynamic Optimization Problems: A Scheduling Approach. Swarm Evol. Comput. 2019, 44, 788–805. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).