Robustness of Artificial Neural Networks Based on Weight Alterations Used for Prediction Purposes

Abstract

Nowadays, due to their excellent prediction capabilities, the use of artificial neural networks (ANNs) in software has significantly increased. One of the most important aspects of ANNs is robustness. Most existing studies on robustness focus on adversarial attacks and complete redundancy schemes in ANNs. Such redundancy methods for robustness are not easily applicable in modern embedded systems. This work presents a study, based on simulations, about the robustness of ANNs used for prediction purposes based on weight alterations. We devise a method to increase the robustness of ANNs directly from ANN characteristics. By using this method, only the most important neurons/connections are replicated, keeping the additional hardware overheads to a minimum. For implementation and evaluation purposes, the networks-on-chip (NoC) case, which is the next generation of system-on-chip, was used as a case study. The proposed study/method was validated using simulations and can be used for larger and different types of networks and hardware due to its scalable nature. The simulation results obtained using different PARSEC (Princeton Application Repository for Shared-Memory Computers) benchmark suite traffic show that a high level of robustness can be achieved with minimum hardware requirements in comparison to other works.

1. Introduction

Neural networks yield excellent prediction results if appropriately trained for use in different application domains [1,2]. They have the power to extract valuable information from complex data and predict trends that cannot be easily detected by other mechanisms. While neural networks have certain prediction capabilities, their accuracy decreases in the presence of small perturbations. This makes it difficult to apply them in critical areas [3].

One of the main research goals of the analysis of robustness is to propose different solutions/architectures with increased robustness [4]. This is one of the fundamental problems that require extensive future research since ANN faults significantly affect the accuracy and reliability of these types of networks.

One of the most well-known solutions for robustness improvement and fault tolerance is to apply triple/dual modular redundancy (n-MR schemes) [5], replicating the entire ANN architecture, but these methods are very restrictive due to additional hardware overheads. This redundancy includes full replications of ANN architecture and is not applicable to modern on-chip systems due to area limitations [6].

Additionally, the robustness of neural networks to adversarial attacks is critical due to security issues that make these neural networks vulnerable [7,8], thus causing poor performance and accuracy. Until recently, researchers concentrated on comparing results based on having/not having adversarial machine learning attacks and providing different solutions. Defenses based on adversarial training have been proposed, but these defenses are often defeated by stronger attacks [8].

Motivated by the above, we focused on the property of robustness of neural networks used for prediction purposes based on weight alterations. Therefore, we examined how the prediction accuracy of ANNs is impacted by weight faults. The networks-on-chip case, which was presented in the framework of one of our previous studies [1], was used as a case study to evaluate the robustness of the ANNs based on simulations. The goal of this work is to discuss the robustness of neural networks to changes in weights that might affect the prediction results. This work discusses and analyzes weight alterations in ANNs based on simulations/implementations and provides a protection/robustness method for ANNs. This method will help to maintain high robustness in ANNs with minimum additional hardware overheads. In this work, the architecture of the ANNs was changed by duplicating only the most important neurons/connections in order to achieve good prediction accuracy for ANNs weight faults. We analyzed the importance of neurons/connections in ANNs based on actual simulations/implementations and how the prediction accuracy of the ANNs is affected in cases of weight faults.

The rest of this paper is organized as follows. Section 2 describes the background and related research. In Section 3, we introduce the methodology and a robust approach for detecting weight faults in ANNs with the support of simulation results and analysis. Section 4 offers a brief conclusion to the paper.

2. Background and Related Research

ANNs and robustness are very popular and active research topics in the literature. Due to adversarial attacks, many approaches have been developed regarding the fault tolerance and robustness of ANNs. The authors of [2] proposed a method based on neural networks in order to detect malicious hosts based on the SYN packets that are exchanged. With the aid of appropriate training, this method achieved 98% accuracy based on specific test data. Moreover, the authors of [3] found that powerful attacks can defeat defensive distillation, demonstrating that by systematically evaluating several possible attacks, better adversarial examples can be found than those in existing approaches. This study also concludes that constructing defenses that are robust to adversarial examples remains challenging. The study of [4] presents a survey on the robustness of deep networks to changes that may affect the samples in practice, such as adversarial perturbations, random noise, and transformations. The authors also discuss different solutions that attempt to increase the robustness of deep networks. Additionally, the authors of [7] study the effectiveness of different types of attacks and propose methods for training a deep-learning-based IDS with the use of different types of neural networks in order to increase the robustness of the networks based on a thread model.

Furthermore, n-MR schemes and redundancy have been proposed as methods for increasing the robustness of ANNs. The authors of [5] propose a novel dual modular redundance framework for DNNs. D2NN checks the fault sensitivity of each neuron in the target DNN based on performance degradation and shows if the neuron is faulty. Next, D2NN duplicates the more sensitive neurons to construct the completed DMR (dual modular redundancy).

Furthermore, theoretical studies and works based on robust metrics have taken into account fault tolerance and robustness. The authors of [9] present a theoretical survey on different defenses against adversarial inputs of machine learning. The following defenses are discussed: techniques based on model training, input validation techniques, and architectural modification techniques. In this study, only the theoretical aspects are presented to show the importance of robustness against adversarial examples and the need for strong, practical countermeasures in the future. The authors of [10] propose a theoretical fault tolerance solution for ANNs based on an evaluation of the different elements of an ANN, which are more appropriate for single faults. Based on this evaluation, they propose the duplication of different parts of an ANN architecture. Furthermore, the authors of [11] present a new version of the communication robustness (CR) metric, simplified communication robustness (SCR), which helps with the calculation of the CR robustness metric for different network topologies. Additionally, this study provides evaluations and discussion about different robustness metrics.

Studies that provide certifications for the robustness of neural networks are presented next. The authors of [8] present a defense method for neural networks with one hidden layer. This is based on certifications that, for a given network and test input, there is no attack that can force the error to exceed a certain threshold: the computation of an upper bound in the worst-case loss scenario. Additionally, they optimized this method with different network parameters, providing an adaptive regularizer that helps robustness. Additionally, the authors of [12] studied the sensitivity of neural networks to weight perturbations. They proposed an efficient approach to compute a certified robustness bound of weight perturbations within neural networks that do not have erroneous outputs. The authors provided a certified weight perturbation region such that DNNs maintained their accuracy if weight perturbations were within that region.

Lastly, different novel robust techniques for neural networks have been presented. The authors of [13] introduced E2CNNs, a new design methodology to improve robustness against memory errors in embedded systems. This work proposes a heuristic method to automate the design of a voter-based ensemble architecture. This design methodology increases the error robustness of CNNs by using ensemble architectures. The authors of [14] studied the sensitivity of weight perturbation in neural networks and its impact on model performance. They further designed a new theory-driven loss function for training generalization and robust neural networks against weight perturbations: bounded weight perturbations. Moreover, the authors of [15] extended the definition of robustness to any type of input for which some alterations can be defined. They proposed the ROBY tool, which accepts different types of data, and some alterations can be performed on these data providing the ability to classify the input data correctly. The authors of [16] present a new scheme for robust DNNs called coded DNN. This alters the internal structure of DNNs by adding redundant neurons and edges to increase reliability—a new middle layer is added. The authors of [17] proposed an approach that is complementary to other forms of defense and replaces the weights of individual neurons with robust analogs derived from the use of Fourier analytic tools. Additionally, the authors of [18] propose a new method called robustness-aware filter pruning (RFP) and utilize this filter pruning method to increase the robustness against adversarial attacks. In the proposed method, the filters that are involved in non-robust features are pruned. Lastly, the authors of [19] designed a novel neuron that uses L∞ distance as its basic operation, known as an L∞-dist neuron. They show that the L∞-dist neuron has a natural 1-Lipschitz function with respect to the L∞ norm, and the neural networks constructed with this neuron (L∞-dist Nets) have the same property [19]. This directly provides a theoretical guarantee of the certified robustness based on the margin of the prediction outputs.

In the following sections, we present a new robustness method to maintain high levels of robustness in ANNs with minimum hardware overheads.

3. Methodology

3.1. Development of the ANNs and Network Traffic

In order to verify the robustness of the developed ANNs, we studied how prediction accuracy is affected by weight alterations in ANNs. For the implementation of the ANNs, we used MATLAB and the nntool. PARSEC benchmark suite was used for the traffic requirements [20]. To collect the ANN training data for predictions, we used NoC as a case study. NoC is an emerging technology that provides high-bandwidth and low-power on-chip communication between many cores. For the purposes of this work and for scalability purposes, we partitioned the NoC topology into smaller parts, and four different ANNs were created, one for each individual partition of NoC topology based on the explanations provided in our previous research [1]. The monitoring of the entire NoC topology/partitions is carried out in parallel using each developed ANN. Each of the four developed ANNs is responsible for monitoring one NoC partition, and the ANN receives data from the specific NoC partition that is used for the training process. The ANNs can be considered independent processing units in NoC topology. Different-sized ANNs were studied, and these have the same structure/architecture depending on the size of the NoC; they differ only in the weights. 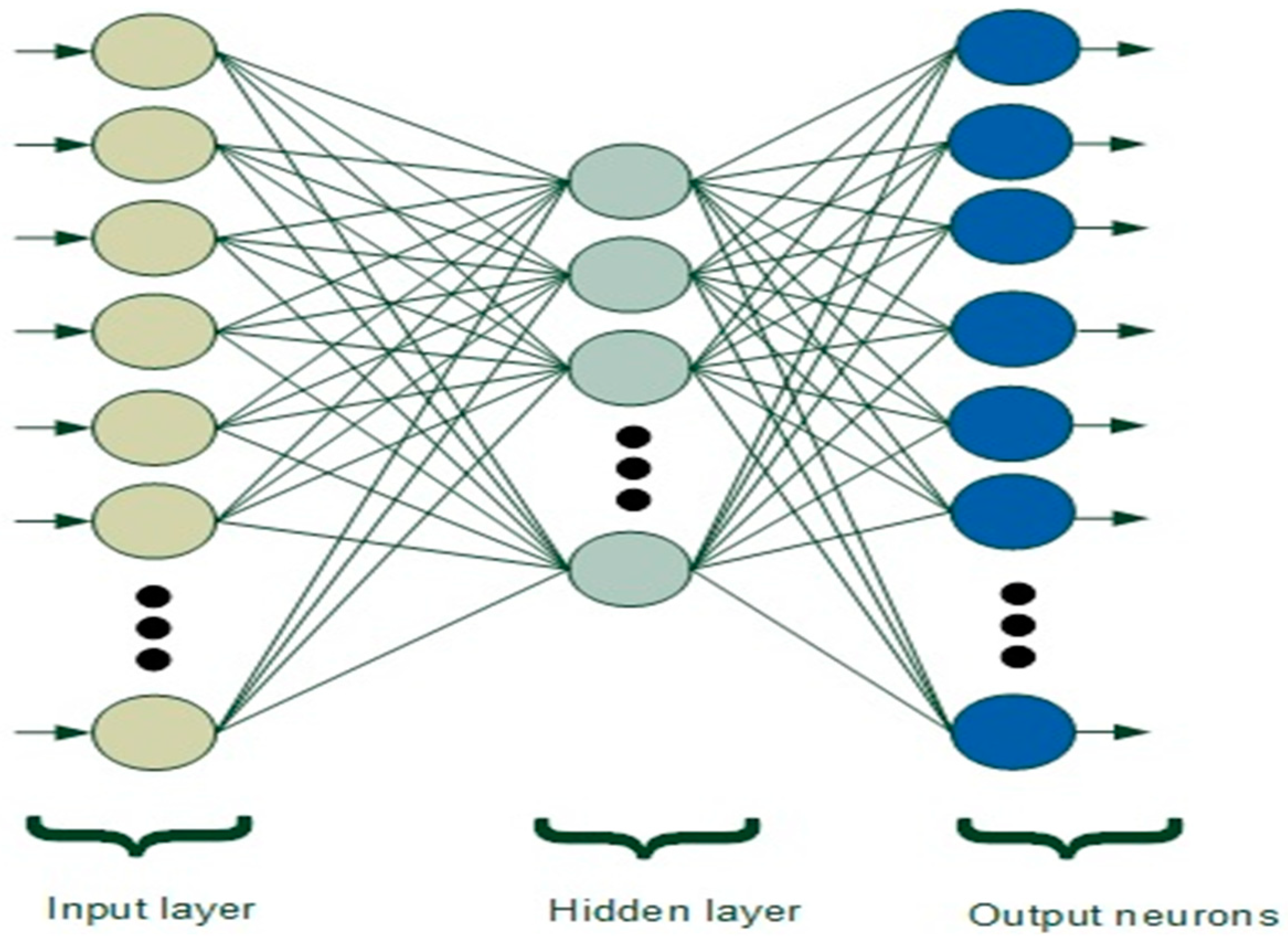Figure 1 presents the structure of the neural network.

In this work, integrated hardware-based ANNs with 19 neurons in the hidden layer were developed and, based on the ANN training and data received from the NoC simulator, intelligently predicted which router might present a fault, as explained in [1]. We used ANNs with one hidden layer, which is sufficient since more hidden layers can introduce a risk of converging to a local minimum and might not improve the model [1]. For the training stage of the developed feed-forward ANNs, we used a back-propagation training algorithm, and the training was carried out offline.

For this work, the size of the ANNs is small, and based on the scalable nature of the calculations, the results are indicative of larger NoCs/ANNs. By using a simple activation function and having a small number of neurons for each ANN, we managed to keep the implementation of the ANNs simple. Each feed-forward ANN uses a hyperbolic tangent as an activation function, which provides simplicity and accuracy. A hyperbolic tangent produces outputs at a scale of [−1, 1]; it is a continuous, symmetric, and asymptotic function that is responsible for processing the output of each neuron in order to feed it to the next adjacent layer.

Inter-router link utilization values from the network-on-chip simulator (inputs to the ANN) are multiplied with the corresponding weights, and the sum of all the weighted inputs of the neuron is calculated. When the computations of each neuron are complete, the result is propagated via the activation function to the output neuron.

In the next sections, we describe the verification of how the prediction accuracy of ANNs was affected by weight alterations using simulations. Based on the results, we propose a method to maintain robustness in accepted margins with minimum additional overheads.

Additionally, network performance and a thorough analysis of the different implementations highly depend on network traffic. In order to achieve more accurate results for our simulations, we used data from the PARSEC benchmark suite, which provides realistic traffic profiles, traces of real applications based on parallel programs, and state-of-the-art algorithms that help with the study of the implemented topologies [20,21,22].

3.2. Simulations to Verify How the Prediction Accuracy of the ANNs Is Generally Affected

Firstly, different random simulations were developed to verify whether weight alterations affect the percentage of correct predictions of the ANNs in general. One NoC topology/partition was randomly chosen, a dedicated ANN is responsible for this partition, and random ANN weight alterations were injected and simulated. Different simulation cases were developed using one, two, three, and four different weight alterations in the case of 8 × 8 NoC topologies with 4 × 5 NoC partitions/ANN sizes. For each weight, one random bit was chosen to be altered. All the different NoC partitions and ANNs were verified in this work. As a starting point, we only used 8 × 8 NoC topologies with 4 × 5 partitions/ANN sizes and changed one bit for each weight in order to verify if the percentage of correct predictions is generally affected. In the following sections, we present more simulations of alterations for more than one bit of different ANN sizes.

Figure 2 and Figure 3 present the results for one, two, three, and four weight alterations in the developed ANNs. Figure 2 presents the results from the simulations in the case of checking all the weights of the ANN: one bit alteration. Figure 3 shows the results in the case of checking the input weights only: one bit alteration. The results show that there is a clear decrease in percentages of the correct predictions of the different simulated cases.

Based on the above graphs/results, we conclude that weight alterations impact the prediction accuracy of the ANNs. Since the accuracy whereby only the input weight alterations are checked decreased below 90% on average, and the accuracy whereby all the weight alterations are checked is above 90% on average, we can conclude that if the alteration is presented in the input weights, the impact on accuracy is larger than if the alteration is presented in the remaining weights. This allows us to assume that the input-hidden connections of the ANN are more influential in the prediction process than the hidden-output connections of the ANN.

3.3. More In-Depth Simulations and Explanations for the Robustness of ANNs Based on Weight Alterations

Next, we checked how the alteration of weights impacts the overall prediction process for each of the different implemented ANNs in more detail. In order to achieve this, different sizes of ANN architectures were developed, and random weight alterations were injected into all of the individual developed ANNs. All the individual ANNs for each partition of the different NoC topologies and all the weights were checked. The randomly chosen bit/bits alterations (one and more bit alterations) of the randomly chosen weight/weights were checked in this work. Figure 4 presents the weight alteration process, and explanations are provided below.

An exhaustive testing process of all the random possibilities of the weight faults is developed for each individual ANN. Thousands of different simulations are developed based on randomly chosen weights and bits for all ANNs. To generate erroneous weights, we tested all the possible random-weight bit/bits alterations for one or more weight errors. For each of these simulation cases, we used PARSEC workloads. All the results were recorded, and based on the prediction results, we managed to conclude on the most important neurons/connections of the ANNs. For the purposes of our method, a neuron/connection is defined as important if the weight/bit alterations cause the ANN to yield erroneous prediction results. Next, we present some of the different simulation cases (

Table 1. Explanations for different simulation cases.

Simulation Case	Description
Case A: One randomly chosen weight error and one randomly chosen bit alteration.	Firstly, we randomly choose one weight. The weight is changed to binary. After this, we randomly chose one bit to be altered. The bit is changed. We change the altered weight back to decimals and continue with the predictions.
Case B: Two randomly chosen weight errors and one randomly chosen bit alteration.	Firstly, we randomly choose two weights. The weights are changed to binary. After this, we randomly chose one bit to be altered for each weight. The bits are changed. We change the altered weights back to decimals and continue with the predictions.
Case C: Two randomly chosen weights and two randomly chosen bits alterations.	Firstly, we randomly choose two weights. The weights are changed to binary. After this, we randomly chose two different bits to be altered for each weight. Both bits are changed. We change the altered weights back to decimals and continue with the predictions.
Case D: Three randomly chosen weights and one randomly chosen bit alteration.	Firstly, we randomly choose three weights. The weights are changed to binary. After this, we randomly chose one bit to be altered for each weight. The bits are changed. We change the altered weights back to decimals and continue with the predictions.

) with results.

Different sizes of the NoCs/ANNs were developed and simulated. We started working with one randomly chosen network-on-chip partition: a dedicated ANN is responsible for each individual partition. All network partitions and different workloads from the PARSEC benchmark suite were verified and presented. Different simulation cases were developed and checked. Table 1 presents some of the developed simulation cases with appropriate descriptions. Figure 5 shows the results concerning the percentage of correct predictions for each of the above-mentioned cases in comparison with the case of no weight faults for different ANN sizes. From the above results, we can conclude that weight changes in the ANNs impact the whole prediction process, and we used thousands of additional simulations to determine the most important ANN neurons for each case (partition and PARSEC workload). In the following section, we present and analyze a method/technique for maintaining the robustness of ANNs in high levels based on replicating the most important neurons/connections.

The amount of redundancy that is needed to achieve good levels of robustness is usually high in overheads. If less redundancy is added, this means that fewer faults will be tolerated. A balance between this redundancy and robustness in additional overheads is needed. Based on our research, we attempted to maintain the robustness of ANNs in accepted margins and have as few overheads as possible by only duplicating the most important neurons/connections. Our method is presented in the next section.

3.4. Replication of the Most Important Neurons/Connections

Next, we present a method in order to achieve robustness for ANNs based on the replication of the most important neurons/connections, addressing the issue of robustness based on redundancy.

Different methods have previously been used for robustness, but these are often restrictive. Most cases are based on replicating complete ANN architecture or replicating a certain number of complete layers in the ANNs. Based on past studies, ANNs are not always fault-tolerant and indicate the need for more robust methods [3].

Based on the results presented in the previous section for each individual ANN, as well as the PARSEC benchmark suite workloads, we managed to identify the most important neurons/connections in the presence of weight (bit) errors. Our method focuses on the replication of these parts in order to achieve robustness for the developed ANNs.

In order to check how many redundant neurons/connections were needed for the different ANN sizes to achieve good robustness levels, different numbers of neurons were replicated and simulated. Figure 6 presents the results from simulations of different numbers of neuron replications for different ANN sizes.

The results show that good robustness results are achieved for the 4 × 5 ANN with 12 neuron replications. For the 4 × 6 ANN, good results are achieved with 14 neuron replications. For the 5 × 6 ANN, good robustness results are achieved with 17 neuron replications. Figure 7 presents the structure of the neural network with redundant neurons/connections (redundant neurons/connections are shown in red).

Figure 8 shows the complete process/steps of our method.

Based on the previous results, since the weight alterations are already known, we determined the most important neurons/connections for specific ANNs under different PARSEC workloads. Next, we replicated the above important neurons/connections of the specific ANN, changing the architecture of the ANN in order to increase its robustness. Based on the new and altered ANN architecture, we carried out simulations to check the prediction accuracy of different ANNs. Different simulations are developed with randomly chosen weights and bits, as explained before. We tested all the possible random weight bit/bits alterations for one and more weight errors. Using the new prediction simulation results, we verified the robustness of the ANNs.

In our method, robustness is achieved via the actual ANN process itself by using the high connectivity of the neurons in the ANNs. Moreover, our method tries to reduce the redundancy needed (in comparison to previous methods) in order to minimize expenses in terms of the additional units and links. Our method is easier to implement in practice in comparison to the other methods that require replications of more neurons/connections (even entire ANNs), and this makes them impractical in reality.

Figure 9 shows that the robust method analyzed above (with redundant neurons/connections) helps to increase the robustness of the ANNs used for prediction purposes. The figure shows the average percentages of correct predictions for each of the above-mentioned cases with redundancy in comparison to cases with no weight faults. The below results show that, by replicating the most important neurons/connections, ANNs can retain a high robustness level (around 98% prediction accuracy); these results are reproducible for larger networks too.

The number of input–hidden–output units remains the same in our study, with only the most important neurons/connections changing. By replicating only these, we kept the overheads to a minimum in comparison to the previous studies that replicated the complete ANN or complete layers x times. Furthermore, our study not only considered single-fault assumptions (as in previous research) but verified all cases of random faults with one and more weights and bit errors.

Lastly, we provide a brief comparison with relevant related studies, as shown in

Table 2. Comparisons with related research.

Work	Overheads	Robustness Levels
D2NN [5] (Dual modular redundancy framework)	DMR—Primary and secondary networks—The primary DNN represents the original DNN, while the secondary DNN is constructed using newly introduced neurons together with parts of the original DNN.	Faults on the secondary network are converted from missed to detected faults, and the fault miss rate is reduced, maintaining good robust levels.
E2CNNs [13] (Convolutional neural networks: ensemble architectures)	The ensemble is built by training a pruned CNN several times. Then, the individual predictions are averaged together to compute the ensemble output. (Additional overheads are needed for the control logic).	A 4-E2CNN increases the accuracy from 12% to 15%.
Our work (NoCs—different cases of PARSEC benchmark suite)	Only the most important neurons/connections are replicated, keeping the overheads to a minimum.	Based on simulated results, high levels of robustness are achieved: ~98% prediction accuracy.

. When compared to both [5,13], our work yields good levels of robustness while still maintaining lower hardware overheads.

4. Conclusions

Our work offers fundamental insights into the robustness of ANNs that are subjected to weight alterations and used for prediction purposes. For simulation purposes, NoC was used as the case study. Thousands of different simulations were created for different NoC/ANN sizes and weight/bit alterations in order to verify how the prediction accuracy of the ANNs is affected. In this work, we verified all the cases of random faults with one or more weight and bit errors. Based on this study, we managed to draw significant conclusions on the robustness of the ANNs based on weight alterations. Additionally, we proposed a robustness method for ANNs based on redundancy. More specifically, the most important neurons/connections, which were defined based on simulations, were replicated. The proposed method can be used for larger networks and different hardware due to its scalable nature, and robustness is achieved through the actual ANN process itself. Our results indicate that a significant amount of redundancy is needed in order to achieve good levels of robustness in ANNs. Based on the analytical results from our simulations, we conclude that the proposed method can maintain the robustness of ANNs at high levels (~98% prediction accuracy). Lastly, our method minimizes additional redundant units and links, keeping the additional hardware overheads and costs to a minimum.