Real-Time Interval Type-2 Fuzzy Control of an Unmanned Aerial Vehicle with Flexible Cable-Connected Payload
Abstract
1. Introduction
Contributions
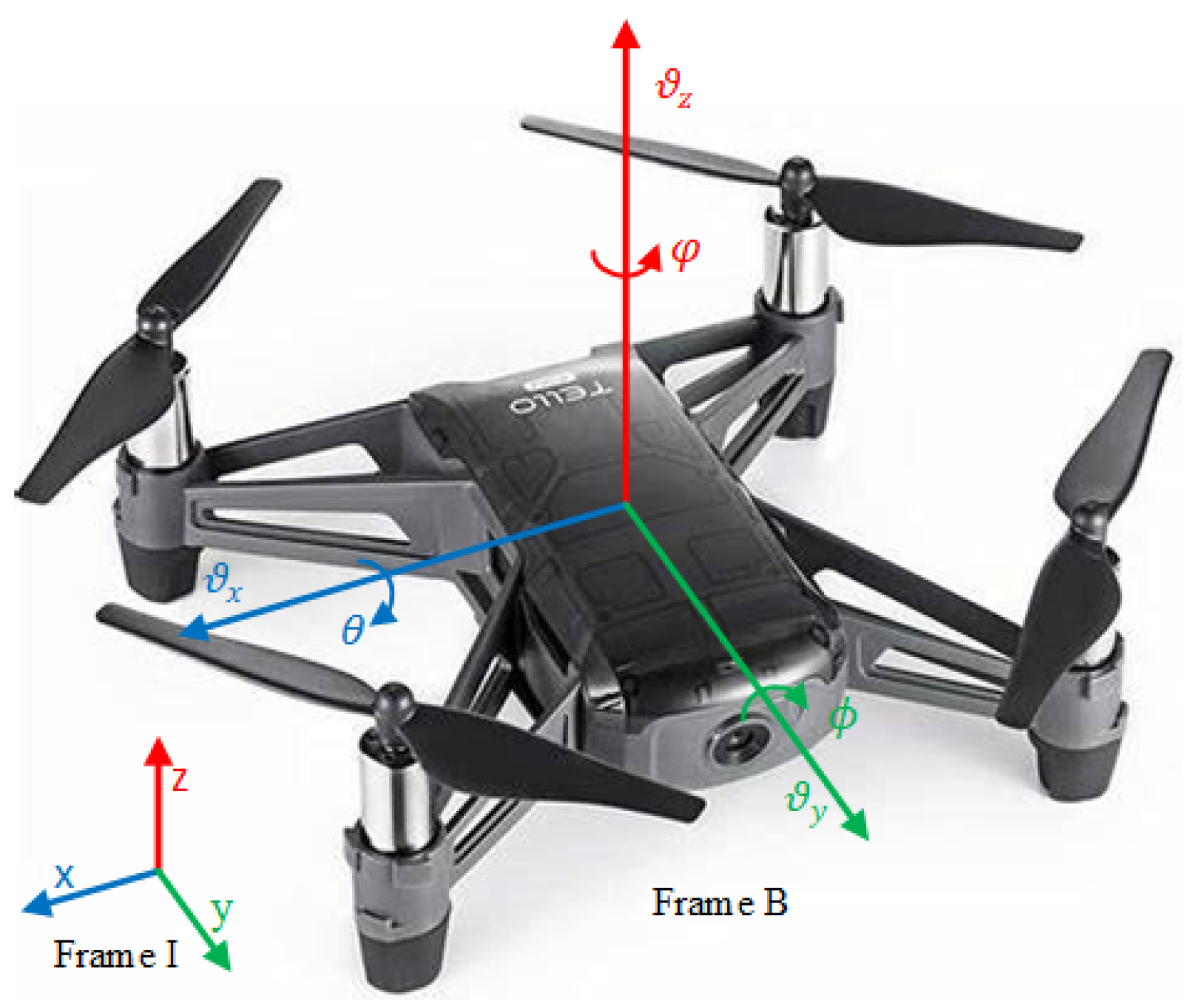
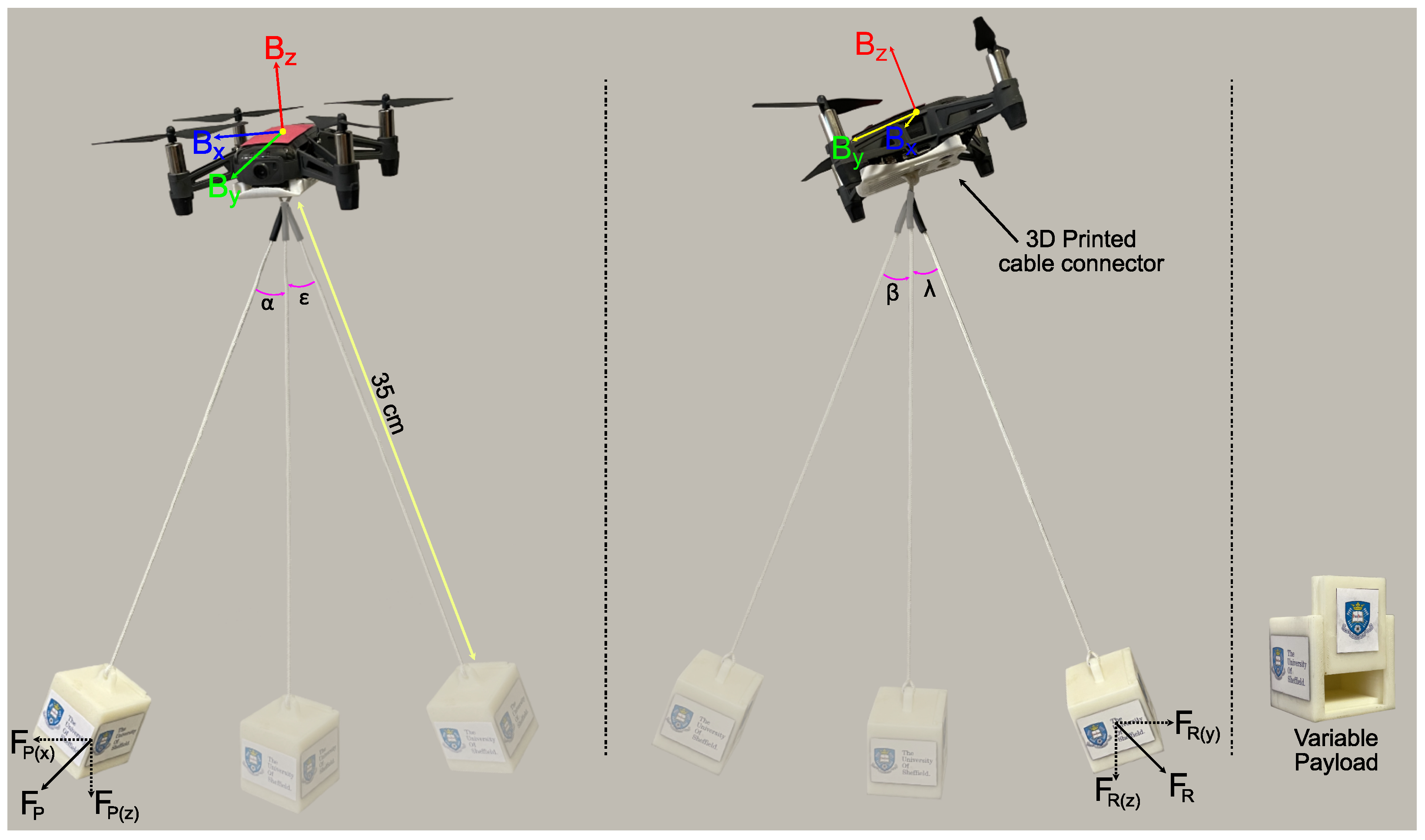
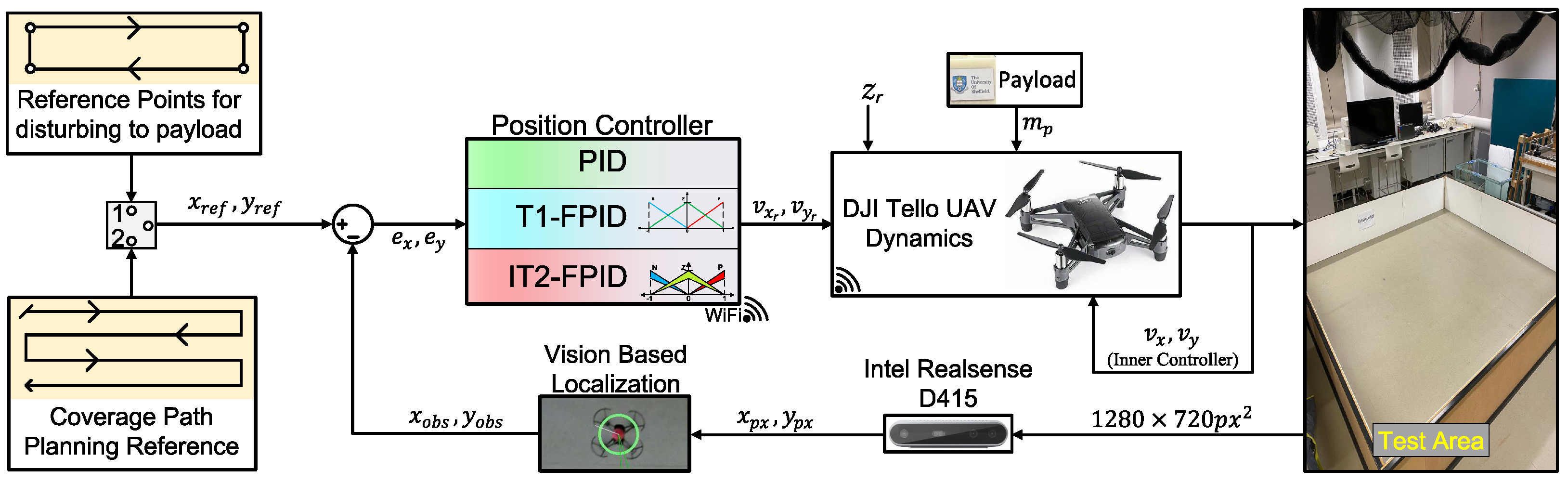
2. UAV Model and the Problem Definition
2.1. Model Dynamics of DJI Tello UAV
2.2. Problem Statement and Challenges
3. Implemented Controllers
3.1. PID Controller
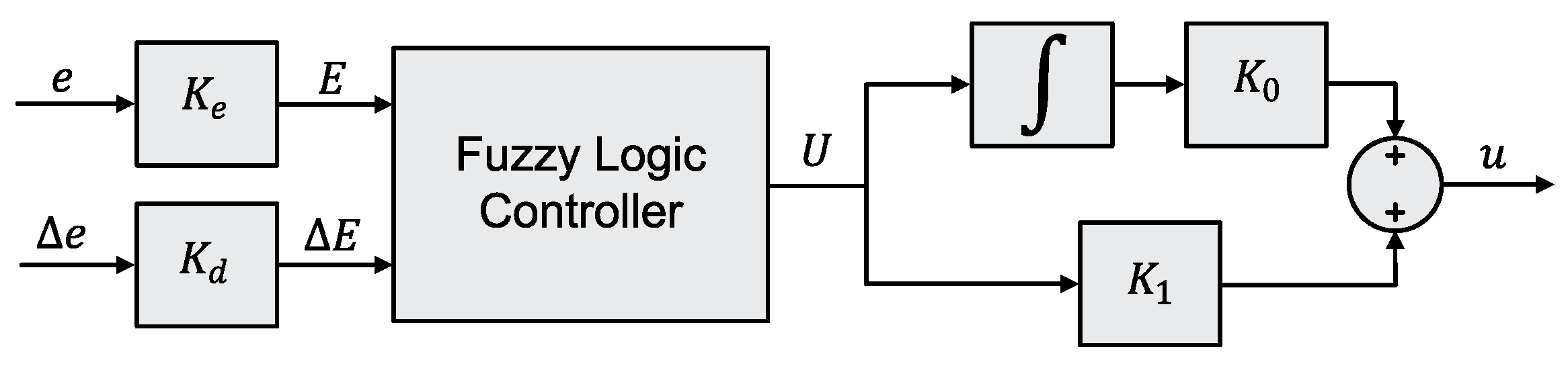
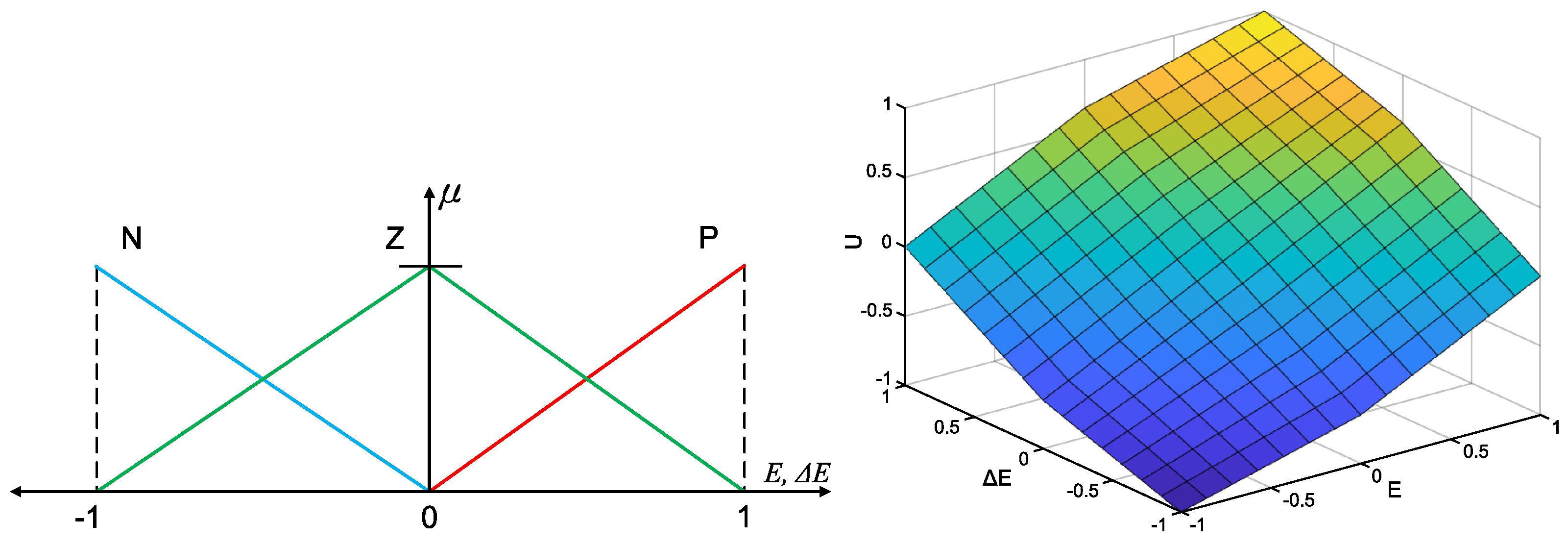
3.2. Type-1 Fuzzy PID Controller
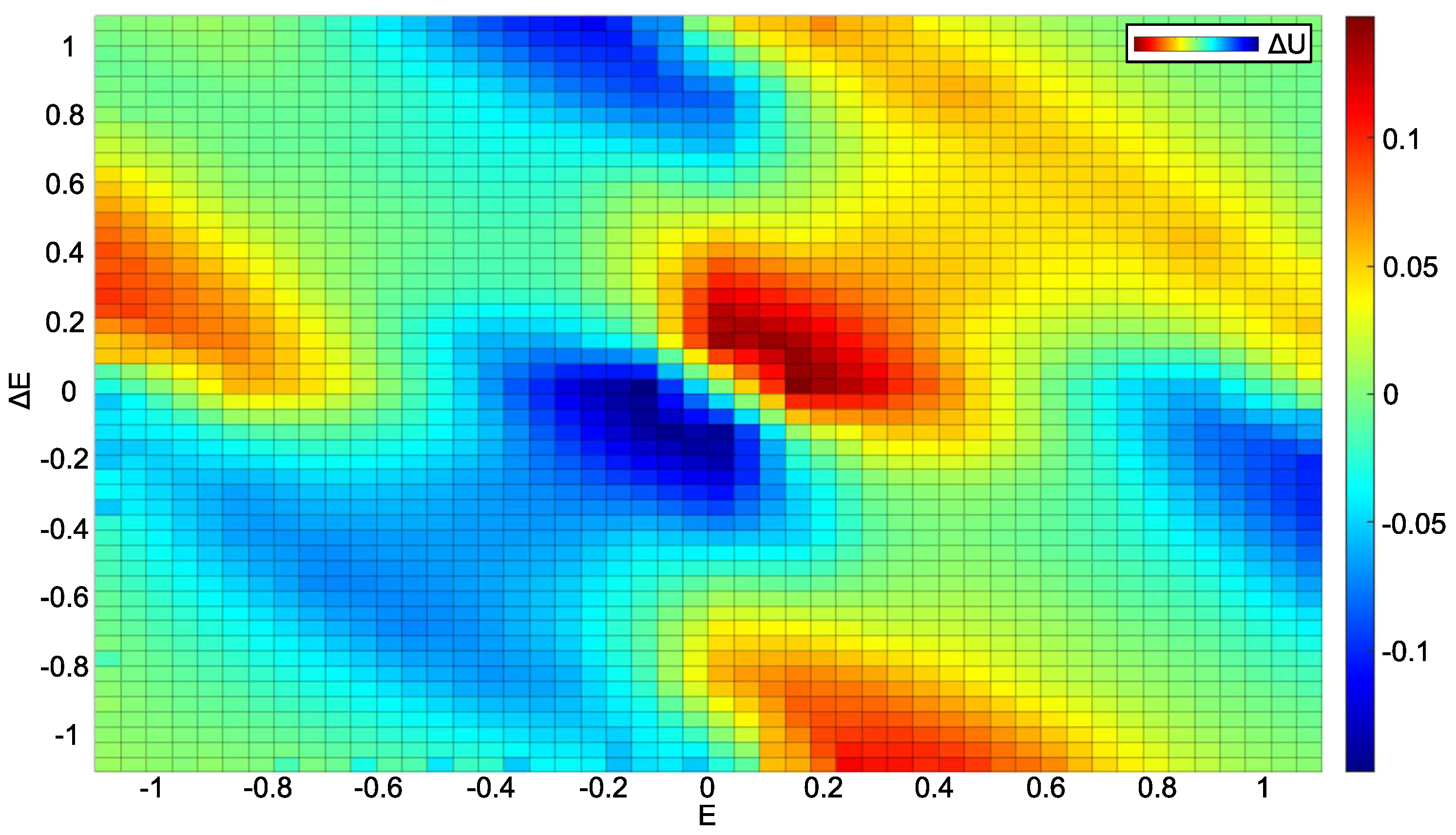
3.3. Interval Type-2 Fuzzy PID Controller
3.4. Optimisation Results and Simulation
4. Indoor Testing Area
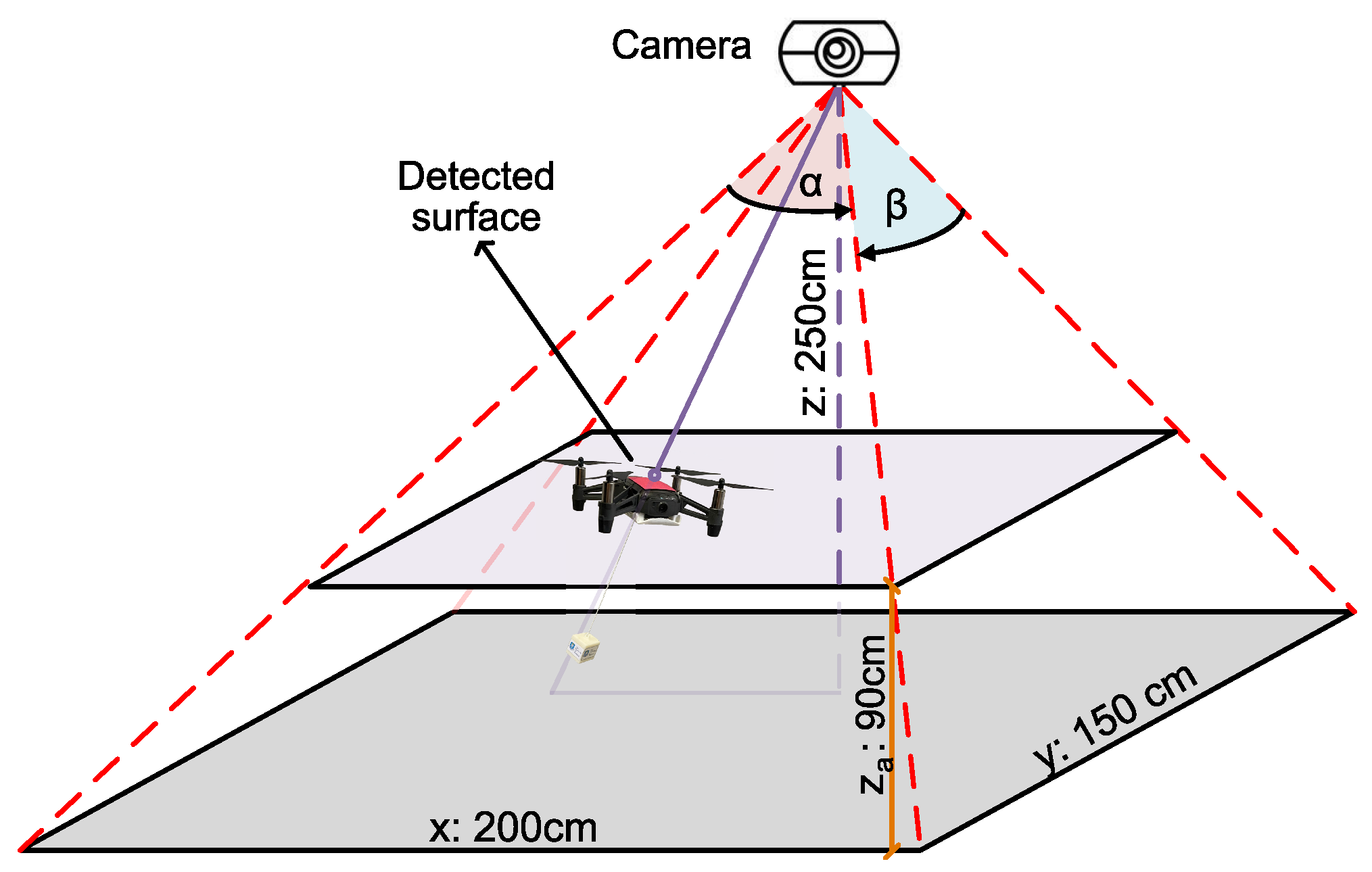
4.1. Intel RealSense Depth Camera and Vision-Based Localisation Method
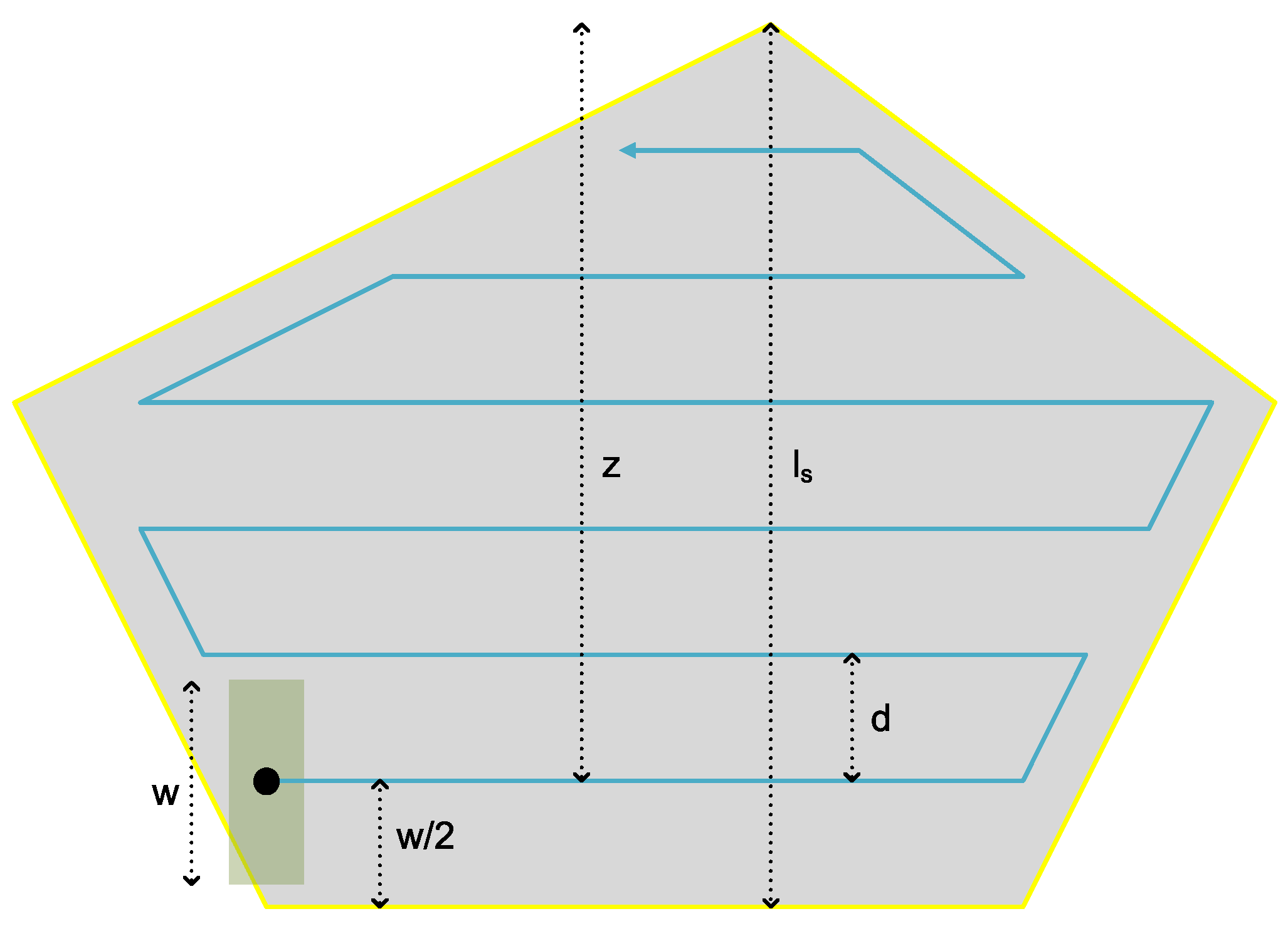
4.2. Coverage Path Planning
| Algorithm 1 Basic CPP algorithm. |
| Step 1: (Farthest vertex v from the edge e) For each edge, find the farthest vertex with respect to Euclidean distance and keep this (e, v) pair and the calculated distance value. Step 2: (Minimum distance pair (e,v)) Compare the distance values and find the (e, v) pair which gives the minimum distance value. Step 3: (Orthogonal direction vector) The optimal line-swept direction is the vector that is orthogonal to the edge from the (e, v) pair found in Step 2, and the rows constructed by the CPP algorithm will be parallel to this edge e. Step 4: (Path construction) The path is defined by the way points that are connected by line segments. These way points are placed in such a way that the line segments connecting them are parallel to the edge on which the polygon width is defined and the distance between a way point and the border of the polygon satisfies the camera footprint requirements. |
5. Real-Time Experimental Results
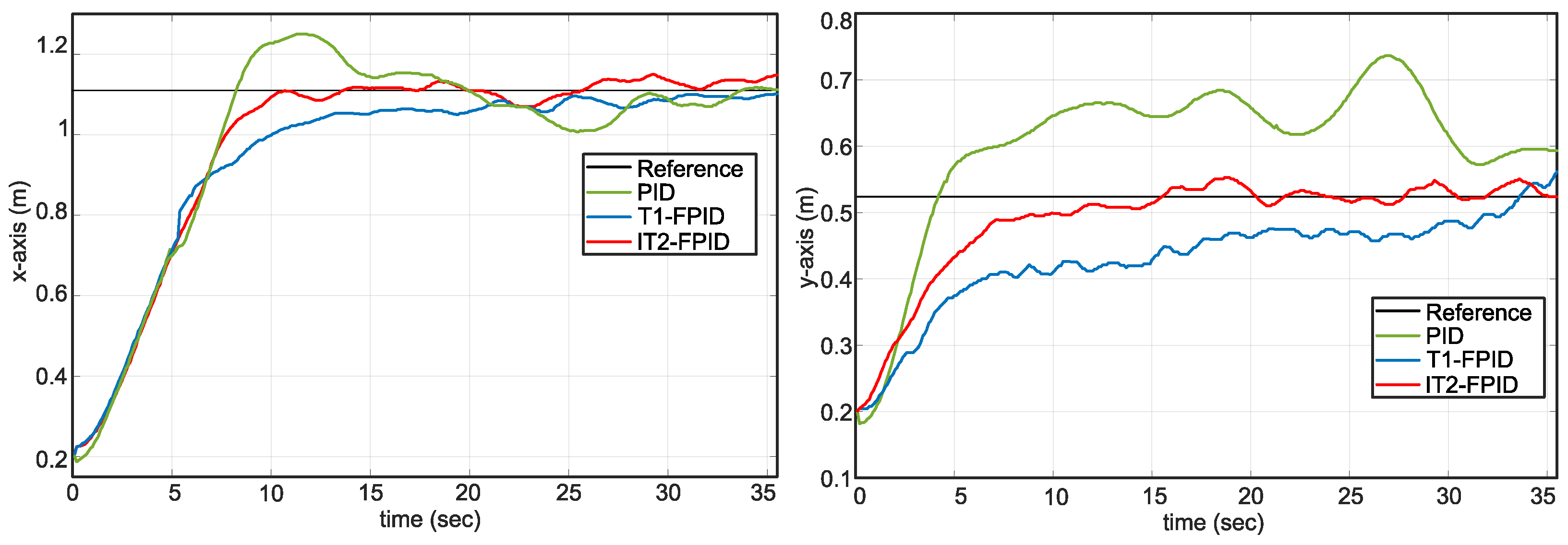
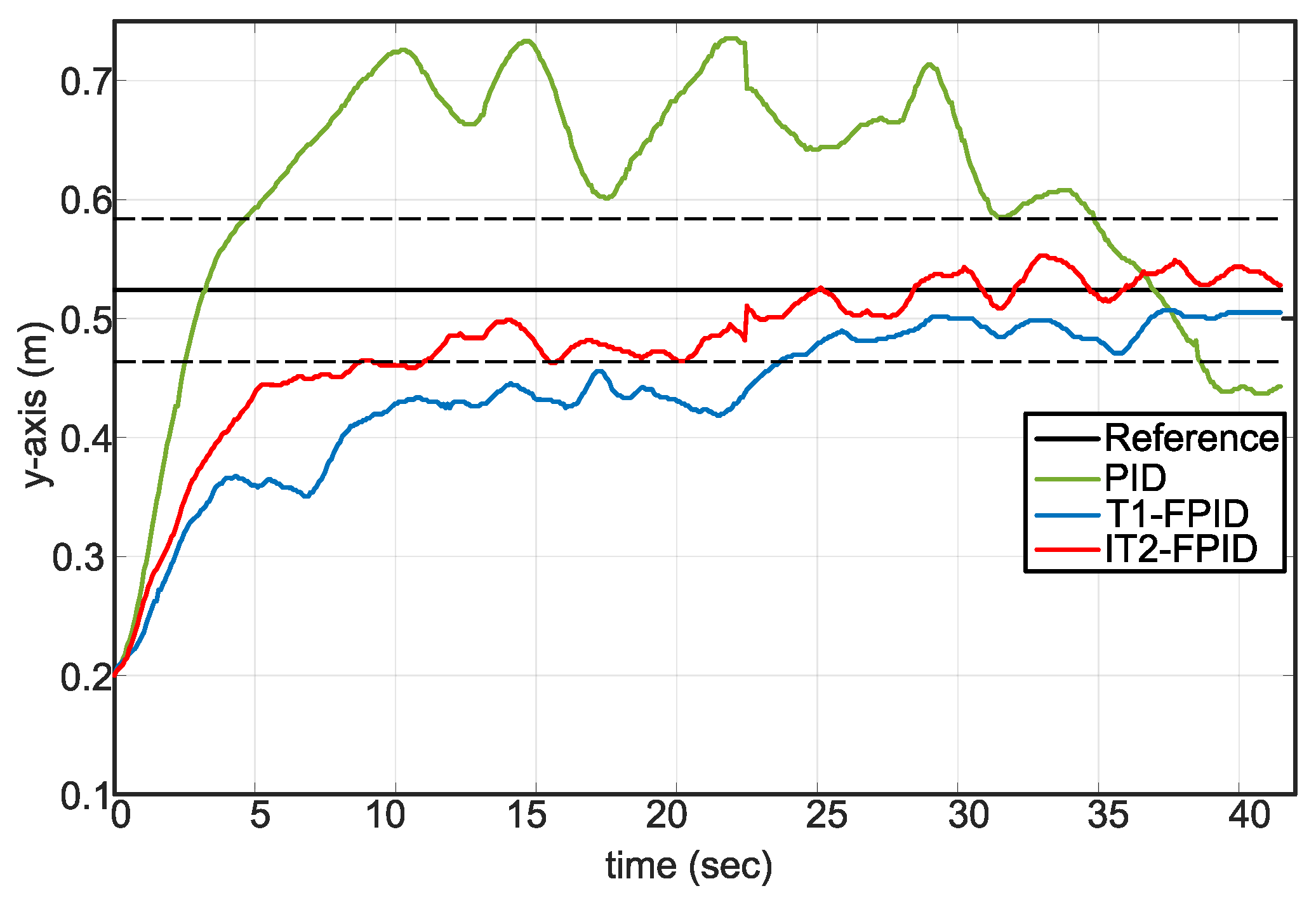
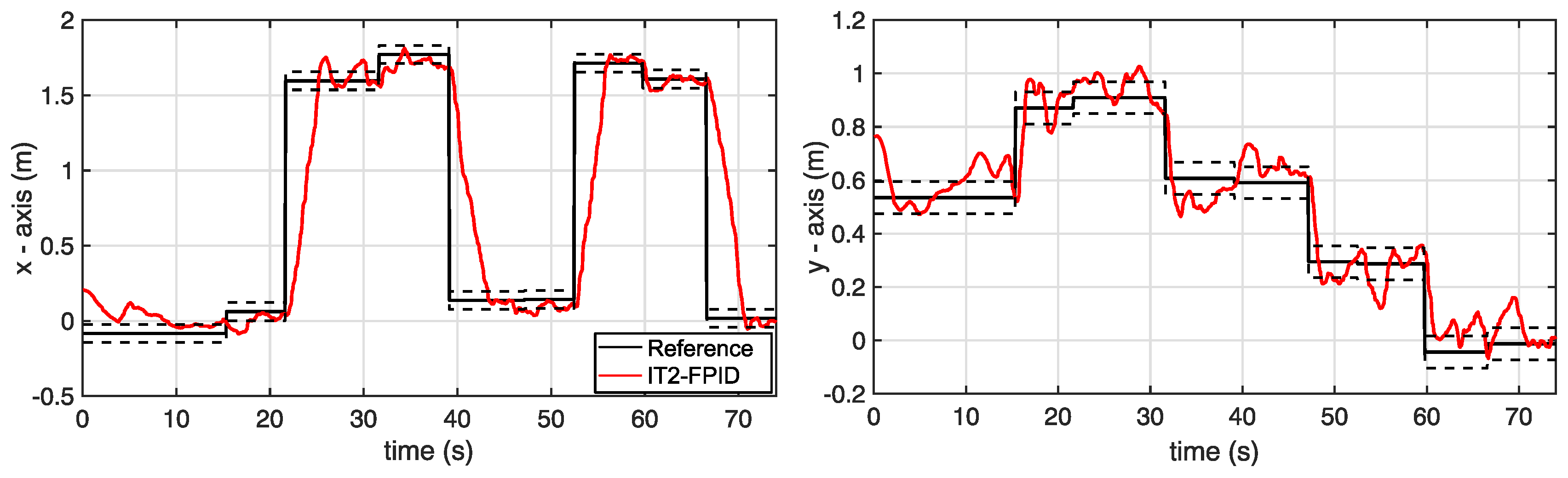
5.1. Set-Point Tracking without Disturbance and the Payload
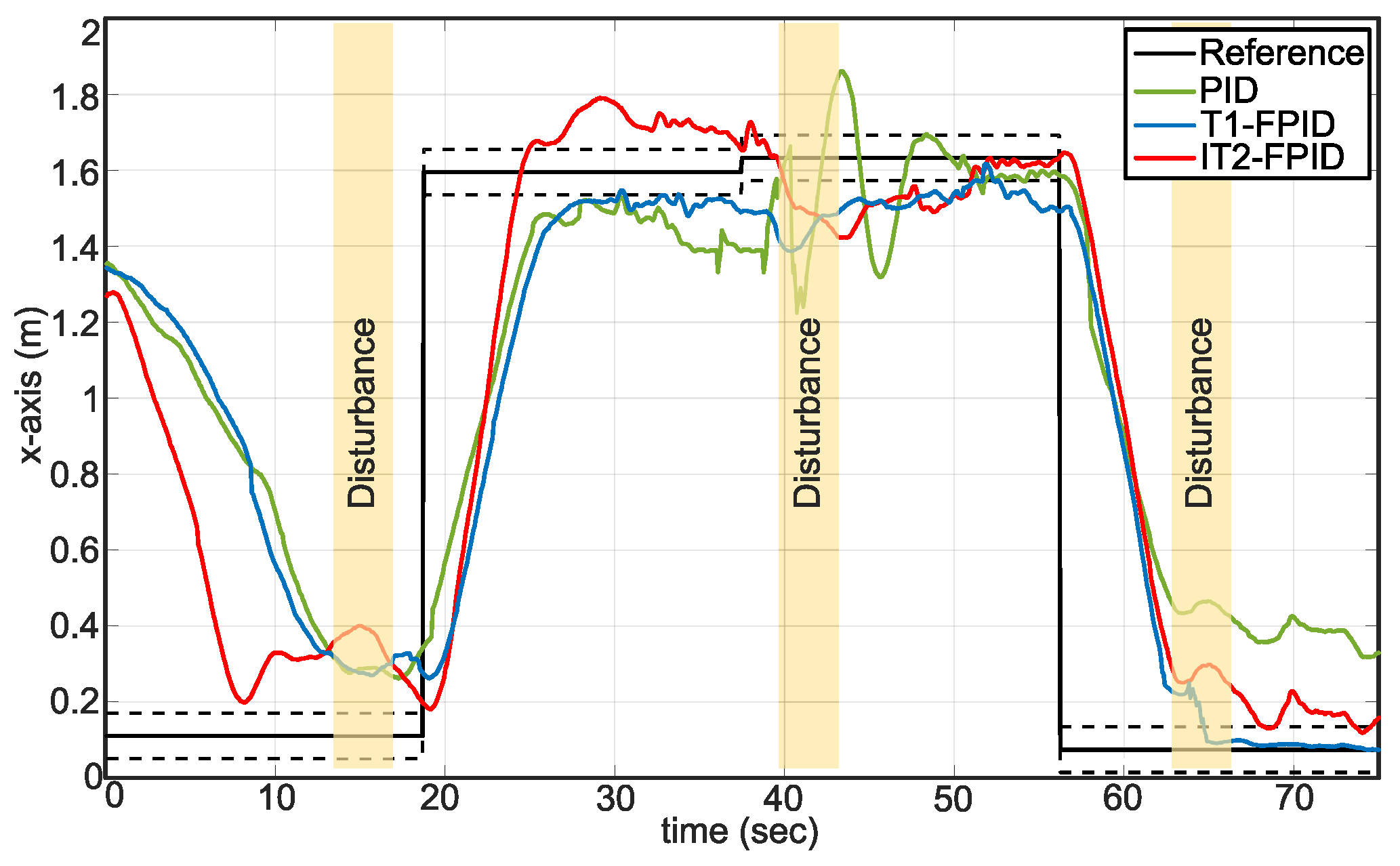
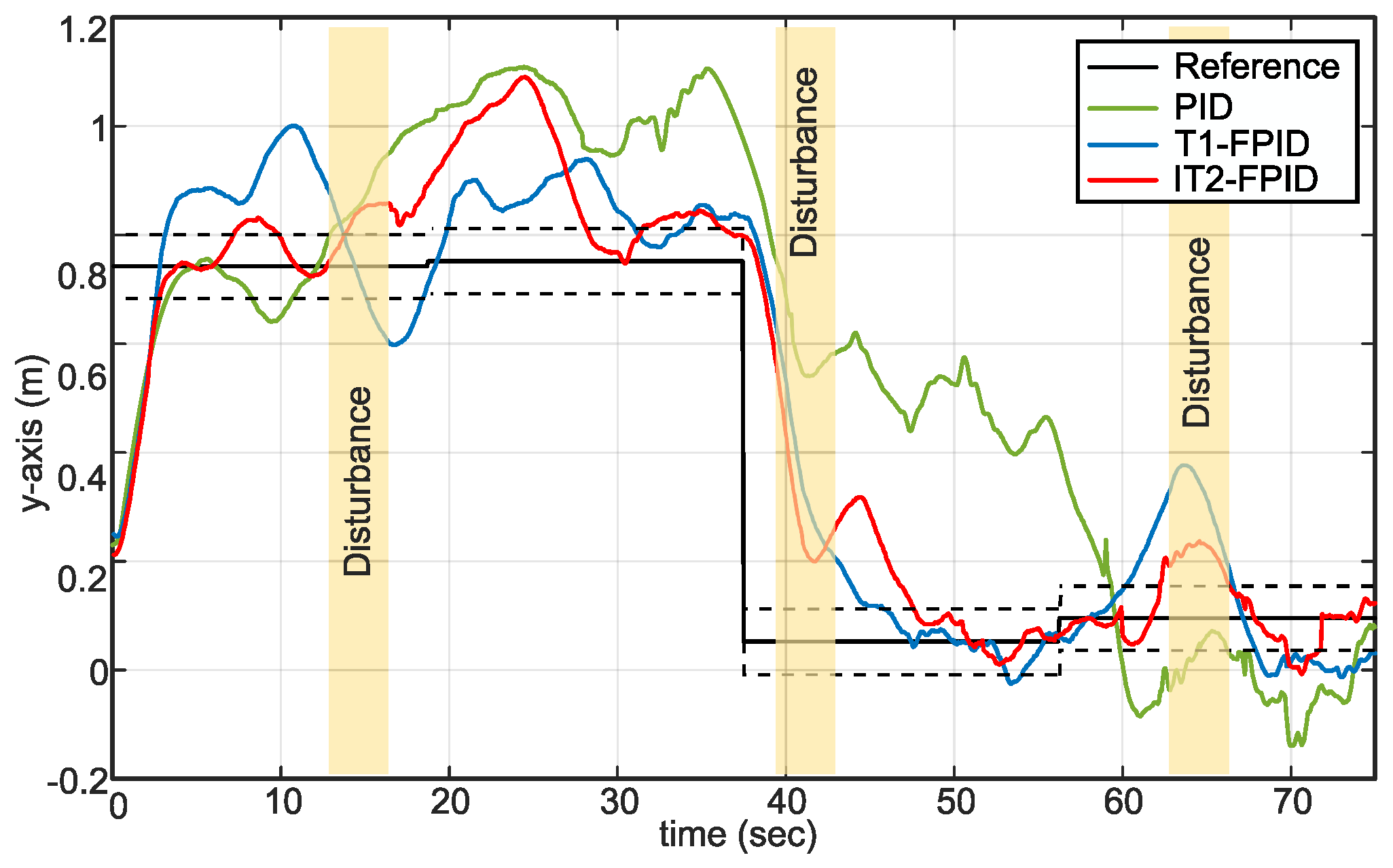
5.2. Set-Point Tracking with Disturbance and the Payload
6. Conclusions and Future Works
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. UAV Linear Model
Appendix B. Big Bang–Big Crunch Optimisation Method
References
- Sun, Z.; Piao, H.; Yang, Z.; Zhao, Y.; Zhan, G.; Zhou, D.; Meng, G.; Chen, H.; Chen, X.; Qu, B.; et al. Multi-agent hierarchical policy gradient for Air Combat Tactics emergence via self-play. Eng. Appl. Artif. Intell. 2021, 98, 104112. [Google Scholar] [CrossRef]
- Bellocchio, E.; Crocetti, F.; Costante, G.; Fravolini, M.L.; Valigi, P. A novel vision-based weakly supervised framework for autonomous yield estimation in agricultural applications. Eng. Appl. Artif. Intell. 2022, 109, 104615. [Google Scholar] [CrossRef]
- Mohamadi, H.E.; Kara, N.; Lagha, M. Heuristic-driven strategy for boosting aerial photography with multi-UAV-aided Internet-of-Things platforms. Eng. Appl. Artif. Intell. 2022, 112, 104854. [Google Scholar] [CrossRef]
- Fu, C.; Ding, F.; Li, Y.; Jin, J.; Feng, C. Learning dynamic regression with automatic distractor repression for real-time UAV tracking. Eng. Appl. Artif. Intell. 2021, 98, 104116. [Google Scholar] [CrossRef]
- Luperto, M.; Amigoni, F. Reconstruction and prediction of the layout of indoor environments from two-dimensional metric maps. Eng. Appl. Artif. Intell. 2022, 113, 104910. [Google Scholar] [CrossRef]
- Argentim, L.M.; Rezende, W.C.; Santos, P.E.; Aguiar, R.A. PID, LQR and LQR-PID on a quadcopter platform. In Proceedings of the International Conference on Informatics, Electronics and Vision (ICIEV), Dhaka, Bangladesh, 17–18 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–6. [Google Scholar]
- Khan, A.A.; Rapal, N. Fuzzy PID controller: Design, tuning and comparison with conventional PID controller. In Proceedings of the 2006 IEEE International Conference on Engineering of Intelligent Systems, Islamabad, Pakistan, 22–23 April 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 1–6. [Google Scholar]
- Candan, F.; Beke, A.; Kumbasar, T. Design and Deployment of Fuzzy PID Controllers to the nano quadcopter Crazyflie 2.0. In Proceedings of the Innovations in Intelligent Systems and Applications (INISTA), Thessaloniki, Greece, 3–5 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Kaplan, M.R.; Eraslan, A.; Beke, A.; Kumbasar, T. Altitude and position control of parrot mambo minidrone with PID and fuzzy PID controllers. In Proceedings of the 11th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 28–30 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 785–789. [Google Scholar]
- Noordin, A.; Mohd Basri, M.A.; Mohamed, Z. Real-Time Implementation of an Adaptive PID Controller for the Quadrotor MAV Embedded Flight Control System. Aerospace 2023, 10, 59. [Google Scholar] [CrossRef]
- Everett, M.F. LQR with Integral Feedback on a Parrot Minidrone. Mass. Inst. Technol. Tech. Rep. 2015, 1, 1–6. [Google Scholar]
- Okasha, M.; Kralev, J.; Islam, M. Design and Experimental Comparison of PID, LQR and MPC Stabilizing Controllers for Parrot Mambo Mini-Drone. Aerospace 2022, 9, 298. [Google Scholar] [CrossRef]
- Barzanooni, E.; Salahshoor, K.; Khaki-Sedigh, A. Attitude flight control system design of UAV using LQG\LTR multivariable control with noise and disturbance. In Proceedings of the 3rd RSI International Conference on Robotics and Mechatronics (ICROM), Tehran, Iran, 7–9 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 188–193. [Google Scholar]
- Zhao, W.; Go, T.H. Quadcopter formation flight control combining MPC and robust feedback linearization. J. Frankl. Inst. 2014, 351, 1335–1355. [Google Scholar] [CrossRef]
- Ganga, G.; Dharmana, M.M. MPC controller for trajectory tracking control of quadcopter. In Proceedings of the 2017 International Conference on Circuit, Power and Computing Technologies (ICCPCT), Kollam, India, 20–21 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Ortiz, J.P.; Minchala, L.I.; Reinoso, M.J. Nonlinear robust H-Infinity PID controller for the multivariable system quadrotor. IEEE Lat. Am. Trans. 2016, 14, 1176–1183. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Sadati, N.; Zamani, I. H∞disturbance attenuation of fuzzy large-scale systems. In Proceedings of the 2011 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2011), Taipei, Taiwan, 27–30 June 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 2364–2368. [Google Scholar]
- Wenzel, K.E.; Masselli, A.; Zell, A. Automatic take off, tracking and landing of a miniature UAV on a moving carrier vehicle. J. Intell. Robot. Syst. 2011, 61, 221–238. [Google Scholar] [CrossRef]
- Palossi, D.; Singh, J.; Magno, M.; Benini, L. Target following on nano-scale unmanned aerial vehicles. In Proceedings of the 7th IEEE International Workshop on Advances in Sensors and Interfaces (IWASI), Vieste, Italy, 15–16 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 170–175. [Google Scholar]
- Greiff, M. Modelling and Control of the Crazyflie Quadrotor for Aggressive and Autonomous Flight by Optical Flow Driven State Estimation. Master’s Thesis, Lund University, Department of Automatic Control, Sweden, Switzerland, 2017. [Google Scholar]
- Souza, R.M.J.A.; Lima, G.V.; Morais, A.S.; Oliveira-Lopes, L.C.; Ramos, D.C.; Tofoli, F.L. Modified artificial potential field for the path planning of aircraft swarms in three-dimensional environments. Sensors 2022, 22, 1558. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, N.P.; Lee, B.H.; Xuan-Mung, N.; Ha, L.N.N.T.; Jeong, H.S.; Lee, S.T.; Hong, S.K. Persistent Charging System for Crazyflie Platform. Drones 2022, 6, 212. [Google Scholar] [CrossRef]
- Belkhale, S.; Li, R.; Kahn, G.; McAllister, R.; Calandra, R.; Levine, S. Model-based meta-reinforcement learning for flight with suspended payloads. IEEE Robot. Autom. Lett. 2021, 6, 1471–1478. [Google Scholar] [CrossRef]
- Rao, J.; Li, B.; Zhang, Z.; Chen, D.; Giernacki, W. Position control of quadrotor uav based on cascade fuzzy neural network. Energies 2022, 15, 1763. [Google Scholar] [CrossRef]
- Lee, D.; Park, W.; Nam, W. Autonomous Landing of Micro Unmanned Aerial Vehicles with Landing-Assistive Platform and Robust Spherical Object Detection. Appl. Sci. 2021, 11, 8555. [Google Scholar] [CrossRef]
- Islam, S.; Liu, P.X.; El Saddik, A. Robust control of four-rotor unmanned aerial vehicle with disturbance uncertainty. IEEE Trans. Ind. Electron. 2014, 62, 1563–1571. [Google Scholar] [CrossRef]
- Qian, L.; Liu, H.H. Path-following control of a quadrotor UAV with a cable-suspended payload under wind disturbances. IEEE Trans. Ind. Electron. 2019, 67, 2021–2029. [Google Scholar] [CrossRef]
- Guo, K.; Jia, J.; Yu, X.; Guo, L.; Xie, L. Multiple observers based anti-disturbance control for a quadrotor UAV against payload and wind disturbances. Control Eng. Pract. 2020, 102, 104560. [Google Scholar] [CrossRef]
- Quintero, S.A.; Hespanha, J.P. Vision-based target tracking with a small UAV: Optimization-based control strategies. Control Eng. Pract. 2014, 32, 28–42. [Google Scholar] [CrossRef]
- Shakeel, T.; Arshad, J.; Jaffery, M.H.; Rehman, A.U.; Eldin, E.T.; Ghamry, N.A.; Shafiq, M. A Comparative Study of Control Methods for X3D Quadrotor Feedback Trajectory Control. Appl. Sci. 2022, 12, 9254. [Google Scholar] [CrossRef]
- Erol, O.K.; Eksin, I. A new optimization method: Big bang–big crunch. Adv. Eng. Softw. 2006, 37, 106–111. [Google Scholar] [CrossRef]
- Abdelmoeti, S.; Carloni, R. Robust control of UAVs using the parameter space approach. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 5632–5637. [Google Scholar]
- DJI Tello, C. DJI Tello EDU, Ryzerobotics. Available online: https://www.ryzerobotics.com/tello-edu (accessed on 16 June 2022).
- Giernacki, W.; Rao, J.; Sladic, S.; Bondyra, A.; Retinger, M.; Espinoza-Fraire, T. DJI Tello Quadrotor as a Platform for Research and Education in Mobile Robotics and Control Engineering. In Proceedings of the 2022 International Conference on Unmanned Aircraft Systems (ICUAS), Dubrovnik, Croatia, 21–24 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 735–744. [Google Scholar]
- Sarabakha, A.; Fu, C.; Kayacan, E.; Kumbasar, T. Type-2 fuzzy logic controllers made even simpler: From design to deployment for UAVs. IEEE Trans. Ind. Electron. 2017, 65, 5069–5077. [Google Scholar] [CrossRef]
- Sakalli, A.; Kumbasar, T.; Mendel, J.M. Towards systematic design of general type-2 fuzzy logic controllers: Analysis, interpretation, and tuning. IEEE Trans. Fuzzy Syst. 2020, 29, 226–239. [Google Scholar] [CrossRef]
- Lee, D.H.; Park, D. An efficient algorithm for fuzzy weighted average. Fuzzy Sets Syst. 1997, 87, 39–45. [Google Scholar] [CrossRef]
- Chang, P.T.; Hung, K.C.; Lin, K.P.; Chang, C.H. A comparison of discrete algorithms for fuzzy weighted average. IEEE Trans. Fuzzy Syst. 2006, 14, 663–675. [Google Scholar] [CrossRef]
- Palma, L.B.; Antunes, R.A.; Gil, P.; Brito, V. Takagi-Sugeno-Kang fuzzy PID control for DC electrical machines. In Proceedings of the 2020 IEEE 14th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Setubal, Portugal, 8–10 July 2020; IEEE: Piscataway, NJ, USA, 2020; Volume 1, pp. 309–316. [Google Scholar]
- Biglarbegian, M.; Melek, W.W.; Mendel, J.M. Design of novel interval type-2 fuzzy controllers for modular and reconfigurable robots: Theory and experiments. IEEE Trans. Ind. Electron. 2010, 58, 1371–1384. [Google Scholar] [CrossRef]
- Kavikumar, R.; Sakthivel, R.; Kwon, O.M.; Selvaraj, P. Robust tracking control design for fractional-order interval type-2 fuzzy systems. Nonlinear Dyn. 2022, 107, 3611–3628. [Google Scholar] [CrossRef]
- Firouzi, B.; Alattas, K.A.; Bakouri, M.; Alanazi, A.K.; Mohammadzadeh, A.; Mobayen, S.; Fekih, A. A Type-2 Fuzzy Controller for Floating Tension-Leg Platforms in Wind Turbines. Energies 2022, 15, 1705. [Google Scholar] [CrossRef]
- Tai, K.; El-Sayed, A.R.; Biglarbegian, M.; Gonzalez, C.I.; Castillo, O.; Mahmud, S. Review of recent type-2 fuzzy controller applications. Algorithms 2016, 9, 39. [Google Scholar] [CrossRef]
- Mathworks, C. Computer Vision Toolbox for Matlab, Matlab. Available online: https://uk.mathworks.com/help/vision/index.html (accessed on 16 June 2022).
- Python.org. Python3. Available online: https://www.python.org/ (accessed on 14 January 2023).
- Torres, M.; Pelta, D.A.; Verdegay, J.L.; Torres, J.C. Coverage path planning with unmanned aerial vehicles for 3D terrain reconstruction. Expert Syst. Appl. 2016, 55, 441–451. [Google Scholar] [CrossRef]
- Cabreira, T.M.; Brisolara, L.B.; Ferreira, P.R., Jr. Survey on coverage path planning with unmanned aerial vehicles. Drones 2019, 3. [Google Scholar] [CrossRef]
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef]
- Intel Realsense. Intel Realsense D415. Available online: https://www.intelrealsense.com/depth-camera-d415 (accessed on 16 June 2022).
- Santos, M.C.; Santana, L.V.; Brandão, A.S.; Sarcinelli-Filho, M.; Carelli, R. Indoor low-cost localization system for controlling aerial robots. Control Eng. Pract. 2017, 61, 93–111. [Google Scholar] [CrossRef]
- Castillo, P.; Lozano, R.; Dzul, A. Stabilization of a mini-rotorcraft having four rotors. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No. 04CH37566), Sendai, Japan, 28 September–2 October 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 3, pp. 2693–2698. [Google Scholar]
- Upasane, S.J.; Hagras, H.; Anisi, M.H.; Savill, S.; Taylor, I.; Manousakis, K. A Big Bang-Big Crunch Type-2 Fuzzy Logic System for Explainable Predictive Maintenance. In Proceedings of the 2021 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Luxembourg, 11–14 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–8. [Google Scholar]
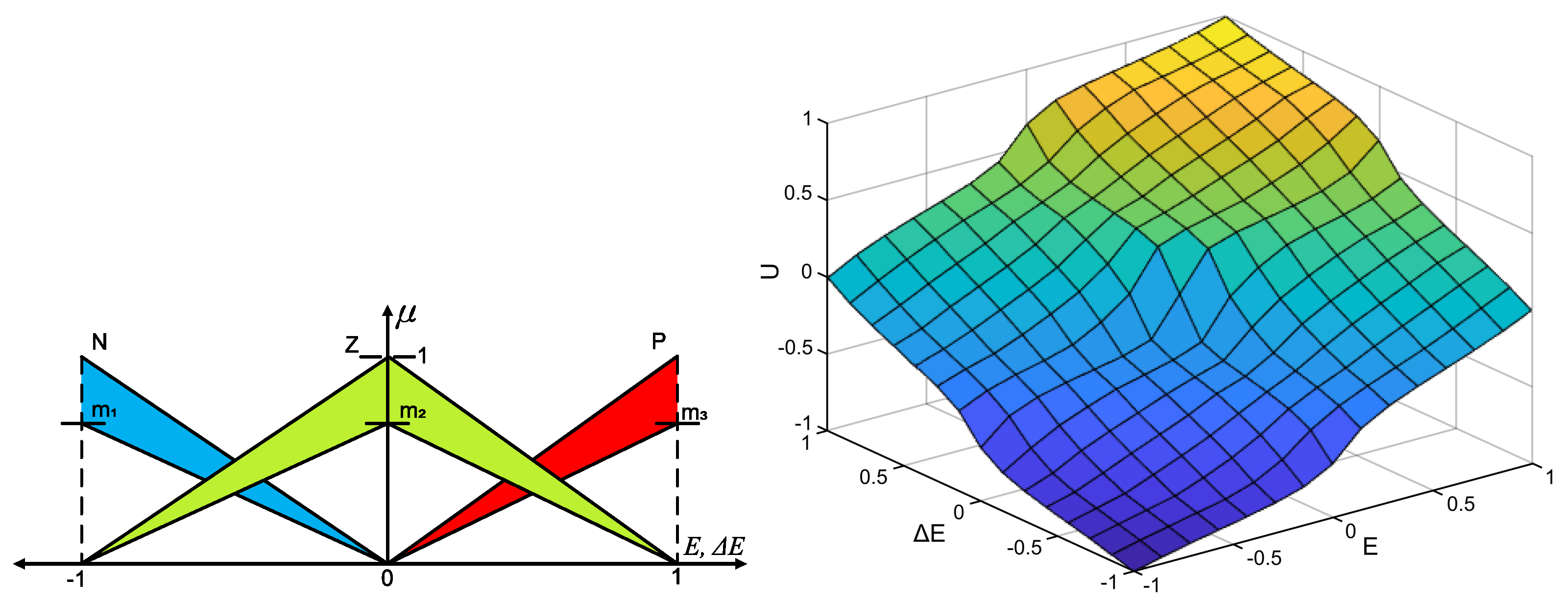




| P | Z | N | |
|---|---|---|---|
| P | PB:1 | PM:0.65 | Z:0 |
| Z | PM:0.65 | Z:0 | NM:−0.65 |
| N | Z:0 | NM:−0.65 | NB:−1 |
| Controller | Parameters | ISE |
|---|---|---|
| PID | , , | 82,133.4 |
| T1-FPID | , , , | 55,128.2 |
| IT2-FPID | , , , , | 36,371.9 |
| HSV | Hue | Saturation | Value |
|---|---|---|---|
| Maximum Values | 160 | 60 | 0 |
| Minimum Values | 200 | 255 | 255 |
| RMSE Values (m) | PID | T1-FPID | IT2-FPID |
|---|---|---|---|
| Set-Point Tracking | 0.2275 | 0.2255 | 0.2218 |
| Under Disturbance | 0.5574 | 0.5490 | 0.4971 |
| CPP Results | 0.5719 | 0.5597 | 0.4540 |
| RMSE Values (m) | PID | T1-FPID | IT2-FPID |
|---|---|---|---|
| Set-Point Tracking | 0.137 | 0.0964 | 0.0805 |
| Under Disturbance | 0.3103 | 0.1877 | 0.1810 |
| CPP Results | 0.1338 | 0.1298 | 0.1068 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Candan, F.; Dik, O.F.; Kumbasar, T.; Mahfouf, M.; Mihaylova, L. Real-Time Interval Type-2 Fuzzy Control of an Unmanned Aerial Vehicle with Flexible Cable-Connected Payload. Algorithms 2023, 16, 273. https://doi.org/10.3390/a16060273
Candan F, Dik OF, Kumbasar T, Mahfouf M, Mihaylova L. Real-Time Interval Type-2 Fuzzy Control of an Unmanned Aerial Vehicle with Flexible Cable-Connected Payload. Algorithms. 2023; 16(6):273. https://doi.org/10.3390/a16060273
Chicago/Turabian StyleCandan, Fethi, Omer Faruk Dik, Tufan Kumbasar, Mahdi Mahfouf, and Lyudmila Mihaylova. 2023. "Real-Time Interval Type-2 Fuzzy Control of an Unmanned Aerial Vehicle with Flexible Cable-Connected Payload" Algorithms 16, no. 6: 273. https://doi.org/10.3390/a16060273
APA StyleCandan, F., Dik, O. F., Kumbasar, T., Mahfouf, M., & Mihaylova, L. (2023). Real-Time Interval Type-2 Fuzzy Control of an Unmanned Aerial Vehicle with Flexible Cable-Connected Payload. Algorithms, 16(6), 273. https://doi.org/10.3390/a16060273








