Combinatorial Generation Algorithms for Some Lattice Paths Using the Method Based on AND/OR Trees †
Abstract
1. Introduction
- Listing: the sequential generation of all objects belonging to the combinatorial set;
- Ranking: the assignment of an individual number (a rank) to an object belonging to the combinatorial set (this requires some way to order the elements of the combinatorial set);
- Unranking: the generation of an object belonging to the combinatorial set by the value of its rank (this requires some way to order the elements of the combinatorial set);
- Random selection: the generation of random objects belonging to the combinatorial set.
2. Materials and Methods
3. Results
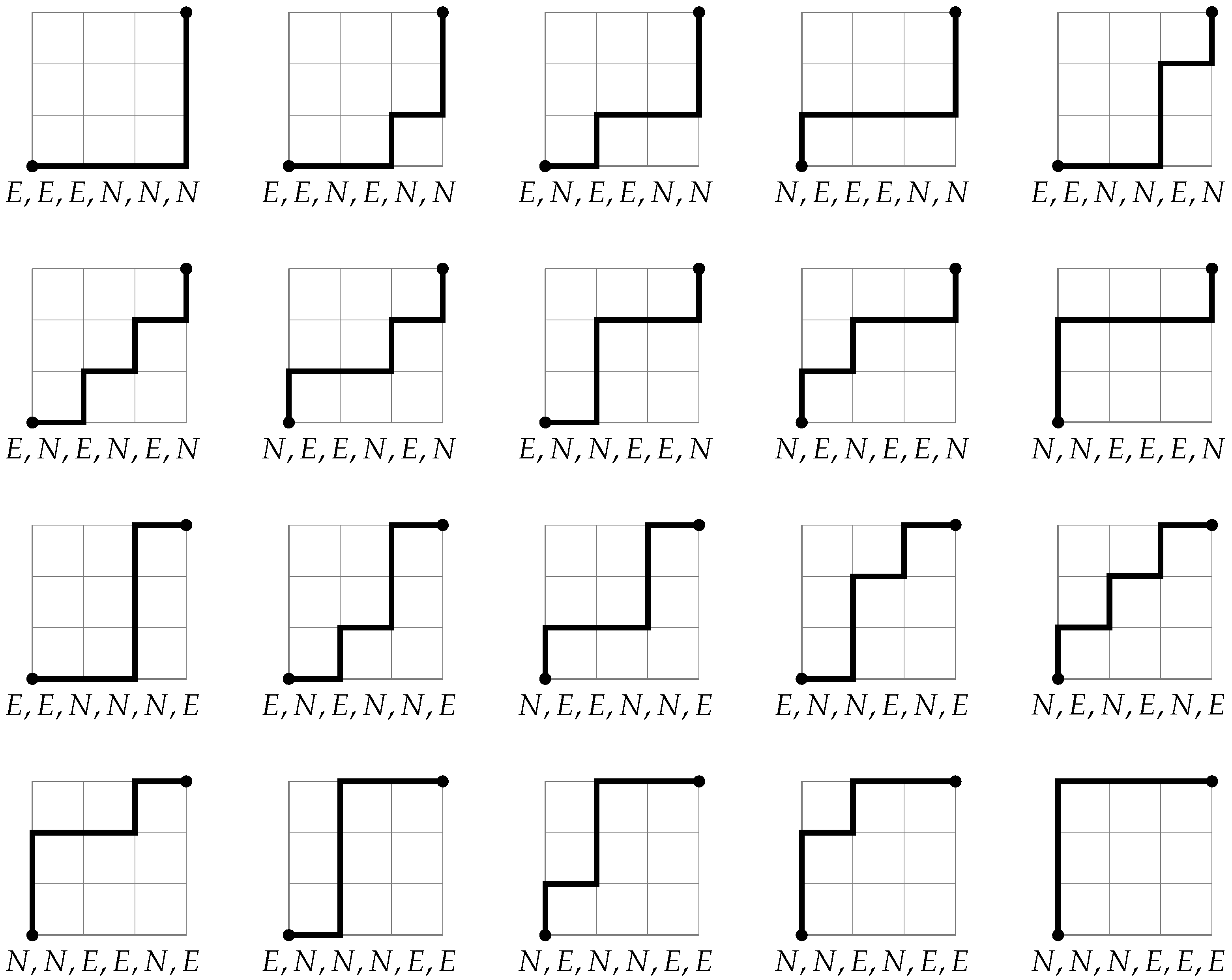
3.1. Combinatorial Generation Algorithms for North-East Lattice Paths
3.1.1. Combinatorial Set
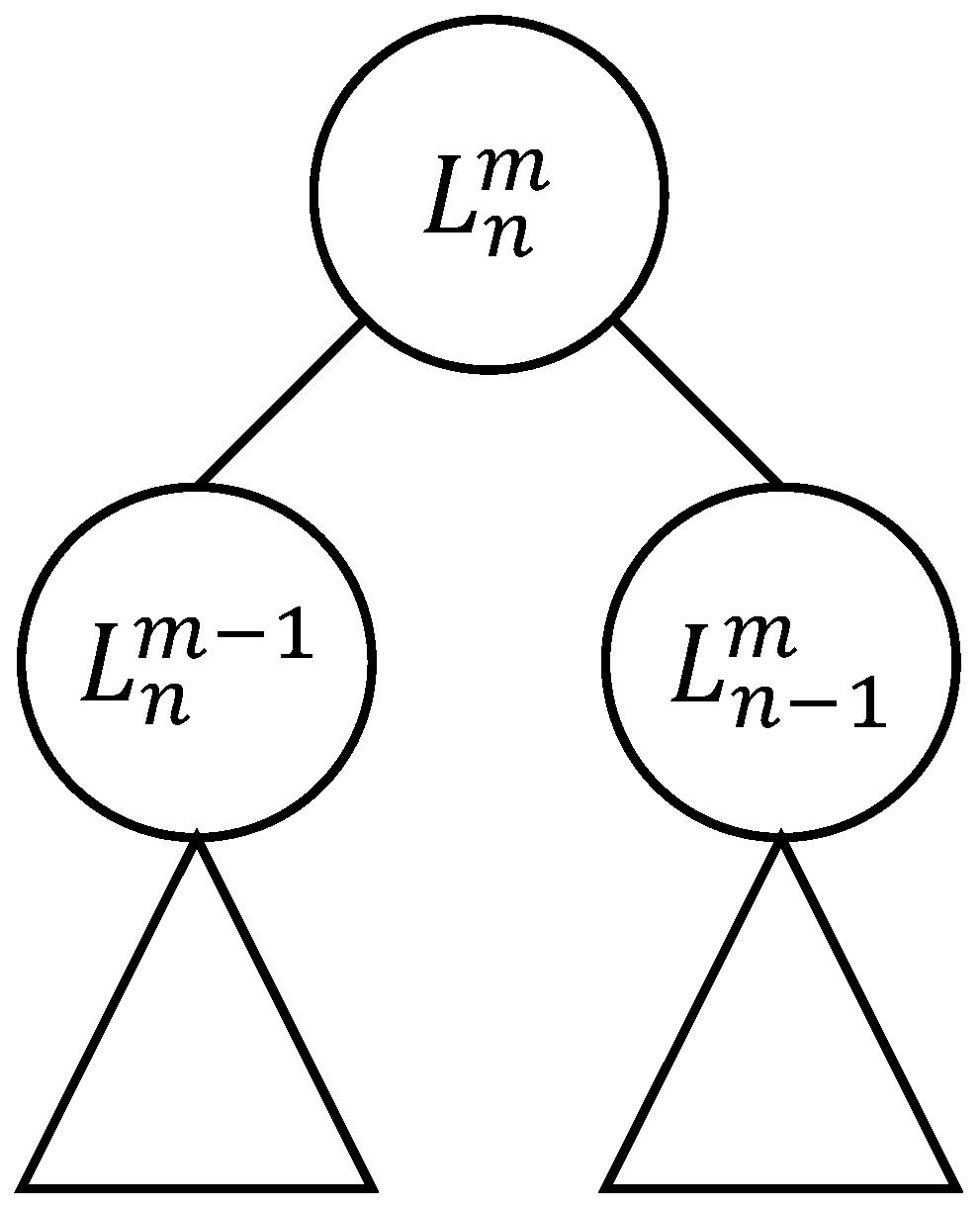
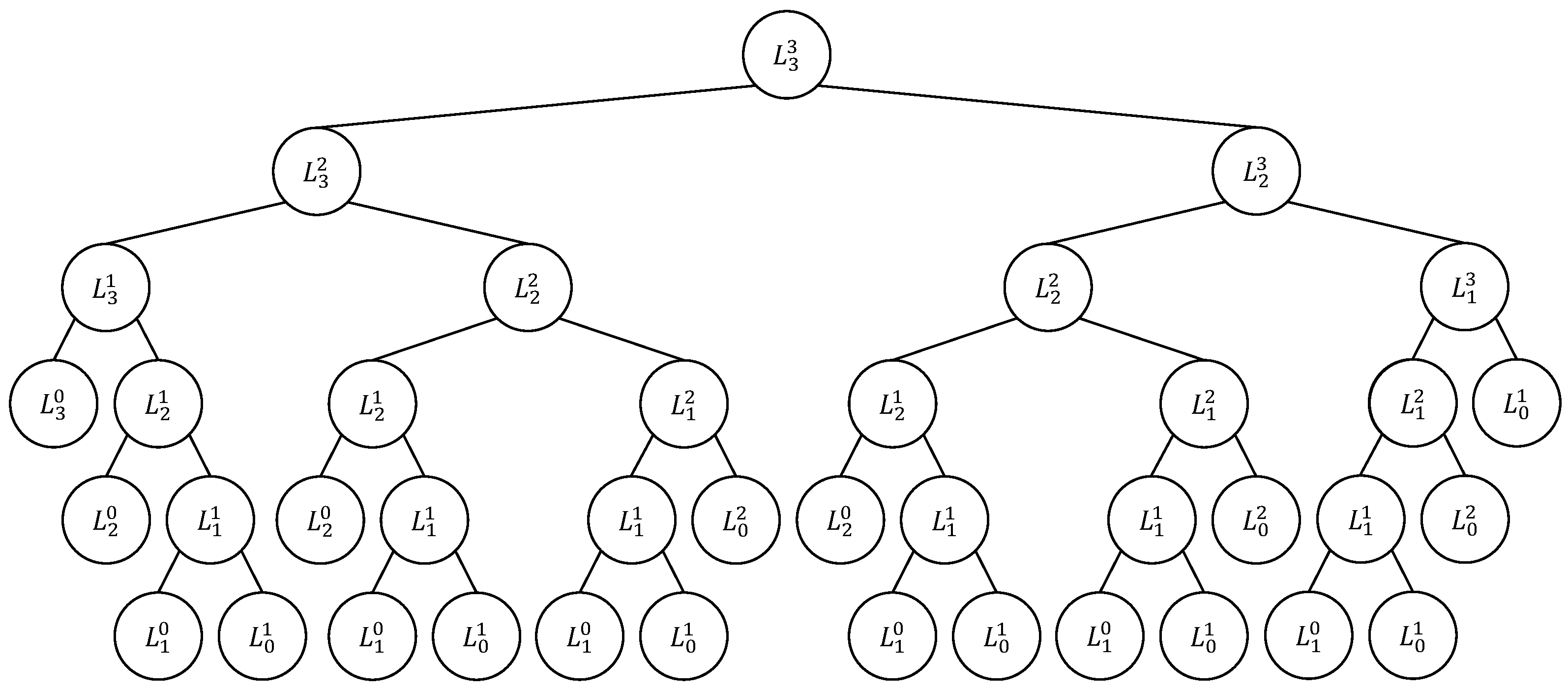
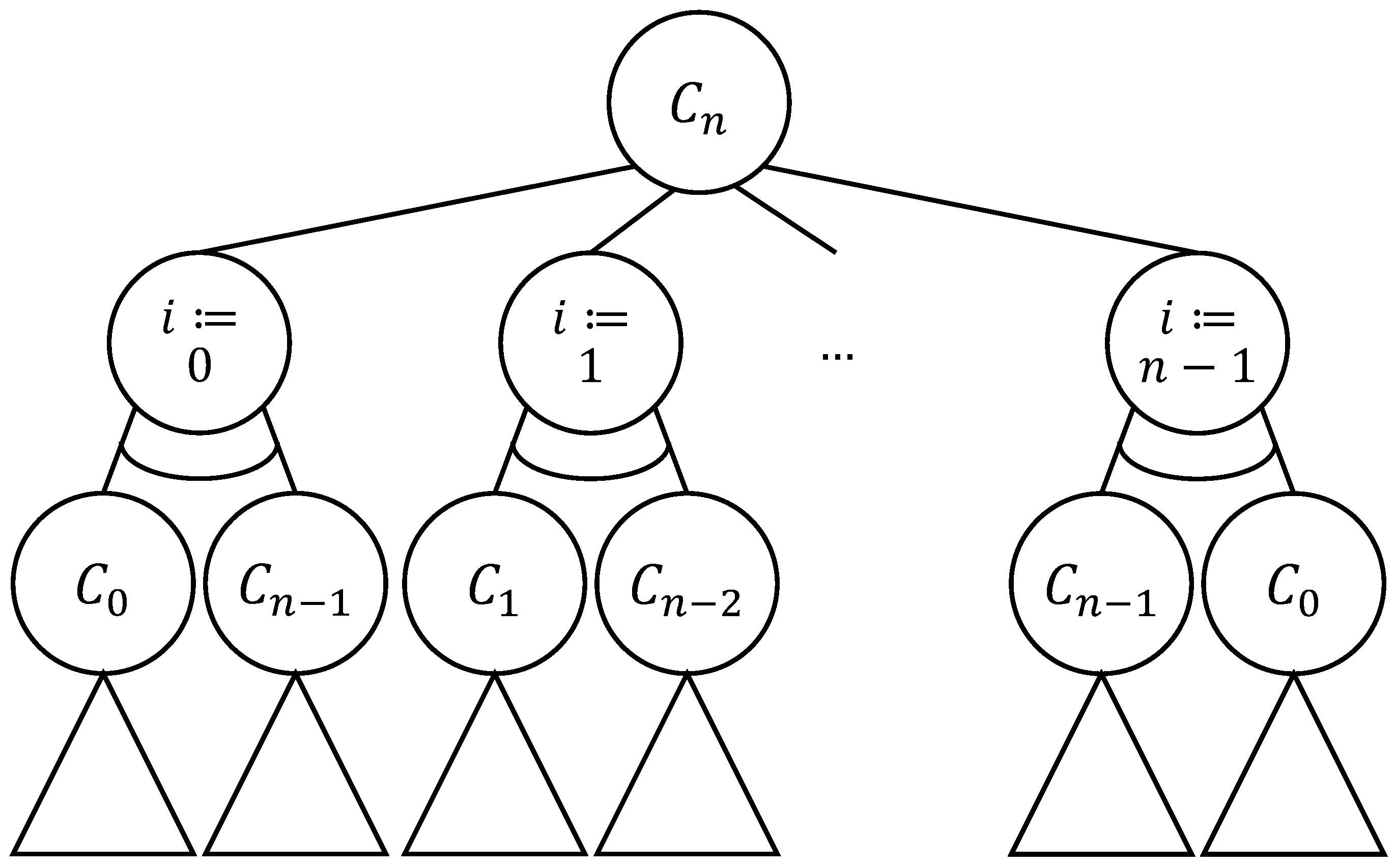
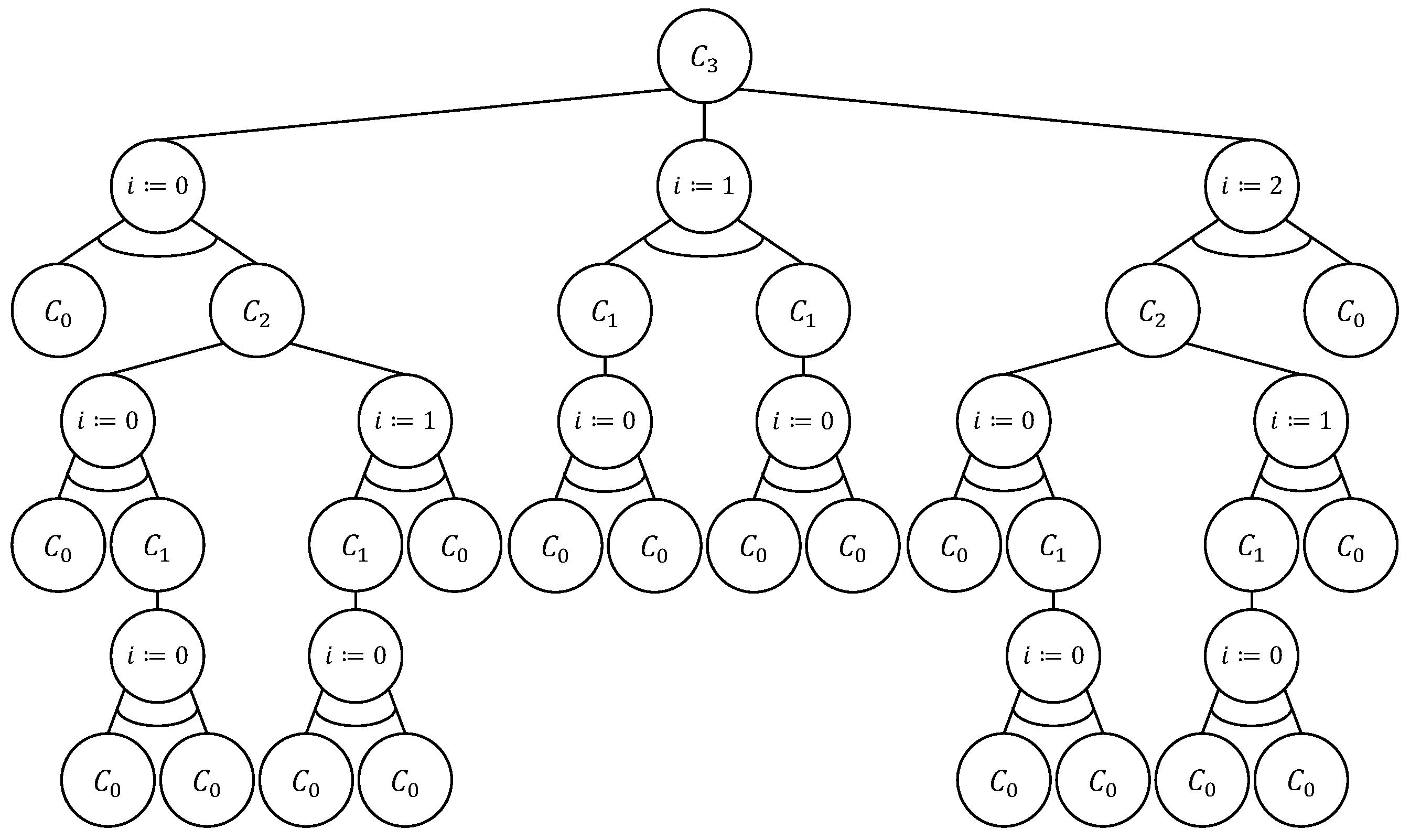
3.1.2. AND/OR Tree Structure
- Each node labeled is a leaf node in the AND/OR tree for ;
- Each node labeled is a leaf node in the AND/OR tree for .
- Each selected left child of the OR node labeled determines the addition of one North-step to the North-East lattice path obtained by the subtree of the node labeled : the resulting lattice path is ;
- Each selected right child of the OR node labeled determines the addition of one East-step to the North-East lattice path obtained by the subtree of the node labeled : the resulting lattice path is ;
- Each leaf node labeled determines the lattice path from to that consists of n East-steps: the resulting lattice path is ;
- Each leaf node labeled determines the lattice path from to that consists of m North-steps: the resulting lattice path is .
3.1.3. Ranking and Unranking Algorithms
| Algorithm 1: An algorithm for ranking a variant of the AND/OR tree for . |
 |
| Algorithm 2: An algorithm for unranking a variant of the AND/OR tree for . |
 |
- Algorithm 1 has at most m recursive calls where (each such recursive call requires one assignment) and has at most n recursive calls where (each such recursive call requires calculations of ). Applying Equation (1), the calculation of has linear time complexity for and for . Hence, Algorithm 1 has polynomial time complexity for and for ;
- Algorithm 2 has at most recursive calls where each such recursive call requires calculations of . Hence, Algorithm 2 has polynomial time complexity for and for .
3.2. Combinatorial Generation Algorithms for Dyck Paths
3.2.1. Combinatorial Set
3.2.2. AND/OR Tree Structure
- Each node labeled is a leaf node in the AND/OR tree for .
- An empty sequence corresponds to the selection of a leaf node labeled ;
- I corresponds to the selected value of i in the AND/OR tree for ;
- corresponds to the variant of the subtree of the node labeled (the left subtree);
- corresponds to the variant of the subtree of the node labeled (the right subtree).
- Each selected child of the OR node labeled determines the addition of one East-step and one North-step to the Dyck -path that merges the Dyck I-path obtained by the subtree of the node labeled and consisting of steps and the Dyck -path obtained by the subtree of the node labeled and consisting of steps: the resulting Dyck n-path is ;
- The subtree of the node labeled (the left subtree) determines the Dyck I-path of the form ;
- The subtree of the node labeled (the right subtree) determines the Dyck -path of the form ;
- Each leaf node labeled determines the empty lattice path.
3.2.3. Ranking and Unranking Algorithms
- Algorithm 3 has at most n recursive calls, where each such recursive call requires calculations of maximum times. Applying Equation (3), the calculation of has linear time complexity . Hence, Algorithm 3 has polynomial time complexity ;
- Algorithm 4 has at most n recursive calls, where each such recursive call requires calculations of maximum times. Hence, Algorithm 4 has polynomial time complexity .
| Algorithm 3: An algorithm for ranking a variant of the AND/OR tree for . |
 |
| Algorithm 4: An algorithm for unranking a variant of the AND/OR tree for . |
 |
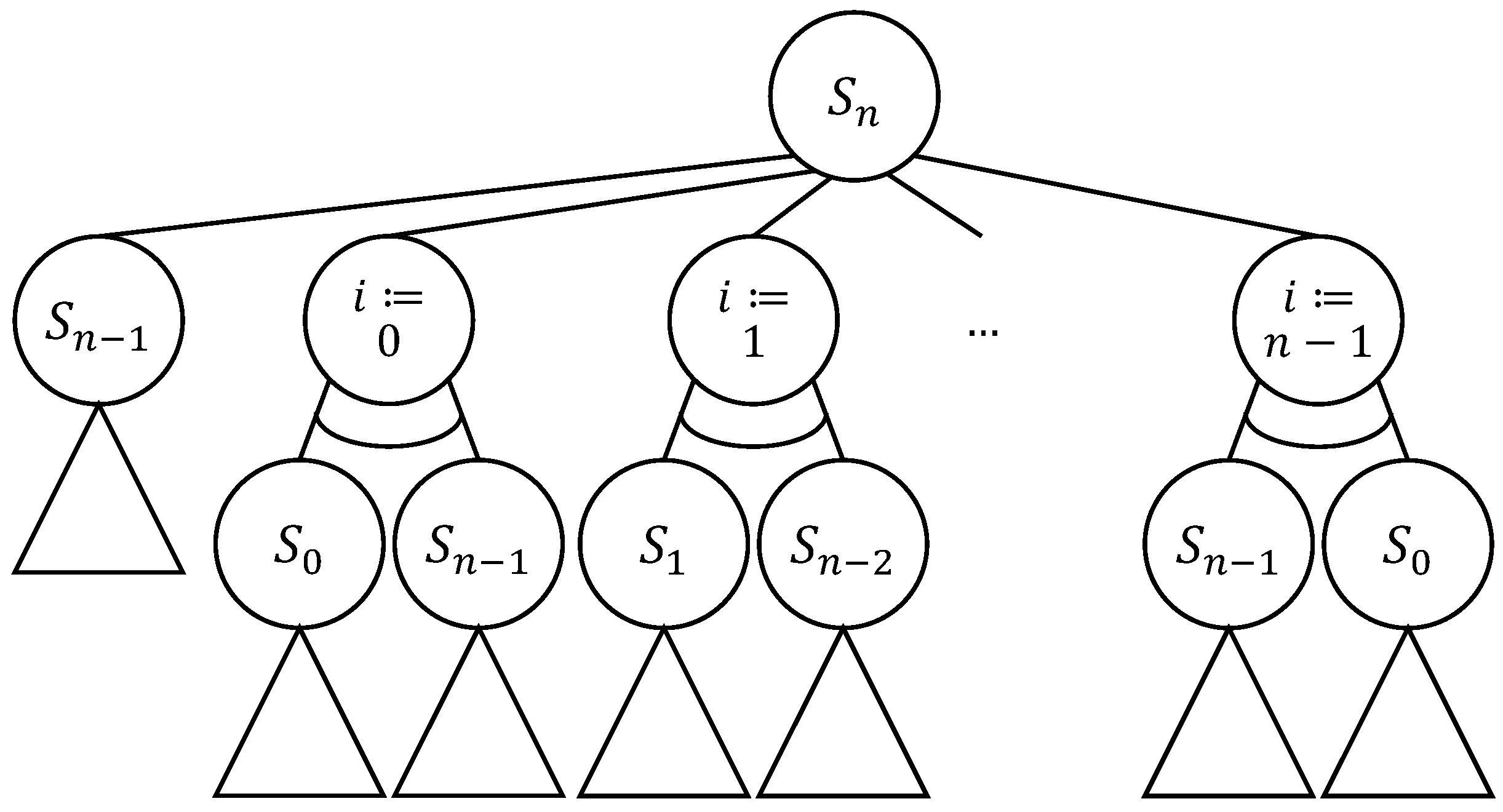
3.3. Combinatorial Generation Algorithms for Delannoy Paths
3.3.1. Combinatorial Set
3.3.2. AND/OR Tree Structure
- Each node labeled is a leaf node in the AND/OR tree for ;
- Each node labeled is a leaf node in the AND/OR tree for .
- Each selected left child of the OR node labeled determines the addition of one North-step to the Delannoy path obtained by the subtree of the node labeled and consisting of k steps: the resulting lattice path is ;
- Each selected middle child of the OR node labeled determines the addition of one East-step to the Delannoy path obtained by the subtree of the node labeled and consisting of k steps: the resulting lattice path is ;
- Each selected right child of the OR node labeled determines the addition of one North-East-step to the Delannoy path obtained by the subtree of the node labeled and consisting of k steps: the resulting lattice path is ;
- Each leaf node labeled determines the Delannoy path from to that consists of n East-steps: the resulting lattice path is ;
- Each leaf node labeled determines the Delannoy path from to that consists of m North-steps: the resulting lattice path is .
3.3.3. Ranking and Unranking Algorithms
| Algorithm 5: An algorithm for ranking a variant of the AND/OR tree for . |
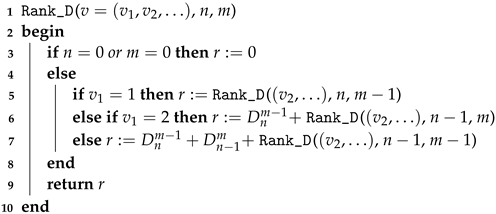 |
| Algorithm 6: An algorithm for unranking a variant of the AND/OR tree for . |
 |
- Algorithm 5 has at most m recursive calls where (each such recursive call requires one assignment), has at most n recursive calls where (each such recursive call requires calculations of ), and has at most recursive calls where (each such recursive call requires calculations of and ). Applying Equation (5), the calculation of has polynomial time complexity for and for . Hence, Algorithm 5 has polynomial time complexity for and for ;
- Algorithm 6 has at most recursive calls where each such recursive call requires calculations of or . Hence, Algorithm 2 has polynomial time complexity for and for .
3.4. Combinatorial Generation Algorithms for Schroder Paths
3.4.1. Combinatorial Set
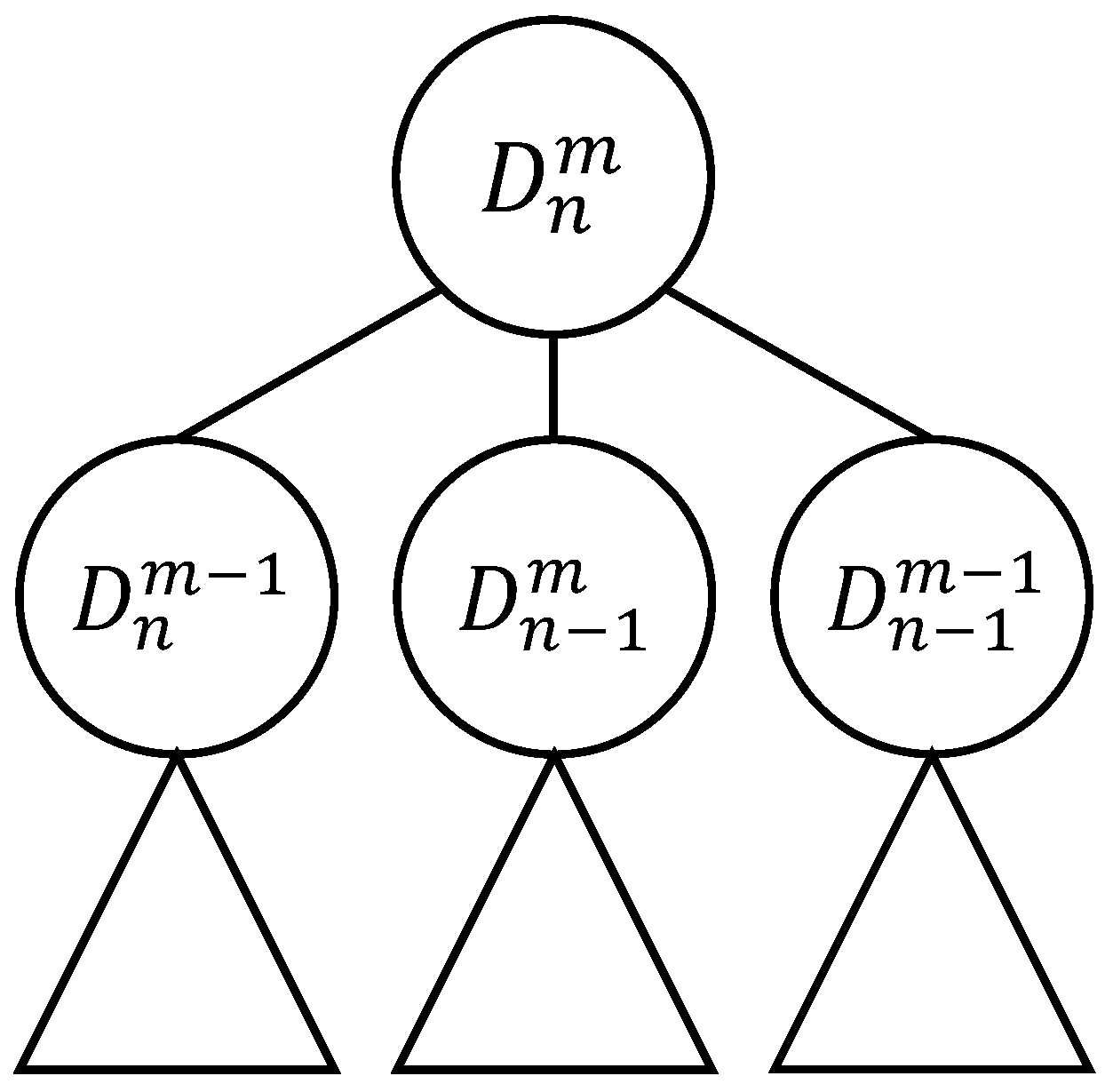
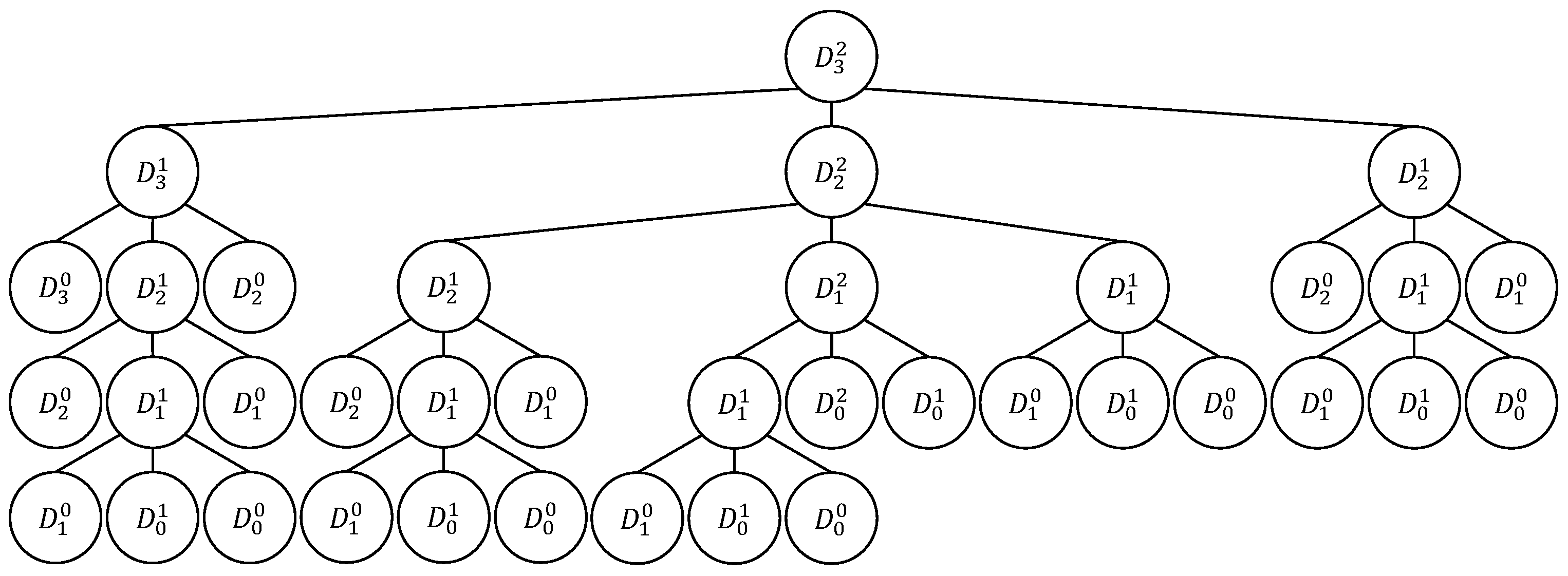
3.4.2. AND/OR Tree Structure
- Each node labeled is a leaf node in the AND/OR tree for .
- If the left child of the OR nodde labeled is selected, then , where
- ;
- corresponds to the variant of the subtree of the node labeled ;
- Otherwise , where
- I corresponds to the selected value of i in the AND/OR tree for ;
- corresponds to the variant of the subtree of the node labeled ;
- corresponds to the variant of the subtree of the node labeled ;
- An empty sequence corresponds to the selection of a leaf node labeled .
- Each selected left child of the OR node labeled determines the addition of one North-East-step to the Schroder -path obtained by the subtree of the node labeled and consisting of k steps: the resulting Schroder n-path is ;
- Each selected child of the OR node labeled determines the addition of one East-step and one North-step to the Schroder -path that merges the Schroder I-path obtained by the subtree of the node labeled and consisting of steps and the Schroder -path obtained by the subtree of the node labeled and consisting of steps: the resulting Schroder n-path is ;
- The subtree of the node labeled (the left subtree) determines the Schroder I-path of the form ;
- The subtree of the node labeled (the right subtree) determines the Schroder -path of the form ;
- Each leaf node labeled determines the empty lattice path ().
3.4.3. Ranking and Unranking Algorithms
- Algorithm 7 has at most n recursive calls where (each such recursive call requires one assignment) and has at most n recursive calls where (each such recursive call requires calculations of maximum times). Applying Equation (7), the calculation of has polynomial time complexity . Hence, Algorithm 7 has polynomial time complexity ;
- Algorithm 8 has at most n recursive calls where (each such recursive call requires calculations of ) and has at most n recursive calls where (each such recursive call requires calculations of maximum times). Hence, Algorithm 8 has polynomial time complexity .
| Algorithm 7: An algorithm for ranking a variant of the AND/OR tree for . |
 |
| Algorithm 8: An algorithm for unranking a variant of the AND/OR tree for . |
 |
3.5. Combinatorial Generation Algorithms for Motzkin Paths
3.5.1. Combinatorial Set
3.5.2. AND/OR Tree Structure
- each node labeled or is a leaf node in the AND/OR tree for .
- If the left child of the OR node labeled is selected, then , where
- ;
- corresponds to the variant of the subtree of the node labeled ;
- Otherwise , where
- I corresponds to the selected value of i in the AND/OR tree for ;
- corresponds to the variant of the subtree of the node labeled ;
- corresponds to the variant of the subtree of the node labeled ;
- An empty sequence corresponds to the selection of a leaf node labeled .
- each selected left child of the OR node labeled determines the addition of one North-East-step to the Motzkin -path obtained by the subtree of the node labeled and consisting of k steps: the resulting Motzkin n-path is ;
- each selected child of the OR node labeled determines the addition of two East-steps and North-steps to the Motzkin -path that merges the Motzkin I-path obtained by the subtree of the node labeled and consisting of steps and the Motzkin -path obtained by the subtree of the node labeled and consisting of steps: the resulting Motzkin n-path is ;
- the subtree of the node labeled (the left subtree) determines the Motzkin I-path of the form ;
- the subtree of the node labeled (the right subtree) determines the Motzkin -path of the form ;
- each leaf node labeled determines the lattice path from to that consists of one North-East-step: the resulting lattice path is ;
- each leaf node labeled determines the empty lattice path ().
3.5.3. Ranking and Unranking Algorithms
- Algorithm 9 has at most n recursive calls where (each such recursive call requires one assignment) and has at most n recursive calls where (each such recursive call requires calculations of maximum times). Applying Equation (9), the calculation of has polynomial time complexity . Hence, Algorithm 9 has polynomial time complexity ;
- Algorithm 10 has at most n recursive calls where (each such recursive call requires calculations of ) and has at most n recursive calls where (each such recursive call requires calculations of maximum times). Hence, Algorithm 10 has polynomial time complexity .
| Algorithm 9: An algorithm for ranking a variant of the AND/OR tree for . |
 |
| Algorithm 10: An algorithm for unranking a variant of the AND/OR tree for . |
 |
3.6. Computational Experiments
4. Discussion
- By calculating (for example, see Line 5 in Algorithm 3 or Lines 5–14 in Algorithm 4), applying a simpler explicit formula without using the summation operator;
- By a preliminary search of the value of the selected child of the OR node (for example, the parameter I defined in Lines 6–14 in Algorithm 4), applying an approximate formula (as in [26]).
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kreher, D.L.; Stinson, D.R. Combinatorial Algorithms: Generation, Enumeration, and Search; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Ruskey, F. Combinatorial Generation. Available online: https://page.math.tu-berlin.de/~felsner/SemWS17-18/Ruskey-Comb-Gen.pdf (accessed on 1 May 2023).
- Knuth, D.E. The Art of Computer Programming, Volume 4A: Combinatorial Algorithms, Part 1; Addison-Wesley Professional: Boston, MA, USA, 2011. [Google Scholar]
- Stanley, R.P. Enumerative Combinatorics: Volume 1, 2nd ed.; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Wallner, M. Combinatorics of Lattice Paths and Tree-Like Structures. Ph.D. Thesis, Institute of Discrete Mathematics and Geometry, Vienna University of Technology, Vienna, Austria, 2016. [Google Scholar]
- Humphreys, K. A history and a survey of lattice path enumeration. J. Statist. Plann. Inference 2010, 140, 2237–2254. [Google Scholar] [CrossRef]
- Krattenthaler, C. Lattice path enumeration. In Handbook of Enumerative Combinatorics; Bona, M., Ed.; CRC Press: New York, NY, USA, 2015; pp. 589–678. [Google Scholar]
- Zaks, S.; Richards, D. Generating trees and other combinatorial objects lexicographically. SIAM J. Comput. 1979, 8, 73–81. [Google Scholar] [CrossRef]
- Bent, S.W. Ranking trees generated by rotations. Lect. Notes Comput. Sci. 1990, 447, 132–142. [Google Scholar]
- Parque, V.; Miyashita, T. An efficient scheme for the generation of ordered trees in constant amortized time. In Proceedings of the 15th International Conference on Ubiquitous Information Management and Communication (IMCOM), Seoul, Republic of Korea, 4–6 January 2021. [Google Scholar]
- Barcucci, E.; Bernini, A.; Pinzani, R. Exhaustive generation of positive lattice paths. In Proceedings of the 11th International Conference on Random and Exhaustive Generation of Combinatorial Structures (GASCom), Athens, Greece, 18–20 June 2018. [Google Scholar]
- Barcucci, E.; Bernini, A.; Pinzani, R. Exhaustive generation of some lattice paths and their prefixes. Theoret. Comput. Sci. 2021, 878–879, 47–52. [Google Scholar] [CrossRef]
- Kuo, T. From enumerating to generating: A linear time algorithm for generating 2D lattice paths with a given number of turns. Algorithms 2015, 8, 190–208. [Google Scholar] [CrossRef]
- The Combinatorial Object Server. Available online: http://combos.org/ (accessed on 1 May 2023).
- Barcucci, E.; Del Lungo, A.; Pergola, E.; Pinzani, R. ECO: A methodology for the enumeration of combinatorial objects. J. Differ. Equ. Appl. 1999, 5, 435–490. [Google Scholar] [CrossRef]
- Flajolet, P.; Zimmerman, P.; Cutsem, B. A calculus for the random generation of combinatorial structures. Theoret. Comput. Sci. 1994, 132, 1–35. [Google Scholar] [CrossRef]
- Shablya, Y.; Kruchinin, D.; Kruchinin, V. Method for developing combinatorial generation algorithms based on AND/OR trees and its application. Mathematics 2020, 8, 962. [Google Scholar] [CrossRef]
- Shablya, Y.; Tokareva, A. Development of combinatorial generation algorithms for some lattice paths using the method based on AND/OR trees. In Proceedings of the 5th Mediterranean International Conference of Pure & Applied Mathematics and Related Areas (MICOPAM), Antalya, Turkey, 27–30 October 2022. [Google Scholar]
- Mohanty, G. Lattice Path Counting and Applications; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- The On-Line Encyclopedia of Integer Sequences. Available online: https://oeis.org/ (accessed on 1 May 2023).
- Mansour, T. Statistics on Dyck paths. J. Integer Seq. 2005, 9, 06.1.5. [Google Scholar]
- Banderier, C.; Schwer, S. Why Delannoy numbers? J. Statist. Plann. Inference 2005, 135, 40–54. [Google Scholar] [CrossRef]
- Shapiro, L.W.; Sulanke, R.A. Bijections for the Schroder numbers. Math. Mag. 2000, 73, 369–376. [Google Scholar] [CrossRef]
- Oste, R.; Van der Jeugt, J. Motzkin paths, Motzkin polynomials and recurrence relations. Electron. J. Combin. 2015, 22, P2.8. [Google Scholar] [CrossRef] [PubMed]
- Maxima, a Computer Algebra System. Available online: https://maxima.sourceforge.io/ (accessed on 1 May 2023).
- Kruchinin, V.; Shablya, Y.; Kruchinin, D. Unranking small combinations of a large set in co-lexicographic order. Algorithms 2022, 15, 36. [Google Scholar] [CrossRef]
- Deutsch, E.; Munarini, E.; Rinaldi, R. Skew Dyck paths. J. Statist. Plann. Inference 2010, 140, 2191–2203. [Google Scholar] [CrossRef]
- Prodinger, H. Skew Dyck paths with catastrophes. Discrete Math. Lett. 2022, 10, 9–13. [Google Scholar]
- Kruchinin, D.; Kruchinin, V.; Shablya, Y. On some properties of generalized Narayana numbers. Quaest. Math. 2022, 45, 1949–1963. [Google Scholar] [CrossRef]












| Lattice Path | Variant of AND/OR Tree | Rank |
|---|---|---|
| 0 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| 15 | ||
| 16 | ||
| 17 | ||
| 18 | ||
| 19 |
| Lattice Path | Variant of AND/OR Tree | Rank |
|---|---|---|
| 0 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
| Lattice Path | Variant of AND/OR Tree | Rank |
|---|---|---|
| 0 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| 15 | ||
| 16 | ||
| 17 | ||
| 18 | ||
| 19 | ||
| 20 | ||
| 21 | ||
| 22 | ||
| 23 | ||
| 24 |
| Lattice Path | Variant of AND/OR Tree | Rank |
|---|---|---|
| 0 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| 15 | ||
| 16 | ||
| 17 | ||
| 18 | ||
| 19 | ||
| 20 | ||
| 21 |
| Lattice path | Variant of AND/OR tree | Rank |
|---|---|---|
| 0 | ||
| 1 | ||
| 2 | ||
| 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shablya, Y. Combinatorial Generation Algorithms for Some Lattice Paths Using the Method Based on AND/OR Trees. Algorithms 2023, 16, 266. https://doi.org/10.3390/a16060266
Shablya Y. Combinatorial Generation Algorithms for Some Lattice Paths Using the Method Based on AND/OR Trees. Algorithms. 2023; 16(6):266. https://doi.org/10.3390/a16060266
Chicago/Turabian StyleShablya, Yuriy. 2023. "Combinatorial Generation Algorithms for Some Lattice Paths Using the Method Based on AND/OR Trees" Algorithms 16, no. 6: 266. https://doi.org/10.3390/a16060266
APA StyleShablya, Y. (2023). Combinatorial Generation Algorithms for Some Lattice Paths Using the Method Based on AND/OR Trees. Algorithms, 16(6), 266. https://doi.org/10.3390/a16060266






