Abstract
This paper examines a calculus-based approach to building model functions in a derivative-free algorithm. This calculus-based approach can be used when the objective function considered is defined via more than one blackbox. Two versions of a derivative-free trust-region method are implemented. The first version builds model functions by using a calculus-based approach, and the second version builds model functions by directly considering the objective function. The numerical experiments demonstrate that the calculus-based approach provides better results in most situations and significantly better results in specific situations.
1. Introduction
Trust-region methods are a popular class of algorithms for finding the solutions of nonlinear minimization optimization problems [1,2]. Trust-region algorithms build a model of the objective function in a neighborhood of the incumbent solution. The region in which the model function behaves similarly to the objective function is called the trust region and is defined through a trust-region radius. The optimization algorithm then finds a point in the trust region at which the model sufficiently decreases. This step is known as the trust-region sub-problem, and the point that provides a sufficient decrease is called the trial point. The value of the objective function is then computed at the trial point. If the ratio of the achieved reduction versus the reduction in the model is sufficient, then the incumbent solution is updated and set to be equal to the trial point. If the ratio is not sufficient, then the trust-region radius is decreased. This method iterates until a stopping condition implies that a local minimizer has been located.
Extensive research has been done on this topic since 1944, when Levenberg published what is known to be the first paper related to trust-region methods [3]. Early work on trust-region methods includes the work of Dennis and Mei [4], Dennis and Schnabel [5], Fletcher [6], Goldfeldt, Quandt, and Trotter [7], Hebden [8], Madsen [9], Moré [10,11], Moré and Sorensen [12], Osborne [13], Powell [14,15,16,17,18], Sorensen [19,20], Steihaug [21], Toint [22,23,24,25], and Winfield [26,27], to name a few. The name trust region seems to have been used for the first time in 1978 by Dennis in [28].
In the works mentioned above, trust-region methods were designed and analyzed under the assumption that first-order information about the objective function is available and that second-order information (i.e., Hessians) may, or may not, be available. In the case in which both first-order and second-order information is not available, or it is hard to directly obtain, derivative-free trust-region (DFTR) methods can be used. This type of method has become more popular in the last two decades due to the rise of blackbox optimization problems. Early works on DFTR methods include those of Conn, Scheinberg, and Toint [29], Marazzi and Nocedal [30], Powell [31,32], and Colson and Toint [33], to name a few.
In 2009, the convergence properties of general DFTR algorithms for unconstrained optimization problems were rigorously investigated [34]. The pseudo-code of an algorithm that converges to a first-order critical point and the pseudo-code of an algorithm that converges to a second-order critical point were provided. A complete review of the DFTR methods for unconstrained optimization problems is available in [35] (Chapters 10 and 11) and [36] (Chapter 11). There now exist several DFTR algorithms for solving unconstrained optimization problems, such as Advanced DFO-TRNS [37], BOOSTERS [38], CSV2 [39], DFO [29,40], UOBYQA [31], and WEDGE [30]. In recent years, DFTR algorithms have also been developed for constrained optimization problems. When an optimization problem is bound-constrained, some of the algorithms available in the literature are BC-DFO [41], BOBYQA [42], ORBIT [43,44], SNOBFIT [45], and TRB-POWELL [46]. Other DFTR algorithms dealing with more general constrained optimization problems include CONDOR [47], CONORBIT [48], DEFT-FUNNEL [49], LCOBYQA [50], LINCOA [51], and S [52].
We define a blackbox as any process that returns an output whenever an input is provided, but where the inner mechanism of the process is not analytically available to the optimizer [36]. In this paper, we consider a situation in which the objective function, is obtained by manipulating several blackboxes. For instance, F could be the product of two functions, say, and , where the function values for are obtained through one blackbox and the function values for are obtained through a different blackbox. An objective function that is defined by manipulating more than one function is called a composite objective function.
Composite objective functions have inspired a particular direction of research under the assumption that the functions involved do not have the same computational costs. For instance, Khan et al. [53] developed an algorithm for minimizing , where is smooth with known derivatives, h is a known nonsmooth piecewise linear function, and f is smooth but expensive to evaluate. In [54], Larson et al. investigated the minimization problem , where h is nonsmooth and inexpensive to compute and f is smooth, but its Jacobian is not available. Recently, Larson and Menickelley developed algorithms for bound-constrained nonsmooth composite minimization problems in which the objective function F has the form , where h is cheap to evaluate, and f requires considerable time to evaluate.
These ideas have led to research on more general calculus-based approaches to approximating gradients or Hessians of composite functions. In [55,56,57], the authors provided calculus rules (integer power, product, quotient, and chain) for (generalized) simplex gradients. These results were advanced to the (generalized) centered simplex gradient in [58] and to the (generalized) simplex Hessian in [59]. In [60], a unified framework that provides general error bounds for gradient and Hessian approximation techniques by using calculus rules was presented.
Previous research has shown that a calculus-based approach to approximating gradients or Hessians can be substantially more accurate than a non-calculus-based approach in several situations [55,58,59,60]. However, it is still unclear if these theoretical results translate to a significant improvement in a derivative-free algorithm. The main goal of this paper is to compare two versions of a DFTR algorithm designed to solve a box-constrained blackbox optimization problem in which the objective function is a composite function: one that employs a calculus-based approach and one that does not employ a calculus-based approach. It is worth emphasizing that it is not our intention to show that the DFTR algorithm developed in this paper is better than state-of-the-art derivative-free algorithms. The main goal is to analyze any benefits resulting from using a calculus-based approach in a DFTR algorithm designed to minimize a composite objective function.
This paper is organized as follows. In Section 2, the context is established and fundamental notions related to the topic of this paper are presented. In Section 3, the pseudo-code of the DFTR algorithm is introduced, and details related to the algorithm are discussed. In Section 4, numerical experiments are conducted to compare the calculus-based approach with the non-calculus-based approach. In Section 5, the results of the numerical experiments are scrutinized. Lastly, the main results of this paper, the limitations of this paper, and future research directions are briefly discussed in Section 6.
2. Background
Unless otherwise stated, we use the standard notation found in [36]. We work in the finite-dimensional space with the inner product . The norm of a vector is denoted as and is taken to be the norm. Given a matrix the induced matrix norm is used.
We denote by the closed ball centered at with radius The identity matrix in is denoted by , and the vector of all ones in is denoted by The Minkowski sum of two sets of vectors A and B is denoted by That is,
In the next sections, we will refer to a calculus-based approach and a non-calculus approach to approximate gradients and Hessians. Let us clarify the meanings of these two approaches.
We begin with the non-calculus-based approach. Let and let be a quadratic interpolation of F at using distinct sample points poised for quadratic interpolation. An approximation of the gradient of F at , denoted by is obtained by computing and an approximation of the Hessian of F at , denoted by is obtained by computing
We now explain the calculus-based approach. Let be constructed using and . Let and be quadratic interpolation functions of and , respectively. When a calculus-based approach is employed and the composite objective function F has the form then
and
Similarly, when the composite objective function F has the form then (assuming )
and
To compute the technique called the (generalized) simplex Hessian is utilized [59]. When the two matrices involved in the computation of the simplex Hessian are square matrices that have been properly chosen, the simplex Hessian is equal to the Hessian of the quadratic interpolation function. The formula for computing simplex Hessians is based on simple matrix algebra. Hence, this technique is straightforward to implement in an algorithm. The formula for computing the simplex Hessian requires the computation of simplex gradients.
Definition 1
([55]). (Simplex gradient). Let . Let be the point of interest. Let with The simplex gradient of f at over T is denoted by and defined by
where
Definition 2
([59]). (Simplex Hessian). Let and let be the point of interest. Let and with The simplex Hessian of f at over S and T is denoted by and defined by
where
The simplex gradient and simplex Hessian do not necessarily require the matrices S and T to be square matrices with a full rank. These two definitions may be generalized by using the Moore–Penrose pseudoinverse of a matrix [55,59].
Last, we recall the definition of a fully linear class of models.
Definition 3
([36]). (Class of fully linear models). Given and we say that is a class of fully linear models of f at x parametrized by Δ if there exists a pair of scalars and such that, given any the model satisfies
Note that a fully linear model is equivalent to a model that is order-1 gradient accurate and order-2 function accurate based on the definitions introduced in [56].
We are now ready to introduce the pseudo-code of the DFTR algorithm that will be used to compare the calculus-based approach with the non-calculus-based approach.
3. Materials and Methods
In this section, the algorithm designed to minimize a box-constrained blackbox optimization problem involving a composite objective function is described. The algorithm will be used to perform our comparison between the calculus-based approach and the non-calculus-based approach in Section 4.
Let be the maximum trust-region radius allowed in the DFTR algorithm. The minimization problem considered is
where is twice continuously differentiable on
where , and the inequalities are taken component-wise. It is assumed that F is a composite function obtained from two blackboxes with similar computational costs.
Before introducing the pseudo-code of the algorithm, let us clarify some details about the model function and the trust-region sub-problem.
The model function built at an iteration k will be denoted by The model is a quadratic function that can be written as
where denotes an approximation of the gradient is a symmetric approximation of the Hessian , and is the independent variable.
When a calculus-based approach is used, both and are built by using the calculus-based approach presented earlier in Section 2. Similarly, if the non-calculus-based approach is used, then both and are built with the non-calculus approach. We define the sampling radius, , as the maximum distance between the incumbent solution and a sampling point used to build the approximations and
The trust-region subproblem solved in the DFTR algorithm (Step 2 of Algorithm 1) at an iteration k is
where is the trust-region radius at an iteration
Recall that the first-order necessary condition for solving (5) is that the projected gradient is equal to zero. The projected gradient of the model function at onto the feasible box, which is delimited by ℓ and u where , is defined by
where the projection operator, is defined component-wise by
Similarly, we define the projected gradient of the objective function at onto the box by
Next, the pseudo-code of our DFTR algorithm is presented. This is essentially the pseudo-code in [34] (Algorithm 4.1), but adapted for a box-constrained problem (see also Algorithm 10.1 in [35] and Algorithm 2.1 in [61]). The algorithm is a first-order method in the sense that it converges to a first-order critical point.
Several details about the pseudo-code require some clarification. The procedure employed in our algorithm to build the model function at an arbitrary iteration k guarantees that the model is fully linear on To see this, first note that when a model is built in Algorithm 1, we always have that the sampling radius It is known that the gradient of a quadratic interpolation function built with sample points poised for quadratic interpolation is The Hessian of this quadratic interpolation is It was shown in [60] that the calculus-based approach to approximating gradients described in (1) and (3) is It was also shown in [59,60] that the calculus-based approach to approximating the Hessians described in (2) and (4) was Hence, and are -accurate. The next proposition shows that if and are both -accurate approximations of the gradient and Hessian at , respectively, then the model function is fully linear on
Proposition 1.
Let and Assume that , where k is any iteration of Algorithm 1. Let the model function be defined as in Equation (7). If is an -accurate approximation of the gradient of F at and is an -accurate approximation of the Hessian of F at then the model is fully linear on
Proof.
For any we have
where is the Lipschitz constant of on and Note that is bounded above, since
Since F is twice continuously differentiable on the box constraint, we have for some nonnegative scalar M independently of Therefore, Letting we obtain
Hence, the first property in Definition 3 is verified. The second property can be obtained by using a similar process to that used in [62] (Proposition 19.1). Therefore, the model is fully linear on □
| Algorithm 1 DFTR pseudo-code. |
|
It follows from Proposition 1 that Algorithm 1 always builds a fully linear model on
In [61], Hough and Roberts analyzed the convergence properties of a DFTR algorithm for an optimization problem of the form
where is closed and convex with a nonempty interior and The main algorithm developed in their paper, Algorithm 2.1, follows the same steps as those of our algorithm. Since a box constraint is a convex closed set with a nonempty interior, the convergence results that were proven in [61] may be applied to Algorithm 1. For completeness, we recall the three assumptions and convergence results of [61].
Assumption 1.
The objective function F is bounded below and continuously differentiable. Furthermore, the gradient is Lipschitz continuous with the constant in
Assumption 2.
There exists such that for all k.
Assumption 3.
There exists a constant such that the computed step satisfies , and the generalized Cauchy decrease condition is
Theorem 1.
Suppose that Algorithm 1 is applied to the minimization problem (5). Suppose that Assumptions 1–3 hold. Then,
To conclude this section, we provide details on the different choices made while implementing Algorithm 1.
3.1. Implementing the Algorithm
Let us begin by specifying the value used for all of the parameters involved in the algorithm. Our choices were influenced by some preliminary numerical results and the values proposed in the literature, such as [1] (Chapter 6).
In our implementation, the parameters are set to:
To build an approximation of the Hessian we compute a simplex Hessian, as defined in Definition 2. Two matrices of directions S and T must be chosen; at every iteration k, the matrices and are set to
Multiplying the identity matrix by to form and guarantees that the sampling radius for building an approximation of the Hessian is equal to Setting and in this fashion creates distinct sample points poised for quadratic interpolation. This implies that the simplex Hessian is equal to the Hessian of the quadratic interpolation function [59]. Clearly, other matrices and could be used, and does not necessarily need to be equal to , nor to always be a multiple of the identity matrix for every iteration More details on how to choose S and T so that the resulting set of sample points is poised for quadratic interpolation can be found in [59].
To build an approximation of the gradient the gradient of the quadratic interpolation function built using the same sample points used to obtain is simply computed. Therefore, building a model requires function evaluations.
Note that the sample points utilized to build and may be outside of the box constraint. This is allowed in our implementation.
To solve the trust-region sub-problem, the Matlab command quadprog with the algorithm trust-region-reflective is used. In theory, this method satisfies Assumption 3.
Based on the preliminary numerical results, the version of Algorithm 1 that is utilized to conduct the numerical experiments in this section does not attempt to improve the accuracy of the model in Step 4. The results obtained suggest that rebuilding a new model function when decreases the efficiency of our algorithm.
Reducing Numerical Errors
We next discuss two strategies that decrease the risk of numerical errors. When the sampling radius is sufficiently small, numerical errors occur while computing and , and this can cause and to be very bad approximations of the gradient and Hessian at To avoid this situation, a minimal sampling radius is defined. Every time the sampling radius is updated in Algorithm 1 (this may happen in Step 1 or Step 5), the rule implemented is the following:
In our implementation, Numerical errors can occur with relatively large values of the sampling radius The following example illustrates this situation. This motivates our choice of setting
Example 1.

Let
Let Set where Note that the sampling radius is Table 1 presents the relative error of the simplex Hessian which is denoted by

Table 1.
Relative error of the simplex Hessian for different values of h.
We see that numerical errors occur at a value of between and .
A maximal sampling radius is also defined to ensure that the sampling radius does not become excessively large when the trust-region radius is large. The parameter is set to Therefore, after checking (10), the following update on is performed:
In Step 3, in the computation of the denominator satisfies
As mentioned in [1] (Section 17.4), to reduce the numerical errors, we use (11) to compute this value.
To compute the ratio we again follow the advice given in [1] (Section 17.4.2) and proceed in the following way. Let , where is the relative machine precision. Let Define
Then,
3.2. Data Profiles
To perform the comparisons in the next section, data profiles were built [63]. The convergence test for the data profiles is
where is a tolerance parameter and is the best known minimum value for each problem p in Let be the number of function evaluations required to satisfy (12) for a problem by using a solver given a maximum number of function evaluations In this paper, the parameter is , where is the dimension of the problem Note that is set to ∞ if (12) is not satisfied after function evaluations. The data profile of a solver is defined by
Three different values of will be used to build the data profiles: .
3.3. Experimental Setup
Algorithm 1 was implemented in Matlab 2021a while using both the calculus-based and non-calculus-based approach to approximating gradients and Hessians. The computer that was utilized had an Intel Core i7-9700 CPU at 3.00 GHz and 16.0 GB of DDR4 RAM at 2666 MHz on a 64-bit version of Microsoft Windows 11 Home. These implementations were tested on a suite of test problems, which are detailed below. The Matlab function fmincon was also tested on each problem for all of the experiments mentioned below. This was done as a validation step to demonstrate that Algorithm 1 was correctly implemented (and reasonably competitive with respect to the currently used methods).
To conclude this section, we present the details of the different situations tested for the product rule and the quotient rule.
3.3.1. Numerical Experiment with the Product Rule
In these numerical experiments, the composite objective function F had the form where Three different situations were considered:
- and were linear functions;
- was a linear function and was a quadratic function;
- and were quadratic functions.
Recall that a linear function has the form
where b and A quadratic function has the form
where is a symmetric matrix. At the beginning of each experiment, the seed of the random number generator was fixed to 54321 by using the command rng. The dimension of the space was between 1 and 30, and it was generated with the command randi. All integers were generated with randi. In each experiment, the coefficients involved in and were integers between −10 and 10 inclusively. Each component of the starting point was an integer between −5 and 5 inclusively. The box constraint was built in the following way:
This created a randomly generated test problem of the form of (5). This problem was solved via Algorithm 1 by using the starting point and by using both versions—the calculus-based approach and the non-calculus-based approach. Each of the three situations listed above was repeated 100 times. Each time, all of the parameters were generated again: the dimension n, the starting point the box constraint , and the functions
3.3.2. Numerical Experiment with the Quotient Rule: Easy Case
In these experiments, the composite objective function took the form where was either a linear function or a quadratic function for . We began by building the function such that its real roots, if any, were relatively far from the box constraint. To do so, each component of the starting point was taken to be an integer between 1 and 100 inclusively. The coefficients in are taken to be integers between 1 and 10 inclusively. When was a quadratic function, note that having all positive entries in the matrix A did not necessary imply that A was positive semi-definite. The box constraint was built in the same fashion as in the previous experiment. Thus, the bounds were
Note that if is a root of then r must have at least one negative component. Since and is an increasing function, there is no root of in the box constraint. Hence, F is twice continuously differentiable on the box constraint. The following four situations were tested:
- and were linear functions;
- was a linear function and was a quadratic function;
- was a quadratic function and was a linear function;
- and were quadratic functions.
Each situation was repeated 100 times.
3.3.3. Numerical Experiment with the Quotient Rule: Hard Case
Last, the quotient rule was tested again, but this time, the function was built so that there was a root of near (but not within) the box constraint. The differences from the previous quotient experiments were the following. Each component of the starting point was taken as an integer between −5 and 5 inclusively. Let , where The coefficients in were taken to be between −10 and 10 inclusively. Before generating the constant c in the minimum value on the box constraint of , say, was found. Then, c was set to Hence, was built such that the minimum value of on the box constraint was 0.001 and for all x in the box constraint.
4. Results
In this section, the data profiles for each of the three experiments are presented. We begin by presenting the data profiles for the product rule. The following nine data profiles (three data profiles per situation) were obtained (Figure 1, Figure 2 and Figure 3). In the following figures, the x-axis represents the independent variable , as defined in Section 3.2. The y-axis represents the percentage of problems solved. For a given tolerance parameter , the robustness of an algorithm was obtained by looking at the value of its curve at the greatest value of in the figures. For example, fmincon solved 100% of the problems for all three values of in Figure 1. For a given percentage of problems solved, the curve with the smallest value of represented the most efficient algorithm, as it used fewer function evaluations to solve a certain percentage of the problems. For example, when in Figure 1, the fmincon algorithm was the most efficient and the most robust of all three algorithms. Roughly speaking, if a curve is on top of all other curves in a data profile, then it was the most efficient and the most robust algorithm on this set of problems for a given value of Testing different values of provides information about the level of accuracy that an algorithm can achieve. Small values of provide information about the capabilities of an algorithm for finding accurate minimizers, and large values of provide information about the capabilities of an algorithm for finding rough approximations of the minimizers.
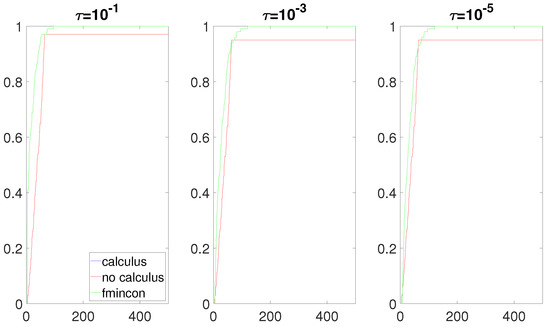
Figure 1.
Data profiles when and when are linear functions.
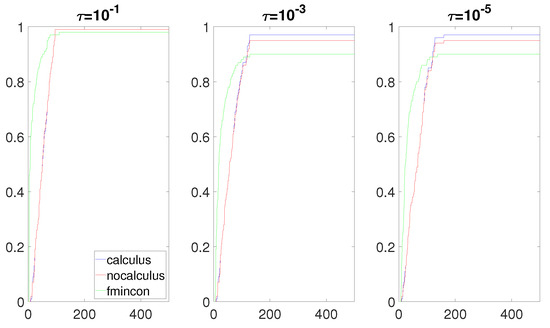
Figure 2.
Data profiles when is a quadratic function, and is a linear function.
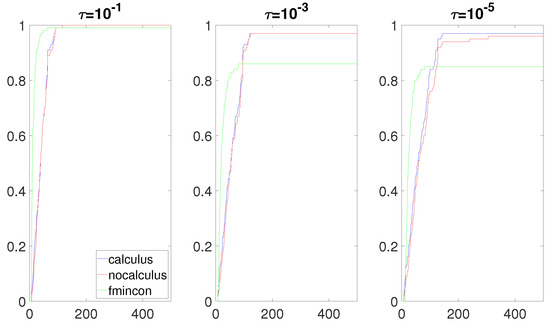
Figure 3.
Data profiles when and when are quadratic functions.
Next, we present the data profiles for the quotient rule as described in Section 3.3.2. The following 12 data profiles were obtained (Figure 4, Figure 5, Figure 6 and Figure 7).
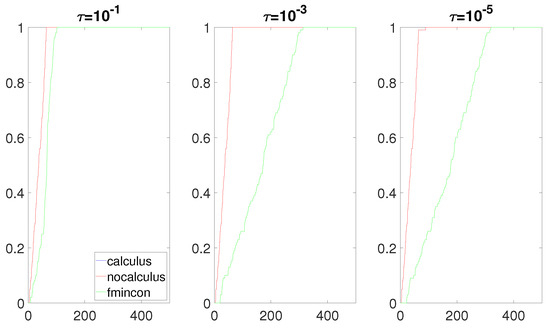
Figure 4.
Data profiles when and when are linear functions.
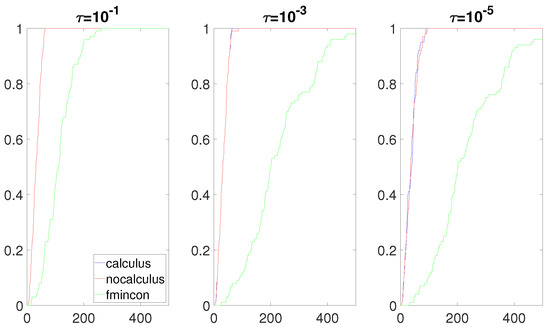
Figure 5.
Data profiles when is a linear function, and is a quadratic function.
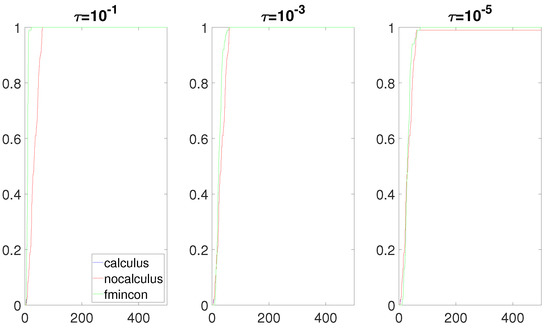
Figure 6.
Data profiles when is a quadratic function, and is a linear function.
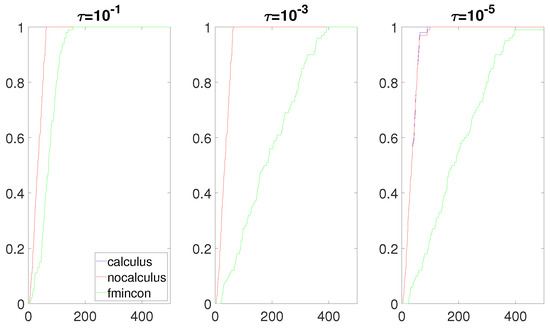
Figure 7.
Data profiles when and when are quadratic functions.
Last, we present the data profiles for the quotient rule as described in Section 3.3.3. The following 12 data profiles were obtained (Figure 8, Figure 9, Figure 10 and Figure 11).
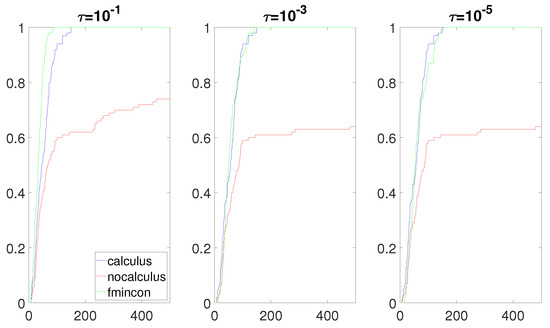
Figure 8.
Data profiles when and when are linear functions.
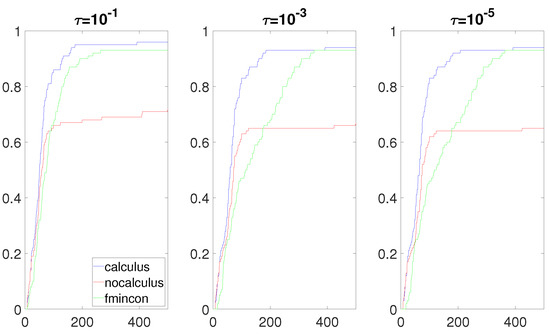
Figure 9.
Data profiles when is a linear function, and is a quadratic function.
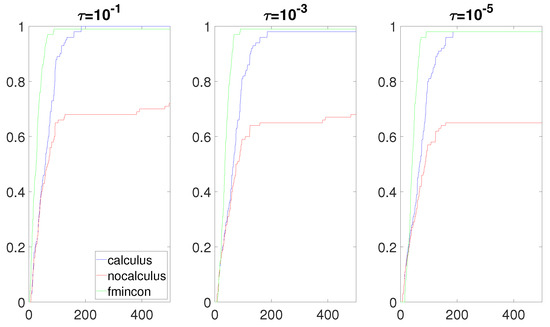
Figure 10.
Data profiles when is a quadratic function, and is a linear function.
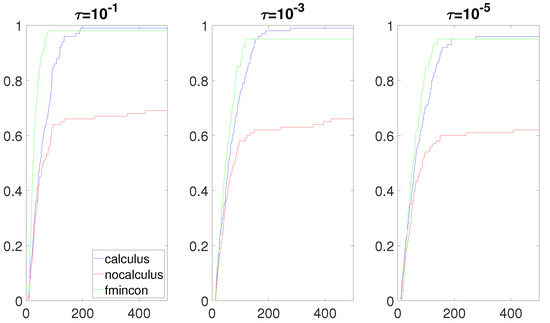
Figure 11.
Data profiles when and when are quadratic functions.
5. Discussion
In this section, the data profiles presented in Section 4 are analyzed. First, the data profiles related to the product rule are scrutinized.
5.1. Numerical Experiment with the Product Rule
Figure 1 agrees with the theory: The calculus-based approach provided the exact same results as the non-calculus-based approach. Indeed, when both and are linear, the theory states that both approaches will build models with an exact gradient and an exact Hessian. As such, both methods should behave identically.
Figure 2 and Figure 3 show that the calculus-based approach was slightly more efficient and robust. Note that the calculus-based approach built the model functions with an exact gradient and an exact Hessian This was not the case with the non-calculus-based approach when F was a cubic function or quartic function. However, the accuracy of the approximate gradients and Hessians in the models was sufficiently good that a significant difference from the exact models built with the calculus-based approach was not made. We also observe that Algorithm 1 was more robust than fmincon for these two situations, which supported that our algorithm is competitive with currently used solvers.
Although there were no drastic differences between the calculus-based approach and the non-calculus-based approach, we conclude that the calculus-based approach was better or at least as good as the non-calculus-based approach in these three situations.
5.2. Numerical Experiment with the Quotient Rule: The Easy Case
We now analyze Figure 4, Figure 5, Figure 6 and Figure 7. The performance of both approaches was almost identical. The calculus-based approach provided slightly better results. Compared to fmincon, Algorithm 1 was competitive and even outperformed fmincon when the numerator of F was a linear function (Figure 4). We note that having no roots of near the box constraint implies that the value of the composite objective function F does not drastically change on the box constraint. In other words, the Lipschitz constant of F on the box constraint is not a huge number. This helped obtain an accurate gradient when using the non-calculus-based approach. As such, in these four situations, the accuracy of the approximate gradients and Hessians computed with the non-calculus-based approach was similar to this computed with the calculus-based approach. Hence, the performance of the non-calculus-based approach was almost as good as that of the calculus-based approach.
5.3. Numerical Experiment with the Quotient Rule: The Hard Case
The most interesting results were obtained when the composite objective function F had the form and had a real root near the box constraint . Figure 8, Figure 9, Figure 10 and Figure 11 clearly show that the calculus-based approach was significantly more efficient and robust than the non-calculus-based approach for these four situations. Note that the composite objective function F was twice continuously differentiable on the box constraint, but F was not twice continuously-differentiable on the expanded box constraint (6). The composite objective function F was also not twice continuously differentiable on Using the non-calculus-based approach, it could be the case that or was undefined if one of the sample points landed exactly on a real root of This was very unlikely and it did not happen during the experiment. When using a calculus-based approach, this issue cannot occur, as and are twice continuously differentiable everywhere. This is clearly an advantage of the calculus-based approach. If a sample point is near a root of the value of F at this point can be a very large number. This could make the accuracy of and very poor when using the non-calculus-based approach.
Note that the Lipschitz constants of and on the box constraint were very large numbers. Hence, the error bounds associated with the approximate gradient and the approximate Hessian were very large numbers (see [59]). This tells us that it is possible to obtain very bad approximations for and when using the non-calculus-based approach.
To see how the non-calculus-based approach can fail to provide accurate approximations of the gradient and Hessian, we present Example 2.
Example 2.

Let
Suppose that The derivative of F at is , and the second-order derivative of F at is . Table 2 provides the value and the relative error associated with the approximations and obtained by using the non-calculus-based approach and for different values of The relative error of the approximation technique is denoted by in the following table.

Table 2.
An example where the non-calculus-based approach provides inaccurate approximations.
Several modifications to Algorithm 1 were tested to see if it was possible to improve the performance of the non-calculus-based approach. None of those modifications resulted in a significant increase in performance for all four situations, which made the non-calculus-based approach competitive with the calculus-based approach.
We observed that numerical errors occurred at for the approximate gradient and at for the approximate Hessian Note that in this experiment, the sampling radius was Assuming that numerical errors do not occur, the theory guarantees that the relative error will be of order for and of order for when is sufficiently small. However, in this experiment, numerical errors occurred before attaining the expected accuracy for and Therefore, in this experiment, and were extremely inaccurate.
6. Conclusions
When dealing with a composite objective function, the numerical results obtained in Section 4 clearly suggest that a calculus-based approach should be used. In particular, in all cases tested, the calculus-based approach was better or as good as the non-calculus-based approach. Since a calculus-based approach is not more difficult to implement than a non-calculus-based approach, the former approach seems to be the best approach to implement and use whenever a composite objective function is optimized.
When the composite objective function was a quotient () and there was a real root of near the box constraint, the calculus-based approach greatly outperformed the other methods. In this case, the sampling radius needed to be very small to obtain a relatively accurate gradient and Hessian when using the non-calculus-based approach. In some situations, numerical errors may occur before obtaining the accuracy required for convergence. In general, based on the results obtained, it seems reasonable to think that a calculus-based approach will outperform a non-calculus-based approach when the Lipschitz constant of the gradient and∖or Hessian of F on the box constraint are large numbers. By increasing the range of numbers allowed to generate the functions and when using the product rule in the experiment described in Section 3.3.1, it is relatively easy to create a test set of problems in which the differences in performance between the calculus-based approach and the non-calculus-based approach are more pronounced than the results presented in this paper (Figure 1, Figure 2 and Figure 3), which are in favor of the calculus-based approach. However, the gain in performance is not as drastic as the results obtained with the quotient rule in our third experiment (Figure 8, Figure 9, Figure 10 and Figure 11). Further investigation is needed to determine situations in which the calculus-based approach significantly outperforms the non-calculus-based approach when using the product rule.
We remark that our implementation of Algorithm 1 is simple. This is intentional, as the goal is to compare the calculus-based approach with the non-calculus-based approach. Nonetheless, we remark that, recently, Nocedal et al. found that a DFTR algorithm that used quadratic models built from a forward-finite-difference gradient and a forward-finite-difference Hessian can be surprisingly competitive with state-of-the-art derivative-free algorithms [64]. From our perspective, now that the calculus-based approach has been established as the superior method within a model-based derivative-free algorithm, the next logical step is to use this knowledge to improve current state-of-the-art software (e.g., [65]). Applying a calculus-based approach to real-world optimization problems is, then, the obvious direction of future research.
Another direction to explore is inspired by model-based methods for high-dimensional blackbox optimization [66]. In [66], the authors used subspace decomposition to reduce a high-dimensional blackbox optimization problem into a sequence of low-dimensional blackbox optimization problems. At each iteration, the subspace was rotated, requiring new models to be frequently constructed. An examination of whether calculus rules could be adapted to help in this situation would be an interesting direction for future research.
This further links to a direction of future research based on underdetermined gradient/Hessian approximations. An underdetermined approximation does not contain accurate information about all entries of a gradient/Hessian, but uses fewer function evaluations than the determined case. It would be valuable to explore if calculus-based approaches could be merged with underdetermined approximations to create more accuracy with a minimal increase in function evaluations.
Author Contributions
W.H. and G.J.-B.: conceptualization, methodology, validation, formal analysis, review, and editing. G.J.-B.: software, writing—original draft preparation, and visualization. W.H.: supervision and funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery Grant 2018-03865.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on Github.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| DFTR | Derivative-free trust region |
References
- Conn, A.; Gould, N.; Toint, P. Trust Region Methods; SIAM: Bangkok, Thailand, 2000. [Google Scholar]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Levenberg, K. A Method for the Solution of Certain Problems in Least Squares. Appl. Math. 1944, 2, 164–168. [Google Scholar]
- Dennis, J.; Mei, H. Two new unconstrained optimization algorithms which use function and gradient values. J. Optim. Theory Appl. 1979, 28, 453–482. [Google Scholar] [CrossRef]
- Dennis, J.; Schnabel, R. Numerical Methods for Unconstrained Optimization and Nonlinear Equations; SIAM: Bangkok, Thailand, 1996. [Google Scholar]
- Fletcher, R. Practical Methods of Optimization: Unconstrained Optimization; Wiley: Hoboken, NJ, USA, 1980; Volume 1. [Google Scholar]
- Goldfeld, S.; Quandt, R.; Trotter, H. Maximization by quadratic hill-climbing. Econom. J. Econom. Soc. 1966, 34, 541–551. [Google Scholar] [CrossRef]
- Hebden, M. An Algorithm for Minimization Using Exact Second Derivatives; Citeseer: Princeton, NJ, USA, 1973. [Google Scholar]
- Madsen, K. An algorithm for minimax solution of overdetermined systems of non-linear equations. IMA J. Appl. Math. 1975, 16, 321–328. [Google Scholar] [CrossRef]
- Moré, J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 1978; pp. 105–116. [Google Scholar]
- Moré, J. Recent developments in algorithms and software for trust region methods. In Mathematical Programming: The State of the Art; Springer: Berlin/Heidelberg, Germany, 1983; pp. 258–287. [Google Scholar]
- Moré, J.; Sorensen, D. Computing a trust region step. SIAM J. Sci. Stat. Comput. 1983, 4, 553–572. [Google Scholar] [CrossRef]
- Osborne, M. Nonlinear least squares—the Levenberg algorithm revisited. J. Aust. Math. Soc. 1976, 19, 343–357. [Google Scholar] [CrossRef]
- Powell, M. A Fortran Subroutine for Solving Systems of Nonlinear Algebraic Equations; Technical Report; Atomic Energy Research Establishment: Oxford, UK, 1970. [Google Scholar]
- Powell, M. A hybrid method for nonlinear equations. In Numerical Methods for Nonlinear Algebraic Equations; Gordon and Breach: London, UK, 1970; pp. 87–114. [Google Scholar]
- Powell, M. A new algorithm for unconstrained optimization. In Nonlinear Programming; Elsevier: Amsterdam, The Netherlands, 1970; pp. 31–65. [Google Scholar]
- Powell, M. Convergence properties of a class of minimization algorithms. In Nonlinear Programming 2; Mangasarian, O.L., Meyer, R.R., Robinson, S.M., Eds.; Elsevier: Amsterdam, The Netherlands, 1975; pp. 1–27. [Google Scholar]
- Powell, M. On the global convergence of trust region algorithms for unconstrained minimization. Math. Program. 1984, 29, 297–303. [Google Scholar] [CrossRef]
- Sorensen, D. Trust-Region Methods for Unconstrained Minimization; U.S. Department of Energy Office of Scientific and Technical Information: Washington, DC, USA, 1981. [Google Scholar]
- Sorensen, D. Newton’s method with a model trust region modification. SIAM J. Numer. Anal. 1982, 19, 409–426. [Google Scholar] [CrossRef]
- Steihaug, T. The conjugate gradient method and trust regions in large scale optimization. SIAM J. Numer. Anal. 1983, 20, 626–637. [Google Scholar] [CrossRef]
- Toint, P. Some numerical results using a sparse matrix updating formula in unconstrained optimization. Math. Comput. 1978, 32, 839–851. [Google Scholar] [CrossRef]
- Toint, P. On the superlinear convergence of an algorithm for solving a sparse minimization problem. SIAM J. Numer. Anal. 1979, 16, 1036–1045. [Google Scholar] [CrossRef]
- Toint, P. Convergence Properties of a Class of Minimization Algorithms That Use a Possibly Unbounded Sequence of Quadratic Approximations; Elsevier: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Toint, P. Towards an efficient sparsity exploiting Newton method for minimization. In Sparse Matrices and Their Uses; Academic Press: London, UK, 1981; pp. 57–88. [Google Scholar]
- Winfield, D. Function minimization by interpolation in a data table. IMA J. Appl. Math. 1973, 12, 339–347. [Google Scholar] [CrossRef]
- Winfield, D. Function and Functional Optimization by Interpolation in Data Tables. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1969. [Google Scholar]
- Dennis, J. A brief introduction to quasi-Newton methods. Numer. Anal. 1978, 22, 19–52. [Google Scholar]
- Conn, A.; Scheinberg, K.; Toint, P. On the convergence of derivative-free methods for unconstrained optimization. In Approximation Theory and Optimization: Tributes to M.J.D. Powell; Cambridge University Press: Cambridge, UK, 1997; pp. 83–108. [Google Scholar]
- Marazzi, M.; Nocedal, J. Wedge trust region methods for derivative free optimization. Math. Program. 2002, 91, 289–305. [Google Scholar] [CrossRef]
- Powell, M. UOBYQA: Unconstrained optimization by quadratic approximation. Math. Program. 2002, 92, 555–582. [Google Scholar] [CrossRef]
- Powell, M. On trust region methods for unconstrained minimization without derivatives. Math. Program. 2003, 97, 605–623. [Google Scholar] [CrossRef]
- Colson, B.; Toint, P. Optimizing partially separable functions without derivatives. Optim. Methods Softw. 2005, 20, 493–508. [Google Scholar] [CrossRef]
- Conn, A.; Scheinberg, K.; Vicente, L. Global convergence of general derivative-free trust-region algorithms to first-and second-order critical points. SIAM J. Optim. 2009, 20, 387–415. [Google Scholar] [CrossRef]
- Conn, A.; Scheinberg, K.; Vicente, L. Introduction to Derivative-Free Optimization; SIAM: Bangkok, Thailand, 2009. [Google Scholar]
- Audet, C.; Hare, W. Derivative-free and Blackbox Optimization; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Liuzzi, G.; Lucidi, S.; Rinaldi, F.; Vicente, L. Trust-region methods for the derivative-free optimization of nonsmooth black-box functions. SIAM J. Optim. 2019, 29, 3012–3035. [Google Scholar] [CrossRef]
- Oeuvray, R.; Bierlaire, M. A new derivative-free algorithm for the medical image registration problem. Int. J. Model. Simul. 2007, 27, 115–124. [Google Scholar] [CrossRef]
- Billups, S.; Larson, J.; Graf, P. Derivative-Free Optimization of Expensive Functions with Computational Error Using Weighted Regression. SIAM J. Optim. 2013, 23, 27–53. [Google Scholar] [CrossRef]
- Conn, A.; Scheinberg, K.; Toint, P. A derivative free optimization algorithm in practice. In Proceedings of the 7th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, St. Louis, MO, USA, 2–4 September 1998; p. 4718. [Google Scholar]
- Gratton, S.; Toint, P.; Tröltzsch, A. An active-set trust-region method for derivative-free nonlinear bound-constrained optimization. Optim. Methods Softw. 2011, 26, 873–894. [Google Scholar] [CrossRef]
- Powell, M. The BOBYQA Algorithm for Bound Constrained Optimization without Derivatives; Cambridge NA Report NA2009/06; University of Cambridge: Cambridge, UK, 2009; pp. 26–46. [Google Scholar]
- Wild, S.; Regis, R.; Shoemaker, C. ORBIT: Optimization by radial basis function interpolation in trust-regions. SIAM J. Sci. Comput. 2008, 30, 3197–3219. [Google Scholar] [CrossRef]
- Wild, S.; Shoemaker, C. Global convergence of radial basis function trust region derivative-free algorithms. SIAM J. Optim. 2011, 21, 761–781. [Google Scholar] [CrossRef]
- Huyer, W.; Neumaier, A. SNOBFIT—Stable noisy optimization by branch and fit. ACM Trans. Math. Softw. (TOMS) 2008, 35, 1–25. [Google Scholar] [CrossRef]
- Arouxét, M.; Echebest, N.; Pilotta, E. Active-set strategy in Powell’s method for optimization without derivatives. Comput. Appl. Math. 2011, 30, 171–196. [Google Scholar]
- Berghen, F.; Bersini, H. CONDOR, a new parallel, constrained extension of Powell’s UOBYQA algorithm: Experimental results and comparison with the DFO algorithm. J. Comput. Appl. Math. 2005, 181, 157–175. [Google Scholar] [CrossRef]
- Regis, R.; Wild, S. CONORBIT: Constrained optimization by radial basis function interpolation in trust regions. Optim. Methods Softw. 2017, 32, 552–580. [Google Scholar] [CrossRef]
- Sampaio, P.; Toint, P. A derivative-free trust-funnel method for equality-constrained nonlinear optimization. Comput. Optim. Appl. 2015, 61, 25–49. [Google Scholar] [CrossRef]
- Gumma, E.; Hashim, M.; Ali, M. A derivative-free algorithm for linearly constrained optimization problems. Comput. Optim. Appl. 2014, 57, 599–621. [Google Scholar] [CrossRef]
- Powell, M. On fast trust region methods for quadratic models with linear constraints. Math. Program. Comput. 2015, 7, 237–267. [Google Scholar] [CrossRef]
- Conejo, P.; Karas, E.; Pedroso, L. A trust-region derivative-free algorithm for constrained optimization. Optim. Methods Softw. 2015, 30, 1126–1145. [Google Scholar] [CrossRef]
- Khan, K.A.; Larson, J.; Wild, S.M. Manifold sampling for optimization of nonconvex functions that are piecewise linear compositions of smooth components. SIAM J. Optim. 2018, 28, 3001–3024. [Google Scholar] [CrossRef]
- Larson, J.; Menickelly, M.; Zhou, B. Manifold Sampling for Optimizing Nonsmooth Nonconvex Compositions. arXiv 2020, arXiv:2011.01283. [Google Scholar] [CrossRef]
- Hare, W.; Jarry-Bolduc, G. Calculus identities for generalized simplex gradients: Rules and applications. SIAM J. Optim. 2020, 30, 853–884. [Google Scholar] [CrossRef]
- Hare, W. A Discussion on Variational Analysis in Derivative-Free Optimization. Set-Valued Var. Anal. 2020, 28, 643–659. [Google Scholar] [CrossRef]
- Regis, R. The calculus of simplex gradients. Optim. Lett. 2015, 9, 845–865. [Google Scholar] [CrossRef]
- Hare, W.; Jarry-Bolduc, G.; Planiden, C. Error bounds for overdetermined and underdetermined generalized centred simplex gradients. arXiv 2020, arXiv:2006.00742. [Google Scholar] [CrossRef]
- Hare, W.; Jarry-Bolduc, G.; Planiden, C. Hessian approximations. arXiv 2020, arXiv:2011.02584. [Google Scholar]
- Chen, Y.; Jarry-Bolduc, G.; Hare, W. Error Analysis of Surrogate Models Constructed through Operations on Sub-models. arXiv 2021, arXiv:2112.08411. [Google Scholar]
- Hough, M.; Roberts, L. Model-Based Derivative-Free Methods for Convex-Constrained Optimization. arXiv 2021, arXiv:2111.05443. [Google Scholar] [CrossRef]
- Audet, C.; Hare, W. Model-based methods in derivative-free nonsmooth optimization. In Numerical Nonsmooth Optimization; Springer: Cham, Switzerland, 2020; pp. 655–691. [Google Scholar]
- Moré, J.; Wild, S. Benchmarking derivative-free optimization algorithms. SIAM J. Optim. 2009, 20, 172–191. [Google Scholar] [CrossRef]
- Shi, H.J.M.; Xuan, M.Q.; Oztoprak, F.; Nocedal, J. On the Numerical Performance of Finite-Difference-Based Methods for Derivative-Free Optimization. Available online: https://doi.org/10.1080/10556788.2022.2121832 (accessed on 1 December 2022).
- Audet, C.; Le Digabel, S.; Rochon Montplaisir, V.; Tribes, C. NOMAD version 4: Nonlinear optimization with the MADS algorithm. arXiv 2021, arXiv:2104.11627. [Google Scholar]
- Cartis, C.; Roberts, L. Scalable Subspace Methods for Derivative-Free Nonlinear Least-Squares Optimization. Available online: https://doi.org/10.1007/s10107-022-01836-1 (accessed on 1 December 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).