1. Introduction
Multivariate data analysis provides several techniques that are useful for examining relationships between variables, analyzing similarities in a set of observations and plotting variables and individuals on factorial planes [
1,
2]. In some cases, a dataset can be presented in time (e.g., years), by survey dimensions, or a specific characteristic associated with a group of variables. Of main interest is the correlation analysis of a group of variables in a dataset, often studied through multiple table methods. In the literature, one such method is multiple factor analysis (MFA) proposed by [
3,
4], which allows leading with qualitative, quantitative, or mixed variable groups [
5]. MFA is among the most used methods for multiple tables and has been applied to sensory and longitudinal data, survey studies, and others [
6,
7,
8]. Given that multiple tables appear in a dataset of individuals, it is possible that some data are missing or unavailable. To perform multivariate analysis when data are unavailable, individuals with unavailable data (NA) or a variable with a high percentage of NA are removed. The removal of individuals or variables in a dataset generates the loss of information; thus, several imputation methods have been developed to estimate the missing data using an optimization criterion [
9,
10,
11,
12].
Husson and Josse [
13] proposed an NA imputation method for MFA called regularized iterative MFA (RIMFA). RIMFA was implemented in the
missMDA library of
R software and is an efficient tool to estimate NAs [
14]. RIMFA imputes data through a conventional MFA over an estimated matrix. RIMFA data imputation is based on the expectation–maximization (EM) algorithm and EM-based principal component analysis (PCA) [
15].
Data imputation is not the only solution for missing data problems. Alternatively, the nonlinear iterative partial least squares (NIPALS) algorithm proposed by Wold [
16,
17] can be used, which does not directly impute the data, but works under the available data principle. This principle serves when an imputation method is not feasible or imputation delivers non-sensical values. Several studies considered the available data principle to solve missing data problems in PCA, multiple correspondence analysis (MCA), the inter-battery method, in state-space models, and others [
18,
19,
20,
21,
22,
23]. In addition, NIPALS presents the same results of a PCA when the dataset does not have NAs [
24]. NIPALS is the most powerful algorithm for partial least squares (PLS) regression methods, which have been used in chemometry, sensometry and genetics [
25], and in cases where datasets include more variables than observations (
). Hence, PLS methods are more suitable for these problems [
26,
27]. In this way, NIPALS offers advantages while working with NAs and datasets with more variables than observations. Moreover, NIPALS is directly related with PCA, which allows NIPALS to be easily adapted to MFA because MFA performs a weighted PCA in its last stage (see
Section 2.1).
Considering NIPALS and the available data principle, this paper proposes the MFA-NIPALS algorithm to solve missing data problems. Specifically, we analyzed the missing data problem in quantitative variable groups and compared the proposed MFA-NIPALS algorithm with classic MFA and RIMFA ones. The Methods section describes these techniques, whereas the Application section presents a dataset to illustrate the performance of the proposed methods and some simulations for comparison and for several percentages of missing data.
3. Applications
In this section, we present two real-world datasets to illustrate the method’s performance, the simulation scenarios, and implementation of methodologies.
3.1. Qualification Dataset
In this dataset, the rows represent students and columns are the qualifications obtained in the subjects of Mathematics, Spanish, and Natural Sciences. We analyzed the student qualifications in a longitudinal way. A similar example can be found in [
37,
38], where Ochoa adapted an MFA.
Table 1 shows the first rows of the data, where
columns (quantitative variables) illustrate three academic periods in a longitudinal way. Using this dataset, we generated random matrices with
observations, each containing a random number of NAs of 5%, 10%,
…, and 30% of
n observations.
As a first step, students’ factorial coordinates
and eigenvalues
were obtained with the classic MFA, RIMFA, and MFA-NIPALS. In the second step, the methods were compared via coordinate correlations of classic MFA versus RIMFA,
, and of classic MFA versus MFA-NIPALS,
. We used version 4.1.0 of
R software for all computations, the
FactoMineR library for classic MFA [
39,
40],
missMDA for RIMFA [
14], and
ade4 for the NIPALS algorithm [
41].
In the next sections, we present the descriptive results, the MFA with complete data, the MFA-NIPALS with 10% of NAs, and simulation results for 5% to 30% of NAs.
MFA with Complete Data
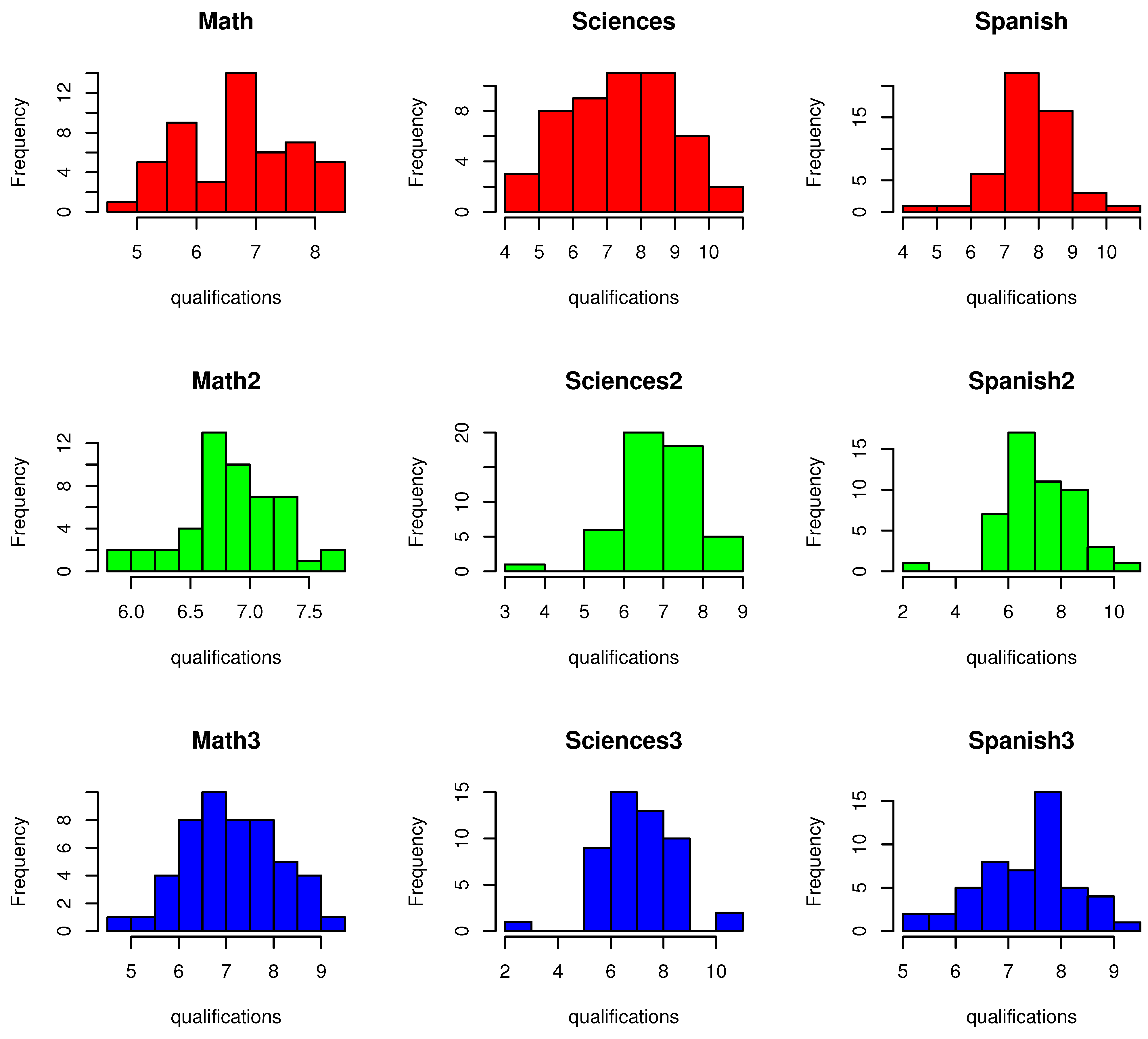
Figure 1 presents a histogram of the qualifications dataset. This first row is related to the first academic period, the second row to the second one, and the third row to the third one.
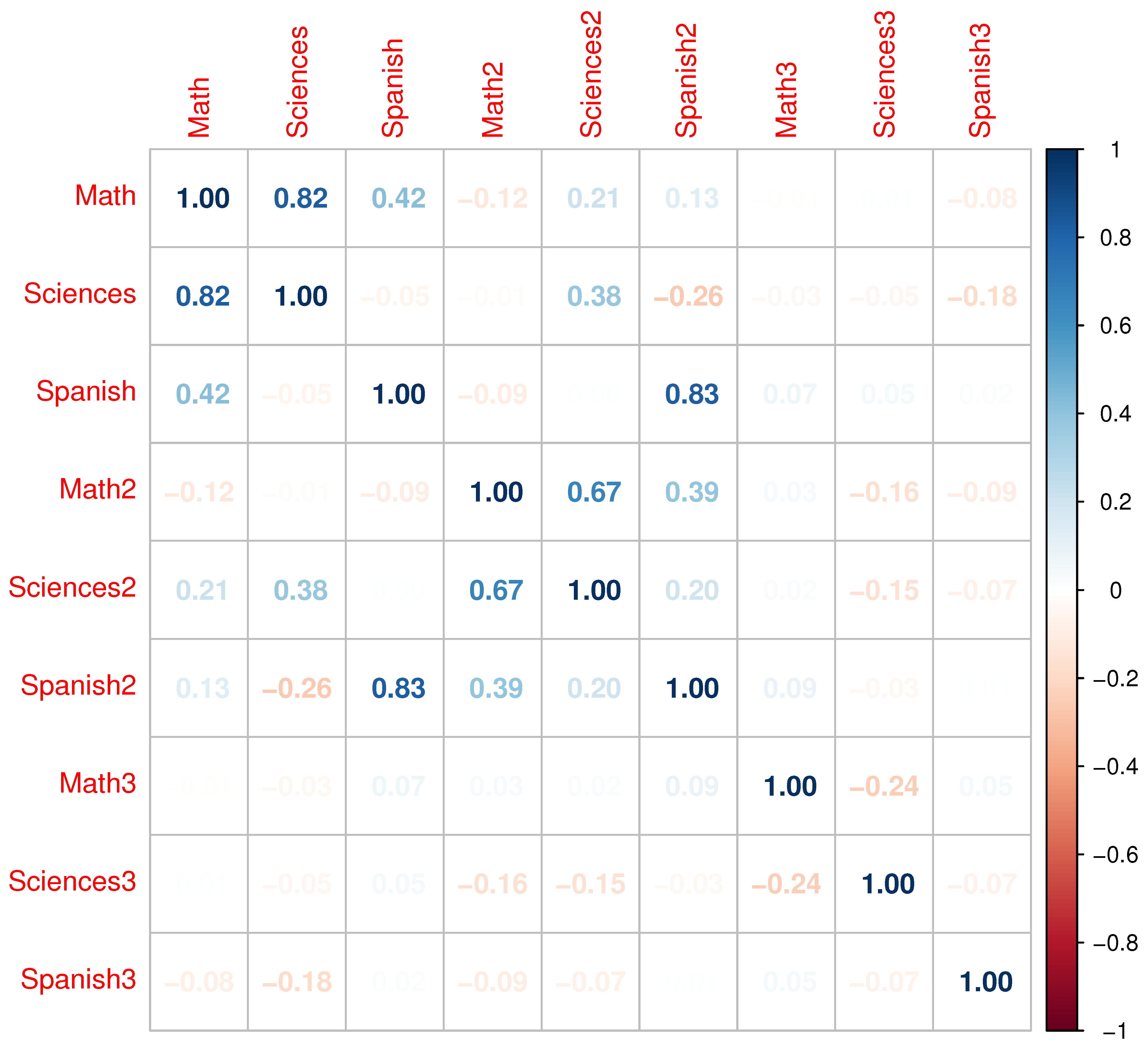
Figure 2 shows the linear correlations between variables, where some correlations higher than 0.6 are highlighted and which are suitable for use in MFA.
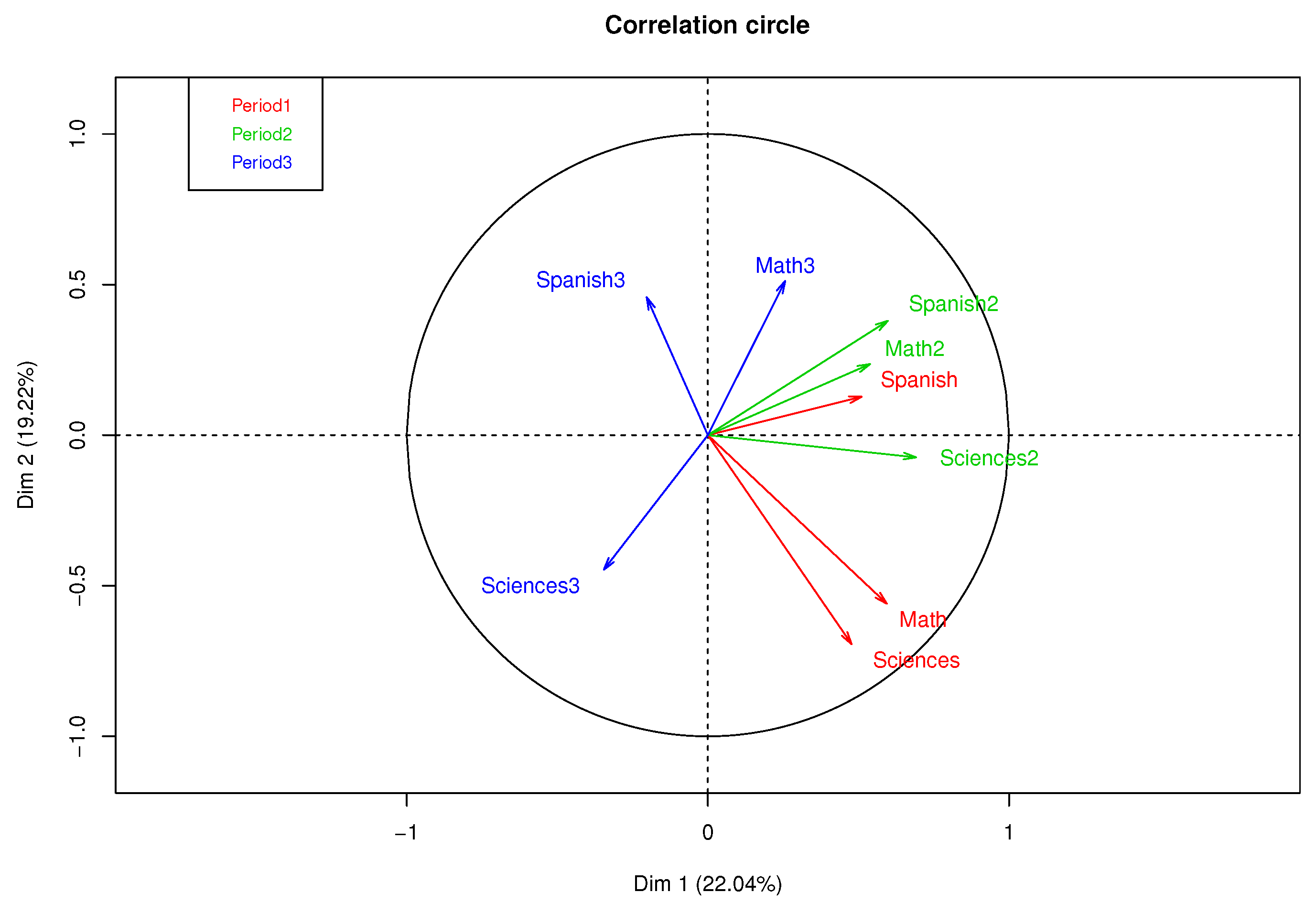
Figure 3 presents a correlation circle of MFA with complete data, where 41.26% of the variance percentage explained was obtained in the first factorial plane. A high correlation between the qualifications of Mathematics and Natural Sciences in the first academic period can be observed, as well as a moderate correlation between Spanish of periods 1 and 2 and a low correlation between subjects in the third period.
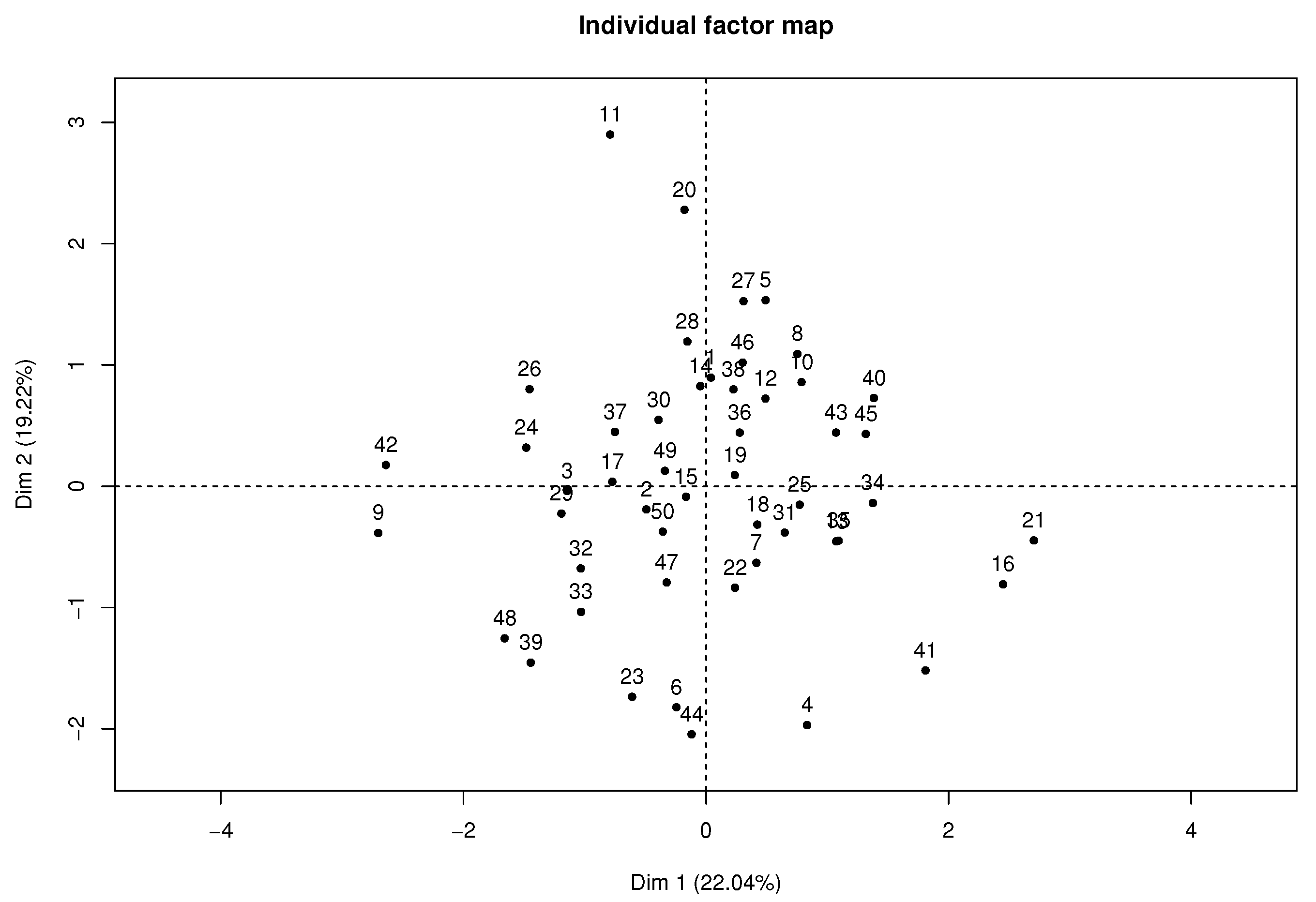
Figure 4 presents the individual factor map where students 11, 21, and 42 highly contribute to the axis, according to their position in the plane far from the average individual or gravity center.
3.1.1. MFA-NIPALS with 10% of NAs
In this section, the main results of the proposed MFA-NIPALS algorithm are presented.
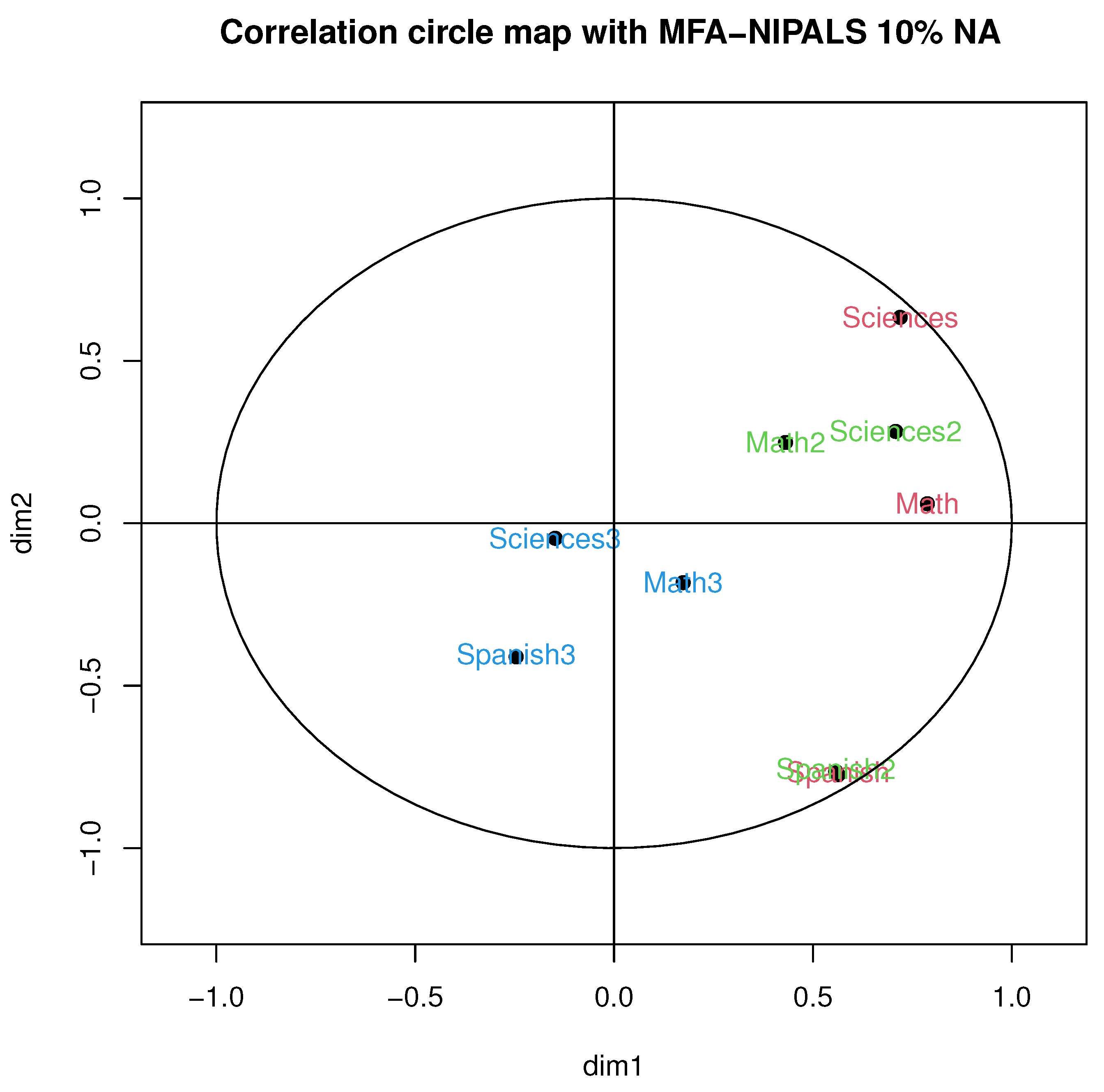
Figure 5 illustrates the correlation circle of MFA-NIPALS with 10% of NA. In particular, a high correlation was obtained in periods 1 and 2 with Spanish, as well as a moderate correlation between Mathematics and Natural Sciences in the first academic period and a low correlation between subjects in the third period, which was, for example, observed with MFA with complete data.
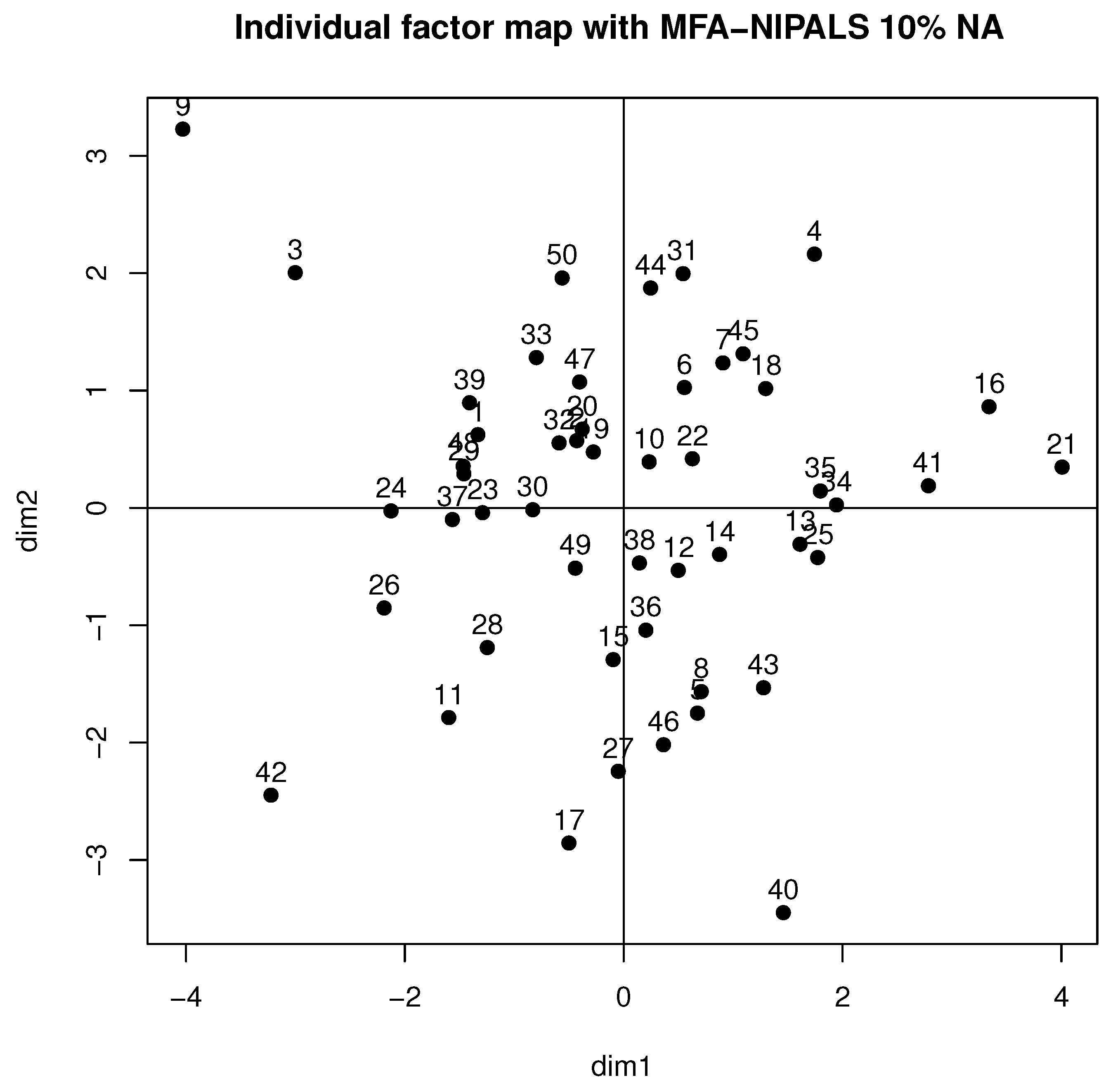
Figure 6 shows the behavior of individuals in the first factorial plane, where similar patterns of a complete data case for students 9, 21, 26, and 42 are highlighted and who highly contributed to the axis, as they are far from the gravity center. Moreover, high variability was detected, which could be produced by the generated NAs of the dataset.
3.1.2. Simulation Scenarios
In this section, results with complete data versus MFA-NIPALS estimates are compared.
Table 2 shows the percentage of variance explained on axes 1 and 2. These percentages increased when the number of NAs rose. Moreover, the percentages of variance explained by MFA-NIPALS were higher than RIMFA ones, which could be influenced by an increment of eigenvectors on axes 1 and 2. In this comparison, RIMFA holds a percentage of variance explained close to MFA with complete data.
Table 3 presents the coordinate correlations with complete data and those estimated by MFA-NIPALS and RIMFA. On axis 1, the highest correlations were detected for MFA-NIPALS and for 30% of NAs, where the RIMFA estimate differed sharply when compared to complete data. For the correlations of axis 2, it can be observed that RIMFA obtained better results than the complete data case. However, a less favorable result was obtained in the case of 30% of NAs.
In summary, MFA-NIPALS performed well on axis 1 and regular on axis 2, indicating that MFA-NIPALS is a good alternative, but more simulation analysis is required to gauge the statistical and computational advantages of MFA-NIPALS versus RIMFA.
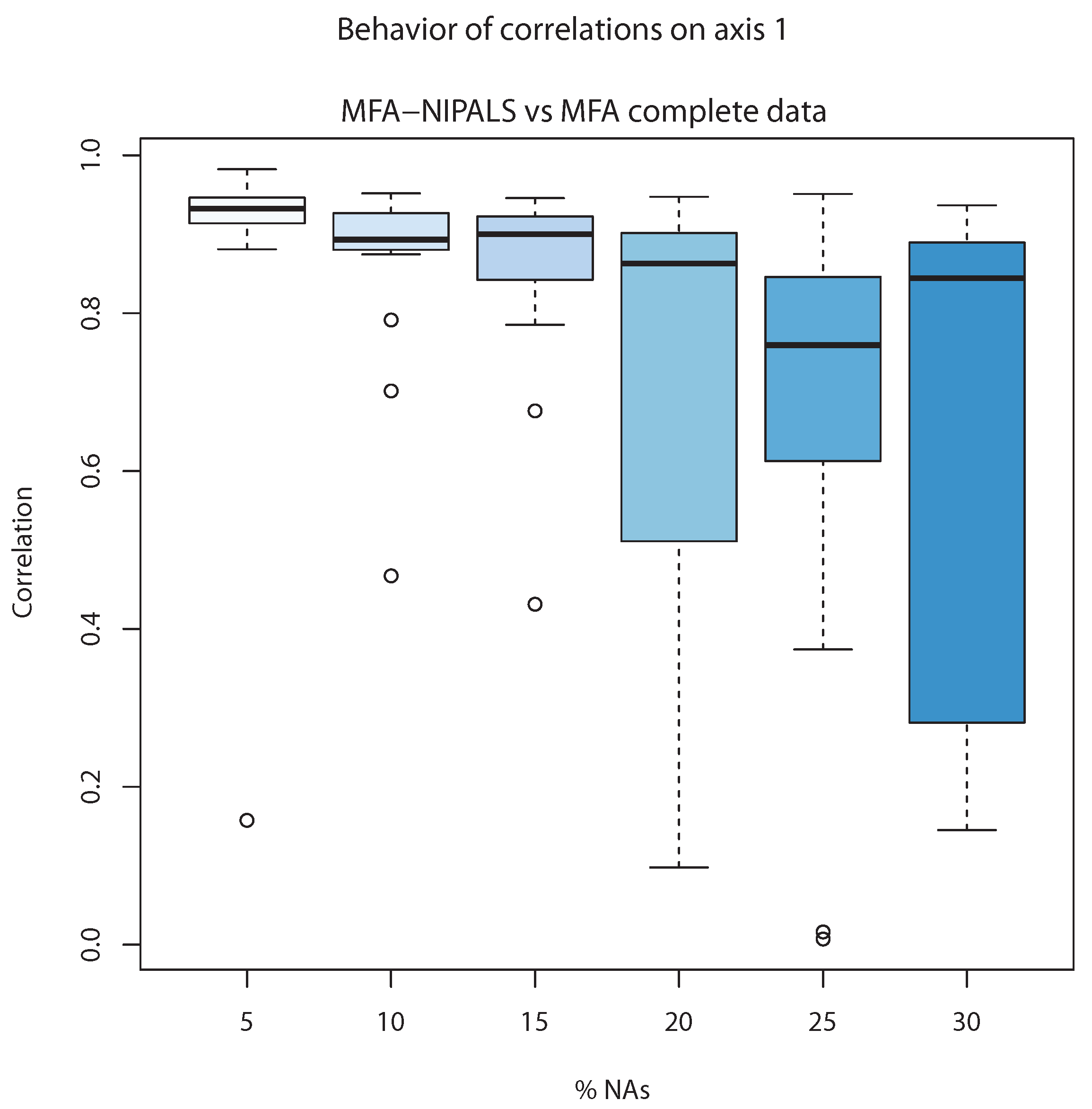
Figure 7 shows the correlation between the first component of individuals of classic MFA (
) and first component of MFA-NIPALS (
). The latter analysis was made with 20 matrices randomly generated for several percentages of NAs. When the percentage of NAs increased to 20%, the median of correlations went farther from 1, indicating less correlation between classic MFA and MFA-NIPALS at 20%, 25%, and 30%. Nevertheless, correlation medians until 15% of NAs were closer to 1, indicating that MFA-NIPALS facilitated favorable results based on estimates related to component
.
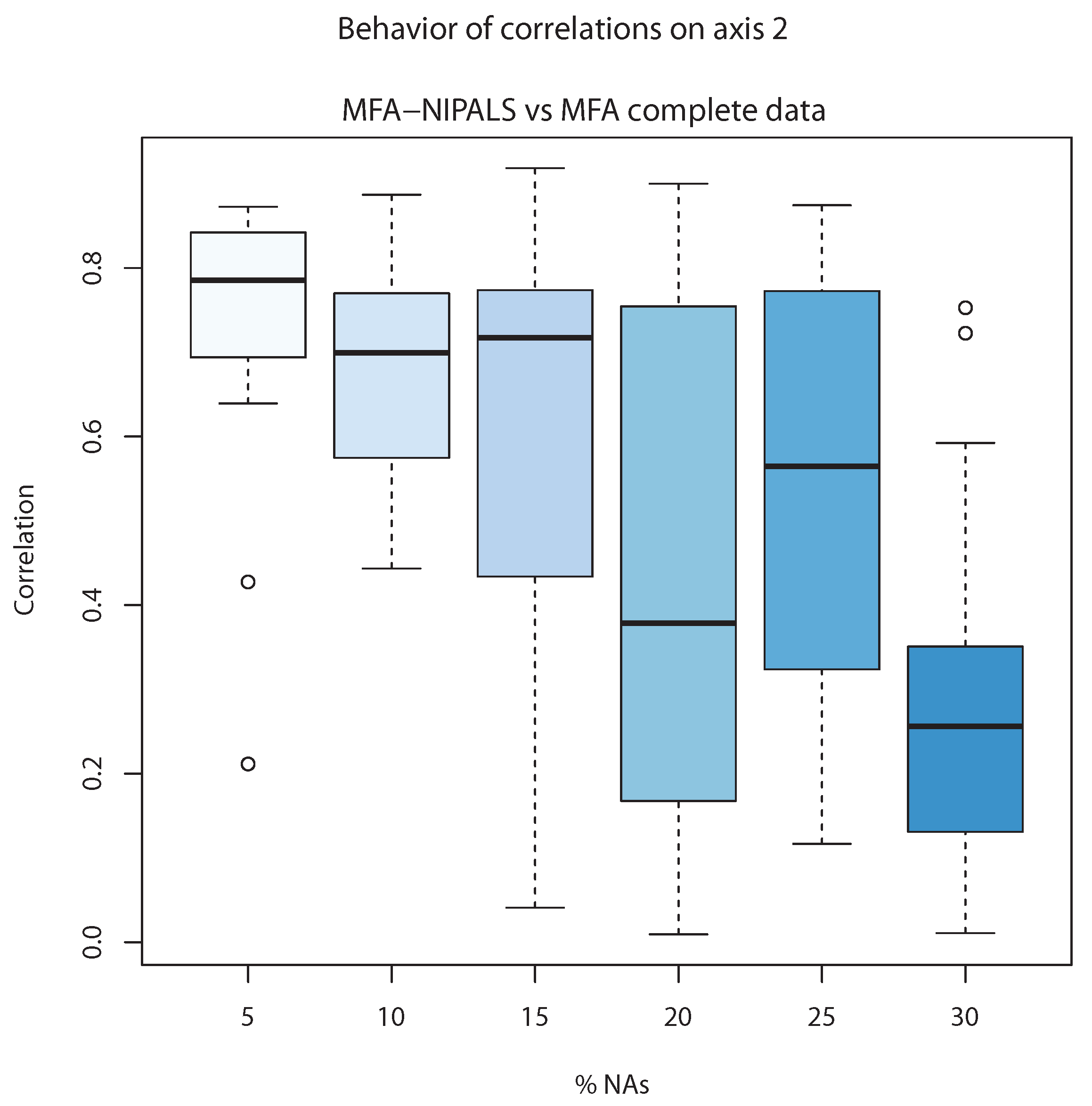
On the other hand,
Figure 8 shows the correlation of the second component of classic MFA (
) and the second component of MFA-NIPALS (
). The correlations are close to 0.8 and in cases until 15% of NAs, whereas above 15%, the lowest correlation is observed, indicating that MFA-NIPALS provided a suitable estimation of the second component
until 15% of NAs.
3.2. Wine Dataset
The wine dataset of the
FactoMineR library has
observations related to Valle de Loira (France) wines and
sensory variables related to wine quality. This dataset contains qualitative and quantitative variables described in [
4,
39]. For this illustration, we considered quantitative variables. First, we deployed the MFA algorithm for a complete dataset. Additionally, a subset with 7% of NAs of total observations was randomly selected to deploy the RIMFA and MFA-NIPALS algorithms. The results were compared in terms of percentage of explained variance and coordinate correlation of the complete dataset versus RIMFA and MFA-NIPALS algorithms.
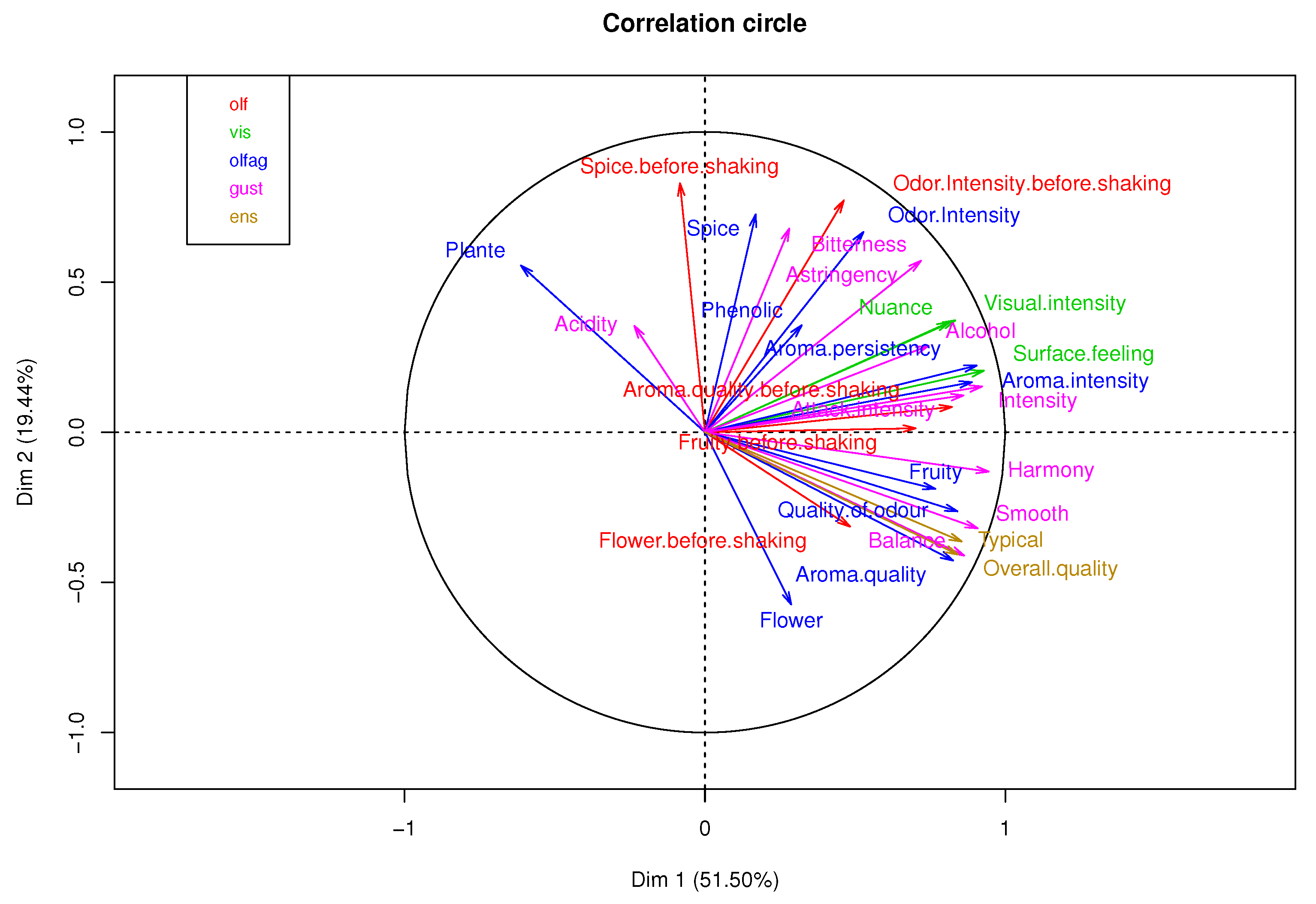
Figure 9 shows the correlation of each table’s variables. The percentage of explained variance in the first two components is 70.94% of the total variability.
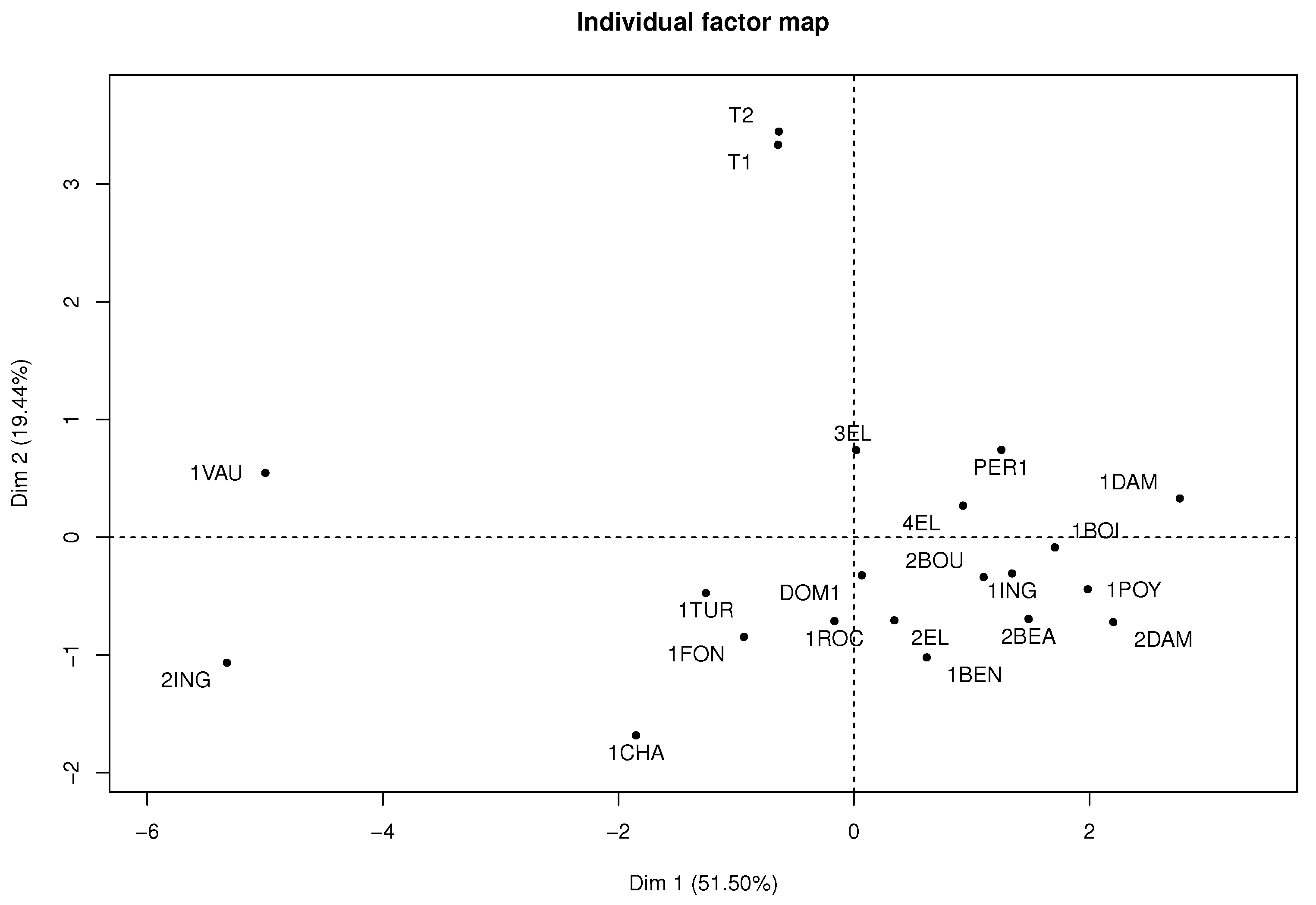
Figure 10 represents each wine in the factorial plane, where wines
T1 and
T2 stand out due to similarities of their sensory variables and atypical features. In addition, the
1VAU and
2ING wines are highlighted on the left of the factorial plane, as they presented similarities and atypical features because they differ greatly from the original wines with average features.
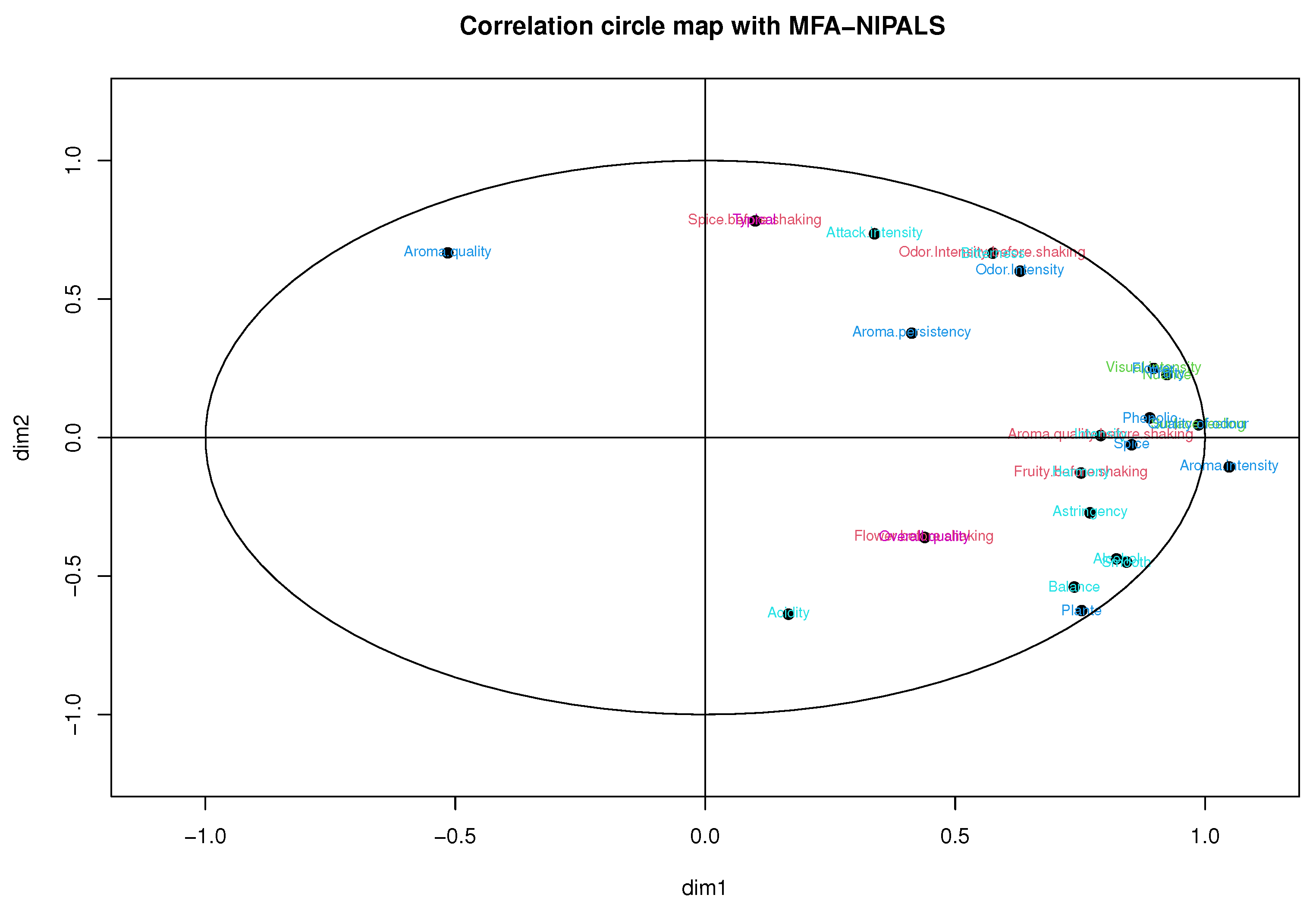
Considering
Figure 11 and
Figure 12, obtained from the MFA-NIPALS algorithm with 7% of NAs, it is evident that the results feature similarities with
Figure 9 and
Figure 10. Moreover, more similarities for wines in the factorial plane are highlighted. In fact, the correlation between the coordinates of wines from MFA and MFA-NIPALS on the first factorial axis is
and
for the second factorial axis. The percentage of explained variance of 72.35%, which is similar to the MFA case with complete dataset, is also highlighted.
For RIMFA, 72.53% of the explained variance was found in the first two factorial axes. Comparing their coordinates versus MFA coordinates using a complete dataset, correlations and were found. Thus, the RIMFA algorithm performed better than the MFA-NIPALS one. Nevertheless, MFA-NIPALS performed better than the MFA algorithm in the estimation of coordinates, where is close to 1.
4. Conclusions and Further Works
We successfully coupled the NIPALS algorithm with MFA for missing data, called the MFA-NIPALS algorithm. The proposed algorithm was implemented with
R software and an alternative method for data imputation with RIMFA was configured. MFA-NIPALS was adapted using the
nipals function of the
ade4 library. Other options such as the
nipals function of the
plsdepot library [
42] could be explored. Karimov et al. [
43] considered phase space reconstruction techniques mainly oriented toward classification tasks, where the integrate-and-differentiate approach is focused on improving identification accuracy through the elimination of classification errors needed for the parameter estimation of nonlinear equations. Further studies could explore the integrate-and-differentiate approach regarding the missing data problem.
Further works could analyze if Gram–Schmidt orthogonalization helps to find better properties for MFA-NIPALS. The literature contains multiple factorial methods, in which the missing data problem has not been addressed with NIPALS, for example, the STATIS-ACT method and canonical correlation analysis (ACC) [
44,
45]. The NIPALS algorithm seems suitable to address missing data in STATIS-ACT and ACC.
Another important concept related to MFS is the RV coefficient of Escoufier [
46,
47], which is a matrix version of the Pearson coefficient of correlation. The RV coefficient between tables
and
is:
where
denotes the trace of matrix
[
36].
The RV coefficient is often used to study the correlation between tables or groups of variables. The coefficients related to the covariance of a pair of tables appear in the numerator of (
18). If
X and
Y include NAs and MFA-NIPALS is used, further work could focus on RV coefficient computation using the available data principle (see
Section 2.4). Another proposal is the use of coordinates between individuals
in the
kth table as an estimation of
X and
Y, since coordinates
do not have NAs when MFA-NIPALS is deployed.
In this paper, MFA-NIPALS was used for longitudinal quantitative variables with the presence of NAs. This approach could be extended to multiple
k qualitative tables using MCA under the available data principle [
19]. This idea allows working with MFA-NIPALS with mixed data using NIPALS for quantitative tables and MCA for qualitative ones. Given that the available data principle reduces computational cost when MFA-NIPALS is used compared to RIMFA, the MFA-NIPALS algorithm is a novel approach to addressing missing data problems in multiple quantitative tables. Nevertheless, further studies are needed to compare MFA-NIPALS with RIMFA across datasets with higher dimensions, analyzing the computational performance of both methods by comparing the estimated coordinates of
(in presence of NAs) with MFA coordinates (of a complete dataset). It is expected that MFA-NIPALS performs better with datasets with more variables than observations (
), where PLS methods have advantages over classic methods [
48].
Based on simulation scenarios, it is recommended to work the MFA-NIPALS proposal until 15% of NAs of the total number of observations. This result is in line with the results by [
24], highlighting the NAs percentage recommended for NIPALS. Moreover, it is recommended to use MFA-NIPALS when data imputation is not feasible. Though the RIMFA algorithm performed well when coordinates are compared to the MFS one, this study showed that the MFA-NIPALS algorithm was a good alternative for NA handling in the MFA. Moreover, our proposal is promising, as it yielded favorable results regarding the percentage of explained variance. It is highly probable that other studies generate even better results by mixing the MFA-NIPALS and RIMFA approaches.