Optimization of Linear Quantization for General and Effective Low Bit-Width Network Compression
Abstract
1. Introduction
- This paper optimizes the linear quantization method with a two-stage technique. The clustering function is separated before mapping from the traditional linear quantization. Specifically, the optimized method applies a modified K-means algorithm to cluster the weights and then uses the uniform partition to map the centroids to fixed-point numbers.
- The results of the K-means algorithm are greatly affected by the initial cluster centroids, which may cause non-convergence. In neural network quantization, the number of cluster centroids can be determined by the bit-width. This paper selects the particle swarm algorithm to obtain the initial cluster centroids to facilitate the convergence of clustering.
- To reduce effectively both the energy consumption and memory cost of DNN models, models are first fine-grained pruning before quantization with low bit-width. The experimental results show that fine-grained pruning does not affect the accuracy of the quantized model. It is safe and necessary to perform pruning before quantization.
2. Related Work
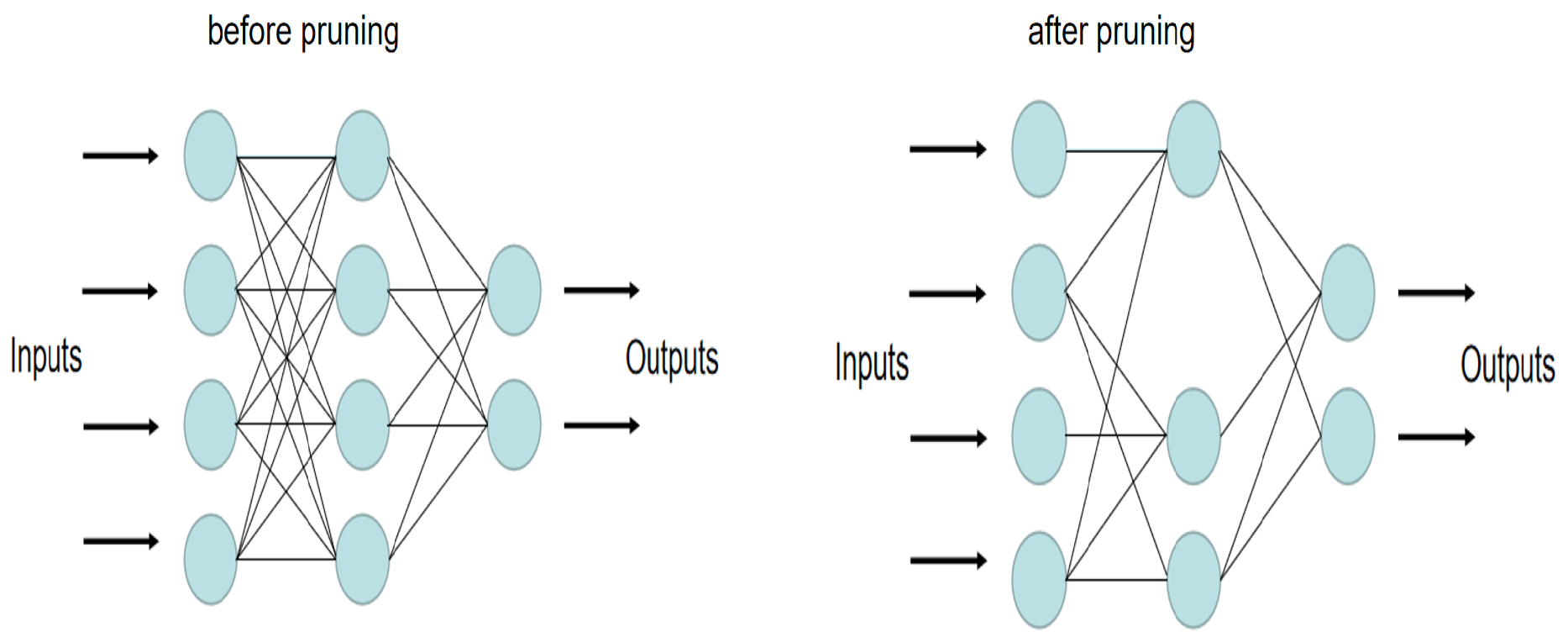
2.1. Fine-Grained Pruning
2.2. Post-Training Quantization
2.2.1. Weight-Sharing Quantization
2.2.2. Uniform Partition Quantization
2.3. Metaheuristic
3. Two-Stage Quantization Method
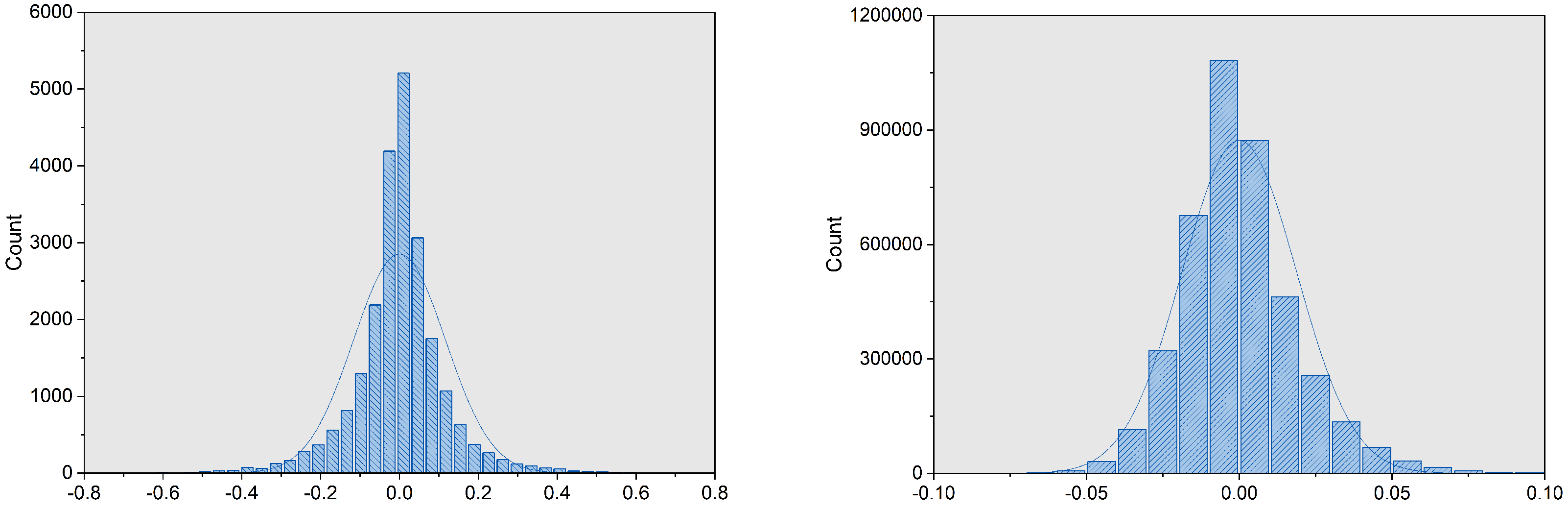
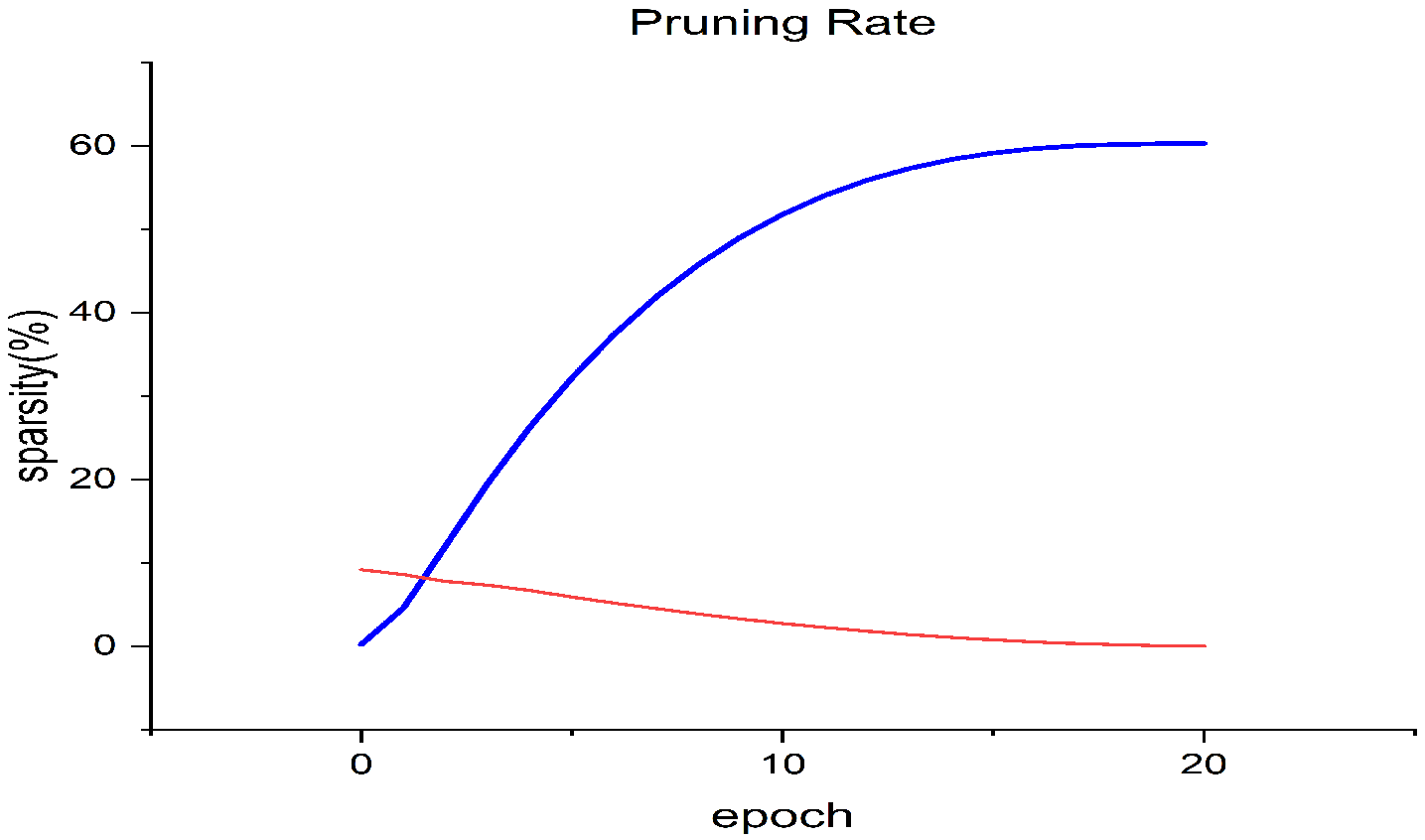
3.1. Pruning
- denotes the target sparsity;
- denotes the initial sparsity;
- denotes the current sparsity.
3.2. Clustering
3.2.1. K-Means
- denotes the i-th weight;
- denotes the centroid of cluster j;
- is the subset of weights that form cluster j.
- (1)
- Random initialization;
- (2)
- Uniform partition;
- (3)
- Initialize by the optimization algorithm.
| Algorithm 1 K-means. |
| Input: Dataset , cluster centorids k |
| Output: Result set |
|
3.2.2. PSO-K-Means
- denotes the average intra-cluster distance;
- denotes the average nearest-cluster distance;
- denotes the silhouette coefficient of one sample;
- denotes the silhouette coefficient of the cluster.
| Algorithm 2 Hybrid PSO-Kmeans. |
| Input: Dataset , cluster centorids k |
| Output: Result set |
|
3.3. Mapping
- r denotes a real number;
- q denotes an n-bit integer.
| Algorithm 3 Mapping. |
| Input: weight matrix after clustering, Quantization bit-width n |
| Output: Result set |
|
4. Experiment
- Top-1 accuracy denotes the accuracy at which the top-ranked category matches the actual results.
- Top-5 accuracy denotes the accuracy at which the top-5 categories match the actual results.
- Total sparsity denotes the proportion of non-zero elements.
4.1. Accuracy Comparison between Linear Quantization and K-Means
4.2. Accuracy Comparison between Different Initialization Methods
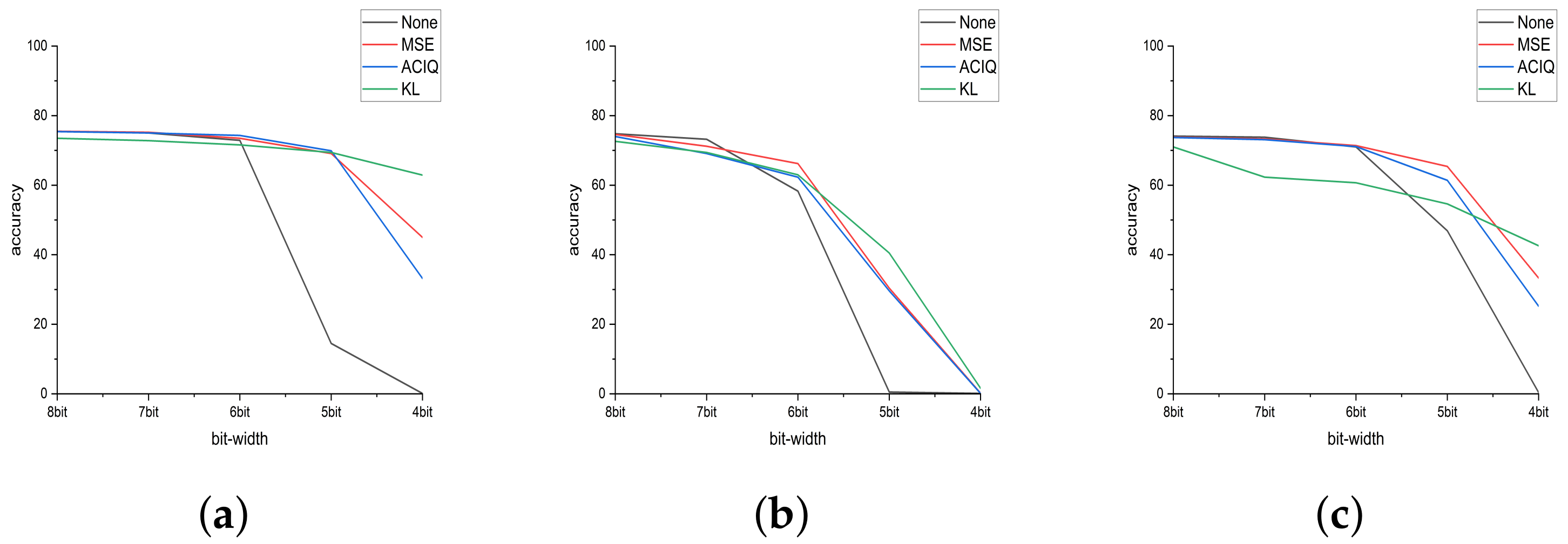
4.3. Accuracy Comparison between Existing Post Quantization Methods Based on Clipping
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Sallam, N.M. Speed control of three phase induction motor using neural network. IJCSIS 2018, 16, 16. [Google Scholar]
- Sallam, N.M.; Saleh, A.I.; Arafat Ali, H.; Abdelsalam, M.M. An Efficient Strategy for Blood Diseases Detection Based on Grey Wolf Optimization as Feature Selection and Machine Learning Techniques. Appl. Sci. 2022, 12, 10760. [Google Scholar] [CrossRef]
- Han, S.; Mao, H.; Dally, W.J. Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding. Fiber 2015, 56, 3–7. [Google Scholar]
- Xu, X.; Ding, Y.; Hu, S.X.; Niemier, M.; Cong, J.; Hu, Y.; Shi, Y. Scaling for edge inference of deep neural networks. Nat. Electron. 2018, 1, 216–222. [Google Scholar] [CrossRef]
- Reed, R.D. Pruning algorithms-a survey. IEEE Trans. Neural Netw. 1993, 4, 740–747. [Google Scholar] [CrossRef] [PubMed]
- Maarif, M.R.; Listyanda, R.F.; Kang, Y.-S.; Syafrudin, M. Artificial Neural Network Training Using Structural Learning with Forgetting for Parameter Analysis of Injection Molding Quality Prediction. Information 2022, 13, 488. [Google Scholar] [CrossRef]
- Zhu, M.; Gupta, S. To prune, or not to prune: Exploring the efficacy of pruning for model compression. arXiv 2017, arXiv:1710.01878. [Google Scholar]
- Vanhoucke, V.; Mao, M.Z. Improving the speed of neural networks on CPUs. In Proceedings of the Deep Learning and Unsupervised Feature Learning Workshop, NIPS 2011, Granada, Spain, 12–17 December 2011. [Google Scholar]
- Courbariaux, M.; Bengio, Y.; David, J.P. BinaryConnect: Training Deep Neural Networks with binary weights during propagations. In Proceedings of the International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Leibe, B.; Matas, J.; Sebe, N.; Welling, M. XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks. In Proceedings of the Computer Vision—ECCV 2016; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; Volume 9908, Chapter 32; pp. 525–542. [Google Scholar]
- Li, F.; Liu, B. Ternary Weight Networks. arXiv 2016, arXiv:1605.04711. [Google Scholar]
- Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Chang, S.E.; Li, Y.; Sun, M.; Shi, R.; So, H.K.-H.; Qian, X.; Wang, Y.; Lin, X. Mix and Match: A Novel FPGA-Centric Deep Neural Network Quantization Framework. In Proceedings of the 2021 IEEE International Symposium on High-Performance Computer Architecture (HPCA), Seoul, Republic of Korea, 27 February 27–3 March 2021. [Google Scholar]
- Migacz, S. 8-bit inference with TensorRT. In Proceedings of the GPU Technology Conference, San Jose, CA, USA, 8–11 May 2017. [Google Scholar]
- Han, S.; Pool, J.; Tran, J.; Dally, W. Learning both Weights and Connections for Efficient Neural Networks. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Zmora, N.; Jacob, G.; Elharar, B.; Zlotnik, L.; Novik, G.; Barad, H.; Chen, Y.; Muchsel, R.; Fan, T.J.; Chavez, R.; et al. NervanaSystems/Distillerv (V0.3.2). Zenodo. 2019. Available online: https://doi.org/10.5281/zenodo.3268730 (accessed on 1 January 2021).
- Miyashita, D.; Lee, E.H.; Murmann, B. Convolutional Neural Networks using Logarithmic Data Representation. arXiv 2016, arXiv:1603.01025. [Google Scholar]
- Chen, W.; Wilson, J.; Tyree, S.; Weinberger, K.; Chen, Y. Compressing Neural Networks with the Hashing Trick. In Proceedings of the International Conference on International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- Wu, J.; Leng, C.; Wang, Y.; Hu, Q.; Cheng, J. Quantized Convolutional Neural Networks for Mobile Devices. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Shin, S.; Hwang, K.; Sung, W. Fixed-point performance analysis of recurrent neural networks. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016. [Google Scholar]
- Banner, R.; Nahshan, Y.; Soudry, D. Post training 4-bit quantization of convolutional networks for rapid-deployment. arXiv 2019, arXiv:1810.05723. [Google Scholar]
- Zhao, R. Improving Neural Network Quantization without Retraining using Outlier Channel Splitting. arXiv 2019, arXiv:1901.09504. [Google Scholar]
- Glover, F. Future paths for integer programming and links to artificial intelligence. Comput. Oper. Res. 1986, 13, 533–549. [Google Scholar] [CrossRef]
- Alorf, A. A survey of recently developed metaheuristics and their comparative analysis. Eng. Appl. Artif. Intell. 2023, 117, 105622. [Google Scholar] [CrossRef]
- Dorigo, M. Optimization, Learning and Natural Algorithms. Ph.D. Thesis, Politecnico di Milano, Milan, Italy, 1992. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle Swarm Optimization. In Proceedings of the IEEE International Joint Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Jain, M.; Singh, V.; Rani, A. A novel nature-inspired algorithm for optimization: Squirrel search algorithm. Swarm Evol. Comput. 2019, 44, 148–175. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Wang, L. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Omran, M.; Salman, A.; Engelbrecht, A.P. Image Classification using Particle Swarm Optimization. In Proceedings of the 4th Asia-Pacific Conference on Simulated Evolution and Learning, Singapore, 18–22 November 2002. [Google Scholar]
- Ballardini, A.L. A tutorial on Particle Swarm Optimization Clusterin. arXiv 2018, arXiv:1809.01942. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Weinberger, K.Q.; van der Maaten, L. Densely connected convolutional networks. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Li, F.-F. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic Differentiation in PyTorch. In Proceedings of the Advances in Neural Information Processing Systems Workshops (NIPS-W), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Sung, W.; Shin, S.; Hwang, K. Resiliency of Deep Neural Networks under Quantization. arXiv 2015, arXiv:1511.06488. [Google Scholar]




| Network | Total Epochs | Initial Sparsity (%) | Final Sparsity (%) |
|---|---|---|---|
| ResNet-18 | 20 | 0 | 60 |
| ResNet-50 | 30 | 0 | 80 |
| Inception-V3 | 25 | 0 | 70 |
| Densenet-121 | 20 | 0 | 60 |
| Network | Top-1 (%) | Top-5 (%) | Total Sparsity (%) |
|---|---|---|---|
| ResNet-18 | 67.664 | 86.486 | 59.92 |
| ResNet-50 | 73.388 | 92.576 | 79.97 |
| Inception-V3 | 67.298 | 87.668 | 68.41 |
| Densenet-121 | 75.050 | 92.516 | 60.28 |
| Network | Bit-Width | Centroids | Linear | K-Means |
|---|---|---|---|---|
| ResNet-18 [33] (69.758) | 8 | 255 | 69.510 | 69.756 |
| 7 | 127 | 69.072 | 69.682 | |
| 6 | 63 | 67.290 | 69.494 | |
| 5 | 31 | 53.586 | 68.066 | |
| 4 | 15 | 1.028 | 61.466 | |
| ResNet-50 [33] (76.13) | 8 | 255 | 75.868 | 76.054 |
| 7 | 127 | 75.232 | 76.080 | |
| 6 | 63 | 72.532 | 75.382 | |
| 5 | 31 | 49.278 | 72.242 | |
| 4 | 15 | 0.234 | 67.736 | |
| DenseNet-121 [34] (74.433) | 8 | 255 | 74.266 | 74.380 |
| 7 | 127 | 73.458 | 74.260 | |
| 6 | 63 | 71.308 | 73.644 | |
| 5 | 31 | 56.260 | 72.738 | |
| 4 | 15 | 1.802 | 64.026 | |
| Inception-v3 [35] (69.538) | 8 | 255 | 69.968 | 69.478 |
| 7 | 127 | 67.942 | 69.288 | |
| 6 | 63 | 61.788 | 67.498 | |
| 5 | 31 | 12.892 | 63.414 | |
| 4 | 15 | 0.086 | 20.946 |
| Network | Bit-Width | Random (Before Pruning) | Random (After Pruning) | Uniform-Partition (After Pruning) | PSO (After Pruning) |
|---|---|---|---|---|---|
| ResNet-18 [33] (69.758) | 8 | 69.560 | 69.432 | 69.312 | 69.422 |
| 7 | 69.178 | 68.758 | 68.848 | 66.398 | |
| 6 | 67.906 | 68.540 | 67.660 | 68.114 | |
| 5 | 61.782 | 64.936 | 60.288 | 66.426 | |
| 4 | 49.134 | 55.328 | 50.720 | 59.594 | |
| ResNet-50 [33] (76.13) | 8 | 75.906 | 75.146 | 75.146 | 75.354 |
| 7 | 75.336 | 75.086 | 74.256 | 75.316 | |
| 6 | 75.280 | 74.620 | 74.182 | 75.050 | |
| 5 | 70.784 | 71.708 | 71.120 | 72.496 | |
| 4 | 60.736 | 65.208 | 64.630 | 67.622 | |
| DenseNet-121 [34] (74.433) | 8 | 74.138 | 74.530 | 74.140 | 74.064 |
| 7 | 73.876 | 73.138 | 73.330 | 74.006 | |
| 6 | 72.468 | 72.992 | 72.402 | 73.786 | |
| 5 | 70.856 | 70.712 | 68.130 | 72.392 | |
| 4 | 54.250 | 54.838 | 60.858 | 60.918 | |
| Inception-v3 [35] (69.538) | 8 | 68.382 | 66.916 | 66.656 | 67.220 |
| 7 | 68.048 | 66.43 | 67.070 | 67.364 | |
| 6 | 64.358 | 66.582 | 65.628 | 65.774 | |
| 5 | 56.420 | 57.200 | 55.514 | 60.958 | |
| 4 | 18.112 | 27.560 | 18.916 | 33.076 |
| Method | Approach | Bit-Width (Weight/Activation) | Top-1 (%) |
|---|---|---|---|
| Baseline | - | W32/A32 | 76.13 |
| none | Linear | W4/A4 | 0.1 |
| MSE [38] | Clip-Linear | W4/A4 | 45.0 |
| ACIQ [22] | Clip-Linear | W4/A4 | 33.2 |
| KL [15] | Clip-Linear | W4/A8 | 62.9 |
| OCS [23] | OCS-Linear | W4/A8 | 63.8 |
| PSO-K-means | Cluster-Map | W4/A4 | 67.622 |
| Method | Approach | Bit-Width (Weight/Activation) | Top-1 (%) |
|---|---|---|---|
| Baseline | - | W32/A32 | 69.538 |
| none | Linear | W4/A4 | 0.1 |
| MSE [38] | Clip-Linear | W4/A4 | 0.2 |
| ACIQ [22] | Clip-Linear | W4/A4 | 0.1 |
| KL [15] | Clip-Linear | W4/A8 | 1.6 |
| OCS [23] | OCS-Linear | W4/A8 | 2.3 |
| PSO-K-means | Cluster-Map | W4/A4 | 33.076 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Zhi, X.; Tong, W. Optimization of Linear Quantization for General and Effective Low Bit-Width Network Compression. Algorithms 2023, 16, 31. https://doi.org/10.3390/a16010031
Yang W, Zhi X, Tong W. Optimization of Linear Quantization for General and Effective Low Bit-Width Network Compression. Algorithms. 2023; 16(1):31. https://doi.org/10.3390/a16010031
Chicago/Turabian StyleYang, Wenxin, Xiaoli Zhi, and Weiqin Tong. 2023. "Optimization of Linear Quantization for General and Effective Low Bit-Width Network Compression" Algorithms 16, no. 1: 31. https://doi.org/10.3390/a16010031
APA StyleYang, W., Zhi, X., & Tong, W. (2023). Optimization of Linear Quantization for General and Effective Low Bit-Width Network Compression. Algorithms, 16(1), 31. https://doi.org/10.3390/a16010031





