Fourier Neural Operator for Fluid Flow in Small-Shape 2D Simulated Porous Media Dataset
Abstract
1. Introduction
- (1)
- Can FNO models perform accurately on small-shape data problems in terms of the prediction error metrics?
- (2)
- How do mode and width affect the performance of FNO models?
- (3)
- Does downsampling have a positive or negative effect on FNO model performance when applied to small-shape data?
- (4)
- Can FNO models satisfy the pattern applicable to porous media problems?
- (5)
- How does the performance of FNO models compare to that of CNN?
2. Problem Setup with Governing Equations
3. Methodology
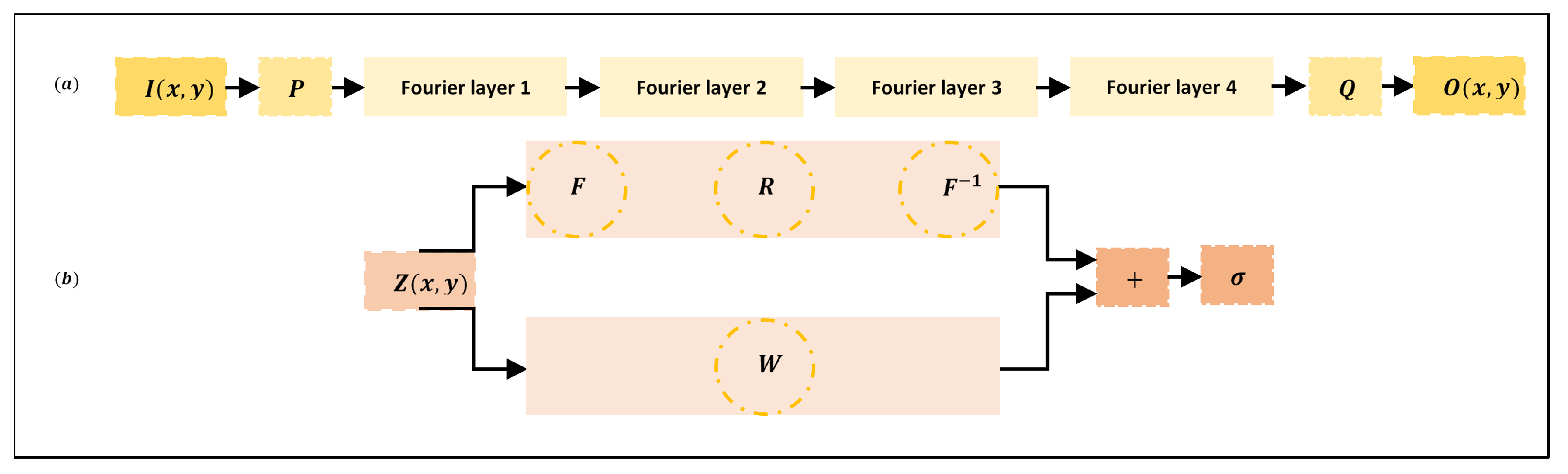
3.1. FNO Architecture
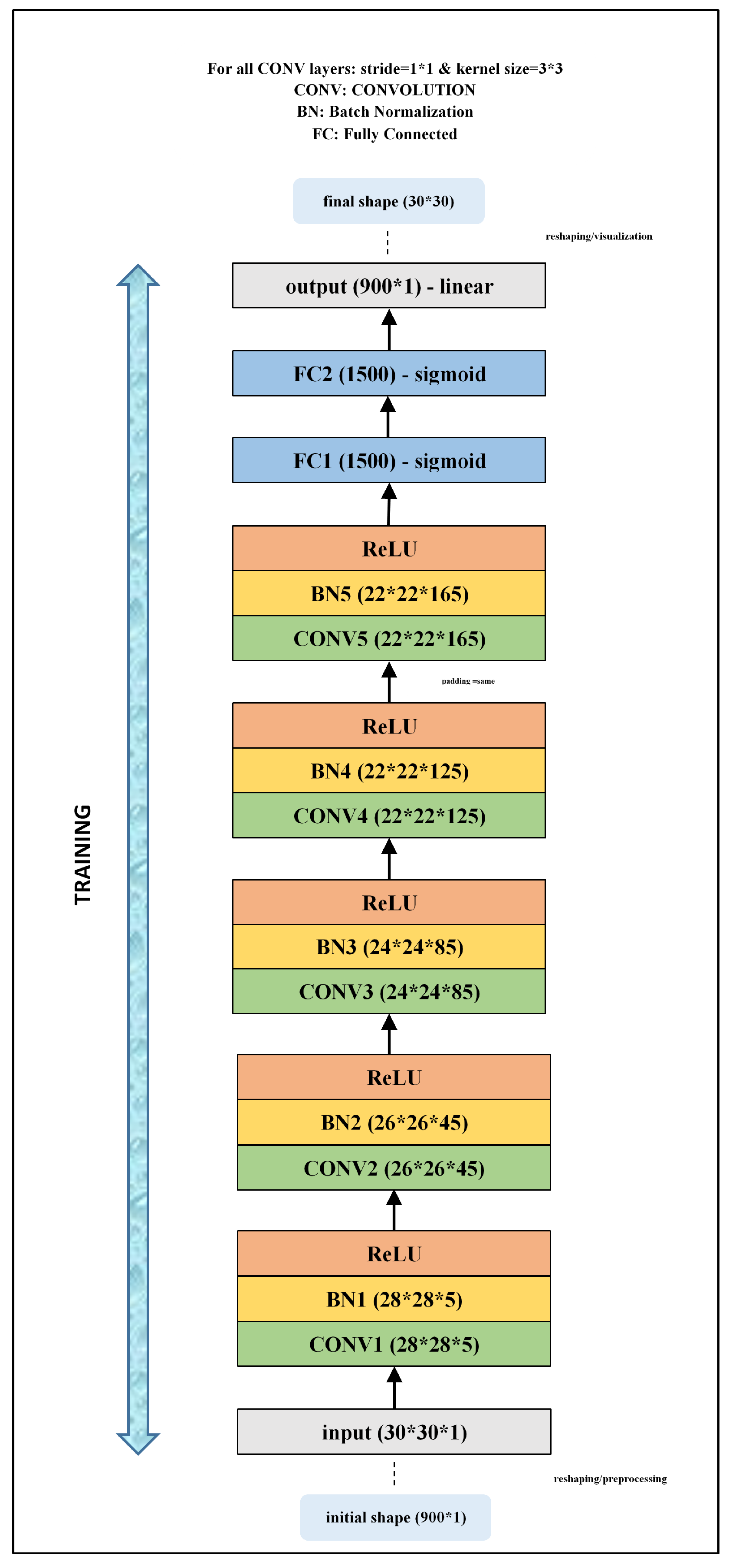
3.2. CNN Architecture
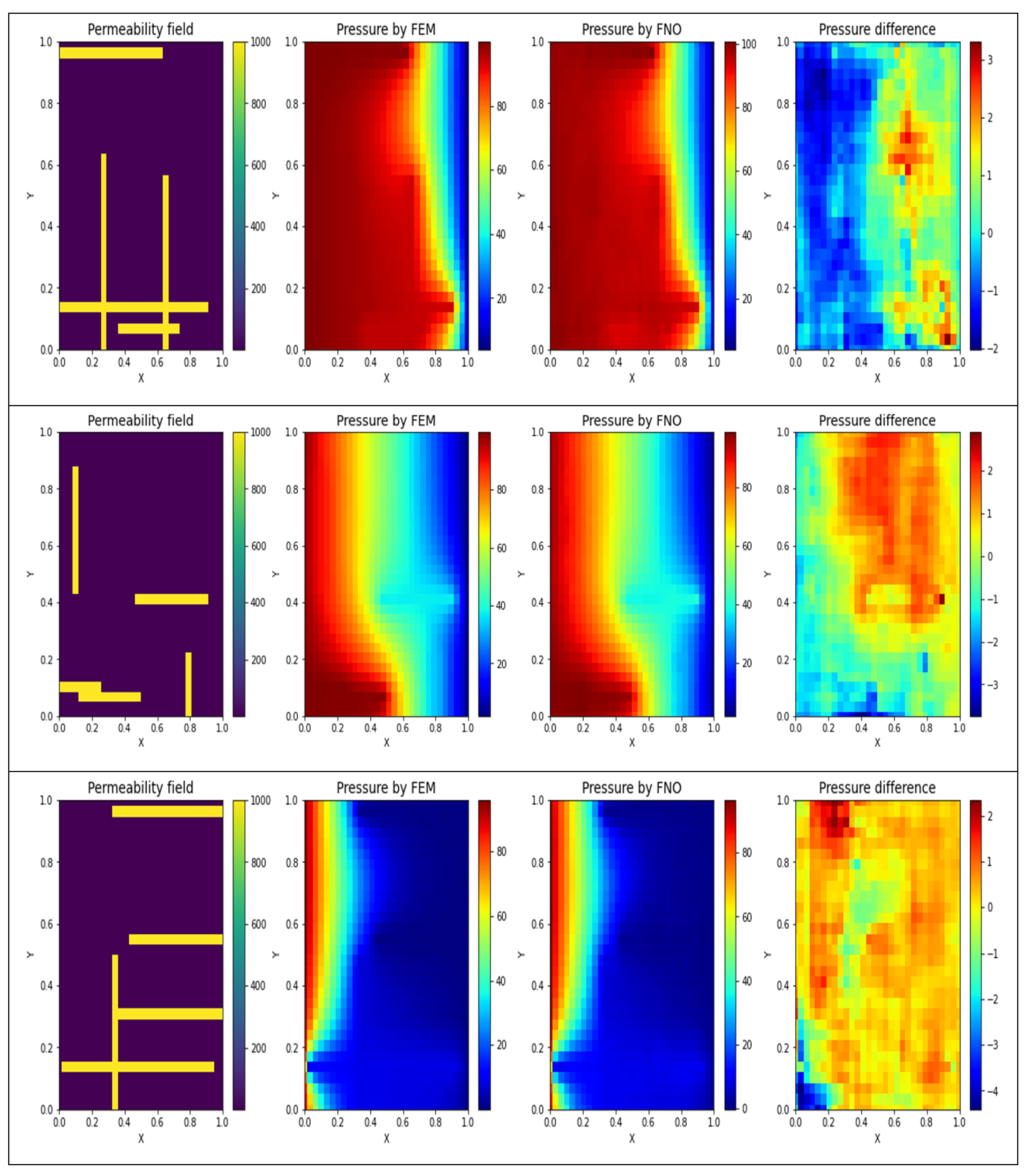
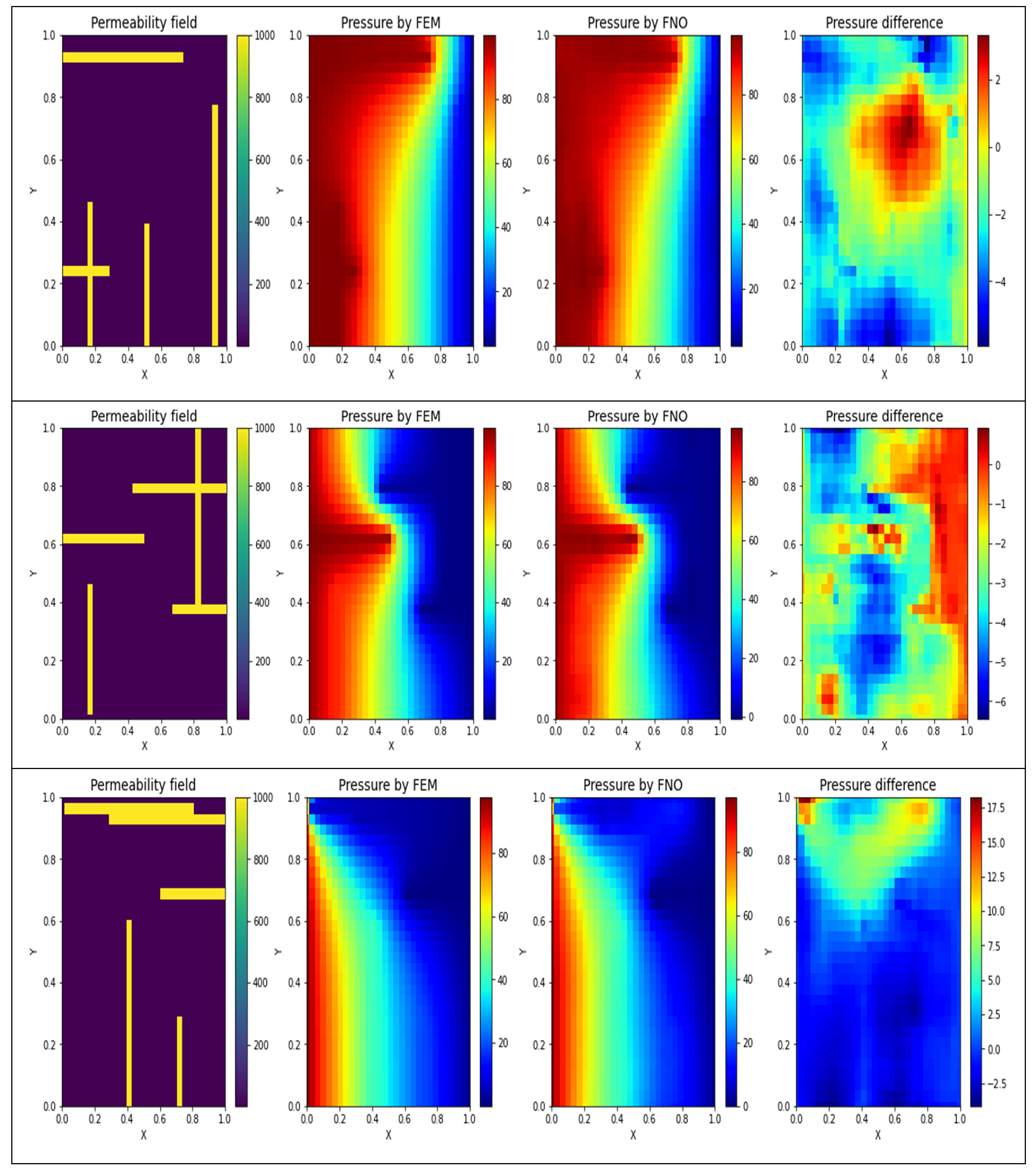
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| first term of | |
| Fourier series coefficient | |
| BC | Boundary Condition |
| BN | Batch Normalization |
| Fourier series coefficient | |
| CNN | Convolutional Neural Network |
| CONV | convolutional layers |
| DL | Deep Learning |
| Laplace pressure | |
| f | source term |
| F | Fourier transform |
| inverse Fourier transform | |
| FC | Fully Connected |
| FEM | Finite Element Method |
| FNO | Fourier Neural Operator |
| i | imaginary number () |
| IC | Initial Condition |
| input layer | |
| permeability of the fracture | |
| permeability of the matrix | |
| LES | Large Eddy Simulation |
| ML | Machine Learning |
| number of fractures | |
| MSE | Mean Squared Error |
| fluid viscosity | |
| NN | Neural Network |
| gradient pressure | |
| divergence velocity | |
| ODE | Ordinary Differential Equation |
| output layer | |
| PDE | Partial Differential Equation |
| PINN | Physics-Informed Neural Network |
| R | linear transform |
| R | coefficient of determination |
| s | angular frequency |
| k | permeability |
| u | Darcy velocity |
| W | local linear transform |
| higher-dimension channel space | |
| output of the fourth (final) Fourier layer |
References
- Golub, G.H.; Ortega, J.M. Scientific Computing and Differential Equations: An Introduction to Numerical Methods; Academic Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Tao, Z.; Cui, Z.; Yu, J.; Khayatnezhad, M. Finite difference modelings of groundwater flow for constructing artificial recharge structures. Iran. J. Sci. Technol. Trans. Civ. Eng. 2022, 46, 1503–1514. [Google Scholar] [CrossRef]
- Fathollahi, R.; Hesaraki, S.; Bostani, A.; Shahriyari, E.; Shafiee, H.; Pasha, P.; Chari, F.N.; Ganji, D.D. Applying numerical and computational methods to investigate the changes in the fluid parameters of the fluid passing over fins of different shapes with the finite element method. Int. J. Thermofluids 2022, 15, 100187. [Google Scholar] [CrossRef]
- Afzal, A.; Saleel, C.A.; Prashantha, K.; Bhattacharyya, S.; Sadhikh, M. Parallel finite volume method-based fluid flow computations using OpenMP and CUDA applying different schemes. J. Therm. Anal. Calorim. 2021, 145, 1891–1909. [Google Scholar] [CrossRef]
- Han, C.; Wang, Y.L.; Li, Z.Y. Numerical Solutions of Space Fractional Variable-Coefficient Kdv–Modified Kdv Equation by Fourier Spectral Method. Fractals 2021, 29, 2150246. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Kumar, A. A meshless method for time fractional nonlinear mixed diffusion and diffusion-wave equation. Appl. Numer. Math. 2021, 160, 146–165. [Google Scholar] [CrossRef]
- Keybondorian, E.; Soltani Soulgani, B.; Bemani, A. Application of ANFIS-GA algorithm for forecasting oil flocculated asphaltene weight percentage in different operation conditions. Pet. Sci. Technol. 2018, 36, 862–868. [Google Scholar] [CrossRef]
- Mohammadi, M.; Safari, M.; Ghasemi, M.; Daryasafar, A.; Sedighi, M. Asphaltene adsorption using green nanocomposites: Experimental study and adaptive neuro-fuzzy interference system modeling. J. Pet. Sci. Eng. 2019, 177, 1103–1113. [Google Scholar] [CrossRef]
- Mai, H.; Le, T.C.; Chen, D.; Winkler, D.A.; Caruso, R.A. Machine learning for electrocatalyst and photocatalyst design and discovery. Chem. Rev. 2022, 122, 13478–13515. [Google Scholar] [CrossRef] [PubMed]
- Kazemi, P.; Ghisi, A.; Mariani, S. Classification of the Structural Behavior of Tall Buildings with a Diagrid Structure: A Machine Learning-Based Approach. Algorithms 2022, 15, 349. [Google Scholar] [CrossRef]
- Chen, W.; Wang, S.; Zhang, X.; Yao, L.; Yue, L.; Qian, B.; Li, X. EEG-based motion intention recognition via multi-task RNNs. In Proceedings of the 2018 SIAM International Conference on Data Mining, SIAM, San Diego, CA, USA, 3–5 May 2018; pp. 279–287. [Google Scholar]
- Choubineh, A.; Chen, J.; Coenen, F.; Ma, F. An innovative application of deep learning in multiscale modeling of subsurface fluid flow: Reconstructing the basis functions of the mixed GMsFEM. J. Pet. Sci. Eng. 2022, 216, 110751. [Google Scholar] [CrossRef]
- Choubineh, A.; Chen, J.; Coenen, F.; Ma, F. A quantitative insight into the role of skip connections in deep neural networks of low complexity: A case study directed at fluid flow modeling. J. Comput. Inf. Sci. Eng. 2022, 23, 014502. [Google Scholar] [CrossRef]
- Pawar, P.; Ainapure, B.; Rashid, M.; Ahmad, N.; Alotaibi, A.; Alshamrani, S.S. Deep Learning Approach for the Detection of Noise Type in Ancient Images. Sustainability 2022, 14, 11786. [Google Scholar] [CrossRef]
- Mijalkovic, J.; Spognardi, A. Reducing the False Negative Rate in Deep Learning Based Network Intrusion Detection Systems. Algorithms 2022, 15, 258. [Google Scholar] [CrossRef]
- Li, Z.; Kovachki, N.; Azizzadenesheli, K.; Liu, B.; Bhattacharya, K.; Stuart, A.; Anandkumar, A. Fourier neural operator for parametric partial differential equations. arXiv 2020, arXiv:2010.08895. [Google Scholar]
- Gallant, A.R.; White, H. There exists a neural network that does not make avoidable mistakes. In Proceedings of the ICNN, San Diego, CA, USA, 24–27 July 1988; pp. 657–664. [Google Scholar]
- Silvescu, A. Fourier neural networks. In Proceedings of the IJCNN’99, International Joint Conference on Neural Networks, Proceedings (Cat. No. 99CH36339), Washington, DC, USA, 10–16 July 1999; Volume 1, pp. 488–491. [Google Scholar]
- Liu, S. Fourier neural network for machine learning. In Proceedings of the 2013 International Conference on Machine Learning and Cybernetics, Tianjin, China, 14–17 July 2013; Volume 1, pp. 285–290. [Google Scholar]
- Wen, G.; Li, Z.; Azizzadenesheli, K.; Anandkumar, A.; Benson, S.M. U-FNO—An enhanced Fourier neural operator-based deep-learning model for multiphase flow. Adv. Water Resour. 2022, 163, 104180. [Google Scholar] [CrossRef]
- Rashid, M.M.; Pittie, T.; Chakraborty, S.; Krishnan, N.A. Learning the stress-strain fields in digital composites using fourier neural operator. iScience 2022, 105452. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Peng, W.; Yuan, Z.; Wang, J. Fourier neural operator approach to large eddy simulation of three-dimensional turbulence. Theor. Appl. Mech. Lett. 2022, 100389. [Google Scholar] [CrossRef]
- Johnny, W.; Brigido, H.; Ladeira, M.; Souza, J.C.F. Fourier Neural Operator for Image Classification. In Proceedings of the 2022 17th Iberian Conference on Information Systems and Technologies (CISTI), Madrid, Spain, 22–25 June 2022; pp. 1–6. [Google Scholar]
- Chen, Z. Reservoir Simulation: Mathematical Techniques in Oil Recovery; SIAM: Philadelphia, PA, USA, 2007. [Google Scholar]
- Fukunaga, K.; Koontz, W.L. Application of the Karhunen-Loeve expansion to feature selection and ordering. IEEE Trans. Comput. 1970, 100, 311–318. [Google Scholar] [CrossRef]
- Lasser, R. Introduction to Fourier Series; CRC Press: Boca Raton, FL, USA, 1996; Volume 199. [Google Scholar]
- Strichartz, R.S. A Guide to Distribution Theory and Fourier Transforms; World Scientific Publishing Company: Hackensack, NJ, USA, 2003. [Google Scholar]
- Subramanian, V. Deep Learning with PyTorch: A Practical Approach to Building Neural Network Models Using PyTorch; Packt Publishing Ltd.: Birmingham, UK, 2018. [Google Scholar]
- Reddi, S.J.; Kale, S.; Kumar, S. On the convergence of adam and beyond. arXiv 2019, arXiv:1904.09237. [Google Scholar]
- Nussbaumer, H.J. The fast Fourier transform. In Fast Fourier Transform and Convolution Algorithms; Springer: Berlin/Heidelberg, Germany, 1981; pp. 80–111. [Google Scholar]
- Joseph, F.J.J.; Nonsiri, S.; Monsakul, A. Keras and TensorFlow: A hands-on experience. In Advanced Deep Learning for Engineers and Scientists; Springer: Cham, Switzerland, 2021; pp. 85–111. [Google Scholar]

| Mode | Width | MSE (Training) | R (Training) | MSE (Testing) | R (Testing) |
|---|---|---|---|---|---|
| 5 | 20 | 2.5543 | 0.9945 | 109.9231 | 0.7661 |
| 5 | 60 | 2.0832 | 0.9955 | 92.2014 | 0.8038 |
| 5 | 100 | 2.0605 | 0.9956 | 89.8219 | 0.8089 |
| 5 | 140 | 1.943 | 0.9958 | 93.8539 | 0.8003 |
| 5 | 180 | 1.878 | 0.996 | 86.3347 | 0.8163 |
| 10 | 20 | 1.8483 | 0.996 | 78.7648 | 0.8324 |
| 10 | 60 | 1.4814 | 0.9968 | 65.4587 | 0.8607 |
| 10 | 100 | 1.4196 | 0.9969 | 60.6803 | 0.8709 |
| 10 | 140 | 1.5745 | 0.9966 | 60.8775 | 0.8705 |
| 10 | 180 | 1.3643 | 0.9971 | 59.8904 | 0.8726 |
| 15 | 20 | 1.7253 | 0.9963 | 65.5664 | 0.8605 |
| 15 | 60 | 1.4007 | 0.997 | 51.0625 | 0.8914 |
| 15 | 100 | 1.4087 | 0.997 | 42.1611 | 0.9103 |
| 15 | 140 | 1.505 | 0.9968 | 53.6779 | 0.8858 |
| 15 | 180 | 1.4966 | 0.9968 | 47.783 | 0.8983 |
| 20 | 20 | 1.5206 | 0.9967 | 60.3367 | 0.8716 |
| 20 | 60 | 1.6387 | 0.9965 | 43.8621 | 0.9067 |
| 20 | 100 | 1.6409 | 0.9965 | 46.167 | 0.9018 |
| 20 | 140 | 1.5687 | 0.9966 | 44.5223 | 0.9053 |
| 20 | 180 | 1.7145 | 0.9963 | 46.8985 | 0.9002 |
| Model | MSE (Training) | R (Training) | MSE (Testing) | R (Testing) |
|---|---|---|---|---|
| FNO ( and ) | 1.4087 | 0.997 | 42.1611 | 0.9103 |
| CNN | 0.3074 | 0.9993 | 86.1818 | 0.8166 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choubineh, A.; Chen, J.; Wood, D.A.; Coenen, F.; Ma, F. Fourier Neural Operator for Fluid Flow in Small-Shape 2D Simulated Porous Media Dataset. Algorithms 2023, 16, 24. https://doi.org/10.3390/a16010024
Choubineh A, Chen J, Wood DA, Coenen F, Ma F. Fourier Neural Operator for Fluid Flow in Small-Shape 2D Simulated Porous Media Dataset. Algorithms. 2023; 16(1):24. https://doi.org/10.3390/a16010024
Chicago/Turabian StyleChoubineh, Abouzar, Jie Chen, David A. Wood, Frans Coenen, and Fei Ma. 2023. "Fourier Neural Operator for Fluid Flow in Small-Shape 2D Simulated Porous Media Dataset" Algorithms 16, no. 1: 24. https://doi.org/10.3390/a16010024
APA StyleChoubineh, A., Chen, J., Wood, D. A., Coenen, F., & Ma, F. (2023). Fourier Neural Operator for Fluid Flow in Small-Shape 2D Simulated Porous Media Dataset. Algorithms, 16(1), 24. https://doi.org/10.3390/a16010024






