Adaptive Piecewise Poly-Sinc Methods for Ordinary Differential Equations
Abstract
1. Introduction
2. Background
2.1. Poly-Sinc Approximation
2.1.1. Lagrange Interpolation
2.1.2. Conformal Mappings and Function Space
2.2. Residual
2.3. Error Analysis
2.4. Collocation Method
2.4.1. Initial Value Problem
2.4.2. Boundary Value Problem
3. Piecewise Collocation Method
3.1. Initial Value Problem
Relaxation Problem
| Algorithm 1: Piecewise Poly-Sinc Algorithm (IVP (11)). |
| input: number of partitions number of Sinc points in the th partition output: : approximate solution Replace with the global approximate solution (10). Solve for the unknowns using the initial condition (12a), continuity Equation (12b), and the set of equations for the residual (13). |
3.2. Hanging Bar Problem
| Algorithm 2: Piecewise Poly-Sinc Algorithm (IVP (14)). |
| input: number of partitions number of Sinc points in the th partition output: : approximate solution Replace with the global approximate solution (10). Solve for the unknowns using initial conditions (20a)–(20b), continuity Equations (20c)–(20d), and the set of equations for the residual (21). |
3.3. Boundary Value Problem
| Algorithm 3: Piecewise Poly-Sinc Algorithm (BVP). |
| input: number of partitions number of Sinc points in the th partition output: : approximate solution Replace with the global approximate solution (10). Solve for the unknowns using boundary conditions (22a)–(22b), continuity Equations (22c)–(22d), and the set of equations for the residual (23). |
4. Adaptive Piecewise Poly-Sinc Algorithm
4.1. Algorithm Description
4.2. Error Analysis
| Algorithm 4: Adaptive Piecewise Poly-Sinc Algorithm. |
 |
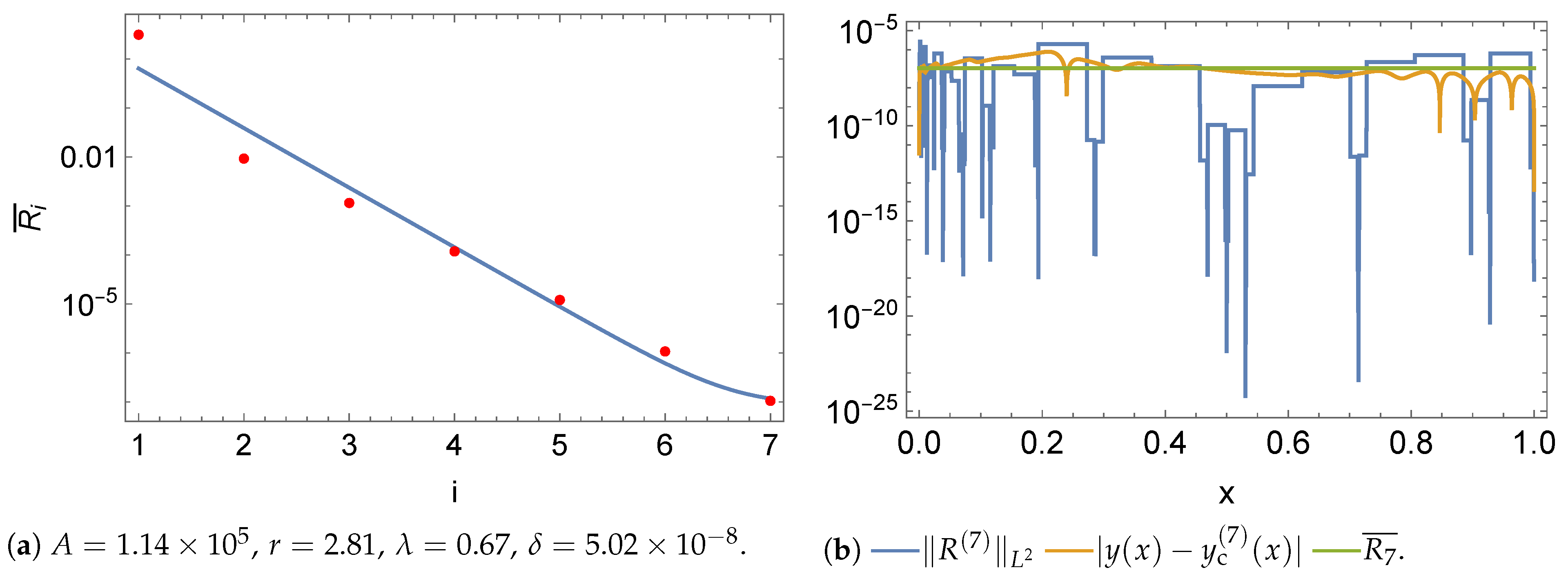
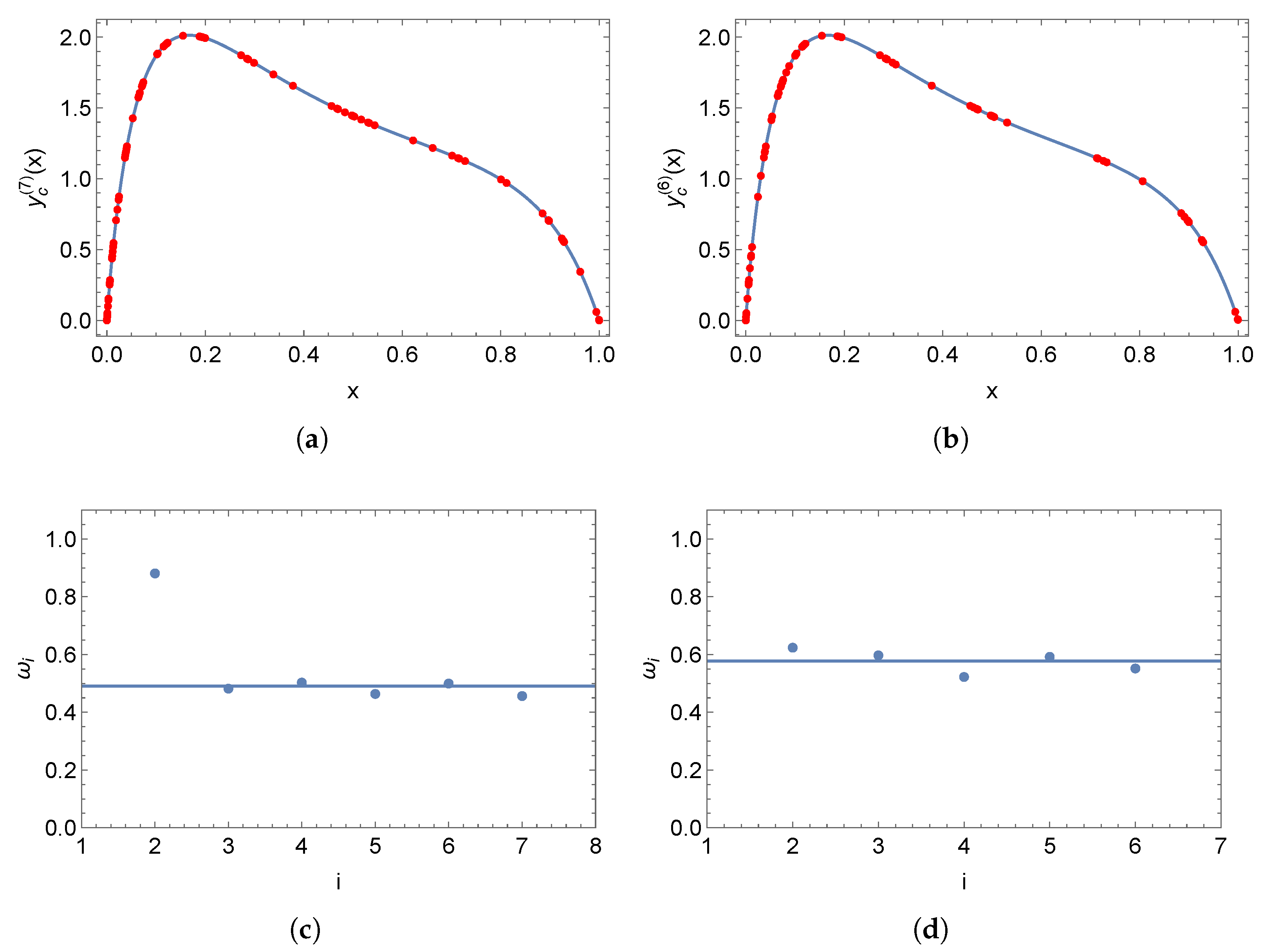
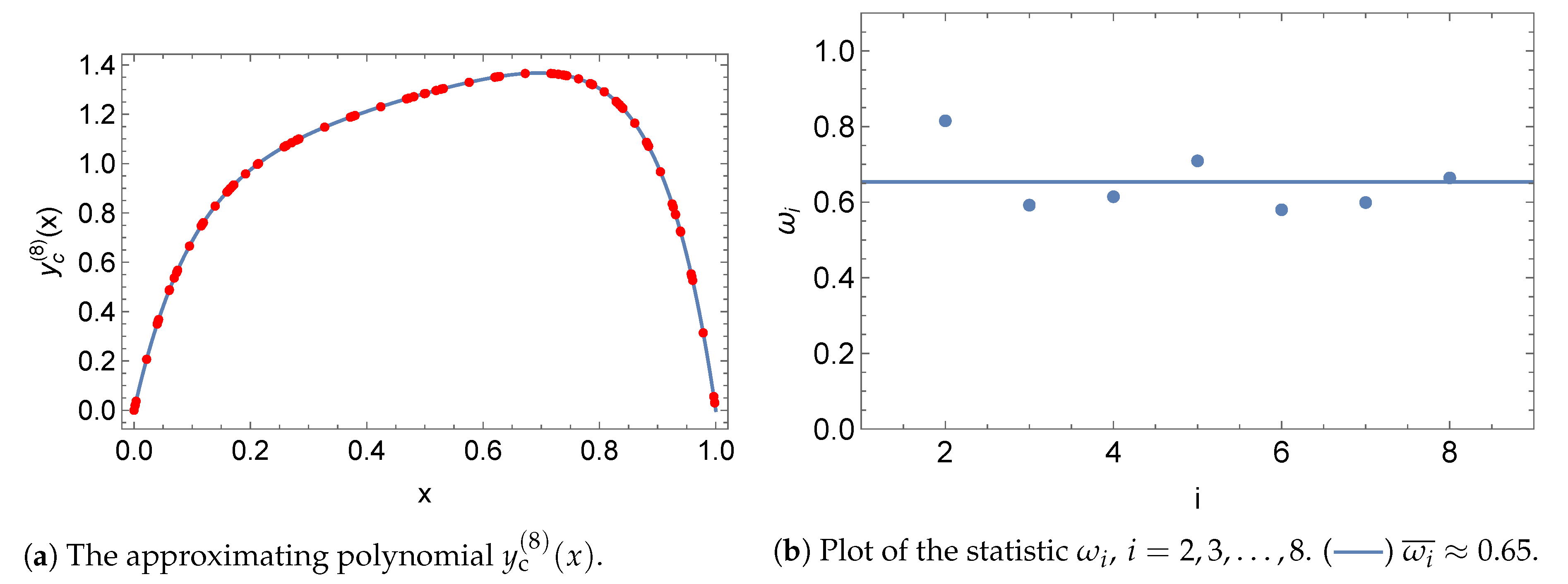
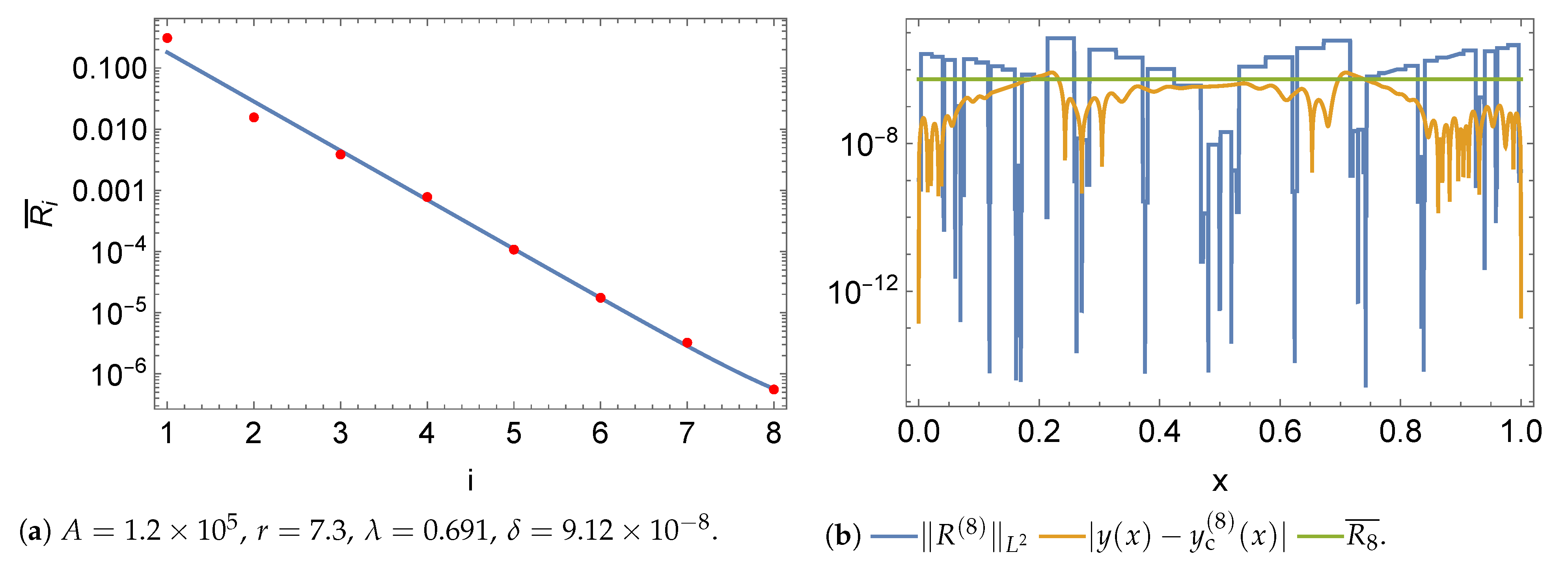
5. Results
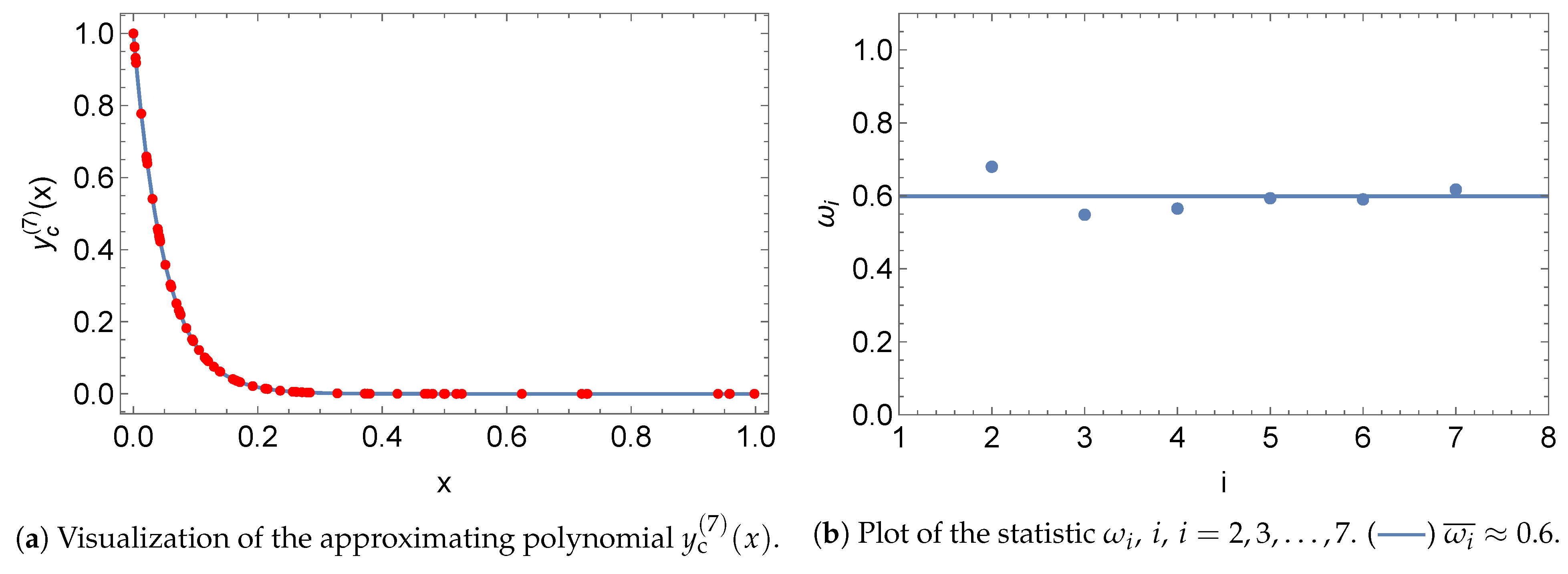
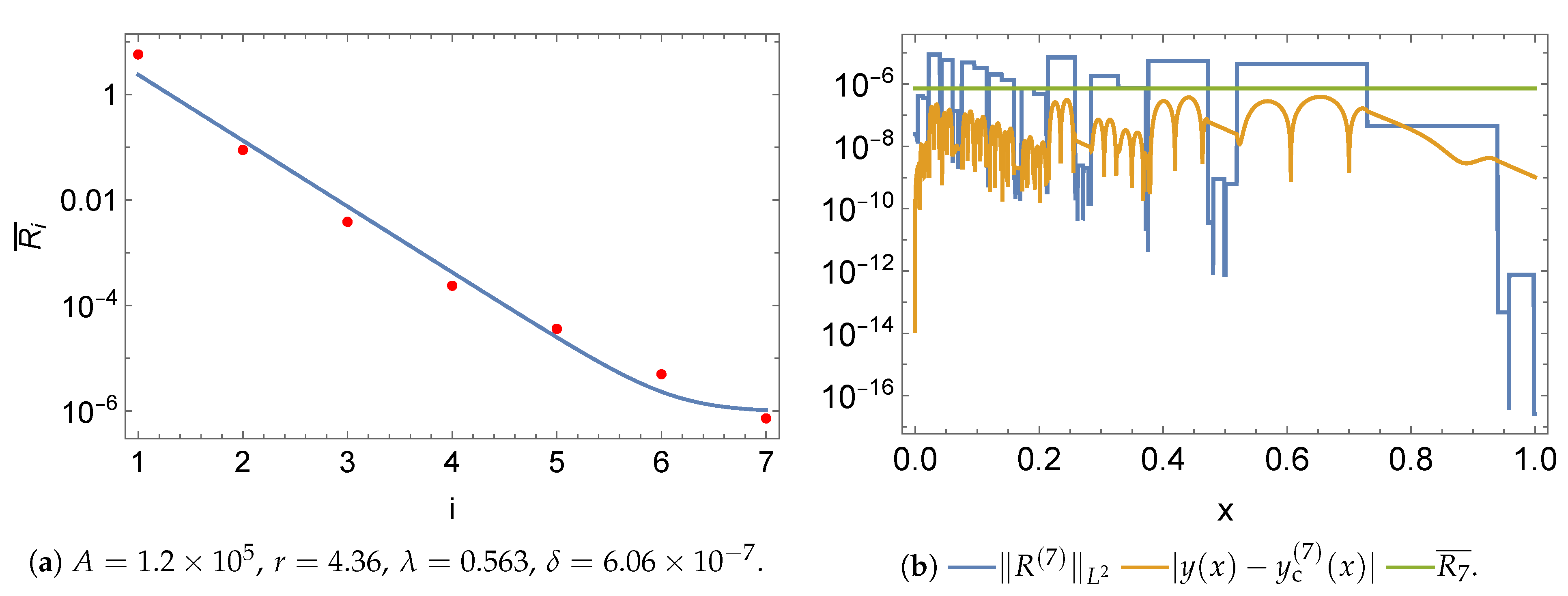
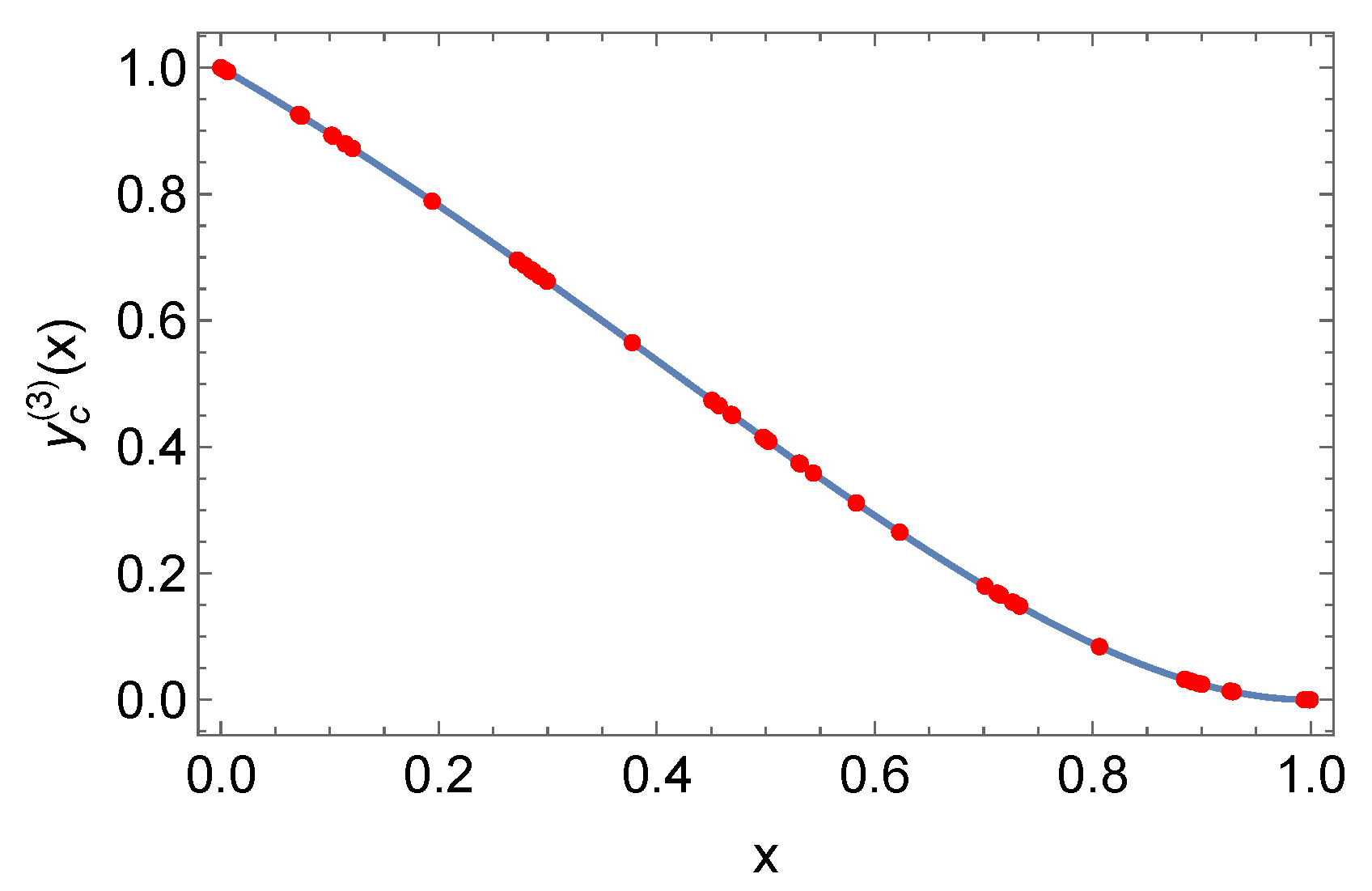
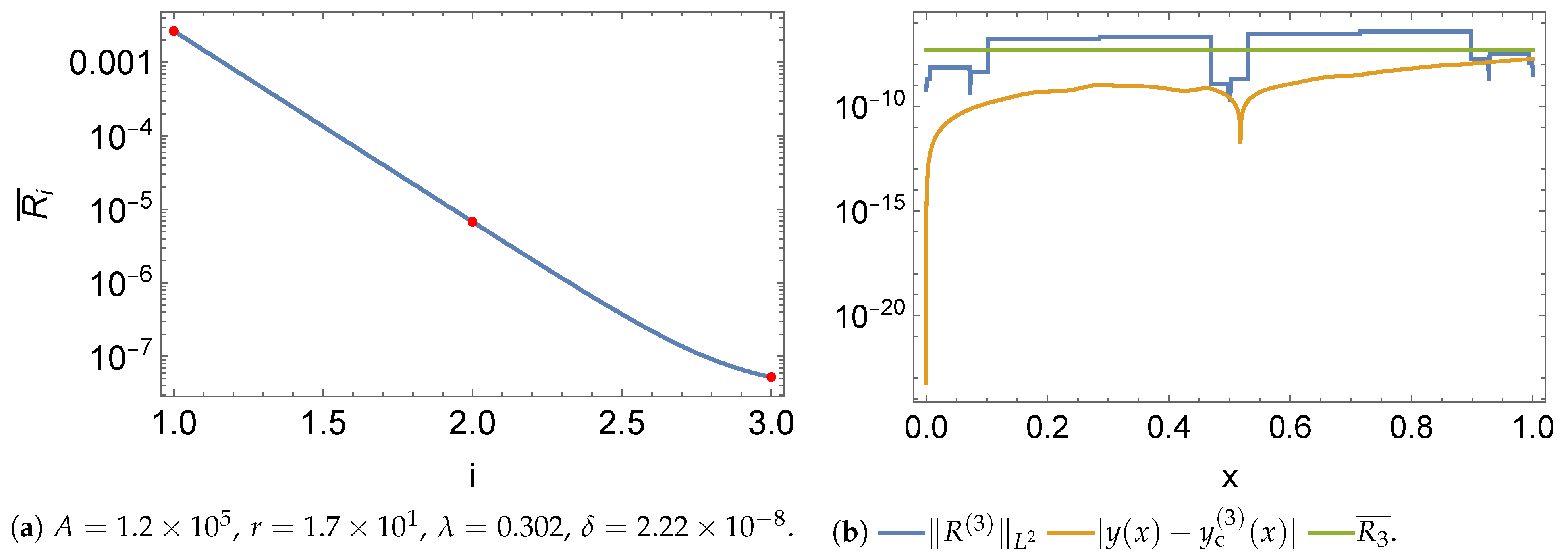
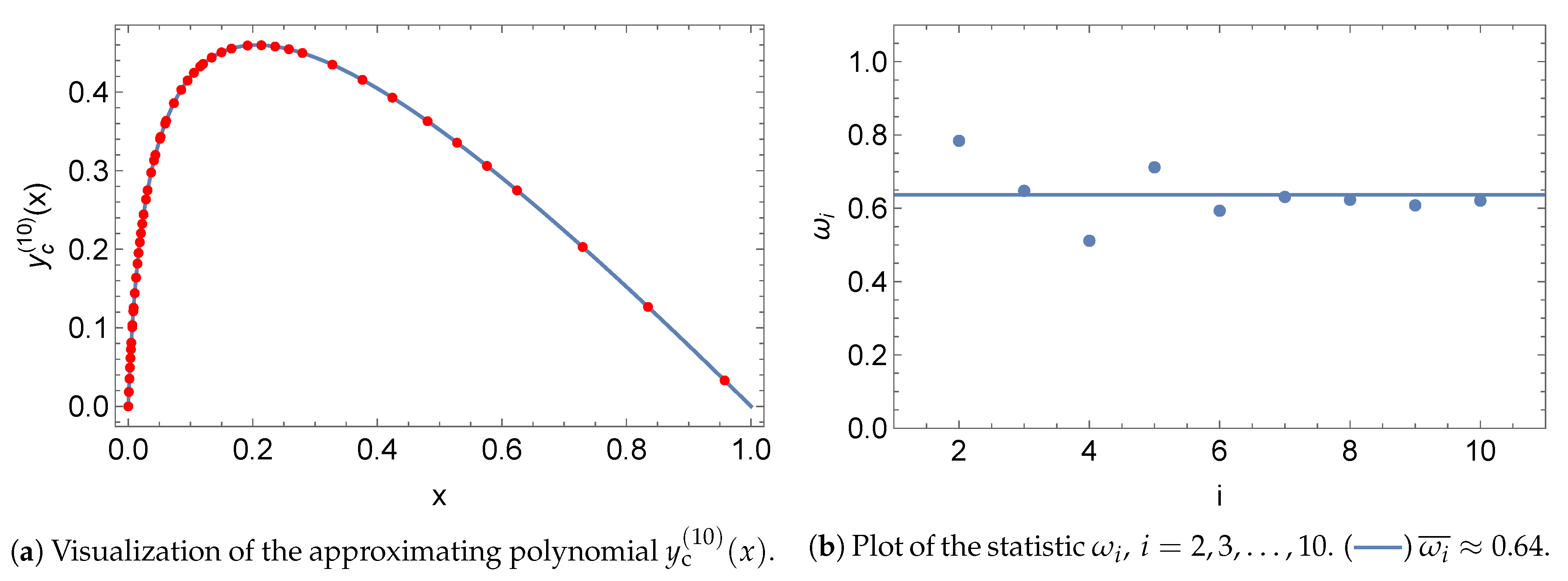
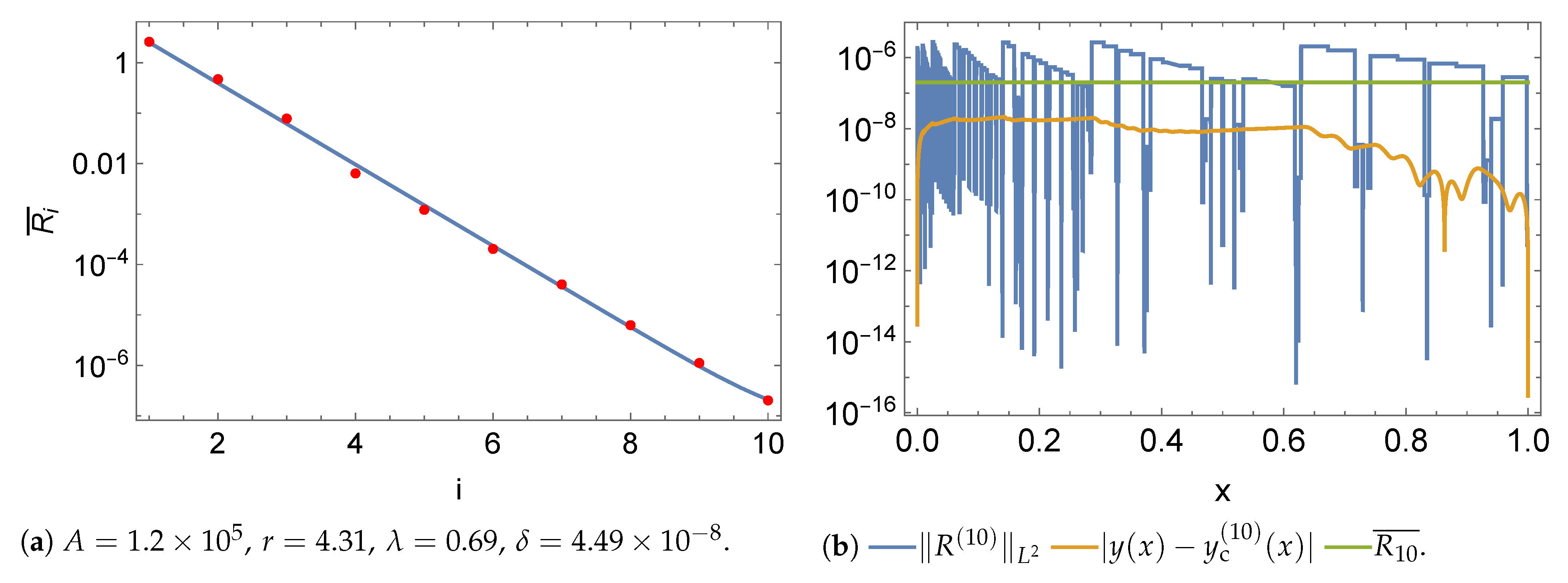
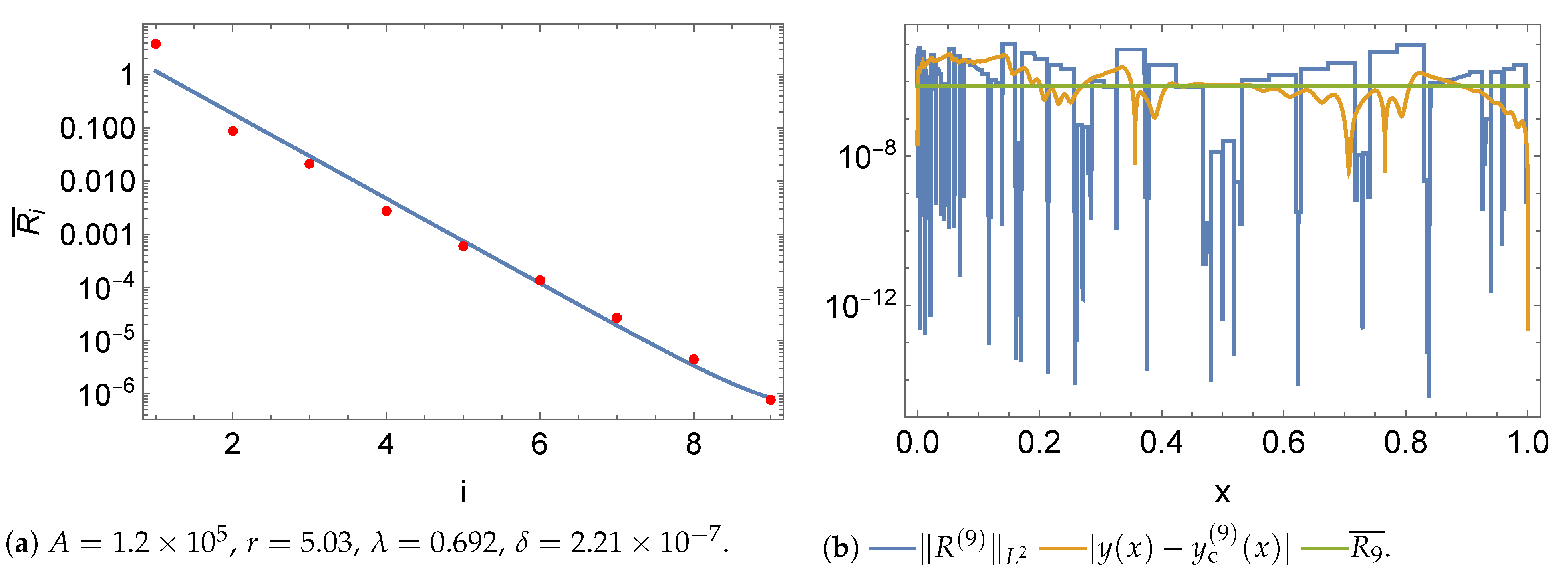
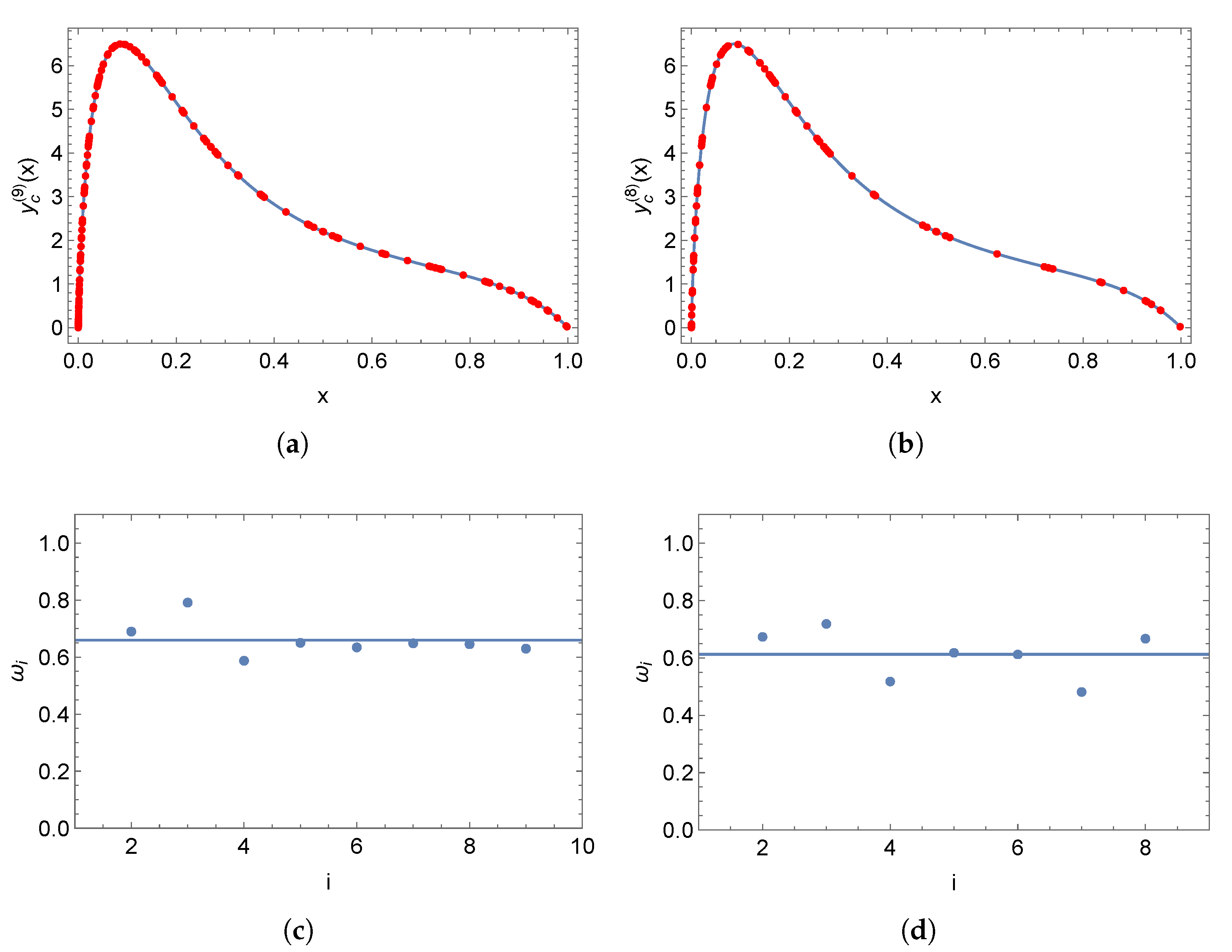
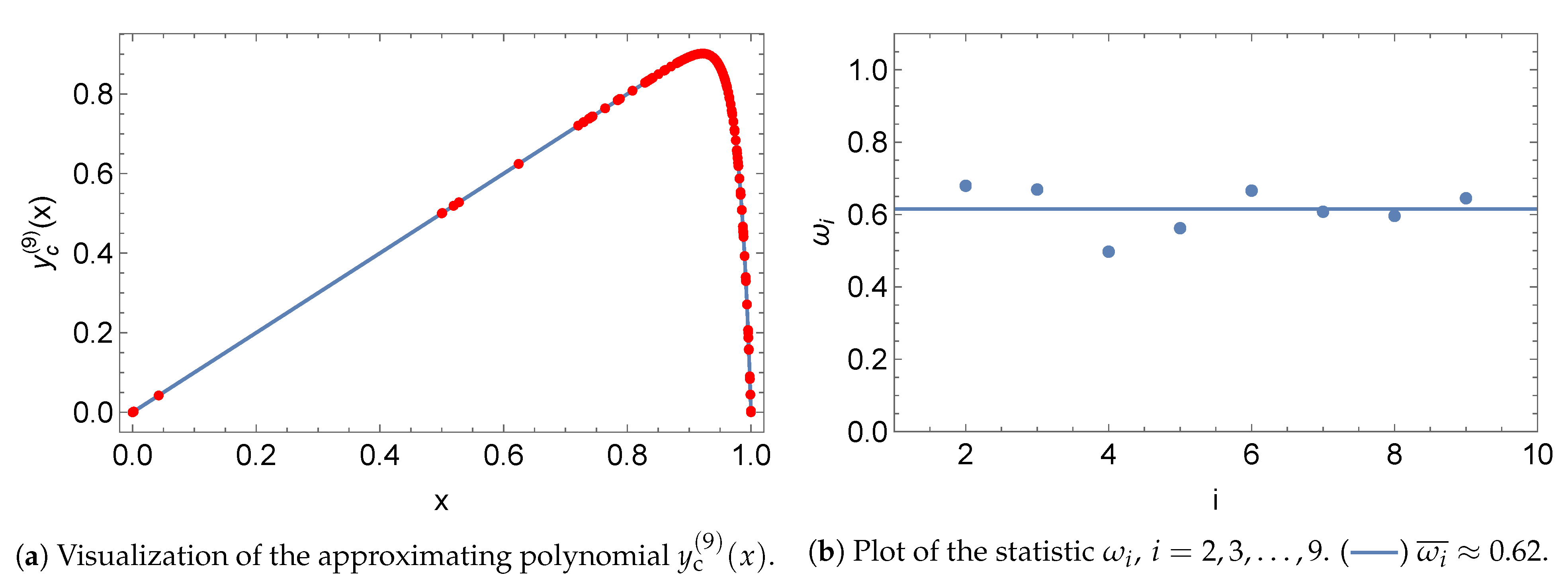
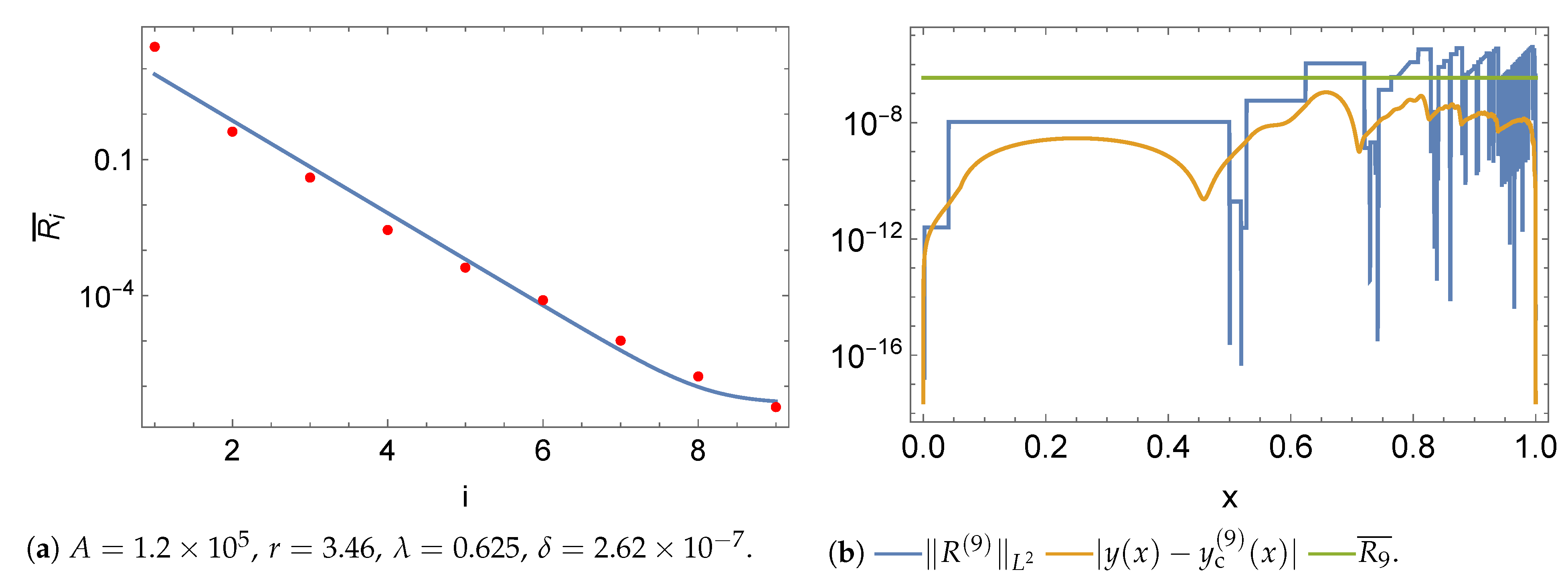
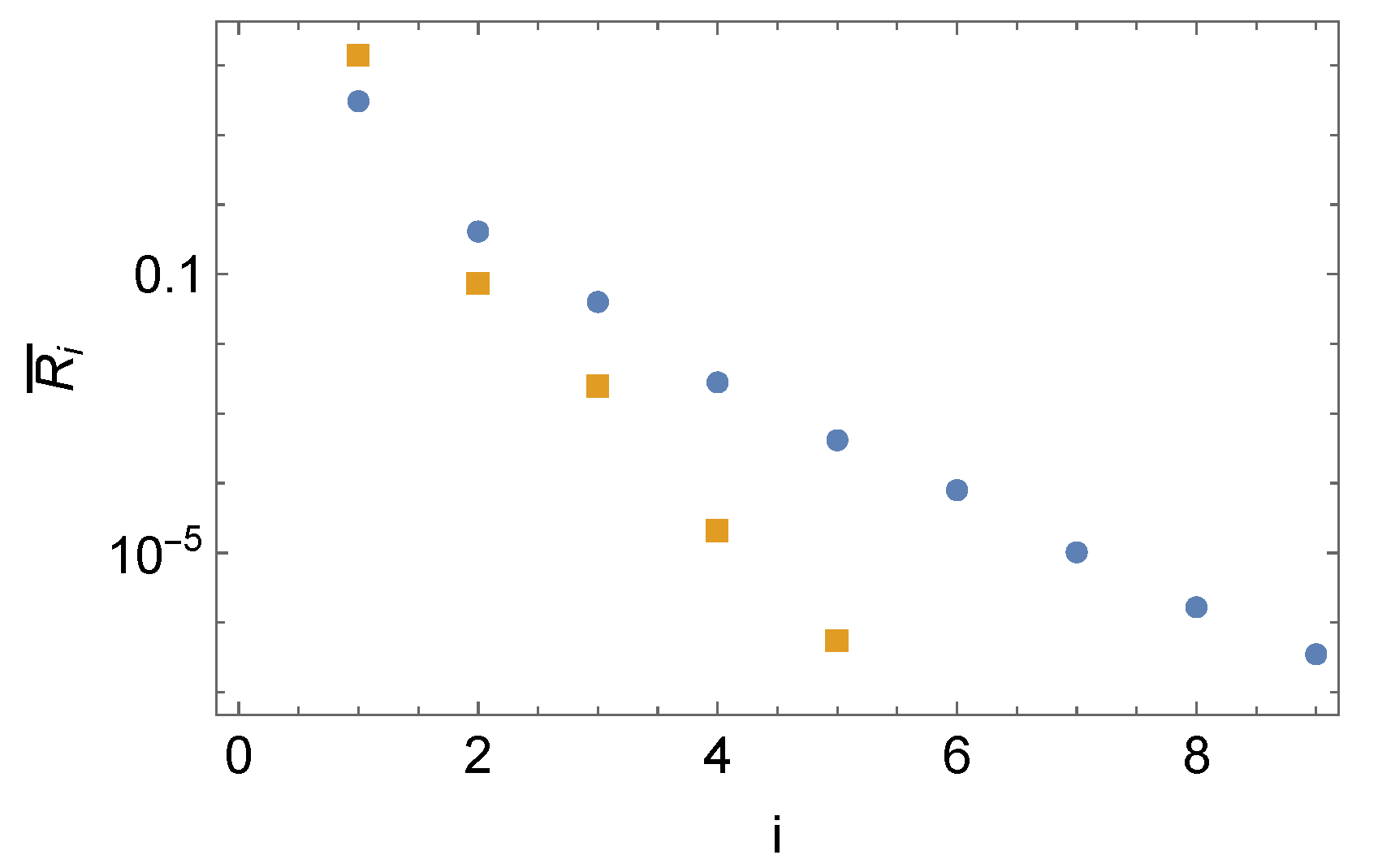
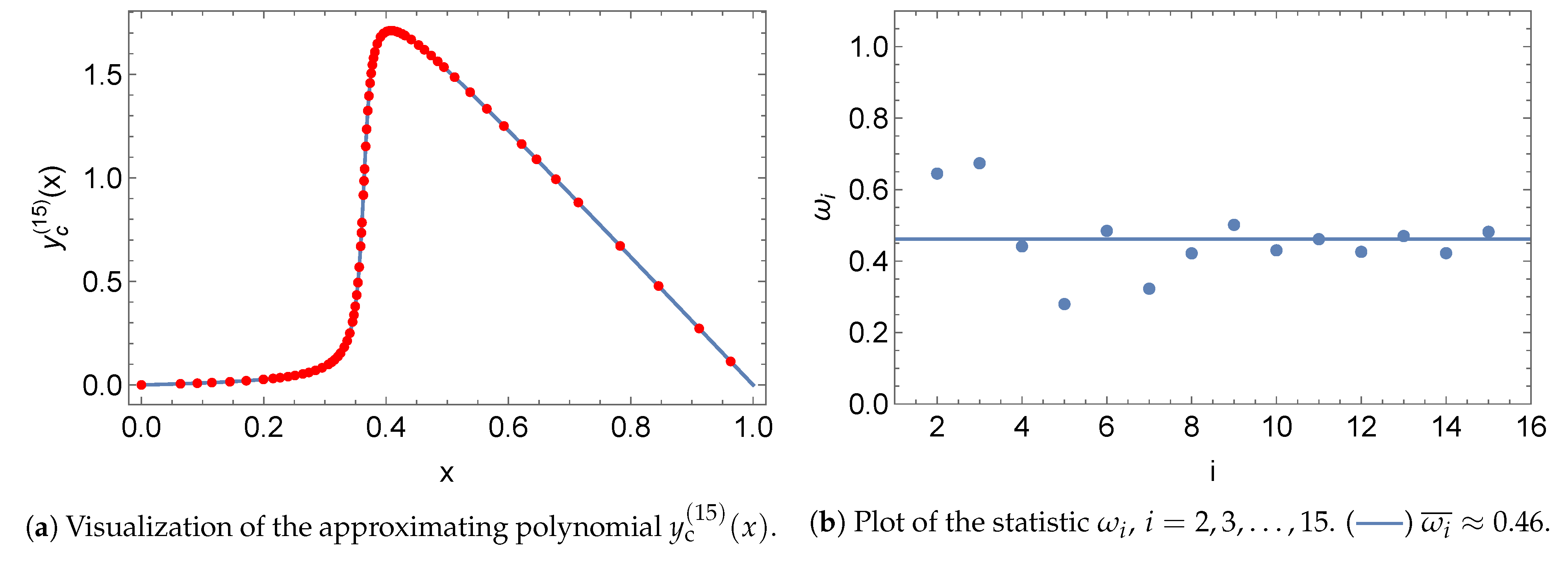
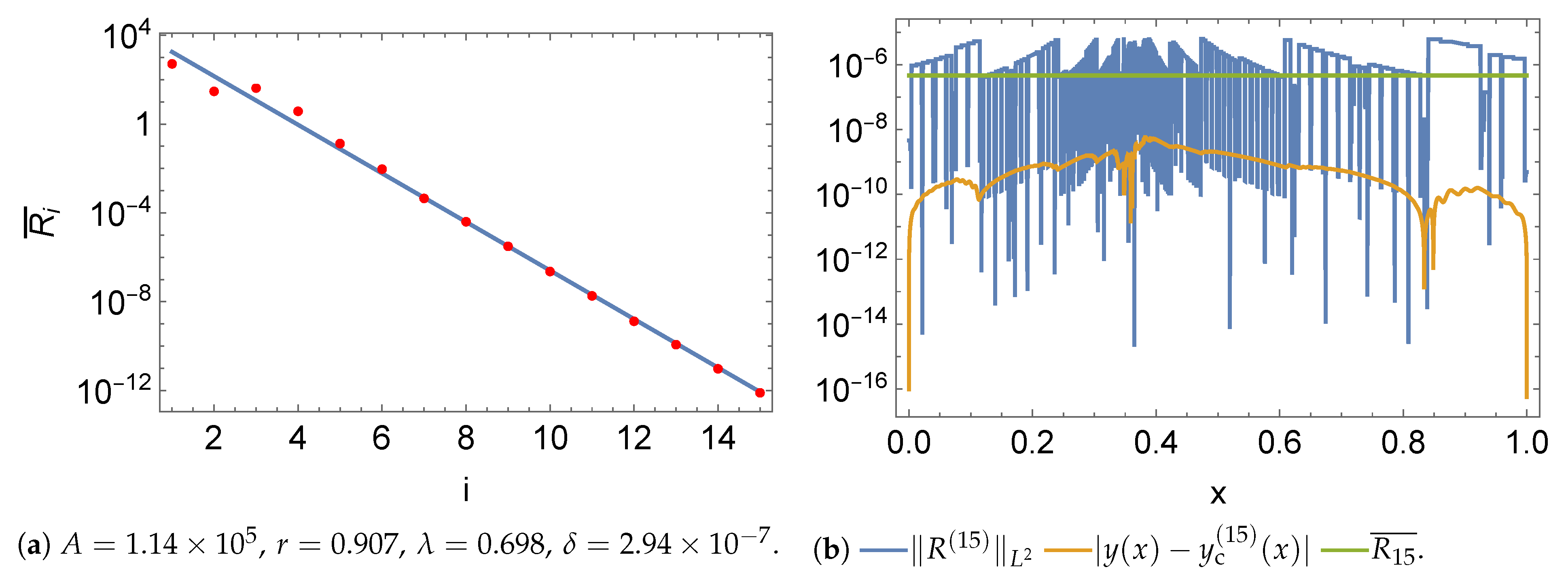
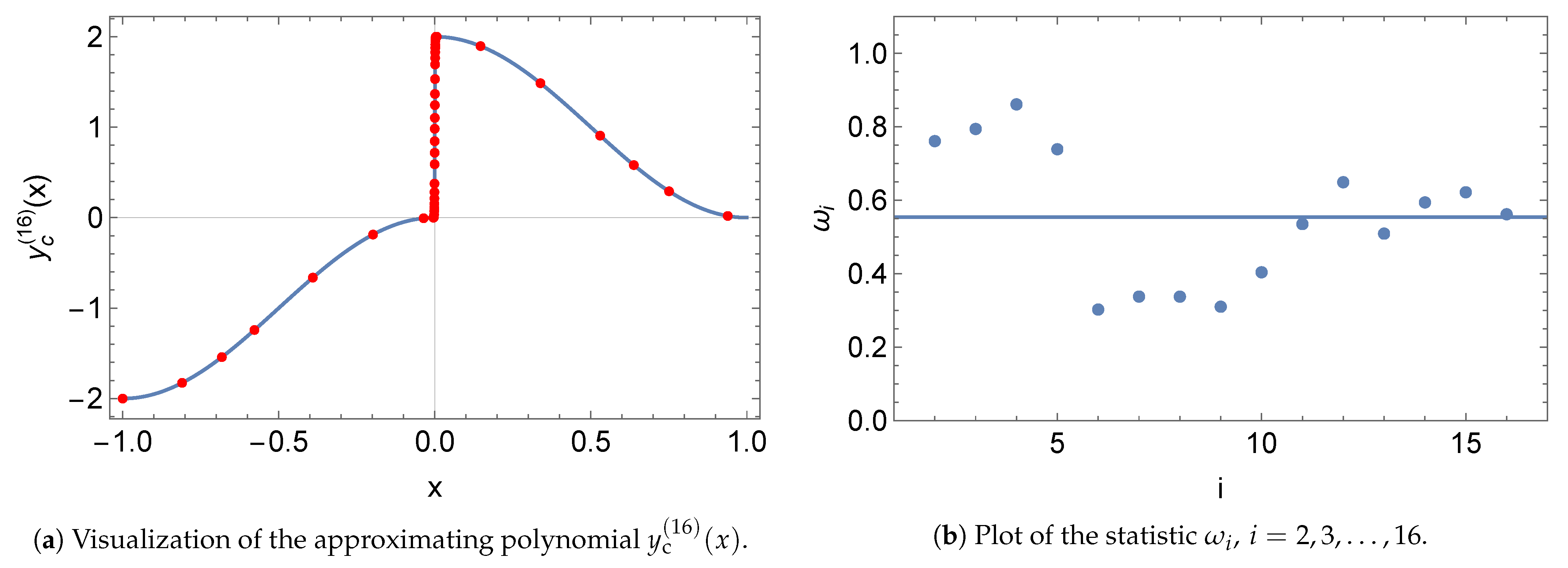
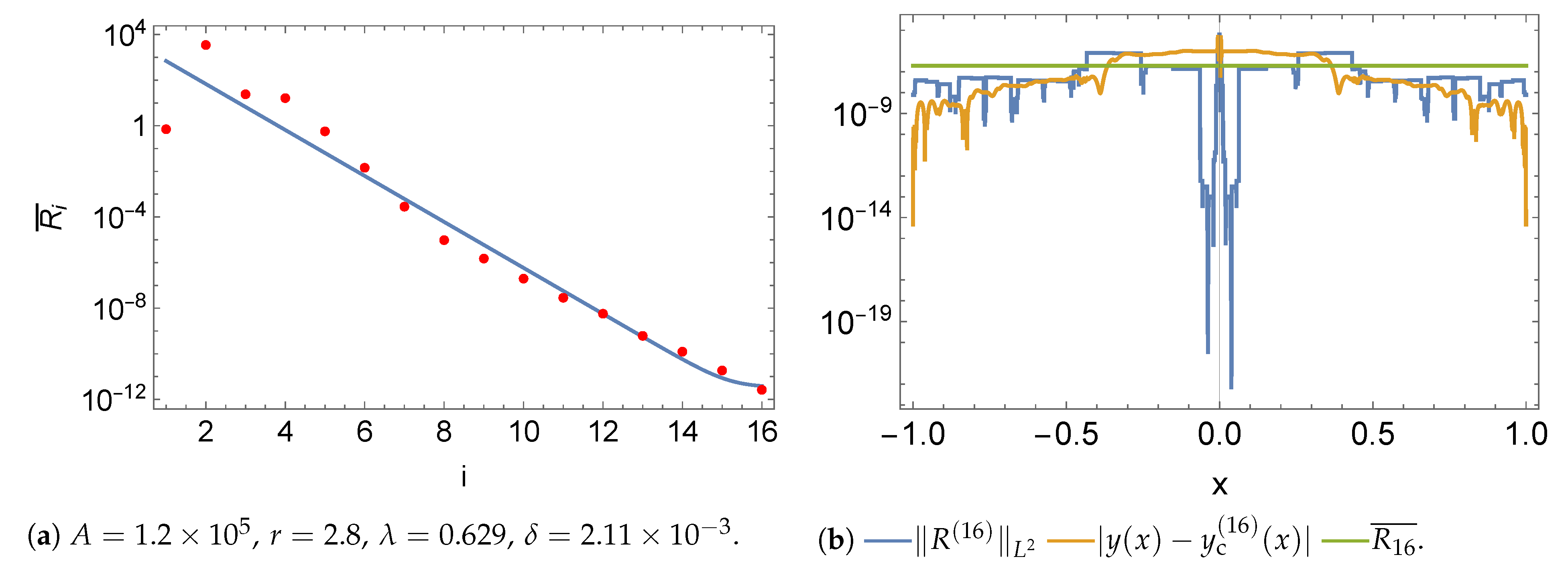
5.1. Norms
5.2. Initial Value Problem
5.3. Boundary Value Problem
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hairer, E.; Nørsett, S.P.; Wanner, G. Solving Ordinary Differential Equations I: Nonstiff Problems; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Hairer, E.; Wanner, G.; Lubich, C. Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Ascher, U.M.; Mattheij, R.M.M.; Russell, R.D. Numerical Solution of Boundary Value Problems for Ordinary Differential Equations; SIAM: Philadelphia, PA, USA, 1995. [Google Scholar]
- Stakgold, I. Boundary Value Problems of Mathematical Physics: Volume I & II; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Axelsson, O.; Barker, V.A. Finite Element Solution of Boundary Value Problems: Theory and Computation; SIAM: Philadelphia, PA, USA, 2001. [Google Scholar]
- Keller, H.B. Numerical Methods for Two-Point Boundary-Value Problems; Dover Publications, Inc.: Mineola, NY, USA, 2018. [Google Scholar]
- Eriksson, K.; Estep, D.; Hansbo, P.; Johnson, C. Introduction to adaptive methods for differential equations. Acta Numer. 1995, 4, 105–158. [Google Scholar] [CrossRef]
- Wright, K. Adaptive methods for piecewise polynomial collocation for ordinary differential equations. BIT Numer. Math. 2007, 47, 197–212. [Google Scholar] [CrossRef]
- Tao, Z.; Jiang, Y.; Cheng, Y. An adaptive high-order piecewise polynomial based sparse grid collocation method with applications. J. Comput. Phys. 2021, 433, 109770. [Google Scholar] [CrossRef]
- Logg, A. Multi-adaptive Galerkin methods for ODEs. I. SIAM J. Sci. Comput. 2003, 24, 1879–1902. [Google Scholar] [CrossRef]
- Logg, A. Multi-adaptive Galerkin methods for ODEs. II. Implementation and applications. SIAM J. Sci. Comput. 2004, 25, 1119–1141. [Google Scholar] [CrossRef]
- Baccouch, M. Analysis of a posteriori error estimates of the discontinuous Galerkin method for nonlinear ordinary differential equations. Appl. Numer. Math. 2016, 106, 129–153. [Google Scholar] [CrossRef]
- Baccouch, M. A posteriori error estimates and adaptivity for the discontinuous Galerkin solutions of nonlinear second-order initial-value problems. Appl. Numer. Math. 2017, 121, 18–37. [Google Scholar] [CrossRef]
- Cao, Y.; Petzold, L. A posteriori error estimation and global error control for ordinary differential equations by the adjoint method. SIAM J. Sci. Comput. 2004, 26, 359–374. [Google Scholar] [CrossRef]
- Kehlet, B.; Logg, A. A posteriori error analysis of round-off errors in the numerical solution of ordinary differential equations. Numer. Algorithms 2017, 76, 191–210. [Google Scholar] [CrossRef]
- Moon, K.S.; Szepessy, A.; Tempone, R.; Zouraris, G.E. A variational principle for adaptive approximation of ordinary differential equations. Numer. Math. 2003, 96, 131–152. [Google Scholar] [CrossRef]
- Moon, K.S.; Szepessy, A.; Tempone, R.; Zouraris, G.E. Convergence rates for adaptive approximation of ordinary differential equations. Numer. Math. 2003, 96, 99–129. [Google Scholar] [CrossRef]
- Moon, K.S.; von Schwerin, E.; Szepessy, A.; Tempone, R. An adaptive algorithm for ordinary, stochastic and partial differential equations. In Recent Advances in Adaptive Computation; American Mathematical Society: Providence, RI, USA, 2005; Volume 383, Contemporary Mathematics; pp. 325–343. [Google Scholar] [CrossRef][Green Version]
- Johnson, C. Error estimates and adaptive time-step control for a class of one-step methods for stiff ordinary differential equations. SIAM J. Numer. Anal. 1988, 25, 908–926. [Google Scholar] [CrossRef]
- Estep, D.; French, D. Global error control for the continuous Galerkin finite element method for ordinary differential equations. RAIRO Modél. Math. Anal. Numér. 1994, 28, 815–852. [Google Scholar] [CrossRef]
- Estep, D.; Ginting, V.; Tavener, S. A posteriori analysis of a multirate numerical method for ordinary differential equations. Comput. Methods Appl. Mech. Eng. 2012, 223/224, 10–27. [Google Scholar] [CrossRef]
- Stenger, F. Polynomial function and derivative approximation of Sinc data. J. Complex. 2009, 25, 292–302. [Google Scholar] [CrossRef][Green Version]
- Stenger, F.; Youssef, M.; Niebsch, J. Improved Approximation via Use of Transformations. In Multiscale Signal Analysis and Modeling; Shen, X., Zayed, A.I., Eds.; Springer: New York, NY, USA, 2013; pp. 25–49. [Google Scholar] [CrossRef]
- Khalil, O.A.; El-Sharkawy, H.A.; Youssef, M.; Baumann, G. Adaptive piecewise Poly-Sinc methods for function approximation. Submitted to Applied Numerical Mathematics. 2022. [Google Scholar]
- Carey, G.F.; Humphrey, D.L. Finite element mesh refinement algorithm using element residuals. In Codes for Boundary-Value Problems in Ordinary Differential Equations; Childs, B., Scott, M., Daniel, J.W., Denman, E., Nelson, P., Eds.; Springer: Berlin/Heidelberg, Germany, 1979; pp. 243–249. [Google Scholar] [CrossRef]
- Carey, G.F. Adaptive refinement and nonlinear fluid problems. Comput. Methods Appl. Mech. Eng. 1979, 17–18, 541–560. [Google Scholar] [CrossRef]
- Carey, G.F.; Humphrey, D.L. Mesh refinement and iterative solution methods for finite element computations. Int. J. Numer. Methods Eng. 1981, 17, 1717–1734. [Google Scholar] [CrossRef]
- Geary, R.C. The ratio of the mean deviation to the standard deviation as a test of normality. Biometrika 1935, 27, 310–332. [Google Scholar] [CrossRef]
- Stenger, F. Handbook of Sinc Numerical Methods; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar] [CrossRef]
- Youssef, M.; Pulch, R. Poly-Sinc solution of stochastic elliptic differential equations. J. Sci. Comput. 2021, 87, 1–19. [Google Scholar] [CrossRef]
- Stenger, F.; El-Sharkawy, H.A.M.; Baumann, G. The Lebesgue Constant for Sinc Approximations. In New Perspectives on Approximation and Sampling Theory: Festschrift in Honor of Paul Butzer’s 85th Birthday; Zayed, A.I., Schmeisser, G., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 319–335. [Google Scholar] [CrossRef]
- Youssef, M.; El-Sharkawy, H.A.; Baumann, G. Lebesgue constant using Sinc points. Adv. Numer. Anal. 2016, 2016. [Google Scholar] [CrossRef]
- Youssef, M.; Baumann, G. Collocation method to solve elliptic equations, bivariate Poly-Sinc approximation. J. Progress. Res. Math. 2016, 7, 1079–1091. [Google Scholar]
- Youssef, M. Poly-Sinc Approximation Methods. Ph.D. Thesis, German University in Cairo, New Cairo, Egypt, 2017. [Google Scholar]
- Youssef, M.; Baumann, G. Troesch’s problem solved by Sinc methods. Math. Comput. Simul. 2019, 162, 31–44. [Google Scholar] [CrossRef]
- Khalil, O.A.; Baumann, G. Discontinuous Galerkin methods using poly-sinc approximation. Math. Comput. Simul. 2021, 179, 96–110. [Google Scholar] [CrossRef]
- Khalil, O.A.; Baumann, G. Convergence rate estimation of poly-Sinc-based discontinuous Galerkin methods. Appl. Numer. Math. 2021, 165, 527–552. [Google Scholar] [CrossRef]
- Stoer, J.; Bulirsch, R. Introduction to Numerical Analysis; Springer: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- Baumann, G.; Stenger, F. Sinc-approximations of fractional operators: A computing approach. Mathematics 2015, 3, 444–480. [Google Scholar] [CrossRef]
- Coddington, E.A. An introduction to Ordinary Differential Equations; Dover Publications, Inc.: Mineola, NY, USA, 1989. [Google Scholar]
- Lund, J.; Bowers, K.L. Sinc Methods for Quadrature and Differential Equations; SIAM: Philadelphia, PA, USA, 1992; Volume 32. [Google Scholar]
- Stenger, F. Numerical Methods Based on Sinc and Analytic Functions; Springer Series in Computational Mathematics; Springer: New York, NY, USA, 1993; Volume 20. [Google Scholar] [CrossRef]
- Youssef, M.; Baumann, G. Solution of nonlinear singular boundary value problems using polynomial-Sinc approximation. Commun. Fac. Sci. Univ. Ank. Sér. A1 Math. Stat. 2014, 63, 41–58. [Google Scholar] [CrossRef]
- Baumann, G. (Ed.) New Sinc Methods of Numerical Analysis; Trends in Mathematics; Birkhäuser/Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Vesely, F.J. Computational Physics: An Introduction; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2001. [Google Scholar]
- Carey, G.; Finlayson, B.A. Orthogonal collocation on finite elements. Chem. Eng. Sci. 1975, 30, 587–596. [Google Scholar] [CrossRef]
- Strang, G. Computational Science and Engineering; Wellesley-Cambridge Press: Wellesley, MA, USA, 2007. [Google Scholar]
- Wazwaz, A.M. Linear and Nonlinear Integral Equations: Methods and Applications; Higher Education Press: Beijing, China; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Haasdonk, B.; Ohlberger, M. Reduced basis method for finite volume approximations of parametrized linear evolution equations. M2AN Math. Model. Numer. Anal. 2008, 42, 277–302. [Google Scholar] [CrossRef]
- Grepl, M.A. Model order reduction of parametrized nonlinear reaction–diffusion systems. Comput. Chem. Eng. 2012, 43, 33–44. [Google Scholar] [CrossRef]
- Nochetto, R.H.; Siebert, K.G.; Veeser, A. Theory of adaptive finite element methods: An introduction. In Multiscale, Nonlinear and Adaptive Approximation; De Vore, R., Kunoth, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 409–542. [Google Scholar] [CrossRef]
- Walpole, R.E.; Myers, R.H.; Myers, S.L.; Ye, K. Probability and Statistics for Engineers and Scientists, 9th ed.; Pearson Education, Inc.: Boston, MA, USA, 2012. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 10th ed.; Dover Publications, Inc.: New York, NY, USA, 1972. [Google Scholar]
- Cruz-Uribe, D.V.; Fiorenza, A. Variable Lebesgue Spaces: Foundations and Harmonic Analysis; Springer: Basel, Switzerland, 2013. [Google Scholar] [CrossRef]
- Gautschi, W. Numerical Analysis; Birkhäuser: Boston, MA, USA, 2012. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Youssef, M.; El-Sharkawy, H.A.; Baumann, G. Multivariate Lagrange interpolation at Sinc points: Error estimation and Lebesgue constant. J. Math. Res. 2016, 8. [Google Scholar] [CrossRef]
- Wolfram Research, Inc. Mathematica, Version 13.0.0; Wolfram Research, Inc.: Champaign, IL, USA, 2021. [Google Scholar]
- Rivière, B. Discontinuous Galerkin Methods for Solving Elliptic and Parabolic Equations: Theory and Implementation; SIAM: Philadelphia, PA, USA, 2008. [Google Scholar]
- Boyce, W.E.; DiPrima, R.C. Elementary Differential Equations and Boundary Value Problems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Ng, E.W.; Geller, M. A table of integrals of the error functions. J. Res. Natl. Bur. Stand. B 1969, 73, 1–20. [Google Scholar] [CrossRef]
- Rachford, H.H.; Wheeler, M.F. An H−1-Galerkin Procedure for the Two-Point Boundary Value Problem. In Mathematical Aspects of Finite Elements in Partial Differential Equations; de Boor, C., Ed.; Academic Press: Cambridge, MA, USA, 1974; pp. 353–382. [Google Scholar] [CrossRef]
- Keast, P.; Fairweather, G.; Diaz, J. A computational study of finite element methods for second order linear two-point boundary value problems. Math. Comput. 1983, 40, 499–518. [Google Scholar] [CrossRef]
- Hemker, P.W. A Numerical Study of Stiff Two-Point Boundary Problems; Mathematical Centre Tracts 80; Mathematisch Centrum: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Ascher, U.; Christiansen, J.; Russell, R.D. A collocation solver for mixed order systems of boundary value problem. Math. Comput. 1979, 33, 659–679. [Google Scholar] [CrossRef]
| Method | Adaptive PW PS | [28] | ([65] Table 13(g)) |
|---|---|---|---|
| Method | Adaptive PW PS | [67] |
|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalil, O.; El-Sharkawy, H.; Youssef, M.; Baumann, G. Adaptive Piecewise Poly-Sinc Methods for Ordinary Differential Equations. Algorithms 2022, 15, 320. https://doi.org/10.3390/a15090320
Khalil O, El-Sharkawy H, Youssef M, Baumann G. Adaptive Piecewise Poly-Sinc Methods for Ordinary Differential Equations. Algorithms. 2022; 15(9):320. https://doi.org/10.3390/a15090320
Chicago/Turabian StyleKhalil, Omar, Hany El-Sharkawy, Maha Youssef, and Gerd Baumann. 2022. "Adaptive Piecewise Poly-Sinc Methods for Ordinary Differential Equations" Algorithms 15, no. 9: 320. https://doi.org/10.3390/a15090320
APA StyleKhalil, O., El-Sharkawy, H., Youssef, M., & Baumann, G. (2022). Adaptive Piecewise Poly-Sinc Methods for Ordinary Differential Equations. Algorithms, 15(9), 320. https://doi.org/10.3390/a15090320






