Abstract
Deep neural networks are exposed to the risk of adversarial attacks via the fast gradient sign method (FGSM), projected gradient descent (PGD) attacks, and other attack algorithms. Adversarial training is one of the methods used to defend against the threat of adversarial attacks. It is a training schema that utilizes an alternative objective function to provide model generalization for both adversarial data and clean data. In this systematic review, we focus particularly on adversarial training as a method of improving the defensive capacities and robustness of machine learning models. Specifically, we focus on adversarial sample accessibility through adversarial sample generation methods. The purpose of this systematic review is to survey state-of-the-art adversarial training and robust optimization methods to identify the research gaps within this field of applications. The literature search was conducted using Engineering Village (Engineering Village is an engineering literature search tool, which provides access to 14 engineering literature and patent databases), where we collected 238 related papers. The papers were filtered according to defined inclusion and exclusion criteria, and information was extracted from these papers according to a defined strategy. A total of 78 papers published between 2016 and 2021 were selected. Data were extracted and categorized using a defined strategy, and bar plots and comparison tables were used to show the data distribution. The findings of this review indicate that there are limitations to adversarial training methods and robust optimization. The most common problems are related to data generalization and overfitting.
1. Introduction
Neural networks are one of the most popular machine learning models, and they have been used in many applications, such as image classification, natural language processing, and other real-time applications [1]. Hence, ensuring the security of neural network models is critical and of substantial importance [2]. Adversarial attacks [2] pose significant threats to existing neural network models, and these attacks could perturb the model’s inputs and cause the model to produce unexpected output results [3]. The perturbed inputs are usually called adversarial samples.
Adversarial samples are the input data computed by an adversarial attack algorithm to make a classifier model misclassify the sample [4]. Normally, an adversarial input sample x’ is computed from a clean input x with a restriction value, called epsilon ε. ε is a variable that controls the strength of the perturbation [5]. The adversarial attack algorithm is responsible for finding the adversarial sample from a clean sample with ε perturbation.
Adversarial training [5] is one of the most promising defensive methods to improve the robustness of a model by reducing the malicious effect caused by adversarial attacks. In general, a training model is able to generalize based on the adversarial sample it was trained against [3,5,6]. Hence, the quality of the adversarial sample provided during the training is important. In recent years, more adversarial training variations have been developed to tackle different shortcomings associated with adversarial training defense methods, such as reducing overfitting, improving generalization, and improving the efficiency of training. However, these problems still exist and there is no guarantee of robustness against adversarial attacks [1], especially when new attack methods are currently being proposed.
In this work, we aim to understand the performance and effectiveness of adversarial training methods. We are particularly interested in the adversarial sample generation components of adversarial training methods. This is important because it is necessary to understand what kind of adversarial samples a model can be trained and generalized on and what the extent of the robustness of the current adversarial training methods is. Normally, adversarial sample generation methods are modified versions of adversarial attacks that are made to fit training schemas [5]. There are some other types of proposals that use non-conventional attack methods in their training schemas, such as generative models or other algorithms [7]. We aim to gather information from existing studies and to analyze the robustness and efficiency improvements and other potential benefits that were brought by those adversary generation components. In addition, we intend to identify the shortcomings, including overfitting, efficiency problems, unachievable robustness, and other research gaps of the adversarial training schema under study.
The end goal of this work is to provide the research community with information about the status of the current development of adversarial training, and the adaption of the newly developed adversarial attacks or other newly developed adversary generation methods. Hence, this work can be viewed as a roadmap to guide other developers and researchers to develop more advanced adversarial sample generation methods to benefit adversarial training.
In the literature, there are few surveys related to the topic of adversarial training. Silva et al. [1] conducted a literature survey of the current advances in adversarial attacks and adversarial defense methods. They described the defensive method in three different categories: gradient masking/obfuscation, robust optimization, and adversarial example detection. They analyzed and discussed the advantages and limitations of each category. The review paper from Wiyatno et al. [2] provided comprehensive information about current adversarial attacks and state-of-the-art defense methods of machine learning models in the image classification domain. Chen et al. [8] provided an overview of the adversarial machine learning topic. Bai et al. [5] provided a review paper that discussed different adversarial training architectures. However, the above literature reviews did not fully cover the recent categories of adversarial training methods and did not focus on the adversarial sample accessibility of each adversarial training method. Furthermore, the literature surveys from Silva et al. [1] and Chen et al. [8] did not expand on the topic of adversarial training and only reviewed some primary categories of adversarial training, while the review by Wiyatno et al. [2] focused only on image classifiers. Chakraborty et al. [9] offered a literature survey about adversarial machine learning. This review included support vector machines, neural networks, deep neural networks, and convolutional neural networks and focused on the application aspect of threats and defenses. Kong et al. [10] also surveyed the application of adversarial attacks in the context of text classification and malware detection. These two papers focused on the application aspect of adversarial training instead of the technical properties of each method. In particular, they did not provide a detailed categorization of adversarial training. Xiao et al. [11] provided a literature review related to the safety and security of deep neural networks. This review looked at safety concerns, verification methods, testing methods, security, and the interpretability of machine learning models. In addition, the review provided information about different adversarial attack methods and some defensive methods, including adversarial training, in terms of adversarial machine learning. However, it did not discuss in detail the categories of adversarial training. It only mentioned two variations of adversarial training, namely projected gradient descent (PGD) adversarial training and ensemble adversarial training.
In this systematic review, we summarize, categorize, compare, and discuss the currently available adversarial training defense methods and the adversary generation methods utilized by adversarial training methods, as well as their limitations and related research gaps. As a systematic review, we followed the guideline provided by Barbara Kitchenham et al. [12] to conduct this review paper. According to Bai et al. [5], adversarial training includes both adversarial regularization and conventional adversarial training methods. Hence, both adversarial regularization and adversarial training methods will be covered in this survey paper. To achieve these objectives, we defined the following as our main research question: What are the limitations of the current adversarial training methods in general and the adversary generation component of adversarial training in particular?
To answer this question, and to gain related insights and conclusions, the following steps were followed:
- Categorize adversarial training methods. The main criteria used for the categorization were the adversarial generation methods, which refer to the standard methods that use adversarial attacks to generate adversarial samples and include these samples in training to improve the robustness of the training model [3].
- Identify the advantages and disadvantages of these adversarial training methods.
The remainder of this paper is organized as follows: Section 2 presents background information on adversarial samples and training and introduces the main concepts that are necessary to understand the subject matter of this paper. The research methodology is presented and discussed in Section 3. Section 4 discusses the categories and details of the adversarial generation methods used by each adversarial training method. Section 5 discusses the current challenges and gaps in adversarial training. Finally, concluding remarks and directions for future work are presented in Section 6.
2. Background
This section provides background information on adversarial samples for modern machine learning models. It also discusses the general schema of adversarial training and explains how adversarial samples are related to current adversarial training schemas. In addition, it provides some historical information for readers to better understand the context and the development of the research.
2.1. Adversarial Samples
The concept of adversarial samples appeared in 2014 when Szegedy et al. [4] proposed the use of the box-constrained optimizer L-BFGS to generate misclassified data samples. The algorithm could find indistinguishable perturbations at L2 distance to cause machine learning models to fail to produce a correct result. This was one of the earliest indications of the existence of adversarial samples.
Later, in 2015, Goodfellow et al. [3] provided a more detailed explanation of the phenomenon of adversarial examples. They found that, when an image is perturbed in a direction, the logit output of the classifier model normally changes in a linear way. They hypothesized that this is caused by the partial linear properties of the activation function of the neurons. With this hypothesis, they proposed the fast gradient sign method (FGSM) to generate adversarial samples of clean images with only the gradient of the loss function. Later, Goodfellow et al. [6] enhanced their previous approach by proposing a more advanced algorithm based on the FGSM to apply perturbations to the input image iteratively, called the basic iterative method (BIM). This algorithm greatly improved the success rate of the generated adversarial samples that attacked the network models. Another improvement was proposed by Madry et al. [13] in 2018 that involved combining the BIM with random initialization. This method is widely used as a benchmark algorithm to test and train a robust model [5]. These methods primarily generate adversarial samples with L∞ norms. The L∞ norm is one of the commonly used distance metrics in adversarial machine learning. The other commonly used metrics include L0 and L2 distance metrics. In this case, the L∞ metric represents the max perturbation across all the input values for the adversarial sample. Based on these findings, the adversarial samples were described as the error caused by the linear properties of the classifier models, which is different from the normal bias and boundary error. The existence of adversarial samples is related to the fundamental properties of the current machine learning models.
In addition to these adversarial attack methods, there are other attack methods that focus on different distance metrics and vulnerabilities of the models. The DeepFool algorithm was proposed by Moosavi-Dezfooli et al. [14] to produce adversarial samples of inputs with reduced perturbation distances compared to the FGSM. The algorithm considered the L2 norm to be the closest decision boundary to generate the adversarial samples. Carlini and Wagner attacks (C&W attacks), proposed by Carlini et al. [15], considered all three distance metrics (L0, L2, L∞) to construct a strong attack. This attack method was proven to be highly effective with high transferability between models. The one-pixel attack proposed by Su et al. [16] constrained the L0 norm to perturb a fixed number of pixels of original inputs by utilizing an evolutionary algorithm. More adversarial attack methods have been developed to produce misclassification samples for machine learning models [2]. Based on these newly developed algorithms, a more general description of adversarial samples could be any malicious data input specifically created for a machine learning model to produce a misclassification result. In this study, we consider this more general description our definition of adversarial samples.
2.2. Adversarial Training
The concept of adversarial training involves training the classifier to generalize the adversarial samples as well as clean samples [5].
In the conventional training schema, shown in Figure 1, the training data pass forward through the model, and prediction loss is backpropagated to improve the classification results [4]. As a result, the model will generalize the distribution of the training data to produce an accurate prediction of their labels. However, a model trained with this normal procedure will be exposed to the threat of adversarial attacks [3]. Adversarial samples were described as linear properties of neural networks by Goodfellow et al. [3]. The more general explanation is that the model will only be able to generalize the training data distribution rather than capture the real distribution due to its linearity.
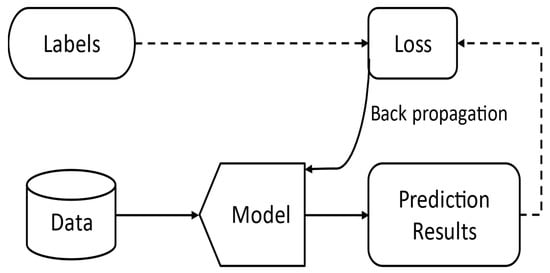
Figure 1.
Conventional training of neural network model.
Adversarial training expands on conventional training methods by adding an extra step into the training procedure, as illustrated in Figure 2. In this way, the model can generalize both clean data and the adversarial data generated by the attack methods utilized in the adversarial training. Therefore, the robustness of the model is improved against adversarial attacks.
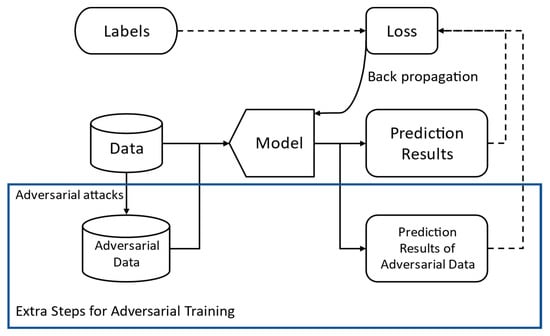
Figure 2.
Adversarial training of neural network model.
Usually, the adversarial samples are generated based on the model’s current state, whereas the latter is based on the previous batch of training steps [3] for any proposed attack method. However, some schemas use a pre-trained model to generate adversarial samples and include them in the training datasets [17]. In this procedure, the attack method involved in the adversarial sample generation will be the focus of this paper. Throughout the paper, we refer to them as the adversarial sample generation method or simply the adversary generator. More details are discussed in Section 4.
Several popular adversarial training methods are also discussed here to provide better context for the general historical development of adversarial training. In 2014, Szegedy et al. [4] proposed the concept of using adversarial samples to train classifier models in order to improve their robustness. Later, in 2015, Goodfellow et al. [3] suggested using the FGSM to generate an adversarial sample in a mix with clean data to train the classifier. The model improved the robustness against this single iteration attack. Madry et al. [13] suggested using a multi-iteration method called projected gradient descent (PGD) to train the model. They showed that when using the fast-single iteration method (FGSM), the trained model is still vulnerable against more strong multi-iteration adversarial samples. They suggested that by using PGD adversarial training, the model would gain universal robustness against adversarial samples. The Modified National Institute of Standards and Technology database (MNIST) model trained by this method could maintain over 90% accuracy under PGD and FGSM attacks. This method has become a baseline method of adversarial training [5].
In recent years, many adversarial training methods have been proposed to improve the performance of the FGSM and PGD adversarial training. The performance improvements have mainly been focused on enhancing robustness, reducing the computation complexity of adversarial training, and reducing the overfitting effect of adversarial training [5]. Details about the advantages and limitations of these methods are discussed in Section 4 and Section 5 in this paper.
3. Survey Methodology
This section provides our review protocol information, including our search strategies, search sources, data collection procedures, and data extraction strategy.
3.1. Search Strategies
In this systematic review, we mainly focus on surveying approaches related to robust optimization or adversarial training in the deep neural network domain with a particular focus on defense against adversarial attacks or adversarial samples. To ensure the overage of papers, we used different terms to describe neural networks and deep neural networks. We also considered “robust optimization”, “adversarial training”, and “adversarial learning” as keywords in our searches. The common phrases used to describe the threat from adversarial attacks include “adversarial sample”, “adversarial example”, “adversarial perturbation”, “adversarial attack”, etc. Based on this, we defined our search query as follows:
(“neural network” OR “deep neural network” OR dnn OR nn OR “deep learning”) AND (“robust optimization” OR “adversarial training” OR “adversarial learning”) AND (defend* OR resist* OR against) AND (“adversarial sample*” OR “adversarial example*” OR “adversarial perturbation*“ OR “adversarial attack”).
3.2. Search Sources
The search was primarily conducted using the Engineering Village engine [18]. Engineering Village is a comprehensive search platform provided by Elsevier (Elsevier is a global publisher of scientific, engineering, and medical content) that includes a wide range of content for engineering research purposes. It has great coverage of digital libraries, such as IEEE and ScienceDirect. The primary indexing databases provided by the Engineering Village that are related to our topic are shown in Table 1. Ei Compendex is one of the most comprehensive literature databases for engineering, which provides over 20 million records of publications. Inspec is a bibliographic database including publishers such as IEEE, AIP, SPIE, and other commercial publishers. Ei Patents includes the engineering patent records from the United States, European Union, and World Patent records [18]. The patent records were also considered since they are good sources to track unique software engineer solutions. Hence, we can use them as indexing sources for their related papers to improve our snowballing process. We decided to use them as a primary indexing tool to search for related papers.

Table 1.
Databases used for this research.
3.3. Inclusion and Exclusion Criteria
We defined our inclusion and exclusion criteria (see Table 2) based on the scope of this study. Since this is an active research field, we expected to find relatively new published papers related to the topic. We searched for both conference papers and journal articles and excluded papers from the following categories: (1) papers that were not written in English, (2) papers with adversarial training approaches deployed for proposes other than defending against adversarial attacks, and (3) papers related to models other than (deep) neural networks. To focus on the most recent research, we included only papers that were published from 2016 to 2021.

Table 2.
Inclusion and exclusion criteria of the papers.
3.4. Data Collection Procedure
The selection process was conducted in November 2021. Figure 3 shows the process of paper inclusion and exclusion.
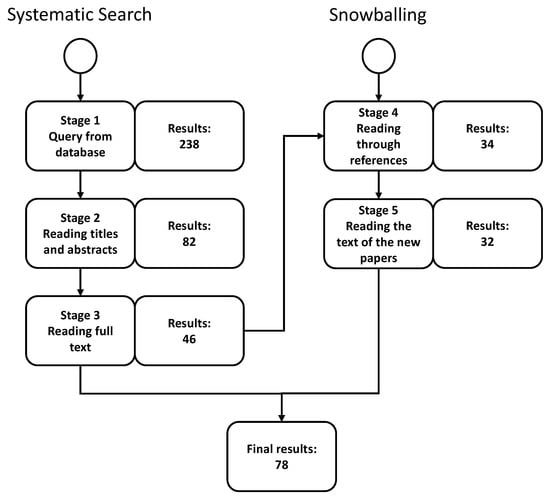
Figure 3.
Collection procedure.
Our search process included a two-step method involving a systematic search and snowballing. We used these two steps to ensure the wide coverage of the papers. The systematic search was conducted first to retrieve the core set of papers. From the retrieved papers, we searched their references to check if there were more related papers that were not retrieved originally. This process is called snowballing, where we expand the collected papers based on the references of the core papers.
The first set of papers was obtained by using the pre-defined search query and the Engineering Village search engine. In addition to the search query, we also defined the “language” and “the time of publication” criteria in the search engine. In this step, we retrieved 238 papers. After this, the obtained papers were screened by reading through the titles and the abstracts, and 82 papers were filtered out based on relevancy. Finally, 46 papers were selected after reviewing the full content of the papers.
After we selected 46 papers, we went through the references of each paper, and 34 new papers were included in this part of the selection. After we went through each new selected paper, we discarded the papers that were out of our pre-defined time of publication (i.e., from 2016 to 2021). As a result, another 32 papers were included in our study. Hence, in total, 78 papers were selected for this survey.
3.5. Data Extraction Strategy
To address our research question, we focused on the adversarial sample generation (or the adversary generator) component of the architecture for each proposed solution. We categorize and sub-categorize all the methods based on their names and functionalities and analyze the details of each method to summarize its advantages and limitations.
The adversary generator’s information is extracted from the papers and used for categorization. Similar methods are categorized as one method if the difference is minor. For example, PGD-10 and PGD are considered to be in the same category since the only difference is the step parameters. On the other hand, a method that is developed from another method but shows a significant improvement is classified into a different category, such as IFGSM and FGSM. Finally, the number of different methods used is summarized for quantitative analysis and comparison.
If an article does not include a specific method, we categorize it in the “other” category. The analyzed data are presented as a bar plot in Figure 4.
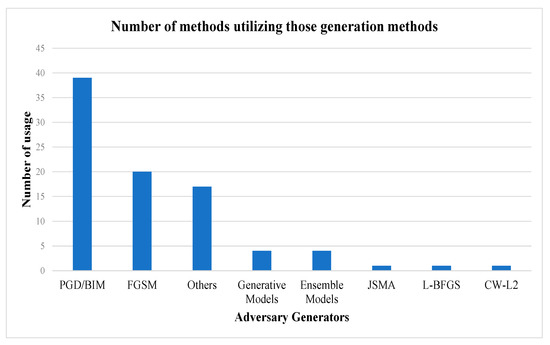
Figure 4.
Distribution of the adversary generators utilized in adversarial training.
4. Findings
This section presents the results and findings of this survey. First, the summary of the results shows the recent publication numbers in related fields. Second, the comparison table is used to represent the major categories, advantages, and disadvantages of the adversary generation method used in adversarial training. Then, the details of each method are reviewed in the following subsections.
4.1. Summary of the Results
The 78 included papers are listed below. Each paper includes a unique solution to the adversarial training schema or proposes an optimization procedure utilizing adversary generation. The distribution of the papers by year of publication is shown below.
From Figure 5, we can see an increasing interest in the research field related to this topic. We think this presents a great opportunity to conduct this research to produce a future roadmap.
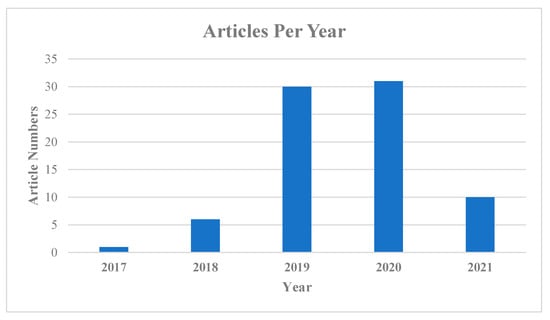
Figure 5.
Number of publications in each year.
Based on the adversary generation approach used in adversarial training methods, we categorize the adversarial training methods as shown in Table 3. Furthermore, we discuss the details of the adversary generation methods and categorize them into further sub-categories whenever applicable.

Table 3.
Comparison table of each adversarial sample generation method in adversarial training.
Adversarial training can be formulated as the following optimization problem:
The inner part of the formula is intended to maximize the loss L of the model f regarding the output label y by adding perturbation δ into the input x. The optimization goal is to minimize the maximum loss of the model. In the following sections, we want to use the inner approximation function to lead the discussion. In general, inner approximation functions are constructed using different attack methods. This approximation is important to determine the upper limit of the adversarial optimization. Generally, the adversarial training method with a similar inner approximation function will share similar benefits and limitations, which are shown in Table 3. However, there might be several improvements built upon these basic methods. The detailed discovery of the outer optimization related to different improvements will be analyzed in the sub-categories to focus on the varieties of adversarial training. Overall, adversarial attacks could be fitted into two more extensive categories: white-box and black-box attacks [2]. The white-box or black-box adversarial generation methods usually share some common properties. The overall structural relationship of the common adversary generation methods studied in this paper is shown in Figure 6. The commonly used acronyms are also shown in the same figure.
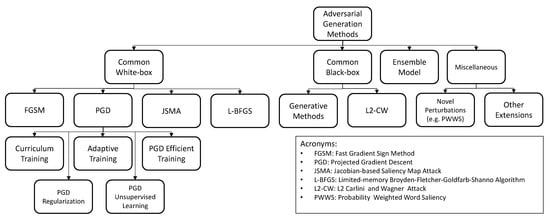
Figure 6.
Overview of the categories of adversarial generation methods.
White-box attacks refer to the adversarial attacks that require the parameter information of the targeted model [2]. This category of methods is the most used method in adversarial training or robustness optimization, as can be seen in Figure 4. The conventional white-box attacks used by adversarial training are referred to as FGSM, IFGSM, PGD, and their variants [2]. These methods utilize the model’s gradient properties to generate adversaries on the L∞ distance metric [2]. Therefore, the algorithm will consider the maximum perturbed input values to measure the significance of the adversarial input compared to the clean input counterpart. Since the perturbation noises are generated using the inner parameters of the victim model, the adversaries generated should be consistent if the model stays the same. The general benefit is that these methods use the internal information of the models to produce relatively efficient and consistent adversaries [2]. However, with the growing interest in this research area, more adversarial attacks could generate adversaries based on different distance metrics [2], which might be unreachable via this type of adversary generation [19].
On the other hand, black-box attack methods are beneficial for adversarial training. The biggest advantage of black-box attacks is that they generally require less information to generate the adversaries; therefore, they are more flexible and model-independent [2]. Furthermore, black-box adversarial attacks usually consider more distance metrics in their perturbation computations [15,16]. Hence, adversarial training based on these methods could provide model robustness against adversarial samples based on these metrics.
We argue that the common black-box attacks are more diverse than other attack methods, as they use different methods and theories to generate the adversarial samples. Furthermore, the black-box adversarial training methods are less popular than the normal white-box adversarial training methods, as shown in Figure 4. Therefore, the knowledge and limitations of these methods used in adversarial training are not discovered. This might be one of the most significant research gaps in the black-box adversarial training methods.
In addition to the methods, advantages, and limitations, the model architectures used to evaluate the training methods are also summarized and listed in Table 3. In general, adversarial training as a defensive method should provide a general improvement in the robustness of most deep learning models. However, the performance might vary between different architectures. With our protocol, we are unable to provide further information about restricted limitations regarding the model architecture. Hence, we directly provide information about model architectures involved in each paper since this information could be useful to consider in future studies.
4.2. Fast Gradient Sign Method
The FGSM is a gradient-based white-box attack proposed by Goodfellow et al. [3]. The formula of the optimization problem can be written as:
where ∇L represents the gradient of the model’s loss function in every input instance regarding the input–label pair (x, y) and x’ represents the perturbed input by adding the sign of the gradient onto input x. This method only requires a one-time calculation to produce a perturbation with an L2 norm constraint. The advantage of this attack in terms of adversarial training relies on its fast computation speed. However, Madry et al. [13] pointed out that this method may not be sufficient to train a robust model. Furthermore, a model trained using this method may have greater accuracy compared to the original clean data [6], which is referred to as the label leakage problem. The disadvantages include overfitting [20].
Other approaches have been proposed to improve the FGSM adversarial training and overcome these disadvantages. Vivek et al. [20] used dropout scheduling to improve the generalization of the model for the training data and reduce the overfitting effect during single-step adversarial training. Huang et al. [21] found that the directions of perturbation generated by the FGSM, and iterative methods might be different due to the landscape of the loss function. Therefore, they proposed a regularization term during the adversarial training to constrain the searched step and to ensure that the perturbation direction of the FGSM is consistent with PGD. In this way, they can improve the performance of FGSM adversarial training to give it the capacity to defend against more advanced attacks. Liu et al. [22] analyzed an enhanced FGSM training to continuously add FGSM perturbation to each epoch. In each epoch, one large perturbation is applied, and the next epoch will reuse the data that the FGSM has attacked, and new perturbations will be applied until the distance reaches a certain threshold. This method reduces the computational complexity while improving the training performance with a single-step method. Wong et al. [23], Andriushchenko et al. [24], Kim et al. [25], Song et al. [26], and Vivek et al. [27] improved the concept of efficient single-step adversarial training through a unique regularizer, loss functions, and domain adaptations. The fast-adversarial training method was found to be more effective during the training compared to efficient PGD adversarial training [23], but Li et al. [28] argued that this fast method has the problem of overfitting. The information on efficient PGD training is presented in Section 4.3. Further improvements also include using the iterative method for adversarial sample generation. We will discuss the details in Section 4.3.
4.3. Projected Gradient Descent and Basic Iterative Method
PGD and BIM/IBGSM are similar. The BIM was proposed by Kurakin et al. [95] and is a modified FGSM that involves converting it into a multi-step optimization. The formula can be written as:
The method uses the same approach as the FGSM to compute small step perturbations and iteratively add the perturbations to the image based on the gradient sign of the input–output pair (x, y). In this formula, x’ represents the perturbation image from the last calculation step and xt+1 is the perturbed sample generated from the current step. In each step, the distance of the perturbation is constrained by α, and the algorithm stops until it reaches a threshold of attack strength.
The PGD method, on the other hand, uses the same schema to generate the adversaries [13]. However, the difference is that the PGD method uses a random initial perturbation of the Lp norm, which creates a randomized data sample within an Lp distance around the original data. This increases the efficiency of finding the adversarial samples.
Madry et al. [13] suggested that the iterative-based attack methods are more effective during adversarial training. These methods provided more precise worst-case perturbations and more generalization toward possible adversarial attacks. As a result, the adversarially trained model with an iterative-based attack can defend against stronger attacks than the model trained by the FGSM. Therefore, these methods are commonly used in adversarial training and robust optimization.
However, the major downside of the PGD and iterative adversarial training is that the computational complexity is significantly increased due to the multiple steps of perturbation noise calculation [2]. Some papers also reported the phenomenon of overfitting still exists in iterative adversarial training [5,39]. Finally, other works showed that the PGD adversarial training could not guarantee robustness against every other type of adversarial sample, especially when the adversary is generated by other Lp metrics [19]. The following sections outline some proposals for improving the iterative adversarial training to solve these shortcomings. A summary of PGD-based adversarial training (PGD AT) is presented in Table 4.

Table 4.
Sub-categories of PGD AT.
4.3.1. Curriculum Training
The curriculum adversarial was proposed in 2018 by Cai et al. [39] to solve the overfitting problem associated with the iterative methods [5]. The curriculum adversarial training uses both weaker attack strength and stronger attack strength to train the model. The method evaluates whether the model can achieve enough accuracy under weaker attack strength settings and then gradually increases the strength after high accuracy is reached. Zhang et al. and Wang et al. [40,41] used a similar approach by monitoring the attack strength of the PGD and incorporating an early stop PGD or dynamic adversarial training.
4.3.2. Adaptive Training
To further obtain accurate adversarial data during the training process, several adaptive adversarial trainings have been proposed that use an adaptive attack strength for each instance of data. Balaji et al. [42], Ding et al. [43], and Cheng et al. [44] describe a situation in which each of the data within the training dataset could have a different distance to the closest decision boundary of the model. Therefore, they propose adaptive adversarial training using PGD with a flexible attack strength depending on the distance between the data and boundary.
4.3.3. Efficient Training
There have also been attempts to solve the heavy computational requirement of the iterative-based attack method during the training process. The free adversarial training model [45] modified the PGD for adversary generation by efficiently reusing the gradient from the backward passing of the training process to produce the adversarial samples. However, Wong et al. [23] argued that the free adversarial training might not actually be faster; therefore, they proposed fast adversarial training as a new training schema (for more information see Section 4.2). The free adversarial training with layer-wise heuristic learning (LHFAT) [46] enhanced the free adversarial training (FAT) method [45], which simultaneously updates the adversaries and model parameters. The layer-wise heuristic learning will update the weights more efficiently. Li et al. [28] also used a combination of the FGSM and PGD to construct an efficient training schema, thus mitigating the effect of overfitting when only using FGSM and reducing the computational time of the PGD. The PGD and FGSM were selected based on whether the model exhibited an overfitting phenomenon.
4.3.4. Adversarial Regularization
Adversarial regularization is another category of training schema that modifies the cost function or regularization terms to cooperate with adversarial training. The general idea is to construct a standalone cost formulation for the purpose of adversarial training to achieve better overall performance of the model. Zhang et al. [47], Kannan et al. [48], Wang et al. [49], and Mao et al. [50] proposed the solutions to corporate PGD adversarial training with a modified regularizer for better performance. Zhang et al. [47] used a method called TRADES to improve the robustness of the model. They presented a concept of a trade-off between standard generalization and adversarial generation. A regularizer with a combination of natural and boundary errors was proposed to minimize the loss of the model to balance the standard accuracy and robustness. The formulation can be written as follows:
where ϕ is any loss function defined, f is the model, λ is a control variable, Y is the output label, and X and X’ are the clean input and perturbed input, respectively. However, Stutz et al. [71] suggested that the model generalization and robustness could coexist. Kannan et al. [48] considered the logit results of the model produced by both clean and adversarial data. They created a regularization term by reducing the distance between the logit pairs. Wang et al. [49] considered the situation when the train data were correctly or incorrectly classified initially and designed two regularizers for each case. Mao et al. [50] adapted a triplet loss to push the samples in different classes further while pulling the sample with the same class closer. Zhong et al. [51] used a similar method, but they only considered the margin between the clean data and the adversarial data.
4.3.5. Unsupervised/Semi-Unsupervised Training
There are also some unsupervised or semi-unsupervised variants of PGD adversarial training. The purpose of unsupervised learning is to solve the potential data hungry problem in machine learning and expand the dataset to provide better generalization. These are the papers that proposed an adversarial training schema by utilizing the unlabeled data [52,53,54,55]. Zhai et al. [54] proposed a unique regularization term by considering the decision boundary’s correctness and stability. They used labeled and unlabeled data to train each of the regularization terms. Uesato et al. [52] used a similar method; however, they also proposed another approach that utilized the pseudo-label from another model with standard generalization. Therefore, they could train a model with a similar standard accuracy compared to the standard model while improving the adversarial accuracy with unlabeled data. Carmon et al. [53] utilized the Gaussian model for generating pseudo-labels for unlabeled data to achieve semi-supervised adversarial learning. Hendrycks et al. [55] used an auxiliary rotation algorithm to improve on original PGD adversarial training. A rotation transformation method is utilized to construct extra data samples to join the self-supervised learning procedure. They claimed that their improved version achieved better robustness and clean accuracy compared to the original PGD adversarial training.
4.3.6. Other Methods Related to PGD and BIM
Maini et al. and Stutz et al. [56,57] used PGD as a base method to discover the potential existence of unseen adversarial samples. Maini et al. [56] combined the different perturbations under multiple distance metrics to find the worst adversarial results. Stutz et al. [57] forced the confidence distribution to change smoothly outside the normal attack distance to reduce the possibility of unseen adversaries.
Dong et al. [58] considered adversarial sample distribution rather than an individual adversarial sample in adversarial training. Yuan et al. and Liu et al. [29,59] used the PGD and FGSM to train the robust GANs network to defend the classifier. Rao et al. [60] targeted the issue when the adversarial attack was used to produce a visible adversarial patch attack. Wan et al. [30] used a Gaussian mixture and a unique regularizer to differentiate the adversarial sample’s features from the normal clean data’s features. Wu et al. [61] proposed a solution against rectangular occlusion attacks, which could be applied to physical space. The attack is based on generating adversarial patterns with the PGD. Ruiz et al. [62] exposed an adversarial attack threat with a GANs face image generator. They proposed a training method to train a robust generative adversarial network. Jiang et al. [63] used a novel network with an extra output head during the adversarial training. Ma et al. [64] tried to apply the adversarial training concept to medical images by searching and adjusting the local decision boundary location. There are a few other examples; they are listed in Table 3.
4.4. L-BFGS and JSMA Methods
There are other well-known white-box attacks that are utilized in adversarial training. The L-BFGS is a white-box attack proposed by Szegedy et al. [4]. This attack uses a flexible objective function to optimize the adversaries. Therefore, the algorithm can be modified easily for different conditions but the optimization problem in this method is relatively difficult to solve [96], which may lead to reduced efficiency in adversarial training. The Jacobian-based saliency map attack (JSMA) is a saliency-based white-box attack method [97] that exploits the idea of the attention saliency map of the model. The perturbations were added to higher attention input instances to impact output space with minimal perturbation distance. These methods were only considered in method-based ensemble adversarial training (MBEAT) [31]; therefore, there is limited information about the limitations of the method when it is used in adversarial training. Zhang et al. [78] used a named YOPO algorithm to freeze the layers of the network while only including the first layer for adversarial sample generation. This method reduced the complexity of the adversarial training.
4.5. Generative Model
The articles on generative models are listed in Table 3. The general idea of those methods includes utilizing generative adversarial networks (GANs) or an auto encode–decoder to generate adversaries. Usually, these methods include unsupervised or semi-unsupervised training concepts. These methods often exploit the current machine learning techniques to auto-generalize a learning model on the adversarial sample distribution to produce adversarial samples. However, Wiyatno et al. [2] reviewed an adversarial attack that uses generative networks to generate adversarial samples and summarized the flaws of the adversaries generated by these methods. One of the flaws is that the adversaries generated by the GANs methods may not be generalized enough compared to other methods. The paper also surveyed another method that uses transformation networks for adversary generation; however, the resulting adversaries often have low transferability, and the generator training process may have catastrophic forgetting properties. Furthermore, there are fewer papers that evaluate these adversarial attacks when they are utilized by adversarial training. Hence, there is a research gap in this area of study.
Wang et al. and Stutz et al. [7,71] proposed the GANs network as a training schema to improve model robustness. Wang et al. [7] used a generative network to discover the adversarial perturbation of a discriminator network. The perturbation strength will be limited by ε after being generated. The two networks were trained jointly as the strength of the adversaries and the robustness of the discriminator increased simultaneously. The generative model could learn the distribution of adversarial perturbations without any supervision. However, the method only considers L∞ norm adversaries. Stutz et al. [71] implemented VAE–GANs to produce an adversarial sample on the manifold of the image data. This type of perturbation limits the perturbation direction in order to find the generalization errors of the decision boundaries within the data samples.
Sreevallabh Chivukula et al. and Bai et al. [72,73] proposed using an auto encode-decoder to generate adversarial samples. Sreevallabh Chivukula et al. [72] used the Stackelberg game concept to form a competition between the generative models. The CAE model was proposed by Bai et al. [73] to construct an encode–decoder structure in the training process. The encoder is the neural network model that provides the prediction, while the decoder responds by producing adversarial samples of the encoder model. In this case, the two models are trained together to improve the robustness of the prediction.
4.6. C&W-L2 Attack
C&W attack is a grey/black-box attack proposed by Carlini et al. [15]. The strength of this attack is that it generates highly transferable adversarial samples to bypass defensive methods such as distillation. Wen et al. [74] trained a detector network as an attachment model to count the attacks. The detector model was trained by the logit output before the SoftMax layer of the victim model was attacked by the C&W attack.
4.7. Ensemble Models
Pang et al. and Tramèr et al. [17,75] proposed and improved the concept of ensemble adversarial training. Ensemble adversarial training considers the adversarial samples of other trained static models and uses them to train a robust model [17]. This method can generate adversaries that represent a more accurate approximation of real adversarial distributions compared to the adversarial samples generated during the adversarial training. Pang et al. [75], Kariyappa et al. [76], and Yang et al. [77] improved upon this concept and lowered the transferability of strong adversarial samples between the ensemble models.
The novelty of this method is that it provides a viable way to decouple the adversary generation from the target training model. This could mean that the adversarial training process could be alternated, in which the adversarial samples are static and could be prepared before the training; therefore, it might partially solve the problem of computational cost in conventional adversarial training [6]. Moreover, the method appears to have better robustness against black-box attacks as the ensemble training can lower the transferability of adversarial samples from other models [17]. However, the trained model might still be vulnerable to white-box attacks such as the iterative least-likely class method and random start FGSM or more powerful black-box adversarial samples [17].
4.8. Novel Perturbation Methods
There are several other related research papers that were published after the year 2017 that we believe it is important to consider here as well. This collection of methods includes novel ways to approximate the inner maximization of adversarial training formulations. Most of them do not use the conventional attack algorithms or use a specially modified version of the attack for some purposes. However, there is insufficient information to draw conclusions regarding limitations and advantages since they are less popular or have been published more recently. Therefore, we propose this as a future research path to verify these novel solutions.
4.8.1. Methods Targeting Specific Application Domains
The PWWS is an adversarial attack that targets text classification [98]. The method approximates the importance of the words presented in the input space related to the output classification. Du et al. [79] utilized PWWS to train a robust text classifier.
Khoda et al. [80] proposed a method to craft malware that can evade the deep learning malware detector. The method uses the Jacobian matrix to find out the most impactful features of the malware related to the output of the deep learning detector and modify them to lower the detection confidence. The method was specialized in the study field of malware detection.
Those adversarial training methods mainly focus on one field of application; therefore, they are not general for constructing a universal framework.
4.8.2. Instance-Wise Perturbation
An instance-wised adversarial attack was proposed by Kim et al. [81] to achieve the goal of self-supervised learning. The goal of this attack is to deviate the model output of an input instance by transforming the image using stochastic augmentation. Therefore, during the training, the classification of the transformed data in the model will be equalized to the original label.
4.8.3. Adversarial Attack with Riemannian Space
Zhang et al. [82] implemented a unique adversarial attack to perturb the input data in Riemannian space. The difference between the proposed attack and the traditional adversarial attack in L2 space is that this attack method considers the perturbation distance in the geometry of the loss function instead of the fixed L2 distance. They propose that this method provides higher precision perturbation.
4.8.4. Boundary-Guided Generation
This method was proposed by Zhou et al. [83] to consider the hidden distribution of the input dataset. A supported vector machine (SVM) was utilized to find the decision boundary over the data distribution. Then, a generative network was used to transfer the adversarial samples close to the boundary of the input data and adjust the decision boundary by training the model using these adversaries. The advantage of this training schema is that it can produce diverse adversarial samples and potentially provide more generalization in terms of the robustness of the model.
4.8.5. Layer-Wised Perturbation
This novel noise generation method was proposed by Liu et al. [84]. In contrast with traditional perturbation, the researchers tried to add perturbation into the intermediate data within each network’s hidden layer. They aimed to improve the robustness of every layer of the network to prevent the negative impact of both the adversarial attack and corrupted data sample. Similarly, Chen et al. [85] proposed a layer-wised adversarial generation by adding the adversarial perturbation into the intermediate layer of the network. The perturbation is calculated using the gradient of the loss function regarding the layer output.
4.8.6. TUP
Wang et al. [86] proposed an adversarial attack method to produce the target universal perturbation (TUP). This type of perturbation will let the model output a false label for most of the input data. The idea of utilizing this adversarial sample determines a weaker decision boundary for the networks.
4.8.7. Self-Supervised Perturbation
Naseer et al. [87] proposed a novel self-supervised perturbation method. The goal of this method is to construct a model-independent self-supervised adversary generator. The optimization objective function of this method is to maximize the output gradient between the original image and the adversarial image while constraining the attack strength within ε distance in L infinite space.
4.8.8. Attack-Less Adversarial Training
This method was proposed in a patent paper by Ho et al. [88] that maps the pixels in an input image to another value instead of using any state-of-the-art adversarial attack method. This approach aimed to train the model on a different form of the necessary features to provide a generalized defense of perturbation and to bypass the problem of overfitting.
4.8.9. Iterative Quantized Local Search
The iterative quantized local search method was proposed by Guo et al. [89] to search the adversaries in a discrete manner. The researchers thought that attacks such as the PGD only search for the perturbation in continuous space but might not be able to apply the found adversaries to a real application. At the same time, search on continuous space is more computationally expensive. Their algorithm tackled these two problems.
4.8.10. Feature Scatter
Zhang et al. [90] utilized the feature scatter method in the training process to prevent label leaks from conventional adversarial training. They formulated their inner maximization optimization problem as optimal transport distance and produced perturbation based on this metric instead of using normal attacks. The formula could be written as:
where D is the optimal transport distance between two distributions of samples. The method minimizes the average loss Lθ regarding each perturbed input–output pair (x’i, yi) under the constraint of maximizing optimal transport distance D between clean and perturbed samples’ distributions.
4.9. Adversarial Training Extension
In this section, some extension methods are introduced to enhance the performance of general adversarial training. These methods might add additional steps to conventional adversarial training, mix multiple training methods, or use different optimization approaches. Most of them did not introduce any new threat models during the training and did not use specific attack methods to train. However, these studies are still valuable for researchers to consider in this research area.
4.9.1. Method-Based Ensemble Adversarial Training
The method-based ensemble adversarial training (MBEAT) utilizes varieties of adversarial attacks in the training process [31]. This method further increases the model’s generalization across the data that are attacked by different attack methods.
4.9.2. Adam Optimizer with Local Linearization Regularizer
Mao et al. [50] used an Adam optimizer and a local linearization regularizer to speed up the robust optimization of the model while maintaining the robustness compared to regular adversarial training.
4.9.3. Adversarial Vertex Mixup
Lee et al. [91] considered a soft label approach to reduce the overfitting effect of adversarial training. They introduced an adversarial vertex on top of the adversarial sample and computed the relative location of the vertex to the samples to produce a soft label of the adversarial training data.
4.9.4. Adversarial Interpolation
Zhang et al. [92] included adversarial samples and their corresponding adversarial labels in the training process. The interpolation method was used to measure the distance between the extracted features of the target image and the clean image and then perturb the clean image in a way so as to close the distance to the target image. They considered this method to produce the adversarial sample with soft labels. The adversarial samples and soft labels could be used in adversarial training.
4.9.5. Adversarial Training with Hypersphere Embedding
Pang et al. [93] included embedding mechanisms in the hypersphere during the training process to improve the overall performance of learning and generalization in adversarial samples.
4.10. Summary of the Findings
The adversarial attacks and defenses are currently one of the hottest topics in this research field. One of the most effective ways to defend against these attacks is adversarial training. The current increase in the number of published papers indicates that there are still many opportunities for the development of adversarial training.
In Section 4, the common adversarial sample generation techniques within adversarial training are analyzed. In this section, we summarize the adversarial training methods based on their primary goals. In summary, the most popular adversarial training methods are the FGSM and PGD, which account for 20 and 35 papers, respectively. Madry et al. [13] proposed the PGD adversarial training as a universal adversarial training method for first-order adversaries. The method implemented by this paper is used as a standard benchmark method for adversarial training and evaluation. There are eighteen papers proposing an efficient adversarial training schema using modified FGSM or PGD for the fast adversarial training process, and one paper heavily modified the adversarial sample generator to achieve the same goal. Seven papers proposed an improvement to traditional PGD adversarial training to reduce the overfitting problem on complex data and improve the adversary generation for every instance of training data. Six papers mainly considered new regularization terms in adversarial training to improve the model robustness. Five papers proposed a semi-supervised adversarial training process with four papers focused on PGD adversaries, while one paper proposed a unique adversarial sample generation method. There are five papers proposing a training method that utilizes black-box adversaries’ generation, four of which include a generative network or auto encode–decode architecture. Two papers proposed a solution to train neural networks against unseen adversarial samples.
4.11. Threats to Validity
In this section, the potential threats to the validity of our study are discussed.
4.11.1. Internal Threats
The primary internal threat to the validity of this study is the selection bias caused by the subjective opinion of the first researcher. The other influential factors also include the bias from the primary search engine used by the study and the categorization method used to summarize the studied papers. The bias from the search engine refers to the influence on the inclusion results and the conclusion of the study caused by the potential favored search results returned by the search engine. Furthermore, the experience and subjective opinion of the first researcher can also influence the definition of the categorization method, and it could also affect the conclusion of the study.
The following steps were used to mitigate the selection bias. First, the papers were filtered out by matching selection criteria. The primary consideration for the criteria included the words within the titles, introductions, keywords, and methodologies of the papers. Papers without any methodology provided were excluded. Then, the papers were evaluated multiple times before inclusion.
To minimize the bias from our primary search engine, we included a snowballing procedure in our paper collection procedure. In this step, further evaluation was conducted to identify the relevancy of the core selected papers and the newly included papers to the topic.
Furthermore, the categorization method used in this study considered each studied method’s methodology. The names of the generation components were used for categorization if they were available, and the descriptions of the components were used if the names were not available to avoid the influence of any subjective opinion on the process. The categories provided by Bai et al. [5] were also considered for our study.
4.11.2. External Threats
The external threats to the validity of the study primarily relate to the coverage of the selected papers. The snowballing method was mentioned in internal threats Section 4.11.1 to expand the coverage of the papers. Considering the active status within the research field of the study, we included every paper that could be found related to a newly proposed method, regardless of its length and writing style. Hence, the study could provide information on less mature ideas as well as well-studied methods. However, we cannot guarantee complete coverage of the topic due to the limitations of this study regarding the time range criteria, limited iteration of the snowballing process, and language criteria.
4.11.3. Construct Validity
The threats to the construct validity relate to the design of the search query and the inclusion and exclusion criteria of the study. To minimize the construct threats, synonyms and acronyms were included in the search query to expand the possible search results. Furthermore, the scope was also completely defined by the search query and inclusion and exclusion criteria to limit our study to the security of the machine learning models.
5. Discussion
5.1. Generalization Problem
In [99], Schmidt et al. discuss model generalization in the standard dataset and adversarial samples and the problem of overfitting. Despite methods proposed to reduce the effect of the limitation, the solution is not guaranteed. There is usually a trade-off between standard and adversarial accuracy in the current robust model, especially in a larger model. Schmidt et al. [99] found that the robust optimization achieved less total accuracy with the same size dataset, indicating that there might be a need for a larger dataset to achieve enough generalization. Therefore, adversarial optimization is potentially more data-hungry than normal training. Schott et al. [19] also said that the traditional gradient-based optimization attack (FGSM and PGD) adversarial training schema might not be able to train a robust model against all possible adversarial samples. Therefore, a more advanced adversary generation method or adversarial samples based on other distance metrics or using other, less popular methods should be considered in future adversarial training methods. Additionally, the current accuracy of the adversarially trained classifier with high dimension adversarial samples is still significantly lower than the standard accuracy [5]. Furthermore, the performance of the model generalization on the black-box adversaries has not been fully studied. We think this could be one of the directions for future adversarial learning research.
5.2. Generalization and Efficiency
To achieve fast adversarial training, there are methods that use a heavily modified version of the PGD or single-step versions of the FGSM as we mentioned in Section 4. However, the trade-off forces the adversarial samples generated to have less precise attacks in general. Although there are some proposed improvements to align the adversaries’ generation performance under weaker attack methods, the performance in most cases is still not ideal, especially for more complex datasets [5,23].
5.3. Against Potential Unseen Adversaries
Recently proposed methods rarely counter the problem of the unseen adversarial samples. Recently, Bai et al. [5] stated that the recent attack methods are not sufficient to work out the hidden adversarial samples. Most adversarial attacks use the preset Lp norm values to control the distance of the perturbation, which might not reflect all possibilities of attacks. There are also constraints that exist for the other methods, such as generative models and evolutionary algorithms [2].
There is a solution that uses multiple Lp norm perturbations to adversarially train the model [56]. Maini et al. suggested considering multiple Lp norms to determine the worst-case perturbation. Another method proposed by Stutz et al. [57] enforced the smooth distribution of confidence during training to ensure the smooth transition over the decision boundary. Dong et al. [58] also considered the distribution of the adversarial samples produced by multiple adversarial attacks.
However, as Bai et al. [5] stated, the current study on unseen adversarial attacks is insufficient. Combining the problem with generalization [5], the data sample we used in the training set and test set does not always reflect the real distribution of the data. There could also be adversarial samples of unseen data points outside the training and test set.
6. Conclusions and Future Work
In this paper, we reviewed the current existing adversarial training methods and approaches to improve the robustness of the neural network classifiers. The goal of this study is to identify the current advances and limitations of this type of robust optimization technique. We selected 78 papers in this review, and the results show that:
- The current research on adversarial training or robust neural network optimization focuses on the FGSM and PGD adversarial samples.
- The major goals of current approaches include balancing standard and adversarial generalization and efficiency. The commonly used methods include modifying the traditional FGSM and PGD and modifying the regularization terms of the training objective function.
- Some other methods have been proposed to be incorporated into adversarial training, such as generative networks and other black-box generation methods.
- Generalization problems have been studied frequently; however, there is still a gap between the standard accuracy, adversarial accuracy, and efficiency of training. Generalization towards unseen adversarial samples has been studied occasionally, but there is potentially more to explore.
To address these challenges, we may require more data samples for both adversarial and non-adversarial samples. Ideally, if we could pre-include the adversarial samples within the training dataset, we can train the model using standard training processes and retain a similar training complexity. We could look into the idea of ensemble adversarial training that uses a simple static model to pre-construct a general standard decision boundary of the data [17]. We can then generate a dataset to conclude potentially vulnerable data points from this pre-train model to train our final robust model.
Furthermore, there are some new adversarial generation methods available in addition to the currently popular methods. The GANs model could be one of the suggestions to produce out-of-set samples. In recent years, GANs have been proven to be effective as adversary generators [100,101]. The concept of using GANs to produce an adversarial but real-looking picture has been utilized in this field of research. A GANs network could be used to capture the latent space representation of adversarial samples. We need more research to evaluate the results when GANs models are used to approximate the inner maximum of the adversarial training. Furthermore, we can also utilize the realistic image generated by GANs and combine the unsupervised learning schema to solve the data-hungry problems. This method could be limited by current GANs limitations; however, it may be a solution to discover more vulnerable data samples in the input space. The evolutionary-based algorithms could also help with solving those problems. The benefit of an evolutionary-based algorithm is that it provides an effective optimal search that could potentially have a wide coverage range of perturbation. The evolutionary attacks have been experiments on the current models and it is an effective method of protecting against them [102,103]. These attacks could also be utilized to solve the inner approximation of adversarial training. By using these methods, we can discover more out-of-set data samples with potential hidden vulnerabilities. This could be a method to defend unseen adversarial samples and provide further generalization for the model. We suggest that they should be considered in robust optimizations.
For the application domain, the adversarial sample was found in recurrent networks and generative models [104,105,106,107,108]. As the current research mainly focuses on computer visions, it is necessary to extend the variety of adversarial training to different applications.
Additionally, there are still gaps in our true understanding of the adversarial samples and adversarial training. Hence, the improved visualization tools regarding the adversarial optimization problems could also help us to explain, understand, and improve the current implementation.
In conclusion, it is challenging to build a natural robust deep learning model. We might need more knowledge and significant modifications to deep neural network models in the future to achieve this goal. Before that, adversarial training might be an effective solution to improve the models’ adversarial robustness. Hence, it is essential to enhance the efficiency and the generalization of adversarial training. Currently, adversarial training primarily improves the robustness of a model involving the collection of data from a dataset. However, there is no guarantee that the training can be generalized to all possible situations in real-life applications. Therefore, new techniques should be developed to expand our current understanding of adversarial optimization. There is still a research gap between recently proposed methods and a robust deep learning model.
Author Contributions
Writing—original draft preparation: W.Z.; supervision and writing—review and editing: S.A. and Q.H.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Natural Sciences and Engineering Research Council of Canada (NSERC).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Silva, S.H.; Najafirad, P. Opportunities and Challenges in Deep Learning Adversarial Robustness: A Survey. arXiv 2020, arXiv:2007.00753. [Google Scholar]
- Wiyatno, R.R.; Xu, A.; Dia, O.; de Berker, A. Adversarial Examples in Modern Machine Learning: A Review. arXiv 2019, arXiv:1911.05268. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and Harnessing Adversarial Examples. arXiv 2015, arXiv:1412.6572. [Google Scholar]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing Properties of Neural Networks. arXiv 2014, arXiv:1312.6199. [Google Scholar]
- Bai, T.; Luo, J.; Zhao, J.; Wen, B.; Wang, Q. Recent Advances in Adversarial Training for Adversarial Robustness. arXiv 2021, arXiv:2102.01356. [Google Scholar]
- Kurakin, A.; Goodfellow, I.; Bengio, S. Adversarial Machine Learning at Scale. arXiv 2017, arXiv:1611.01236. [Google Scholar]
- Wang, H.; Yu, C.-N. A Direct Approach to Robust Deep Learning Using Adversarial Networks. arXiv 2019, arXiv:1905.09591. [Google Scholar]
- Chen, K.; Zhu, H.; Yan, L.; Wang, J. A Survey on Adversarial Examples in Deep Learning. J. Big Data 2020, 2, 71–84. [Google Scholar] [CrossRef]
- Chakraborty, A.; Alam, M.; Dey, V.; Chattopadhyay, A.; Mukhopadhyay, D. Adversarial Attacks and Defences: A Survey. arXiv 2018, arXiv:1810.00069. [Google Scholar] [CrossRef]
- Kong, Z.; Xue, J.; Wang, Y.; Huang, L.; Niu, Z.; Li, F. A Survey on Adversarial Attack in the Age of Artificial Intelligence. Wirel. Commun. Mob. Comput. 2021, 2021, 4907754. [Google Scholar] [CrossRef]
- Huang, X.; Kroening, D.; Ruan, W.; Sharp, J.; Sun, Y.; Thamo, E.; Wu, M.; Yi, X. A Survey of Safety and Trustworthiness of Deep Neural Networks: Verification, Testing, Adversarial Attack and Defence, and Interpretability. Comput. Sci. Rev. 2020, 37, 100270. [Google Scholar] [CrossRef]
- Kitchenham, B.; Charters, S. Guidelines for Performing Systematic Literature Reviews in Software Engineering; Technical Report; Keele University: Keele, UK; Durham University: Durham, UK, 2007; Volume 2. [Google Scholar]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards Deep Learning Models Resistant to Adversarial Attacks. arXiv 2019, arXiv:1706.06083. [Google Scholar]
- Moosavi-Dezfooli, S.-M.; Fawzi, A.; Frossard, P. DeepFool: A Simple and Accurate Method to Fool Deep Neural Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2574–2582. [Google Scholar]
- Carlini, N.; Wagner, D. Towards Evaluating the Robustness of Neural Networks. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2017; pp. 39–57. [Google Scholar]
- Su, J.; Vargas, D.V.; Sakurai, K. One Pixel Attack for Fooling Deep Neural Networks. IEEE Trans. Evol. Computat. 2019, 23, 828–841. [Google Scholar] [CrossRef]
- Tramèr, F.; Kurakin, A.; Papernot, N.; Goodfellow, I.; Boneh, D.; McDaniel, P. Ensemble Adversarial Training: Attacks and Defenses. arXiv 2020, arXiv:1705.07204. [Google Scholar]
- About Engineering Village|Elsevier. Available online: https://www.elsevier.com/solutions/engineering-village#:~:text=Engineering%20Village%20is%20a%20search,needs%20of%20world%20class%20engineers (accessed on 13 July 2022).
- Schott, L.; Rauber, J.; Bethge, M.; Brendel, W. Towards the First Adversarially Robust Neural Network Model on MNIST. arXiv 2018, arXiv:1805.09190. [Google Scholar]
- Vivek, B.S.; Venkatesh Babu, R. Single-Step Adversarial Training With Dropout Scheduling. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 947–956. [Google Scholar]
- Huang, T.; Menkovski, V.; Pei, Y.; Pechenizkiy, M. Bridging the Performance Gap between FGSM and PGD Adversarial Training. arXiv 2020, arXiv:2011.05157. [Google Scholar]
- Liu, G.; Khalil, I.; Khreishah, A. Using Single-Step Adversarial Training to Defend Iterative Adversarial Examples. In Proceedings of the Proceedings of the Eleventh ACM Conference on Data and Application Security and Privacy, Virtual Event USA, 26–28 April 2021; pp. 17–27. [Google Scholar]
- Wong, E.; Rice, L.; Kolter, J.Z. Fast Is Better than Free: Revisiting Adversarial Training. arXiv 2020, arXiv:2001.03994. [Google Scholar]
- Andriushchenko, M.; Flammarion, N. Understanding and Improving Fast Adversarial Training. Adv. Neural Inf. Process. Syst. 2020, 33, 16048–16059. [Google Scholar]
- Kim, H.; Lee, W.; Lee, J. Understanding Catastrophic Overfitting in Single-Step Adversarial Training. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar]
- Song, C.; He, K.; Wang, L.; Hopcroft, J.E. Improving the Generalization of Adversarial Training with Domain Adaptation. arXiv 2019, arXiv:1810.00740. [Google Scholar]
- Vivek, B.S.; Babu, R.V. Regularizers for Single-Step Adversarial Training. arXiv 2020, arXiv:2002.00614. [Google Scholar]
- Li, B.; Wang, S.; Jana, S.; Carin, L. Towards Understanding Fast Adversarial Training. arXiv 2020, arXiv:2006.03089. [Google Scholar]
- Yuan, J.; He, Z. Adversarial Dual Network Learning With Randomized Image Transform for Restoring Attacked Images. IEEE Access 2020, 8, 22617–22624. [Google Scholar] [CrossRef]
- Wan, W.; Chen, J.; Yang, M.-H. Adversarial Training with Bi-Directional Likelihood Regularization for Visual Classification. In Computer Vision—ECCV 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.-M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 12369, pp. 785–800. ISBN 9783030585853. [Google Scholar]
- Qin, Y.; Hunt, R.; Yue, C. On Improving the Effectiveness of Adversarial Training. In Proceedings of the ACM International Workshop on Security and Privacy Analytics—IWSPA’19, Richardson, TX, USA, 27 March 2019; ACM Press: New York, NY, USA, 2019; pp. 5–13. [Google Scholar]
- Laugros, A.; Caplier, A.; Ospici, M. Addressing Neural Network Robustness with Mixup and Targeted Labeling Adversarial Training. In Computer Vision—ECCV 2020 Workshops; Bartoli, A., Fusiello, A., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 12539, pp. 178–195. ISBN 9783030682378. [Google Scholar]
- Li, W.; Wang, L.; Zhang, X.; Huo, J.; Gao, Y.; Luo, J. Defensive Few-Shot Adversarial Learning. arXiv 2019, arXiv:1911.06968. [Google Scholar]
- Liu, J.; Jin, Y. Evolving Hyperparameters for Training Deep Neural Networks against Adversarial Attacks. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019; pp. 1778–1785. [Google Scholar]
- Ren, Z.; Baird, A.; Han, J.; Zhang, Z.; Schuller, B. Generating and Protecting Against Adversarial Attacks for Deep Speech-Based Emotion Recognition Models. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 7184–7188. [Google Scholar]
- Song, C.; Cheng, H.-P.; Yang, H.; Li, S.; Wu, C.; Wu, Q.; Chen, Y.; Li, H. MAT: A Multi-Strength Adversarial Training Method to Mitigate Adversarial Attacks. In Proceedings of the 2018 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Hong Kong, China, 8–11 July 2018; pp. 476–481. [Google Scholar]
- Gupta, S.K. Reinforcement Based Learning on Classification Task Could Yield Better Generalization and Adversarial Accuracy. arXiv 2020, arXiv:2012.04353. [Google Scholar]
- Chen, E.-C.; Lee, C.-R. Towards Fast and Robust Adversarial Training for Image Classification. In Computer Vision—ACCV 2020; Ishikawa, H., Liu, C.-L., Pajdla, T., Shi, J., Eds.; Springer International Publishing: Cham, Switzerland, 2021; Volume 12624, pp. 576–591. ISBN 9783030695347. [Google Scholar]
- Cai, Q.-Z.; Du, M.; Liu, C.; Song, D. Curriculum Adversarial Training. arXiv 2018, arXiv:1805.04807. [Google Scholar]
- Zhang, J.; Xu, X.; Han, B.; Niu, G.; Cui, L.; Sugiyama, M.; Kankanhalli, M. Attacks Which Do Not Kill Training Make Adversarial Learning Stronger. In Proceedings of the 37th International Conference on Machine Learning, PMLR, Online, 21 November 2020; pp. 11278–11287. [Google Scholar]
- Wang, Y.; Ma, X.; Bailey, J.; Yi, J.; Zhou, B.; Gu, Q. On the Convergence and Robustness of Adversarial Training. arXiv 2022, arXiv:2112.08304. [Google Scholar]
- Balaji, Y.; Goldstein, T.; Hoffman, J. Instance Adaptive Adversarial Training: Improved Accuracy Tradeoffs in Neural Nets. arXiv 2019, arXiv:1910.08051. [Google Scholar]
- Ding, G.W.; Sharma, Y.; Lui, K.Y.C.; Huang, R. MMA Training: Direct Input Space Margin Maximization through Adversarial Training. arXiv 2020, arXiv:1812.02637. [Google Scholar]
- Cheng, M.; Lei, Q.; Chen, P.-Y.; Dhillon, I.; Hsieh, C.-J. CAT: Customized Adversarial Training for Improved Robustness. arXiv 2020, arXiv:2002.06789. [Google Scholar]
- Shafahi, A.; Najibi, M.; Ghiasi, A.; Xu, Z.; Dickerson, J.; Studer, C.; Davis, L.S.; Taylor, G.; Goldstein, T. Adversarial Training for Free! arXiv 2019, arXiv:1904.12843. [Google Scholar]
- Zhang, H.; Shi, Y.; Dong, B.; Han, Y.; Li, Y.; Kuang, X. Free Adversarial Training with Layerwise Heuristic Learning. In Image and Graphics; Peng, Y., Hu, S.-M., Gabbouj, M., Zhou, K., Elad, M., Xu, K., Eds.; Springer International Publishing: Cham, Switzerland, 2021; Volume 12889, pp. 120–131. ISBN 9783030873578. [Google Scholar]
- Zhang, H.; Yu, Y.; Jiao, J.; Xing, E.; Ghaoui, L.E.; Jordan, M. Theoretically Principled Trade-off between Robustness and Accuracy. In Proceedings of the 36th International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 24 May 2019; pp. 7472–7482. [Google Scholar]
- Kannan, H.; Kurakin, A.; Goodfellow, I. Adversarial Logit Pairing. arXiv 2018, arXiv:1803.06373. [Google Scholar]
- Wang, Y.; Zou, D.; Yi, J.; Bailey, J.; Ma, X.; Gu, Q. Improving Adversarial Robustness Requires Revisiting Misclassified Examples. In Proceedings of the 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Mao, C.; Zhong, Z.; Yang, J.; Vondrick, C.; Ray, B. Metric Learning for Adversarial Robustness. arXiv 2019, arXiv:1909.00900. [Google Scholar]
- Zhong, Y.; Deng, W. Adversarial Learning With Margin-Based Triplet Embedding Regularization. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 6548–6557. [Google Scholar]
- Uesato, J.; Alayrac, J.-B.; Huang, P.-S.; Stanforth, R.; Fawzi, A.; Kohli, P. Are Labels Required for Improving Adversarial Robustness? arXiv 2019, arXiv:1905.13725. [Google Scholar]
- Carmon, Y.; Raghunathan, A.; Schmidt, L.; Liang, P.; Duchi, J.C. Unlabeled Data Improves Adversarial Robustness. arXiv 2019, arXiv:1905.13736. [Google Scholar]
- Zhai, R.; Cai, T.; He, D.; Dan, C.; He, K.; Hopcroft, J.; Wang, L. Adversarially Robust Generalization Just Requires More Unlabeled Data. arXiv 2019, arXiv:1906.00555. [Google Scholar]
- Hendrycks, D.; Mazeika, M.; Kadavath, S.; Song, D. Using Self-Supervised Learning Can Improve Model Robustness and Uncertainty. arXiv 2019, arXiv:1906.12340. [Google Scholar]
- Maini, P.; Wong, E.; Kolter, J.Z. Adversarial Robustness Against the Union of Multiple Perturbation Models. In Proceedings of the 37th International Conference on Machine Learning, Virtual Event, 21 November 2020. [Google Scholar]
- Stutz, D.; Hein, M.; Schiele, B. Confidence-Calibrated Adversarial Training: Generalizing to Unseen Attacks. In Proceedings of the 37th International Conference on Machine Learning, PMLR, Virtual Event, 21 November 2020; pp. 9155–9166. [Google Scholar]
- Dong, Y.; Deng, Z.; Pang, T.; Su, H.; Zhu, J. Adversarial Distributional Training for Robust Deep Learning. Adv. Neural Inf. Process. Syst. 2020, 33, 8270–8283. [Google Scholar]
- Liu, G.; Khalil, I.; Khreishah, A. GanDef: A GAN Based Adversarial Training Defense for Neural Network Classifier. In ICT Systems Security and Privacy Protection; Dhillon, G., Karlsson, F., Hedström, K., Zúquete, A., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Volume 562, pp. 19–32. ISBN 9783030223113. [Google Scholar]
- Rao, S.; Stutz, D.; Schiele, B. Adversarial Training Against Location-Optimized Adversarial Patches. In Computer Vision—ECCV 2020 Workshops; Bartoli, A., Fusiello, A., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 12539, pp. 429–448. ISBN 9783030682378. [Google Scholar]
- Wu, T.; Tong, L.; Vorobeychik, Y. Defending Against Physically Realizable Attacks on Image Classification. arXiv 2020, arXiv:1909.09552. [Google Scholar]
- Ruiz, N.; Bargal, S.A.; Sclaroff, S. Disrupting Deepfakes: Adversarial Attacks Against Conditional Image Translation Networks and Facial Manipulation Systems. In Computer Vision—ECCV 2020 Workshops; Bartoli, A., Fusiello, A., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 12538, pp. 236–251. ISBN 9783030668228. [Google Scholar]
- Jiang, Y.; Ma, X.; Erfani, S.M.; Bailey, J. Dual Head Adversarial Training. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021. [Google Scholar]
- Ma, L.; Liang, L. Increasing-Margin Adversarial (IMA) Training to Improve Adversarial Robustness of Neural Networks. arXiv 2022, arXiv:2005.09147. [Google Scholar]
- Zhang, C.; Liu, A.; Liu, X.; Xu, Y.; Yu, H.; Ma, Y.; Li, T. Interpreting and Improving Adversarial Robustness of Deep Neural Networks With Neuron Sensitivity. IEEE Trans. Image Process. 2021, 30, 1291–1304. [Google Scholar] [CrossRef]
- Bouniot, Q.; Audigier, R.; Loesch, A. Optimal Transport as a Defense Against Adversarial Attacks. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10 January 2021; pp. 5044–5051. [Google Scholar]
- Rakin, A.S.; He, Z.; Fan, D. Parametric Noise Injection: Trainable Randomness to Improve Deep Neural Network Robustness against Adversarial Attack. arXiv 2018, arXiv:1811.09310. [Google Scholar]
- Xu, H.; Liu, X.; Li, Y.; Jain, A.; Tang, J. To Be Robust or to Be Fair: Towards Fairness in Adversarial Training. In Proceedings of the 38th International Conference on Machine Learning, PMLR, Virtual Event, 1 July 2021; pp. 11492–11501. [Google Scholar]
- Xu, M.; Zhang, T.; Li, Z.; Liu, M.; Zhang, D. Towards Evaluating the Robustness of Deep Diagnostic Models by Adversarial Attack. Med. Image Anal. 2021, 69, 101977. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, H. Bilateral Adversarial Training: Towards Fast Training of More Robust Models Against Adversarial Attacks. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 6628–6637. [Google Scholar]
- Stutz, D.; Hein, M.; Schiele, B. Disentangling Adversarial Robustness and Generalization. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 6969–6980. [Google Scholar]
- Sreevallabh Chivukula, A.; Yang, X.; Liu, W. Adversarial Deep Learning with Stackelberg Games. In Neural Information Processing; Gedeon, T., Wong, K.W., Lee, M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Volume 1142, pp. 3–12. ISBN 9783030368074. [Google Scholar]
- Bai, W.; Quan, C.; Luo, Z. Alleviating Adversarial Attacks via Convolutional Autoencoder. In Proceedings of the 2017 18th IEEE/ACIS International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD), Kanazawa, Japan, 26–28 June 2017; pp. 53–58. [Google Scholar]
- Wen, J.; Hui, L.C.K.; Yiu, S.-M.; Zhang, R. DCN: Detector-Corrector Network Against Evasion Attacks on Deep Neural Networks. In Proceedings of the 2018 48th Annual IEEE/IFIP International Conference on Dependable Systems and Networks Workshops (DSN-W), Luxembourg, 25–28 June 2018; pp. 215–221. [Google Scholar]
- Pang, T.; Xu, K.; Du, C.; Chen, N.; Zhu, J. Improving Adversarial Robustness via Promoting Ensemble Diversity. In Proceedings of the 36th International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 24 May 2019; pp. 4970–4979. [Google Scholar]
- Kariyappa, S.; Qureshi, M.K. Improving Adversarial Robustness of Ensembles with Diversity Training. arXiv 2019, arXiv:1901.09981. [Google Scholar]
- Yang, H.; Zhang, J.; Dong, H.; Inkawhich, N.; Gardner, A.; Touchet, A.; Wilkes, W.; Berry, H.; Li, H. DVERGE: Diversifying Vulnerabilities for Enhanced Robust Generation of Ensembles. Adv. Neural Inf. Process. Syst. 2020, 33, 5505–5515. [Google Scholar]
- Zhang, D.; Zhang, T.; Lu, Y.; Zhu, Z.; Dong, B. You Only Propagate Once: Accelerating Adversarial Training via Maximal Principle. arXiv 2019, arXiv:1905.00877. [Google Scholar]
- Du, X.; Yu, J.; Li, S.; Yi, Z.; Liu, H.; Ma, J. Combating Word-Level Adversarial Text with Robust Adversarial Training. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18 July 2021; pp. 1–8. [Google Scholar]
- Khoda, M.; Imam, T.; Kamruzzaman, J.; Gondal, I.; Rahman, A. Selective Adversarial Learning for Mobile Malware. In Proceedings of the 2019 18th IEEE International Conference on Trust, Security and Privacy in Computing and Communications/13th IEEE International Conference on Big Data Science and Engineering (TrustCom/BigDataSE), Rotorua, New Zealand, 5–8 August 2019; pp. 272–279. [Google Scholar]
- Kim, M.; Tack, J.; Hwang, S.J. Adversarial Self-Supervised Contrastive Learning. Adv. Neural Inf. Process. Syst. 2020, 33, 2983–2994. [Google Scholar]
- Zhang, S.; Huang, K.; Zhang, R.; Hussain, A. Generalized Adversarial Training in Riemannian Space. In Proceedings of the 2019 IEEE International Conference on Data Mining (ICDM), Beijing, China, 8–11 November 2019; pp. 826–835. [Google Scholar]
- Zhou, X.; Tsang, I.W.; Yin, J. Latent Adversarial Defence with Boundary-Guided Generation. arXiv 2019, arXiv:1907.07001. [Google Scholar]
- Liu, A.; Liu, X.; Yu, H.; Zhang, C.; Liu, Q.; Tao, D. Training Robust Deep Neural Networks via Adversarial Noise Propagation. IEEE Trans. Image Process. 2021, 30, 5769–5781. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, N. Layer-Wise Adversarial Training Approach to Improve Adversarial Robustness. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Wang, L.; Chen, X.; Tang, R.; Yue, Y.; Zhu, Y.; Zeng, X.; Wang, W. Improving Adversarial Robustness of Deep Neural Networks by Using Semantic Information. Knowl.-Based Syst. 2021, 226, 107141. [Google Scholar] [CrossRef]
- Naseer, M.; Khan, S.; Hayat, M.; Khan, F.S.; Porikli, F. A Self-Supervised Approach for Adversarial Robustness. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 259–268. [Google Scholar]
- Ho, J.; Lee, B.-G.; Kang, D.-K. Attack-Less Adversarial Training for a Robust Adversarial Defense. Appl. Intell. 2022, 52, 4364–4381. [Google Scholar] [CrossRef]
- Guo, Y.; Ji, T.; Wang, Q.; Yu, L.; Li, P. Quantized Adversarial Training: An Iterative Quantized Local Search Approach. In Proceedings of the 2019 IEEE International Conference on Data Mining (ICDM), Beijing, China, 8–11 November 2019; pp. 1066–1071. [Google Scholar]
- Zhang, H.; Wang, J. Defense Against Adversarial Attacks Using Feature Scattering-Based Adversarial Training. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Curran Associates, Inc.: New York, NY, USA, 2019; Volume 32. [Google Scholar]
- Lee, S.; Lee, H.; Yoon, S. Adversarial Vertex Mixup: Toward Better Adversarially Robust Generalization. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 272–281. [Google Scholar]
- Zhang, H.; Xu, W. Adversarial Interpolation Training: A Simple Approach for Improving Model Robustness. In Proceedings of the 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Pang, T.; Yang, X.; Dong, Y.; Xu, K.; Zhu, J.; Su, H. Boosting Adversarial Training with Hypersphere Embedding. Adv. Neural Inf. Process. Syst. 2020, 33, 7779–7792. [Google Scholar]
- Qin, C.; Martens, J.; Gowal, S.; Krishnan, D.; Dvijotham, K.; Fawzi, A.; De, S.; Stanforth, R.; Kohli, P. Adversarial Robustness through Local Linearization. arXiv 2019, arXiv:1907.02610. [Google Scholar]
- Kurakin, A.; Goodfellow, I.; Bengio, S. Adversarial Examples in the Physical World; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Zhang, J.; Li, C. Adversarial Examples: Opportunities and Challenges. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 2578–2593. [Google Scholar] [CrossRef]
- Papernot, N.; McDaniel, P.; Jha, S.; Fredrikson, M.; Celik, Z.B.; Swami, A. The Limitations of Deep Learning in Adversarial Settings. In Proceedings of the 2016 IEEE European Symposium on Security and Privacy (EuroS&P), Saarbruecken, Germany, 21–24 March 2016. [Google Scholar]
- Ren, S.; Deng, Y.; He, K.; Che, W. Generating Natural Language Adversarial Examples through Probability Weighted Word Saliency. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; Association for Computational Linguistics: Stroudsburg, PA, USA, 2019; pp. 1085–1097. [Google Scholar]
- Schmidt, L.; Santurkar, S.; Tsipras, D.; Talwar, K.; Mądry, A. Adversarially Robust Generalization Requires More Data. arXiv 2018, arXiv:1804.11285. [Google Scholar]
- Xiao, C.; Li, B.; Zhu, J.-Y.; He, W.; Liu, M.; Song, D. Generating Adversarial Examples with Adversarial Networks. arXiv 2019, arXiv:1801.02610. [Google Scholar]
- Zhao, Z.; Dua, D.; Singh, S. Generating Natural Adversarial Examples. arXiv 2018, arXiv:1710.11342. [Google Scholar]
- Wang, L.; Yang, K.; Wang, W.; Wang, R.; Ye, A. MGAAttack: Toward More Query-Efficient Black-Box Attack by Microbial Genetic Algorithm. In Proceedings of the Proceedings of the 28th ACM International Conference on Multimedia, Seattle, WA, USA, 12 October 2020; ACM: New York, NY, USA, 2020; pp. 2229–2236. [Google Scholar]
- Chen, J.; Su, M.; Shen, S.; Xiong, H.; Zheng, H. POBA-GA: Perturbation Optimized Black-Box Adversarial Attacks via Genetic Algorithm. Comput. Secur. 2019, 85, 89–106. [Google Scholar] [CrossRef]
- Das, S.D.; Basak, A.; Mandal, S.; Das, D. AdvCodeMix: Adversarial Attack on Code-Mixed Data. In Proceedings of the 5th Joint International Conference on Data Science & Management of Data (9th ACM IKDD CODS and 27th COMAD), Bangalore, India, 8 January 2022; ACM: New York, NY, USA, 2022; pp. 125–129. [Google Scholar]
- Papernot, N.; McDaniel, P.; Swami, A.; Harang, R. Crafting Adversarial Input Sequences for Recurrent Neural Networks. In Proceedings of the MILCOM 2016—2016 IEEE Military Communications Conference, Baltimore, MD, USA, 1–3 November 2016; pp. 49–54. [Google Scholar]
- Kereliuk, C.; Sturm, B.L.; Larsen, J. Deep Learning and Music Adversaries. IEEE Trans. Multimed. 2015, 17, 2059–2071. [Google Scholar] [CrossRef]
- Liu, X.; Hsieh, C.-J. From Adversarial Training to Generative Adversarial Networks. In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Taori, R.; Kamsetty, A.; Chu, B.; Vemuri, N. Targeted Adversarial Examples for Black Box Audio Systems. In Proceedings of the 2019 IEEE Security and Privacy Workshops (SPW), San Francisco, CA, USA, 19–23 May 2019; pp. 15–20. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).