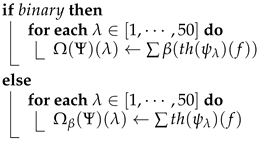Abstract
Recent studies have been evaluating the presence of patterns associated with the occurrence of cancer in different types of tissue present in the individual affected by the disease. In this article, we describe preliminary results for the automatic detection of cancer (Walker 256 tumor) in laboratory animals using preclinical microphotograph images of the subject’s liver tissue. In the proposed approach, two different types of descriptors were explored to capture texture properties from the images, and we also evaluated the complementarity between them. The first texture descriptor experimented is the widely known Local Phase Quantization (LPQ), which is a descriptor based on spectral information. The second one is built by the application of a granulometry given by a family of morphological filters. For classification, we have evaluated the algorithms Support Vector Machine (SVM), k-Nearest Neighbor (k-NN) and Logistic Regression. Experiments carried out on a carefully curated dataset developed by the Enteric Neural Plasticity Laboratory of the State University of Maringá showed that both texture descriptors provide good results in this scenario. The accuracy rates obtained using the SVM classifier were 96.67% for the texture operator based on granulometry and 91.16% for the LPQ operator. The dataset was made available also as a contribution of this work. In addition, it is important to remark that the best overall result was obtained by combining classifiers created using both descriptors in a late fusion strategy, achieving an accuracy of 99.16%. The results obtained show that it is possible to automatically perform the identification of cancer in laboratory animals by exploring texture properties found on the tissue taken from the liver. Moreover, we observed a high level of complementarity between the classifiers created using LPQ and granulometry properties in the application addressed here.
1. Introduction
Cancer is the second biggest cause of death worldwide, accounting for nearly 10 million deaths in 2020 [1]. This disease starts from the transformation of normal cells into tumor cells, in a multi-stage process that generally progresses from a pre-cancerous lesion to a malignant tumor. Different parts from the human body may be affected by this transformation. In this vein, several research studies have been developed aiming to investigate how these lesions happen in different types of tissue.
One of these investigations is under development in the Enteric Neural Plasticity Laboratory of the State University of Maringá. In that work, the researchers have been evaluating the transformations provoked by Walker 256 tumor in the cells contained in samples of tissue taken from the liver of laboratory rats in a preclinical scenario. By visually inspecting those images, they noticed that different patterns are present when samples taken from healthy and sick individuals are compared.
In this work, we describe results obtained in preliminary investigations developed aiming to accomplish the automatic identification of cancer using the aforementioned images. For this purpose, we decided to explore the textural properties of the images, inspired in another biomedical application previously investigated by our research group [2]. In that work, we evaluated the use of some widely known texture operators for the identification of chronic degenerative diseases from images taken from other types of tissue.
As far as we know, the automatic identification of cancer, using a spectral texture descriptor and granulometry-based properties of the tissue taken from the liver, is proposed for the first time in this work. Furthermore, we also investigate the complementarity between classifiers created on both scenarios (i.e., the LPQ texture operator [3], and a granulometry-based descriptor [4,5,6]). The experimental results demonstrate the existence of a high level of complementarity between both on the task evaluated here.
Taking it into account, we describe the following Research Questions (RQ) we intend to answer in this work:
- RQ1: What is the performance of LPQ to support cancer identification in a Walker 256 tumor model on microphotograph of rats liver?
- RQ2: What is the performance of granulometry-based descriptors (GBD) to support cancer identification in a Walker 256 tumor model on microphotographs of rat liver?
- RQ3: Is it possible to obtain better results for cancer identification in a Walker 256 tumor model by combining classifiers created using LPQ and GBD in this scenario?
The classification was performed using three of the most widely known shallow classifiers: k-NN, Logistic Regression, and SVM. The choice of shallow classifiers is justified by the size of the dataset, which is too small to feed deep learning models.
The remaining of this work is organized as follows: In Section 2, we describe some remarkable related works. Section 3 presents the main facts related to the dataset used in this work. In Section 4, we describe details about the feature extraction design adopted here. In Section 5, the methodology used for classification is showed in details. In Section 6, results and discussions are presented. Finally, we describe our concluding remarks.
2. Related Works
In a more general context, Matos et al. [7] recently described a review on the use of machine learning methods for histopathological image analysis. In that work, the authors easily found 2524 scientific works already published in the period between 2008 and 2020, using five widely known research portal engines (i.e., IEEExplore, ACM Digital Library, Science Direct, Web of Science and Scopus). In that work, the authors described the systematic review according to a taxonomy which takes into account some important aspects of machine learning methods: the use of segmentation as a preprocessing strategy; the use of handcrafted or non-handcrafted features; and the use of shallow or deep learning methods.
The choice for works from the literature related to this one is not such a trivial task, because this relationship may be seen from different perspectives, considering different arrangements. One of these possibilities is to make the stratification of the works in terms of the tissue/organ from which the images were obtained. In this vein, the work presented by Nativ et al. [8] is worth mentioning here. In that work, they proposed a particular image analysis technique to automatically identify the steatotic state of livers. The proposal was based on a carefully designed image analysis based on the segmentation of liver cellular and tissue structures. Following, some metrics were obtained from the segmented structures and used with a k-means unsupervised clustering algorithm. The authors claim that the proposed method overcame the performance of the strategies already presented at that moment.
Shi et al. [9] also performed automated liver fat quantification. For this purpose, they developed a pipeline in which high-relevant pixel-level features are firstly extracted from hematoxylin–eosin stained images. Following, the boundaries between nuclei, fat and other components are found clustering pixels using an unsupervised strategy. Finally, the fat regions are identified based on the use of morphological operations. The authors claim that the proposed approach presented a high accuracy and adaptability in fat droplets quantification.
Deeply analyzing the literature, we still found one more work closely related to this one. Thiran and Macq [10] performed morphological feature extraction for the Classification of Digital Images of Cancerous Tissues. The authors used a dataset composed of images from lungs and digestive tract obtained by biopsy. The proposal was based on the use of mathematical morphology to segment the nuclei of the cell, as the shape is an important attribute to make it. The sequence of operations used to perform this segmentation was the following: morphological opening, morphological reconstruction, and lastly, a threshold. Once the nuclei was segmented, the set of features was extracted using, once again, morphological operations to capture measures related to Nucleocytoplasmic Ratio, Anisonucleosis, Nuclear Deformity, and Hyperchromasia. Finally, they proposed a score obtained from these four values and used it to decide whether a given tissue is cancerous or not.
3. Dataset
The dataset used in this work was created by researchers of the Enteric Neural Plasticity Laboratory of the State University of Maringá. For this, male adult rats, of the Wistar (Rattus norvegicus) lineage were used. All the proceedings involving the animals were previously approved by the “Standing Committee on Ethics in Animals Experimentation” of the university.
The animals were randomly separated into a control group (C) and Walker tumor group (TW). Animals from the TW group were inoculated with Walker 256 tumor cells. The dataset is composed of 120 microphotographs taken from samples of rat liver tissue. The images are divided in two classes: control (C), containing 60 microphotographs taken from six healthy rats (10 from each rat) and Walker 256 tumor (TW), containing 60 microphotographs taken from six rats (ten from each rat) with the Walker 256 tumor.
The liver samples were made in a semi-serialized manner with 5 m cuts; they were stained with haematoxylin and eosin. The images were obtained using the camera Moticam® 2500 5.0 Mega Pixel (Motic China Group Co, Shanghai, China) coupled to the microscope Motic BA 400 (Motic China Group Co., Shanghai, China). The images were collected with magnification of and resolution of pixels, which corresponds to an area of 35,369.85 per image. Figure 1 and Figure 2 show samples from the classes C and TW, respectively. Some details about the images are summarized in Table 1, and additional information about the dataset can be found in [11]. The dataset used in this work was made freely available (https://github.com/Sersasj/Liver_Dataset, accessed on 1 April 2022) for research purposes in such a way that other researchers can benefit from it and properly compare the results obtained using different techniques with those obtained here.
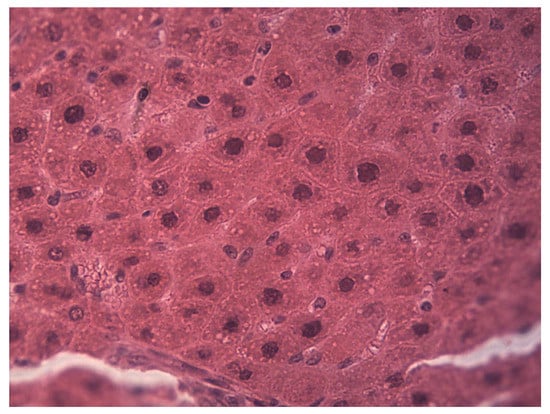
Figure 1.
Liver microphotograph from the control group (C).
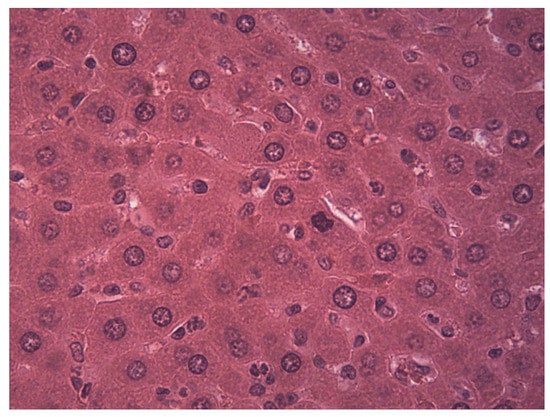
Figure 2.
Liver microphotograph from the Walker 256 tumor group (TW).

Table 1.
Dataset characteristics.
4. Feature Extraction
This section describes the descriptors used in this work: Local Phase Quantization (LPQ) and a granulometry-based descriptor. The rationale behind this choice is the following. Firstly, we chose LPQ because this operator is supposed to achieve a good performance when the images may be affected by blur, which is a noise that frequently occurs in this type of image due to the nature of the collection process, as we can see in the bottom right corner of Figure 1. Next, we decided to evaluate a granulometry-based descriptor [4,5], supposing that both could have a high level of complementarity.
4.1. Local Phase Quantization (LPQ)
Blurring in images can limit the analysis of texture information, and such degradation can happen for a number of reasons. Algorithms that enable image blur removal are computationally intensive and may introduce new artifacts, so algorithms that can analyze textures in a robust way are desired.
Ojansivu and Heikkila [3] proposed a texture descriptor insensitive to blur based on the quantized phase of the discrete Fourier transform, which is called Local Phase Quantization (LPQ). The information of the local phase of an image of size is given by the Short-Term Fourier Transform in Equation (1), being defined by the Equation (2), where and is a 2D frequency vector
Only four complex coefficients are considered in LPQ, which correspond to the 2D frequency , , , , where . The STFT (Equation (1)) is expressed using the vector described in Equation (3) with being the STFT basis vector at a frequency u and , a vector of size containing the values of the image pixels in the m × m neighborhood of x.
Here, is denoted as a matrix containing the neighborhood of all image pixels and , where and . and represent, respectively, the real and imaginary parts of a complex number, and the transformation matrix is given by .
Ojansivu and Heikkila [3] assume that the function of an image is the result of the first-order Markov process, where the correlation coefficient between two pixels and is exponentially related to their distance. The vector f is defined by a covariance matrix of size according to the Equation (4), and the covariance matrix of the Fourier coefficients can be obtained by . As long as D is not a diagonal matrix, the coefficients are correlated and may become not correlated through , where V is an orthogonal matrix derivative from the singular value decomposition (SVD) of a matrix D, which is .
The coefficients are quantized using Equation (5), in which are components of E. The coefficients are represented as integer values between 0 and 255 using the binary code obtained from Equation (6).
At last, a histogram of these integer values from all images positions is used to make a 256-dimensional feature vector used for classification. The pseudocode for LPQ is described in Algorithm 1.
| Algorithm 1: Pseudocode for LPQ based descriptors. |
|
4.2. Granulometry-Based Descriptors (GBD)
Mathematical Morphology (MM) is an algebraic theory that studies the decomposition of operators between complete lattices in terms of elementary operators (erosion and dilation) and operations (union, intersection and negation) [4,12]. It is a field of non-linear digital image processing tools, and it is widely applied to process and analyze topological and geometrical structures.
Two basic and important morphological operators are the openings and closings [4,5]. Openings are morphological filters with the following properties:
- increasingness: .
- idempotence: .
- anti-extensivity: .
Closings operators are also morphological filters which are increasing, idempotent and extensive ().
Considering images as a surface, an opening operator filters bright smaller peaks while maintaining the bigger ones. On the other hand, a closing operator sieves smaller darker valleys while preserving the bigger ones. Such removal depends on the type of the filter. For instance, structural openings remove peaks where a structuring element can not be fit [6]. More, the higher the size of the structuring element, the higher the amount of filtered structures.
This paper uses three types of openings:
Definition 1
(Structural opening). Let f be an image. Let B be a structuring element [12]. The structural opening [4,5] is given by
where and are, respectively, the dilation and erosion of f by a structuring element B [12].
Definition 2
(Opening by reconstruction). Let f be an image. Let B be a structuring element. Let be a structuring element that denotes connectivity [13]. The opening by reconstruction is given by
where is the morphological reconstruction of g from f [5].
Definition 3
(Area opening). Let f be an image. Let . The graylevel area opening [14] of parameter λ is given by
where is the threshold of f with parameter h [14]. In this paper, for simplicity, the graylevel area opening will be called area opening.
This paper also uses three types of closings:
Definition 4
(Structural closing). Let f be an image. Let B be a structuring element. The structural closing [4,5,12] is given by
Definition 5
(Closing by reconstruction). Let f be an image. Let B be a structuring element. Let be a structuring element denoting connectivity. The closing by reconstruction [13] is given by
where is the morphological dual reconstruction of g from f [13].
Definition 6
(Area closing). Let f be an image. Let . The graylevel area closing [14] of parameter λ is given by
where is the negation of f [4]. Again, for simplicity, the graylevel area closing will be called area closing.
Figure 3 shows a detailed view of the pixels affected by application of two morphological filters, an opening by reconstruction and a closing by reconstruction. In each case, the affected pixels are highlighted in green.
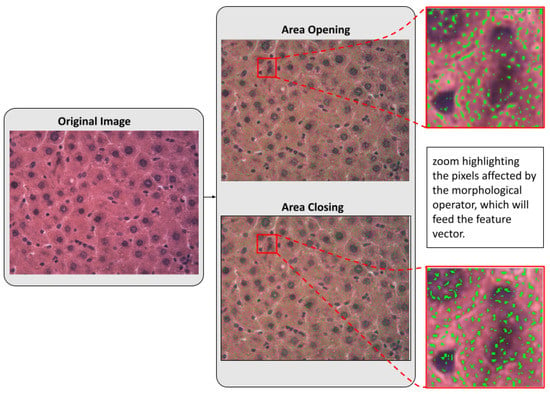
Figure 3.
Pixels affected by application of a opening by reconstruction and of a closing by reconstruction, using a disk structuring element with radius one.
Definition 7
(Granulometry). A granulometry [4,5] is a family of openings , which has the following property:
Definition 8
(Anti-granulometry). An anti-granulometry is given by a family of closings , such that
(In this paper, for simplicity, all granulometries and anti-granulometries will be called granulometry.)
Let be a granulometry. In the granulometric analysis, the amount of sieved structures by is computed for each increment of . Let be the size distribution of such that , is the amount of sieved structures by [5]. Note that since increases as is incremented, is an increasing function.
Definition 9
(Opening Top-Hat). Let f be an image. The opening top-hat is given by
Definition 10
(Closing Top-Hat). Let f be an image. The closing top-hat is given by
Note that the opening top-hat and closing top-hat are residual operators, which gives the sieved structures (the residue) by application of their respective morphological filters.
Let be a granulometry. Let be the sum of all intensities from an image f. The size distribution of is given by,
In this measurement, gives the sum of the volumes of all structures sieved by .
Let be the binarization function, which is given by
Let be a granulometry. The binary size distribution is given by
In this measurement, gives the number of pixels of all structures sieved by .
Each one of the GBD assessed in this work is built as described in Algorithm 2.
| Algorithm 2: Pseudocode for Granulometry-Based Descriptors. |
|
Table 2 summarizes the set of twelve GBD tested in this work. Figure 4 illustrates the construction of a size distribution from a granulometry given by a family of openings by reconstruction. For each , a disk structuring element of radius was used by the filter . The residue of such a filter is summed and taken as the -th component of the feature vector.

Table 2.
Granulometry-based descriptors.
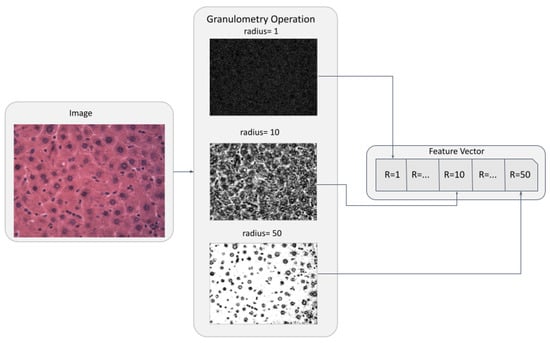
Figure 4.
GBD generated by an opening by reconstruction. A disk-structuring element with radius was used for each .
Figure 5 and Figure 6 show two sets of binary size distributions computed for each image from the dataset introduced in Section 3. In this example, 120 binary size distributions were computed: the blue curves are related to control images; the red ones are related to the Walker 256 tumor images.
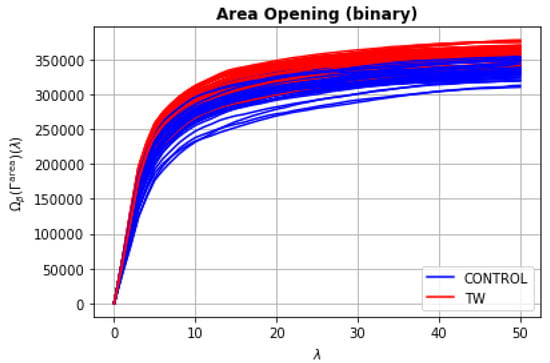
Figure 5.
Binary size distributions from an area opening granulometry, . One size distribution was computed for each image from the dataset introduced in Section 3.
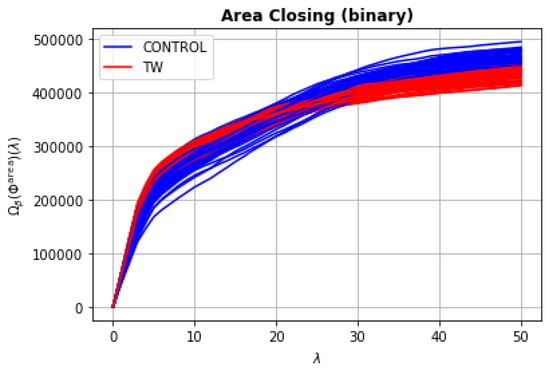
Figure 6.
Binary size distributions from an area closing granulometry, . One size distribution was computed for each image from the dataset introduced in Section 3.
5. Methodology Used For Classification
In this work, we have chosen three of the most popular classifiers algorithms frequently used in different classification scenarios. Figure 7 illustrates the general overview of the methodology used for classification.
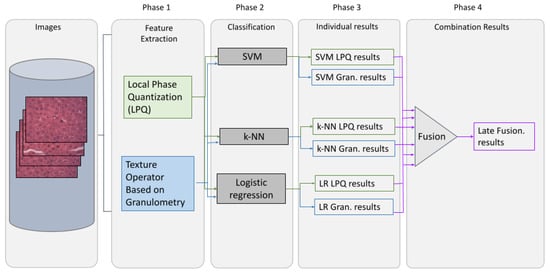
Figure 7.
General overview of the methodology used for classification.
As we can see, in phase 1, the extraction of the handcrafted features is performed. The texture operators used are those already described in Section 4. Next, in phase 2, the classification is carried out using one of the three classifiers described in this section. In phase 3, the results are evaluated considering each possible combination in isolation. Finally, in phase 4, the fusions combining the outputs of the classifiers with the best individual performances are evaluated, using late fusion strategies (i.e., max rule, sum rule and product rule) proposed by Kittler et al. [15]. Equations (17)–(19) describe the mathematical details behind the max, product and sum combinations rules, respectively. In these equations, x is the pattern to be classified, c is the number of classes involved in the problem, n is the number of classifiers involved in the combination, represents a class, with , and is the probability that x belongs to the class according to the classifier i.
Three classifiers’ algorithms were applied in this work: Support Vector Machines (SVM), K-Nearest Neighbor and Logistic Regression.
SVM: Support Vector Machine (SVM) was first proposed by Vladmir Vapnik [16]. The SVM algorithm is able to perform the classification by determining a hyperplane that best separates the classes in the training data [17]. In this work, we used the Gaussian kernel, and cost and gamma parameters were tuned using a grid search.
k-NN: k-NN is an instance-based algorithm widely used for classification. The K-Nearest Neighbor algorithm for binary classifications is considered simple when compared to other machine learning algorithms [18]. Despite its simplicity, k-NN is still one of the top 10 classification algorithms in machine learning [19]. This simplicity lies in the fact that it assumes all instances as points in the dimensional space and uses a distance metric (e.g., the Euclidean distance is frequently used in this case) to decide whether the element belongs to class A or class B [18,20]. In the experiments, various numbers of neighbors were tested, and k = 5 was chosen as it performed better than the other odd values.
Logistic Regression: Logistic Regression is a special case of Regression [21]. Logistic Regression uses the following equation:
in which and are associated with every independent variable and are calculated by the likelihood method based on the dataset. Reglog is a statistical technique that establishes a relationship between the variable of interest and the probability of the outcome occurring; this probability has the value of success (1) and failure (0) [21]. The values and assume the value that maximizes the probability of the observed sample [22].
The choice for shallow learning methods in this work is basically justified by the following aspects: (i) the number of samples available in the dataset is quite limited, which makes it not appropriate to be addressed using deep learning methods; (ii) the accuracy rates achieved using handcrafted features and shallow learning proved to be suitable to address the problem both in terms of accuracy and computational time.
6. Experimental Results and Discussion
In this section, we describe the results obtained using the LPQ descriptor, the GBD and the late fusion between them. As there were six animals per class (i.e., control and TW), we decided to organize the data making cross-validation such a way one subject per class was taken to compose the test set for each round of training.
Let us call the six control subjects , , , , and and the six subjects affected by Walker tumor , , , , and . One control subject and one TW subject were separated to be tested on a model trained using all the remaining subjects. For example, in the first round, was tested on a model trained using . On the second round, was used for the test, and so on, characterizing a six-fold cross-validation. This strategy was used to avoid the presence of samples taken from the same subject both on test and training sets simultaneously, which could introduce a bias on the classifier.
6.1. Results Obtained Using LPQ
Table 3 presents the accuracies found using SVM, k-NN and Logistic Regression classifiers, fed by the LPQ feature vector. Window sizes 3, 5, 7 and 9 were experimented. The best results were achieved using the SVM classifier with features vectors built using window sizes 5, 7 and 9.

Table 3.
Classification accuracy using LPQ descriptor.
As we can see, an accuracy of 91.67% was achieved with , and ; with these results, we can now confirm our first research question (RQ1), that it is possible to perform cancer identification exploring a spectral-based texture descriptor on microphotographs of rat liver.
6.2. Results Obtained Using GBD
Table 4 and Table 5 present the accuracies obtained using SVM, k-NN and Logistic Regression classifiers, trained with the feature vectors created using the GBD described in Section 6.2. The tables are divided according to the descriptor obtained by the closing and opening morphological operations. Table 4 represents, respectively, Area Closing (AC), Area Closing Binary (BinAC), Structural Closing (SC), Structural Closing Binary (BinSC), Reconstruction Closing (RC) and Reconstruction Closing Binary (BinRC). Table 5 represents, respectively, Area Opening (AO), Area Opening Binary (BinAO), Structural Opening (SO), Structural Opening Binary (BinSO), Reconstruction Opening (RO) and Reconstruction Opening Binary (BinRO).

Table 4.
Classification accuracy using closing vectors.

Table 5.
Classification accuracy using opening vectors.
The accuracies achieved with the vectors extracted using the Closing operation, as shown in Table 4, in almost all classifiers are superior to the accuracies achieved with the Opening vectors, as shown in Table 5. It is noticeable that the Area Closing Binary (BinAC) achieved the best results when compared to other morphological filters, reaching the 96.67% mark using SVM and 95.83% using k-NN () classifier.
The Reconstruction Opening (RO) vector, as shown in Table 5, obtained the lowest accuracies in all experiments, 50.83%, with the Logistic Regression classifier.
The results obtained using vectors obtained by the granulometry operations were very divergent; AC, BinAC and BinSC performed even better than LPQ, and others such as SO and RO obtained very poor results. Concerning our RQ2, we can conclude it is possible to perform cancer identification exploring some granulometry filters described in Section 4, but not all of them.
6.3. Results Obtained Using Late Fusion strategies
Finally, aiming to achieve better results, the sum, max and product combination rules were employed as a late fusion strategy. In all cases, the sum rule obtained the best results. Due to this, we decided to describe in Table 6 only the results obtained with this rule. The results described were obtained combining the three classifiers chosen among those with the best performance in the experiments described previously.

Table 6.
Accuracies obtained with late fusion combinations.
The best overall results obtained in this work, i.e., 99.16% of accuracy, were obtained in two different scenarios. The first one occurred in the combination between –SVM, BinAC–5-NN and BinSC–Reg. It is worth mentioning that in isolation, these classifiers had reached, respectively, 91.67%, 95.83% and 92.50%, as can be seen in the first section of Table 6.
The second scenario in which the best rate was obtained happened when the classifiers –SVM, AC–SVM and BinAC–5-NN were combined. In isolation, these classifiers had reached, respectively, 91.67%, 95.00% and 95.83%, as can be seen in the second section of Table 6.
An accuracy of 98.33% was reached by combining –SVM, AC–SVM and BinSC–SVM. In isolation, these classifiers had reached, respectively, 91.67%, 95.00% and 82.50%, as can be seen in the third section of Table 6.
6.4. Discussions
Aiming to check whether or not there is a statistical difference between the best results obtained using LPQ, Opening Vectors, Closing Vectors, and the best late fusion result, we performed the Friedman statistical test.
The Friedman test was made using the accuracies obtained by the Late Fusion (–SVM, BinAC–5-NN and BinSC–Reg), BinAC–SVM, BinAO–SVM and –SVM classifiers. The accuracies were computed over each folder, as described in the beginning of Section 6. The test presented a p-value of 0.0299; considering = 0.05, we can conclude that the performance of the classifiers are not all equivalent to each other.
Furthermore, the selected classifiers were ranked according to their accuracies, as can be seen in Table 7. As a result, the superior performance of the Late Fusion technique is attested.

Table 7.
Classifiers ranking.
In respect to RQ3, we can conclude that classifiers built with LPQ and GBD presented a good level of complementarity to each other. As a consequence of this complementarity, the late fusion obtained the best overall results reported in this work.
7. Concluding Remarks
We proposed a method for cancer identification exploring texture properties taken from microphotographs of rat liver. For this, we used the LPQ spectral texture operator, a widely used descriptor, especially when the images may be affected by blur, a noise that typically occurs in images such as those used in this work. We also experimented with GBD, and lastly, we investigated the complementarity between classifiers created in both scenarios by using late fusion strategies.
Experiments performed on a dataset created by researchers from Enteric Neural Plasticity Laboratory of the State University of Maringá confirm the efficiency of the proposed strategies in isolation. In addition, we noticed an important level of complementarity between the classifiers created using both descriptors experimented. The best result obtained using LPQ was 91.16% of accuracy. In this way, it is possible to state that cancer can be identified in the Walker 256 tumor model using the LPQ texture operator with reasonably good rates, answering RQ1. For GBD, the best result obtained was 96.67% of accuracy, which responds positively to RQ2. Finally, the best overall result was obtained combining classifiers created using both LPQ and GBD descriptors, achieving 99.16% of accuracy. Thus, we can state that RQ3 was also positively answered.
Finally, we make a brief comment regarding the main limitation of this work. As happens in several works that deal with biomedical images, the main difficulty faced here refers to the limited size of the dataset, which makes it more difficult to create a more robust model and to make comparisons. Aiming to mitigate this issue, we performed the Friedman statistical test, and we confirmed that there is a meaningful difference between the results obtained by combining both strategies investigated here and the results obtained by each strategy in isolation.
As future work, we intend to expand our investigations using an additional dataset currently under development. This dataset is also being created by researchers from Enteric Neural Plasticity Laboratory of the State University of Maringá. In this new version of the dataset, two new classes will be included: treated control and treated Walker 256 tumor. Other tests using granulometry, such as pattern spectrum and others, are also planned to be made.
Author Contributions
Conceptualization, M.F.T.C., S.A.S.J., F.C.F., J.V.C.M.P., J.N.Z. and Y.M.G.C.; Data curation, C.C.O.B.; Funding acquisition, Y.M.G.C.; Investigation, M.F.T.C., S.A.S.J. and F.C.F.; Methodology, M.F.T.C., S.A.S.J., F.C.F. and Y.M.G.C.; Project administration, F.C.F. and Y.M.G.C.; Supervision, F.C.F. and Y.M.G.C.; Validation, M.F.T.C., S.A.S.J., C.C.O.B., F.C.F., J.V.C.M.P. and Y.M.G.C.; Visualization, J.N.Z.; Writing—original draft, M.F.T.C., S.A.S.J., F.C.F. and Y.M.G.C.; Writing—review and editing, M.F.T.C., S.A.S.J., F.C.F., J.V.C.M.P., J.N.Z. and Y.M.G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been partly supported by the Brazilian agencies National Council for Scientific and Technological Development (CNPq) and Coordination for the Improvement of Higher Education Personnel (CAPES).
Institutional Review Board Statement
Ethical review and approval were waived for this study due to the use of rats during the image acquisition phase of the dataset construction. The study follows the ethical principles under the terms set out in the Brazilian federal Law 11,794 (October 2008) and the Decree 66,689 (July 2009) established by the Brazilian Society of Science on Laboratory Animals (SBCAL). All the proceedings were submitted and approved by the Standing Committee on Ethics in Animals Experimentation of the State University of Maringá under Protocol number 8617130120.
Informed Consent Statement
Not applicable.
Data Availability Statement
The dataset used in this study will be made available in due course on GitHub at: https://github.com/Sersasj/Liver_Dataset (accessed on 1 April 2022).
Acknowledgments
We thank the support of the Enteric Neural Plasticity Laboratory and Intelligent Interactive Systems Laboratory of the State University of Maringá. We also thank the Brazilian agencies National Council for Scientific and Technological Development (CNPq), and Coordination for the Improvement of Higher Education Personnel (CAPES).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AC | Area Closing |
| AO | Area Opening |
| BinAC | Area Closing (binary) |
| BinAO | Area Opening (binary) |
| BinRC | Closing by Reconstruction (binary) |
| BinSC | Structural Closing (binary) |
| BinSO | Structural Opening (binary) |
| BinRO | Opening by Reconstruction (binary) |
| C | Control group |
| GBD | Granulometry-Based Descriptors |
| k-NN | k-Nearest Neighbor |
| LPQ | Local Phase Quantization |
| MM | Mathematical Morphology |
| RGB | Red, Green and Blue color space |
| RC | Closing by Reconstruction |
| RQ | Research Question |
| RO | Opening by Reconstruction |
| SC | Structural Closing |
| SE | Structuring Element |
| SO | Structural Opening |
| STFT | Shor-Time Fourier Transform |
| SVM | Support Vector Machine |
| TW | Walker 256 Tumor |
References
- Ferlay, J.; Ervik, M.; Lam, F.; Colombet, M.; Mery, L.; Piñeros, M.; Znaor, A.; Soerjomataram, I.; Bray, F. Global Cancer Observatory: Cancer Today; International Agency for Research on Cancer: Lyon, France, 2018; pp. 1–6. [Google Scholar]
- Felipe, G.Z.; Zanoni, J.N.; Sehaber-Sierakowski, C.C.; Bossolani, G.D.; Souza, S.R.; Flores, F.C.; Oliveira, L.E.; Pereira, R.M.; Costa, Y.M. Automatic chronic degenerative diseases identification using enteric nervous system images. Neural Comput. Appl. 2021, 33, 15373–15395. [Google Scholar] [CrossRef]
- Ojansivu, V.; Heikkilä, J. Blur insensitive texture classification using local phase quantization. In International Conference on Image and Signal Processing; Springer: Berlin/Heidelberg, Germany, 2008; pp. 236–243. [Google Scholar]
- Najman, L.; Talbot, H. Mathematical Morphology: From Theory to Applications; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Dougherty, E.R.; Lotufo, R.A. Hands-On Morphological Image Processing; SPIE Press: Bellingham, WA, USA, 2003; Volume 59. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing; Prentice Hall: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- De Matos, J.; Ataky, S.T.M.; de Souza Britto, A.; Soares de Oliveira, L.E.; Lameiras Koerich, A. Machine learning methods for histopathological image analysis: A review. Electronics 2021, 10, 562. [Google Scholar] [CrossRef]
- Nativ, N.I.; Chen, A.I.; Yarmush, G.; Henry, S.D.; Lefkowitch, J.H.; Klein, K.M.; Maguire, T.J.; Schloss, R.; Guarrera, J.V.; Berthiaume, F.; et al. Automated image analysis method for detecting and quantifying macrovesicular steatosis in hematoxylin and eosin–stained histology images of human livers. Liver Transplant. 2014, 20, 228–236. [Google Scholar] [CrossRef] [PubMed]
- Shi, P.; Chen, J.; Lin, J.; Zhang, L. High-throughput fat quantifications of hematoxylin-eosin stained liver histopathological images based on pixel-wise clustering. Sci. China Inf. Sci. 2017, 60, 092108. [Google Scholar] [CrossRef]
- Thiran, J.P.; Macq, B. Morphological feature extraction for the classification of digital images of cancerous tissues. IEEE Trans. Biomed. Eng. 1996, 43, 1011–1020. [Google Scholar] [CrossRef] [PubMed]
- Bernardo, C.C.O. Effect of supplementation with l-glutationa 1% on the liver of wistar rats implanted with walker’s tumor 256. Master’s Thesis, Maringá State University, Maringá, Brazil, 2021. [Google Scholar]
- Haralick, R.M.; Sternberg, S.R.; Zhuang, X. Image analysis using mathematical morphology. In IEEE Transactions on Pattern Analysis and Machine Intelligence; IEEE: Piscataway, NJ, USA, 1987; pp. 532–550. [Google Scholar]
- Vincent, L. Morphological grayscale reconstruction in image analysis: Applications and efficient algorithms. IEEE Trans. Image Process. 1993, 2, 176–201. [Google Scholar] [CrossRef] [PubMed]
- Vincent, L. Grayscale area openings and closings, their efficient implementation and applications. In Proceedings of the First Workshop on Mathematical Morphology and Its Applications to Signal Processing, Barcelona, Spain, 10–14 May 1993; pp. 22–27. [Google Scholar]
- Kittler, J.; Hatef, M.; Duin, R.P.; Matas, J. On combining classifiers. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 226–239. [Google Scholar] [CrossRef]
- Vapnik Vladimir, N. The Nature of Statistical Learning Theory; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Kowalczyk, A. Support Vector Machine Succinctly; Syncfusion: Morrisville, NC, USA, 2017. [Google Scholar]
- Shalev-Shwartz, S. Understanding Machine Learning: From Theory to Algorithms; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
- Zhang, S. Cost-sensitive KNN classification. Neurocomputing 2020, 391, 234–242. [Google Scholar] [CrossRef]
- Mitchell, T.M. Machine Learning; MacGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Application in R; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).