Abstract
In this paper, we present the results of nonlinearity detection in Hedge Fund price returns. The main challenge is induced by the small length of the time series, since the return of this kind of asset is updated once a month. As usual, the nonlinearity of the return time series is a key point to accurately assess the risk of an asset, since the normality assumption is barely encountered in financial data. The basic idea to overcome the hypothesis testing lack of robustness on small time series is to merge several hypothesis tests to improve the final decision (i.e., the return time series is linear or not). Several aspects on the index/decision fusion, such as the fusion topology, as well as the shared information by several hypothesis tests, have to be carefully investigated to design a robust decision process. This designed decision rule is applied to two databases of Hedge Fund price return (TASS and SP). In particular, the linearity assumption is generally accepted for the factorial model. However, funds having detected nonlinearity in their returns are generally correlated with exchange rates. Since exchange rates nonlinearly evolve, the nonlinearity is explained by this risk factor and not by a nonlinear dependence on the risk factors.
1. Introduction
Hedge Funds (HFs) have generated a lot of curiosity and have introduced a lot of questions [1,2,3,4,5,6,7,8,9,10], first due to their performance (sometimes negative) with respect to usual markets and second to their very particular and complex financial nature. Usual classifications of HFs [11,12] are based either on a particular goal or mechanism, i.e., they are directional, (Fixed Income, Hedge/Non Hedge Equity) or on the assets on which they are applied, i.e., they are non-directional (Macro, Distressed Securities, Commodities Trading Advisor). The manager behavior (trend follower or not) is another feature that has some effects on the HF returns. Due to the out performance, we can question the validity of the simple factorial model,
where is the HF price returns, the risk free return and a market risk factor. conveys the skill of the HF manager to generate profits, are the regression (loading) coefficients on the risk factor and the idiosyncratic risk or the error term or residuals. This model is widely accepted, in particular, for mutual funds and has been straightforwardly extended to HFs with the idea that coefficient are close to 0 ([9]; although, in this paper, only 22% of the funds statistically verify this property, see also [8]). However, mutual funds of assets are obviously linked to the market risk factors, while HF may have fairly different mechanisms to generate profits as stated above. In particular, in some of them, leverage mechanisms are used to outperform the other funds as previously stated [5]. In this case, we can question whether the linear dependence on the risk factors is still valid. In fact, the modeling of Equation (1), is the corner stone to analyze the fund performance (either mutual or hedge), for deriving the skill of the fund manager (i.e., ) or to estimate the exposure to a given risk factor. The risk factors are generally a priori identified and depend on the authors and their number varying from 7 (the well admitted proposal of [2]) to 31 (the return explanation by a given risk factor is generally not verified through conditional independence testing [13] or Bayesian network [14] for instance). The idea of this paper is to propose a method to directly classify HFs according to their price return (i.e., their performance) model. When observing a time series (TS, in our case, the HF price returns), a natural idea is to determine the equations governing this TS (quantitative model). Amin and Kat [15], Leland [16], Kosowki et al. [4], Lo [10], and Agarwal [17] have noticed that the HF price returns exhibit non-Gaussian skewness and kurtosis. Usually, non-Gaussian statistics are thought to be generated by some nonlinearities [10].
- For instance, Leland [16] proposes a price return model based on the nonlinear payoff model developed by Dybvig [18,19] but without statistical validation of this model.
- Patton proposed in [9] an extension of Equation (1) by adding powered risk factors.
- Patton and Ramadorai [8] and Lo [10] proposed a model with a loading factor having different values depending on the risk factor (i.e., and, thus nonlinearly, depends on ), the simplest loading function being a threshold model. This threshold model possibly conveys the less or more liquid periods [5].
- Similarly, Lo [10] proposed to add switching the random variable to the factorial model of Equation (1), this switching variable explains the phase locking behavior observed in crisis periods.
The idea of including nonlinear terms in Equation (1) is supported by the fact that usual risk factors have a normal distribution [17]. Thus, if the risk factors are normal (right side of Equation (1)) and the returns are non-normal (left side of Equation (1)), then a straightforward explanation is some nonlinearities. The main goal of this paper is to provide an algorithm to validate the linearity of the HF return model. The nonlinearity detection problem in an observed TS has led to the definition of several Hypothesis Testing (HT). In the signal processing community, tests based on the bispectrum have generated some interest (see [20,21,22,23]), and a comparison of the non parametric tests is given in [24]). In the econometric community, nonlinearity tests are generally based on linear/nonlinear parametric models. For both approaches, the detection of nonlinearity in HF price returns is a challenge since the return TS contain few samples, HF prices being generally updated once a month. Thus, a ten year record provides only 120 samples. In fact, the bispectrum (and its normalized version) is known to have a high variance and its estimate needs a fairly large number of samples to provide robust results. On the other hand, parametric tests are generally slightly more efficient for small TS length but they imply some underlying hypothesis on the model driving the TS under the null hypothesis. For instance, the models used in the parametric tests (AR-STAR) are infinite memory processes (i.e., the AutoCorrelation Function, ACF, has an infinite support), while the TS of asset returns, and in particular, HF returns, are finite memory. Moreover, the robustness of this last class of tests decreases when the model parameter number increases (as seen again below). Thus, a straightforward idea is to merge several HT to improve the detection. In order to expose the process of TS nonlinearity detection, the fusion algorithm and its application to HFs, we develop two points:
- The first is to expose the design of this HT fusion algorithm. Hypotheses have to be carefully defined and the fusion process carefully designed to avoid false conclusions on HT and fusion algorithm robustness, as previously stated. In particular, several points are generally overlooked in operational decisions, such as the pdf under the null hypothesis, key features in the decision process, or the information shared by several HT.
- The second aim of the paper is the application of the decision rule to detect nonlinearity in HF price returns. We first inspect whether there is a relationship with the a priori classification and the nonlinearity detection in two databases. These databases, respectively, provided by TASS and Standard and Poors (S&P), contain several styles of HFs and we seek to inspect whether some styles exhibit nonlinear feature, unlike the others.
All the fusion methods need a “learning” base on which some parameters of the fusion process have to be estimated (see [25]). A “validation” base is used to verify the efficiency of these estimated parameters over data not involved in their estimates. An underlying assumption made thorough this paper is that HF returns are stationary up to the third order (since all the HT need this assumption). Obviously, this assumption is questionable, but due to the dependence of each HT on a management style, as well as the low rate of price updating, it seems realistic (we discuss this point again in Section 4.2). To expose our results, the paper is organized as follows. In Section 2, we present the hypothesis definition, the robustness criterion and the 12 statistical indices used in the fusion process step, while the topology and fusion approaches are presented in Section 3. In Section 4, this decision rule is applied to detect nonlinearities in simulated TS and HF returns.
2. Nonlinearity Detection Hypothesis Testing
As many financial TS, HF price returns exhibit non-symmetrical statistics [15,26], a fairly common confusion is to relate the non-symmetry of the statistics to nonlinearity (see the tutorial [27] for the generation of a non-symmetrical distribution induced by the phase coupling due to nonlinear systems). We must point out that the linearity does not imply the gaussianity. When the input noise of the linear system is non-symmetrical, the output TS is also non-symmetrical, although linear. On the other hand, some nonlinear systems can exhibit statistics close to the normal ones (for instance, if we sum a large number of nonlinear terms, then the central limit theorem ensures that we have asymptotical normal statistics). The statistical “linear” modeling of a TS means that the estimated statistics of this TS can be modeled as those of the output of a linear system, the input data of which are not available (these conditions are usually assumed for predicting and modeling systems). Thus, the null and the alternative hypothesis can be written as:
- : The signal can be modeled as the output of a linear system driven by an iid (independent and identically distributed) non-symmetric random excitation.
- : The signal cannot be modeled as the output of a linear system driven by an iid non symmetric random excitation and we decide that the system is nonlinear (driven by a normal excitation). In this case, the input is assumed to be Gaussian, since considering other input statistics only involves an additional nonlinear transform.
For instance, has been identified as a possible factorial model in [8], when non-normal residuals are observed. On the other side, is suggested for the same factorial model in [17] when transforming normal statistics of the risk factors into non-normal statistics of the HF returns. In what follows, with a slight abuse of language, we use the term “linear” and “nonlinear” TS for the sake of simplicity. Moreover, the HT have been designed (or redesigned) in order to be right sided. In other words, a positive index q is derived from the observed TS. If q is below a threshold T, is accepted and then the decision, denoted u, is equal to 0 (or 1 otherwise). Similarly, the decision can also be made from the probability:
where (resp is the index pdf under hypothesis (resp ) if , then . Thus, three quantities can be merged from several HT as detailed in Section 2.2.
- The estimated index denoted of the jth HT.
- The probability , derived from the estimated index value and the pdf of the estimated probability under (see Equation (2)), denoted .
- The decision , provided by after fixing the threshold on the probability (i.e., fixing the p-value), this threshold/p-value being possibly different for each HT.
The first approach is the more straightforward, but induces merged quantities with very different ranges of values. The last two have the advantage of merging similar quantities (i.e., a probability in the range or binary quantities, the decision ), but they require perfectly knowing the statistical index under to derive these two quantities. A final decision based on each HT decision adds a hyperparameter, the threshold T/p-value, which can be HT dependent. In our case, the fusion algorithm depends on these two last quantities, leading to two fusion topologies, as seen in Section 3.1. In the next subsection, we inspect the robustness under .
2.1. Robustness
- The HT robustness involves correctly defining a performance metric for the HT (such a comparison has already been completed, see [24,28,29], but with non rigorous definition of the two hypotheses, as seen below). As usual, two types of error are possible, the TIEP (Type I Error Probability), denoted that is the probability of rejecting the null hypothesis although right; and the Type II Error Probability (TIIEP, i.e., the error of accepting the null hypothesis although false, denoted ). The usual HT decision making involves fixing , thus deriving threshold T using the index pdf function under and then comparing the index to this value, leading to the acceptance or rejection of . Admitting that the two errors have the same importance in the decision process, the mean Bayesian risk of the HT (see [25] chapter one) is equal to:This criterion is the parameter to minimize as the metric of performance in what follows.
- In order to rigorously estimate the HT robustness and derive the parameters needed for the HT fusion algorithm, TS under the two hypotheses have to be simulated. However, the (linear/nonlinear) TS sets have to be carefully designed. The nonlinear TS set can be derived from nonlinear models. In this paper and in [30], we consider three kinds of second-order nonlinear system:As usual, in TS modeling, the excitation is assumed to be iid white normal noise, while is assumed to convey the statistical properties of the observed TS. Volterra models (4a) are easily derived by nonlinear expansion for differentiable nonlinear transfer function and the ACF finite length model, unlike the other two (when the summation upper bounds are finite). There are necessary conditions for the stability of QARMA ((4c), Quadratic Autoregressive Moving Average Model, see [31,32,33]) or bilinear ((4b), see [34,35,36] for instance), extensively used in econometric TS modeling. A first inspection of the polynomial models of Equations (4a)–(4c) shows that these models contain two kernels, a first linear kernel and a quadratic one. Thus, for nonlinear systems, the excitation variance induces different weights of each (linear/quadratic) kernel and thus fairly different outputs. For instance, a weak variance induces a strong weight of the linear kernel output and thus an almost linear TS, making the nonlinearity detection fairly difficult. For this reason, the metric performance (Equation (3)) also depends on the NonLinear Energy Ratio (NLER, that is the energy from the quadratic kernel over the total energy). In what follows, we have considered NLER values of 0.25, 0.5 and 0.75 (i.e., weakly, fairly, strongly nonlinear systems).
- The system simulating the linear system (hypotheses ) also has to be carefully designed. In fact, for each generated output of nonlinear systems, the corresponding output linear system requires:
- 1.
- Having the same second order moment, i.e., the same ACF and then the same Power Spectrum Density (PSD). In fact, the second order moment has an effect on the variance of the estimated indices. Thus, after estimating the theoretical ACF/PDF by choosing one of the three models, initializing the model parameters and the excitation variance (see above), we derive the theoretical ACF of the output; this ACF is used to calculate the transfer function of the linear system. This requirement of having the same ACF under the two hypotheses is preserved by the surrogate data method (that can be seen as a Bootstrap method for nonlinearity detection, see [37,38,39,40]), used for deriving a linear TS, and then the index pdf under , from an observed and possibly nonlinear TS.
- 2.
- Being non Gaussian. In the previously mentioned papers on the HT robustness, the excitation is Gaussian under . Indeed, comparing a linear Gaussian TS and a skewed nonlinear TS induces a normality HT, which is much easier than a nonlinearity HT. The surrogate data method loosens this requirement (since the equivalent linear TS is normal) inducing an overperformance of the HT. The excitation, in the case, has to have a zero mean and a skewness, providing the same value of skewness for the linear/nonlinear TS.
Thus, the linear and nonlinear TS (i.e., the two hypotheses TS set) have the same ACF at all lags and the same third-order moment at lag (0,0), as seen below. - A last point is that the statistical index pdf derived on hypothesis is derived under the asymptotical assumption using the central limit theorem for instance. As observed in [30], for the HT presented below, we observe a strong departure between the statistical index pdf (under ) and the theoretical pdf, turning the decision, linear/nonlinear, non-robust. In order to make a robust decision, the pdf under has to derived for the learning base, as described in Section 4.1.
2.2. Tested Nonlinearity Hypothesis Tests
The twelve indices we tested (summed up in Table 1) were divided into two main classes, the parametric tests and the non-parametric ones. The non-parametric HT class can also be divided into the time domain test and Fourier domain test, as seen in the next section.

Table 1.
Indices and references.
2.2.1. Non-Parametric Fourier Domain Tests
Non-parametric tests of the Fourier domain are mainly based on the third-order moment and the bispectrum defined as:
is called a bifrequency, the skewness being derived from the third-order moment at lag . Under hypothesis , the bispectrum verifies:
Several tests have been proposed to test whether the modeling of the estimated bispectrum as the triple product of a linear transfer function is valid or not. Subba et al. [22] and Hinich [20] proposed two tests for nonlinearity detection based on the bicoherence (normalized bispectrum). However, these tests have been shown to not be very robust due to the bicoherence estimate variance. The problem of bispectrum estimates (and the phase unrolling for the biceptrum for the indices presented below) have been tackled in [24,46]. Nonredundant bispectrum support is depicted by the triangle in Figure 1, the symmetry relationships being given the aforementioned papers. Two indices are based upon the bispectrum:
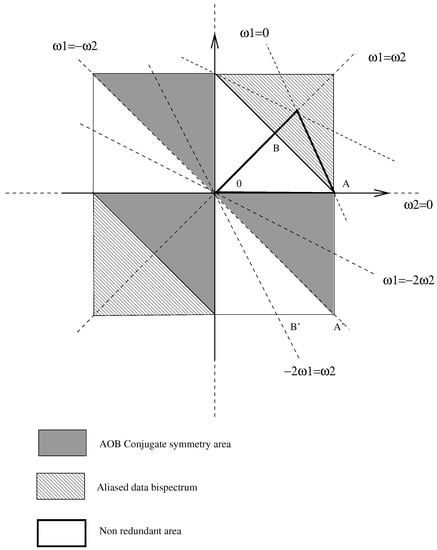
Figure 1.
Bispectrum support and symmetry.
- The first selected index was proposed by Erdem and Tekalp in [23] and uses the bicepstrum (defined as the inverse Fourier transform of the bispectrum logarithm), which has the property of being null outside the lines (see Equation (6)). In [24], Le Caillec and Garello derive an HT based on the test of the nullity of the bicepstrum components outside these three lines. This index is denoted in the latter part of the same paper.
- In the same paper, they propose another based on two relationships involving, respectively, the bispectrum phase (at different bifrequencies) and the bispectrum magnitude logarithm (also at different bifrequencies).where is the bispectrum phase and an arbitrary lag. These properties being verified for a linear TS, we then form two sets of variables from the relationship of Equation (7). The test estimates the two variables (for all the possible bifrequencies) linking the bispectrum phase and the log-magnitude in Equation (7). After normalization (in order to have a unit variance for both variables [24]), index is given by the interquartile of the concatenated variables.
2.2.2. Non-Parametric Time Domain Tests
In this class, we have also selected two indices:
- The idea developed by Hjellvik and Tjøstheim in [41] compares the best nonlinear predictor at lag k, i.e., the conditional mathematical expectation denoted with the best linear predictor, i.e., the value of the TS at lag k multiplied by the correlation coefficient with , with . This test estimates the conditional mean as well as the pdf of with a Kernel Density Estimate (KDE, i.e., a Regressogram/Nadaraya-Watson estimate). The final index is given by the mean square error between the best predictor (calculated with the estimated pdf). In the same article, the authors propose a similar test based on a parametric model as seen in Section 2.3.
- The last non parametric index, , was exposed in [40] by Paluš. It is given by the difference between the dimensional redundancy and the linear redundancy. The dimensional redundancy is defined as the entropy of the TS samples (multiplied by ) minus the joined entropy of adjacent TS samples. The linear redundancy is defined as half the difference of the sum of logarithms of the diagonal entries of the covariance matrix minus the sum of logarithms of the eigenvalues of the same covariance matrix. Under , these two quantities are equal (for practical decision we use the absolute value of the difference in order to have a right sided HT, as previously stated). The limiting parameter of this approach is the “embedding dimension” . In Section 4, we set as in [40].
2.3. Tests Based on Parametric Linear and Nonlinear Models
As stated in the introduction, the purpose of the parametric tests is first to identify a linear system and to test whether the residuals (denoted that is the difference between the predicted values by the estimated AR model and the real values or in others words an estimate of model excitation, see Equations (4a)–(4c)) contain nonlinear terms (with the underlying assumption that the identified linear model captures only the linear part, this being not so obvious, see [24,47] for a discussion). As usual, the aim of the tests is to verify that the residuals are white. For these tests, the AR model identification is assumed to be performed with a least squares solution (i.e., by solving the Yule–Walker equations). In many articles, the order of the AR model is assumed to be known. In practical situations of Section 4.1 and Section 4.2, the Bayesian Information Criterion (BIC) is applied to determine the order of the AR model (see [48] for the BIC and [49] for an exhaustive review of the order selection criteria). Several tests over the residual whiteness are proposed.
- Tsay index: In [29], Tsay improves a test proposed by Keenan [50] derived from the one-degree test (of additivity) by Tukey [51]. In this paper, we consider only the Tsay indices (F and C tests) since they provide slightly better results than Keenan’s indices. After the model identification and the residual estimation, we regress the TS squared samples over the TS samples at previous lags and we estimate the new residuals (obviously this step involves Higher Order Statistics, HOS, as explicitly mentioned in Keenan [50] and Section 2.2.1). The last step involves finding a correlation between the residuals of the TS fitting and the residuals of the squared TS fitting. If the TS is linear, then the two kinds of residuals are uncorrelated. This property is verified by using the F-distribution test. We denote this index in the rest of the paper. Due to bad results of a Volterra model, Tsay proposes a second test based on the correlation of the squared residuals with the TS samples. This test is the C test and is denoted in the latter part of this paper.
- Luukkonen et al. index. The test proposed by Luukkonen et al. is based on whether the TS can be modeled by a Smooth Transition AutoRegressive (STAR) model. By expanding the STAR model up to the third order, this model can be rewritten as a Nonlinear AutoRegressif model containing nonlinear terms , , and . The HT of nonlinearity is based on the test of the nullity of the nonlinear kernel coefficients. As for the Tsay index, the first step involves calculating the residual after regression of over an AR model and we denote , the sum of the squared residuals. Finally, the residuals are regressed (using a mean least squares criterion) on , , and , (then HOS are also involved in this step). The squared sum of these new residuals is denoted leading to the nonlinearity index , N being the TS length. This procedure being fairly complicated due the large number of parameters to be estimated, the authors propose a simpler test based on a reduced QARMA model (4b). In this test, the index is then given by where is the sum of the squared residuals of the nonlinear regression of over and (see [42]). Other nonlinear models are difficult to identify, in particular Volterra model, except in simplified cases such a Wiener and Hammerstein second-order models [52,53,54].
- BDS test: The idea developed by Brock et al. in [43], always verifies that the residuals are white, is close to Order Statistics (see [55]). They define the sequence The distance between two sequences is defined as The index is based on the number of sequences whose distance is below a given threshold Index is defined as the difference between the number of sequences of length m (with a distance below the threshold) with the number of sequences of length 1 powered at m (with a distance also below the threshold). This difference is normalized in order that the index has standard normal statistics. When the model is well fitted, the noise is iid and the index is close to 0. In this index, two parameters have to be fixed. The first is the sequence length m (if we choose m too small, then will be always close to 0 whatever the model is) and the second is the value of (in fact, if is too small, then the number of close sequences will not be large enough for a robust estimate of ). In Section 4, we test the values , and , , , with being the standard deviation of the residuals.
- Peña and Rodriguez test. Peña and Rodriguez in [44] propose a test based on the logarithm of the determinant of the correlation matrix of the squared residuals. In other words, we havewhere is the normalized correlation matrix of the squared residuals (the normalizing coefficient is and the size of this square matrix of dimension m, k being the lag of the correlation coefficient). The idea behind this test is to verify that the correlation matrix is diagonal (i.e., the residuals are white and then the model is well fitted). In this test, the parameter m has to be chosen. As proposed by the authors, m is determined by the greatest correlation length in the residual. This estimation of the correlation is performed as the MA order estimation described below.
- Hjellvik and Tjøstheim test on residuals. Always with the idea of comparing the best predictor and the linear predictor (see Section 2.2.2), Hjellvik and Tjøstheim compare the two predictors for the residuals (always under an AR model fitting). The idea behind this calculation is to find nonlinear terms in the residuals, as stated in the introduction to this section. In this case, the index is also defined as the mean square error between the two predictors.
- The main drawback of the previously presented approaches is to be based on an AR model and then they assumed that the process is infinite memory. In [45], we propose a HT based on an MA model (i.e., with finite ACF), that is of particular interest in our case since HF returns are assumed to verify this property of finite memory. The order of the MA process is to detect a lag above which the autocorrelation function is null. Such an order estimate can be performed either by a Ljung-Box test or with a Hotteling by estimating the correlation sequence over subsignals (in the results of Section 4, we use four sub signals). We estimate the MA parameters by a Giannakis’ formula since we have (see [56,57]). Unlike the AR model, MA are not necessarily invertible (the transfer function can vanish). Since the residual are not available as for the previous indices, we propose to verify that the estimated coefficients agree with the estimated ACF as:where is the estimated MA order, is the estimated second-order moment, is the MA coefficient estimated by a Giannakis’ formula and is estimated to minimize . When the TS is the output of a linear MA model, then is theoretically null, but non-null under , (see [45], for practical implementation).
As seen, all these HT are different, but they can share either an underlying modeling (e.g., AR) or statistical quantities (e.g., bispectrum) and the question of their redundancy/complementarity can be raised. We detail the fusion process in the next section, with firstly a discussion on the information redundancy between the HT.
3. HT Fusion Algorithms
Before presenting the tested approaches of fusion in the last section, we first focus on the topology of these fusion methods since according to the topology the shared information has to be included in the decision process.
3.1. Topology and Mutual Information
Basically, we distinguish three kinds of topology for the fusion algorithm:
- The first is to consider jointly the results of the HT (i.e., the probability ) and make a decision from all these values. Thus, we have to classify the TS (linear/nonlinear) with an array of probabilities. This topology is named centralized topology.
- In the second, each HT makes a decision, and the final decision is performed from these individual decisions. The classification is performed from an array of the decision. This framework is a parallel distributed decision.
- Finally, the last topology is called a serial (or sequential) distributed decision. Each detector can make a decision depending on the robustness of the decision, for instance. This approach can be interesting when all the HT do not have the same reliability using first the more robust and then the others if needed.
The topology is a key feature, in particular, for the redundancy borne by each index. In particular, the first two topologies pose the problem of the information shared by several entries. It is obvious that some HT share close information, all making a false decision on a TS; for instance, the final decision of the fusion would also be false if the information redundancy is not detected and processed. A fairly admitted quantity to estimate the shared information, under the two hypotheses, is the Mutual Information (MI) as:
where is the joint probability of and estimates and is the marginal pdf (same for ), see Section 2. In Section 4, we estimated the MI for the two hypotheses, all the lengths and all the systems according to the Ahmad entropy estimate ([13,58]).
3.2. Fusion Methods
In [30], we tested fusion rules. In what follows, we consider having selected some indices to perform the fusion (see Table 2). Obliviously, the selection is based on the HT robustness according to the estimated values of the criterion of Equation (3) over the learning base.
- Neural Network on probability and Entropy/Log-Probability (NN and NNL). The first two methods are based on Neural Networks (NNs). Details of the architecture are given in [30]. We use the learning base to train the NN and estimate the results on the validation base. The first NN has for input the probability for all the indices of Section 2, assuming that the NN discard the non-pertinent input (i.e., non robust HT, but also shared information in order to robustify the final decision), the output being 0 or 1 according to the hypothesis. For the same kind of NN, the same process is developed over the Log-Probability and then the NN input is the entropy. The idea being to ease the elimination of the shared information but possibly losing the robustness information borne by the probabilities.
- Maximum Likehood (ML). Obviously, since we have a labeled (linear/nonlinear) database, we can estimate the joint multivariate density pdf of all the probabilities and make the decision:In this case, the (resp. ) is the joint probability density of the , under (resp. ). The threshold is fixed according to value . This joint probability could be estimated either on all the HT or by only considering the more robust ones, as previously stated.
- Optimized Decision (OD). This approach [59] first concatenates the decision of each HT into an array , the final decision being made as:(resp. ) is the probability of under (resp. ). Thus, has possible values, n being the number of selected HT. One advantage of the approach is that it is set to different TIEP for each decision, but it needs an operational research of all the p-values to take into account, the possible correlation between the decisions, this optimization being performed over a predefined bounded grid.
- Decision with Security Offset (DSO). This approach needs first to rank the HT according to the performance over the learning based. The idea is to make this ranking using first the most robust HT, except when its decision is not sure, i.e., when the pdf at the estimated value is close to:When there is not a decision, the second-most robust test is tested. The process is repeated, in case of failure, until the less robust HT. If none of the HT can provide a “robust” decision, in the meaning of Equation (13), then the final decision is given by the more robust (i.e., first) HT. and are estimated over the learning basis, by an exhaustive search, in order to minimize .
- Maximum of Entropy (ME). One of the few papers [25,60], taking into account the MI between the indices in the final decision. This decision is given by:where and , and thus, is the entropy (i.e., the uncertainty) of the hypothesis conditionally to the final decision . Unlike the ML, the thresholds are given by the data according to their MI. However, the main difficulty is to estimate the coefficient since a recursive optimization process between the acceptation region and the estimate of this coefficient has to be performed ([30], Section 3 of [60], Chapter 7 [25]).
- Geometric Mean (GM). An ad-hoc approach is obviously to estimate a fused probability as the weighted geometric mean of the probability of each HT:In [30], it is shown that entropy of the weighted geometric mean is a linear combination of the entropy of each HT weighted by . These weights are obviously derived from the learning base by an optimization process, the decision being made on the value of p. As seen in the results of [30], the more robust is an HT, the higher is its weight; in some cases, a single HT can concentrate all the mass.

Table 2.
Tested methods of HT fusion.
Table 2.
Tested methods of HT fusion.
| Method | Type | Merged Quantity | Ref. |
|---|---|---|---|
| Neural networks on probability (NN) | Centralized | Probability | [61] |
| Neural networks on log-probability (NNL) | Centralized | Entropy | [61] |
| Maximum likehood (ML) | Centralized | Probability | [25] |
| Optimal decision (OD) | Parallel distributed | Decision | [59] |
| Decision with security offset (DSO) | Serial distributed | Probability | [25] |
| Maximum of entropy (ME) | Parallel distributed | Decision | [25,60] |
| Geometric mean (GM) | Centralized | Probability |
4. Results
Before presenting the main findings of this paper, the nonlinearity detection in HF returns, we briefly expose the results of [30].
4.1. Nonlinearity Detection in Small Simulated TS
As stated in the introduction, the first step is to generate the two bases for choosing the fusion algorithm. For this, for each basis, we generate 10 systems of each quadratic model of Equations (4a)–(4c), with randomly chosen parameters, under the stability constraint for the bilinear and QARMA models. The normal excitation variance is calculated for NLER equal to 0.25, 0.5, 0.75. For all 90 cases (30 nonlinear models and 3 NLER values), we generate one thousand trials of nonlinear TS and the corresponding linear TS (but also surrogate data as seen in [30]), over which the 12 indices have been estimated (in fact, using different hyperparameter values of some HT, or for instance, we have estimated 23 indices). This process has been repeated for the TS of length , 256, 512, 1024, 2048 and 4096 (under assessing the effect of the TS length on the HT performance), leading to more than 50 million index estimates. We have reproduced for each index in Table 3 and for the fusion methods in Table 4.

Table 3.
Mean (multiplied by ) for all models and all NLERs.

Table 4.
(multiplied by ) for all models and all NLERs for the different fusion methods, learning base (left) and test base (right).
- As stated in the Introduction, robustness for a small TS length (, see first line of Table 3) is generally weak. Two HT give fairly good results and . Indices , , and are less robust but not totally inefficient, unlike the remaining HT. As expected, the performance in the HT depends on the nonlinear system. For instance , and lead to fairly good decisions on QARMA models. outperforms the others for bilinear/Volterra models. Moreover, the NLER, as previously stated, interferes in the performance. Weakly nonlinear TS led to poor results, in particular, for all TS lengths. Other details, in particular, on the optimal hyperparameters are given in [30].
- Amazingly, the MI under the two hypotheses (see Tables 4 and 5 of [30]), does not make clusters appear inside the 12 HT, all the pairs of HT having the same MI level, even for the closest ones (e.g., and ). The only conclusions that we can draw from the MI estimates are: first, the MI increases with the TS length, the HT giving the same decision as they become more robust; second, the MI is slightly higher under , the HT giving a similar decision for nonlinear TS unlike the case.
- Obviously, for the selection of our fusion method, we mainly consider the results on the validation basis. In particular, even for NNs, we obtain the best results over the learning basis, while the DSO method gives the best results on the validation basis. The performance remains close for all TS lengths, except for the ML method that improves by passing from to . As seen, the input data is a key feature for neural networks, since the NN with entropy as input underperform the NN with probability as input; the reason being that the entropy is not discriminant, as seen in the previous point. As seen, the performance improvement is slight, passing from from 0.21 for alone to 0.18 for the DSO and as seen in [30] for , the decision is performed by the most robust HT, i.e., at the outset or at the outcome of the DSO process.
According the these results, considering the case and the ranked indices , , , , and , we perform the DSO method on the HF returns according to the parameters computed over the simulated TS. Obviously, we object that the possible nonlinearity of HF price returns is not necessarily a second-order model, as in Equations (4a)–(4c). However, since there no available nonlinear system models for HF returns, we can only consider these simple models. Moreover, these models are known to be able to mimic/approximate a lot of nonlinear systems [33,62].
4.2. Hedge Fund Nonlinearity
The decision rule on the nonlinearity has then been applied over two databases provided by TASS and S&P, the first one containing HF recorded from 1992 to 2003 (i.e., 132 samples), the second one 120 samples from 1996 to 2006. As stated in the introduction, the low number of samples makes the statistical decisions fairly difficult [5,9,63]. However, the statistical properties of HF returns are known to vary over time [8,9,63]. Then, largest return time series can violate the stationarity assumption needed for our tests (see Section 2). Only fully recorded TS have been considered in the results presented below. This induces a survivor bias, theoretically not relevant in our case, since we are not interested in the relative performance, but we discuss this point again below. Another bias can be relevant in the nonlinearity detection case. Since the HF prices are declarative, managers may smooth their returns [5] to reduce high returns for augmenting these returns when low or negative. This smoothing has been observed through serial correlation of the returns. Such “saturation” effects can induce nonlinearities. Results on the two HF bases are given in Table 5. Two main conclusions can be drawn from this table.

Table 5.
Classification of Hedge funds according to the decision rule of nonlinearity for the TASS base (second and third column) and the S&P base (fourth and fifth column).
- The first one is that the number of TS classified as nonlinear is much greater in the TASS base than in the S&P base. For instance, 53.9% are classified as nonlinear for the first HF base, but only 36.3% for the second one.
- According to Table 5, we can observe four situations:
- The HFs mostly classified as linear in the two bases. For instance, Event-driven, Emerging Market, Fixed Income and Distressed Securities.
- The HFs mostly classified as nonlinear in the two bases (for the reason exposed in the previous point, an equivalent number of linear/nonlinear HFs in the S& P base leads to a conclusion of nonlinearity detection). These nonlinear styles are Equity Hedge, Equity Non Hedge and Managed Future.
- The Hedge funds equivalently classified as nonlinear or linear in both bases. Four styles are in this category, Funds of Funds, Sector, Macro and Relative Values Arbitrage. As observed in [17], Macro has near normal statistics but are sometimes classified as nonlinear.
- The last family is that classified as nonlinear in a base and linear in the other one. These styles are Convertible arbitrage, Merger Arbitrage and Equity Market Neutral. For this last family no conclusion can be drawn.
For the first family of HFs, the factorial linear model is valid. Moreover, the evolution of the pertinent risk factors is also governed by a linear equation. For the second family, the linearity of the model is rejected. Two reasons can explain the nonlinearity in the HF price return. The first one is that the price return does not depend linearly on the risk factors. The second reason is that the risk factors are nonlinear TS. A first indication is given by observing that these three HF styles are negatively and strongly correlated with the exchange rate (see [64] chapter 11) with a coefficient correlation respectively equal to −0.14, −0.17, −0.15, but the exchange rates are known to nonlinearly evolve [65]. Thus, the nonlinearity detected for the family of funds is due to the risk factor and not to a nonlinearity in the factorial model. This point is confirmed by observing that the linear HFs do not depend on the exchange rate (correlation coefficients equal to −0.03, 0.03, 0.06). The exception is the Fixed Income style with a positive correlation coefficient of 0.15. In fact, Exchange rate has been pointed out as a leverage factor in some HFs (but not in all the cases, as detailed on the Quantum Georges Soros’ fund in [63]). Amazingly, the emerging market HFs are not classified as nonlinear, although the exchange rate is also assumed to be a key factor in these funds [63]. As also noted in this paper, this exposure depends on the level really invested in local currencies. The linearity of the emerging market HF price return is observed despite the turbulent times related to the multiple currency and financial crises (Mexican crisis of December 1994; Asian crisis since July 1997; Brazilian devaluation of January 1999; Turkish liquidity crises of 2000–2001…). The linearity is also declared for Exchange Rate HFs. A possible reason is that in these funds the nonlinearities between all the exchange rates can cancel each other out.
The third family can be explained by observing that the funds are very diversified and thus there can be a specific risk factor (on a specific sector of the HF for instance) that explains why some HF are classified as nonlinear and the others as linear. A final and global conclusion of this study is that the linear factorial model is generally validated. When nonlinearities are observed, they can be explained by the nonlinear evolution of a special risk factor (the exchange rate). This is in accordance with Patton’s observation [9] that the heavy tails of the market returns are uncorrelated with the heavy tail of HF returns leading to a conclusion that these heavy tails are due to a skewed idiosyncratic risk (downside risk aversion), and not to a common factor risk. As stated in this section, the survivor bias may also have a part explanation of the overall acceptance of a linear factorial model. We can assume that the HFs, for which the factorial model is nonlinear, have disappeared due to a higher risk exposure and only those with a linear factorial model have survived.
As stated in the introduction, except the parameter the parameter may vary [8] over time, and seems to be less informative in the HF case than the information ratio [4,17,66]. In particular, the estimated values of in Equation (1), after a regression of the HF returns over of the previously identified risk factors, can be impacted by residual nonlinearities (not removed by the linear regression see [32]). In fact, the question of determining the real value of is a key point of HF management, obviously for the overall HF performance and the manager’s skill evaluation, but, above all, for the level of fees claimed by the managers [67].
A last point for which the impact of nonlinearities has to be taken into account is the design of fund of HFs, as initially proposed by Brandt et al. [6,7] for mutual funds and extended to HFs by Joenväärä et al. [1]. In fact, this design/management is based over the regression/clustering of fund characteristics, the factorial model of Equation (1) being one of these characteristics. Thus, including nonlinear terms in the HF characteristics could improve the fund of HFs performance.
Finally, from an algorithmic point of view, due to the weak improvement of HT fusion for small time series, another method to perform the difficult task of nonlinearity detection in small time series could be the use of Long Short Time Memory neural networks. The basis to train the neural network could be the same as for estimating the fusion process parameters. A question is to possibly redesign the activation function to detect nonlinearity (i.e., phase coupling) instead of using well established functions as the Relu activation.
5. Conclusions
In this paper, we have presented several results. The first one is the robustness of HT for nonlinearity detection in small TS. The second result is a decision rule derived from the results of the robustness estimation step. The last point is the application of the decision rule to the HF price return. From the results of this last section, we have deduced that when nonlinearities are detected, they are due to the nonlinear evolution of a risk factor, the exchange rate, and not the nonlinearity in the factorial model, thus validating results previously derived under the linear factorial model.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
This study did not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Joenväärä, J.; Kaupplia, M.; Kahra, H. Hedge fund portfolio Selection with characteristics. J. Bank. Financ. 2021, 132, 106232. [Google Scholar] [CrossRef]
- Fung, W.; Hsieh, D. Hedge fund Benchmark: A risk based approach. Financ. Anal. J. 2004, 60, 63–80. [Google Scholar] [CrossRef]
- Fung, W.; Hsieh, D.; Naik, N.; Ramadorai, T. Hedge fund, Risk and Capital Formation. J. Financ. 2008, 63, 1777–1803. [Google Scholar] [CrossRef]
- Kosowski, R.; Naik, N.; Teo, M. Do the hedge funds deliver alpha? A Bayesian and bootstrap analysis. J. Financ. Econ. 2007, 84, 229–264. [Google Scholar] [CrossRef]
- Titman, S.; Tiu, C. Do the best Hedge Funds Hedge? Rev. Financ. Stud. 2011, 24, 123–168. [Google Scholar] [CrossRef]
- Brandt, M.; Santa-Clara, P.; Valkanov, R. Parametric portfolio policies: Exploiting characteristics in the cross-section of equity return. Rev. Financ. Stud. 2009, 22, 3411–3447. [Google Scholar] [CrossRef]
- Brandt, M.; Santa-Clara, P. Dynamic portfolio selection by augmenting the asset space. J. Financ. 2006, 61, 2187–2217. [Google Scholar] [CrossRef]
- Patton, A.; Ramadorai, T. On the High-Frequency Dynamics of Hedge Fund Risk exposures. J. Financ. 2013, LXVIII, 597–635. [Google Scholar] [CrossRef]
- Patton, A. Are “Market Neutral” Hedge Funds Really Market Neutral? Rev. Econ. Stud. 2009, 27, 2495–2530. [Google Scholar] [CrossRef]
- Lo, A. Risk management for Hedge Funds: Introduction and Overview. Financ. Anal. J. 2001, 57, 3731–3777. [Google Scholar] [CrossRef]
- Agarwal, V.; Naik, N. Multi-Period Performance Persistence Analysis of Hedge Funds. J. Financ. Quant. Anal. 2000, 35, 327–339. [Google Scholar] [CrossRef]
- Akermann, C.; McEnally, R.; Ravencraft, D. The performance of hedge funds: Risk, return and incentives. J. Financ. 1999, 54, 833–874. [Google Scholar] [CrossRef]
- Le Caillec, J.-M. Testing conditional independence to determine shared information in a data/signal fusion process. Signal Process. 2018, 143, 7–19. [Google Scholar] [CrossRef]
- Barber, D. Bayesian Reasoning and Machine Learning; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Amin, G.; Kat, H. Hedge Funds Performance 1990–2000: Do the “Money Machine” Really add values. J. Financ. Quant. Anal. 2003, 38, 251–274. [Google Scholar] [CrossRef]
- Leland, H. Beyond Mean-Variance: Risk and Performance Measures for Portfolios with Nonsymmetric Distribution; Working Paper; Haas School of Business: Berkely, CA, USA, 1999. [Google Scholar]
- Agarwal, V.; Naik, N. Performance Evaluation of Hedge Funds with Options-Based and By-and-Hold Strategies; Technical Report; Centre for Hedge Fund Research and Education: Londa, France, 2000. [Google Scholar]
- Dybvig, P. Distributional Analysis of Portfolio Choice. J. Bus. 1988, 61, 369–393. [Google Scholar] [CrossRef]
- Dybvig, P. Inefficient dynamic strategies or How to throw away a million dollars in the stock market. Rev. Financ. Stud. 1988, 1, 67–88. [Google Scholar] [CrossRef]
- Hinich, M. Testing For Gaussianity and linearity of a stationary time series. J. Time Ser. Anal. 1980, 3, 169–176. [Google Scholar] [CrossRef]
- Priestley, M. Non-Linear and Non Stationary Time Series Analysis; Academic Press, Harcourt Brace Jonavich: London, UK, 1988. [Google Scholar]
- Subba Rao, T.; Gabr, M. A test for linearity of time series analysis. J. Time Ser. Anal. 1982, 1, 145–158. [Google Scholar]
- Tekalp, A.; Erdem, A. Higher-Order Spectrum Factorization in One and Two Dimensions with Applications in Signal Modeling and Nonminimum Phase System Identification. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 1537–1549. [Google Scholar] [CrossRef]
- Le Caillec, J.-M.; Garello, R. Comparison of statistical indices using third order spectra for nonlinearity detection. Signal Process. 2004, 3, 499–525. [Google Scholar] [CrossRef]
- Varshney, P. Distributed Detection and Data Fusion; Springer: New York, NY, USA, 1997. [Google Scholar]
- Amenc, N.; Curtis, S.; Martellini, L. The Alpha and Omega of Hedge Fund Performance Measurement; Working Paper; Edhec Risk and Asset Management Research Center: Nice, France, 2003. [Google Scholar]
- Nikias, C.; Mendel, J. Signal Processing With Higher Order Spectra. IEEE Signal Mag. 1993, 10, 10–37. [Google Scholar] [CrossRef]
- Peña, D.; Rodriguez, J. Detecting nonlinearity in time series by model selection criteria. Int. J. Forecast. 2005, 21, 731–748. [Google Scholar] [CrossRef]
- Tsay, R. Nonlinearity Test for Time Series. Biometrika 1986, 73, 461–466. [Google Scholar] [CrossRef]
- Le Caillec, J.-M.; Montagner, J. Fusion of hypothesis testing for nonlinearity detection in small time series. Signal Process. 2013, 93, 1295–1307. [Google Scholar] [CrossRef]
- Chen, S.; Billings, S. Representation of non-linear systems: The NARMAX model. Int. J. Control 1989, 3, 1013–1032. [Google Scholar] [CrossRef]
- Le Caillec, J.-M.; Garello, R. Nonlinear system identification using autoregressive quadratic models. Signal Process. 2001, 81, 357–379. [Google Scholar] [CrossRef]
- Leontaritis, I.; Billings, S. Input-output parametric models for nonlinear systems part II: Stochastic nonlinear model. Int. J. Control 1985, 329–344. [Google Scholar] [CrossRef]
- Brillinger, D. A study of Second and Third-Order Spectral procedures and maximum likehood in the identification of a Bilinear system. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1238–1245. [Google Scholar] [CrossRef]
- Lee, J.; Mathews, V. A stability condition for certain bilinear systems. IEEE Trans. Signal Process. 1994, 42, 1871–1873. [Google Scholar]
- Mohler, R. Bilinear Control Processes; Academic: New York, NY, USA, 1973. [Google Scholar]
- Schreiber, T.; Schmitz, A. Improved Surrogate Data for Nonlinearity Tests. Phys. Rev. Lett. 1996, 77, 635–638. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Surrogate time series. Physica D 2000, 142, 346–382. [Google Scholar] [CrossRef]
- Theiler, J.; Eubank, S.; Longtin, A.; Galdrikian, B.; Farmer, J. Testing for nonlinearity in time series: The method of surrogate data. Physica D 1992, 58, 77–94. [Google Scholar] [CrossRef]
- Paluš, M. Testing for nonlinearity using redundancies: Quantitative and qualitative aspects. Physica D 1995, 80, 186–205. [Google Scholar] [CrossRef]
- Hjellvik, V.; Tjøstheim, D. Nonparametric tests of linearity for time series. Biometrika 1995, 82, 351–368. [Google Scholar] [CrossRef]
- Luukkonen, R.; Saikkonen, P.; Teräsvirta, T. Testing Linearity Againt Smooth Transition Autoregressive Models. Biometrika 1988, 75, 491–499. [Google Scholar] [CrossRef]
- Brock, W.; Dechert, W.; Scheinkman, J.; LeBaron, B. A Test for independence based on the correlation dimension. Econom. Rev. 1996, 15, 197–235. [Google Scholar] [CrossRef]
- Peña, D.; Rodriguez, J. The log of the determinant of the autocorrelation matrix for testing goodness of fit in time series. J. Stat. Plan. Inference 2006, 8, 2706–2718. [Google Scholar] [CrossRef]
- Le Caillec, J.-M. Hypothesis testing for nonlinearity detection based on an MA model. IEEE Trans. Signal Process. 2008, 56, 816–821. [Google Scholar] [CrossRef]
- Le Caillec, J.-M.; Garello, R. Asymptotic bias and variance of conventional bispectrum estimates for 2-D signals. Multidimens. Syst. Signal Process. 2005, 10, 49–84. [Google Scholar] [CrossRef]
- Bondon, P.; Benidir, M.; Picinbono, B. Polyspectrum modeling Using Linear or Quadratic Filters. IEEE Trans. Signal Process. 1993, 41, 692–702. [Google Scholar] [CrossRef][Green Version]
- Djurić, P. Asymptotic MAP Criteria for model selection. IEEE Trans. Signal Process. 1998, 46, 2726–2734. [Google Scholar] [CrossRef]
- Stoica, P.; Selén, Y. A review of information criterion rules. IEEE Signal Process. Mag. 2004, 21, 36–42. [Google Scholar] [CrossRef]
- Keenan, D.M. A Tukey Nonadditivity-Type Test for Times Series Nonlinearity. Biometrika 1985, 72, 39–44. [Google Scholar] [CrossRef]
- Tukey, J. One degree of freedom for non-additivity. Biometrics 1949, 5, 232–242. [Google Scholar] [CrossRef]
- Le Caillec, J.-M. Time series nonlinearity modeling: A Giannakis formula type approach. Signal Process. 2003, 83, 1759–1788. [Google Scholar] [CrossRef]
- Le Caillec, J.-M. Time Series Modeling by a Second-Order Hammerstein System. IEEE Signal Process. 2008, 56, 96–110. [Google Scholar] [CrossRef]
- Le Caillec, J.-M. Spectral inversion of second order Volterra models based on the blind identification of Wiener models. Signal Process. 2011, 91, 2541–2555. [Google Scholar] [CrossRef]
- David, H. Order Statistics, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1981. [Google Scholar]
- Giannakis, G. Cumulants: A Powerful Tool in Signal processing. Proc. IEEE 1987, 75, 1333–1334. [Google Scholar] [CrossRef]
- Giannakis, G.; Swami, A. On Estimating Non-causal Non-minimum Phase ARMA Models of Non Gaussian Processes. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 478–495. [Google Scholar] [CrossRef]
- Ahmad, I.; Lin, P. A non parametric estimation of the entropy for absolutely continuous distributions. IEEE Trans. Inf. Theory 1976, 22, 372–375. [Google Scholar] [CrossRef]
- Drakopoulos, E.; Lee, C. Optimum multisensor Fusion of Correlated Local Decisions. IEEE Trans. Aerosp. Electron. Syst. 1991, 27, 593–606. [Google Scholar] [CrossRef]
- Pomorski, D. Entropy based optimization for binary detection networks. In Proceedings of the 3rd International Conference on Information Fusion, Paris, France, 10–13 July 2000; Volume II, pp. ThC4–ThC10. [Google Scholar]
- Cybenko, G. Approximations by superpositions of sigmoidal functions. Math. Control Signals, Syst. 1989, 4, 303–314. [Google Scholar] [CrossRef]
- Schetzen, J. The Volterra and Wiener Theories of Nonlinear Systems; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Brealey, R.; Kaplanis, E. Changes in the Factor Exposure of Hedge Funds; Technical Report; London School of Business: London, UK, 2001. [Google Scholar]
- Amenc, N.; Bonnet, S.; Henry, G.; Martellini, L.; Weytens, A. La Gestion Alternative; Economica: Paris, France, 2004. [Google Scholar]
- Sarantis, N. Modeling nonlinearities in real effective exchange rate. J. Int. Money Financ. 1999, 18, 27–45. [Google Scholar] [CrossRef]
- Brown, S.; Goetzmann, W.; Ibbotson, R. Offshore Hedge Funds: Survival and Performance 1989–1995. J. Bus. 1999, 72, 91–117. [Google Scholar] [CrossRef]
- Hutchinson, M.C.; Nguyen, M.H.Q.; Mulcahy, M. Private Hedge fund firm’ incentive and performance: Evidence from audited filings. Eur. J. Financ. 2022, 28, 291–306. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).