Abstract
For the feature selection problem, we propose an efficient privacy-preserving algorithm. Let D, F, and C be data, feature, and class sets, respectively, where the feature value and the class label are given for each and . For a triple , the feature selection problem is to find a consistent and minimal subset , where ‘consistent’ means that, for any , if for , and ‘minimal’ means that any proper subset of is no longer consistent. On distributed datasets, we consider feature selection as a privacy-preserving problem: assume that semi-honest parties and have their own personal and . The goal is to solve the feature selection problem for without sacrificing their privacy. In this paper, we propose a secure and efficient algorithm based on fully homomorphic encryption, and we implement our algorithm to show its effectiveness for various practical data. The proposed algorithm is the first one that can directly simulate the CWC (Combination of Weakest Components) algorithm on ciphertext, which is one of the best performers for the feature selection problem on the plaintext.
1. Introduction
1.1. Motivation
This study proposes a secure feature selection protocol that works effectively as a preprocessor for traditional machine learning (ML). Let us consider a scenario where different data owners are interested in private ML model training (e.g., logistic regression [], SVM [,], and decision tree [,]) on their combined data. There is a large advantage to securely training these ML models on distributed data due to competitive advantage or privacy regulations. Feature selection is the problem of finding a subset of relevant features for model training. Using well-chosen features can lead to more accurate models, as well as speedup during model training [].
Consider a data set D associated with a feature set F and a class variable C, where all feature values and the corresponding class label are defined for each datum . In Table 1, for example, we show a concrete example. Given a triple , the feature selection problem is to find a minimal that is relevant to the class C. The relevance of is evaluated, for example, by , which measures the mutual information between and C. On the other hand, is minimal, if any proper subset of is no longer consistent.

Table 1.
An example dataset shown in [].
To the best of our knowledge, the most common method for identifying favorable features is to choose features that show higher relevance in some statistical measures. Individual feature relevance can be estimated using statistical measures such as mutual information and Bayesian risk. For example, at the bottom row of Table 1, the mutual information score of each feature to class labels is described. We can see that is more important than , because . and of Table 1 will be chosen to explain C based on the mutual information score. However, a closer examination of D reveals that and cannot uniquely determine C. In fact, we find and with and but . On the other hand, we can see that and uniquely determine C using the formula while . As a result, the traditional method based on individual feature relevance scores misses the correct answer.
Thus, we concentrate on the concept of consistency: is considered to be consistent if, for any , for all implies . In machine learning research, consistency-based feature selection has received a lot of attention [,,,,]. CWC (Combination of Weakest Components) [] is the simplest of such consistency-based feature selection algorithms, and even though CWC uses the most rigorous measure, it shows one of the best performances in terms of accuracy as well as computational speed compared to other methods []. Throughout the proposed secure protocol, none of the parties learns the values of the data as all computations are done over ciphertexts. Next, the parties train an ML model over the pre-processed data using existing privacy-preserving training protocols (e.g., logistic regression training [] and decision tree []). Finally, they can disclose the trained model for common use.
To design a secure protocol for feature selection, we focus on the framework of homomorphic encryption. Given a public key encryption scheme E, let denote a ciphertext of integer m; if can be computed from and without decrypting them, then E is said to be additive homomorphic, and if can also be computed, then E is said to be fully homomorphic. Furthermore, modern public key encryption must be probabilistic: when the same message m is encrypted multiple times, the encryption algorithm produces different ciphertexts of .
Various homomorphic encryption schemes have been proposed to satisfy these homomorphic properties over the last two decades. The first additive homomorphic encryption was proposed by Paillier []. Somewhat homomorphic encryption that allows a sufficient number of additions and a limited number of multiplications has also been proposed [,,], and we can use these cryptosystems to compute more difficult problems, such as the inner product of two vectors. Gentry [] proposed the first fully homomorphic encryption (FHE) with an unlimited number of additions and multiplications, and since then, useful libraries for fully homomorphic encryption have been developed, particularly for bitwise operations and floating-point operations. TFHE [,] is known as the fastest fully homomorphic encryption that is optimized for bitwise operations.
For the private feature selection problem, we use TFHE to design and implement our algorithm. In this case, we assume two semi-honest parties and : each party complies with the protocol but tries to infer as much as possible about the secret from the information obtained. The parties have their own private data and and they jointly compute advantageous features for while maintaining their privacy. The goal is to jointly compute the CWC algorithm result on without revealing any other information.
In this paper, we describe the simplest case where there are two data owners, and they perform the cooperative secure computation. More generally, there are many data owners, and they encrypt with their own public keys. Since homomorphic operations cannot be applied to two data encrypted with different public keys, a simple approach would be for the server to attempt to re-encrypt them with some common public key. However, there is no guarantee that the server or the new public key can be trusted. To solve this problem, the framework of multi-key homomorphic encryption was proposed. This allows FHE operations on data encrypted with different keys, i.e., we can extend the two-party computation model to a more general case because TFHE has the required property. Using this property, its application to the framework of oblivious neural network inference [] has been proposed.
This should be a realistic requirement, if one wants to draw some conclusions from data that are privately distributed over more than one party. Multi-party computation (MPC) can provide effective technical solutions to realize this requirement in many cases. In MPC, certain computations that essentially rely on the distributed data are performed through cooperation among the parties. In particular, fully homomorphic encryption (FHE) is one of the critical tools of MPC. One of the most significant advantages of FHE-based MPC is thought to be that FHE realizes outsourced computation in a simple and straightforward manner: parties encrypt their private data with their public keys and send the encrypted data to a single trusted party with sufficient computational power to perform the required computation; although the computational results of the trusted party may be incorrect, if some malicious parties send incorrect data, honest parties are at least convinced that their private data have not been stolen as far as the cryptosystem used is secure. In contrast, when a party shares his/her secret with other parties to perform MPC, even if it uses a secure secret sharing scheme, collusion of a sufficient number of compromised parties may reveal the party’s secret. In general, it is difficult to prove the security of MPC protocols for the situation where we cannot deny the existence of active malicious parties, and hence, the security is very often proven assuming that all the parties are at worst semi-honest. In reality, however, even this relaxed assumption is unable to hold. Thus, the property that a party can protect its private data only relying on its own efforts should be counted as an important advantage of FHE-based MPC.
On the other hand, the current implementations of FHE are thought to be significantly inefficient, and consequently, their ranges of application are actually limited. This is currently true, but may not be true in the future: the Goldwasser–Mmicali (GM) cryptosystem [] is considered as the first scheme with provable security. Unfortunately, because the GM cryptosystem encrypts data in a bitwise manner, it has turned out not to have sufficient efficiency in time and memory to be used in the real world. In 2001, however, RSA-OAEP was finally proven to have both provable security and realistic efficiency [,], and is widely used through SSL/TLS. Thus, studying FHE-based MPC does not merely have theoretical meaning, but also will yield significant contributions in terms of application to the real world in the future.
In this paper, we propose an MPC protocol which relies on FHE-based outsourced computation as well as mutual cooperation among parties. The target of our protocol is to perform the computation of CWC, a feature selection algorithm known to be accurate and efficient, preserving the privacy of the participating parties. If we fully perform CWC by FHE-based outsourced computation, we have to pay unnecessarily large costs in time in the phase of sorting the features of CWC. Therefore, in our proposed scheme, we add ingenuity so that two parties cooperate with each other to sort the features efficiently.
Converting CWC into its privacy-preserving version based on different primitives of MPC—for example, based on secret sharing techniques—is not only interesting but also useful both in theory and in practice. We will pursue this direction as well in our future work.
1.2. Our Contribution and Related Work
Table 2 summarizes the complexities of the proposed algorithms in comparison to the original CWC on plaintext. The baseline is a naive algorithm that can simulate the original CWC [] over ciphertext using TFHE operations. The bottleneck of private feature selection exists in the sorting task over ciphertext, as we mention in the related work below. Our main contribution is the improved algorithm, shown as ‘improved’, which significantly reduces the time complexity caused by the sorting task. We also implement the improved algorithm and demonstrate its efficiency through experiments in comparison to the baseline.

Table 2.
Time and space complexities of the baseline and improved algorithms for secure CWC, where k is the number of features and are the numbers of positive and negative data, respectively. We assume that the time of the respective operation (e.g., encryption/addition/multiplication/comparison) in FHE is .
There are mainly two private computation models, secret sharing-based MPC and public key-based MPC, and secret sharing-based MPC currently has an advantage. On the other hand, we focus on the convenience of FHE. Public key-based MPC can establish a simple mechanism to obtain results while keeping the learning model possessed by the server and the personal information of many data owners confidential from each other, relying only on cryptographic strength. The secret sharing-based MPC is faster but requires at least two trusted parties that do not collude with each other, which creates a different problem to cryptographic strength.
Other drawbacks of public key-based MPC are its security against the chosen plaintext attack (CPA) and computational cost. TFHE is, however, computationally secure against the chosen ciphertext attack (CCA), which assumes a stronger adversary than CPA so that an attacker cannot obtain meaningful information from plaintext or ciphertext within polynomial time.
In this section, we discuss related work on private feature selection as well as the benefits of our method. Rao [] et al. proposed a homomorphic encryption-based private feature selection algorithm. Their protocol allows the additive homomorphic property only, which invariably leaks statistical information about the data. Anaraki and Samet [] proposed a different method based on the rough set theory, but their method suffers from the same limitations as Rao et al., and neither method has been implemented. Banerjee et al. [], and Sheikhalishahi and Martinellil [] have proposed MPC-based algorithms that guarantee security by decomposing the plaintext into shares, as a different approach to the private feature selection, while achieving cooperative computation. Li et al. [] improved the MPC protocol on the aforementioned flaw and demonstrated its effectiveness through experiments.
These methods avoid partial decoding under the assumption that the mean of feature values provides a good criterion for feature selection. This assumption, however, is heavily dependent on data. The most important task in general feature selection is feature value-based sorting, and CWC and its variants [,,] demonstrated the effectiveness of sorting with the consistency measure and its superiority over other methods. On ciphertext, this study realizes the sorting-based feature selection algorithm (e.g., CWC).
We focus on the learning decision tree by MPC [] as another study that employs sorting for private ML, where the sorting is limited to the comparison of N values of fixed length in time by a sorting network. In the case of CWC, however, the algorithm must sort N data points, each of which has a variable length of up to M, so a naive method requires time. Our algorithm reduces this complexity to , which is significantly smaller than the naive algorithm depending on M and N. Through experiments, we confirm this for various data, including real datasets for ML.
Although sorting itself is not ML, a fast-sorting algorithm is an important preprocess for ML model training. In the previous result [], it was shown that sorting-based feature selection can classify with higher accuracy than other heuristic methods. Furthermore, preprocessing by sorting has proven to be an important task in decision tree model training []. On the other hand, it is also well known that sorting can speed up ML model training. For example, in SVM, which is widely used in text classification and pattern recognition, the problem of finding the convex hull of n points in Euclidean space can be reduced from to time by preprocessing it with an appropriate sorting algorithm.
2. Preliminaries
2.1. Consistency Measure
First of all, we review the notion of the consistency measure employed in our problem. A consistency measure for a feature set F is a function to represent how far the data deviate from a consistent state and is required to satisfy determinisity ( if and only if F is consistent) and monotonicity ( implies ). The following consistency measures satisfy this requirement.
- , F is consistent; 1, otherwise (binary consistency [])
- (ICR [])
- (rough set [])
- (inconsistent pair [])
The fully homomorphic encryption used in this study is specialized for binary operations. Therefore, among these consistency measures, we employ .
2.2. CWC Algorithm over Plaintext
We generally assume that the dataset D associated with F and C contains no errors, i.e., if for all i, . When D contains such errors, they are removed beforehand and D contains not more than one with the same feature values.
In Algorithm 1, we describe the original algorithm for finding a minimal consistent feature for two-class data. Given D with and , a datum of is referred to as a positive datum and of is referred to as a negative datum. Let n represent the number of positive data and . We consider two-dimensional bit array such that, for any and , if and otherwise, where is the p-th positive datum and is the q-th negative datum . means that is not consistent with the pair because despite . Recall that is said to be consistent only if implies for any . As a result, is defined to be the number of 1s in .
For a subset , is said to be consistent, if for any and , there exists i such that and hold. CWC uses this to remove irrelevant features from F in order to build a minimal consistent feature set. We note that finding the smallest consistent feature set is clearly NP-hard. There is a simple reduction from the minimum set cover to this problem as follows: given with the intention that is regarded as in CWC, covering any element of S corresponds to the condition that for any , there exists at least one i such that .
Since the point of is that it contains information, for every pair of data across different classes, whether is consistent with the pair or not, it can be easily extended to multi-class data that have more than two classes. Although we focus on two-class data for the sake of simplicity, for multi-class data, the -factors in the complexities are replaced with the number of pairs of data across different classes, which is upper bounded by . Moreover, in extending to multi-class data, it is convenient to consider as an appropriately serialized one-dimensional bit string because there is no way to represent it as a dense two-dimensional bit array. Hence, in what follows, we treat as a bit string.
| Algorithm 1 The algorithm CWC for plaintext |
|
Table 3 shows an example of D, and Table 4 shows the corresponding . Consider the behavior of CWC in this case. All are computed as preprocessing. Then, the features are sorted by the order and . By the consistency order , CWC checks whether can be removed from the current F. Using the consistency measure, CWC removes and and the resulting is the output. In fact, we can predict the class of x by the logical operation .

Table 3.
An example dataset D with and . The data consist of two positive data and five negative data .

Table 4.
The bit string for the example dataset D of Table 3. Each column is 0 if . For example, because only for the two pairs and .
2.3. Security Model
2.3.1. Indistinguishable Random Variables
Let denote the set of natural numbers. A function is called negligible, if . Let and be sequences of random variables such that and are defined over the same sample space. We say that X and Y are indistinguishable, denoted by , if, and only if, is a negligible function.
2.3.2. Security of Multi-Party Computation (MPC)
Although the discussion of this section can be extended to MPC schemes which involve more than two parties, merely for simplicity, we focus on the case where only two parties are involved.
A two-party protocol is a pair of PPT Turing machines with input and random tapes. Let be an input of and be an output of , respectively.
We assume a semi-honest adversary and consider a protocol , replacing in by , where takes as input and apparently follows the protocol. Let denote the random variable representing the output of , and we define the class .
On the other hand, let denote the functionality that the protocol is trying to realize, i.e., is a PPT that simulates the honest so that . Here, we assume a completely reliable third party, denoted by . In this ideal world, for this and any adversary acting as with input , possibly , we define the random variable , where denotes the i-th component of the output of for . Similarly, we denote the class .
Using such random variables, we define the security of protocol as follows.
Definition 1.
It is said that a protocol Π securely realizes a functionality if, for any attacker against Π, there exists an adversary , and holds.
The definitions stated above can be intuitively explained as follows. Exactly conforming to the protocol, a semi-honest adversary plays the role of to steal any secrets. The information sources which can take advantage of are the following three:
- 1.
- the input tape to ;
- 2.
- the conversation with ;
- 3.
- the execution of the protocol.
While the information that can obtain from the first and third sources is exactly and , respectively, we call the information from the second source a view.
To denote it, we use the symbol .
Since the protocol inevitably requires that obtains the information of and , the security of the protocol questions what can obtain, in addition to what can be computationally inferred from and . If there exists such information, its source must be .
The security criterion of simulatability requires that can be simulated on the input of and . In more formal terms, there exists a PPT Turing machine Sim that outputs a view on the input of and such that the output view cannot be distinguished from by any PPT Turing machine. When is simulatable, we see that Sim can generate by itself what Sim can obtain from . Therefore, Sim cannot cannot obtain any information in addition to what Sim can compute from and .
2.3.3. IND-CPA
Indistinguishability against chosen plaintext attack (IND-CPA) is an important criterion for the secrecy of a public key cryptosystem. We let denote a public key cryptosystem consisting of key generation, encryption, and decryption algorithms. To describe IND-CPA, we introduce the IND-CPA game played between an adversary and an oracle : is a PPT Turing machine, and k is the security parameter.
- 1.
- generates a public key pair .
- 2.
- generates two messages of the same length arbitrarily and throws a query to .
- 3.
- On receipt of , selects uniformly at random, computes , and replies to with c.
- 4.
- guesses on b by examining c and outputs the guess bit .
We view b and as random variables whose underlying probability space is defined to represent the choices of the public key pair, b and . The advantage of the adversary is defined as follows to represent the advantage of over tossing a fair coin to guess ’s secret b:
when we let
We have
This definition of the advantage is consistent with the common definition found in many textbooks:
Definition 2.
A public key cryptosystem Π is secure in the sense of IND-CPA, or simply IND-CPA secure, if as a function in k is a negligible function.
2.4. TFHE: A Faster Fully Homomorphic Encryption
The proposed private feature selection is based on FHE. We review the TFHE [], one of the fastest libraries for bitwise addition (this means XOR ‘⊕’) and bitwise multiplication (AND ‘·’) over ciphertext. On TFHE, any integer is encrypted bitwise: For ℓ-bit integer , we denote its bitwise encryption by , for short. These bitwise operations are denoted by and for and the ciphertexts and . The same symbol is used to represent an encrypted array. For example, when x and y are integers of length ℓ and , respectively, denotes
TFHE allows all arithmetic and logical operations via the elementary operations and . In this section, we will consider how to build the adder and comparison operations. Let represent ℓ-bit integers and represent the i-th bit of , respectively. Let represent the i-th carry-in bit and is the i-th bit of the sum . Then, we can obtain by the bitwise operations of ciphertexts using and . We can construct other operations such as subtraction, multiplication, and division based on the adder. For example, is obtained by , where is the bit complement of y obtained by for all i-th bits. On the other hand, we examine the comparison. We want to obtain without decrypting x and y where if and otherwise. We can obtain the logical bit for as the most significant bit of over ciphertexts here. Similarly, for the equality test, we can compute the encrypted bit .
Adopting these operations of TFHE, we design a secure multi-party CWC. In this paper, we omit the details of TFHE (see, e.g., [,]).
We should note that the secrecy of TFHE definitely impacts the security of our scheme. In fact, in our two-party feature selection scheme, the party B sends his/her inputs in an encrypted form to the party A, and A performs the computation of feature selection on the encrypted inputs. If the encrypted inputs could be easily infiltrated, any ingenious devices to secure the scheme would be meaningless.
Therefore, in designing our scheme, it was a matter of course to require our FHE cryptosystem to be IND-CPA secure. In fact, TFHE is known to be IND-CPA secure. Regarding this, we should note the following:
- By definition, encryption with an ID-CPA cryptosystem is probabilistic. That is, the result of encryption unpredictably differs every time the encryption is performed. For this reason, by , we denote a ciphertext generated at time t. In particular, the notation of means that the ciphertext has been generated at a time different from any other encryption events.
- When we consider the IND-CPA security of an FHE cryptosystem, we should note that the way in which the oracle generates c with is not unique. For example, the oracle may compute c from two ciphertexts of additive shares of , say and , by . The IND-CPA security of an FHE cryptosystem should require that cannot guess b with effective advantage, no matter how c has been generated. This, however, holds, if the result of performing and distributes uniformly, and TFHE is known to satisfy this condition.
3. Algorithms
3.1. Baseline Algorithm
We present the baseline algorithm, a privacy-preserving variant of CWC. In this subsection, we consider a two-party protocol, in which a party has its private data and outsources CWC computation to another party , where this protocol can be extended to more than two data owners using the multi-key homomorphic encryption []. During the computation, party should not gain other information than the number n of positive data, the number m of negative data, and the number k of features. It should be noted that party can hide the actual number of data by inserting dummy data and telling the inflated numbers n and m. Dummy data can be distinguished by adding an extra bit that indicates that the datum is a dummy if the bit is 1. The values of features and dummy bits of data in each class are encrypted by ’s public key and sent to .
The baseline algorithm consists of three tasks: computing encrypted bit string , sorting s, and executing feature selection on s. In the baseline algorithm, all inputs are encrypted and they are not decrypted until the computation is completed. Thus, for simplicity, we omit the notation E in the following presentation.
3.1.1. Computing
We can compute by , where and represent the dummy bits for data and , respectively. becomes 0 if is inconsistent for the pair of and . Since we want to ignore the influence of dummy data, the part ‘’ is added to make the whole value 1 (meaning that it is consistent) when one of and is a dummy. It takes time and space in total.
3.1.2. Sorting s
We can compute in encrypted form by summing up the values in in time (noting that each operation on integers of bits takes time). Instead, we can set an upper bound of the bits used to store the consistency measure to reduce the time complexity to .
Then, sorting s in the incremental order of consistency measures can be accomplished using any sorting network in which comparison and swap are performed in encrypted form, without leaking information about feature ordering. It should be noted that in this approach, the algorithm must spend time to swap (or pretend to swap) two-bit strings and original feature indices of bits regardless of whether the two features are actually swapped or not. Because this is the most complex part of our baseline algorithm, we will demonstrate how to improve it. Using an AKS sorting network [] of size , the total time for sorting s is .
In our experiments, we employ a more practical sorting network of Batcher’s odd-even mergesort [] of size . A simple oblivious radix sort [] in the algorithm under the assumption that the bit length of each integer is constant was recently proposed.
3.1.3. Selecting Features
Let be the sorted list of features. We first compute a sequence of bit strings of length each such that for any and ; namely, is the bit array storing the cumulative or each position h for . Note that indicates that the set of features is inconsistent with regard to a pair satisfying , and is inconsistent if and only if the bit string contains 0. See Table 5 for Zs in our running example. The computation requires time and space.

Table 5.
Sorted s for the example dataset D of Table 3 and the corresponding s.
We simulate Algorithm 1 on encrypted s and Zs for feature selection. Furthermore, we use two 0-initialized bit arrays, R of length k and S of length . is meant to store 1 if the i-th feature (in sorted order) is selected. S is used to keep track of the cumulative or for the bit strings of the currently selected features. Namely, is set to if ℓ features have been selected at this time.
Assume that we are in the i-th iteration of the loop of Algorithm 1. Note that, at this time, F contains features and currently selected features, and is consistent if is 1. Because we keep in F if is inconsistent, the algorithm sets . After computing , we can correctly update S by for every in time. Therefore, the total computational time is .
3.1.4. Summing Up Analysis
The sorting step takes time. Because CWC works with any consistent measure, we do not need to use in full accuracy, so we assume that is set to be constant. Under the assumption, we obtain the following theorem.
Theorem 1.
For the two-party feature selection problem, we can securely simulate CWC in time and space without revealing the private data of the parties under the assumption that TFHE is secure.
Proof.
According to the discussion above, computing for all features takes time and space, sorting features takes time, and selecting features takes time.
Finally, party computes in time an integer array P with , which stores the original indices of selected features. In the outsourcing scenario, party simply sends P to party as the result of CWC. In the joint computing scenario, party randomly shuffles P to conceal to . As a result, we can securely simulate CWC in time and space. □
3.2. Improvement of Secure CWC
Sorting is a major bottleneck for private CWC. The reason for this is that pointers cannot be moved across ciphertexts. For example, consider the case of a secure integer. Let the variables x and y contain integers a and b, respectively. In this case, by performing the secure operation , the result is obtained as . Using this logical bit c, we can swap the values of x and y in time, satisfying by the secure operation and .
In the case of CWC, however, each integer i of feature is associated with the bit string . Since any x cannot be decrypted, we cannot swap the pointers appropriately. Therefore, the baseline algorithm swaps explicitly. As a result, the computation time for sorting increases to . Our main contribution is to improve this complexity to by reducing the cost for such explicit sorting.
Based on the FHE, we propose the improved secure CWC (Algorithm 2), which reduces the time complexity to . An example run of Algorithm 2 is illustrated in Figure 1. As shown in this example, the party can securely sort k randomized features in time using a suitable sorting network, and then, according to the result of sorting, swaps each associated bit string of length in time. Following this preprocessing, the parties securely obtain minimal consistent features by decrypting the output of CWC. Finally, we have the following result.
| Algorithm 2 Improved secure CWC between parties and |
|
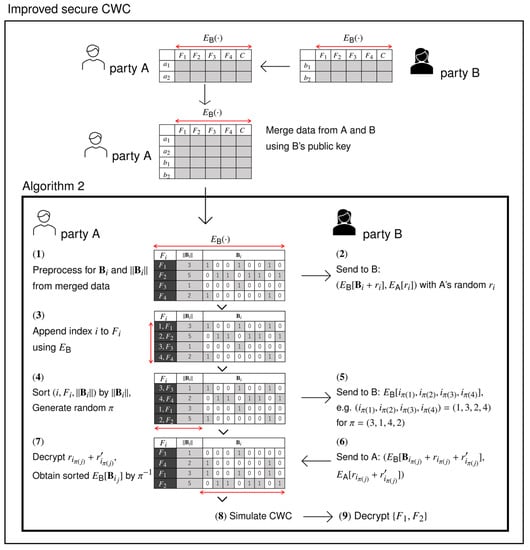
Figure 1.
An example run of Algorithm 2. For simplicity, we omit the clock time in each ciphertext. (1): Parties and jointly compute and for each feature (same as the baseline algorithm). (2): securely sends ; cannot learn anything. (3): appends encrypted index i for each . (4): sorts only by . (5): sends the sorted indices with random permutation; cannot learn anything. (6): sends ; cannot learn anything from it. (7): decrypts the noise and obtains the correct order of ; cannot learn anything. (8): simulates CWC the same as the baseline. (9): Party share the resulting features.
Theorem 2.
Algorithm 2 can simulate CWC in time and space under the assumption that FHE executes each bit operation in time.
Proof.
Compared to the baseline, additional space is required for and and . Thus, the space complexity remains . For the time complexity, the main task is to sort k-triple in the increasing order of . The improved algorithm sorts only the pairs of integers, where the size of is bits. For each , we can check if in time and we can swap them in time using homomorphic operations in FHE. It follows that the time for sorting all is time. After sorting the pairs, the algorithm moves all to the correct positions according to the rank of . This cost is . Therefore, time complexity is . □
Theorem 3.
Algorithm 2 is secure under the assumption that the employed FHE is IND-CPA secure.
Proof.
We show the security by constructing simulators for parties and , respectively.
’s view (what can obtain from ) is the following:
- for ;
- .
Their probability distributions are uniform and independent of each other. Hence, the simulator for can replace them with
- for and , which are selected uniformly at random;
- for , which is selected uniformly at random.
Note that, even if an adversary knows , it is computationally impossible to distinguish between and by the IND-CPA security of the cryptosystem .
Next, we construct a simulator Sim for the party . Although what can obtain from is
this is equivalent to after decryption and permutation.
On the other hand, the sequence is not explicitly given to , and recognizes it through the alignment between
- and
- .
Therefore, we define ’s view to be
with .
On the other hand, we define the view that should generate as follows. While can generate with , needs ’s cooperation to generate . Without ’s cooperation, selects uniformly at random, and generates its own view to be
Sim can compute from and taking advantage of the homomorphic property of the encryption system .
Furthermore, we define a distinguisher as a PPT Turing machine that tries to distinguish between and on the input of
When we let and , the advantage of is defined as .
We show that, if ’s advantage is not negligible, we can construct a PPT attacker that can break the IND-CPA security of the encryption system with a non-negligible advantage. Our attacker plays the IND-CPA game, exploiting an oracle as follows:
- 1.
- generates with ;
- 2.
- lets and and throws a query to ;
- 3.
- selects uniformly at random and sends to ;
- 4.
- initializes by inputting ;
- 5.
- First query. throws to the query: ;
- 6.
- If replies with , outputs 1 and terminates.
- 7.
- Second query. generates by adding to c. Note that holds. throws to the query: .
- 8.
- If replies with , outputs 1 and terminates.
- 9.
- outputs 2.
We evaluate ’s advantage as follows. We assume . The probability of this case is . The probability that replies with to the first query or replies with to the second query is
since the first and second queries are mutually independent.
When assuming , we see that is negligible. Otherwise, can be used as an attacker to break the IND-CPA security of . Therefore, is negligible. Consequently, we have
Since we assume that is not negligible, neither is . □
4. Experiments
We implemented the baseline and improved algorithms for secure CWC in C++ using the TFHE library (https://tfhe.github.io/tfhe (accessed on 28 January 2021)).
The experiments were carried out on a machine equipped with an Intel Core i7-6567U (3.30 GHz) processor and 16GB of RAM. In the following, m (resp. n) is the number of positive (resp. negative) data and k is the number of features.
Table 6 summarizes the running time of the baseline algorithm (naive implementation of Algorithm 1 using TFHE) for random data generated for and . The complexity analysis shows that the running time increases in proportion to . This experimental result confirms this in real data. The table clearly shows that the sorting process is the bottleneck.

Table 6.
Running time (s) of baseline algorithm (naive secure CWC). Task 1: computing s. Task 2: sorting s. Task 3: feature selection.
Table 7 compares the running time of preprocessing in the baseline and improved algorithms. According to the results, the proposed algorithm significantly improves the bottleneck in naive CWC for secure computing. We should note that the baseline and improved algorithms both compute exactly the same solution as the CWC on plaintexts. We also show the details of the improved algorithm: ‘sorting’ means the time for sorting of the triples of integers; ‘other task’ means the time for remaining tasks, including generating/adding/subtracting random noise , moving , decrypting integers, etc.

Table 7.
Running time (s) of baseline and improved algorithms. Here, ‘baseline’ is same as Task 2 in Table 6 (i.e., the bottleneck); ‘improved:’ is the running time of corresponding task in the improved algorithm, where ‘sorting’ and ‘other tasks’ are the details.
Table 8 displays the running time of the improved algorithm for real data available from the UCI Machine Learning Repository (https://archive.ics.uci.edu/ml/index.php (accessed on 26 January 2022)), because, since these datasets contain more than three feature/class values, we treated them as a binary classification between one feature/class and the other.

Table 8.
Running time (s) of improved algorithm for real data in UCI Machine Learning Repository.
We demonstrated that the proposed algorithm works well for real-world multi-level feature selection problems. We only evaluated the running time in this experiment, but the relevance of the extracted features is guaranteed because the secure CWC algorithm produces the same solution as the original [].
5. Conclusions
On the basis of fully homomorphic encryption, we proposed a faster private feature selection algorithm that allows us to securely compute functional features from distributed private datasets. Our algorithm can simulate the original CWC algorithm, which chooses favorable features by sorting. In addition to the improvement in computational complexity, the proposed algorithm solves the private feature selection problem in practical time for a variety of real data. One of the remaining challenges is to improve sorting at a lower cost because CWC does not always require exact sorting. Then, ambiguous sorting possibly reduces the computation time, maintaining solution quality. At this time, the proposed algorithm is not applicable to real numbers for feature value. This is because TFHE [] is not suitable for floating-point operations. Extending the TFHE library to enable secure feature selection for real-valued data is a future challenge.
A well-known feature selection method is to filter features by computing Gini impurity scores []. In this method, the optimal threshold for filtering is determined by the order of sorting of each feature. However, since sorting is time-consuming even for secret sharing-based MPC [], a simpler method of determining the threshold by calculation has been proposed [], and its effectiveness has been confirmed by experiments. On the other hand, this study focuses on consistency measure-based feature selection. As we mentioned previously, the consistency measure-based method has been confirmed to have advantages over other methods. This study proposes the first secure protocol that enables consistency measure-based feature selection in practical time.
We next compare our proposal with other methods in the framework of private feature selection. A secret sharing-based MPC using the distributed secure sum is proposed []. In this method, it is known that statistical information about the data is leaked during the computation. The authors in [] propose an honest-majority three-party protocol that improves on the drawback of []. This method is fast but requires at least two trusted parties. In addition, [] considered both semi-honest and malicious adversaries, but in this study, the parties are assumed to be semi-honest. A feature selection using homomorphic encryption was proposed in []. This method uses only the additive homomorphic property in a two-party model, which limits its computational power. Therefore, statistical information about the data is leaked because partial decryption is required during communication between the parties. Moreover, this protocol has not been implemented. The recent approach by [] is not based on cryptography and does not provide a formal privacy guarantee, and it leaks information through the disclosure of intermediate representations. Although our method is inferior to secret sharing-based MPC in terms of practical computing time, it can handle feature selection from many data owners, even in situations where only they themselves can be trusted, and does not leak information during computation.
In addition, we discuss future issues and prospects related to secret computation with FHE, which were not discussed in detail in this study. First, this study assumes that the data are consistent, which cannot be applied to real-world data. If the data are inconsistent, e.g., when the data are merged, there are two entries with the same feature values they but are classified into different classes, the party can ignore these entries without decoding. Since the outsourced party can perform a comparison of two integers without decoding, they can use the encrypted logical bit to change the class label of these irrelevant entries to a special value, effectively ignoring them.
Next, we consider how to speed up the computation of real numbers using FHE. CKKS [] and TFHE are the current state-of-the-art methods for computing real numbers on FHE. CKKS speeds up arithmetic operations on real numbers by converting reals to integers through scaling, performing arithmetic operations on the integers, and then converting the results back to reals. However, CKKS has the drawback that it cannot compute nonlinear functions (e.g., ReLU) or perform comparison operations, making it difficult to apply to ML. On the other hand, TFHE can evaluate comparison operations and NAND circuits, making all computations theoretically possible. Unfortunately, the runtime on TFHE has an overhead of approximately 10,000 times that on the plaintext, and thus the GPGPU-based architecture is currently being studied for speedup. Currently, the fastest implementation is around 20 times faster than algorithms on CPUs []. Thus, the application and speedup of TFHE to ML is a promising research area for the future.
In conclusion, it should be noted that with the development of FHE, practical algorithms for more challenging problems such as large-scale genome analysis (GWAS) [,] and deep learning [,,] are emerging.
Author Contributions
Conceptualization, H.S.; methodology, T.I., K.S. and H.S.; software, S.O., J.T. and M.K.; validation, S.O., J.T. and M.K.; formal analysis, T.I., K.S. and H.S.; investigation, T.I., K.S. and H.S.; resources, S.O., J.T. and M.K.; data curation, S.O., J.T. and M.K.; writing—original draft preparation, T.I., K.S. and H.S.; writing—review and editing, T.I., K.S. and H.S.; visualization, H.S.; supervision, H.S.; project administration, H.S.; funding acquisition, H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by JSPS KAKENHI (Grant Number 21H05052, 18H04098).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, S.; Zhang, Y.; Dai, W.; Lauter, K.; Kim, M.; Tang, Y.; Xiong, H.; Jiang, X. HEALER: Homomorphic computation of ExAct Logistic rEgRession for secure rare disease variants analysis in GWAS. Bioinformatics 2015, 32, 211–218. [Google Scholar]
- Liu, F.; Ng, W.K.; Zhang, W. Encrypted SVM for Outsourced Data Mining. In Proceedings of the 2015 IEEE 8th International Conference on Cloud Computing, New York, NY, USA, 20 August 2015; pp. 1085–1092. [Google Scholar]
- Qiu, G.; Huo, H.; Gui, X.; Dai, H. Privacy-Preserving Outsourcing Scheme for SVM on Vertically Partitioned Data. Secur. Commun. Netw. 2022, 2022, 9983463. [Google Scholar]
- Bost, R.; Ada Popa, R.; Tu, S.; Goldwasser, S. Machine learning classification over encrypted data. In Proceedings of the Network and Distributed System Security Symposium, San Diego, CA, USA, 8–11 February 2015. [Google Scholar]
- Khedr, A.; Gulak, G.; Vaikuntanathan, V. SHIELD: Scalable Homomorphic Implementation of Encrypted Data-Classifiers. IEEE Trans. Comput. 2016, 65, 2848–2858. [Google Scholar]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar]
- Shin, K.; Kuboyama, T.; Hashimoto, T.; Shepard, D. SCWC/SLCC: Highly scalable feature selection algorithms. Information 2017, 8, 159. [Google Scholar]
- Shin, K.; Xu, X.M. Consistency-based feature selection. In Proceedings of the 13th International Conference on Knowledge-Based and Intelligent Information and Engineering Systems, Santiago, Chile, 28–30 September 2009; pp. 28–30. [Google Scholar]
- Almuallim, H.; Dietteric, T.G. Learning boolean concepts in the presence of many irrelevant features. Artif. Intell. 1994, 69, 279–305. [Google Scholar]
- Liu, H.; Motoda, H.; Dash, M. A monotonic measure for optimal feature selection. In Proceedings of the 10th European Conference on Machine Learning, Chemnitz, Germany, 21–23 April 1998; pp. 101–106. [Google Scholar]
- Shin, K.; Fernandes, D.; Miyazaki, D. Consistency measures for feature selection: A formal definition, relative sensitivity comparison, and a fast algorithm. In Proceedings of the 22nd International Joint Conference on Artificial Intelligence, Barcelona, Spain, 16–22 July 2011; pp. 1491–1497. [Google Scholar]
- Zhao, Z.; Liu, H. Searching for interacting features. In Proceedings of the 20th International Joint Conference on Artificial Intelligence, Hyderabad, India, 6–12 January 2007; pp. 1156–1161. [Google Scholar]
- De Cock, M.; Dowsley, R.; Nascimento, A.C.A.; Railsback, D.; Shen, J.; Todoki, A. High performance logistic regression for privacy-preserving genome analysis. BMC Med. Genom. 2021, 14, 23. [Google Scholar]
- Breiman, L.; Friedman, J.; Stone, C.; Olshen, R. Classification and Regression Trees, 1st ed.; Taylor and Francis: Oxfordshire, UK, 1984. [Google Scholar]
- Paillier, P. Public-key cryptosystems based on composite degree residuosity classes. In Proceedings of the International Conference on the Theory and Application of Cryptographic Techniques, Prague, Czech Republic, 2–6 May 1999; pp. 223–238. [Google Scholar]
- Attrapadung, N.; Hanaoka, G.; Mitsunari, S.; Sakai, Y.; Shimizu, K.; Teruya, T. Efficient two-level homomorphic encryption in prime-order bilinear groups and a fast implementation in webassembly. In Proceedings of the 2018 on Asia Conference on Computer and Communications Security, Incheon, Korea, 4 June 2018; pp. 685–697. [Google Scholar]
- Boneh, D.; Goh, E.J.; Nissim, K. Evaluating 2-DNF formulas on ciphertexts. In Proceedings of the Theory of Cryptography Conference, Cambridge, MA, USA, 10–12 February 2005; pp. 325–341. [Google Scholar]
- Brakerski, Z.; Gentry, C.; Vaikuntanathan, V. (leveled) fully homomorphic encryption without bootstrapping. In Proceedings of the 3rd Innovations in Theoretical Computer Science, Cambridge, MA, USA, 8–10 January 2012; pp. 309–325. [Google Scholar]
- Gentry, C. Fully homomorphic encryption using ideal lattices. In Proceedings of the 41st ACM Symposium on Theory of Computing, Bethesda, MD, USA, 31 May–2 June 2009; pp. 169–178. [Google Scholar]
- Chillotti, I.; Gama, N.; Georgieva, M.; Izabachène, M. TFHE: Fast fully homomorphic encryptionover the torus. J. Cryptol. 2020, 33, 34–91. [Google Scholar]
- Chillotti, I.; Gama, N.; Georgieva, M.; Izabachène, M. TFHE: Fast Fully Homomorphic Encryption Library, August 2016. Available online: https://tfhe.github.io/tfhe (accessed on 28 January 2021).
- Chen, H.; Dai, W.; Kim, M.; Song, Y. Efficient Multi-Key Homomorphic Encryption with Packed Ciphertexts with Application to Oblivious Neural Network Inference. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, London, UK, 11–15 November 2019; pp. 395–412. [Google Scholar]
- Goldwasser, S.; Micali, S. Probabilistic Encryption. J. Comput. Syst. Sci. 1984, 28, 270–299. [Google Scholar]
- Fujisaki, E.; Okamoto, T.; Pointcheval, D.; Stern, J. RSA-OAEP is secure under the RSA assumption. In Proceedings of the 21st Annual International Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2001; pp. 260–274. [Google Scholar]
- Bellare, M.; Rogaway, P. Optimal Asymmetric Encryption. In Proceedings of the Workshop on the Theory and Application of Cryptographic Techniques, Perugia, Italy, 9–12 May 1994; pp. 92–111. [Google Scholar]
- Rao, V.; Long, Y.; Eldardiry, H.; Rane, S.; Rossi, R.A.; Torres, F. Secure two-party feature selection. arXiv 2019, arXiv:1901.00832. [Google Scholar]
- Anarakia, J.R.; Samet, S. Privacy-preserving feature selection: A survey and proposing a new set of protocols. arXiv 2020, arXiv:2008.07664. [Google Scholar]
- Banerjee, M.; Chakravarty, S. Privacy preserving feature selection for distributed data using virtual dimension. In Proceedings of the 20th ACM International Conference on Information and Knowledge Management, Glasgow Scotland, UK, 24–28 October 2011; pp. 2281–2284. [Google Scholar]
- Sheikhalishahi, M.; Martinelli, F. Privacy-utility feature selection as a privacy mechanism in collaborative data classification. In Proceedings of the 26th International Conference on Enabling Technologies: Infrastructure for Collaborative Enterprises, Poznan, Poland, 21–23 June 2017; pp. 244–249. [Google Scholar]
- Li, X.; Dowsley, R.; Cock, M.D. Privacy-preserving feature selection with secure multiparty computation. In Proceedings of the 38th International Conference on Machine Learning, Online, 18–24 July 2021; pp. 6326–6336. [Google Scholar]
- Abspoel, M.; Escudero, D.; Volgushev, N. Secure training of decision trees with continuous attribute. Proc. Priv. Enhancing Technol. 2021, 2021, 167–187. [Google Scholar]
- Dash, M.; Liu, H. Consistency-based search in feature selection. Articial Intell. 2003, 151, 155–176. [Google Scholar]
- Pawlak, Z. Rough Sets, Theoretical Aspects of Reasoning about Data; Kluwer Academic Publishers: Alphen aan den Rijn, The Netherlands, 1991. [Google Scholar]
- Arauzo-Azofra, A.; Benitez, J.M.; Castro, J.L. Consistency measures for feature selection. J. Intell. Inf. Syst. 2008, 30, 273–292. [Google Scholar]
- Ajtai, M.; Szemerédi, E.; Komlós, J. An O(nlogn) sorting network. In Proceedings of the 15th Annual ACM Symposium on Theory of Computing, Boston, MA, USA, 25–27 April 1983; pp. 1–9. [Google Scholar]
- Batcher, K.E. Sorting networks and their applications. In Proceedings of the American Federation of Information Processing Societies Spring Joint Computing Conference, Atlantic City, NJ, USA, 30 April–2 May 1968; pp. 307–314. [Google Scholar]
- Hamada, K.; Chida, K.; Ikarashi, D.; Takahashi, K. Oblivious Radix Sort: An Efficient Sorting Algorithm for Practical Secure Multi-party Computation (iacr.org). 2014. Available online: https://eprint.iacr.org/2014/121 (accessed on 26 January 2022).
- Goodrich, M. Zig-zag sort: A simple deterministic data-oblivious sorting algorithm running in O(nlogn) time. In Proceedings of the 46th Annual ACM Symposium on Theory of Computing, New York, NY, USA, 31 May–3 June 2014; pp. 684–693. [Google Scholar]
- Ye, X.; Li, H.; Imakura, A.; Sakurai, T. Distributed collaborative feature selection based on intermediate representation. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 4142–4149. [Google Scholar]
- Cheon, J.H.; Kim, A.; Kim, M.; Song, Y. Homomorphic encryption for arithmetic of approximate numbers. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Online, 30 November 2017; pp. 409–437. [Google Scholar]
- Matsuoka, K.; Hoshizuki, Y.; Sato, T.; Bian, S. Towards Better Standard Cell Library: Optimizing Compound Logic Gates for TFHE. In Proceedings of the 9th on Workshop on Encrypted Computing & Applied Homomorphic Cryptography, New York, NY, USA, 15 November 2021; pp. 63–68. [Google Scholar]
- Bos, J.W.; Lauter, K.; Naehrig, M. Private predictive analysis on encrypted medical data. J. Biomed. Inform. 2014, 50, 234–243. [Google Scholar]
- Lauter, K.; López-Alt, A.; Naehrig, M. Private Computation on Encrypted Genomic Data. In Proceedings of the 3rd International Conference on Cryptology and Information Security in Latin America, Florianópolis, Brazil, 17–19 September 2014; pp. 3–27. [Google Scholar]
- Dowlin, N.; Gilad-Bachrach, R.; Laine, K.; Lauter, K.; Naehrig, M.; Wernsing, J. CryptoNets: Applying neural networks to Encrypted data with high throughput and accuracy. In Proceedings of the 33rd International Conference on International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 201–210. [Google Scholar]
- Bourse, F.; Minelli, M.; Minihold, M.; Paillier, P. Fast Homomorphic Evaluation of Deep Discretized Neural Networks. In Proceedings of the 38th Annual International Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2018; pp. 483–512. [Google Scholar]
- Badawi, A.A.; Jin, C.; Lin, J.; Fook Mun, C.; Jun Jie, S.; Hong Meng Tan, B.; Nan, X.; Mi Mi Aung, K.; Chandrasekhar, V.R. Towards the AlexNet Moment for Homomorphic Encryption: HCNN, the First Homomorphic CNN on Encrypted Data With GPUs. IEEE Trans. Emerg. Top. Comput. 2021, 9, 1330–1343. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).